Analysis of Wave Distribution Simulated by WAVEWATCH-III Model in Typhoons Passing Beibu Gulf, China
Abstract
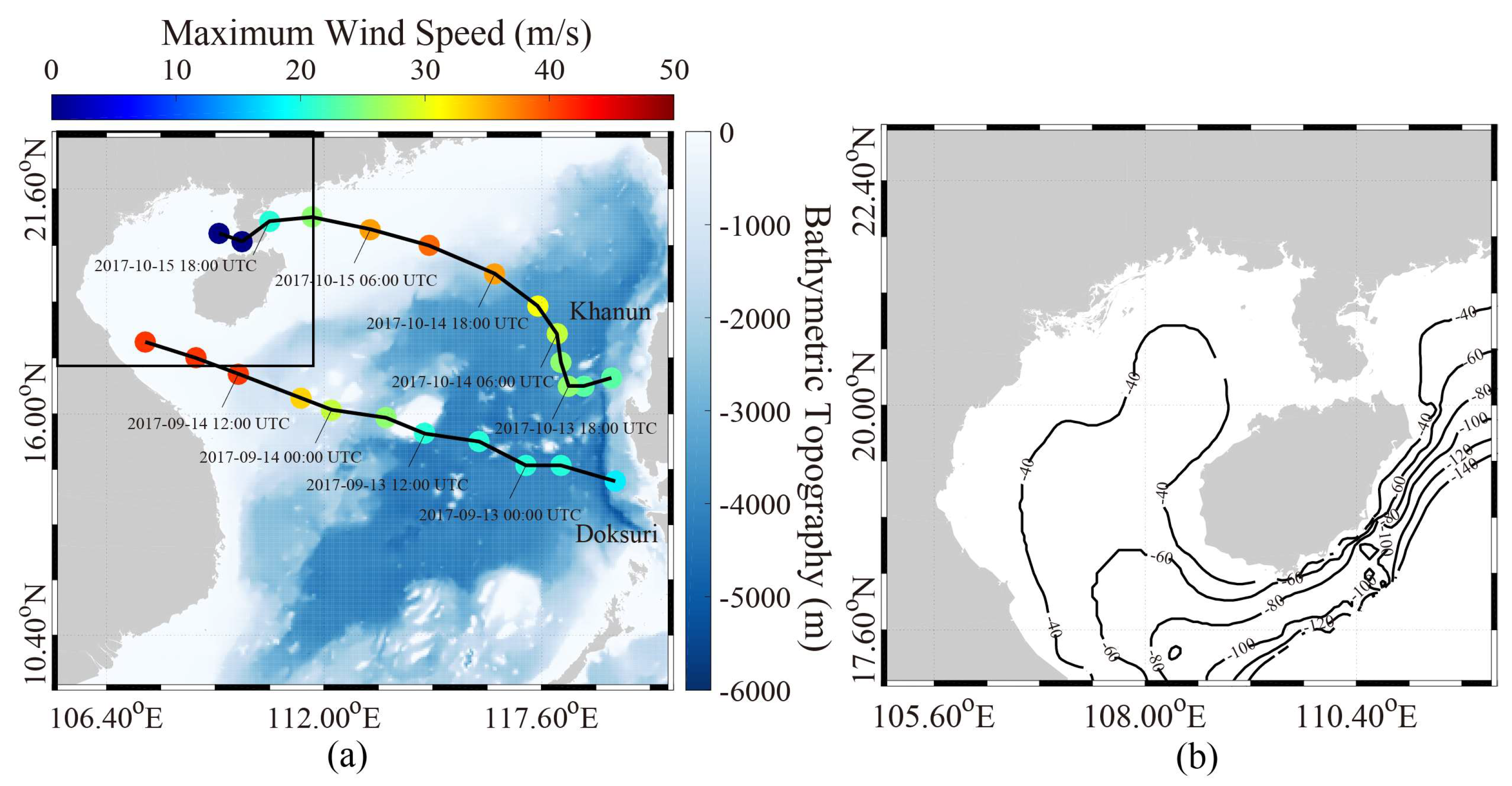
1. Introduction
2. Data Collection
3. Four Optional Packages of Nonlinear Terms and Model Setup
3.1. DIA Package
3.2. WRT Package
3.3. GMD Package
- The definition of quadruplets is expanded.
- The equations mentioned in Section 3.1 are improved for arbitrary depths, even at extremely shallow waters, e.g., Beibu Gulf where the water depth is shallower than 5 m.
- The use of multiple quadruplets is introduced.
3.4. Model Setup
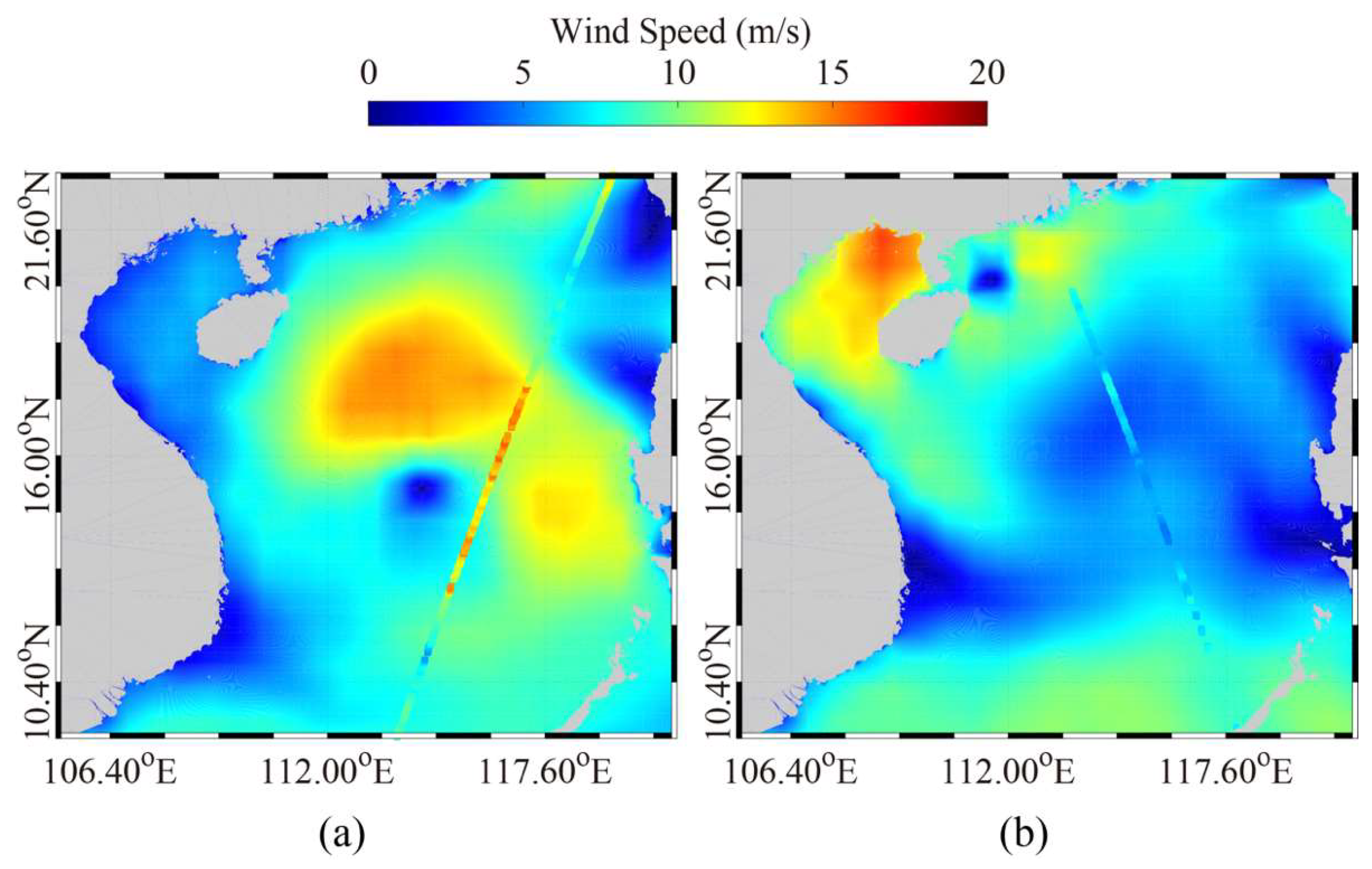
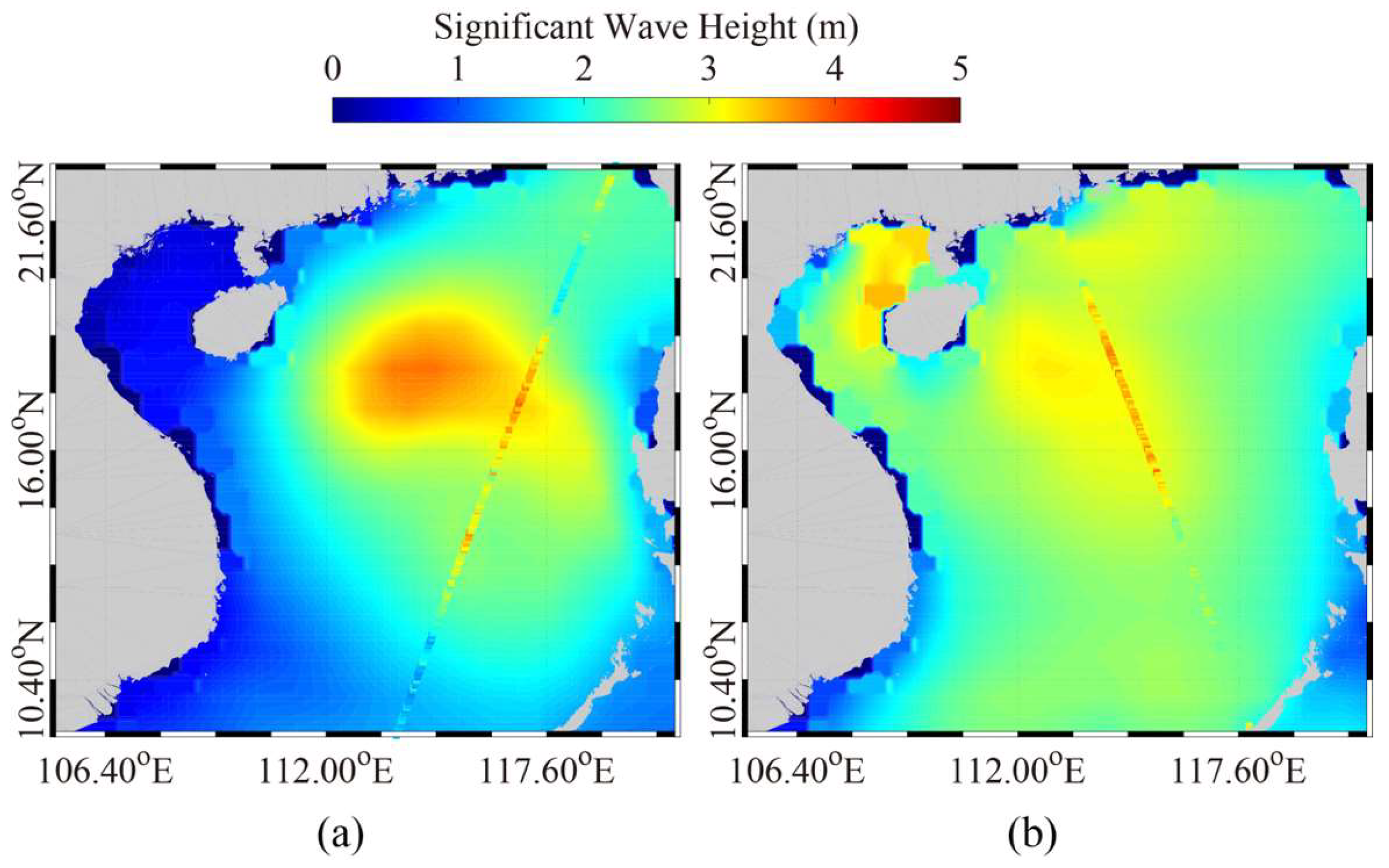
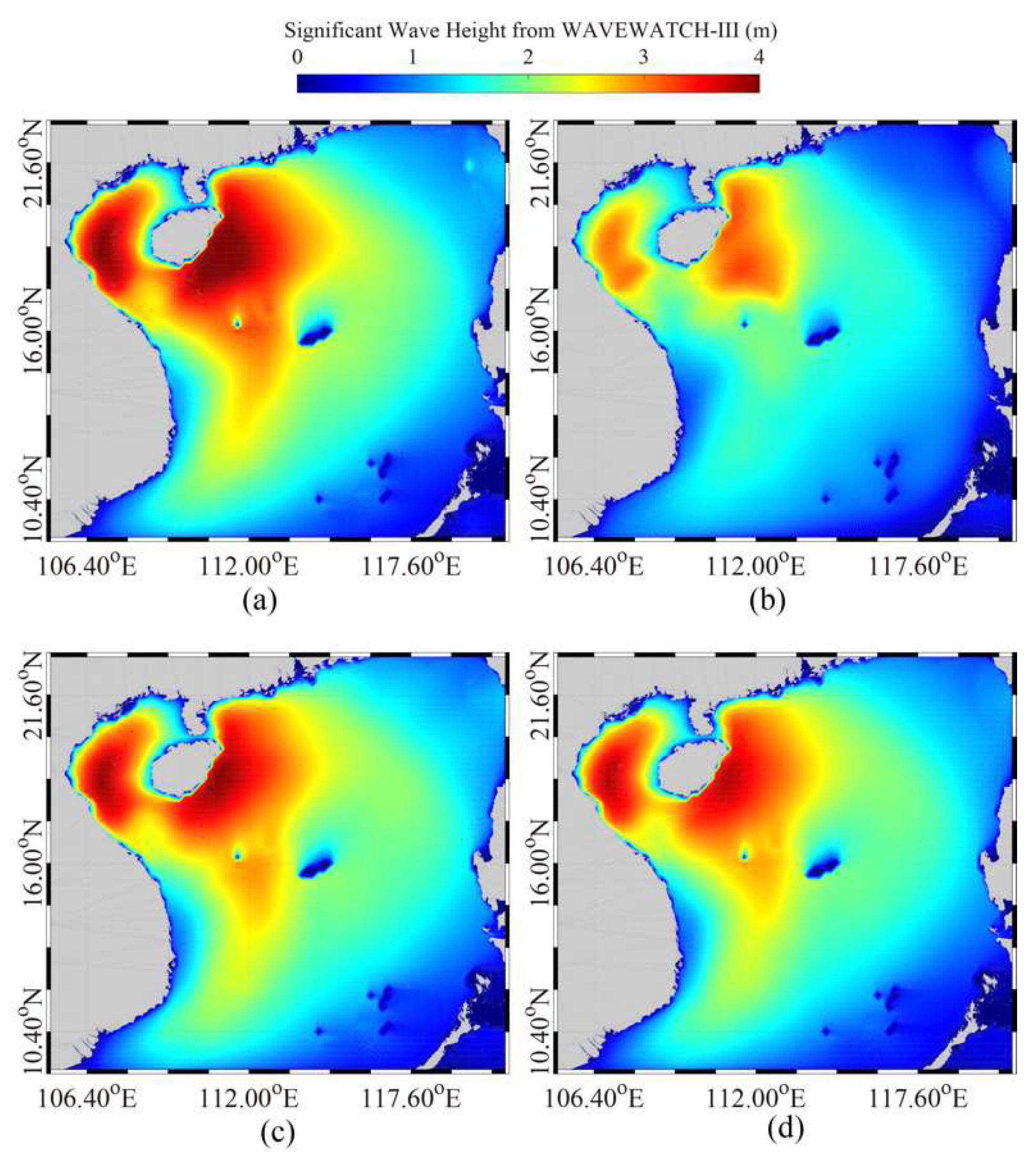
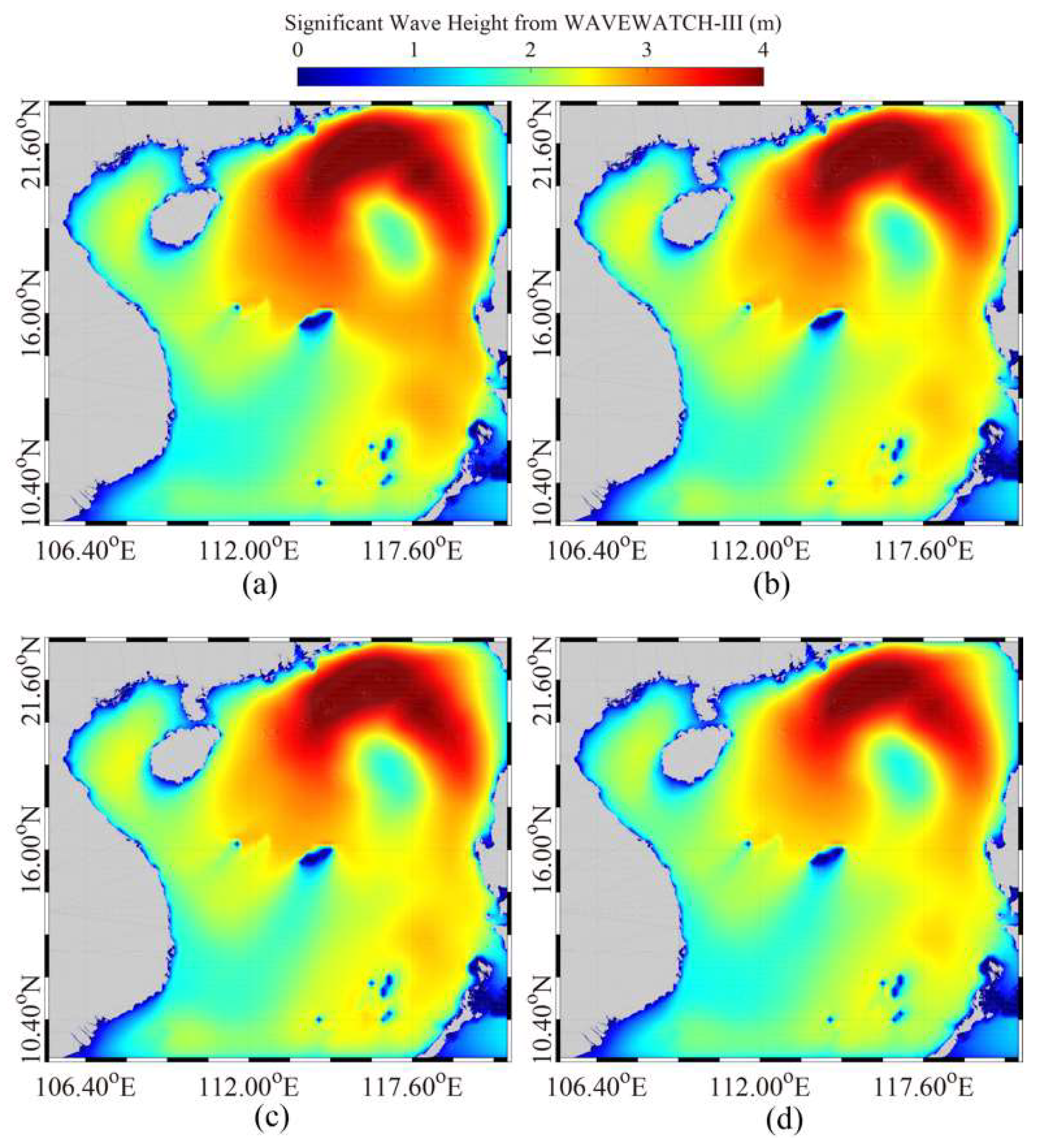
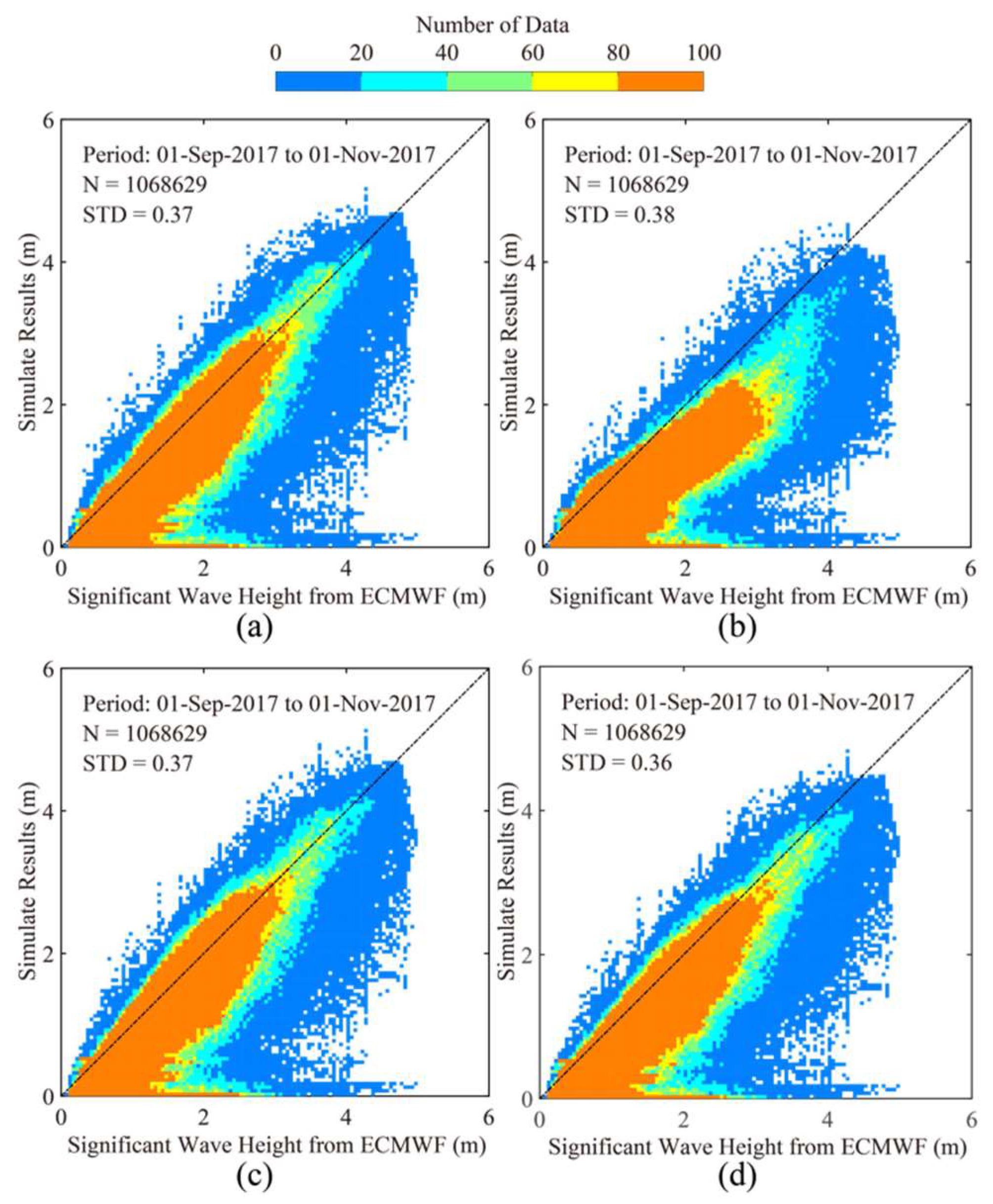
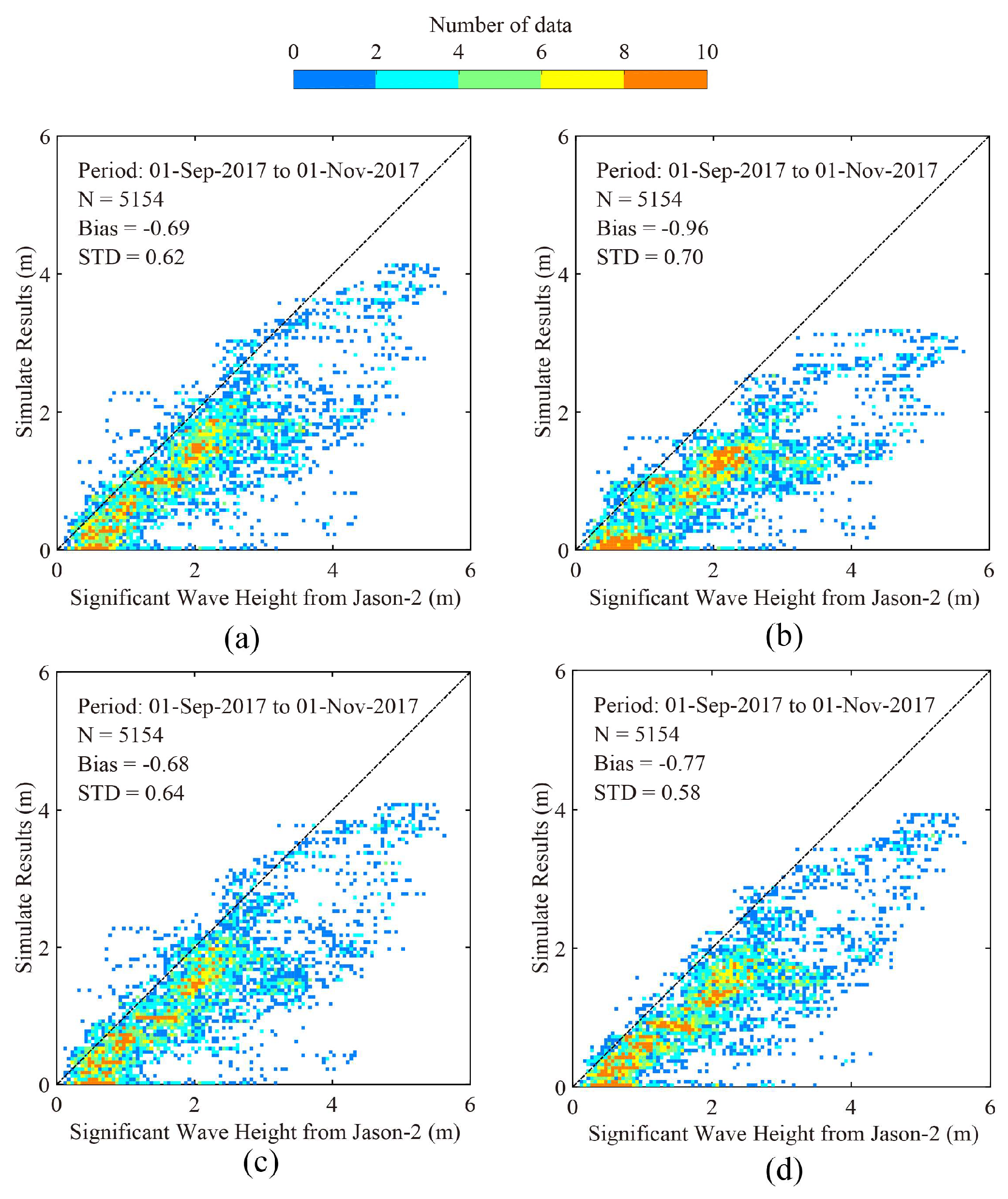
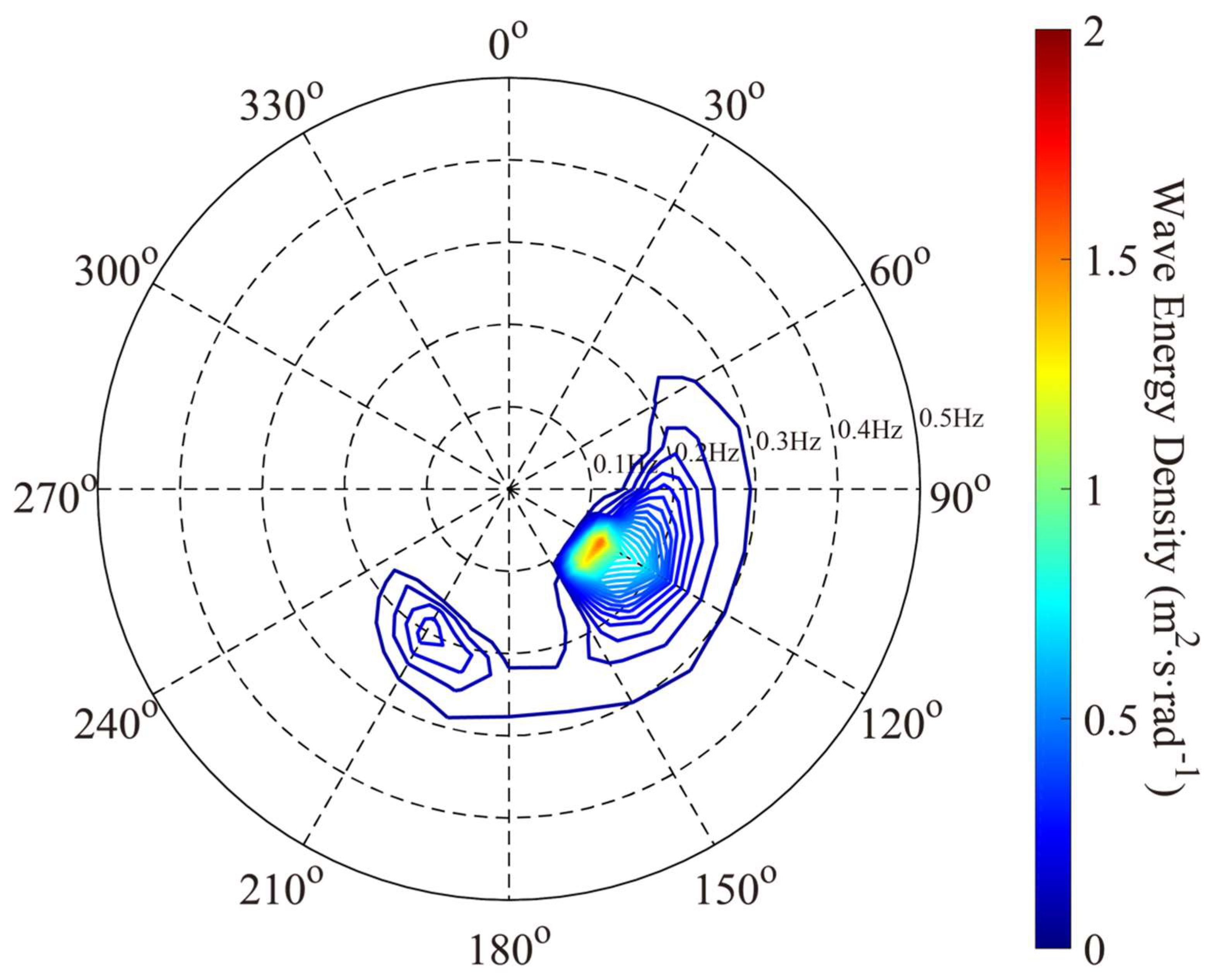
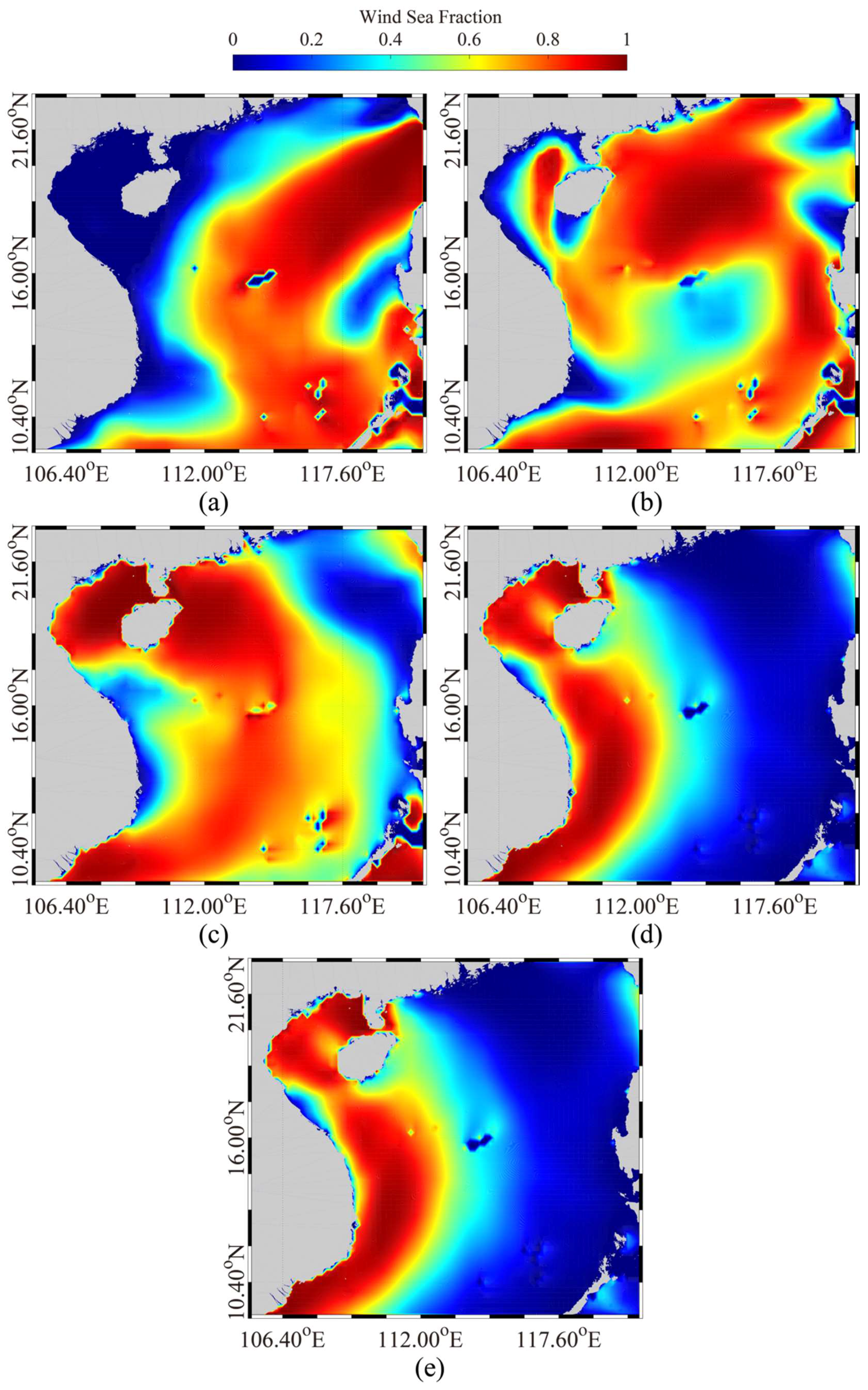
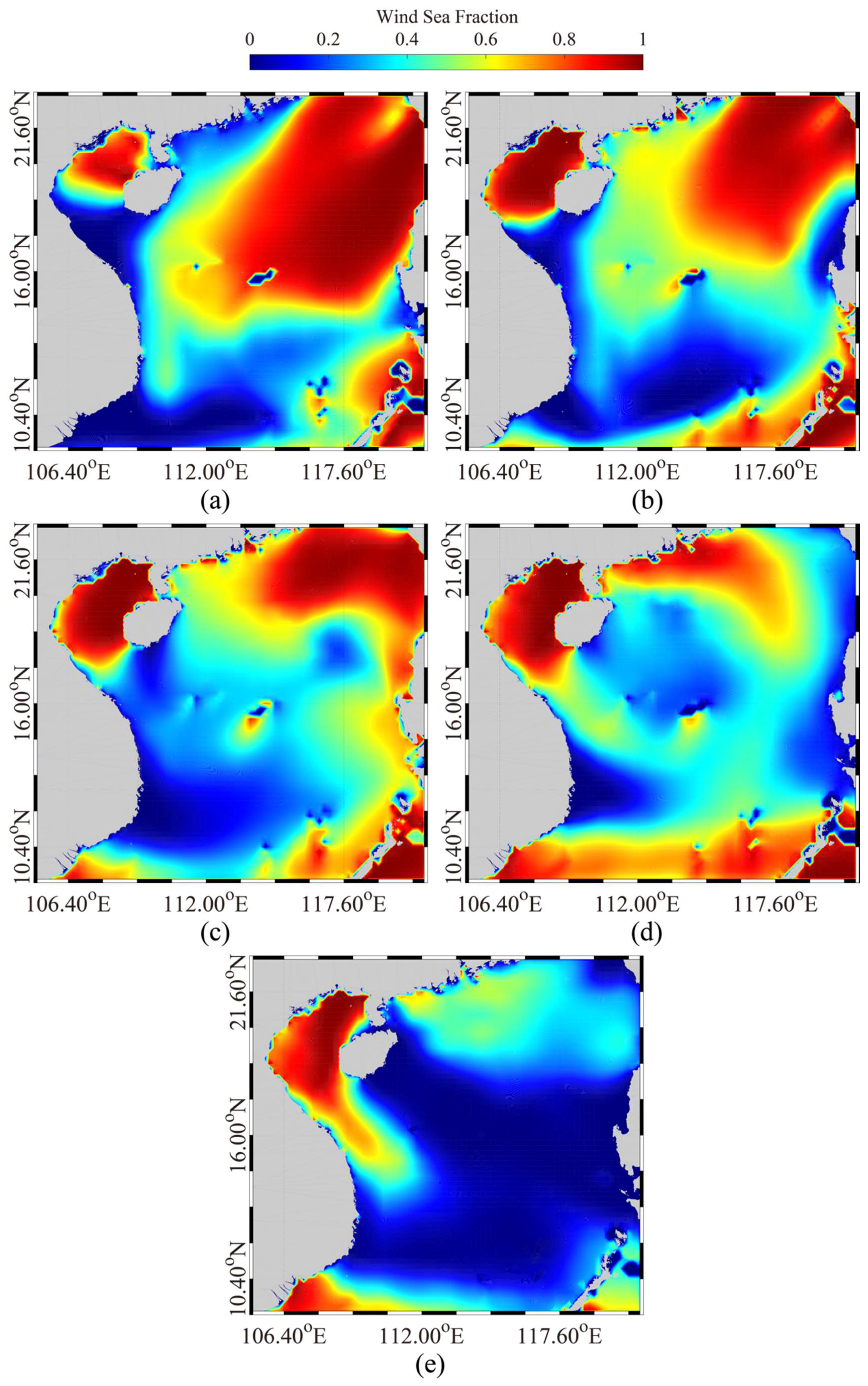
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, C.B.; Zhao, B.B.; Deng, B.; Wu, Z.Y. Numerical simulation of typhoon storm surge in the Beibu Gulf and hazardous analysis at key areas. Marin Forec. 2017, 34, 32–40. (In Chinese) [Google Scholar]
- Chen, B.; Chen, X.Y.; Dong, D.X.; Shi, M.C.; Qiu, S.F. Analysis of the influence of water level change in Guangxi nearshore caused by typhoon landed in the north of Beibu Gulf. Guangxi Sci. 2015, 22, 245–249. (In Chinese) [Google Scholar]
- Zeng, W.G.; Wu, F. Risk assessment on geological disaster caused by typhoon and rainstorm in Beibu Gulf economic zone of Guangxi Zhuang autonomous region. Chin. J. Geol. Hazard Contr. 2017, 28, 121–127. (In Chinese) [Google Scholar]
- Quilfen, Y.; Tournadre, J.; Chapron, B. Altimeter dual-frequency observations of surface winds, waves, and rain rate in tropical cyclone Isabel. J. Geophys. Res. 2006, 111, C01004. [Google Scholar] [CrossRef]
- Kudryavtseva, N.A.; Soomere, T. Validation of the multi-mission altimeter wave height data for the Baltic Sea region. Est. J. Earth Sci. 2016, 65, 161–175. [Google Scholar] [CrossRef]
- Liu, Q.X.; Babanin, A.V.; Guan, C.L.; Zieger, S.; Sun, J.; Jia, Y. Calibration and validation of HY-2 altimeter wave height. J. Atmos. Ocean Technol. 2016, 33, 919–936. [Google Scholar] [CrossRef]
- The WAMDI Group. The WAM Model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Bi, F.; Song, J.B.; Wu, K.J.; Xu, Y. Evaluation of the simulation capability of the Wavewatch II model for Pacific Ocean wave. Acta Oceanol. Sin. 2015, 34, 43–57. [Google Scholar] [CrossRef]
- Zheng, K.W.; Sun, J.; Guan, C.L.; Shao, W.Z. Analysis of the global swell and wind-sea energy distribution using WAVEWATCH III. Adv. Meteorol. 2016, 2016, 8419580. [Google Scholar] [CrossRef]
- Shukla, R.P.; Kinter, J.L.; Shin, C.S. Sub-seasonal prediction of significant wave heights over the Western Pacific and Indian Oceans, part II: The impact of ENSO and MJO. Ocean Model. 2018, 123, 1–15. [Google Scholar] [CrossRef]
- He, H.L.; Xu, Y. Wind-wave hindcast in the Yellow Sea and the Bohai Sea from the year 1988 to 2002. Acta Oceanol. Sin. 2016, 35, 46–53. [Google Scholar] [CrossRef]
- Zheng, K.W.; Osinowo, A.; Sun, J.; Hu, W. Long term characterization of sea conditions in the East China Sea using significant wave height and wind speed. J. Ocean Univ. China 2018, 17, 733–743. [Google Scholar] [CrossRef]
- Li, S.Q.; Guan, S.D.; Hou, Y.J.; Liu, Y.; Bi, F. Evaluation and adjustment of altimeter measurement and numerical hindcast in wave height trend estimation in China’s coastal seas. Int. J. Appl. Earth Obs. 2018, 67, 161–172. [Google Scholar] [CrossRef]
- Montoya, R.D.; Arias, A.O.; Royero, J.C.O.; Ocampo-Torres, F.J. A wave parameters and directional spectrum analysis for extreme winds. Ocean Eng. 2013, 67, 100–118. [Google Scholar] [CrossRef]
- Gallagher, S.; Tiron, R.; Dias, F. A long-term nearshore wave hindcast for Ireland: Atlantic and Irish Sea coasts (1979–2012). Ocean Dyn. 2014, 64, 1163–1180. [Google Scholar] [CrossRef]
- Fan, Y.; Lin, S.J.; Held, I.M.; Yu, Z.; Tolman, H.L. Global ocean surface wave simulation using a coupled atmosphere-wave model. J. Clim. 2012, 25, 6233–6252. [Google Scholar] [CrossRef]
- Guo, L.; Perrie, W.; Long, Z.; Toulany, B.; Sheng, J. The impacts of climate change on the autumn North Atlantic wave climate. Atmos. Ocean 2018, 53, 491–509. [Google Scholar] [CrossRef]
- Gallagher, S.; Gleeson, E.; Tiron, R.; Mcgrath, R.; Dias, F. Wave climate projections for Ireland for the end of the 21st century including analysis of EC-Earth winds over the North Atlantic Ocean. Int. J. Climatol. 2016, 36, 4592–4607. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. Bound waves and triad interactions in shallow water. Ocean Eng. 1993, 20, 359–388. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity wave spectrum, Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Moeini, M.H.; Etemad-Shahidi, A.; Chegini, V. Wave modeling and extreme value analysis off the northern coast of the Persian Gulf. Appl. Ocean Res. 2010, 32, 209–218. [Google Scholar] [CrossRef]
- He, H.L.; Song, J.B.; Bai, Y.; Xu, Y.; Wang, J.; Fan, B. Climate and extrema of ocean waves in the East China Sea. Sci. China Earth Sci. 2018, 61, 1–15. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; Haan, S.D. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. 2007, 112, C03006. [Google Scholar] [CrossRef]
- Hersbach, H. Comparison of C-Band scatterometer CMOD5. N equivalent neutral winds with ECMWF. J. Atmos. Ocean. Technol. 2010, 27, 721–736. [Google Scholar] [CrossRef]
- Shao, W.Z.; Wang, J.; Li, X.F.; Sun, J. An empirical algorithm for wave retrieval from co-polarization X-Band SAR imagery. Remote Sens. 2017, 9, 711. [Google Scholar] [CrossRef]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015, 2, 331–345. [Google Scholar] [CrossRef]
- Liu, Q.X.; Babanin, A.V.; Zieger, S.; Young, I.R.; Guan, C.L. Wind and wave climate in the Arctic ocean as observed by altimeters. J. Clim. 2016, 29, 7957–7975. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnett, T.P. Computations and parameterizations of the non-linear energy transfer in a gravity-wave spectrum, Part 2: Parameterizations of the non-linear energy transfer for application in wave models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- The WAVEWATCH III Development Group (WW3DG). User Manual and System Documentation of WAVEWATCH III Version 5.16. Tech. Note 329; Technical Note, MMAB Contribution; NOAA/NWS/NCEP/MMAB: College Park, MD, USA, 2016; Volume 276, p. 326. [Google Scholar]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum: Part 2. Conservation theorems. J. Fluid Mech. 1963, 15, 273–281. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum: Part 3. Evaluation of the energy flux and swell-sea interaction for a Neumann spectrum. J. Fluid Mech. 1963, 15, 385–398. [Google Scholar] [CrossRef]
- Webb, D.J. Non-linear transfers between sea waves. Deep Sea Res. 1978, 25, 279–298. [Google Scholar] [CrossRef]
- Tracy, B.; Resion, D.T. Theory and Calculation of the Non-Linear Energy Transfer between Sea Waves in Deep Water; WES Report 11; US Army Corps of Engineer: Washington, DC, USA, 1982. [Google Scholar]
- Resio, D.T.; Perrie, W. A numerical study of non-linear energy fluxes due to wave-wave interactions. Part 1: Methodology and basic results. J. Fluid Mech. 1991, 223, 603–629. [Google Scholar] [CrossRef]
- Herterich, K.; Hasselmann, K. A similarity relation for the non-linear energy transfer in a finite-depth gravity-wave spectrum. J. Fluid Mech. 1980, 97, 215–224. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF reanalysis interim and the NECP climate forecast system reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Chu, P.C.; Cheng, K.F. South China Sea wave characteristics during typhoon Muifa passage in winter 2004. J. Oceanogr. 2008, 64, 1–21. [Google Scholar] [CrossRef]
- Hanson, J.L.; Jensen, R.E. Wave System Diagnostics for Numerical Wave Models. In Proceedings of the 8th International Workshop on Wave Hindcasting and Forecasting, North Shore, HI, USA, 14–19 November 2014. JCOMM Tech. 2004, Rep. 29, WMO/TD-No. 1319. [Google Scholar]
- Zhang, J.; Wang, W.; Guan, C. Analysis of the global swell distributions using ECMWF Re-analyses wind wave data. J. Ocean Univ. China 2011, 10, 325–330. [Google Scholar] [CrossRef]
- Xu, Y.; He, H.; Song, J.; Hou, Y.; Li, F. Observations and modeling of typhoon waves in the South China Sea. J. Phys. Oceanogr. 2017, 47, 1307–1324. [Google Scholar] [CrossRef]
- Chu, P.C.; Qi, Y.; Chen, Y.; Shi, P.; Mao, Q. South China Sea wind-wave characteristics. Part 1: Validation of WAVEWATCH-III using TOPEX/Poseidon data. J. Atmos. Ocean. Technol. 2004, 21, 1718–1733. [Google Scholar] [CrossRef]
- Cao, X.F.; Shi, H.Y.; Shi, M.C.; Guo, P.F.; Wu, L.Y.; Ding, Y. Model-simulated coastal trapped waves stimulated by typhoon in northwestern South China Sea. J. Ocean Univ. China 2017, 16, 965–977. [Google Scholar] [CrossRef]
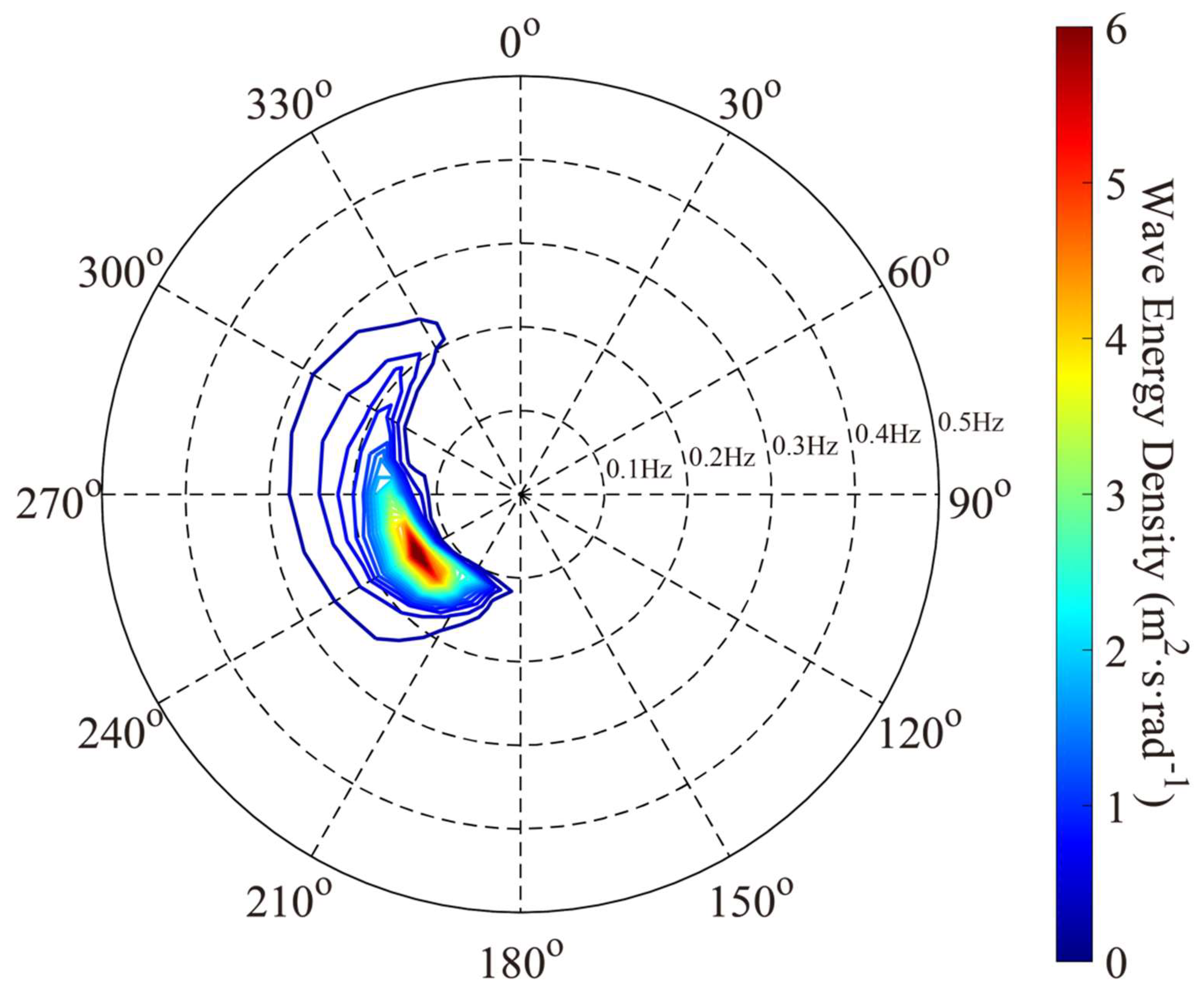
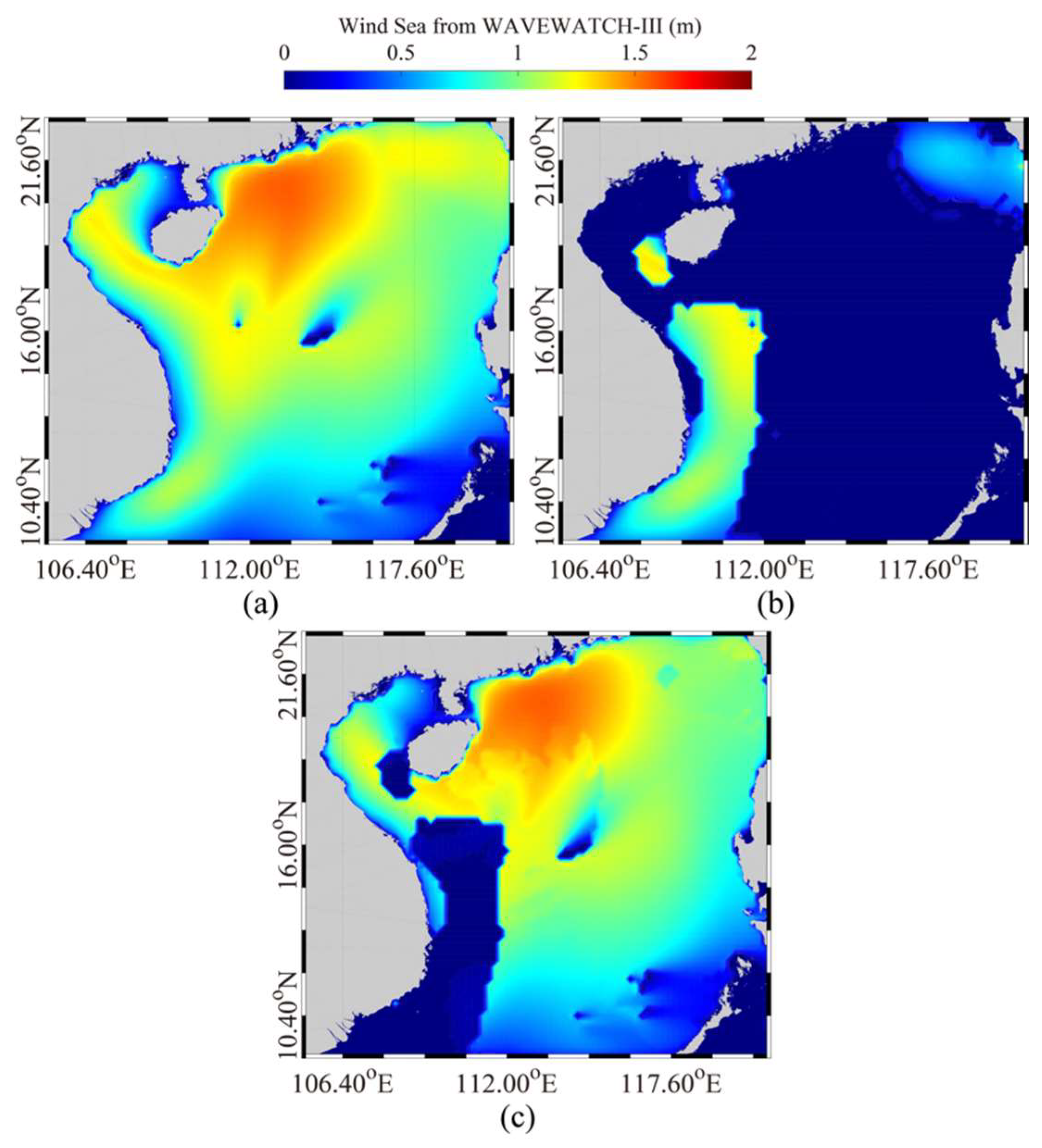
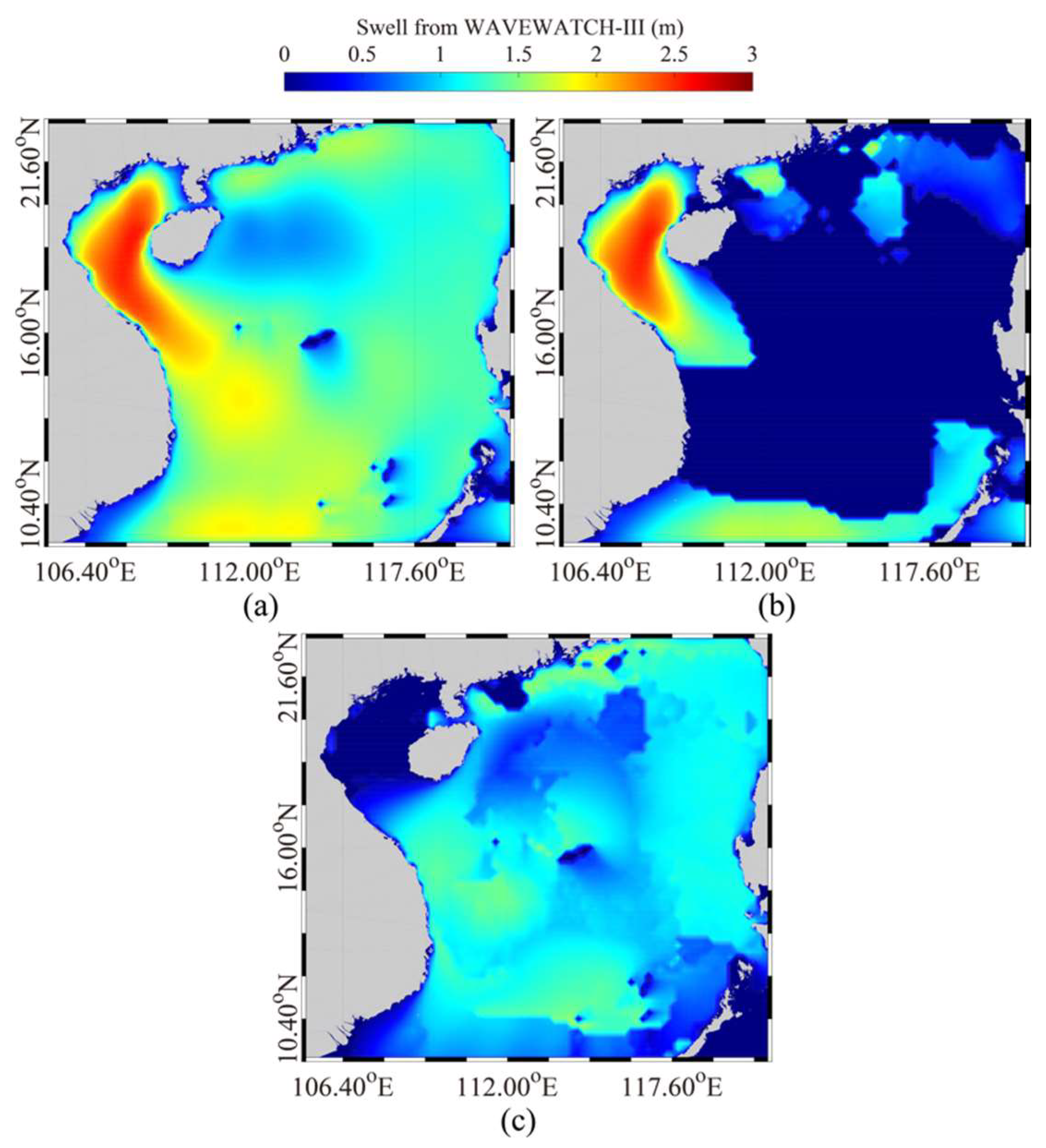
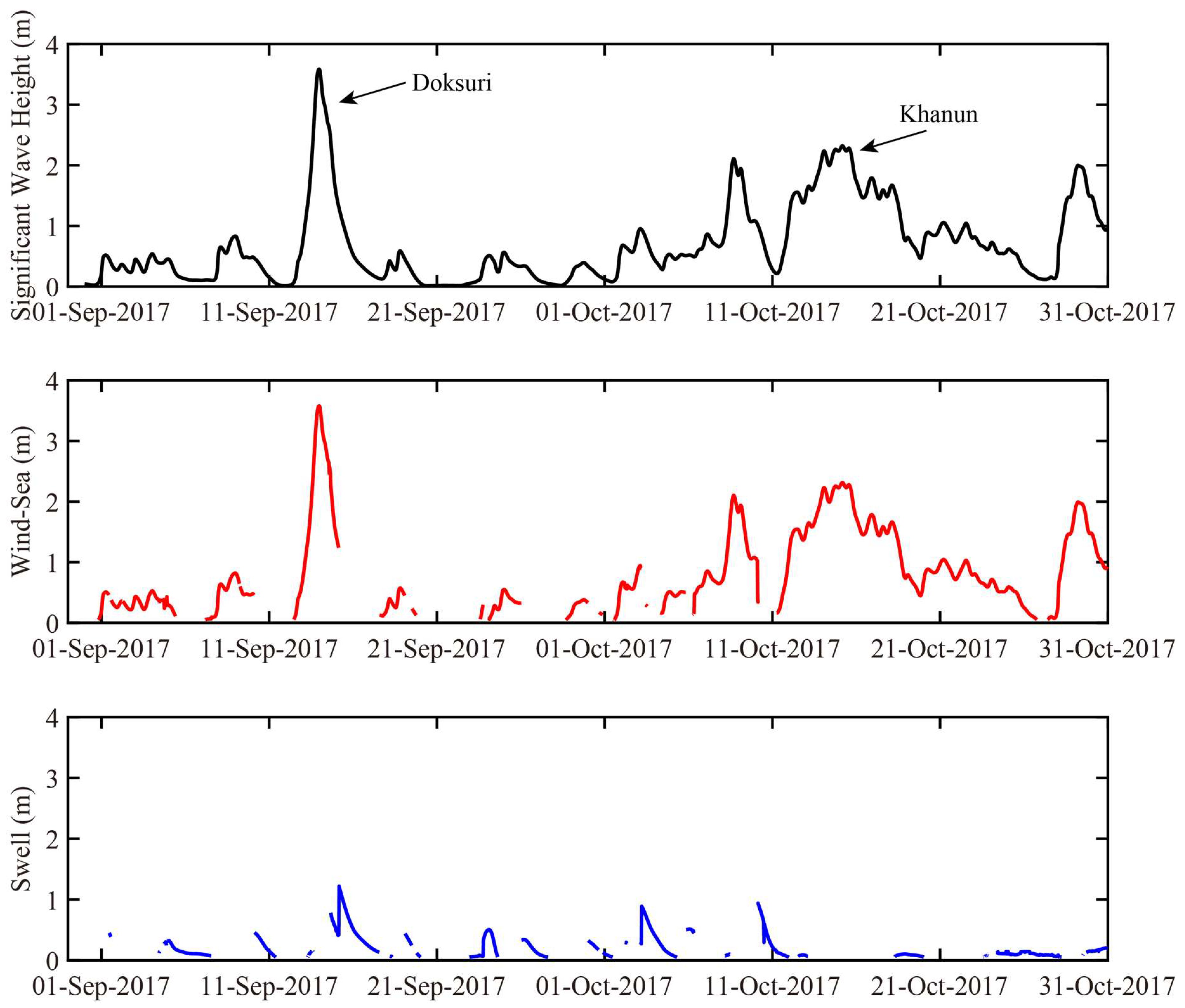
| Package Name | nq | m | n | λ | μ | θ12 | Cdeep | Cshal |
|---|---|---|---|---|---|---|---|---|
| GMD1 | 3 | 0.00 | −3.5 | 0.126 | 0.00 | −1.0 | 4.790 × 107 | 0.00 |
| 0.237 | 0.00 | −1.0 | 2.200 × 107 | 0.00 | ||||
| 0.319 | 0.00 | −1.0 | 1.110 × 107 | 0.00 | ||||
| GMD2 | 5 | 0.00 | −3.5 | 0.066 | 0.018 | 21.4 | 0.170 × 109 | 0.00 |
| 0.127 | 0.069 | 19.6 | 0.127 × 109 | 0.00 | ||||
| 0.228 | 0.065 | 2.0 | 0.443 × 108 | 0.00 | ||||
| 0.295 | 0.196 | 40.5 | 0.210 × 108 | 0.00 | ||||
| 0.369 | 0.226 | 11.5 | 0.118 × 108 | 0.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, W.; Sheng, Y.; Li, H.; Shi, J.; Ji, Q.; Tan, W.; Zuo, J. Analysis of Wave Distribution Simulated by WAVEWATCH-III Model in Typhoons Passing Beibu Gulf, China. Atmosphere 2018, 9, 265. https://doi.org/10.3390/atmos9070265
Shao W, Sheng Y, Li H, Shi J, Ji Q, Tan W, Zuo J. Analysis of Wave Distribution Simulated by WAVEWATCH-III Model in Typhoons Passing Beibu Gulf, China. Atmosphere. 2018; 9(7):265. https://doi.org/10.3390/atmos9070265
Chicago/Turabian StyleShao, Weizeng, Yexin Sheng, Huan Li, Jian Shi, Qiyan Ji, Wei Tan, and Juncheng Zuo. 2018. "Analysis of Wave Distribution Simulated by WAVEWATCH-III Model in Typhoons Passing Beibu Gulf, China" Atmosphere 9, no. 7: 265. https://doi.org/10.3390/atmos9070265
APA StyleShao, W., Sheng, Y., Li, H., Shi, J., Ji, Q., Tan, W., & Zuo, J. (2018). Analysis of Wave Distribution Simulated by WAVEWATCH-III Model in Typhoons Passing Beibu Gulf, China. Atmosphere, 9(7), 265. https://doi.org/10.3390/atmos9070265






