Subpixel-Based Precipitation Nowcasting with the Pyramid Lucas–Kanade Optical Flow Technique
Abstract
1. Introduction
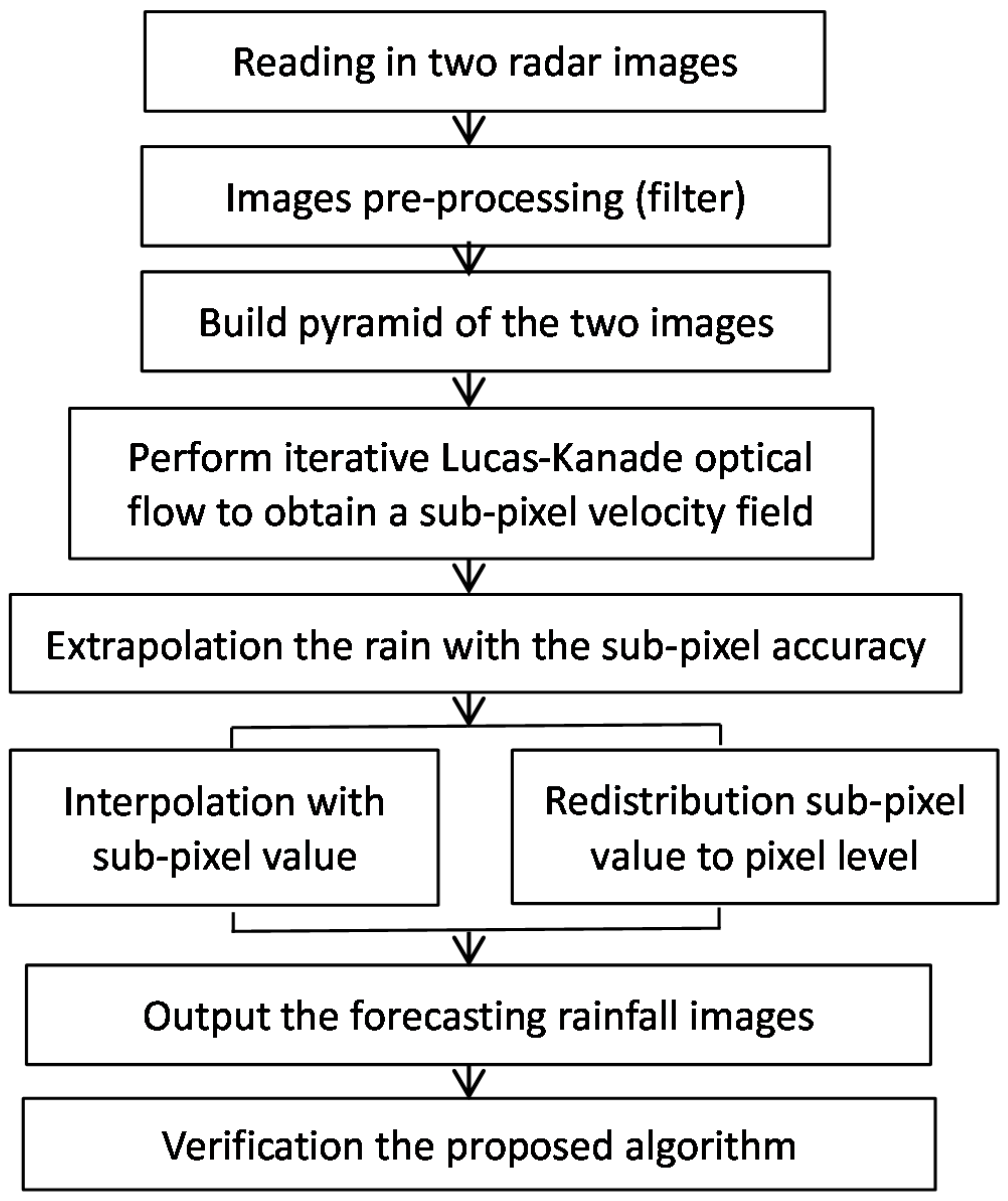
2. Methodology
2.1. Extrapolation-Based Nowcasting Algorithm
2.2. Subpixel Nowcasting Algorithm
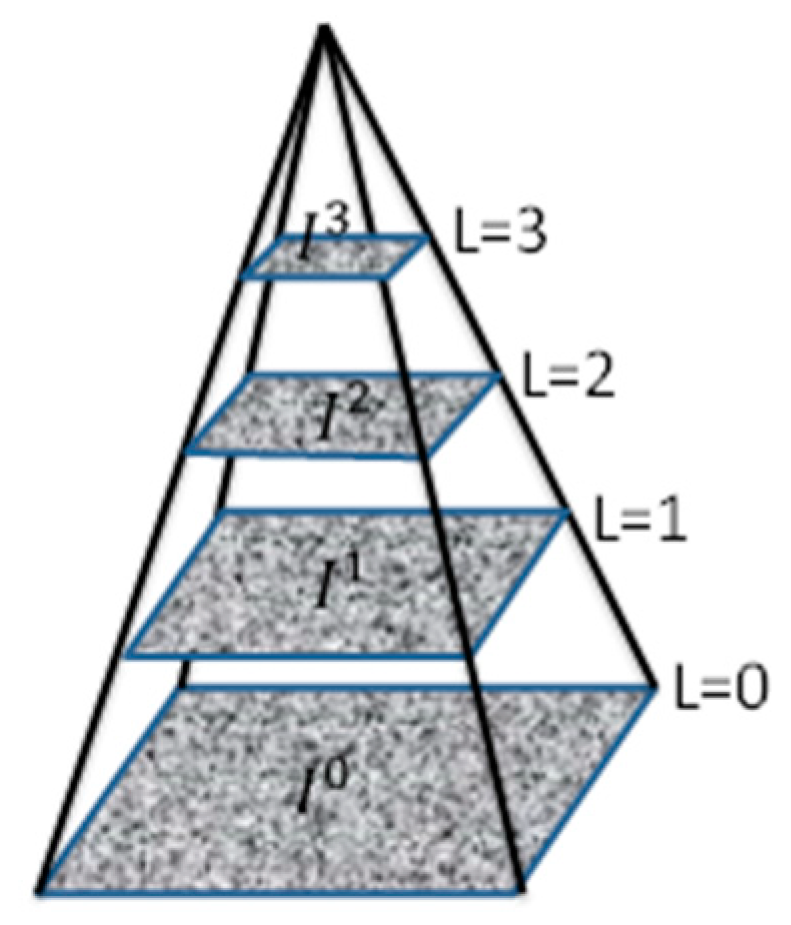
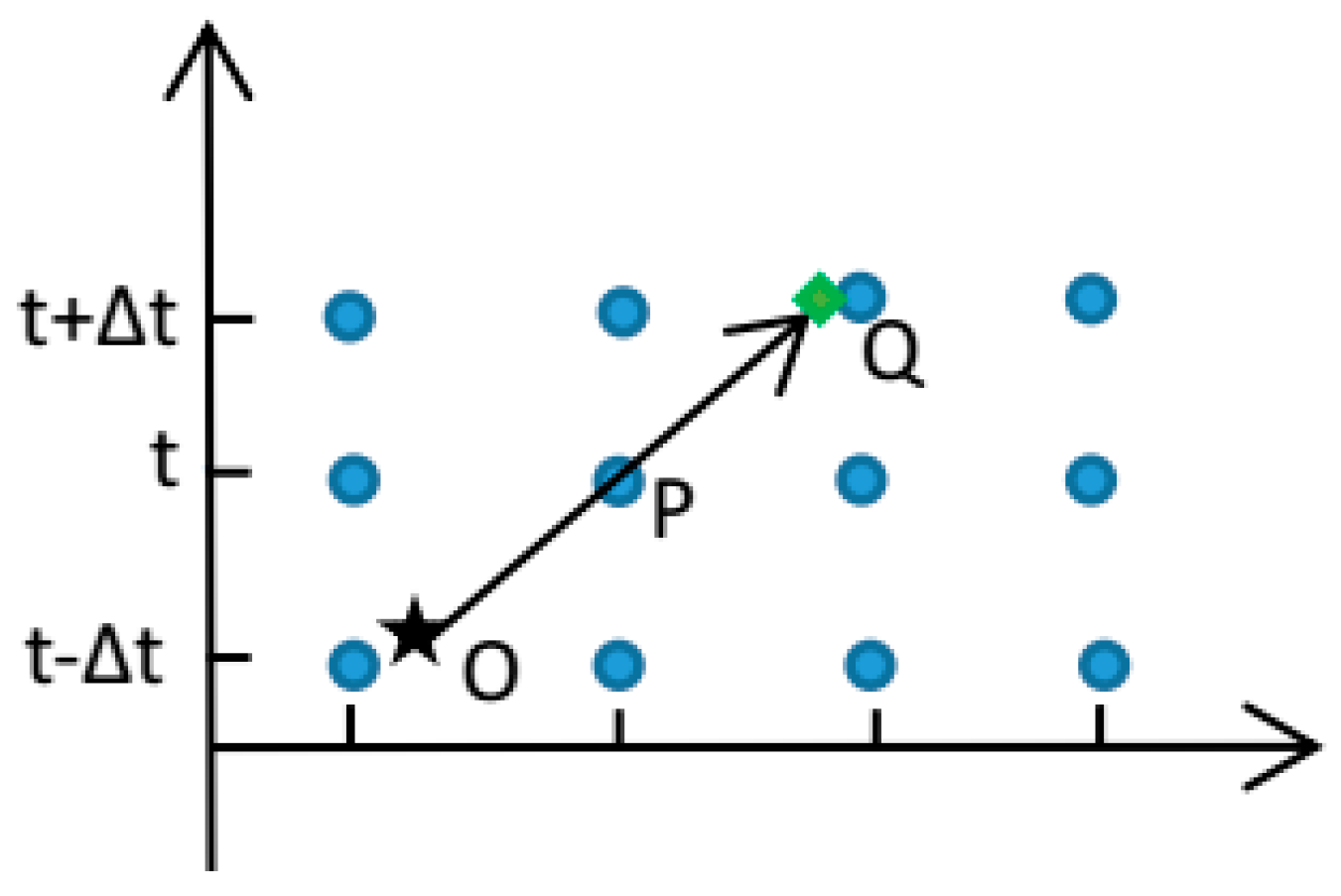
2.2.1. Subpixel-Based Tracking with the Pyramidal Lucas–Kanade Optical Flow Model
- (a)
- Construct, recursively, a Gaussian pyramid composed of the two radar images using Equation (7). The level value L is set as four.
- (b)
- Compute the subpixel value using bilinear interpolation method between integer pixels at each level, which is critical to obtaining optical flow in subpixel accuracy.
- (c)
- Initialize the guess of the top-level optical flow:
- (d)
- Let L = Lm.
- (e)
- Use the standard Lucas–Kanade algorithm Equations (3)–(6) to compute the residual optical flow at level L.
- (f)
- The optical flow at level L−1 can be estimated with the following Equation (8):The coefficient of 2 means the image size of the L − 1 layer is twice the size of the L layer, either on the x-axis or the y-axis.
- (g)
- Let L = L − 1, and go to step (e) and loop execution step (e) to step (f) until L = 0.
- (h)
- In the end, the optical flow at level L = 0 (original image) is estimated with the following Equation (9):
- (i)
- Smoothness constraint: the obtained in step (h) is sensitive to noise, and the velocity field must be smoothed. Here, the velocity field obtained above is smoothed with the Bowler smooth scheme based on the average of the eight nearest neighbors [23].
2.2.2. Rainfall Extrapolation
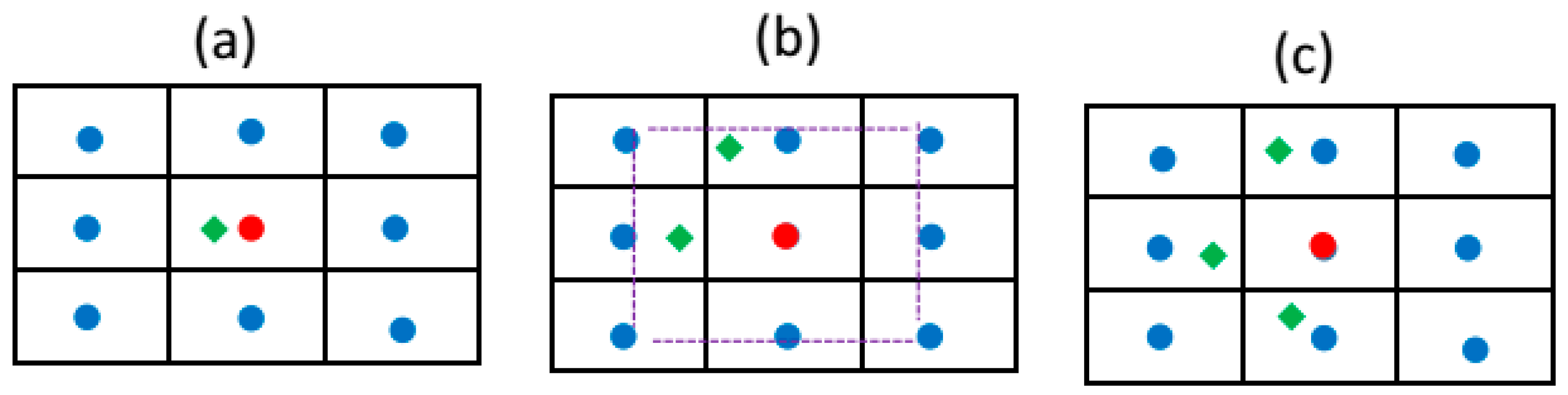
2.2.3. Redistribution of Subpixel Value to Integer Pixel
- (a)
- If there is only a green point in the windows (Figure 4a), determine whether the point located in the grid of red point; if yes, assign the green point value to the red point, else, desert this green point and keep the value of red point unchanged.
- (b)
- If there are two green points in the windows, determine whether the two points are located on the same side of the red dot grid (Figure 4b), for example, the region of the purple dot line. If these green points are not located on the same side, estimate the value of the red point using the two points and the inverse distance method, else, desert these green points.
- (c)
- If there are more than three green points in the windows (Figure 4c), estimate the value of the red point by using the surrounding points and the inverse distance method.
- (d)
- Repeat the process until all the pixel values surrounded by the red point are identified and estimated. The redistribution process refines the motion field up to pixel level.
2.2.4. Spatial Interpolation
- (a)
- Identify the pixels in the extrapolation image which is neighboring in the original image.
- (b)
- If the non-data pixels in the extrapolation image are in the neighbor of the rainy pixels (use the 3 × 3 windows), then use the rainy pixels, and the inverse distance method to calculate the non-data pixels’ value. Then, assign the value to these non-data pixels.
- (c)
- Repeat steps (a)–(b) until all non-data pixels, which are surrounded by the neighboring rainy pixels, are identified and estimated. These pixels are located in the storm spot.
- (d)
- Estimate the pixels which are located on the edge of a storm patch using only three neighboring rainy pixels by the same method as used in the four rainy points as mentioned in steps (b)–(c).
2.3. Verification
2.3.1. Pixel-Based Verification
2.3.2. Object-Based Verification
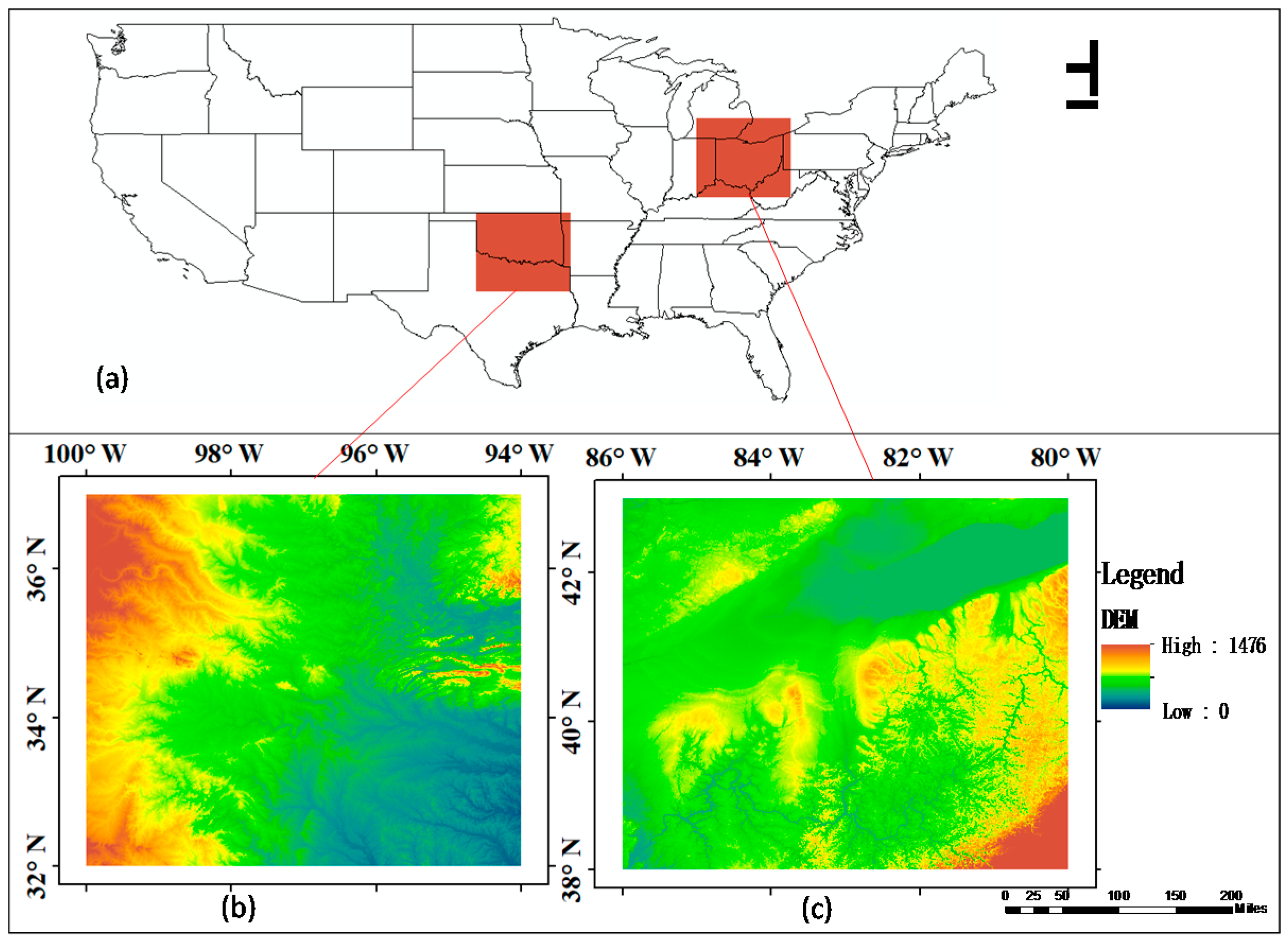
3. Data
4. Results and Discussion
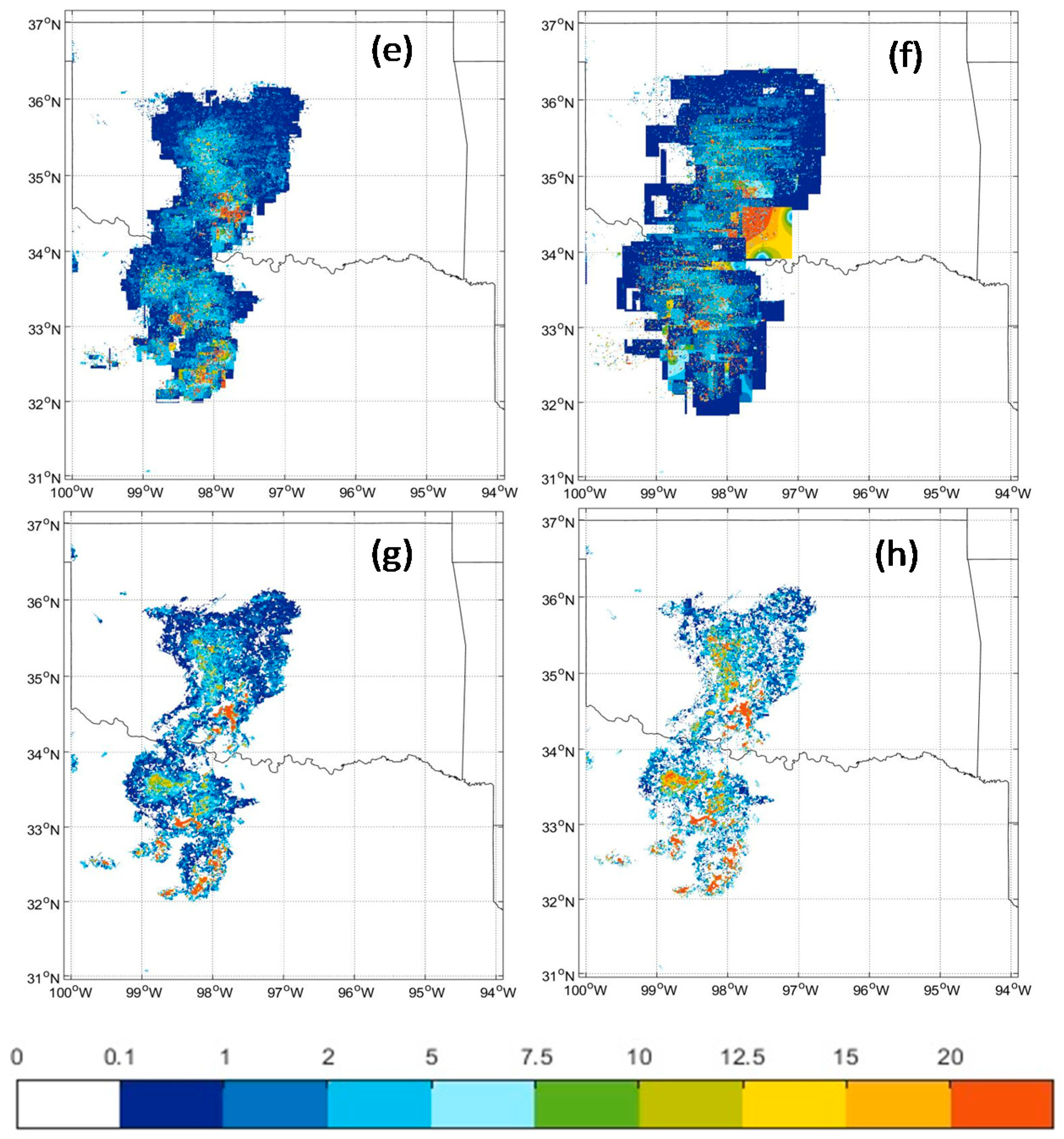
4.1. The Performance of SPLK in the Selected Events
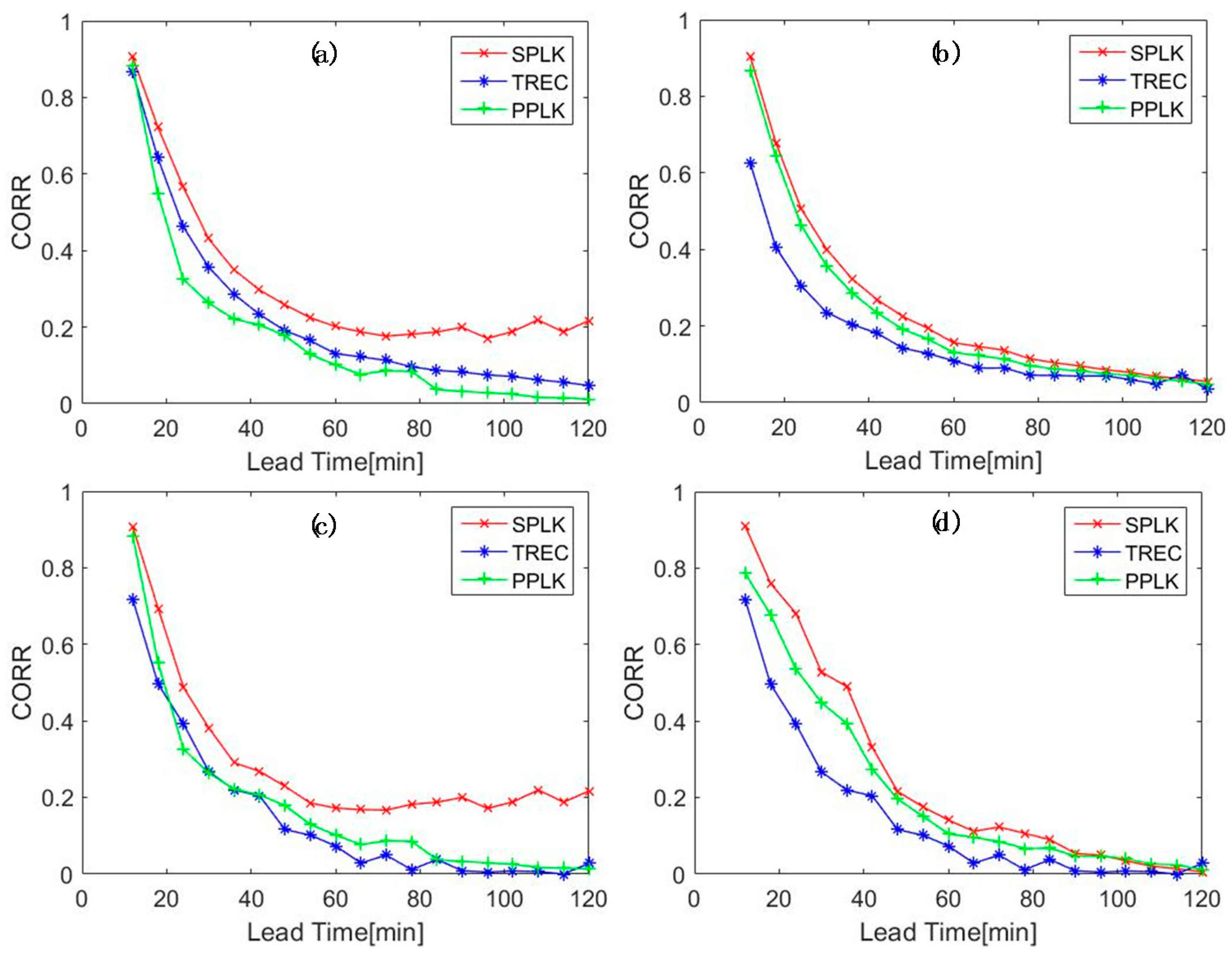
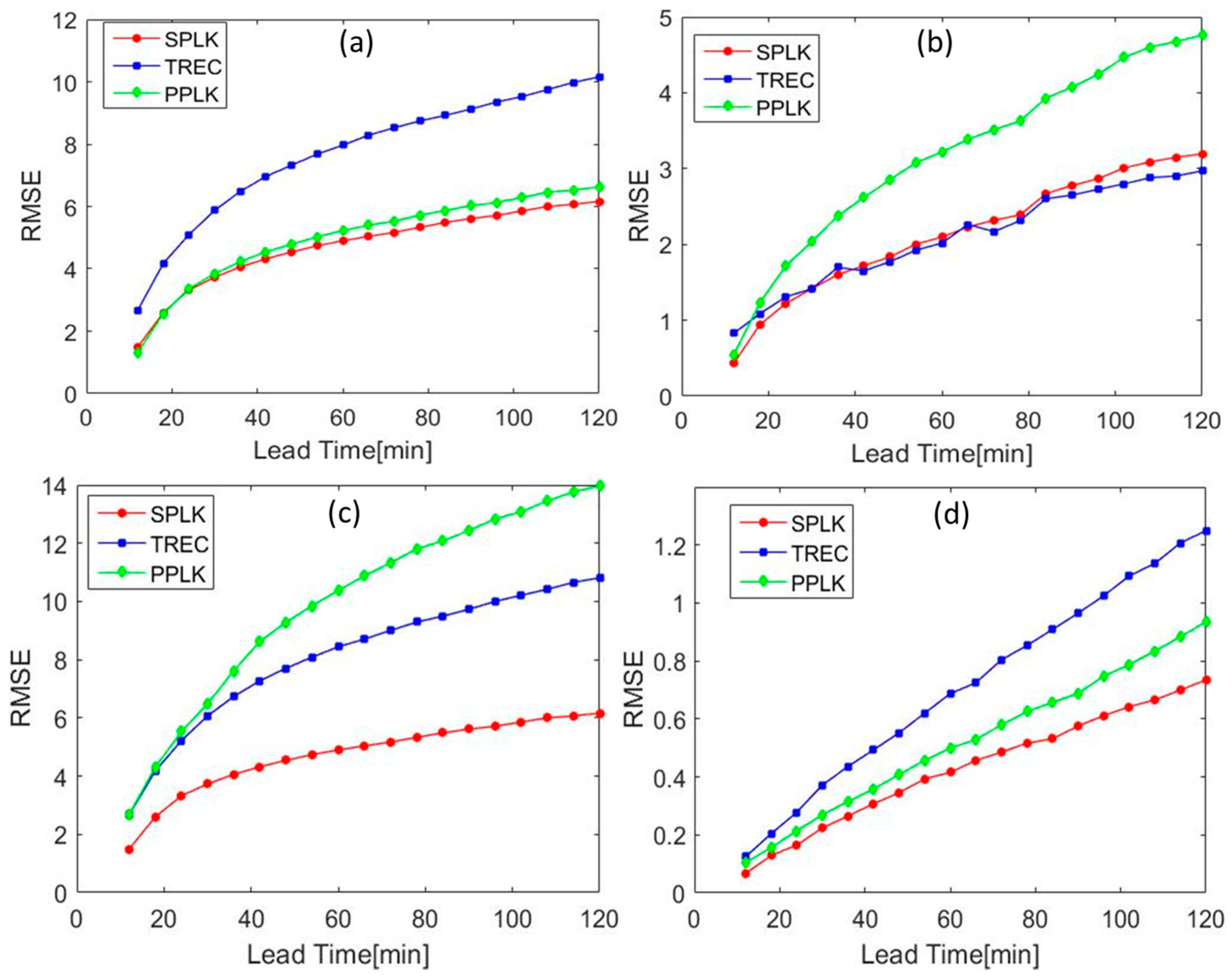
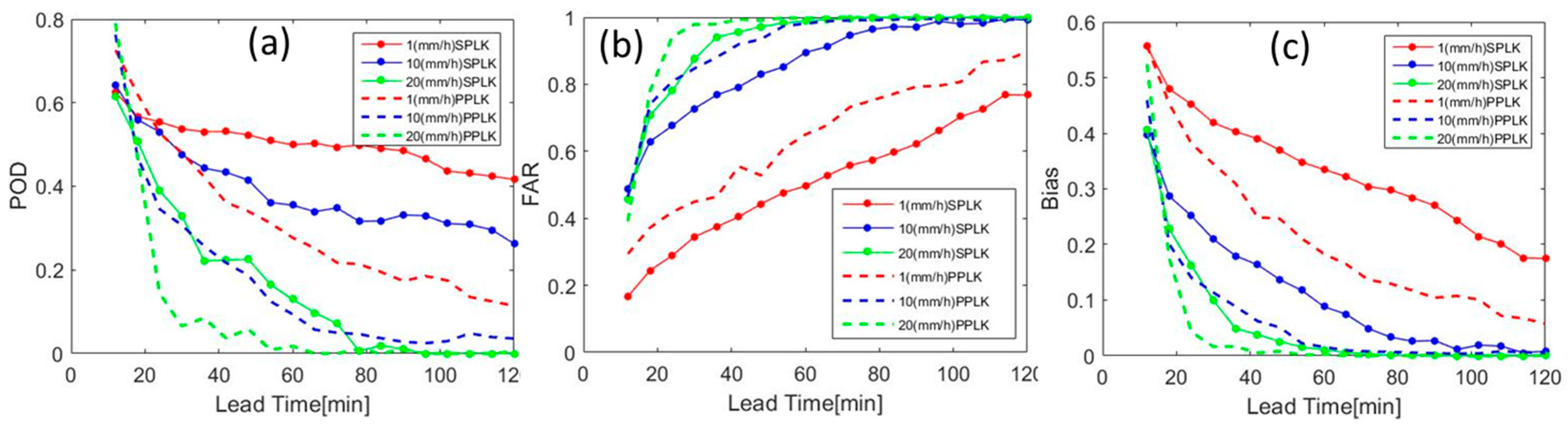
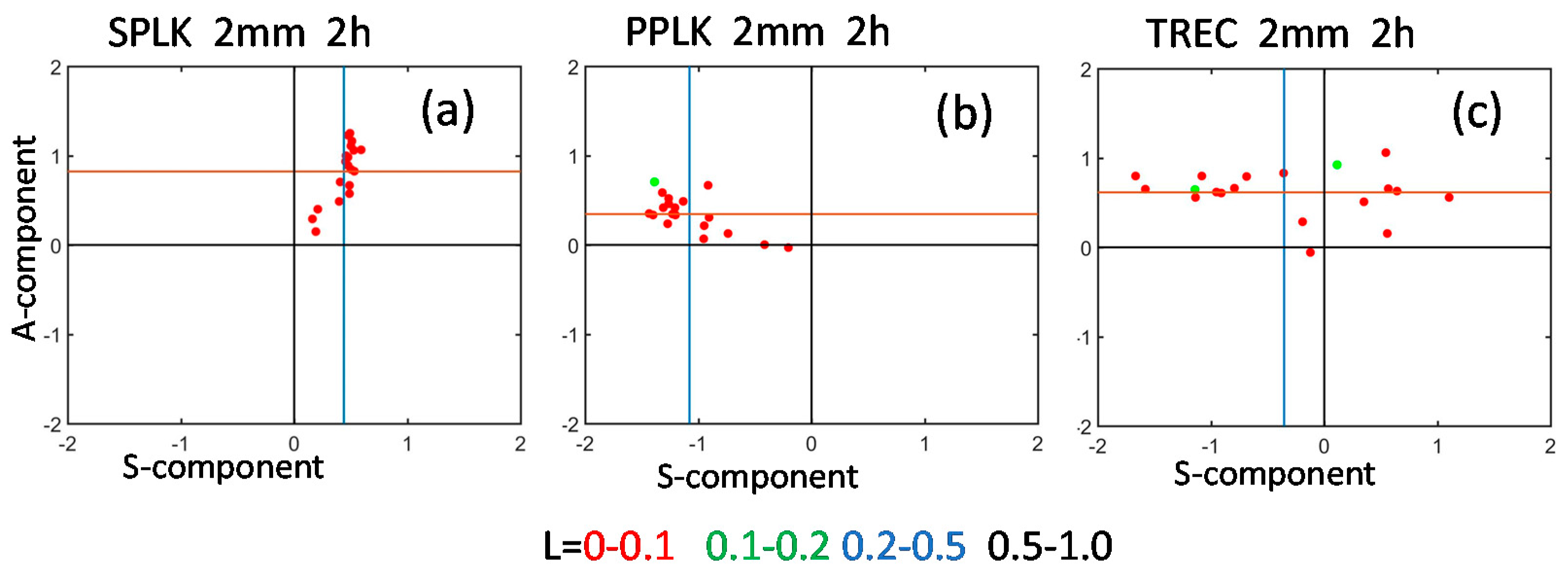
4.2. Comparison of the SPLK with TREC and PPLK Method
5. Summary and Conclusions
- (1)
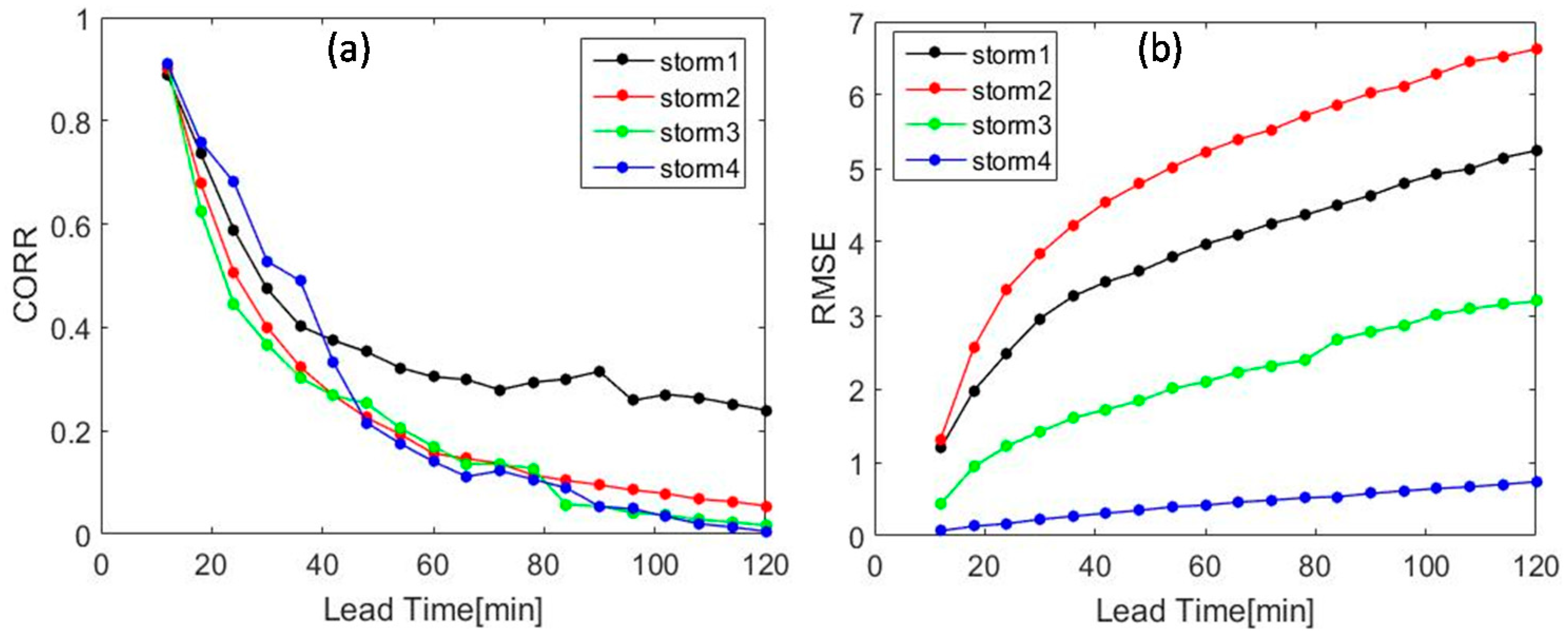
- The SPLK can improve the accuracy of precipitation forecasting within the 2 h lead time. The experiment results (Figure 7 and Figure 8, Table 2) indicate that SPLK has the capability of improving the predictability of storm positions and intensities with high CORR, and low RMSE and SAL components. The SPLK shows good performances in complicated storms, especially in the small-scale and fast-moving storms.
- (2)
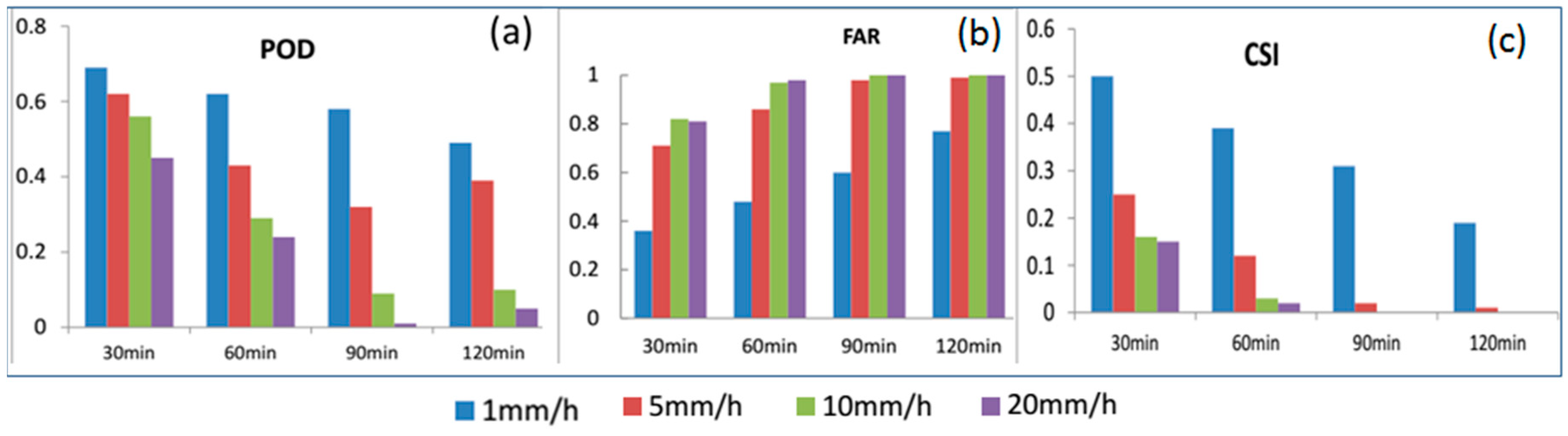
- The SPLK achieved better performance than both TREC and PPLK. Compared with the TREC, SPLK improves the predictability about 15–20% with the measured CORR and RMSE (Figure 10 and Figure 11), especially in the small-scale severe storms. Compared with PPLK, SPLK shows better accuracy in both heavy rain events (>20 mm/h) and light rain events (<10 mm/h) with the better POD, FAR, and CSI during the 2 h lead time (Figure 12).
- (3)
- The SAL verification results indicate that SPLK is superior to PPLK in capturing the precipitation location (L) and structure (S) with the component values close to zero, and more stable to the TREC in capturing the precipitation band.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, J.; Xue, M.; Wilson, J.; Ballard, P.S.; Onvlee, J.; Joe, P.; Barker, M.; Li, P.-W.; Golding, B.; Xu, M.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.-l.; Sorooshian, S.; Gourley, J.J.; Lakshmanan, V.; Hong, Y.; Bellerby, T. Quantitative precipitation nowcasting: A lagrangian pixel-based approach. Atmos. Res. 2012, 118, 418–434. [Google Scholar] [CrossRef]
- Golding, B. Nimrod: A system for generating automated very short range forecasts. Meteorol. Appl. 1998, 5, 1–16. [Google Scholar] [CrossRef]
- Ganguly, A.R.; Bras, R. Distributed quantitative precipitation forecasting using information from radar and numerical weather prediction models. J. Hydrometeorol. 2002, 4, 1168–1180. [Google Scholar] [CrossRef]
- Wiener, M.D.G. Titan: Thunderstorm identification, tracking, analysis, and nowcasting—A radar-based methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.-l.; Sorooshian, S.; Gourley, J.J.; Hong, Y.; Behrangi, A. Short-term quantitative precipitation forecasting using an object-based approach. J. Hydrol. 2013, 483, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, D.-G.; Li, Z.-L.; Hong, Y. A new methodology for pixel-quantitative precipitation nowcasting using a pyramid lucas kanade optical flow approach. J. Hydrol. 2015, 529, 354–364. [Google Scholar] [CrossRef]
- Sokol, Z.; Pesice, P. Nowcasting of precipitation—Advective statistical forecast model (sam) for the czech republic. Atmos. Res. 2012, 103, 70–79. [Google Scholar] [CrossRef]
- Johnson, J.L.; MacKeen, P.; Witt, A.; De Wayne Mitchell, E.; Stumpf, G.; Eilts, M.; Thomas, K.W. The storm cell identification and tracking algorithm: An enhanced WSR-88d algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Yeung, L.H.; Wong, W.K.; Chan, P.K.; Lai, E.S. Applications of the Hong Kong Observatory nowcasting system SWIRLS-2 in support of the 2008 Beijing Olympic Games. BMJ 2009, 2, 1977. [Google Scholar] [CrossRef]
- Mueller, C.; Saxen, T.; Roberts, R.; Wilson, J.; Betancourt, T.; Dettling, S.; Oien, N.; Yee, J. Ncar auto-nowcast system. Weather Forecast. 2003, 18, 545–561. [Google Scholar] [CrossRef]
- Haiden, T.; Kann, C.; Wittmann, A.; Pistotnik, G.; Bica, B.; Gruber, C. The Integrated Nowcasting through Comprehensive Analysis (INCA) System and Its Validation over the Eastern Alpine Region. Weather Forecast. 2011, 26, 166–183. [Google Scholar] [CrossRef]
- Wang, G.; Hong, Y.; Liu, L.; Wong, W.K.; Zahraei, A.; Lakshmanan, V. Inter-comparison of radar-based nowcasting schemes in the jianghuai river basin, china. Meteorol. Appl. 2015, 22, 289–300. [Google Scholar] [CrossRef]
- Grecu, M.; Krajewski, W.F. A large-sample investigation of statistical procedures for radar-based short-term quantitative precipitation forecasting. J. Hydrol. 2000, 239, 69–84. [Google Scholar] [CrossRef]
- Woo, W.-C.; Wong, W.-K. Operational application of optical flow techniques to radar-based rainfall nowcasting. Atmosphere 2017, 8, 48. [Google Scholar] [CrossRef]
- Novo, S.; Martínez, D.; Puentes, O. Tracking, analysis, and nowcasting of cuban convective cells as seen by radar. Meteorol. Appl. 2014, 21, 585–595. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale-dependence of the predictability of precipitation from continental radar images. Part I: Description of the methodology. Mon. Weather Rev. 2002, 130, 2859. [Google Scholar] [CrossRef]
- Diamond, D.H.; Heyns, P.S.; Oberholster, A.J. Accuracy evaluation of sub-pixel structural vibration measurements through optical flow analysis of a video sequence. Measurement 2017, 95, 166–172. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Li, J.; Li, Z.; Schmit, T.J.; Bai, W. Advanced infrared sounder subpixel cloud detection with imagers and its impact on radiance assimilation in nwp. Geophys. Res. Lett. 2014, 41, 1773–1780. [Google Scholar] [CrossRef]
- Javh, J.; Slavič, J.; Boltežar, M. The subpixel resolution of optical-flow-based modal analysis. Mech. Syst. Signal Process. 2017, 88, 89–99. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative technique of image registration and its application to stereo. In Proceedings of the 7th International Joint Conference on Artificial intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 73, pp. 674–679. [Google Scholar]
- Bowler, N.E.H.; Pierce, C.E.; Seed, A. Development of a precipitation nowcasting algorithm based upon optical flow techniques. J. Hydrol. 2004, 288, 74–91. [Google Scholar] [CrossRef]
- Wolfson, M.; Forman, B.; Hallowell, R.; Moore, M. The growth and decay storm tracker. In Proceedings of the 8th Conference on Aviation, Range, and Aerospace Meteorology, Dallas, TX, USA, 10–15 January 1999. [Google Scholar]
- Lakshmanan, V.; Smith, T. Data mining storm attributes from spatial grids. J. Atmos. Ocean. Technol. 2009, 26, 2353–2365. [Google Scholar] [CrossRef]
- Bellon, A.; Lovejoy, S.; Austin, G. Combining satellite and radar data for the short-range forecasting of precipitation. Mon. Weather Rev. 2003, 108, 1554–1566. [Google Scholar] [CrossRef]
- Tuttle, J.D.; Foote, B. Determination of the boundary layer airflow from a single doppler radar. J. Atmos. Ocean. Technol. 1990, 7, 218–232. [Google Scholar] [CrossRef]
- Laroche, S.; Zawadzki, I. A variational analysis method for retrieval of three-dimensional wind field from single-doppler radar data. J. Atmos. Sci. 1994, 51, 2664–2682. [Google Scholar] [CrossRef]
- Bouguet, J.Y. Pyramidal implementation of the Lucas Kanade feature tracker description of the algorithm. OpenCV Doc. 1999, 22, 363–381. [Google Scholar]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef]
- Bouguet, J.-Y. Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm. OpenCV Doc. 2001, 22, 363–381. [Google Scholar]
- Lyu, Y.; Yang, Y.; Ru, J. Gesture motion detection algorithm based on optical flow method. In Proceedings of the 2015 IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 10–11 October 2015; pp. 128–132. [Google Scholar]
- Ulbrich, U.; Fink, A.; Klawa, M.; Pinto, J. Three extreme storms over europe in december 1999. Weather 2012, 56, 70–80. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Ebert, E.E.; Wilson, L.J.; Brown, B.G.; Nurmi, P.; Brooks, H.E.; Bally, J.; Jaeneke, M. Verification of nowcasts from the wwrp sydney 2000 forecast demonstration project. Weather Forecast. 2004, 19, 73–96. [Google Scholar] [CrossRef]
- Wernli, H.; Paulat, M.; Hagen, M.; Frei, C. SAL—A novel quality measure for the verification of Quantitative Precipitation Forecasts. Mon. Weather Rev. 2008, 136, 4470–4487. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.; et al. Multi-radar multi-sensor (MRMS) quantitative precipitation estimation: Initial operating capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Wilson, J.; Roberts, R. Summary of convective storm initiation and evolution during IHOP: Observational and modeling perspective. Mon. Weather Rev. 2006, 134, 23–47. [Google Scholar] [CrossRef]


| Storm Event | Start-Time (yyyymmdd-hhmm) | Spatial Coverage | Mean Velocity | Description |
|---|---|---|---|---|
| T1 | 20151018-0300 | 30 km/h | Frontal rain | |
| T2 | 20160603-1150 | 40 km/h | Convective rain | |
| T3 | 20150815-1450 | 60 km/h | Organized thunderstorm | |
| T4 | 20150801-0000 | 10 km/h | cyclonic | |
| T5 | 20150920-2030 | 50 km/h | Frontal rain | |
| T6 | 20150801-1200 | 20 km/h | Convective rain | |
| T7 | 20160816-1240 | 36 km/h | Convective rain | |
| T8 | 20160619-0840 | 40 km/h | Localized thunderstorms |
| Lead Time | Case | S | A | L |
|---|---|---|---|---|
| 30 min | storm1 | 0.2660 | 0.5022 | 0.0604 |
| storm2 | 0.3996 | 0.4864 | 0.0235 | |
| storm3 | 0.3498 | 0.5075 | 0.0104 | |
| storm4 | 0.4908 | 0.9372 | 0.0839 | |
| 60 min | storm1 | 1.1044 | 0.9994 | 0.1276 |
| storm2 | 1.7340 | 0.9527 | 0.0760 | |
| storm3 | 0.5013 | 0.8488 | 0.0532 | |
| storm4 | 1.2269 | 1.1193 | 0.1347 | |
| 90 min | storm1 | 1.5339 | 1.3932 | 0.1587 |
| storm2 | 1.6550 | 1.0625 | 0.1382 | |
| storm3 | 0.5277 | 1.0615 | 0.0635 | |
| storm4 | 1.5784 | 1.4312 | 0.1480 | |
| 120 min | storm1 | 1.4840 | 1.6312 | 0.1506 |
| storm2 | 1.7911 | 1.2628 | 0.2407 | |
| storm3 | 0.4945 | 1.2503 | 0.0552 | |
| storm4 | 1.5561 | 1.6578 | 0.1779 | |
| average | storm1 | 1.0971 | 1.1315 | 0.1243 |
| storm2 | 1.3825 | 0.9464 | 0.1163 | |
| storm3 | 0.4808 | 0.9118 | 0.0489 | |
| storm4 | 1.2131 | 1.2864 | 0.1361 |
| Lead Time | SPLK | PPLK | TREC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| POD | FAR | CSI | POD | FAR | CSI | POD | FAR | CSI | |
| 12 min | 0.848 | 0.182 | 0.713 | 0.735 | 0.227 | 0.604 | 0.692 | 0.253 | 0.561 |
| 30 min | 0.746 | 0.447 | 0.630 | 0.533 | 0.363 | 0.409 | 0.723 | 0.435 | 0.464 |
| 60 min | 0.689 | 0.537 | 0.527 | 0.434 | 0.466 | 0.315 | 0.743 | 0.587 | 0.361 |
| 90 min | 0.452 | 0.793 | 0.356 | 0.427 | 0.580 | 0.269 | 0.504 | 0.750 | 0.201 |
| 120 min | 0.370 | 0.904 | 0.060 | 0.372 | 0.728 | 0.192 | 0.329 | 0.826 | 0.158 |
| average | 0.621 | 0.573 | 0.457 | 0.500 | 0.473 | 0.358 | 0.598 | 0.570 | 0.349 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; He, Z.; Chen, S.; Mai, X.; Zhang, A.; Hu, B.; Li, Z.; Tong, X. Subpixel-Based Precipitation Nowcasting with the Pyramid Lucas–Kanade Optical Flow Technique. Atmosphere 2018, 9, 260. https://doi.org/10.3390/atmos9070260
Li L, He Z, Chen S, Mai X, Zhang A, Hu B, Li Z, Tong X. Subpixel-Based Precipitation Nowcasting with the Pyramid Lucas–Kanade Optical Flow Technique. Atmosphere. 2018; 9(7):260. https://doi.org/10.3390/atmos9070260
Chicago/Turabian StyleLi, Ling, Zhengwei He, Sheng Chen, Xiongfa Mai, Asi Zhang, Baoqing Hu, Zhi Li, and Xinhua Tong. 2018. "Subpixel-Based Precipitation Nowcasting with the Pyramid Lucas–Kanade Optical Flow Technique" Atmosphere 9, no. 7: 260. https://doi.org/10.3390/atmos9070260
APA StyleLi, L., He, Z., Chen, S., Mai, X., Zhang, A., Hu, B., Li, Z., & Tong, X. (2018). Subpixel-Based Precipitation Nowcasting with the Pyramid Lucas–Kanade Optical Flow Technique. Atmosphere, 9(7), 260. https://doi.org/10.3390/atmos9070260




