Impact of Subgrid-Scale Modeling in Actuator-Line Based Large-Eddy Simulation of Vertical-Axis Wind Turbine Wakes
Abstract
1. Introduction
2. Large-Eddy Simulation Framework
2.1. LES Governing Equations
2.2. Subgrid-Scale Parametrization
2.2.1. Standard Smagorinsky Model
2.2.2. Lagrangian Scale-Dependent Dynamic Smagorinsky Model
2.2.3. Anisotropic Minimum Dissipation Model
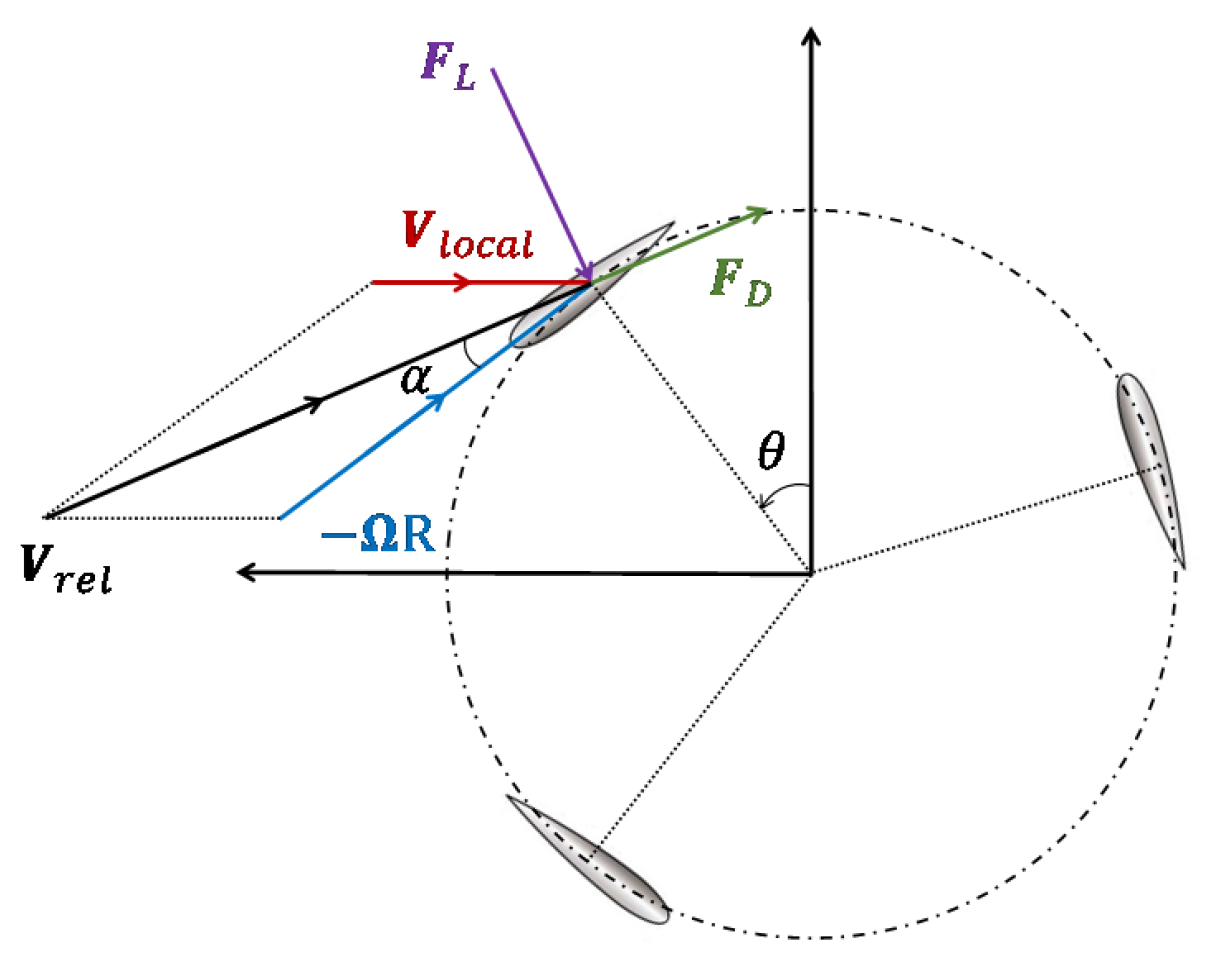
2.3. Wind Turbine Parametrization
2.4. Numerical Setup
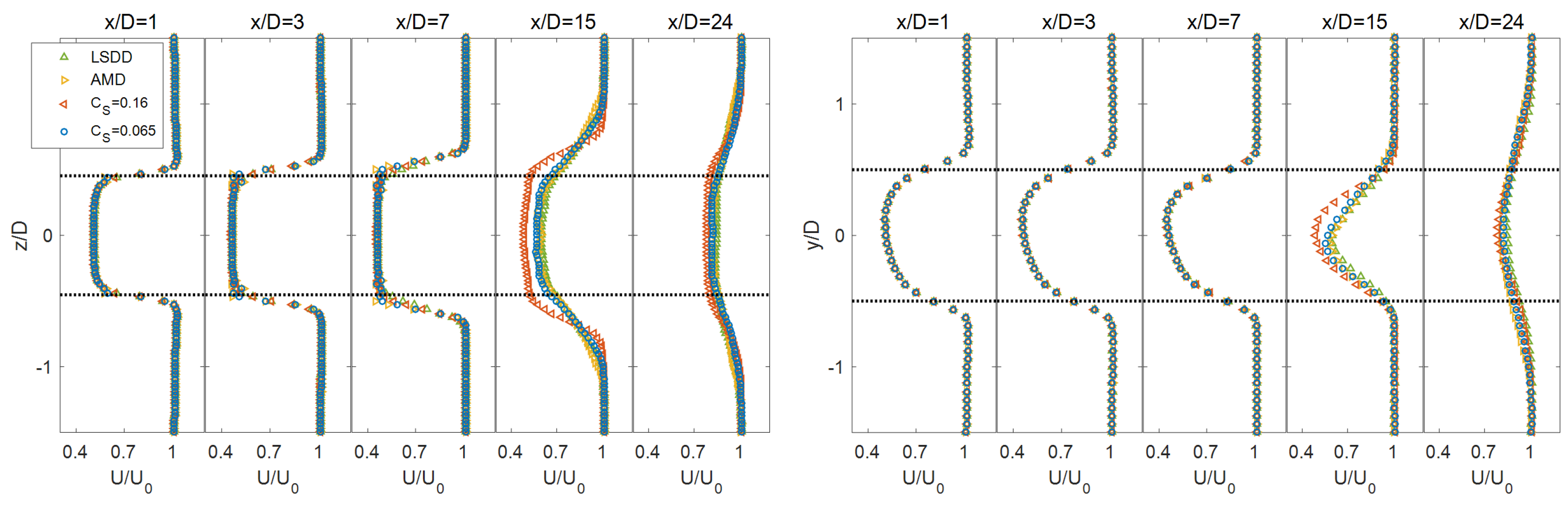
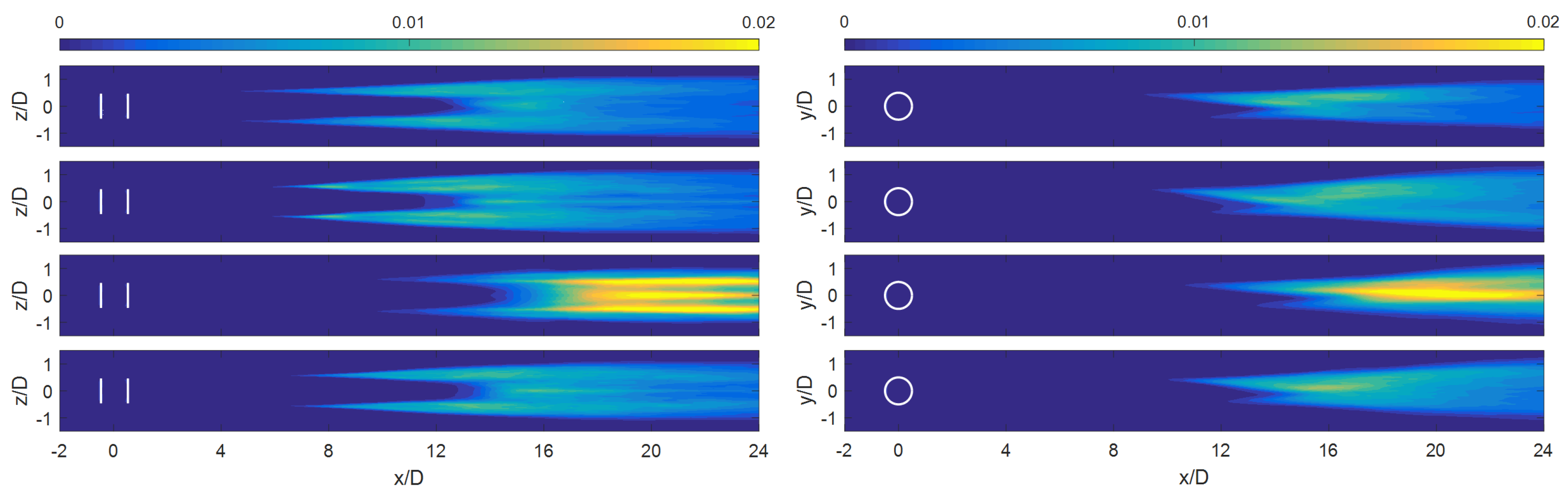
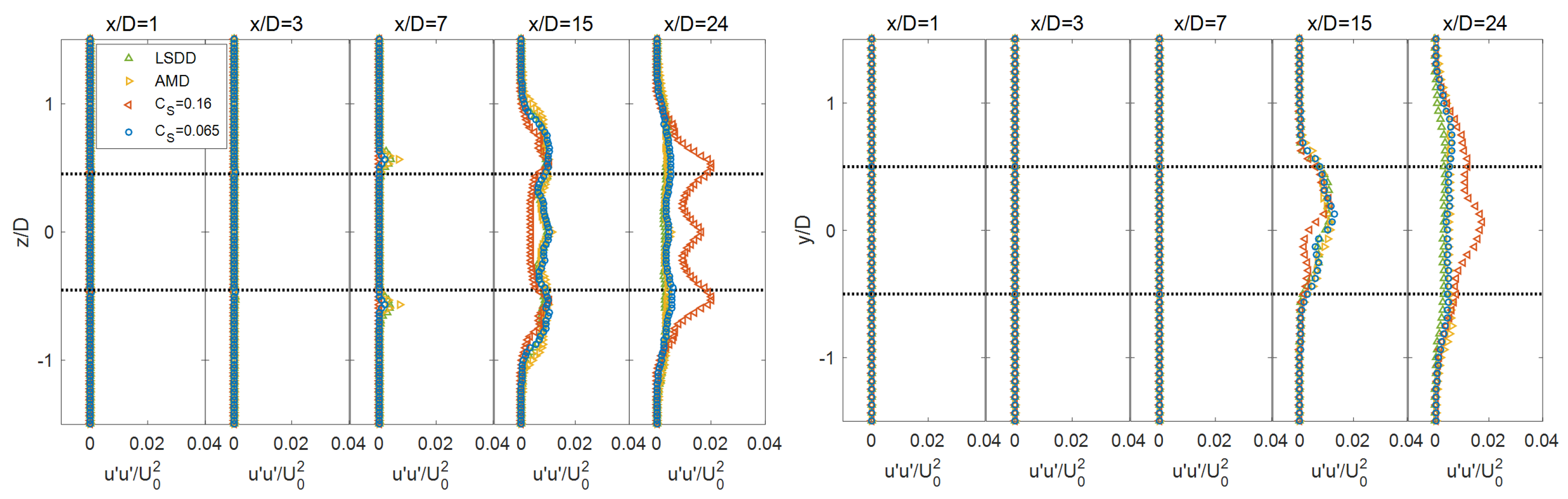
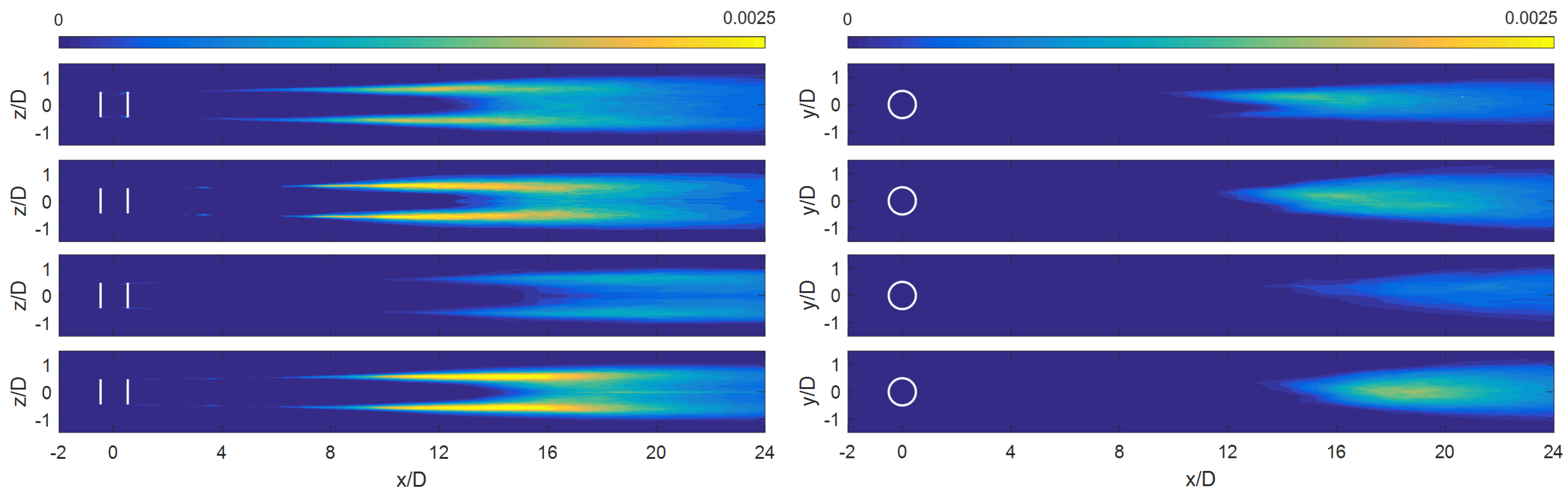
3. Results
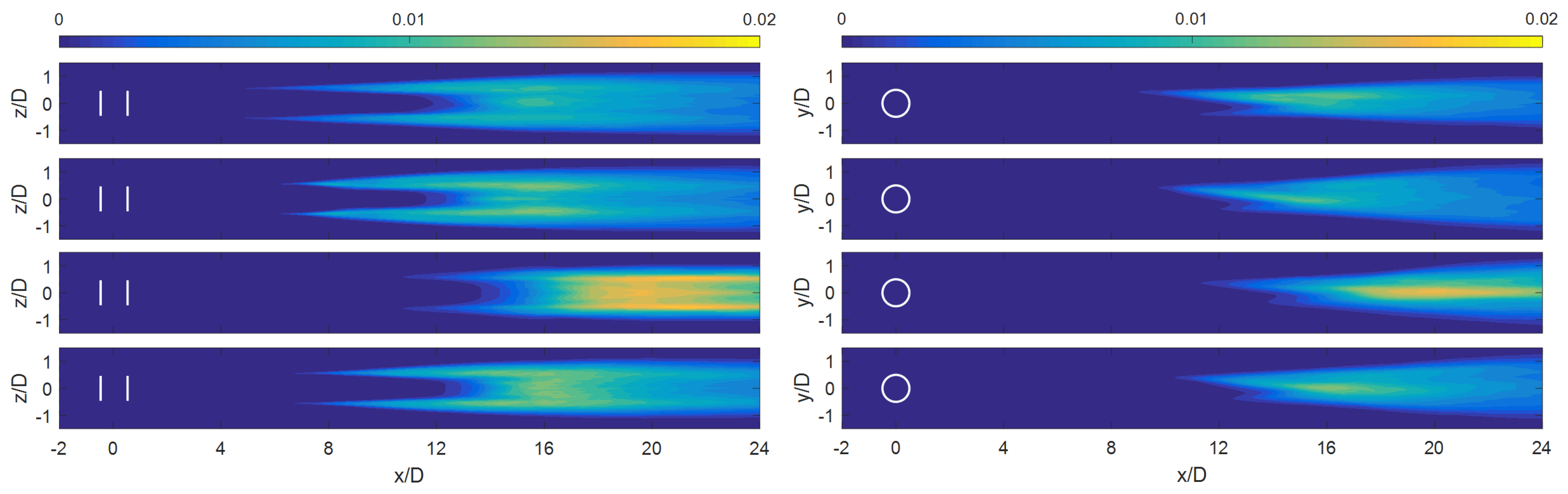
4. Resolved-Scale Turbulent Kinetic Energy Budget
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
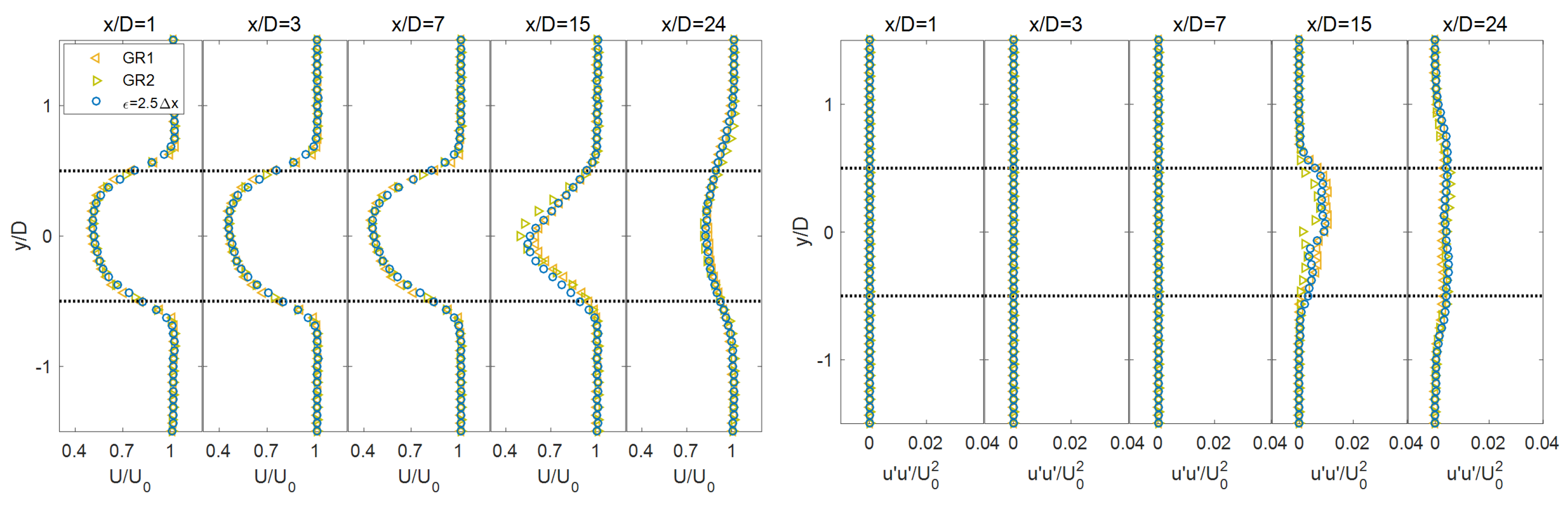
Appendix A. Effects of the Smearing Parameter and Grid Resolution
References
- Araya, D.B.; Craig, A.E.; Kinzel, M.; Dabiri, J.O. Low-order modeling of wind farm aerodynamics using leaky Rankine bodies. J. Renew. Sustain. Energy 2014, 6, 063118. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Battisti, L.; Zanne, L.; Dell’Anna, S.; Dossena, V.; Persico, G.; Paradiso, B. Aerodynamic Measurements on a Vertical Axis Wind Turbine in a Large Scale Wind Tunnel. J. Energy Resour. Technol. 2011, 133, 031201. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Characterising the near-wake of a cross-flow turbine. J. Turbul. 2015, 16, 392–410. [Google Scholar] [CrossRef]
- Araya, D.B.; Dabiri, J.O. A comparison of wake measurements in motor-driven and flow-driven turbine experiments. Exp. Fluids 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Posa, A.; Parker, C.M.; Leftwich, M.C.; Balaras, E. Wake structure of a single vertical axis wind turbine. Int. J. Heat Fluid Flow 2016. [Google Scholar] [CrossRef]
- Ryan, K.J.; Coletti, F.; Elkins, C.J.; Dabiri, J.O.; Eaton, J.K. Three-dimensional flow field around and downstream of a subscale model rotating vertical axis wind turbine. Exp. Fluids 2016, 57, 1–15. [Google Scholar] [CrossRef]
- Araya, D.B.; Colonius, T.; Dabiri, J.O. Transition to bluff-body dynamics in the wake of vertical-axis wind turbines. J. Fluid Mech. 2017, 813, 346–381. [Google Scholar] [CrossRef]
- Craig, A.E.; Dabiri, J.O.; Koseff, J.R. Low order physical models of vertical axis wind turbines. J. Renew. Sustain. Energy 2017, 9, 013306. [Google Scholar] [CrossRef]
- Rolin, V.; Porté-Agel, F. Experimental investigation of vertical-axis wind-turbine wakes in boundary layer flow. Renew. Energy 2018, 118, 1–13. [Google Scholar] [CrossRef]
- Kadum, H.; Friedman, S.; Camp, E.H.; Cal, R.B. Development and scaling of a vertical axis wind turbine wake. J. Wind Eng. Ind. Aerodyn. 2018, 174, 303–311. [Google Scholar] [CrossRef]
- Kinzel, M.; Mulligan, Q.; Dabiri, J.O. Energy exchange in an array of vertical-axis wind turbines. J. Turbul. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Brownstein, I.D.; Kinzel, M.; Dabiri, J.O. Performance enhancement of downstream vertical-axis wind turbines. J. Renew. Sustain. Energy 2016, 8, 053306. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Large Eddy Simulation of Vertical Axis Wind Turbine Wakes. Energies 2014, 7, 890–912. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. A Large-Eddy Simulation Study of Vertical Axis Wind Turbine Wakes in the Atmospheric Boundary Layer. Energies 2016, 9, 366. [Google Scholar] [CrossRef]
- Lam, H.; Peng, H. Study of wake characteristics of a vertical axis wind turbine by two-and three-dimensional computational fluid dynamics simulations. Renew. Energy 2016, 90, 386–398. [Google Scholar] [CrossRef]
- Hezaveh, S.H.; Bou-Zeid, E.; Lohry, M.W.; Martinelli, L. Simulation and wake analysis of a single vertical axis wind turbine. Wind Energy 2016, 20, 713–730. [Google Scholar] [CrossRef]
- Abkar, M.; Dabiri, J.O. Self-similarity and flow characteristics of vertical-axis wind turbine wakes: An LES study. J. Turbul. 2017, 18, 373–389. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Montazeri, H.; Blocken, B. Effect of the shaft on the aerodynamic performance of urban vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 616–630. [Google Scholar] [CrossRef]
- Mehta, D.; Van Zuijlen, A.; Koren, B.; Holierhoek, J.; Bijl, H. Large eddy simulation of wind farm aerodynamics: A review. J. Wind Eng. Ind. Aerodyn. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Stevens, R.J.; Meneveau, C. Flow structure and turbulence in wind farms. Ann. Rev. Fluid Mech. 2017, 49, 311–339. [Google Scholar] [CrossRef]
- Breton, S.P.; Sumner, J.; Sørensen, J.N.; Hansen, K.S.; Sarmast, S.; Ivanell, S. A survey of modelling methods for high-fidelity wind farm simulations using large eddy simulation. Phil. Trans. R. Soc. A 2017, 375, 20160097. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.T.; Porté-Agel, F. Large-Eddy Simulation of Wind-Turbine Wakes: Evaluation of Turbine Parametrisations. Bound.-Lay. Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Sarlak, H.; Meneveau, C.; Sørensen, J.N. Role of subgrid-scale modeling in large eddy simulation of wind turbine wake interactions. Renew. Energy 2015, 77, 386–399. [Google Scholar] [CrossRef]
- Sarlak, H.; Meneveau, C.; Sørensen, J.N.; Mikkelsen, R. Quantifying the impact of subgrid scale models in actuator-line based LES of wind turbine wakes in laminar and turbulent inflow. In Direct and Large-Eddy Simulation IX; Springer: Berlin, Germany, 2015; pp. 169–175. [Google Scholar]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Meneveau, C. Large eddy simulation of wind turbine wakes: Detailed comparisons of two codes focusing on effects of numerics and subgrid modeling. J. Phys. Conf. Ser. 2015, 625, 012024. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Yilmaz, A.E.; Sarlak, H.; Johnson, P.L.; Sørensen, J.N.; Meyers, J.; Meneveau, C. Comparison of four large-eddy simulation research codes and effects of model coefficient and inflow turbulence in actuator-line-based wind turbine modeling. J. Renew. Sustain. Energy 2018, 10, 033301. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lilly, D.K. The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, Yorktown Height, NY, USA, 4–16 November 1966; p. 167. [Google Scholar]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 1982, 118, 341–377. [Google Scholar] [CrossRef]
- Piomelli, U.; Moin, P.; Ferziger, J.H. Model consistency in large eddy simulation of turbulent channel flows. Phys. Fluids 1988, 31, 1884–1891. [Google Scholar] [CrossRef]
- Vreman, B.; Geurts, B.; Kuerten, H. Large-eddy simulation of the turbulent mixing layer. J. Fluid Mech. 1997, 339, 357–390. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A Scale-Dependent Dynamic Model for Large-Eddy Simulation: Application to a Neutral Atmospheric Boundary Layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 2005, 17, 025105. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Piomelli, U. High Reynolds number calculations using the dynamic subgrid-scale stress model. Phys. Fluids A 1993, 5, 1484–1490. [Google Scholar] [CrossRef]
- Meneveau, C.; Katz, J. Scale-invariance and turbulence models for large-eddy simulation. Ann. Rev. Fluid Mech. 2000, 32, 1–32. [Google Scholar] [CrossRef]
- Khani, S.; Waite, M.L. Large eddy simulations of stratified turbulence: The dynamic Smagorinsky model. J. Fluid Mech. 2015, 773, 327–344. [Google Scholar] [CrossRef]
- Meneveau, C.; Lund, T.S.; Cabot, W.H. A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef]
- Stoll, R.; Porté-Agel, F. Dynamic subgrid-scale models for momentum and scalar fluxes in large-eddy simulations of neutrally stratified atmospheric boundary layers over heterogeneous terrain. Water Resour. Res. 2006, 42, W01409. [Google Scholar] [CrossRef]
- Verstappen, R. When does eddy viscosity damp subfilter scales sufficiently? J. Sci. Comput. 2011, 49, 94–110. [Google Scholar] [CrossRef]
- Rozema, W.; Bae, H.J.; Moin, P.; Verstappen, R. Minimum-dissipation models for large-eddy simulation. Phys. Fluids 2015, 27, 085107. [Google Scholar] [CrossRef]
- Abkar, M.; Bae, H.; Moin, P. Minimum-dissipation scalar transport model for large-eddy simulation of turbulent flows. Phys. Rev. Fluids 2016, 1, 041701. [Google Scholar] [CrossRef]
- Abkar, M.; Moin, P. Large-Eddy Simulation of Thermally Stratified Atmospheric Boundary-Layer Flow Using a Minimum Dissipation Model. Bound.-Lay. Meteorol. 2017, 165, 405–419. [Google Scholar] [CrossRef]
- Verstappen, R.; Rozema, W.; Bae, H. Numerical scale separation in large-eddy simulation. In Proceedings of the Summer Program 2014, Stanford, CA, USA, 6 July–1 August 2014; pp. 417–426. [Google Scholar]
- Noll, R.B.; Ham, N.D. Dynamic Stall of small Wind Systems; Technical Report; Aerospace Systems Inc.: Burlington, MA, USA, 1983. [Google Scholar]
- Glauert, H. Airplane propellers. In Aerodynamic Theory; Durand, W.F., Ed.; Dover Publications: Mineola, NY, USA, 1963; pp. 169–360. [Google Scholar]
- Sørensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluid Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, J.; Mikkelsen, R. Actuator line simulation of wake of wind turbine operating in turbulent inflow. J. Phys. Conf. Ser. 2007, 75, 012063. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Simulation of Turbulent Flow Inside and Above Wind Farms: Model Validation and Layout Effects. Bound.-Lay. Meteorol. 2013, 146, 181–205. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. The Effect of Free-Atmosphere Stratification on Boundary-Layer Flow and Power Output from Very Large Wind Farms. Energies 2013, 6, 2338–2361. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Mean and turbulent kinetic energy budgets inside and above very large wind farms under conventionally-neutral condition. Renew. Energy 2014, 70, 142–152. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. A new wind-farm parameterization for large-scale atmospheric models. J. Renew. Sustain. Energy 2015, 7, 013121. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of the Coriolis force on the structure and evolution of wind turbine wakes. Phys. Rev. Fluids 2016, 1, 063701. [Google Scholar] [CrossRef]
- Yang, X.I.; Abkar, M. A hierarchical random additive model for passive scalars in wall-bounded flows at high Reynolds numbers. J. Fluid Mech. 2018, 842, 354–380. [Google Scholar] [CrossRef]
- Moeng, C. A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 46, 2311–2330. [Google Scholar] [CrossRef]
- Albertson, J.D.; Parlange, M.B. Surfaces length scales and shear stress: Implications for land-atmosphere interactions over complex terrain. Water Resour. Res. 1999, 35, 2121–2132. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Zang, T. Spectral Methods in Fluid Dynamics; Springer: Berlin, Germany, 1988. [Google Scholar]
- Möllerström, E.; Ottermo, F.; Hylander, J.; Bernhoff, H. Noise Emission of a 200 kW Vertical Axis Wind Turbine. Energies 2015, 9, 19. [Google Scholar] [CrossRef]
- Möllerström, E.; Ottermo, F.; Goude, A.; Eriksson, S.; Hylander, J.; Bernhoff, H. Turbulence influence on wind energy extraction for a medium size vertical axis wind turbine. Wind Energy 2016, 19, 1963–1973. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Airfoil Sections through 180 Degrees Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report SAND80-2114; Sandia National Laboratories: Livermore, CA, USA, 1981. [Google Scholar]
- Tseng, Y.H.; Meneveau, C.; Parlange, M.B. Modeling flow around bluff bodies and predicting urban dispersion using large eddy simulation. Environ. Sci. Technol. 2006, 40, 2653–2662. [Google Scholar] [CrossRef] [PubMed]
- Abkar, M.; Porté-Agel, F. A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions. J. Turbul. 2012, 13, 1–18. [Google Scholar] [CrossRef]
- Munters, W.; Meneveau, C.; Meyers, J. Turbulent Inflow Precursor Method with Time-Varying Direction for Large-Eddy Simulations and Applications to Wind Farms. Bound.-Lay. Meteorol. 2016, 159, 305–328. [Google Scholar] [CrossRef]
- Abkar, M.; Sharifi, A.; Porté-Agel, F. Wake flow in a wind farm during a diurnal cycle. J. Turbul. 2016, 17, 420–441. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bergeles, G.; Michos, A.; Athanassiadis, N. Velocity vector and turbulence in the symmetry plane of a Darrieus wind generator. J. Wind Eng. Ind. Aerodyn. 1991, 37, 87–101. [Google Scholar] [CrossRef]
- Ferreira, C.J.S.; van Bussel, G.J.; van Kuik, G.A. Wind tunnel hotwire measurements, flow visualization and thrust measurement of a VAWT in skew. J. Sol. Energy Eng. 2006, 128, 487–497. [Google Scholar] [CrossRef]
- Rolin, V.; Porté-Agel, F. Wind-tunnel study of the wake behind a vertical axis wind turbine in a boundary layer flow using stereoscopic particle image velocimetry. J. Phys. Conf. Ser. 2015, 625, 012012. [Google Scholar] [CrossRef]
- Parker, C.M.; Leftwich, M.C. The effect of tip speed ratio on a vertical axis wind turbine at high Reynolds numbers. Exp. Fluids 2016, 57, 1–11. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of atmospheric stability on wind turbine wakes: A large-eddy simulation study. Phys. Fluids 2015, 27, 035104. [Google Scholar] [CrossRef]
- Ivanell, S.; Sørensen, J.; Mikkelsen, R.; Henningson, D. Analysis of numerically generated wake structures. Wind Energy 2009, 12, 63–80. [Google Scholar] [CrossRef]


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abkar, M. Impact of Subgrid-Scale Modeling in Actuator-Line Based Large-Eddy Simulation of Vertical-Axis Wind Turbine Wakes. Atmosphere 2018, 9, 257. https://doi.org/10.3390/atmos9070257
Abkar M. Impact of Subgrid-Scale Modeling in Actuator-Line Based Large-Eddy Simulation of Vertical-Axis Wind Turbine Wakes. Atmosphere. 2018; 9(7):257. https://doi.org/10.3390/atmos9070257
Chicago/Turabian StyleAbkar, Mahdi. 2018. "Impact of Subgrid-Scale Modeling in Actuator-Line Based Large-Eddy Simulation of Vertical-Axis Wind Turbine Wakes" Atmosphere 9, no. 7: 257. https://doi.org/10.3390/atmos9070257
APA StyleAbkar, M. (2018). Impact of Subgrid-Scale Modeling in Actuator-Line Based Large-Eddy Simulation of Vertical-Axis Wind Turbine Wakes. Atmosphere, 9(7), 257. https://doi.org/10.3390/atmos9070257




