Micro-Scale Properties of Different Bora Types
Abstract
1. Introduction
2. Methods and Data
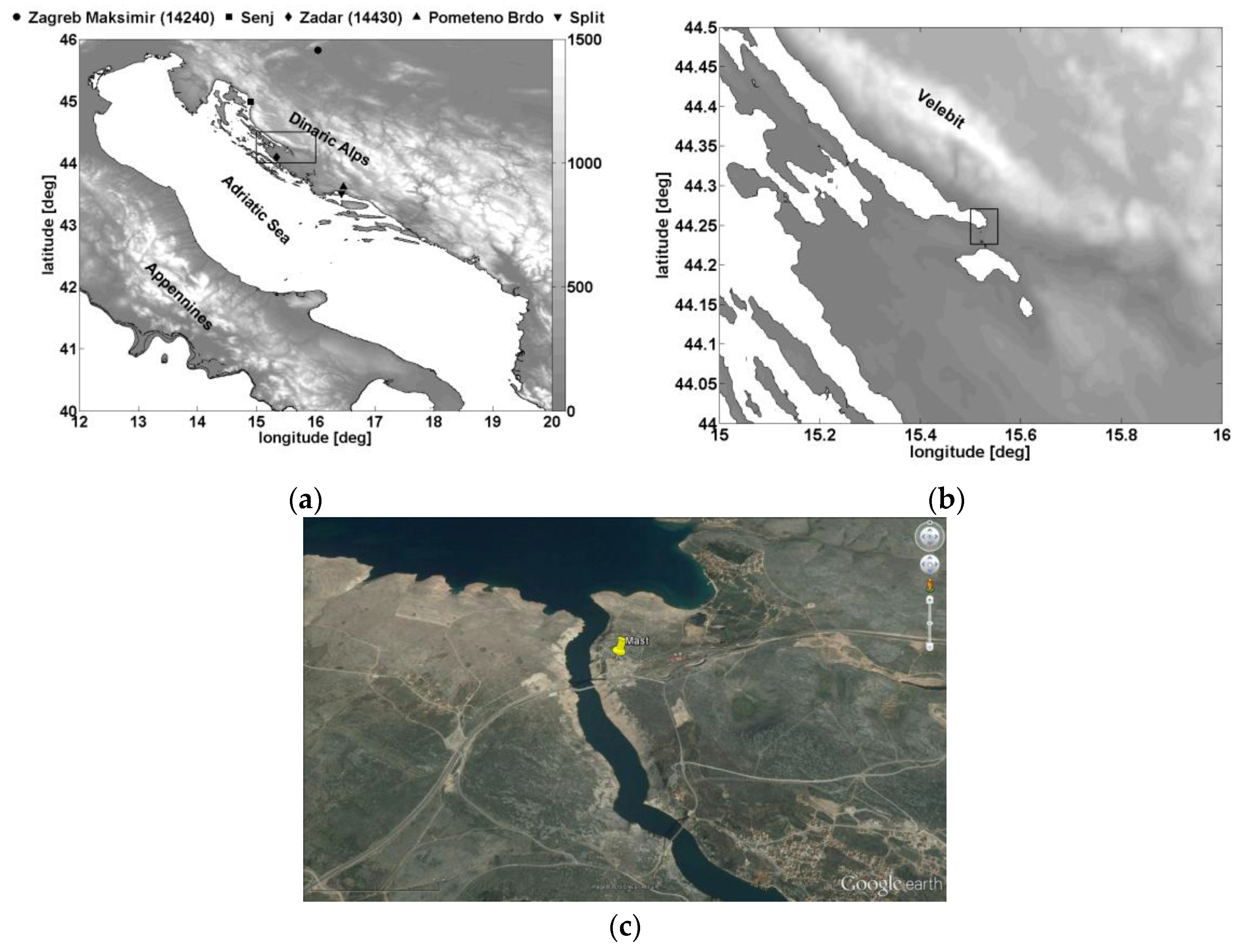
2.1. Measurement Site and Instruments
2.2. Data Quality Check
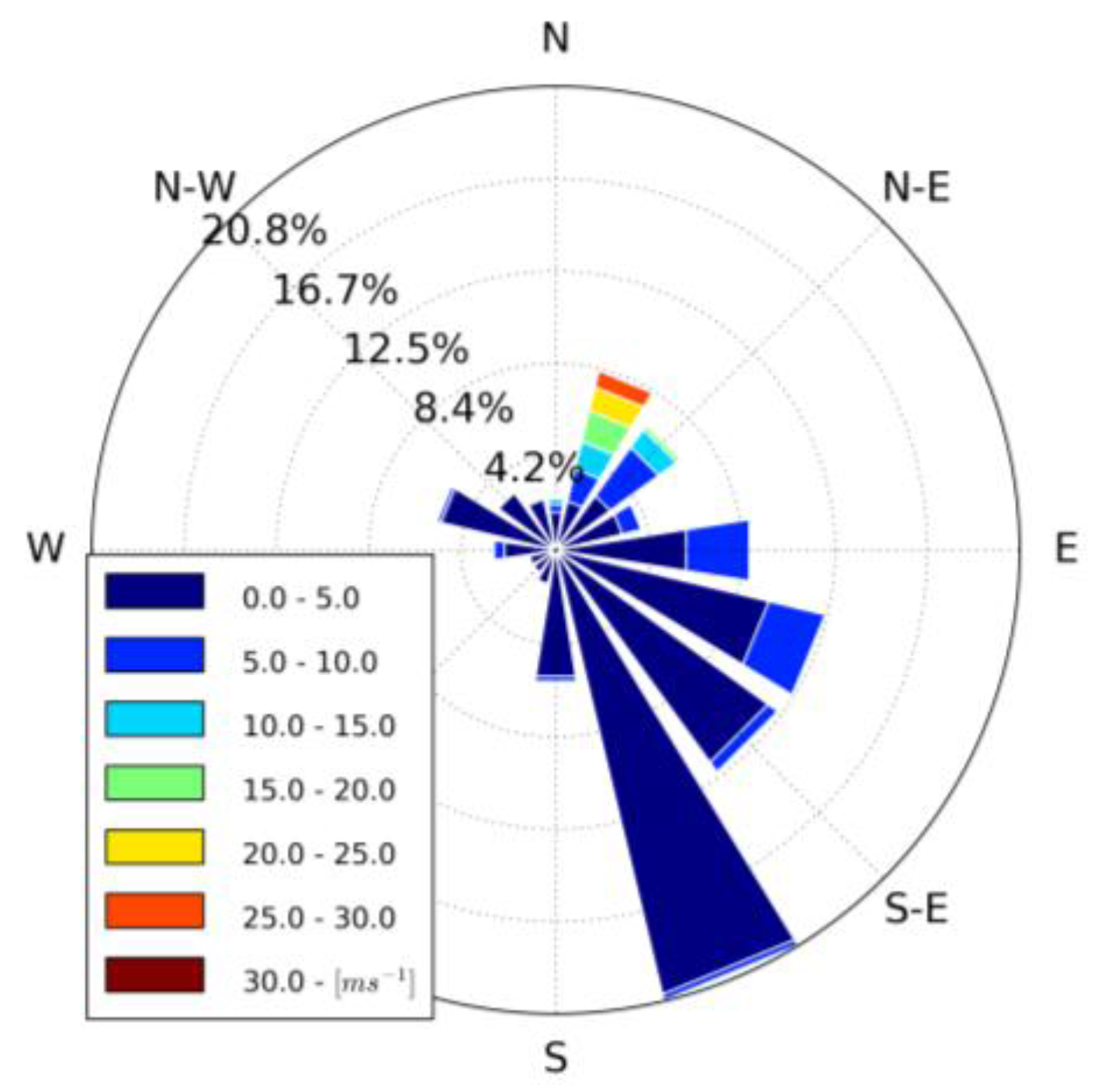
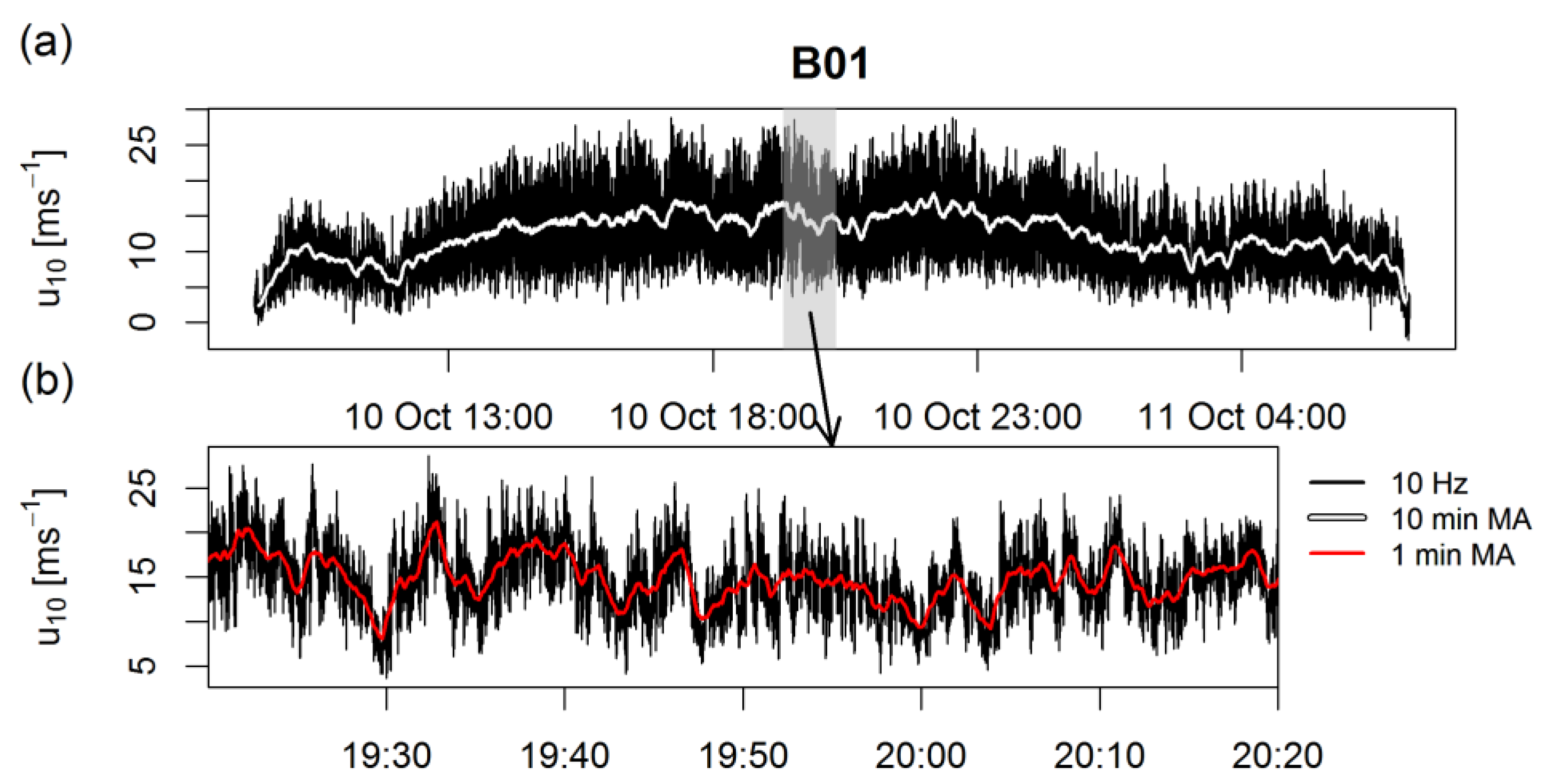
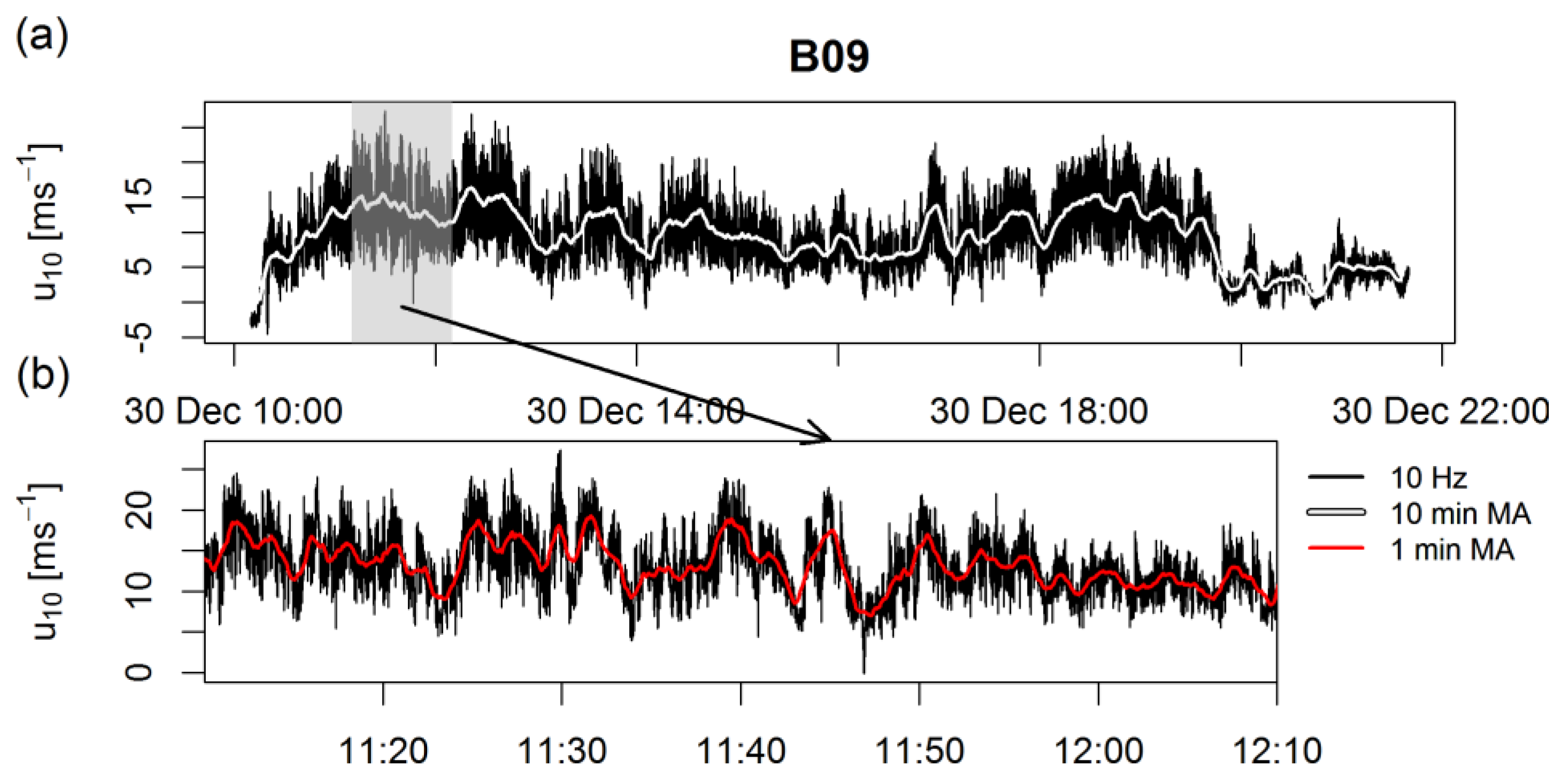
2.3. Criteria for Bora Episode Detection and Selection
2.4. Bora Turbulence Spectra
2.5. Taylor Hypothesis
2.6. Stability Parameter and Friction Velocity
2.7. Monin–Obukhov Similarity Functions
2.8. Turbulence Kinetic Energy Budget
2.9. Wind Profiles
3. Results and Discussion
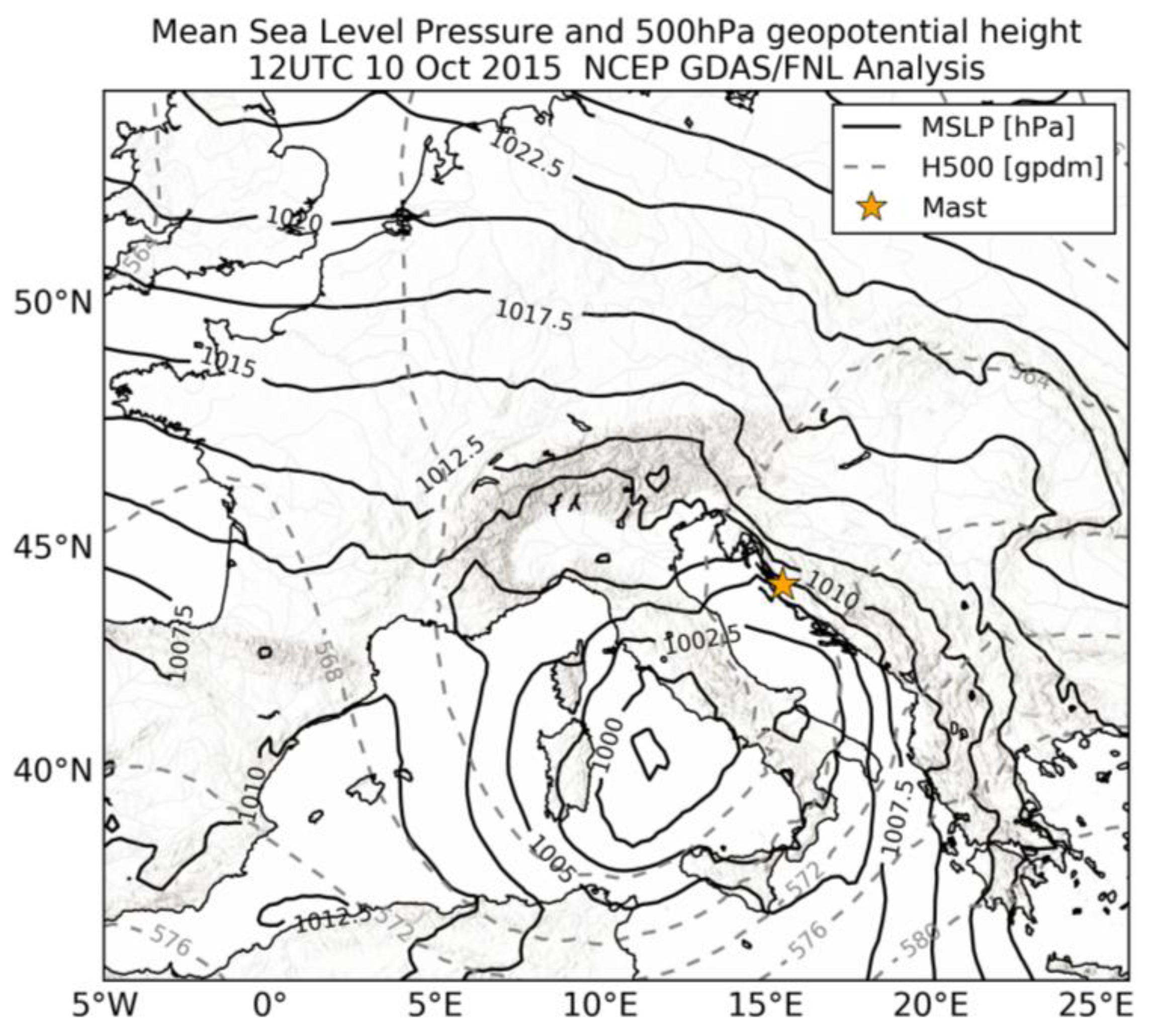
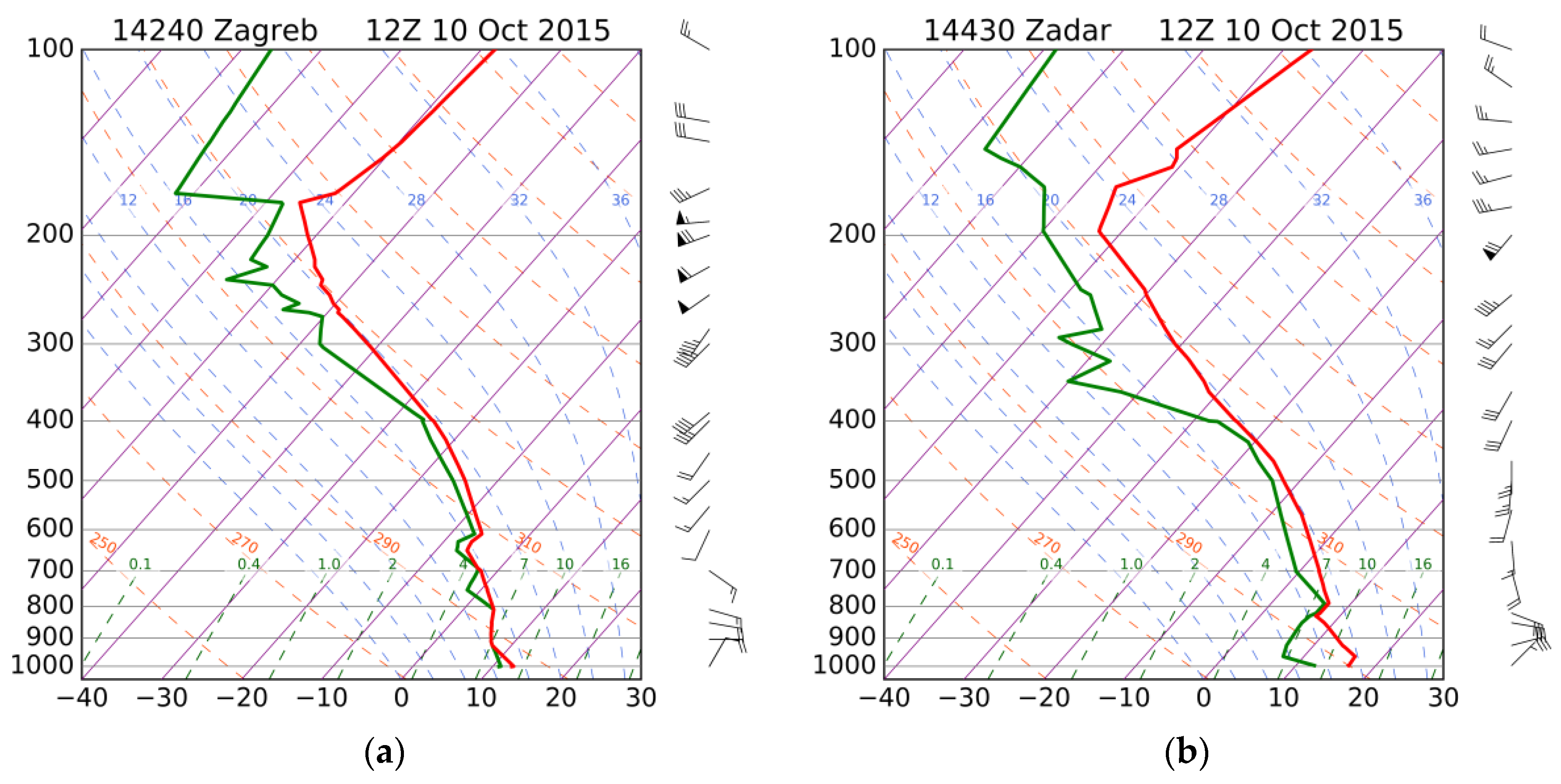
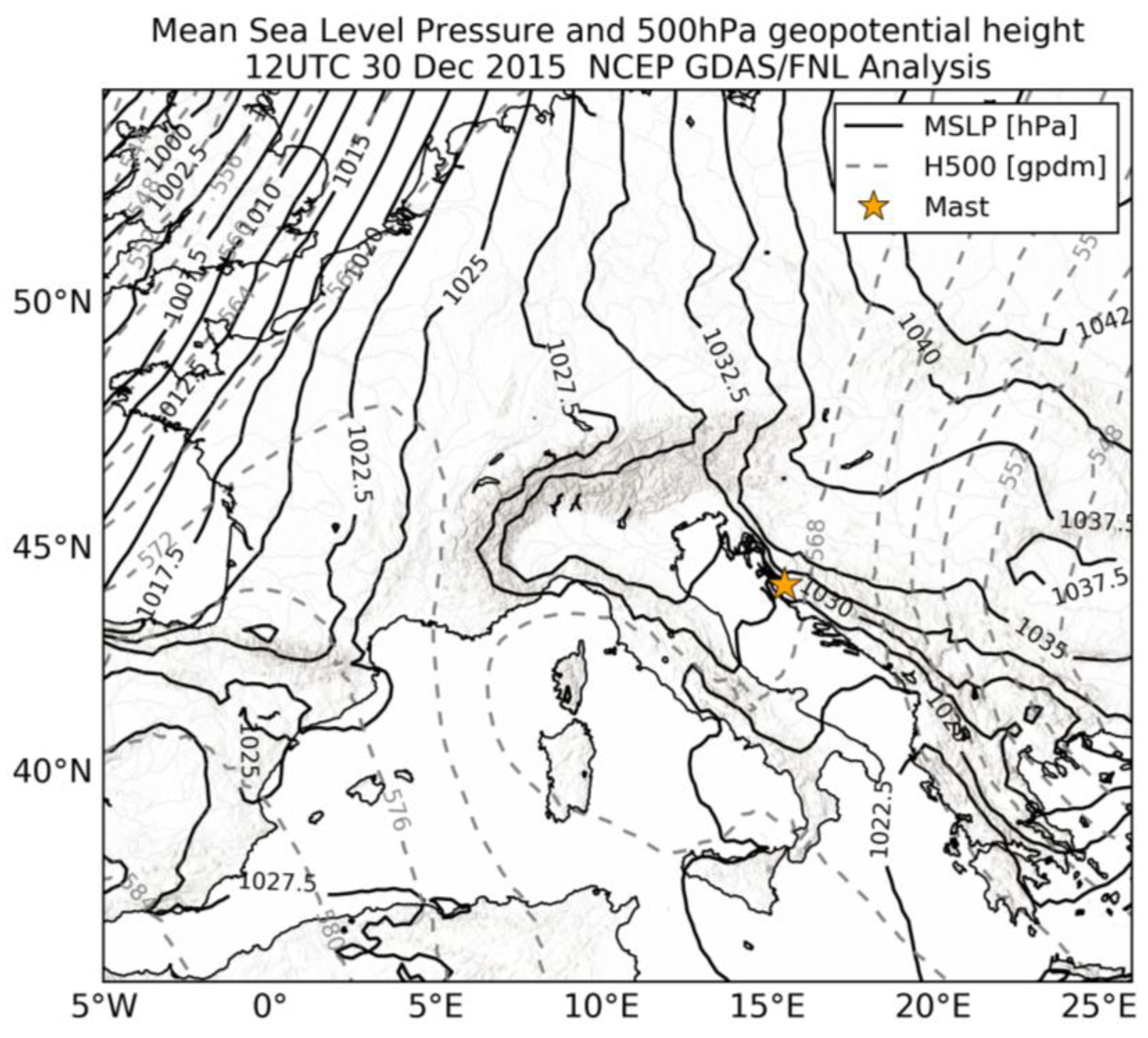
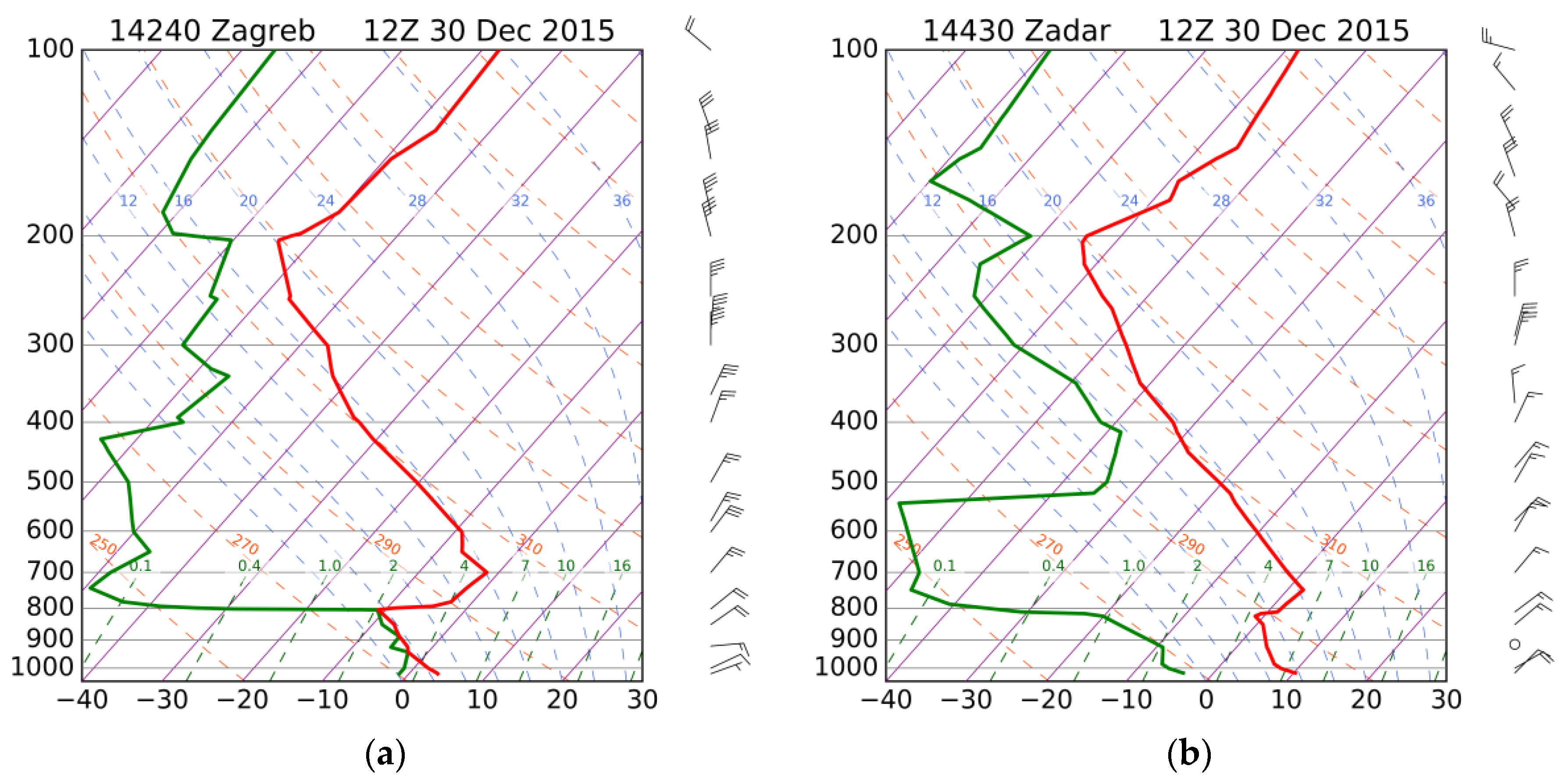
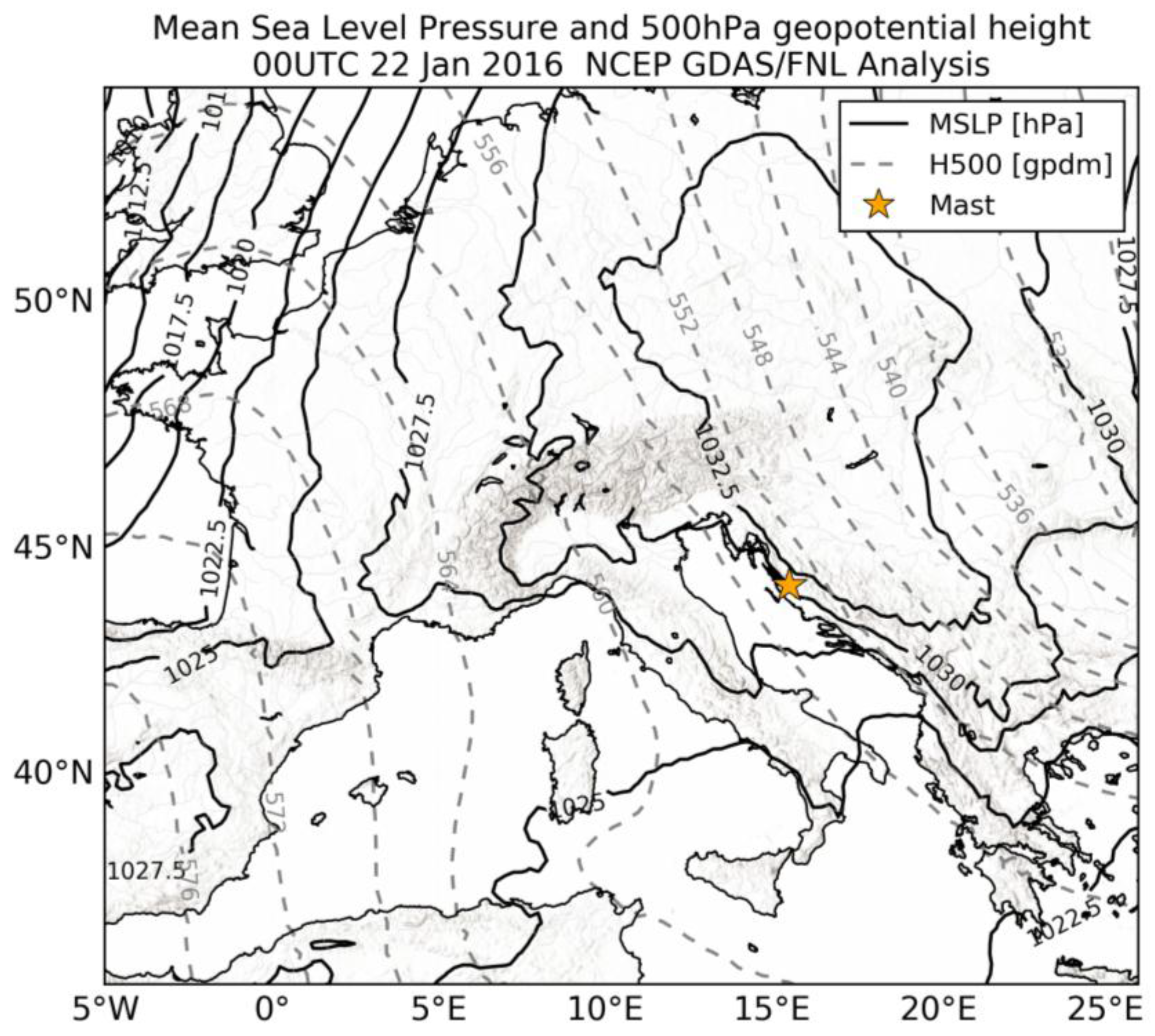
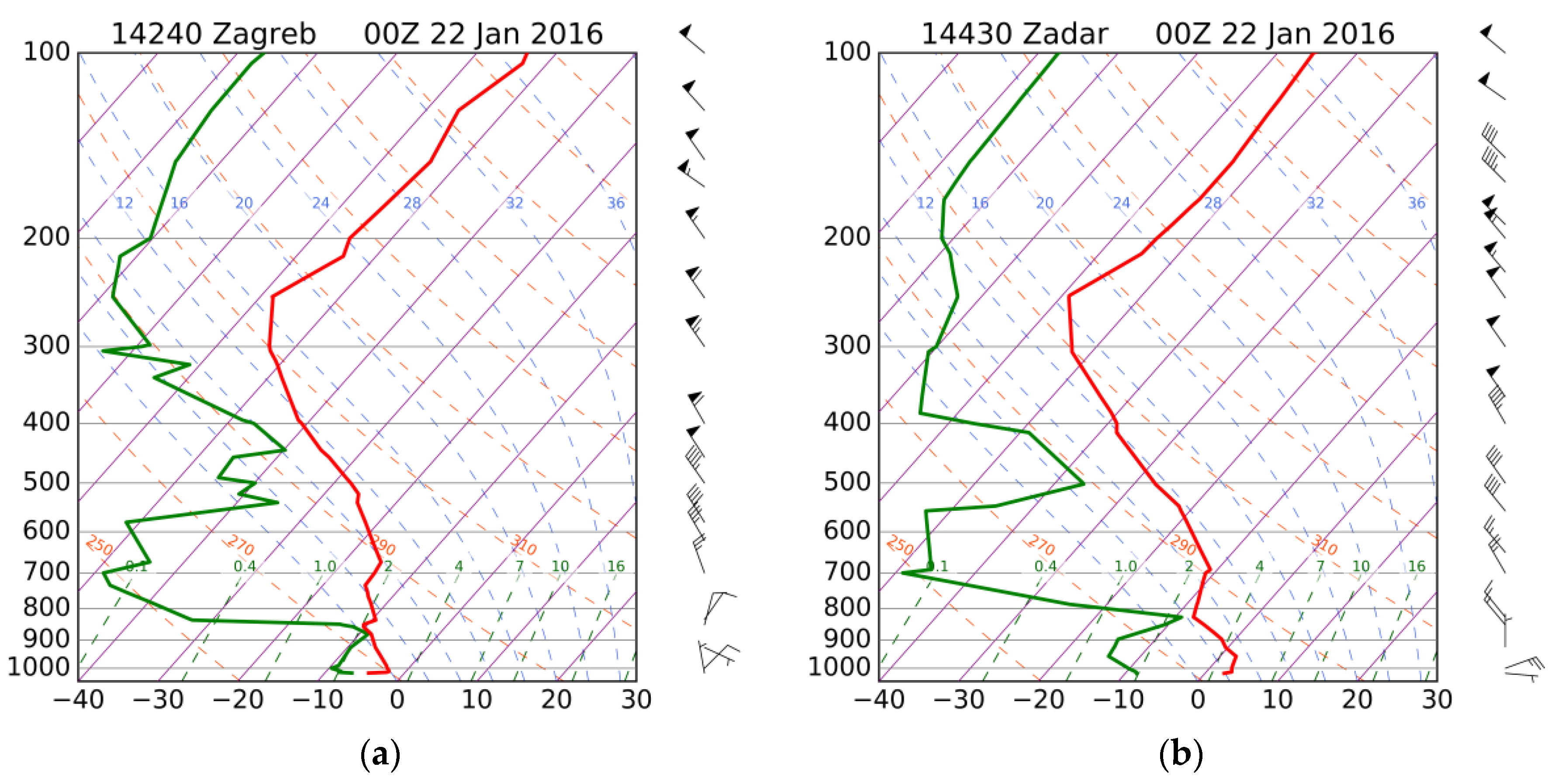
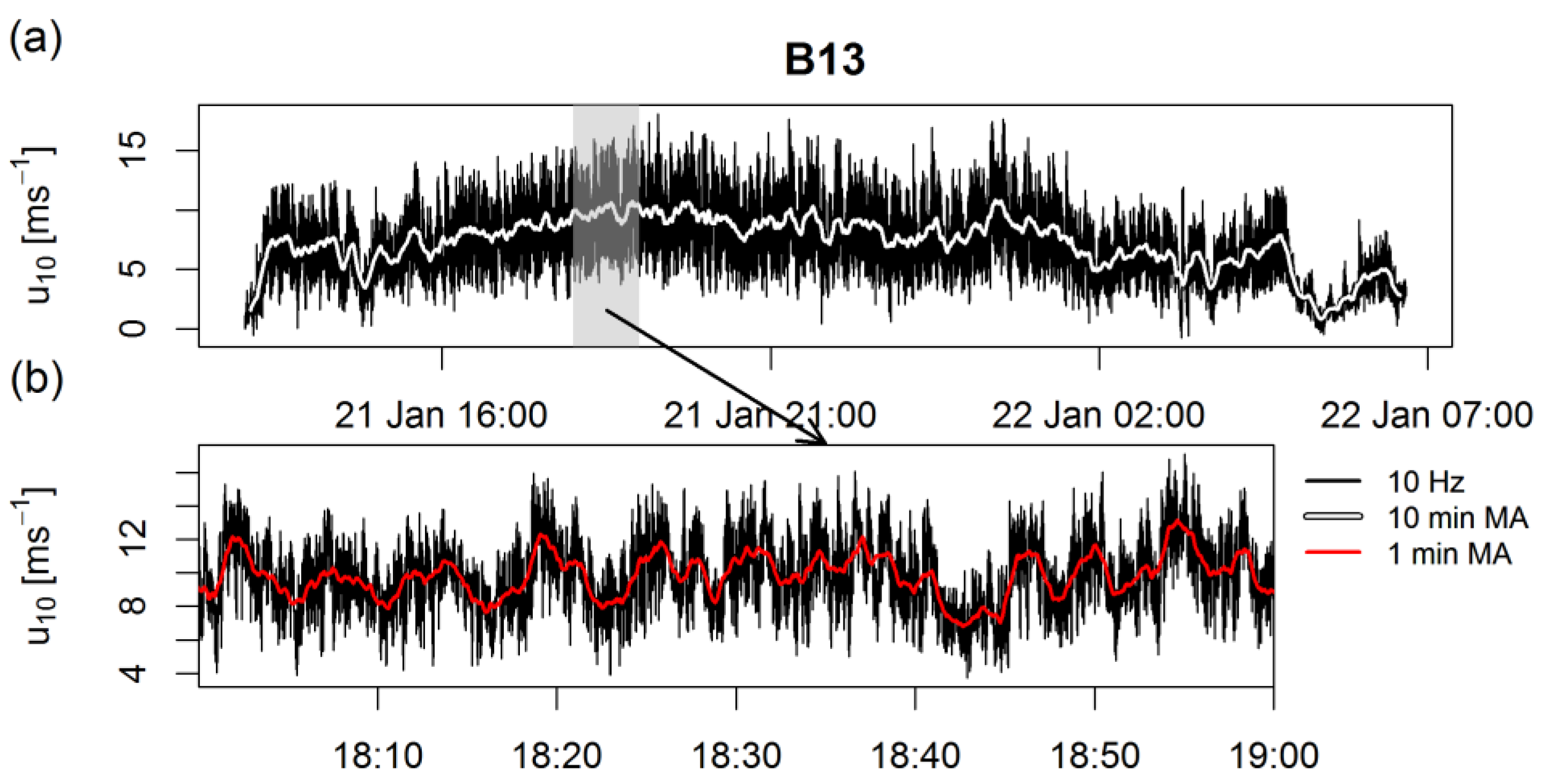
3.1. Selected Bora Episodes
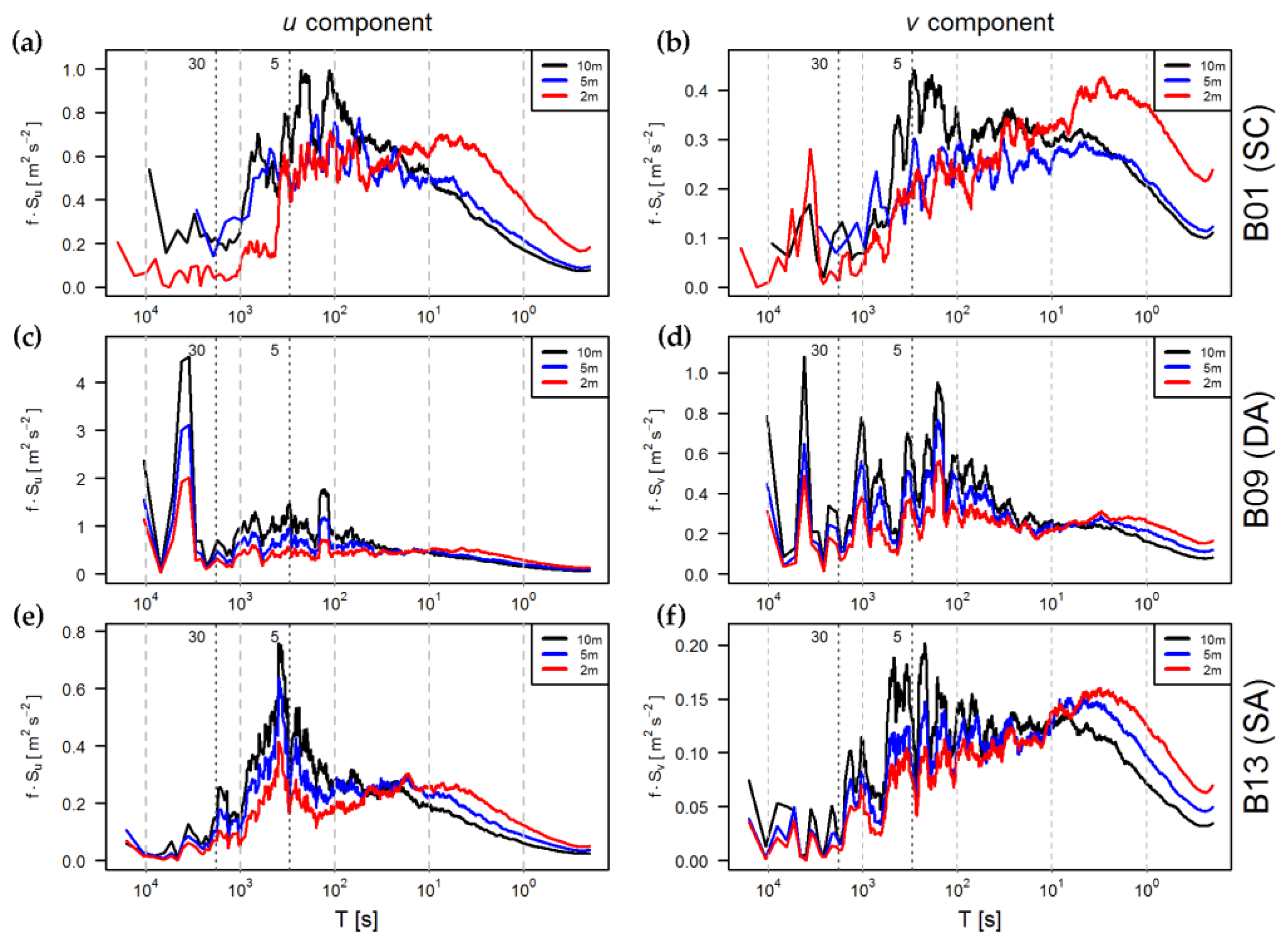
3.2. Bora Spectra
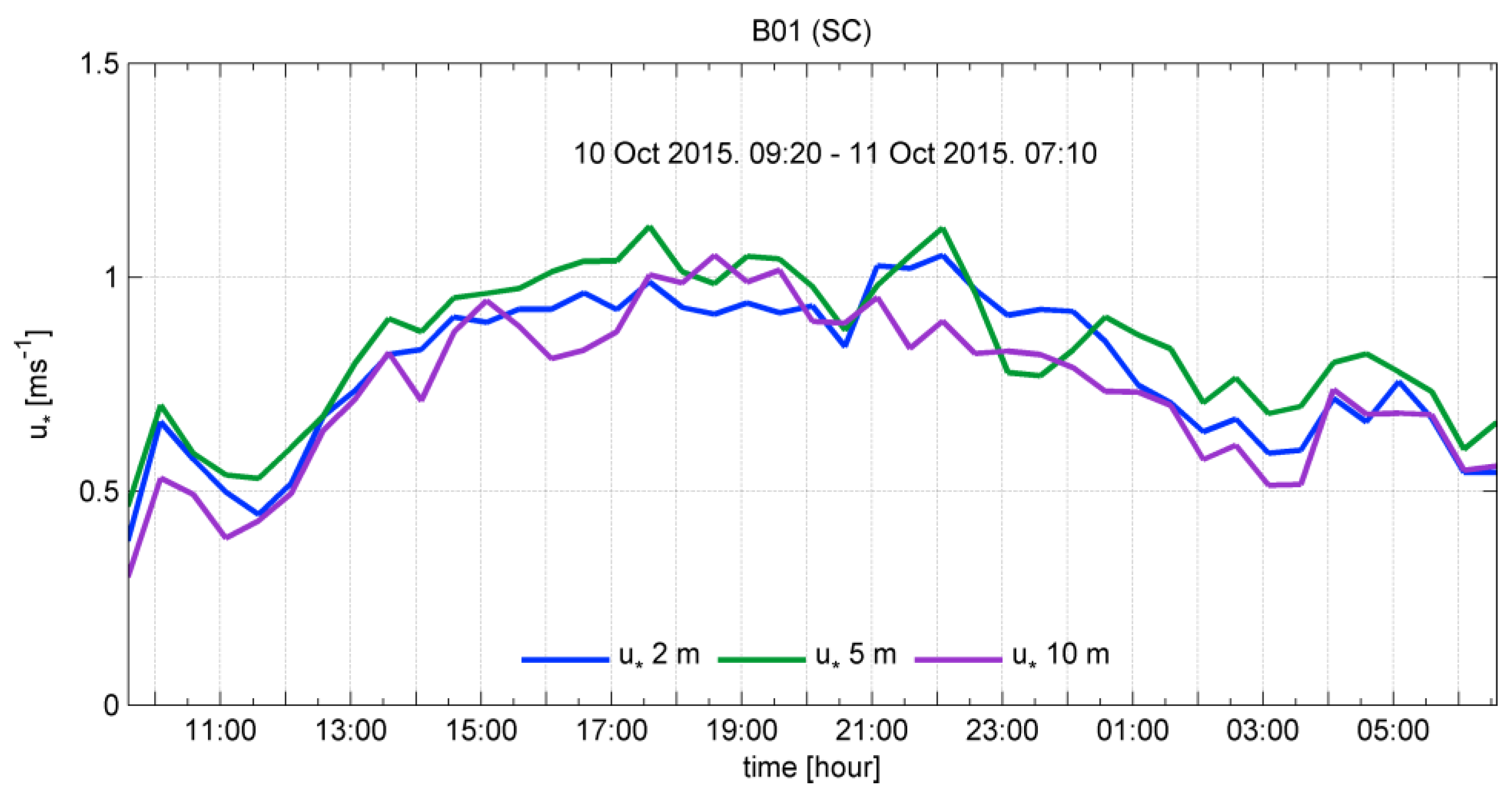
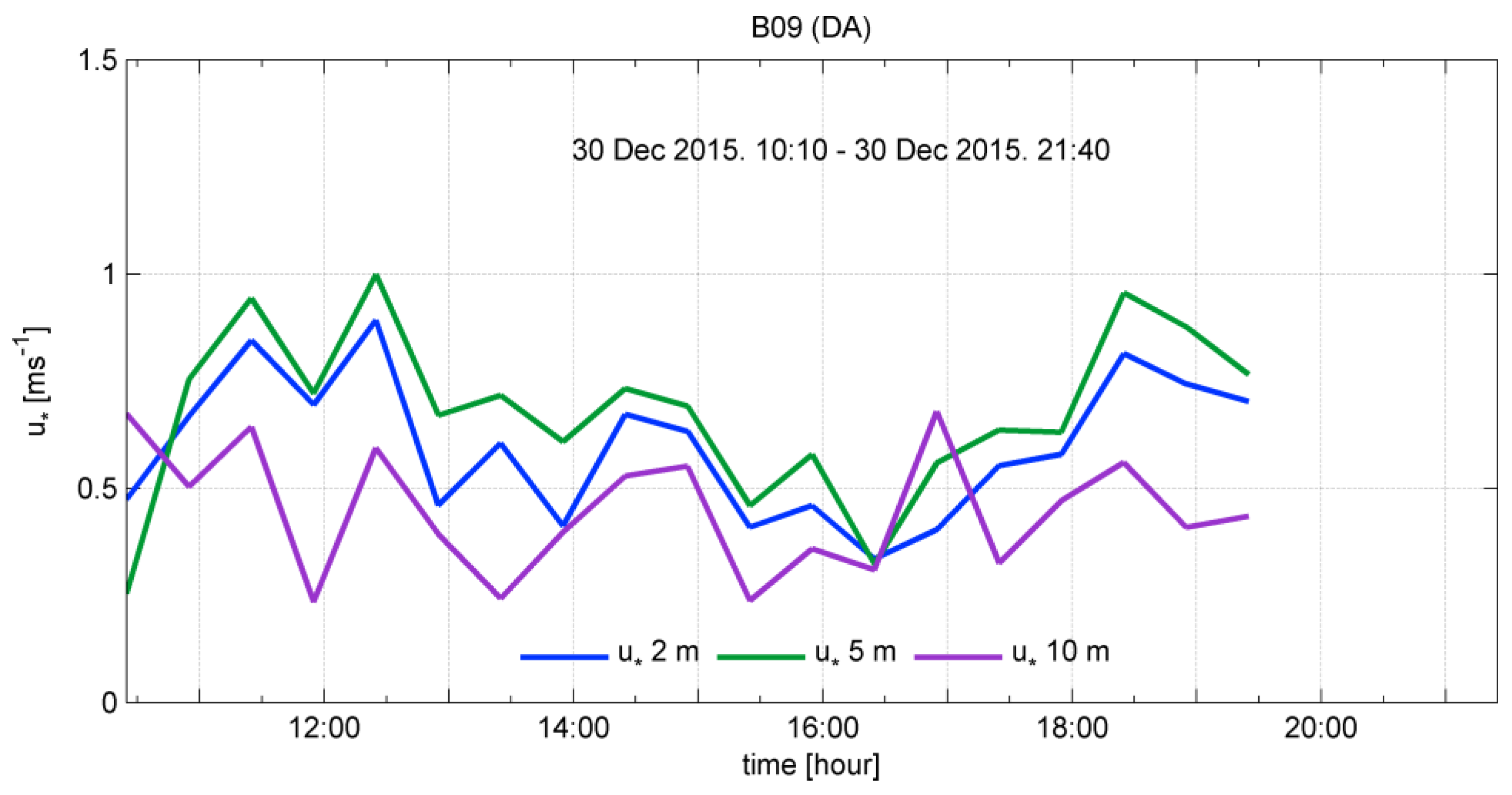
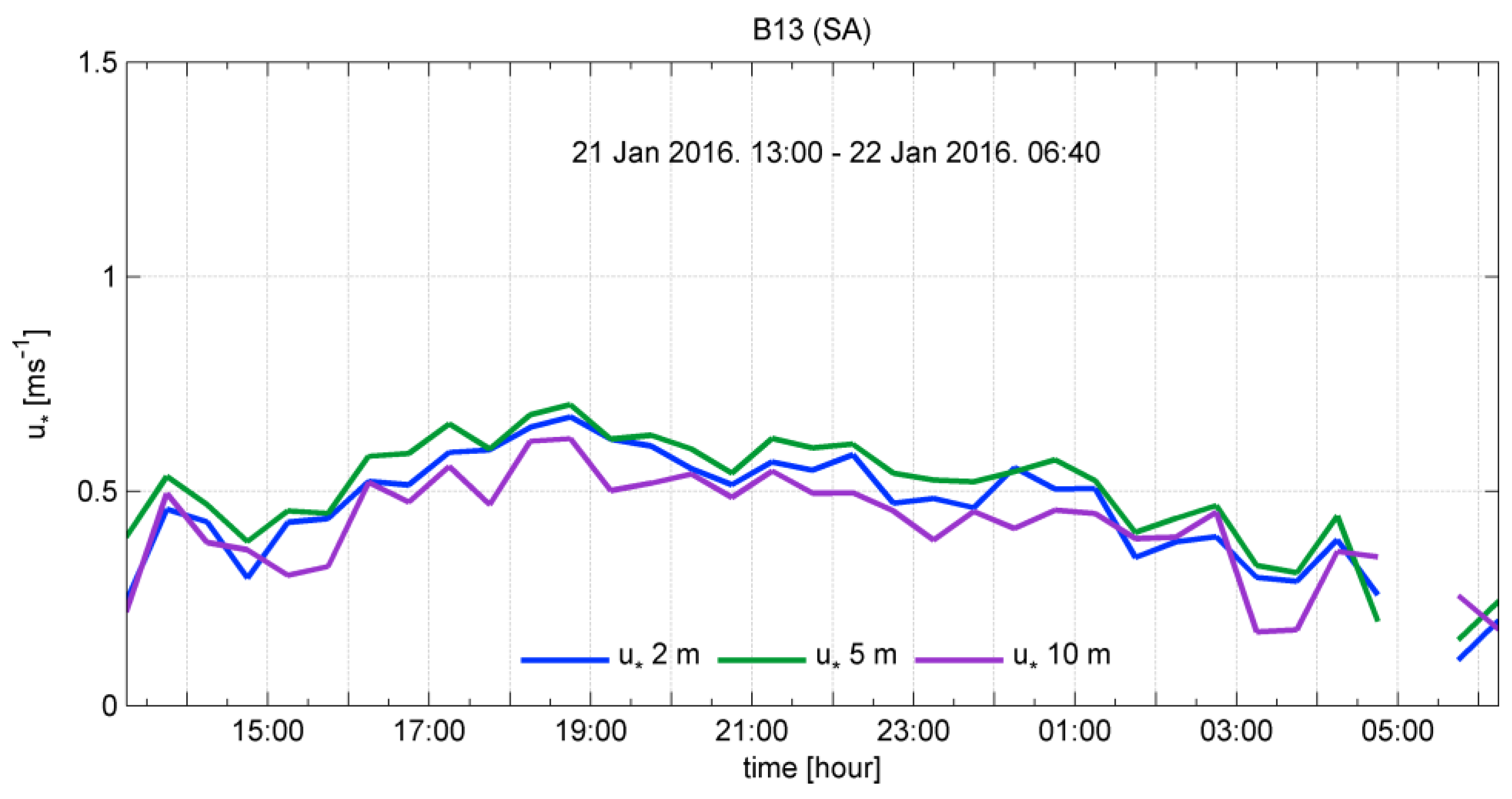
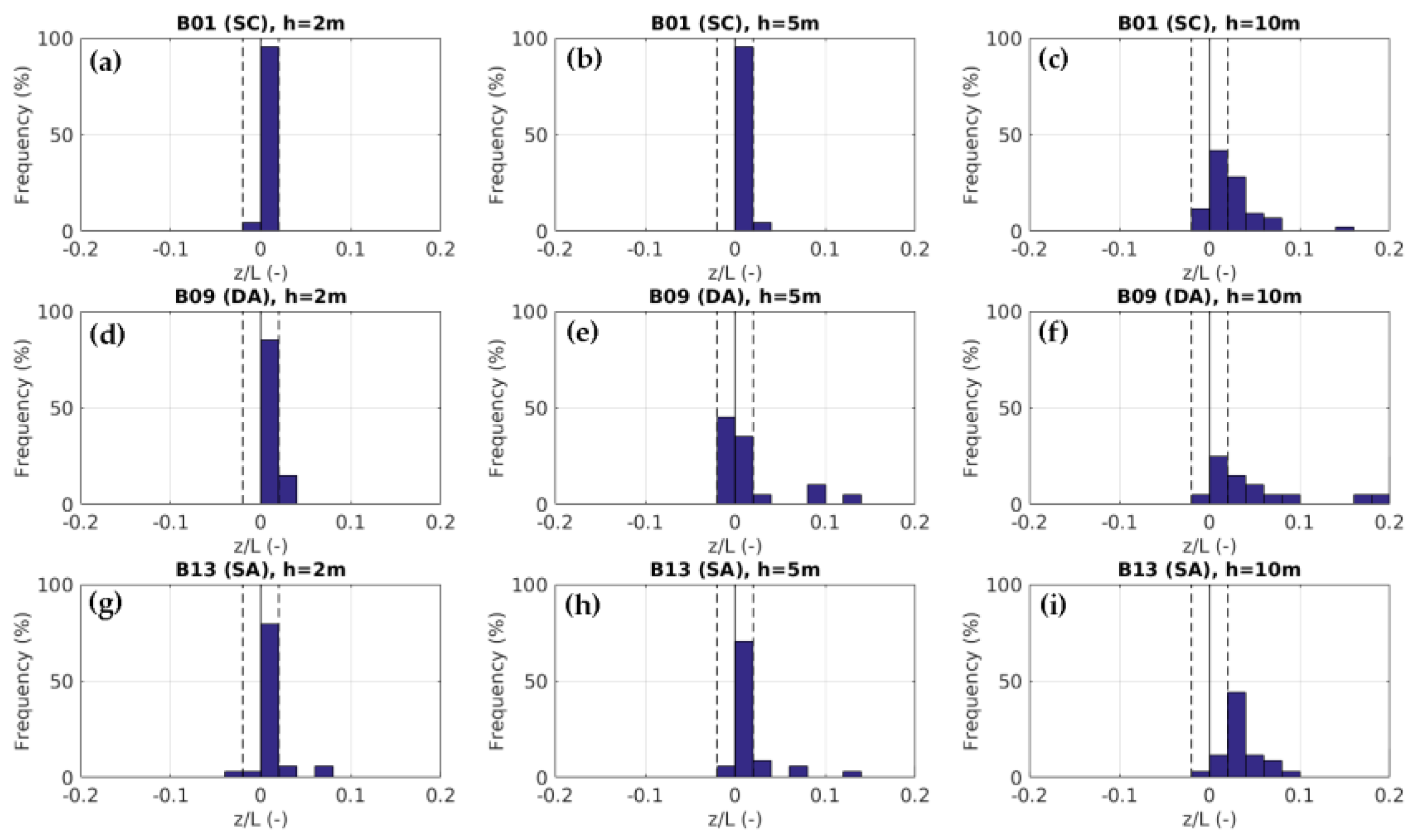
3.3. Friction Velocity and Stability Parameter
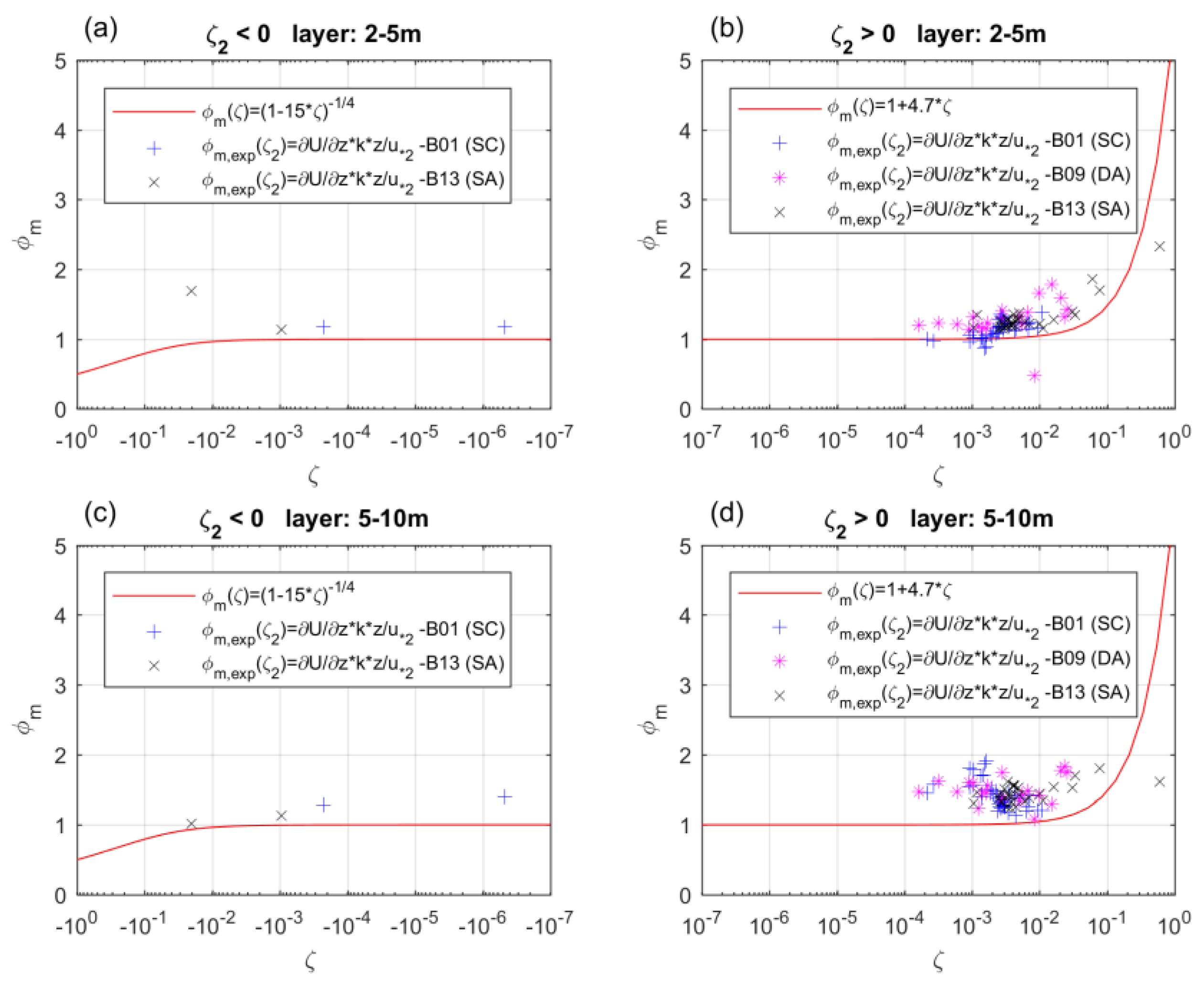
3.4. Monin–Obukhov Similarity Functions
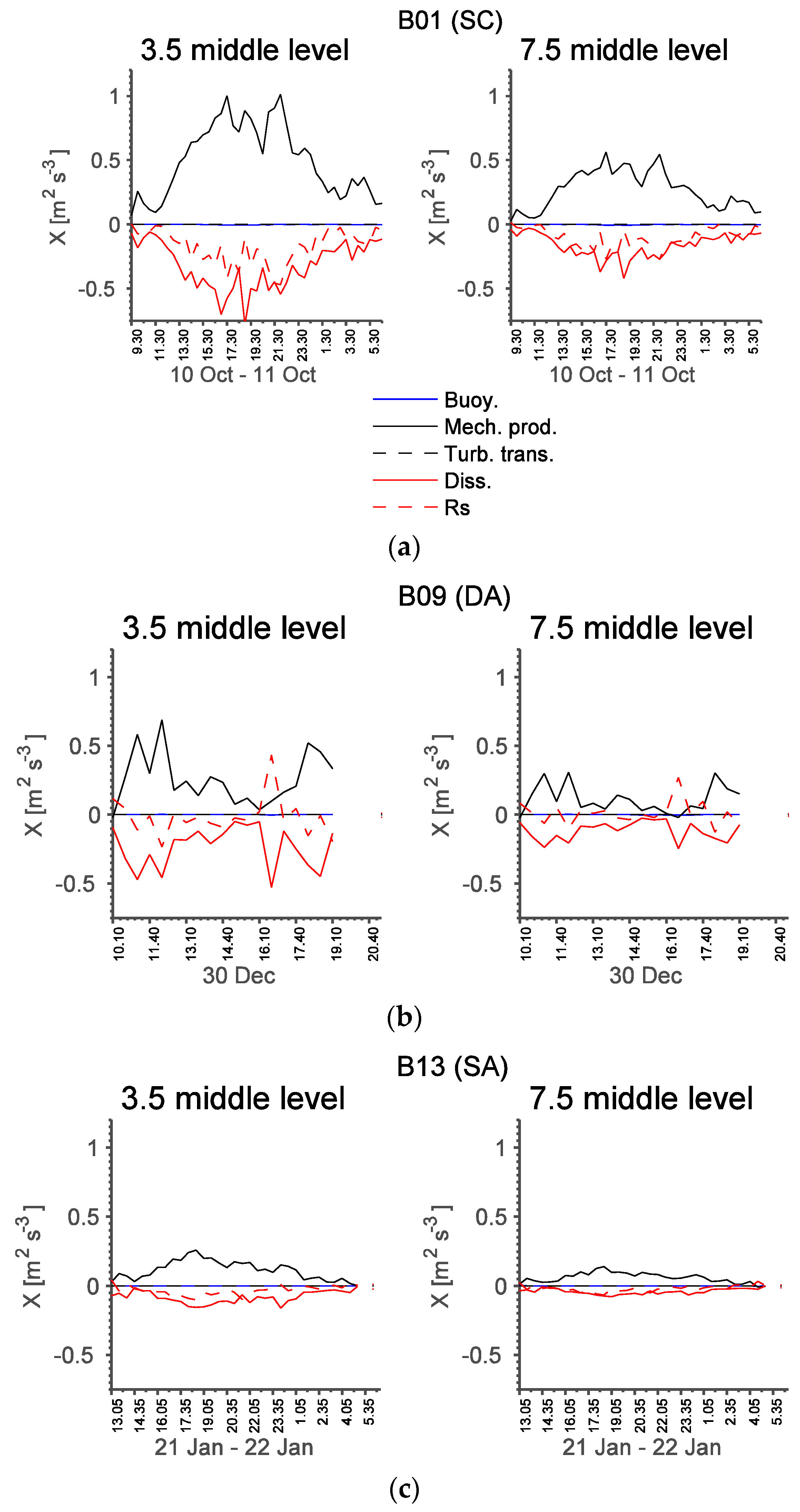
3.5. Turbulence Kinetic Energy Budget
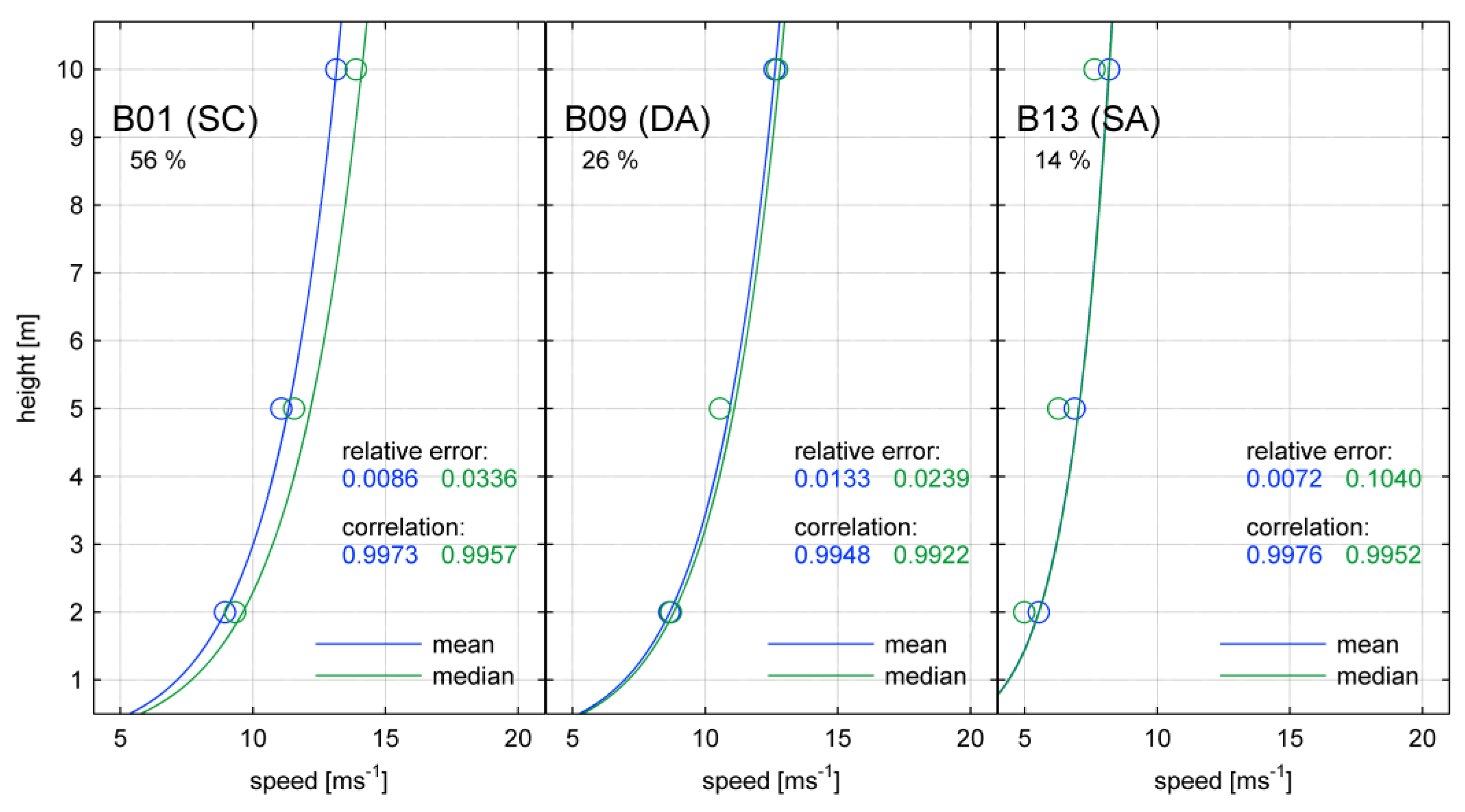
3.6. Wind Profiles
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lepri, P.; Vecenaj, Z.; Kozmar, H.; Grisogono, B. Bora wind characteristics for engineering applications. Wind Struct. 2017, 24, 579–611. [Google Scholar] [CrossRef]
- Smith, R.B. Aerial observations of the Yugoslavian bora. J. Atmos. Sci. 1987, 44, 269–297. [Google Scholar] [CrossRef]
- Defant, F. Local winds. Compendium of Meteorology; American Meteorological Society: Boston, MA, USA, 1951; pp. 655–672. [Google Scholar]
- Jurčec, V. On mesoscale characteristics of bora conditions in Yugoslavia. In Weather and Weather Maps; Birkhäuser: Basel, Switzerland, 1981; pp. 640–657. [Google Scholar]
- Kuettner, J.; O’ Neill, T. ALPEX-the GARP mountain subprogram. Bull. Am. Meteorol. Soc. 1981, 62, 793–805. [Google Scholar]
- Smith, R.B. On severe downslope winds. J. Atmos. Sci. 1985, 42, 2597–2603. [Google Scholar] [CrossRef]
- Durran, D.R. Another look at downslope windstorms. Part I: The development of analogs to supercritical flow in an infinitely deep, continuously stratified fluid. J. Atmos. Sci. 1986, 43, 2527–2543. [Google Scholar] [CrossRef]
- Bencetić Klaić, Z.; Belušić, D.; Grubišić, V.; Gabela, L.; Ćoso, L. Mesoscale airflow structure over the northern Croatian coast during MAP IOP—A major bora event. Geofizika 2003, 20, 23–61. [Google Scholar]
- Grubišíc, V. Bora-driven potential vorticity banners over the Adriatic. Q. J. R. Meteorol. Soc. 2004, 130, 2571–2603. [Google Scholar] [CrossRef]
- Gohm, A.; Mayr, G. Numerical and observational case-study of a deep Adriatic Bora. Q. J. R. Meteorol. Soc. 2005, 131, 1363–1392. [Google Scholar] [CrossRef]
- Grisogono, B.; Belušić, D. A review of recent advances in understanding the meso-and microscale properties of the severe Bora wind. Tellus A 2009, 61, 1–16. [Google Scholar] [CrossRef]
- Jurčec, V. The Adriatic frontal bora type. Croat. Meteorol. J. 1988, 23, 13–25. [Google Scholar]
- Kuzmić, M.; Grisogono, B.; Li, X.; Lehner, S. Examining deep and shallow Adriatic bora events. Q. J. R. Meteorol. Soc. 2015, 141, 3434–3438. [Google Scholar] [CrossRef]
- Lukšić, I. Tipovi strujanja zraka iznad Zagreba za vrijeme bure na Sjevernom Jadranu (Upper Level Flow Types at Zagreb During the Bora in the Northern Adriatic). In Papers from VII Climatological Conference; Federal Hydrometorological Institute: Belgrade, Serbia, 1972; pp. 111–129. [Google Scholar]
- Gohm, A.; Mayr, G.J.; Fix, A.; Giez, A. On the onset of bora and the formation of rotors and jumps near a mountain gap. Q. J. R. Meteorol. Soc. 2008, 134, 21–46. [Google Scholar] [CrossRef]
- Pullen, J.; Doyle, J.D.; Haack, T.; Dorman, C.; Signell, R.P.; Lee, C.M. Bora event variability and the role of air-sea feedback. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Poje, D. Wind persistence in Croatia. Int. J. Climatol. 1992, 12, 569–586. [Google Scholar] [CrossRef]
- Pasarić, M.; Orlić, M. Djelovanje atmosfere na Jadran: danas te u uvjetima očekivanih klimatskih promjena. Geofizika 2004, 21, 69–87. [Google Scholar]
- Belušić, A.; Prtenjak, M.T.; Güttler, I.; Ban, N.; Leutwyler, D.; Schär, C. Near-surface wind variability over the broader Adriatic region: Insights from an ensemble of regional climate models. Clim. Dyn. 2017, 1–26. [Google Scholar] [CrossRef]
- Mohorovicic, A. Interesting cloud pictures over the Bay of Buccari (with a comment from the editor J. Hann) (Interessante Wolkenbildung ber der Bucht von Buccari). Meteorol. Z 1889, 24, 56–58. [Google Scholar]
- Yoshino, M. Local Wind Bora; University of Tokyo Press: Tokyo, Japan, 1976. [Google Scholar]
- Stiperski, I.; Ivančan-Picek, B.; Grubišić, V.; Bajić, A. Complex bora flow in the lee of Southern Velebit. Q. J. R. Meteorol. Soc. 2012, 138, 1490–1506. [Google Scholar] [CrossRef]
- Glasnović, D.; Jurčec, V. Determination of upstream bora layer depth. Meteorol. Atmos. Phys. 1990, 43, 137–144. [Google Scholar] [CrossRef]
- Klemp, J.B.; Durran, D.R. Numerical modelling of Bora winds. Meteorol. Atmos. Phys. 1987, 36, 215–227. [Google Scholar] [CrossRef]
- Watanabe, K. Bora and Man: Weather Forecasts and Prognosis of Bora by the Fishermen’s Traditional Way of Observation on the Croatian Coast. In Local Wind Bora; Yoshino, M.M., Ed.; University of Tokyo Press: Tokyo, Japan, 1976; pp. 267–274. [Google Scholar]
- Petkovšek, Z. Gravity waves and bora gusts. Ann. Meteorol. 1982, 19, 108–110. [Google Scholar]
- Petkovšek, Z. Main bora gusts—A model explanation. Geofizika 1987, 4, 41–50. [Google Scholar]
- Belušić, D.; Pasarić, M.; Orlić, M. Quasi-periodic bora gusts related to the structure of the troposphere. Q. J. R. Meteorol. Soc. 2004, 130, 1103–1121. [Google Scholar] [CrossRef]
- Belušić, D.; Žagar, M.; Grisogono, B. Numerical simulation of pulsations in the bora wind. Q. J. R. Meteorol. Soc. 2007, 133, 1371–1388. [Google Scholar] [CrossRef]
- Babić, N.; Večenaj, Ž.; Kozmar, H.; Horvath, K.; De Wekker, S F.; Grisogono, B. On turbulent fluxes during strong winter bora wind events. Bound. Layer Meteorol. 2016, 158, 331–350. [Google Scholar] [CrossRef]
- Peltier, W.R.; Scinocca, J.F. The origin of severe downslope windstorm pulsations. J. Atmos. Sci. 1990, 47, 2853–2870. [Google Scholar] [CrossRef]
- Belušić, D.; Grisogono, B. Disappearance of pulsations in severe downslope windstorms. Croat. Meteorol. J. 2005, 40, 84–87. [Google Scholar]
- Večenaj, Ž.; Belušić, D.; Grisogono, B. Characteristics of the near-surface turbulence during a bora event. Annales Geophysicae 2010, 28, 155–163. [Google Scholar] [CrossRef]
- Večenaj, Ž.; Belušić, D.; Grubišić, V.; Grisogono, B. Along-coast features of bora-related turbulence. Bound. Layer Meteorol. 2012, 143, 527–545. [Google Scholar] [CrossRef]
- Lepri, P.; Kozmar, H.; Večenaj, Ž.; Grisogono, B. A summertime near-ground velocity profile of the Bora wind. Wind Struct. 2014, 19, 505–522. [Google Scholar] [CrossRef]
- Lepri, P.; Večenaj, Ž.; Kozmar, H.; Grisogono, B. Near-ground turbulence of the Bora wind in summertime. J. Wind Eng. Ind. Aerodyn. 2015, 147, 345–357. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Ivančan-Picek, B.; Grubišić, V.; Stiperski, I.; Xiao, M.; Bajić, A. “Zadar calm” during severe Bora. In Proceedings of the 29th International Conference on Alpine Meteorology, Extended Abstracts, Chambery, France, 4–8 June 2007. [Google Scholar]
- Telišman Prtenjak, M.; Belušić, D. Formation of reversed lee flow over the north-eastern Adriatic during bora. Geofizika 2009, 26, 145–155. [Google Scholar]
- Deutscher Wetterdienst (DWD) Surface Analysis Charts. Available online: http://www1.wetter3.de/Archiv/archiv_dwd.html (accessed on 28 November 2016).
- National Centers for Environmental Prediction, National Weather Service and U.S. Department of Commerce. NOAA NCEP GDAS/FNL 0.25 Degree Global Tropospheric Analyses and Forecast Grids. Available online: https://doi.org/10.5065/D65Q4T4Z (accessed on 10 March 2017).
- University of Wyoming Department of Atmospheric Science Sounding Data from University of Wyoming Database. Available online: http://weather.uwyo.edu/upperair/sounding.html (accessed on 28 November 2016).
- Reynolds, O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Proc. R. Soc. Lond. 1894, 56, 40–45. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology, 1st ed.; Stull, R.B., Ed.; Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 1988; Volume 13, ISBN 978-90-277-2768-8. [Google Scholar]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Albertson, J.D.; Parlange, M.B.; Kiely, G.; Eichinger, W.E. The average dissipation rate of turbulent kinetic energy in the neutral and unstable atmospheric surface layer. J. Geophys. Res. Atmos. 1997, 102, 13423–13432. [Google Scholar] [CrossRef]
- Fortuniak, K.; Pawlak, W.; Siedlecki, M. Integral turbulence statistics over a central European city centre. Bound. Layer Meteorol. 2013, 146, 257–276. [Google Scholar] [CrossRef]
- Večenaj, Ž.; De Wekker, S.F.; Grubišić, V. Near-surface characteristics of the turbulence structure during a mountain-wave event. J. Appl. Meteorol. Climatol. 2011, 50, 1088–1106. [Google Scholar] [CrossRef]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Dmowska, R., Holton, J.R., Eds.; International Geophysics Series; Elsevier Academic Press: Burlington, MA, USA, 2004; ISBN 978-0-12-354015-7. [Google Scholar]
- Babić, K.; Bencetić Klaić, Z.; Večenaj, Ž. Determining a turbulence averaging time scale by Fourier analysis for the nocturnal boundary layer. Geofizika 2012, 29, 35–51. [Google Scholar]
- Belušić, D.; Pasarić, M.; Pasarić, Z.; Orlić, M.; Grisogono, B. A note on local and non-local properties of turbulence in the bora flow. Meteorol. Z. 2006, 15, 301–306. [Google Scholar] [CrossRef]
- Tampieri, F. Turbulence and Dispersion in the Planetary Boundary Layer; Physics of Earth and Space Environments; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-43602-9. [Google Scholar]
- Večenaj, Ž.; De Wekker, S.F. Determination of non-stationarity in the surface layer during the T-REX experiment. Q. J. R. Meteorol. Soc. 2015, 141, 1560–1571. [Google Scholar] [CrossRef]

| Bora Type | Abbreviation |
|---|---|
| shallow cyclonic | SC |
| shallow anticyclonic | SA |
| deep cyclonic | DC |
| deep anticyclonic | DA |
| frontal | F |
| Episode | Start | End | Duration | Avg U | Max U | Max G | Type |
|---|---|---|---|---|---|---|---|
| B01 | 10 October 2015. 09:20 | 11 October 2015. 07:10 | 0 days 21:50 | 12.16 | 18.21 | 27.94 | SC |
| B02 | 21 October 2015. 16:00 | 23 October 2015. 01:40 | 1 day 09:40 | 13.35 | 20.12 | 35.68 | SC/DC |
| B03 | 23 October 2015. 11:30 | 24 October 2015. 00:30 | 0 days 13:00 | 8.08 | 13.53 | 24.18 | DC/DA |
| B04 | 30 October 2015. 03:30 | 1 November 2015. 12:30 | 2 days 09:00 | 7.16 | 12.88 | 21.02 | SA |
| B05 | 21 November 2015. 15:50 | 22 November 2015. 00:40 | 0 days 08:50 | 10.31 | 16.77 | 26.34 | F/SC |
| B06 | 22 November 2015. 08:20 | 22 November 2015. 20:10 | 0 days 11:50 | 7.44 | 12.26 | 18.60 | SC |
| B07 | 26 November 2015. 01:30 | 28 November 2015. 04:00 | 2 days 02:30 | 17.69 | 31.05 | 45.47 | SC/DC |
| B08 | 10 Decemebr 2015. 01:40 | 10 Decemebr 2015. 12:00 | 0 days 10:20 | 16.57 | 25.66 | 36.10 | SA/DA |
| B09 | 30 Decemebr 2015. 10:10 | 30 Decemebr 2015. 21:40 | 0 days 11:30 | 9.58 | 16.46 | 26.90 | DA |
| B10 | 3 January 2016. 12:40 | 3 January 2016. 19:00 | 0 days 06:20 | 5.92 | 9.62 | 16.35 | SC/F |
| B11 | 15 January 2016. 23:30 | 17 January 2016. 04:10 | 1 day 04:40 | 18.02 | 28.40 | 40.18 | SC/DC |
| B12 | 17 January 2016. 14:50 | 18 January 2016. 07:30 | 0 days 16:40 | 20.82 | 28.78 | 39.68 | SC/SA |
| B13 | 21 January 2016. 13:00 | 22 January 2016. 06:40 | 0 days 17:40 | 7.25 | 10.91 | 17.42 | SA |
| B14 | 3 February 2016. 22:40 | 4 February 2016. 16:50 | 0 days 18:10 | 19.17 | 25.83 | 37.27 | F/SC |
| Episode | Height (m) | Mean | Med | Max | Min | SD |
|---|---|---|---|---|---|---|
| B01 (SC) | 2 | 0.782 | 0.830 | 1.051 | 0.384 | 0.177 |
| 5 | 0.838 | 0.832 | 1.118 | 0.465 | 0.171 | |
| 10 | 0.739 | 0.737 | 1.051 | 0.299 | 0.186 | |
| B09 (DA) | 2 | 0.580 | 0.592 | 0.892 | 0.247 | 0.177 |
| 5 | 0.656 | 0.681 | 0.999 | 0.246 | 0.214 | |
| 10 | 0.435 | 0.421 | 0.679 | 0.171 | 0.154 | |
| B13 (SA) | 2 | 0.454 | 0.477 | 0.673 | 0.106 | 0.138 |
| 5 | 0.497 | 0.530 | 0.701 | 0.153 | 0.135 | |
| 10 | 0.419 | 0.451 | 0.622 | 0.171 | 0.120 |
| Episode | Height (m) | Mean | Med | Max | Min | SD |
|---|---|---|---|---|---|---|
| B01 (SC) | 2 | 0.003 | 0.003 | 0.011 | 0.000 | 0.002 |
| 5 | 0.008 | 0.008 | 0.024 | 0.000 | 0.005 | |
| 10 | 0.025 | 0.020 | 0.147 | −0.010 | 0.028 | |
| B09 (DA) | 2 | 0.007 | 0.003 | 0.026 | 0.000 | 0.008 |
| 5 | 0.018 | 0.001 | 0.126 | −0.003 | 0.038 | |
| 10 | 0.198 | 0.045 | 1.160 | −0.004 | 0.307 | |
| B13 (SA) | 2 | 0.027 | 0.004 | 0.617 | −0.021 | 0.106 |
| 5 | 0.039 | 0.009 | 0.401 | −0.017 | 0.093 | |
| 10 | 0.099 | 0.028 | 0.815 | −0.301 | 0.223 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šoljan, V.; Belušić, A.; Šarović, K.; Nimac, I.; Brzaj, S.; Suhin, J.; Belavić, M.; Večenaj, Ž.; Grisogono, B. Micro-Scale Properties of Different Bora Types. Atmosphere 2018, 9, 116. https://doi.org/10.3390/atmos9040116
Šoljan V, Belušić A, Šarović K, Nimac I, Brzaj S, Suhin J, Belavić M, Večenaj Ž, Grisogono B. Micro-Scale Properties of Different Bora Types. Atmosphere. 2018; 9(4):116. https://doi.org/10.3390/atmos9040116
Chicago/Turabian StyleŠoljan, Vinko, Andreina Belušić, Kristina Šarović, Irena Nimac, Stjepana Brzaj, Jurica Suhin, Martin Belavić, Željko Večenaj, and Branko Grisogono. 2018. "Micro-Scale Properties of Different Bora Types" Atmosphere 9, no. 4: 116. https://doi.org/10.3390/atmos9040116
APA StyleŠoljan, V., Belušić, A., Šarović, K., Nimac, I., Brzaj, S., Suhin, J., Belavić, M., Večenaj, Ž., & Grisogono, B. (2018). Micro-Scale Properties of Different Bora Types. Atmosphere, 9(4), 116. https://doi.org/10.3390/atmos9040116





