Abstract
The exchange of heat, momentum, and mass in the atmosphere over mountainous terrain is controlled by synoptic-scale dynamics, thermally driven mesoscale circulations, and turbulence. This article reviews the key challenges relevant to the understanding of exchange processes in the mountain boundary layer and outlines possible research priorities for the future. The review describes the limitations of the experimental study of turbulent exchange over complex terrain, the impact of slope and valley breezes on the structure of the convective boundary layer, and the role of intermittent mixing and wave–turbulence interaction in the stable boundary layer. The interplay between exchange processes at different spatial scales is discussed in depth, emphasizing the role of elevated and ground-based stable layers in controlling multi-scale interactions in the atmosphere over and near mountains. Implications of the current understanding of exchange processes over mountains towards the improvement of numerical weather prediction and climate models are discussed, considering in particular the representation of surface boundary conditions, the parameterization of sub-grid-scale exchange, and the development of stochastic perturbation schemes.
1. Introduction
The study of earth–atmosphere exchange processes plays a prominent role in meteorology and in many related disciplines, e.g., climate science, hydrology, cryospheric science, and agricultural science. Exchange is the transfer of fluid properties through a surface, and it may occur either at the boundary of a fluid (e.g., earth–atmosphere exchange) or across an imaginary surface within the fluid (e.g., between the atmospheric boundary layer and the free atmosphere). Transport is a synonym of exchange, while flux denotes the rate of exchange of a quantity per unit area.
Exchange processes at the land surface and within the atmospheric boundary layer (ABL) are represented in numerical weather prediction (NWP) and climate simulation models by empirically tuned and inherently uncertain parameterization schemes [1,2]. The uncertainties of these parameterizations limit the accuracy of weather and climate forecasts, especially for near-surface atmospheric parameters [3,4,5,6].
The parameterization of earth–atmosphere exchange emphasizes the role of small-scale turbulent processes and uses methods (e.g., Reynolds averaging and decomposition) and concepts (e.g., scaling based on dimensional analysis) from boundary-layer meteorology [7]. While this approach may be appropriate over flat and homogeneous terrain, it proves overly simplistic when applied to exchange processes over mountainous terrain [8,9].
In fact, airflow over orography generates a broad range of phenomena, which encompass all scales of atmospheric motion. Mountains impact the atmospheric flow by modifying synoptic-scale advection processes and generating planetary waves [10], producing mesoscale organized motions [11,12,13,14] and altering micro-scale turbulent mixing [15,16]. The spatial scales of the orographic impact are dictated by landforms, ranging from O (10 m) for an isolated slope to O (10 m) for a mountain range. The relevant temporal scales range from seconds (for turbulence bursts in stably stratified flows) to tens of minutes (for the turnover time of a large turbulent convective eddy) to a few days (for frontal passages over major mountain ranges). Several mountain weather phenomena, like breeze systems, have a pronounced daily periodicity [17,18]. A further layer of complexity results from the fact that, besides orography, other land properties feature small-scale variability in the vicinity of mountains, e.g., land cover, vegetation, soil moisture [19] and the presence of water bodies [20,21].
In the last few decades, the cooperative deployment of ground-based and airborne sensors during international field campaigns (ALPEX [22] in 1981–1982, PYREX [23] in 1990, MAP [24] in 1999, and the HyMeX SOP1 [25] in 2012) provided fine-scale measurements of the weather conditions around large mountain barriers (Alps, Pyrenees) during selected intensive observation periods. While these research programmes addressed a broad range of scientific questions, a number of other campaigns targeted specific phenomena, generally in mountain areas with relatively limited geographical extent (ASCOT [26], BLLAST [27], COLPEX [28], COPS [29], CUPIDO [30], DOMEX [31], MATERHORN [32], METCRAX [33], METCRAX II [34], PAP [35], PCAPS [36], Pic 2005 [37], TRACT [38], T-REX [39], VERTIKATOR [40], VOTALP [41], and VTMX [42]). Although they did not focus primarily on exchange in the ABL over mountains, all of these experimental efforts indirectly led to significant progress in the understanding of the relevant processes. A summary of the insights emerging from these observations and from the related theoretical and numerical studies can be found in a few monographs and review articles [15,43,44,45]. More recently, results from field campaigns and long-term observational programmes, focusing specifically on exchange processes over heterogeneous terrain, have appeared in the literature (i-Box [46], HVAMS [47]). Building on this bulk of knowledge, we synthesize the current understanding of exchange processes in the atmosphere over mountainous terrain and propose some possibilities for future research.
Prospects for progress in understanding exchange processes over mountains rely on three elements. First, dense measurement networks that exploit remote sensing platforms and targeted observations are needed to map the state of the atmosphere near mountains in three dimensions [48]. Second, it is necessary to make use of high-resolution NWP models, using discretization methods with sufficient accuracy and stability over steep terrain [49], appropriate sub-grid-scale (SGS) process parameterizations, and initial and boundary conditions that represent the multi-scale variability of the atmosphere over and near mountains [50]. Third, it is essential to achieve a better conceptual understanding of the processes at play between the synoptic- and micro-scale ends of the spectrum of atmospheric motions, including their cross-scale interactions. The present contribution focuses primarily on the latter aspect, in particular on thermally driven dry processes. Dynamically driven processes and moist convective processes [51] are covered elsewhere in this journal issue.
2. Understanding the Atmospheric Boundary Layer Over Mountains
2.1. General Considerations
The daily cycle of the surface radiation and energy balance leads to alternating phases of heating and cooling in the lowest atmospheric layers. Where the terrain is flat and homogeneous, stratification and buoyancy effects enhance turbulence during the day and suppress it at night. Dimensional analysis permits describing the impact of the buoyant production/loss of turbulence on the vertical profiles of atmospheric properties as a function of a limited set of scaling variables [7]. These scaling variables are combined with other quantities (e.g., vertical gradients) into non-dimensional groups which, in the ideal case, are related to each other by universally valid scaling laws that can be determined empirically. The generally accepted framework for the formulation of scaling laws in the lowest part of the ABL, i.e., the surface layer (SL), is the Monin–Obukhov similarity theory (MOST). The key scaling parameter in MOST is the Obukhov length, which is related to the ratio between mechanical production and buoyant production or loss of turbulence in the steady-state and horizontally uniform SL [7,52,53,54].
Where landforms or land cover are spatially heterogeneous, the daily cycle of the ABL is not only affected by turbulence enhancement and suppression but also by baroclinicity due to differential heating or cooling, which leads to organized air motions, such as breezes. In the vicinity of mountains, breeze systems respond to thermal contrasts at the scales of an individual slope, of a valley, or of a whole mountain range [17,18]. These thermally driven wind systems typically have high Rossby number and therefore are approximately aligned to the mesoscale or microscale horizontal pressure gradients imposed by differential heating [11]. Under weak synoptic flow, surface pressure gradients depend quasi-hydrostatically on the temperature perturbations in the overlying atmosphere. Consequently, thermally driven circulations typically have their maximum intensity near the ground, where pressure gradients are strongest. These flows, in particular slope and valley winds in fair-weather conditions, are prominent features of the atmosphere in mountainous regions and, together with turbulent mixing, they control exchange processes.
Another difference between the ABL over flat and homogeneous terrain and the ABL over mountains is that, as clarified in the following sections, strong horizontal gradients are relatively common in the latter case, for instance in connection with nocturnal valley-exit jets, diurnal flow along curved valleys, or mountain venting above mountain tops. Consequently, it may be inappropriate to assume that the vertical exchange is much more efficient than the horizontal one over mountainous terrain.
The specific features of the ABL over mountainous areas are described in greater detail in the following sections, which summarize the current status of knowledge and outline possibilities for future research, beginning with micrometeorological aspects (Section 2.2) and proceeding with thermally driven circulations (Section 2.3) and the dynamics of the convective (Section 2.4) and stable (Section 2.5) boundary layers. A short summary of the ABL processes in which multi-scale interactions are most relevant is also provided (Section 2.6).
2.2. Micrometeorology and Scaling in the Layer Near the Surface
2.2.1. The Surface Energy Balance in Complex Terrain
The ABL is commonly defined as “that part of the troposphere that is directly influenced by the presence of the earth’s surface, and responds to surface forcings with a timescale of about an hour or less” [7]. The most important driver of the temporal and spatial variability of the ABL is the surface energy balance (SEB). Ideally, the terms of the SEB include net radiation, sensible and latent heat fluxes in the atmosphere, and ground heat flux (Figure 1a). Two of these terms (the sensible and latent heat fluxes) are normally evaluated from atmospheric measurements at some height above the ground using the eddy-covariance method or, more rarely, profile methods based on flux-gradient similarity [55]. For this reason, the experimental characterization of the SEB actually refers to a three-dimensional volume (i.e., to an atmospheric layer near the surface and not to the surface itself; Figure 1b). Therefore, additional terms are included in the SEB to represent energy storage in the control volume [56].
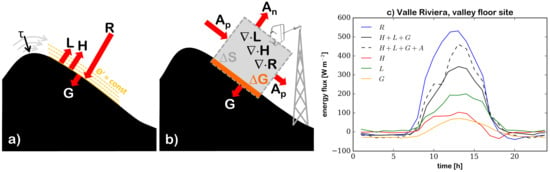
Figure 1.
The surface energy balance in complex terrain (adapted from [56,57,58]). (a) The components of the budget are R (net radiation), H (sensible heat flux), L (latent heat flux), and G (ground heat flux). In the ideal case, the energy balance refers to the interface between the atmosphere and the ground. Because an ideal surface has no mass and cannot store energy, the balance is closed. Since perturbation isentropes are generally parallel to the ground, the most appropriate reference frame for eddy-covariance measurements has one axis normal to the ground [58]. Flux components along the other axes are not negliglible in general. The same considerations apply to the Reynolds stress (). (b) In practice, the experimental characterization of the energy balance refers to a sampling volume. Energy conservation implies that . A represents the advective flux, while and represent storage in the atmosphere and in the ground. Imperfect estimation of the storage terms and of the flux divergences implies lack of closure. In particular, advection effects (represented by and in the figure, for the components parallel and normal to the surface, respectively) are generally neglected but can be important over heterogeneous terrain. (c) Daily cycle of the energy balance components at a measurement site at the floor of the Riviera Valley, averaged over 7 days with weak synoptic forcing [57]. Accounting for horizontal and vertical advection effects, estimated from nearby mesonet stations, reduces the underclosure of the energy balance (an estimation of is included in G, while is negligible in this case).
Measurements usually indicate an underclosure of the SEB, even over homogeneous and flat terrain [56,59]. This means that the sum of the surface turbulent sensible and latent heat fluxes is less than the available energy (net radiation minus ground heat flux). The potential explanations for this are a matter of ongoing scientific debate [60]. Implications are non-trivial, considering for instance that NWP and climate models postulate the closure of the SEB in order to constrain the land–atmosphere exchange.
Over complex orography, a number of factors impact the SEB and need to be taken into account in order to interpret its lack of closure. These factors include the inherent horizontal heterogeneity [15,47], the corresponding local advection processes [57,61], slope effects on the available radiant energy [62,63], the potential failure of the vertically-constant-flux assumption in the SL [64], and others.
To illustrate the significance of the SEB closure problem in complex terrain, Figure 1c shows the energy balance for the lowest layer at a valley floor site in the Riviera Valley in Southern Switzerland [65]. The difference between the available energy and the sum of the heat fluxes in Figure 1c largely exceeds the uncertainty that can be attributed to measurement errors. Therefore, underclosure due to measurement error, often advocated for ideal sites, can be excluded in this case. For this particular location, vertical advection accounts for a considerable part of the underclosure [57]. However, in the general case, other terms in the energy budget, not routinely observed (e.g., horizontal advection and horizontal flux divergence), need to be taken into account in order to fully understand the SEB in complex terrain.
Given the very few existing SEB closure studies in complex mountainous terrain, systematic evaluation of field data is necessary in order to formulate any SEB correction for parameterizations in numerical models.
2.2.2. Data Processing Methods
The current understanding of atmospheric turbulence over mountainous terrain suffers fundamentally from the violation of the basic assumptions of existing micrometeorological theory: these assumptions include horizontal homogeneity, no slopes, stationarity, approximately constant turbulent fluxes along the vertical, and Kolmogorov’s local isotropy assumption for the inertial subrange of the turbulence spectrum [66]. Any effort to systematically study local exchange processes (and hence turbulence) over mountainous terrain (e.g., i-Box [46]) needs in the first place to revisit these assumptions.
In this respect, data quality control and post-processing techniques play a crucial role, particularly in connection with the eddy-covariance method. For instance, the definition of the most appropriate coordinate system (slope-normal vs. vertical third coordinate—especially for the heat flux) and the associated post-processing of turbulence data (in terms of anemometer tilt correction) has triggered some discussion [58,67], but no agreement within the scientific community has yet been reached. While it is clear that post-processing matters and that it can substantially affect the estimation of turbulent fluxes and variances [16,58,68], no convincing arguments have been put forward yet that support the superiority of any of the possible options (e.g., tilt correction using double rotation or any of the various versions of planar-fit rotation) over the others.
Besides tilt correction, another non-trivial problem is the determination of the turbulence averaging scale (TAS), that is, the optimal time interval that has to be used when estimating fluxes and variances from turbulence-resolving measured time-series. Typically, the determination of the appropriate TAS is based on detecting the time scale that matches the mesoscale energy gap, i.e., the low-energy intermediate range in the kinetic energy spectrum of atmospheric motions [69]. Often, no obvious mesoscale gap can be found in the Fourier spectra of measurements from complex terrain [70,71,72]. Therefore, the determination of the TAS has to rely on more complex techniques, such as the ogive method [73], multi-resolution flux decomposition [74], or wavelet analysis [75]. Adjusting the TAS to the data instead of using a constant averaging interval has been shown to improve the consistency of turbulence statistics, in particular by reducing the scatter of observational data around theoretical similarity relationships [76]. It is, however, unclear whether a unique approach to TAS determination can be recommended at all measurement sites and whether orographic complexity has any systematic impact on the TAS.
2.2.3. Fundamental Properties of Turbulence Over Complex Terrain
The ambiguities posed by data post-processing (e.g., TAS determination) reflect a fundamental lack of knowledge about the properties of the flow structures that are responsible for mixing in complex terrain: for instance, how isotropic they are, how their time and length scales are most appropriately defined, how these scales change in time and space, and how they are affected by the terrain geometry.
For this reason, methodologies to determine the degree of (an-)isotropy and (non-)stationarity in turbulence measurements are an important component of any micrometeorological investigation in complex orography. While methods to deal with non-stationarity have been in use for some time now [77], turbulence anisotropy over mountainous terrain is a scarcely explored issue that deserves further investigation [78,79]. A new metric to characterize turbulence anisotropy [80] has recently been used to demonstrate that different states of anisotropy correspond to different similarity relations, especially for horizontal variances, and to confirm that separating the experimental data according to anisotropy significantly improves the match to MOST scaling laws. Since anisotropy in complex terrain may be related to terrain features [81], systematic anisotropy analysis could help identify turbulence properties that hold generally for any complex terrain site and that can be used to generalize scaling laws.
As previously mentioned, scaling laws for SL processes are generally based on MOST. Since many of the pre-requisites of this theory are almost invariably not fulfilled over mountainous terrain, no universal scaling behaviour according to MOST (that is, correspondence to the well-established universal MOST functions) has been reported over complex orography so far. Local scaling has been suggested as an alternative [64,82], but it is a much less powerful approach than MOST, because the scaling functions need to be established for each site separately [83]. For this reason, the use of local SL scaling in numerical models is not yet feasible. Extensions to MOST for including the impact of surface heterogeneity (e.g., local slope) on scaling laws have not proven successful so far [83].
Besides limiting the applicability of scaling approaches, horizontal heterogeneity in mountainous terrain also leads to significant small-scale variability of turbulence characteristics [47,58,84], particularly in stable boundary layers. This aspect is discussed in greater detail in Section 2.5.
2.3. Daytime Thermally Driven Winds
The small-scale end of thermally driven baroclinic circulations over mountainous terrain corresponds to slope winds. These flows react very quickly (on a timescale of minutes) to changes in the sensible heat flux at the surface, and they are almost invariably turbulent. Turbulence is generated over slopes mostly by buoyancy effects during the day and by wind shear at night. It can be negligible or absent only in short periods in weak synoptic flow, for instance during the morning and evening transitions of the daily cycle or under overcast skies.
In the past, nocturnal katabatic (downslope) winds have been investigated much more extensively than daytime anabatic (upslope) winds. Upslope flows are harder to measure and to simulate than downslope flows, because they extend to a higher altitude above ground and they contain a wider spectrum of convectively driven scales of motion.
There are two main reasons for investigating upslope winds further. First, quantifying the vertical transport determined locally by upslope circulations allows testing, and possibly improving, the existing surface-layer and boundary-layer parameterizations. If these do not represent the exchange over mountainous terrain accurately, then specific exchange parameterizations are required. These should rely on a decomposition of the vertical transport into a turbulent component and an advective slope circulation component [85]. Second, the thermodynamic impact of thermally forced upslope circulations on the atmosphere above mountains can impact dynamical processes such as orographic blocking [86] and has implications towards convective preconditioning and convective initiation [51]. These two perspectives on the properties of upslope winds refer to largely distinct spatial scales, namely a single point along a slope in one case, and a whole mountain ridge in the other. Herein, we refer to them as the pointwise and ridge-scale perspectives, respectively.
2.3.1. Pointwise Perspective on Upslope Winds
From the pointwise perspective, the basic physics of fluid flow over a heated or cooled slope is described by the 1942 Prandtl model [87,88,89]. This is a closed-form solution of the Navier–Stokes equations, providing slope-normal profiles of equilibrium laminar flow over homogeneous slopes. A few extensions of this model have been proposed as an attempt to introduce some additional complexity while keeping the problem mathematically tractable [90,91]. For instance, extended Prandtl models include the effects of slope curvature [92], differential heat fluxes along the slope [93], unsteady behaviour due to daily periodicity [94], and turbulent mixing in the form of a gradually varying eddy viscosity [95,96,97]. Generally speaking, none of these extensions successfully removes all of the restrictions under which the Prandtl model is valid.
Prandtl-type model results compare rather favourably with observations in the case of katabatic winds [88]; in particular, variable-eddy-viscosity models successfully predict that the height of the katabatic jet maximum and the height at which the temperature anomaly vanishes do not coincide (the former being smaller than the latter), as often suggested by observations [96]. The applicability of Prandtl profiles in the case of anabatic winds is instead dramatically reduced under weakly stratified conditions, due to convective mixing [88,94,98]. The Prandtl model has already been used to quantify the mesoscale heat and mass fluxes due to slope winds [85], but further investigations are necessary in order to understand if its applicability in this context is warranted in general.
Bulk steady-state models [99] provide an alternative approach for estimating transport by slope winds. While the Prandtl model provides a continuous one-dimensional representation of the flow field over a slope, bulk models only evaluate a few integral properties of the slope wind layer. Starting from the heat and mass balance over a uniform slope, bulk models estimate steady-state fluxes a-priori, given the surface heat flux, the environmental stratification, the slope angle [99] and possibly a turbulent detrainment parameter [100]. Relatively complex bulk models, which relax the homogeneity and stationarity conditions but are not analytically solvable, also exist [101]. Bulk slope flow models seem to work well for simple slope geometries and in stably stratified sections of the valley atmosphere [100,102]. Consequently, in regions with sufficient stratification, the slope-flow-induced mass flux is primarily determined by factors external to the slope wind layer and is largely independent of turbulent processes. Given the bulk mass flux along the slope, the vertical transport of passive tracers (pollutants and moisture) can in principle be estimated, while for the heat flux a parameterization of the temperature excess in the slope wind layer is required [100]. The bulk approach seems to provide a viable methodology to quantify transport by upslope winds, but effective ways to remove model singularities in neutral conditions, estimate turbulent detrainment from the slope wind layer, and account for spatial heterogeneity have not yet been devised.
At present, because of the above-mentioned limitations, neither Prandtl-type nor bulk models offer an acceptable solution to the problem of estimating the heat and mass fluxes due to daytime slope winds. In principle, idealized large-eddy simulations (LES) of the atmosphere over a heated inclined plane are a useful way to make progress. Such simulations, which integrate the governing equations in a rotated reference frame (with axes parallel and normal to the slope), were pioneered in the late 1980s [98]. They were used, for instance, to investigate the impact of the slope angle on the slope-normal profiles of first- and second-order turbulence moments and to investigate the effect of surface roughness on the bulk energy and mass fluxes in the slope wind layer. Little progress has been made ever since. Poorly investigated issues include (1) the conditions under which upslope flow is disrupted by convective instability, leading to the formation of coherent turbulent structures (rolls, plumes) and eventually to enhanced mixing between the slope flow layer and the rest of the valley atmosphere [103]; (2) the response of the flow to the spatial variability of the lower boundary condition and of the atmosphere above the slope wind layer; (3) the morning and evening transitions, in particular the small-scale coherent structures that develop in these periods and that determine the phase lag of the wind reversal at different heights; (4) the relative contribution of upslope flow and horizontal entrainment to the mass flux within thermal plumes at mountain tops [104].
A further reason to run turbulence-resolving simulations of upslope flows would be the possibility of using numerical results to test surface-layer scaling laws specifically devised for sloping terrain, in close analogy to existing studies addressing flow over flat and homogeneous terrain [105].
2.3.2. Ridge-Scale Perspective on Upslope Winds
Taking the ridge-scale perspective, the impact of daytime slope flows on the atmosphere above an isolated mountain can, to a certain extent, be modelled using linear theory. The Crook and Tucker (CT) model [106] extends the well-known theory of continuously stratified, steady-state, hydrostatic, and frictionless flow over a mountain by representing diurnal heating as an exponentially decaying function with height. Over higher terrain, the upward shift of this function causes a local heating-rate excess relative to the surroundings at the same height. The steady-state linear solutions of the CT model exhibit vertically propagating thermally forced gravity waves (featuring descent upstream of the ridge and ascent downwind), which interfere destructively with mechanically forced mountain waves. The CT model also suggests that ridges oriented along the flow direction drive the strongest thermal circulations. This result follows logically from the representation of a mountain as a localized heat source: when the ridge is elongated in the flow direction, air parcels spend more time over the heat source and acquire larger buoyancy.
The applicability of the CT model is limited to continuously stratified, steady-state, and non-dissipative flows. More recent linear models represent the effects of the daytime convective boundary layer (CBL) and of daily variations by incorporating the CT lower boundary condition into a two-layer, linear, time-varying, and dissipative model [107,108]. The resulting semi-analytic solutions differ strongly from those of the CT model under weaker winds (where the advective time-scale for impinging flow to cross the terrain becomes comparable to the daily timescale), and include surface-based convergence and an ascending convective “core” over the high terrain, surrounded by weak downdrafts. These solutions resemble real upslope circulations [109,110], but they quantitatively disagree with nonlinear solutions from idealized numerical simulations if realistic heating rates are applied. In this nonlinear regime, which prevails in most real-world situations, the ascent contracts to a very narrow core over the crest, while the surrounding descent broadens and weakens. This asymmetry arises from nonlinear advection by the circulation itself.
Thermally forced upslope circulations have also been quantified using thermodynamic heat-engine theory [107,108,111,112,113,114]. Although this theory does not solve for the full dynamical response, it provides accurate diagnoses of the thermal-circulation strength based on limited information (the surface thermal contrast between the mountain crest and base, and estimates of the relevant length scales). Thus, it arguably offers the most promise for the efficient representation of sub-grid thermal circulations in NWP parameterizations.
2.3.3. Valley Winds
Along-valley winds develop as a result of the larger amplitude of the daily temperature oscillations in the atmosphere of a valley in comparison to the atmosphere above a plain [99]. They may occur even if the daily temperature range at the floor of the valley is not larger than over the plain, because the pressure field at the surface is affected hydrostatically by heating anomalies aloft [115,116,117,118] (Figure 2). Valley winds can also arise because of temperature differences between air columns located at different points along a valley’s axis [17].
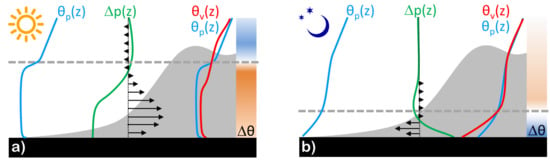
Figure 2.
Thermally driven winds in a valley with horizontal floor (adapted from [18,115,117]). (a) During the day, the atmosphere in the valley (red profile, ) is warmer than that over the plain (blue profiles, ). The largest imbalances () are often found near mountain top level. Horizontal pressure differences () result quasi-hydrostatically from the vertically integrated temperature imbalances, and are typically largest at the valley floor. The wind responds to the pressure gradient and is decelerated by friction near the ground. Deeper convective mixing in the valley causes an elevated cool anomaly, which may drive an upper-level return flow. (b) The opposite situation occurs at night.
Compared to slope winds, valley winds evolve over longer time scales. The pressure gradient to which the up-valley flow responds is established in a few hours. Normally, it takes about six hours before an approximately steady state is reached [119]. The surface wind itself reacts to changes of the pressure gradient on a timescale of 30–45 min [118,120,121].
The larger amplitude of daily temperature fluctuations in valleys has been traditionally explained by means of the valley volume effect and the related concept of the topographic amplification factor (TAF) [122,123]. Topographic amplification of the daily temperature range is caused by the atmospheric volume below a given reference height being smaller over a valley than over a plain. Energy conservation then implies that, given the same heat input per unit surface area, temperature will increase faster in the valley (provided that the valley atmosphere can be treated as a closed thermodynamic system).
The importance of the volume effect in comparison to other mechanisms has been explored in detail using idealized numerical simulations [100,116,117,124,125,126]. It is important to clearly distinguish between the local perspective of valley heating (i.e., the processes leading to a local temperature change, such as subsidence in a stably stratified atmosphere) and the bulk perspective (i.e., the processes leading to a change of the mean temperature of the whole valley atmosphere). For a “pure,” thermally driven along-valley wind (i.e., no other external forcing, uniform surface properties), the valley volume effect is regarded as the primary cause of the larger temperature amplitude in the bulk of the valley atmosphere and hence of the along-valley wind [100,125]. During the transition periods, however, advection may also play an important role at the local scale. For instance, during the morning (evening) transition, slope winds are compensated by subsidence (ascent) in the valley core. This vertical advection effect, which involves the compression (expansion) of a stable air mass, combines with the horizontal advection caused by the pre-existing down-valley (up-valley) flow and contributes to the warming (cooling) of the valley atmosphere at specific locations [116,125,127]. During these transition phases, the combined effect of horizontal and vertical advection coincides with the daily evolution of the driving force of the valley wind system (e.g., advective warming during the morning transition). However, apart from the transition phases, the total advection generally opposes the driving force (for instance, up-valley and up-slope winds cause overall advective cooling during the day) [125].
The theoretical arguments used to explain along-valley winds generally do not lead to exact quantitative estimates of their intensity. Finding quantitative links between the intensity of breeze systems and the magnitude of their forcing factors (heat fluxes and topography) is important in order to fully understand the possible feedbacks between different classes of thermally driven flow. For instance, lakes [20,128] and densely populated urban areas [129,130,131,132] have distinctive thermal fingerprints and induce their own thermally direct circulation systems. Although it is conceivable that the latter may either intensify or obliterate orographically induced breezes, depending on the direction of the respective perturbation pressure gradients, consolidated knowledge on this theme is still lacking.
One approach to estimate a priori the intensity of the along-valley wind and the associated exchange fluxes is to use simple linear and non-linear conceptual models [133,134,135]. These models are capable of predicting the time evolution of the along-valley wind, but their results are very sensitive to key empirical parameters and they are only applicable to simple valley geometries. An alternative method is to investigate the quasi-steady-state limit of the valley wind system [119], in which all relevant parts of the system are in an approximate steady state. The approach highlights the key balances associated with the along-valley circulation and allows for the derivation of a scaling relation for the steady-state along-valley wind and the associated exchange fluxes as functions of valley geometry, valley size, atmospheric stratification, and radiative forcing. In contrast to simple dynamical models, the steady-state scaling is also applicable to complex valley geometries. The use of the complete scaling relation, however, requires the estimation of the depth of the valley inflow layer as an input. Further investigations are required to assess the suitability of the steady-state assumption for various situations.
Besides theory development, progress in understanding valley winds and their role in exchange processes should also capitalize on observational data from a broader range of geographical areas. A considerable portion of the current knowledge on valley winds derives from the painstaking study of the atmospheric circulation in a handful of valleys at mid-latitudes, e.g., the Inn Valley in the Austrian Alps [99,136]. Measurements at new sites often reveal unexpected phenomena, such as the recent finding that the daily surface temperature range in the Adige Valley in the Italian Alps is not larger than that in the adjacent Po Plain during valley wind days [118]. New observations of valley winds should focus in particular on mountainous regions in tropical and sub-tropical areas, which have been studied only marginally until now [137,138,139,140].
Observations should rely not only on ground-based but also on airborne measurements. In this respect, methods to estimate accurately the three-dimensional state of the valley atmosphere from observations along aircraft trajectories [20,128,141,142,143] and from airborne remote sensing [144] have received limited attention so far and should be further improved. Additional considerations on the need of integrating in-situ and remote-sensing measurements for a better understanding of exchange processes in valleys are offered elsewhere in this journal issue [48].
2.4. The Convective Boundary Layer Over Mountainous Terrain
The CBL typically has a simple three-layered structure over flat and homogeneous terrain (proceeding from bottom to top: the surface, mixed, and entrainment layers). Due to the interaction between flows at different scales (e.g., synoptic flow, valley wind, and slope flows), the CBL over mountains has an altogether different structure (Figure 3), as discussed in depth elsewhere in this journal issue [145] and in previous reviews [146]. The present discussion is limited to two specific aspects, namely the interplay between advective and turbulent exchange and the definition of the vertical extent of the CBL over mountains.
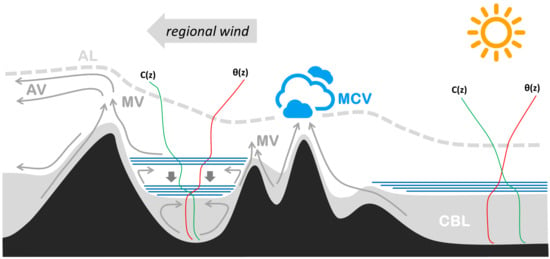
Figure 3.
Exchange processes in the daytime boundary layer over mountainous terrain (adapted from [15,99,146,147,148]). Grey shading indicates the ground-based mixed layer (CBL). MV, AV, and MCV denote, respectively, mountain venting, advective venting, and mountain-cloud venting. Arrows indicate airflow, while and indicate vertical profiles of pollutant concentration and potential temperature, respectively. Horizontal blue lines represent layers with enhanced static stability, which favour the separation of up-slope flows from the ground. Down-pointing arrows represent valley-core subsidence. The dashed line indicates the top of the regional aerosol layer (AL).
2.4.1. Advective and Turbulent Exchange in the CBL Over Mountainous Terrain
Slope and valley winds are important drivers of heat and mass exchange over mountainous terrain. As such, they play a decisive role in determining the vertical extent and the horizontal and vertical variability of the CBL. In particular, the CBL in valleys is locally influenced by the horizontal cold air advection operated by up-valley winds and, if the valley core is stably stratified, by the vertical warm air advection due to the sinking motions that compensate upslope winds [124,149,150,151,152,153].
The transport of near-surface air by thermally driven winds towards the mountain ridges, and then upwards over slopes [154], is often referred to as topographic or mountain venting (MV in Figure 3). Unlike updrafts over flat terrain, which follow a random pattern dictated by the dominant mode of convective instability, the updrafts responsible for mountain venting are anchored to prominent orographic features. Thermally driven convergence enhances vertical transport right over ridges [155], possibly also initiating moist convection [156,157,158,159] (MCV in Figure 3). Because of mountain venting, a deep layer above the mountain crest is affected by daily variations of atmospheric properties, such as moisture, pollutants, temperature or turbulence. Studies have shown that pollutants and moisture can be transported vertically for more than 1000 m above mountain tops [148,160,161,162]. Turbulence advection towards an elevated layer around ridge height [100,124,152,161] may also contribute to a reduction of atmospheric static stability, thus enhancing vertical mixing.
Besides the vertical exchange, thermally driven circulations also affect the horizontal exchange. For instance, at low levels near coastal mountains, sea breezes and up-valley winds often superimpose and enhance the horizontal inland transport of moist air [144,151,161,163,164,165]. At high elevations over ridges, instead, the above-mentioned mountain venting can locally increase humidity and aerosol content [161], generating horizontal gradients of these quantities. In concert with horizontal advection by the mean wind (which can either be driven from the synoptic conditions or result from mesoscale processes), these horizontal gradients are responsible for advective venting [147,161,162]. Advective venting (AV in Figure 3) generates warm elevated mixed layers, which often have a strong inversion at their base [166]. Because of their thermal structure, elevated mixed layers can considerably influence the growth of the ground-based mixed-layer over the surrounding lower terrain or over a valley [166,167,168]. Evidence of multiple layering is often found in the atmosphere near complex orography [169], and ground-based mixed layers (grey shading in Figure 3) are often reported to be shallow [15,115,124,150,170,171] or non-existent [151] in valleys.
Another horizontal exchange process was identified near the floor of valleys with a curved axis, e.g., the Riviera Valley in Southern Switzerland [127,150]. Horizontal airflow along a curved valley is subject to centrifugal acceleration , which can cause cross-valley flow. During daytime, centrifugal cross-valley flow can alter the development of the CBL. Near bends in the valley axis, the relatively cold up-valley flow is pushed towards the outer slope. Consequently, isentropes are displaced upwards near the slope. Since the resulting cross-valley pressure gradient does not balance the centrifugal force exactly at all heights, local imbalances drive a secondary cross-valley circulation that brings air from the outer slope to the inner slope near the valley floor and in the opposite direction aloft. For further details, see Figure 11 in [150]. In the area where this circulation has been observed, cold air advection near the ground and warm air advection aloft have been connected to the local suppression of mixed layer growth.
2.4.2. The Vertical Extent of the CBL Over Complex Orography
The multi-faceted impact of thermally driven breezes on the structure of the CBL near mountains makes it challenging to determine its vertical extent. Over flat terrain, the upper boundary of the CBL is sharply defined. It coincides with the mixing height and depends primarily on the thermal structure of the atmosphere and on the intensity of turbulent exchange (quantified, for instance, by the bulk Richardson number) [172,173]. The previous discussion of the importance of mountain venting and of horizontal exchange processes clearly suggests that this scheme is not adequate for the ABL over mountains [127,146,150].
The multi-layer structure of the daytime atmosphere over mountains is often identified in observations and simulations. Lidar observations, increasingly used to determine the vertical extent of the CBL, often reveal elevated aerosol layers, transported by mountain-induced exchange processes. The top of these aerosol layers (AL in Figure 3) is not always equivalent to the CBL determined using thermodynamic profiles and can be a source of confusion when determining a relevant ‘mixing height’ scale over mountainous terrain [142]. It could be argued that the top of the aerosol layer is a more relevant height scale for mixing processes over mountainous terrain, but its relationship to the traditionally defined CBL height is largely uncertain [102,146,148,162]. Since the quantification of vertical exchange depends partly on an estimate of the vertical extent of mixing and transport processes, more research is needed in defining and identifying the relevant transport and mixing height scales.
So far, much of the focus on daytime boundary layers in mountainous terrain has been on the temporal and spatial evolution of the CBL top as defined in traditional boundary layer studies. CBLs in valleys and basins have received most attention and are relatively well observed and understood compared to CBLs over slopes and mountain tops. Observations typically highlight the importance of the interaction between local, meso-, and synoptic scale flows with resulting convergence and divergence zones that influence CBL top behaviour. For mountain ranges, different spatial patterns of variability of the CBL top have been observed, including terrain-following and level CBL heights [146]. Factors such as atmospheric stability, synoptic wind speed, vertical and horizontal scales of the orography and the presence of embedded valleys have been found to be important. Deep CBLs are less terrain-following than shallow ones, and the CBL top is subject to larger vertical displacements over orographic features that have a large horizontal extent [174]. Conclusions on whether advection effects make the CBL height more uniform over mountains differ between observations [175] and theoretical models [176]. Clearly, conclusive and general statements are still difficult to make and warrant the need for more observations and systematic numerical studies of the CBL over complex topography.
The discussion in Section 2.4.1 and Section 2.4.2 and the schematic depiction in Figure 3 describe different aspects of the diurnal exchange over mountains using a variety of terms (e.g., mountain and advective venting, mixed layer, convective boundary layer, and aerosol layer). Although all of these expressions refer to specific aspects of CBL processes over mountains, their use can be a source of confusion if the context is not specified accurately. The pressing need of specifying a comprehensive and unambiguous definition of the mountain boundary layer (MBL) is apparent [145].
2.5. The Stable Boundary Layer Over Mountainous Terrain
During the nighttime, stabilization of the air due to radiative cooling over complex orography supports the propagation of internal gravity waves, causes drainage flows, and can lead to cold air pool formation. These factors add complexity to nocturnal exchange processes in the stable boundary layer (SBL) over complex terrain (Figure 4).
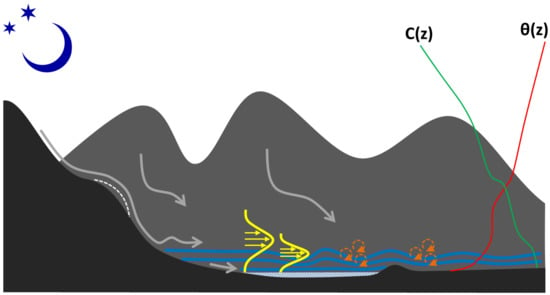
Figure 4.
Nocturnal boundary-layer processes over mountainous terrain. Radiative cooling at the valley floor causes the formation of a stable layer near the ground (blue lines). Drainage flow develops along slopes (grey lines). Drainage flow typically has a low-level wind maximum very close to the surface, but it can detach from the ground above stable layers or at convexities in the slope profile (white dashed line). Sheltered areas beneath separated flow are typically less turbulent. If the valley geometry is favourable (for instance, if the cross-section becomes narrower or there are humps on the valley floor), cold air pools and eventually fog may form (white shaded area). If a cold-air pool is present, the down-valley flow typically flows over it (yellow arrows and profiles). Gravity waves may propagate along the top of the surface-based stable layer, forming undulations along the down-valley jet. Increased wind shear at wave troughs enhances turbulence, leading to localized and intermittent mixing episodes (orange whirls). Layering in the profiles of potential temperature and scalar concentration is often observed. After days with strong insolation, a well-mixed near-neutral residual layer may be present in the valley core. The vertical scale of the figure is exaggerated near the valley floor.
2.5.1. The Stable Boundary Layer at the Valley Floor
Orographically induced processes in the stable boundary layer can control whether turbulent exchange has a role in the nocturnal surface energy budget or not. Valleys with a sloping floor and with a cross-sectional area increasing down-valley can sustain continuous drainage [177,178]. In these conditions, the down-valley flow exhibits a wind speed maximum right above the ground, similar to a low-level jet; turbulence is maintained by shear production, the length scale of the largest eddies can reach 100 m or more, stratification is weak, and, likely, turbulence is only slightly anisotropic.
In contrast, basins and valleys with a flat floor or with blocking obstacles downstream allow for the formation of strong surface-based inversions and cold air pools [28,36,179,180] (blue lines and white shaded area in Figure 4). The time-scale of nocturnal cooling is typically shorter in basins and valleys than it is over flat terrain [181]. The formation of cold air pools is favoured by certain geometric properties of the orography (e.g., the sky-view factor and altitude), but their intensity and persistence depend on a few meteorological factors, mostly determined at the synoptic scale (the presence of a cold and dry air mass, weak winds, and a cloudless sky) [182,183].
Cold air pools decouple the near-surface layer from the overlying flow, which may be either synoptic or thermally driven. Stratification in cold air pools decreases turbulence intensity but, even in such stable conditions, turbulent mixing is possible [184]. Short-lived mixing events can occur when wind shear across the top of the cold pool becomes strong enough to make the Richardson number (Ri) subcritical [185] (yellow wind profiles and orange whirls in Figure 4). When this happens, mixing removes momentum from the free-atmosphere flow, shear decreases, and turbulence is suppressed again. These mixing events are inherently intermittent and, because they are driven top-down by the dynamical instability of the flow (i.e., subcritical Ri below a jet), they may not be linked at all to the near-surface conditions [186]. While the origin of these sporadic shear-driven mixing events is qualitatively well understood, their quantitative description (for instance, for parameterization purposes) remains challenging.
2.5.2. The Stable Boundary Layer Over Slopes
Downslope flows are invariably turbulent for two reasons. First, the katabatic jet maximum is always very close to the surface, implying that turbulence production by shear is always large. Consequently, the atmosphere rarely becomes very stable at slope sites, at least those that are not affected by cold-air pools at the valley floor [187]. Second, buoyant turbulence production (instead of loss) may occur over steep slopes even in statically stable conditions [188,189]. Despite being essentially turbulent, katabatic flows or other flows with a low-level wind maximum do not match the standard ABL structure [185,190,191]. Therefore, the applicability of MOST or of local scaling approaches for katabatic flow has been called into question [192] and is a matter of on-going debate [191].
Arguments against the use of local scaling approaches for slope sites can be understood considering the joint role of advection processes and of terrain heterogeneity. Besides causing significant turbulent mixing, katabatic winds advect heat and air mass along the slope, and the coupling between advection and spatial heterogeneity necessarily implies that, at any point along the slope, turbulence is not entirely determined by local effects. The heat budget at one point may be affected by upstream thermal heterogeneity, while changes in the slope roughness and angle may alter the wind speed and therefore the intensity of turbulence downstream, possibly even causing flow separation [58] (dashed white line in Figure 4). Similarly, mixing in the SBL is affected by terrain curvature, with convex areas being sheltered and therefore less turbulent [47,84].
An implication of these considerations is that wind direction can have an impact on the local turbulent fluxes at a slope site, because of the directional variability of the fetch. In addition, turbulent mixing at slope sites may be enhanced by low-frequency non-turbulent flow disturbances; the mechanisms of the enhancement depend on the flow, being different between thermally driven katabatic and dynamically driven downslope winds [193]. Future research should be directed at finding methods to incorporate such non-local effects in scaling laws for the SBL, and at answering the general question whether terrain complexity makes land–atmosphere exchange more efficient in the SBL.
2.5.3. The Role of Gravity Waves
Internal gravity waves (IGWs) occur ubiquitously in the SBL [194]. Just like turbulent motions, transient wave disturbances appear in measured records as fluctuations with respect to a background ambient flow. However, turbulent and wave fluctuations are connected to physically distinct transport processes: mixing in one case and wave-energy radiation in the other.
Understanding the interplay between waves and turbulence in the SBL depends on the ability to disentangle turbulent and wave fluxes, that is, to decompose fluctuations into a turbulent component and a wave component. The related knowledge is sparse or sketchy, mostly because the relevant phenomena are non-stationary and in disequilibrium with the ambient flow. From a theoretical perspective, methods to distinguish waves from turbulence may rely on considering their different properties, e.g., their dominant wavelengths or frequencies, energy transport speed, mixing efficiency, ability to transport scalar quantities, correlations between pressure, temperature, and wind speed fluctuations, and potential vorticity [194]. However, in practice, no straightforward and universally accepted approach to the problem seems to exist at present.
There are several practical reasons why wave–turbulence interactions in the SBL are important. First, both waves and turbulence are momentum sinks, i.e., they exert drag. In the SBL, IGW may transport momentum between small-scale terrain and the lowermost critical level [195]. The related wave drag can be of the same amplitude of, or even larger than, the turbulent drag [196,197,198]; it has a significant impact on the SBL dynamics, but it can also affect larger scales of motion [199].
Second, interactions with IGW may lead to a global intermittency of turbulence, i.e., temporally and spatially limited turbulence patches. In fact, wind speed perturbations induced by waves can enhance shear and thereby promote the onset of mechanically generated turbulence (orange whirls in Figure 4), which then also affects heat transport [186,200]. Actually, intermittent turbulence can be triggered in the SBL by a range of diverse sub-mesoscale (submeso) motions, of which orographically generated IGW are just one example [194,201,202,203]. The impact of such submeso motions on turbulent transport is not accounted for by MOST and other classical theories of turbulence.
A lack of theoretical understanding has hindered the development of parameterizations for unresolved submeso-motions and wave–turbulence interactions. Recent advancements in parameterizing the SBL followed from recognizing that the onset of turbulence is not associated with a unique critical value of the Richardson number [204] and that the Prandtl number is stability-dependent [205]. However, the few existing wave-like drag parameterizations are still far from being fully adequate [194,198,206].
2.6. Multiscale Interactions
The preceding discussion encompassed the concept of multiscale interaction, that is, a state in which atmospheric exchange is affected by weather processes evolving over distinctly different spatial and temporal scales. Often, the transfer of kinetic energy between different scales of atmospheric motion over mountainous terrain is controlled by the presence or absence of atmospheric layers with enhanced static stability. These stable layers can be either ground-based or elevated and, if stratification is very strong, they can even be associated with temperature inversions.
Stable layers in valleys effectively control whether the valley atmosphere is coupled or decoupled with the overlying free atmosphere (Figure 5). Some of the processes that create stable layers over complex orography occur also over flat and homogeneous terrain (e.g., radiative cooling in the SBL, large-scale subsidence, differential advection, and turbulent entrainment by overshooting thermals in the CBL). Other relevant processes, especially during daytime, are specific to the ABL over mountainous terrain (e.g., subsidence compensating anabatic flow, layering due to mountain, and advective venting).
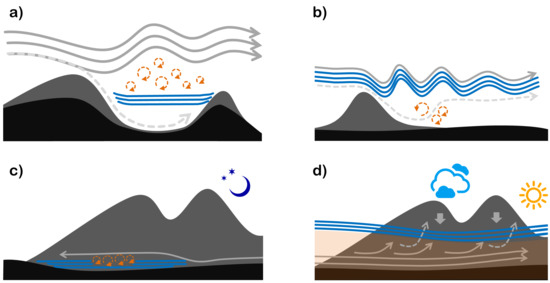
Figure 5.
Role of stable layers (blue lines) in controlling multi-scale interactions. (a) Airflow over a valley, with (continuous grey lines) or without (dashed grey line) a stable layer below the mountain-top level, results, respectively, in elevated turbulence (orange whirls) and small-amplitude waves or in valley flushing and large-amplitude waves (adapted from [210]). (b) Airflow past an isolated mountain with (continous grey line) or without (dashed grey line) a low-level inversion above mountain-top level. In the former case, non-hydrostatic lee waves develop. In the latter, a large-amplitude hydrostatic wave forms, possibly conducive to boundary-layer separation and related turbulence (orange whirls). (c) Turbulent erosion of ground-based stable layers underneath a down-valley flow. (d) Confinement of moist air (orange shading) beneath a stable layer during daytime, possibly destabilizing the atmosphere. Thermally driven breezes advect air from the plain and upwards along the slopes (grey lines). Part of the upslope flow pierces the stable layer and causes mountain venting (dashed grey lines). Valley-core subsidence (down-pointing arrows) displaces the stable layer downwards.
Stable layers suppress turbulence, resist erosion by wind shear, hinder vertical exchange, and control the propagation of gravity wave modes. In more practical terms:
- Stable layers below mountain crest control whether the valley atmosphere is sheltered from or exposed to synoptic cross-valley flow (e.g., Foehn; Figure 5a). Processes controlling whether ambient flow overflows or flushes the valley atmosphere [207,208,209,210,211] have obvious air-quality implications for large urban areas in mountains [142,212].
- Inversion layers above mountain tops control the amplitude and wavelength of propagating and trapped wave modes (Figure 5b). Low-level inversions exceeding critical strength or located above critical height trap wave energy in the underlying boundary layer [213]. Some authors described the impact of stable layers on gravity waves as if it were that of a virtual topography [214]. The analogy might be inappropriate because, unlike orography, stable layers evolve over meteorological time-scales and are affected by the ambient flow. However, just like orography, low-level stable layers can affect gravity wave drag (the removal of momentum from the synoptic flow) in ways that have not yet been completely explored.
- Ground-based stable layers control intermittent turbulent exchange in the stable boundary layer, effectively turning it off when they are strong enough to decouple the SBL from the overlying nocturnal jet, suppressing shear turbulence production (Figure 5c).
- Elevated stable layers trap heat and moisture underneath them (Figure 5d). In combination with horizontal advection towards mountainous regions, elevated stable layers may thus favour the accumulation of moist static energy within valleys and the establishment of convectively or potentially unstable conditions. Furthermore, wind shear across stable layers might aid convective organization and enhance storm longevity [215].
At present, exploring the formation, evolution, and destruction of stable layers or inversions in valleys under a variety of weather conditions seems a promising approach to make sense of multi-scale interactions in the atmosphere over mountainous terrain.
3. Representing the Mountain Atmosphere in Weather Prediction Models
3.1. Modelling Surface Exchange
Numerical weather prediction models and the atmospheric component of climate models require the fluxes of momentum, sensible heat, water substance, and other trace constituents to be specified at the interface between the earth and the atmosphere. Because present-day operational models almost invariably adopt a terrain-following vertical coordinate, this interface coincides with the lowest computational level above the ground.
The representation of the lower boundary condition generally uses a bulk approach, because models do not resolve explicitly the turbulent eddies that mediate near-surface exchange. Typically, only vertical fluxes are modelled, in the tacit assumption that the deviation of vertical-coordinate isosurfaces from the true horizontal is small. For any prognostic variable , its vertical flux at the surface is assumed to be proportional to between the atmosphere and the surface through a bulk transfer coefficient. Land-surface models (LSMs) combine geospatial information about land properties with tendencies from several parameterization schemes (ABL, radiation, microphysics, and, optionally, convection) to specify the bulk transfer coefficients and to update the land state variables, such as soil temperature and moisture content [1]. From this concise overview, the need of special provisions for complex-orography conditions in some aspects of LSMs is apparent.
Firstly, bulk transfer relationships must be specified in a way that accounts for the effects of both resolved and unresolved orography. The stability-dependent formulation of bulk transfer coefficients typically accounts for adiabatic effects using results from MOST. In light of the deficiencies of MOST over complex orography (Section 2.2), a thorough re-evaluation of the formulation of bulk transfer coefficients, wall functions, and boundary-layer parameterization constants is warranted for complex-terrain applications. Given the observed impact of terrain curvature and directional fetch variability on turbulent fluxes (Section 2.5.2), it seems necessary to explore ways of incorporating unresolved variations of these properties into flux parameterizations.
Furthermore, it is necessary to abandon the flat-boundary approximation in the formulation of the surface stress and heat fluxes. It has been demonstrated that failing to account for the horizontal flux components can lead to substantial errors in the modelling of surface exchange when the resolved topography is steep [216]. Eliminating the flat-boundary approximation is also necessary in NWP models that do not use a terrain-following coordinate system, e.g., those that represent terrain using the immersed boundary method [217]. Future developments in NWP will likely lead to an increasing use of unstructured computational grids based on finite-volume numerical methods. Even in this context, correct specification of surface fluxes at the lower boundary will be a critical aspect, and it might require the adaptation of closure approaches borrowed from computational fluid dynamics applications.
Radiation modelling needs to account for complex-orography conditions. The parameterization of the shortwave component typically lacks a representation of orographic shading, where solar radiation is blocked by prominent orography [218]. In contrast, self-shading due to the orientation of a sloping surface with respect to the sun is generally accounted for. The representation of the longwave component, instead, typically neglects the radiation emitted by the surrounding elevated terrain, which might be an important contribution to the nocturnal radiative budget at sites with concave orography (e.g., valley floors and dolines).
Finally, because regional NWP models will likely adopt sub-km grid spacing in the foreseeable future, consistency will require an improved treatment of surface fields with high spatial variability and possibly a patchy spatial structure, e.g., soil moisture (which has a marked altitudinal dependence and is affected by runoff), snow cover [6], and urban land-cover [219].
3.2. Modelling Turbulent and Advective Exchange within the CBL
The ability of NWP and climate models to simulate the CBL structure and the vertical exchange over mountainous terrain is strongly sensitive to the horizontal grid resolution [169,220]. Models that do not sufficiently resolve the complex network of valleys embedded in large-scale mountain ranges might require specific parameterizations to account for SGS orographically driven exchange processes. Such parameterizations would have to take into account various atmospheric, diabatic, and orographic factors.
The atmospheric and diabatic factors controlling the transport and exchange of heat and mass are the ambient (large-scale) wind speed and direction, the static stability of the valley atmosphere, the radiative forcing, and the associated surface sensible heat flux, as well as latent heat release in clouds [102,103,221]. The most important geometric factors are the valley width and depth, the inclination of the valley floor, and the along-valley variability of the valley cross-section [121,126,162]. For example, deeper and narrower valleys produce stronger up-valley winds and stronger vertical mass flux out of the valley [126].
The impact of some of these factors on the vertical exchange can be summarized into a single parameter. For example, the total export of mass of some arbitrary tracer out of the valley atmosphere by diurnal thermally driven flows increases with decreasing stability and increasing surface heating. Therefore, the resistance of the valley atmosphere to vertical exchange can be quantified by the ratio between the energy required to neutralize the valley atmosphere (which is stably stratified in the early morning) and the total energy provided by the surface sensible heat flux in the course of the day. This ratio is referred to as the breakup parameter, B [102]. If B < 1, the turbulent and advective exchange processes caused by diurnal heating remove any valley inversion, enhancing vertical transport towards the free atmosphere. LES studies of CBL development in valleys have shown that the fraction of tracer mass that is exported out the valley atmosphere decreases exponentially with increasing B. Hence, the tracer mass turnover can be effectively parameterized by B [102]. Similar results have been found for the export of heat [221]. Because B is affected by valley width, crest height, forcing amplitude, and stratification, it quantifies the joint impact of all these factors on the total heat export from the valley atmosphere.
Despite these encouraging results, several difficulties need to be mastered in order to improve the parameterization of exchange processes over complex terrain for NWP and climate models. First, one key problem is how to characterize the SGS variability of terrain characteristics, atmospheric stability, and heat flux. In this respect, borrowing techniques from gravity wave drag parameterization [222] seems to be a promising approach. More specifically, the SGS orography can be concisely described by a set of grid-scale-dependent statistical measures describing its standard deviation, asymmetry, and convexity [223]. Parameterization development can rely on coarse-graining studies based on high-resolution LES, designed to resolve explicitly a broad range of scales of motion over wide domains with complex orography. Spectral decomposition of the simulation output (e.g., using Fourier analysis) would show how the unresolved contribution to the vertical heat and mass fluxes depends on arbitrarily chosen cut-off scales and on the corresponding unresolved orography descriptors.
A second challenge is to determine and prescribe the instantaneous unresolved orographically induced vertical fluxes of mass and heat, as needed by a parameterization scheme that should be active at each time step during model integrations. No viable methodology to solve this problem exists so far, because the breakup parameter method has only been used to parameterize the total, i.e., time-integrated, exchange [102,221]. To illustrate the possible approaches to the problem, it is useful to recall some basic aspects of ABL parameterization.
From the perspective of transport and exchange phenomena, thermally driven circulations in the CBL over mountains are analogous to large convective eddies, i.e., they perturb local mixing and invalidate the assumption of down-gradient turbulent diffusion along the vertical. The concept of down-gradient vertical diffusion, which is the foundation of most boundary-layer parameterization schemes, is concisely expressed as , where is any physical variable, w is the vertical wind component, z is the vertical coordinate, is a positive-definite eddy exchange coefficient, primes denote turbulent fluctuations, and angle brackets indicate Reynolds averaging. Evidence against the validity of the down-gradient exchange assumption over complex orography (e.g., demonstrations that vertical gradients can have the same sign as vertical fluxes) has been provided in the literature. For instance, in the upper portion of the valley CBL, around and above mountain tops, the atmosphere is generally statically stable ( > 0, being the potential temperature), while the spatially-averaged heat flux is upward ( > 0) [126].
Exchange parameterization schemes for the atmosphere over mountainous terrain should acknowledge the fact that, in general, SGS exchange over complex orography is affected by both turbulent mixing and mesoscale advection processes. This situation is best modelled by generalizing non-local mixing parameterizations to complex-orography scenarios. Non-local mixing schemes modify the down-gradient assumption either by including a counter-gradient correction , [224,225], or by including an additional mixing term , [226]. The second strategy has become popular in the context of shallow convection parameterization, where it is known as the mass-flux approach [227]; in fact, is normally taken as proportional to the mass flux associated with an ensemble of narrow updrafts. In either case, the correction term ( or ) represents the impact on the exchange process of large-scale flow structures, which are not necessarily turbulent.
A detailed analysis of the existing formulations of the eddy exchange coefficient , the counter-gradient correction , and the mass-flux factor is beyond the scope of the present paper. It is sufficient to mention that a few key parameters involved in their definition (e.g., the mixing length, the CBL depth, and the fractional area of updrafts) are typically unaware of the SGS orography variability. Therefore, future attempts at improving exchange parameterizations over complex terrain should consider introducing SGS orography descriptors in their formulation.
3.3. Stochastic Boundary-Layer Parameterization
The grid spacing adopted by current operational limited-area NWP models is of the order of 1 km [187,228]. This relatively high resolution resolves most fine-scale terrain and, combined with non-hydrostatic dynamics, allows for the explicit representation of some mesoscale phenomena, including deep moist convection and part of the spectrum of thermally driven breezes. However, the lack of mesoscale detail in the initial conditions of the forecasts, the fast growth of forecast errors at small spatial scales [229,230], and the rapid downscale propagation of small initial errors at the large scales [231] imply that high-resolution predictions are not necessarily more skillful than low-resolution ones. In addition, parameterization schemes that are appropriate at coarse resolutions may be inadequate for km-scale or sub-km-scale simulations, in particular for ABL mixing [232]. These considerations point to the need of complementing high-resolution forecasts with an evaluation of their uncertainty and explain the increasing efforts devoted to the development of limited-area ensemble prediction systems (EPSs) [233,234,235,236,237].
Modern EPSs rely not only on perturbed initial conditions but also on a model error representation that aims at quantifying the forecast uncertainty arising from an imperfect model design or from unknown physical processes [238]. One way of accounting for model errors is to introduce stochastic perturbations in some aspects of the parameterization schemes adopted by the ensemble members (multi-physics ensembles [239] offer another approach to the problem).
Stochastic perturbations help to compensate for the typical underdispersiveness of ensembles, especially at short forecast ranges [236]. Ensembles are underdispersive when the variance between the ensemble members (the ensemble spread) is too small compared to the mean square error of the ensemble mean. In a reliable ensemble, where ensemble spread and error are consistent, the spread is a good estimate of the expected forecast uncertainty. An underdispersive ensemble, instead, underestimates forecast uncertainty. A widely used approach to increase ensemble spread, the SPPT (stochastically-perturbed parameterized tendencies) scheme [240,241], superimposes column-wise multiplicative noise, with pre-determined spatial and temporal correlation scales, to the parameterized tendencies of dynamic and thermodynamic variables. This approach proved successful at improving reliability, especially for near-surface variables, but is not free of drawbacks. For instance, because it introduces stochastic perturbations in the whole simulation domain, the SPPT approach might reduce accuracy in areas where the forecast is not underdispersive.
Current attempts at improving stochastic parameterizations are directed at developing SPP (stochastically perturbed parameter) schemes [241,242,243], where stochastic perturbations are imposed at the parameter level instead of the tendency level. Knowledge of physical processes is instrumental in the development of this type of schemes and suggests what parameters might be more appropriately subject to stochastic perturbation.
By way of example, a non-exhaustive list of the major sources of model uncertainty over mountainous terrain in fair-weather conditions might include (1) the parameters of any scaling law used to prescribe the surface fluxes of heat, moisture, and momentum—because of the aforementioned insufficient knowledge of scaling laws over complex terrain; (2) soil moisture and temperature—because of the quick response of thermally driven flows, and therefore of vertical mixing, to potentially unresolved variations of the surface energy balance; (3) shortwave radiation, affected by intermittent and unresolved cloudiness—for the same reasons as above; (4) the parameters governing turbulent entrainment at the top of the ABL—because advection by possibly unresolved thermally driven flows obliterates turbulent entrainment processes and prevents the formation of strong capping inversions; (5) the boundary-layer height (in first-order turbulence closures) or the mixing length (in order-1.5 turbulence closures)—because fine-scale terrain variability is typically not considered in their estimation.
The introduction of stochastic parameterizations in high-resolution EPS is at an early stage of development and, to the authors’ knowledge, no attempts have yet been published to specifically investigate their applicability over complex terrain. In fact, the topic is a major challenge for the mountain meteorology community. Considering the proven inability of km-scale simulations to resolve the whole spectrum of thermally driven flows over orography [169], the large uncertainty about the relevant physics, and the substantial SGS variability that needs to be accounted for, forecasts of ABL processes in complex terrain can be anticipated to benefit greatly from any progress in the development of limited-area EPS.
4. Conclusions
The exchange of heat, mass and momentum in the atmosphere over mountainous terrain is affected by turbulence, thermally driven mesoscale circulations, and synoptic-scale dynamics. This article has provided a concise review of the current state of knowledge of this topic, addressing primarily the investigation of turbulence over complex terrain, the impact of slope and valley breezes on the structure of the convective boundary layer, and the roles that katabatic winds, intermittent mixing, and wave–turbulence interaction play in the stable boundary layer.
Possible research directions for the future have been identified and discussed. Progress in understanding turbulent exchange (Section 2.2) should be pursued by
- studying systematically the surface energy balance at mountainous sites to understand the factors that determine its lack of closure;
- achieving a more thorough understanding of the implications of data processing (e.g., anemometer tilt correction and the determination of the turbulence averaging scale) on the estimate of turbulence statistics with the eddy-covariance method;
- studying the origins of turbulence anisotropy, in particular whether orographic variability has any direct or indirect impact on it;
- extending similarity theory by accounting for horizontal heterogeneity in landforms and land-cover, in order to improve the accuracy of scaling laws over complex orography.
Research on diurnal boundary layer processes (Section 2.3 and Section 2.4) should aim at
- quantifying the vertical heat and mass fluxes due to diurnal anabatic flow, in particular over heterogeneous slopes and during transition phases, to understand whether the existing boundary-layer parameterizations model the bulk effects of these circulations well enough;
- modelling the intensity of thermally driven valley and plain-to-mountain flows, using either equilibrium models based on the concept of topographic amplification or heat-engine theory;
- improving the existing approaches to map the three-dimensional state of the atmosphere over valleys and near ridges from sparse measurements;
- evaluating the scales of vertical and horizontal mixing in the CBL over mountains and how they depend on orography and weather conditions; in particular, the spatial and temporal variability of the upper boundary of the aerosol layer and of the convective boundary layer, and how they are affected by mountain and advective venting.
Priorities in the investigation of stable boundary layer dynamics (Section 2.5) include
- making progress in discriminating turbulent fluctuations in field quantities (which cause local mixing of momentum and heat) from wave oscillations (which instead radiate wave energy and momentum);
- quantifying (possibly parameterizing) the extent to which turbulent fluxes are enhanced by the intermittent mixing generated by low-level jets and wave–turbulence interactions, and how orography affects intermittent mixing.
Distinctively, exchange processes over mountainous terrain are affected by atmospheric motions on a broad range of spatial and temporal scales. It is argued (Section 2.6) that studying in depth the mechanisms that generate and dissipate stable layers in the atmosphere, both at daytime and at night, will help decipher the multi-scale interactions that affect exchange processes over mountains.
Better knowledge of exchange processes over mountainous terrain can result in improved NWP and climate models (Section 3). Modelling aspects that require a special treatment of complex-orography processes include the representation of surface boundary conditions, the parameterization of sub-grid-scale exchange, and the stochastic perturbation approaches used in ensemble prediction systems to quantify model-error uncertainty.
Acknowledgments
S.F.J.D.W.’s contribution was funded by an NSF award ATM-1151445. B.G. and Ž.V. acknowledge support from the Croatian Science Foundation (HrZZ), project VITCLIC, PKP-2016-06-2975. J.S. was supported by the Hans Ertel Centre for Weather Research; this German research network of universities, research institutes, and the Deutscher Wetterdienst is funded by the BMVI (Federal Ministry of Transport and Digital Infrastructure). The work of I.S., A.G., and S.S. was funded by the Austrian Science Fund (FWF), through grants T781-N32, P 23918-N21, and P 24726-N27, respectively. The authors are grateful to three anonymous reviewers, who helped improve the manuscript.
Author Contributions
S.S. designed the paper outline, wrote text for all sections, and prepared all figures. The other authors provided concepts and text for individual paper sections. B.A.: Section 2.4; J.C.: Section 2.1 and Section 2.5; S.F.J.D.W.: Section 2.4; A.G.: Section 3.2; B.G.: Section 2.5; N.K.: Section 2.4; D.K.: Section 2.3; M.W.R.: Section 1 and Section 2.2; J.S.: Section 2.3; I.S.: Section 2.2 and Section 2.5; Ž.V.: Section 2.2; D.Z.: Section 2.3. M.W.R. and D.Z. encouraged the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABL | Atmospheric Boundary Layer |
| AL | Aerosol Layer |
| ALPEX | Alpine Experiment |
| ASCOT | Atmospheric Studies in Complex Terrain |
| AV | Advective Venting |
| BLLAST | Boundary-Layer Late Afternoon and Sunset Turbulence Experiment |
| CBL | Convective Boundary Layer |
| COLPEX | Cold-Air Pooling Experiment |
| COPS | Convective and Orographically induced Precipitation Study |
| CT | Crook and Tucker linear model |
| CUPIDO | Cumulus Photogrammetric, In-Situ, and Doppler Observations |
| DOMEX | Dominica Experiment: Orographic Precipitation in the Tropics |
| EPS | Ensemble Prediction System |
| HVAMS | Hudson Valley Ambient Meteorology Study |
| HYMEX SOP1 | Hydrological Cycle in the Mediterranean Experiment, Special Observation Period 1 |
| i-Box | Innsbruck Box |
| IGW | Internal Gravity Waves |
| LES | Large-Eddy Simulation |
| LSM | Land-Surface Model |
| MAP | Mesoscale Alpine Programme |
| MATERHORN | Mountain Terrain Atmospheric Modeling and Observations Program |
| MBL | Mountain Boundary Layer |
| MCV | Mountain-Cloud Venting |
| METCRAX | Meteor Crater Experiment |
| MOST | Monin-Obukhov Similarity Theory |
| MV | Mountain Venting |
| NWP | Numerical Weather Prediction |
| PAP | Pollution Atmospheric in the Pyrenees |
| PCAPS | Persistent Cold-Air Pool Study |
| PYREX | Momentum Budget over the Pyrénées Experiment |
| SBL | Stable Boundary Layer |
| SEB | Surface Energy Balance |
| SGS | Sub-Grid-Scale |
| SL | Surface Layer |
| SPPT | Stochastically Perturbed Parameterized Tendencies |
| T-REX | Terrain-induced Rotor Experiment |
| TAF | Topographic Amplification Factor |
| TAS | Turbulence Averaging Scale |
| TRACT | Transport of Air Pollutants Over Complex Terrain |
| VERTIKATOR | Vertikaler Austausch und Orographie (Vertical Transport and Orography) |
| VOTALP | Vertical Ozone Transports in the Alps |
| VTMX | Vertical Transport and Mixing |
References
- Stensrud, D.J. Parameterization Schemes. Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Baklanov, A.A.; Grisogono, B.; Bornstein, R.; Mahrt, L.; Zilitinkevich, S.S.; Taylor, P.; Larsen, S.E.; Rotach, M.W.; Fernando, H.J.S. The Nature, Theory, and Modeling of Atmospheric Planetary Boundary Layers. Bull. Am. Meteorol. Soc. 2011, 92, 123–128. [Google Scholar] [CrossRef]
- Arnold, D.; Morton, D.; Schicker, I.; Seibert, P.; Rotach, M.W.; Horvath, K.; Dudhia, J.; Satomura, T.; Müller, M.; Zängl, G.; et al. High Resolution Modelling in Complex Terrain. Report on the HiRCoT 2012 Workshop, Vienna, 21–23 February 2012; Technical Report, BOKU-Met Report 21; BOKU-Met: Vienna, Austria, 2012. [Google Scholar]
- King, J.C.; Connolley, W.M.; Derbyshire, S.H. Sensitivity of modelled Antarctic climate to surface and boundary-layer flux parametrizations. Q. J. R. Meteorol. Soc. 2001, 127, 779–794. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Lüthi, D.; Litschi, M.; Schär, C. Land-atmosphere coupling and climate change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, E.; Giovannini, L.; Zardi, D.; de Franceschi, M. Optimization of Noah and Noah_MP WRF Land Surface Schemes in Snow-Melting Conditions over Complex Terrain. Mon. Weather Rev. 2017, 145, 4727–4745. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Rotach, M.W.; Wohlfahrt, G.; Hansel, A.; Reif, M.; Wagner, J.; Gohm, A. The World is Not Flat: Implications for the Global Carbon Balance. Bull. Am. Meteorol. Soc. 2014, 95, 1021–1028. [Google Scholar] [CrossRef]
- Rotach, M.W.; Gohm, A.; Lang, M.N.; Leukauf, D.; Stiperski, I.; Wagner, J.S. On the Vertical Exchange of Heat, Mass, and Momentum Over Complex, Mountainous Terrain. Front. Earth Sci. 2015, 3, 76. [Google Scholar] [CrossRef]
- Smith, R.B. The Influence of Mountains on the Atmosphere. Adv. Geophys. 1979, 21, 87–230. [Google Scholar]
- Atkinson, B.W. Topographically induced circulations. In Meso-Scale Atmospheric Circulations; Chapter Part II; Academic Press: Cambridge, MA, USA, 1981; pp. 25–122. [Google Scholar]
- Lin, Y.L. Orographically forced flows. In Mesoscale Dynamics; Cambridge University Press: Cambridge, UK, 2007; Chapter 5; pp. 109–183. [Google Scholar]
- Markowski, P.; Richardson, Y. Orographic mesoscale phenomena. In Mesoscale Meteorology in Midlatitudes; Wiley: Hoboken, NJ, USA, 2010; Chapter Part IV; pp. 315–366. [Google Scholar]
- Jiménez, M.A.; Cuxart, J. A study of the nocturnal flows generated in the north side of the Pyrenees. Atmos. Res. 2014, 145–146, 244–254. [Google Scholar] [CrossRef]
- Rotach, M.W.; Zardi, D. On the boundary-layer structure over highly complex terrain: Key findings from MAP. Q. J. R. Meteorol. Soc. 2007, 133, 937–948. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D.; Tagliazucca, M.; Tampieri, F. Analysis of second-order moments in surface layer turbulence in an Alpine valley. Q. J. R. Meteorol. Soc. 2009, 135, 1750–1765. [Google Scholar] [CrossRef]
- Whiteman, C.D. Mountain Meteorology. Fundamentals and Applications; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Zardi, D.; Whiteman, D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting: Recent Progress and Current Challenges; Chow, F., De Wekker, S., Snyder, B., Eds.; Springer Atmospheric Sciences; Springer: Dordrecht, The Netherlands, 2013; pp. 35–119. [Google Scholar]
- Schicker, I.; Arnold Arias, D.; Seibert, P. Influences of updated land-use datasets on WRF simulations for two Austrian regions. Meteorol. Atmos. Phys. 2016, 128, 279–301. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G.; Giovannini, L. Analysis of the diurnal development of a lake-valley circulation in the Alps based on airborne and surface measurements. Atmos. Chem. Phys. 2014, 14, 9771–9786. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Zardi, D.; de Franceschi, M. Climatological characteristics of the Ora del Garda wind in the Alps. Int. J. Climatol. 2015, 35, 4103–4115. [Google Scholar] [CrossRef]
- Davies, H.C.; Pichler, H. Mountain meteorology and ALPEX—An introduction. Meteorol. Atmos. Phys. 1990, 43, 3–4. [Google Scholar] [CrossRef]
- Bougeault, P.; Clar, A.J.; Benech, B.; Carissimo, B.; Pelon, J.; Richard, E. Momentum Budget over the Pyrénées: The PYREX Experiment. Bull. Am. Meteorol. Soc. 1990, 71, 806–818. [Google Scholar] [CrossRef]
- Bougeault, P.; Binder, P.; Buzzi, A.; Dirks, R.; Kuettner, J.; Houze, R.; Smith, R.B.; Steinacker, R.; Volkert, H. The MAP Special Observing Period. Bull. Am. Meteorol. Soc. 2001, 82, 433–462. [Google Scholar] [CrossRef]
- Ducrocq, V.; Braud, I.; Davolio, S.; Ferretti, R.; Flamant, C.; Jansa, A.; Kalthoff, N.; Richard, E.; Taupier-Letage, I.; Ayral, P.A.; et al. HyMeX-SOP1: The Field Campaign Dedicated to Heavy Precipitation and Flash Flooding in the Northwestern Mediterranean. Bull. Am. Meteorol. Soc. 2013, 95, 1083–1100. [Google Scholar] [CrossRef]
- Clements, W.E.; Archuleta, J.A.; Gudiksen, P.H. Experimental Design of the 1984 ASCOT Field Study. J. Appl. Meteorol. 1989, 28, 405–413. [Google Scholar] [CrossRef]
- Lothon, M.; Lohou, F.; Pino, D.; Couvreux, F.; Pardyjak, E.R.; Reuder, J.; Vilȁ-Guerau de Arellano, J.; Durand, P.; Hartogensis, O.; Legain, D.; et al. The BLLAST field experiment: Boundary-Layer Late Afternoon and Sunset Turbulence. Atmos. Chem. Phys. 2014, 14, 10931–10960. [Google Scholar] [CrossRef]
- Price, J.D.; Vosper, S.; Brown, A.; Ross, A.; Clark, P.; Davies, F.; Horlacher, V.; Claxton, B.; McGregor, J.R.; Hoare, J.S.; et al. COLPEX: Field and Numerical Studies over a Region of Small Hills. Bull. Am. Meteorol. Soc. 2011, 92, 1636–1650. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Behrendt, A.; Kottmeier, C.; Corsmeier, U.; Barthlott, C.; Craig, G.C.; Hagen, M.; Althausen, D.; Aoshima, F.; Arpagaus, M.; et al. The Convective and Orographically-induced Precipitation Study (COPS): The scientific strategy, the field phase, and research highlights. Q. J. R. Meteorol. Soc. 2011, 137, 3–30. [Google Scholar] [CrossRef]
- Damiani, R.; Geerts, B.; Demko, J.; Haimov, S.; French, J.; Zehnder, J.; Razdan, A.; Hu, J.; Petti, J.; Leuthold, M.; et al. The Cumulus, Photogrammetric, In Situ, and Doppler Observations Experiment of 2006. Bull. Am. Meteorol. Soc. 2008, 89, 57–73. [Google Scholar] [CrossRef]
- Smith, R.B.; Minder, J.R.; Nugent, A.D.; Storelvmo, T.; Kirshbaum, D.J.; Warren, R.; Lareau, N.; Palany, P.; James, A.; French, J. Orographic Precipitation in the Tropics: The Dominica Experiment. Bull. Am. Meteorol. Soc. 2012, 93, 1567–1579. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Pardyjak, E.R.; Di Sabatino, S.; Chow, F.K.; De Wekker, S.F.J.; Hoch, S.W.; Hacker, J.; Pace, J.C.; Pratt, T.; Pu, Z.; et al. The MATERHORN: Unraveling the Intricacies of Mountain Weather. Bull. Am. Meteorol. Soc. 2015, 96, 1945–1967. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Hoch, S.W.; Hahnenberger, M.; Muschinski, A.; Hohreiter, V.; Behn, M.; Cheon, Y.; Zhong, S.; Yao, W.; Fritts, D.; et al. Metcrax 2006: Meteorological Experiments in Arizona’s Meteor Crater. Bull. Am. Meteorol. Soc. 2008, 89, 1665–1680. [Google Scholar] [CrossRef]
- Lehner, M.; Whiteman, C.D.; Hoch, S.W.; Crosman, E.T.; Jeglum, M.E.; Cherukuru, N.W.; Calhoun, R.; Adler, B.; Kalthoff, N.; Rotunno, R.; et al. The METCRAX II Field Experiment: A Study of Downslope Windstorm-Type Flows in Arizona’s Meteor Crater. Bull. Am. Meteorol. Soc. 2016, 97, 217–235. [Google Scholar] [CrossRef]
- Ezcurra, A.; Benech, B.; Echelecou, A.; Santamaría, J.M.; Herrero, I.; Zulueta, E. Influence of local air flow regimes on the ozone content of two Pyrenean valleys. Atmos. Environ. 2013, 74, 367–377. [Google Scholar] [CrossRef]
- Lareau, N.P.; Crosman, E.; Whiteman, C.D.; Horel, J.D.; Hoch, S.W.; Brown, W.O.J.; Horst, T.W. The Persistent Cold-Air Pool Study. Bull. Am. Meteorol. Soc. 2013, 94, 51–63. [Google Scholar] [CrossRef]
- Gheusi, F.; Ravetta, F.; Delbarre, H.; Tsamalis, C.; Chevalier-Rosso, A.; Leroy, C.; Augustin, P.; Delmas, R.; Ancellet, G.; Athier, G.; et al. Pic 2005, a field campaign to investigate low-tropospheric ozone variability in the Pyrenees. Atmos. Res. 2011, 101, 640–665. [Google Scholar] [CrossRef]
- Larsen, S.; Fiedler, F.; Borrell, P. (Eds.) Exchange and Transport of Air Pollutants over Complex Terrain and the Sea; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Grubišić, V.; Doyle, J.D.; Kuettner, J.; Dirks, R.; Cohn, S.A.; Pan, L.L.; Mobbs, S.; Smith, R.B.; Whiteman, C.D.; Czyzyk, S.; et al. The Terrain-Induced Rotor Experiment: A Field Campaign Overview Including Observational Highlights. Bull. Am. Meteorol. Soc. 2008, 89, 1513–1533. [Google Scholar] [CrossRef]
- Weissmann, M.; Braun, F.J.; Gantner, L.; Mayr, G.J.; Rahm, S.; Reitebuch, O. The Alpine Mountain–Plain Circulation: Airborne Doppler Lidar Measurements and Numerical Simulations. Mon. Weather Rev. 2005, 133, 3095–3109. [Google Scholar] [CrossRef]
- Wotawa, G.; Kromp-Kolb, H. The research project VOTALP—General objectives and main results. Atmos. Environ. 2000, 34, 1319–1322. [Google Scholar] [CrossRef]
- Doran, J.C.; Fast, J.D.; Horel, J. The VTMX 2000 campaign. Bull. Am. Meteorol. Soc. 2002, 83, 537–551. [Google Scholar] [CrossRef]
- Blumen, W.E. Atmospheric Processes over Complex Terrain; Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1990. [Google Scholar]
- Barry, R.G. Mountain Weather and Climate, 3rd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Chow, F.; De Wekker, S.; Snyder, B. Mountain Weather Research and Forecasting: Recent Progress and Current Challenges; Springer Atmospheric Sciences; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Rotach, M.W.; Stiperski, I.; Fuhrer, O.; Goger, B.; Gohm, A.; Obleitner, F.; Rau, G.; Sfyri, E.; Vergeiner, J. Investigating Exchange Processes over Complex Topography: The Innsbruck Box (i-Box). Bull. Am. Meteorol. Soc. 2017, 98, 787–805. [Google Scholar] [CrossRef]
- Medeiros, L.E.; Fitzjarrald, D.R. Stable Boundary Layer in Complex Terrain. Part I: Linking Fluxes and Intermittency to an Average Stability Index. J. Appl. Meteorol. Climatol. 2014, 53, 2196–2215. [Google Scholar] [CrossRef]
- Emeis, S.; Kalthoff, N.; Adler, B.; Pardyjak, E.; Paci, A.; Junkermann, W. High-resolution observation of transport and exchange processes in mountainous terrain. Atmosphere 2018. in preparation. [Google Scholar]
- Chow, F.K.; Schär, C.; Ban, N.; Lundquist, K.A.; Schlemmer, L.; Shi, X. Crossing multiple gray zones in the transition from mesoscale to microscale simulation over complex terrain. Atmosphere 2018. in preparation. [Google Scholar]
- Hacker, J.; Draper, C.; Madaus, L. Challenges and Opportunities for Data Assimilation in Mountainous Environments. Atmosphere 2018. submitted. [Google Scholar]
- Kirshbaum, D.J.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist orographic convection: Physical mechanisms and links to surface-exchange processes. Atmosphere 2018, 9, 80. [Google Scholar] [CrossRef]
- Pal Arya, S. Introduction to Micrometeorology; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence: Models and Methods for Engineering Applications; Wiley: Hoboken, NJ, USA, 1984. [Google Scholar]
- Foken, T. Micrometeorology, 2nd ed.; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Cuxart, J.; Conangla, L.; Jiménez, M.A. Evaluation of the surface energy budget equation with experimental data and the ECMWF model in the Ebro Valley. J. Geophys. Res. Atmos. 2015, 120, 1008–1022. [Google Scholar] [CrossRef]
- Rotach, M.W.; Andretta, M.; Calanca, P.; Weigel, A.; Weiss, A. Boundary layer characteristics and turbulent exchange mechanisms in highly complex terrain. Acta Geophys. 2008, 56, 194–219. [Google Scholar] [CrossRef]
- Stiperski, I.; Rotach, M.W. On the Measurement of Turbulence Over Complex Mountainous Terrain. Bound. Layer Meteorol. 2016, 159, 97–121. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171–172, 137–152. [Google Scholar] [CrossRef]
- Cuxart, J.; Wrenger, B.; Martínez-Villagrasa, D.; Reuder, J.; Jonassen, M.O.; Jiménez, M.A.; Lothon, M.; Lohou, F.; Hartogensis, O.; Dünnermann, J.; et al. Estimation of the advection effects induced by surface heterogeneities in the surface energy budget. Atmos. Chem. Phys. 2016, 16, 9489–9504. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Albin, H.; Niedrist, G.; Scholz, K.; Enrico, T.; Peng, Z. On the energy balance closure and net radiation in complex terrain. Agric. For. Meteorol. 2016, 226–227, 37–49. [Google Scholar]
- Matzinger, N.; Andretta, M.; Gorsel, E.V.; Vogt, R.; Ohmura, A.; Rotach, M.W. Surface radiation budget in an Alpine valley. Q. J. R. Meteorol. Soc. 2003, 129, 877–895. [Google Scholar] [CrossRef]
- Nadeau, D.F.; Pardyjak, E.R.; Higgins, C.W.; Parlange, M.B. Similarity Scaling Over a Steep Alpine Slope. Bound. Layer Meteorol. 2013, 147, 401–419. [Google Scholar] [CrossRef]
- Rotach, M.W.; Calanca, P.; Graziani, G.; Gurtz, J.; Steyn, D.G.; Vogt, R.; Andretta, M.; Christen, A.; Cieslik, S.; Connolly, R.; et al. Turbulence Structure and Exchange Processes in an Alpine Valley: The Riviera Project. Bull. Am. Meteorol. Soc. 2004, 85, 1367–1385. [Google Scholar] [CrossRef]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Oldroyd, H.J.; Pardyjak, E.R.; Huwald, H.; Parlange, M.B. Adapting Tilt Corrections and the Governing Flow Equations for Steep, Fully Three-Dimensional, Mountainous Terrain. Bound. Layer Meteorol. 2016, 159, 539–565. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D. Evaluation of Cut-off Frequency and Correction of Filter-Induced Phase Lag and Attenuation in Eddy Covariance Analysis of Turbulence Data. Bound. Layer Meteorol. 2003, 108, 289–303. [Google Scholar] [CrossRef]
- Vinnichenko, N.K. The kinetic energy spectrum in the free atmosphere—1 second to 5 years. Tellus 1970, 22, 158–166. [Google Scholar] [CrossRef]
- Večenaj, Ž.; De Wekker, S.F.J.; Grubišić, V. Near-Surface Characteristics of the Turbulence Structure during a Mountain-Wave Event. J. Appl. Meteorol. Climatol. 2010, 50, 1088–1106. [Google Scholar] [CrossRef]
- Večenaj, Ž.; Belušić, D.; Grubišić, V.; Grisogono, B. Along-Coast Features of Bora-Related Turbulence. Bound. Layer Meteorol. 2012, 143, 527–545. [Google Scholar] [CrossRef]
- Babić, N.; Večenaj, Ž.; De Wekker, S.F.J. Spectral gap characteristics in a daytime valley boundary layer. Q. J. R. Meteorol. Soc. 2017, 143, 2509–2523. [Google Scholar] [CrossRef]
- Oncley, S.P.; Friehe, C.A.; Larue, J.C.; Businger, J.A.; Itsweire, E.C.; Chang, S.S. Surface-Layer Fluxes, Profiles, and Turbulence Measurements over Uniform Terrain under Near-Neutral Conditions. J. Atmos. Sci. 1996, 53, 1029–1044. [Google Scholar] [CrossRef]
- Howell, J.F.; Mahrt, L. Multiresolution Flux Decomposition. Bound. Layer Meteorol. 1997, 83, 117–137. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. The Cospectral Gap and Turbulent Flux Calculations. J. Atmos. Ocean. Technol. 2003, 20, 660–672. [Google Scholar] [CrossRef]
- Večenaj, Ž.; De Wekker, S.F.J. Determination of non-stationarity in the surface layer during the T-REX experiment. Q. J. R. Meteorol. Soc. 2015, 141, 1560–1571. [Google Scholar] [CrossRef]
- Babić, N.; Večenaj, Ž.; De Wekker, S.F.J. Flux–Variance Similarity in Complex Terrain and Its Sensitivity to Different Methods of Treating Non-stationarity. Bound. Layer Meteorol. 2016, 159, 123–145. [Google Scholar] [CrossRef]
- Lampert, A.; Pätzold, F.; Jiménez, M.A.; Lobitz, L.; Martin, S.; Lohmann, G.; Canut, G.; Legain, D.; Bange, J.; Martínez-Villagrasa, D.; et al. A study of local turbulence and anisotropy during the afternoon and evening transition with an unmanned aerial system and mesoscale simulation. Atmos. Chem. Phys. 2016, 16, 8009–8021. [Google Scholar] [CrossRef]
- Stiperski, I.; Calaf, M. Dependence of near-surface similarity scaling on the anisotropy of atmospheric turbulence. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- Carruthers, D.J.; Hunt, J.C.R. Fluid Mechanics of Airflow over Hills: Turbulence, Fluxes, and Waves in the Boundary Layer. In Atmospheric Processes Over Complex Terrain; Meteorological Monographs; Blumen, W., Ed.; American Meteorological Society: Boston, MA, USA, 1990; Volume 23, pp. 83–103. [Google Scholar]
- Moraes, O.L.L.; Acevedo, O.C.; Degrazia, G.A.; Anfossi, D.; da Silva, R.; Anabor, V. Surface layer turbulence parameters over a complex terrain. Atmos. Environ. 2005, 39, 3103–3112. [Google Scholar] [CrossRef]
- Sfyri, E.; Rotach, M.; Stiperski, I.; Bosveld, F.; Obleitner, F.; Lehner, M. Scalar flux similarity in the layer near the surface over mountainous terrain. Bound. Layer Meteorol. 2018. submitted. [Google Scholar]
- Medeiros, L.E.; Fitzjarrald, D.R. Stable Boundary Layer in Complex Terrain. Part II: Geometrical and Sheltering Effects on Mixing. J. Appl. Meteorol. Climatol. 2015, 54, 170–188. [Google Scholar] [CrossRef]
- Noppel, H.; Fiedler, F. Mesoscale Heat Transport Over Complex Terrain By Slope Winds—A Conceptual Model And Numerical Simulations. Bound. Layer Meteorol. 2002, 104, 73–97. [Google Scholar] [CrossRef]
- Kirshbaum, D.J. On upstream blocking over heated mountain ridges. Q. J. R. Meteorol. Soc. 2017, 143, 53–68. [Google Scholar] [CrossRef]
- Prandtl, L. Führer durch die Strömungslehre; Vieweg und Sohn: Braunschweig, Germany, 1942. [Google Scholar]
- Defant, F. Zur Theorie der Hangwinde, nebst Bemerkungen zur Theorie der Berg- und Talwinde. Arch. Meteorol. Geophys. Bioklimatol. A 1949, 1, 421–450. [Google Scholar]
- Haiden, T. On the Pressure Field in the Slope Wind Layer. J. Atmos. Sci. 2003, 60, 1632–1635. [Google Scholar] [CrossRef]
- Gutman, L.N.; Malbakhov, V.M. On the theory of katabatic winds of Antarctic. Meteorol. Issled. 1964, 9, 150–155. (In Russian) [Google Scholar]
- Fedorovich, E.; Shapiro, A. Oscillations in Prandtl slope flow started from rest. Q. J. R. Meteorol. Soc. 2017, 143, 670–677. [Google Scholar] [CrossRef]
- Zammett, R.J.; Fowler, A.C. Katabatic Winds on Ice Sheets: A Refinement of the Prandtl Model. J. Atmos. Sci. 2007, 64, 2707–2716. [Google Scholar] [CrossRef]
- Egger, J. On the Linear Two-Dimensional Theory of Thermally Induced Slope Winds. Beitr. Phys. Atmos. 1981, 54, 465–481. [Google Scholar]
- Zardi, D.; Serafin, S. An analytic solution for time-periodic thermally driven slope flows. Q. J. R. Meteorol. Soc. 2015, 141, 1968–1974. [Google Scholar] [CrossRef]
- Ye, Z.J.; Segal, M.; Pielke, R.A. Effects of Atmospheric Thermal Stability and Slope Steepness on the Development of Daytime Thermally Induced Upslope Flow. J. Atmos. Sci. 1987, 44, 3341–3354. [Google Scholar] [CrossRef]
- Grisogono, B.; Oerlemans, J. Katabatic Flow: Analytic Solution for Gradually Varying Eddy Diffusivities. J. Atmos. Sci. 2001, 58, 3349–3354. [Google Scholar] [CrossRef]
- Giometto, M.G.; Grandi, R.; Fang, J.; Monkewitz, P.A.; Parlange, M.B. Katabatic Flow: A Closed-Form Solution with Spatially-Varying Eddy Diffusivities. Bound. Layer Meteorol. 2017, 162, 307–317. [Google Scholar] [CrossRef]
- Schumann, U. Large-eddy simulation of the up-slope boundary layer. Q. J. R. Meteorol. Soc. 1990, 116, 637–670. [Google Scholar] [CrossRef]
- Vergeiner, I.; Dreiseitl, E. Valley winds and slope winds—Observations and elementary thoughts. Meteorol. Atmos. Phys. 1987, 36, 264–286. [Google Scholar] [CrossRef]
- Schmidli, J. Daytime Heat Transfer Processes over Mountainous Terrain. J. Atmos. Sci. 2013, 70, 4041–4066. [Google Scholar] [CrossRef]
- Kuwagata, T.; Kondo, J. Observation and modeling of thermally induced upslope flow. Bound. Layer Meteorol. 1989, 49, 265–293. [Google Scholar]
- Leukauf, D.; Gohm, A.; Rotach, M.W. Quantifying horizontal and vertical tracer mass fluxes in an idealized valley during daytime. Atmos. Chem. Phys. 2016, 16, 13049–13066. [Google Scholar] [CrossRef]
- Leukauf, D.; Gohm, A.; Rotach, M.W.; Wagner, J.S. The Impact of the Temperature Inversion Breakup on the Exchange of Heat and Mass in an Idealized Valley: Sensitivity to the Radiative Forcing. J. Appl. Meteorol. Climatol. 2015, 54, 2199–2216. [Google Scholar] [CrossRef]
- Hocut, C.; Liberzon, D.; Fernando, H. Separation of upslope flow over a uniform slope. J. Fluid Mech. 2015, 775, 266–287. [Google Scholar] [CrossRef]
- Khanna, S.; Brasseur, J.G. Analysis of Monin–Obukhov similarity from large-eddy simulation. J. Fluid Mech. 1997, 345, 251–286. [Google Scholar] [CrossRef]
- Crook, N.A.; Tucker, D.F. Flow over Heated Terrain. Part I: Linear Theory and Idealized Numerical Simulations. Mon. Weather Rev. 2005, 133, 2552–2564. [Google Scholar] [CrossRef]
- Kirshbaum, D.J. On Thermally Forced Circulations over Heated Terrain. J. Atmos. Sci. 2013, 70, 1690–1709. [Google Scholar] [CrossRef]
- Kirshbaum, D.J.; Wang, C.C. Boundary Layer Updrafts Driven by Airflow over Heated Terrain. J. Atmos. Sci. 2014, 71, 1425–1442. [Google Scholar] [CrossRef]
- Braham, R.R.; Draginis, M. Roots of orographic cumuli. J. Meteorol. 1960, 17, 214–226. [Google Scholar] [CrossRef]
- Raymond, D.; Wilkening, M. Mountain-Induced Convection under Fair Weather Conditions. J. Atmos. Sci. 1980, 37, 2693–2706. [Google Scholar] [CrossRef]
- Souza, E.P.; Rennó, N.O.; Silva Dias, M.A.F. Convective Circulations Induced by Surface Heterogeneities. J. Atmos. Sci. 2000, 57, 2915–2922. [Google Scholar] [CrossRef]
- Rennó, N.O.; Ingersoll, A.P. Natural Convection as a Heat Engine: A Theory for CAPE. J. Atmos. Sci. 1996, 53, 572–585. [Google Scholar] [CrossRef]
- Tian, W.; Parker, D.J. A Modeling Study and Scaling Analysis of Orographic Effects on Boundary Layer Shallow Convection. J. Atmos. Sci. 2003, 60, 1981–1991. [Google Scholar] [CrossRef]
- Wang, C.C.; Kirshbaum, D.J. Thermally Forced Convection over a Mountainous Tropical Island. J. Atmos. Sci. 2015, 72, 2484–2506. [Google Scholar] [CrossRef]
- Rampanelli, G.; Zardi, D. A Method to Determine the Capping Inversion of the Convective Boundary Layer. J. Appl. Meteorol. 2004, 43, 925–933. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Daytime Development of the Boundary Layer over a Plain and in a Valley under Fair Weather Conditions: A Comparison by Means of Idealized Numerical Simulations. J. Atmos. Sci. 2011, 68, 2128–2141. [Google Scholar] [CrossRef]
- Schmidli, J.; Rotunno, R. Influence of the Valley Surroundings on Valley Wind Dynamics. J. Atmos. Sci. 2012, 69, 561–577. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Serafin, S.; Zardi, D. The thermally driven diurnal wind system of the Adige Valley in the Italian Alps: Thermally Driven Wind System of Adige Valley. Q. J. R. Meteorol. Soc. 2017, 143, 2389–2402. [Google Scholar] [CrossRef]
- Schmidli, J.; Rotunno, R. The Quasi-Steady State of the Valley Wind System. Front. Earth Sci. 2015, 3, 79. [Google Scholar] [CrossRef]
- Nickus, U.; Vergeiner, I. The thermal structure of the Inn valley atmosphere. Arch. Meteorol. Geophys. Bioklimatol. 1984, A33, 195–215. [Google Scholar]
- Wagner, J.S.; Gohm, A.; Rotach, M.W. Influence of along-valley terrain heterogeneity on exchange processes over idealized valleys. Atmos. Chem. Phys. 2015, 15, 6589–6603. [Google Scholar] [CrossRef]
- Wagner, A. Theorie und Beobachtung der periodischen Gebirgswinde. Gerlands Beitr. Geophys. 1938, 52, 408–449. [Google Scholar]
- Steinacker, R. Area-Height Distribution of a Valley and its Relation to the Valley Wind. Beitr. Phys. Atmos. 1984, 57, 64–71. [Google Scholar]
- Rampanelli, G.; Zardi, D.; Rotunno, R. Mechanisms of Up-Valley Winds. J. Atmos. Sci. 2004, 61, 3097–3111. [Google Scholar] [CrossRef]
- Schmidli, J.; Rotunno, R. Mechanisms of Along-Valley Winds and Heat Exchange over Mountainous Terrain. J. Atmos. Sci. 2010, 67, 3033–3047. [Google Scholar] [CrossRef]
- Wagner, J.S.; Gohm, A.; Rotach, M.W. The impact of valley geometry on daytime thermally driven flows and vertical transport processes: Impact of Valley Geometry on Thermally Driven Flows. Q. J. R. Meteorol. Soc. 2015, 141, 1780–1794. [Google Scholar] [CrossRef]
- Weigel, A.P.; Chow, F.K.; Rotach, M.W.; Street, R.L.; Xue, M. High-Resolution Large-Eddy Simulations of Flow in a Steep Alpine Valley. Part II: Flow Structure and Heat Budgets. J. Appl. Meteorol. Climatol. 2006, 45, 87–107. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Atmospheric boundary layer structures associated with the Ora del Garda wind in the Alps as revealed from airborne and surface measurements. Atmos. Res. 2013, 132–133, 473–489. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Analysis of the Urban Thermal Fingerprint of the City of Trento in the Alps. J. Appl. Meteorol. Climatol. 2011, 50, 1145–1162. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M.; Chen, F. Numerical simulations of boundary-layer processes and urban-induced alterations in an Alpine valley. Int. J. Climatol. 2014, 34, 1111–1131. [Google Scholar] [CrossRef]
- Rendón, A.M.; Salazar, J.F.; Palacio, C.A.; Wirth, V.; Brötz, B. Effects of Urbanization on the Temperature Inversion Breakup in a Mountain Valley with Implications for Air Quality. J. Appl. Meteorol. Climatol. 2014, 53, 840–858. [Google Scholar] [CrossRef]
- Rendón, A.M.; Salazar, J.F.; Palacio, C.A.; Wirth, V. Temperature Inversion Breakup with Impacts on Air Quality in Urban Valleys Influenced by Topographic Shading. J. Appl. Meteorol. Climatol. 2015, 54, 302–321. [Google Scholar] [CrossRef]
- Vergeiner, I. An elementary valley wind model. Meteorol. Atmos. Phys. 1987, 36, 255–263. [Google Scholar] [CrossRef]
- Egger, J. Simple models of the valley-plain circulation Part I: Minimum resolution model. Meteorol. Atmos. Phys. 1987, 36, 231–242. [Google Scholar]
- Egger, J. Thermally forced flows: Theory. In Atmospheric Processes over Complex Terrain; Blumen, W., Ed.; Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1990; Volume 23, pp. 43–58. [Google Scholar]
- Zängl, G. A reexamination of the valley wind system in the Alpine Inn Valley with numerical simulations. Meteorol. Atmos. Phys. 2004, 87, 241–256. [Google Scholar] [CrossRef]
- Doran, J.C.; Zhong, S. Thermally Driven Gap Winds into the Mexico City Basin. J. Appl. Meteorol. 2000, 39, 1330–1340. [Google Scholar] [CrossRef]
- Egger, J.; Bajrachaya, S.; Egger, U.; Heinrich, R.; Reuder, J.; Shayka, P.; Wendt, H.; Wirth, V. Diurnal Winds in the Himalayan Kali Gandaki Valley. Part I: Observations. Mon. Weather Rev. 2000, 128, 1106–1122. [Google Scholar] [CrossRef]
- Zängl, G.; Egger, J.; Wirth, V. Diurnal Winds in the Himalayan Kali Gandaki Valley. Part II: Modeling. Mon. Weather Rev. 2001, 129, 1062–1080. [Google Scholar] [CrossRef]
- Egger, J.; Bajrachaya, S.; Heinrich, R.; Kolb, P.; Lämmlein, S.; Mech, M.; Reuder, J.; Schäper, W.; Shakya, P.; Schween, J.; et al. Diurnal Winds in the Himalayan Kali Gandaki Valley. Part III: Remotely Piloted Aircraft Soundings. Mon. Weather Rev. 2002, 130, 2042–2058. [Google Scholar] [CrossRef]
- Schnitzhofer, R.; Norman, M.; Wisthaler, A.; Vergeiner, J.; Harnisch, F.; Gohm, A.; Obleitner, F.; Fix, A.; Neininger, B.; Hansel, A. A multimethodological approach to study the spatial distribution of air pollution in an Alpine valley during wintertime. Atmos. Chem. Phys. 2009, 9, 3385–3396. [Google Scholar] [CrossRef]
- Gohm, A.; Harnisch, F.; Vergeiner, J.; Obleitner, F.; Schnitzhofer, R.; Hansel, A.; Fix, A.; Neininger, B.; Emeis, S.; Schäfer, K. Air Pollution Transport in an Alpine Valley: Results From Airborne and Ground-Based Observations. Bound. Layer Meteorol. 2009, 131, 441–463. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Residual kriging analysis of airborne measurements: Application to the mapping of atmospheric boundary-layer thermal structures in a mountain valley. Atmos. Sci. Lett. 2013, 14, 79–85. [Google Scholar] [CrossRef]
- De Wekker, S.F.J.; Godwin, K.S.; Emmitt, G.D.; Greco, S. Airborne Doppler Lidar Measurements of Valley Flows in Complex Coastal Terrain. J. Appl. Meteorol. Climatol. 2012, 51, 1558–1574. [Google Scholar] [CrossRef]
- Lehner, M.; Rotach, M.W.R. Current challenges in understanding and predicting transport and exchange in the atmosphere over mountainous terrain. Atmosphere 2018. in preparation. [Google Scholar]
- De Wekker, S.F.J.; Kossmann, M. Convective Boundary Layer Heights Over Mountainous Terrain—A Review of Concepts. Front. Earth Sci. 2015, 3, 77. [Google Scholar] [CrossRef]
- Kossmann, M.; Corsmeier, U.; De Wekker, S.F.; Fiedler, F.; Vögtlin, R.; Kalthoff, N.; Güsten, H.; Neininger, B. Observations of handover processes between the atmospheric boundary layer and the free troposphere over mountainous terrain. Beitr. Phys. Atmos. 1999, 72, 329–350. [Google Scholar]
- De Wekker, S.F.J.; Steyn, D.G.; Nyeki, S. A Comparison Of Aerosol-Layer And Convective Boundary-Layer Structure Over A Mountain Range During Staaarte’ 97. Bound. Layer Meteorol. 2004, 113, 249–271. [Google Scholar] [CrossRef]
- Whiteman, C.D. Breakup of Temperature Inversions in Deep Mountain Valleys: Part I. Observations. J. Appl. Meteorol. 1982, 21, 270–289. [Google Scholar] [CrossRef]
- Weigel, A.P.; Rotach, M.W. Flow structure and turbulence characteristics of the daytime atmosphere in a steep and narrow Alpine valley. Q. J. R. Meteorol. Soc. 2004, 130, 2605–2627. [Google Scholar] [CrossRef]
- Khodayar, S.; Kalthoff, N.; Fiebig-Wittmaack, M.; Kohler, M. Evolution of the atmospheric boundary-layer structure of an arid Andes Valley. Meteorol. Atmos. Phys. 2008, 99, 181–198. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Daytime Heat Transfer Processes Related to Slope Flows and Turbulent Convection in an Idealized Mountain Valley. J. Atmos. Sci. 2010, 67, 3739–3756. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Structure of the Atmospheric Boundary Layer in the Vicinity of a Developing Upslope Flow System: A Numerical Model Study. J. Atmos. Sci. 2010, 67, 1171–1185. [Google Scholar] [CrossRef]
- Fast, J.D.; Zhong, S. Meteorological factors associated with inhomogeneous ozone concentrations within the Mexico City basin. J. Geophys. Res. Atmos. 1998, 103, 18927–18946. [Google Scholar] [CrossRef]
- Lu, R.; Turco, R.P. Air Pollutant Transport in a Coastal Environment. Part I: Two-Dimensional Simulations of Sea-Breeze and Mountain Effects. J. Atmos. Sci. 1994, 51, 2285–2308. [Google Scholar] [CrossRef]
- Ching, J.K.S.; Shipley, S.T.; Browell, E.V. Evidence for cloud venting of mixed layer ozone and aerosols. Atmos. Environ. 1988, 22, 225–242. [Google Scholar] [CrossRef]
- Kalthoff, N.; Adler, B.; Wieser, A.; Kohler, M.; Träumner, K.; Handwerker, J.; Corsmeier, U.; Khodayar, S.; Lambert, D.; Kopmann, A.; et al. KITcube—A mobile observation platform for convection studies deployed during HyMeX. Meteorol. Z. 2013, 22, 633–647. [Google Scholar] [CrossRef]
- Panosetti, D.; Böing, S.; Schlemmer, L.; Schmidli, J. Idealized Large-Eddy and Convection-Resolving Simulations of Moist Convection over Mountainous Terrain. J. Atmos. Sci. 2016, 73, 4021–4041. [Google Scholar] [CrossRef]
- Langhans, W.; Schmidli, J.; Fuhrer, O.; Bieri, S.; Schär, C. Long-Term Simulations of Thermally Driven Flows and Orographic Convection at Convection-Parameterizing and Cloud-Resolving Resolutions. J. Appl. Meteorol. Climatol. 2013, 52, 1490–1510. [Google Scholar] [CrossRef]
- Henne, S.; Furger, M.; Nyeki, S.; Steinbacher, M.; Neininger, B.; de Wekker, S.F.J.; Dommen, J.; Spichtinger, N.; Stohl, A.; Prévôt, A.S.H. Quantification of topographic venting of boundary layer air to the free troposphere. Atmos. Chem. Phys. 2004, 4, 497–509. [Google Scholar] [CrossRef]
- Adler, B.; Kalthoff, N. Multi-scale Transport Processes Observed in the Boundary Layer over a Mountainous Island. Bound. Layer Meteorol. 2014, 153, 515–537. [Google Scholar] [CrossRef]
- Lang, M.N.; Gohm, A.; Wagner, J.S. The impact of embedded valleys on daytime pollution transport over a mountain range. Atmos. Chem. Phys. 2015, 15, 11981–11998. [Google Scholar] [CrossRef]
- Adler, B.; Kalthoff, N.; Kohler, M.; Handwerker, J.; Wieser, A.; Corsmeier, U.; Kottmeier, C.; Lambert, D.; Bock, O. The Variability of Water Vapour over the Mountainous Island of Corsica. Q. J. R. Meteorol. Soc. 2016, 142, 335–346. [Google Scholar] [CrossRef]
- Bischoff-Gauß, I.; Kalthoff, N.; Fiedler, F. The Impact of Secondary Flow Systems on Air Pollution in the Area of São Paulo. J. Appl. Meteorol. 1998, 37, 269–287. [Google Scholar] [CrossRef]
- Bischoff-Gauß, I.; Kalthoff, N.; Khodayar, S.; Fiebig-Wittmaack, M.; Montecinos, S. Model Simulations of the Boundary-Layer Evolution over an Arid Andes Valley. Bound. Layer Meteorol. 2008, 128, 357–379. [Google Scholar] [CrossRef]
- Arritt, R.W.; Wilczak, J.M.; Young, G.S. Observations and Numerical Modeling of an Elevated Mixed Layer. Mon. Weather Rev. 1992, 120, 2869–2880. [Google Scholar] [CrossRef]
- Kalthoff, N.; Horlacher, V.; Corsmeier, U.; Volz-Thomas, A.; Kolahgar, B.; Geiß, H.; Möllmann-Coers, M.; Knaps, A. Influence of valley winds on transport and dispersion of airborne pollutants in the Freiburg-Schauinsland area. J. Geophys. Res. Atmos. 2000, 105, 1585–1597. [Google Scholar] [CrossRef]
- Kuwagata, T.; Kimura, F. Daytime Boundary Layer Evolution in a Deep Valley. Part II: Numerical Simulation of the Cross-Valley Circulation. J. Appl. Meteorol. 1997, 36, 883–895. [Google Scholar] [CrossRef]
- Wagner, J.S.; Gohm, A.; Rotach, M.W. The Impact of Horizontal Model Grid Resolution on the Boundary Layer Structure over an Idealized Valley. Mon. Weather Rev. 2014, 142, 3446–3465. [Google Scholar] [CrossRef]
- Kalthoff, N.; Bischoff-Gauß, I.; Fiebig-Wittmaack, M.; Fiedler, F.; Thürauf, J.; Novoa, E.; Pizarro, C.; Castillo, R.; Gallardo, L.; Rondanelli, R.; et al. Mesoscale Wind Regimes in Chile at 30°S. J. Appl. Meteorol. 2002, 41, 953–970. [Google Scholar] [CrossRef]
- De Wekker, S.F.J.; Steyn, D.G.; Fast, J.D.; Rotach, M.W.; Zhong, S. The performance of RAMS in representing the convective boundary layer structure in a very steep valley. Environ. Fluid Mech. 2005, 5, 35–62. [Google Scholar] [CrossRef][Green Version]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound. Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Kalthoff, N.; Binder, H.J.; Kossmann, M.; VÖgtlin, R.; Corsmeier, U.; Fiedler, F.; Schlager, H. Temporal evolution and spatial variation of the boundary layer over complex terrain. Atmos. Environ. 1998, 32, 1179–1194. [Google Scholar]
- Kossmann, M.; Vögtlin, R.; Corsmeier, U.; Vogel, B.; Fiedler, F.; Binder, H.J.; Kalthoff, N.; Beyrich, F. Aspects of the convective boundary layer structure over complex terrain. Atmos. Environ. 1998, 32, 1323–1348. [Google Scholar] [CrossRef]
- Stull, R. A theory for mixed-layer-top levelness over irregular topography. In Proceedings of the 10th AMS Symposium on Turbulence and Diffusion, 29 September–2 October, Portland, OR, USA; 1992; pp. 92–94. [Google Scholar]
- Arduini, G.; Staquet, C.; Chemel, C. Interactions between the Nighttime Valley-Wind System and a Developing Cold-Air Pool. Bound. Layer Meteorol. 2016, 161, 49–72. [Google Scholar] [CrossRef]
- Arduini, G.; Chemel, C.; Staquet, C. Energetics of Deep Alpine Valleys in Pooling and Draining Configurations. J. Atmos. Sci. 2017, 74, 2105–2124. [Google Scholar] [CrossRef]
- Cuxart, J. Nocturnal basin low-level jets: An integrated study. Acta Geophys. 2008, 56, 100–113. [Google Scholar] [CrossRef]
- Martínez, D.; Jiménez, M.A.; Cuxart, J.; Mahrt, L. Heterogeneous Nocturnal Cooling in a Large Basin under Very Stable Conditions. Bound. Layer Meteorol. 2010, 137, 97–113. [Google Scholar] [CrossRef]
- De Wekker, S.F.J.; Whiteman, C.D. On the Time Scale of Nocturnal Boundary Layer Cooling in Valleys and Basins and over Plains. J. Appl. Meteorol. Climatol. 2006, 45, 813–820. [Google Scholar] [CrossRef]
- Dorninger, M.; Whiteman, C.D.; Bica, B.; Eisenbach, S.; Pospichal, B.; Steinacker, R. Meteorological Events Affecting Cold-Air Pools in a Small Basin. J. Appl. Meteorol. Climatol. 2011, 50, 2223–2234. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Haiden, T.; Pospichal, B.; Eisenbach, S.; Steinacker, R. Minimum Temperatures, Diurnal Temperature Ranges, and Temperature Inversions in Limestone Sinkholes of Different Sizes and Shapes. J. Appl. Meteorol. 2004, 43, 1224–1236. [Google Scholar] [CrossRef]
- Cuxart, J.; Jiménez, M.A. Mixing Processes in a Nocturnal Low-Level Jet: An LES Study. J. Atmos. Sci. 2007, 64, 1666–1679. [Google Scholar] [CrossRef]
- Banta, R. Stable-boundary-layer regimes from the perspective of the low-level jet. Acta Geophys. 2008, 56, 58–87. [Google Scholar] [CrossRef]
- Mahrt, L. Stratified Atmospheric Boundary Layers. Bound. Layer Meteorol. 1999, 90, 375–396. [Google Scholar] [CrossRef]
- Goger, B.; Rotach, M.W.; Gohm, A.; Fuhrer, O.; Stiperski, I.; Holtslag, A. The Impact of 3D Effects on the Simulation of Turbulence Kinetic Energy Structure in a Major Alpine Valley. Bound. Layer Meteorol. 2018, in press. [Google Scholar] [CrossRef]
- Horst, T.W.; Doran, J.C. The Turbulence Structure of Nocturnal Slope Flow. J. Atmos. Sci. 1988, 45, 605–616. [Google Scholar] [CrossRef]
- Oldroyd, H.J.; Pardyjak, E.R.; Higgins, C.W.; Parlange, M.B. Buoyant Turbulent Kinetic Energy Production in Steep-Slope Katabatic Flow. Bound. Layer Meteorol. 2016, 161, 405–416. [Google Scholar] [CrossRef]
- Banta, R.M.; Pichugina, Y.L.; Newsom, R.K. Relationship between Low-Level Jet Properties and Turbulence Kinetic Energy in the Nocturnal Stable Boundary Layer. J. Atmos. Sci. 2003, 60, 2549–2555. [Google Scholar] [CrossRef]
- Grachev, A.A.; Leo, L.S.; Di Sabatino, S.; Fernando, H.J.S.; Pardyjak, E.R.; Fairall, C.W. Structure of Turbulence in Katabatic Flows Below and Above the Wind-Speed Maximum. Bound. Layer Meteorol. 2016, 159, 469–494. [Google Scholar] [CrossRef]
- Parmhed, O.; Oerlemans, J.; Grisogono, B. Describing surface fluxes in katabatic flow on Breidamerkurjökull, Iceland. Q. J. R. Meteorol. Soc. 2004, 130, 1137–1151. [Google Scholar] [CrossRef]
- Litt, M.; Sicart, J.E.; Helgason, W.D.; Wagnon, P. Turbulence Characteristics in the Atmospheric Surface Layer for Different Wind Regimes over the Tropical Zongo Glacier (Bolivia, 16°S). Bound. Layer Meteorol. 2015, 154, 471–495. [Google Scholar] [CrossRef]
- Sun, J.; Nappo, C.J.; Mahrt, L.; Belušić, D.; Grisogono, B.; Stauffer, D.R.; Pulido, M.; Staquet, C.; Jiang, Q.; Pouquet, A.; et al. Review of wave-turbulence interactions in the stable atmospheric boundary layer. Rev. Geophys. 2015, 53, 956–993. [Google Scholar] [CrossRef]
- Nappo, C.J.; Chimonas, G. Wave Exchange between the Ground Surface and a Boundary-Layer Critical Level. J. Atmos. Sci. 1992, 49, 1075–1091. [Google Scholar] [CrossRef]
- Chimonas, G.; Nappo, C.J. Wave drag in the planetary boundary layer over complex terrain. Bound. Layer Meteorol. 1989, 47, 217–232. [Google Scholar] [CrossRef]
- Grisogono, B. Dissipation of Wave Drag in the Atmospheric Boundary Layer. J. Atmos. Sci. 1994, 51, 1237–1243. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Holtslag, A.A.M.; Nappo, C.J.; van de Wiel, B.J.H.; Mahrt, L. Exploring the Possible Role of Small-Scale Terrain Drag on Stable Boundary Layers over Land. J. Appl. Meteorol. Climatol. 2008, 47, 2518–2530. [Google Scholar] [CrossRef]
- Tsiringakis, A.; Steeneveld, G.J.; Holtslag, A.A.M. Small-scale orographic gravity wave drag in stable boundary layers and its impact on synoptic systems and near-surface meteorology: Orographic Gravity Wave Drag in Stable Boundary Layers. Q. J. R. Meteorol. Soc. 2017, 143, 1504–1516. [Google Scholar] [CrossRef]
- Sun, J.; Mahrt, L.; Nappo, C.; Lenschow, D.H. Wind and Temperature Oscillations Generated by Wave-Turbulence Interactions in the Stably Stratified Boundary Layer. J. Atmos. Sci. 2014, 72, 1484–1503. [Google Scholar] [CrossRef]
- Mahrt, L. Stably Stratified Atmospheric Boundary Layers. Annu. Rev. Fluid Mech. 2014, 46, 23–45. [Google Scholar] [CrossRef]
- Hoover, J.D.; Stauffer, D.R.; Richardson, S.J.; Mahrt, L.; Gaudet, B.J.; Suarez, A. Submeso Motions within the Stable Boundary Layer and Their Relationships to Local Indicators and Synoptic Regime in Moderately Complex Terrain. J. Appl. Meteorol. Climatol. 2014, 54, 352–369. [Google Scholar] [CrossRef]
- Vercauteren, N.; Mahrt, L.; Klein, R. Investigation of interactions between scales of motion in the stable boundary layer. Q. J. R. Meteorol. Soc. 2016, 142, 2424–2433. [Google Scholar] [CrossRef]
- Galperin, B.; Sukoriansky, S.; Anderson, P.S. On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Lett. 2007, 8, 65–69. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. On the turbulent Prandtl number in the stable atmospheric boundary layer. Bound. Layer Meteorol. 2007, 125, 329–341. [Google Scholar] [CrossRef]
- Nappo, C.J. An Introduction to Atmospheric Gravity Waves, 2nd ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Jiang, Q.; Doyle, J.D. Diurnal Variation of Downslope Winds in Owens Valley during the Sierra Rotor Experiment. Mon. Weather Rev. 2008, 136, 3760–3780. [Google Scholar] [CrossRef]
- Mayr, G.J.; Armi, L. The Influence of Downstream Diurnal Heating on the Descent of Flow across the Sierras. J. Appl. Meteorol. Climatol. 2010, 49, 1906–1912. [Google Scholar] [CrossRef]
- Armi, L.; Mayr, G.J. The Descending Stratified Flow and Internal Hydraulic Jump in the Lee of the Sierras. J. Appl. Meteorol. Climatol. 2011, 50, 1995–2011. [Google Scholar] [CrossRef]
- Strauss, L.; Serafin, S.; Grubišić, V. Atmospheric Rotors and Severe Turbulence in a Long Deep Valley. J. Atmos. Sci. 2016, 73, 1481–1506. [Google Scholar] [CrossRef]
- Adler, B.; Kalthoff, N. The Impact of Upstream Flow on the Atmospheric Boundary Layer in a Valley on a Mountainous Island. Bound. Layer Meteorol. 2016, 158, 429–452. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D. Study of wintertime high pollution episodes during the Brenner-South ALPNAP measurement campaign. Meteorol. Atmos. Phys. 2009, 103, 237–250. [Google Scholar] [CrossRef]
- Sachsperger, J.; Serafin, S.; Grubišić, V. Lee Waves on the Boundary-Layer Inversion and Their Dependence on Free-Atmospheric Stability. Front. Earth Sci. 2015, 3, 626–633. [Google Scholar] [CrossRef]
- Armi, L.; Mayr, G.J. Virtual and Real Topography for Flows across Mountain Ranges. J. Appl. Meteorol. Climatol. 2015, 54, 723–731. [Google Scholar]
- Scheffknecht, P.; Serafin, S.; Grubišić, V. A long-lived supercell over mountainous terrain. Q. J. R. Meteorol. Soc. 2018, 143, 2973–2986. [Google Scholar] [CrossRef]
- Epifanio, C.C. A Method for Imposing Surface Stress and Heat Flux Conditions in Finite-Difference Models with Steep Terrain. Mon. Weather Rev. 2007, 135, 906–917. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An Immersed Boundary Method Enabling Large-Eddy Simulations of Flow over Complex Terrain in the WRF Model. Mon. Weather Rev. 2012, 140, 3936–3955. [Google Scholar] [CrossRef]
- Colette, A.; Chow, F.K.; Street, R.L. A Numerical Study of Inversion-Layer Breakup and the Effects of Topographic Shading in Idealized Valleys. J. Appl. Meteorol. 2003, 42, 1255–1272. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Characterization of the Thermal Structure inside an Urban Canyon: Field Measurements and Validation of a Simple Model. J. Appl. Meteorol. Climatol. 2013, 52, 64–81. [Google Scholar] [CrossRef]
- Duine, G.J.; De Wekker, S.F.J. The effects of horizontal grid spacing on simulated daytime boundary layer depths in an area of complex terrain in Utah. Environ. Fluid Mech. 2017. [Google Scholar] [CrossRef]
- Leukauf, D.; Gohm, A.; Rotach, M.W. Toward Generalizing the Impact of Surface Heating, Stratification, and Terrain Geometry on the Daytime Heat Export from an Idealized Valley. J. Appl. Meteorol. Climatol. 2017, 56, 2711–2727. [Google Scholar] [CrossRef]
- Kim, Y.J.; Eckermann, S.D.; Chun, H.Y. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmos.-Ocean 2003, 41, 65–98. [Google Scholar]
- Kim, Y.J.; Arakawa, A. Improvement of Orographic Gravity Wave Parameterization Using a Mesoscale Gravity Wave Model. J. Atmos. Sci. 1995, 52, 1875–1902. [Google Scholar] [CrossRef]
- Deardorff, J.W. The Counter-Gradient Heat Flux in the Lower Atmosphere and in the Laboratory. J. Atmos. Sci. 1966, 23, 503–506. [Google Scholar] [CrossRef]
- Stevens, B. Quasi-Steady Analysis of a PBL Model with an Eddy-Diffusivity Profile and Nonlocal Fluxes. Mon. Weather Rev. 2000, 128, 824–836. [Google Scholar] [CrossRef]
- Ertel, H. Der Vertikale Turbulenz-Wärmestorm in der Atmosphäre. Meteorol. Z. 1942, 59, 250–253. [Google Scholar]
- Soares, P.M.M.; Miranda, P.M.A.; Siebesma, A.P.; Teixeira, J. An eddy-diffusivity/mass-flux parametrization for dry and shallow cumulus convection. Q. J. R. Meteorol. Soc. 2004, 130, 3365–3383. [Google Scholar] [CrossRef]
- De Morsier, G.; Fuhrer, O.; Arpagaus, M. Challenges for a new 1 km non-hydrostatic model over the Alpine Area. In Proceedings of the 15th Conference on Mountain Meteorology, Steamboat Springs, CO, USA, 20–24 August 2012. [Google Scholar]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Zhang, F. Intrinsic versus Practical Limits of Atmospheric Predictability and the Significance of the Butterfly Effect. J. Atmos. Sci. 2016, 73, 1419–1438. [Google Scholar] [CrossRef]
- Durran, D.R.; Gingrich, M. Atmospheric Predictability: Why Butterflies Are Not of Practical Importance. J. Atmos. Sci. 2014, 71, 2476–2488. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Toward Numerical Modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Eckel, F.A.; Mass, C.F. Aspects of Effective Mesoscale, Short-Range Ensemble Forecasting. Weather Forecast. 2005, 20, 328–350. [Google Scholar] [CrossRef]
- Frogner, I.L.; Haakenstad, H.; Iversen, T. Limited-area ensemble predictions at the Norwegian Meteorological Institute. Q. J. R. Meteorol. Soc. 2006, 132, 2785–2808. [Google Scholar] [CrossRef]
- Bowler, N.E.; Arribas, A.; Mylne, K.R.; Robertson, K.B.; Beare, S.E. The MOGREPS short-range ensemble prediction system. Q. J. R. Meteorol. Soc. 2008, 134, 703–722. [Google Scholar] [CrossRef]
- Montani, A.; Cesari, D.; Marsigli, C.; Paccagnella, T. Seven years of activity in the field of mesoscale ensemble forecasting by the COSMO-LEPS system: Main achievements and open challenges. Tellus A 2011, 63, 605–624. [Google Scholar] [CrossRef]
- Wang, Y.; Bellus, M.; Wittmann, C.; Steinheimer, M.; Weidle, F.; Kann, A.; Ivatek-Šahdan, S.; Tian, W.; Ma, X.; Tascu, S.; et al. The Central European limited-area ensemble forecasting system: ALADIN-LAEF. Q. J. R. Meteorol. Soc. 2011, 137, 483–502. [Google Scholar] [CrossRef]
- Berner, J.; Achatz, U.; Batté, L.; Bengtsson, L.; Cámara, A.D.L.; Christensen, H.M.; Colangeli, M.; Coleman, D.R.B.; Crommelin, D.; Dolaptchiev, S.I.; et al. Stochastic Parameterization: Toward a New View of Weather and Climate Models. Bull. Am. Meteorol. Soc. 2017, 98, 565–588. [Google Scholar] [CrossRef]
- Hacker, J.P.; Ha, S.Y.; Snyder, C.; Berner, J.; Eckel, F.A.; Kuchera, E.; Pocernich, M.; Rugg, S.; Schramm, J.; Wang, X. The U.S. Air ForceWeather Agency’s mesoscale ensemble: scientific description and performance results. Tellus A 2011, 63, 625–641. [Google Scholar] [CrossRef][Green Version]
- Buizza, R.; Milleer, M.; Palmer, T.N. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2007, 125, 2887–2908. [Google Scholar] [CrossRef]
- Leutbecher, M.; Lock, S.J.; Ollinaho, P.; Lang, S.T.K.; Balsamo, G.; Bechtold, P.; Bonavita, M.; Christensen, H.M.; Diamantakis, M.; Dutra, E.; et al. Stochastic representations of model uncertainties at ECMWF: State of the art and future vision: Stochastic Representations of Model Uncertainties. Q. J. R. Meteorol. Soc. 2017, 143, 2315–2339. [Google Scholar] [CrossRef]
- Hacker, J.P.; Snyder, C.; Ha, S.Y.; Pocernich, M. Linear and non-linear response to parameter variations in a mesoscale model. Tellus A 2011, 63, 429–444. [Google Scholar] [CrossRef]
- Kober, K.; Craig, G.C. Physically Based Stochastic Perturbations (PSP) in the Boundary Layer to Represent Uncertainty in Convective Initiation. J. Atmos. Sci. 2016, 73, 2893–2911. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).