Estimating Hourly Beam and Diffuse Solar Radiation in an Alpine Valley: A Critical Assessment of Decomposition Models
Abstract
1. Introduction
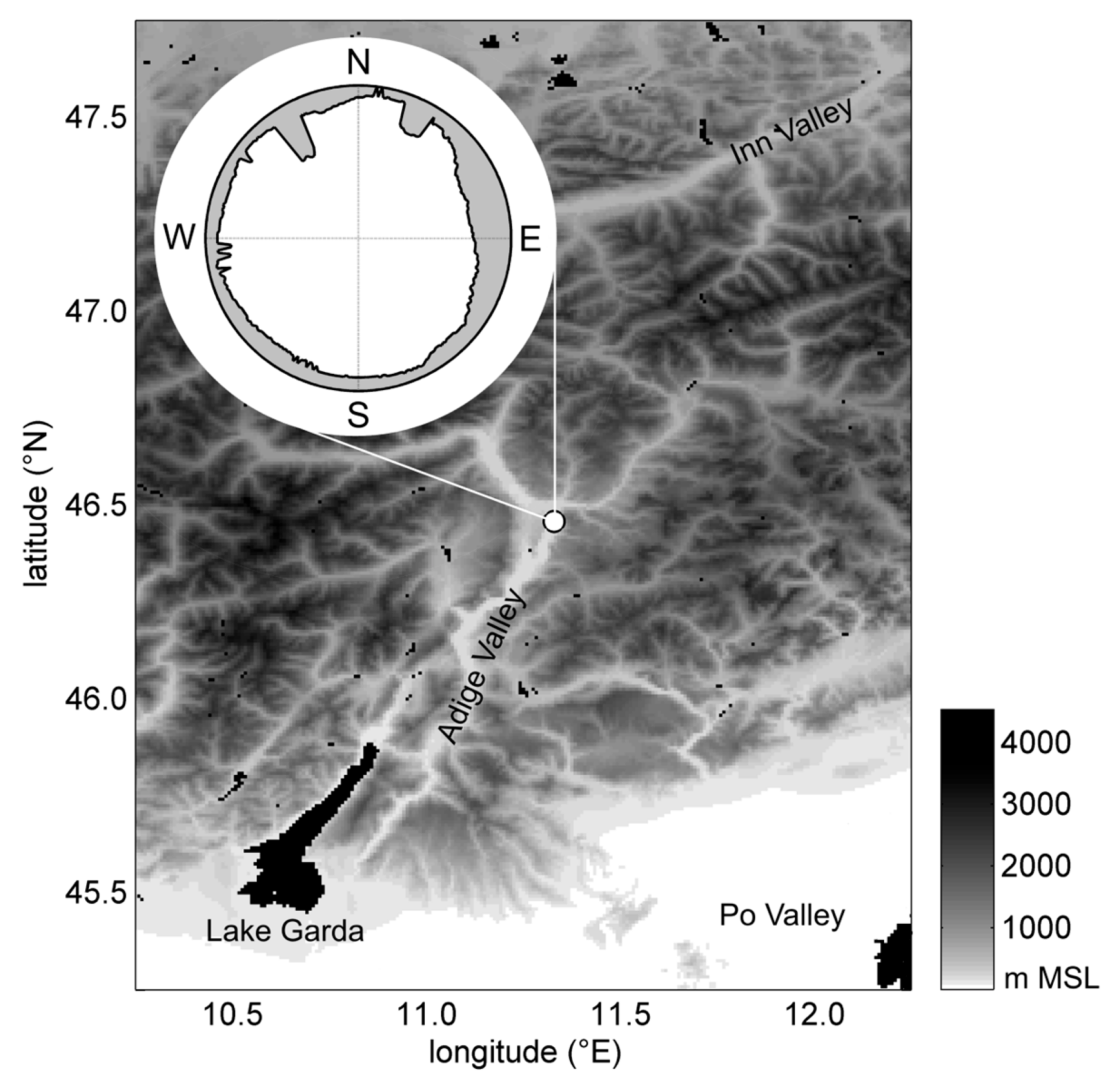
- The characterization of the local climatology of diffuse and beam radiation for a weather station in the Adige Valley, south of the city of Bolzano (eastern Italian Alps), on the basis of four years of hourly observations of global horizontal irradiation (GHI), diffuse horizontal irradiation (DHI), and direct normal irradiation (DNI);
- The investigation and the discussion of the effects of the complex orography in a mountain valley environment on the diffuse fraction of solar radiation, as well as on the performance of decomposition models;
- The evaluation and the comparison of a significant number of state-of-the-art decomposition models for the site of interest, in order to identify the best-performing model(s) and assess the accuracy that can be achieved for DHI and DNI estimates at a typical Alpine valley site, as well as the sensitivity of such accuracy to different weather conditions;
- The calibration of simple local decomposition models for the Bolzano station, to explore the possibility of obtaining unbiased and accurate local estimates with minimum computational efforts.
2. Data and Methods
2.1. The Experimental Dataset
2.2. Validation and Calibration of the Decomposition Models
3. Results and Discussion
3.1. Local Climatology of Diffuse and Beam Radiation
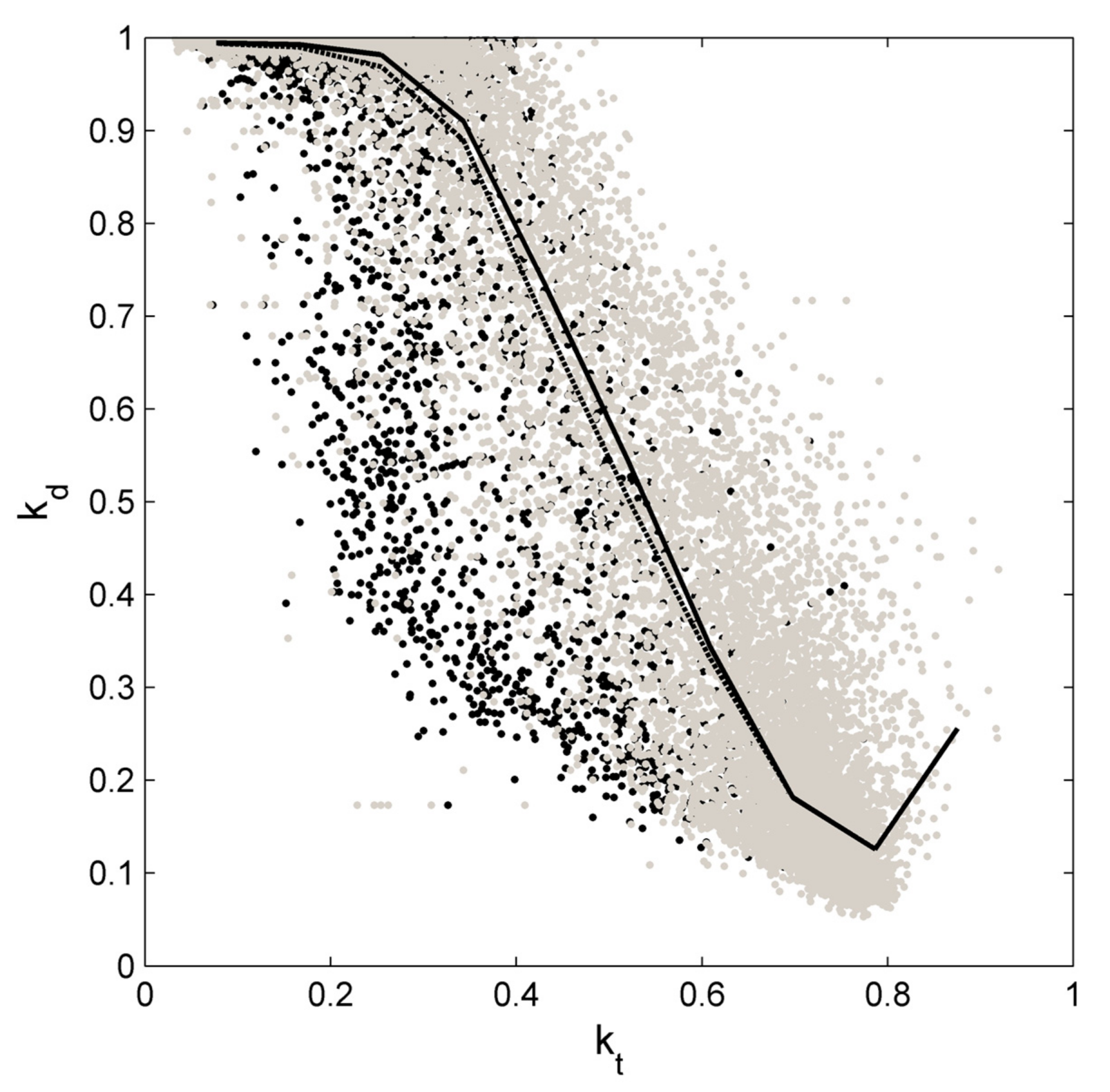
3.2. Effects of Complex Orography on the Diffuse Fraction
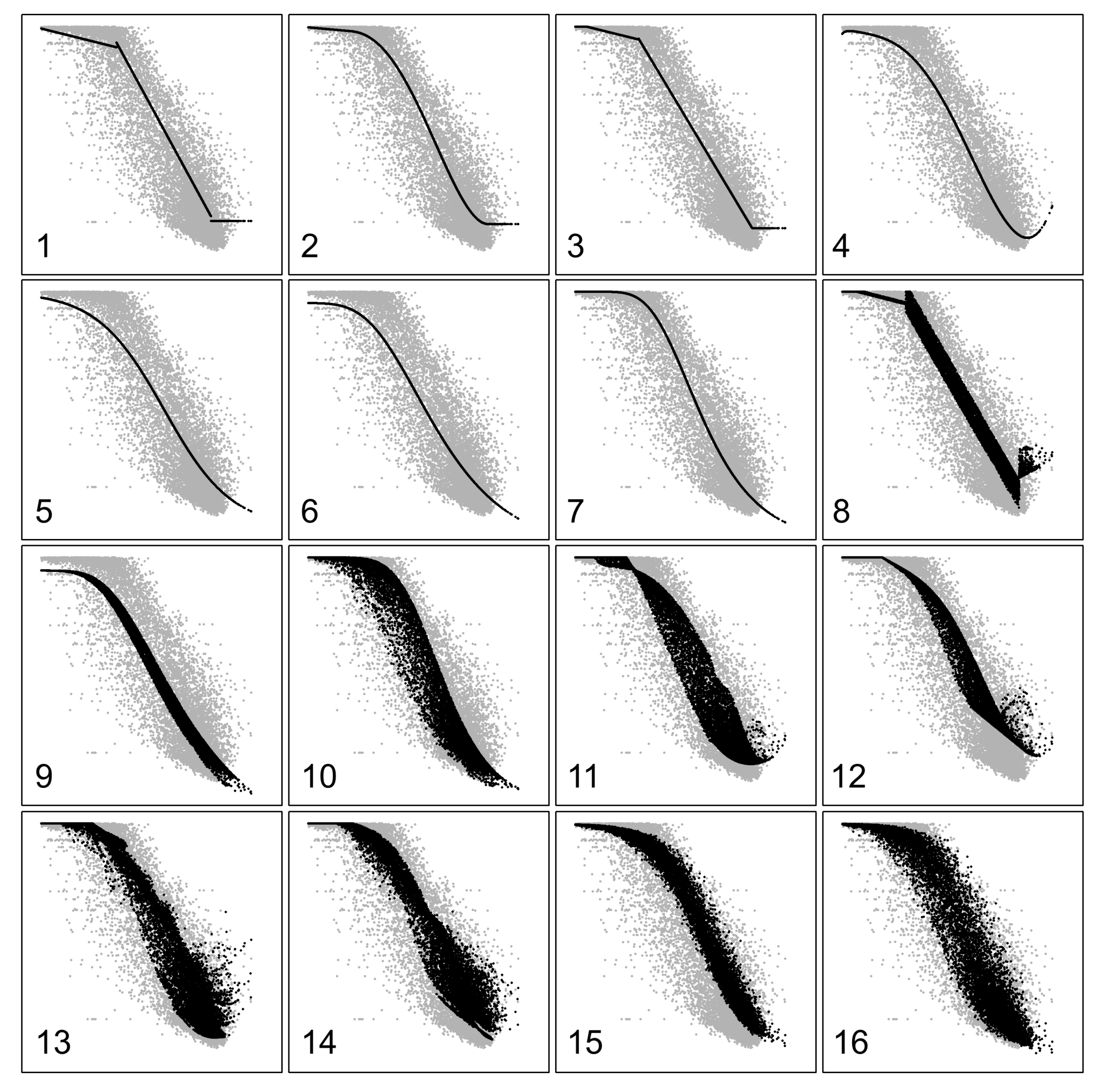
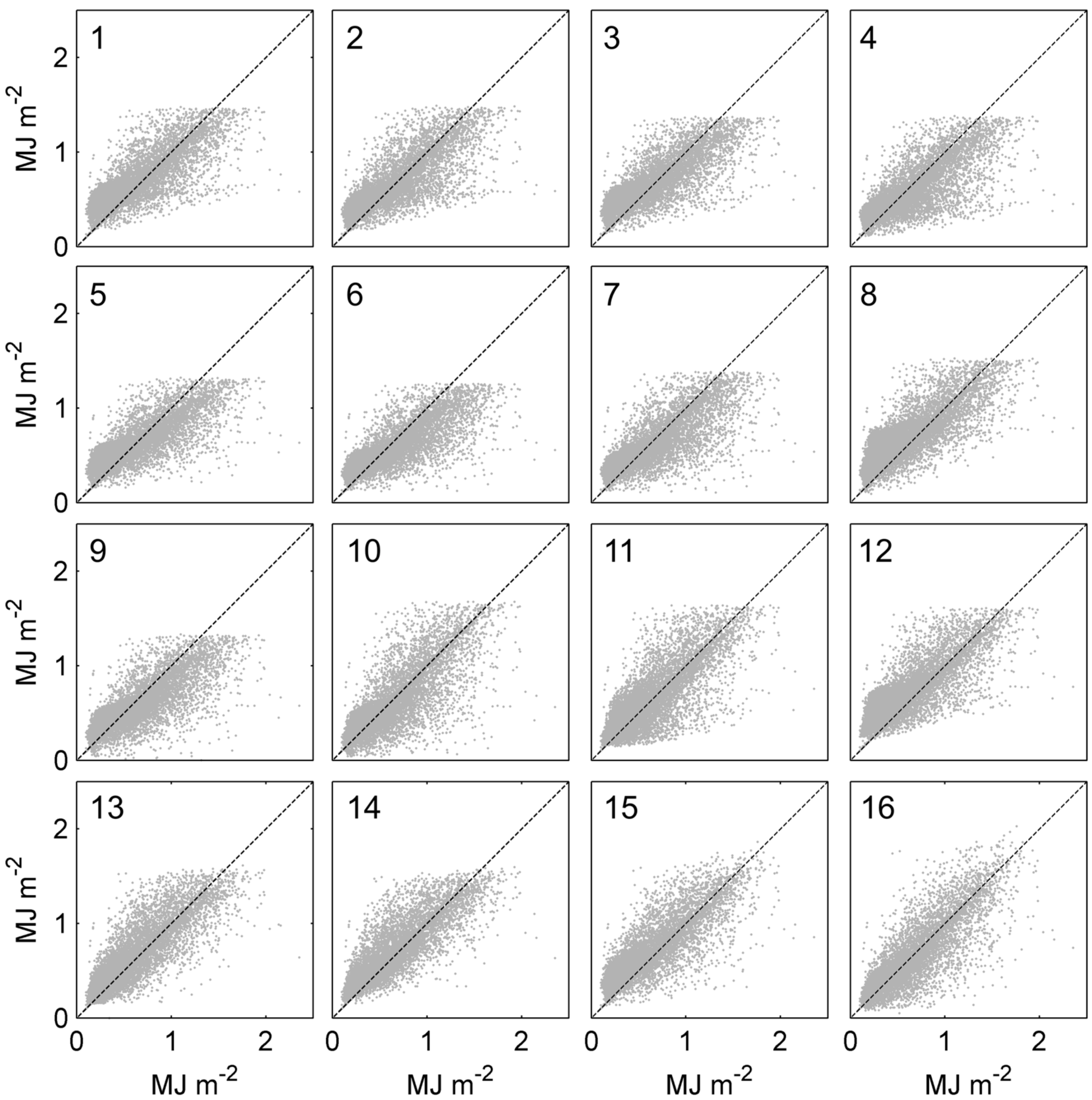
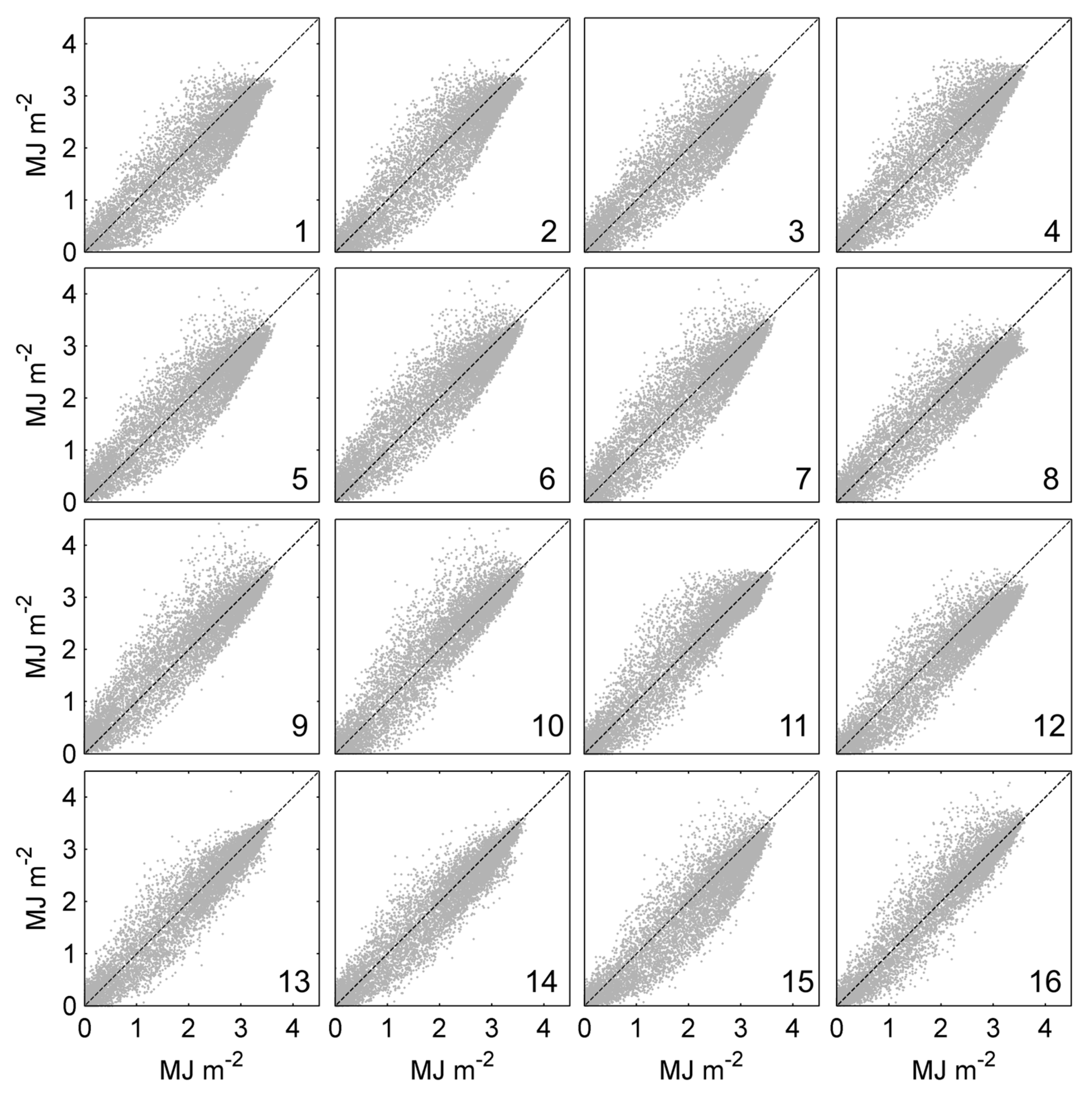
3.3. Comparison of the Decomposition Models
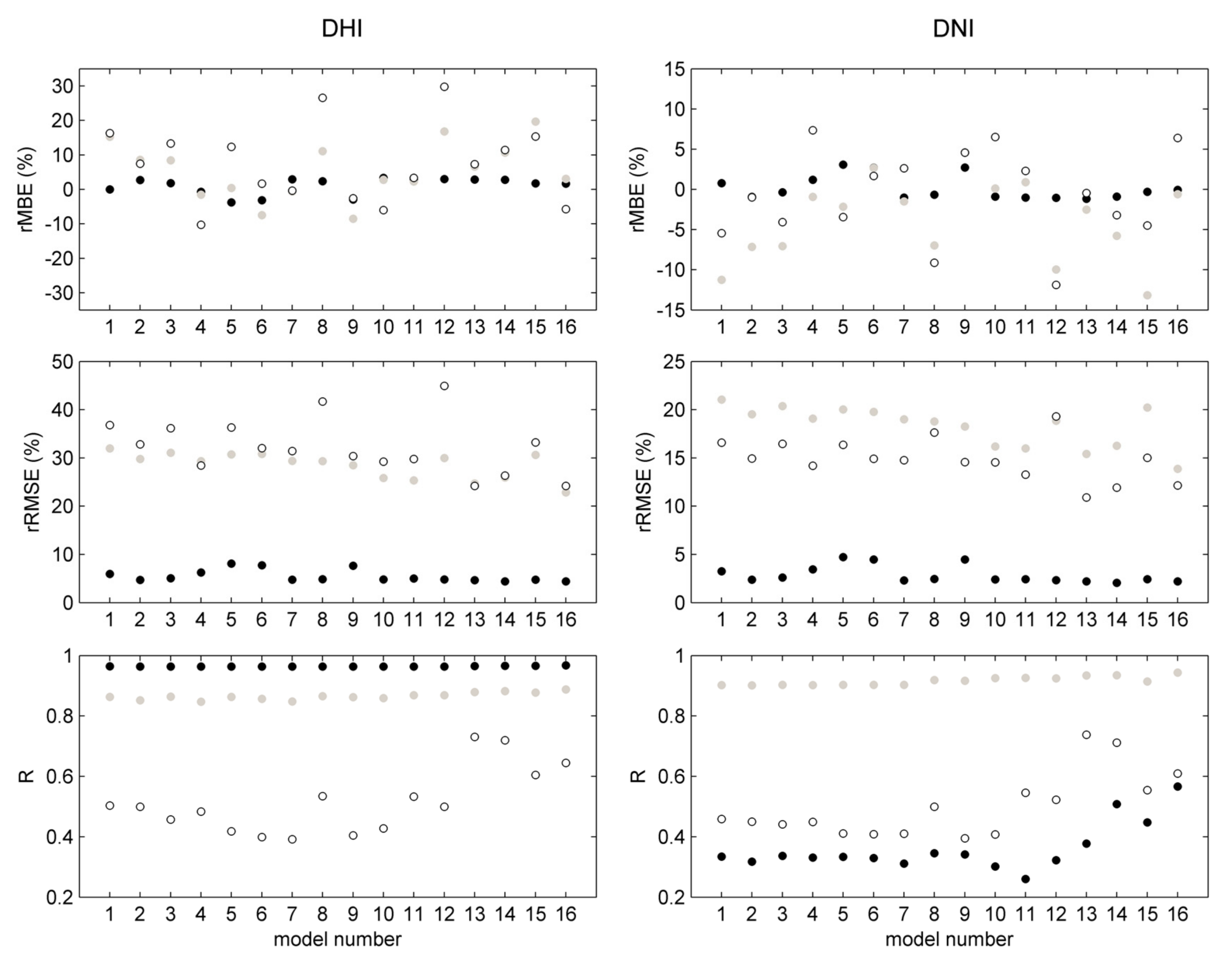
3.3.1. Accuracy of the Models
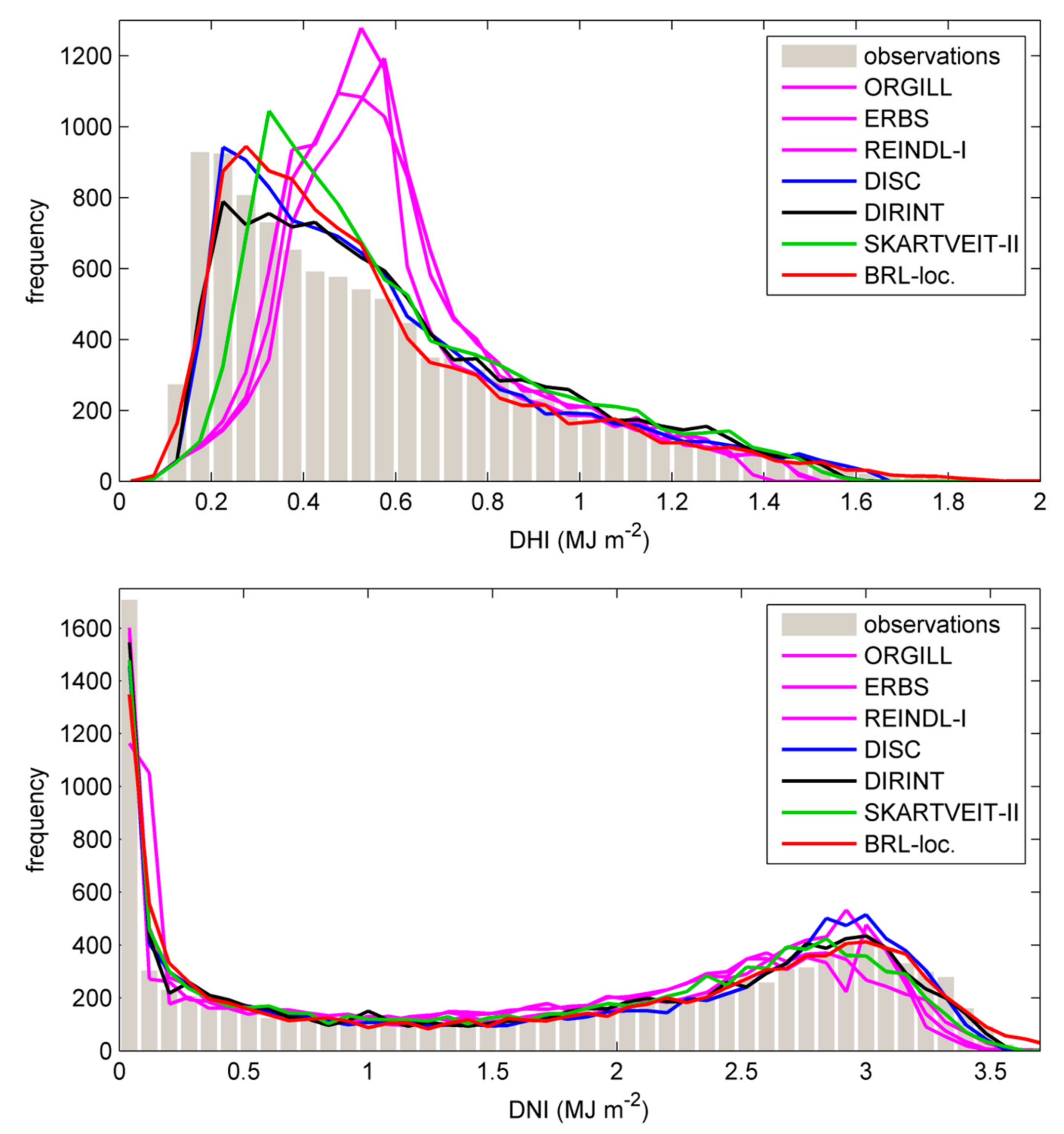
3.3.2. Goodness-of-Fit of the Models
3.4. Model Results under Different Sky Conditions
4. Conclusions
- Observations affected by orographic shadows present a kt–kd distribution very different from the rest of the data and high decomposition errors. Although they do not alter too much the overall decomposition results (because of their relative scarcity), these data are excluded from further analyses. Also, the modification of kd according to the local SVF value is found to be potentially significant for the results of the decomposition models at Alpine sites.
- Concerning the overall decomposition accuracy, in general, the literature models overestimate the measured DHI (with positive biases often exceeding 10%) and underestimate DNI (with negative biases often above 5%). With respect to MAE and RMSE, the average accuracy of the literature models is around 27% and 37% for DHI, and 14% and 20% for DNI, i.e., comparable to the values obtained by similar studies carried out for flat, homogeneous regions. The use of additional predictors generally (but not always) implies better model performances, especially when a variability/persistence index is included (cf. [33]).
- Confirming results previously reported in the literature, DIRINT and SKARTVEIT-II are the best-performing models, although they provide non-negligible biases (cf. [33]). The third best model, DISC, shows the lowest bias among the literature models (3%) and a frequency distribution very similar to the observed one (like DIRINT). On the other hand, SKARTVEIT-I (included in the HelioMont algorithm, which provides satellite-based radiation estimates for the Alps [26]) and ORGILL are the worst-performing models, respectively, for diffuse and beam radiation.
- Apart from a null bias, the local calibration of BRL is found to allow performances comparable or even better than those of DIRINT and SKARTVEIT-II (for DHI: MAE = 20%, RMSE = 32%; for DNI: MAE = 12%, RMSE = 17%). Moreover, BRL is much simpler and is computationally inexpensive (cf. also the recent results from the application and adjustment of the BRL model to hourly and minute data in Brazil [69]).
- All models reproduce more accurately the observations relative to overcast conditions than those corresponding to partially cloudy and clear skies. Including a variability (or intermittency)/persistence index among the predictors improves the modeling of the cloud-related enhancement of diffuse radiation under clear skies (scattered clouds) [33,70,71].
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huld, T.; Paietta, E.; Zangheri, P.; Pinedo Pascua, I. Assembling Typical Meteorological Year Data Sets for Building Energy Performance Using Reanalysis and Satellite-Based Data. Atmosphere 2018, 9, 53. [Google Scholar] [CrossRef]
- Gueymard, C.A. Direct and indirect uncertainties in the prediction of tilted irradiance for solar engineering applications. Sol. Energy 2009, 83, 432–444. [Google Scholar] [CrossRef]
- Grigiante, M.; Mottes, F.; Zardi, D.; de Franceschi, M. Experimental solar radiation measurements and their effectiveness in setting up a real-sky irradiance model. Renew. Energy 2011, 36, 1–8. [Google Scholar] [CrossRef]
- Myers, D.R. Solar radiation modeling and measurements for renewable energy applications: Data and model quality. Energy 2005, 30, 1517–1531. [Google Scholar] [CrossRef]
- Paulescu, M.; Paulescu, E.; Gravila, P.; Badescu, V. Weather Modeling and Forecasting of PV Systems Operation, 1st ed.; Springer: London, UK, 2013; p. 358. ISBN 978-1-4471-4649-0. [Google Scholar] [CrossRef]
- Castro-Diez, Y.; Alados-Arboledas, L.; Jiménez, J.I. A model for climatological estimations of global, diffuse, and direct solar radiation on a horizontal surface. Sol. Energy 1989, 42, 417–424. [Google Scholar] [CrossRef]
- El-Metwally, M. Simple new methods to estimate global solar radiation based on meteorological data in Egypt. Atmos. Res. 2004, 69, 217–239. [Google Scholar] [CrossRef]
- Boata, R.S.; Gravila, P. Functional fuzzy approach for forecasting daily global solar irradiation. Atmos. Res. 2012, 112, 79–88. [Google Scholar] [CrossRef]
- Pandey, P.K.; Soupir, M.L. A new method to estimate average hourly global solar radiation on the horizontal surface. Atmos. Res. 2012, 114–115, 83–90. [Google Scholar] [CrossRef]
- Manzano, A.; Martín, M.L.; Valero, F.; Armenta, C. A single method to estimate the daily global solar radiation from monthly data. Atmos. Res. 2015, 166, 70–82. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Orgill, J.F.; Hollands, K.G.T. Correlation equation for hourly diffuse radiation on a horizontal surface. Sol. Energy 1977, 19, 357–359. [Google Scholar] [CrossRef]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Skartveit, A.; Olseth, J.A. A model for the diffuse fraction of hourly global radiation. Sol. Energy 1987, 38, 271–274. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse fraction correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Louche, A.; Notton, G.; Poggi, P.; Simonnot, G. Correlations for direct normal and global horizontal irradiation on a French Mediterranean site. Sol. Energy 1991, 46, 261–266. [Google Scholar] [CrossRef]
- Torres, J.L.; De Blas, M.; García, A.; de Francisco, A. Comparative study of various models in estimating hourly diffuse solar irradiance. Renew. Energy 2010, 35, 1325–1332. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Alsamamra, H.; Tovar-Pescador, J.; Pozo-Vázquez, D. Proposal of a regressive model for the hourly diffuse solar radiation under all sky conditions. Energ. Convers. Manag. 2010, 51, 881–893. [Google Scholar] [CrossRef]
- Lauret, P.; Boland, J.; Ridley, B. Bayesian statistical analysis applied to solar radiation modelling. Renew. Energy 2013, 49, 124–127. [Google Scholar] [CrossRef]
- Maxwell, E.L. A Quasi-Physical Model for Converting Hourly Global Horizontal to Direct Normal Insolation; Report SERI/TR-215-3087; Solar Energy Research Institute: Golden, CO, USA, 1987. [Google Scholar]
- Perez, R.; Ineichen, P.; Maxwell, E.; Seals, R.; Zelenka, A. Dynamic global-to-direct irradiance conversion models. ASHRAE Trans. 1992, 3578, 354–369. [Google Scholar]
- Skartveit, A.; Olseth, J.A.; Tuft, M.E. An hourly diffuse fraction model with correction for variability and surface albedo. Sol. Energy 1998, 63, 173–183. [Google Scholar] [CrossRef]
- Remund, J.; Müller, S.C. Solar Radiation and Uncertainty Information of Meteonorm 7. In Proceedings of the 26th European Photovoltaic Solar Energy Conference and Exhibition, Hamburg, Germany, 5–9 September 2011; pp. 4388–4390. [Google Scholar] [CrossRef]
- Blanc, P.; Gschwind, B.; Lefèvre, M.; Wald, L. The HelioClim Project: Surface Solar Irradiance Data for Climate Applications. Remote Sens. 2011, 3, 343–361. [Google Scholar] [CrossRef]
- Šúri, M.; Remund, J.; Cebecauer, T.; Dumortier, D.; Wald, L.; Huld, T.; Blanc, P. First Steps in the Cross-Comparison of Solar Resource Spatial Products in Europe. In Proceedings of the EUROSUN 2008—1st International Conference on Solar Heating, Cooling and Buildings, Lisbon, Portugal, 7–10 October 2008. [Google Scholar]
- Stöckli, R. The HelioMont Surface Radiation Processing; Scientific Report, 93; Federal Office of Meteorology and Climatology, MeteoSwiss: Zurich, Switzerland, 2013; p. 122. [Google Scholar]
- Olmo, F.J.; Batlles, F.J.; Alados-Arboledas, L. Performance of global to direct/diffuse decomposition models before and after the eruption of Mt. Pinatubo, June 1991. Sol. Energy 1996, 57, 433–443. [Google Scholar] [CrossRef]
- Batlles, F.J.; Rubio, M.A.; Tovar, J.; Olmo, F.J.; Alados-Arboledas, L. Empirical modeling of hourly direct irradiance by means of hourly global irradiance. Energy 2000, 25, 675–688. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation on an hourly basis of solar diffuse irradiations from global data for horizontal surfaces in Ajaccio. Energy Convers. Manag. 2004, 45, 2849–2866. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Tymvios, F.S.; Assimakopoulos, V.D.; Kaltsounides, N.A. Comparative study of various correlations in estimating hourly diffuse fraction of global solar radiation. Renew. Energy 2006, 31, 2492–2504. [Google Scholar] [CrossRef]
- Ineichen, P. Comparison and validation of three global-to-beam irradiance models against ground measurements. Sol. Energy 2008, 82, 501–512. [Google Scholar] [CrossRef]
- Bertrand, C.; Vanderveken, G.; Journée, M. Evaluation of decomposition models of various complexity to estimate the direct solar irradiance over Belgium. Renew. Energy 2015, 74, 618–626. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Performance of Separation Models to Predict Direct Irradiance at High Frequency: Validation over Arid Areas. In Proceedings of the EUROSUN 2014—International Conference on Solar Energy and Buildings, Aix-Les-Bains, France, 16–19 September 2014. [Google Scholar]
- Gueymard, C.A.; Ruiz-Arias, J.A. Extensive worldwide validation and climate sensitivity analysis of direct irradiance predictions from 1-min global irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Tovar, J.; Olmo, F.J.; Alados-Arboledas, L. Local-Scale Variability of Solar Radiation in a Mountainous Region. J. Appl. Meteorol. 1995, 34, 2316–2322. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.A.; Dunlop, E.D.; Ossenbrink, H.A. Potential of solar electricity generation in the European Union member states and candidate countries. Sol. Energy 2007, 81, 1295–1305. [Google Scholar] [CrossRef]
- Castelli, M.; Stöckli, R.; Zardi, D.; Tetzlaff, A.; Wagner, J.E.; Belluardo, G.; Zebisch, M.; Petitta, M. The HelioMont method for assessing solar irradiance over complex terrain: Validation and improvements. Remote Sens. Environ. 2014, 152, 603–613. [Google Scholar] [CrossRef]
- Rampanelli, G.; Zardi, D.; Rotunno, R. Mechanisms of Up-Valley Winds. J. Atmos. Sci. 2004, 61, 3097–3111. [Google Scholar] [CrossRef]
- Rotach, M.; Zardi, D. On the boundary layer structure over highly complex terrain: Key findings from MAP. Q. J. R. Meteorol. Soc. 2007, 133, 937–948. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Daytime Heat Transfer Processes Related to Slope Flows and Turbulent Convection in an Idealized Mountain Valley. J. Atmos. Sci. 2010, 67, 3739–3756. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Structure of the atmospheric boundary layer in the vicinity of a developing upslope flow system: A numerical model study. J. Atmos. Sci. 2010, 67, 1171–1185. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Daytime development of the boundary layer over a plain and in a valley under fair weather conditions: A comparison by means of idealized numerical simulations. J. Atmos. Sci. 2011, 68, 2128–2141. [Google Scholar] [CrossRef]
- Zardi, D.; Whiteman, C.D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting—Recent Progress and Current Challenges; Chow, K.F., De Wekker, S.F.J., Snyder, J.B., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 35–119. [Google Scholar] [CrossRef]
- Zardi, D.; Serafin, S. An analytic solution for daily-periodic thermally-driven slope flow. Q. J. R. Meteorol. Soc. 2015, 141, 1968–1974. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Serafin, S.; Zardi, D. The thermally driven diurnal wind system of the Adige Valley in the Italian Alps. Q. J. R. Meteorol. Soc. 2017, 143, 2389–2402. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D. Study of wintertime high pollution episodes during the Brenner-South ALPNAP measurement campaign. Meteorol. Atmos. Phys. 2009, 103, 237–250. [Google Scholar] [CrossRef]
- Rada, E.C.; Ragazzi, M.; Zardi, D.; Laiti, L.; Ferrari, A. PCDD/F environmental impact from municipal solid waste bio-drying plant. Chemosphere 2011, 84, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Ragazzi, M.; Tirler, W.; Angelucci, G.; Zardi, D.; Rada, E.C. Management of atmospheric pollutants from waste incineration processes: The case of Bozen. Waste Manag. Res. 2013, 31, 235–240. [Google Scholar] [CrossRef] [PubMed]
- Grenier, J.C.; De La Casinière, A.; Cabot, T. Atmospheric Turbidity Analyzed by Means of Standardized Linke’s Turbidity Factor. J. Appl. Meteorol. 1995, 34, 1449–1458. [Google Scholar] [CrossRef]
- Belluardo, G.; Pichler, M.; Moser, D.; Nikolaeva-Dimitrova, M. One-year comparison of different thin film technologies at Bolzano airport test installation. In Fuelling the Future: Advances in Science and Technologies for Energy Generation, Transmission and Storage; Mendez-Vilas, A., Ed.; BrownWalker Press: Boca Raton, FL, USA, 2012; p. 614. [Google Scholar]
- Moser, D.; Pichler, M.; Nikolaeva-Dimitrova, M. Filtering procedures for reliable outdoor temperature coefficients in different photovoltaic technologies. J. Sol. Energy Eng. 2013, 136, 021006. [Google Scholar] [CrossRef]
- IEC (International Electrotechnical Commission). International Standard IEC61724: Photovoltaic System Performance Monitoring: Guidelines for Measurement, Data Exchange, and Analysis; IEC: Geneva, Switzerland, 1998. [Google Scholar]
- Younes, S.; Claywell, R.; Muneer, T. Quality control of solar radiation data: Present status and proposed new approaches. Energy 2005, 30, 1533–1549. [Google Scholar] [CrossRef]
- Journée, M.; Bertrand, C. Quality control of solar radiation data within the RMIB solar measurements network. Sol. Energy 2011, 85, 72–86. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; García-Marín, A.P.; Zardi, D. A method for detecting spurious precipitation signals from automatic weather stations in irrigated areas. Int. J. Climatol. 2015, 35, 1556–1568. [Google Scholar] [CrossRef]
- Laiti, L.; Andreis, D.; Zottele, F.; Giovannini, L.; Panziera, L.; Toller, G.; Zardi, D. A Solar Atlas for the Trentino Region in the Alps: Quality Control of Surface Radiation Data. Energy Proced. 2014, 59, 336–343. [Google Scholar] [CrossRef]
- ESRA (European Society of Regional Anaesthesia). European Solar Radiation Atlas, 4th ed.; Greif, J., Scharmer, K., Eds.; Presses de l’Ecole des Mines de Paris: Paris, France, 2000. [Google Scholar]
- Rigollier, C.; Bauer, O.; Wald, L. On the clear sky model of the 4th European Solar Radiation Atlas with respect to the Heliosat method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef]
- Remund, J.; Wald, L.; Page, J. Chain of algorithms to calculate advanced radiation parameters. In Proceedings of the International Solar Energy Society (ISES) Solar World Congress 2003, Göteborg, Sweden, 14–19 June 2003. [Google Scholar]
- Linke, F. Transmission-Koeffizient und Trübungsfaktor. Beitr. Phys. Atmos. 1922, 10, 91–103. [Google Scholar]
- Nash, J.E.; Suttcliffe, J.V. River flow forecasting through conceptual models, part I. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Boland, J.; Huang, J.; Ridley, B. Decomposing global solar radiation into its direct and diffuse components. Renew. Sustain. Energy Rev. 2013, 28, 749–756. [Google Scholar] [CrossRef]
- Roesch, A.; Wild, M.; Ohmura, A.; Dutton, E.G.; Long, C.N.; Zhang, T. Assessment of BSRN radiation records for the computation of monthly means. Atmos. Meas. Tech. 2011, 4, 339–354. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System (PVGIS), Geographical Assessment of Solar Resource and Performance of Photovoltaic Technology. Available online: re.jrc.ec.europa.eu/pvgis (accessed on 31 December 2015).
- 3PClim—Past, Present and Perspective Climate of Tirol, Südtirol-Alto Adige and Veneto. Available online: www.3pclim.eu (accessed on 31 December 2015).
- Liu, B.Y.H.; Jordan, R.C. Daily insolation on surfaces tilted towards the equator. ASHRAE Trans 1962, 67, 526–541. [Google Scholar]
- Ridley, B.; Boland, J.; Lauret, P. Modelling of diffuse solar fraction with multiple predictors. Renew. Energy 2010, 35, 478–483. [Google Scholar] [CrossRef]
- Lemos, L.F.L.; Starke, A.R.; Boland, J.; Cardemil, J.M.; Machado, R.D.; Colle, S. Assessment of solar radiation components in Brazil using the BRL model. Renew. Energy 2017, 108, 569–580. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, G.; Nunnari, S. A new fine-grained classification strategy for solar daily radiation patterns. Pattern Recogit. Lett. 2016, 81, 110–117. [Google Scholar] [CrossRef]
- Starke, A.R.; Lemos, L.F.L.; Boland, J.; Cardemil, J.M.; Colle, S. Resolution of the Cloud Enhancement Problem for One-Minute Diffuse Radiation Prediction. Renew. Energy 2018, in press. [Google Scholar] [CrossRef]
- Mueller, R.; Träger-Chatterjee, C. Brief Accuracy Assessment of Aerosol Climatologies for the Retrieval of Solar Surface Radiation. Atmosphere 2014, 5, 959–972. [Google Scholar] [CrossRef]
- Mueller, R.; Pfeifroth, U.; Traeger-Chatterjee, C. Towards Optimal Aerosol Information for the Retrieval of Solar Surface Radiation Using Heliosat. Atmosphere 2015, 6, 863–878. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D. Evaluation of cut-off frequency and correction of filter-induced phase lag and attenuation in eddy covariance analysis of turbulence data. Bound.-Lay Meteorol. 2003, 108, 289–303. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D.; Tagliazucca, M.; Tampieri, F. Analysis of second order moments in the surface layer turbulence in an Alpine valley. Q. J. R. Meteorol. Soc. 2009, 135, 1750–1765. [Google Scholar] [CrossRef]
- Serafin, S.; Adler, B.; Cuxart, J.; De Wekker, S.F.J.; Gohm, A.; Grisogono, B.; Kalthoff, N.; Kirshbaum, D.J.; Rotach, M.W.; Schmidli, J.; et al. Exchange Processes in the Atmospheric Boundary Layer Over Mountainous Terrain. Atmosphere 2018, 9, 102. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Analysis of the urban thermal fingerprint of the city of Trento in the Alps. J. Appl. Meteorol. Clim. 2011, 50, 1145–1162. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Characterization of the Thermal Structure inside an Urban Canyon: Field Measurements and Validation of a Simple Model. J. Appl. Meteorol. Clim. 2013, 52, 64–81. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M.; Chen, F. Numerical simulations of boundary-layer processes and urban-induced alterations in an Alpine valley. Int. J. Climatol. 2014, 34, 1111–1131. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Residual Kriging analysis of airborne measurements: Application to the mapping of Atmospheric Boundary-Layer thermal structures in a mountain valley. Atmos. Sci. Lett. 2013, 14, 79–85. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Atmospheric boundary layer structures associated with the Ora del Garda wind in the Alps as revealed from airborne and surface measurements. Atmos. Res. 2013, 132–133, 473–489. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G.; Giovannini, L. Analysis of the diurnal development of a lake-valley circulation in the Alps based on airborne and surface measurements. Atmos. Chem. Phys. 2014, 14, 9771–9786. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Zardi, D.; de Franceschi, M. Climatological characteristics of the Ora del Garda wind in the Alps. Int. J. Climatol. 2015, 35, 4103–4115. [Google Scholar] [CrossRef]
- Panziera, L.; Giovannini, L.; Laiti, L.; Zardi, D. The relation between circulation types and regional Alpine climate. Part I: Synoptic climatology of Trentino. Int. J. Climatol. 2015, 35, 4655–4672. [Google Scholar] [CrossRef]
- Panziera, L.; Giovannini, L.; Laiti, L.; Zardi, D. The relation between circulation types and regional Alpine climate. Part II: The dependence of the predictive skill on the vertical level of the classification for Trentino. Int. J. Climatol. 2016, 36, 2189–2199. [Google Scholar] [CrossRef]
| Model Type | Model Number | Author(s) (Year) | Model Acronym | Predictors |
|---|---|---|---|---|
| single predictor | 1 | Orgill and Hollands (1977) [12] | ORGILL | kt |
| 2 | Erbs et al. (1982) [13] | ERBS | kt | |
| 3 | Reindl et al. (1990) [15] | REINDL-I | kt | |
| 4 | Louche et al. (1991) [16] | LOUCHE | kt | |
| 5 | Torres et al. (2010) [17] | TORRES | kt | |
| 6 | Ruiz-Arias et al. (2010) [18] | RUIZ-I | kt | |
| 7 | local calibration of Ruiz-Arias et al. (2010) [18] | RUIZ-I-loc. | kt | |
| multiple predictors | 8 | Reindl et al. (1990) [15] | REINDL-II | kt h |
| 9 | Ruiz-Arias et al. (2010) [15] | RUIZ-II | kt m | |
| 10 | local calibration of Ruiz-Arias et al. (2010) [18] | RUIZ-II-loc. | kt m | |
| 11 | Maxwell (1987) [20] | DISC | kt m | |
| 12 | Skartveit and Olseth (1987) [14] | SKARTVEIT-I | kt h | |
| with variability predictor | 13 | Perez et al. (1992) [21] | DIRINT | kt h Ψ |
| 14 | Skartveit et al. (1998) [22] | SKARTVEIT-II | kt Ψ | |
| 15 | Lauret et al. (2013) [19] | BRL | kt t h Kt Ψ | |
| 16 | local calibration of Lauret et al. (2013) [19] | BRL-loc. | kt t h Kt Ψ |
| Month | Bolzano Observations | PVGIS-CMSAF | ||||||
|---|---|---|---|---|---|---|---|---|
| Ig | Id | Ibn | kd | Ig | Id | Ibn | kd | |
| Jan. | 4.81 | 2.18 | 7.49 | 0.45 | 5.33 | 2.72 | 8.03 | 0.51 |
| Feb. | 8.21 | 3.52 | 11.36 | 0.43 | 9.22 | 3.87 | 13.03 | 0.42 |
| Mar. | 13.11 | 4.67 | 16.35 | 0.36 | 14.51 | 6.38 | 15.34 | 0.44 |
| Apr. | 16.40 | 7.09 | 14.12 | 0.43 | 17.75 | 7.63 | 16.09 | 0.43 |
| May | 20.75 | 7.82 | 17.66 | 0.38 | 21.35 | 9.18 | 17.35 | 0.43 |
| Jun. | 21.38 | 8.36 | 16.33 | 0.39 | 22.90 | 9.85 | 18.25 | 0.43 |
| Jul. | 21.74 | 7.69 | 18.85 | 0.35 | 23.65 | 8.51 | 21.20 | 0.36 |
| Aug. | 19.39 | 6.23 | 19.66 | 0.32 | 19.87 | 7.35 | 19.12 | 0.37 |
| Sep. | 14.67 | 5.02 | 16.51 | 0.34 | 15.34 | 6.29 | 15.80 | 0.41 |
| Oct. | 9.32 | 3.70 | 11.87 | 0.40 | 9.86 | 4.73 | 11.23 | 0.48 |
| Nov. | 4.90 | 2.23 | 7.26 | 0.45 | 5.69 | 2.96 | 7.88 | 0.52 |
| Dec. | 3.73 | 1.77 | 6.45 | 0.48 | 4.25 | 2.29 | 6.88 | 0.54 |
| Model | MBE | MAE | RMSE | rMBE | rMAE | rRMSE | R | E | FVU | KSI | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ORGILL | 0.07 | 0.17 | 0.22 | 13.28 | 29.58 | 38.69 | 0.820 | 0.622 | 39.85 | 284 |
| 2 | ERBS | 0.04 | 0.15 | 0.21 | 7.35 | 26.95 | 37.23 | 0.817 | 0.650 | 41.83 | 246 |
| 3 | REINDL-I | 0.05 | 0.16 | 0.21 | 9.01 | 28.75 | 38.09 | 0.817 | 0.634 | 49.02 | 287 |
| 4 | LOUCHE | −0.02 | 0.14 | 0.21 | −4.27 | 25.52 | 37.78 | 0.806 | 0.640 | 45.96 | 232 |
| 5 | TORRES | 0.02 | 0.16 | 0.21 | 3.69 | 29.09 | 38.34 | 0.811 | 0.629 | 57.09 | 303 |
| 6 | RUIZ-I | −0.02 | 0.15 | 0.22 | −3.81 | 27.71 | 38.76 | 0.810 | 0.621 | 59.43 | 296 |
| 7 | RUIZ-I-loc. | 0.00 | 0.15 | 0.21 | 0.00 | 26.29 | 37.94 | 0.803 | 0.637 | 49.70 | 251 |
| 8 | REINDL-II | 0.08 | 0.17 | 0.22 | 14.84 | 29.63 | 38.98 | 0.820 | 0.616 | 30.56 | 279 |
| 9 | RUIZ-II | −0.03 | 0.14 | 0.21 | −5.74 | 25.93 | 37.61 | 0.814 | 0.643 | 48.77 | 234 |
| 10 | RUIZ-II-loc. | 0.00 | 0.13 | 0.21 | 0.00 | 23.74 | 36.97 | 0.817 | 0.655 | 13.96 | 95 |
| 11 | DISC | 0.02 | 0.13 | 0.20 | 2.71 | 23.68 | 35.48 | 0.834 | 0.682 | 11.44 | 61 |
| 12 | SKARTVEIT-I | 0.11 | 0.17 | 0.23 | 18.94 | 31.02 | 40.71 | 0.820 | 0.582 | 21.92 | 303 |
| 13 | DIRINT | 0.04 | 0.12 | 0.18 | 6.27 | 21.48 | 31.82 | 0.871 | 0.745 | 12.21 | 119 |
| 14 | SKARTVEIT-II | 0.05 | 0.13 | 0.18 | 9.74 | 22.80 | 32.51 | 0.870 | 0.733 | 18.20 | 172 |
| 15 | BRL | 0.09 | 0.15 | 0.21 | 15.54 | 27.53 | 37.05 | 0.845 | 0.653 | 20.66 | 246 |
| 16 | BRL-loc. | 0.00 | 0.12 | 0.18 | 0.00 | 20.47 | 32.29 | 0.864 | 0.737 | 8.40 | 63 |
| Model | MBE | MAE | RMSE | rMBE | rMAE | rRMSE | R | E | FVU | KSI | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ORGILL | −0.13 | 0.29 | 0.39 | −7.51 | 16.88 | 22.55 | 0.954 | 0.898 | 10.22 | 241 |
| 2 | ERBS | −0.07 | 0.26 | 0.36 | −4.18 | 15.42 | 21.20 | 0.956 | 0.910 | 9.04 | 128 |
| 3 | REINDL-I | −0.09 | 0.28 | 0.37 | −5.06 | 16.39 | 21.80 | 0.954 | 0.904 | 9.56 | 178 |
| 4 | LOUCHE | 0.04 | 0.26 | 0.36 | 2.10 | 15.09 | 21.04 | 0.956 | 0.911 | 8.90 | 57 |
| 5 | TORRES | −0.03 | 0.28 | 0.37 | −1.78 | 16.49 | 21.30 | 0.955 | 0.909 | 9.12 | 176 |
| 6 | RUIZ-I | 0.04 | 0.27 | 0.36 | 2.35 | 15.85 | 21.07 | 0.955 | 0.911 | 8.93 | 150 |
| 7 | RUIZ-I-loc. | 0.00 | 0.26 | 0.36 | −0.07 | 15.07 | 20.90 | 0.955 | 0.912 | 8.78 | 68 |
| 8 | REINDL-II | −0.11 | 0.27 | 0.35 | −6.71 | 15.92 | 20.70 | 0.962 | 0.914 | 8.61 | 208 |
| 9 | RUIZ-II | 0.07 | 0.26 | 0.35 | 4.33 | 14.95 | 20.54 | 0.959 | 0.915 | 8.48 | 150 |
| 10 | RUIZ-II-loc. | 0.04 | 0.23 | 0.34 | 2.06 | 13.55 | 19.92 | 0.962 | 0.920 | 7.98 | 89 |
| 11 | DISC | 0.02 | 0.22 | 0.32 | 1.07 | 13.03 | 18.61 | 0.965 | 0.930 | 6.96 | 70 |
| 12 | SKARTVEIT-I | −0.16 | 0.28 | 0.36 | −9.24 | 16.47 | 21.20 | 0.964 | 0.910 | 9.03 | 277 |
| 13 | DIRINT | −0.03 | 0.20 | 0.29 | -1.65 | 11.93 | 16.80 | 0.972 | 0.943 | 5.67 | 55 |
| 14 | SKARTVEIT-II | −0.07 | 0.22 | 0.30 | -4.18 | 12.67 | 17.34 | 0.971 | 0.940 | 6.04 | 132 |
| 15 | BRL | −0.14 | 0.27 | 0.37 | −8.36 | 15.80 | 21.85 | 0.958 | 0.904 | 9.60 | 257 |
| 16 | BRL-loc. | 0.01 | 0.20 | 0.30 | 0.81 | 11.53 | 17.14 | 0.972 | 0.940 | 5.90 | 47 |
| RUIZ-I | RUIZ-I-loc. | RUIZ-II | RUIZ-II-loc. | BRL | BRL-loc. | |
|---|---|---|---|---|---|---|
| a0 | 0.952 | 1.000 | 0.944 | 0.998 | −5.32 | −6.67 |
| a1 | 1.041 | 1.071 | 1.538 | 1.018 | 7.28 | 6.72 |
| a2 | 2.300 | 2.642 | 2.808 | 3.244 | −0.03 | 0.06 |
| a3 | −4.702 | −5.343 | −5.759 | −3.003 | −0.0047 | −0.0072 |
| a4 | - | - | 2.276 | −3.572 | 1.72 | 2.01 |
| a5 | - | - | −0.125 | −0.495 | 1.08 | 2.47 |
| a6 | - | - | 0.013 | 0.035 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laiti, L.; Giovannini, L.; Zardi, D.; Belluardo, G.; Moser, D. Estimating Hourly Beam and Diffuse Solar Radiation in an Alpine Valley: A Critical Assessment of Decomposition Models. Atmosphere 2018, 9, 117. https://doi.org/10.3390/atmos9040117
Laiti L, Giovannini L, Zardi D, Belluardo G, Moser D. Estimating Hourly Beam and Diffuse Solar Radiation in an Alpine Valley: A Critical Assessment of Decomposition Models. Atmosphere. 2018; 9(4):117. https://doi.org/10.3390/atmos9040117
Chicago/Turabian StyleLaiti, Lavinia, Lorenzo Giovannini, Dino Zardi, Giorgio Belluardo, and David Moser. 2018. "Estimating Hourly Beam and Diffuse Solar Radiation in an Alpine Valley: A Critical Assessment of Decomposition Models" Atmosphere 9, no. 4: 117. https://doi.org/10.3390/atmos9040117
APA StyleLaiti, L., Giovannini, L., Zardi, D., Belluardo, G., & Moser, D. (2018). Estimating Hourly Beam and Diffuse Solar Radiation in an Alpine Valley: A Critical Assessment of Decomposition Models. Atmosphere, 9(4), 117. https://doi.org/10.3390/atmos9040117





