Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data †
Abstract
1. Introduction
2. Case Study and Datasets
3. Methods
3.1. Kriging Methods
- Ordinary kriging—OK
- Ordinary kriging for uncertain data—OKUD
- Kriging with External Drift with radar rainfall as covariate—KED
- Kriging with External Drift for uncertain data with radar rainfall as covariate—KEDUD
3.2. Variogram and Covariance Function
3.3. Kriging for Uncertain Data (KUD)
3.4. Synthetic Experiment
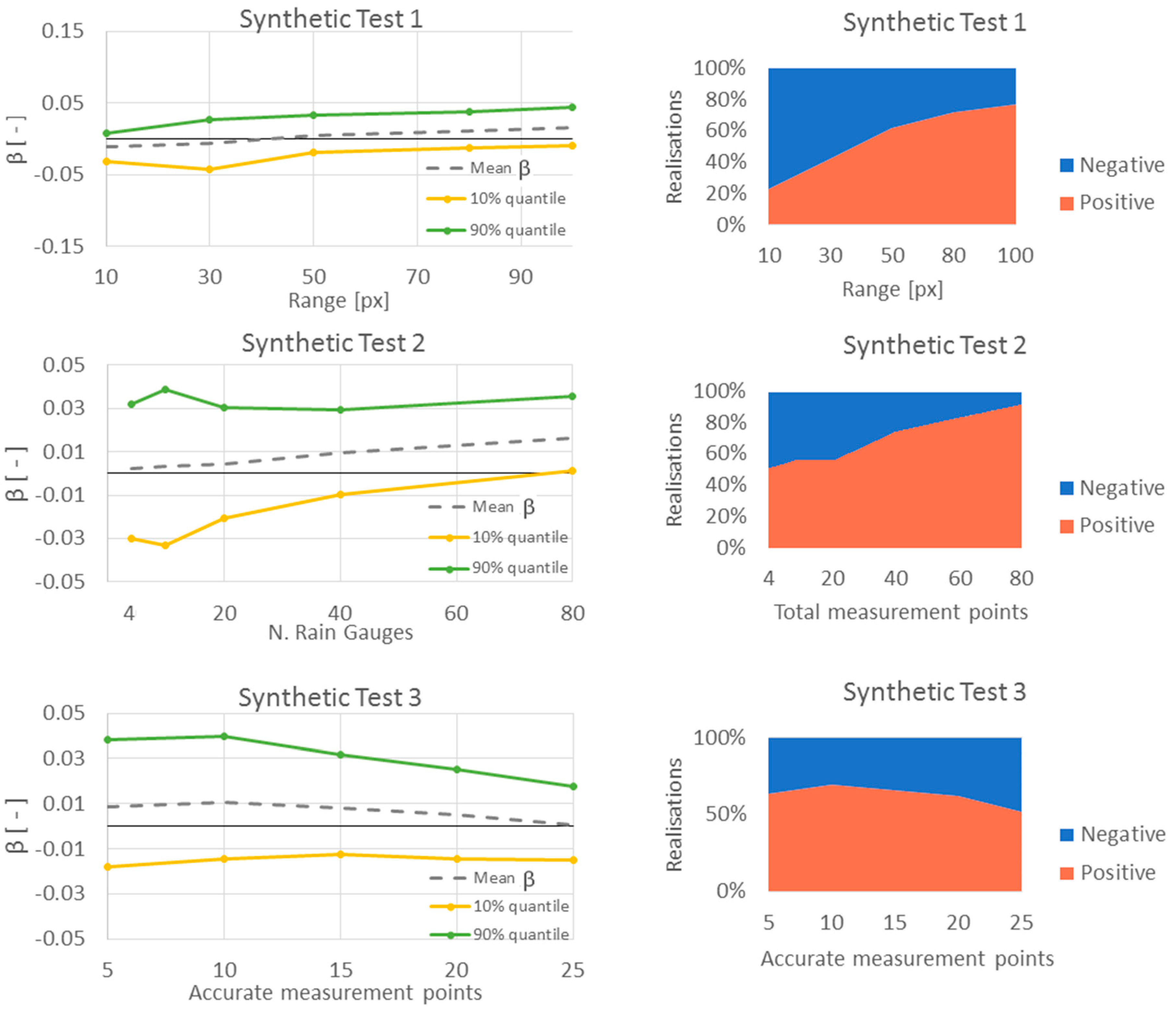
3.4.1. First Synthetic Experiment: Field Spatial Variability
3.4.2. Second Synthetic Experiment: Rain Gauge Density
3.4.3. Third Synthetic Experiment: Sampling Point Accuracy
3.4.4. KUD Performance Evaluation
3.5. Rain Gauge Uncertainty Estimation for the Case Study
3.5.1. KNMI Automatic Rain Gauges
3.5.2. Tipping-Bucket Rain Gauges
3.5.3. KNMI Manual Rain Gauges
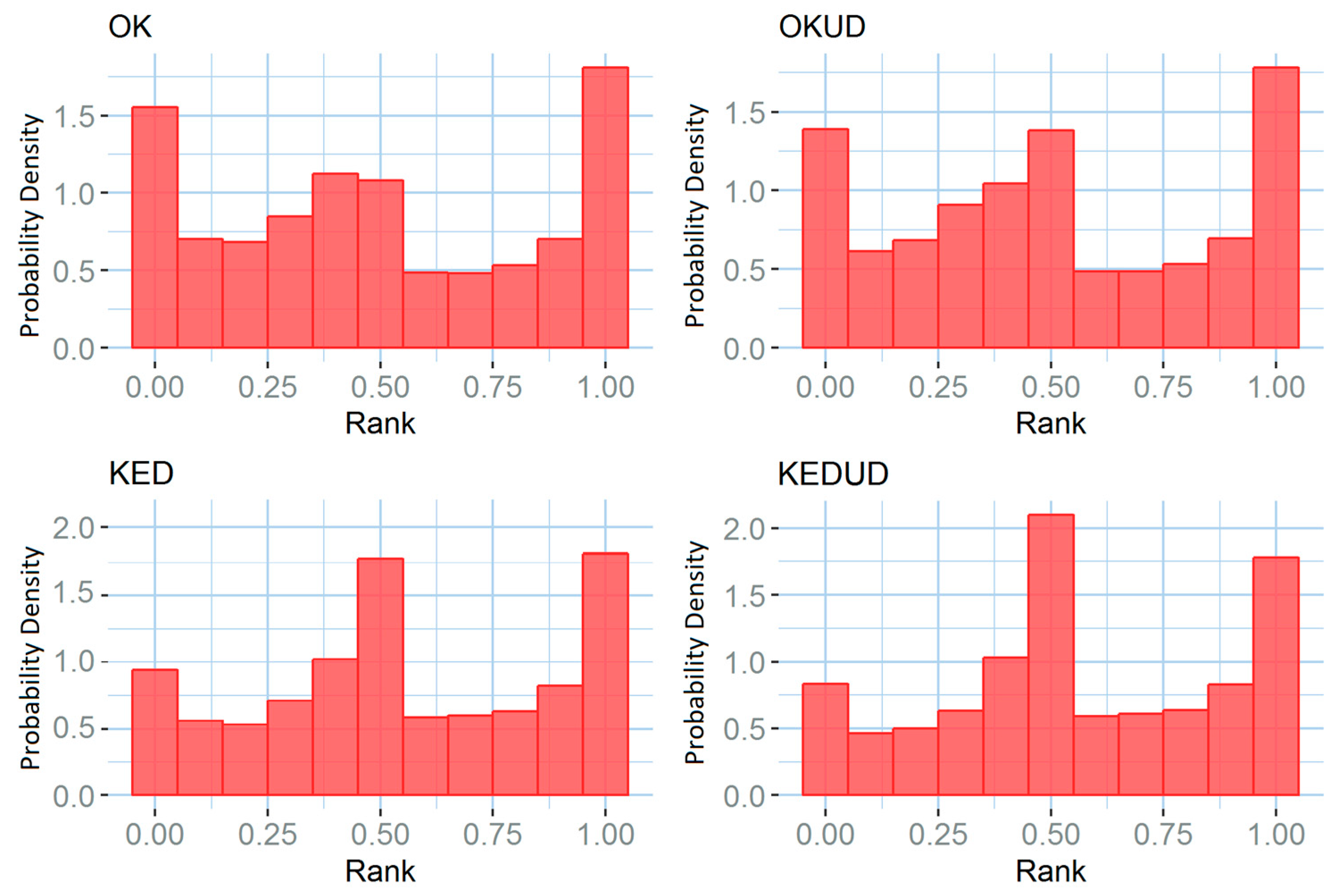
3.5.4. Result Evaluation Methods
4. Results and Discussion
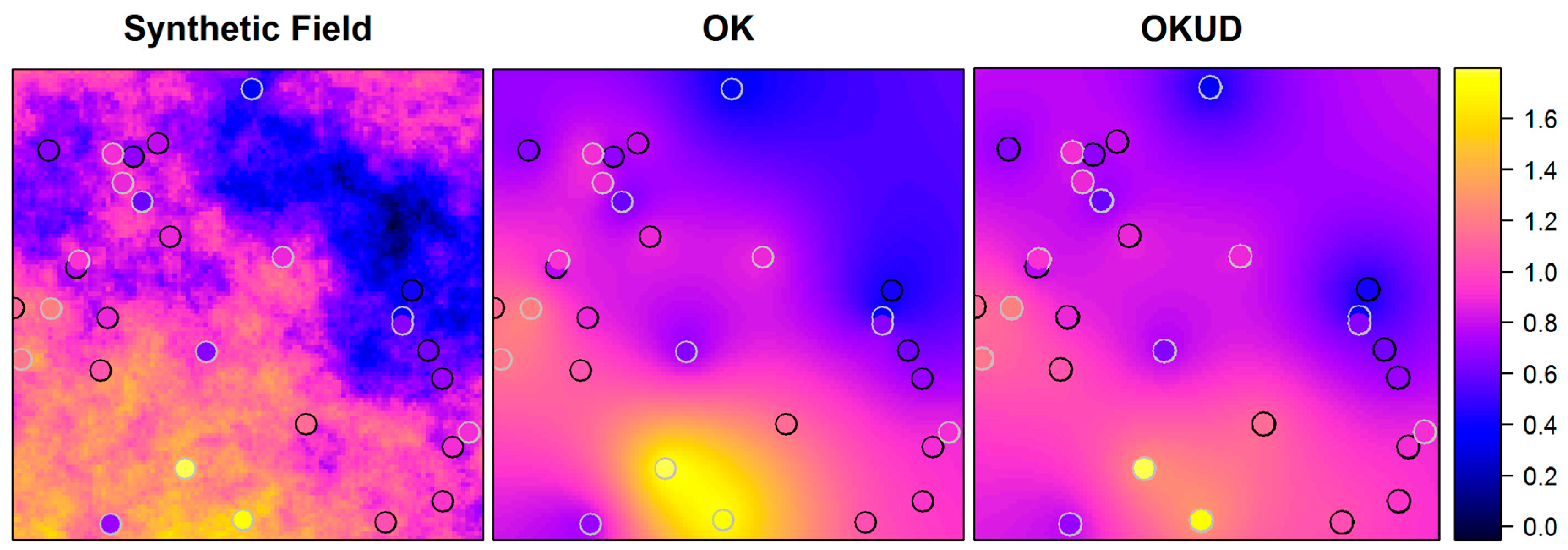
4.1. Synthetic Experiment Results and Discussion
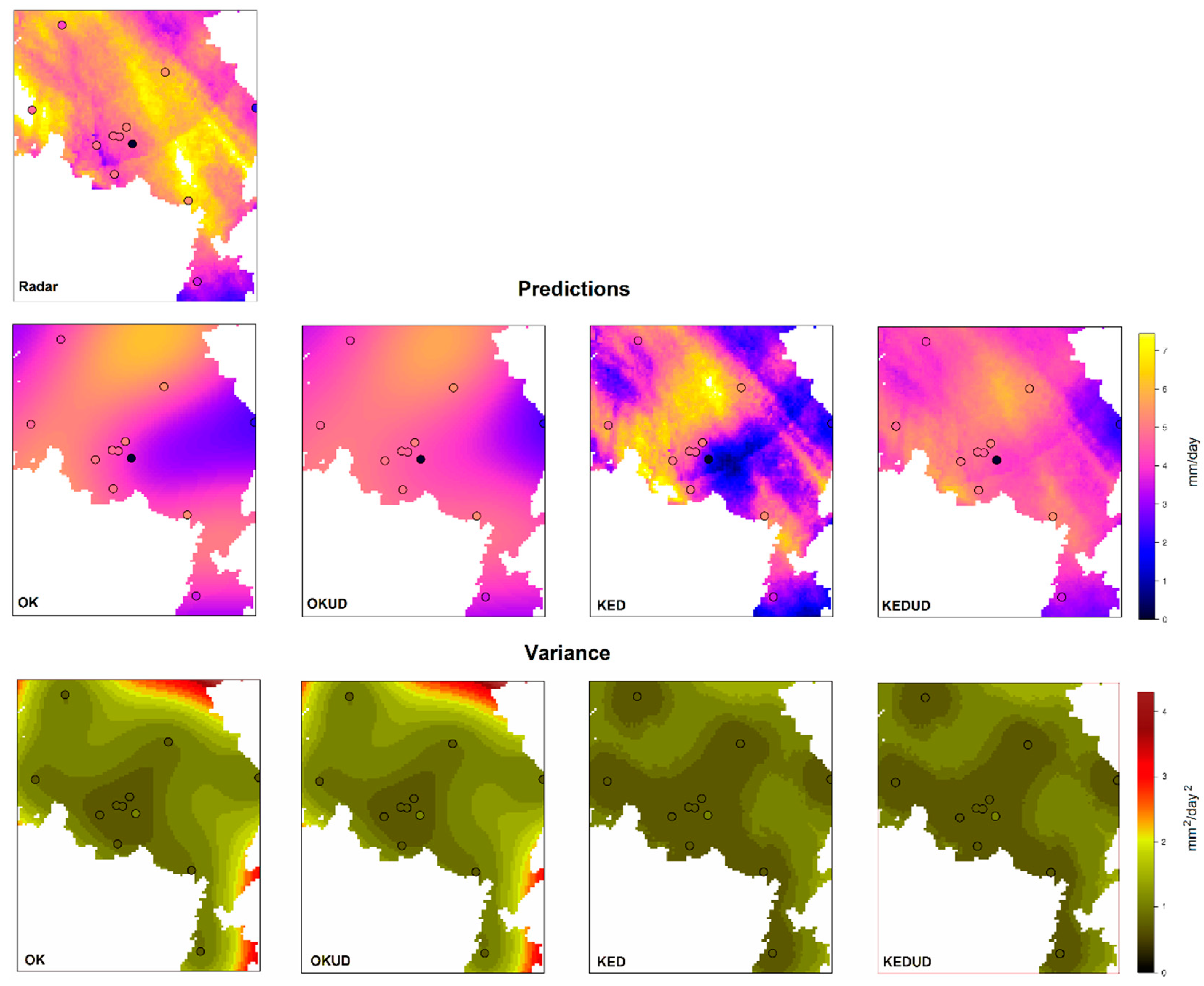
4.2. Case Study Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Ellerbæk Nielsen, J.; Ten Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. Discuss. 2009, 5, 2975–3003. [Google Scholar] [CrossRef]
- Berndt, C.; Rabiei, E.; Haberlandt, U. Geostatistical merging of rain gauge and radar data for high temporal resolutions and various station density scenarios. J. Hydrol. 2014, 508, 88–101. [Google Scholar] [CrossRef]
- Jewell, S.A.; Gaussiat, N. An assessment of kriging-based rain-gauge-radar merging techniques. Q. J. R. Meteorol. Soc. 2015, 141, 2300–2313. [Google Scholar] [CrossRef]
- Clark, I. Statistics or geostatistics? Sampling error or nugget effect? J. S. Afr. Inst. Min. Metall. 2010, 110, 307–312. [Google Scholar]
- Cressie, N.A.C. Statistics for Spatial Data, Revised ed.; Kohn Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Germann, U.; Berenguer, M.; Sempere-Torres, D.; Zappa, M. REAL—Ensemble radar precipitation estimation for hydrology in mountainous region. Q. J. R. Meteorol. Soc. 2009, 135, 445–456. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Empirically based modelling of radar-rainfall uncertainties for a C-band radar at different time-scales. Q. J. R. Meteorol. Soc. 2009, 1438, 1424–1438. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F.; Villarini, G. Product-Error-Driven Uncertainty Model for Probabilistic Quantitative Precipitation Estimation with NEXRAD Data. J. Hydrometeorol. 2007, 8, 1325–1347. [Google Scholar] [CrossRef]
- Rico-Ramirez, M.A.; Liguori, S.; Schellart, A.N.A. Quantifying radar-rainfall uncertainties in urban drainage flow modelling. J. Hydrol. 2015, 528, 17–28. [Google Scholar] [CrossRef]
- Sevruk, B. Adjustment of tipping-bucket precipitation gauge measurements. Atmos. Res. 1996, 42, 237–246. [Google Scholar] [CrossRef]
- Nešpor, V.; Sevruk, B. Estimation of wind-induced error of rainfall gauge measurements using a numerical simulation. J. Atmos. Ocean. Technol. 1999, 16, 450–464. [Google Scholar] [CrossRef]
- Habib, E.H.; Meselhe, E.A.; Aduvala, A. V Effect of Local Errors of Tipping-Bucket Rain Gauges on Rainfall-Runoff Simulations. J. Hydrol. Eng. 2008, 13, 488–496. [Google Scholar] [CrossRef]
- Molini, A.; Lanza, L.G.; La Barbera, P. The impact of tipping-bucket raingauge measurement errors on design rainfall for urban-scale applications. Hydrol. Process. 2005, 19, 1073–1088. [Google Scholar] [CrossRef]
- Steiner, M.; Smith, J.A.; Burges, S.J.; Alonso, C.V.; Darden, R.W. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 1999, 35, 2487–2503. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Rahimi, A.R. On-line detection of errors in tipping-bucket raingauges. J. Hydrol. 2003, 278, 197–212. [Google Scholar] [CrossRef]
- Luyckx, G.; Berlamont, J. Simplified Method to Correct Rainfall Measurements from Tipping Bucket Rain Gauges. In Proceedings of the World Water and Environmental Resources Congress, Orlando, FL, USA, 20–24 May 2001; pp. 767–776. [Google Scholar]
- Ciach, G.J. Local Random Errors in Tipping-Bucket Rain Gauge Measurements. J. Atmos. Ocean. Technol. 2003, 20, 752–759. [Google Scholar] [CrossRef]
- Lebel, T.; Bastin, G.; Obled, C.; Creutin, J.D. On the accuracy of areal rainfall estimation: A. case study. Water Resour. Res. 1987, 23, 2123–2134. [Google Scholar] [CrossRef]
- Habib, E.; Ciach, G.J.; Krajewski, W.F. A method for filtering out raingauge representativeness errors from the verification distributions of radar and raingauge rainfall. Adv. Water Resour. 2004, 27, 967–980. [Google Scholar] [CrossRef]
- Hasan, M.M.; Sharma, A.; Johnson, F.; Mariethoz, G.; Seed, A. Correcting bias in radar Z–R relationships due to uncertainty in point rain gauge networks. J. Hydrol. 2014, 519, 1668–1676. [Google Scholar] [CrossRef]
- Bringi, V.N.; Rico-Ramirez, M.A.; Thurai, M. Rainfall Estimation with an Operational Polarimetric C-Band Radar in the United Kingdom: Comparison with a Gauge Network and Error Analysis. J. Hydrometeorol. 2011, 12, 935–954. [Google Scholar] [CrossRef]
- De Marsily, G. Quantitative Hydrogeology, 1st ed.; Academic Press: San Diego, CA, USA, 1986. [Google Scholar]
- Mazzetti, C.; Todini, E. Combining Weather Radar and Raingauge Data for Hydrologic Applications. In Flood Risk Management: Research and Practice; Samuels, P., Huntington, S., Allsop, W., Harrop, J., Eds.; Taylor & Francis Group: London, UK, 2009; ISBN 9780415485074. [Google Scholar]
- Krajewski, W.F.; Ciach, G.J. Towards Probabilistic Quantitative Precipitation WSR-88D Algorithms: Preliminary Studies and Problem Formulation; National Oceanic and Atmospheric Administration/National Weather Service: Iowa City, IA, USA, 2003; p. 59.
- Brandsma, T. Comparison of Automatic and Manual Precipitation Networks in The Netherlands; Royal Netherlands Meteorological Institute: De Bilt, The Netherlands, 2014; p. 42. [Google Scholar]
- Wauben, W. WMO Laboratory Intercomparison of Rainfall Intensity Gauges; Instrumental Department, INSA-IO, KNMI: De Bilt, the Netherlands, 2006; p. 164. [Google Scholar]
- Overeem, A.; Holleman, I.; Buishand, A. Derivation of a 10-Year Radar-Based Climatology of Rainfall. J. Appl. Meteorol. Climatol. 2009, 48, 1448–1463. [Google Scholar] [CrossRef]
- Cecinati, F.; Wani, O.; Rico-Ramirez, M.A. Comparing Approaches to Deal With Non-Gaussianity of Rainfall Data in Kriging-Based Radar-Gauge Rainfall Merging. Water Resour. Res. 2017. [Google Scholar] [CrossRef]
- Marcotte, D. Fast variogram computation with FFT. Comput. Geosci. 1996, 22, 1175–1180. [Google Scholar] [CrossRef]
- Nerini, D.; Besic, N.; Sideris, I.; Germann, U.; Foresti, L. A non-stationary stochastic ensemble generator for radar rainfall fields based on the short-space Fourier transform. Hydrol. Earth Syst. Sci. 2017, 21, 2777–2797. [Google Scholar] [CrossRef]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Gómez-Hernández, J.J. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.F.; Kruger, A. Sampling Errors of Tipping-Bucket Rain Gauge Measurements. J. Hydrol. Eng. 2001, 6, 159–166. [Google Scholar] [CrossRef]
- Cecinati, F.; de Niet, A.; Sawicka, K.; Rico-Ramirez, M.A. Optimal Temporal Resolution of Rainfall for Urban Applications and Uncertainty Propagation. Water 2017, 9, 762. [Google Scholar] [CrossRef]
- Hamill, T.M. Interpretation of Rank Histograms for Verifying Ensemble Forecasts. Mon. Weather Rev. 2001, 129, 550–560. [Google Scholar] [CrossRef]
- Cecinati, F.; Moreno Ródenas, A.M.; Rico-Ramirez, M.A. Integration of rain gauge errors in radar-rain gauge merging techniques. In Proceedings of the 10th World Congress on Water Resources and Environment, Athens, Greece, 8 July 2017; pp. 279–285. [Google Scholar]
- Erdin, R.; Frei, C.; Künsch, H.R. Data Transformation and Uncertainty in Geostatistical Combination of Radar and Rain Gauges. J. Hydrometeorol. 2012, 13, 1332–1346. [Google Scholar] [CrossRef]

| ID | Provider | Use | Number | Type | Temporal Resolution | Intensity resolution |
|---|---|---|---|---|---|---|
| EM | Municipality of Eindhoven | Modelling | 3 | Tipping bucket | 1 min | 0.25 mm |
| DWB | Dommel Water Board | Modelling | 3 | Tipping bucket | 1 min | 0.1 mm |
| KNMI-A | KNMI | Modelling | 7 | Floating device | 12 s | 0.001 mm |
| KNMI-M | KNMI | Validation | 35 | Manual | 1 day | 0.1 mm |
| Experiment 1 | Experiment 2 | Experiment 3 | |
|---|---|---|---|
| Tested variable | Range | Number of rain gauges | Accurate/less accurate rain gauge ratio |
| Tested values | (10, 30, 50, 80, 100) | (4, 10, 20, 40, 80) | (5/25, 10/20, 15/15, 20/10, 25/5) |
| Number of realisation | 500 for each range value | 500 for each tested number of rain gauges | 500 for each tested rain gauge ratio |
| Number of accurate rain gauges | 10 | 2, 5, 10, 20, 40 | 5, 10, 15, 20, 25 |
| Number of less accurate rain gauges | 10 | 2, 5, 10, 20, 40 | 25, 20, 15, 10, 5 |
| Range value [pixels] | 10, 30, 50, 80, 100 | 50 | 50 |
| Sill [ ] | 0.1 | 0.1 | 0.1 |
| Mean [ ] | 1 | 1 | 1 |
| RMSE | MRTE | BIAS | |
|---|---|---|---|
| OK | 2.49 | 0.32 | −0.38 |
| OKUD | 2.46 | 0.30 | −0.35 |
| KED | 2.48 | 0.28 | −0.39 |
| KEDUD | 2.08 | 0.22 | −0.37 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cecinati, F.; Moreno-Ródenas, A.M.; Rico-Ramirez, M.A.; Ten Veldhuis, M.-c.; Langeveld, J.G. Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data. Atmosphere 2018, 9, 446. https://doi.org/10.3390/atmos9110446
Cecinati F, Moreno-Ródenas AM, Rico-Ramirez MA, Ten Veldhuis M-c, Langeveld JG. Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data. Atmosphere. 2018; 9(11):446. https://doi.org/10.3390/atmos9110446
Chicago/Turabian StyleCecinati, Francesca, Antonio M. Moreno-Ródenas, Miguel A. Rico-Ramirez, Marie-claire Ten Veldhuis, and Jeroen G. Langeveld. 2018. "Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data" Atmosphere 9, no. 11: 446. https://doi.org/10.3390/atmos9110446
APA StyleCecinati, F., Moreno-Ródenas, A. M., Rico-Ramirez, M. A., Ten Veldhuis, M.-c., & Langeveld, J. G. (2018). Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data. Atmosphere, 9(11), 446. https://doi.org/10.3390/atmos9110446





