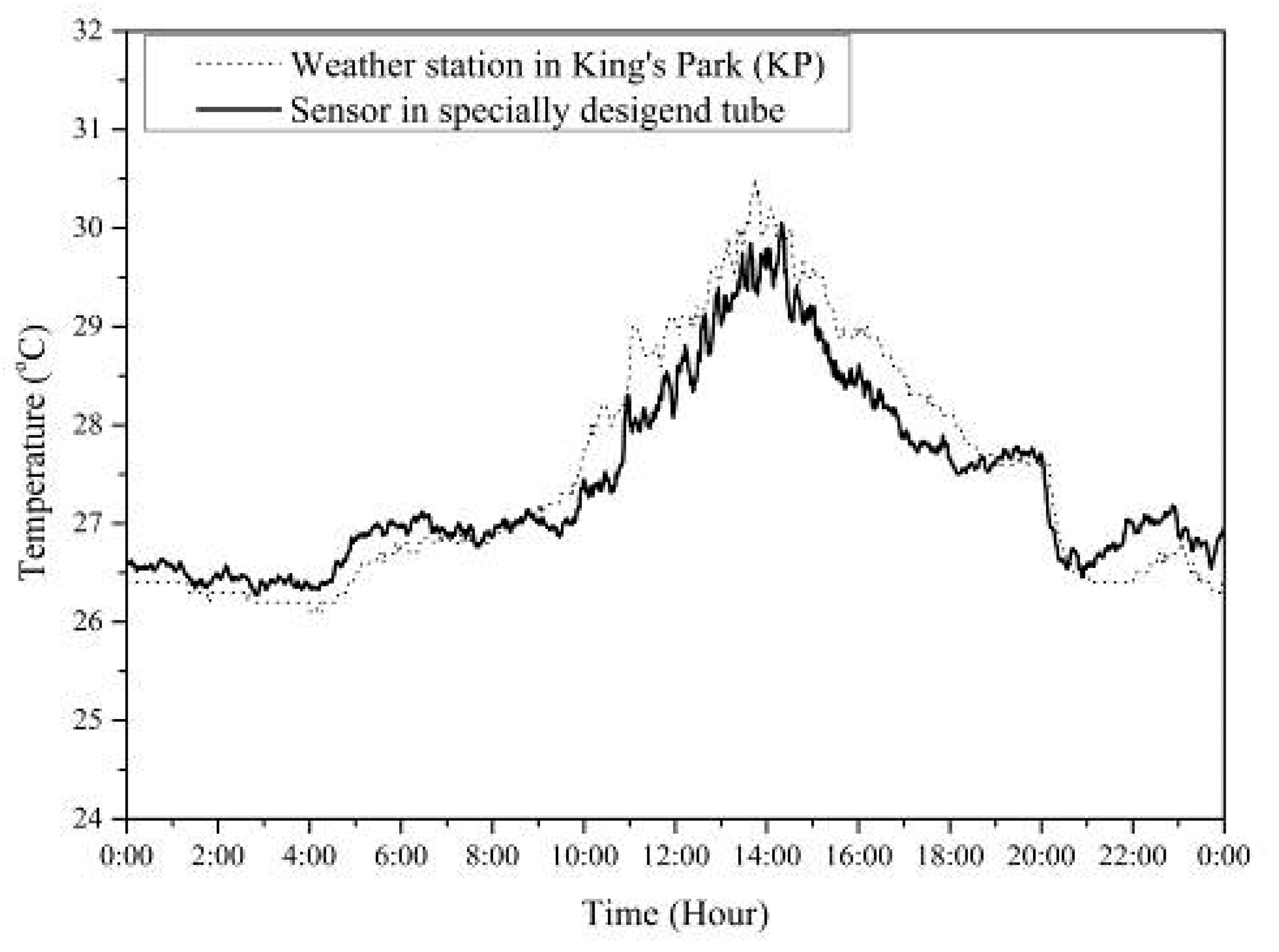
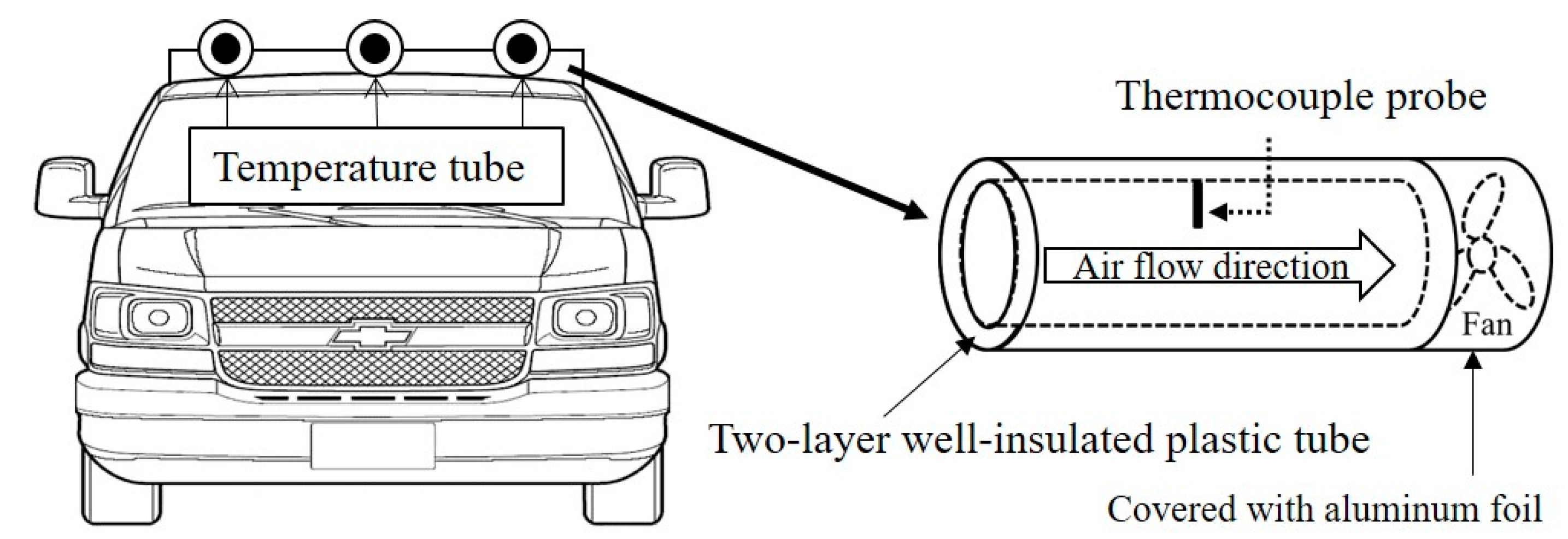
3.1. Model Description
Yang et al. [
39] developed a model to determine the air temperature in the city, which is referred to as zero-dimensional City Air Temperature (zero-CAT) model. However, the ventilation rate and the anthropogenic heat in the zero-CAT model is not applicable for the street, especially in a compact high-rise city such as Hong Kong. The model is improved in this section.
The original model is based on the zero-dimensional mesoscale model to determine urban surface temperature originally developed by Silva et al. [
37]. The zero-CAT model cataloged the urban fabric into different types and linked the air and surface temperature together through an analytical solution of urban air temperature. Two assumptions are made to simplify the city to a simple and ideal control volume for the zero-CAT model (
Figure 5).
- (1)
The city is composed of buildings, streets, plants, and vehicles. The underlying surface is concrete with uniform distribution for the city area. The plan area (
) includes the area of the green zone (
), such as plants and parks; the area of the streets covered by pavement (
); and the building roof area (
). The total area of the surfaces (
) in the control volume includes both the plan area (
) and the surface area of the buildings (
), including wall surfaces and the roof of buildings. The relation of the terms is shown in Equations (1) and (2).
The plan area coverage ratio
, calculated by Equation (3), represents the density of the city. The frontal area ratio
, is calculated by the area of the wall of the building which facing the inflow (
) and the total plan area, as shown in Equation (4) [
45]
- (2)
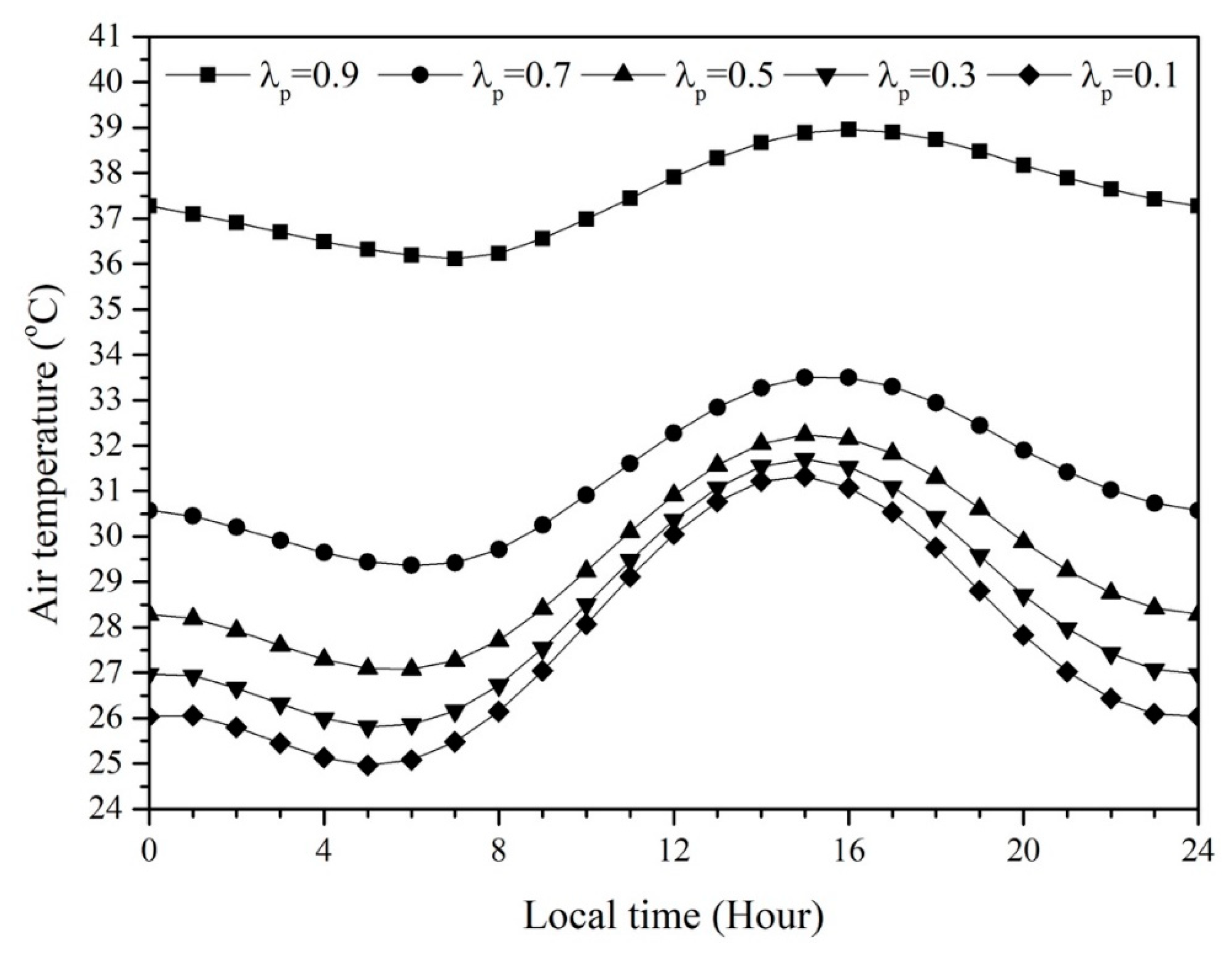
The airflow is assumed to be fully mixed, so the air temperature (
) distribution in the domain is uniform. The temperature distribution in the thermal mass except for the underlying surface is also assumed to be uniform, and the surface temperature is referred to as
. The rural air temperature
is also uniform. The air temperature from the representative rural station was used as the temperature of the incoming air [
39].
With all assumptions, two heat balance equations are used in the city, one for the outdoor air and one for the surface temperature. The balance equation of the urban air is
where
is the density of the air,
is the heat capacity of the air,
is the ventilation rate,
is the sensible heat flux transfer coefficient, and
is the anthropogenic heat.
The surface energy balance equation is:
where
is the thermal mass of the urban area. The terms on the right side are the different energy terms gained in the control volume. The term
is the solar radiation absorbed by the urban fabric,
is the solar radiation,
is the albedo of the volume, and
and
are the conductive heat flux into vegetated areas and roads, respectively.
is calculated by
, where
is the conductivity of the surface type
, and
is the representative depth in which the diurnal temperature variation is ignored.
is the subsurface of
type temperature. The term
is the conductive heat flux into building walls, which is also represented as
.
and
are the velocity of building roofs and walls.
is the indoor air temperature.
is the evapotranspiration heat flux from a natural vegetated surface.
represents the convection heat transfer from the total urban surfaces, which is calculated by
. The last term is the long wave radiation heat loss to the sky; the calculation is simplified to
.
is the gradient of the linearized function and
is the sky temperature. More details can be found in Yang et al. [
39].
3.2. Ventilation Rate
Assume an ideal city with same length and width (
L), and the building height is
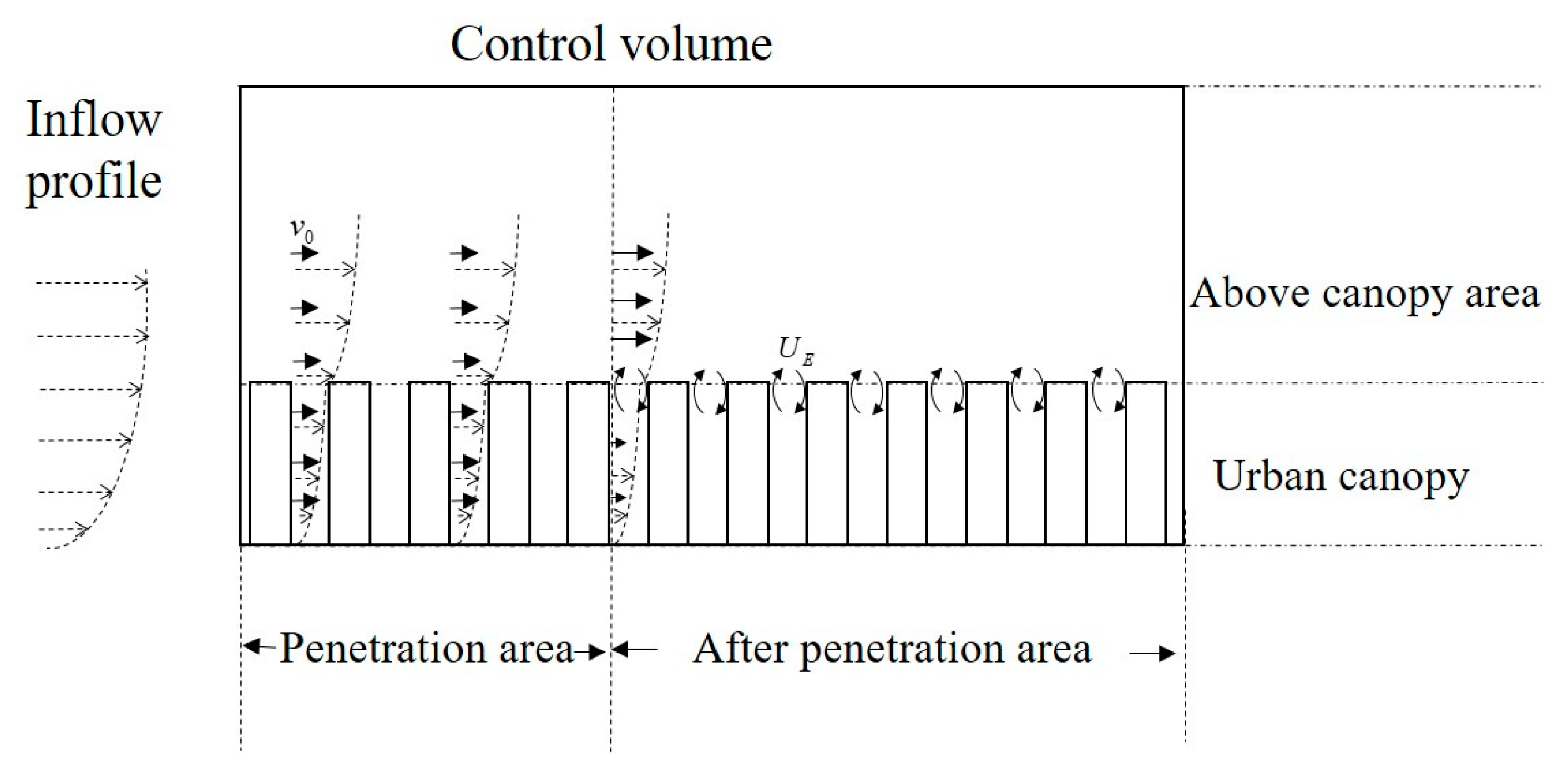
H. The air change rate in the city includes the rate in the penetration area and that after the penetration area. The penetration area is the area where the dominant vertical transport was driven by the mean velocity, and the dominant vertical transport in the area after the penetration area was driven by turbulence, as shown in
Figure 6. The length of the penetration area is determined by penetration depth (
), which is calculated by Equation (7), suggested by Belcher et al. [
46].
where
usually equals 2, and the adjustment length
is
for low-rise and
for high-rise city [
39].
In the after penetration area, the dominant vertical transport is turbulence, which can be calculated by spatially averaged vertical velocity between urban canopy and above the canopy area, named as exchange velocity
. It balances the momentum between urban canopy and above the canopy area, and the definition is also shown in
Figure 6.
The total air change rate in the model includes the air change rate in both the penetration area and after the penetration area, as shown in Equation (8).
where
is exchange velocity.
is the effective velocity of the inflow from the rural. In the penetration area, the air change rate is
. The rural wind follows the log law. The exchange velocity (
) is calculated by Equation (9) [
47].
where
is the velocity above the urban canopy, which is the velocity at 2
H as shown in many other studies for city [
48].
is the velocity in the urban canopy. The friction velocity
is defined as Equation (10).
The morphology method instead of wind tunnel experiment is adopted here because the geometry of the surface roughness elements such as reference height , displacement height and roughness length , could easily be obtained and changed for the ideal city.
Bentham and Britter [
47] also found that the velocity in the urban canopy
is different for low-rise and high-rise buildings, as shown in Equations (11) and (12).
However, for very high and compact area, the model is not applicable. Yuan et al. [
48] found that
is almost constant when frontal area ratio
is larger than 0.4.
in the high and compact city can be calculated by Equation (13).
The relationship between roughness height
, zero displacement
, frontal area ratio
and plan area ratio
from Grimmond and Oke [
45] was directly used in the mentioned study, and was also adopted in this study. Combining these parameters with Equations (10)–(13), the relationship between frontal area ratio
and
is shown in
Figure 7. When
increases, the velocity in the urban canopy decreases.
The effective velocity can be rewritten to a function of . The rural wind follows the log law (Equation (8)), and is the wind at 2H. Effective velocity can be calculated by Equation (14).
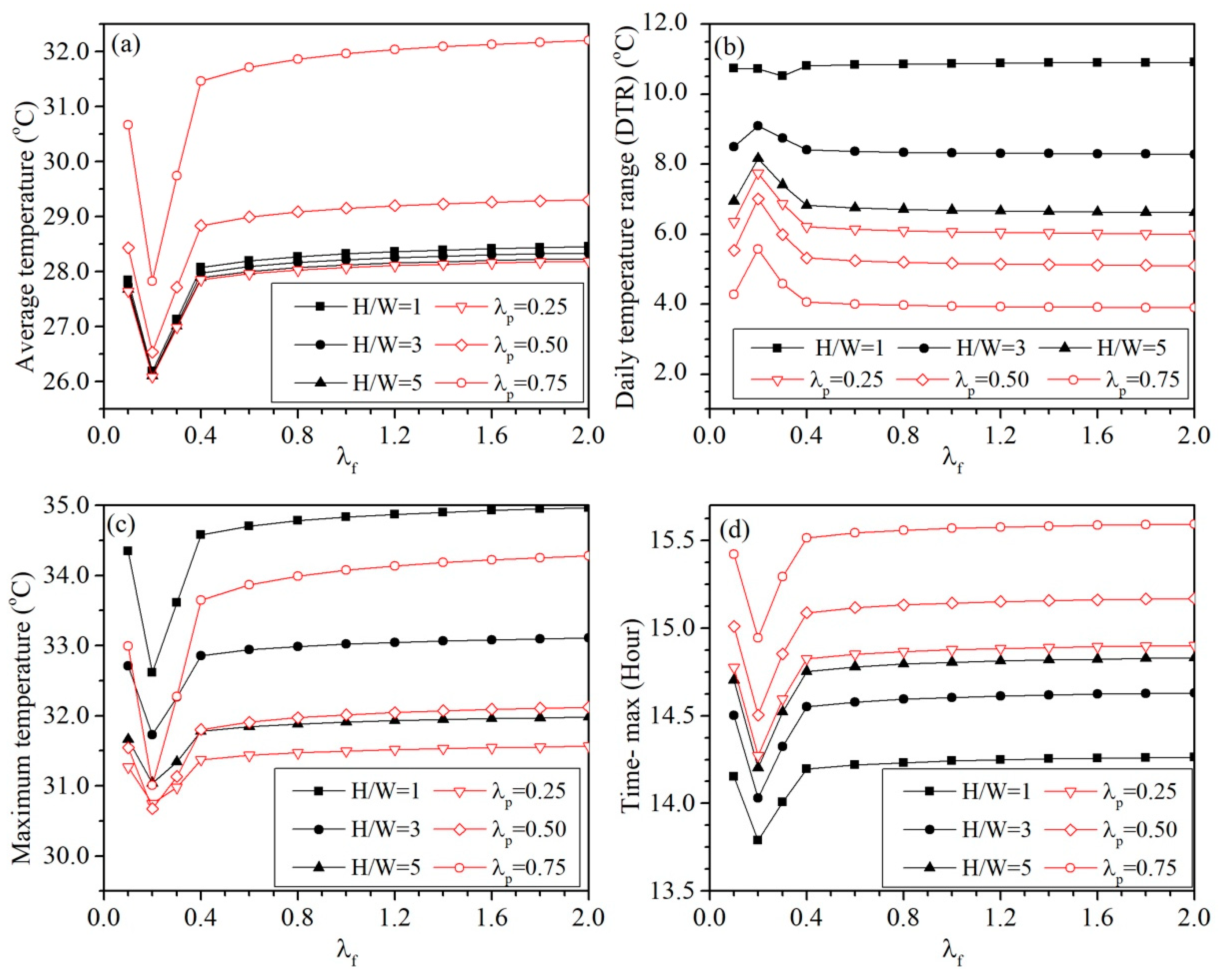
The length of the city L is proportional to the building height H. . Equation (8) becomes
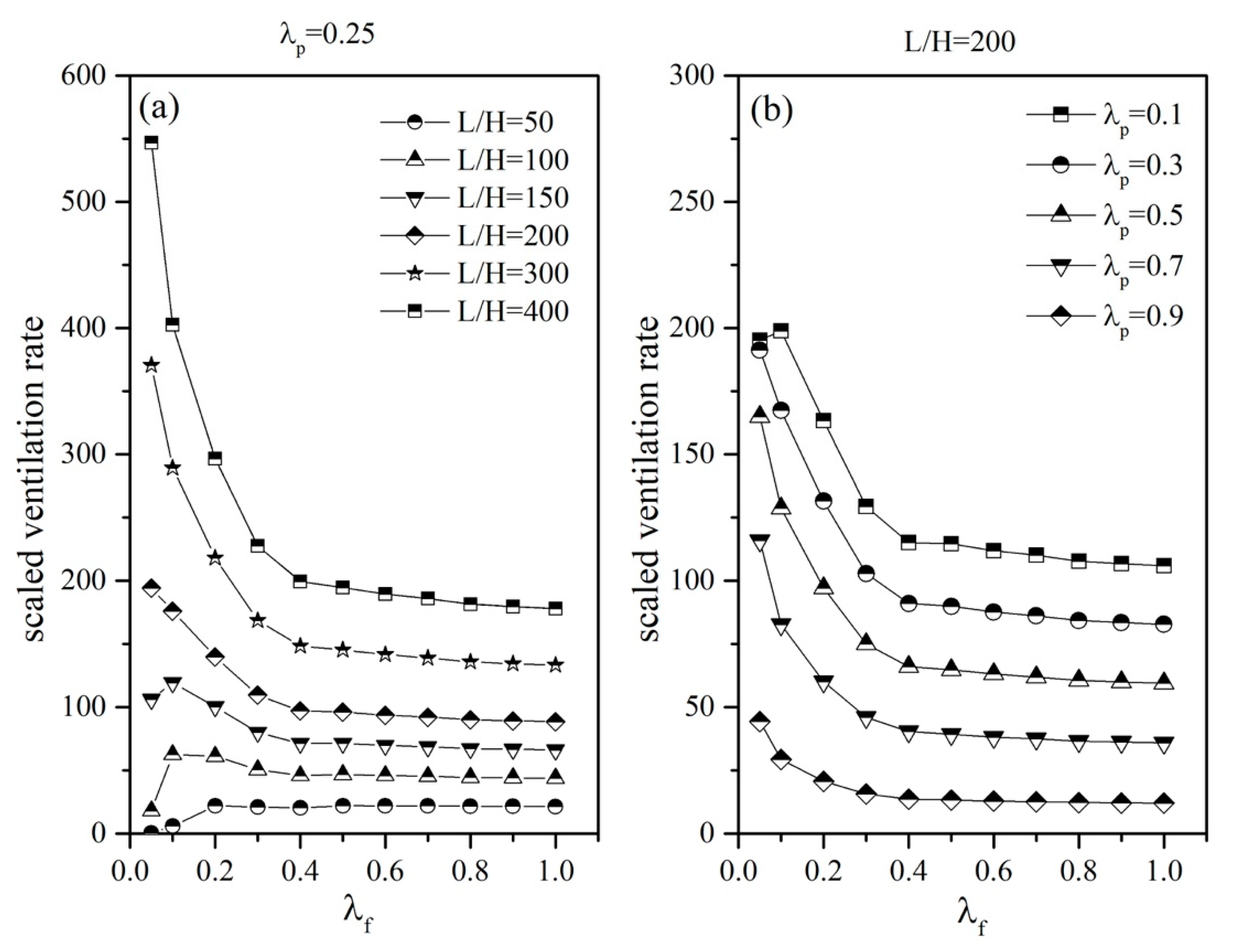
Figure 8a shows the total air change rate with different city length and
. The density (
) is 0.25. In general, the ventilation rate is larger when the city is bigger. Because the area dominated by vertical velocity, which is the after-penetration area, is larger than the area in the small city. When the city is large enough (larger than 200
H), the ventilation rate decreases with
. This is because the city has large
usually has large
H/W ratio, which leads to small exchange velocity. However, for the small city, the ventilation rate increases first when
is smaller than 0.2. When
increases, the penetration depth (
) decreases, and term
increase, while the exchange velocity decreases. Therefore, a maximum ventilation rate appears when
is 0.2. A large city is usually larger than 200
H long. We used
L/H = 200 as a constant to discuss the impact of
.
Figure 8b shows the ventilation rate with different
and
for a general city (
L/H = 200). When
increases, the city becomes more compact, and the ventilation rate smaller.
3.3. Anthropogenic Heat
In the ideal city, the distribution of anthropogenic heat is assumed to be uniform. The anthropogenic heat includes several parts: metabolism, industry, buildings and transports.
- (a)
The heat flux generated from metabolism, industry and buildings
In the study area (i.e., District Yau Tsim Mong), the population density is 40,000 persons per square kilometer [
49], and the corresponding metabolic heat flux is on the order of 10 W m
−2 [
50]. The heat flux generated from industry is ignored as there is almost no industry [
51]. The heat flux generated from buildings is calculated by Equation (16) according to Sailor [
50] and Yang et al. [
41].
where
is 50 W m
−2 and the
is the height of each floor, which is assumed to be 3 m.
- (b)
The heat flux generated from traffic
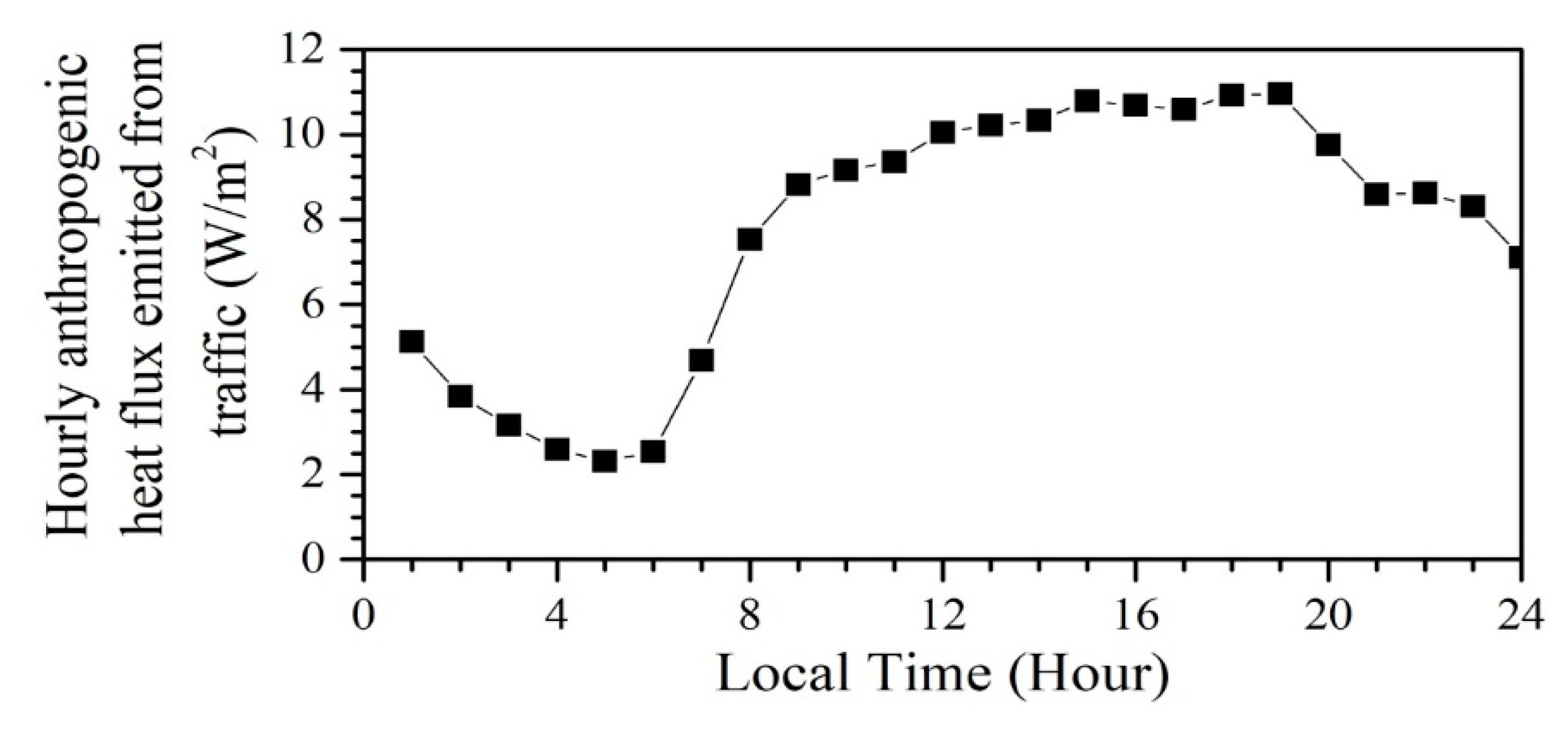
The hourly anthropogenic heat flux emitted from traffic
is calculated from Equation (17) [
52,
53].
where
is local time,
is the hourly total number of vehicles of class
consuming fuel type
and travelling on road segment
at hour
,
(J m
−1) is the energy used per vehicle of class
consuming fuel type
, and
is the vehicle distance travelled on road segment
(m).
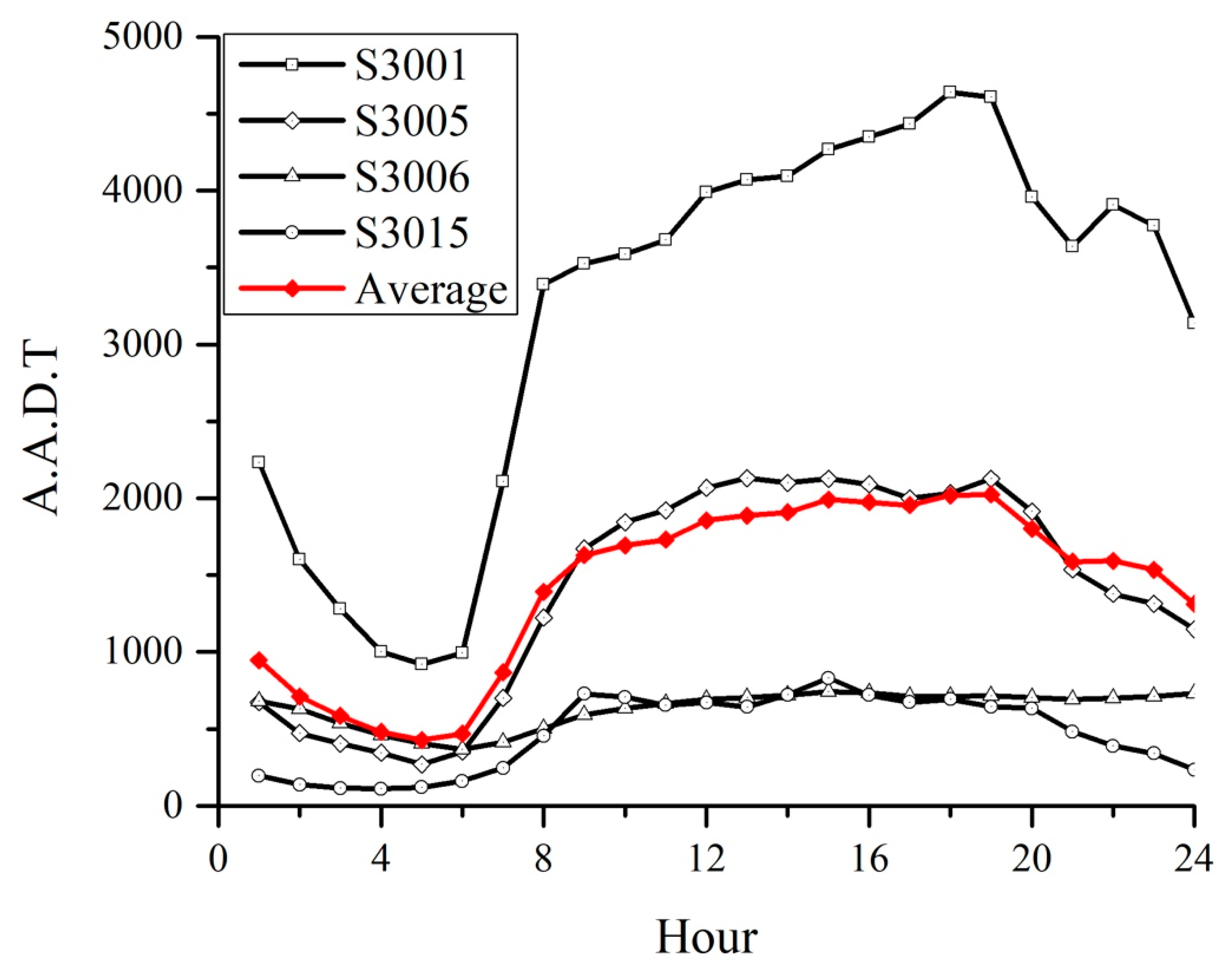
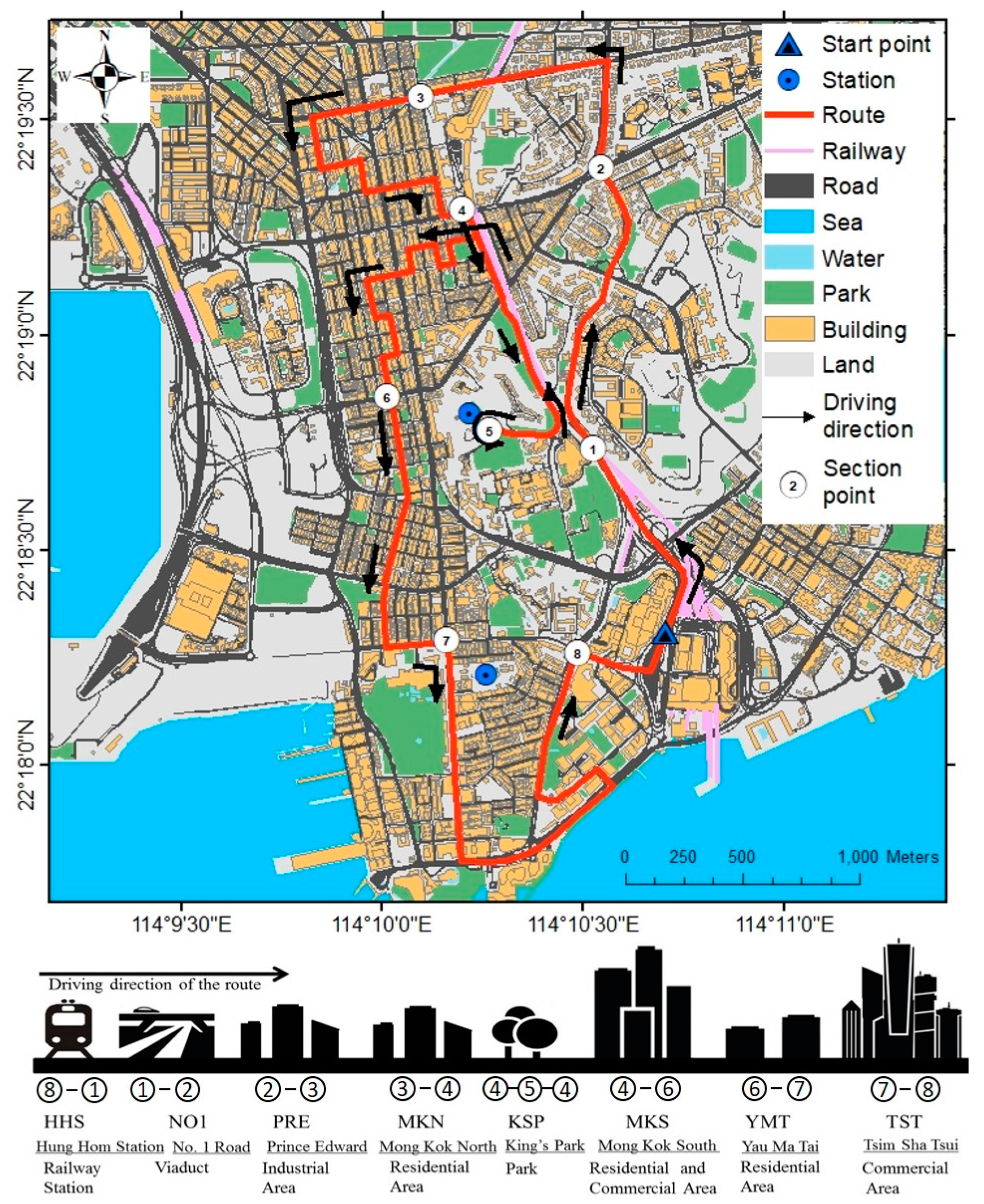
Assume the traffic flow in the ideal city is uniform. We averaged the Annual Average Daily Traffic (A.A.D.T) from four monitored station in the different part of the design route [
54], and used it as the uniform traffic flow. The averaged A.A.D.T are shown in
Appendix C.
Table 2 shows the percentage of each class among the vehicles and the energy used for each vehicle class in Hong Kong. The latter was similar to Singapore [
53]. It was assumed all cars in Hong Kong use unleaded petrol. The total area and total road length of the road segment are evaluated from Google Earth. Finally, the hourly anthropogenic heat flux released from transport in the experiment area was calculated, as shown in
Figure 9.