Abstract
Ozone is a key trace gas in the troposphere; because it is a greenhouse gas, it is very reactive, and it is potentially toxic to humans, fauna, and vegetation. The main sink processes for ozone are chemical reactions and the turbulent deposition flux to the earth’s surface. The deposition process itself is rather complex: The interactions between co-varying drivers such as the tropospheric ozone concentration, turbulence, and chemical reactions are not well understood. In the case of ozone deposition to vegetation, another aspect that must be studied is the role of stomatal regulation for a wide range of conditions. Therefore, we measured turbulent deposition fluxes of ozone with the eddy covariance technique during the peak of the growing season in 2014 over a managed, rewetted peatland in NW Germany. The deposition flux was large during the day (up to −15 nmol m−2 s−1) and relatively small during the night (between −1 and −2 nmol m−2 s−1). Flux partitioning by applying the surface resistance analogy and further analysis showed that the stomatal uptake was smaller than non-stomatal deposition. The correction of stomatal conductance with the gross primary production (GPP) improved the estimation of day- and nighttime stomatal deposition fluxes. Statistical analysis confirmed that the friction velocity (u*) was the single most important driver of non-stomatal ozone deposition and that relationships with other environmental drivers are not linear and highly variable. Further research is needed to develop a better process understanding of non-stomatal ozone deposition, to quantify the role of surface deposition to the ozone budget of the atmospheric boundary layer, and to estimate uncertainties associated with the partitioning of ozone deposition into stomatal and non-stomatal fluxes.
1. Introduction
Tropospheric ozone is an important greenhouse gas and is harmful to humans, as it impairs lung function [1]. Its average mixing ratio has more than doubled over the past 150 years [2]; the background mixing ratio today in Europe is approximately 30 ppb and is continuously increasing [3]. Ozone is not directly emitted into the atmosphere by anthropogenic emissions, but it is formed through photochemical reactions involving precursors—mainly nitrogen oxides (NOx) and volatile organic compounds (VOC)—from both natural and anthropogenic origins [4]. The sinks of tropospheric ozone are manifold and have been studied previously in detail: Ozone reacts with various trace gases such as hydroperoxyl radicals (HO2), biogenic VOC [5], and nitric oxide (NO) [6,7]. It also reacts with aerosol particles [8,9] and undergoes direct photolysis through short-wave solar radiation [6]. Another sink mechanism is its deposition on the earth’s surface [10]. Once in contact with a given surface (vegetation, soil, or water), ozone will react readily and be decomposed; thus, its deposition is a terminal process [11,12]. For vegetation, two ozone deposition pathways act in parallel: First, ozone is deposited on plants’ surfaces, such as on their cuticles or twig and stem surfaces. Second, ozone can enter the plants’ stomata, reach the sub-stomatal cavity and thus impact photosynthesis and other physiological processes [13,14]. This may eventually cause alterations of plant morphology [15] and crop yield losses [16]. However, the stomatal ozone flux preceding these effects cannot be directly quantified on an ecosystem scale. Efforts to quantify this flux by indirect methods have only been made for a few ecosystems so far [17,18,19,20,21,22,23].
In this study, we focus on the ozone deposition process on vegetation, specifically on the partitioning between stomatal and non-stomatal fluxes [22,24,25]. We performed this study on a mid-latitude peatland ecosystem, which is managed with the goal of bringing it back to a natural or at least semi-natural state. While most studies on ozone deposition to peat- and wetlands have been conducted using mesocosm and microcosm experiments [26,27,28,29], only few studies have considered the larger picture and deal with ozone deposition to these ecosystems as a whole [30,31,32,33]. To our knowledge, there is only one study on ozone deposition to a mid-latitude peatland on the ecosystem scale [21]; thus, here we aim to add valuable information that can improve the characterization of ozone deposition to these ecosystems.
We applied the eddy covariance technique as well as the surface resistance analogy to first quantify the overall ozone deposition flux () and then partition this flux into stomatal (i.e., uptake by vegetation through stomatal gas exchange, ) and non-stomatal fluxes () during the peak of the growing season. We performed a driver analysis of non-stomatal deposition velocities and analyzed the relationship between the stomatal ozone fluxes and gross primary productivity under different environmental ozone concentrations.
2. Materials and Methods
2.1. Study Site and Study Period
In NW Germany, natural peat has been widely cut through the past centuries and is still cut today. Once drained, a large portion of the soils have been used for intensive agricultural activities. Over the past decades, some of the cut areas have started to be restored in order to regain the natural properties of these ecosystems, such as reestablishing the groundwater level to be near the soil surface.
Our study site is located within the Mittleres Wietingsmoor (MWM) and north of the village Freistatt within the Diepholzer Moorniederung, a peatland consisting mainly of bogs. This Diepholz peatland extends over 1575 ha, of which 1176 ha are under high-priority nature protection. Until the 1970s, peat was cut manually here; after that and up until 1995, it was cut using industrial machinery. Overall, up to 1.3 m of peat was cut. In 1982, restoration started in some areas and was extended and intensified after 1999 [34,35].
The actual site (52°39′8″ N, 8°39′12″ E) is within an open, rewetted grassland with Juncus effuses being the dominant species. In wetter areas, we found Eriophorum vaginatum and Sphagnum cuspidatum, while Holcus lanatus appeared in dryer patches. The average vegetation height increased from 81 cm to 85 cm from the beginning to the end of our experimental period. The area is kept free of woody vegetation through regular sheep grazing.
The experimental period was from 30 June through 4 August 2014. Due to rather frequent and sometimes extensive power losses before 15 July, we limit our data analysis to the period 15 July through 4 August 2014.
2.2. Instrumentation
The eddy covariance setup consisted of three main components. First, a CSAT3 (Campbell Scientific Logan, UT, USA) ultrasonic anemometer was employed to measure the 3D wind vector and the sonic temperature. It was mounted at a height of z = 2.42 m above ground level and oriented to the southwest. Second, a LI-7200 CO2/H2O enclosed-path gas analyzer (LI-COR, Inc., Lincoln, NE, USA) measured the CO2 and the water vapor concentration. Its intake tube was 0.5 m long and had an inner diameter of 5.3 mm. The inlet was mounted 4 cm to the north and 22 cm above the center of the ultrasonic anemometer. Third, a CLD 88 O3 (ECO PHYSICS AG, Dürnten, Switzerland) ozone analyzer was used to measure the mixing ratio of O3 () with the gas phase chemiluminescence method after O3 reacted with NO, which was offered in surplus. The instrument has a measurement range from 0.5 ppb to 5000 ppb and the lag time within the analyzer is below 1 second. The inlet of a 16 mm inner diameter Teflon tube was located 13 cm to the northeast of the center of the ultrasonic anemometer. The data acquisition frequency for all instruments described so far was 5 Hz. Whenever needed, ozone mixing ratios (, in units ppb) were converted to concentrations (, in units of µg m−3 or nmol m−3) by using actual air temperature (Tair) and pressure data.
Further, low-frequency measurements were made for air temperature (Tair) and relative air humidity (rH) with an HMP45A (Vaisala, Helsinki, Finnland) within a radiation shield at 2 m above ground. A four-channel CNR 4 radiometer (Kipp & Zonen B.V., Delft, Netherlands) was employed for the measurement of longwave and shortwave radiation (upwelling and downwelling, respectively), and a Young Typ 61302 V sensor measured the air pressure. These measurements were collected at 1 Hz and aggregated to 10-min averages. The photograph in Figure 1 (left) shows the instrumented field site.

Figure 1.
Photograph of the micrometeorological flux site in the Mittleres Wietingsmoor, NW Germany (left). Areal view (from Bing Maps) of the site with the overlaid daytime (light blue) and nighttime (purple) flux footprint during the experimental period (see Section 2.3 for more details) (right). Contour lines correspond to the 20%, 40%, 60% and 80% contributions to the flux footprints calculated according to Kljun et al. [36].
2.3. Data Analysis
2.3.1. Eddy Covariance
The sensible heat flux (H), latent heat flux (LE), flux of CO2 () and were calculated with the software EddyPro 6.2.0 (Licor Bioscience) [37] (see Equation (1), Section 2.3.2, for the calculation of the ozone flux). Raw data processing and flux calculation included de-spiking [38], double rotation of the 3D wind components, block averaging, lag correction with covariance maximization within defined bounds, corrections for sensor separation according to Horst and Lenschow [39], high-frequency corrections according to Ibrom et al. [40], and high-pass filtering effects according to Moncrieff et al. [41]. Additionally, the ozone fluxes were corrected for the dilution of the ozone concentration by water vapor, which was not measured within the instrument [42]. The calculated fluxes were quality controlled for stationarity and integral turbulence characteristics [43]. The CO2 storage term was estimated using the 1-point storage correction and then added to the CO2 fluxes to derive the net ecosystem exchange (NEE). Nocturnal data were filtered for low friction velocity (u*) values. The u* threshold (0.1 m s−1) was estimated following Papale et al. [44].
Data quality control was performed according to Mauder and Foken [45] and resulted in three classes: QC_0 data are considered to be of very good quality, QC_1 data are of acceptable quality, and QC_2 data should not be considered for scientific data analysis. Further, data sets that are associated with low u* values (u* < 0.1 m s−1) are considered problematic because the respective turbulence is not sufficiently established. After removal of QC_2 data and those with low u* values (see Section 3.1 for details), the remaining data set was gap-filled with marginal distribution sampling as described in Reichstein et al. [46]. Statistical analyses (Section 3.2 and Section 3.3) were performed with non-gap-filled data.
Subsequently, NEE was partitioned into gross primary productivity (GPP) and ecosystem respiration (Reco) by using daytime flux partitioning with light response curves [47] as implemented in REddyProc 1.0.0 for R [48].
The flux footprints were calculated as described in Kljun et al. [36] for half-hour fluxes when the u* threshold was exceeded. Nighttime fluxes were calculated whenever the global radiation (i.e., the shortwave, downwelling radiation Rg) was below or equal to 5 W m−2, while daytime conditions were defined for global radiation values above 200 W m−2. With this classification, the transition periods around sunrise and sunset were excluded from the analysis.
Co-spectra were computed for the vertical wind component in conjunction with temperature and O3, respectively, for each half hour. Frequency-class binned averages were then used to calculate ensemble co-spectra from good-quality data and well-developed turbulence conditions for individual stability classes. Reference co-spectra for temperature and vertical wind were calculated according to Kaimal and Finnigan [49].
The stability of the boundary layer was determined from the ultrasonic anemometer data as (z-d)/L with L being the Monin-Obukhov length and d the displacement height (d = 0.67 · z). Neutral stability conditions were defined as −0.03 ≤ z/L ≤ 0.03, stable conditions as z/L > 0.03, and unstable conditions as z/L < −0.03, respectively.
2.3.2. Resistance Terms and Deposition Velocity
was measured with the eddy covariance method as described above on the basis of high-frequency measurement of and the vertical wind component w (Equation (1) in [24]),
where the primes describe the deviations of individual data points from the half-hour means and the overbar indicates the half-hour averages. Further, can be expressed in terms of concentration gradients and resistance terms (Equation (4) in [24]):
Here, is the ambient O3 concentration at measurement height and is the concentration within the sub-stomatal cavities, which can be assumed to be zero [50]. The total resistance against the O3 deposition is equal to the sum (Equation (2)), where the aerodynamic resistance () and the bulk leaf boundary layer resistance for ozone () are computed from ultrasonic anemometer data as (Equations (8) and (9) in [50])
and (Equation (6) in [50])
Here, σv is the standard deviation of the lateral wind component, u* is the friction velocity, u is the horizontal wind velocity, Sc = 1.07 is the Schmidt number for ozone and Pr = 0.72 is the Prandtl number [51]. The surface resistance can now be calculated from Equation (2) with and by using the measured ozone flux (Equation (1)) and the ambient ozone concentration :
Following the reasoning of Gerosa et al. [25] and Fares et al. [17], can be divided into and (Equation (9) in [24]),
happens together with the exchange flux of CO2 and H2O vapor through the plant stomata. includes all other O3 sinks in the vegetation including plant, water, soil surfaces, and chemical reactions. It is further presumed that the flux-resistance concept can be applied for both terms on the right-hand side of Equation (6) separately while using an ozone concentration near the surfaces (Equation (9) in [24]):
Note that is not measured but will be computed as a residual once and are known (see below, Equations (8)–(12). The surface resistance , which is known from Equation (5), can be partitioned into two resistances acting in parallel, the stomatal () and the non-stomatal () resistances (Equation (9) in [21]):
To calculate the stomatal resistance of ozone, , we use the estimate of the stomatal conductance for water vapor from the Penman-Monteith approach (gsto,PM) and the molecular diffusivities for water vapor and ozone (Equation (4) in [11]),
where β is the Bowen ratio H / ET, s is the slope of the water vapor saturation curve (Pa K−1), and γ is the psychrometric constant (kPa K−1). is the bulk leaf boundary layer resistance for water vapor, which is computed from Equation (4) with the Schmidt number for water vapor (0.68; [51]). We calculated the water vapor pressure deficit (VPD) in Equation (9) from the difference between , which is saturation vapor pressure (kPa) at the temperature at canopy surface level Tsurf, and e, which is the vapor pressure (kPa) at measurement level z. This procedure was proposed by Gerosa et al. (Equation (12) in [24]), who suggest calculating as
and this calculation is valid as long as no direct evaporation takes place. To account for “computational contamination” of the stomatal water vapor conductance in Equation (9) from direct evaporation, we applied a correction after Lamaud et al. [11]. For this purpose, the slope of the regression line α between and GPP is computed for conditions during daytime and rH < 60% only. Under these conditions, the direct evaporation from wet surfaces is at its minimum (zero), and the stomatal conductance for water vapor and CO2 are related by the constant α. This ratio is used to compute the stomatal conductance of ozone for all conditions (Equation (5) in [11]):
Now, can be directly calculated as
and can be calculated from Equation (8), from Equation (7), and the flux partitioning can be derived from Equation (6). This routine was applied for each 30-min interval of the measurement period.
The deposition velocity is typically considered as the inverse of , while, by convention, a minus sign is introduced into Equation (11) (Equation (7) in [50]):
Additionally, the deposition velocity can be calculated from measured data directly as (Equation (9) in [11])
In analogy to eqs. 8 and 11, ozone deposition velocities towards the stomata are defined as , and towards all non-stomatal surfaces as . Note that equals .
2.4. Statistical Driver Analysis
Statistical analyses were performed with R 3.2.2 [48]. A relative importance analysis was carried out using the relaimpo package [52] with the Lindeman, Merenda and Gold method (LMG). The contribution of each predictor variable (see below) to the total R2 between the modelled and the measured non-stomatal deposition velocity was calculated by first averaging the contributions of each variable according to different ordering of predictor variables within one model, and then averaging the results of step 1 for each variable across multiple linear models of different sizes (different numbers of predictor variables included). This procedure needs to be applied when the predictor variables are correlated to each other, as their order influences the individual contributions to the total R2 within the multiple linear model [52]. The following predictor variables were used for the relative importance analysis of , , VPD, Tair, u*, LE, GPP, Rg and rH. The selection was based on variables which were identified as potential predictors for ozone fluxes in the literature. To better understand the relationships between the drivers and , the latter was binned according to the various drivers for graphical display.
2.5. Regional Ozone Analysis
To understand the spatial representativeness of the ozone concentrations in the study region MWM, regression and correlation analyses of hourly were performed between MWM and two air quality measurement stations of the State of Lower-Saxony, which are operated by the Lufthygienisches Überwachungssystem Niedersachsen (LÜN). The LÜN stations Südoldenburg (SO) and Allertal (AT) were 61 and 68 km in northwestern and east-northeastern directions from MWM, respectively. Data from the LÜN stations were provided as hourly concentrations. For this analysis, the MWM data were averaged to hourly .
3. Results and Discussion
3.1. Flux Data Quality Control
The eddy covariance method is widely employed to analyze fluxes of energy (H, LE) and , and respective data quality assurance protocols are well established. We applied these protocols in our data analysis as described in Section 2.3 for the computation of all fluxes including those of O3. The resulting data gaps are reported in Table 1. Altogether, 12% of the time series showed data gaps from power outages at the site. Additionally, 5–13% of the data were flagged because they did not fulfill the requirements of stationarity and/or integral turbulence characteristics (QC_2). Further, 18–23% of the good-quality data were flagged because of low u* values.

Table 1.
Frequency (%) of data sets within the quality control classes QC_0, QC_1, and QC_2 for , , LE, and H. The sum of the three classes plus the data that were not available due to power failures (NA, 12%) is 100% for each flux. The last column contains the frequency (%) of good data (QC_0 and QC_1) below the u*-threshold.
The analysis of co-spectra is an additional diagnostic procedure to evaluate the quality of flux estimates in terms of spectral characteristics of the turbulent transport and the instrumental setup. The dashed blue line in Figure 2 shows a theoretical co-spectrum model [49] of the vertical wind component with temperature, which represents H. Deviations from the modelled co-spectrum in the high-frequency range result from dampening of ambient fluctuations within the intake tube and the time lag resulting from sensor separation [53], while low- and mid-frequency deviations are rather caused by non-stationarities, trends, or by low-frequency fluctuations within the analyzed time series (e.g., [54]). High similarity of measured data with the modelled co-spectra thus indicates a good coverage of the ambient turbulence by the employed measurement setup. Figure 2 shows that the ensemble co-spectra are in good agreement with the low- to mid- frequency range of the modelled co-spectrum, while the high-frequency range is dampened and becomes noise dominated at normalized frequencies above 2.3. On the other hand, the co-spectra w’T’ were noise dominated only at normalized frequencies above 3.0, but not dampened (Figure 2). Dampening effects of the ozone flux, as shown in Figure 2, are accounted for in each half-hour flux computation through spectral corrections as described in Section 2.3. The spectral correction factors had a median of 1.23, an inner quartile range of 0.13, and the 10th and 90th percentiles were 1.12 and 1.40.
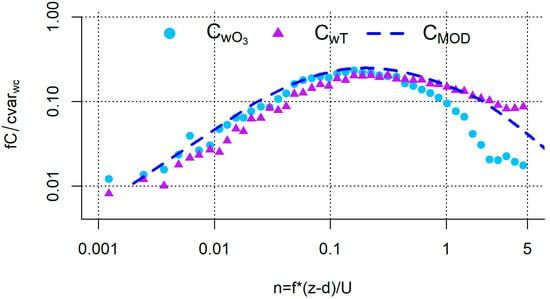
Figure 2.
Ensemble co-spectra of the vertical wind component w with ( blue circles) and with T (w’T’, purple triangles). The co-spectral model for w’T’ after Kaimal and Finnigan [49] is shown as a blue dashed line. The normalized frequency of 1 corresponds to a real frequency of 0.5 Hz.
3.2. General Meteorology and Flux Pattern
An eleven-day time series of selected meteorological, ecosystem flux, and ozone data is shown in Figure 3. Clear diurnal cycles are evident for all depicted parameters. The solar radiation (top panel) indicates that most days were partly cloudy. Tair reached maxima between 20.7 °C and 28.4 °C, while the minima were between 12.0 °C and 18.0 °C. The VPD (second panel) was low during most of the nights and had a maximum of 23.8 hPa on 1 August at 16:30 h. The diurnal cycle of u*, with mostly very low values during the nights and moderate values during the days, indicates a diurnal cycle of turbulence intensity and wind pattern. The boundary layer was stable during the nights (positive z/L, third panel from below) and unstable during the days (negative z/L). The diurnal cycles of GPP, LE, and H (panels 4–6 from top in Figure 3) were typical expressions of a hot, mostly sunny, and relatively calm high-pressure summer period in central Europe. Intense upwelling fluxes of long-wave radiation led to negative radiation balances during the nights (both not shown in detail) and to negative, downward fluxes of H.
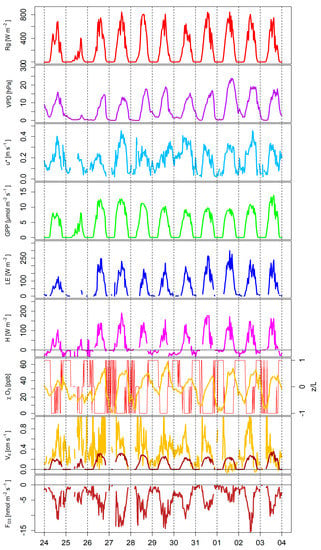
Figure 3.
Eleven-day time series of (from top to bottom) Rg, VPD, u*, GPP, LE, H, and z/L, brown), (yellow), and in the Mittleres Wietingsmoor, NW Germany, during late July and early August, 2014. z/L is set equal to 1 for values > 0.03, −1 for values < −0.03, and 0 for values between these thresholds. Gaps in the time series correspond to bad data quality of the eddy covariance data or to malfunctioning of the instruments.
(third panel from bottom in Figure 3) was highest during the late afternoon hours between 17 h and 20 h local time; the minima were sometimes very low (0.5 ppb on 27 July) and occurred during the early morning hours between 4 h and 7 h local time. These patterns of were very similar to the patterns detected at the LÜN stations SO and AT. R2 values of 0.69 and 0.75 between MWM on the one hand and AT and SO on the other (both p < 0.001), respectively, indicate a good agreement of ozone data between the sites (see Supplementary Material (Figure S1) for details). The slopes of the correlation lines revealed that the concentration measurements at MWM were about 25% to 30% lower than those at the LÜN stations. The nighttime data fit generally better between the sites than the peak concentrations during the days.
During the nights, the near-surface ozone decreased due to non-stomatal deposition (see Section 3.3 for more details) from a shallow, stable boundary layer to the surface, and potentially due to chemical reactions with gases such as NO. During the days, increased rapidly in the morning due to break-up of the stable nocturnal boundary layer (Figure 3 drop of z/L from positive to negative values) and down-mixing of ozone from the residual layer. Furthermore, rather slow production of additional ozone occurred during the course of the days [55].
The stomatal and non-stomatal deposition velocities are shown in the second panel from below (Figure 3). The stomatal deposition velocity is driven by GPP (Equation (11)) and is thus zero at night. The non-stomatal deposition velocity is generally larger than . On 1 August during the daytime, is larger than , and even becomes slightly negative for individual half hours. Even though is rather high, with values around 50 ppb, is low with daytime values of 4–6 nmol m−2 s−1. The mismatch between GPP and (low at high GPP) caused to become negative. We could not find any evidence for instrumental malfunctioning that could have caused the low . The wind direction was south-southwest, which was not common during our measurement period. Therefore, we can only assume that spatial heterogeneity in surface properties (i.e., much lower LAI or open water surfaces) likely caused the low on this day.
The measured ozone fluxes are shown in the bottom panel of Figure 3. They were negative throughout with large deposition fluxes up to about −15 nmol m−2 s−1 occurring during the midday hours.
3.3. O3-Flux Partitioning
The turbulent deposition flux of ozone, was partitioned into and (Equation (6)) for each half hour. Figure 4 shows the median diurnal courses of these individual fluxes. is generally larger than . Both and follow a diurnal pattern. is driven by the conductance of the stomata (and thus related to GPP) and by . It is zero during the nights, and the total is established by . is larger than for most of the daytime as well, except during the afternoon hours, when and are about equal to each other.
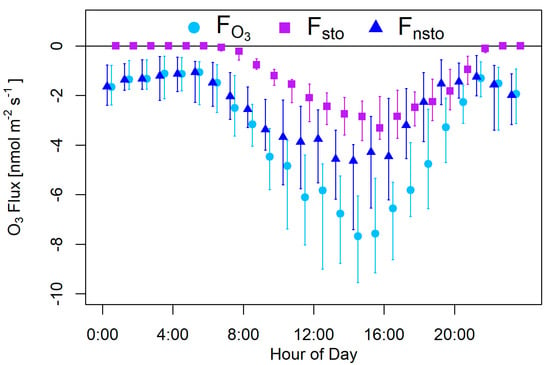
Figure 4.
Ozone deposition flux () partitioning between stomatal () and non-stomatal () contributions. Medians and interquartile ranges are shown for each 1-h interval of the day.
For situations when no evaporation is present, (Equation (9)) can be used to calculate instead of (Equation (11)). Using this simplification leads to an overestimation of the amount of the nocturnal by about 1 nmol m−2 s−1, (nocturnal ≈ −1 nmol m−2 s−1) and a root mean square error (RMSE) between the simplified and the correct approach of 1.3 nmol m−2 s−1 (details not shown in detail). This overestimate stems from nocturnal evaporation, of which a considerable portion was interpreted to be a stomatal flux when applying the simplification. For daytime conditions, the RMSE between the two methods was 1.7 nmol m−2 s−1 and as calculated with the simplified approach is mostly higher, which suggests that also during daytime, a certain amount of evaporation falsely contributed to the computed transpiration flux and thus to . Therefore, taking the GPP into account when calculating the stomatal conductance (Equation (11)) and thus leads to much better results.
The partitioning of into and allows us to disentangle different processes driving . Figure 5 shows a plot of the stomatal flux versus GPP with used to color-code individual data points. As GPP and are the main drivers of , a dependence of the slopes of regressions for various classes is to be expected in this plot. The larger is, the larger (with larger negative numbers) is. However, there remains a scatter in Figure 5 due to the fact that it is not the ambient ozone concentration that is used to compute but the surface ozone concentration (Equation (7)). This surface concentration is computed for each half hour and it introduces the variability in the computation of from measured data.
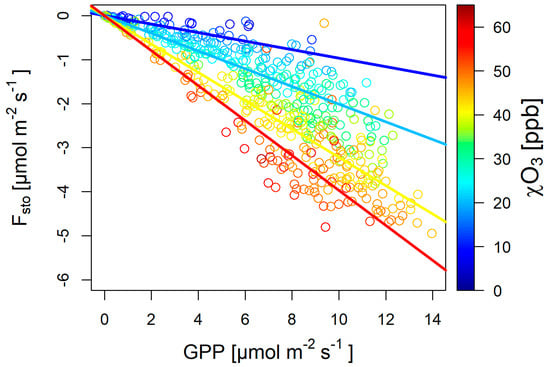
Figure 5.
Scatter plots of stomatal ozone flux () versus gross primary productivity (GPP) during daytime hours (Rg > 10 W m−2). Symbols are color-coded according to the ozone mixing ratio (side bar). Lines are regressions for (blue) with slope –0.097, (light blue) with slope −0.201, (yellow) with slope −0.321, and , (red) with slope −0.397, respectively. All regression lines were forced to have an intercept of 0 and had an R2 > 0.92 and a p < 0.001.
The more important non-stomatal flux is the residual of flux computations (Equation (6)). According to general understanding, it should be associated with the surface area available for deposition and its properties (e.g., LAI and surface wetness) and atmospheric turbulence (expressed as u*). Figure 6 presents the results of the driver analysis for . Overall (lowest panel in Figure 6), an R2 of about 26% was achieved, of which u* and Rg together account for 50%. The low R2 value shows that a large portion of the variability of cannot be explained with the data and analytical tools employed. A graphical presentation of the relationships between and environmental drivers (Figure 6, top 6 panels) shows that most relationships are not linear and contain much scatter, which explains the low value of R2 for the multiple linear model.
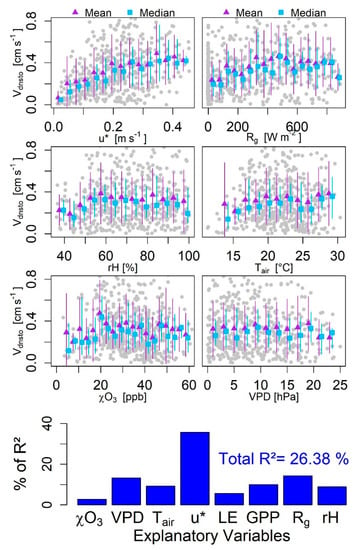
Figure 6.
Top panels: Relationships between (y-axes) and u*, Rg, rH, Tair, and VPD shown as grey full circles. Purple triangles are means ± standard deviations; light blue squares are medians with 25th and 75th percentiles. Bottom panel: Relative importance analysis of the drivers of ; bars indicate the percentage that each variable contributes to the total R2 of all variables.
Nevertheless, the observed relationships between and environmental drivers at our site are in agreement with the work of Altimir et al. [56], Lamaud et al. [11], Fares et al. [24], Coyle et al. [23], and Hogg et al. [57]. Even though all these measurements were performed in different ecosystems, the respective results agree with ours in that the relationships between fluxes and drivers are not linear and that the scatter in these relationships is large.
Following a suggestion given by Fowler et al. and Cape et al. [21,58], we calculated the dependency of to thermal decomposition at the surface, and we found that our site had 25% higher activation energy as compared to the Auchencorth Moss in Fowler et al. [21].
3.4. O3-Flux Partitioning Uncertainties
Generally speaking, the partitioning of into and works well. Nevertheless, there are several sources of uncertainty that have not yet been reported in the literature. When using the Penman-Monteith approach to calculate the stomatal conductance (or stomatal resistance) for H2O (ep. 9), the molecular diffusivities of H2O and O3, of and , are employed. The values of this ratio as employed by various authors [51,50,59] vary between 1.67 and 1.51, which translates to a variation of by about 10%.
The exclusion of direct evaporation from plant surfaces and open water surfaces is stated, and Lamaud et al. [11] proposed a method to account for this issue by using the relationship between GPP and stomatal conductance under conditions with relative humidity below 60% (Equation (11)). However, the effect of soil evaporation can not be corrected for with this method. Most likely, soil evaporation can only be excluded if additional soil evaporation measurements are performed.
Finally, additional uncertainty originates from the GPP data which were used when applying the correction according to Equation (11). In our case, we separated the net ecosystem flux (NEE) of CO2 into GPP and ecosystem respiration (Reco) by estimating the daytime Reco from light response curves [47]. This yields a GPP of 0 µmol m−2 s−1 during the night. When using nighttime data instead and extrapolating these values to the daytime through a temperature relationship [46], the nocturnal GPP is not necessarily zero. Rather, it fluctuates around 0 and could eventually cause negative stomatal conductance during the night. Additionally, the daytime GPP values as calculated from these two methods would differ from each other as well.
4. Conclusions
Ozone deposition fluxes () were measured during the peak of the growing season at a peatland in NW Germany. The employed eddy covariance setup for the O3 fluxes and employing the gas phase chemiluminescence method after reaction of O3 with NO showed good co-spectral characteristics even though the signal was damped in the mid- to high-frequency range, most likely caused by the intake tube.
The ozone fluxes were partitioned into stomatal () and non-stomatal () fluxes by using resistance analogy. The use of the Penman-Monteith approach to estimate led to an overestimate of the stomatal conductance and thus of and . The inclusion of GPP into the computational routine led to a clear improvement of the estimate of . The stomatal flux is thus rather well understood and can thus be parameterized and modeled with the stomatal conductance and the ambient ozone concentration. For further measurements of to vegetated surfaces, we recommend measuring and applying the corrections employing GPP to determine . However, further research needs to be performed in order to quantify the effect of various routines to separate NEE into GPP and Reco on the flux partitioning of ozone.
The non-stomatal flux, which is computed as the residual (Equation (6)), was larger than , is less well defined, and more difficult to parameterize or to model. Atmospheric turbulence plays the single most important role in non-stomatal ozone flux; however, the overall coefficient of determination between the flux and drivers was rather poor, i.e., only 26%. Further research on ozone deposition should focus on longer time series covering all seasons, on various types of ecosystems, and other types of surfaces in order to better understand the non-stomatal ozone deposition flux.
Supplementary Materials
The following are available online at www.mdpi.com/2073-4433/8/9/175/s1, Figure S1: Scatter plots (1-3 from top) with correlation line (red), 1:1 line (black), linear fit, and coefficient of determination for the respective ozone concentrations.
Acknowledgments
We are deeply indebted to many persons and institutions who made this research possible. Geerd Smidt of the Europäisches Fachzentrum Moor helped to identify a suitable peatland for our analysis. The owner of the land, v. Bodelschwinghsche Stiftung Bethel, represented by J. Ermshausen, provided access and electricity supply. The legal permit was given by the nature conservancy authority of the Landkreis Diepholz. We thank Land Niedersachsen for providing ozone data from their Lufthygienisches Überwachungssystem Niedersachsen LÜN (www.umwelt.niedersachsen.de). M.J. Deventer and E. Braeckevelt helped during data acquisition. Last but not least, we thank the three anonymous reviewers for their constructive feedback on an earlier version of this manuscript and C. Brennecka for language editing of the final version.
Author Contributions
Tarek S. El-Madany conducted all data analyses and wrote the manuscript together with Otto Klemm. Katharina Niklasch performed the field experiments as part of her Master’s thesis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kahle, J.J.; Neas, L.M.; Devlin, R.B.; Case, M.W.; Schmitt, M.T.; Madden, M.C.; Diaz-Sanchez, D. Interaction Effects of Temperature and Ozone on Lung Function and Markers of Systemic Inflammation, Coagulation, and Fibrinolysis: A Crossover Study of Healthy Young Volunteers. Environ. Health Perspect. 2014, 123, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Vingarzan, R. A review of surface ozone background levels and trends. Atmos. Environ. 2004, 38, 3431–3442. [Google Scholar] [CrossRef]
- Royal Society (Great Britain); Fowler, D. Ground-Level Ozone in the 21st Century: Future Trends, Impacts and Policy Implications; The Royal Society: London, UK, 2008; ISBN 978-0-85403-713-1. [Google Scholar]
- Finlayson-Pitts, Barbara J.; Pitts, James N. Chemistry of the Upper and Lower Atmosphere; Academic Press: San Diego, London, 1999; ISBN 0-12-257060-X. [Google Scholar]
- Zenone, T.; Hendriks, C.; Brilli, F.; Fransen, E.; Gioli, B.; Portillo-Estrada, M.; Schaap, M.; Ceulemans, R. Interaction between isoprene and ozone fluxes in a poplar plantation and its impact on air quality at the European level. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Akimoto, H. Atmospheric Reaction Chemistry; Springer Atmospheric Sciences; Springer: Tokyo, Japan, 2016; ISBN 978-4-431-55868-2. [Google Scholar]
- De Arellano, J.V.-G.; Duynkerke, P.G.; Builtjes, P.J.H. The divergence of the turbulent diffusion flux in the surface layer due to chemical reactions: The NO-O3-NO2 system. Tellus. B 1993, 45, 23–33. [Google Scholar] [CrossRef]
- Mogili, P.K.; Kleiber, P.D.; Young, M.A.; Grassian, V.H. Heterogeneous Uptake of Ozone on Reactive Components of Mineral Dust Aerosol: An Environmental Aerosol Reaction Chamber Study. J. Phys. Chem. A 2006, 110, 13799–13807. [Google Scholar] [CrossRef] [PubMed]
- Cwiertny, D.M.; Young, M.A.; Grassian, V.H. Chemistry and Photochemistry of Mineral Dust Aerosol. Annu. Rev. Phys. Chem. 2008, 59, 27–51. [Google Scholar] [CrossRef] [PubMed]
- Galbally, I.E.; Roy, C.R. Destruction of ozone at the earth’s surface. Q. J. R. Meteorol. Soc. 1980, 106, 599–620. [Google Scholar] [CrossRef]
- Lamaud, E.; Loubet, B.; Irvine, M.; Stella, P.; Personne, E.; Cellier, P. Partitioning of ozone deposition over a developed maize crop between stomatal and non-stomatal uptakes, using eddy-covariance flux measurements and modelling. Agric. For. Meteorol. 2009, 149, 1385–1396. [Google Scholar] [CrossRef]
- Stella, P.; Personne, E.; Loubet, B.; Lamaud, E.; Ceschia, E.; Béziat, P.; Bonnefond, J.M.; Irvine, M.; Keravec, P.; Mascher, N.; et al. Predicting and partitioning ozone fluxes to maize crops from sowing to harvest: The Surfatm-O3 model. Biogeosciences 2011, 8, 2869–2886. [Google Scholar] [CrossRef]
- Guidi, L.; Nali, C.; Lorenzini, G.; Filippi, F.; Soldatini, G.F. Effect of chronic ozone fumigation on the photosynthetic process of poplar clones showing different sensitivity. Environ. Pollut. 2001, 113, 245–254. [Google Scholar] [CrossRef]
- Calatayud, A.; Ramirez, J.W.; Iglesias, D.J.; Barreno, E. Effects of ozone on photosynthetic CO2 exchange, chlorophyll a fluorescence and antioxidant systems in lettuce leaves. Physiol. Plant. 2002, 116, 308–316. [Google Scholar] [CrossRef]
- Biswas, D.K.; Xu, H.; Li, Y.G.; Sun, J.Z.; Wang, X.Z.; Han, X.G.; Jiang, G.M. Genotypic differences in leaf biochemical, physiological and growth responses to ozone in 20 winter wheat cultivars released over the past 60 years. Glob. Change Biol. 2008, 14, 46–59. [Google Scholar] [CrossRef]
- Avnery, S.; Mauzerall, D.L.; Liu, J.; Horowitz, L.W. Global crop yield reductions due to surface ozone exposure: 1. Year 2000 crop production losses and economic damage. Atmos. Environ. 2011, 45, 2284–2296. [Google Scholar] [CrossRef]
- Fares, S.; McKay, M.; Holzinger, R.; Goldstein, A.H. Ozone fluxes in a Pinus ponderosa ecosystem are dominated by non-stomatal processes: Evidence from long-term continuous measurements. Agric. For. Meteorol. 2010, 150, 420–431. [Google Scholar] [CrossRef]
- Stella, P.; Kortner, M.; Ammann, C.; Foken, T.; Meixner, F.X.; Trebs, I. Measurements of nitrogen oxides and ozone fluxes by eddy covariance at a meadow: Evidence for an internal leaf resistance to NO2. Biogeosciences 2013, 10, 5997–6017. [Google Scholar] [CrossRef]
- Zona, D.; Gioli, B.; Fares, S.; De Groote, T.; Pilegaard, K.; Ibrom, A.; Ceulemans, R. Environmental controls on ozone fluxes in a poplar plantation in Western Europe. Environ. Pollut. 2014, 184, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Gerosa, G.; Marzuoli, R.; Cieslik, S.; Ballarin-Denti, A. Stomatal ozone fluxes over a barley field in Italy. “Effective exposure” as a possible link between exposure- and flux-based approaches. Atmos. Environ. 2004, 38, 2421–2432. [Google Scholar] [CrossRef]
- Fowler, D.; Flechard, C.; Cape, J.N.; Storeton-West, R.L.; Coyle, M. Measurements of ozone deposition to vegetation quantifying the flux, the stomatal and non-stomatal components. Water. Air. Soil Pollut. 2001, 130, 63–74. [Google Scholar] [CrossRef]
- Coe, H.; Gallagher, M.; Choularton, T.; Dore, C. Canopy Scale Measurements of Stomatal and Cuticular O3 Uptake by Sitka Spruce. Atmos. Environ. 1995, 29, 1413–1423. [Google Scholar] [CrossRef]
- Coyle, M.; Nemitz, E.; Storeton-West, R.; Fowler, D.; Cape, J.N. Measurements of ozone deposition to a potato canopy. Agric. For. Meteorol. 2009, 149, 655–666. [Google Scholar] [CrossRef][Green Version]
- Fares, S.; Weber, R.; Park, J.-H.; Gentner, D.; Karlik, J.; Goldstein, A.H. Ozone deposition to an orange orchard: Partitioning between stomatal and non-stomatal sinks. Environ. Pollut. 2012, 169, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Gerosa, G.; Vitale, M.; Finco, A.; Manes, F.; Ballarin-Denti, A.; Cieslik, S. Ozone uptake by an evergreen Mediterranean Forest (Quercus ilex) in Italy. Part I: Micrometeorological flux measurements and flux partitioning. Atmos. Environ. 2005, 39, 3255–3266. [Google Scholar] [CrossRef]
- Williamson, J.L.; Mills, G.; Hayes, F.; Jones, T.; Freeman, C. How do increasing background concentrations of tropospheric ozone affect peatland plant growth and carbon gas exchange? Atmos. Environ. 2016, 127, 133–138. [Google Scholar] [CrossRef][Green Version]
- Niemi, R.; Martikainen, P.J.; Silvola, J.; Holopainen, T. Ozone effects on Sphagnum mosses, carbon dioxide exchange and methane emission in boreal peatland microcosms. Sci. Total Environ. 2002, 289, 1–12. [Google Scholar] [CrossRef]
- Toet, S.; Oliver, V.; Ineson, P.; McLoughlin, S.; Helgason, T.; Peacock, S.; Stott, A.W.; Barnes, J.; Ashmore, M. How does elevated ozone reduce methane emissions from peatlands? Sci. Total Environ. 2017, 579, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Rinnan, R.; Impiö, M.; Silvola, J.; Holopainen, T.; Martikainen, P.J. Carbon dioxide and methane fluxes in boreal peatland microcosms with different vegetation cover? Effects of ozone or ultraviolet-B exposure. Oecologia 2003, 137, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Aalto, T.; Hatakka, J.; Lallo, M. Tropospheric methane in northern Finland: seasonal variations, transport patterns and correlations with other trace gases. Tellus. B 2007, 59, 251–259. [Google Scholar] [CrossRef]
- Tuovinen, J.P.; Aurela, M.; Laurila, T. Resistances to ozone deposition to a flark fen in the northern aapa mire zone. J. Geophys. Res. Atm. 1984–2012 1998, 103, 16953–16966. [Google Scholar] [CrossRef]
- Moore, K.E.; Fitzjarrald, D.R.; Wofsy, S.C.; Daube, B.C.; Munger, J.W.; Bakwin, P.S.; Crill, P. A season of heat, water vapor, total hydrocarbon, and ozone fluxes at a subarctic fen. J. Geophys. Res.-Atm. 1994, 99, 1937–1952. [Google Scholar] [CrossRef]
- Munger, J.W.; Wofsy, S.C.; Bakwin, P.S.; Fan, S.-M.; Goulden, M.L.; Daube, B.C.; Goldstein, A.H.; Moore, K.E.; Fitzjarrald, D.R. Atmospheric deposition of reactive nitrogen oxides and ozone in a temperate deciduous forest and a subarctic woodland: 1. Measurements and mechanisms. J. Geophys. Res. Atm. 1984–2012 1996, 101, 12639–12657. [Google Scholar] [CrossRef]
- Schmatzler, B.; Schmatzler, E. Moorland: Moorlandschaften in Niedersachsen nach industriellem Torfabbau, 1st ed.; IVG: Ratingen, Germany, 2010; ISBN 978-3-00-031560-2. [Google Scholar]
- BUND Diepholzer Moorniederung, Mittleres Wietingsmoor - Historisch eine Besonderheit, Kranichschutz and Kranich erleben I. Available online: http://www.naturpark-duemmer.de/fileadmin/content/Zum_download/fly_mw.pdf (accessed on 24 June 2017).
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Fratini, G.; Mauder, M. Towards a consistent eddy-covariance processing: An intercomparison of EddyPro and TK3. Atm. Meas. Tech. 2014, 7, 2273–2281. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atm. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Horst, T.W.; Lenschow, D.H. Attenuation of Scalar Fluxes Measured with Spatially-displaced Sensors. Bound.-Layer Meteorol. 2009, 130, 275–300. [Google Scholar] [CrossRef]
- Ibrom, A.; Dellwik, E.; Flyvbjerg, H.; Jensen, N.O.; Pilegaard, K. Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems. Agric. For. Meteorol. 2007, 147, 140–156. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, Detrending, and Filtering of Eddy Covariance Time Series. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Lee, X., Massman, W.J., Law, B.E., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2004; pp. 7–31. [Google Scholar]
- Ibrom, A.; Dellwik, E.; Larsen, S.E.; Pilegaard, K. On the use of the Webb–Pearman–Leuning theory for closed-path eddy correlation measurements. Tellus. B 2007, 59, 937–946. [Google Scholar] [CrossRef]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3. 2011. Available online: https://epub.uni-bayreuth.de/342/1/ARBERG046.pdf (accessed on 28 May 2011).
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Glob. Change Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation: SEPARATION OF NEE INTO GPP AND RECO. Glob. Change Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: https://www.R-project.org/ (accessed on 23 July 2015).
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Laisk, A.; Kull, O.; Moldau, H. Ozone concentration in leaf intercellular air spaces is close to zero. Plant. Physiol. 1989, 90, 1163–1167. [Google Scholar] [CrossRef] [PubMed]
- Hicks, B.B.; Baldocchi, D.D.; Meyers, T.P.; Hosker, R.P.; Matt, D.R. A preliminary multiple resistance routine for deriving dry deposition velocities from measured quantities. Water. Air. Soil Pollut. 1987, 36, 311–330. [Google Scholar] [CrossRef]
- Grömping, U. Relative importance for linear regression in R: the package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Fratini, G.; Ibrom, A.; Arriga, N.; Burba, G.; Papale, D. Relative humidity effects on water vapour fluxes measured with closed-path eddy-covariance systems with short sampling lines. Agric. For. Meteorol. 2012, 165, 53–63. [Google Scholar] [CrossRef]
- Moncrieff, J.B.; Massheder, J.M.; deBruin, H.; Elbers, J.; Friborg, T.; Heusinkveld, B.; Kabat, P.; Scott, S.; Soegaard, H.; Verhoef, A. A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide. J. Hydrol. 1997, 189, 589–611. [Google Scholar] [CrossRef]
- Klemm, O. Local and regional ozone: A student study project. J. Chem. Educ. 2001, 78, 1641–1646. [Google Scholar] [CrossRef]
- Altimir, N.; Kolari, P.; Tuovinen, J.-P.; Vesala, T.; Bäck, J.; Suni, T.; Kulmala, M.; Hari, P. Foliage surface ozone deposition: a role for surface moisture? Biogeosciences 2006, 3, 209–228. [Google Scholar] [CrossRef]
- Hogg, A.; Uddling, J.; Ellsworth, D.; Carroll, M.A.; Pressley, S.; Lamb, B.; Vogel, C. Stomatal and non-stomatal fluxes of ozone to a northern mixed hardwood forest. Tellus. B 2007, 59, 514–525. [Google Scholar] [CrossRef]
- Cape, J.N.; Hamilton, R.; Heal, M.R. Reactive uptake of ozone at simulated leaf surfaces: Implications for “non-stomatal” ozone flux. Atmos. Environ. 2009, 43, 1116–1123. [Google Scholar] [CrossRef]
- Massman, W.J. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O-3, SO2, NH3, N2O, NO, AND NO2 in air, O-2 AND N-2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).