Stomatal and Non-Stomatal Turbulent Deposition Flux of Ozone to a Managed Peatland
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Study Period
2.2. Instrumentation
2.3. Data Analysis
2.3.1. Eddy Covariance
2.3.2. Resistance Terms and Deposition Velocity
2.4. Statistical Driver Analysis
2.5. Regional Ozone Analysis
3. Results and Discussion
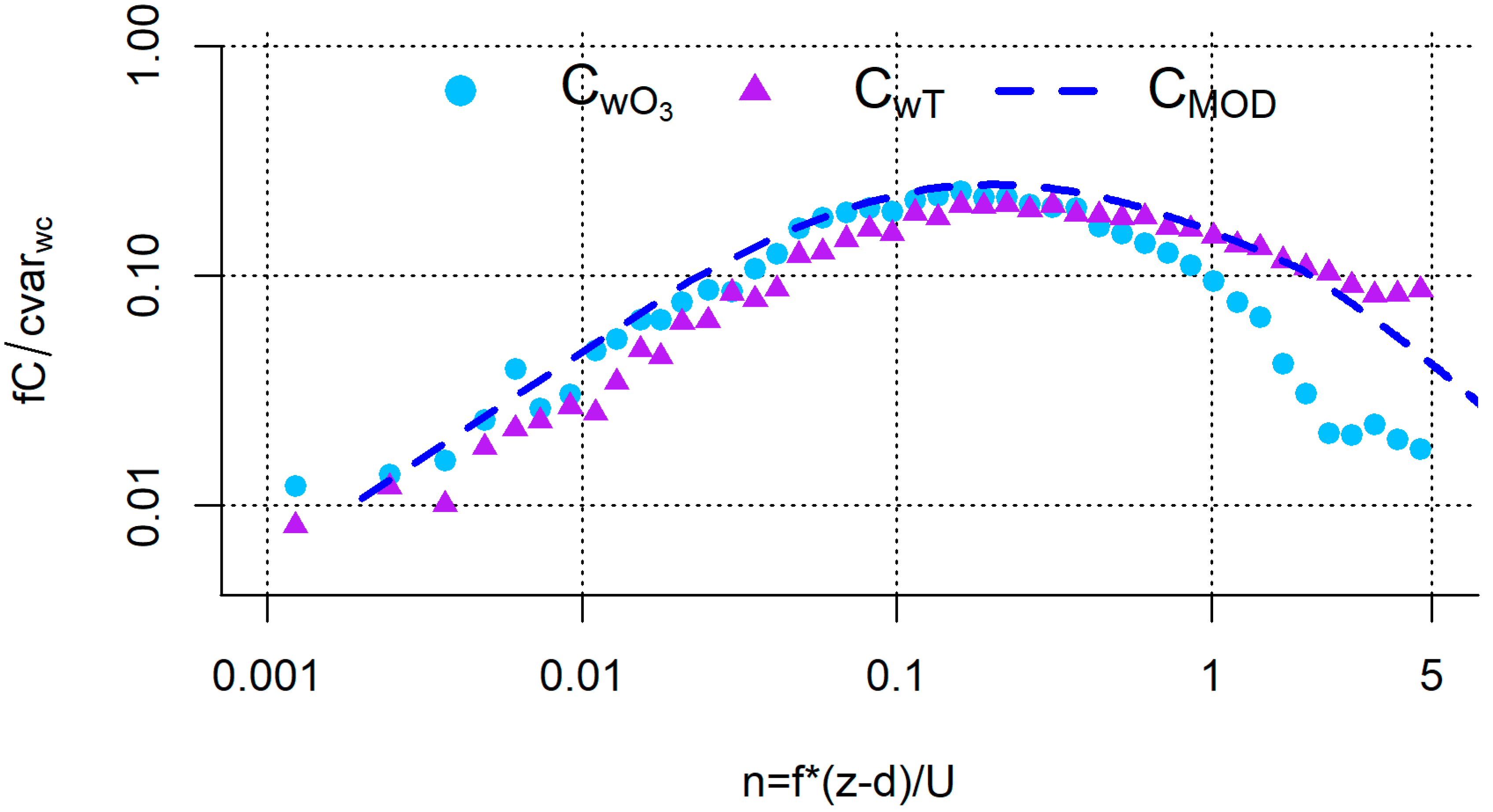
3.1. Flux Data Quality Control
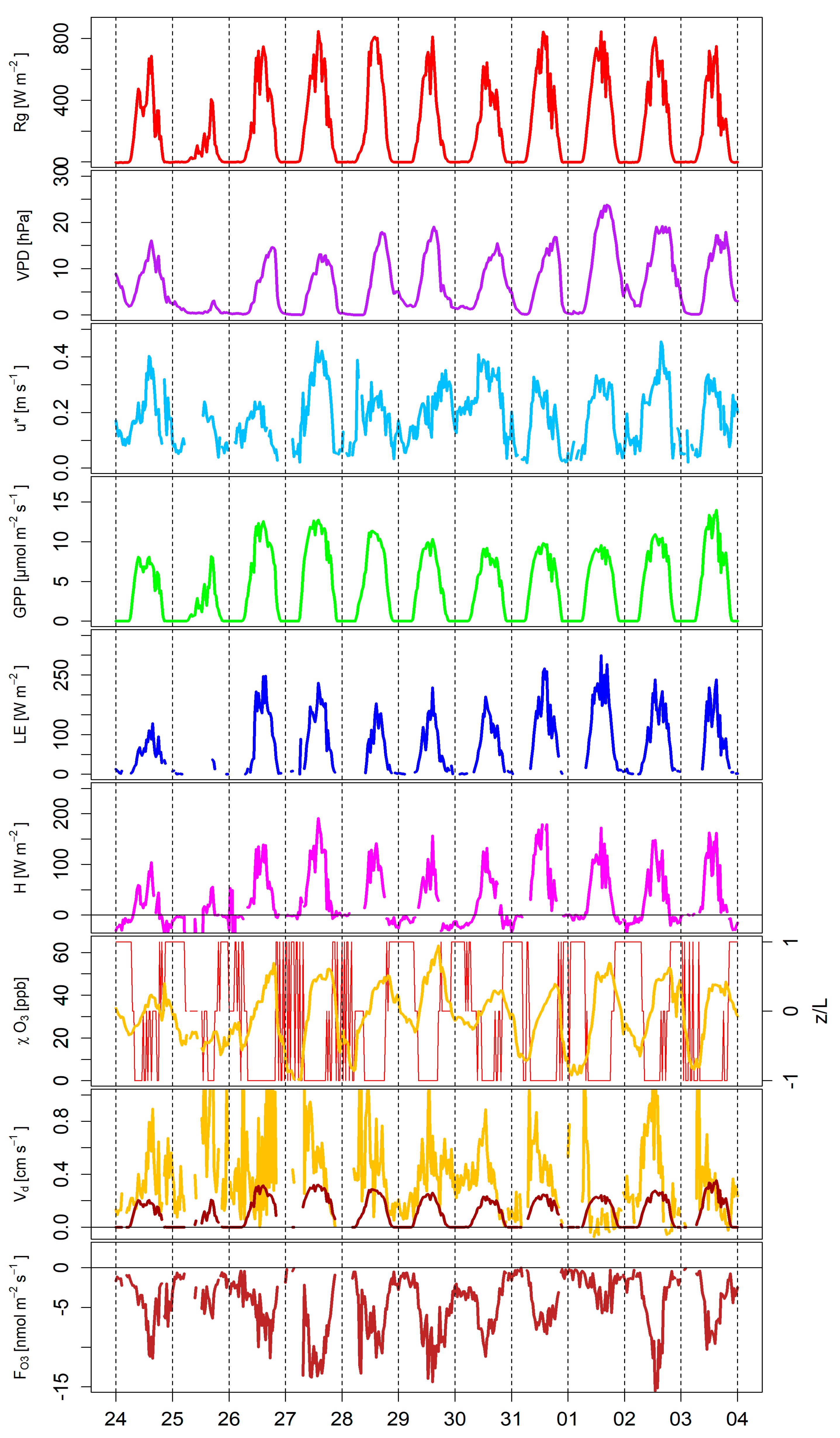
3.2. General Meteorology and Flux Pattern
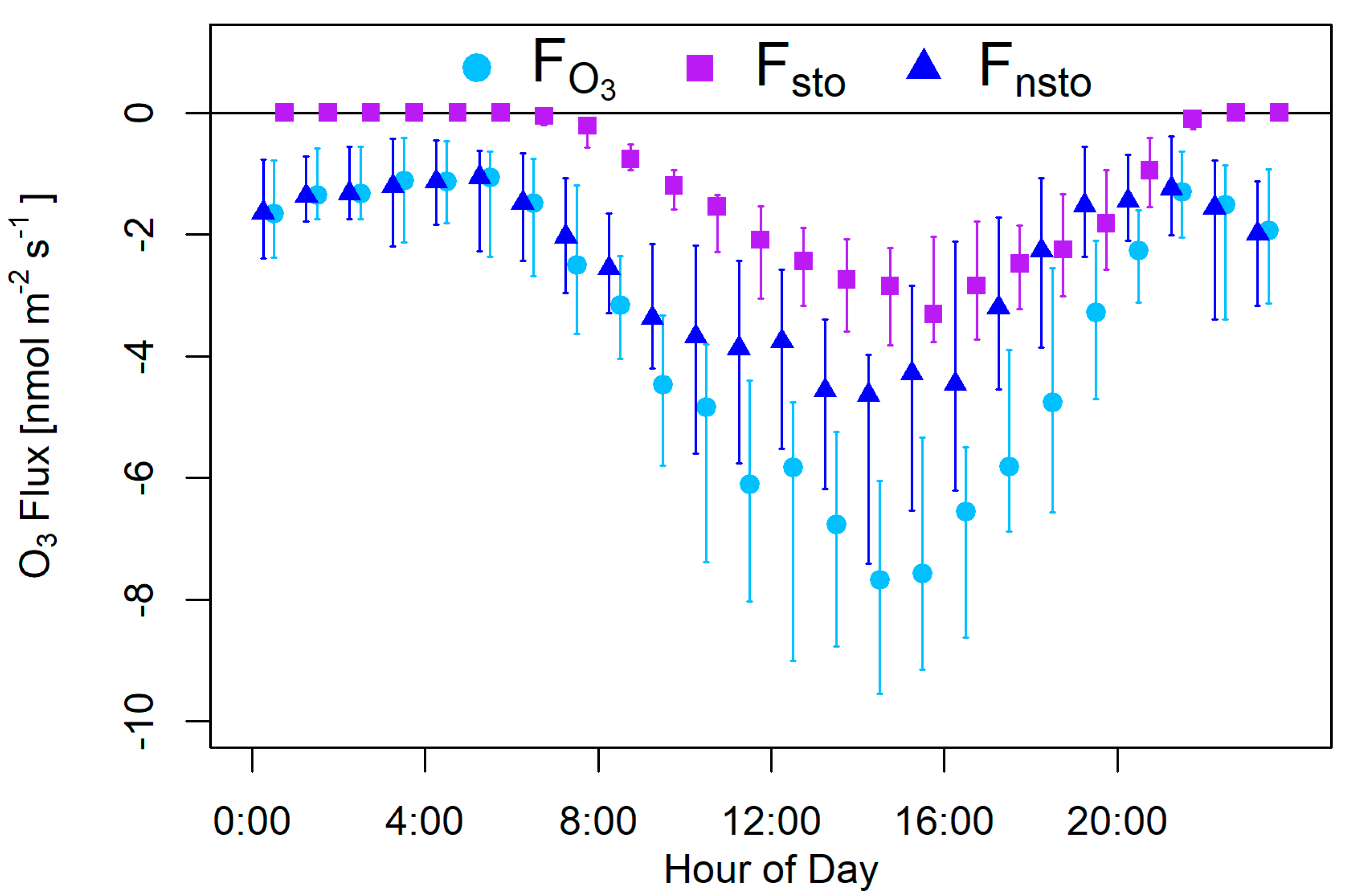
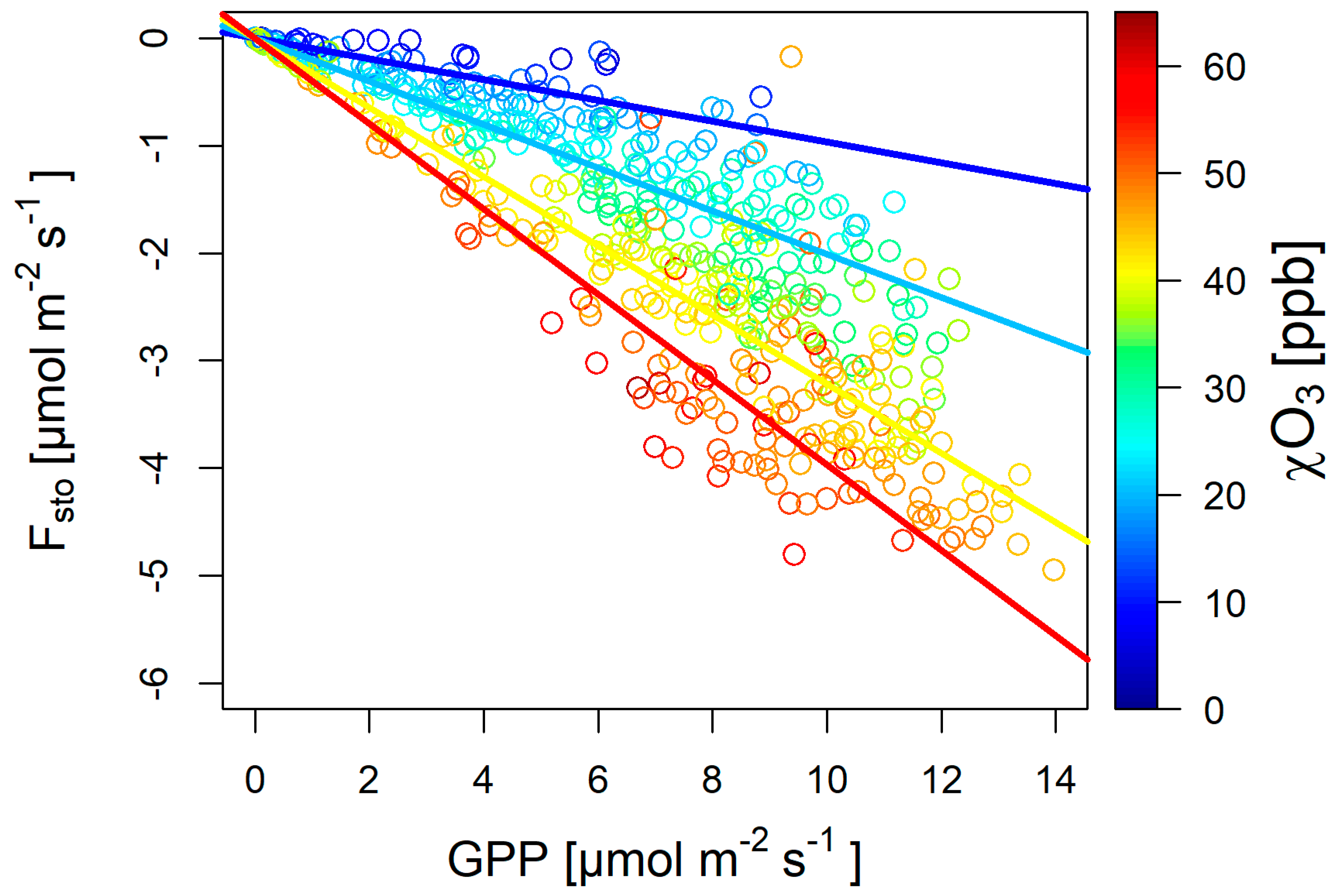
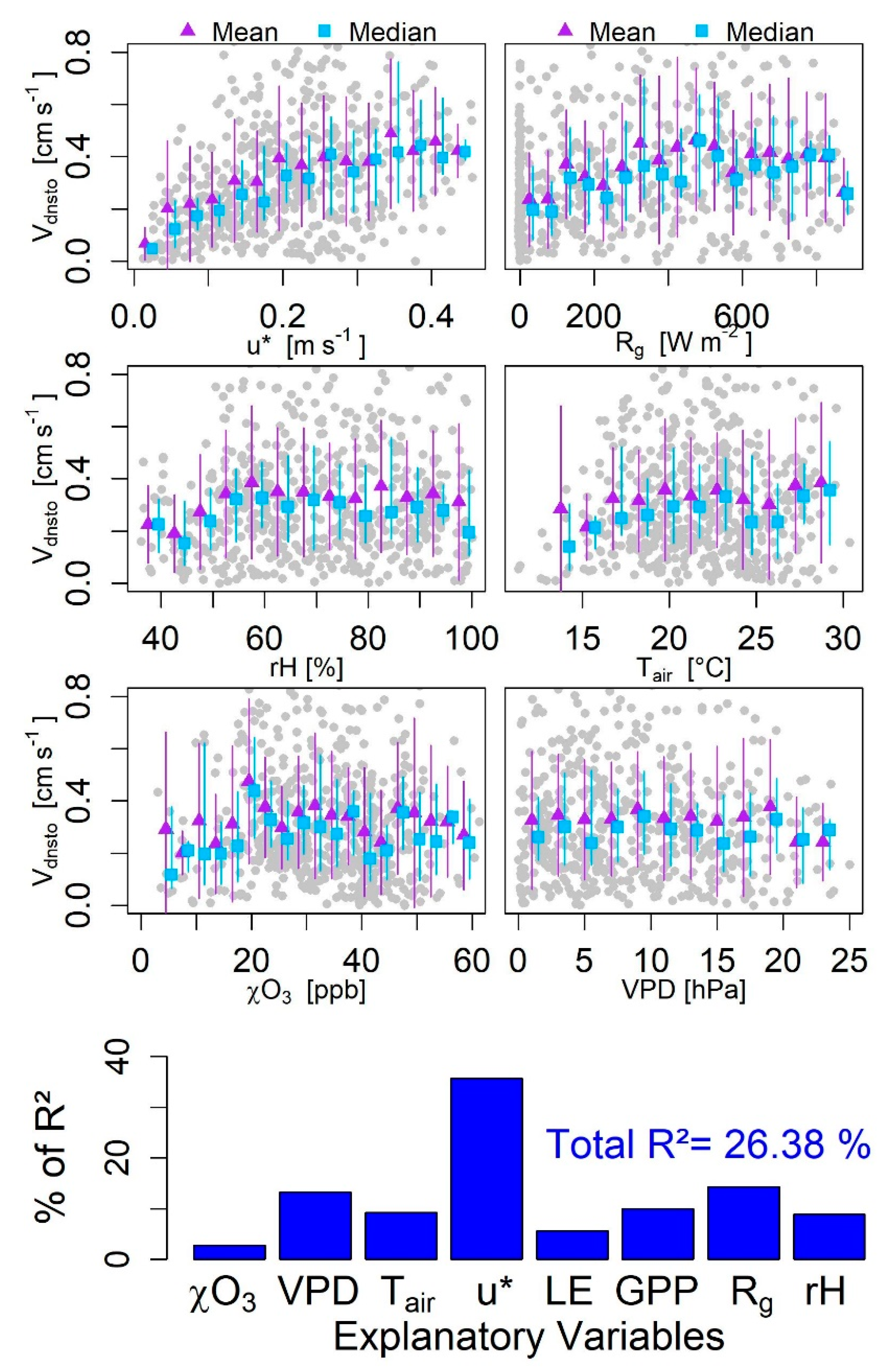
3.3. O3-Flux Partitioning
3.4. O3-Flux Partitioning Uncertainties
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kahle, J.J.; Neas, L.M.; Devlin, R.B.; Case, M.W.; Schmitt, M.T.; Madden, M.C.; Diaz-Sanchez, D. Interaction Effects of Temperature and Ozone on Lung Function and Markers of Systemic Inflammation, Coagulation, and Fibrinolysis: A Crossover Study of Healthy Young Volunteers. Environ. Health Perspect. 2014, 123, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Vingarzan, R. A review of surface ozone background levels and trends. Atmos. Environ. 2004, 38, 3431–3442. [Google Scholar] [CrossRef]
- Royal Society (Great Britain); Fowler, D. Ground-Level Ozone in the 21st Century: Future Trends, Impacts and Policy Implications; The Royal Society: London, UK, 2008; ISBN 978-0-85403-713-1. [Google Scholar]
- Finlayson-Pitts, Barbara J.; Pitts, James N. Chemistry of the Upper and Lower Atmosphere; Academic Press: San Diego, London, 1999; ISBN 0-12-257060-X. [Google Scholar]
- Zenone, T.; Hendriks, C.; Brilli, F.; Fransen, E.; Gioli, B.; Portillo-Estrada, M.; Schaap, M.; Ceulemans, R. Interaction between isoprene and ozone fluxes in a poplar plantation and its impact on air quality at the European level. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Akimoto, H. Atmospheric Reaction Chemistry; Springer Atmospheric Sciences; Springer: Tokyo, Japan, 2016; ISBN 978-4-431-55868-2. [Google Scholar]
- De Arellano, J.V.-G.; Duynkerke, P.G.; Builtjes, P.J.H. The divergence of the turbulent diffusion flux in the surface layer due to chemical reactions: The NO-O3-NO2 system. Tellus. B 1993, 45, 23–33. [Google Scholar] [CrossRef]
- Mogili, P.K.; Kleiber, P.D.; Young, M.A.; Grassian, V.H. Heterogeneous Uptake of Ozone on Reactive Components of Mineral Dust Aerosol: An Environmental Aerosol Reaction Chamber Study. J. Phys. Chem. A 2006, 110, 13799–13807. [Google Scholar] [CrossRef] [PubMed]
- Cwiertny, D.M.; Young, M.A.; Grassian, V.H. Chemistry and Photochemistry of Mineral Dust Aerosol. Annu. Rev. Phys. Chem. 2008, 59, 27–51. [Google Scholar] [CrossRef] [PubMed]
- Galbally, I.E.; Roy, C.R. Destruction of ozone at the earth’s surface. Q. J. R. Meteorol. Soc. 1980, 106, 599–620. [Google Scholar] [CrossRef]
- Lamaud, E.; Loubet, B.; Irvine, M.; Stella, P.; Personne, E.; Cellier, P. Partitioning of ozone deposition over a developed maize crop between stomatal and non-stomatal uptakes, using eddy-covariance flux measurements and modelling. Agric. For. Meteorol. 2009, 149, 1385–1396. [Google Scholar] [CrossRef]
- Stella, P.; Personne, E.; Loubet, B.; Lamaud, E.; Ceschia, E.; Béziat, P.; Bonnefond, J.M.; Irvine, M.; Keravec, P.; Mascher, N.; et al. Predicting and partitioning ozone fluxes to maize crops from sowing to harvest: The Surfatm-O3 model. Biogeosciences 2011, 8, 2869–2886. [Google Scholar] [CrossRef]
- Guidi, L.; Nali, C.; Lorenzini, G.; Filippi, F.; Soldatini, G.F. Effect of chronic ozone fumigation on the photosynthetic process of poplar clones showing different sensitivity. Environ. Pollut. 2001, 113, 245–254. [Google Scholar] [CrossRef]
- Calatayud, A.; Ramirez, J.W.; Iglesias, D.J.; Barreno, E. Effects of ozone on photosynthetic CO2 exchange, chlorophyll a fluorescence and antioxidant systems in lettuce leaves. Physiol. Plant. 2002, 116, 308–316. [Google Scholar] [CrossRef]
- Biswas, D.K.; Xu, H.; Li, Y.G.; Sun, J.Z.; Wang, X.Z.; Han, X.G.; Jiang, G.M. Genotypic differences in leaf biochemical, physiological and growth responses to ozone in 20 winter wheat cultivars released over the past 60 years. Glob. Change Biol. 2008, 14, 46–59. [Google Scholar] [CrossRef]
- Avnery, S.; Mauzerall, D.L.; Liu, J.; Horowitz, L.W. Global crop yield reductions due to surface ozone exposure: 1. Year 2000 crop production losses and economic damage. Atmos. Environ. 2011, 45, 2284–2296. [Google Scholar] [CrossRef]
- Fares, S.; McKay, M.; Holzinger, R.; Goldstein, A.H. Ozone fluxes in a Pinus ponderosa ecosystem are dominated by non-stomatal processes: Evidence from long-term continuous measurements. Agric. For. Meteorol. 2010, 150, 420–431. [Google Scholar] [CrossRef]
- Stella, P.; Kortner, M.; Ammann, C.; Foken, T.; Meixner, F.X.; Trebs, I. Measurements of nitrogen oxides and ozone fluxes by eddy covariance at a meadow: Evidence for an internal leaf resistance to NO2. Biogeosciences 2013, 10, 5997–6017. [Google Scholar] [CrossRef]
- Zona, D.; Gioli, B.; Fares, S.; De Groote, T.; Pilegaard, K.; Ibrom, A.; Ceulemans, R. Environmental controls on ozone fluxes in a poplar plantation in Western Europe. Environ. Pollut. 2014, 184, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Gerosa, G.; Marzuoli, R.; Cieslik, S.; Ballarin-Denti, A. Stomatal ozone fluxes over a barley field in Italy. “Effective exposure” as a possible link between exposure- and flux-based approaches. Atmos. Environ. 2004, 38, 2421–2432. [Google Scholar] [CrossRef]
- Fowler, D.; Flechard, C.; Cape, J.N.; Storeton-West, R.L.; Coyle, M. Measurements of ozone deposition to vegetation quantifying the flux, the stomatal and non-stomatal components. Water. Air. Soil Pollut. 2001, 130, 63–74. [Google Scholar] [CrossRef]
- Coe, H.; Gallagher, M.; Choularton, T.; Dore, C. Canopy Scale Measurements of Stomatal and Cuticular O3 Uptake by Sitka Spruce. Atmos. Environ. 1995, 29, 1413–1423. [Google Scholar] [CrossRef]
- Coyle, M.; Nemitz, E.; Storeton-West, R.; Fowler, D.; Cape, J.N. Measurements of ozone deposition to a potato canopy. Agric. For. Meteorol. 2009, 149, 655–666. [Google Scholar] [CrossRef][Green Version]
- Fares, S.; Weber, R.; Park, J.-H.; Gentner, D.; Karlik, J.; Goldstein, A.H. Ozone deposition to an orange orchard: Partitioning between stomatal and non-stomatal sinks. Environ. Pollut. 2012, 169, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Gerosa, G.; Vitale, M.; Finco, A.; Manes, F.; Ballarin-Denti, A.; Cieslik, S. Ozone uptake by an evergreen Mediterranean Forest (Quercus ilex) in Italy. Part I: Micrometeorological flux measurements and flux partitioning. Atmos. Environ. 2005, 39, 3255–3266. [Google Scholar] [CrossRef]
- Williamson, J.L.; Mills, G.; Hayes, F.; Jones, T.; Freeman, C. How do increasing background concentrations of tropospheric ozone affect peatland plant growth and carbon gas exchange? Atmos. Environ. 2016, 127, 133–138. [Google Scholar] [CrossRef][Green Version]
- Niemi, R.; Martikainen, P.J.; Silvola, J.; Holopainen, T. Ozone effects on Sphagnum mosses, carbon dioxide exchange and methane emission in boreal peatland microcosms. Sci. Total Environ. 2002, 289, 1–12. [Google Scholar] [CrossRef]
- Toet, S.; Oliver, V.; Ineson, P.; McLoughlin, S.; Helgason, T.; Peacock, S.; Stott, A.W.; Barnes, J.; Ashmore, M. How does elevated ozone reduce methane emissions from peatlands? Sci. Total Environ. 2017, 579, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Rinnan, R.; Impiö, M.; Silvola, J.; Holopainen, T.; Martikainen, P.J. Carbon dioxide and methane fluxes in boreal peatland microcosms with different vegetation cover? Effects of ozone or ultraviolet-B exposure. Oecologia 2003, 137, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Aalto, T.; Hatakka, J.; Lallo, M. Tropospheric methane in northern Finland: seasonal variations, transport patterns and correlations with other trace gases. Tellus. B 2007, 59, 251–259. [Google Scholar] [CrossRef]
- Tuovinen, J.P.; Aurela, M.; Laurila, T. Resistances to ozone deposition to a flark fen in the northern aapa mire zone. J. Geophys. Res. Atm. 1984–2012 1998, 103, 16953–16966. [Google Scholar] [CrossRef]
- Moore, K.E.; Fitzjarrald, D.R.; Wofsy, S.C.; Daube, B.C.; Munger, J.W.; Bakwin, P.S.; Crill, P. A season of heat, water vapor, total hydrocarbon, and ozone fluxes at a subarctic fen. J. Geophys. Res.-Atm. 1994, 99, 1937–1952. [Google Scholar] [CrossRef]
- Munger, J.W.; Wofsy, S.C.; Bakwin, P.S.; Fan, S.-M.; Goulden, M.L.; Daube, B.C.; Goldstein, A.H.; Moore, K.E.; Fitzjarrald, D.R. Atmospheric deposition of reactive nitrogen oxides and ozone in a temperate deciduous forest and a subarctic woodland: 1. Measurements and mechanisms. J. Geophys. Res. Atm. 1984–2012 1996, 101, 12639–12657. [Google Scholar] [CrossRef]
- Schmatzler, B.; Schmatzler, E. Moorland: Moorlandschaften in Niedersachsen nach industriellem Torfabbau, 1st ed.; IVG: Ratingen, Germany, 2010; ISBN 978-3-00-031560-2. [Google Scholar]
- BUND Diepholzer Moorniederung, Mittleres Wietingsmoor - Historisch eine Besonderheit, Kranichschutz and Kranich erleben I. Available online: http://www.naturpark-duemmer.de/fileadmin/content/Zum_download/fly_mw.pdf (accessed on 24 June 2017).
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Fratini, G.; Mauder, M. Towards a consistent eddy-covariance processing: An intercomparison of EddyPro and TK3. Atm. Meas. Tech. 2014, 7, 2273–2281. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atm. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Horst, T.W.; Lenschow, D.H. Attenuation of Scalar Fluxes Measured with Spatially-displaced Sensors. Bound.-Layer Meteorol. 2009, 130, 275–300. [Google Scholar] [CrossRef]
- Ibrom, A.; Dellwik, E.; Flyvbjerg, H.; Jensen, N.O.; Pilegaard, K. Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems. Agric. For. Meteorol. 2007, 147, 140–156. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, Detrending, and Filtering of Eddy Covariance Time Series. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Lee, X., Massman, W.J., Law, B.E., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2004; pp. 7–31. [Google Scholar]
- Ibrom, A.; Dellwik, E.; Larsen, S.E.; Pilegaard, K. On the use of the Webb–Pearman–Leuning theory for closed-path eddy correlation measurements. Tellus. B 2007, 59, 937–946. [Google Scholar] [CrossRef]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3. 2011. Available online: https://epub.uni-bayreuth.de/342/1/ARBERG046.pdf (accessed on 28 May 2011).
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Glob. Change Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation: SEPARATION OF NEE INTO GPP AND RECO. Glob. Change Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: https://www.R-project.org/ (accessed on 23 July 2015).
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Laisk, A.; Kull, O.; Moldau, H. Ozone concentration in leaf intercellular air spaces is close to zero. Plant. Physiol. 1989, 90, 1163–1167. [Google Scholar] [CrossRef] [PubMed]
- Hicks, B.B.; Baldocchi, D.D.; Meyers, T.P.; Hosker, R.P.; Matt, D.R. A preliminary multiple resistance routine for deriving dry deposition velocities from measured quantities. Water. Air. Soil Pollut. 1987, 36, 311–330. [Google Scholar] [CrossRef]
- Grömping, U. Relative importance for linear regression in R: the package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Fratini, G.; Ibrom, A.; Arriga, N.; Burba, G.; Papale, D. Relative humidity effects on water vapour fluxes measured with closed-path eddy-covariance systems with short sampling lines. Agric. For. Meteorol. 2012, 165, 53–63. [Google Scholar] [CrossRef]
- Moncrieff, J.B.; Massheder, J.M.; deBruin, H.; Elbers, J.; Friborg, T.; Heusinkveld, B.; Kabat, P.; Scott, S.; Soegaard, H.; Verhoef, A. A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide. J. Hydrol. 1997, 189, 589–611. [Google Scholar] [CrossRef]
- Klemm, O. Local and regional ozone: A student study project. J. Chem. Educ. 2001, 78, 1641–1646. [Google Scholar] [CrossRef]
- Altimir, N.; Kolari, P.; Tuovinen, J.-P.; Vesala, T.; Bäck, J.; Suni, T.; Kulmala, M.; Hari, P. Foliage surface ozone deposition: a role for surface moisture? Biogeosciences 2006, 3, 209–228. [Google Scholar] [CrossRef]
- Hogg, A.; Uddling, J.; Ellsworth, D.; Carroll, M.A.; Pressley, S.; Lamb, B.; Vogel, C. Stomatal and non-stomatal fluxes of ozone to a northern mixed hardwood forest. Tellus. B 2007, 59, 514–525. [Google Scholar] [CrossRef]
- Cape, J.N.; Hamilton, R.; Heal, M.R. Reactive uptake of ozone at simulated leaf surfaces: Implications for “non-stomatal” ozone flux. Atmos. Environ. 2009, 43, 1116–1123. [Google Scholar] [CrossRef]
- Massman, W.J. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O-3, SO2, NH3, N2O, NO, AND NO2 in air, O-2 AND N-2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]

| QC_0 | QC_1 | QC_2 | NA | Below u*-Threshold | |
|---|---|---|---|---|---|
| 59 | 24 | 5 | 12 | 23 | |
| 53 | 25 | 9 | 12 | 21 | |
| LE | 50 | 25 | 13 | 12 | 18 |
| H | 60 | 20 | 8 | 12 | 22 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Madany, T.S.; Niklasch, K.; Klemm, O. Stomatal and Non-Stomatal Turbulent Deposition Flux of Ozone to a Managed Peatland. Atmosphere 2017, 8, 175. https://doi.org/10.3390/atmos8090175
El-Madany TS, Niklasch K, Klemm O. Stomatal and Non-Stomatal Turbulent Deposition Flux of Ozone to a Managed Peatland. Atmosphere. 2017; 8(9):175. https://doi.org/10.3390/atmos8090175
Chicago/Turabian StyleEl-Madany, Tarek S., Katharina Niklasch, and Otto Klemm. 2017. "Stomatal and Non-Stomatal Turbulent Deposition Flux of Ozone to a Managed Peatland" Atmosphere 8, no. 9: 175. https://doi.org/10.3390/atmos8090175
APA StyleEl-Madany, T. S., Niklasch, K., & Klemm, O. (2017). Stomatal and Non-Stomatal Turbulent Deposition Flux of Ozone to a Managed Peatland. Atmosphere, 8(9), 175. https://doi.org/10.3390/atmos8090175





