Next Article in Journal
Validation of MODIS-Aqua Aerosol Products C051 and C006 over the Beijing-Tianjin-Hebei Region
Next Article in Special Issue
The Madden-Julian Oscillation: A Tool for Regional Seasonal Precipitation Outlooks?
Previous Article in Journal
Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method
Previous Article in Special Issue
Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 8
Issue 9
10.3390/atmos8090171
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Remote Ocean Response to the Madden–Julian Oscillation during the DYNAMO Field Campaign: Impact on Somali Current System and the Seychelles–Chagos Thermocline Ridge

by
Toshiaki Shinoda
1,*,
Weiqing Han
2,
Luis Zamudio
3,
Ren-Chieh Lien
4 and
Masaki Katsumata
5
1
Department of Physical and Environmental Sciences, Texas A&M University-Corpus Christi, Corpus Christi, TX 78412, USA
2
Department of Atmospheric and Oceanic Sciences, University of Colorado, Denver, CO 80203, USA
3
Center for Ocean-Atmospheric Prediction Studies, Florida State University, Tallahassee, FL 32306, USA
4
Applied Physical Laboratory, University of Washington, Seattle, WA 98195, USA
5
Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Yokosuka 237-0061, Japan
*
Author to whom correspondence should be addressed.
Atmosphere 2017, 8(9), 171; https://doi.org/10.3390/atmos8090171
Submission received: 15 August 2017 / Revised: 9 September 2017 / Accepted: 10 September 2017 / Published: 13 September 2017
(This article belongs to the Special Issue Madden-Julian Oscillation)
Browse Figures
Versions Notes

Abstract

:
During the CINDY/DYNAMO field campaign, exceptionally large upper ocean responses to strong westerly wind events associated with the Madden–Julian oscillation (MJO) were observed in the central equatorial Indian Ocean. Strong eastward equatorial currents in the upper ocean lasted more than one month from late November 2011 to early January 2012. The remote ocean response to these unique MJO events are investigated using a high resolution (1/25°) global ocean general circulation model along with the satellite altimeter data. The local ocean response to the MJO events are realistically simulated by the global model based on the comparison with the data collected during the field campaign. The satellite altimeter data show that anomalous sea surface height (SSH) associated with the strong eastward jets propagated eastward as an equatorial Kelvin wave. The positive SSH anomalies then partly propagate westward as a reflected Rossby wave. The SSH anomalies associated with the reflected Rossby wave in the southern hemisphere propagate all the way to the western boundary. These remote ocean responses are well simulated by the global model. The analysis of the model simulation indicates the significant influence of reflected Rossby waves on sub-seasonal variability of Somali current system near the equator. The analysis further suggests that the reflected Rossby wave causes a substantial change in the structure of the Seychelles–Chagos thermocline ridge, which contributes to significant SST anomalies.

1. Introduction

The Cooperative Indian Ocean experiment on intraseasonal variability (CINDY)/Dynamics of the MJO (DYNAMO) international field campaign was conducted in boreal fall 2011 through winter 2011/2012 with the goal of expediting our understanding of the physical and dynamical processes key to Madden–Julian Oscillation (MJO) initiation in the Indian Ocean [1]. During the field campaign, three episodes of large-scale convection associated with the MJO propagated eastward over the Indian Ocean. The equatorial low-level westerly winds associated with the MJO-induced convection were particularly strong during the second and third events in late November and December, e.g., [1,2,3]. These westerly wind events provide a significant source of fluxes of momentum and heat into the ocean, e.g., [4], causing large upper ocean responses including strong anomalous currents, changes of thermocline depth, and temperature. The upper ocean variability produced by these MJO events were well monitored by the arrays of surface mooring and ship observations in the central Indian Ocean during the intensive observing period of the field campaign (1 October 2011–15 January 2012; [1,3,5]). This study investigates remote ocean responses to the MJO events observed during the field campaign, in which the local upper ocean response was exceptionally strong.
A number of previous studies reported significant remote upper ocean responses to wind forcing near the equator in the central Indian Ocean through equatorial and coastal wave propagation. These remote areas include Indonesian Seas, e.g., [6,7,8,9,10], northern Indian Ocean, e.g., [11,12,13,14], and the western tropical Indian Ocean, e.g., [15,16,17]. Many of these studies discuss the remote ocean response to semiannual westerlies along the equator, which generate eastward zonal currents during boreal spring and fall [18]. For example, semiannual equatorial winds generate equatorial Kelvin and reflected Rossby waves, which influence upper ocean structures in the entire equatorial Indian Ocean, e.g., [19,20]. A recent study suggests that semiannual reflected Rossby waves can impact mixed layer temperature around the region of Somali current near the equator based on numerical model simulations [17]. As described above, the eastward zonal jet in the equatorial Indian Ocean is also generated by the MJO, but the amplitude of the reflected Rossby waves for the typical MJO is generally much weaker than those associated with semiannual wind forcing, e.g., [21]. Yet, some of the strong MJO events could influence western Indian Ocean through reflected Rossby waves e.g., [2,15,16]. However, the impact of the MJO-induced equatorial waves on the western boundary region including the Somali current system has not been reported so far.
The remote ocean response to strong MJO events during the CINDY/DYNAMO field campaign has been described by satellite observations [2]. In response to strong equatorial westerlies associated with MJO events, eastward jets with a large zonal extent, which cover the almost entire Indian Ocean basin, were accelerated along the equator in late November 2011. Large positive sea surface height (SSH) anomalies are found near the eastern boundary in late December to early January right after the strong equatorial jet is generated. Satellite observations suggest that these SSH anomalies partly propagate westward by radiating Rossby waves from the eastern boundary and they reach the area of shallowest thermocline near the equator, which is known as the Seychelles–Chagos thermocline ridge (SCTR), e.g., [22,23,24,25], where sea surface temperatures (SSTs) are sensitive to small changes of the thermocline depth and surface forcing.
While satellite observations provide estimates of surface manifestation of the local and remote response of the upper ocean, they do not describe details of internal fluctuations. In situ observations, such as research moored array for African–Asian–Australian monsoon analysis and prediction (RAMA) and DYNAMO buoys, provide subsurface variability, but these data are available only for the limited areas and periods. Accordingly, numerical model simulations are able to provide further information on large-scale upper ocean variability once validated with observations. Recent high resolution models are able to resolve upper ocean structure near the boundary including the narrow western boundary, which is difficult to monitor by satellite observations. This study investigates the upper ocean variability in response to the MJO events observed during the CINDY/DYNAMO filed campaign using a high resolution numerical model simulation. In particular, the remote ocean responses, including currents, especially the western boundary current, and the thermocline variability associated with Rossby and Kelvin waves are emphasized. Also, the variation of subsurface structure of SCTR associated with the Rossby wave propagation is investigated. The model’s ability to simulate local and remote responses to the MJO events is evaluated based on the comparison with in-situ data collected during CINDY/DYNAMO and satellite observations.

2. Experiment

2.1. Model and Experiment

The ocean model used in this study is the Hybrid Coordinate Ocean Model (HYCOM), which is a community ocean model with a generalized vertical coordinate [26]. The hybrid coordinate is isopycnal in the open, stratified ocean, but smoothly reverts to a terrain-following coordinate in shallow coastal regions, and to z-level coordinates in the mixed layer and/or unstratified seas. The K-profile parameterization [27] is used for vertical mixing in the model.
The model version used in this study is for the global domain, with horizontal resolution of 1/25° and 41 layers in the vertical [28]. The global HYCOM simulation was spun up for 10 years with climatological atmospheric forcing fields derived from ERA-40. Then the model was integrated for the period of 2008–2012 with 3-hourly archived operational forcing from the navy operational global atmospheric prediction system (NOGAPS) [29], but with the long-term annual mean replaced by the long-term mean from ERA-40. A more realistic mean state could be obtained by using these hybrid winds. Also, the hybrid wind set reduces spurious spin-up effects at the beginning of the interannual simulations initialized from ERA-40. The observational data are not assimilated in the model simulation.

2.2. Observational Data for Model Evaluation

2.2.1. DYNAMO and RAMA Buoy Data

In situ data collected from surface moorings during DYNAMO [30] and RAMA program [31] are used to evaluate upper ocean variability in the model simulations. The data from the DYNAMO surface moorings located at 0°, 78°56′ E and 1°30′ S, 78°45′ E are used. A major focus of the evaluation is on upper ocean thermal structure including the thermocline depth variability generated by strong westerly winds, since this study primarily discusses the remote ocean variability through oceanic wave propagation. Upper ocean temperature data collected by moored Conductivity, Temperature, Depth (CTD) sensors are used for the comparison. Subsurface CTD measurements in DYNAMO moorings were taken every 2 min at 1, 5, 10, 15, 20, 30, 40, 50, 60, 70, 80, 90, 101, 150, 200, 300, and 500 m. In addition, near-surface velocity data taken by acoustic Doppler current profilers (ADCPs) on the DYNAMO and RAMA moorings are used to evaluate the model simulations of equatorial jet produced by strong westerly winds.

2.2.2. SeaSoar, XBT, CTD, and XCTD Measurements

Upper ocean temperature data collected by SeaSoar, expendable bathythermograph (XBT), CTD and XCTD during CINDY/DYNAMO are used to validate the variation of thermocline structure simulated by the model. During the mooring deployment period of the DYNAMO experiment, 68 XBT casts were deployed in 9–18 September 2011 along 78.5° E with a nominal 0.25° latitudinal resolution between 12° S and 2° N. XBT measured temperature and pressure between surface and 1100 m depth with a vertical resolution of 0.6 m. XBT data were averaged into 2 m depth bins. Shipboard CTD profiles were made at each of three mooring positions during the mooring deployment. XBT and temperature measurements taken by shipboard CTD showed a good agreement and confirmed their quality. During the mooring recovery cruise, the meridional structure of temperature and salinity along 78.5° E was captured in 19–23 January using a SeaSoar, a towed vehicle with impeller-forced wings allowing its undulation in the upper ocean. CTD sensors mounted on the SeaSoar measured temperature, salinity, and pressure between ~10 m and ~350 m depth at a vertical resolution of ~2 m.
During CINDY experiment, the shipboard CTD measurements from the surface to 1000 m were conducted at (8.0° S, 80.5° E) and (5.1° S, 78.1° E) on 28–30 November. Also, the XCTD was towed (down to 1000 m) every 0.5° in latitude between these CTD stations and Equator, 80° E. Using these data, the meridional section of temperature near 79° E during this period is constructed. Further details on the observations and data processing are described in the cruise report [32].

2.2.3. Satellite Observations

Sea surface height (SSH) obtained from archiving, validation, and interpretation of satellite oceanographic (AVISO) data are used to describe local and remote ocean responses and to evaluate those simulated by the model. The data are provided for the daily average on a 0.25° × 0.25° grid.

3. Results

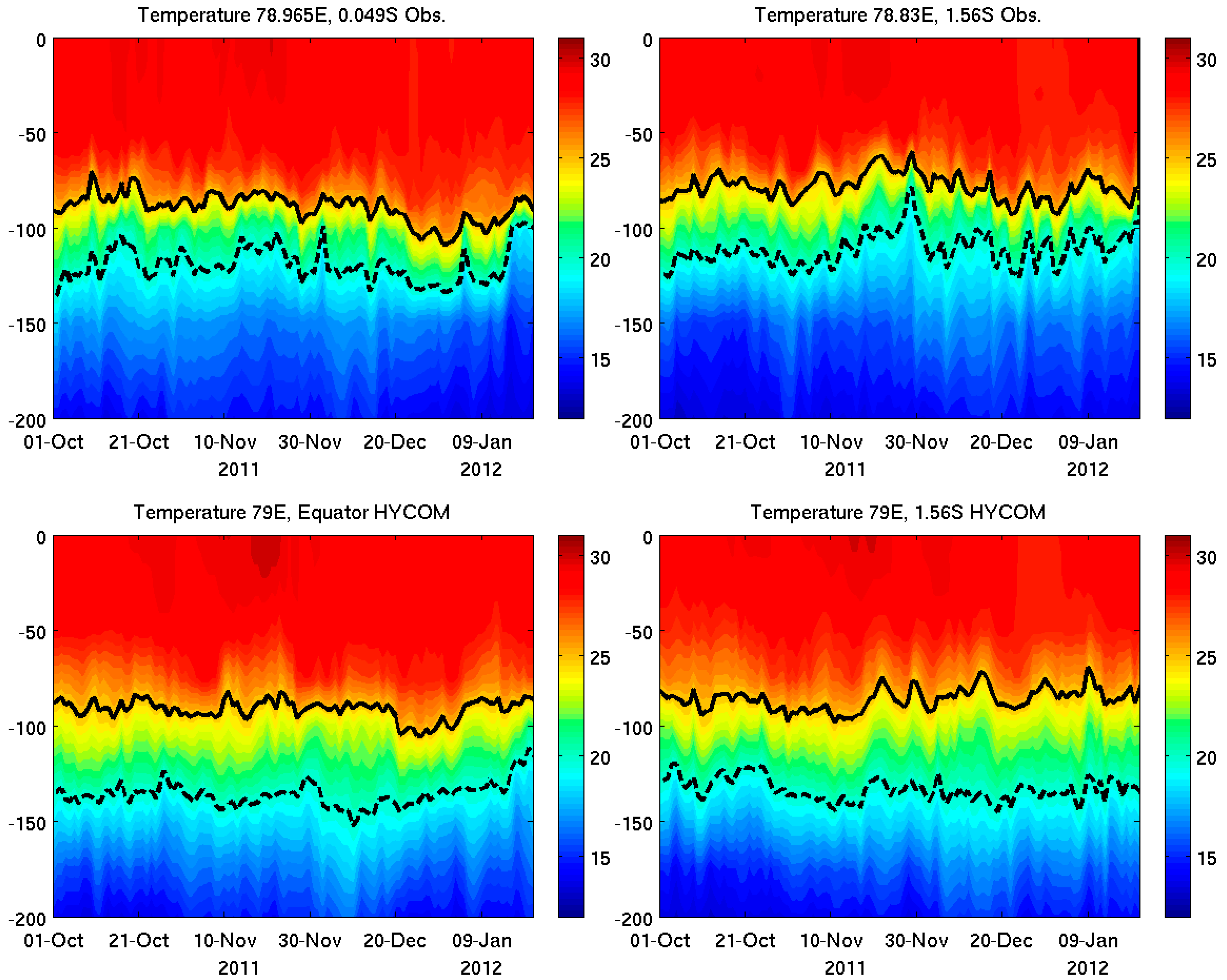
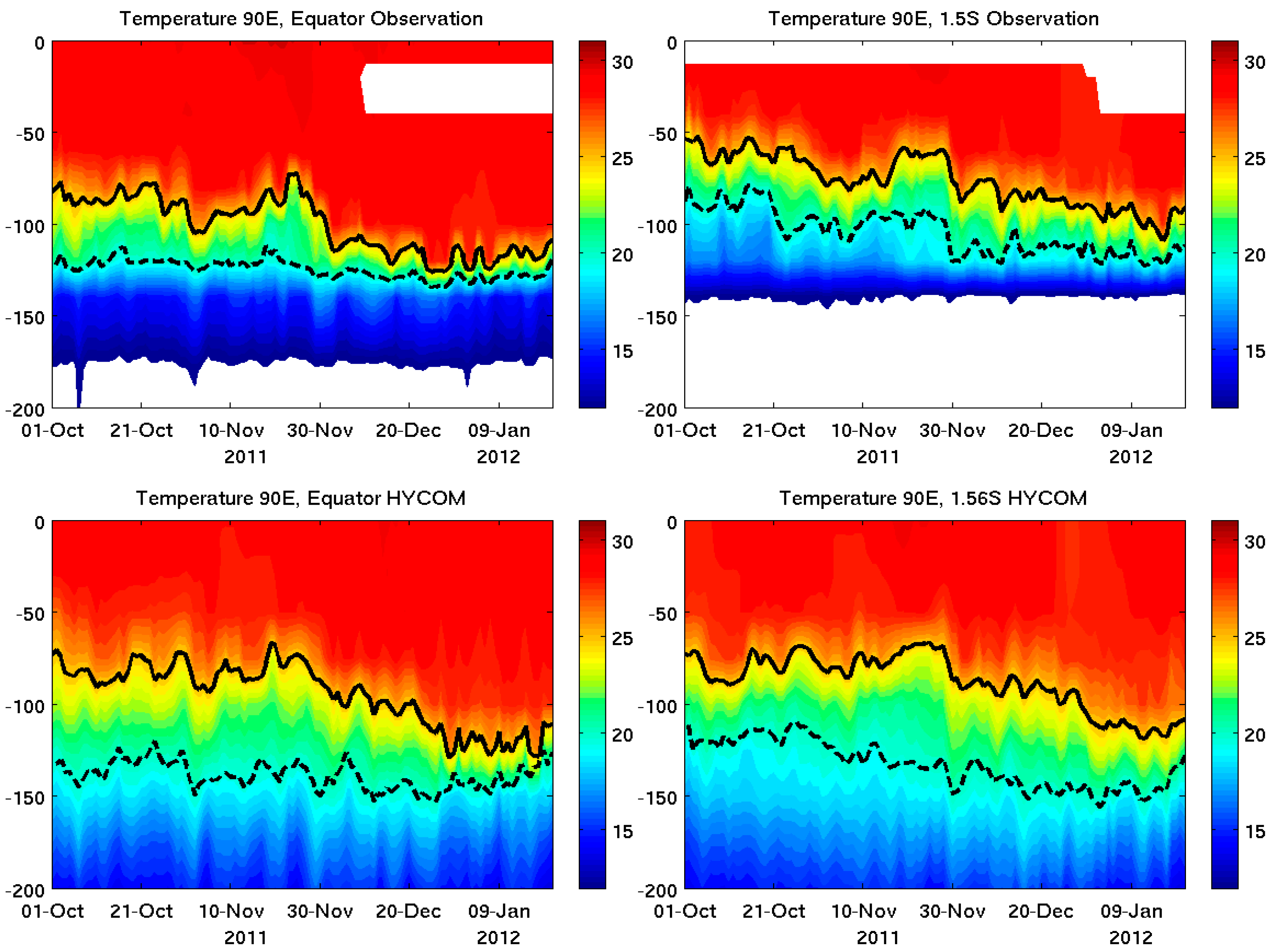
3.1. Comparison of the Model Simulation with Observations

The model simulation used in this study has been compared previously with some of the data collected during DYNAMO [10]. While the previous comparison demonstrates that the model is able to simulate the ocean response to the MJO reasonably well, further comparisons, including the variation of thermocline structure, are performed here using additional data sets.

3.1.1. Local Ocean Response to MJO Forcing

Since the major focus of this study is to identify the remote ocean processes associated with wave propagations, the variability of thermocline depth in the model simulation is first compared with the observed data. Figure 1 shows the time series of temperature in October 2011–mid-January 2012 at DYNAMO surface mooring locations from the model simulation and observations. During this period, the variation of the thermocline depth at this location is small. The average thermocline depth in the model agree with observations reasonably well, although the model tends to generate the thermocline a little deeper than observations. The average depth of 20 °C isotherm (D20; dashed lines in figures) of observation and the model at 79° E, Equator is 120 m and 133 m, respectively, and those at 79° E, 1.56° S are 111 m and 128 m. While large variations of thermocline depth are not observed during this period at these locations, occasional small changes are captured by the model. For example, a D20 shoaling of about 25 m at 79° E, Equator is observed in early January, which is simulated by the model.
The depth of 25 °C isotherm (D25), which is located near the top of the thermocline, is also shown in Figure 1. D25 simulated by the model agrees with observations better than D20, indicating that the isothermal layer thickness is well simulated by the model but the model thermocline is not sharp enough. The smaller vertical temperature gradient in the equatorial thermocline is a common problem found in most ocean models.
Figure 2 displays the comparison of upper ocean temperature time series from the model with the RAMA mooring data at 90° E, Equator and 90° E, 1.5° S. While the observed D20 does not vary much at 90° E, Equator, D25 gradually increases during this period. These variations are well captured by the model. At 90° E, 1.5° S, D20 gradually increases by about 30 m in observations, which is consistent with the model simulation. However, as in the comparison at 79° E, the model tends to produce a deeper D20 than observations. Nevertheless, the model is able to simulate observed thermocline variability reasonably well.
Westerly winds associated with the MJO events during the field campaign generated strong equatorial jets [2,5,10,33]. In order to validate the simulation of equatorial jets, the model surface zonal currents are compared with the RAMA and DYNAMO mooring data in the central equatorial Indian Ocean (Figure 3). The observed equatorial zonal current variations agree well with those in the model. In particular, the rapid acceleration in late November is well simulated by the model. The zonal currents continue to be strong in December (~1 m/s) after the acceleration. This is because there is no clear suppressed phase between the two MJO events in late November and December, and thus weakening of the westerlies occur for only a short period of time during December, e.g., [2].

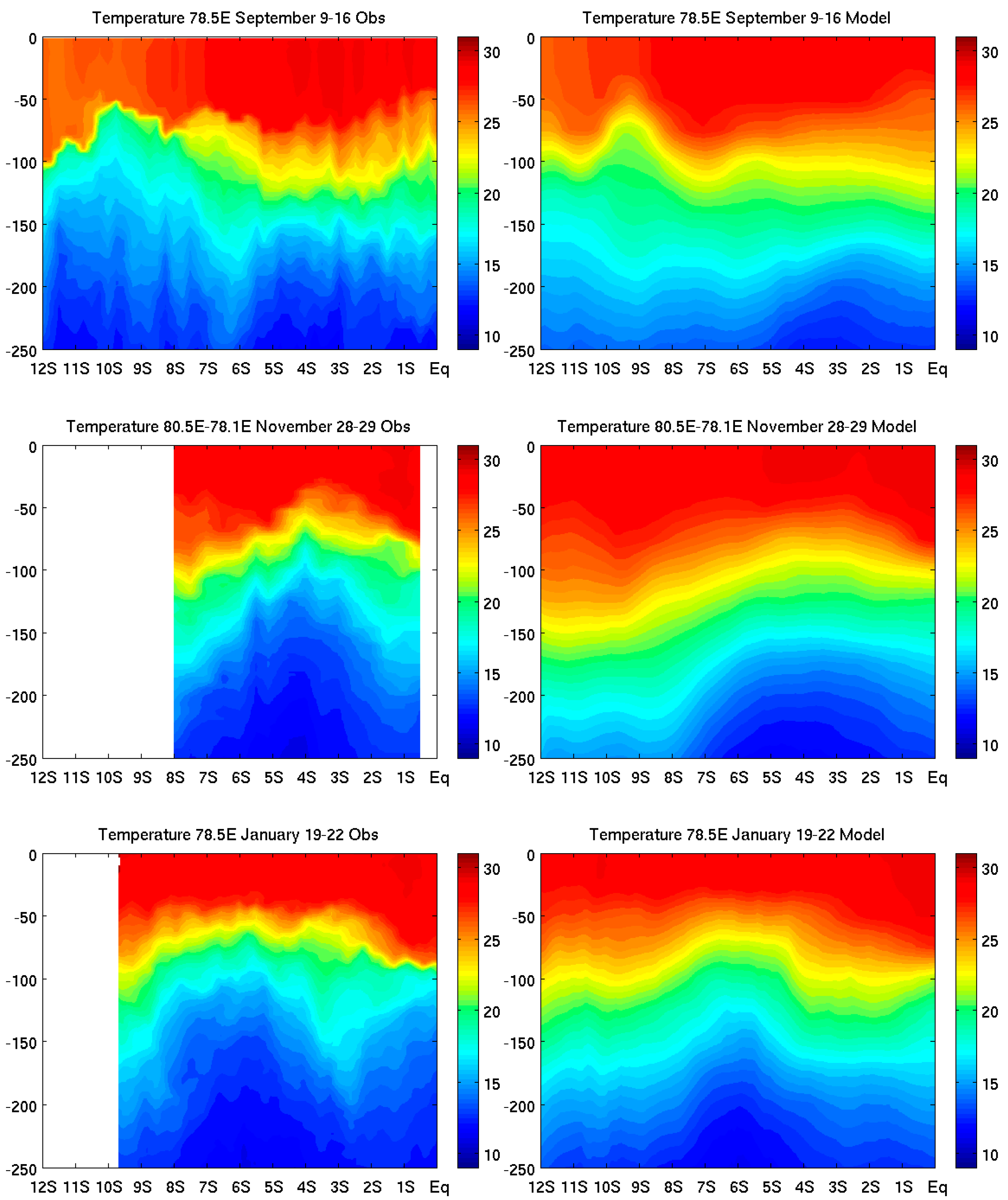
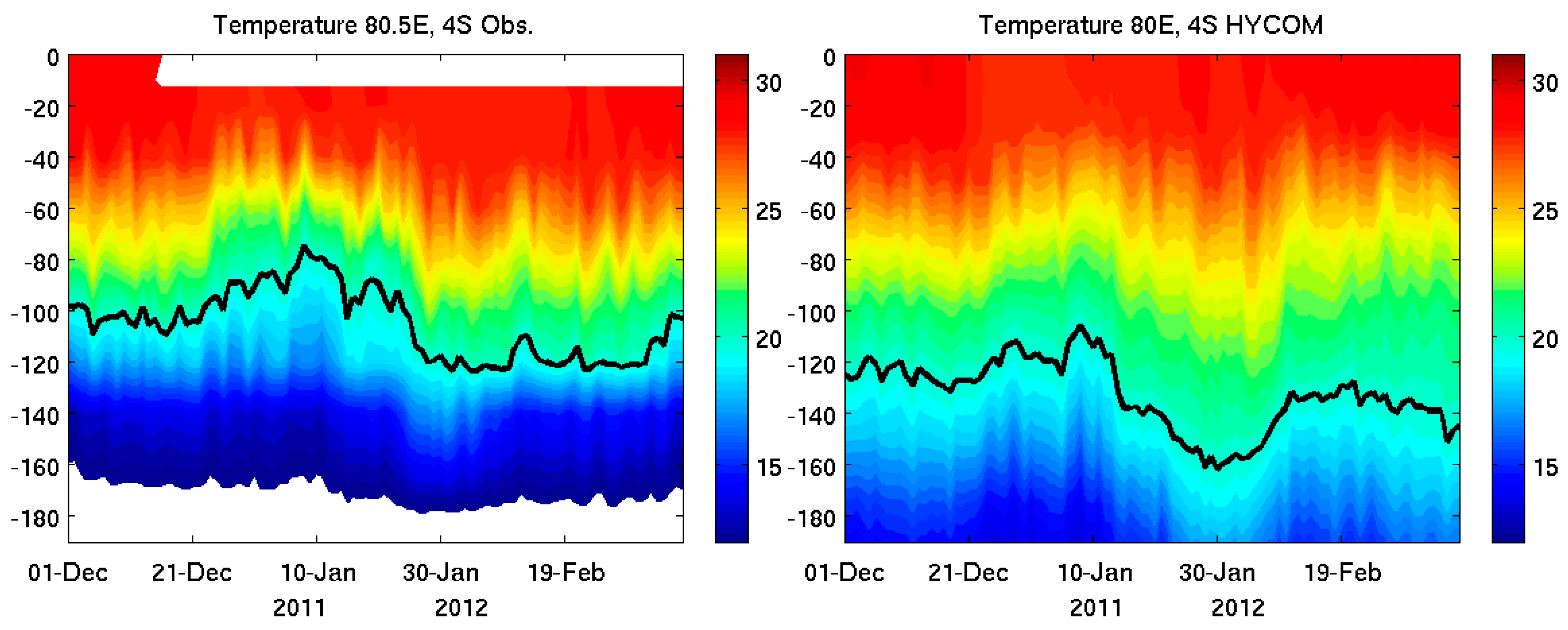
3.1.2. Thermocline Ridge

While the center of SCTR is located in the western part of the tropical Indian Ocean around 60° E–65° E, it extends farther east, including the locations of CINDY/DYNAMO ocean observations. As described in Section 2, temperature measurements along 79° E were conducted three times (early September, late November, and mid-January) during CINDY/DYNAMO. A comparison of these observations demonstrates the meridional migration of SCTR at this location (Figure 4, left panels). During early September, the shallowest thermocline is located around 9° S–10° S. Then, the shallowest thermocline is migrated to around 4° S in late November. In mid-January 2012, the SCTR at this longitude is found centering around 6° S. The observed meridional migration is well simulated by the model (Figure 4, right panels), indicating that major physical processes that modulate the SCTR structure are well represented in the model. However, there are some quantitative differences between the model and observations. For example, the structure of the lower part of the thermocline in the model during early September does not agree well with the observation. Nevertheless, the overall agreement suggests that the model simulation is adequate to be used to discuss the variation of SCTR structure. Although the SCTR meridional migration observed in the area of DYNAMO observation is not a major focus in this study, possible dynamical processes affecting the migration are further discussed in Section 4.

3.2. Large-Scale Variability

In the previous section, it is demonstrated that the model is able to simulate variations of thermocline depth including the location of SCTR and zonal currents in the central equatorial Indian Ocean reasonably well based on the comparison with in-situ observations. In this section, large-scale upper ocean variability in response to the MJO events in the model simulation, including that in the remote ocean areas, is described and compared with the satellite-derived data.

3.2.1. Equatorial Kelvin Wave

Figure 5 shows the longitude-time diagram of SSH anomalies from satellite observations and the model. In response to the MJO event in late November, a prominent signal of eastward propagation of SSH anomaly is evident in observations. The propagation speed is about 2.8 m/s, which is close to the phase speed of the first baroclinic mode equatorial Kelvin wave in this region, e.g., [34,35]. The model is able to simulate the downwelling Kelvin wave with the amplitude comparable to the observations (Figure 5). Note that the differnce in anomaly fields between model and observation is partly due to the climatology calculated for different periods. While the climamatological seasonal cycle of satellite observation is computed for the period 2000–2014, the model seasonal cycle is calculated for the 5-year period (2008–2012) of the simulation.
Figure 5 (third panel) shows the longitude-time diagram of surface zonal current anomaly near the equator from the model simulation. The rapid acceleration of eastward jet in late November is evident in almost the entire Indian Ocean basin. The large-scale eastward currents continue to be strong until early January. While the strong anomalous currents are found in both western and eastern parts in the basin in late November, the anomalous currents are stronger in the eastern part around 80° E–90° E in late December. This distribution of zonal current anomaly is consistent with the spatial pattern of westerly winds, in which the stronger westerlies are found in the eastern Indian Ocean in late December (Figure 5, right panel), [2]. Note that the eastward propagation of zonal current can be detected, but it is not as clear as that of SSH because equatorial zonal currents often include other large signals such as Rossby waves and Yoshida jet [33,36].
As a result of eastward currents associated with Kelvin waves and strong zonal jets directly driven by westerlies in the eastern Indian Ocean, a significant SSH increase (~15 cm) is found in the large areas (6° N–8° S) near the coast of Sumatra in late December–early January due to the strong convergence of zonal currents at the eastern boundary (Figure 5 and Figure 6). The D20 anomaly associated with the increase of SSH exceeds 25 m near the eastern boundary (Figure 6). The alongshore (northwesterly) winds south of the equator in late December [2] could also enhance the increase of SSH and deepening of the thermocline.
The eastward propagation of SSH is also evident in mid to late October (Figure 5). However, SSH increase near the eastern boundary is not as large as that associated with later events. This is because the westerly wind anomalies near the equator associated with the MJO during this period are weaker although atmospheric convection is comparable to later events (Figure 5 right panel), e.g., [1,2].

3.2.2. Reflected Rossby Wave

As shown in the previous section, a pronounced increase of SSH and the deepening of the thermocline along the coast of Sumatra and Java in late December due to the convergence of zonal current associated with equatorial jets are well simulated by the model. These positive SSH anomalies could propagate westward by radiating Rossby waves from the eastern boundary, e.g., [19,35,37]. Figure 7a shows the satellite-derived SSH variations near the equator (left panel) and around 4° S (right panel) where the SSH amplitude of equatorial Rossby wave is maximum, e.g., [37]. The periods include those after the occurrence of large positive SSH anomalies at the eastern boundary during late December–early January. The westward propagation throughout the entire Indian Ocean basin during early January to mid-March is clearly evident in observations. The model is able to simulate the westward propagation of the observed SSH well (Figure 7b). The phase speed (~0.88 m/s) is consistent with the first baroclinic mode Rossby wave in this region. The SSH signals of phase speeds slower than the first baroclinic mode are also evident, and as a result, weaker positive SSH anomalies are found in the eastern side of maximum SSH anomalies. These signals could be due to the higher baroclinic modes (e.g., [2]). A similar westward propagation of D20 is also evident during this period (not shown). It should be noted that a similar westward propagation of SSH anomalies is evident at 4° N at least in the eastern side of the basin, but it is not as clear as that at 4° S in the western side of the basin probably because it is disturbed by the coast of south India and Sri Lanka (not shown), e.g., [38].
The model simulation of the Rossby wave is further confirmed by the comparison with the RAMA mooring data at 80.5° E, 4° S (Figure 8). During mid to late January, when the reflected Rossby wave passed at this location, the mooring data indicate that the thermocline becomes deeper by about 20–30 m. This deepening of the thermocline is simulated well by the model.

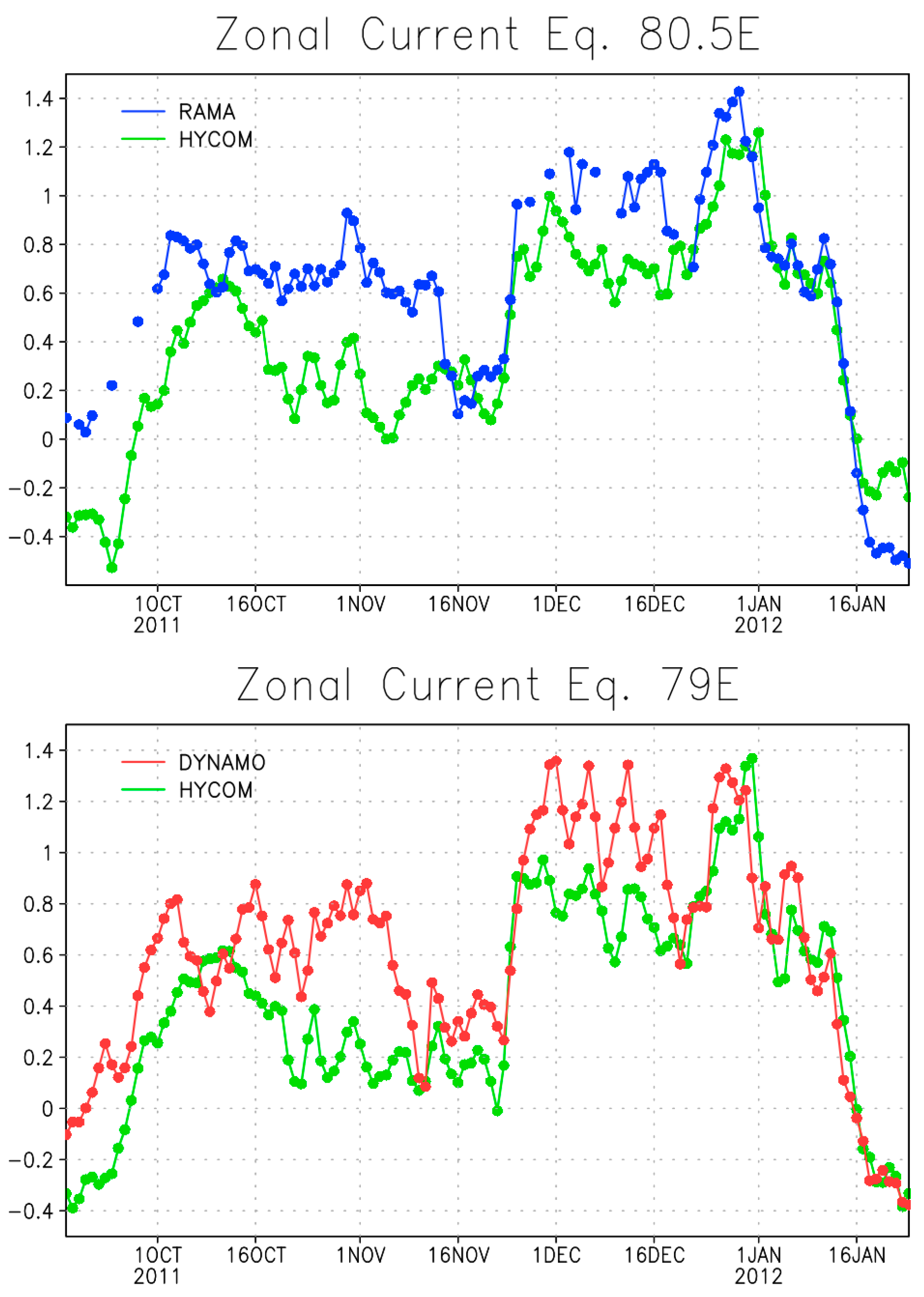
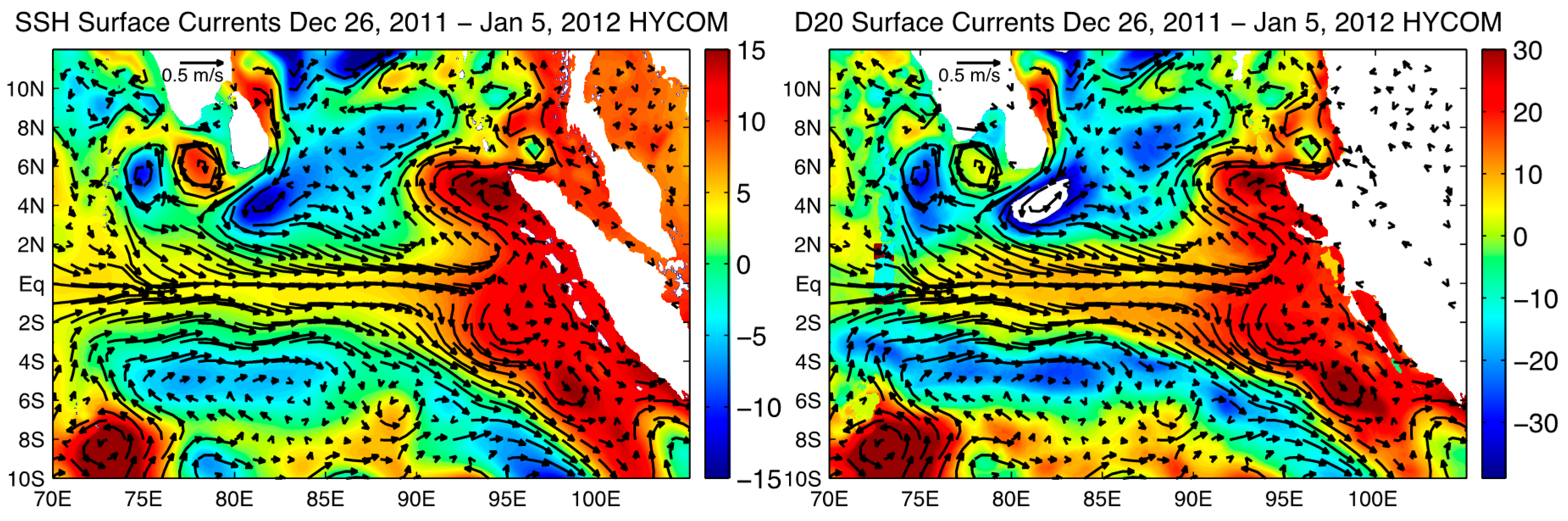
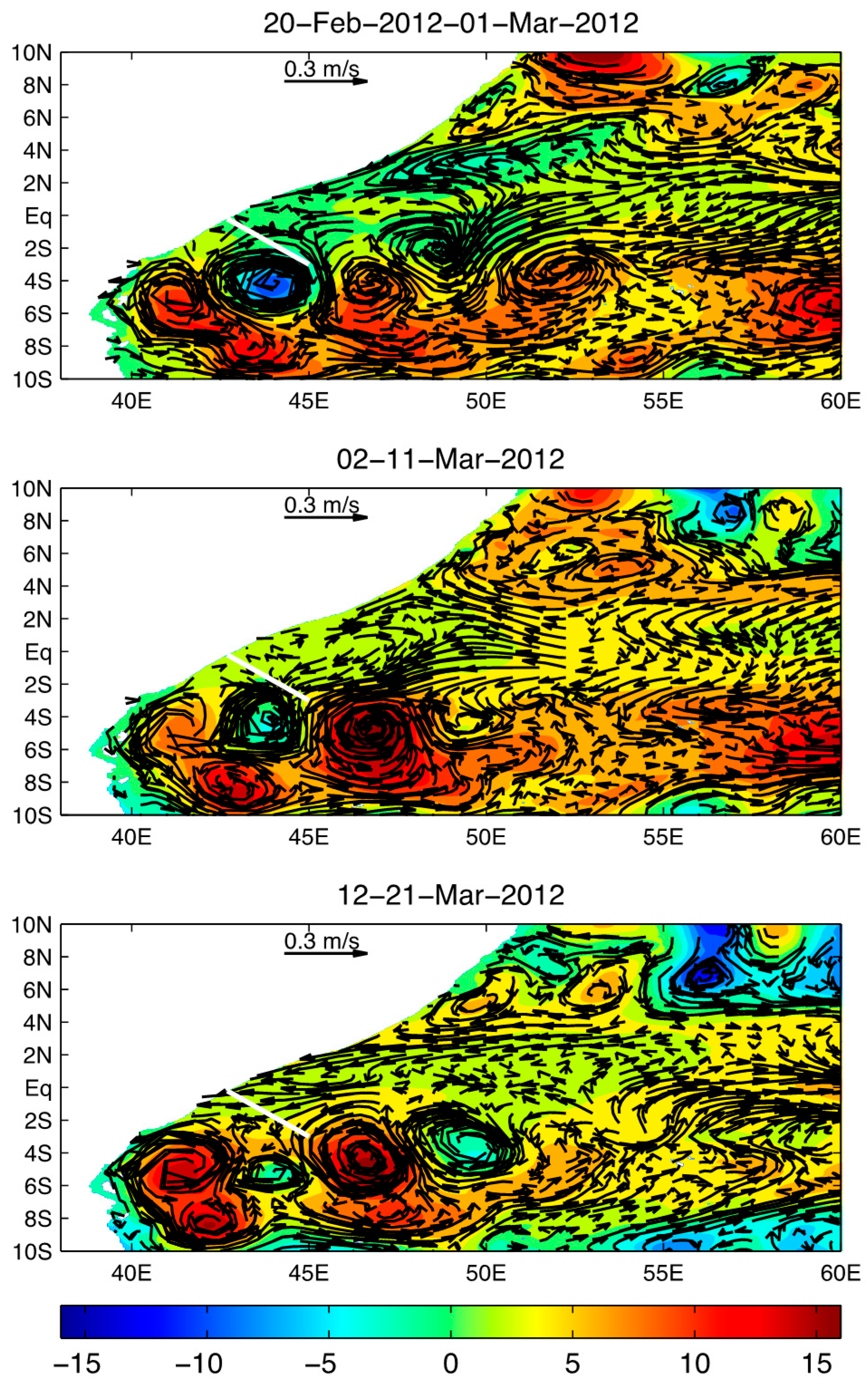
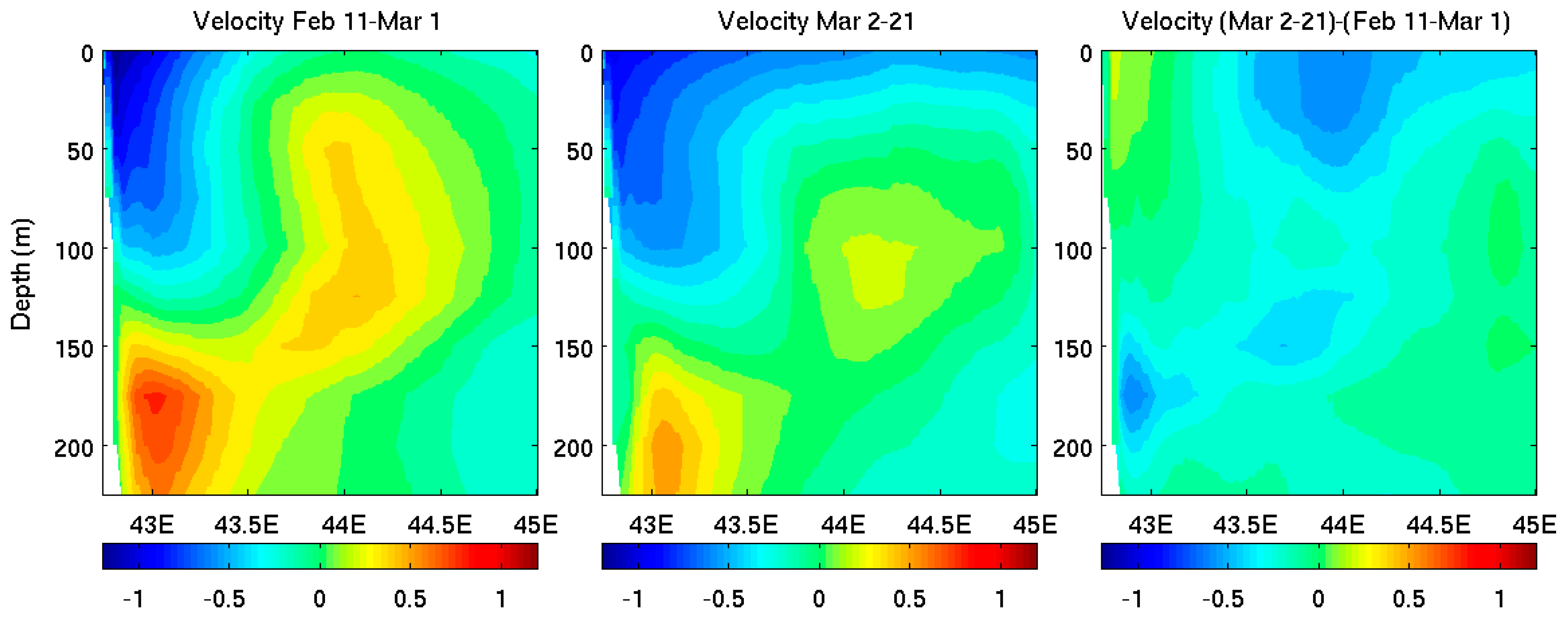
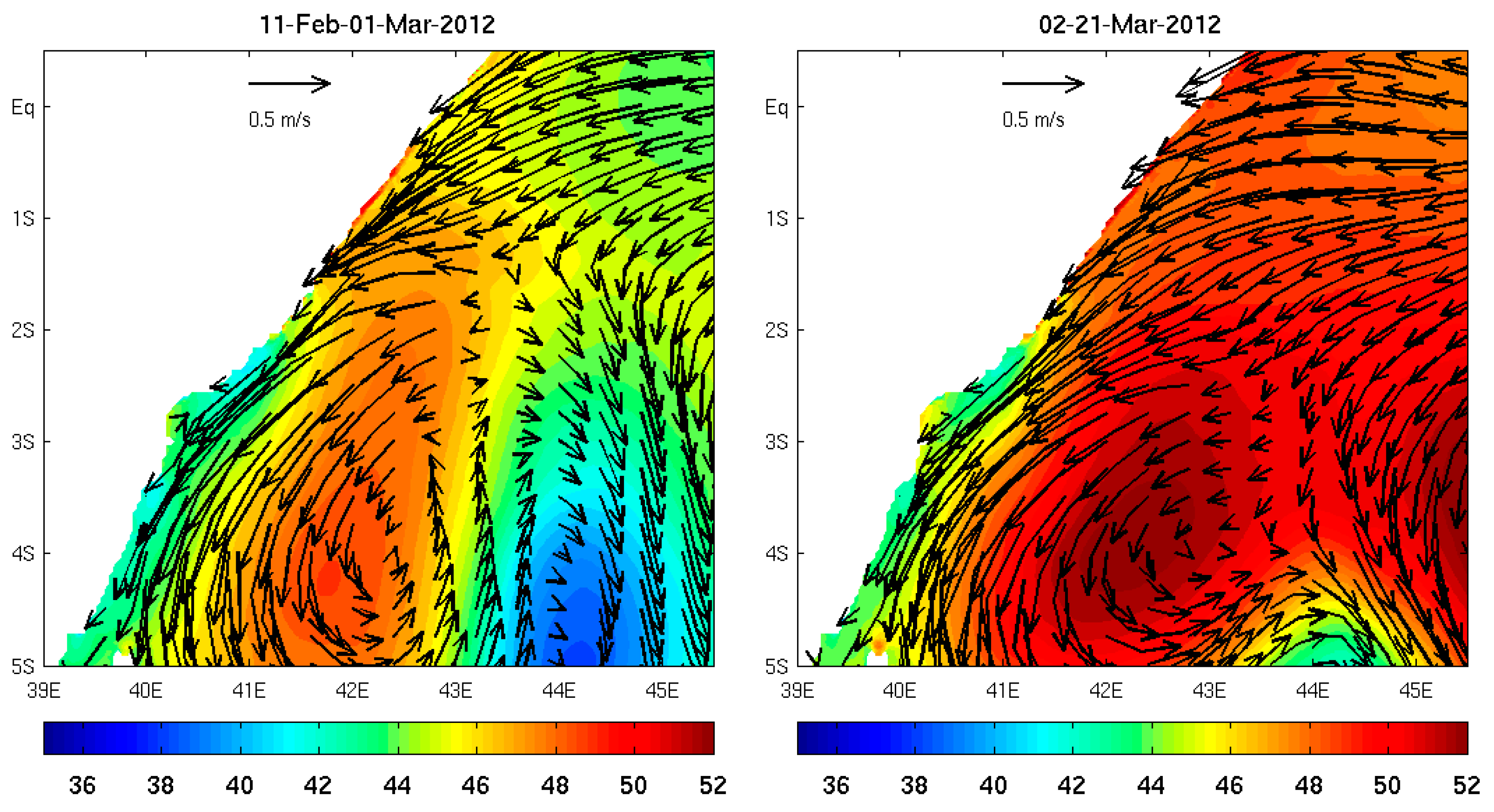
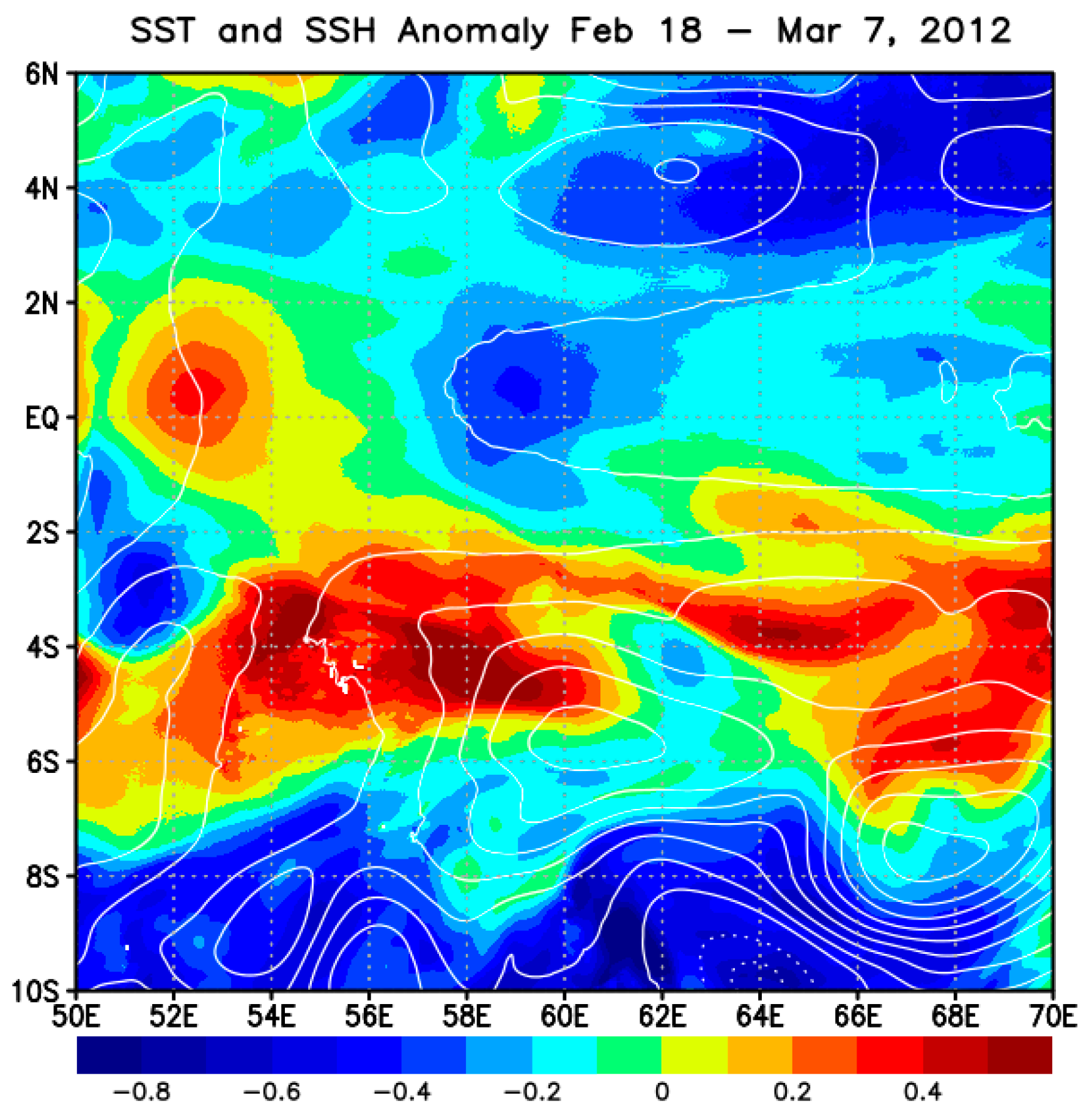
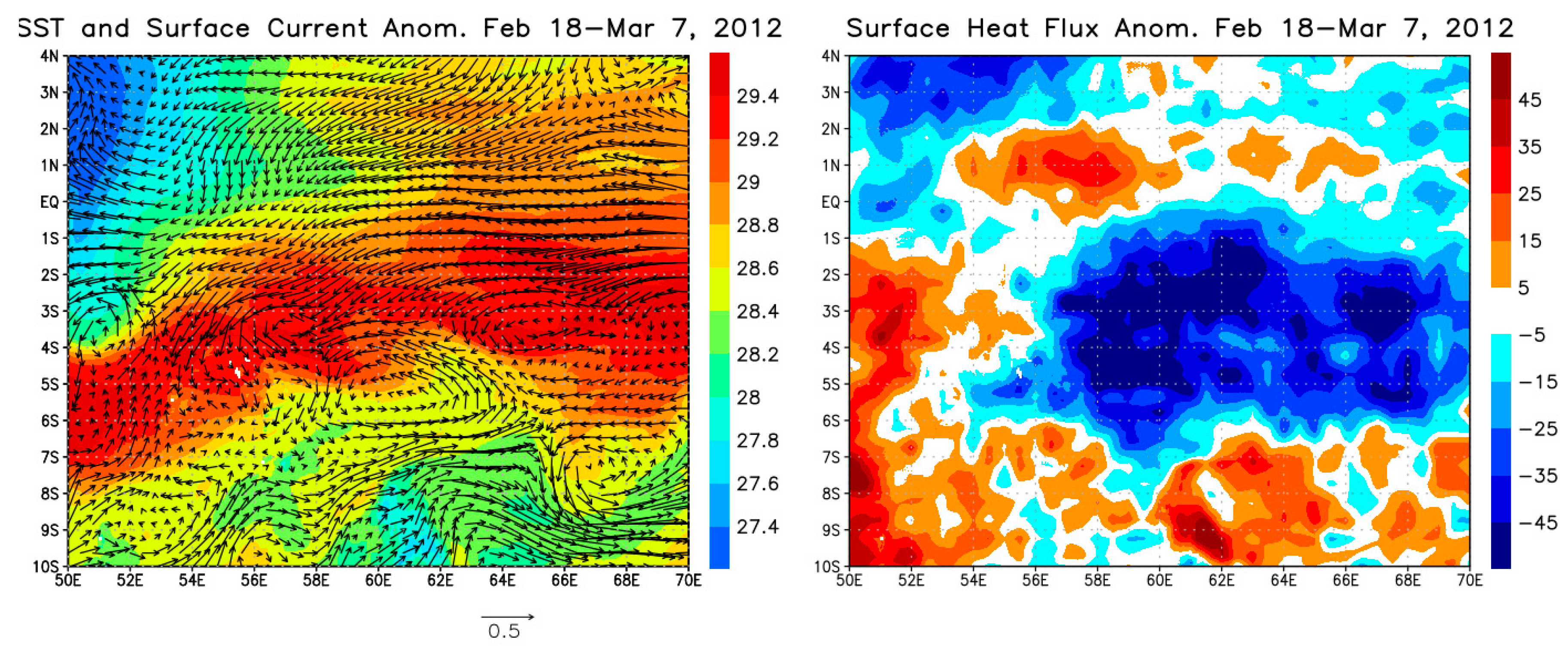
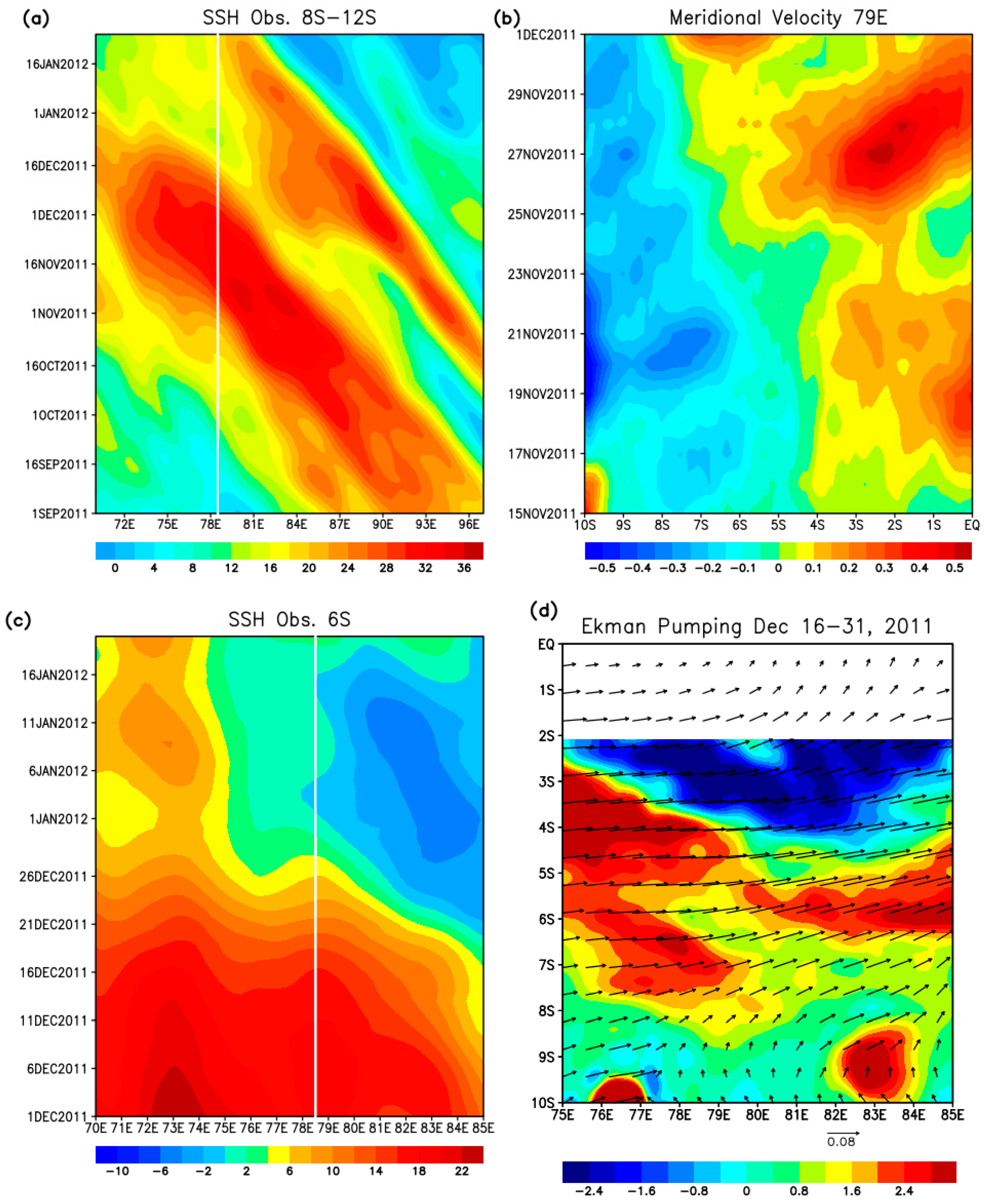
3.2.3. Influence on Somali Current System

Somali current is one of the western boundary currents in the Indian Ocean, and has been extensively studied since the 1960s. It is unique in that the current direction changes seasonally due to the monsoon reversal, with complex vertical and horizontal structures such as a two-gyre system and prominent undercurrents, e.g., [39,40]. The influence of the remotely forced variability on the Somali current system has been discussed in many studies, e.g., [23,41,42,43,44]. For example, a recent study [44] indicates that Rossby waves propagated from the central Indian Ocean drive the onset of northward currents around 6° N in April, which are associated with a precursor of the Great Whirl. These studies, however, focused mostly on the seasonal variation of the Somali current system. The subseasonal variability, such as that generated by the MJO, has not been previously investigated. This section discusses the influence of MJO-induced remote ocean variability on the Somali current system.
As shown in Figure 7, the reflected Rossby wave propagates all the way to the western boundary, and thus they may influence the upper ocean structure in the western boundary current region. Figure 9 shows the surface current anomaly in the western side of the basin during the period when the reflected Rossby wave is propagating in this region. The westward propagation of anomalous westward currents near the equator is evident, and the significant changes of alongshore current anomaly near the boundary is found between equator and 4° S, when the wave reaches the boundary (Figure 9, bottom panel).
Figure 10 shows the alongshore velocity along the cross section indicated by the white line in Figure 9. The high-resolution model is able to generate narrow strong currents in the upper 100 m near the boundary, in which the alongshore (southwestward) velocity exceeds 1 m/s. Also, northeastward undercurrents around the depth of 150–200 m are evident. The structure of the boundary currents is consistent with observations during this season at least qualitatively, e.g., [39,40]. It should be noted, however, that a further quantitative comparison is not possible because of the lack of in situ observations especially during this season.
The comparison of the Somali current structure between the periods before and after the arrival of reflected Rossby wave shows its substantial influence (Figure 10). While the current right near the boundary during late February is similar to that in early to mid-March, strong alongshore currents are found in much broader areas during mid-March. The spatial pattern of surface currents near the boundary during these periods are shown in Figure 11. The broadening of alongshore currents are found in almost the entire region between equator and 4° S near the boundary. In addition, the narrow boundary current is significantly enhanced by about 20 cm/s between 2° S and 4° S, in association with the increase of SSH centered around 4° S.

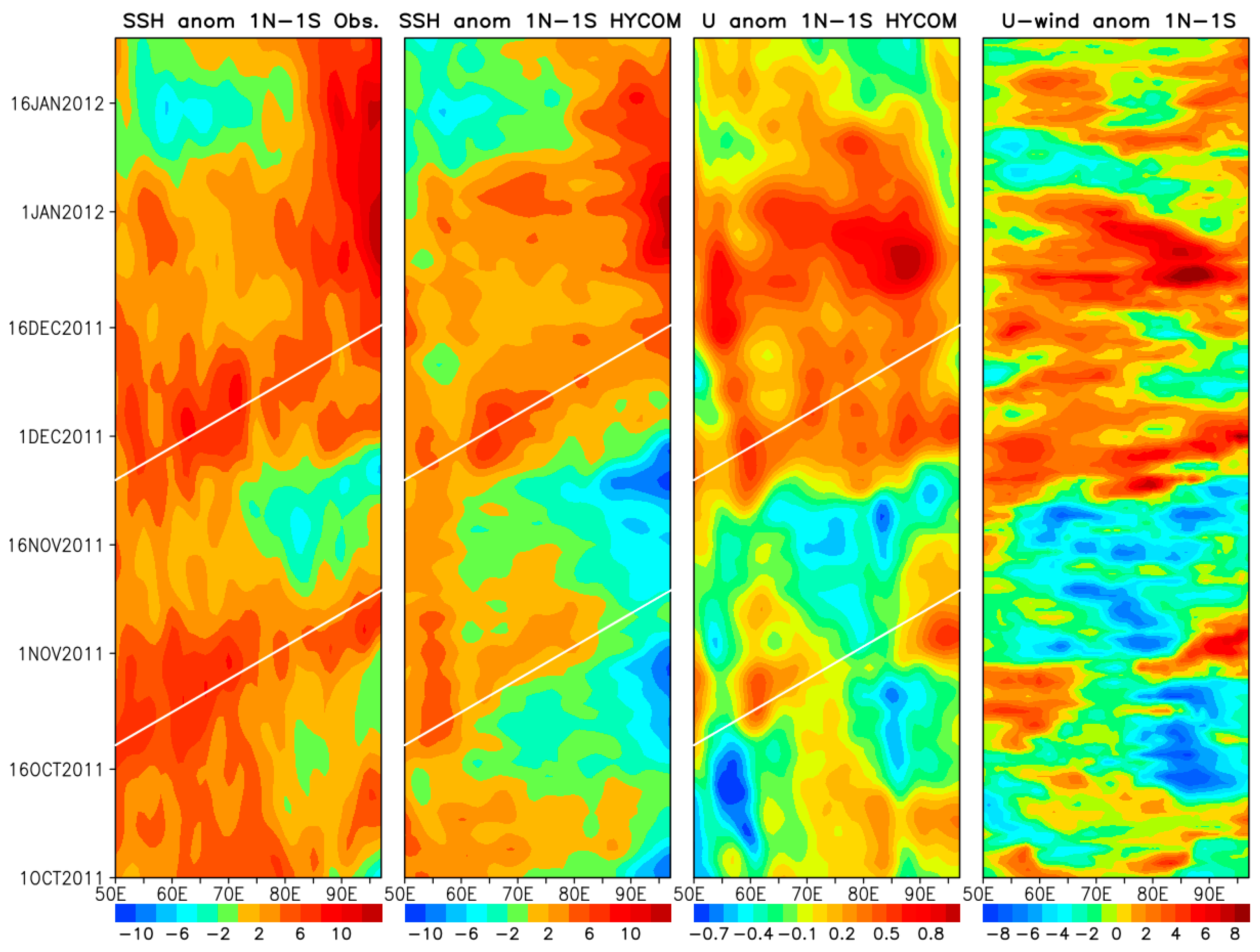
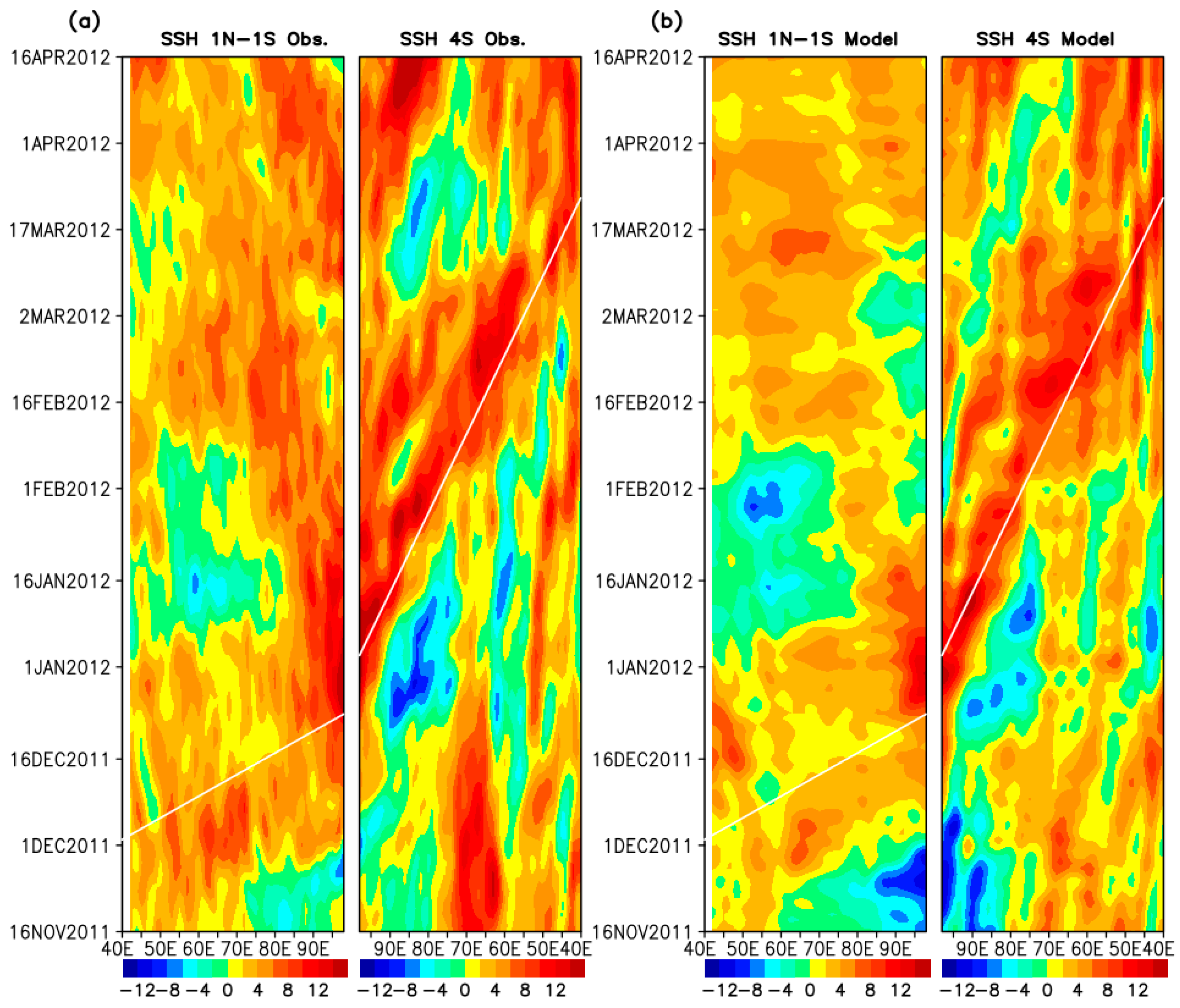
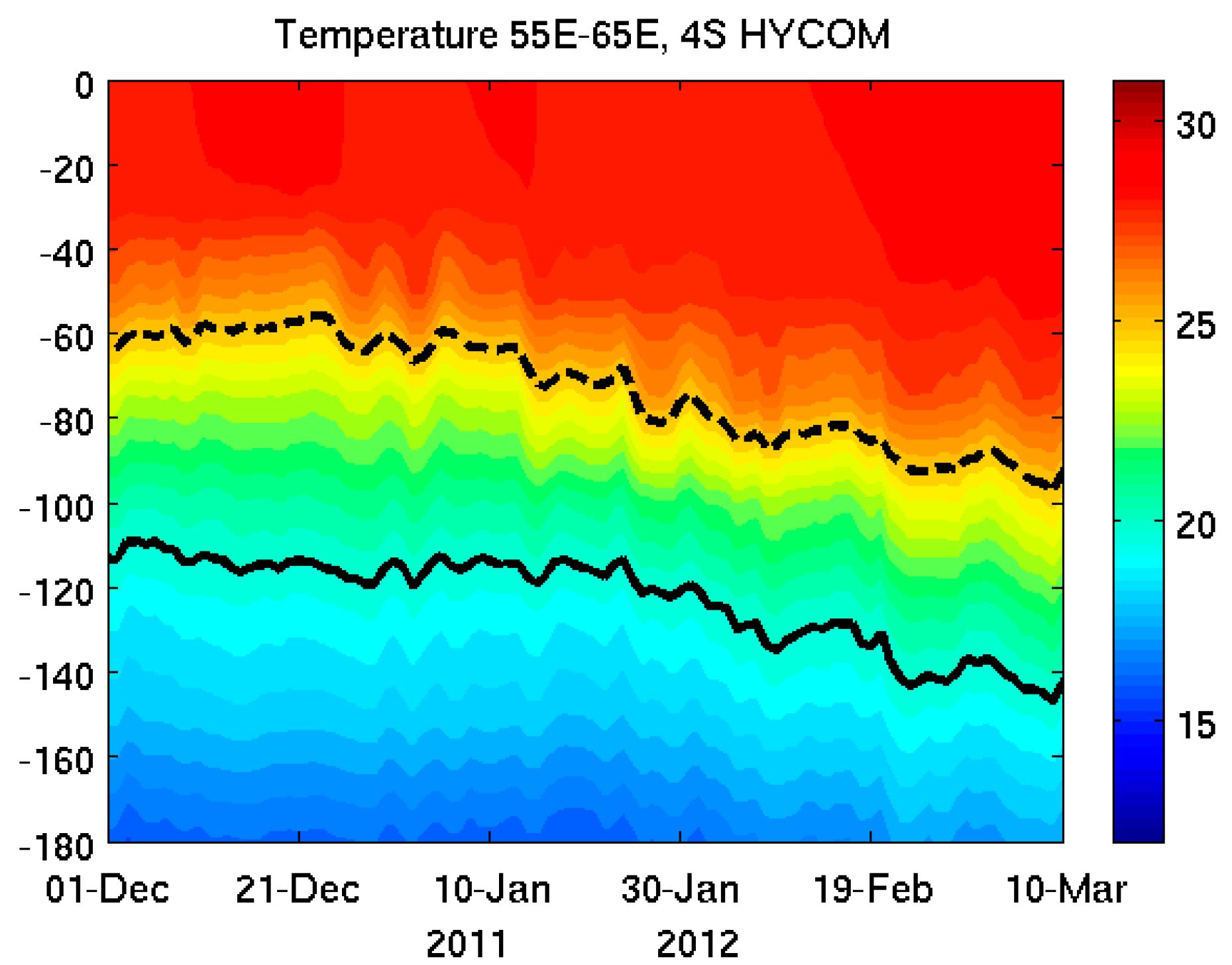
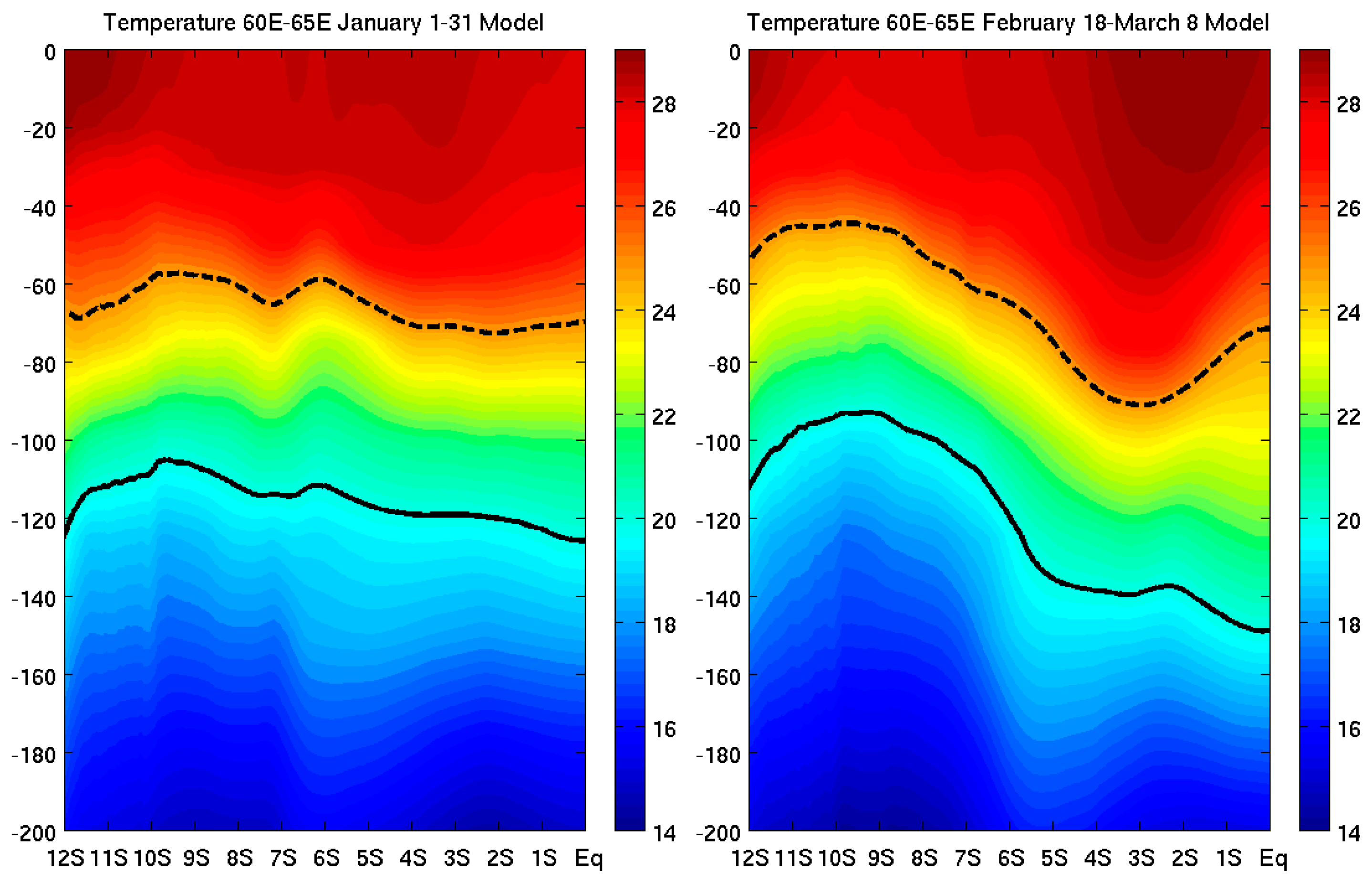
3.2.4. Influence on the Seychelles–Chagos Thermocline Ridge Region

While previous studies suggest significant remote ocean responses in the western Indian Ocean to MJO forcing [15,16], most of these studies did not specifically focus on the SCTR region where SST is very sensitive to the small change of thermocline depth and surface forcing. A possible impact of the reflected Rossby waves generated by the MJO on the SCTR region is suggested in a recent study [2] based on the analysis of satellite altimeter data. However, these studies did not emphasize subsurface variability such as the structure of the thermocline in SCTR. Changes of SCTR structure associated the propagation of reflected Rossby waves and their possible impact on SST are discussed in this section.
A significant amplitude of reflected Rossby wave passed through the center of SCTR around 60° E during February–early March. Figure 12 shows the time series of temperature profile at 55° E–65° E, 4° S from the model simulation. The deepening of the thermocline associated with the propagation of Rossby wave is found from February, and the SST warming associated with the deepening of the thermocline is evident.
The meridional sections of temperature around the center of SCTR before and after the arrival of Rossby wave are compared in Figure 13. The meridional structure of SCTR was substantially changed after the arrival of reflected Rossby wave during late February–early March. Because of the downwelling Rossby wave in the northern part of SCTR, the north-south slope of the thermocline becomes much steeper as the Rossby wave is passing through this location. In association with the change of meridional structure of SCTR, the location of the maximum SST is shifted northward. The warmest SST and upper ocean temperature is connected to the deep thermocline around 3° S–5° S, although the location of the maximum changes with depth. Also, the SST contrast between northern and southern parts of SCTR is much stronger after the arrival of the Rossby wave.
The spatial distribution of SST and SSH anomalies from the model simulation near the SCTR region during late February–early March are shown in Figure 14. A significant positive SST anomaly, which exceeds 0.3 °C, is evident around 4° S. SSH anomalies are also positive around 4° S although they are somewhat noisy due to active mesoscale eddies south of 6° S. These positive SST and SSH anomalies around 4° S are associated with the Rossby wave propagation through the SCTR region during this period.
Figure 15 shows SST and the anomaly of surface current for the same period (18 February–7 March). Significant anomalous currents are found in the areas of large SST gradient around 4° S. In particular, the meridional component of anomalous currents crosses the area of a large meridional SST gradient. However, these currents cause both warming and cooling by the heat advection. For example, colder waters from the south are advected northward around 4° S, 62° E, where a significant cooling anomaly is found (Figure 14).
A recent study [45] suggests that the zonal heat advection primarily generate the western Indian Ocean intraseasonal SST anomalies associated with downwelling Rossby waves, based on the composite analysis. Such an impact of zonal advection could be also inferred for this event (Figure 15). For example, westward currents around 55° E near the equator flow through the region of large zonal SST gradient. Hence the analysis indicates that the zonal and meridional heat advection significantly influence SST in the SCTR region. However, horizontal advection described here occurs in a smaller scale than the overall warming with a relatively large zonal extent shown in Figure 14. Accordingly, the SST warming with the large zonal extent (~20°) found around 4° S for this event cannot be fully explained by the horizontal heat advection alone.
Surface heat flux anomalies during this period (Figure 15, right panel) show a cooling most of the areas of positive SST anomaly in the SCTR region, indicating that the anomalous warming is not generated by surface heat fluxes. Hence these analyses suggest that deepening of the thermocline associated with reflected Rossby wave significantly contributes to the positive SST anomalies shown in Figure 14.
Recent studies [15,16,45,46] suggest that reflected Rossby waves generated by the MJO in the Indian Ocean may play an important role in generating a subsequent MJO. Because of the deepening of the thermocline in the western Indian Ocean due to the propagation of Rossby waves, a significant SST warming could be generated, which in turn could act as a trigger of the initiation of convection. In fact, atmospheric convection was initiated in the western and central Indian Ocean during March 2012, and it was developed to MJO, which propagated to the western Pacific in late March [1]. Accordingly, our results of model simulation are consistent with their mechanism (hypothesis) for the possible generation of a subsequent MJO event. However, the MJO events during the field campaign, which produced the exceptionally large amplitude of reflected Rossby waves, are unique in that they occurred within one month without a clear suppressed phase between the events. Because of the persistent westerly winds in late November and December, large-scale strong equatorial jets lasted more than one month, which in turn generated a substantial deepening of the thermocline at the eastern boundary. Such large thermocline depth anomalies might be required for the Rossby wave to influence the SST in the SCTR region, and it is uncertain how often such large amplitude of reflected Rossby waves have been generated by the MJO, which could have the impact similar to the events during DYNAMO. Further studies that examine the details on the remote upper ocean response to several other strong MJO events, including the SCTR thermocline structure, are necessary.

4. Discussion

The results in this study suggest that the meridional structure of SCTR can be substantially changed due to the remote ocean response to the MJO (Figure 13). As shown in Figure 4, a large change of the SCTR meridional structure was also observed during DYNAMO (September 2011–January 2012) in the central Indian Ocean, which could affect the SST and in turn may influence the MJO. Hence it is worthwhile to further discuss the possible physical mechanism that causes the variation of SCTR meridional structure during DYNAMO.
Since the period of DYNAMO observations shown in Figure 4 covers boreal fall and winter, the variation is likely to include the seasonal cycle. The processes that control the seasonal cycle of SCTR are examined in previous studies, e.g., [25,47]. For example, Hermes and Reason [25] indicated that the annual cycle of SCTR is a result of complex interaction between the ocean response to local and remote forcing based on numerical model experiments. On the other hand, Yokoi et al. [47] suggest that the seasonal variation of SCTR is primarily controlled by local wind forcing. These studies, however, focused on the center of the SCTR (55° E–65° E), and the processes in the area of DYNAMO observations are not emphasized.
Figure 16a shows the SSH variation derived from satellite altimeter around 10° S during DYNAMO, which includes the seasonal cycle. The downwelling annual Rossby wave during boreal fall and winter is evident, in which the amplitude and period are consistent with those reported in previous studies [48,49]. The propagation of this annual Rossby wave results in a significant deepening of the thermocline during mid-October-December in the area of DYNAMO observations. The subsequent Rossby wave with a relatively short time scale also reaches the DYNAMO observation area in January, which maintains the deep thermocline generated by the annual Rossby wave. Note that the annual Rossby wave around this latitude does not affect the center of SCTR (~60° E) where the shallowest thermocline is found (Figure 16a).
Around 4° S in November, the propagation of the Rossby wave, which can cause a large upwelling, is not clearly evident in the SSH data (not shown). Therefore, the local wind stress is likely to contribute primarily to the upwelling. Figure 16b shows the evolution of the meridional velocity in the upper 50 m in mid to late November 2011. In late November, a rapid acceleration of equatorward currents centered around 2° S is found, which is associated with the acceleration of eastward jet on the equator (Figure 3). As a result of equatorial convergence caused by westerly winds, a strong meridional divergence centered around 4° S is generated and thus the resultant upwelling changes the structure of SCTR. Hence, the shallow thermocline at 4° S during this period is generated by equatorial westerly winds around this longitude associated with the MJO onset. The smaller divergence around 4° S generated by weaker westerlies is evident before the onset of MJO convection in late November (Figure 16b), which also contributes to the shoaling of the thermocline.
Figure 16c shows SSH variations at 6° S in December–January. A rapid decrease of SSH (and thus a strong upwelling) around 6° S, 79° E–85° E is evident in mid- to late December, and the upwelling during this period mostly contributes to the shallow thermocline observed in mid-January. Also, the propagation of Rossby wave generated east of the DYNAMO area maintains the shallow thermocline in early to mid-January. The upwelling around 79° E and the Rossby wave are generated due to the winds around these areas (Figure 16d). The maximum of upward Ekman pumping velocity is found around 6° S, 79° E–85° E during this period, which is mostly due to the strong westerly winds associated with the MJO (see also Figure 3 in [2]). These analyses demonstrate that a meridional migration of SCTR in the DYNAMO area is caused by a combination of annual Rossby wave and MJO-induced wind stress. Although these SCTR changes are not generated by the reflected Rossby wave such as those discussed in the previous section, the results suggest that intraseasonal variation of wind stress produced by the MJO can largely alter the SCTR structure. It should be noted that the impact of the reflected Rossby wave on the thermocline structure, which is similar to that shown in Figure 10, is also found around the DYNAMO observation areas (not shown). The north-south slope of the thermocline depth around 4° S–6° S becomes much sharper during and after the reflected Rossby wave propagation in late January–early February.
While the analysis of the model simulations and satellite observations in this study clearly demonstrate that the reflected Rossby wave generated by MJO events during DYNAMO propagated all the way to the western boundary, the intraseasonal variabiily of local winds could modify the upper ocean structure during the wave propagation. The analysis of the wind data along the path of Rossby wave does not indicate the singnificant role of local wind forcing, including SCTR and the western boundary region (not shown). However, it is still desirable to completely isolate and further quantify the effect of local wind forcing by additional sensitivity experiments for the longer period. Such experiments, which remove reflected Rossby waves, have been conducted previously using coarse resolution models, e.g., [17,20,35]. Although the sensitivity experiments with a very high resolution model such as that used in this study are still challenging and beyond the scope of this study, it may be pursued in our future research.
As discussed in Section 3, the Somali current system reveals a remarkable seasonal cycle, including the area near the equator. The transition from southward to northward current near the equator occurs around March/April before the onset of the Indian summer monsoon [40]. During DYNAMO, the reflected Rossby wave generated by MJO events reach the western boundary early to mid-March, which largely enhanced southward currents near the boundary. Because this is the period right before the seasonal reversal of the current direction, it is possible that such subseasonal variability could impact the seasonal transition process. A further analysis of the model simulation indicates that the northward Somali current is generated in mid-April in the model, in which the direction of the current around 2° S–3° S rapidly changed and the northward current was accelarated to about 1 m/s within a few days (not shown). Such a rapid transition could be a result from the enhanced southward currents in the southern hemisphere due to the reflected Rossby wave right before the current reversal. Hence the results of this study suggest that remotely-forced subseasonal variability near the boundary could possibly contribute to dynamical processes affecting the seasonal reversal of Somali current system.
The analysis of the model simulation suggests the significant contribution of reflected Rossby waves on the SST variability in SCTR. However, it should be noted that processes controlling intraseasonal SST in the SCTR region is still a subject of debate, e.g., [50]. For example, the relative importance of ocean dynamical processes and surface fluxes for the intraseasonal SST variation largely depends on the location within the SCTR, e.g., [51]. In addition, processes controlling the intraseasonal SST is affected by interannual variability and event-to-event variability, e.g., [51,52]. Furthermore, significant uncertainties in the mixed layer heat budget, which most previous studies rely on, still exist due partly to the difficulty of quantifying the vertical mixing processes around the mixed layer depth including entrainment and vertical advection. A further quantitative discussion on the impact of the thermocline depth change on SSTs requires an accurate estimate of both intraseasonal variability and climatology of the entrainment heat flux in SCTR, which are likely to contain large uncertainties. Therefore, at least the longer integration of models with high horizontal and vertical resolutions and extensive analysis are necessary to further confirm the results in this study. Such model simulation and analysis are still difficult at this stage, but could hopefully be feasible in the near future.

5. Conclusions

This study investigates the remote ocean response to MJO events observed during CINDY/DYNAMO field campaign using high resolution (1/25°) global ocean general circulation model and satellite observations. A particular emphasis is given to the impact on the Somali current system through the reflected Rossby wave propagation, which has not been reported in previous studies. During the DYNAMO field campaign, two strong MJO events were observed within a month without a clear suppressed phase between them, and these events generated exceptionally strong ocean responses. Strong eastward currents along the equator in the Indian Ocean lasted more than one month from late November 2011 to early January 2012. These unique MJO events resulted in very strong remote ocean responses.
During the field campaign, the westerlies associated with these MJO events generate strong equatorial eastward jets and downwelling near the eastern boundary. The equatorial currents and associated thermocline depth variation are shown to be realistically simulated by the global ocean model based on the comparison with the data collected during the field campaign. The satellite altimeter data show that anomalous sea surface height (SSH) associated with the strong eastward jets propagated eastward as an equatorial Kelvin wave. The positive SSH anomalies then partly propagate westward as a reflected Rossby wave. The SSH fluctuations in the southern hemisphere propagate all the way to the western boundary. These remote ocean responses are well simulated by the global ocean model. For the first time, the impact of the reflected Rossby wave generated by the MJO on the Somali current system is investigated based on the analysis of the model simulation. The result demonstrates the significant influence of reflected Rossby waves on the sub-seasonal variability of Somali current system and upper ocean structure near the western boundary. The southward Somali current is largely enhanced in the broad area around the western boundary between Equator and 4° S.
While the influence of reflected Rossby waves associated with the strong MJO on the western Indian Ocean SSTs has been reported in previous studies, the variation of subsurface (thermocline) structure around the Seychelles–Chagos thermocline ridge (SCTR) region, where SSTs are very sensitive to a small change of thermocline depth, has not been emphasized. The analysis of the model simulation indicates the substantial change of the SCTR meridional structure associated with the reflected Rossby wave. The deepening of the thermocline of about 20 m around 4° S is found after the reflected Rossby wave reaches the SCTR region, which results in the sharper north-south slope of the thermocline depth. Significant SST anomalies associated with the deepening of the thermocline, which exceed 0.3 °C, are found within SCTR, and thus such a change could influence the subsequent atmospheric convection associated with MJO initiation.

Acknowledgments

The TAO Project Office of NOAA/PMEL provided the RAMA mooring time series data. The altimeter products are produced by SSALTO/DUACS and are distributed by AVISO. Grants of computer time for the modeling work were provided by the Department of Defense (DoD) High Performance Computing Modernization Program, and the model simulations were performed at the Navy DoD Supercomputing Resources Center, Stennis Space Center, MS. Computing resources were also provided by the Climate Simulation Laboratory at NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation, and the HPC system at the Texas A&M University. We appreciate valuable comments from anonymous reviewers. This research is supported by NOAA grants NA15OAR431074 and NA17OAR4310256, NSF grants OCE-1658218 and AGS-1347132, and NASA grant NNX17AH25G.

Author Contributions

Toshiaki Shinoda conceived, designed, and conducted the analysis of model simulation and in-situ and satellite data. Weiqing Han provided valuable suggestions and stimulating discussion on the analysis. Luis Zamudio conducted a global ocean model simulation. Ren-Chieh Lien conducted observations of moorings, XBT, and SeaSoar, and helped in the analysis of the data. Masaki Katsumata conducted observations of XCTD and CTD, and helped in the analysis of the data; Toshiaki Shinoda wrote the paper, and other co-authors assisted in writing it.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yoneyama, K.; Zhang, C.; Long, C.N. Tracking pulses of the Madden-Julian oscillation. Bull. Am. Meteorol. Soc. 2013, 94, 1871–1891. [Google Scholar] [CrossRef]
  2. Shinoda, T.; Jensen, T.G.; Flatau, M.; Chen, S.; Han, W.; Wang, C. Large-scale oceanic variability associated with the Madden-Julian oscillation during the CINDY/DYNAMO field campaign from satellite observations. Remote Sens. 2013, 5, 2072–2092. [Google Scholar] [CrossRef]
  3. Gottschalck, J.; Roundy, P.; Schreck, C.; Vintzileos, A.; Zhang, C. Large-scale Atmospheric and Oceanic Conditions During the 2011–2012 DYNAMO Field Campaign. Mon. Weather Rev. 2013, 141, 4173–4196. [Google Scholar] [CrossRef]
  4. De Szoeke, S.; Edson, J.; Marion, J.; Fairall, C.; Bariteau, L. The MJO and Air-Sea Interaction in TOGA COARE and DYNAMO. J. Clim. 2015, 28, 597–622. [Google Scholar] [CrossRef]
  5. Moum, J.N.; de Szoeke, S.P.; Smyth, W.D.; Edson, J.B.; DeWitt, H.L.; Moulin, A.J.; Thompson, E.J.; Zappa, C.J.; Rutledge, S.A.; Johnson, H.R.; et al. Air-Sea Interactions from Westerly Wind Bursts during the November 2011 MJO in the Indian Ocean. Bull. Am. Meteorol. Soc. 2013, 95, 1185–1199. [Google Scholar] [CrossRef]
  6. Sprintall, J.; Gordon, A.L.; Murtugudde, R.; Susanto, R.D. A semiannual Indian Ocean forced Kelvin wave observed in the Indonesian seas in May 1997. J. Geophys. Res. 2000, 105, 17217–17230. [Google Scholar] [CrossRef]
  7. Susanto, R.D.; Ffield, A.; Gordon, A.; Adi, T.R. Variability of Indonesian throughflow with Makassar Strait: 2004–2009. J. Geophys. Res. 2012, 117, C09013. [Google Scholar] [CrossRef]
  8. Pujiana, K.; Gordon, A.L.; Sprintall, J. Intraseasonal Kelvin waves in Makassar Strait. J. Geophys. Res. 2013, 118, 2023–2034. [Google Scholar] [CrossRef]
  9. Shinoda, T.; Han, W.; Metzger, E.J.; Hurlburt, H.E. Seasonal variation of the Indonesian through flow in Makassar Strait. J. Phys. Oceanogr. 2012, 42, 1099–1123. [Google Scholar] [CrossRef]
  10. Shinoda, T.; Han, W.; Jensen, T.; Zamudio, L.; Metzger, E.J.; Lien, R.-C. Impact of the Madden-Julian Oscillation on the Indonesian Throughflow during the CINDY/DYNAMO field campaign. J. Clim. 2016, 29, 6085–6108. [Google Scholar] [CrossRef]
  11. Potemra, J.T.; Luther, M.E.; O’Brien, J.J. The Seasonal Circulation of the Upper Ocean in the Bay of Bengal. J. Geophys. Res. 1991, 96, 12667–12683. [Google Scholar] [CrossRef]
  12. Vinayachandran, P.N.; Yamagata, T. Monsoon Response of the Sea around Sri Lanka: Generation of Thermal Domes and Anticyclonic Vortices. J. Phys. Oceangr. 1998, 28, 1946–1960. [Google Scholar] [CrossRef]
  13. Han, W.; Webster, P.J. Forcing mechanisms of sea level interannual variability in the Bay of Bengal. J. Phys. Oceanogr. 2002, 32, 216–239. [Google Scholar] [CrossRef]
  14. Rao, R.R.; Girish Kumar, M.S.; Ravichandran, M.; Rao, A.R.; Gopalakrishna, V.V.; Thadathil, P. Interannual variability of Kelvin wave propagation in the wave guides of the equatorial Indian Ocean, the coastal Bay of Bengal and the southeastern Arabian Sea during 1993–2006. Deep Sea Res. 2010, 57, 1–13. [Google Scholar] [CrossRef]
  15. Webber, B.G.M.; Matthews, A.J.; Heywood, K.J. A dynamical ocean feedback mechanism for the Madden-Julian oscillation. Q. J. R. Meteorol. Soc. 2010, 136, 740–754. [Google Scholar] [CrossRef] [Green Version]
  16. Webber, B.G.M.; Matthews, A.J.; Heywood, K.J.; Stevens, D.P. Ocean Rossby waves as a triggering mechanism for primary Madden-Julian events. Q. J. R. Meteorol. Soc. 2012, 138, 514–527. [Google Scholar] [CrossRef] [Green Version]
  17. Tozuka, T.; Nagura, M.; Yamagata, T. Influence of the reflected Rossby waves on the western Arabian Sea upwelling region. J. Phys. Oceanogr. 2014, 44, 1424–1438. [Google Scholar] [CrossRef]
  18. Wyrtki, K. An equatorial jet in the Indian Ocean. J. Clim. 1973, 181, 262–264. [Google Scholar] [CrossRef] [PubMed]
  19. Jensen, T.G. Equatorial variability and resonance in a wind-driven Indian Ocean model. J. Geophys. Res. 1993, 98, 22533–22552. [Google Scholar] [CrossRef]
  20. Han, W.; McCreary, J.P.; Anderson, D.L.T.; Mariano, A.J. Dynamics of the eastward surface jets in the equatorial Indian Ocean. J. Phys. Oceanogr. 1999, 29, 2191–2209. [Google Scholar] [CrossRef]
  21. Marshall, A.G.; Hendon, H.H. Impacts of the MJO in the Indian Ocean and on the Western Australian coast. Clim. Dyn. 2014, 42, 579–595. [Google Scholar] [CrossRef]
  22. Woodberry, K.E.; Luther, M.E.; O’Brien, J. The wind-driven seasonal circulation in the southern tropical Indian Ocean. J. Geophys. Res. 1989, 94, 17985–18002. [Google Scholar] [CrossRef]
  23. McCreary, J.P., Jr.; Kundu, P.K.; Molinari, R.L. A numerical investigation of dynamics, thermodynamics and mixed-layer processes in the Indian Ocean. Prog. Oceanogr. 1993, 31, 181–244. [Google Scholar] [CrossRef]
  24. Xie, S.-P.; Annamalai, H.; Schott, F.A.; McCreary, J.P., Jr. Structure and mechanism of South Indian Ocean climate variability. J. Clim. 2002, 15, 864–878. [Google Scholar] [CrossRef]
  25. Hermes, J.; Reason, C.J.C. Annual cycle of the South Indian Ocean (Seychelles-Chagos) thermocline ridge in a regional ocean model. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
  26. Bleck, R. An oceanic general circulation model framed in Hybrid Isopycnic-Cartesian Coordinates. Ocean Model. 2002, 4, 55–88. [Google Scholar] [CrossRef]
  27. Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
  28. Hurlburt, H.E.; Metzger, E.J.; Sprintall, J.; Riedlinger, S.N.; Arnone, R.A.; Shinoda, T.; Xu, X. Circulation in the Philippine Archipelago simulated by 1/12° and 1/25° global HYCOM and EAS NCOM. Oceanography 2011, 24, 28–47. [Google Scholar] [CrossRef]
  29. Rosmond, T.E.; Teixeira, J.; Peng, M.; Hogan, T.F.; Pauley, R. Navy Operational Global Atmospheric Prediction System: Forcing for ocean models. Oceanography 2002, 15, 99–108. [Google Scholar] [CrossRef]
  30. Chi, N.-H.; Lien, R.-C.; D’Asaro, E.A.; Ma, B.B. The surface mixed layer heat budget from mooring observations in the Central Indian Ocean during Madden-Julian oscillation events. J. Geophys. Res. Ocean 2014, 119, 4638–4652. [Google Scholar] [CrossRef]
  31. McPhaden, M.J.; Meyers, G.; Ando, K.; Masumoto, Y.; Murty, V.S.N.; Ravichandran, M.; Syamsudin, F.; Vialard, J.; Yu, L.; Yu, W. RAMA: The Research Moored Array for African-Asian-Australian Monsoon Analysis and Prediction. Bull. Am. Meteorol. Soc. 2009, 90, 459–480. [Google Scholar] [CrossRef]
  32. JAMSTEC. R/V Mirai MR11-07 Cruise Report. 2011. Available online: http://www.godac.jamstec.go.jp/catalog/doc_catalog/metadataDisp/MR11-07_leg1-2_all (accessed on 15 September 2017).
  33. Jensen, T.G.; Shinoda, T.; Chen, S.; Flatau, M. Ocean response to CINDY/DYNAMO MJOs in air-sea coupled COAMPS. J. Meteorol. Soc. Jpn. 2015, 93A, 157–178. [Google Scholar] [CrossRef]
  34. Moore, D.W.; McCreary, J.P. Excitation of intermediate frequency equatorial waves at a western ocean boundary: With application to observations from the western Indian Ocean. J. Geophys. Res. 1990, 95, 5219–5231. [Google Scholar] [CrossRef]
  35. Han, W. Origins and dynamics of the 90-day and 30–60 day variations in the equatorial Indian Ocean. J. Phys. Oceanogr. 2005, 35, 708–728. [Google Scholar] [CrossRef]
  36. Yoshida, K. A theory of the Cromwell current (the equatorial undercurrent) and of equatorial upwelling—An interpretation in a similarity to a coastal circulation. J. Oceanogr. Soc. Jpn. 1959, 15, 159–170. [Google Scholar] [CrossRef]
  37. Moore, D.W.; Philander, S.G.H. Modeling of the tropical oceanic circulation. In The Sea; Wiley: New York, NY, USA, 1977; Volume 6. [Google Scholar]
  38. Vialard, J.; Shenoi, S.S.C.; McCreary, J.P.; Shankar, D.; Durand, F.; Fernando, V.; Shetye, S.R. Intraseasonal response of the northern Indian Ocean coastal waveguide to the Madden-Julian Oscillation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
  39. Knox, R.A.; Anderson, D.L.T. Recent advances in the study of the low-latitude ocean circulation. Prog. Oceanogr. 1985, 14, 259–317. [Google Scholar] [CrossRef]
  40. Schott, F.; McCreary, J.P. The monsoon circulation of the Indian Ocean. Prog. Oceanogr. 2001, 51, 1–123. [Google Scholar] [CrossRef]
  41. Lighthill, M.J. Dynamic responseof the Indian Ocean to onset of the Southwest Monsoon. Philos. Trans. R. Soc. Lond. 1969, 265, 45–92. [Google Scholar] [CrossRef]
  42. Hurlburt, H.E.; Thompson, J.D. A numerical model of the Somali Current. J. Phys. Oceanogr. 1976, 6, 646–664. [Google Scholar] [CrossRef]
  43. Luther, M.E.; O’Brien, J.J. A model of the seasonal circulation in the Arabian Sea forced by observed winds. Prog. Oceanogr. 1985, 1, 353–385. [Google Scholar] [CrossRef]
  44. Beal, L.M.; Hormann, V.; Lumpkin, R.; Foltz, G.R. The response of the surface circulation of the Arabian Sea to monsoonal forcing. J. Phys. Oceanogr. 2013, 43, 2008–2022. [Google Scholar] [CrossRef]
  45. Rydbeck, A.V.; Jensen, T.G.; Nyadjro, E. Intraseasonal sea surface warming in the western Indian Ocean by oceanic equatorial Rossby waves. Geophys. Res. Lett. 2017, 44, 4224–4232. [Google Scholar] [CrossRef]
  46. Rydbeck, A.V.; Jensen, T.G. Oceanic impetus for convective onset of the Madden-Julian Oscillation in the western Indian Ocean. J. Clim. 2017, 30, 4299–4316. [Google Scholar] [CrossRef]
  47. Yokoi, T.; Tozuka, T.; Yamagata, T. Seasonal variation of the Seychelles Dome. J. Clim. 2008, 21, 3740–3754. [Google Scholar] [CrossRef]
  48. Perigaud, C.; Delecluse, P. Annual sea level variations in the southern tropical Indian Ocean from Geosat and shallow-water simulations. J. Geophys. Res. 1992, 97, 20169–20178. [Google Scholar] [CrossRef]
  49. Seiki, A.; Katsumata, M.; Horii, T.; Hasegawa, T.; Richards, K.J.; Yoneyama, K.; Shirooka, R. Abrupt cooling associated with the oceanic Rossby wave and lateral advection during CINDY2011. J. Geophys. Res. 2013, 118, 5523–5535. [Google Scholar] [CrossRef]
  50. DeMott, C.A.; Klingaman, N.P.; Woolnough, S.J. Atmosphere-ocean coupled processes in the Madden-Julian oscillation. Rev. Geophys. 2015, 53, 1099–1154. [Google Scholar] [CrossRef]
  51. Halkides, D.J.; Waliser, D.E.; Lee, T.; Menemenlis, D.; Guan, B. Quantifying the processing controlling intraseasonal mixed-layer temperature variability in the tropical Indian Ocean. J. Geophys. Res. Oceans 2015, 120, 692–715. [Google Scholar] [CrossRef]
  52. Li, Y.; Han, W.; Shinoda, T.; Wang, C.; Ravichandran, M.; Wang, J.-W. Revisiting the Wintertime Intraseasonal SST Variability in the Tropical South Indian Ocean: Impact of the Ocean Interannual Variation. J. Phys. Oceanogr. 2014, 44, 1886–1907. [Google Scholar] [CrossRef]
Atmosphere 08 00171 g001 550
Figure 1. Time series of temperature profile from DYNAMO (Dynamics of the MJO) moorings at Equator, 79° E (upper left panel), 1.5° S, 79° E (upper right panel), from the HYCOM (Hybrid Coordinate Ocean Model) simulation at Equator, 79° E (lower left panel), and 1.5° S, 79° E (lower right panel). Solid (dashed) lines indicate 25° C (20° C) isotherm contours.
Figure 1. Time series of temperature profile from DYNAMO (Dynamics of the MJO) moorings at Equator, 79° E (upper left panel), 1.5° S, 79° E (upper right panel), from the HYCOM (Hybrid Coordinate Ocean Model) simulation at Equator, 79° E (lower left panel), and 1.5° S, 79° E (lower right panel). Solid (dashed) lines indicate 25° C (20° C) isotherm contours.
Atmosphere 08 00171 g001
Atmosphere 08 00171 g002 550
Figure 2. Time series of temperature profile from research moored array for African–Asian–Australian monsoon analysis and prediction (RAMA) mooring at Equator, 90° E (upper left panel), 1.5° S, 90° E (upper right panel), from the HYCOM simulation at Equator, 90° E (lower left panel), and 1.5° S, 79° E (lower right panel). Solid (dashed) lines indicate 25 °C (20 °C) isotherm contours.
Figure 2. Time series of temperature profile from research moored array for African–Asian–Australian monsoon analysis and prediction (RAMA) mooring at Equator, 90° E (upper left panel), 1.5° S, 90° E (upper right panel), from the HYCOM simulation at Equator, 90° E (lower left panel), and 1.5° S, 79° E (lower right panel). Solid (dashed) lines indicate 25 °C (20 °C) isotherm contours.
Atmosphere 08 00171 g002
Atmosphere 08 00171 g003 550
Figure 3. Upper panel: Time series of surface zonal velocity (m/s) at Equator, 80.5° E from the RAMA mooring (blue line) and HYCOM simulation (green line). Lower panel: Time series of surface zonal velocity (m/s) at Equator, 79° E from the DYNAMO mooring (red line) and HYCOM simulation (green line). The model velocity of the uppermost layer (1 m thickness) and the velocity measurements at the shallowest depth from DYNAMO (4 m) and RAMA (10 m) moorings are used as the surface velocity.
Figure 3. Upper panel: Time series of surface zonal velocity (m/s) at Equator, 80.5° E from the RAMA mooring (blue line) and HYCOM simulation (green line). Lower panel: Time series of surface zonal velocity (m/s) at Equator, 79° E from the DYNAMO mooring (red line) and HYCOM simulation (green line). The model velocity of the uppermost layer (1 m thickness) and the velocity measurements at the shallowest depth from DYNAMO (4 m) and RAMA (10 m) moorings are used as the surface velocity.
Atmosphere 08 00171 g003
Atmosphere 08 00171 g004 550
Figure 4. Temperature along 78.5° E (top panels and bottom panels), and 80.5° E–78.1° E (middle panels) from observations (left panels) and model simulations (right panels) for the periods of 9–16 September 2011 (top panels), 28–29 November 2011 (middle panels), and 19–22 January 2012 (bottom panels).
Figure 4. Temperature along 78.5° E (top panels and bottom panels), and 80.5° E–78.1° E (middle panels) from observations (left panels) and model simulations (right panels) for the periods of 9–16 September 2011 (top panels), 28–29 November 2011 (middle panels), and 19–22 January 2012 (bottom panels).
Atmosphere 08 00171 g004
Atmosphere 08 00171 g005 550
Figure 5. Longitude-time diagram of sea surface height (SSH) anomaly (cm) averaged over 1° N–1° S from satellite observations (left panel), from HYCOM simulation (second panel from the left), zonal velocity anomaly (m/s) from HYCOM simulation (third panel from the left), and surface zonal wind anomaly (m/s) used for the HYCOM simulation (right panel). White lines indicate the phase speed of 2.8 m/s. SSH and zonal velocity data are averaged on a 1° × 1° grid, and a 9-point smoothing is applied in the longitude-time plane.
Figure 5. Longitude-time diagram of sea surface height (SSH) anomaly (cm) averaged over 1° N–1° S from satellite observations (left panel), from HYCOM simulation (second panel from the left), zonal velocity anomaly (m/s) from HYCOM simulation (third panel from the left), and surface zonal wind anomaly (m/s) used for the HYCOM simulation (right panel). White lines indicate the phase speed of 2.8 m/s. SSH and zonal velocity data are averaged on a 1° × 1° grid, and a 9-point smoothing is applied in the longitude-time plane.
Atmosphere 08 00171 g005
Atmosphere 08 00171 g006 550
Figure 6. Left panel: Surface velocity (arrow) and SSH (cm; shading) anomalies during 26 December 2011–5 January 2012 from the HYCOM simulation. Right panel: Same as left panel except for 20 °C isotherm depth anomaly (m; shading).
Figure 6. Left panel: Surface velocity (arrow) and SSH (cm; shading) anomalies during 26 December 2011–5 January 2012 from the HYCOM simulation. Right panel: Same as left panel except for 20 °C isotherm depth anomaly (m; shading).
Atmosphere 08 00171 g006
Atmosphere 08 00171 g007 550
Figure 7. (a) Longitude time diagram of SSH (cm) at 1° N–1° S (left panel) and 3.5° S–4.5° S (right panel) from the satellite altimeter data. The horizontal axis (longitude) is flipped in the right panel. The white lines of the left (right) panel indicate the phase speed 2.8 (0.88) m/s. (b) Same as (a) except from the HYCOM simulation. SSH data are averaged on a 1° × 1° grid, and a 9-point smoothing is applied in the longitude-time plane.
Figure 7. (a) Longitude time diagram of SSH (cm) at 1° N–1° S (left panel) and 3.5° S–4.5° S (right panel) from the satellite altimeter data. The horizontal axis (longitude) is flipped in the right panel. The white lines of the left (right) panel indicate the phase speed 2.8 (0.88) m/s. (b) Same as (a) except from the HYCOM simulation. SSH data are averaged on a 1° × 1° grid, and a 9-point smoothing is applied in the longitude-time plane.
Atmosphere 08 00171 g007
Atmosphere 08 00171 g008 550
Figure 8. Time series of temperature profile from RAMA mooring at 4° S, 80.5° E (left panel) and HYCOM simulation (right panel).
Figure 8. Time series of temperature profile from RAMA mooring at 4° S, 80.5° E (left panel) and HYCOM simulation (right panel).
Atmosphere 08 00171 g008
Atmosphere 08 00171 g009 550
Figure 9. Surface currents (m/s; arrows) and SSH (cm; shading) anomalies during 20 February–1 March 2012 (upper panel), 2–11 March (middle panel), and 12–21 March (bottom panel) from the HYCOM simulation.
Figure 9. Surface currents (m/s; arrows) and SSH (cm; shading) anomalies during 20 February–1 March 2012 (upper panel), 2–11 March (middle panel), and 12–21 March (bottom panel) from the HYCOM simulation.
Atmosphere 08 00171 g009
Atmosphere 08 00171 g010 550
Figure 10. Alongshore velocity (m/s) section along the white line in Figure 9 during 11 February–1 March 2012 (left panel), 2–21 March (middle panel), and the difference between the left and middle panels (right panel) from the HYCOM simulation. The positive values indicate northeastward current component perpendicular to the white line.
Figure 10. Alongshore velocity (m/s) section along the white line in Figure 9 during 11 February–1 March 2012 (left panel), 2–21 March (middle panel), and the difference between the left and middle panels (right panel) from the HYCOM simulation. The positive values indicate northeastward current component perpendicular to the white line.
Atmosphere 08 00171 g010
Atmosphere 08 00171 g011 550
Figure 11. Surface current (m/s) and SSH (cm) from the model simulation for the period 11 February–1 March 2012 (left panel) and 2–21 March 2012 (right panel).
Figure 11. Surface current (m/s) and SSH (cm) from the model simulation for the period 11 February–1 March 2012 (left panel) and 2–21 March 2012 (right panel).
Atmosphere 08 00171 g011
Atmosphere 08 00171 g012 550
Figure 12. Time series of temperature profile at 4° S, 55° E–65° E from the HYCOM simulation. Solid (dashed) lines indicate 20 °C (25 °C) isotherm contours.
Figure 12. Time series of temperature profile at 4° S, 55° E–65° E from the HYCOM simulation. Solid (dashed) lines indicate 20 °C (25 °C) isotherm contours.
Atmosphere 08 00171 g012
Atmosphere 08 00171 g013 550
Figure 13. Temperature along 60° E–65° E for the period 1–31 January (left panel) and 18 February–8 March (right panel) from model simulations. Solid (dashed) lines indicate 20 °C (25 °C) isotherm contours.
Figure 13. Temperature along 60° E–65° E for the period 1–31 January (left panel) and 18 February–8 March (right panel) from model simulations. Solid (dashed) lines indicate 20 °C (25 °C) isotherm contours.
Atmosphere 08 00171 g013
Atmosphere 08 00171 g014 550
Figure 14. Average SST (°C; shading) and SSH (cm; contour) anomalies during 18 February–7 March 2012. Only positive values of SSH contour are shown, with the contour interval of 2 cm starting from 1 cm.
Figure 14. Average SST (°C; shading) and SSH (cm; contour) anomalies during 18 February–7 March 2012. Only positive values of SSH contour are shown, with the contour interval of 2 cm starting from 1 cm.
Atmosphere 08 00171 g014
Atmosphere 08 00171 g015 550
Figure 15. Left panel: Average SST (sea surface temperatures) (°C; shading) and surface current anomaly (m/s; arrows) during 18 February–7 March 2012. Right panel: Same as the upper panel except for net surface heat flux anomaly (W/m2) used for the HYCOM simulation.
Figure 15. Left panel: Average SST (sea surface temperatures) (°C; shading) and surface current anomaly (m/s; arrows) during 18 February–7 March 2012. Right panel: Same as the upper panel except for net surface heat flux anomaly (W/m2) used for the HYCOM simulation.
Atmosphere 08 00171 g015
Atmosphere 08 00171 g016 550
Figure 16. (a) Longitude-time diagram of SSH from altimeter data averaged over 8° S–12° S. The white line indicates the location of DYNAMO observations (78.5° E). (b) Longitude-time diagram of meridional velocity averaged over 0–50 m depth along 79° E. (c) Same as (a) except for the averaging latitudes 5.5° S–6.5° S. (d) Ekman pumping velocity (×10−5 m/s; shading) and wind stress (N/m2; arrows) for the period 16–31 December. Positive values indicate upward velocity.
Figure 16. (a) Longitude-time diagram of SSH from altimeter data averaged over 8° S–12° S. The white line indicates the location of DYNAMO observations (78.5° E). (b) Longitude-time diagram of meridional velocity averaged over 0–50 m depth along 79° E. (c) Same as (a) except for the averaging latitudes 5.5° S–6.5° S. (d) Ekman pumping velocity (×10−5 m/s; shading) and wind stress (N/m2; arrows) for the period 16–31 December. Positive values indicate upward velocity.
Atmosphere 08 00171 g016

Share and Cite

MDPI and ACS Style

Shinoda, T.; Han, W.; Zamudio, L.; Lien, R.-C.; Katsumata, M. Remote Ocean Response to the Madden–Julian Oscillation during the DYNAMO Field Campaign: Impact on Somali Current System and the Seychelles–Chagos Thermocline Ridge. Atmosphere 2017, 8, 171. https://doi.org/10.3390/atmos8090171

AMA Style

Shinoda T, Han W, Zamudio L, Lien R-C, Katsumata M. Remote Ocean Response to the Madden–Julian Oscillation during the DYNAMO Field Campaign: Impact on Somali Current System and the Seychelles–Chagos Thermocline Ridge. Atmosphere. 2017; 8(9):171. https://doi.org/10.3390/atmos8090171

Chicago/Turabian Style

Shinoda, Toshiaki, Weiqing Han, Luis Zamudio, Ren-Chieh Lien, and Masaki Katsumata. 2017. "Remote Ocean Response to the Madden–Julian Oscillation during the DYNAMO Field Campaign: Impact on Somali Current System and the Seychelles–Chagos Thermocline Ridge" Atmosphere 8, no. 9: 171. https://doi.org/10.3390/atmos8090171

APA Style

Shinoda, T., Han, W., Zamudio, L., Lien, R.-C., & Katsumata, M. (2017). Remote Ocean Response to the Madden–Julian Oscillation during the DYNAMO Field Campaign: Impact on Somali Current System and the Seychelles–Chagos Thermocline Ridge. Atmosphere, 8(9), 171. https://doi.org/10.3390/atmos8090171

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop