Abstract
Many recent studies have characterized the Madden–Julian Oscillation (MJO) as a moisture mode, suggesting that its amplification and eastward propagation result from processes that build up moisture to the east of the MJO’s convective center, including frictionally driven boundary layer convergence, surface fluxes, and shallow convection. Discussions of MJO moistening under this theory often implicitly assume an Eulerian framework; i.e., that local increases in moisture result from physical processes acting in the same location as the moistening is observed. In this study, the authors examine MJO moistening in a Lagrangian framework using a model that simulates atmospheric circulations by predicting the motions of individual air parcels. Back trajectories are presented for parcels in moist convecting regions of the MJO, and the effects of different physical processes on their moisture and moist static energy budgets are quantified. The Lagrangian MJO simulations suggest that much of the low-level moist air in heavily precipitating regions of the MJO arrives via the mid troposphere, coming from nearby equatorial regions, where it has been moistened largely by convective processes. Consequently, a thorough understanding of MJO moistening requires knowledge of the origin of the moist air and information about remote moisture sources.
1. Introduction
The Madden–Julian Oscillation (MJO) [1,2,3,4] is a planetary-scale weather disturbance that propagates slowly eastward over the equatorial Indian and west-Pacific Oceans. It is the dominant mode of intraseasonal variability in the tropics [5], is coupled to Asian, Australian, and North American monsoons [6,7], and modulates tropical cyclogenesis in all tropical ocean basins [8,9]. Despite decades of study, scientists have not reached a consensus on the MJO’s most fundamental dynamics, with many physical and dynamical processes postulated to be part of its mechanism(s) including moisture convergence by atmospheric waves [10,11,12] surface fluxes [13,14] radiation [15], extratropical influences [16], and frictionally driven boundary layer convergence to the east of the MJO’s convective center [17,18]. Moreover, the MJO has been notoriously difficult to simulate with climate models [19] with even recent climate simulations producing MJOs that are too weak, lack sufficient eastward propagation, and/or have the wrong period [20].
In recent years, one popular way of thinking about the MJO is as a moisture mode [14,21] with many studies seeking to understand its mechanism(s) of moistening and drying [22,23,24]. The moisture mode concept is consistent with the observation that high rain rates are correlated with regions of high column integrated moisture in the tropics in general [25,26]. Moreover, several studies have noted a relationship between a model’s ability to simulate the MJO and its represention of moist convection’s interaction with environmental moisture, e.g., [22,27,28]. There is a growing consensus that the low-level Rossby gyres that develop in response to the MJO’s heat source [29,30,31] advect off-equatorial dry air into the western side of the MJO, which shuts down moist convection, and enhances the MJO’s eastward propagation [12,24,32]. However, there is debate about the mechanism(s) of the moistening on the eastern side of the MJO’s convective center. Some studies point to the moistening effects of shallow convection that is frequently observed to the east of the MJO’s deep convection [31,33,34,35], which transports boundary layer moisture upward, and imports moist static energy (and moisture) from remote locations by driving low-level convergence and mid-level divergence through its bottom heavy heating profile [35,36,37,38]. Other studies emphasize the importance of boundary layer processes for moistening, including frictional convergence in the region of low pressure to the east of the MJO’s convective center [17,18], and enhanced evaporation in regions of enhanced easterlies to the east of the MJO [39,40], although observations do not fully support this last theory [41]. Another factor that potentially contributes to the moistening to the east of the MJO’s convection is a weakening of meridional winds above the boundary layer that import dry air from off-equatorial locations [12,42].
One especially puzzling aspect of the MJO is that, in principle, it should be straightforward to simulate most if not all of its proposed mechanisms in a conventional climate model [43]. For example, such models have sophisticated radiation schemes, can model frictional boundary layer convergence, variations in surface fluxes due to winds, and the large-scale circulations that develop in response to parameterized convective heatings. While conventional climate models can be tuned to generate slow-moving, planetary scale equatorial convective systems, which mimic the MJO at least in horizontal structure and propagation, such tuning is often detrimental to the model’s basic state [44]. Clearly, if it were easy to tune for a strong and realistic MJO and a good basic state, MJO representations would be better than they are at this point in simulations used to study climate change [20].
In this study, we use a recently developed Lagrangian atmospheric model (LAM) to study the mechanism(s) of moistening and drying in the MJO. In contrast to the Eulerian modeling framework, realistic MJOs are surprisingly easy to simulate in a Lagrangian one, with weak MJOs present in the first set of LAM tropical channel simulations published [45], and strong MJOs with realistic vertical and horizontal structures appearing in subsequent LAM aquaplanet runs [12,42,46]. Here, we use an improved version of the LAM that includes continents, variable surface topography, as well as modified physical parameterizations. These features make simulated MJOs even more realistic than those in previous studies, and also contribute improvements to the model’s basic state. We take advantage of two key properties of the LAM: (1) the ability to identify a given air parcel’s position at all previous times with no extra computations or interpolation; and (2) the capacity to completely partition a parcel’s moisture and moist static energy budget with minimal numerical errors due only to floating point round off. We address two questions: (1) where does the moist air in the lower atmosphere in regions of heavy rainfall in MJOs originate; and (2) what physical processes give this air high moisture and high moist static energy?
This paper is organized as follows: Section 2 describes the Lagrangian atmospheric model; Section 3 describes our key modeling results: (1) the global LAM’s simulation of the atmosphere’s basic state and tropical convective variability; (2) composite simulated structure and evolution of the MJO; and (3) case studies of two kinds of MJOs in which in which origins of moist air in precipitating regions are determined; Section 4 discusses our results in light of related studies; and Section 5 highlights our main conclusions.
2. Experiments
2.1. Lagrangian Atmospheric Model (LAM)
The LAM simulates atmospheric motions by tracking individual mass elements referred to as “air parcels”. Each parcel is assumed to have a horizontal mass distribution that is fixed in the parcel’s frame of reference (Figure 1a). Horizontal accelerations are predicted by calculating the pressure force on each parcel with a viscosity term included to account for unresolved momentum transport between parcels. Non-convective vertical motions are determined by mass continuity; i.e., a parcel moves up or down when it slides over irregular bottom topography and/or other parcels. Typically, parcels with higher potential temperatures lie above those with lower potential temperatures (Figure 1a). The LAM is based on a numerical method that was first applied to lakes and oceans (see review by [46]), and later modified to handle compressible parcels by [45]. For more details on the model’s numerics the reader is referred to these two studies.
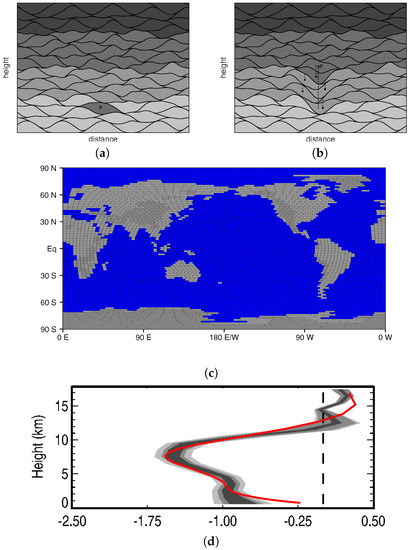
Figure 1.
The Lagrangian atmospheric model. (a,b) conforming parcel concept and convective parameterization (from [12]). Local heating causes parcel P to become warmer than its neighbors (darker shades denote higher potential temperatures), and the convective parameterization raises P to its level of neutral buoyancy. Dashed lines trace paths of parcel centers with significant vertical displacements. (c) the new spherical land and ocean geometry. (d) net radiative heating (K/day) over the West Pacific Warm Pool for the radiation scheme (red) compared with observationally based estimates from [48].
One unique feature of the LAM is its convective parameterization, which is referred to as “Lagrangian overturning” (Figure 1a,b). When local heating causes a given air parcel to become warmer than its neighbors (Figure 1a), it is moved vertically so that stable and/or neutral stratification is restored (Figure 1b), thereby mimicing the vertical transport by convective plumes in nature. In moist regions, condensation continuously heats rising parcels, allowing for deep convective updrafts. Note also that when a warm parcel rises, nearby parcels subside (Figure 1b), which is also true of air around convective updrafts in nature. A portion of falling precipitation evaporates into parcels it passes through on its way to the ground [42]. Note that parcels are much larger than convective cells in nature, so that mass transports by individual parcels model the collective effects of many updrafts or downdrafts [42].
One new feature of the LAM is a global spherical geometry that includes continents with variable topography (Figure 1c). The global domain is divided into boxes that have approximately constant width in actual distance (i.e., there are fewer longitudinal divisions at higher latitudes). This grid is used for the purposes of column physics and calculating the acceleration of parcels due to pressure. Within a parcel radius of the poles, a spherical projection is used for calculating parcel motions so there are no singularities; elsewhere standard latitude and longitude coordinates are used. The LAM has a simple land surface model, with a single layer of ground with a 25 mm water-holding capacity, a heat capacity equivalent to that of 0.1 m of water, and a constant albedo.
The radiation scheme evolved from the idealized method of [47], but has been modified to include moisture-radiation interactions [42], and has been extensively tuned to approximate observationally based estimates of net radiative forcing over the western Pacific warm pool (Figure 1d) [48]. The scheme does not include the radiative affects of clouds. Other model parameters such as the mixing of convective updrafts with their environment and evaporation rates (Table 1; mixing and evaporation rates have units ) have been tuned so that the model has realistic profiles of temperature and moisture in the tropics (e.g., see Figure 13 from [42]) as well as adequate representations of global precipitation, zonal winds, and tropical convective systems for a model of its complexity. For more details on the LAM’s column physics and surface fluxes, the reader is referred to [42].

Table 1.
Lagrangian model parameters.
The LAM is run in a configuration similar to that of the Atmospheric Model Intercomparision Project (AMIP) [49], with prescribed sea surface temperatures (SSTs), but predicted land surface temperatures. Results from two simulations are presented in this study: a coarser-resolution run forced with SSTs observed from 1998–2009, and a shorter duration finer-resolution run for the period 1998–2000 (Table 1). The longer duration of the the coarser-resolution run is used to establish a model climatology and the finer-resolution run is used to study moisture pathways MJO case studies. While it is difficult to precisely define the equivalent Eulerian resolution of the LAM [42], and the coarser-resolution run has an approximate low-latitude resolution of 1.88/3.75 degrees latitude/longitude, and the finer-resolution run has an approximate resolution of 1.33/2.67 degrees latitude/longitude.
2.2. Rainfall Observations
Observations from the Global Precipitation Climatology Project [50] are used evaluate the rainfall climatology of the LAM as well as its tropical convective variability. Annual average rainfall is calculated on a grid with a one degree resolution in both latitude and longitude for the years 1998–2009. Wavenumber frequency spectra are calculated for the same data set following the method of [5].
3. Results
3.1. LAM Basic State and Tropical Convective Variability
3.1.1. Average Global Circulation
While the focus of this paper and previous work involving the LAM has been on tropical convective systems, we begin by briefly reviewing several aspects of the model’s simulation of the atmosphere’s time-average global state, since this is the first study conducted with the global version of the LAM that includes continents.
The LAM’s annual average rainfall (Figure 2a) exhibits many features seen in observationally based estimates (e.g., Figure 2b) including heavy rainfall over the warm waters of the Indian and west Pacific Oceans and the Amazon basin, an intertropical convergence zone (ITCZ) that encircles the tropics and lies to the north of the equator in the east Pacific and Atlantic Oceans, prominent storm tracks to the east of North America and Asia, and dry regions over Northern Africa, continental Australia, and to the west of continents in the subtropics. Similarly, the gross features of the zonal mean zonal wind field are captured (Figure 2c,d), with zonal jets at mid latitudes peaking around 25–30 m/s near 200 hPa, and low-level easterlies in the tropics. There is a bias towards stronger than observed easterlies near the surface at low latitudes (Figure 2c), and a westerly bias at upper-levels in the tropics, the causes of which are not known at this time.
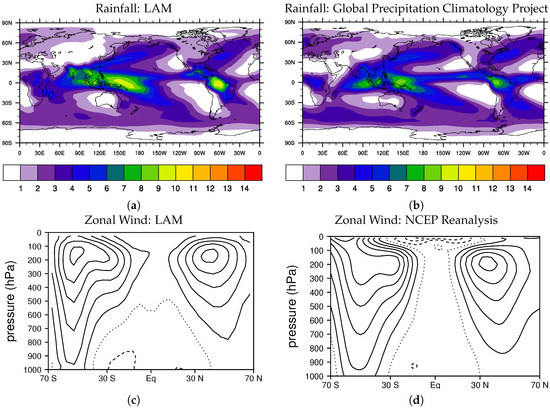
Figure 2.
Annual average (a,b) rainfall and (c,d) zonal wind. Panels (a,c) show fields simulated with the Lagrangian Atmospheric Model, and panels (b,d) are based on observations. Rainfall is shaded with a 1 mm/day increment, and zonal wind is contoured with a 5 m/s interval with the zero contour dotted and negative contours dashed.
There are some biases in the simulated precipitation field due in part to the use of a constant land surface albedo, such as too much rainfall over Saudia Arabia, and lower than observed rainfall over the Atlantic Ocean (Figure 2a). However, considering the idealized nature of the LAM’s physical parameterizations, and its radically different numerics and convective scheme, which have been tested and refined much less than those used in conventional climate models, the global basic state is more realistic than we expected at this stage. Indeed, the annual precipitation field (Figure 2a) has a pattern correlation with observations that is already competitive with climate models used in the fifth phase of the coupled model intercomparison project (CMIP5) [51]). While some work needs to be done to understand and remove the biases in the zonal wind field, it is sufficiently realistic at this time for simulating the MJO, which is the main focus of this study.
The LAM reproduces the observed band of weak low-level westerlies near the equator over the Indo-Pacific warm pool, which shifts southward during the boreal winter and extends eastward to near the Dateline at this time, and which has been theorized to be important for the development of the MJO (Figure 3; compare with Figure 7 from [52]).
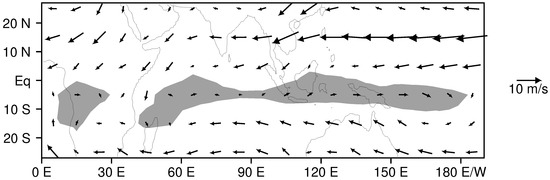
Figure 3.
Average 850 hPa flow for December through March for the lower-resolution LAM simulation with regions of westerlies shaded light gray.
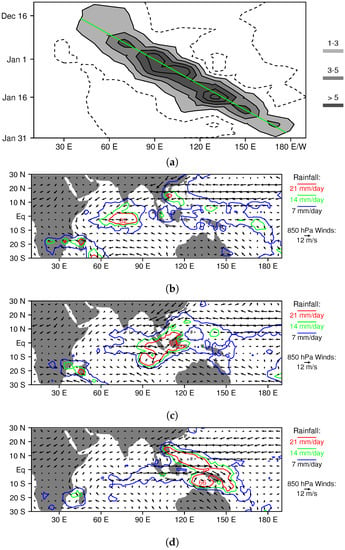
Figure 7.
Horizontal structure and propagation of the December 1998/January 1999 MJO simulated with the higher-resolution version of the LAM. (a) time series of time-filtered equatorial (15 S–15 N) rainfall. (b–d) rainfall and 850 hPa winds for 27 December, 7 January, and 17 January, respectively.
3.1.2. Tropical Convective Variability
In order to examine the LAM’s tropical convective variability, we constructed wavenumber frequency diagrams of equatorial rainfall for symmetric and antisymmetric components. We follow the methodogy of [5], dividing the raw spectra by a smoothed background spectra, so that dispersion signals of convectively coupled equatorial waves are easy to discern. The simulated spectra (Figure 4a,c) contain all of the major wave types that are present in observations from the Global Precipitation Climatology Project [50] (Figure 4b,d) including Kelvin waves, equatorial Rossby waves, mixed Rossby-gravity waves, and eastward and westward inertio-gravity waves. The signal of the MJO is also well represented with a prominent peak for eastward wave numbers 1–4 in the MJO frequency range, a near zero change in frequency with respect to zonal wavenumber [53], and the spectral gap between the MJO and Rossby wave signals (compare Figure 4a,b). There is also a spectral gap between the MJO and Kelvin wave signals, but it occurs at a higher wavenumber in the LAM than it does in the observations (Figure 4a,b). To make it easy for the reader to compare the LAM’s spectra with those for conventional climate models, we have used the same contour interval and shading scheme in Figure 4 as used by [20] for climate simulations. Overall, the LAM’s signal of convectively coupled equatorial waves and the MJO compares favorably with those in other models. Like most models, raw spectral power drops off too rapidly at higher wavenumbers and frequencies (not shown), but tests show that this is at least partly a resolution issue. Moreover, since the MJO is a low frequency and low wavenumber phenomena, its absolute amplitude is actually quite realistic, as is discussed further in the following section.
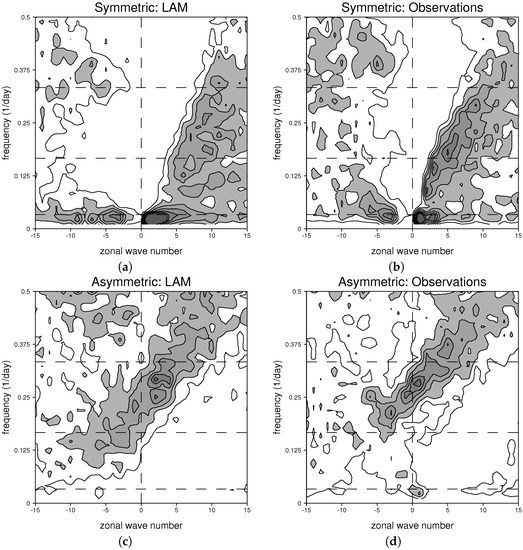
Figure 4.
(a,c) simulated and (b,d) observed wavenumber frequency spectra, each divided by a smoothed background spectra (following [5]).
3.1.3. Simulated MJO Structure
Before we talk about the mechanisms of moistening and drying in simulated MJOs, we establish that the LAM produces realistic MJO structure. Following the method of [12], we construct a composite LAM MJO by tracking the MJO precipition signal, and examining vertical and horizontal structure in the frame of reference of the convective envelope for three stages in its life cycle: developing, mature, and dissipating (illustrated in Figure 5b). Note that we elected to compare with the composite MJO from [12] for two reasons: (1) it is based purely on observations with no contribution from a model forecast; and (2) we believe that the key to understanding the MJO is explaining the development and movement of its convective envelope.
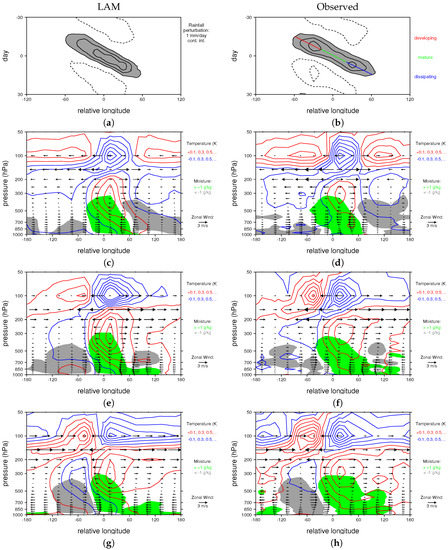
Figure 5.
Composite Madden Julian Oscillation for the LAM (left panels) and observations (right panels, adapted from [12]). (a,b) rainfall times series (1 mm/day contour interval, perturbations greater than 1 mm/day are shaded gray, and negative contours are dashed). Composite vertical structures for (c,d) developing, (e,f) mature, and (g,h) dissipating stages. Green (gray) shading denotes a positive (negative) moisture anomaly of greater (less) than 1 (−1) g/kg. Temperature is contoured with red (blue) contours indicating positive (negative) perturbations. Vectors illustrate the zonal flow.
Figure 5 compares simulated (left panels) and observed (right panels) composite MJO structure. In both the model and in nature, the MJO convective envelope travels about one-third of the way around the world at a speed of roughly 5 m/s, as is apparent in the composite time series of equatorial rainfall (Figure 5a,b). Peak amplitudes are the same in each case (between 3 and 4 mm/day), although the observed MJO exhibits a double peak owing to reduced precipitation anomalies over the Maritime Continent that is not present in the LAM MJO. We suspect that the simplified land surface model as well as the relatively low model resolution inhibit the LAM’s ability to capture that effects of islands, which have been hypothesized to cause the minimum in MJO convection over the Maritime continent [54] . Note that achieving a realistic eastward propagation for the MJO is not trivial; Hung et al. [20] found that only one or two out of 20 CMIP5 models tested properly simulated the MJO’s eastward propragation. Eastward propagating negative precipitation anomalies precede and trail the MJO’s convective signal in both the model and observations (Figure 5a,b).
The LAM also captures the evolution of key features of the MJO’s vertical structure. During the developing stage (Figure 5c,d), there is a tilted moisture anomaly near the MJO’s convective center (located at longitude 0 by construction), which extends about 60 degrees eastward in the lower troposphere. By the mature stage, the low-level moisture anomaly has spread more than 120 degrees east of the convective center at very low-levels underneath a mid-level dry anomaly (Figure 5e,f). By the dissipating stage dry anomalies have disappeared to the east of the convective center, but they have deepened and intensified on the west side of the MJO (Figure 5g,h). There is a mid- to upper-tropospheric warm anomaly that peaks near 300 hPa just east of the MJO’s convective center, which lies beneath a cool anomaly near the tropopause, both of which expand eastward throughout the convective life cycle (Figure 5c–h). By the dissipating stage, the warm anomaly wraps all the way around the world, rising to join a warm anomaly near the tropopause, which is located just west of the MJO’s convective center (Figure 5g,h). The model also reproduces the evolution of the observed zonal wind field, with low-level (upper-level) easterlies (westerlies) that expand eastward from the convective center throughout the life cycle, and low-level (upper-level) westerlies (easterlies) that persist to the west of the convective center (Figure 5c–h).
Figure 6 shows the composite horizontal structure of simulated and observed MJOs throughout the convective life cycle, including deep-tropospheric shear and temperature perturbations. During the developing stage, there is an elongated equatorial cool anomaly lying to the west of the MJO colocated with upper level easterly shear in both the LAM and in nature (Figure 6a,b). As noted by [12], this is the signature of a first baroclinic Kelvin wave, which likely plays a role in the MJO’s convective initiation, by contributing large-scale upward motion where rainfall is developing. By the Mature stage, this cool anomaly has disappeared, and a warm anomaly accompanied by upper-level westerly shear is growing eastward from the region of enhanced convection (shaded gray in Figure 6c,d). Off-equatorial anticyclonic flow is also apparent to the west of the MJO convective center at this time. By the dissipating stage, the warm Kelvin wave has propagated most of the way around the world, and it is contributing large-scale subsidence in the dry region to the west of the MJO convective center in both the model and in nature (Figure 6e,f).
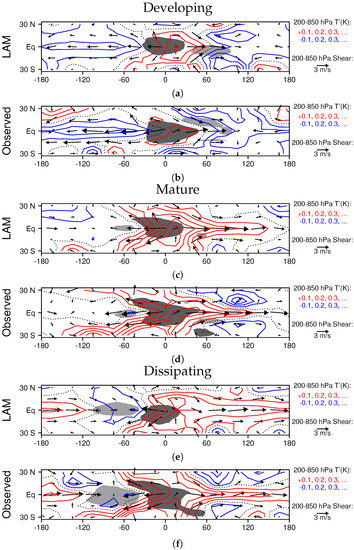
Figure 6.
Composite MJO horizontal structure for (a,b) developing, (c,d) mature, and (e,f) dissipating stages. Dark shading indicates rainfall perturbations of greater that 1 mm/day, and light shading indicates perturbations of less than 1 mm/day.
As noted by [12], while the Matsuno–Gill model of the atmospheric response to an equatorial heat source [29,30,31,55] resembles the mature MJO structure shown in Figure 6c,d, it does not capture the evolution of large scale features seen in the observations and the LAM (Figure 6a–f). In particular, the cool Kelvin wave that helps to initiate MJO convection (Figure 6a,b) likely forms in response to the negative convective anomaly that precedes the MJO (Figure 5a,b), and the elongated warm Kelvin wave that grows eastward from the MJO’s convective center is not in a steady state (as it is in the Matsuno–Gill model owing to an unrealistically high damping coefficient). For now, we postpone a full discussion of the the implications of these results for the dynamics of the MJO, and note only that LAM captures the observed evolution of both vertical structure and large scale wave features in the MJO, suggesting that it has the same mechanism(s) as are operating in nature.
3.2. Moisture Transport in Higher-Resolution Case Studies
Since the LAM is not yet coded to run in parallel, we have not conducted many higher resolution runs to this point, but we have carried out a few such simulations to test the sensitivity of MJO structure to resolution and examine smaller-scale features embedded in the MJO. In this section, we examine moisture transport in two MJOs simulated with the higher resolution version of the LAM. We begin by studying a classical boreal winter MJO, with convection that remains concentrated near the equator throughout its lifetime, and which maintains a strong convective signal from the western Indian Ocean to the dateline. The second case, which forms in the boreal spring, generates twin cyclones over the Indian Ocean, and has a weaker signal of eastward propagation after this point.
3.2.1. Boreal Winter MJO
As noted by [56], MJO convective complexes typically propagate eastward near the equator in the boreal winter and spring (see their Figure 6a). The December 1998/January 1999 case simulated with the higher-resolution version of the LAM is no exception. Average equatorial rainfall perturbations of greater than 1 mm/day originate in the western Indian Ocean in mid December, and propagate steadily eastward until late January (Figure 7a). Low-level westerly winds develop behind the convective complex (Figure 7b–d), and they become especially strong when convection is over the Western Pacific, which is not uncommon for a boreal winter MJO [33]. Throughout most of the lifetime of this MJO, there is a broad fetch of low-level easterlies north of the equator over the Pacific Ocean (Figure 7b–d).
In order to understand the origins of moist air in the heavily raining region over the western Pacific, we compute back trajectories for parcels located between 153 and 157 E, 3 and 7 S and 700 and 1000 hPa on 20 January. This region is shown as a large aqua box in each panel of Figure 8, and it was selected because it is a region of heavy rainfall, which is located near the center of the location of COARE sounding arrays (Coupled Ocean Atmosphere Response Experiment; [57]). The 17 January locations of the parcels that end up in this region are marked with small aqua boxes in Figure 8. Almost all of them are in the mid-troposphere on 17 January (Figure 8b), with most located to the west of 140 E (Figure 8a,b). The mean trajectory of these parcels, which is denoted with a long black arrow in each panel of Figure 8 with its tip in the large aqua box, is eastward/southeastward and downward. It may seem surprising that the mean parcel trajectory into the aqua box points downward, considering it lies in a region with heavy rainfall, which has a mean upward motion. This happens because we are selectively sampling parcels that are not in deep convective updrafts during this time by chosing those that end up in the lower troposphere; parcels in deep convective updrafts that contribute most of the upward motion rapidly ascend into the upper troposphere.
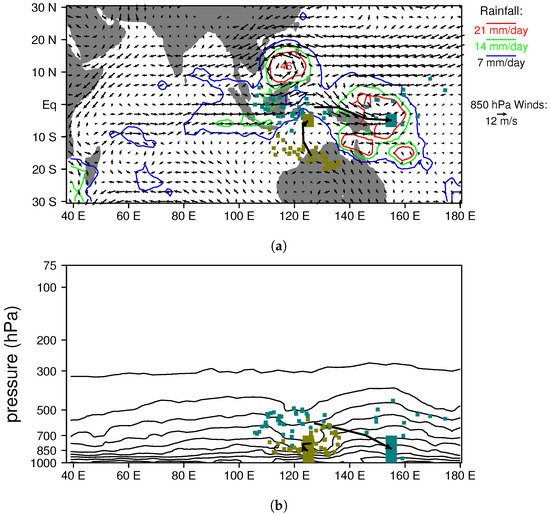
Figure 8.
Back trajectory analysis of moist (aqua) and dry (gold) regions in the December 1998/January 1999 MJO simulated with the higher-resolution version of the LAM. (a) 20 January rainfall and 850-hPa flow. All parcels centered within the large aqua and gold boxes on 20 January are tracked backwards in time three days, and their positions on 17 January are marked with small colored boxes. The mean parcel path over the three days for each region is shown with a thick black line. Average specific humidity over 3–7 S is contoured in panel (b) with a 2 g/kg contour interval. Note that, in the moist region with heavy rainfall (large aqua box), most parcels have come from mid-levels in the atmosphere over the Maritime Continent, whereas, in the dry region with light rain (large gold box), parcels have come from the lower troposphere near or over northwest Australia.
We also performed the same kind of analyis for a region with light rainfall located between 123 and 127 E, 3 and 7 S, and 700 and 1000 hPa, which is shaded gold in Figure 8. Most of the parcels that end up in this region are located in the lower troposphere near the northwest coast of Australia three days earlier (see small golden boxes in Figure 8). Figure 8b also shows contours of specific humidity for 3–7 S on 20 January. Moisture contours dip downward, indicating dryness in the vicinity of the gold box, and bulge upward, indicating a moist column in the vicinity of the aqua box. This result is consistent with the observation of [26] that high rain rates in the tropics are correlated with high column water contents, and the concept of the MJO as a moisture mode [14,21].
However, why is the atmosphere so moist in the vicinity of the aqua box, and so dry near the gold box on 20 January? Figure 9a,c,e address this question by showing the moisture budget for the mean parcel trajectory into each region (i.e., the average moisture tendency and budget contributions for the moist and dry collections of parcels). The moist sample starts only slightly moister than the dry sample on January 17, but has a greater increase in moisture over the three-day period (Figure 9a). Examining the contribution of individual budget terms reveals that, while there are greater surface fluxes for the dry parcels owing to their proximity to the ocean (Figure 9e), this is more than compensated by the large evaporation into parcels entering the moist region (Figure 9c). In other words, the moist sample traverses the mid levels of the atmosphere in a region with active convection, and the evaporation of falling rain moistens these parcels as they descend into the aqua box, whereas the dry sample flows through a region with little rainfall, and the parcels moisten more slowly. The amount of moistening from mixing (which is the physical process in our model that simultaneously models entrainment and detrainment) is not that different between the two sets of parcels (Figure 9c,e).
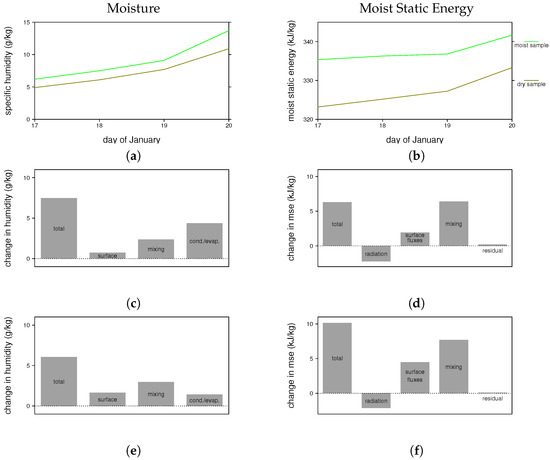
Figure 9.
Moisture and moist static energy budgets for the mean parcel trajectories shown in Figure 8. (a,b) evolution of moisture and moist static energy for parcels entering the moist (green) and dry (gold) regions, respectively; (c,d) contributions to changes in moisture and moist static energy for the moist sample from surface fluxes, radiation, mixing with convective updrafts, and/or evaporation/condensation of hydrometeors; (e,f) contributions to changes in moisture and moist static energy for the dry sample from surface fluxes, radiation, mixing with convective updrafts, and/or evaporation/condensation of hydrometeors.
Perhaps even more important than quantifying the sources of moisture, is becoming aware of just how broad the spread of parcels is; they span half the troposphere and more than 70 degrees in longitude just three days prior to entering the aqua box (Figure 8b). Many previous studies implicity discuss moistening to the east of the MJO’s convective center as occurring at low-levels in a material column of air (e.g., through shallow convection or frictional boundary layer convergence). In contrast, in the LAM the moistening is occuring at a variety of levels over a very large region. This suggests that accurately modeling both remote moisture sources and large-scale trajectories is necesseary for properly simulating MJO moistening.
In Figure 9b,d,f, we consider the moist static energy budget of the two groups of air parcels. The dry sample starts with a substantially lower moist static energy on 17 January, which is largely due to the difference in the average height of the two samples (i.e., if the moist static energy is written as gz + Cp T + Lq, where g is gravity, z is height, Cp is the specific heat at constant pressure, T is temperature, L is the latent heat of vaporization, and q is specific humidity, then most of the difference in the two samples comes from the first term). While the increase in moist static energy is greater for the dry sample (Figure 9d,f), owing primarily to higher surface fluxes, it is not enough greater to close the gap. We conclude that the air in the aqua box, where it is heavily raining, has a higher moist static energy primarily because it started at a higher height three days prior.
3.2.2. Boreal Spring MJO
The second MJO event we consider, which occurs in April 1998 of model time, has several key differences from the first case. First, it occurs in the late spring, near the typical time of transition to the Indian monsoon season, and consequently has less pronounced eastward propagation and stronger northward propagation when it reaches the eastern Indian Ocean (compare Figure 7 and Figure 10. In this way, it is more like the eastward/northward (EN) mode noted by [56], and consistent with the late springtime MJO climatology of [58], which is of a fundamentally different nature than that for the boreal winter MJO (see their Figure 4a). A weaker southward propagating branch of convection breaks off at the same time as the northward propagating one, so that on 21 April there is a classic twin cyclone pattern, with very strong low-level westerlies on the equator between the cyclones (Figure 10d).
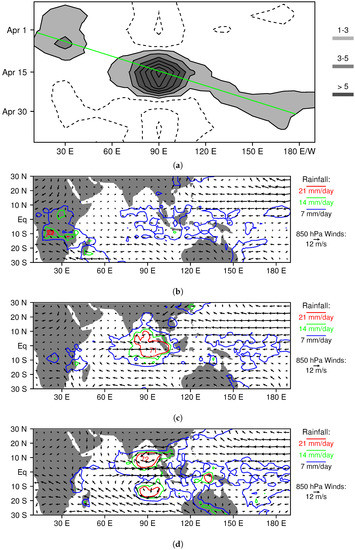
Figure 10.
Horizontal structure and propagation of the April 1998 MJO simulated with the higher-resolution version of the LAM. (a) time series of time-filtered equatorial (15 S–15 N) rainfall; (b–d) rainfall and 850 hPa winds for 5 April, 12 April, and 21 April, respectively.
Figure 11 shows back trajectories of parcels, just prior to the development of the twin cyclones, for heavily (aqua) and lightly (gold) raining regions on 9 April. In this case, there are weaker winds, so we track parcels seven days backwards in time to understand their origins, and their sources of moisture and moist static energy. The parcels in the moist region, which is located over the southern Bay of Bengal, generally come from the mid troposphere well to the east of the region of heavy rainfall (Figure 11a,b). Parcels in the dry region originate in lower levels in the atmosphere over in the Arabian Sea. As in the previous case, the moist sample starts with a similar specific humidity to that for the dry sample (Figure 12a), but gains more moisture from the detrainment from convective updrafts (labeled mixing) and the evaparation of hydrometeors (Figure 12c,e). In other words, the moist parcels become moister because they traverse the mid troposphere in a region with active convection prior to descending to low levels over the Bay of Bengal. Also similar to the previous case, the parcels in the moist region start with a higher moist static energy (MSE) than those in the dry region, and the MSE difference is maintained during the 7-day period (Figure 12b,d,f),
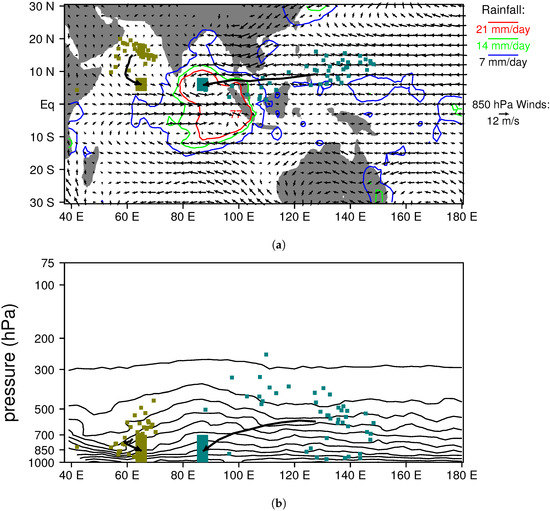
Figure 11.
Back trajectory analysis of moist (aqua) and dry (gold) regions in the April 1998 MJO simulated with the higher-resolution version of the LAM. (a) 9 April rainfall and 850-hPa flow. All parcels centered within the large aqua and gold boxes on 9 April are tracked backwards in time seven days, and their positions on 2 April are marked with small colored boxes. The mean parcel path over the seven days for each region is shown with a thick black line. Average specific humidity over 3–9 N is contoured in panel (b) with a 2 g/kg contour interval. Note that in the moist region with heavy rainfall (large aqua box) most parcels have come from mid-levels in the atmosphere over the equatorial western Pacific, whereas in the dry region with light rain (large gold box), parcels have come from the lower troposphere over the northern Arabian Sea.
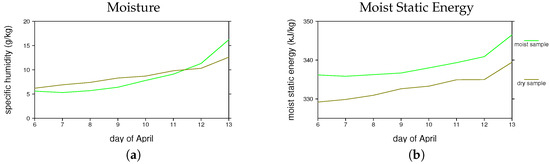
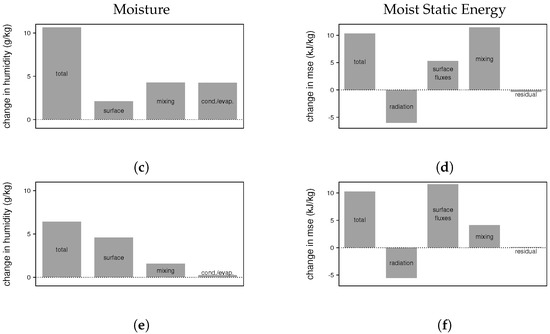
Figure 12.
Moisture and moist static energy budgets for the mean parcel trajectories shown in Figure 11. (a,b) evolution of moisture and moist static energy for parcels entering the moist (green) and dry (gold) regions. (c,d) contributions to changes in moisture and moist static energy for the moist sample from surface fluxes, radiation, mixing with convective updrafts, and/or evaporation/condensation of hydrometeors. (e,f) contributions to changes in moisture and moist static energy for the dry sample from surface fluxes, radiation, mixing with convective updrafts, and/or evaporation/condensation of hydrometeors.
Despite the differences in the propagation of the second case, we reach the same general conclusion about the origin of moist air in the heavily raining region: it comes from the middle troposphere near the equator, and it is moistened by mixing (detrainment) from convective plumes and evaporation of hydrometeors as it descends to the region with the most intense convection.
4. Discussion
The global Lagrangian atmospheric simulations presented in this paper provide a new perspective on the mechanism of the MJO. In particular, they point to the equatorial middle troposphere as the source of moist air for regions with heavy rainfall. Air in this region starts with a similar moisture content and higher moist static energy than air entering drier regions of the MJO, which comes from low-level off-equatorial locations. As the descending air approaches the MJO’s convective center, detrainment from rising convective plumes and evaporation of falling hydrometeors add additional moisture.
Ultimately, the sources of moisture for the mid-level air must tie into one or more of several moistening mechanisms previously hypothesized to be at work in the MJO, such as enhanced surface fluxes owing to stronger winds [39], frictionally driven boundary layer convergence [17,18], or low-level convergence driven by shallow convection [35,38]. The moisture is carried to mid levels by convective plumes, and then deposited either through detrainment or evaporation of hydrometeors. However, the failure of a model to include the mid-level leg of the journey could easily lead to deficiencies in the simulation of the MJO, such as a lack of eastward propagation, or inaccuracies in the period or amplitude of the MJO [20]. For example, in a typical MJO, the strongest westerlies and moisture perturbations are elevated several kilometers above the surface [31], and consequently the horizontal advective tendency of mid-level moisture perturbations is much greater than that for near-surface moisture perturbations.
Another point implicit in our results is that the MJO’s convective sensitivity to mid-level moisture may not come entirely from convective entrainment effects (i.e., how the buoyancy of rising plumes is affected by mixing with drier mid-level air), but also because mid-level air becomes the boundary layer air on a several-day time scale (e.g., Figure 8b). Simply cranking up the entrainment rate, and not including the mid-level moisture pathway diagnosed here, might enhance MJO-like systems, but at least partially for the wrong reasons. Several biases in climate models that were tuned to have strong MJOs were noted by [44], some by increasing convection’s sensitivity to mid-level moisture. Observations indicate that changes in mid- and upper-level humidity are one of the key large-scale changes that accompany the MJO [59] and the trajectories shown in Figure 8 and Figure 11 illustrate how these changes can affect the buoyancy of boundary layer air on a relatively short time scale (i.e., compared to that of the MJO).
One of the features that’s striking about the comparison between the LAM and observed composite MJOs (Figure 5), is how closely the upper tropospheric/lower stratospheric temperature perturbations match over the global tropics. What is not clear at this point is whether this is just a consequence of accurately modeling the evolution of the MJO’s convective heating [36], or if it is a necessary ingredient for properly simulating the MJO. Several salient features in high levels of the atmosphere that accompany the MJO’s deep convection have been noted by [59] and several references therein. It is also not clear at this point what the key is to the LAM’s success at simulating the MJO; i.e., whether it is the Lagrangian convective parameterization, the Lagrangian numerics, or some other aspect of the model’s physical parameterizations [12,42,45].
5. Conclusions
This study presents global, fully-Lagrangian simulations of the earth’s atmosphere. We focus on understanding and interpreting one key result of these simulations: a robust Madden–Julian Oscillation that includes realistic evolution of vertical and horizontal structures over its convective life cycle. Using back-trajectory analysis, we show that moist air in heavily raining regions of the MJO originates in the middle troposphere in equatorial locations, and it further moistens as it descends into the region of most intense convection owing to mixing with convective updrafts (i.e., detrainment) and evaporation of hydrometeors. The Lagrangian MJO simulations also suggest that much of the moist air that fuels MJO convection comes from remote locations and moisture sources.
Acknowledgments
This research was supported by the National Science Foundation of the United States of America under the Division of Atmospheric and Geospace Science (AGS) through grants AGS-1116885 and AGS-1561066.
Author Contributions
Patrick Haertel conceived, designed and performed the numerical experiments; Patrick Haertel and William R. Boos conceived the analyis of parcel trajectories, moisture and moist static energy budgets; and Katherine Straub analyzed GPCP data and computed wavenumber frequency diagrams of LAM and GPCP data. Patrick Haertel wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Observations of the 40–50-day tropical oscillation—A review. Mon. Weather Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Wheeler, M.; Kiladis, G.N. Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber—Frequency domain. J. Atmos. Sci. 1999, 56, 374–399. [Google Scholar] [CrossRef]
- Wu, M.L.C.; Schubert, S.; Huang, N.E. The development of the South Asian summer monsoon and the intraseasonal oscillation. J. Clim. 1999, 12, 2054–2075. [Google Scholar] [CrossRef]
- Lorenz, D.J.; Hartmann, D.L. The effect of the MJO on the North American monsoon. J. Clim. 2006, 19, 333–343. [Google Scholar] [CrossRef]
- Liebmann, B.; Hendon, H.H.; Glick, J.D. The relationship between tropical cyclones of the western Pacific and Indian Oceans and the Madden–Julian oscillation. J. Meteorol. Soc. Jpn. Ser. II 1994, 72, 401–412. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Modulation of eastern North Pacific hurricanes by the Madden—Julian oscillation. J. Clim. 2000, 13, 1451–1460. [Google Scholar] [CrossRef]
- Lau, K.; Peng, L. Origin of low-frequency (intraseasonal) oscillations in the tropical atmosphere. Part I: Basic theory. J. Atmos. Sci. 1987, 44, 950–972. [Google Scholar] [CrossRef]
- Seo, K.H.; Song, E.J. Initiation of boreal summer intraseasonal oscillation: Dynamic contribution by potential vorticity. Mon. Weather Rev. 2012, 140, 1748–1760. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Budsock, A. Transforming circumnavigating Kelvin waves that initiate and dissipate the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2015, 141, 1586–1602. [Google Scholar] [CrossRef]
- Emanuel, K.A.; David Neelin, J.; Bretherton, C.S. On large-scale circulations in convecting atmospheres. Q. J. R. Meteorol. Soc. 1994, 120, 1111–1143. [Google Scholar] [CrossRef]
- Sobel, A.; Maloney, E. Moisture modes and the eastward propagation of the MJO. J. Atmos. Sci. 2013, 70, 187–192. [Google Scholar] [CrossRef]
- Raymond, D.J. A new model of the Madden–Julian oscillation. J. Atmos. Sci. 2001, 58, 2807–2819. [Google Scholar] [CrossRef]
- Straus, D.M.; Lindzen, R.S. Planetary-scale baroclinic instability and the MJO. J. Atmos. Sci. 2000, 57, 3609–3626. [Google Scholar] [CrossRef]
- Wang, B.; Rui, H. Dynamics of the coupled moist Kelvin–Rossby wave on an equatorial β-plane. J. Atmos. Sci. 1990, 47, 397–413. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Frictional moisture convergence in a composite life cycle of the Madden–Julian oscillation. J. Clim. 1998, 11, 2387–2403. [Google Scholar] [CrossRef]
- Lin, J.L.; Kiladis, G.N.; Mapes, B.E.; Weickmann, K.M.; Sperber, K.R.; Lin, W.; Wheeler, M.C.; Schubert, S.D.; Del Genio, A.; Donner, L.J.; et al. Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals. J. Clim. 2006, 19, 2665–2690. [Google Scholar] [CrossRef]
- Hung, M.P.; Lin, J.L.; Wang, W.; Kim, D.; Shinoda, T.; Weaver, S.J. MJO and convectively coupled equatorial waves simulated by CMIP5 climate models. J. Clim. 2013, 26, 6185–6214. [Google Scholar] [CrossRef]
- Raymond, D.J.; Fuchs, Ž. Moisture modes and the Madden–Julian oscillation. J. Clim. 2009, 22, 3031–3046. [Google Scholar] [CrossRef]
- Kim, D.; Xavier, P.; Maloney, E.; Wheeler, M.; Waliser, D.; Sperber, K.; Hendon, H.; Zhang, C.; Neale, R.; Hwang, Y.T.; et al. Process-oriented MJO simulation diagnostic: Moisture sensitivity of simulated convection. J. Clim. 2014, 27, 5379–5395. [Google Scholar] [CrossRef]
- Hannah, W.M.; Maloney, E.D. The moist static energy budget in NCAR CAM5 hindcasts during DYNAMO. J. Adv. Mode. Earth Syst. 2014, 6, 420–440. [Google Scholar] [CrossRef]
- Sobel, A.; Wang, S.; Kim, D. Moist static energy budget of the MJO during DYNAMO. J. Atmos. Sci. 2014, 71, 4276–4291. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M. Modeling tropical convergence based on the moist static energy budget. Mon. Weather Rev. 1987, 115, 3–12. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Peters, M.E.; Back, L.E. Relationships between water vapor path and precipitation over the tropical oceans. J. Clim. 2004, 17, 1517–1528. [Google Scholar] [CrossRef]
- Del Genio, A.D.; Wu, J.; Wolf, A.B.; Chen, Y.; Yao, M.S.; Kim, D. Constraints on cumulus parameterization from simulations of observed MJO events. J. Clim. 2015, 28, 6419–6442. [Google Scholar] [CrossRef]
- Klingaman, N.; Woolnough, S. Using a case-study approach to improve the Madden–Julian oscillation in the Hadley Centre model. Q. J. R. Meteorol. Soc. 2014, 140, 2491–2505. [Google Scholar] [CrossRef]
- Gill, A. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
- Houze, R.A., Jr.; Chen, S.S.; Kingsmill, D.E.; Serra, Y.; Yuter, S.E. Convection over the Pacific warm pool in relation to the atmospheric Kelvin-Rossby wave. J. Atmos. Sci. 2000, 57, 3058–3089. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Straub, K.H.; Haertel, P.T. Zonal and vertical structure of the Madden–Julian oscillation. J. Atmos. Sci. 2005, 62, 2790–2809. [Google Scholar] [CrossRef]
- Pritchard, M.S.; Bretherton, C.S. Causal evidence that rotational moisture advection is critical to the superparameterized Madden–Julian oscillation. J. Atmos. Sci. 2014, 71, 800–815. [Google Scholar] [CrossRef]
- Lin, X.; Johnson, R.H. Heating, moistening, and rainfall over the western Pacific warm pool during TOGA COARE. J. Atmos. Sci. 1996, 53, 3367–3383. [Google Scholar] [CrossRef]
- Johnson, R.H.; Rickenbach, T.M.; Rutledge, S.A.; Ciesielski, P.E.; Schubert, W.H. Trimodal characteristics of tropical convection. J. Clim. 1999, 12, 2397–2418. [Google Scholar] [CrossRef]
- Haertel, P.T.; Kiladis, G.N.; Denno, A.; Rickenbach, T.M. Vertical-mode decompositions of 2-day waves and the Madden–Julian oscillation. J. Atmos. Sci. 2008, 72. [Google Scholar] [CrossRef]
- Haertel, P.T.; Kiladis, G.N. Dynamics of 2-day equatorial waves. Dynamics 2004. [Google Scholar] [CrossRef]
- Peters, M.E.; Bretherton, C.S. Structure of tropical variability from a vertical mode perspective. Theor. Comput. Fluid Dyn. 2006, 20, 501–524. [Google Scholar] [CrossRef]
- Raymond, D.J.; Sessions, S.L. Evolution of convection during tropical cyclogenesis. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction model of intraseasonal oscillations in the tropics. J. Atmos. Sci. 1987, 44, 2324–2340. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M.; Cook, K.H. Evaporation-wind feedback and low-frequency variability in the tropical atmosphere. J. Atmos. Sci. 1987, 44, 2341–2348. [Google Scholar] [CrossRef]
- Lin, X.; Johnson, R.H. Kinematic and thermodynamic characteristics of the flow over the western Pacific warm pool during TOGA COARE. J. Atmos. Sci. 1996, 53, 695–715. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Fedorov, A. Lagrangian overturning and the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2014, 140, 1344–1361. [Google Scholar] [CrossRef]
- Randall, D.A. Beyond deadlock. Geophys. Res. Lett. 2013, 40, 5970–5976. [Google Scholar] [CrossRef]
- Kim, D.; Sobel, A.H.; Maloney, E.D.; Frierson, D.M.; Kang, I.S. A systematic relationship between intraseasonal variability and mean state bias in AGCM simulations. J. Clim. 2011, 24, 5506–5520. [Google Scholar] [CrossRef]
- Haertel, P.T.; Straub, K.H. Simulating convectively coupled Kelvin waves using Lagrangian overturning for a convective parametrization. Q. J. R. Meteorol. Soc. 2010, 136, 1598–1613. [Google Scholar] [CrossRef]
- Haertel, P. A Lagrangian method for simulating geophysical fluids. Lagrangian Model. Atmos. 2012, 85–98. [Google Scholar] [CrossRef]
- Frierson, D.M.; Held, I.M.; Zurita-Gotor, P. A gray-radiation aquaplanet moist GCM. Part I: Static stability and eddy scale. J. Atmos. Sci. 2006, 63, 2548–2566. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; McGarragh, G. A 10-year climatology of tropical radiative heating and its vertical structure from TRMM observations. J. Clim. 2010, 23, 519–541. [Google Scholar] [CrossRef]
- Gates, W.L.; Boyle, J.S.; Covey, C.; Dease, C.G.; Doutriaux, C.M.; Drach, R.S.; Fiorino, M.; Gleckler, P.J.; Hnilo, J.J.; Marlais, S.M.; et al. An overview of the results of the Atmospheric Model Intercomparison Project (AMIP I). Bull. Am. Meteorol. Soc. 1999, 80, 29–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M. Seasonality in the Madden–Julian oscillation. J. Clim. 2004, 17, 3169–3180. [Google Scholar] [CrossRef]
- Majda, A.J.; Stechmann, S.N. The skeleton of tropical intraseasonal oscillations. Proc. Natl. Acad. Sci. USA 2009, 106, 8417–8422. [Google Scholar] [CrossRef] [PubMed]
- Inness, P.M.; Slingo, J.M. The interaction of the Madden–Julian oscillation with the maritime continent in a GCM. Q. J. R. Meteorol. Soc. 2006, 132, 1645–1667. [Google Scholar] [CrossRef]
- Matsuno, T. Quasi-geostrophic motions in the equatorial area. J. Meteorol. Soc. Jpn. Ser. II 1966, 44, 25–43. [Google Scholar] [CrossRef]
- Wang, B.; Rui, H. Synoptic climatology of transient tropical intraseasonal convection anomalies: 1975–1985. Meteorol. Atmos. Phys. 1990, 44, 43–61. [Google Scholar] [CrossRef]
- Ciesielski, P.E.; Johnson, R.H.; Haertel, P.T.; Wang, J. Corrected TOGA COARE sounding humidity data: Impact on diagnosed properties of convection and climate over the warm pool. J. Clim. 2003, 16, 2370–2384. [Google Scholar] [CrossRef]
- Yasunaga, K. Seasonality and regionality of the Madden–Julian oscillation and convectively coupled equatorial waves. SOLA 2011, 7, 153–156. [Google Scholar] [CrossRef]
- Johnson, R.H.; Ciesielski, P.E. Structure and properties of Madden–Julian oscillations deduced from DYNAMO sounding arrays. J. Atmos. Sci. 2013, 70, 3157–3179. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).