Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation
Abstract
:1. Introduction
2. Experiments
2.1. Lagrangian Atmospheric Model (LAM)
2.2. Rainfall Observations
3. Results
3.1. LAM Basic State and Tropical Convective Variability
3.1.1. Average Global Circulation
3.1.2. Tropical Convective Variability
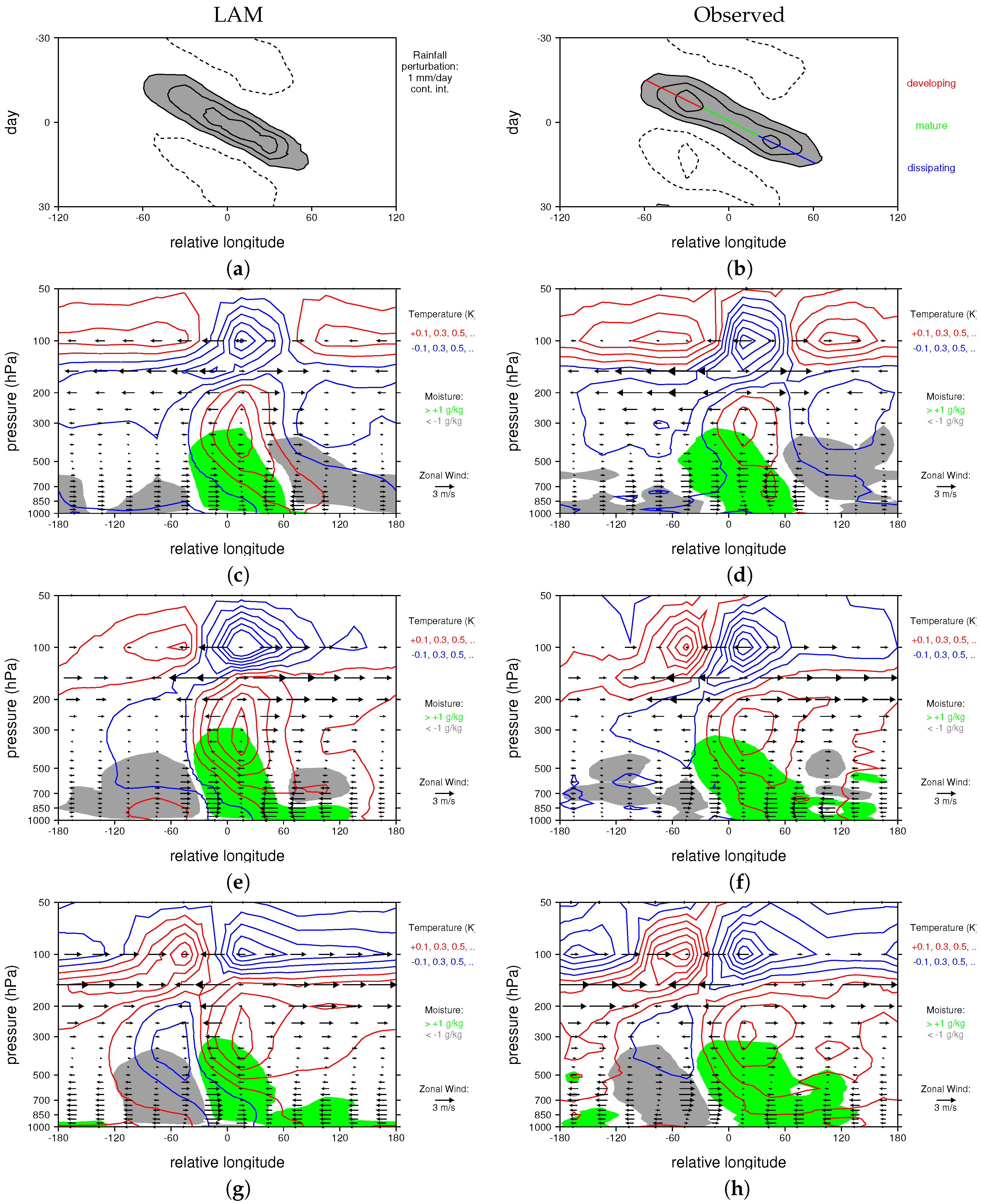
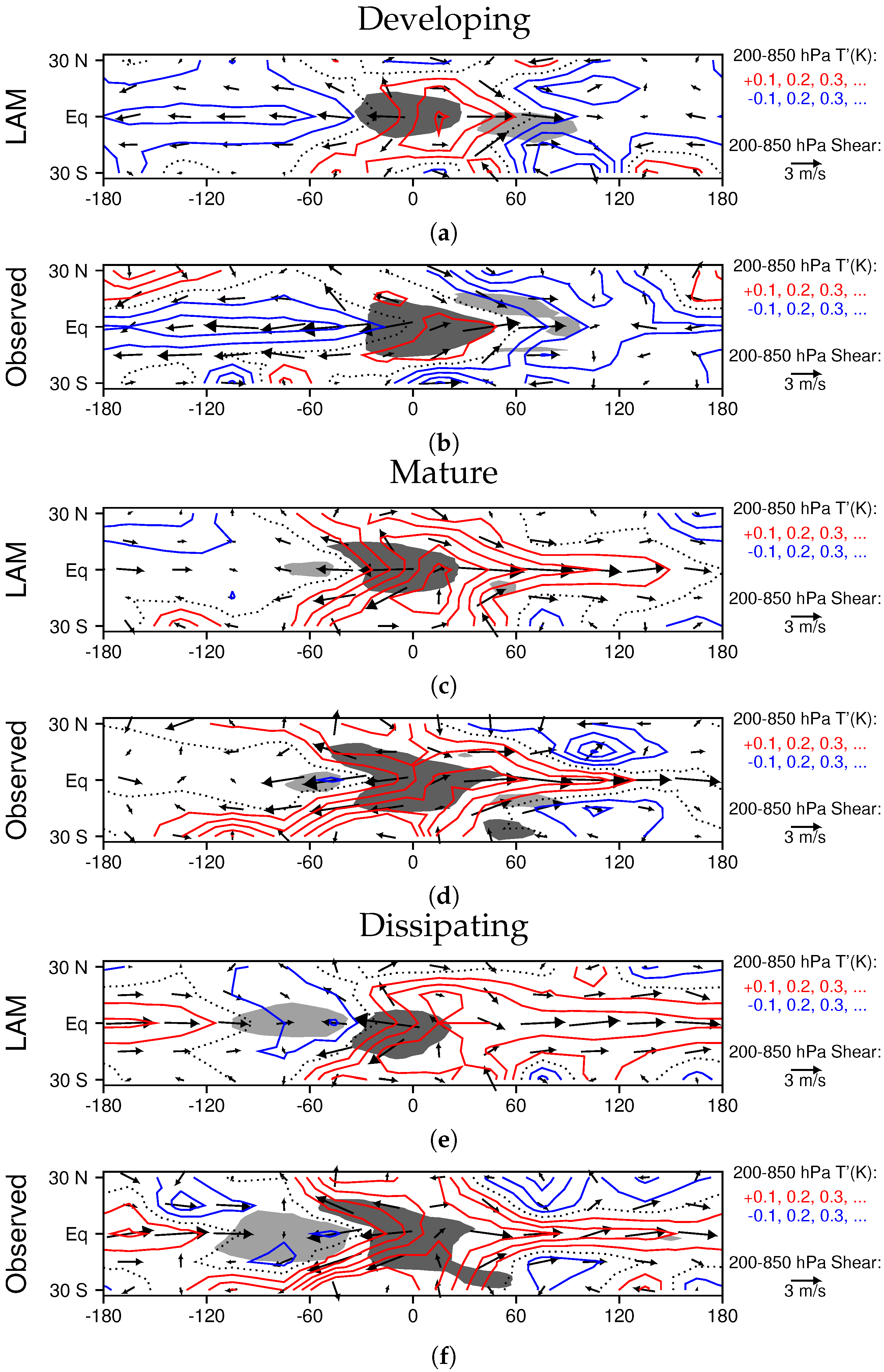
3.1.3. Simulated MJO Structure
3.2. Moisture Transport in Higher-Resolution Case Studies
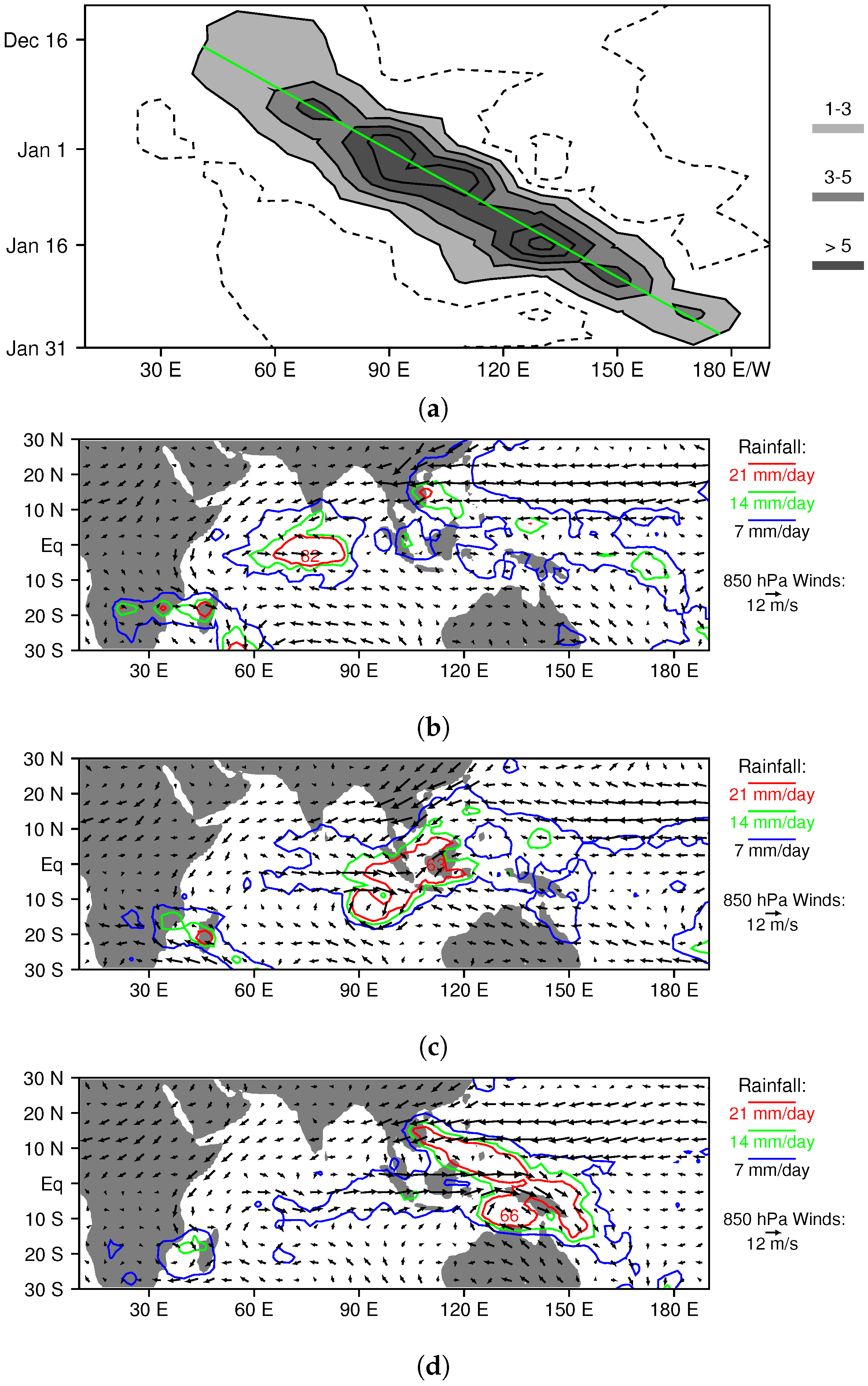
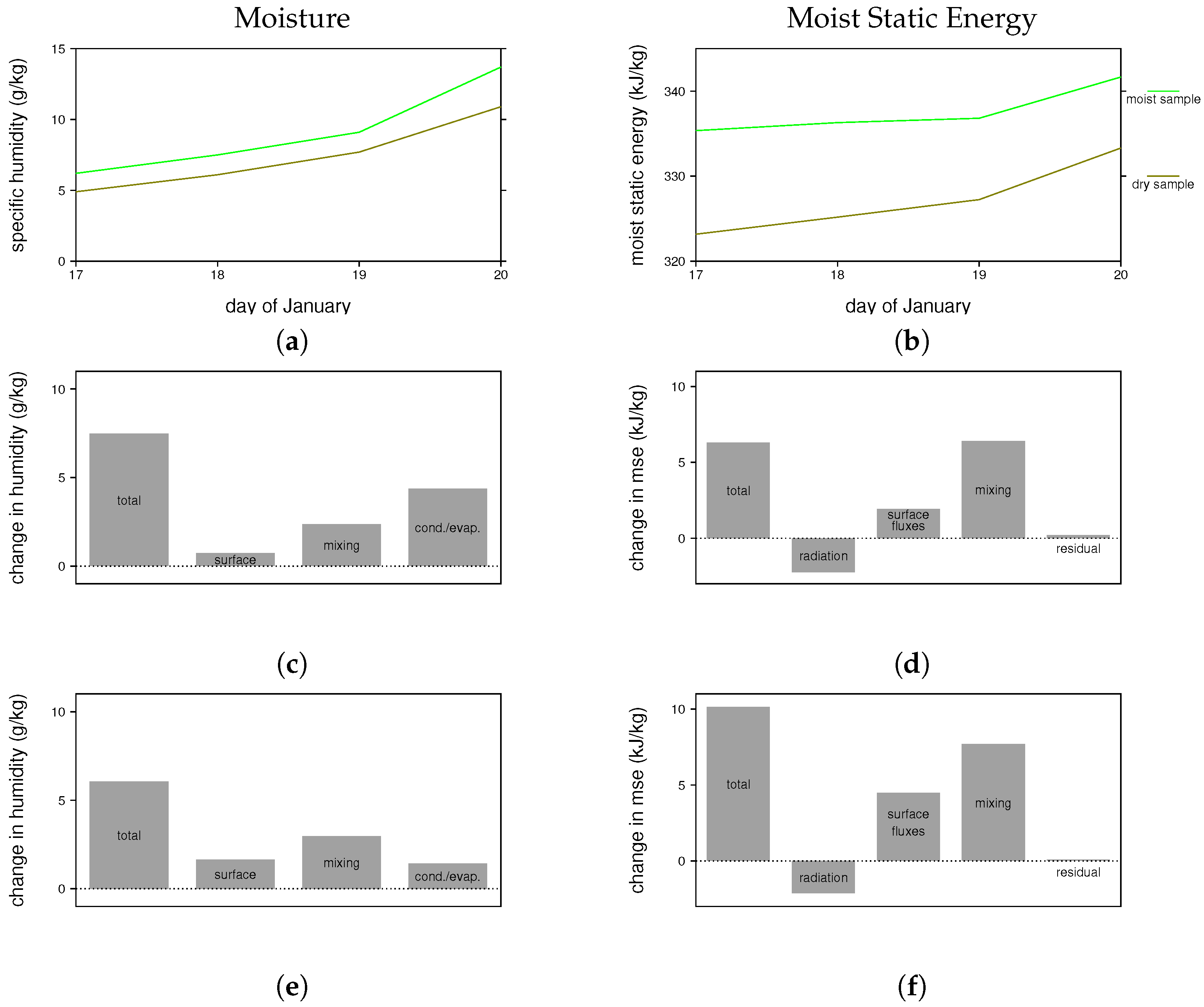
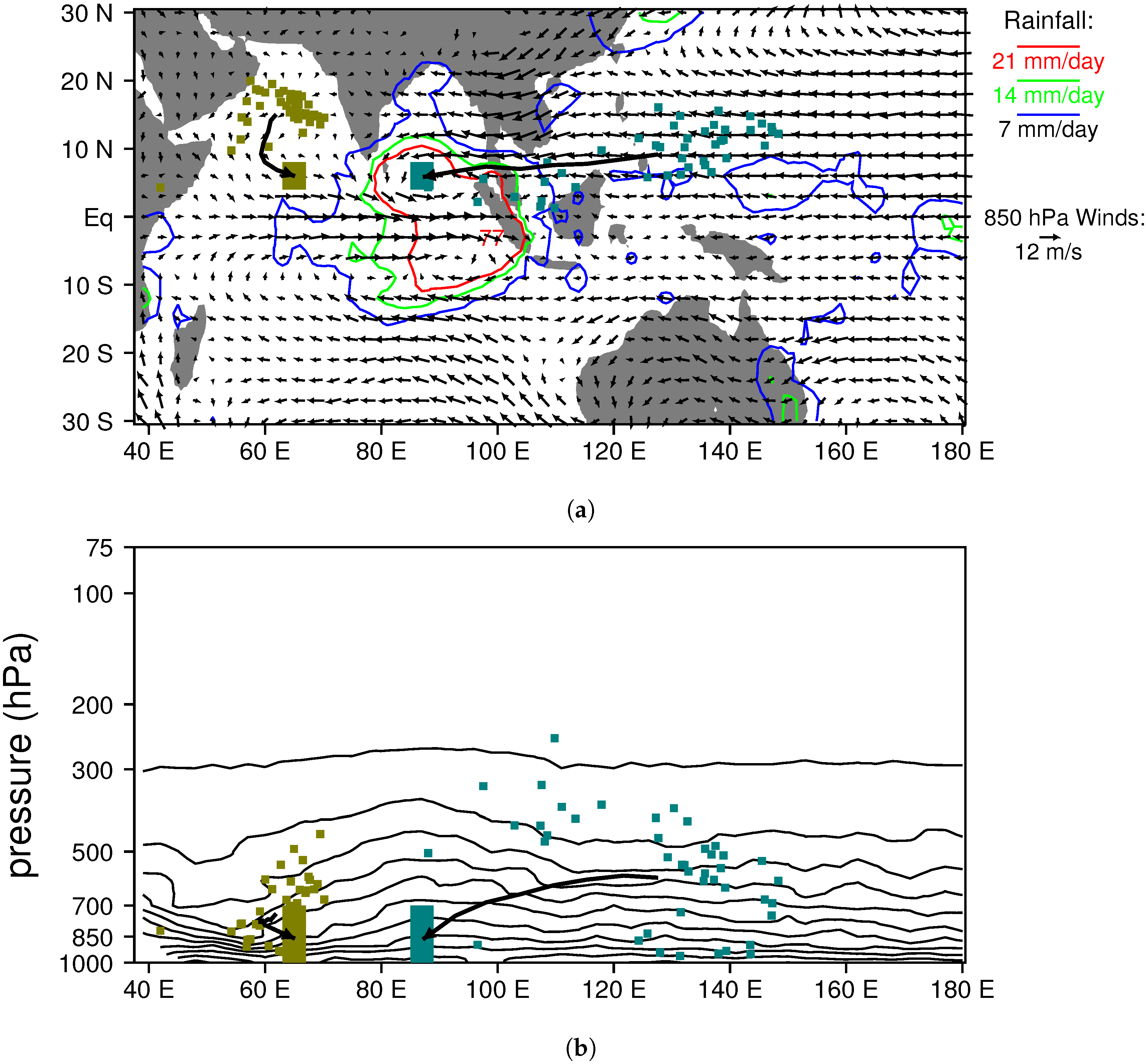
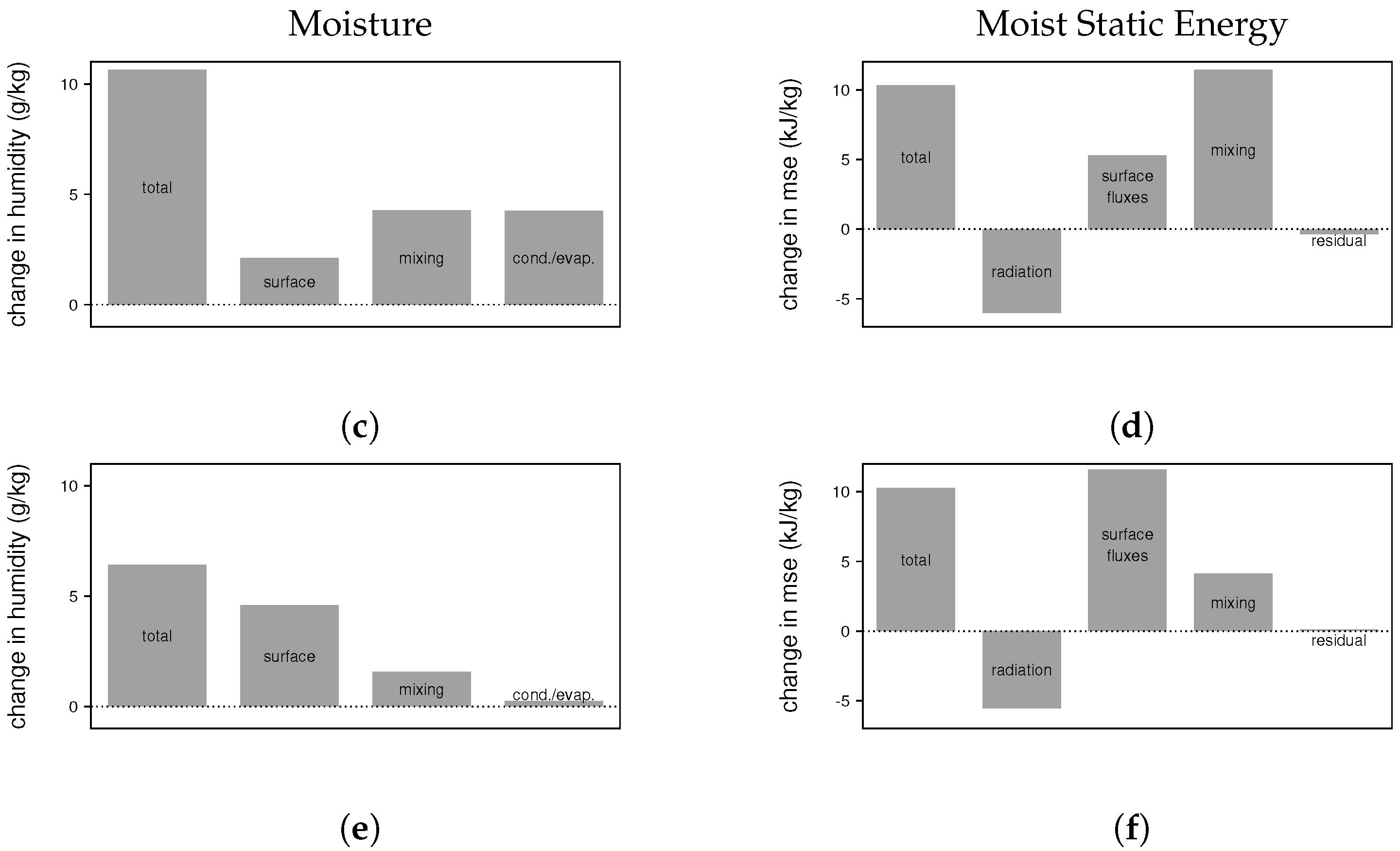
3.2.1. Boreal Winter MJO
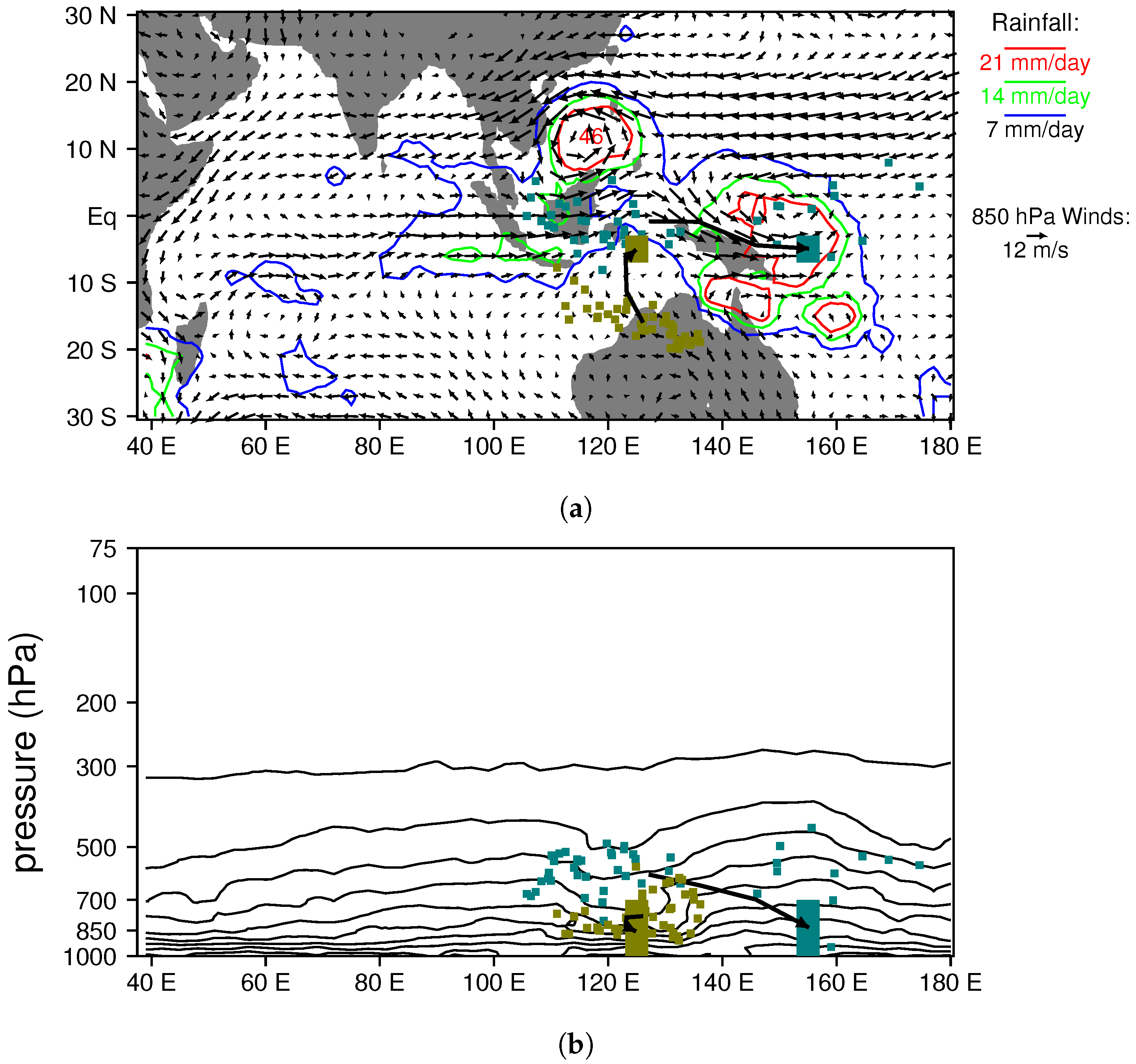
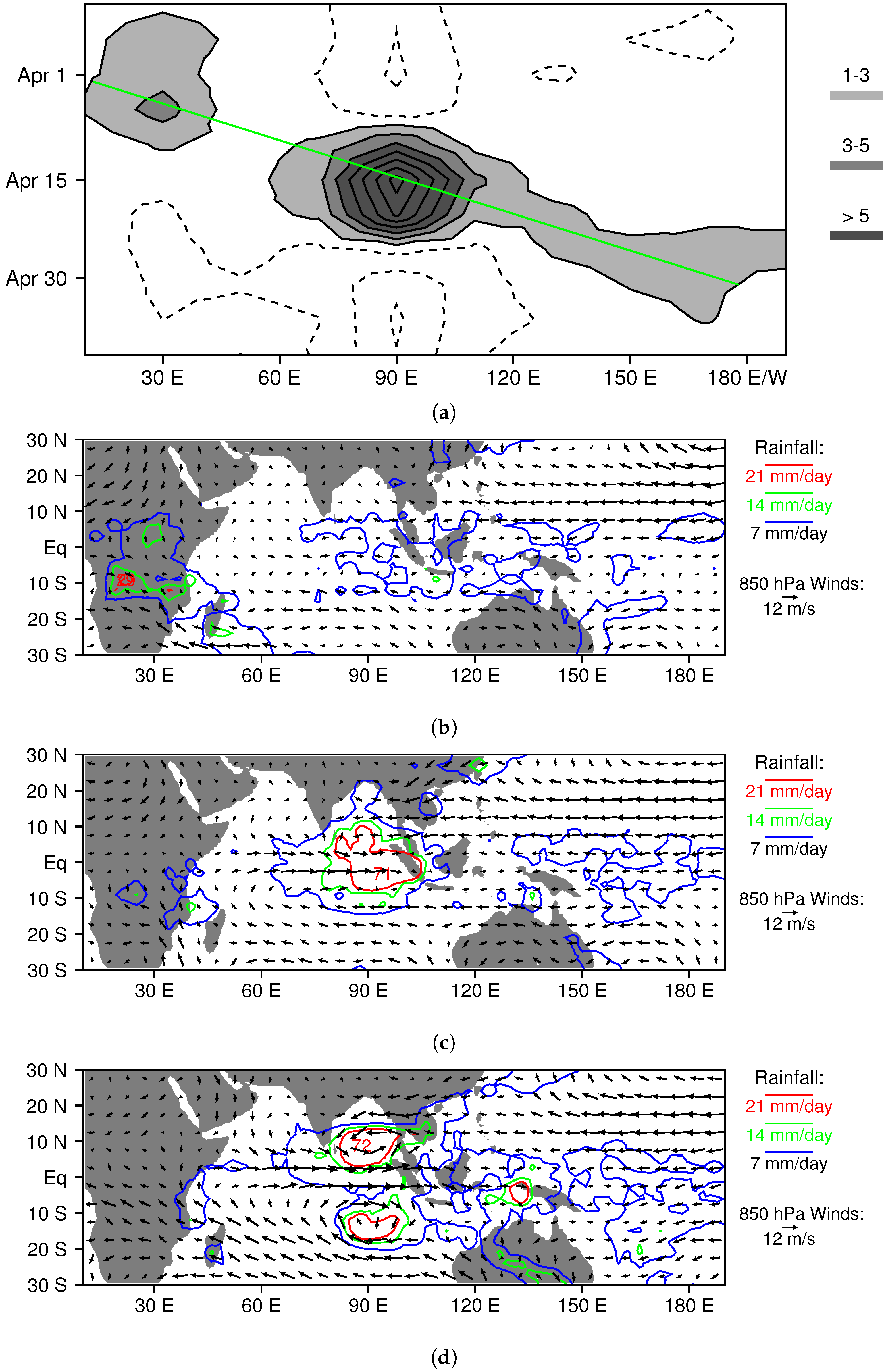
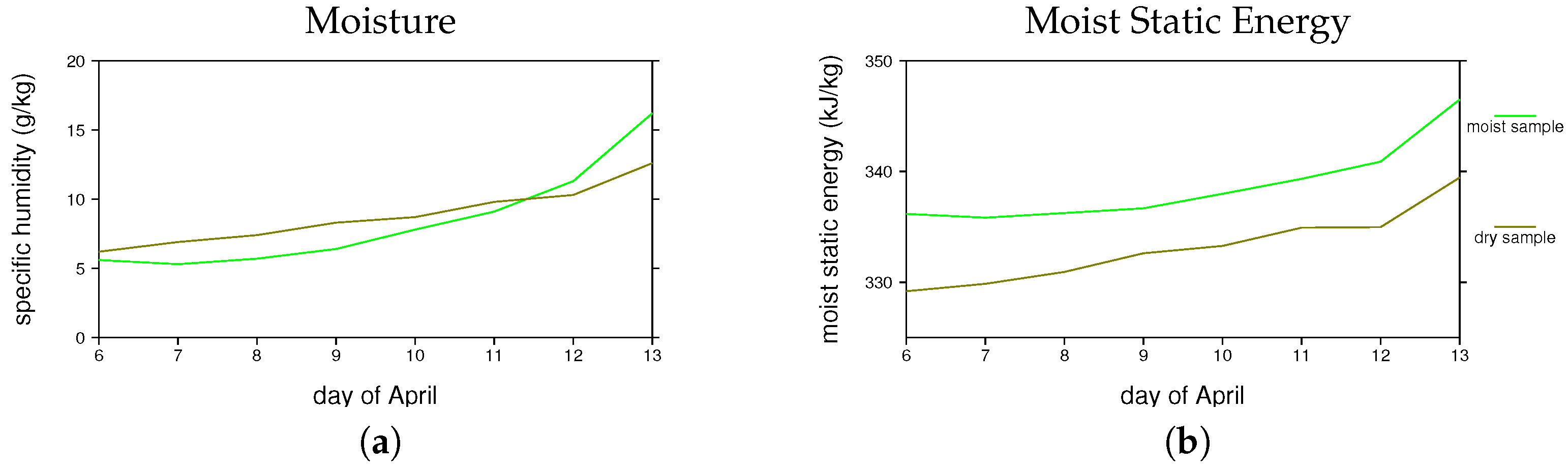
3.2.2. Boreal Spring MJO
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Observations of the 40–50-day tropical oscillation—A review. Mon. Weather Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Wheeler, M.; Kiladis, G.N. Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber—Frequency domain. J. Atmos. Sci. 1999, 56, 374–399. [Google Scholar] [CrossRef]
- Wu, M.L.C.; Schubert, S.; Huang, N.E. The development of the South Asian summer monsoon and the intraseasonal oscillation. J. Clim. 1999, 12, 2054–2075. [Google Scholar] [CrossRef]
- Lorenz, D.J.; Hartmann, D.L. The effect of the MJO on the North American monsoon. J. Clim. 2006, 19, 333–343. [Google Scholar] [CrossRef]
- Liebmann, B.; Hendon, H.H.; Glick, J.D. The relationship between tropical cyclones of the western Pacific and Indian Oceans and the Madden–Julian oscillation. J. Meteorol. Soc. Jpn. Ser. II 1994, 72, 401–412. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Modulation of eastern North Pacific hurricanes by the Madden—Julian oscillation. J. Clim. 2000, 13, 1451–1460. [Google Scholar] [CrossRef]
- Lau, K.; Peng, L. Origin of low-frequency (intraseasonal) oscillations in the tropical atmosphere. Part I: Basic theory. J. Atmos. Sci. 1987, 44, 950–972. [Google Scholar] [CrossRef]
- Seo, K.H.; Song, E.J. Initiation of boreal summer intraseasonal oscillation: Dynamic contribution by potential vorticity. Mon. Weather Rev. 2012, 140, 1748–1760. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Budsock, A. Transforming circumnavigating Kelvin waves that initiate and dissipate the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2015, 141, 1586–1602. [Google Scholar] [CrossRef]
- Emanuel, K.A.; David Neelin, J.; Bretherton, C.S. On large-scale circulations in convecting atmospheres. Q. J. R. Meteorol. Soc. 1994, 120, 1111–1143. [Google Scholar] [CrossRef]
- Sobel, A.; Maloney, E. Moisture modes and the eastward propagation of the MJO. J. Atmos. Sci. 2013, 70, 187–192. [Google Scholar] [CrossRef]
- Raymond, D.J. A new model of the Madden–Julian oscillation. J. Atmos. Sci. 2001, 58, 2807–2819. [Google Scholar] [CrossRef]
- Straus, D.M.; Lindzen, R.S. Planetary-scale baroclinic instability and the MJO. J. Atmos. Sci. 2000, 57, 3609–3626. [Google Scholar] [CrossRef]
- Wang, B.; Rui, H. Dynamics of the coupled moist Kelvin–Rossby wave on an equatorial β-plane. J. Atmos. Sci. 1990, 47, 397–413. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Frictional moisture convergence in a composite life cycle of the Madden–Julian oscillation. J. Clim. 1998, 11, 2387–2403. [Google Scholar] [CrossRef]
- Lin, J.L.; Kiladis, G.N.; Mapes, B.E.; Weickmann, K.M.; Sperber, K.R.; Lin, W.; Wheeler, M.C.; Schubert, S.D.; Del Genio, A.; Donner, L.J.; et al. Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals. J. Clim. 2006, 19, 2665–2690. [Google Scholar] [CrossRef]
- Hung, M.P.; Lin, J.L.; Wang, W.; Kim, D.; Shinoda, T.; Weaver, S.J. MJO and convectively coupled equatorial waves simulated by CMIP5 climate models. J. Clim. 2013, 26, 6185–6214. [Google Scholar] [CrossRef]
- Raymond, D.J.; Fuchs, Ž. Moisture modes and the Madden–Julian oscillation. J. Clim. 2009, 22, 3031–3046. [Google Scholar] [CrossRef]
- Kim, D.; Xavier, P.; Maloney, E.; Wheeler, M.; Waliser, D.; Sperber, K.; Hendon, H.; Zhang, C.; Neale, R.; Hwang, Y.T.; et al. Process-oriented MJO simulation diagnostic: Moisture sensitivity of simulated convection. J. Clim. 2014, 27, 5379–5395. [Google Scholar] [CrossRef]
- Hannah, W.M.; Maloney, E.D. The moist static energy budget in NCAR CAM5 hindcasts during DYNAMO. J. Adv. Mode. Earth Syst. 2014, 6, 420–440. [Google Scholar] [CrossRef]
- Sobel, A.; Wang, S.; Kim, D. Moist static energy budget of the MJO during DYNAMO. J. Atmos. Sci. 2014, 71, 4276–4291. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M. Modeling tropical convergence based on the moist static energy budget. Mon. Weather Rev. 1987, 115, 3–12. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Peters, M.E.; Back, L.E. Relationships between water vapor path and precipitation over the tropical oceans. J. Clim. 2004, 17, 1517–1528. [Google Scholar] [CrossRef]
- Del Genio, A.D.; Wu, J.; Wolf, A.B.; Chen, Y.; Yao, M.S.; Kim, D. Constraints on cumulus parameterization from simulations of observed MJO events. J. Clim. 2015, 28, 6419–6442. [Google Scholar] [CrossRef]
- Klingaman, N.; Woolnough, S. Using a case-study approach to improve the Madden–Julian oscillation in the Hadley Centre model. Q. J. R. Meteorol. Soc. 2014, 140, 2491–2505. [Google Scholar] [CrossRef]
- Gill, A. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
- Houze, R.A., Jr.; Chen, S.S.; Kingsmill, D.E.; Serra, Y.; Yuter, S.E. Convection over the Pacific warm pool in relation to the atmospheric Kelvin-Rossby wave. J. Atmos. Sci. 2000, 57, 3058–3089. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Straub, K.H.; Haertel, P.T. Zonal and vertical structure of the Madden–Julian oscillation. J. Atmos. Sci. 2005, 62, 2790–2809. [Google Scholar] [CrossRef]
- Pritchard, M.S.; Bretherton, C.S. Causal evidence that rotational moisture advection is critical to the superparameterized Madden–Julian oscillation. J. Atmos. Sci. 2014, 71, 800–815. [Google Scholar] [CrossRef]
- Lin, X.; Johnson, R.H. Heating, moistening, and rainfall over the western Pacific warm pool during TOGA COARE. J. Atmos. Sci. 1996, 53, 3367–3383. [Google Scholar] [CrossRef]
- Johnson, R.H.; Rickenbach, T.M.; Rutledge, S.A.; Ciesielski, P.E.; Schubert, W.H. Trimodal characteristics of tropical convection. J. Clim. 1999, 12, 2397–2418. [Google Scholar] [CrossRef]
- Haertel, P.T.; Kiladis, G.N.; Denno, A.; Rickenbach, T.M. Vertical-mode decompositions of 2-day waves and the Madden–Julian oscillation. J. Atmos. Sci. 2008, 72. [Google Scholar] [CrossRef]
- Haertel, P.T.; Kiladis, G.N. Dynamics of 2-day equatorial waves. Dynamics 2004. [Google Scholar] [CrossRef]
- Peters, M.E.; Bretherton, C.S. Structure of tropical variability from a vertical mode perspective. Theor. Comput. Fluid Dyn. 2006, 20, 501–524. [Google Scholar] [CrossRef]
- Raymond, D.J.; Sessions, S.L. Evolution of convection during tropical cyclogenesis. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction model of intraseasonal oscillations in the tropics. J. Atmos. Sci. 1987, 44, 2324–2340. [Google Scholar] [CrossRef]
- Neelin, J.D.; Held, I.M.; Cook, K.H. Evaporation-wind feedback and low-frequency variability in the tropical atmosphere. J. Atmos. Sci. 1987, 44, 2341–2348. [Google Scholar] [CrossRef]
- Lin, X.; Johnson, R.H. Kinematic and thermodynamic characteristics of the flow over the western Pacific warm pool during TOGA COARE. J. Atmos. Sci. 1996, 53, 695–715. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Fedorov, A. Lagrangian overturning and the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2014, 140, 1344–1361. [Google Scholar] [CrossRef]
- Randall, D.A. Beyond deadlock. Geophys. Res. Lett. 2013, 40, 5970–5976. [Google Scholar] [CrossRef]
- Kim, D.; Sobel, A.H.; Maloney, E.D.; Frierson, D.M.; Kang, I.S. A systematic relationship between intraseasonal variability and mean state bias in AGCM simulations. J. Clim. 2011, 24, 5506–5520. [Google Scholar] [CrossRef]
- Haertel, P.T.; Straub, K.H. Simulating convectively coupled Kelvin waves using Lagrangian overturning for a convective parametrization. Q. J. R. Meteorol. Soc. 2010, 136, 1598–1613. [Google Scholar] [CrossRef]
- Haertel, P. A Lagrangian method for simulating geophysical fluids. Lagrangian Model. Atmos. 2012, 85–98. [Google Scholar] [CrossRef]
- Frierson, D.M.; Held, I.M.; Zurita-Gotor, P. A gray-radiation aquaplanet moist GCM. Part I: Static stability and eddy scale. J. Atmos. Sci. 2006, 63, 2548–2566. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; McGarragh, G. A 10-year climatology of tropical radiative heating and its vertical structure from TRMM observations. J. Clim. 2010, 23, 519–541. [Google Scholar] [CrossRef]
- Gates, W.L.; Boyle, J.S.; Covey, C.; Dease, C.G.; Doutriaux, C.M.; Drach, R.S.; Fiorino, M.; Gleckler, P.J.; Hnilo, J.J.; Marlais, S.M.; et al. An overview of the results of the Atmospheric Model Intercomparison Project (AMIP I). Bull. Am. Meteorol. Soc. 1999, 80, 29–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M. Seasonality in the Madden–Julian oscillation. J. Clim. 2004, 17, 3169–3180. [Google Scholar] [CrossRef]
- Majda, A.J.; Stechmann, S.N. The skeleton of tropical intraseasonal oscillations. Proc. Natl. Acad. Sci. USA 2009, 106, 8417–8422. [Google Scholar] [CrossRef] [PubMed]
- Inness, P.M.; Slingo, J.M. The interaction of the Madden–Julian oscillation with the maritime continent in a GCM. Q. J. R. Meteorol. Soc. 2006, 132, 1645–1667. [Google Scholar] [CrossRef]
- Matsuno, T. Quasi-geostrophic motions in the equatorial area. J. Meteorol. Soc. Jpn. Ser. II 1966, 44, 25–43. [Google Scholar] [CrossRef]
- Wang, B.; Rui, H. Synoptic climatology of transient tropical intraseasonal convection anomalies: 1975–1985. Meteorol. Atmos. Phys. 1990, 44, 43–61. [Google Scholar] [CrossRef]
- Ciesielski, P.E.; Johnson, R.H.; Haertel, P.T.; Wang, J. Corrected TOGA COARE sounding humidity data: Impact on diagnosed properties of convection and climate over the warm pool. J. Clim. 2003, 16, 2370–2384. [Google Scholar] [CrossRef]
- Yasunaga, K. Seasonality and regionality of the Madden–Julian oscillation and convectively coupled equatorial waves. SOLA 2011, 7, 153–156. [Google Scholar] [CrossRef]
- Johnson, R.H.; Ciesielski, P.E. Structure and properties of Madden–Julian oscillations deduced from DYNAMO sounding arrays. J. Atmos. Sci. 2013, 70, 3157–3179. [Google Scholar] [CrossRef]
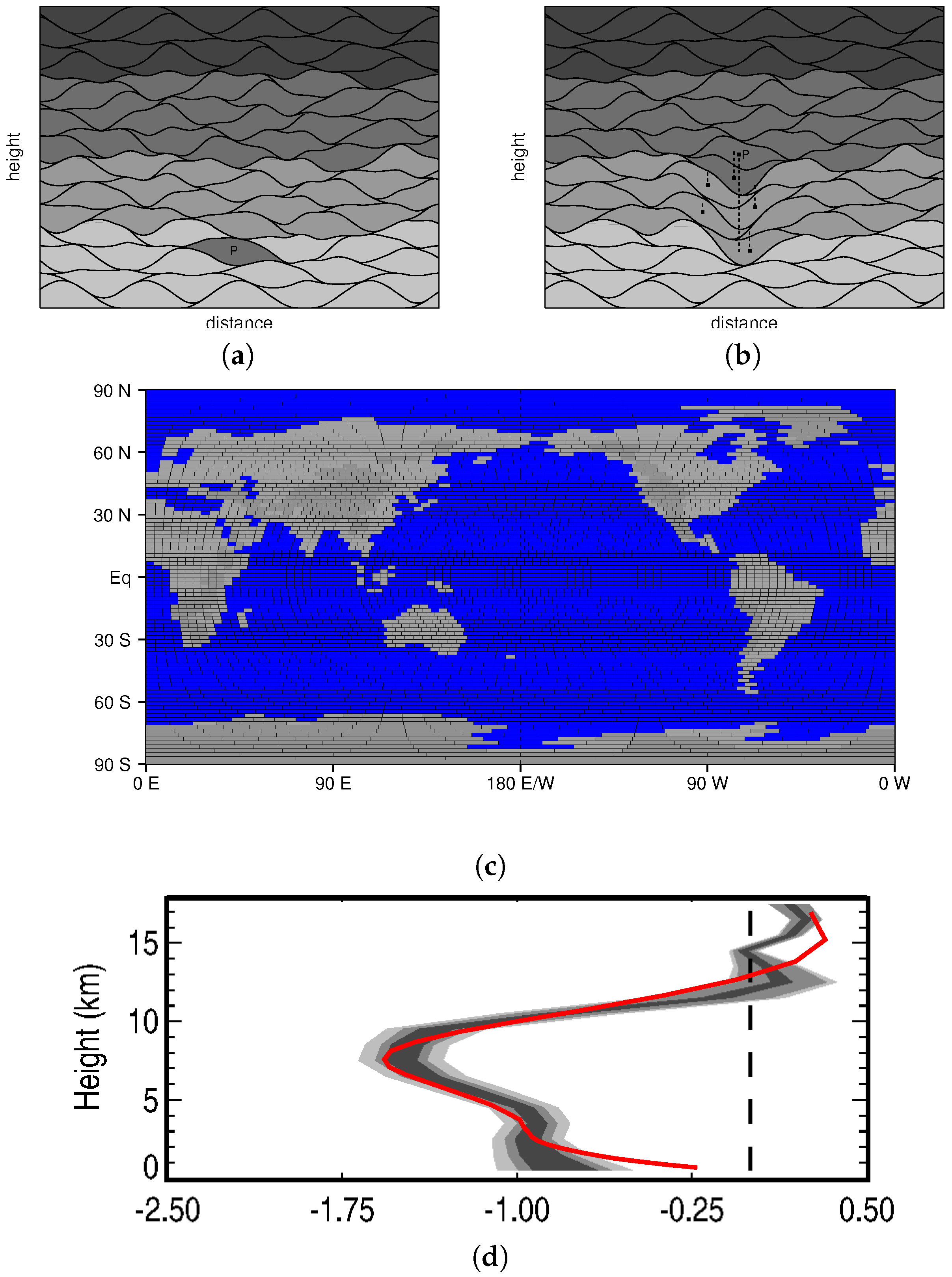
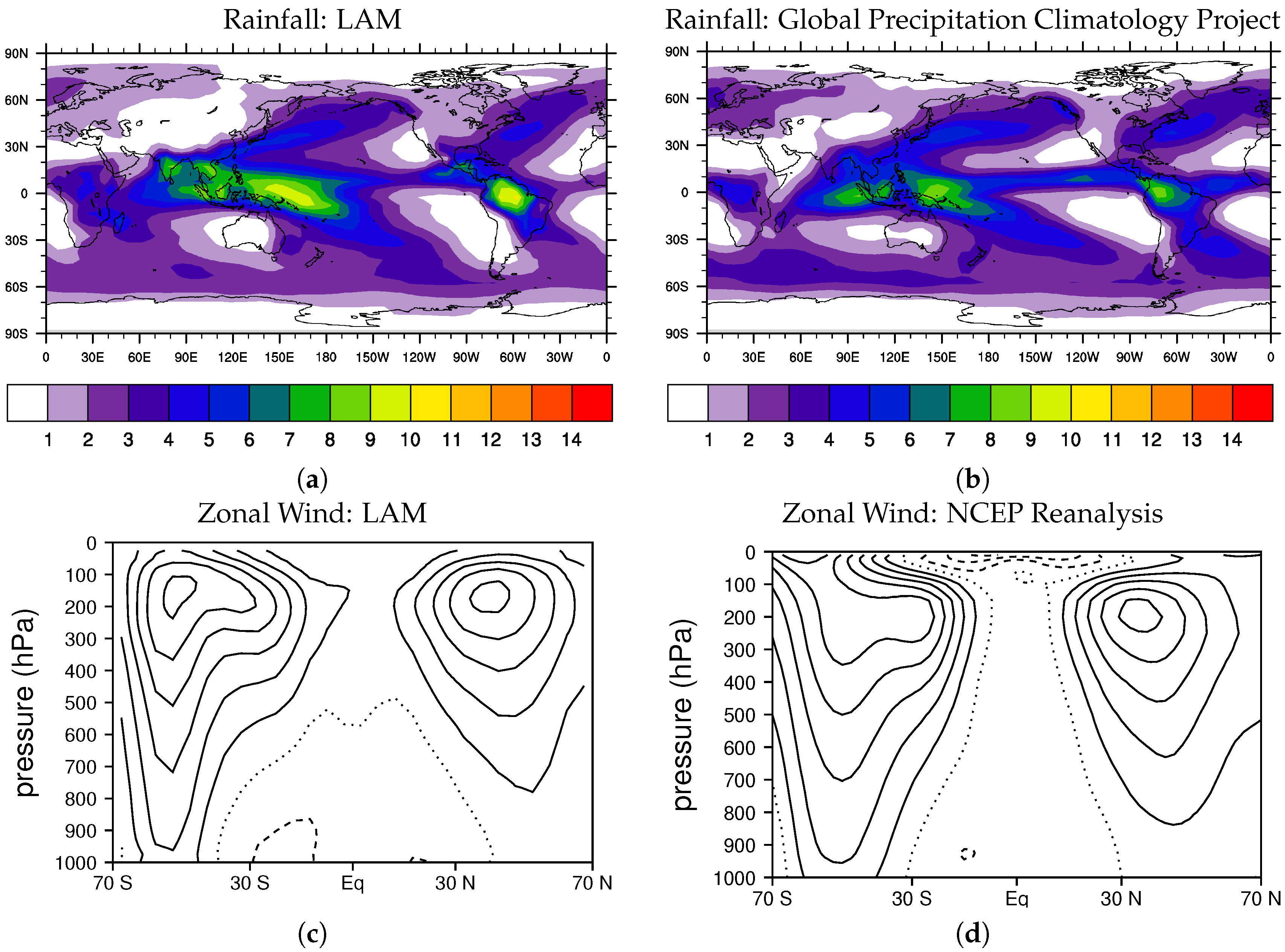
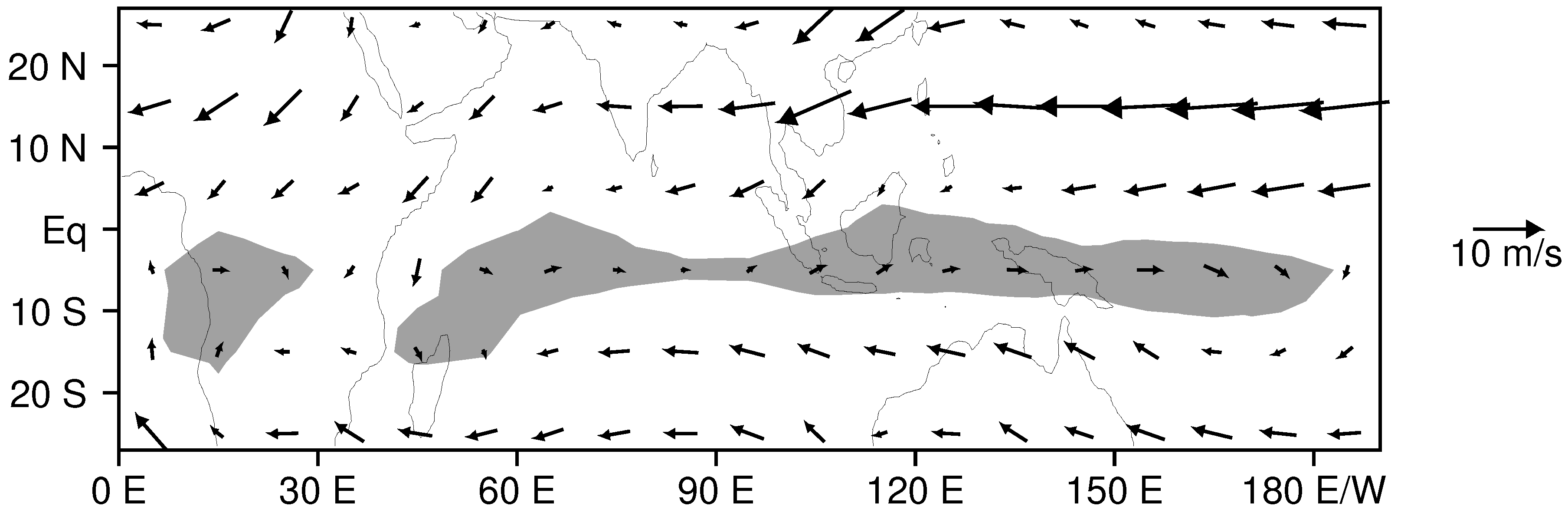
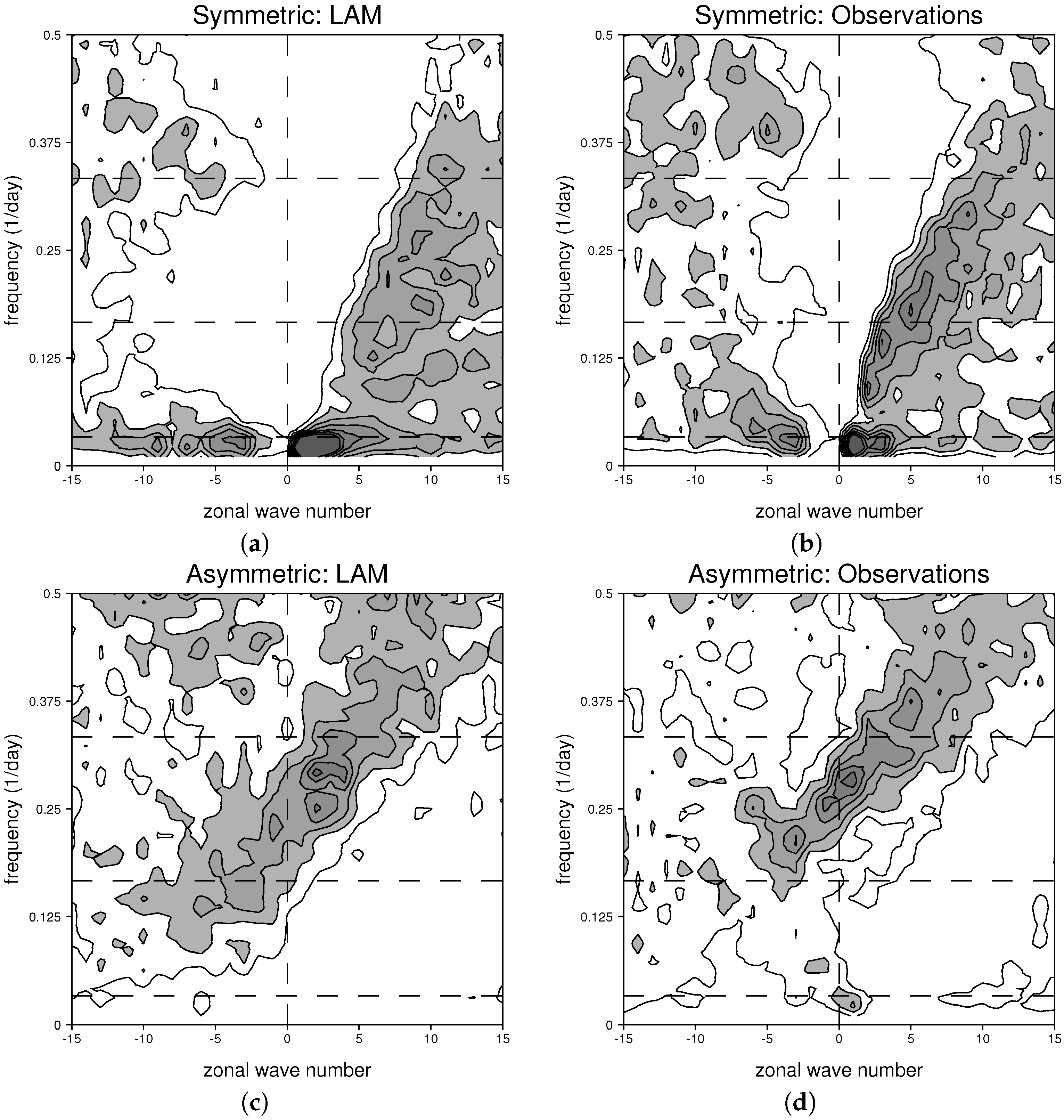
| Run | Resolution (Lat/lon) | Years | Mixing | Evaporation |
|---|---|---|---|---|
| climatology | 1.88/3.75 | 1998–2009 | ||
| mjo case studies | 1.33/2.67 | 1998–2000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haertel, P.; Boos, W.R.; Straub, K. Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation. Atmosphere 2017, 8, 158. https://doi.org/10.3390/atmos8090158
Haertel P, Boos WR, Straub K. Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation. Atmosphere. 2017; 8(9):158. https://doi.org/10.3390/atmos8090158
Chicago/Turabian StyleHaertel, Patrick, William R. Boos, and Katherine Straub. 2017. "Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation" Atmosphere 8, no. 9: 158. https://doi.org/10.3390/atmos8090158
APA StyleHaertel, P., Boos, W. R., & Straub, K. (2017). Origins of Moist Air in Global Lagrangian Simulations of the Madden–Julian Oscillation. Atmosphere, 8(9), 158. https://doi.org/10.3390/atmos8090158




