A Support Vector Machine Hydrometeor Classification Algorithm for Dual-Polarization Radar
Abstract
:1. Introduction
2. The SVM Hydrometeor Classification Algorithm
2.1. Support Vector Machine Description
2.2. Support Vector Machine Implementation of HCA
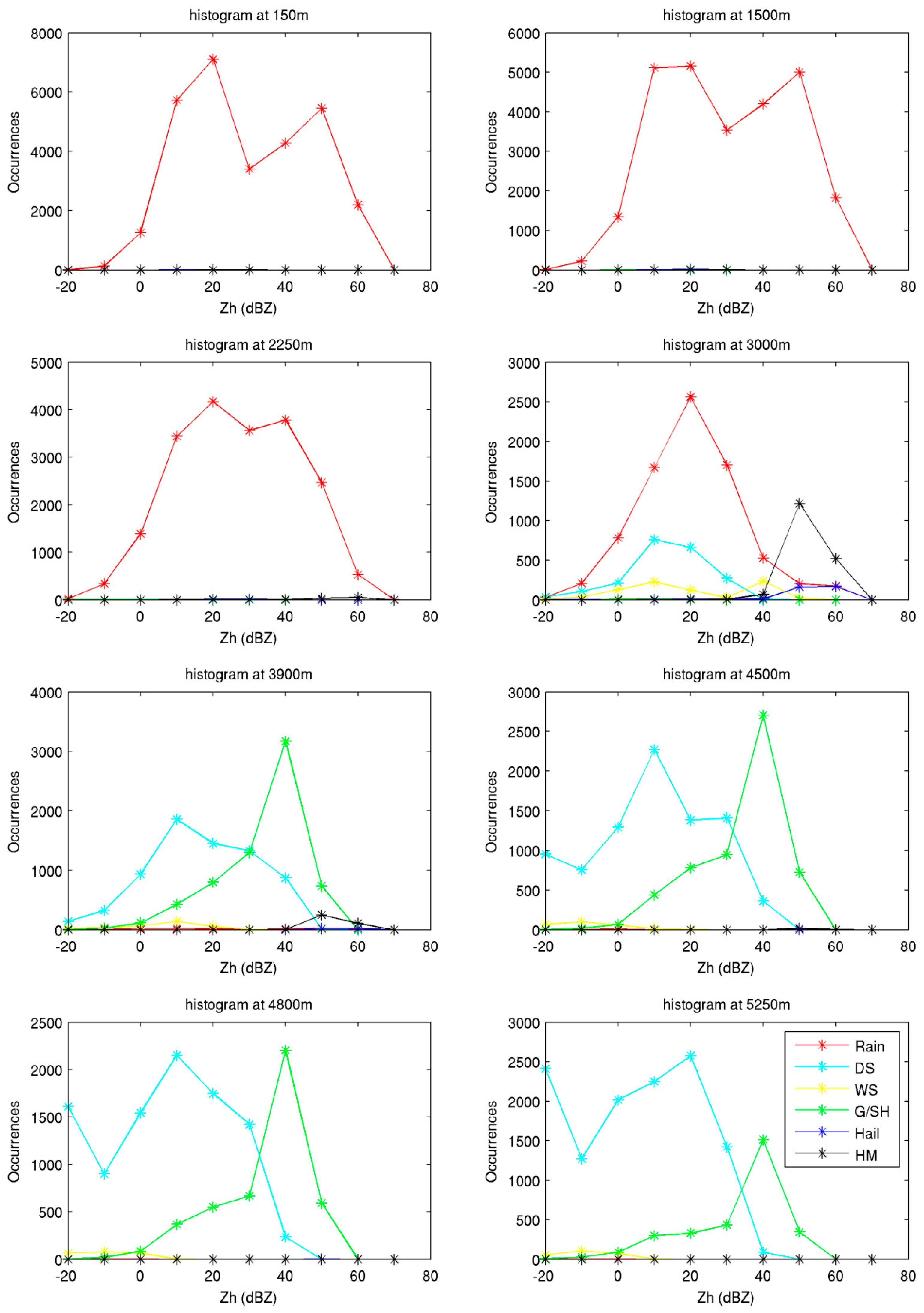
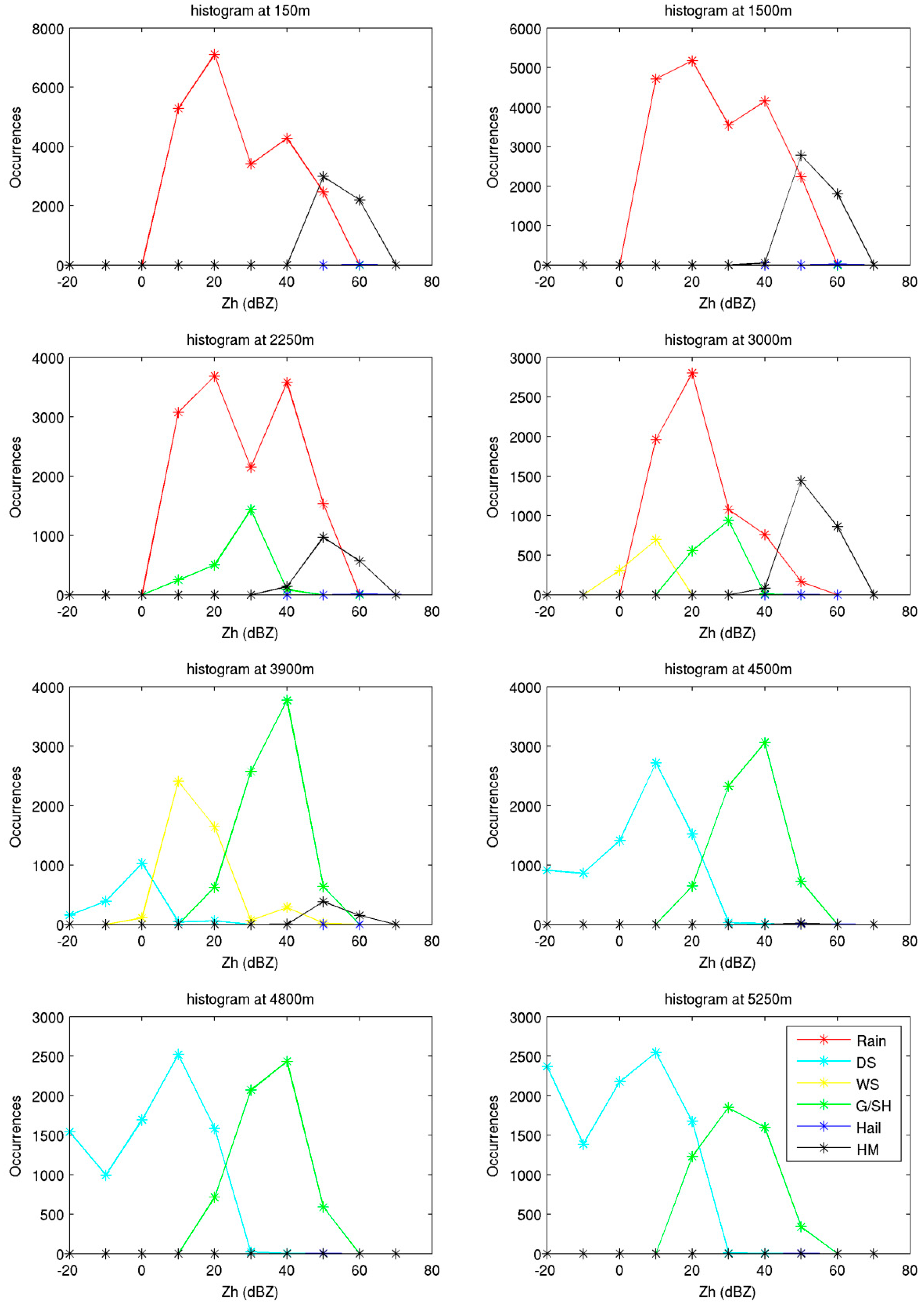
- Rain: this class includes, light rain, moderate rain and heavy rain (characteristics of convective events). For this reason, Zh spans from 10 to 60 dBZ and Zdr assumes positive values due to the oblate shape of rain. The liquid hydrometeors are typically detectable below the melting layer (ML).
- Dry Snow: this class includes all the non-wet ice particles, such as aggregates, plates, and columns, which determine the relatively low values of Zh. Such particles are typically detectable above the ML.
- Wet Snow: this class typically refers to ice particles in the melting phase, which typically present in the ML. These hydrometeors are usually ice particles or aggregated ice particles covered by a film of water that result in high values of Zh.
- Graupel: these hydrometeors are detectable both above and within the melting layer: usually these particles melt below the ML, but they may reach the ground during convective events with intense downdraft. They are smaller than hail and thus are associated with Zh values lower than those found in hail. They produce Zdr levels around 0, but conical graupel can produce negative Zdr values.
- Hail: the presence of hailstones characterizes convective events. They are typically found in the core of the deep convective cells and are detectable from the ground up to several kilometers above the ML. The updraft of the convective cell drives the growth of these particles, whose dimensions can reach the order of centimeters. Hailstones have high variability in their size and shape distribution. A typical signature of these particles is high values of Zh and Zdr and Kdp values around 0 (due to tumbling).
- Hail Mix: these hydrometeors occur from ground to few kilometers above the ML. The hydrometeors in this class are representative of a mix, present within the radar resolution volume, of raindrops lifted by updraft, supercooled raindrops, hail, small hail, and graupel. The typical signature is high values of Zh and low values of ρhv (these values decrease for the increase of hail amount of different size and increases with increasing mixing) while Zdr spans from negative to positive values.
- Unreliable data removal. pixel affected by ground clutter, anomalous propagation, and non-meteorological targets were identified and removed by applying a set of thresholds on Zh and on the standard deviations of φdp and Zdr [28].
- Attenuation correction for Zh and Zdr. Measurements propagated along paths below the 0°C level are corrected using a linear relation of Kdp with specific attenuation and specific differential attenuation (Ah, Adp, respectively) i.e., Ah,dp = γh,dpKdp. The parameterizations adopted to obtain γh,dp coefficients at X-band and C-band are performed by T-matrix scattering simulations using three years of disdrometer observations collected in Rome by a disdrometer [30].
- Correction of polarimetric variables for elevation angle. The values of the polarimetric variables of the same ensemble of scatterers change with the elevation angle. The most affected are Zdr and Kdp, while Zh typically does not change more than 1 dBZ, which is the intrinsic uncertainty due to noise. In general, Zdr and Kdp exhibit their maxima at 0° elevation and their values gradually decrease to 0 when reaching vertical incidence. In this work, Zdr and Kdp are corrected for elevation angles by recalculating their values as observed at 0° of elevation [31].
- Estimation of 0 °C level. The 0 °C level is estimated using vertical profiling soundings from the closest sounding station. If the processing is referred to the AWR, this level can be estimated directly from measurements collected by devices on-board an airplane.
- Input SVM data organization. The dual-polarization measurements Zh, Zdr, Kdp, and ρhv (or σ(Фdp) at C-band) and the height of 0° level are stored in an organized structure. The organization for the data access is made by n-tuples (a row of the whole structure contains a single n-tuple of polarimetric features).
3. SVM HCA Validation Using a Simulated Scenario
3.1. Set-Up of a Weather Scenario and Simulation of Radar Observations
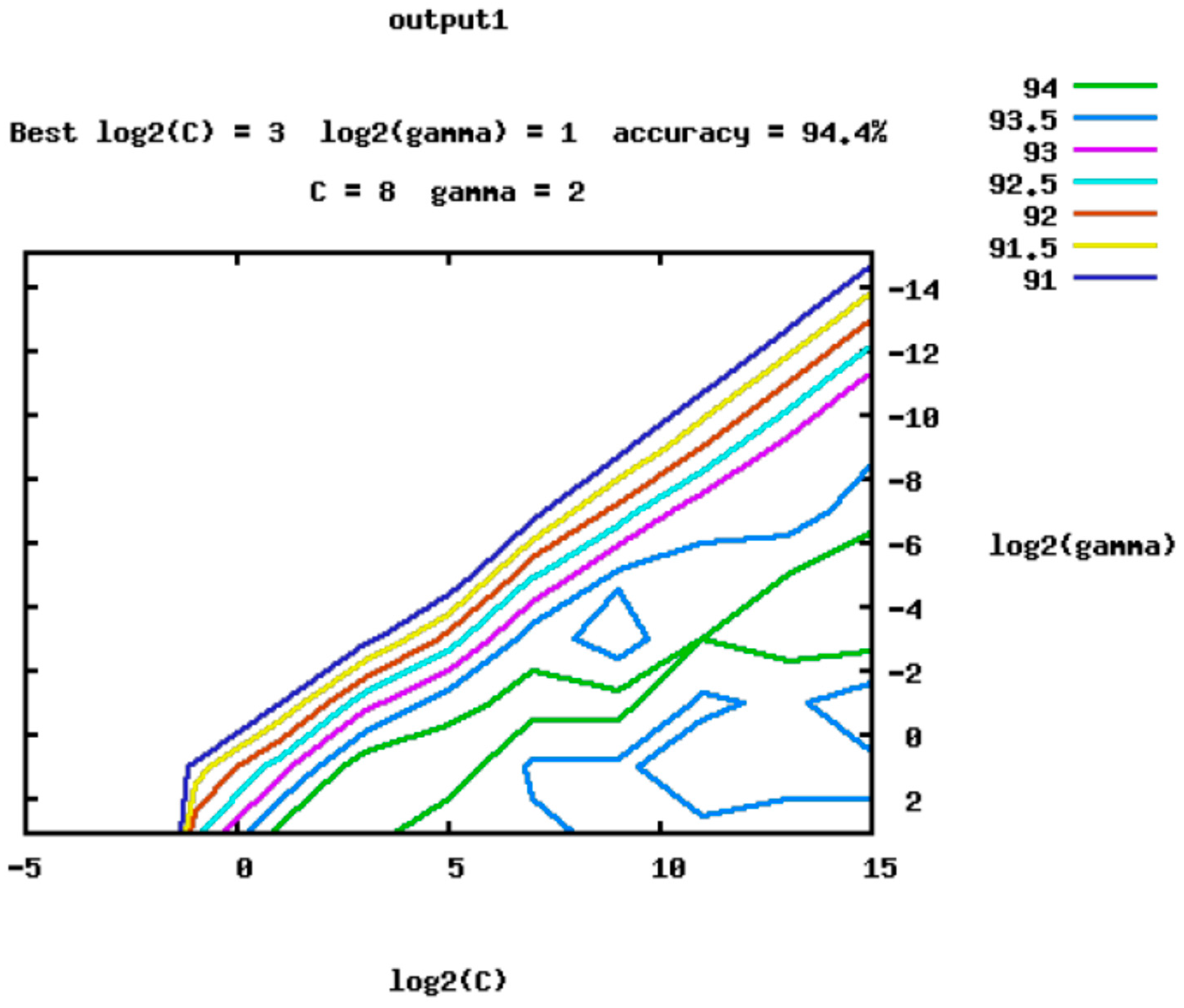
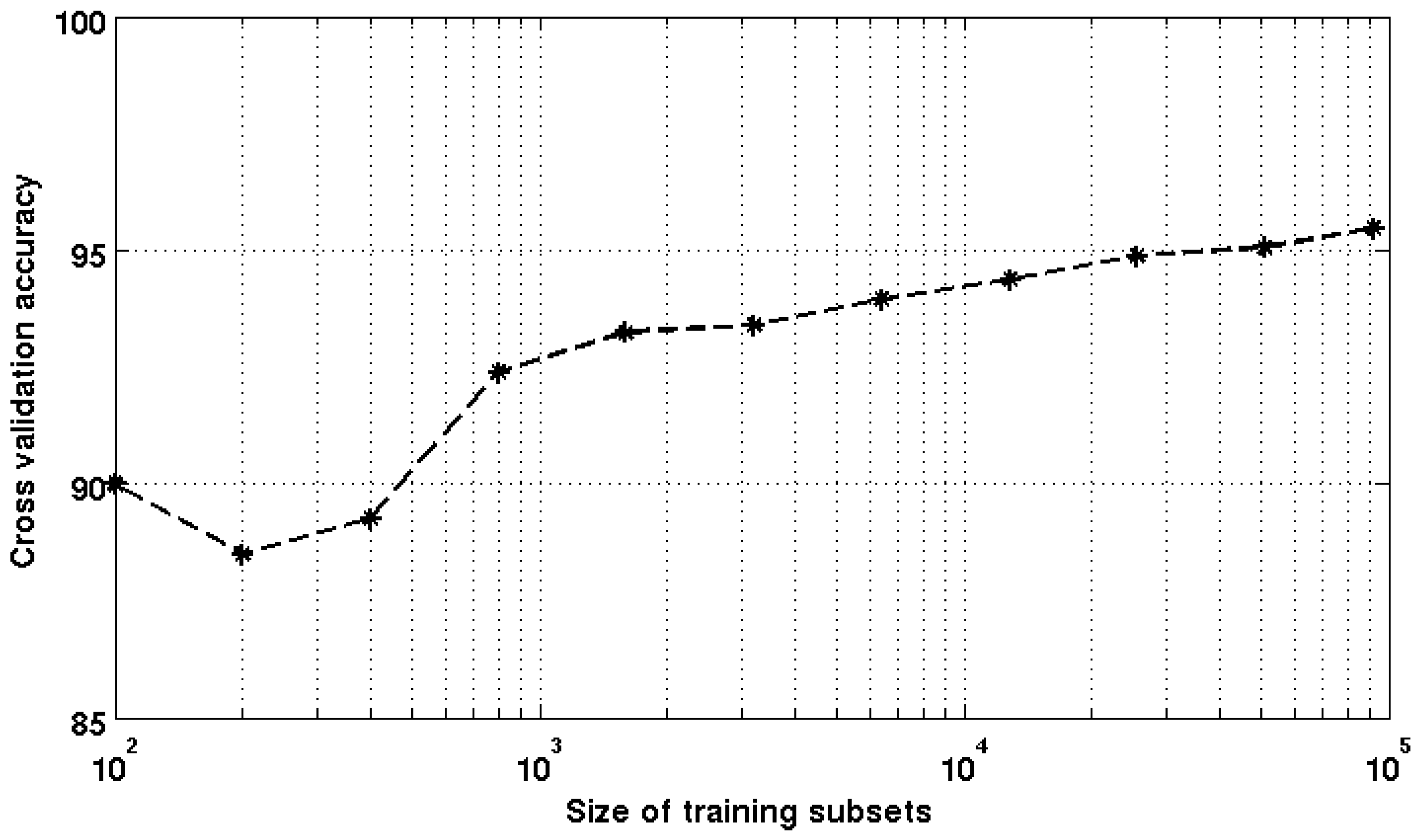
3.2. SVM Parameters Optimization
3.3. SVM HCA Validation Using WRF Model Output
4. Evaluation of the SVM Hydrometeor Classification with Real Measurements
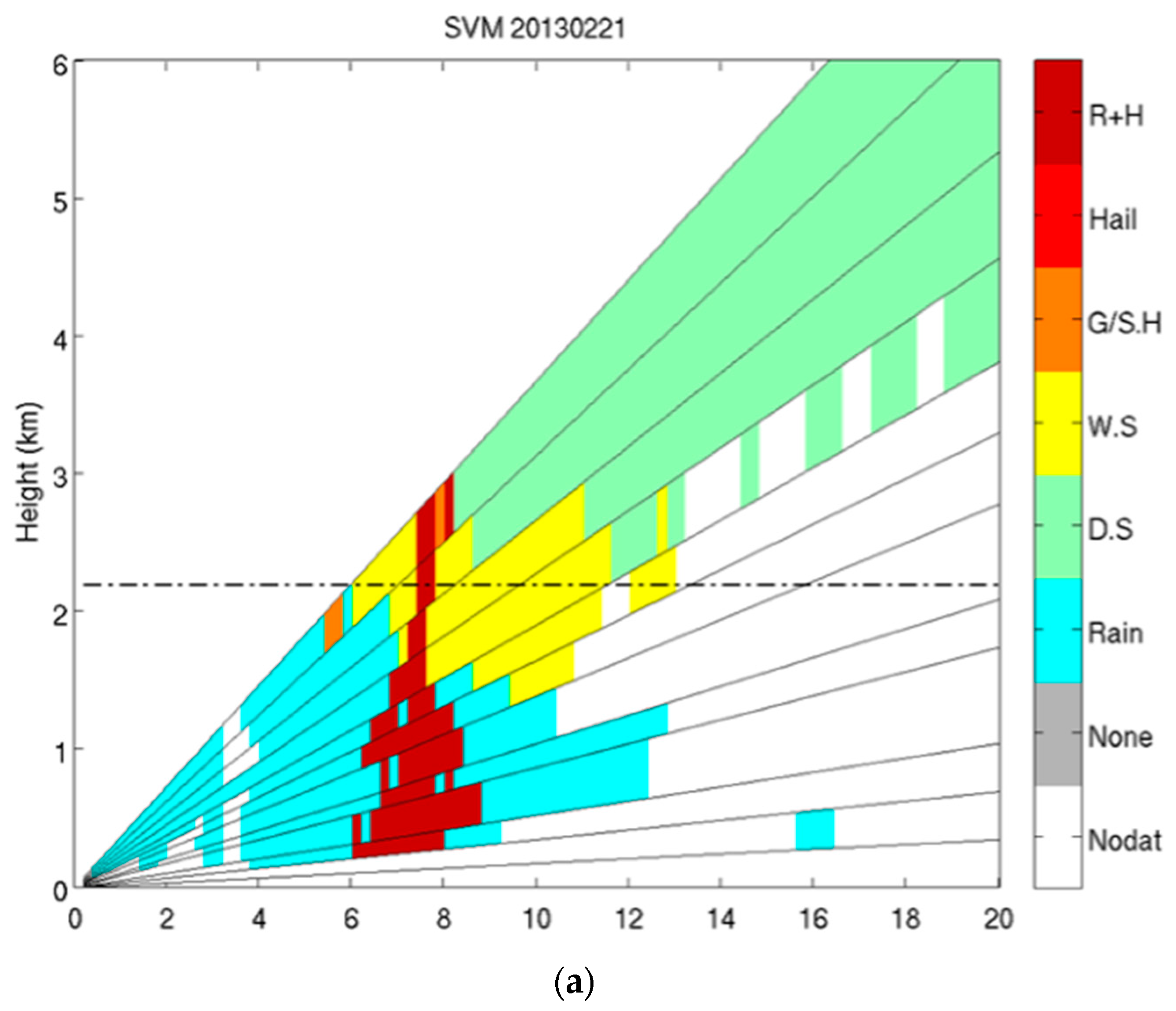
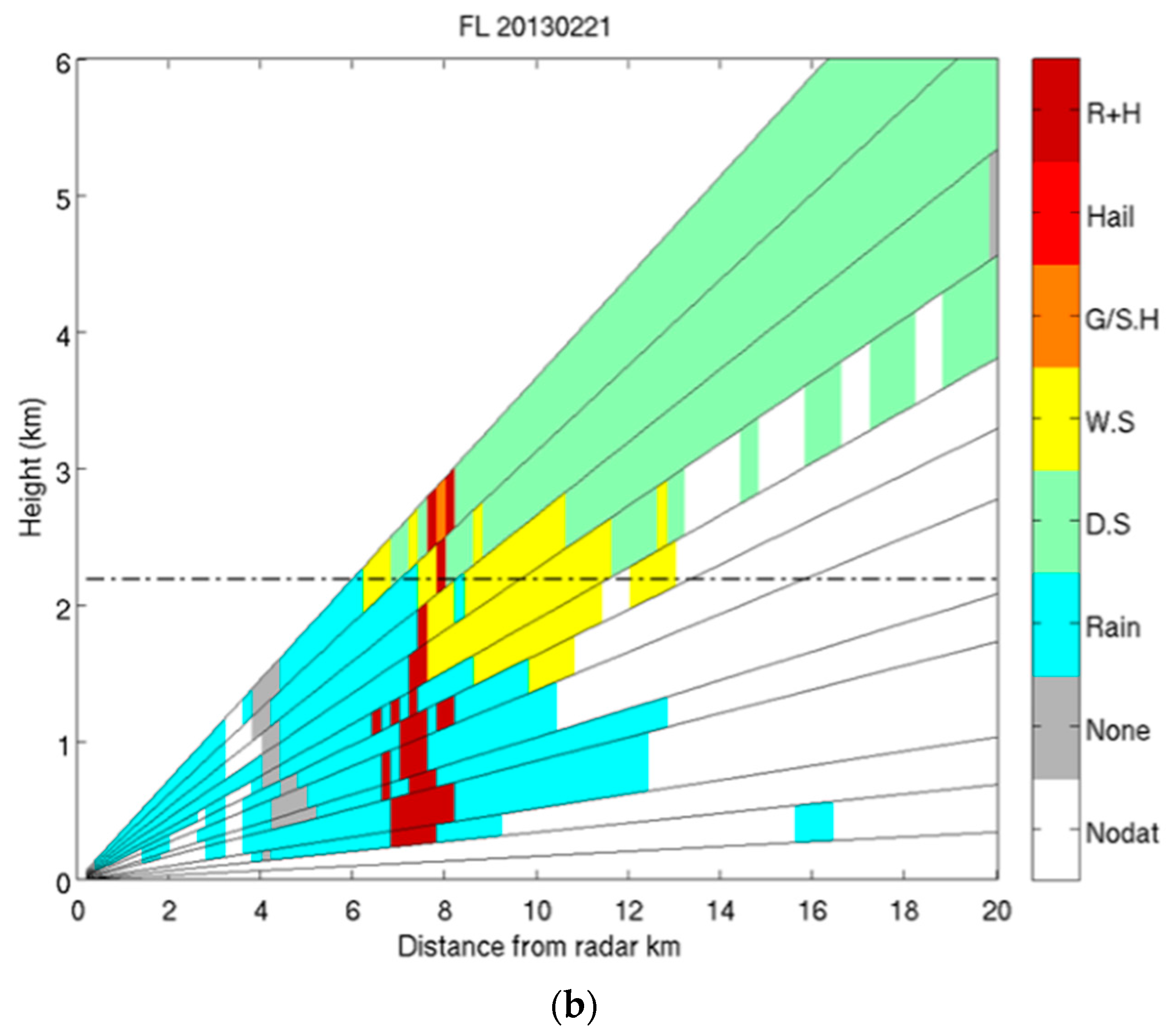
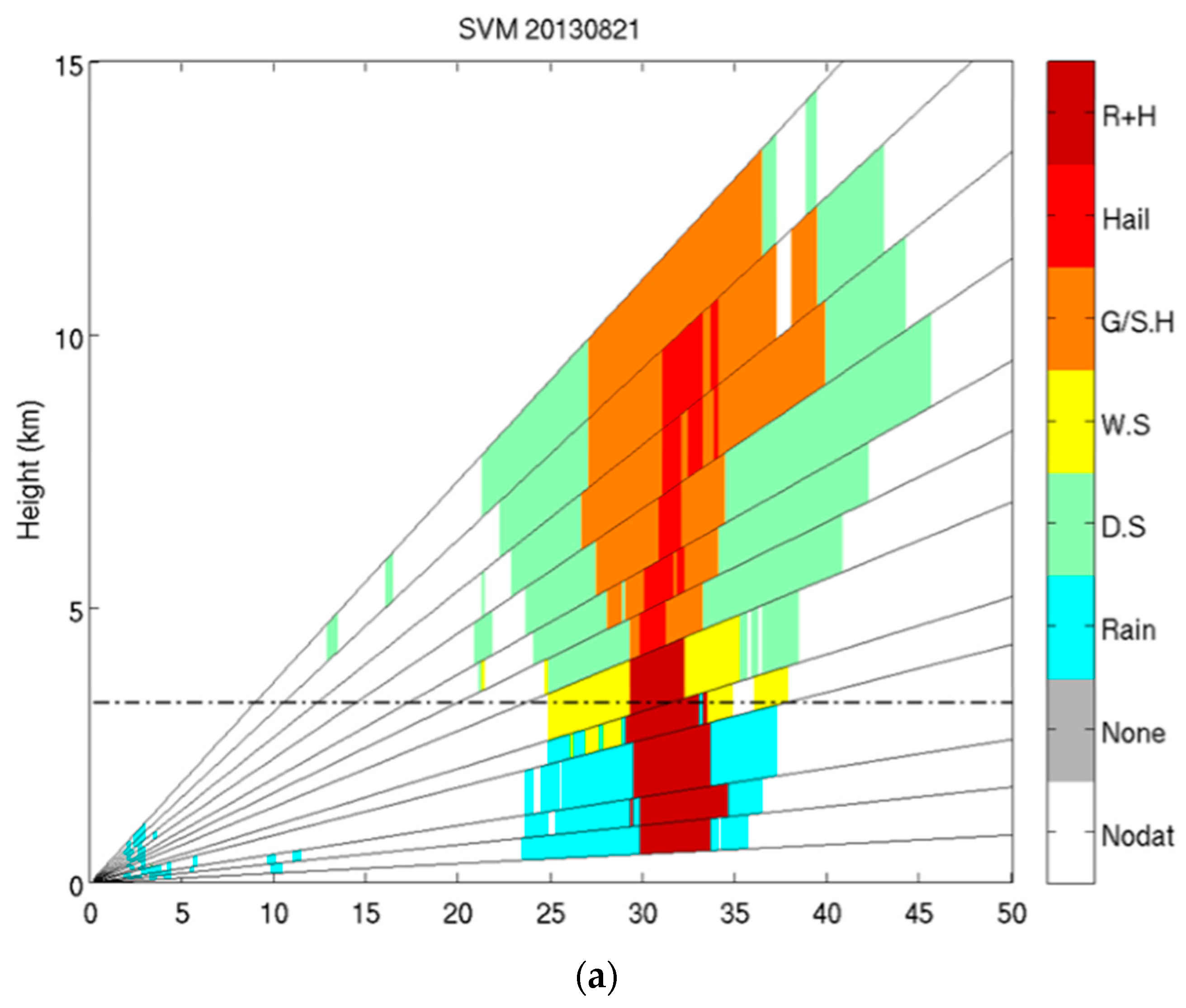
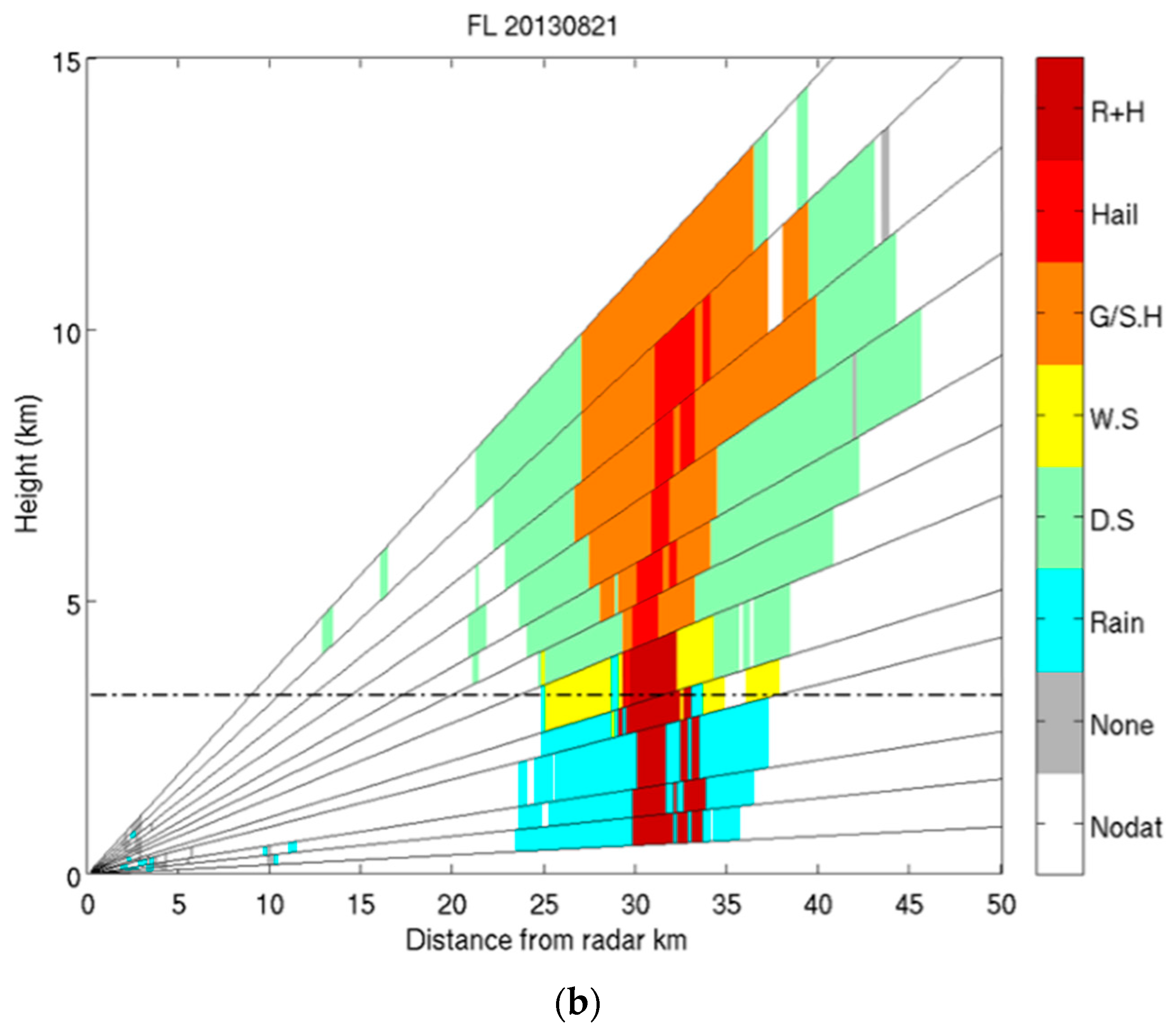
4.1. C-Band Dataset
4.2. X-Band Dataset
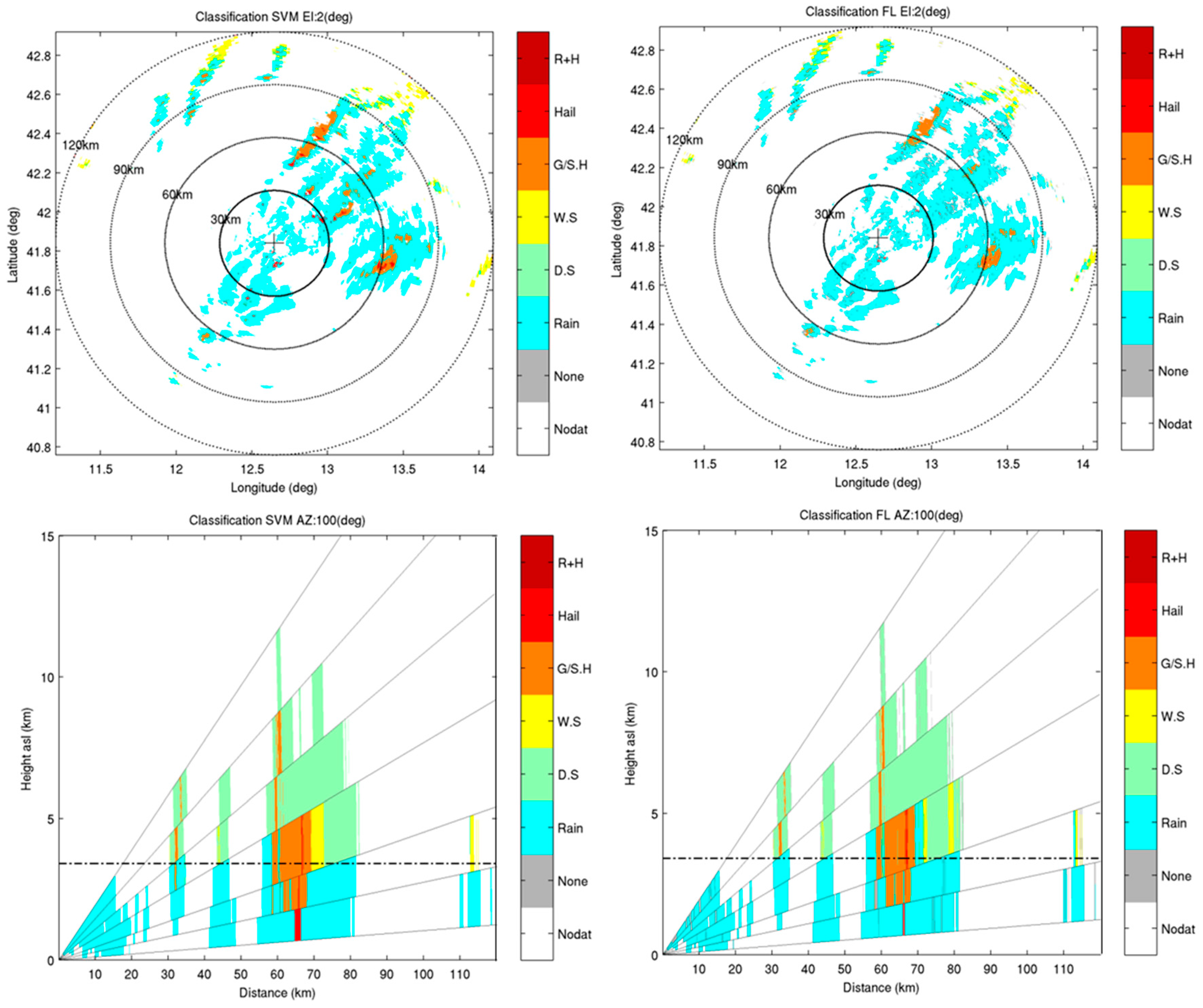
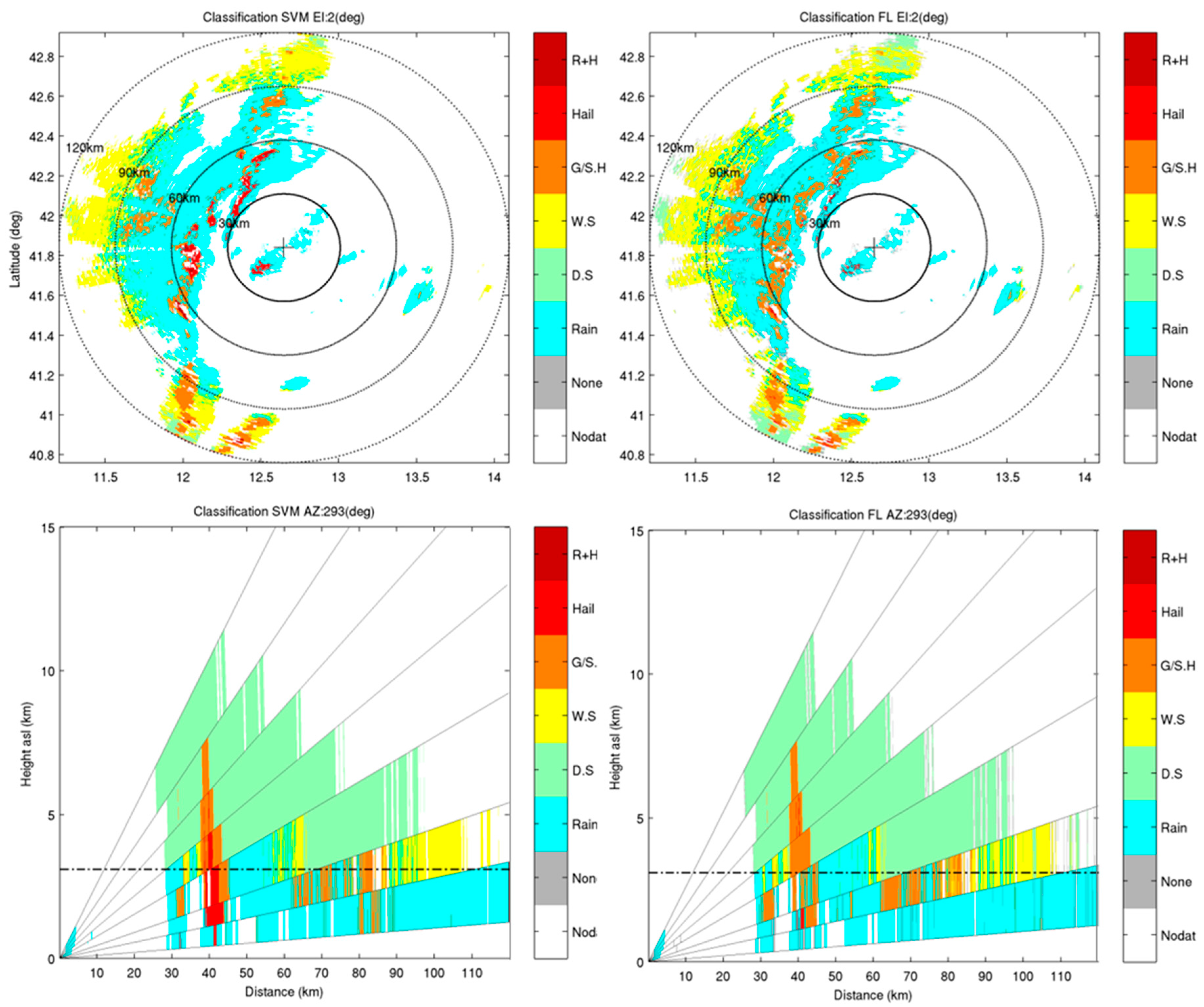
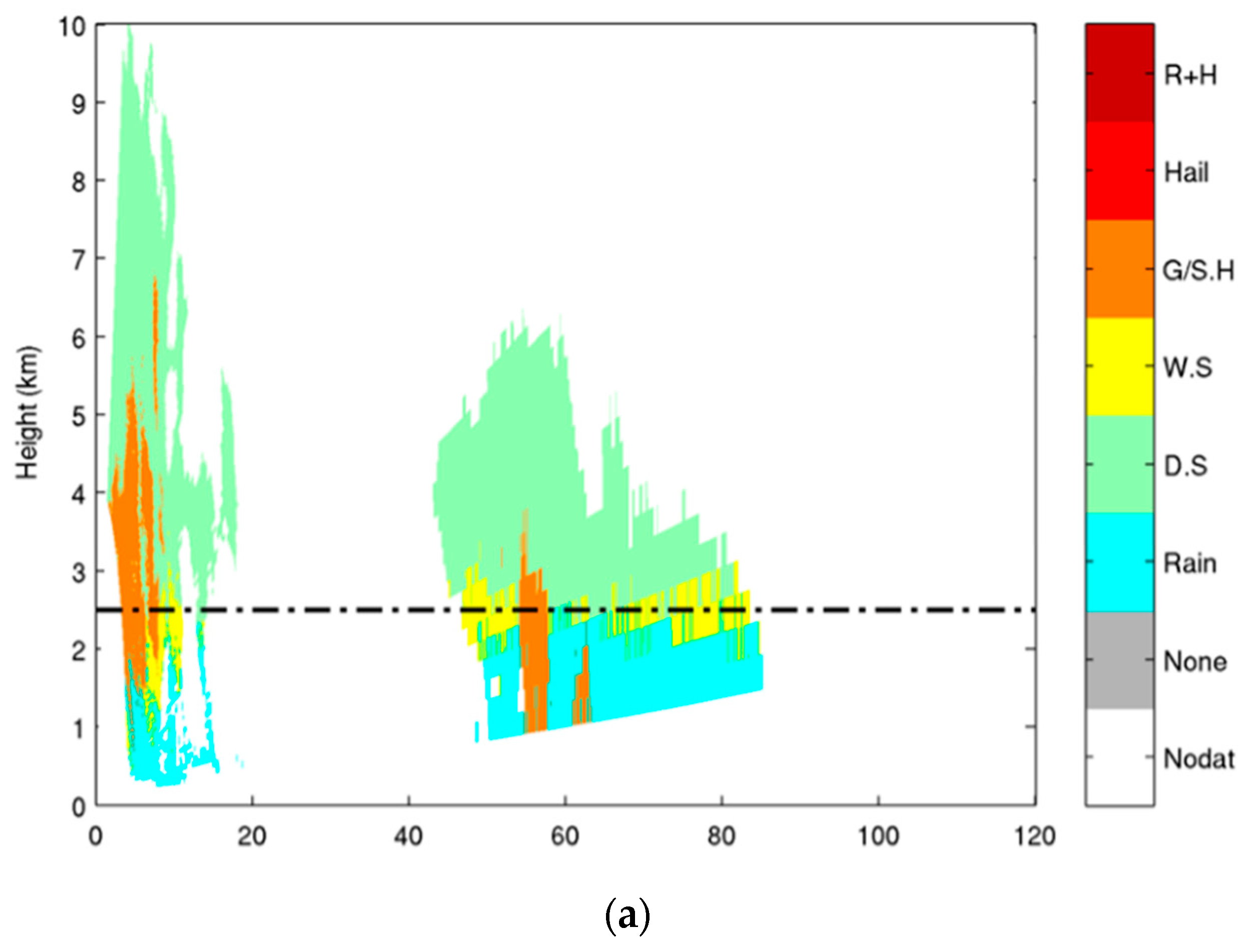
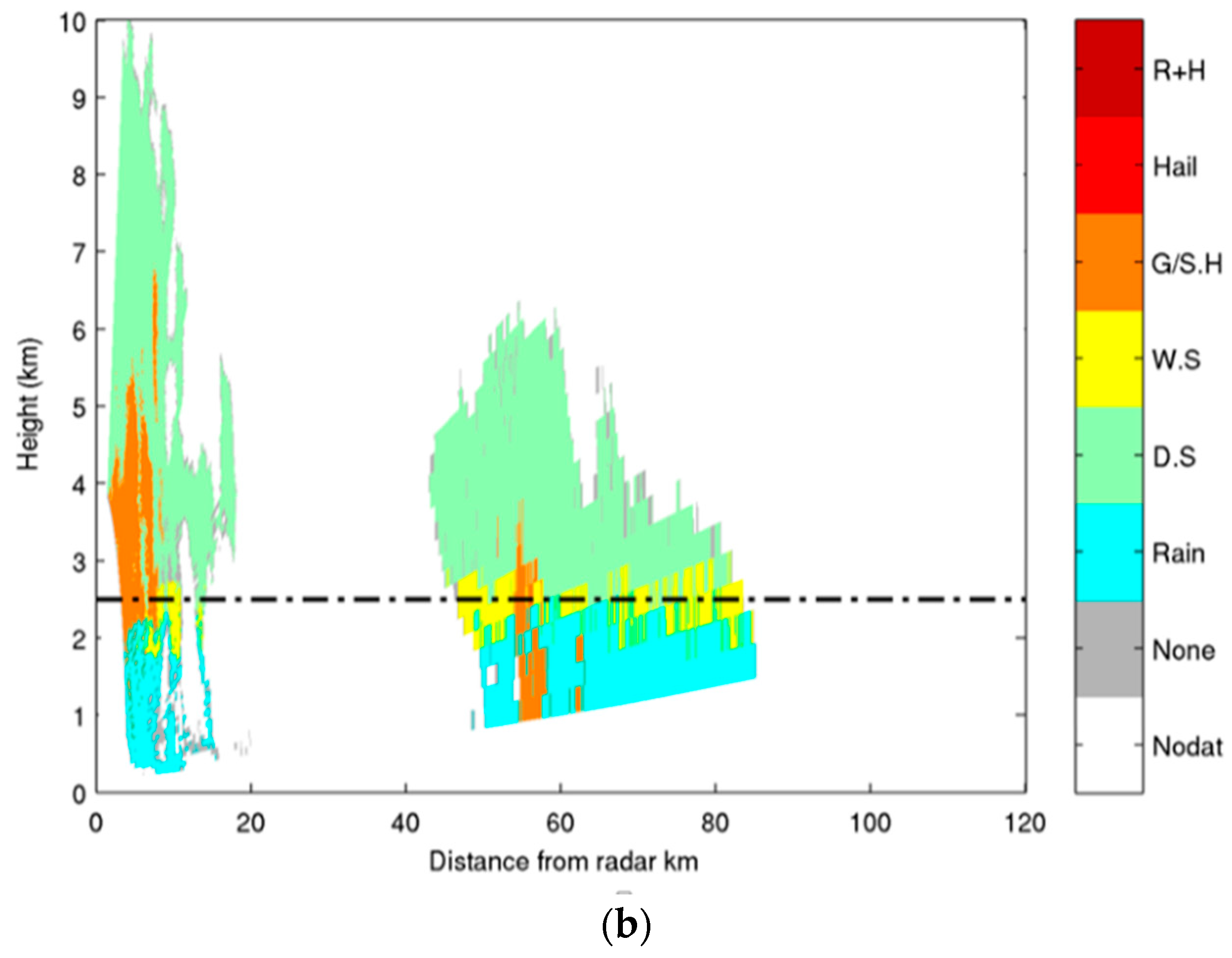
4.3. Comparison of Results from SVM and FL Classification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| CPU | 2 GHz Core i7 Intel |
| Display Touch Screen | 8″ XGA 1024 × 768 Pixels |
| Memory | 4GB DDR3 1066 MHz |
| Ethernet | 4 full duplex Ethernet channels (10/100 Base) |
| USB ports | 1 USB port on display unit, 2 USB ports on electronic unit |
| Operating System | Certified Linux Operating System, DO178 Level C |
Appendix B
References
- Liu, H.; Chandrasekar, V. Classification of hydrometeor type based on multiparameter radar measurements: Development of a fuzzy logic and neuro fuzzy systems and in-situ verification. J. Atmos. Ocean. Technol. 2000, 17, 140–164. [Google Scholar] [CrossRef]
- Straka, M.; Zrnic, D.S.; Ryzhkov, A.V. Bulk hydrometeor classification and quantification using polarimetric radar data: Synthesis of relations. J. Appl. Meteorol. 2000, 39, 1341–1372. [Google Scholar] [CrossRef]
- Dolan, B.; Rutledge, S.A. A theory-based hydrometeor identification algorithm for X-band polarimetric radars. J. Atmos. Ocean. Technol. 2009, 26, 2071–2088. [Google Scholar] [CrossRef]
- Dolan, B.; Rutledge, S.A.; Lim, S.; Chandrasekar, V.; Thurai, M. A robust C-band hydrometeor identification algorithm and application to a long-term polarimetric radar dataset. J. Appl. Meteorol. Climatol. 2013, 52, 2162–2186. [Google Scholar] [CrossRef]
- Zrnić, D.S.; Ryzhkov, A.; Straka, J.; Liu, Y.; Vivekanandan, J. Testing A Procedure for Automatic Classification of Hydrometeor Types. J. Atmos. Ocean. Technol. 2001, 18, 892–913. [Google Scholar] [CrossRef]
- Marzano, F.S.; Scaranari, D.; Vulpiani, G.; Montopoli, M. Supervised classification and estimation of hydrometeors using C-band dual-polarized radars: A Bayesian approach. IEEE Trans. Geosci. Remote Sens. 2008, 46, 85–98. [Google Scholar] [CrossRef]
- Al-Sakka, H.; Boumahmoud, A.A.; Fradon, B.; Frasier, S.J.; Tabary, P. A new fuzzy logic Hydrometeor Classification Scheme applied to the French X-, C-, and S-band polarimetric radars. J. Appl. Meteorol. Climatol. 2013, 52, 2328–2344. [Google Scholar] [CrossRef]
- Thompson, E.J.; Rutledge, S.A.; Dolan, B.; Chandrasekar, V.V.; Cheong, B. A Dual-Polarization Radar Hydrometeor Classification Algorithm for Winter Precipitation. J. Atmos. Ocean. Technol. 2014, 31, 1457–1481. [Google Scholar] [CrossRef]
- Roberto, N.; Adirosi, E.; Baldini, L.; Casella, D.; Dietrich, S.; Gatlin, P.; Panegrossi, G.; Petracca, M.; Sanò, P.; Tokay, A. Multi-sensor analysis of convective activity in central Italy during the HyMeX SOP 1.1. Atmos. Meas. Technol. 2016, 9, 535–552. [Google Scholar] [CrossRef]
- Bechini, R.; Chandrasekar, V. A semisupervised robust hydrometeor classification method for dual-polarization radar applications. J. Atmos. Ocean. Technol. 2015, 32, 22–47. [Google Scholar] [CrossRef]
- Grazioli, J.; Tuia, D.; Berne, A. Hydrometeor classification from polarimetric radar measurements: A clustering approach. Atmos. Meas. Tech. 2015, 8, 149–170. [Google Scholar] [CrossRef] [Green Version]
- Besic, N.; Figuerasi Ventura, J.; Grazioli, J.; Gabella, M.; Germann, U.; Berne, A. Hydrometeor classification through statistical clustering of polarimetric radar measurements: A semi-supervised approach. Atmos. Meas. Tech. 2016, 9, 4425–4445. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Lee, Y.; Wahba, G.; Ackerman, S.A. Cloud classification of satellite radiance data by multicategory support vector machines. J. Atmos. Ocean. Technol. 2004, 21, 159–169. [Google Scholar] [CrossRef]
- Grazioli, J.; Tuia, D.; Monhart, S.; Schneebeli, M.; Raupach, T.; Berne, A. Hydrometeor classification from two-dimensional video disdrometer data. Atmos. Meas. Tech. 2014, 7, 2869–2882. [Google Scholar] [CrossRef]
- Yanovsky, F.; Ostrovsky, Y.; Marchuk, V. Hydrometeor Type and Turbulence Intensity Recognition with Doppler-Polarimetric Radar. In Proceedings of the Radar Conference, Amsterdam, The Netherlands, 30–31 October 2008. [Google Scholar]
- Lim, S.; Chandrasekar, V.; Bringi, V.N. Hydrometeor classification system using dual-polarization radar measurements: Model improvements and in situ verification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 792–801. [Google Scholar] [CrossRef]
- Roberto, N.; Baldini, L.; Adirosi, E.; Lischi, S.; Lupidi, A.; Cuccoli, F.; Barcaroli, E.; Facheris, L. Test and validation of particle classification based on meteorological model and weather simulator. In Proceedings of the 13th European Radar Conference (EuRAD), London, UK, 11–13 October 2016. [Google Scholar]
- Lupidi, A.; Lischi, S.; Berizzi, F.; Cuccoli, F.; Roberto, N.; Baldini, L. Validation of the advanced polarimetric Doppler weather radar simulator with Polar55C Real Observations. In Proceedings of the 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014. [Google Scholar]
- Lischi, S.; Lupidi, A.; Martorella, M.; Cuccoli, F.; Facheris, L.; Baldini, L. Advanced Polarimetric Doppler Weather Radar Simulator. In Proceedings of the 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Boser, B.E.; Guyon, I.; Vapnik, V. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector network. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (assessed on 21 June 2017).
- Baldini, L.; Gorgucci, E.; Chandrasekar, V.; Peterson, W. Implementations of CSU Hydrometeor Classification Scheme for C-Band Polarimetric Radars. Available online: https://ams.confex.com/ams/32Rad11Meso/techprogram/paper_95865.htm (assessed on 21 June 2017).
- Vulpiani, G.; Baldini, L.; Roberto, N. Characterization of Mediterranean hail-bearing storms using an operational polarimetric X-band radar. Atmos. Meas. Tech. 2015, 8, 4681–4698. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Vulpiani, G.; Montopoli, M.; DelliPasseri, L.; Gioia, A.; Giordano, P.; Marzano, F.S. On the use of dual-polarized C-bandradar for operational rainfall retrieval in mountainous areas. J. Appl. Meteorol. Climatol. 2012, 51, 405–425. [Google Scholar] [CrossRef]
- Adirosi, E.; Baldini, L.; Roberto, N.; Vulpiani, G.; Russo, F. Using disdrometer measured raindrop size distributions to establish weather radar algorithms. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2015; pp. 110–128. [Google Scholar]
- Baldini, L.; Roberto, N.; Gorgucci, E.; Fritz, J.; Chandrasekar, V. Analysis of dual polarization images of precipitating clouds collected by the COSMO SkyMed constellation. Atmos. Res. 2013, 144, 21–37. [Google Scholar] [CrossRef]
- Michalakes, J.; Dudhia, J.; Gill, D.; Henderson, T.; Klemp, J.; Skamarock, W.; Wang, W. The Weather Reseach and Forecast Model: Software Architecture and Performance. In Use of High Performance Computing in Meteorology, Proceedings of the 11th ECMWF Workshop on the Use of High Performance Computing in Meteorology; Reading, England, October 2004; World Scientific: Singapore, 2005. [Google Scholar]
- Milbrandt, J.A.; Yau, M.K. A multimoment bulk microphysics parameterization. Part I: Analysis of the role of the spectral shape parameter. J. Atmos. Sci. 2005a, 62, 3051–3064. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A multimoment bulk microphysics parameterization. Part II: A proposed three-moment closure and scheme description. J. Atmos. Sci. 2005b, 62, 3065–3081. [Google Scholar] [CrossRef]
- Montopoli, M.; Roberto, N.; Adirosi, E.; Gorgucci, E.; Baldini, L. Investigation of Weather Radar Quantitative Precipitation Estimation Methodologies in Complex Orography. Atmosphere 2017, 8, 34. [Google Scholar] [CrossRef]
- Sebastianelli, S.; Russo, F.; Napolitano, F.; Baldini, L. On precipitation measurements collected by a weather radar and a rain gauge network. Nat. Hazards Earth Syst. Sci. 2013, 13, 605–623. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Featuresfor Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Haralick, R.M.; Linda, G.S. Computer and Robot Vision; Addison-Wesley Longman: Boston, MA, USA, 1992; pp. 28–48. [Google Scholar]
- Federal Aviation Administration: Guidelines for the Certification, Airworthiness, and Operational Use of Electronic Flight Bags. Available online: https://www.faa.gov/documentLibrary/media/Advisory_Circular/AC_120-76C.pdf (assessed on 21 June 2017).
- Sermi, F.; Cuccoli, F.; Mugnai, C.; Facheris, L. Aircraft hazard evaluation for critical weather avoidance. MetroAeroSpace 2015. [Google Scholar] [CrossRef]
- Serafino, G. Multi-objective Aircraft Trajectory Optimization for Weather Avoidance and Emissions Reduction. In International Workshop on Modelling and Simulation for Autonomous Systems; Springer: Cham, Switzerland, 2015; pp. 226–239. [Google Scholar]
| Rain | DS | WS | Graupel | Hail | HM | |
|---|---|---|---|---|---|---|
| qrain | >90% | 0 | >30% | 0 | 0 | >30% |
| qsnow | 0 | >90% | >60% | 0 | 0 | 0 |
| qgraup | 0 | 0 | >90% | 0 | ||
| qhail | 0 | 0 | 0 | >90% | >60% |
| Model (WRF) | |||||||
|---|---|---|---|---|---|---|---|
| Predicted (SVM) | Rain | DS | WS | Graupel | Hail | HM | |
| 51,390.0 | 1252.5 | 6289.0 | 567.0 | 210.0 | 913.5 | ||
| Rain | 51,447.0 | 1275.0 | 6320.0 | 592.5 | 222.0 | 941.0 | |
| 51,511.0 | 1290.0 | 6351.0 | 610.5 | 231.5 | 967.0 | ||
| 823.0 | 41,477.5 | 9689.0 | 5136.0 | 6.0 | 6.0 | ||
| DS | 835.5 | 41,524.0 | 9702.5 | 5172.0 | 8.0 | 7.0 | |
| 852.0 | 41,585.5 | 9714.5 | 5209.0 | 10.0 | 9.0 | ||
| 902.0 | 1940.0 | 2308.0 | 2382.0 | 13.0 | 172.0 | ||
| WS | 917.0 | 1964.0 | 2327.0 | 2422.5 | 16.0 | 180.0 | |
| 935.5 | 1993.0 | 2345.0 | 2454.5 | 20.0 | 190.0 | ||
| 4566.5 | 7401.5 | 916.5 | 17,119.0 | 2.0 | 17.0 | ||
| Graupel | 4601.0 | 7457.5 | 951.0 | 17,168.5 | 4.0 | 22.0 | |
| 4648.5 | 7515.5 | 980.5 | 17,219.5 | 6.0 | 27.0 | ||
| 1087.0 | 0.0 | 0.0 | 48.5.0 | 1311.0 | 1627.5 | ||
| Hail | 1112.5 | 0.0 | 0.0 | 56.5 | 1352.5 | 1668.0 | |
| 1151.0 | 0.0 | 0.0 | 67.0 | 1407.0 | 1719.0 | ||
| 7059.5 | 0.0 | 0.0 | 124.5 | 16,346.0 | 16,029.0 | ||
| HM | 7106.5 | 0.0 | 0.0 | 135.0 | 16,396.0 | 16,082.5 | |
| 7144.5 | 0.0 | 1.0 | 147.0 | 16,443.0 | 16,120.0 | ||
| None | Energy | Entropy | Homogeneity | S | |
|---|---|---|---|---|---|
| 20121015 1738UTC | |||||
| SVM | 0 | 0.424 | 0.369 | 0.957 | 281 |
| FL | 2404 | 0.341 | 0.365 | 0.893 | 323 |
| None | Energy | Entropy | Homogeneity | S | |
|---|---|---|---|---|---|
| 20130821 0450UTC | |||||
| SVM | 0 | 0.255 | 0.951 | 0.977 | 29 |
| FL | 73 | 0.247 | 0.939 | 0.958 | 37 |
| 20130221 1520UTC | |||||
| SVM | 0 | 0.333 | 0.689 | 0.952 | 17 |
| FL | 24 | 0.336 | 0.678 | 0.937 | 19 |
| None | Energy | Entropy | Homogeneity | S | |
|---|---|---|---|---|---|
| SVM | 0 | 0.645 | 0.105 | 0.933 | 87 |
| 0 | 0.820 | 0.339 | 0.964 | 448.5 | |
| 0 | 0.981 | 0.784 | 0.996 | 1691.5 | |
| FL | 900.5 | 0.414 | 0.102 | 0.790 | 77.5 |
| 3062.5 | 0.663 | 0.334 | 0.861 | 473.5 | |
| 9527.5 | 0.790 | 0.776 | 0.917 | 2126 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberto, N.; Baldini, L.; Adirosi, E.; Facheris, L.; Cuccoli, F.; Lupidi, A.; Garzelli, A. A Support Vector Machine Hydrometeor Classification Algorithm for Dual-Polarization Radar. Atmosphere 2017, 8, 134. https://doi.org/10.3390/atmos8080134
Roberto N, Baldini L, Adirosi E, Facheris L, Cuccoli F, Lupidi A, Garzelli A. A Support Vector Machine Hydrometeor Classification Algorithm for Dual-Polarization Radar. Atmosphere. 2017; 8(8):134. https://doi.org/10.3390/atmos8080134
Chicago/Turabian StyleRoberto, Nicoletta, Luca Baldini, Elisa Adirosi, Luca Facheris, Fabrizio Cuccoli, Alberto Lupidi, and Andrea Garzelli. 2017. "A Support Vector Machine Hydrometeor Classification Algorithm for Dual-Polarization Radar" Atmosphere 8, no. 8: 134. https://doi.org/10.3390/atmos8080134







