Parameterization of the Aerosol Upscatter Fraction as Function of the Backscatter Fraction and Their Relationships to the Asymmetry Parameter for Radiative Transfer Calculations
Abstract
:1. Introduction
2. Average Aerosol Upscatter Fraction
3. Henyey-Greenstein (HG) Phase Function, Asymmetry Parameter, and Its Range in the Atmosphere
3.1. Henyey-Greenstein (HG) Phase Function and Asymmetry Parameter g
3.2. Range of the Asymmetry Parameter
3.2.1. Principal Considerations
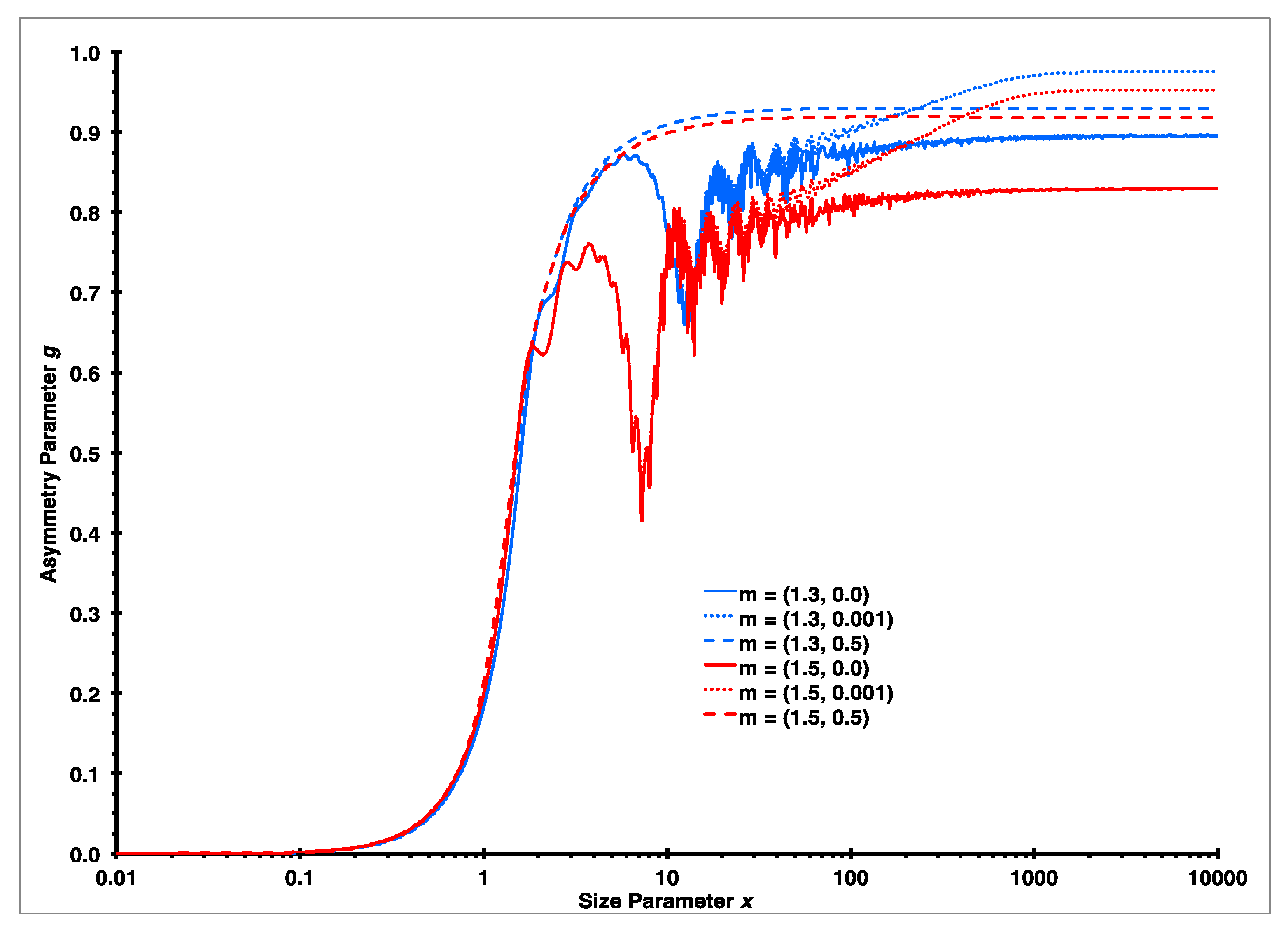
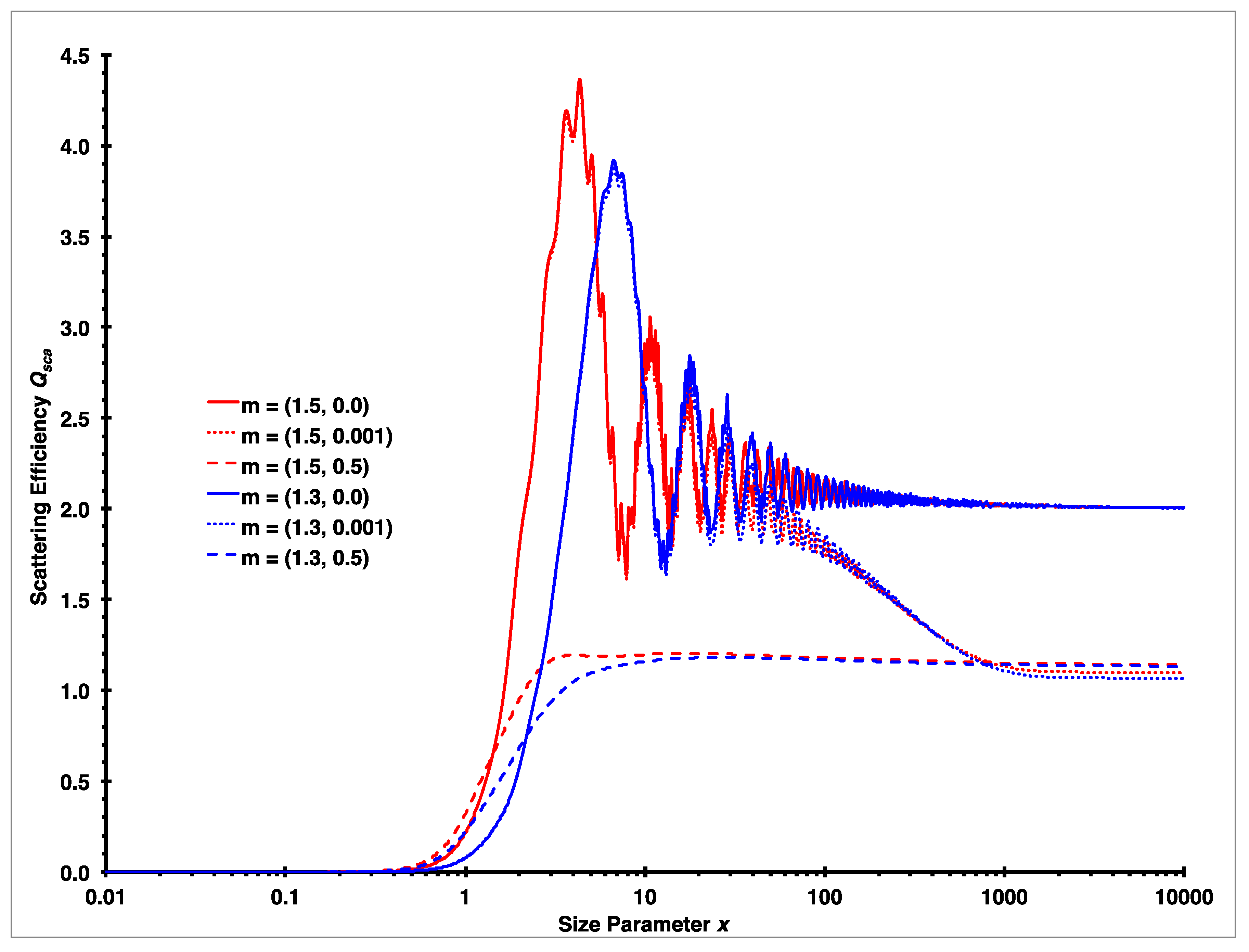
3.2.2. Mie Calculations of the Asymmetry Parameter g
3.2.3. Measurements of the Asymmetry Parameter g in the Ambient Atmosphere
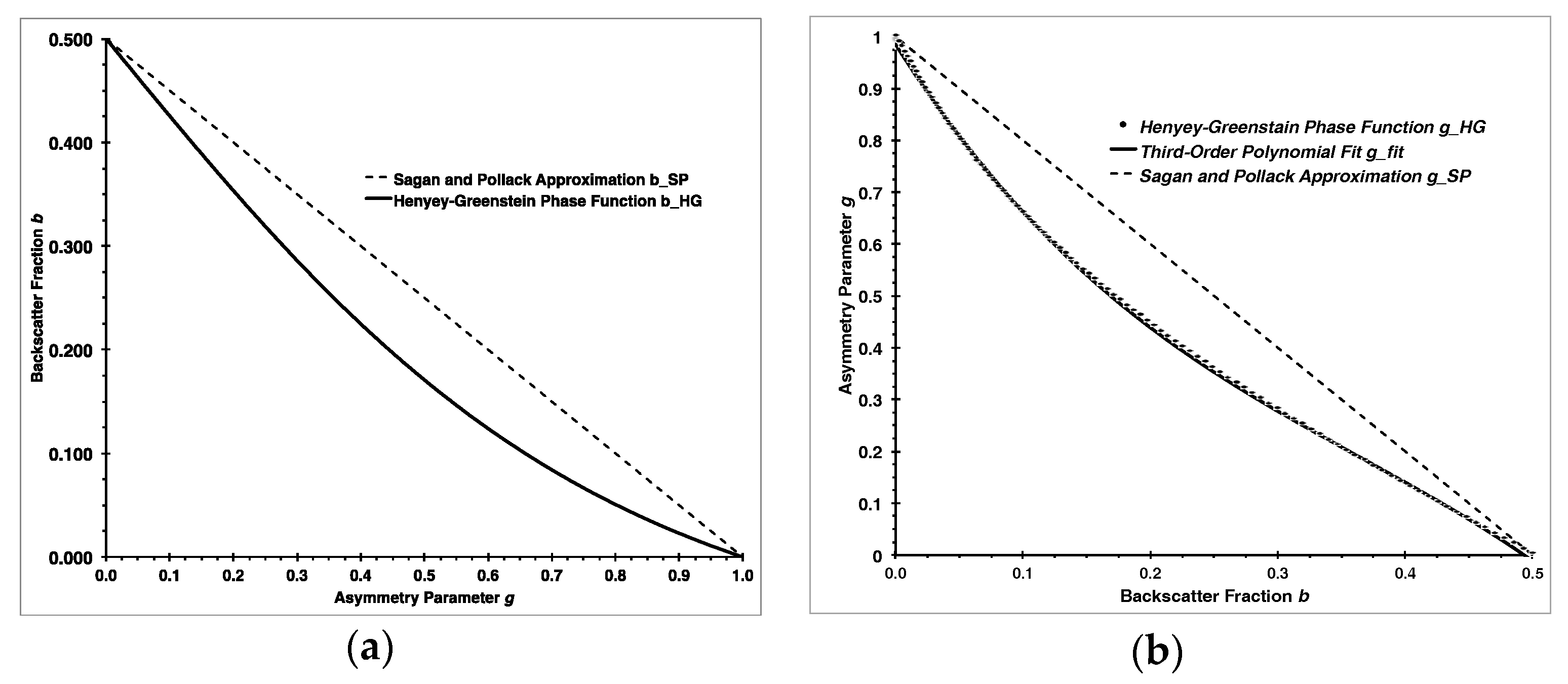
3.3. Backscatter Fraction for Henyey-Greenstein (HG) Phase Function: Solutions and Approximations
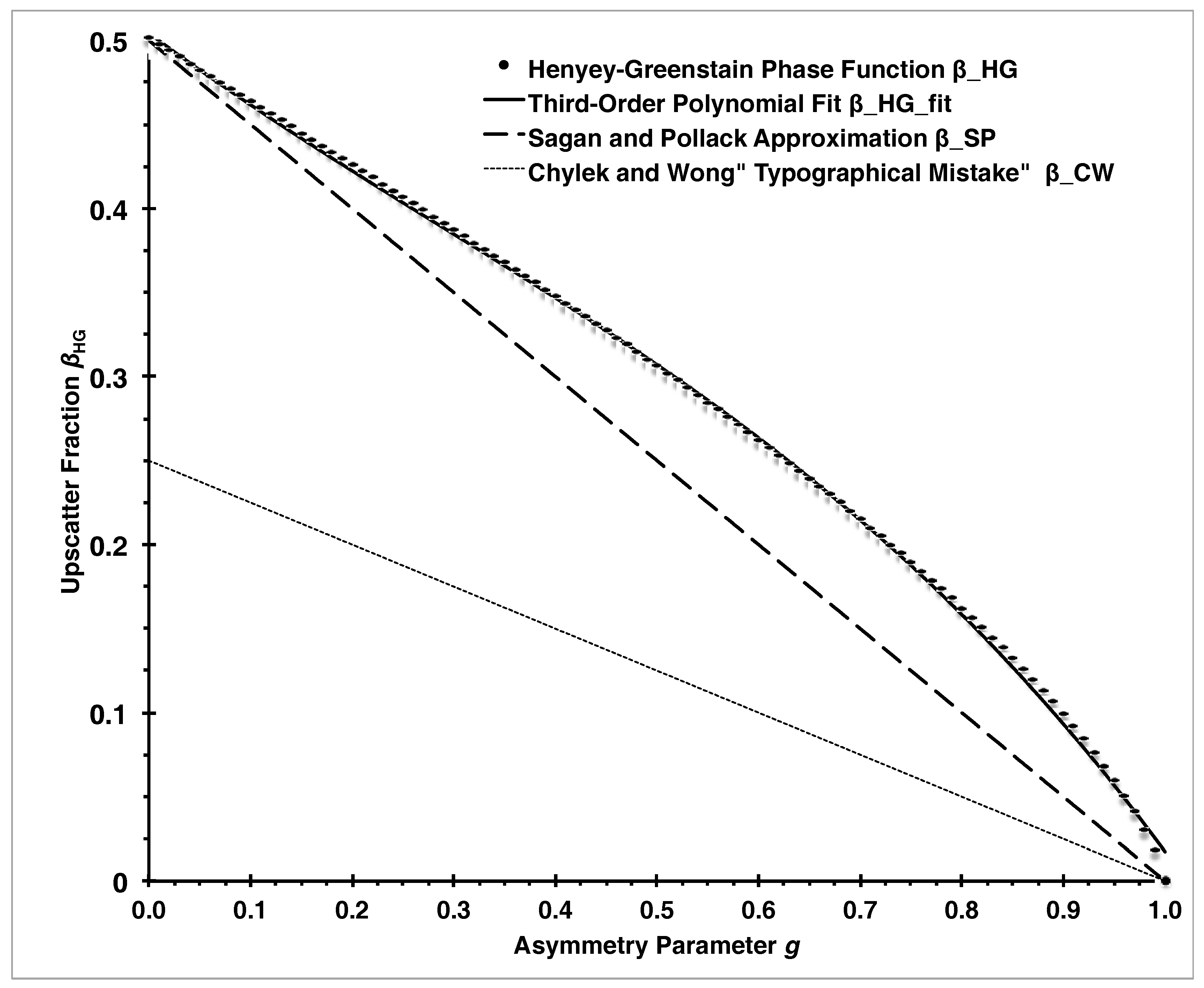
3.4. Upscatter Fraction for Henyey-Greenstein (HG) Phase Function: Solutions and Approximations
3.5. Relationship and Approximations between Average Upscatter Fraction and Backscatter Fraction for Henyey-Greenstein (HG) Phase Function
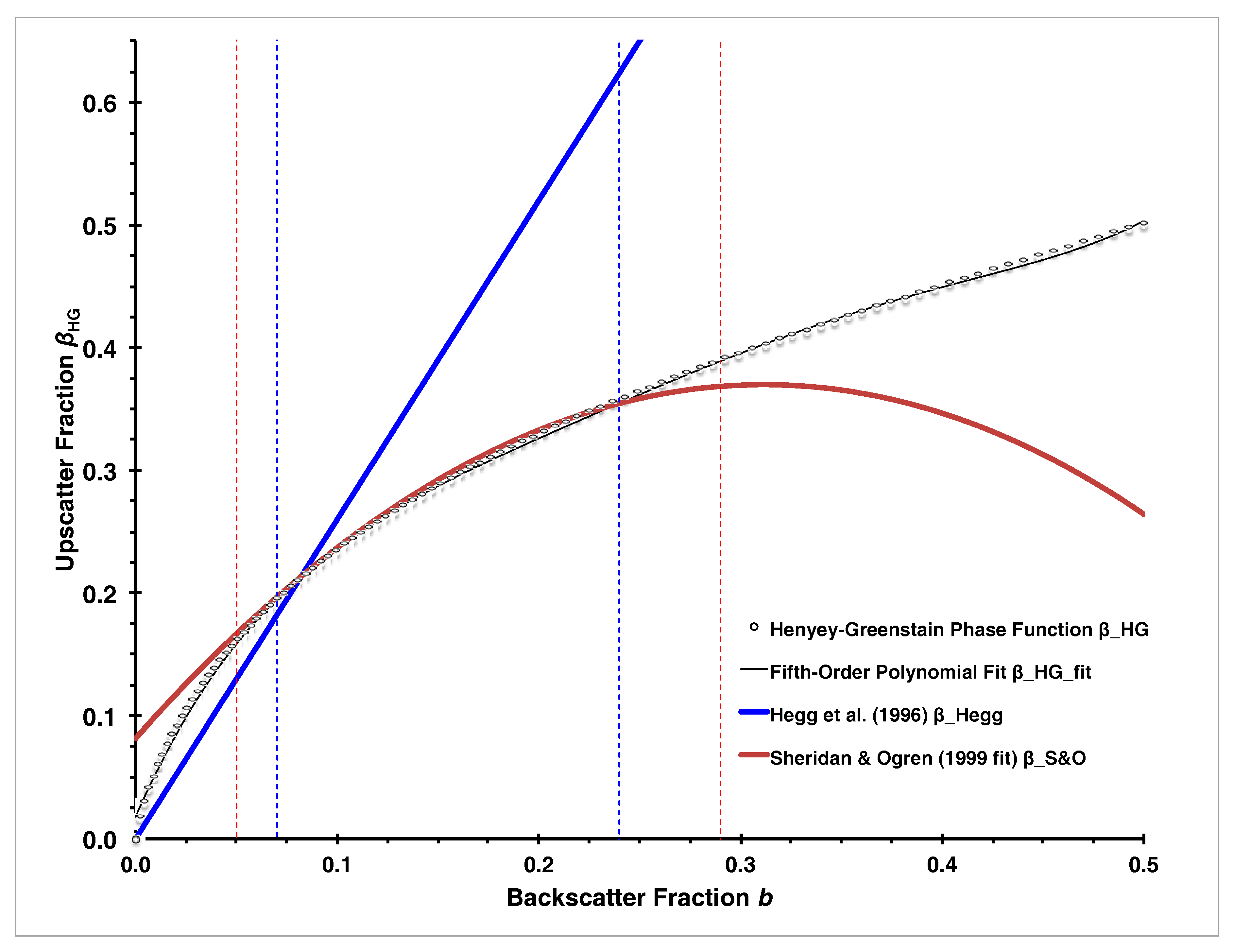
3.5.1. Approximation by Hegg, et al. [24]
3.5.2. Approximation by Sheridan and Ogren [32]
4. Conclusions
- b(g)
- Equation (8), analytical, exact;
- g(b)
- Equation (10), third order polynomial approximation with RSME = 0.0051;
- Equation (14), third order polynomial approximation with RSME = 0.0029;
- Equation (15), fifth order polynomial approximation with RSME = 0.0031.
Acknowledgments
Conflicts of Interest
Symbols
| Name | Symbol | Unit |
| aerosol asymmetry parameter | g | |
| aerosol backscatter fraction | b | |
| aerosol optical thickness | τ | |
| aerosol radiative forcing | ΔFaer | W/m2 |
| atmospheric transmittance above aerosol layer | Tatm | |
| average aerosol upscatter fraction | β | |
| fractional cloud cover | Acld | degree |
| particle radius | r | m |
| particle size parameter | x | |
| refractive index, complex | m | |
| refractive index, real | n | |
| refractive index, imaginary | k | |
| scattering angle | θ | degree |
| scattering efficiency | Qsca | |
| scattering phase function | p | |
| single scattering albedo | ω | |
| solar constant | s0 | W/m2 |
| solar zenith angle | θ0 | degree |
| surface reflectance | Rsurf |
References
- Charlson, R.J.; Langner, J.; Rodhe, H.; Leovy, C.B.; Warren, S.G. Perturbation of the northern-hemisphere radiative balance by backscattering from anthropogenic sulfate aerosols. Tellus 1991, 43AB, 152–163. [Google Scholar] [CrossRef]
- Chýlek, P.; Wong, J. Effect of absorbing aerosol on global radiation budget. Geophys. Res. Lett. 1995, 22, 929–931. [Google Scholar] [CrossRef]
- Haywood, J.M.; Shine, K.P. The effect of anthropogenic sulfate and soot aerosol on the clear-sky planetary radiation budget. Geophys. Res. Lett. 1995, 22, 603–606. [Google Scholar] [CrossRef]
- Hassan, T.; Moosmüller, H.; Chung, C.E. Coefficients of an analytical aerosol forcing equation determined with a monte-carlo radiation model. J. Quant. Spectrosc. Radiat. Transfer 2015, 164, 129–136. [Google Scholar] [CrossRef]
- Andrews, E.; Sheridan, P.J.; Fiebig, M.; McComiskey, A.; Ogren, J.A.; Arnott, W.P.; Covert, D.S.; Elleman, R.; Gasparini, R.; Collins, D.; et al. Comparison of methods for deriving aerosol asymmetry parameter. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, S.E. The whitehouse effect—shortwave radiative forcing of climate by anthropogenic aerosols: An overview. J. Aerosol Sci. 1996, 27, 359–382. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Grams, G.W. The backscattered fraction in two-stream approximations. J. Atmos. Sci. 1976, 33, 2440–2451. [Google Scholar] [CrossRef]
- Henyey, L.G.; Greenstein, J.L. Diffuse radiation in the galaxy. Astrophys. J. 1941, 93, 70–83. [Google Scholar] [CrossRef]
- Boucher, O. On aerosol direct shortwave forcing and the henyey-greenstein phase function. J. Atmos. Sci. 1998, 55, 128–134. [Google Scholar] [CrossRef]
- Marshall, S.F.; Covert, D.S.; Charlson, R.J. Relationship between asymmetry parameter and hemispheric backscatter ratio: Implications for climate forcing by aerosols. Appl. Opt. 1995, 34, 6306–6311. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I.; Hovenier, J.W.; Travis, L.D. Light Scattering by Nonspherical Particles: Theory, Measurements, and Applications; Academic Press: San Diego, CA, USA, 2000; pp. 1–690. [Google Scholar]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover Publications: New York, NY, USA, 1981; pp. 1–470. [Google Scholar]
- Mie, G. Beiträge zur optik trüber medien, speziell kolloidaler metallösungen. Ann. Physik 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
- Moosmüller, H.; Arnott, W.P. Particle optics in the rayleigh regime. J. Air Waste Manag. Assoc. 2009, 59, 1028–1031. [Google Scholar] [CrossRef] [PubMed]
- Fiebig, M.; Ogren, J.A. Retrieval and climatology of the aerosol asymmetry parameter in the NOAA aerosol monitoring network. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Arnott, W.P.; University of Nevada, Reno, NV, USA. Personal Communication, 2012.
- Ramachandran, S.; Rajesh, T.A. Asymmetry parameters in the lower troposphere derived from aircraft measurements of aerosol scattering coefficients over tropical India. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Gopal, K.R.; Arafath, S.M.; Lingaswamy, A.P.; Balakrishnaiah, G.; Kumari, S.P.; Devi, K.U.; Reddy, N.S.K.; Reddy, K.R.O.; Reddy, M.P.; Reddy, R.R.; et al. In-situ measurements of atmospheric aerosols by using integrating nephelometer over a semi-arid station, southern India. Atmos. Environ. 2014, 86, 228–240. [Google Scholar] [CrossRef]
- Formenti, P.; Andreae, M.O.; Lelieveld, J. Measurements of aerosol optical depth above 3570 m asl in the North Atlantic free troposphere: Results from ACE-2. Tellus 2000, 52B, 678–693. [Google Scholar] [CrossRef]
- Hegg, D.A.; Covert, D.S.; Rood, M.J.; Hobbs, P.V. Measurements of aerosol optical properties in marine air. J. Geophys. Res. 1996, 101, 12893–12903. [Google Scholar] [CrossRef]
- Hegg, D.A.; Hobbs, P.V.; Gassó, S.; Nance, J.D.; Rangno, A.L. Aerosol measurements in the Arctic relevant to direct and indirect radiative forcing. J. Geophys. Res. 1996, 101, 23349–23363. [Google Scholar] [CrossRef]
- Ichoku, C.; Andreae, M.O.; Andreae, T.W.; Meixner, F.X.; Schebeske, G.; Formenti, P.; Maenhaut, W.; Cafmeyer, J.; Ptasinski, J.; Karnieli, A.; et al. Interrelationships between aerosol characteristics and light scattering during late winter in an Eastern Mediterranean arid environment. J. Geophys. Res.-Atmos. 1999, 104, 24371–24393. [Google Scholar] [CrossRef]
- Andrews, E.; Ogren, J.A.; Bonasoni, P.; Marinoni, A.; Cuevas, E.; Rodríguez, S.; Sun, J.Y.; Jaffe, D.A.; Fischer, E.V.; Baltensperger, U.; et al. Climatology of aerosol radiative properties in the free troposphere. Atmos. Res. 2011, 102, 365–393. [Google Scholar] [CrossRef]
- Ma, N.; Birmili, W.; Müller, T.; Tuch, T.; Cheng, Y.; Xu, W.; Zhao, C.; Wiedensohler, A. Tropospheric aerosol scattering and absorption over central Europe: A closure study for the dry particle state. Atmos. Chem. Phys. 2014, 14, 6241–6259. [Google Scholar] [CrossRef]
- Sagan, C.; Pollack, J.B. Anisotropic nonconservative scattering and the clouds of venus. J. Geophys. Res. 1967, 72, 469–477. [Google Scholar] [CrossRef]
- Chýlek, P.; Los Alamos National Laboratory, Los Alamos, NM, USA. Personal Communication, 2011.
- Anderson, T.L.; Covert, D.S.; Marshall, S.F.; Laucks, M.L.; Charlson, R.J.; Waggoner, A.P.; Ogren, J.A.; Caldow, R.; Holm, R.L.; Quant, F.R.; et al. Performance characteristics of a high-sensitivity, three-wavelength, total scatter/backscatter nephelometer. J. Atmos. Ocean. Technol. 1996, 13, 967–986. [Google Scholar] [CrossRef]
- Müller, T.; Laborde, M.; Kassell, G.; Wiedensohler, A. Design and performance of a three-wavelength led-based total scatter and backscatter integrating nephelometer. Atmos. Meas. Tech. 2011, 4, 1291–1303. [Google Scholar] [CrossRef]
- Sheridan, P.J.; Ogren, J.A. Observations of the vertical and regional variability of aerosol optical properties over central and eastern North America. J. Geophys. Res. 1999, 104, 16793–16805. [Google Scholar] [CrossRef]
- Formenti, P.; Andreae, M.O.; Andreae, T.W.; Ichoku, C.; Schebeske, G.; Kettle, J.; Maenhaut, W.; Cafmeyer, J.; Ptasinsky, J.; Karnieli, A.; et al. Physical and chemical characteristics of aerosols over the negev desert (Israel) during summer 1996. J. Geophys. Res. 2001, 106, 4871–4890. [Google Scholar] [CrossRef]
- Anderson, T.L.; Covert, D.S.; Wheeler, J.D.; Harris, J.M.; Perry, K.D.; Trost, B.E.; Jaffe, D.J.; Ogren, J.A. Aerosol backscatter fraction and single scattering albedo: Measured values and uncertainties at a coastal station in the Pacific Northwest. J. Geophys. Res. 1999, 104, 26793–26807. [Google Scholar] [CrossRef]
| Range of g | Method | Location | Reference |
|---|---|---|---|
| 0.36–0.71 | Novel Algorithm | Global NOAA Network | Fiebig and Ogren [18] |
| 0.5–0.8 | Mie Retrieval | Oklahoma, USA | Andrews, et al. [5] |
| 0.3–0.6 | Nephelometer Retrieval | Tropical India | Ramachandran and Rajesh [20] |
| 0.53–0.65 | Nephelometer Retrieval | Southern India | Gopal, et al. [21] |
| 0.72–0.73 | Mie Retrieval | Canari Islands, Spain | Formenti, et al. [22] |
| 0.44–0.72 | Nephelometer Retrieval | Marine West Coast, USA | Hegg, et al. [23] |
| 0.37–0.75 | Nephelometer Retrieval | Prudhoe Bay, AK, USA | Hegg, et al. [24] |
| 0.40–0.66 | Nephelometer Retrieval | Negev Desert, Israel | Ichoku, et al. [25] |
| 0.26–0.77 | Nephelometer Retrieval | Northern, Mid-Latitudes | Andrews, et al. ([26]; Figure 3f) |
| 0.34–0.73 | Nephelometer Retrieval | Melpitz, East Germany | Ma, et al. [27] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moosmüller, H.; Ogren, J.A. Parameterization of the Aerosol Upscatter Fraction as Function of the Backscatter Fraction and Their Relationships to the Asymmetry Parameter for Radiative Transfer Calculations. Atmosphere 2017, 8, 133. https://doi.org/10.3390/atmos8080133
Moosmüller H, Ogren JA. Parameterization of the Aerosol Upscatter Fraction as Function of the Backscatter Fraction and Their Relationships to the Asymmetry Parameter for Radiative Transfer Calculations. Atmosphere. 2017; 8(8):133. https://doi.org/10.3390/atmos8080133
Chicago/Turabian StyleMoosmüller, Hans, and John A. Ogren. 2017. "Parameterization of the Aerosol Upscatter Fraction as Function of the Backscatter Fraction and Their Relationships to the Asymmetry Parameter for Radiative Transfer Calculations" Atmosphere 8, no. 8: 133. https://doi.org/10.3390/atmos8080133






