Street-Level Ventilation in Hypothetical Urban Areas
Abstract
:1. Introduction
2. Methodology
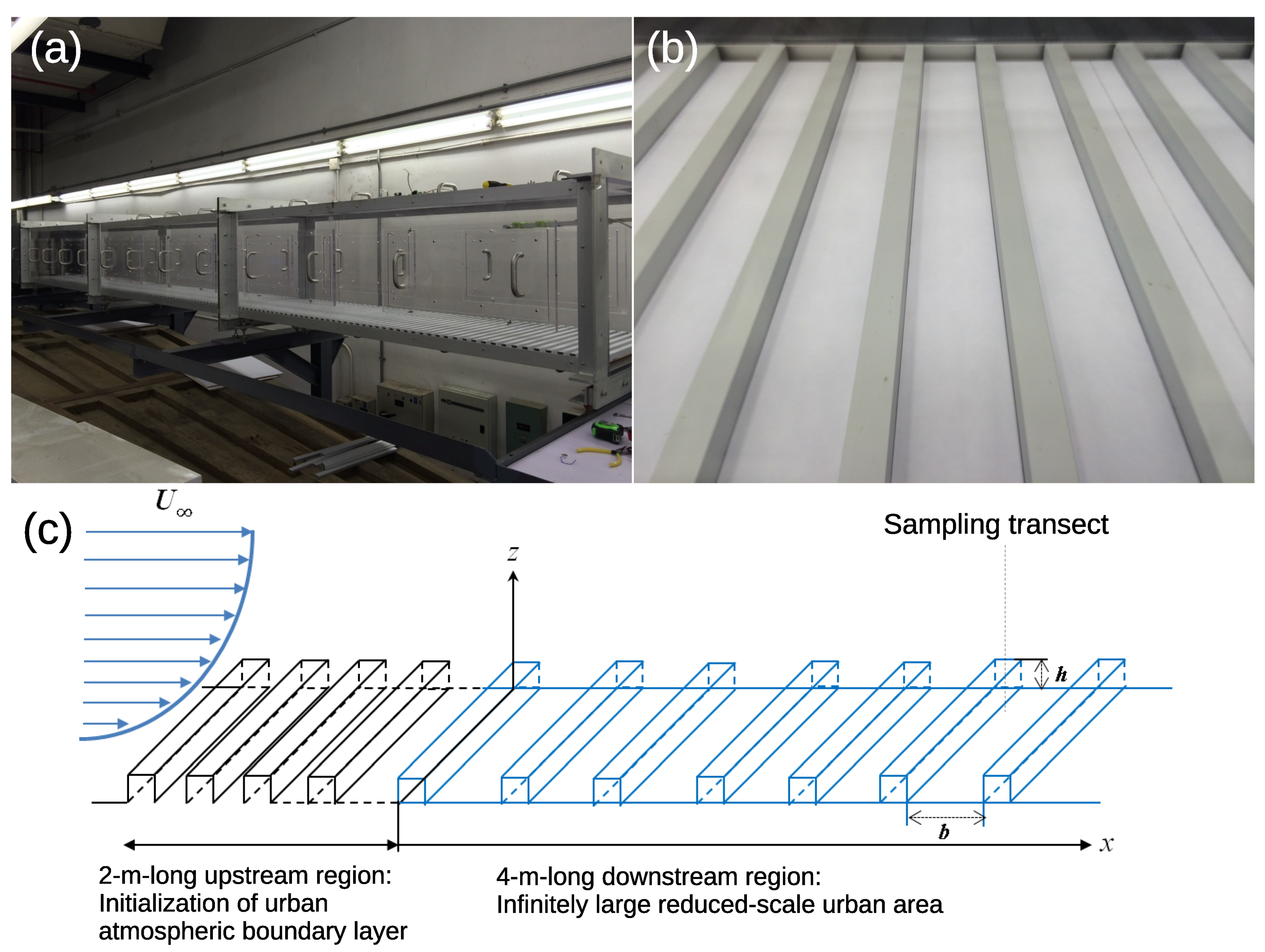
2.1. Wind Tunnel Infrastructure
2.2. Idealized Urban Surfaces
2.3. Hot-Wire Anemometry
3. Results and Discussion
3.1. Thickness of TBL and ISL
3.2. Friction Velocity
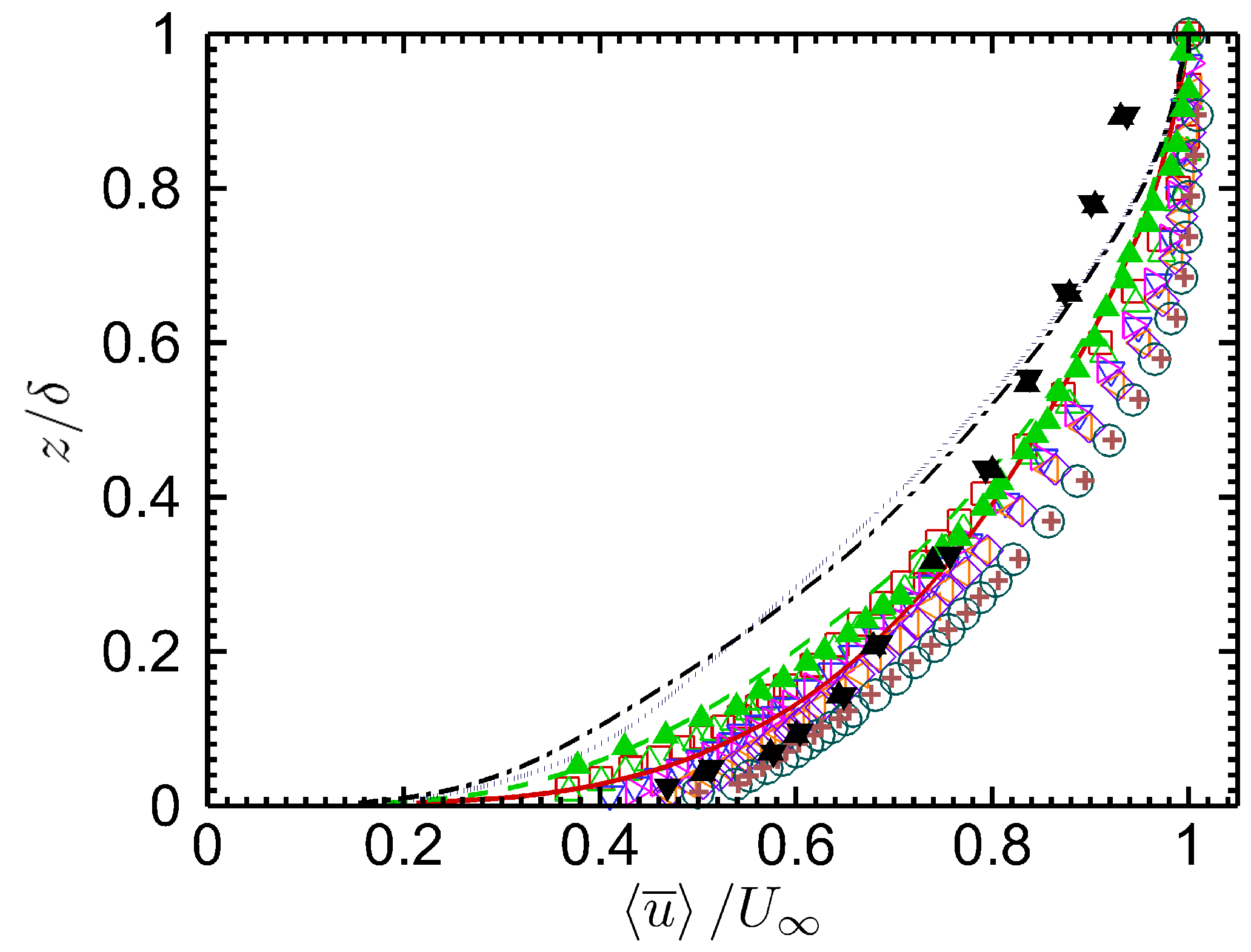
3.3. Wind Speed Profiles
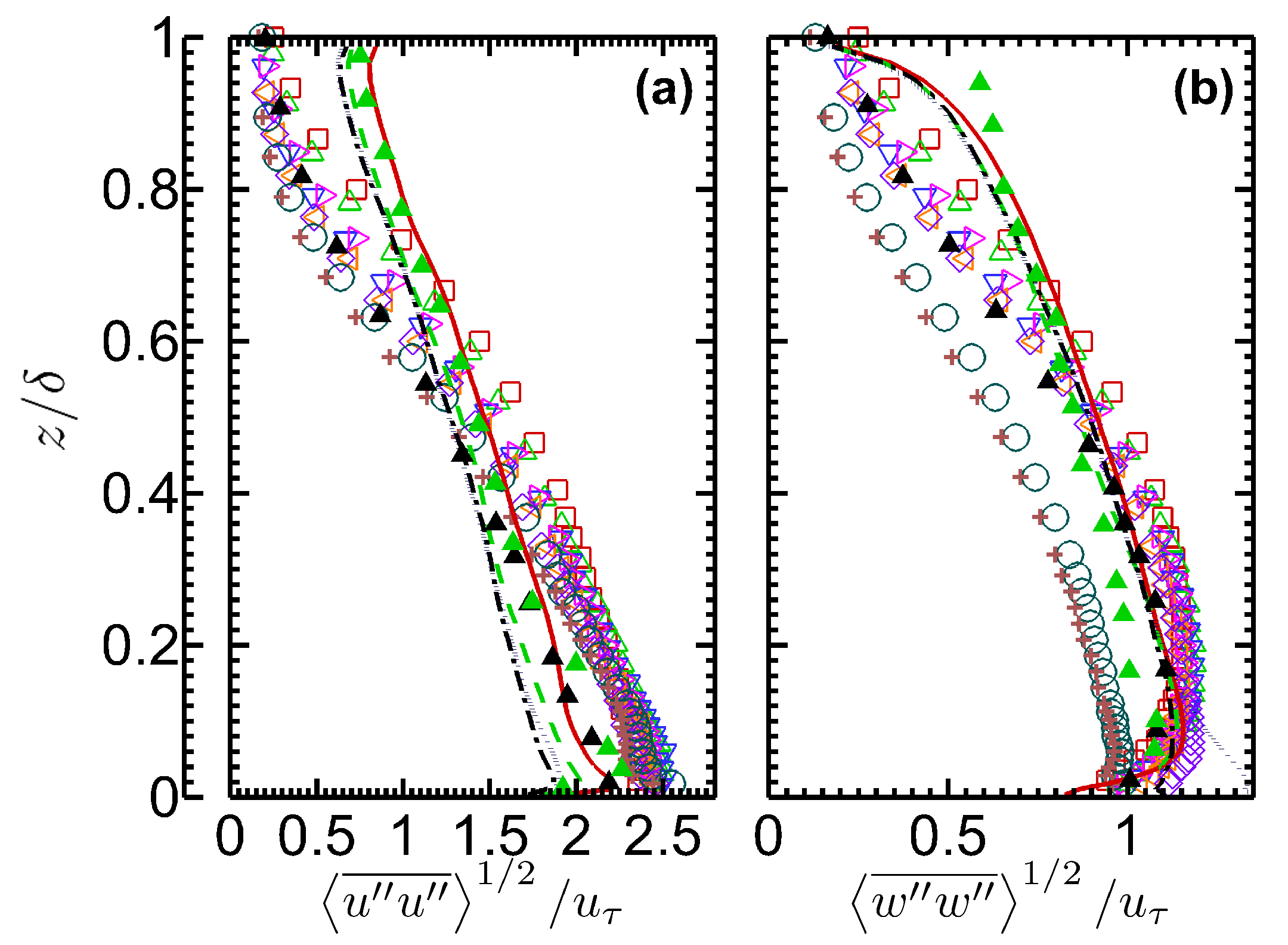
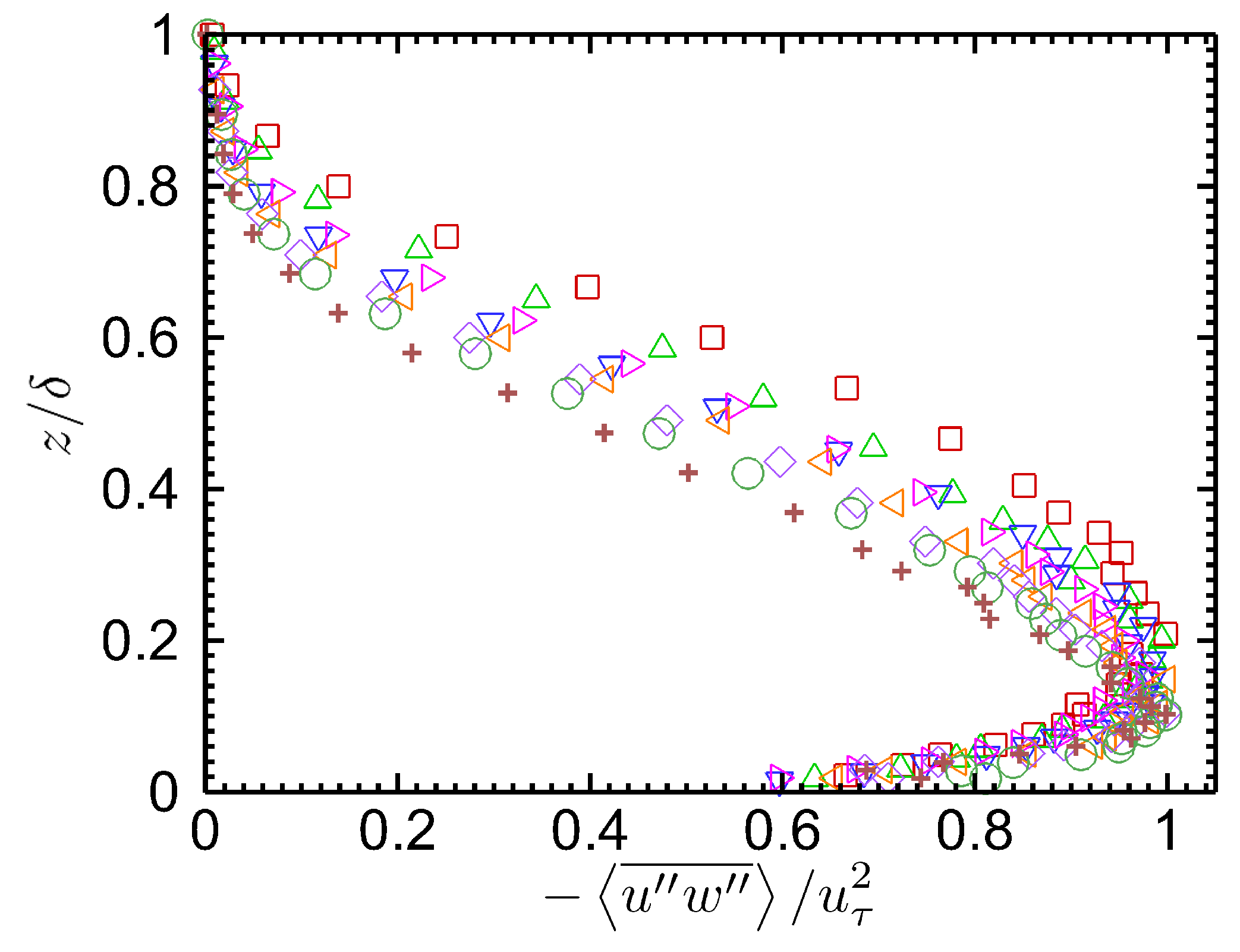
3.4. Turbulence Profiles
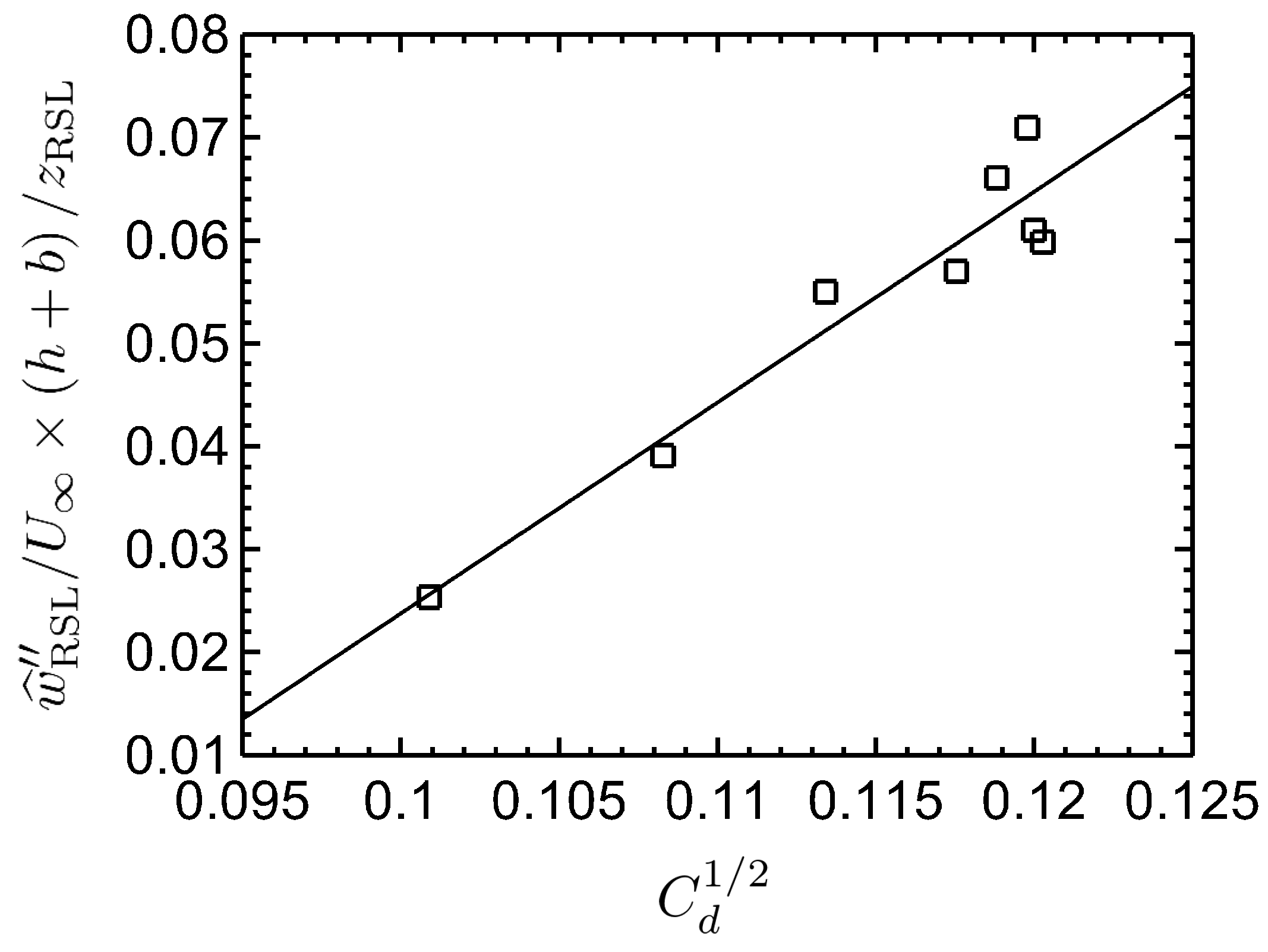
3.5. Street-Level Ventilation Estimate
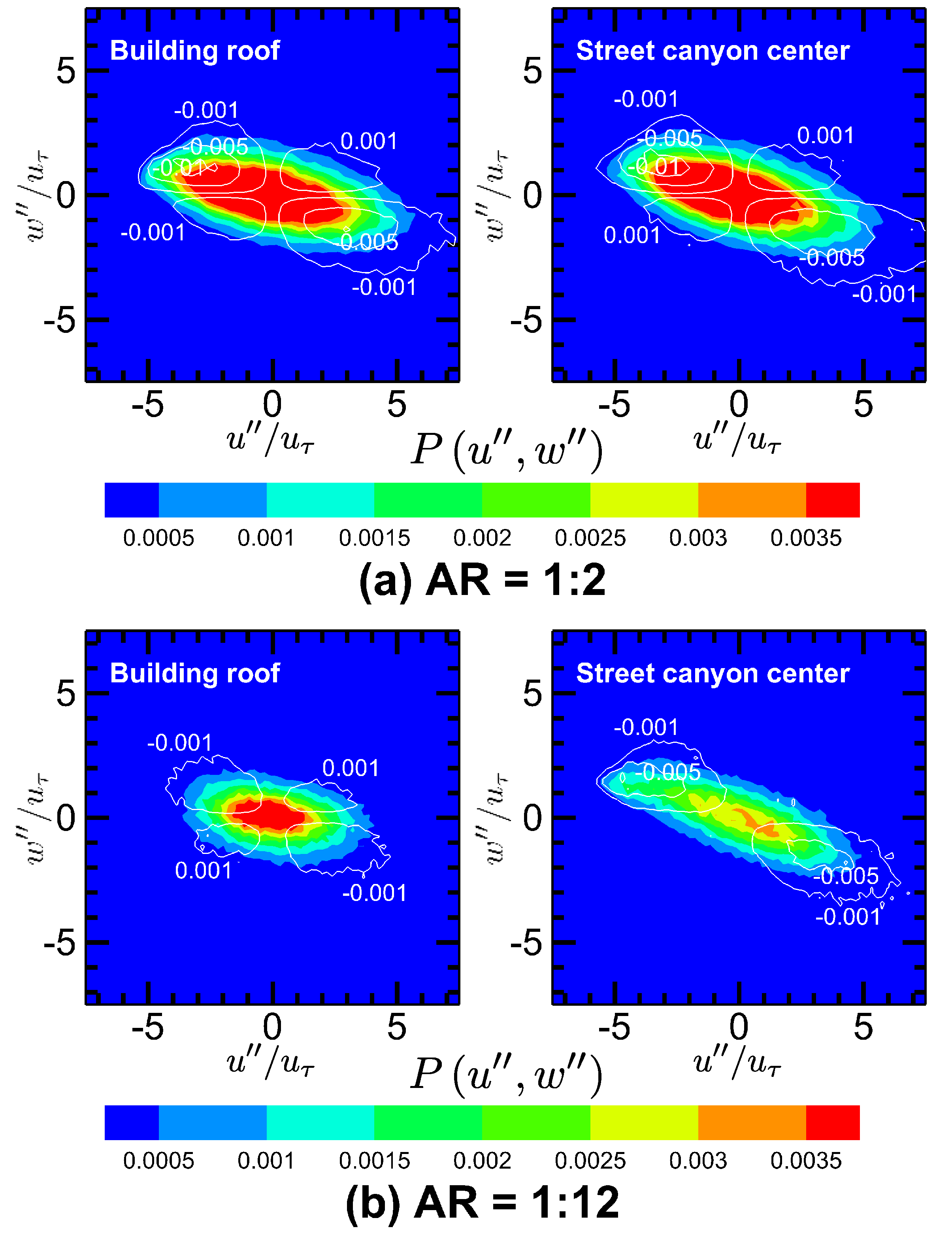
3.6. Quadrant Analysis
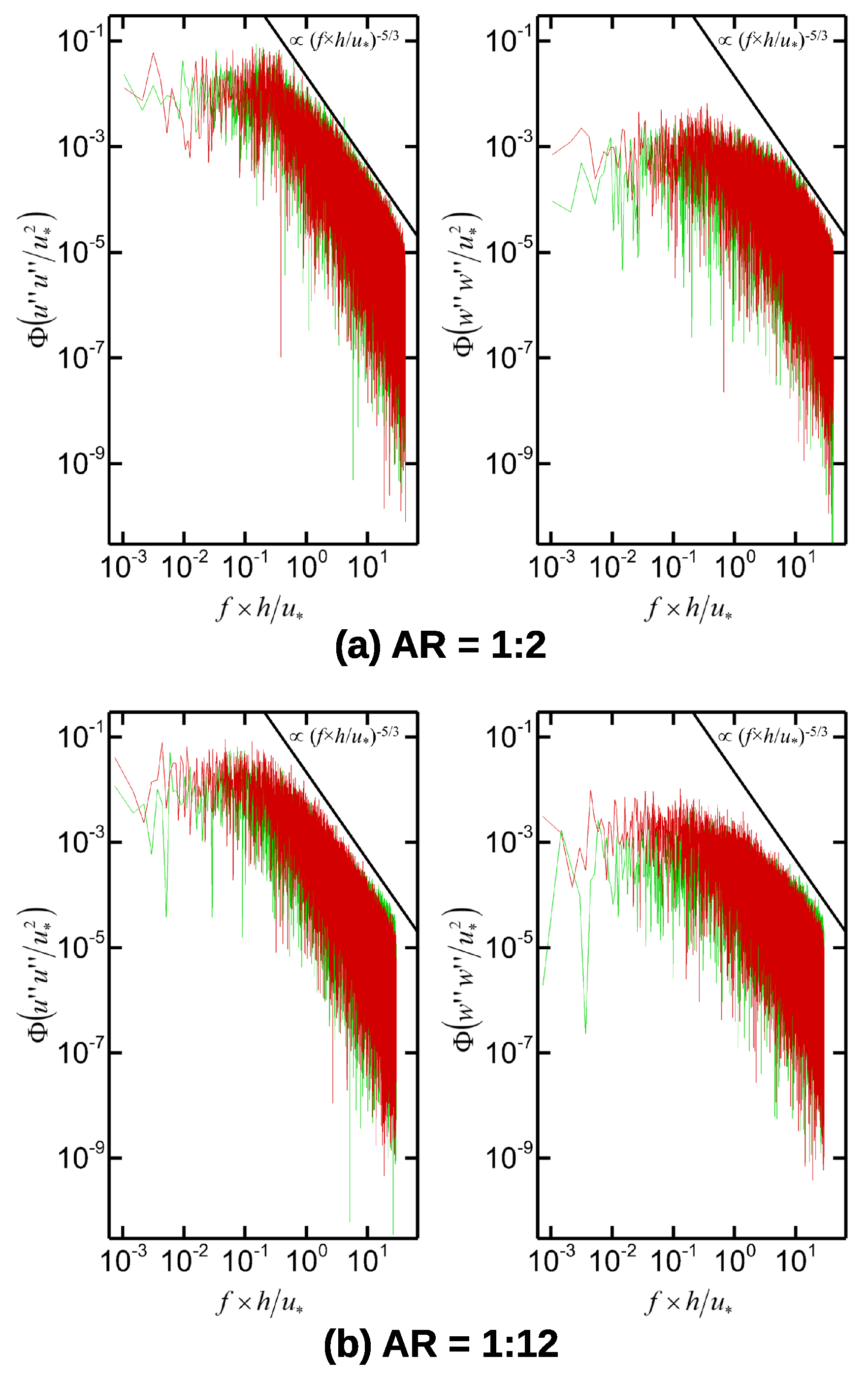
3.7. Frequency Spectrum
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deweerdt, S. The urban downshift. Nature 2016, 531, S52–S53. [Google Scholar] [CrossRef] [PubMed]
- Wigginton, N.S.; Fahrenkamp-Uppenbrink, J.; Wible, B.; Malakoff, D. Cities are the future. Science 2016, 352, 904–905. [Google Scholar] [CrossRef] [PubMed]
- Parrish, D.D.; Zhu, T. Clean air for megacities. Science 2009, 326, 674–675. [Google Scholar] [CrossRef] [PubMed]
- Fernando, H.J.S. Fluid dynamics of urban atmospheres in complex terrain. Annu. Rev. Fluid Mech. 2010, 42, 365–389. [Google Scholar] [CrossRef]
- Claus, J.; Krogstad, P.A.; Castro, I.P. Some measurements of surface drag in urban-type boundary layers at various wind angles. Bound. Layer Meteorol. 2012, 145, 407–422. [Google Scholar] [CrossRef]
- Ricci, A.; Burlando, M.; Freda, A.; Repetto, M.P. Wind tunnel measurements of the urban boundary layer development over a historical district in Italy. Build. Environ. 2017, 111, 192–206. [Google Scholar] [CrossRef]
- Tse, K.T.; Hitchcock, P.A.; Kwok, K.C.S.; Thepmongkorn, S.; Chan, C.M. Economic perspectives of aerodynamic treatments of square tall buildings. J. Wind Eng. Ind. Aerodyn. 2009, 97, 455–467. [Google Scholar] [CrossRef]
- Aly, A.M. Atmospheric boundary-layer simulation for the built environment: Past, present and future. Build. Environ. 2014, 75, 206–221. [Google Scholar] [CrossRef]
- Stabile, L.; Arpino, F.; Buonanno, G.; Russi, A.; Frattolillo, A. A simplified benchmark of ultrafine particle dispersion in idealized urban street canyons: A wind tunnel study. Build. Environ. 2015, 93, 186–198. [Google Scholar] [CrossRef]
- Panagiotou, I.; Neophytou, M.K.A.; Hamlyn, D.; Britter, R.E. City breathability as quantified by the exchange velocity and its spatial variation in real inhomogeneous urban geometries: An example from central London urban area. Sci. Total Environ. 2013, 442, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Hang, J.; Wang, Q.; Chen, X.; Sandberg, M.; Zhu, W.; Buccolieri, R.; Di Sabatino, S. City breathability in medium density urban-like geometries evaluated through the pollutant transport rate and the net escape velocity. Build. Environ. 2015, 94, 166–182. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; van Beeck, J.P.A.J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Kubota, T.; Miura, M.; Tominaga, Y.; Mochida, A. Wind tunnel tests on the relationship between building density and pedestrian-level wind velocity: Development of guidelines for realizing acceptable wind environment in residential neighborhoods. Build. Environ. 2008, 43, 1699–1708. [Google Scholar] [CrossRef]
- Jiménez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 2004, 36, 173–196. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Djenidi, L.; Antonia, R.A.; Talluru, K.M. Drag of a turbulent boundary layer with transverse 2D circular rods on the wall. Exp. Fluids 2015, 56, 121–129. [Google Scholar] [CrossRef]
- Hagishima, A.; Tanimoto, J.; Nagayama, K.; Meno, S. Aerodynamic parameters of regular arrays of rectangular blocks with various geometries. Bound. Layer Meteorol. 2009, 132, 315–337. [Google Scholar] [CrossRef]
- Karimpour, A.; Kaye, N.B.; Baratian-Ghorghi, Z. Modeling the neutrally stable atmospheric boundary layer for laboratory scale studies of the built environment. Build. Environ. 2012, 49, 203–211. [Google Scholar] [CrossRef]
- Krogstad, P.-Å.; Antonia, R.A. Surface roughness effects in turbulent boundary layers. Exp. Fluids 1999, 27, 450–460. [Google Scholar] [CrossRef]
- Antonia, R.A.; Krogstad, P.-Å. Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 2001, 28, 139–157. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Pollution removal effectiveness of the pedestrian ventilation system. J. Wind Eng. Ind. Aerodyn. 2011, 99, 46–58. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. A procedure to quantify the impact of mitigation techniques on the urban ventilation. Build. Environ. 2012, 47, 410–420. [Google Scholar] [CrossRef]
- Kanda, I.; Yamao, Y. Velocity adjustment and passive scalar diffusion in and above an urban canopy in response to various approach flows. Bound. Layer Meteorol. 2011, 141, 415–441. [Google Scholar] [CrossRef]
- Carpentieri, M.; Hayden, P.; Robins, A.G. Wind tunnel measurements of pollutant turbulent fluxes in urban intersections. Atmos. Enviorn. 2012, 46, 669–674. [Google Scholar] [CrossRef]
- Chung, J.; Hagishima, A.; Ikegaya, N.; Tanimoto, J. Wind-tunnel study of scalar transfer phenomena for surfaces of block arrays and smooth walls with dry patches. Bound. Layer Meteorol. 2015, 157, 219–236. [Google Scholar] [CrossRef]
- Raupach, M.R.; Hughes, D.E.; Cleugh, H.A. Momentum absorption in rough-wall boundary layers with sparse roughness elements in random and clustered distributions. Bound. Layer Meteorol. 2006, 120, 201–218. [Google Scholar] [CrossRef]
- Tachie, M.F.; Bergstrom, D.J.; Balachandar, R. Roughness effects in low-Reθ open-channel turbulent boundary layers. Exp. Fluids 2003, 35, 338–346. [Google Scholar] [CrossRef]
- Pascheke, F.; Barlow, J.F.; Robins, A.G. Wind-tunnel modelling of dispersion from a scalar area source in urban-like roughness. Bound. Layer Meteorol. 2008, 126, 103–124. [Google Scholar] [CrossRef]
- Ikegaya, N.; Hagishima, A.; Tanimoto, J.; Tanaka, Y.; Narita, K.-I.; Zaki, S.A. Geometric dependence of the scalar transfer efficiency over rough surfaces. Bound. Layer Meteorol. 2012, 143, 357–377. [Google Scholar] [CrossRef]
- Barlow, J.F.; Harman, I.N.; Belcher, S.E. Scalar fluxes from urban street canyons. Part I: Laboratory simulation. Bound. Layer Meteorol. 2004, 113, 369–385. [Google Scholar] [CrossRef]
- Salizzoni, P.; Soulhac, L.; Mejean, P. Street canyon ventilation and atmospheric turbulence. Atmos. Environ. 2009, 43, 5056–5067. [Google Scholar] [CrossRef]
- Takimoto, H.; Sato, A.; Barlow, J.F.; Ryo, M.; Inagaki, A.; Onomura, S.; Kanda, M. Particle image velocimetry measurements of turbulent flow within outdoor and indoor urban scale models and flushing motions in urban canopy layers. Bound. Layer Meteorol. 2011, 140, 295–314. [Google Scholar] [CrossRef]
- Perret, L.; Savory, E. Large-scale structures over a single street canyon immersed in an urban-type boundary layer. Bound. Layer Meteorol. 2013, 148, 111–131. [Google Scholar] [CrossRef]
- Djenidi, L.; Antonia, R.A.; Anselmet, F. LDA measurements in a turbulent boundary layer over a d-type rough wall. Exp. Fluids 1994, 16, 323–329. [Google Scholar] [CrossRef]
- Schultz, M.P.; Flack, K.A. Outer layer similarity in fully rough turbulent boundary layers. Exp. Fluids 2005, 38, 328–340. [Google Scholar] [CrossRef]
- Smits, A.J.; McKeon, B.J.; Marusic, I. High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 2011, 43, 353–375. [Google Scholar] [CrossRef]
- Squire, D.T.; Morrill-Winter, C.; Hutchins, N.; Schultz, M.P.; Klewicki, J.C.; Marusic, I. Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 2016, 795, 210–240. [Google Scholar] [CrossRef]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 2007, 592, 263–293. [Google Scholar] [CrossRef]
- Flack, K.A.; Schultz, M.P. Roughness effects on wall-bounded turbulent flows. Phys. Fluids 2014, 101305. [Google Scholar] [CrossRef]
- De Ridder, K. Bulk transfer relations for the roughness sublayer. Bound. Layer Meteorol. 2010, 134, 257–267. [Google Scholar] [CrossRef]
- Kastner-Kelin, P.; Rotach, M.W. Mean flow and turbulence characteristics in an urban roughness sublayer. Bound. Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Smeets, C.J.P.P.; van den Broeke, M.R. The parameterisation of scalar transfer over rough ice. Bound. Layer Meteorol. 2008, 128, 339–355. [Google Scholar] [CrossRef]
- Castro, I.P.; Cheng, H.; Reynolds, R. Turbulence over urban-type roughness: Deductions from wind-tunnel measurements. Bound. Layer Meteorol. 2006, 118, 109–131. [Google Scholar] [CrossRef]
- Mihailovic, D.T.; Rao, S.T.; Hogrefe, C.; Clark, R.D. An approach for the aggregation of aerodynamic surface parameters in calculating the turbulent fluxes over heterogeneous surfaces in atmospheric models. Environ. Fluid Mech. 2002, 2, 339–355. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Bldg. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Perry, A.E.; Schofield, W.H.; Joubert, P.N. Rough wall turbulent boundary layers. J. Fluid Mech. 1969, 37, 383–413. [Google Scholar] [CrossRef]
- Baetke, F.; Werner, H.; Wengle, H. Numerical simulation of turbulent flow over surface-mounted obstacles with sharp edges and corners. J. Fluid Mech. 1990, 35, 129–147. [Google Scholar] [CrossRef]
- Bruun, H.H. Interpretation of a hot wire signal using a universal calibration law. J. Sci. Instrum. 1971, 4, 225–231. [Google Scholar] [CrossRef]
- Aydin, E.M.; Leutheusser, H.J. Plane-Couette flow between smooth and rough walls. Exp. Fluids 1991, 11, 302–312. [Google Scholar] [CrossRef]
- Snyder, W.H.; Castro, I.P. The critical Reynolds number for rough-wall boundary layers. J. Wind Eng. Ind. Aerodyn. 2002, 90, 41–54. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994; p. 316. [Google Scholar]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Bound. Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Ho, Y.-K. Wind-Tunnel Study of Turbulent Boundary Layer over Idealised Urban Roughness with Application to Urban Ventilation Problem. Ph.D. Thesis, The University of Hong Kong, Hong Kong, China, 2017; 237p. [Google Scholar]
- Takimoto, H.; Inagaki, A.; Kanda, M.; Sato, A.; Michioka, T. Length-scale similarity of turbulent organized structures over surfaces with different roughness types. Bound. Layer Meteorol. 2013, 147, 217–236. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, C.-H. Time scale analysis of chemically reactive pollutants over urban roughness in the atmospheric boundary layer. Int. J. Environ. Pollut. 2017. accepted. [Google Scholar]
- Burattini, P.; Leonardi, S.; Orlandi, P.; Antonia, R.A. Comparison between experiment and direct numerical simulations in a channel flow with roughness on one wall. J. Fluid Mech. 2008, 600, 403–426. [Google Scholar] [CrossRef]
- Rafailidis, S. Influence on building area density and roof shape on the wind characteristics above a town. Bound. Layer Meteorol. 1997, 85, 255–271. [Google Scholar] [CrossRef]
- Keirsbulck, L.; Labraga, L.; Mazouz, A.; Tournier, C. Influence of surface roughness on anisotropy in a turbulent boundary layer flow. Exp. Fluids 2002, 33, 497–499. [Google Scholar] [CrossRef]
- Nourmohammadi, K.; Hopke, P.K.; Stukel, J.J. Turbulent air flow over rough surfaces II. Turbulent flow parameters. J. Fluids Eng. 1985, 107, 55–60. [Google Scholar] [CrossRef]
- Panofsky, H.A. The atmospheric boundary layer below 150 meters. Annu. Rev. Fluid Mech. 1974, 107, 147–177. [Google Scholar] [CrossRef]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in a boundary layer with two-dimensional roughness. J. Fluid Mech. 2009, 635, 75–101. [Google Scholar] [CrossRef]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 2011, 676, 172–190. [Google Scholar] [CrossRef]
- Smalley, R.J.; Leonardi, S.; Antonia, R.A.; Djenidi, L.; Orlandi, P. Reynolds stress anisotropy of turbulent rough wall layers. Exp. Fluids 2002, 33, 31–37. [Google Scholar] [CrossRef]
- Reynolds, R.T.; Castro, I.P. Measurements in an urban-type boundary layer. Exp. Fluids 2008, 45, 141–156. [Google Scholar] [CrossRef]
- Ho, Y.-K.; Liu, C.-H. A wind tunnel study of flows over idealised urban surfaces with roughness sublayer corrections. Theor. Appl. Climatol. 2016, 1–16. [Google Scholar] [CrossRef]
- Liu, C.-H.; Leung, D.Y.C.; Barth, M.C. On the prediction of air and pollutant exchange rates in street canyons of different aspect ratios using large-eddy simulation. Atmos. Environ. 2005, 39, 1567–1574. [Google Scholar] [CrossRef]
- Ho, Y.-K.; Liu, C.-H.; Wong, M.S. Preliminary study of the parameterisation of street-level ventilation in idealised two-dimensional simulations. Build. Environ. 2015, 89, 345–355. [Google Scholar] [CrossRef]
- Liu, C.H.; Ng, C.T.; Wong, C.C.C. A theory of ventilation estimate over hypothetical urban areas. J. Hazard. Mater. 2015, 296, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Wallace, J.M. Quadrant analysis in turbulence research: History and evolution. Annu. Rev. Fluid Mech. 2016, 48, 131–158. [Google Scholar] [CrossRef]
- Immer, M.; Allegrini, J.; Carmeliet, J. Time-resolved and time-averaged stereo-PIV measurements of a unit-ratio cavity. Exp. Fluids 2016, 57, 101–118. [Google Scholar] [CrossRef]
- Hong, J.; Katz, J.; Schultz, M.P. Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 2011, 667, 1–37. [Google Scholar] [CrossRef]
| Types of Idealized Urban Surface | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | ||
| Rib [mm] | Size h | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 |
| Separation b | 38 | 57 | 76 | 95 | 114 | 152 | 190 | 228 | |
| Size of a repeating unit l (= h + b) [mm] | 57 | 76 | 95 | 114 | 133 | 171 | 209 | 247 | |
| Aspect ratio (= ) | 1:2 | 1:3 | 1:4 | 1:5 | 1:6 | 1:8 | 1:10 | 1:12 | |
| Boundary layer thickness | [mm] | 244 | 248 | 283 | 284 | 294 | 294 | 304 | 304 |
| Sampling location | [mm] | 3705 | 3686 | 3609 | 3648 | 3590 | 3562 | 3571 | 3619 |
| 195 | 194 | 190 | 192 | 189 | 187 | 188 | 190 | ||
| Number of profiles in a repeating unit | 7 | 7 | 7 | 7 | 7 | 9 | 9 | 9 | |
| Velocity [m s] | Free-stream | ||||||||
| Mean | |||||||||
| Friction velocity | [m s] | ||||||||
| Drag coefficient f (= ) [] | |||||||||
| Reynolds number | (= ) | 195,168 | 207,495 | 239,729 | 242,190 | 250,614 | 247,520 | 276,800 | 278,400 |
| (= ) | 15,200 | 15,900 | 16,100 | 16,200 | 16,200 | 16,000 | 17,300 | 17,400 | |
| (= ) | 12,500 | 13,100 | 13,800 | 13,900 | 14,100 | 14,000 | 15,500 | 15,600 | |
| (= ) | 864 | 983 | 1060 | 1127 | 1138 | 1138 | 1229 | 1277 | |
| Quadrants | Events | ||
|---|---|---|---|
| 1 | Outward interaction | + | + |
| 2 | Ejection | − | + |
| 3 | Inward interaction | − | − |
| 4 | Sweep | + | − |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, Y.-K.; Liu, C.-H. Street-Level Ventilation in Hypothetical Urban Areas. Atmosphere 2017, 8, 124. https://doi.org/10.3390/atmos8070124
Ho Y-K, Liu C-H. Street-Level Ventilation in Hypothetical Urban Areas. Atmosphere. 2017; 8(7):124. https://doi.org/10.3390/atmos8070124
Chicago/Turabian StyleHo, Yat-Kiu, and Chun-Ho Liu. 2017. "Street-Level Ventilation in Hypothetical Urban Areas" Atmosphere 8, no. 7: 124. https://doi.org/10.3390/atmos8070124
APA StyleHo, Y.-K., & Liu, C.-H. (2017). Street-Level Ventilation in Hypothetical Urban Areas. Atmosphere, 8(7), 124. https://doi.org/10.3390/atmos8070124





