Research on the Fine-Scale Spatial Uniformity of Natural Rainfall and Rainfall from a Rainfall Simulator with a Rotary Platform (RSRP)
Abstract
:1. Introduction
2. Experiments
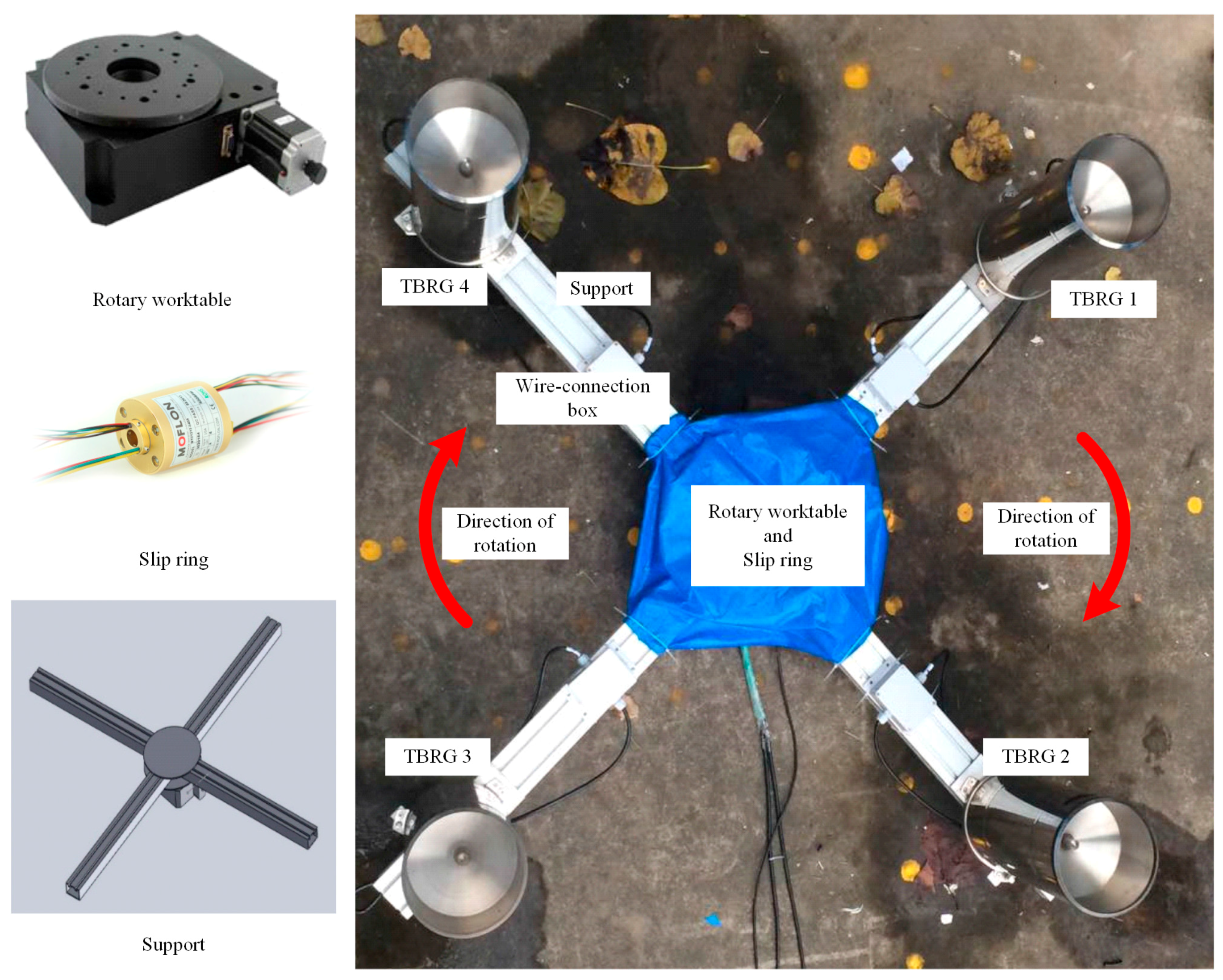
2.1. Rainfall Simulator with a Rotary Platform (RSRP)
2.2. Quantification of the Spatial Uniformity of Natural Rainfall and Analysis of Influencing Factors
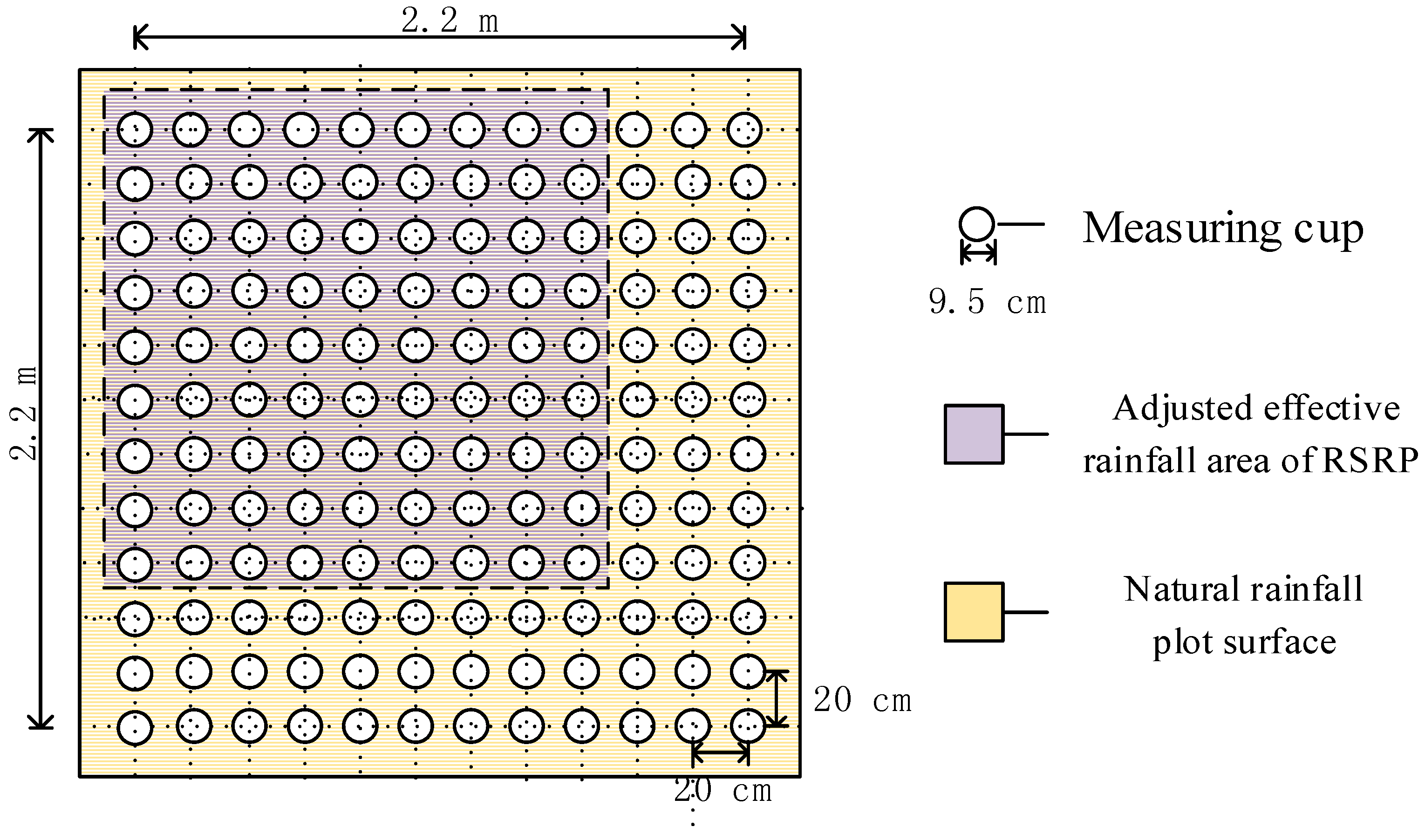
2.2.1. Quantification of the Spatial Uniformity of Natural Rainfall
2.2.2. Analysis of Factors Influencing Spatial Uniformity of Natural Rainfall
3. Results and Discussion
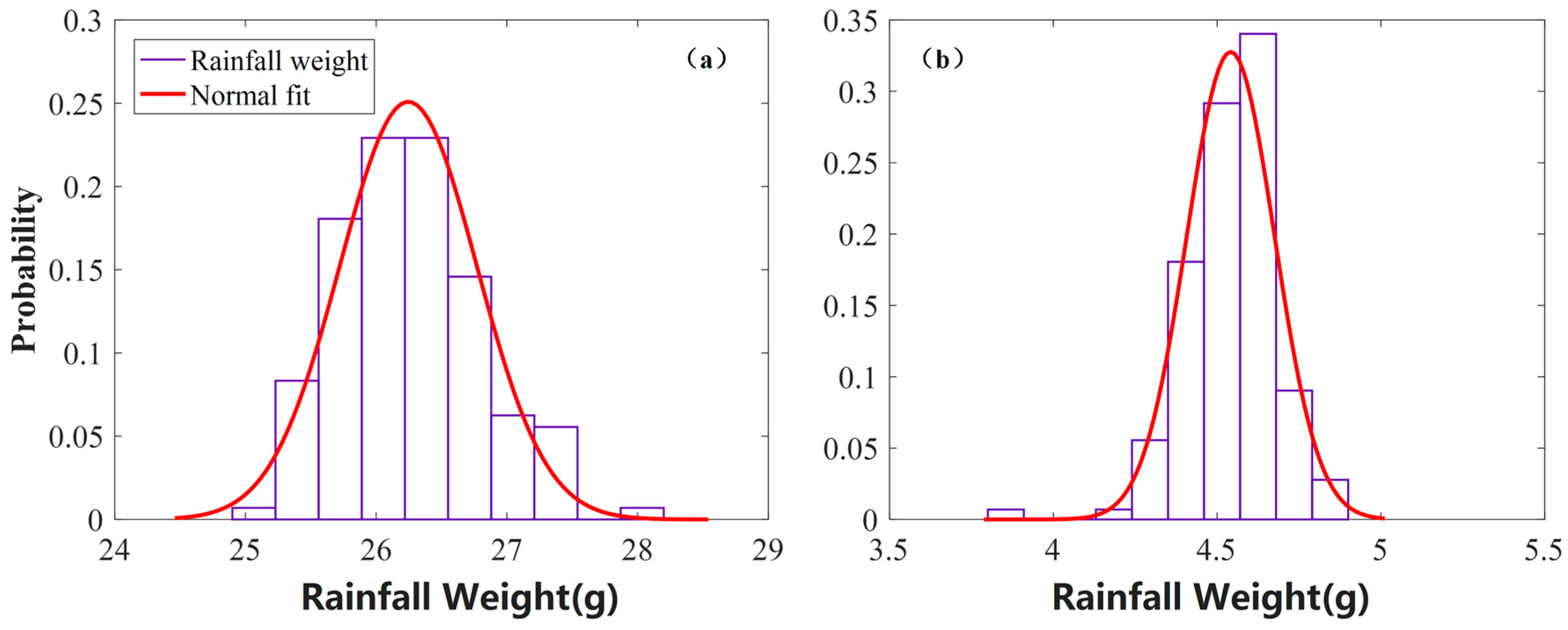
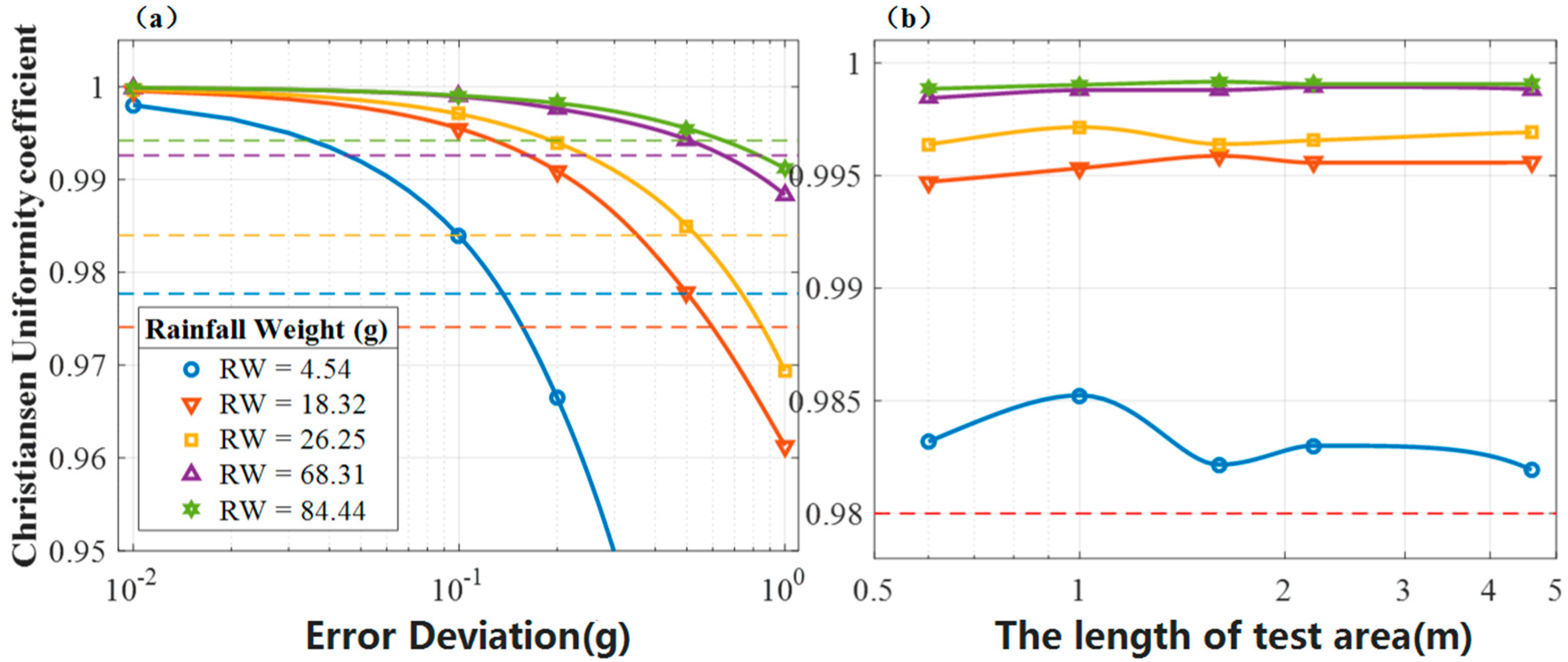
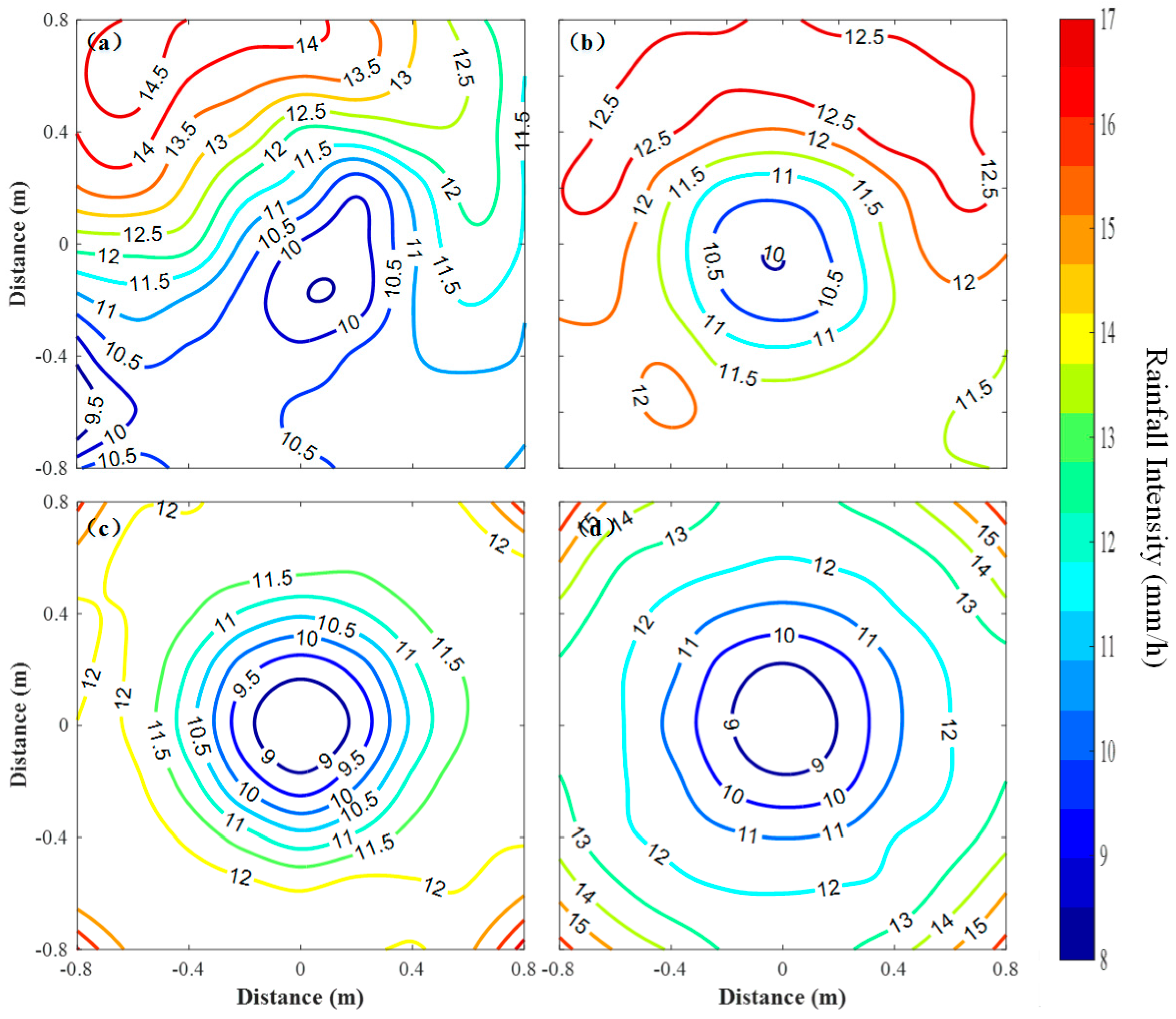
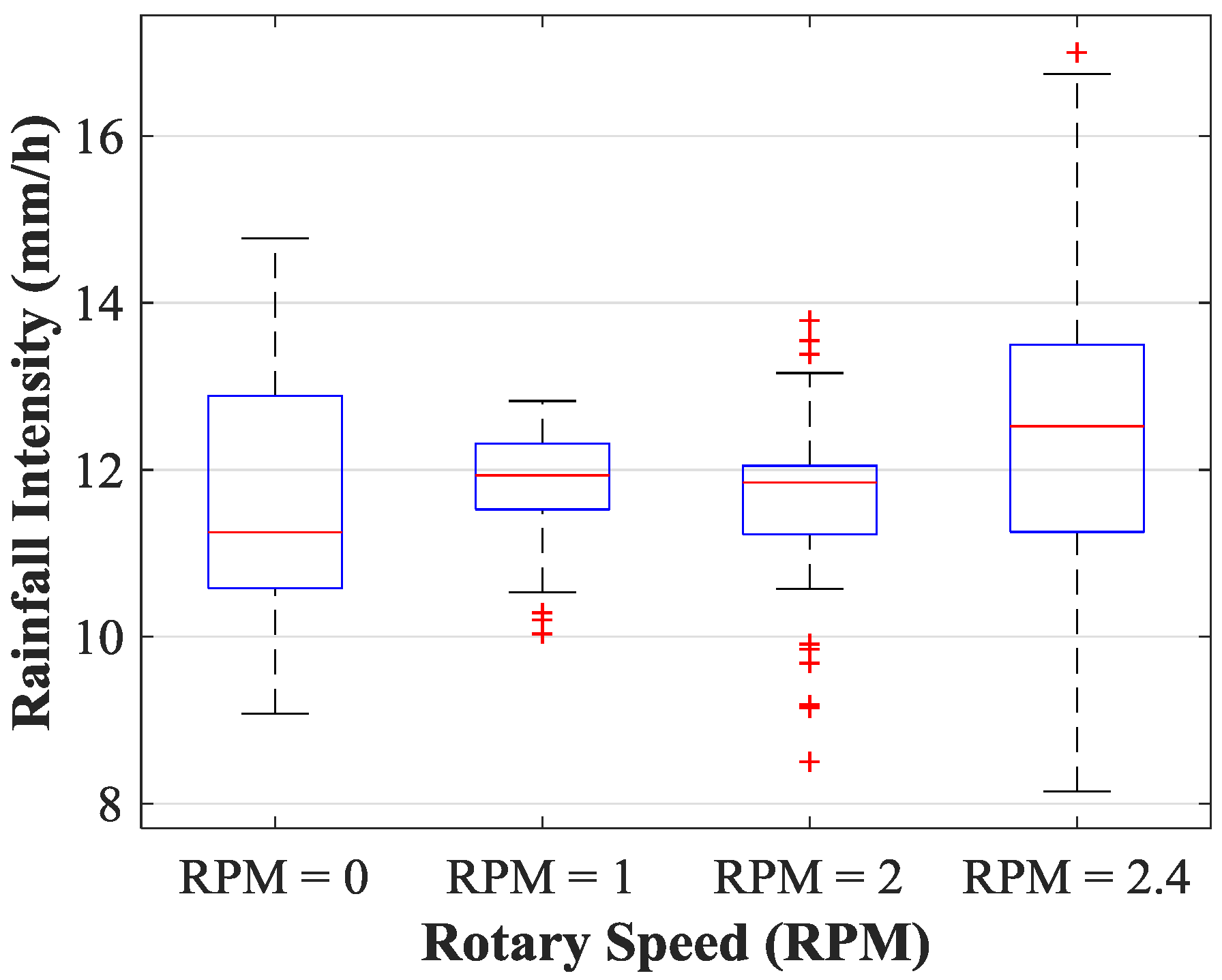
3.1. Spatial Uniformity Evaluation of the Rainfall Simulator with a Rotary Platform
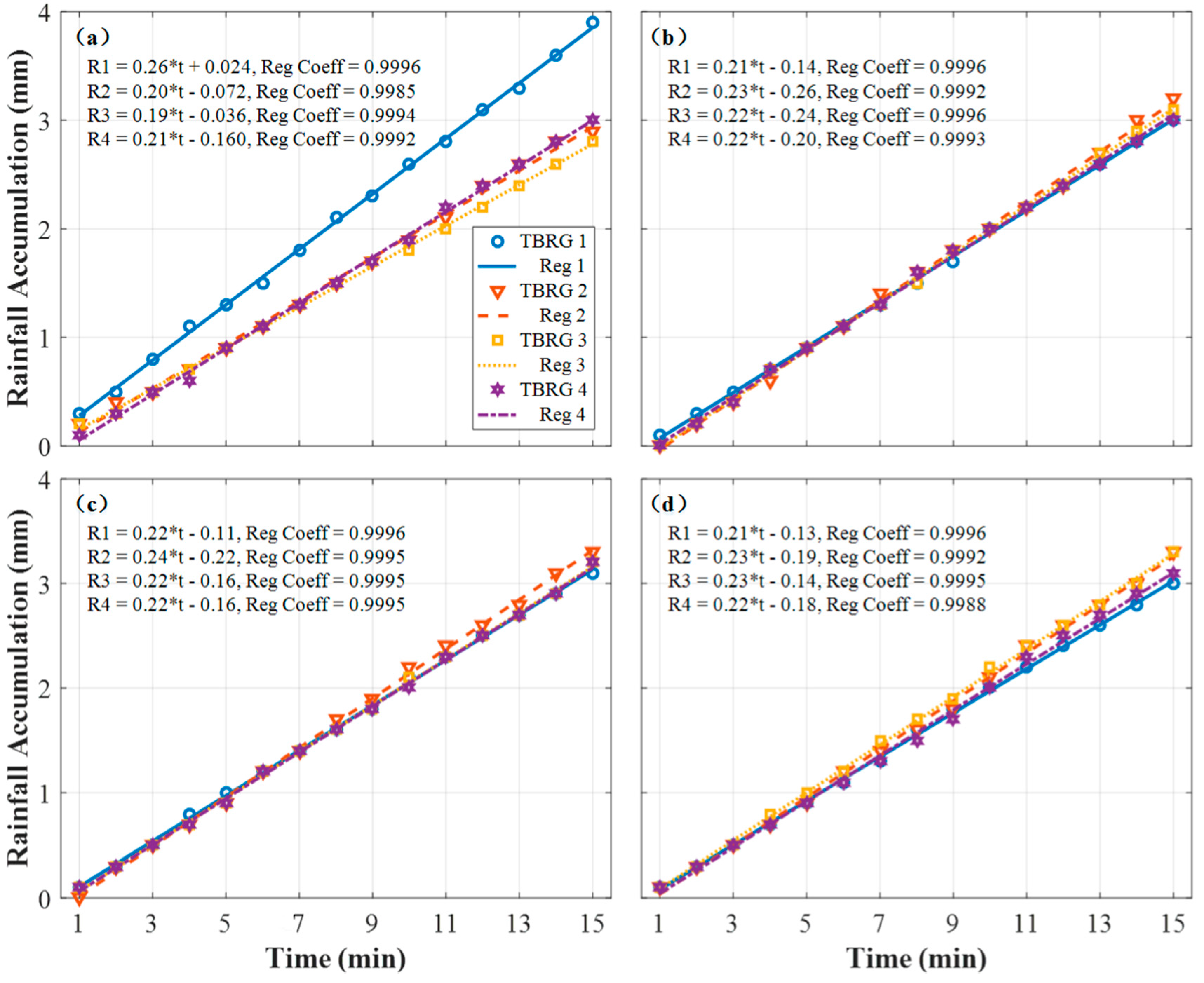
3.2. TBRG Tests of the Rainfall Simulator with a Rotary Platform
4. Conclusions
Abbreviations
| RSRP | Rainfall Simulator with a Rotary Platform |
| RS | Rainfall Simulator |
| TBRG | Tipping bucket rain gauge |
| AREA | Adjusted effective rainfall area |
| CU | Christiansen Uniformity coefficient |
| RA | Rainfall accumulation |
| RI | Rainfall intensity |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dunkerley, D. Rain event properties in nature and in rainfall simulation experiments: A comparative review with recommendations for increasingly systematic study and reporting. Hydrol. Process. 2008, 22, 4415–4435. [Google Scholar] [CrossRef]
- Iserloh, T.; Ries, J.B.; Arnáez, J.; Boix-Fayos, C.; Butzen, V.; Cerdà, A.; Echeverría, M.T.; Fernández-Gálvez, J.; Fister, W.; Geißler, C.; et al. European small portable rainfall simulators: A comparison of rainfall characteristics. Catena 2013, 110, 100–112. [Google Scholar] [CrossRef]
- Liu, X.C.; Gao, T.C.; Liu, L. A comparison of rainfall measurements from multiple instruments. Atmos. Meas. Tech. 2013, 6, 1585–1595. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Sieck, L.C.; Burges, S.J.; Steiner, M. Challenges in obtaining reliable measurements of point rainfall. Water Resour. Res. 2007, 43, 1–23. [Google Scholar] [CrossRef]
- Abudi, I.; Carmi, G.; Berliner, P. Rainfall simulator for field runoff studies. J. Hydrol. 2012, 454, 76–81. [Google Scholar] [CrossRef]
- Ries, J.B.; Iserloh, T.; Seeger, M.; Gabriels, D. Rainfall simulations—Constraints, needs and challenges for a future use in soil erosion research. Z. Geomorphol. Suppl. Issues 2013, 57, 1–10. [Google Scholar] [CrossRef]
- Colli, M.; Stagnaro, M.; Lanza, L.; La Barbera, P. Metrological requirements for a laboratory rainfall simulator. In Proceedings of the 10th International Workshop on Precipitation in Urban Areas, Pontresina, Switzerland, 1–5 December 2015; pp. 1–6. [Google Scholar]
- Liu, B.; Wang, X.L.; Su, T.; Kang, Z.J. The uniformity tests of a rainfall generator. In Proceedings of the 5th International Conference on Civil Engineering and Transportation, Guangzhou, China, 28–29 November 2015; Atlantis Press: Paris, France, 2015; pp. 1933–1937. [Google Scholar]
- Moazed, H.; Bavi, A.; Boroomand-Nasab, S.; Naseri, A.; Albaji, M. Effects of climatic and hydraulic parameters on water uniformity coeffcient in solid set systems. J. Appl. Sci. 2010, 10, 1792–1796. [Google Scholar]
- Egodawatta, P. Translation of Small-Plot Scale Pollutant Build-Up and Wash-Off Measurements to Urban Catchment Scale. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 3 December 2007. [Google Scholar]
- Kathiravelu, G. Review on design requirements of a rainfall simulator for urban stormwater studies. In Proceedings of the 2014 Stormwater Queensland Conference, Townsville, Australia, 6–8 August 2014; pp. 1–13. [Google Scholar]
- Chevone, B.I.; Yang, Y.S.; Winner, W.E.; Storks-Cotter, I.; Long, S.J. A Rainfall Simulator for Laboratory Use in Acidic Precipitation Studies. J. Air Pollut. Control Assoc. 1984, 34, 355–359. [Google Scholar] [CrossRef]
- Hemmati, A.; Torab-Mostaedi, M.; Shirvani, M.; Ghaemi, A. A study of drop size distribution and mean drop size in a perforated rotating disc contactor (PRDC). Chem. Eng. Res. Des. 2015, 96, 54–62. [Google Scholar] [CrossRef]
- Strebel, M.; Stienkemeier, F.; Mudrich, M. Improved setup for producing slow beams of cold molecules using a rotating nozzle. Phys. Rev. A 2010, 81, 537–542. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Liu, B.; Wang, X.L.; Kang, Z.J.; Hang, T.Y.; Su, T. The experimental research on the factors of rainfall intensity and raindrop properties of a rainfall generator. China Meas. Test. 2017, 2, 125–129. [Google Scholar]
- Löfflermang, M.; Joss, J. An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. J. Atmos. Ocean. Technol. 2000, 2, 130–139. [Google Scholar] [CrossRef]
- Christiansen, J.E. The uniformity of application of water by sprinkler systems. Agric. Eng. 1941, 3, 89–92. [Google Scholar]
- Kostinski, A.B.; Larsen, M.L.; Jameson, A.R. The texture of rain: Exploring stochastic micro-structure at small scales. J. Hydrol. 2006, 328, 38–45. [Google Scholar] [CrossRef]
- Jameson, A.R.; Larsen, M.L.; Kostinski, A.B. Disdrometer Network Observations of Finescale Spatial-Temporal Clustering in Rain. J. Atmos. Sci. 2015, 72, 1648–1666. [Google Scholar] [CrossRef]
- Habib, E.; Lee, G.; Kim, D.; Ciach, G.J. Ground-Based Direct Measurement. In Rainfall: State of the Science; American Geophysical Union: Washington, DC, USA, 2013; pp. 61–77. [Google Scholar]
- Santana, M.A.A.; Guimarães, P.L.O.; Lanza, L.G.; Vuerich, E. Metrological analysis of a gravimetric calibration system for tipping-bucket rain gauges. Meteorol. Appl. 2015, 22, 879–885. [Google Scholar] [CrossRef]
- Colli, M. Assessing the Accuracy of Precipitation Gauges a CFD Approach to Model Wind Induced Errors. Ph.D. Thesis, University of Genova, Genoa, Italy, 30 March 2014. [Google Scholar]
- Isidoro, J.M.G.P.; de Lima, J.L.M.P. Hydraulic system to ensure constant rainfall intensity (over time) when using nozzle rainfall simulators. Hydrol. Res. 2015, 46, 705–710. [Google Scholar] [CrossRef]
- Zemke, J.J. Runoff and soil erosion assessment on forest roads using a small scale rainfall simulator. Hydrology 2016, 3, 25. [Google Scholar] [CrossRef]

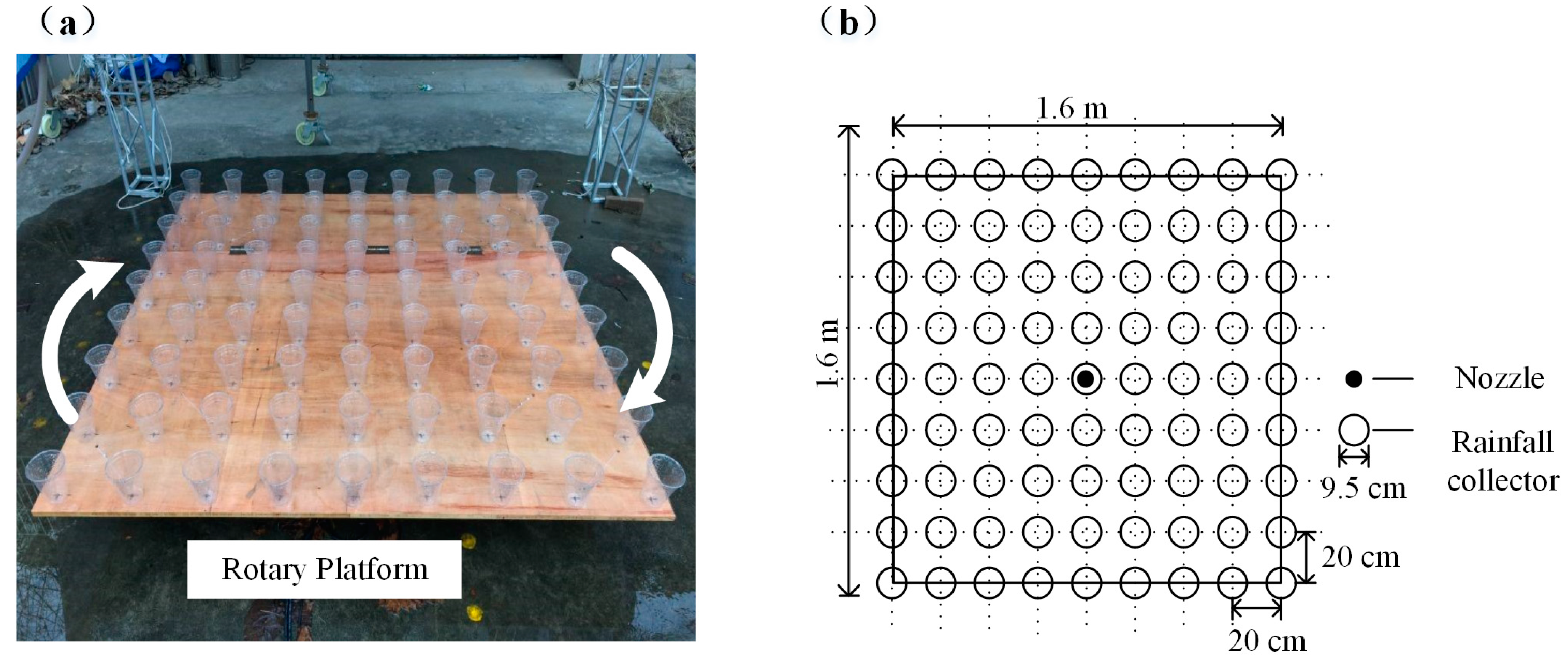
| Rainfall Events | Date | Duration (h) | (g) | RA (mm) | σ (g) | CU | |
|---|---|---|---|---|---|---|---|
| No.1 | 2015.12.02 | 4.5 | 26.25 | 3.70 | 0.52 | 0.0198 | 98.40% |
| No.2 | 2015.12.05 | 3.2 | 4.54 | 0.64 | 0.13 | 0.0286 | 97.77% |
| No.3 | 2016.01.03 | 34.4 | 84.44 | 11.91 | 0.61 | 0.0072 | 99.42% |
| No.4 | 2016.01.08 | 12.7 | 68.31 | 9.64 | 0.59 | 0.0086 | 99.26% |
| No.5 | 2016.01.15 | 8.6 | 18.32 | 2.58 | 0.51 | 0.0278 | 97.41% |
| Rotary Speed | CU | The Maximum Deviation of Rainfall Weight (G) | ||||
|---|---|---|---|---|---|---|
| (RPM) | 1.6 × 1.6 (m) | 1.2 × 1.2 (m) | 0.8 × 0.8 (m) | 1.6 × 1.6 (m) | 1.2 × 1.2 (m) | 0.8 × 0.8 (m) |
| 0 | 89.43% | 90.06% | 92.24% | 13.45 | 12.36 | 9.11 |
| 1 | 95.87% | 95.09% | 94.81% | 6.59 | 6.59 | 6.43 |
| 2 | 94.00% | 92.82% | 92.39% | 12.48 | 8.84 | 8.01 |
| 2.4 | 89.26% | 91.00% | 91.19% | 20.91 | 12.57 | 9.08 |
| Number | RA (mm) | Average RA (mm) | ||
|---|---|---|---|---|
| 1st | 2nd | 3rd | ||
| TBRG 1 | 3.1 | 3.1 | 3.0 | 3.1 |
| TBRG 2 | 3.2 | 3.2 | 3.1 | 3.2 |
| TBRG 3 | 3.3 | 3.2 | 3.2 | 3.2 |
| TBRG 4 | 3.1 | 3.1 | 3.1 | 3.1 |
| Rotary Speed (RPM) | RA (mm) | The Maximum RA Bias (mm) | Consistent RI Values | |||
|---|---|---|---|---|---|---|
| TBRG 1 | TBRG 2 | TBRG 3 | TBRG 4 | |||
| 0 | 3.9 | 2.9 | 2.8 | 3.0 | 1.1 | 3 |
| 1 | 3.0 | 3.2 | 3.1 | 3.0 | 0.2 | 6 |
| 2 | 3.1 | 3.3 | 3.2 | 3.2 | 0.2 | 6 |
| 3 | 3.0 | 3.3 | 3.3 | 3.1 | 0.3 | 8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Wang, X.; Shi, L.; Liu, X.; Kang, Z.; Chen, Z. Research on the Fine-Scale Spatial Uniformity of Natural Rainfall and Rainfall from a Rainfall Simulator with a Rotary Platform (RSRP). Atmosphere 2017, 8, 113. https://doi.org/10.3390/atmos8070113
Liu B, Wang X, Shi L, Liu X, Kang Z, Chen Z. Research on the Fine-Scale Spatial Uniformity of Natural Rainfall and Rainfall from a Rainfall Simulator with a Rotary Platform (RSRP). Atmosphere. 2017; 8(7):113. https://doi.org/10.3390/atmos8070113
Chicago/Turabian StyleLiu, Bo, Xiaolei Wang, Lihua Shi, Xichuan Liu, Zhaojing Kang, and Zhentao Chen. 2017. "Research on the Fine-Scale Spatial Uniformity of Natural Rainfall and Rainfall from a Rainfall Simulator with a Rotary Platform (RSRP)" Atmosphere 8, no. 7: 113. https://doi.org/10.3390/atmos8070113
APA StyleLiu, B., Wang, X., Shi, L., Liu, X., Kang, Z., & Chen, Z. (2017). Research on the Fine-Scale Spatial Uniformity of Natural Rainfall and Rainfall from a Rainfall Simulator with a Rotary Platform (RSRP). Atmosphere, 8(7), 113. https://doi.org/10.3390/atmos8070113





