Role of Wind Filtering and Unbalanced Flow Generation in Middle Atmosphere Gravity Wave Activity at Chatanika Alaska
Abstract
:1. Introduction
2. Experiments
2.1. Rayleigh LiDAR
2.2. Meteorological Reanalysis
3. Results
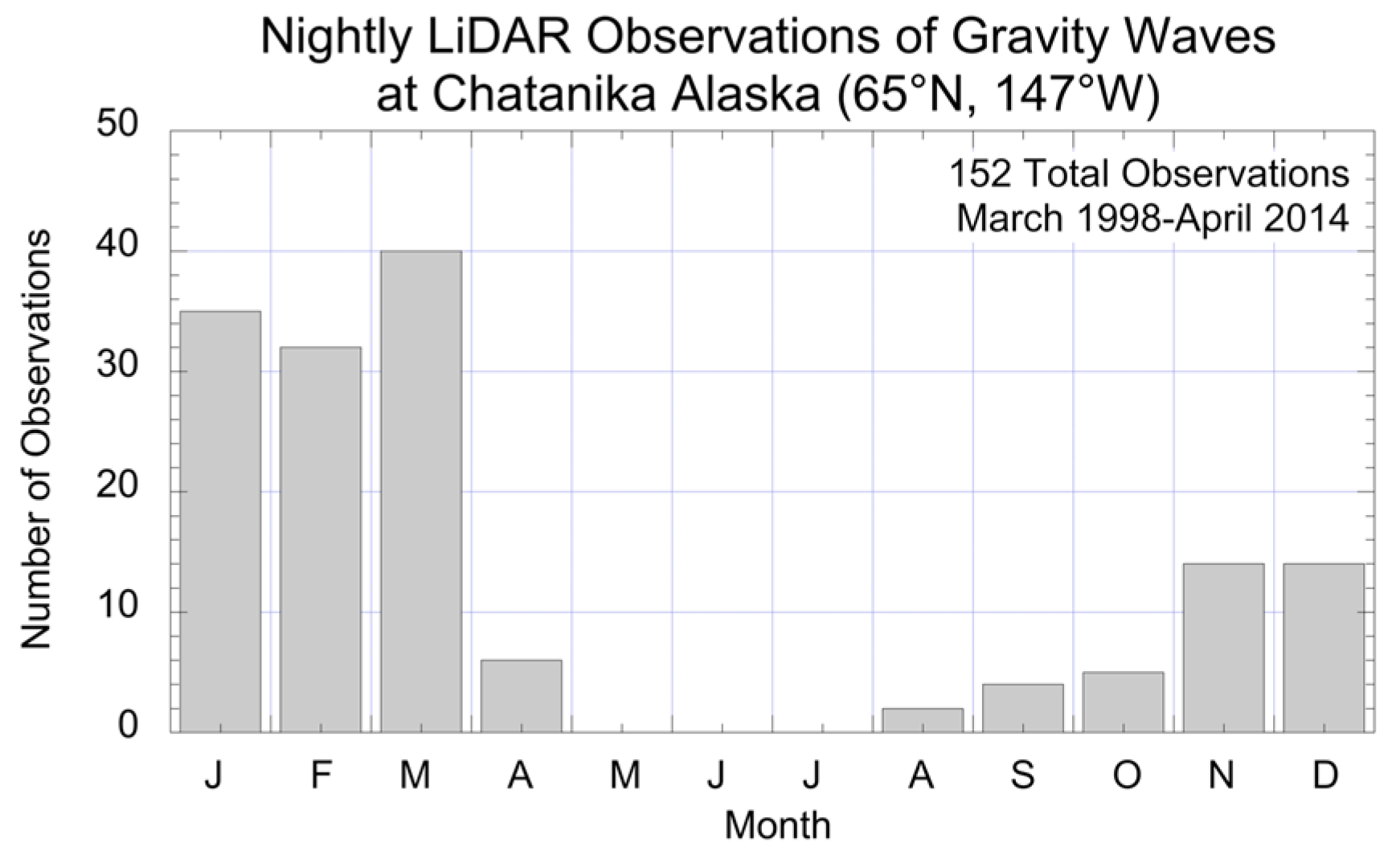
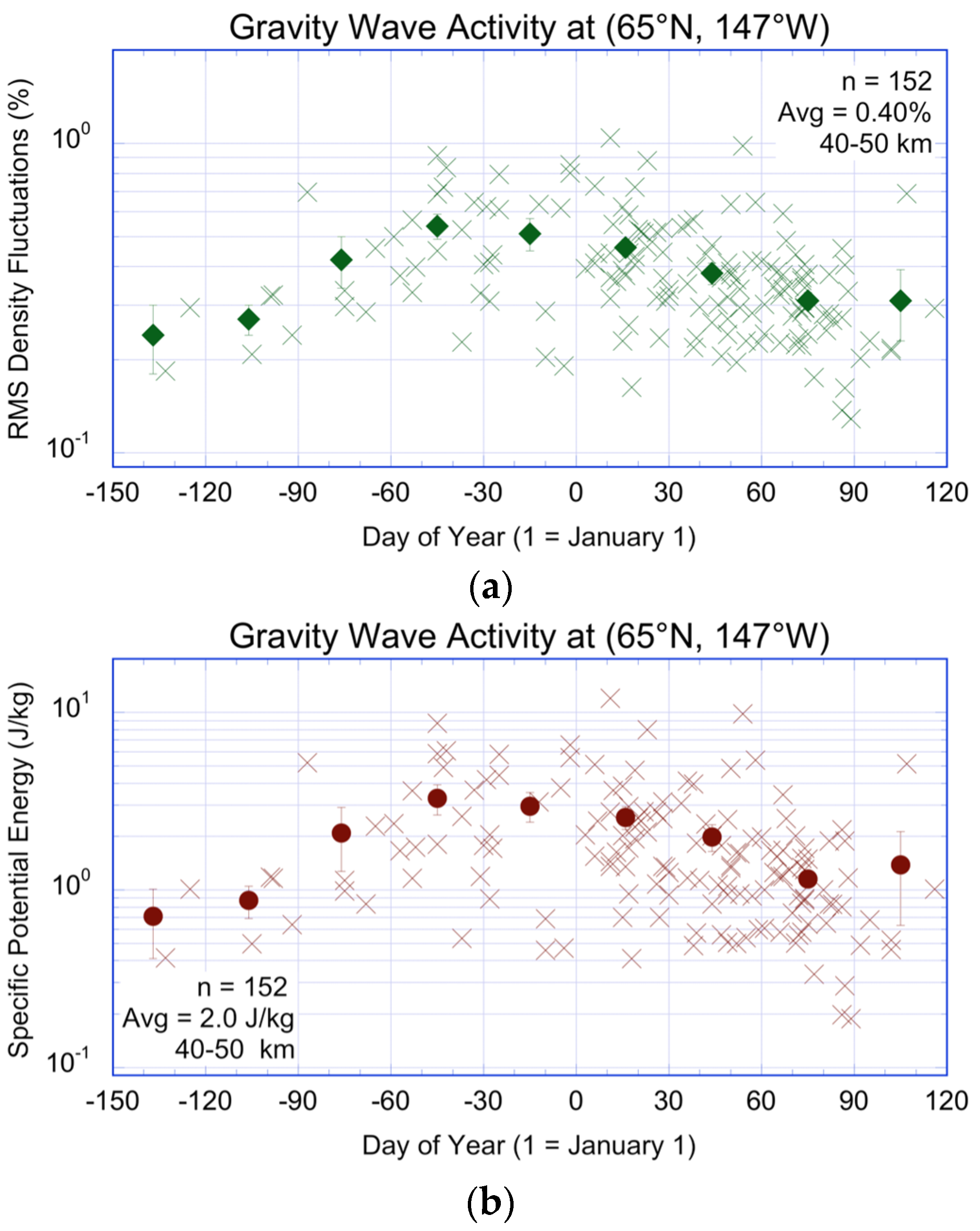
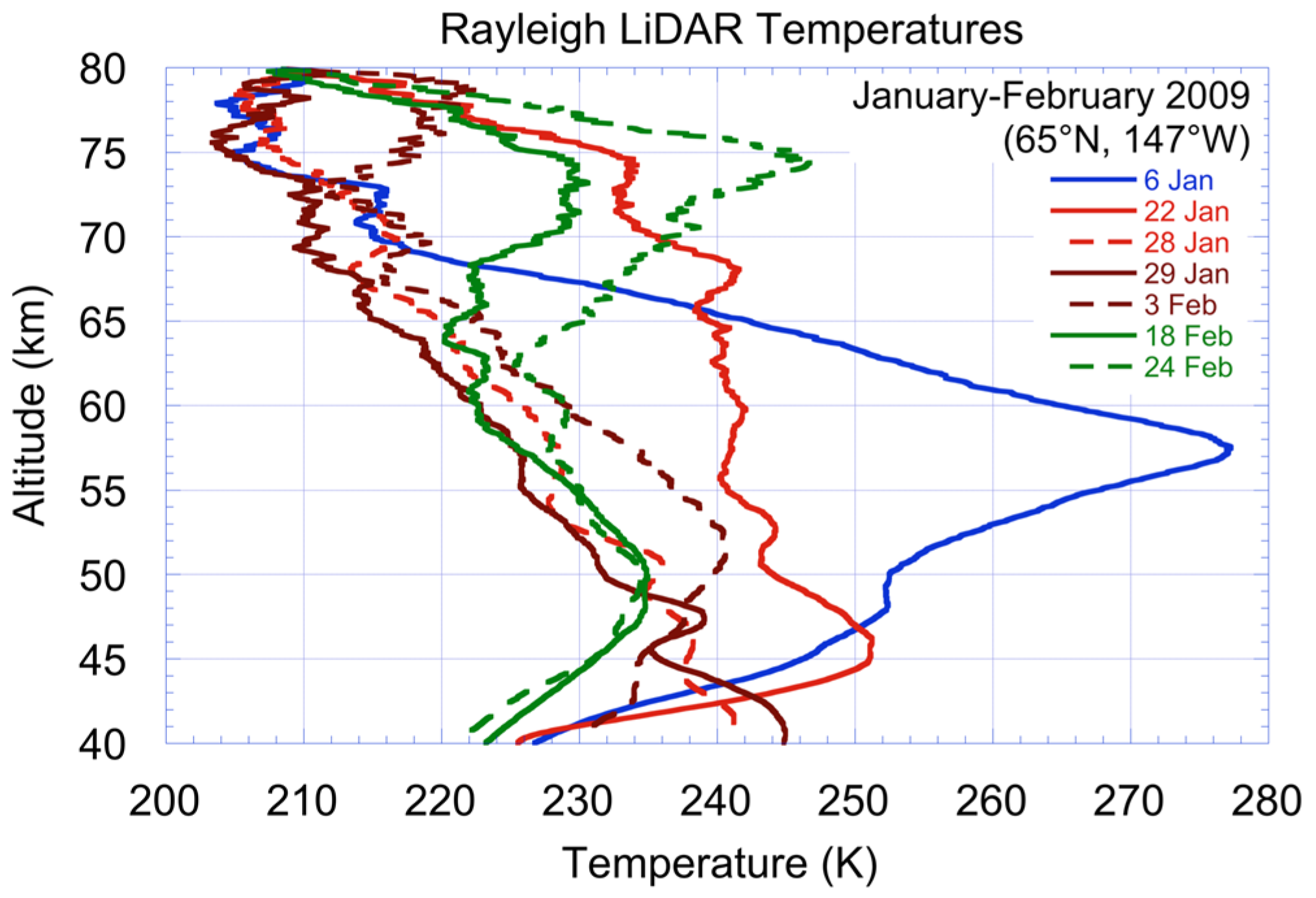
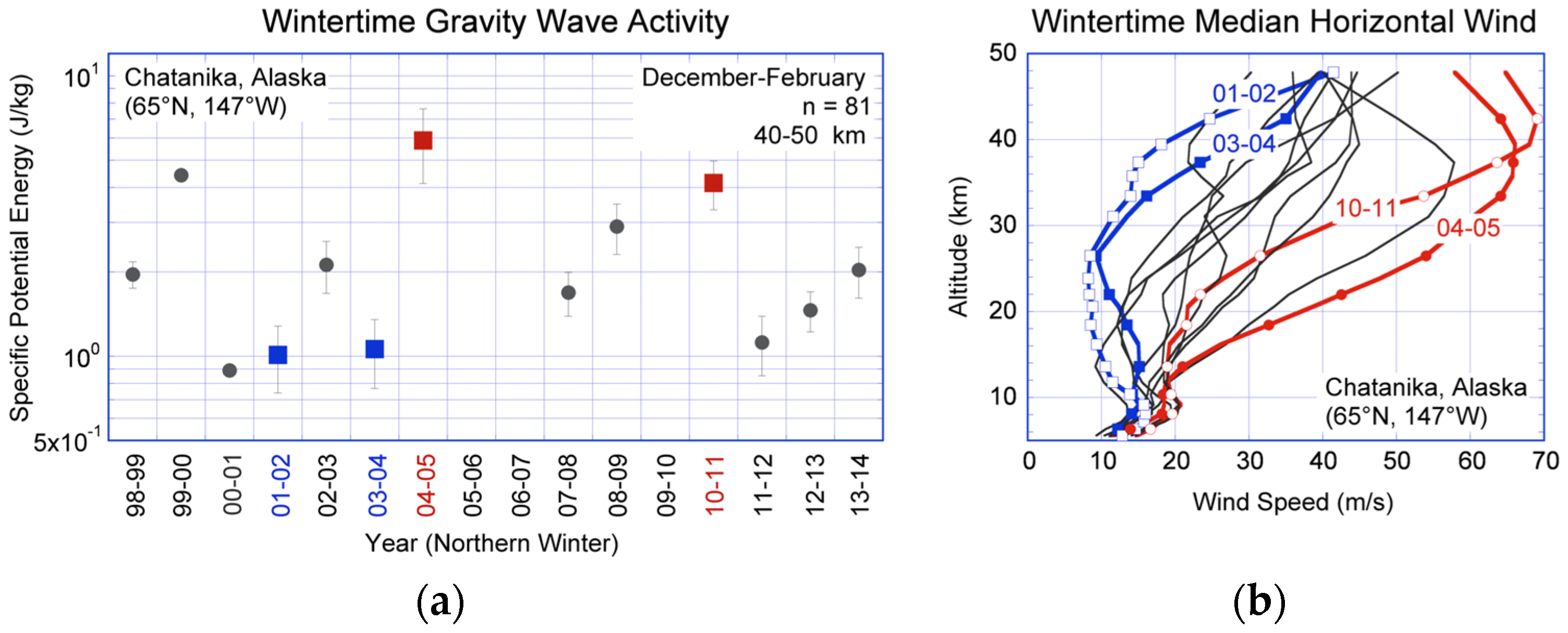
3.1. Rayleigh LiDAR Measurements of Gravity Wave Activity
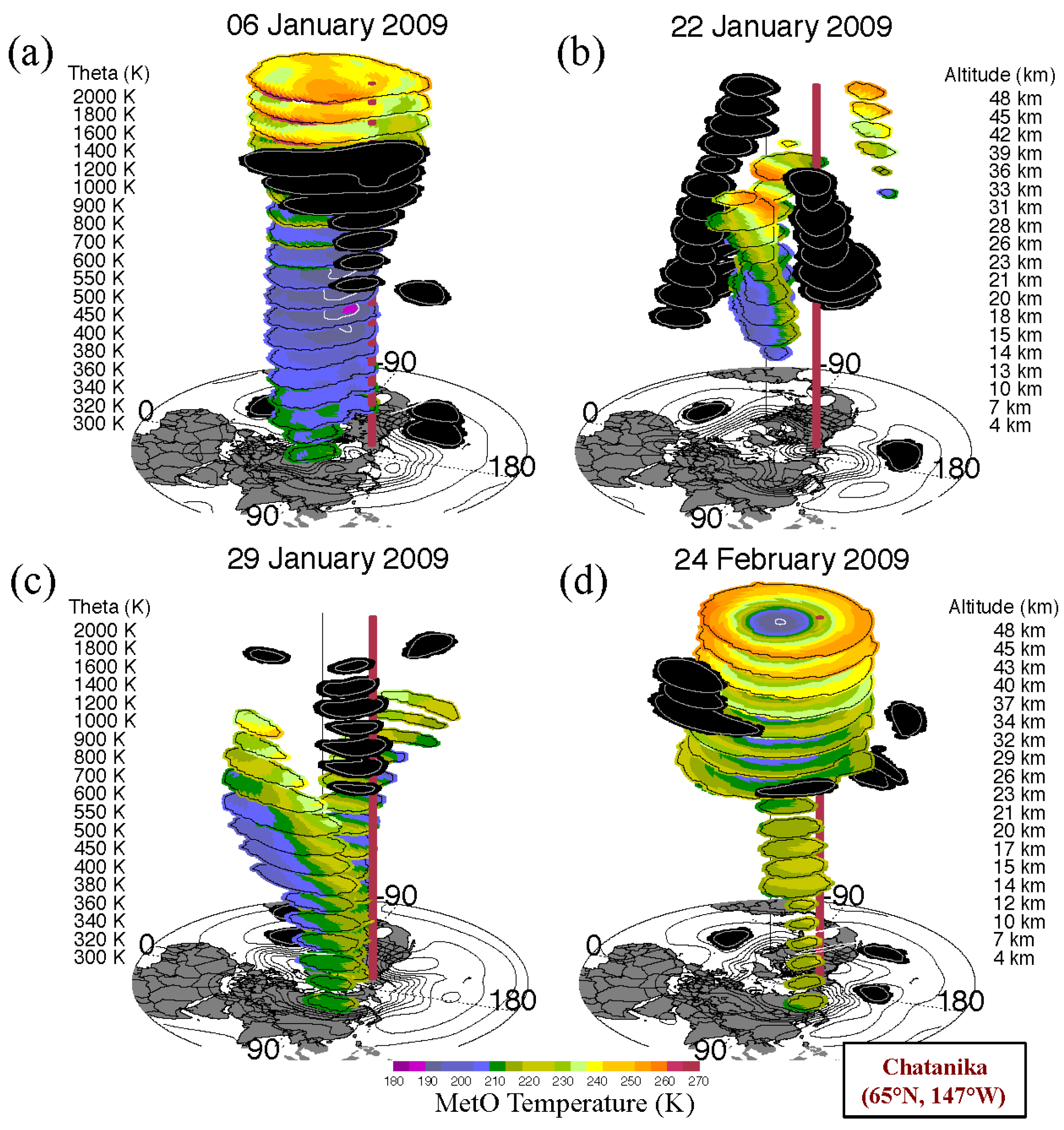
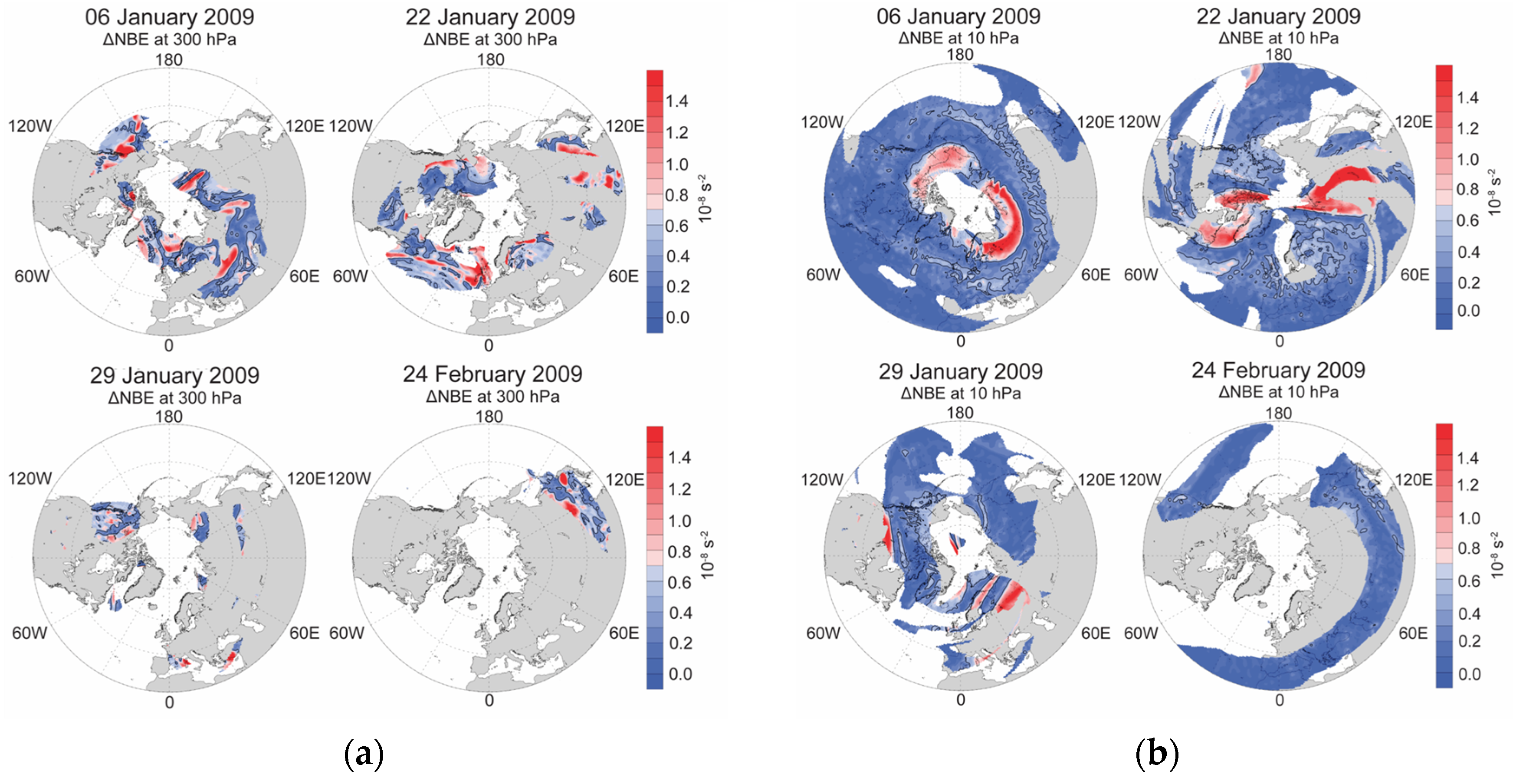
3.2. The 2009 Stratospheric Sudden Warming
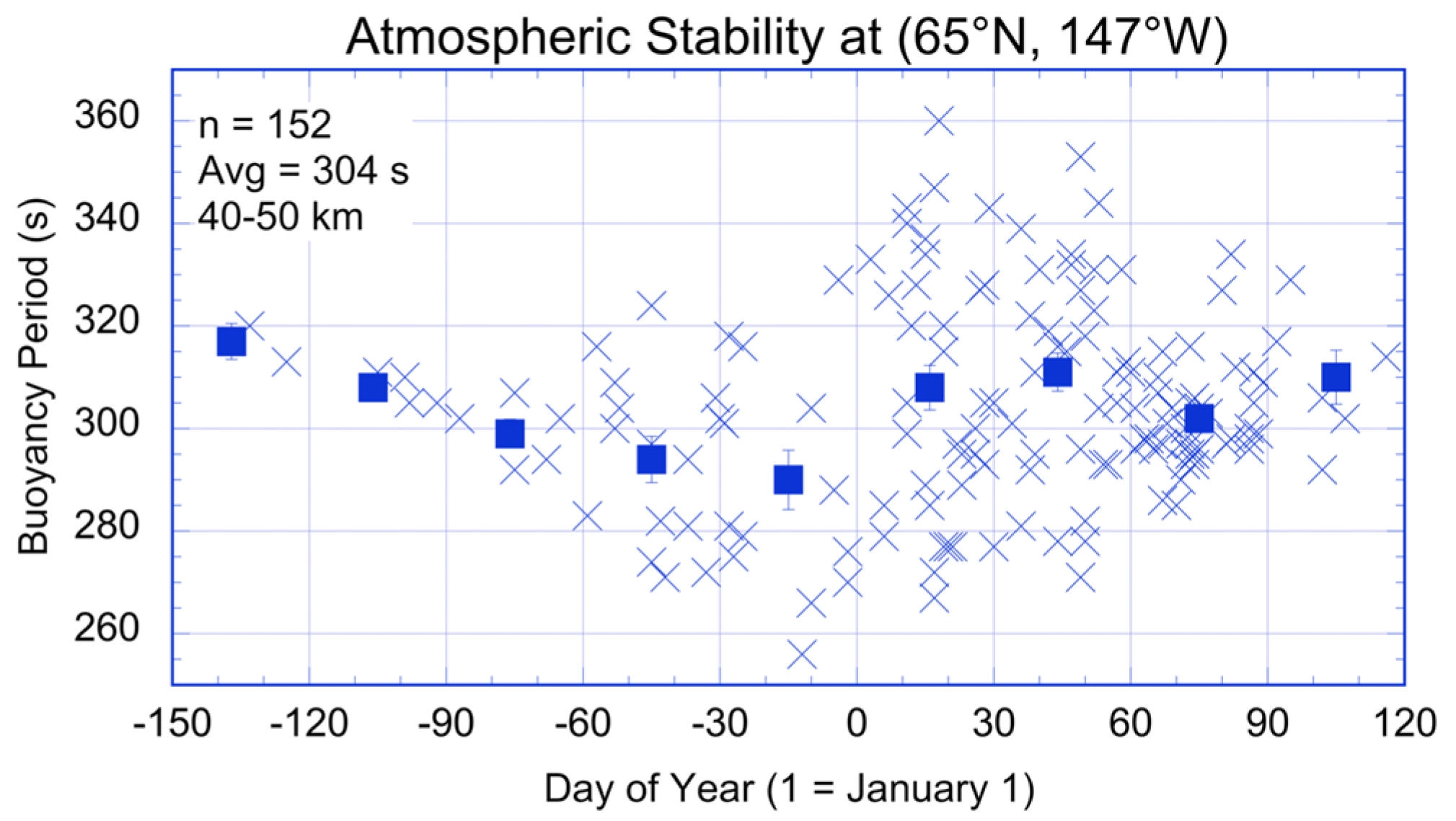
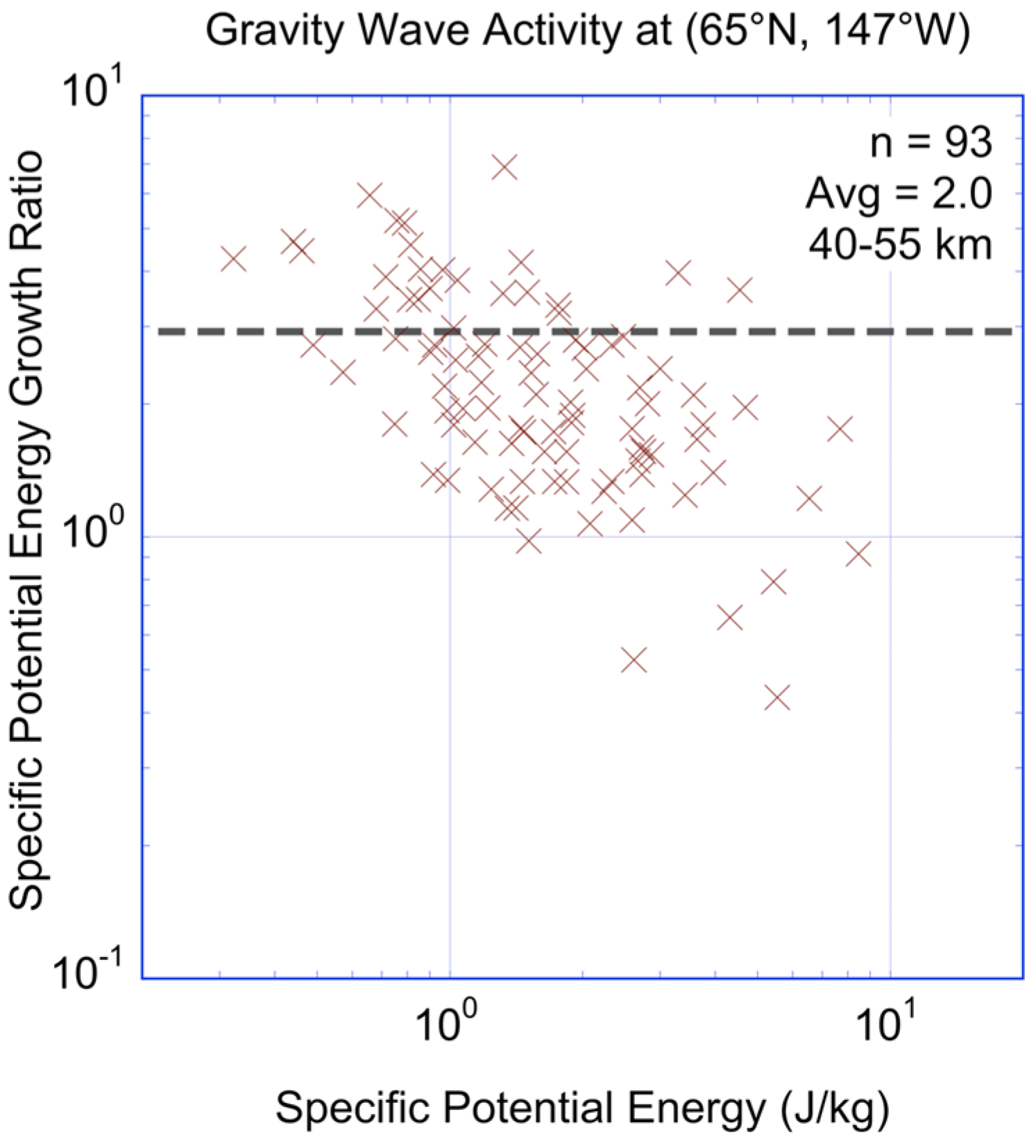
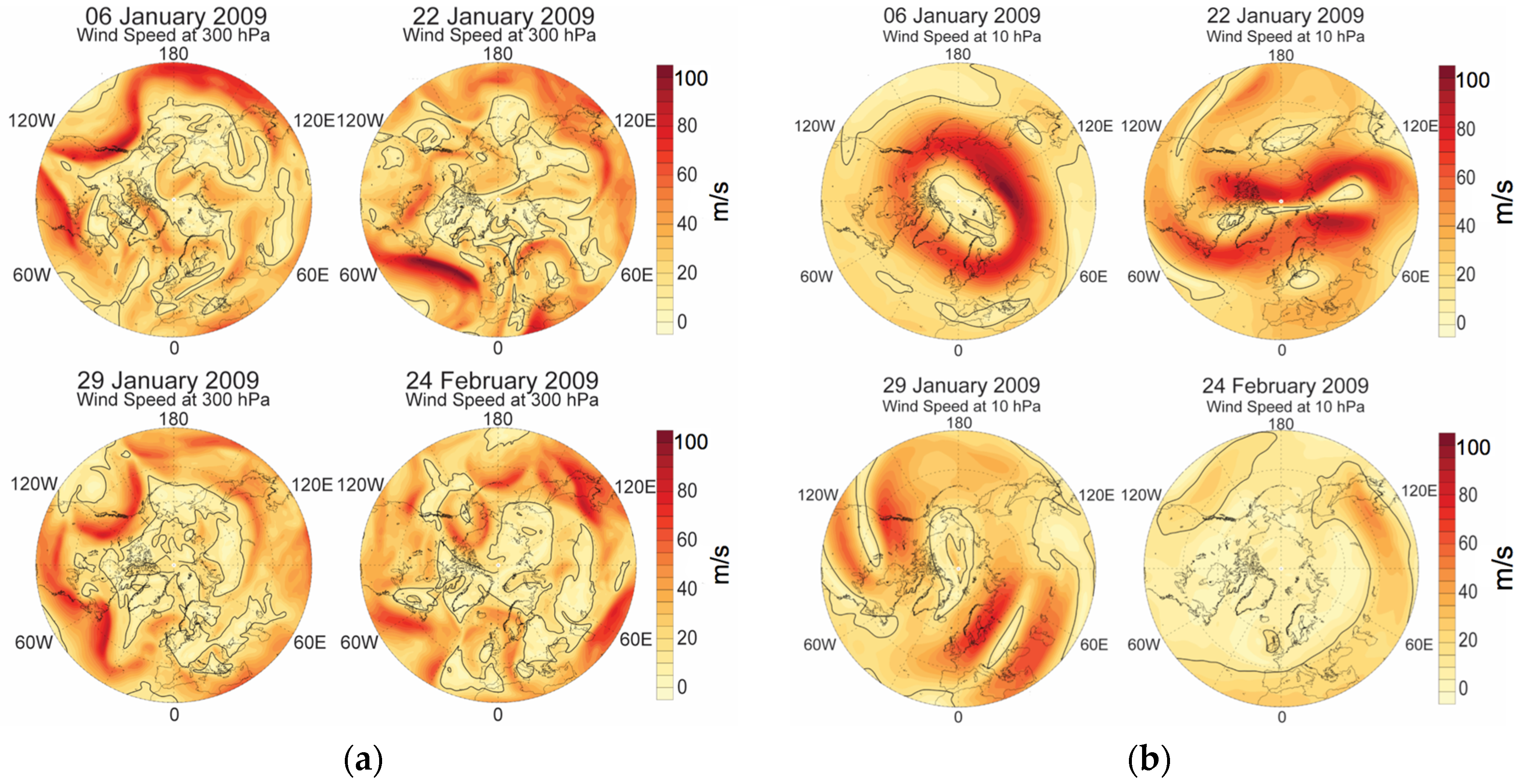
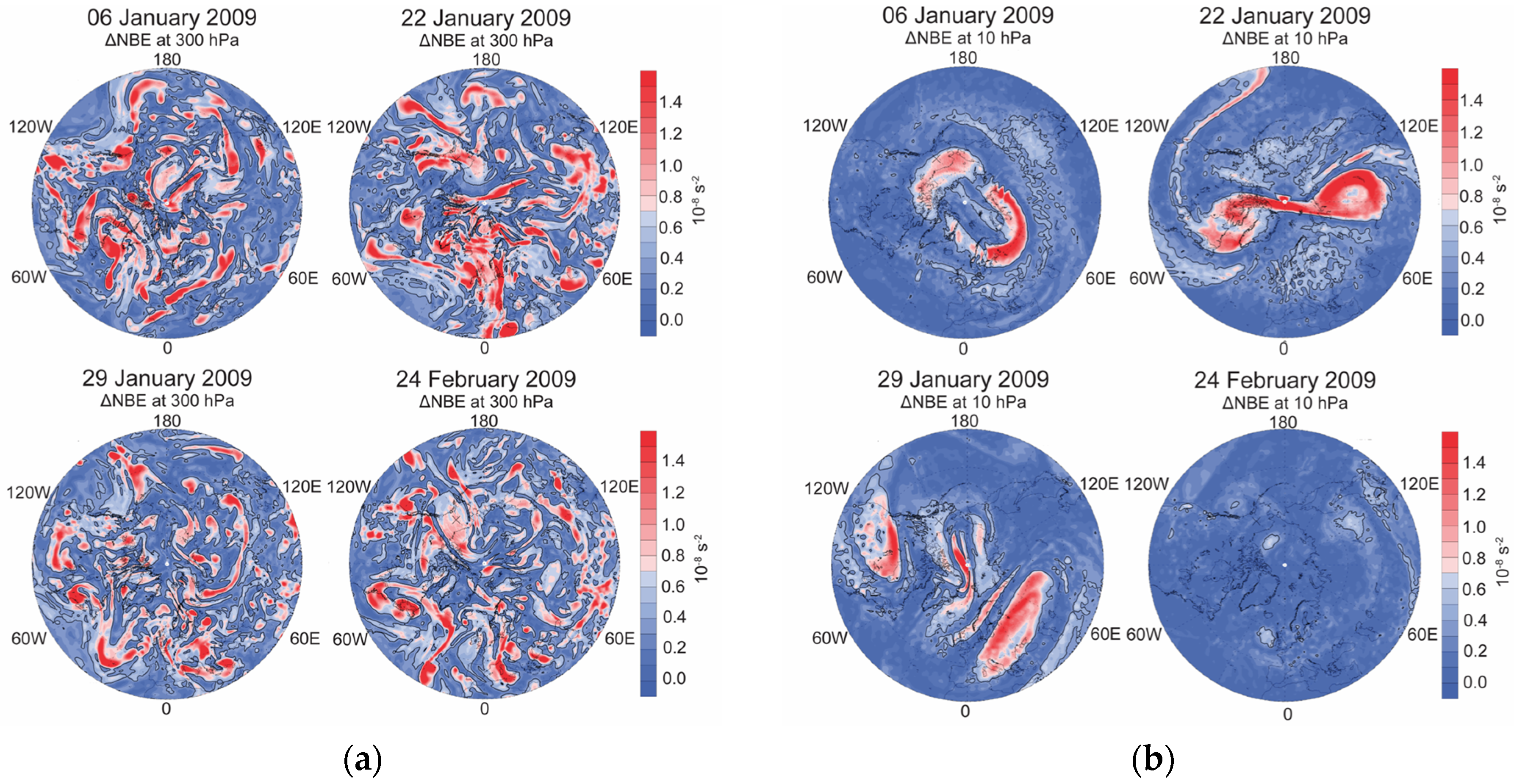
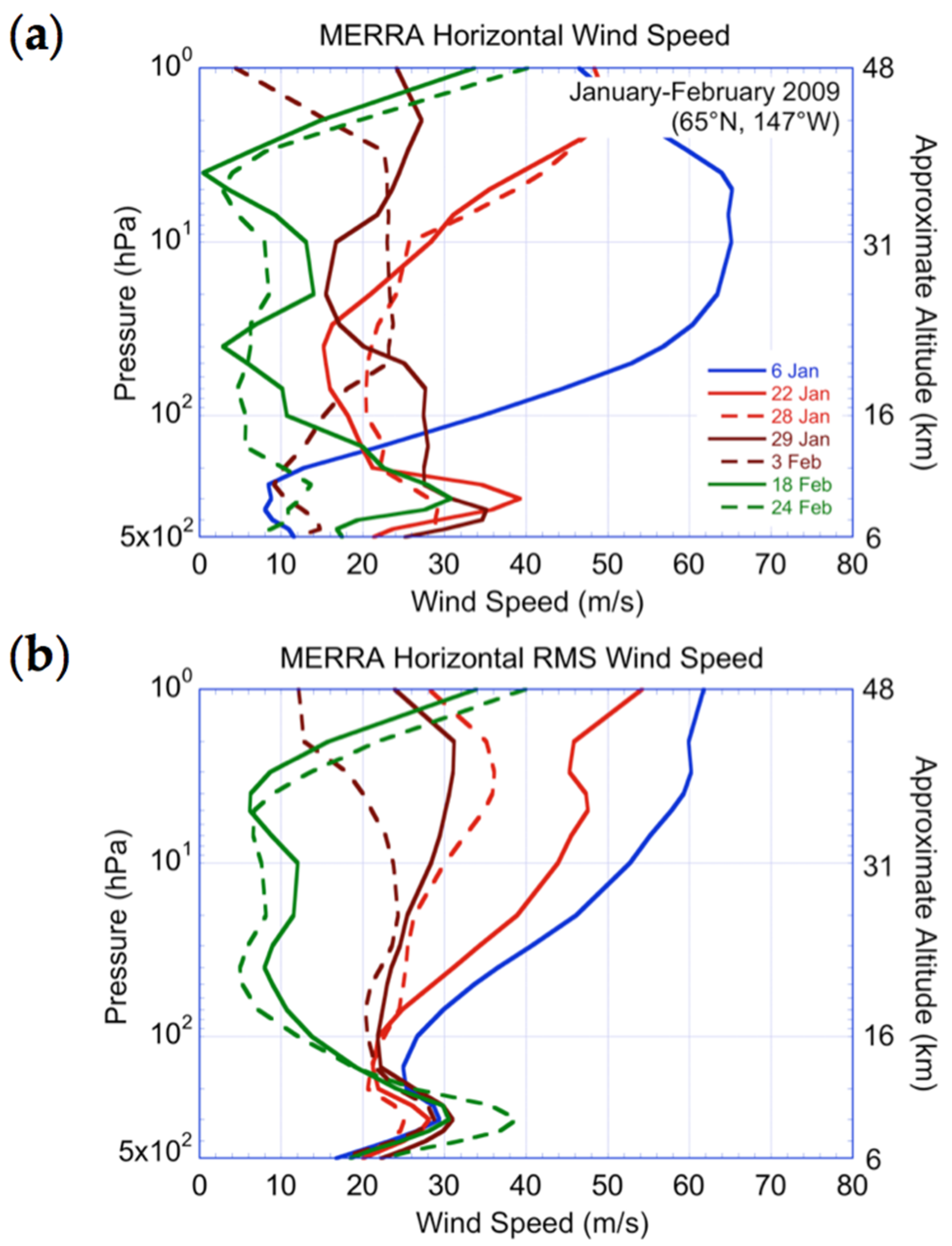
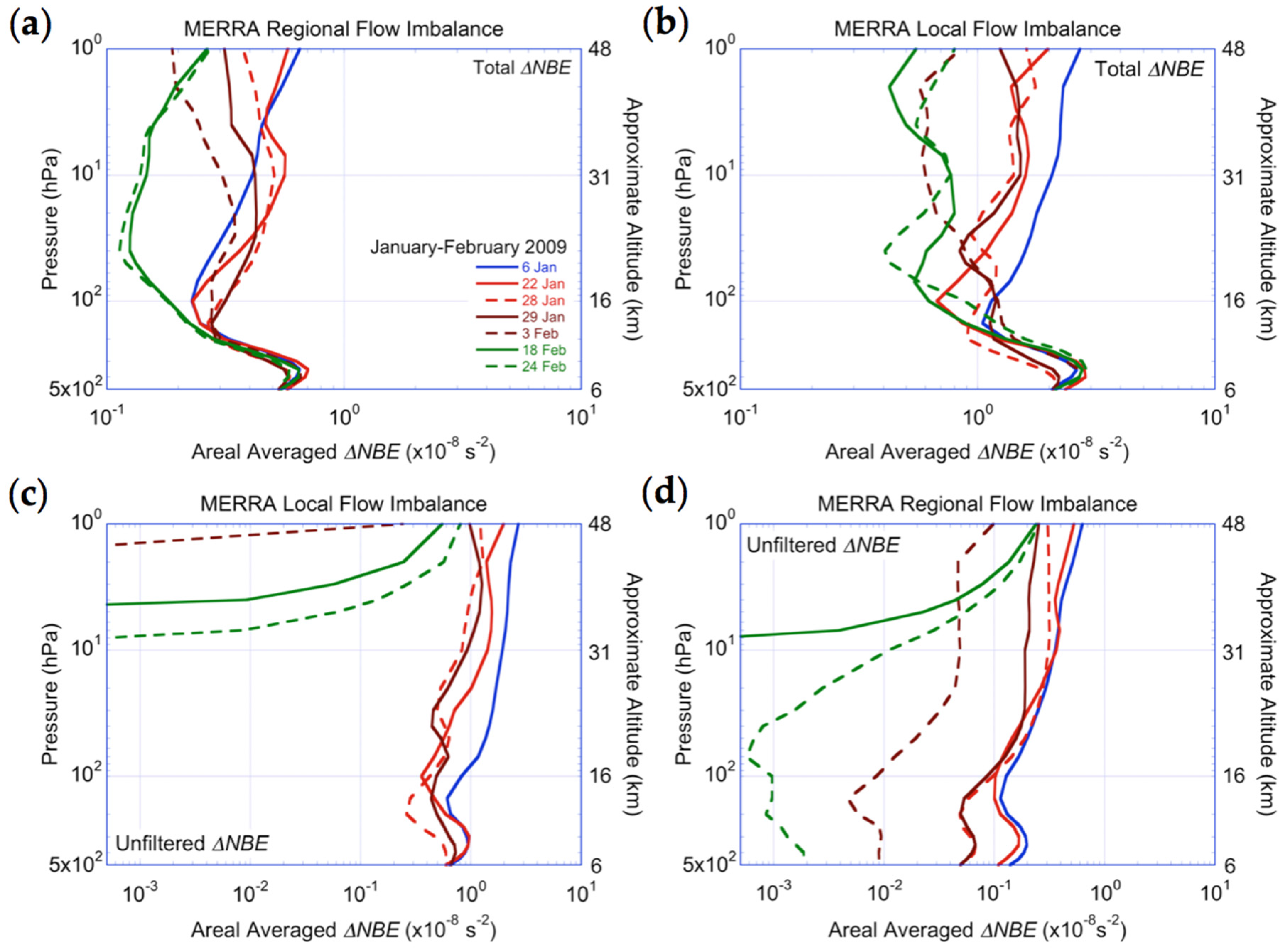
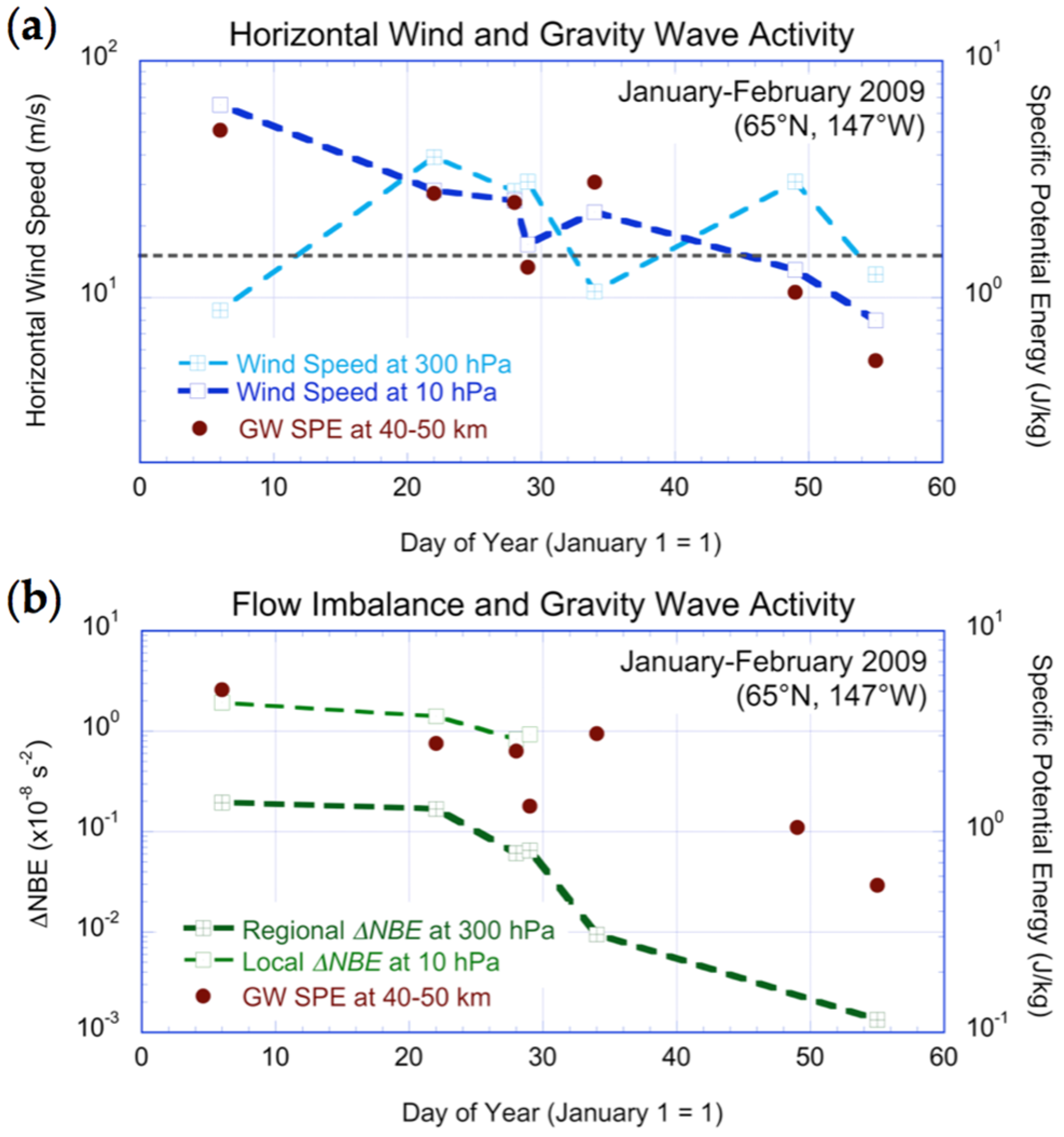
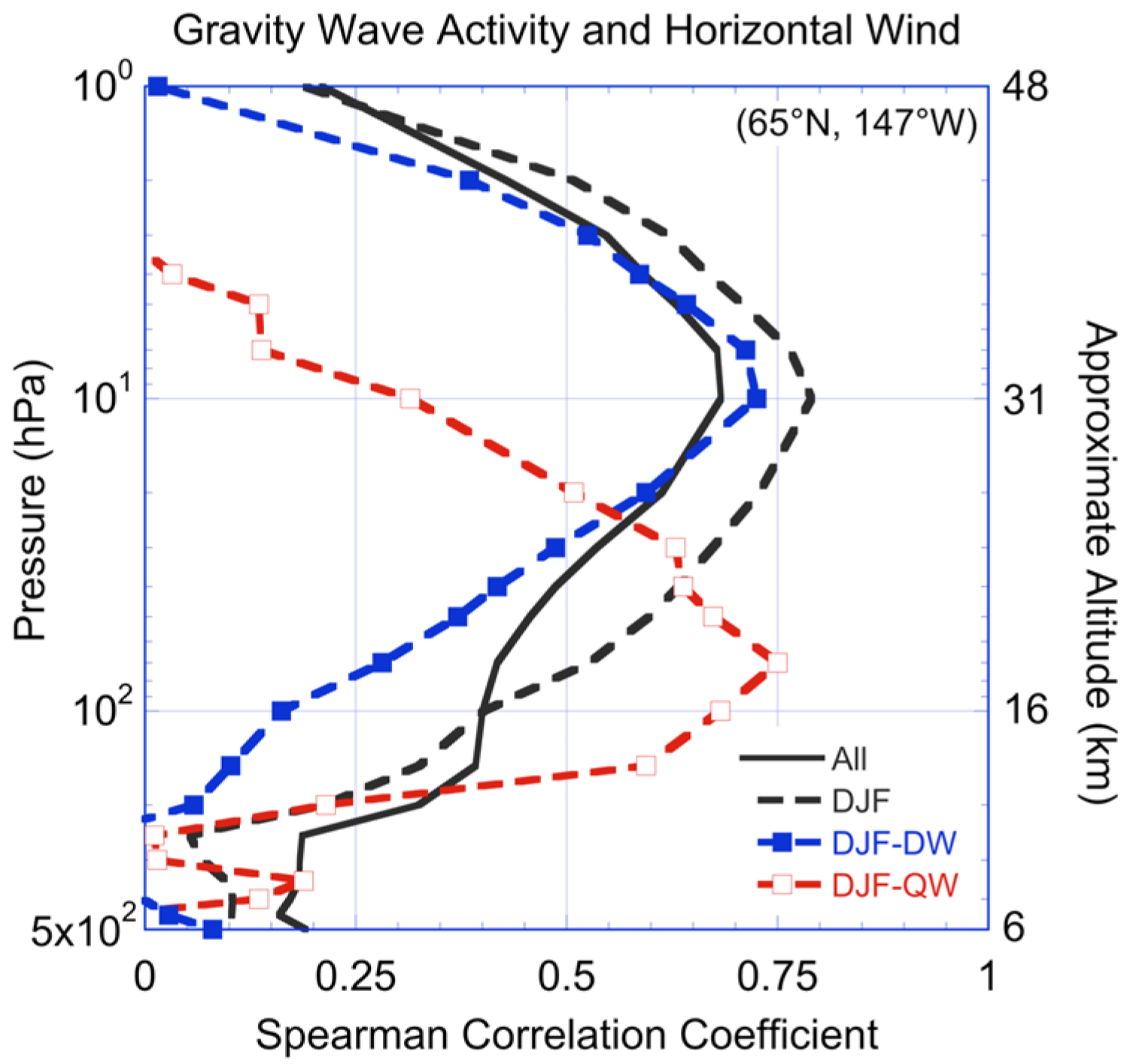
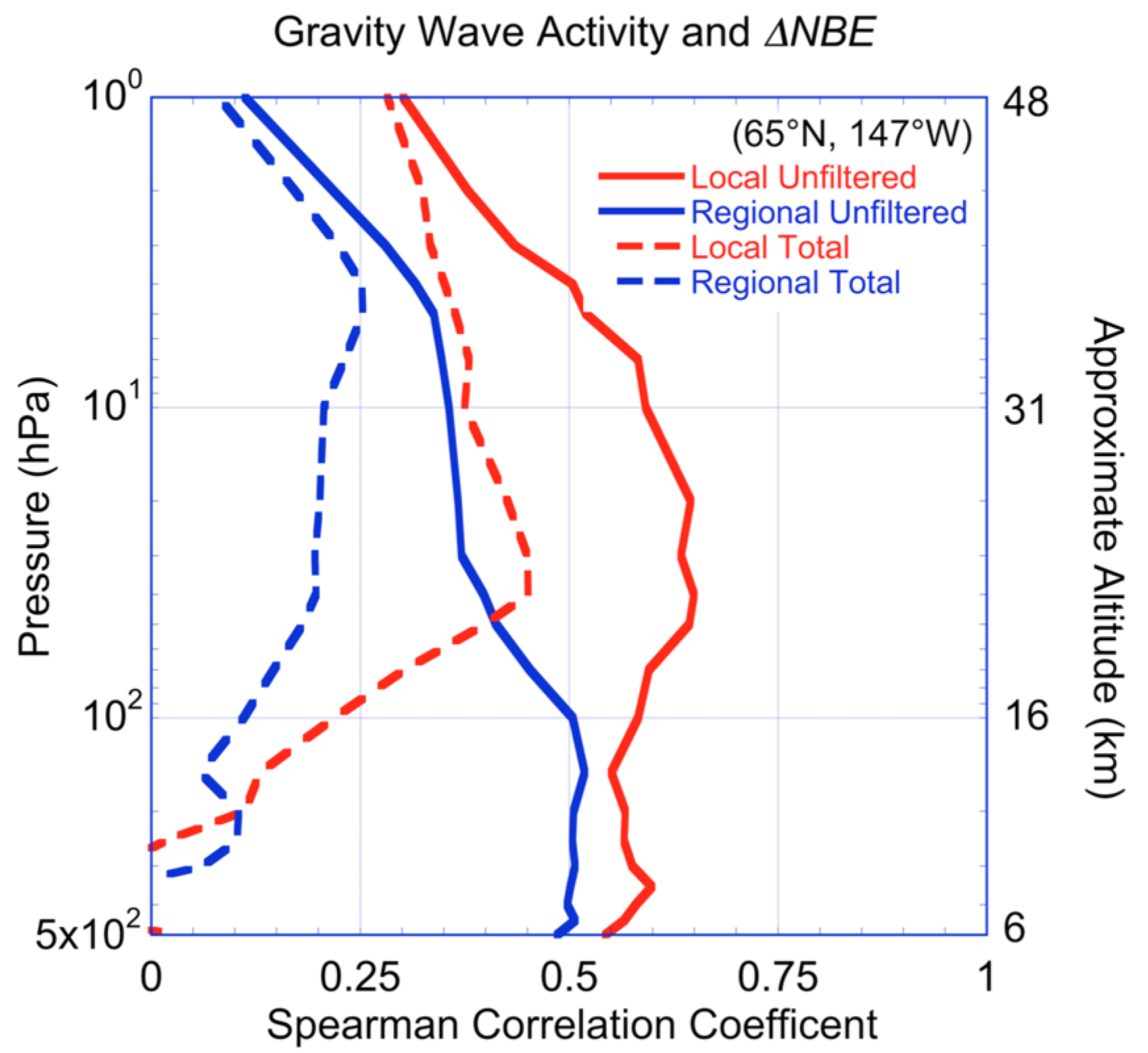
3.3. Correlation between Gravity Wave Activity and Winds and Ageostrophy
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Houghton, J.T. The stratosphere and mesosphere. Q. J. R. Meteorol. Soc. 1978, 104, 1–29. [Google Scholar] [CrossRef]
- Plumb, R.A.; Vincent, R.A. Introduction to special issue on middle atmosphere. Pure Appl. Geophys. 1989, 130, 149–150. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Alexander, M.J.; Sato, K. Gravity wave dynamics and climate: An update from the SPARC gravity wave activity. SPARC Newsl. 2015, 44, 9–13. [Google Scholar]
- Fritts, D.C.; Smith, R.B.; Taylor, M.J.; Doyle, J.D.; Eckermann, S.D.; Dörnbrack, A.; Rapp, M.; Williams, B.P.; Pautet, P.-D.; Bossert, K.; et al. The Deep Propagating Gravity Wave Experiment (DEEPWAVE): An Airborne and Ground-Based Exploration of Gravity Wave Propagation and Effects from Their Sources throughout the Lower and Middle Atmosphere. Bull. Am. Meteorol. Soc. 2016, 97, 425–453. [Google Scholar] [CrossRef]
- Chandran, A.; Collins, R.L.; Garcia, R.R.; Marsh, D.R. A case study of an elevated stratopause generated in the Whole Atmosphere Community Climate Model. Geophys. Res. Lett. 2011, 38, L08804. [Google Scholar] [CrossRef]
- Chandran, A.; Collins, R.L.; Garcia, R.R.; Marsh, D.R.; Harvey, V.L.; Yue, J.; de la Torre, J. A climatology of elevated stratopause events in the whole atmosphere community climate model. J. Geophys. Res. 2013, 118, 1234–1246. [Google Scholar] [CrossRef]
- Chandran, A.; Collins, R.L.; Harvey, V.L. Stratosphere-mesosphere coupling during stratospheric sudden warming events. Adv. Space Res. 2014, 53, 1265–1289. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Alexander, M.J.; Orsolini, Y.J.; Wu, D.L.; Richter, J.H.; Yamashita, C. Mesoscale simulation of gravity waves during the 2008–2009 major stratospheric sudden warming. J. Geophys. Res. 2011, 116, D17104. [Google Scholar] [CrossRef]
- Ren, S.; Polavarapu, S.; Beagley, S.R.; Nezlin, Y.; Rochon, Y.J. The impact of gravity wave drag mesospheric analyses of the 2006 stratospheric major warming. J. Geophys. Res. 2011, 116, D19116. [Google Scholar] [CrossRef]
- Rossby, C.G. On the mutual adjustment of pressure and velocity distributions in certain simple current systems. II. J. Mar. Res. 1938, 7, 239–263. [Google Scholar] [CrossRef]
- Cahn, A. An investigation of the free oscillations of a simple current system. J. Atmos. Sci. 1945, 2, 113–119. [Google Scholar] [CrossRef]
- Obukhov, A. On the question of geostrophic wind (in Russian). Bull. USSR Acad. Sci. Geograph. Geophys. Ser. 1949, 13, 281–306. [Google Scholar]
- Plougonven, R.; Zhang, F. Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 2014, 52, 33–76. [Google Scholar] [CrossRef]
- Fritts, D.C.; Luo, Z. Gravity wave excitation by geostrophic adjustment of the jet stream, part I, Two-dimensional forcing. J. Atmos. Sci. 1992, 49, 681–697. [Google Scholar] [CrossRef]
- Sato, K.; Yoshiki, M. Gravity wave generation around the polar vortex in the stratosphere revealed by 3-hourly radiosonde observations at Syowa Station. J. Atmos. Sci. 2008, 65, 3719–3735. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Gravity wave activity during stratospheric sudden warmings in the 2007–2008 Northern Hemisphere winter. J. Geophys. Res. 2009, 114, D18108. [Google Scholar] [CrossRef]
- Thurairajah, B.; Collins, R.L.; Harvey, V.L.; Lieberman, R.S.; Mizutani, K. Rayleigh lidar observations of reduced gravity wave activity during the formation of an elevated stratopause in 2004 at Chatanika, Alaska (65° N, 147° W). J. Geophys. Res. 2010, 115, D13109. [Google Scholar] [CrossRef]
- Thurairajah, B.; Collins, R.L.; Harvey, V.L.; Lieberman, R.S.; Gerding, M.; Mizutani, K.; Livingston, J.M. Gravity wave activity in the Arctic stratosphere and mesosphere during the 2007–2008 and 2008–2009 stratospheric sudden warming events. J. Geophys. Res. 2010, 115, D00N06. [Google Scholar] [CrossRef]
- Collins, R.L.; Lehmacher, G.A.; Larsen, M.F.; Mizutani, K. Estimates of vertical eddy diffusivity in the upper mesosphere in the presence of a mesospheric inversion layer. Ann. Geophys. 2011, 29, 2019–2029. [Google Scholar] [CrossRef] [Green Version]
- Irving, B.K.; Collins, R.L.; Lieberman, R.S.; Thurairajah, B.; Mizutani, K. Mesospheric Inversion Layers at Chatanika, Alaska (65° N, 147° W): Rayleigh lidar observations and analysis. J. Geophys. Res. Atmos. 2014, 119, 11235–11249. [Google Scholar] [CrossRef]
- SPARC intercomparison of middle atmosphere climatologies. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20030020951.pdf (accessed on 18 January 2017).
- Randel, W.; Udelhofen, P.; Fleming, E.; Geller, M.; Gelman, M.; Hamilton, K.; Karoly, D.; Ortland, D.; Pawson, S.; Swinbank, R.; et al. The SPARC intercomparison of middle-atmosphere climatologies. J. Clim. 2004, 17, 986–1003. [Google Scholar] [CrossRef]
- Gill, H.E. Atmosphere–Ocean Dynamics; Academic Press Inc.: New York, NY, USA, 1982; p. 662. [Google Scholar]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Champion, K.S.W.; Cole, A.E.; Kantor, A.J. Standard and Reference Atmospheres. In Handbook of Geophysics and the Space Environment; Jursa, A.S., Ed.; Air Force Geophysics Laboratory: Hanscom AFB, MA, USA, 1985; pp. 14:1–14:43. [Google Scholar]
- Petterssen, S. On the relation between vorticity, deformation, and divergence and the configuration of the pressure field. Tellus 1953, 5, 231–237. [Google Scholar] [CrossRef]
- Zhang, F.; Koch, S.E.; Davis, C.A.; Kaplan, M.L. A survey of unbalanced flow diagnostics and their application. Adv. Atmos. Sci. 2000, 17, 205–218. [Google Scholar] [CrossRef]
- Zhang, F.; Koch, S.E.; Davis, C.A.; Kaplan, M.L. Wavelet analysis and the governing dynamics of a large-amplitude mesoscale gravity-wave event along the East Coast of the United States. Q. J. R. Meteorol. Soc. 2001, 127, 2209–2245. [Google Scholar] [CrossRef]
- Hertzog, A.; Souprayen, C.; Hauchecorne, A. Observation and backward trajectory of an inertia-gravity wave in the lower stratosphere. Ann. Geophys. 2001, 19, 1141–1155. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1992; pp. 1–963. [Google Scholar]
- Hoffmann, L.; Xue, X.; Alexander, M.J. A global view of stratospheric gravity wave hotspots located with Atmospheric Infrared Sounder observations. J. Geophys. Res. Atmos. 2013, 118, 416–434. [Google Scholar] [CrossRef]
- Mzé, N.; Hauchecorne, A.; Keckhut, P.; Thétis, M. Vertical distribution of gravity wave potential energy from long-term Rayleigh lidar data at a northern middle-latitude site. J. Geophys. Res. Atmos. 2014, 119, 12069–12083. [Google Scholar] [CrossRef]
- Kaifler, B.; Kaifler, M.; Ehard, B.; Dörnbrack, A.; Rapp, M.; Fritts, D.C. Influences of source conditions on mountain wave penetrations into the stratosphere and mesosphere. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Harvey, V.L.; Pierce, R.B.; Fairlie, T.D.; Hitchman, M.H. A climatology of stratospheric polar vortices and anticyclones. J. Geophys. Res. 2002, 107, 4442. [Google Scholar] [CrossRef]
- Harvey, V.L.; Randall, C.E.; Hitchman, M.H. Breakdown of potential vorticity-based equivalent latitude as a vortex-centered coordinate in polar winter mesosphere. J. Geophys. Res. 2009, 114, D22105. [Google Scholar] [CrossRef]
- Ern, M.; Trinh, Q.T.; Kaufmann, M.; Krisch, I.; Preusse, P.; Ungermann, J.; Zhu, Y.; Gille, J.C.; Mlynczak, M.G.; Russell, J.M.; et al. Satellite observations of middle atmosphere gravity wave absolute momentum flux and of its vertical gradient during recent stratospheric warming. Atmos. Chem. Phys. 2016, 16, 9983–10019. [Google Scholar] [CrossRef]
- Ehard, B.; Achtert, P.; Gumbel, J. Long-term lidar observations of wintertime gravity wave activity over northern Sweden. Ann. Geophys. 2014, 32, 1395–1405. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Lübken, F.-J. Seasonal changes in gravity wave activity measured by lidars at mid-latitudes. Atmos. Chem. Phys. 2008, 8, 6775–6787. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Carswell, A.I. Lidar observations of gravity wave activity in the upper stratosphere over Toronto. J. Geophys. Res. 1995, 100, 14113–14124. [Google Scholar] [CrossRef]
- Wilson, R.; Chanin, M.L.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar 2. Climatology. J. Geophys. Res. 1991, 96, 5169–5183. [Google Scholar] [CrossRef]
- Duck, T.J.; Whiteway, J.A.; Carswell, A.I. The gravity wave–arctic stratospheric vortex interaction. J. Atmos. Sci. 2001, 58, 3581–3596. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Dunkerton, T.J. Generation of inertia-gravity waves in a simulated life cycle of baroclinic instability. J. Atmos. Sci. 1995, 52, 3695–3716. [Google Scholar] [CrossRef]
- Wu, D.L.; Eckermann, S.D. Global gravity wave variances from Aura MLS: Characteristics and interpretation. J. Atmos. Sci. 2008, 65, 3695–3718. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Triplett, C.C.; Collins, R.L.; Nielsen, K.; Harvey, V.L.; Mizutani, K. Role of Wind Filtering and Unbalanced Flow Generation in Middle Atmosphere Gravity Wave Activity at Chatanika Alaska. Atmosphere 2017, 8, 27. https://doi.org/10.3390/atmos8020027
Triplett CC, Collins RL, Nielsen K, Harvey VL, Mizutani K. Role of Wind Filtering and Unbalanced Flow Generation in Middle Atmosphere Gravity Wave Activity at Chatanika Alaska. Atmosphere. 2017; 8(2):27. https://doi.org/10.3390/atmos8020027
Chicago/Turabian StyleTriplett, Colin C., Richard L. Collins, Kim Nielsen, V. Lynn Harvey, and Kohei Mizutani. 2017. "Role of Wind Filtering and Unbalanced Flow Generation in Middle Atmosphere Gravity Wave Activity at Chatanika Alaska" Atmosphere 8, no. 2: 27. https://doi.org/10.3390/atmos8020027
APA StyleTriplett, C. C., Collins, R. L., Nielsen, K., Harvey, V. L., & Mizutani, K. (2017). Role of Wind Filtering and Unbalanced Flow Generation in Middle Atmosphere Gravity Wave Activity at Chatanika Alaska. Atmosphere, 8(2), 27. https://doi.org/10.3390/atmos8020027



