ELF Electromagnetic Waves from Lightning: The Schumann Resonances
Abstract
:1. Introduction
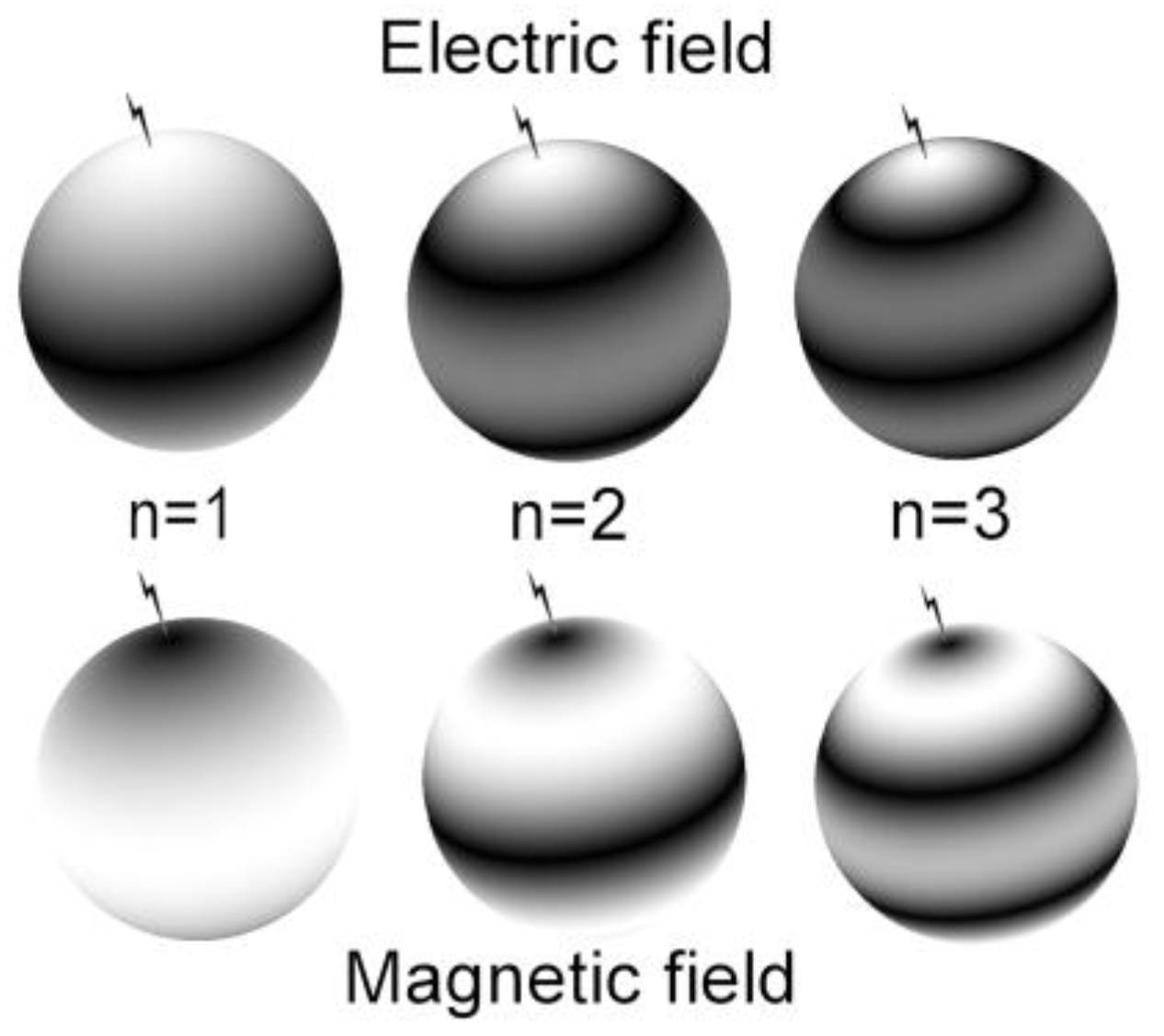
2. Theoretical Background
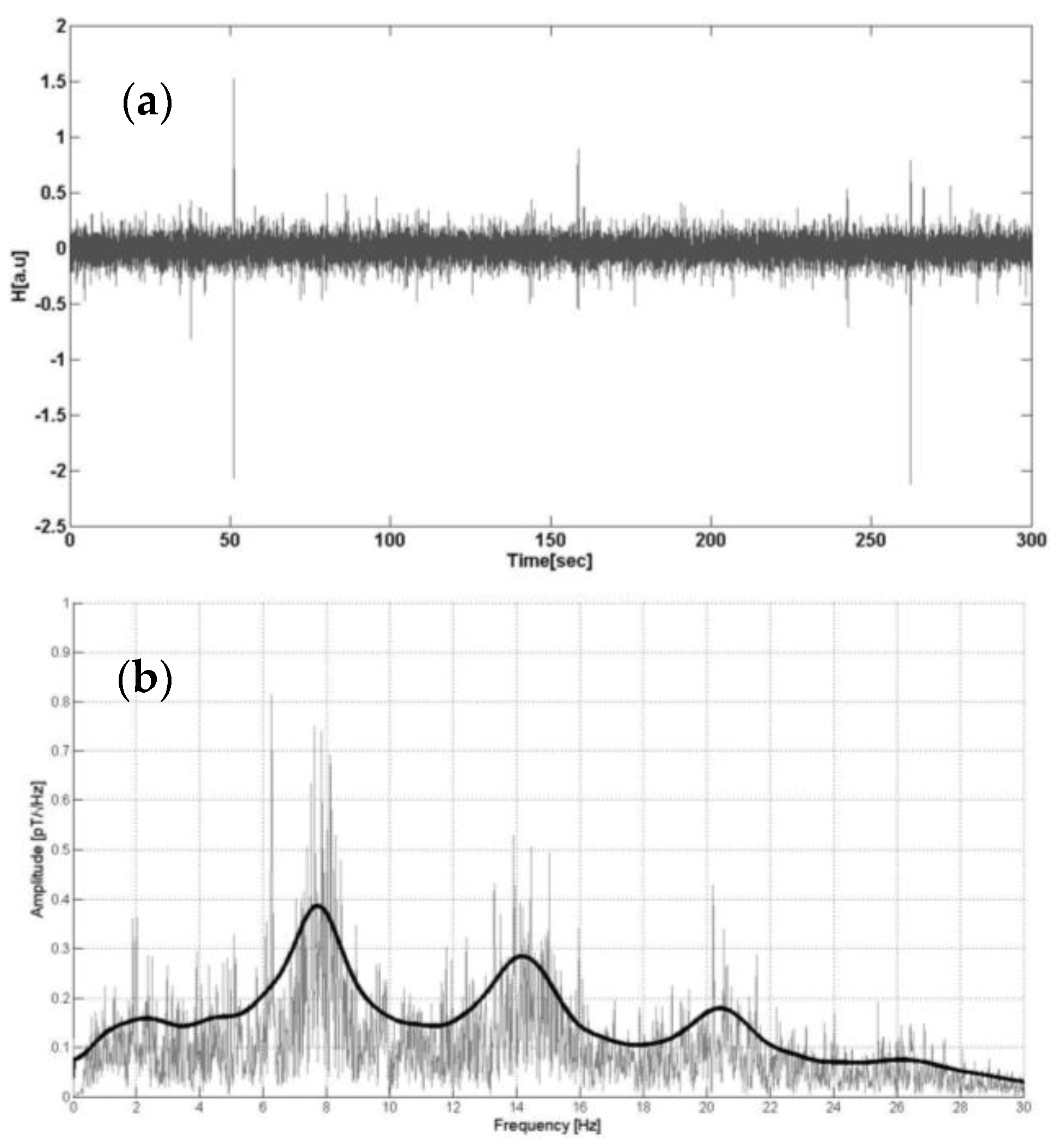
3. SR Measurements
4. Applications of SR Research
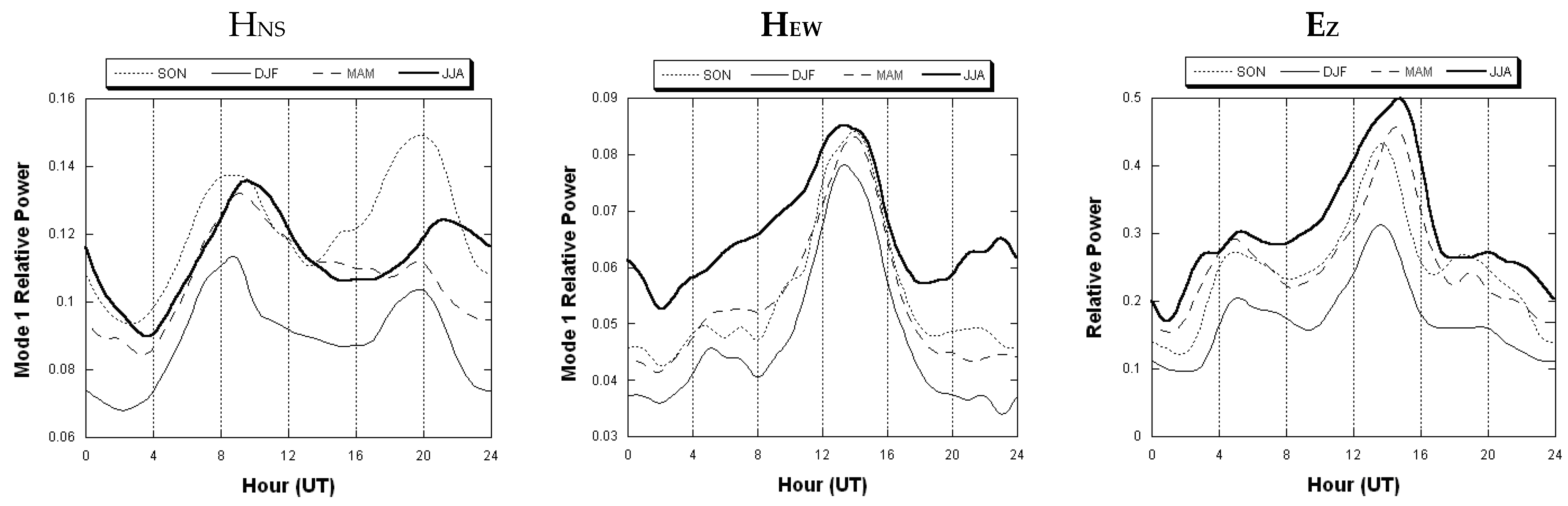
4.1. SR Background Observations of Global Lightning Activity
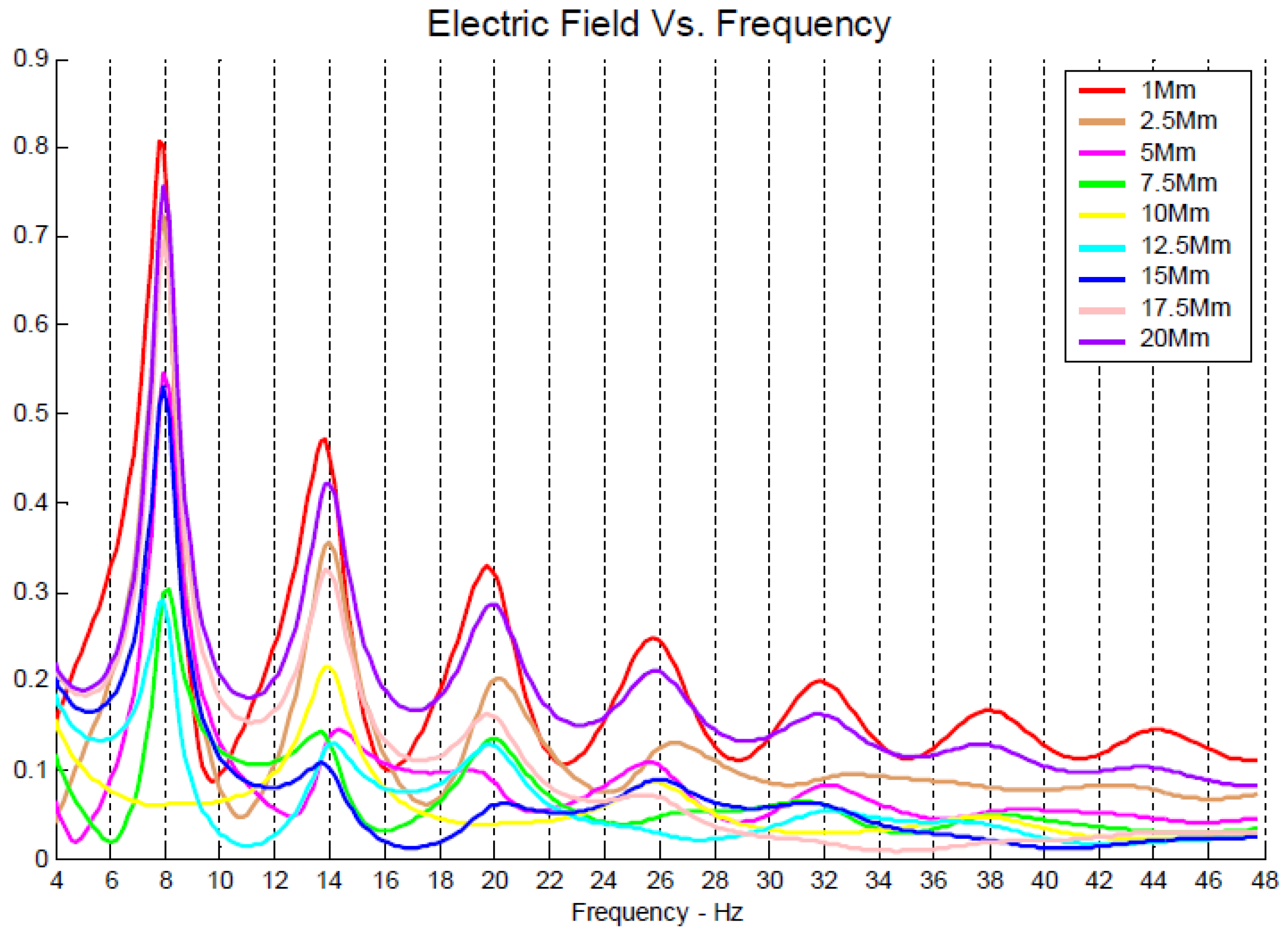
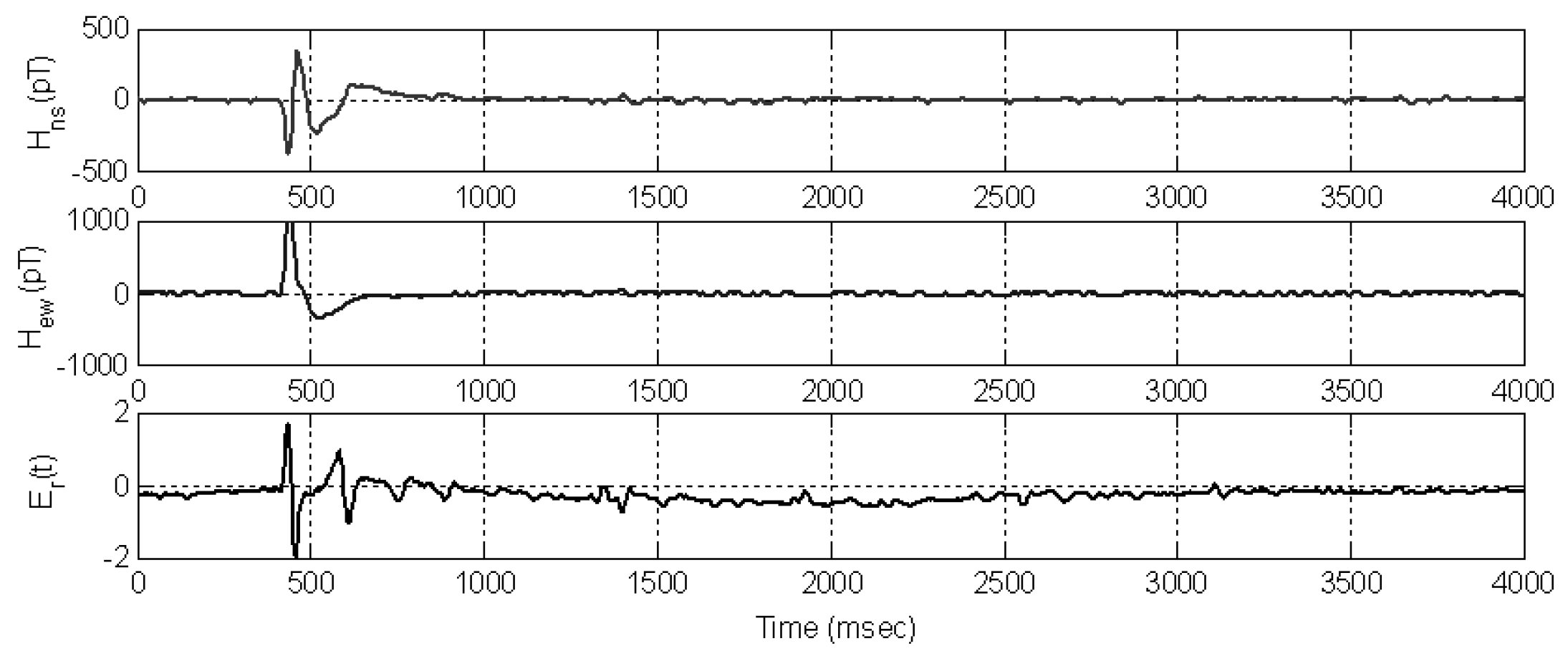
4.2. SR Transient Measurements of Global Lightning Activity
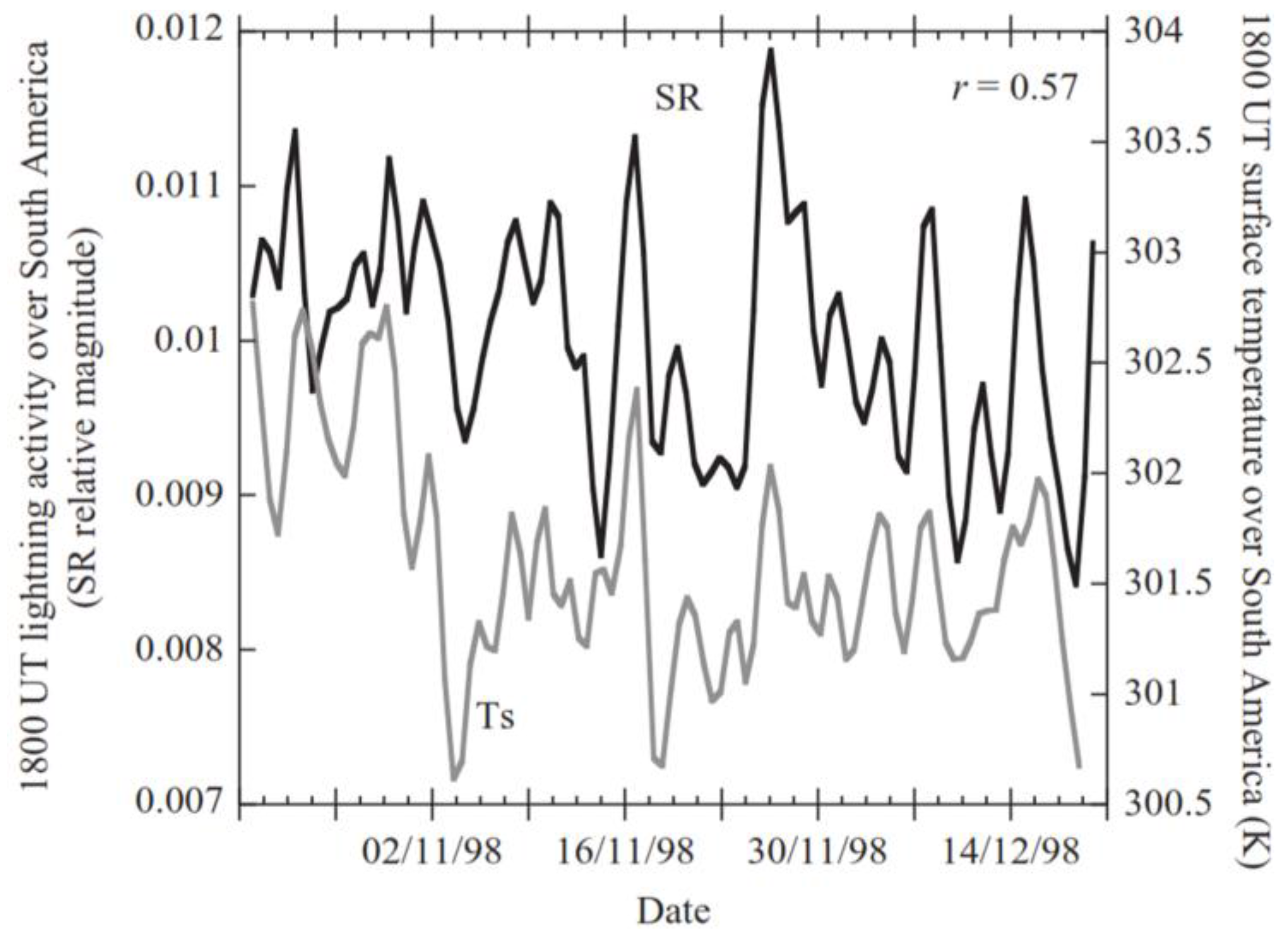
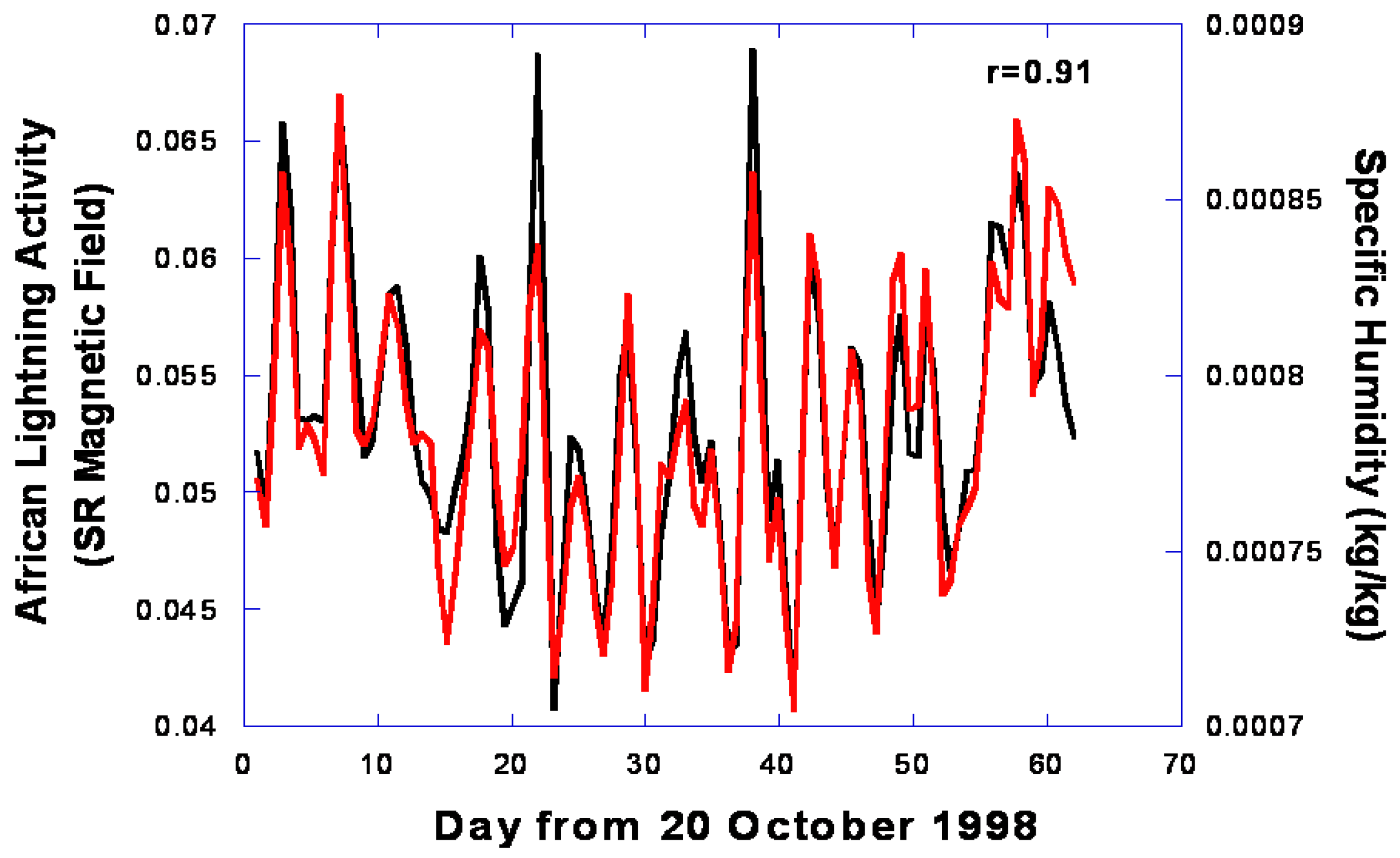
4.3. Using SR as A Climate Research Tool
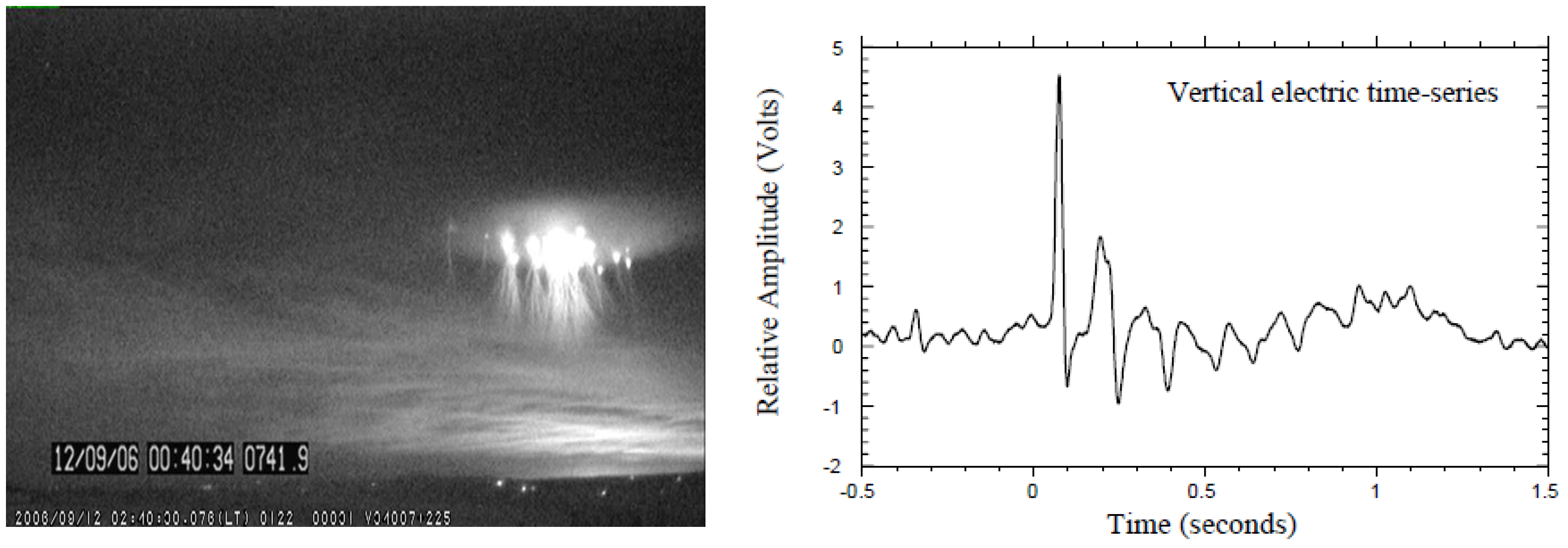
4.4. SR in Transient Luminous Events Research
4.5. SR in Extraterrestrial Lightning Research
5. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Besser, B.P. Synopsis of the historical development of Schumann resonances. Radio Sci. 2007. [Google Scholar] [CrossRef]
- Schumann, W.O. Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphärenhülle umgeben ist. Z. und Naturf. 1952, 7, 149–154. [Google Scholar] [CrossRef]
- Tesla, N. The Transmission of electrical energy without wires as a means of furthering world peace. Electr. World Eng. 1905, 7, 21–24. [Google Scholar]
- Schumann, W.O. Über die Dämpfung der elektromagnetischen Eigenschwingnugen des Systems Erde—Luft—Ionosphäre. Z. und Naturf. 1952, 7, 250–252. [Google Scholar]
- Schumann, W.O. Über die Ausbreitung sehr Langer elektriseher Wellen um die Signale des Blitzes. Nuovo Cimento 1952, 9, 1116–1138. [Google Scholar] [CrossRef]
- Schumann, W.O.; König, H. Über die Beobactung von Atmospherics bei geringsten Frequenzen. Naturwiss 1954, 41, 183–184. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C. Measurement of the spectrum of radio noise from 50 to 100 c/s. J. Res. NBS 1960, 64, 415–418. [Google Scholar]
- Balser, M.; Wagner, C. Observations of earth-ionosphere cavity resonances. Nature 1960, 188, 638–641. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C. Diurnal power variations of the earth-ionosphere cavity modes and their relationship to worldwide thunderstorm activity. J. Geophys. Res. 1962, 67, 619–625. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C. On frequency variations of the earth-ionosphere cavity modes. J. Geophys. Res. 1962, 67, 4081–4083. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C. Effect of a high-altitude nuclear detonation on the earth-ionosphere cavity. J. Geophys. Res. 1963, 68, 4115–4118. [Google Scholar] [CrossRef]
- Gendrin, R.; Stefant, R. Effet de l’explosion thermonucleaire a tres haute altitude du 9 juillet 1962 sur la resonance de la cavite Terre-ionosphere: Resultats experimentaux. C.R. Acad. Sci. Paris 1962, 255, 2273–2275. [Google Scholar]
- Wait, J.R. Historical background and introduction to the special issue on extremely low frequency (ELF) communication. IEEE Trans. Commun. 1974, 22, 353–354. [Google Scholar] [CrossRef]
- Wait, J.R. Propagation of ELF electromagnetic waves and project Sanguine/Seafarer. IEEE J. Oceanic Eng. 1977, 2, 161–172. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bannister, P.R. Reception of ELF signals at antipodal distance. Radio Sci. 1998, 33, 83–88. [Google Scholar] [CrossRef]
- Yano, M.; Ida, Y.; Hobara, Y.; Hayakawa, M.; Nickolaenko, A.P. Reception of ELF transmitter signals at Moshiri, Japan, and their propagation characteristics. Radio Sci. 2010, 45. [Google Scholar] [CrossRef]
- Holzer, R.E. World thunderstorm activity and extremely low frequency sferics. In Recent Advances in Atmospheric Electricity; Smith, L.G., Ed.; Pergamon Press: Oxford, UK, 1958; pp. 599–602. [Google Scholar]
- Nickolaenko, A.P.; Rabinowicz, L.M. Study of the annual changes of global lightning distribution and frequency variations of the first Schumann resonance mode. J. Atoms. Terr. Phys. 1995, 57, 1345–1348. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Rabinowicz, L.M.; Hayakawa, M. Analyses of the ULF/ELF records performed in a seismo-active region. J. Atmos. Electr. 1998, 18, 1–10. [Google Scholar]
- Heckman, S.J.; Williams, E.; Boldi, B. Total global lightning inferred from Schumann resonance measurements. J. Geophys. Res. 1998, 103, 31775–31779. [Google Scholar] [CrossRef]
- Yang, H.; Pasko, V.P.; Sa´tori, G. Seasonal variations of global lightning activity extracted from Schumann resonances using a genetic algorithm method. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Rabinowicz, L.M. On the possibility of existence of global electromagnetic resonances on the planets of Solar system. Space Res. 1982, 20, 82–89. [Google Scholar]
- Nickolaenko, A.P.; Rabinowicz, L.M. On the applicability of extremely low frequency global resonances in the studies of lightning activity at Venus. Space Res. 1987, 25, 301–308. [Google Scholar]
- Pechony, O.; Price, C. Schumann resonance parameters calculated with a partially uniform knee model on Earth, Venus, Mars, and Titan. Radio Sci. 2004, 39. [Google Scholar] [CrossRef]
- Price, C.; Rind, D. The effect of global warming on lightning frequencies. In Proceedings of the AMS 16th Conference on Severe Storms; American Meteorological Society: Alberta, AB, Canada, 1990. [Google Scholar]
- Williams, E.R. The Schumann resonance: A global tropical thermometer. Science 1992, 256, 1184–1186. [Google Scholar] [CrossRef] [PubMed]
- Boccippio, D.J.; Williams, E.R.; Heckman, S.J.; Lyons, W.A.; Baker, I.T.; Boldi, R. Sprites, ELF transients, and positive ground strokes. Science 1995, 269, 1088–1091. [Google Scholar] [CrossRef] [PubMed]
- Haung, H.G.; Williams, E.; Boldi, R.; Heckman, S.; Lyons, W.; Taylor, M.; Nelson, T.; Wong, C. Criteria for sprites and elves based on Schumann resonance observations. J. Geophys. Res. 1999, 104, 16943–16964. [Google Scholar] [CrossRef]
- Price, C.; Asfur, M.; Lyons, W.; Nelson, T. An improved ELF/VLF method for globally geolocating sprite-produced lightning. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Sato, M.; Fukunishi, H.; Kikuchi, M.; Yamagishi, H.; Lyons, W.A. Validation of sprite-inducing cloud-to-ground lightning based on ELF observations at Syowa station in Antarctica. J. Atoms. Terr. Phys. 2003, 65, 607–614. [Google Scholar] [CrossRef]
- Sato, M.; Fukunishi, H. Global sprite occurrence locations and rates derived from triangulation of transient Schumann resonance events. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Volland, H. Atmospheric Electrodynamics; Springer Science & Business Media: Berlin, Germany, 1984. [Google Scholar]
- Wait, J.R. Electromagnetic Waves in Stratified Media; Pergamon Press: Oxford, UK, 1962. [Google Scholar]
- Galejs, J. Terrestrial Propagation of Long Electromagnetic Waves; Pergamon Press: Oxford, UK, 1972. [Google Scholar]
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth-Ionosphere Cavity; Kluwer Academic Publishers: Dordrecht, Boston, London, 2002. [Google Scholar]
- Kemp, D.T.; Jones, D.L. A new technique for the analysis of transient ELF electromagnetic disturbances within the Earth–ionosphere cavity. J. Atmos. Terr. Phys. 1971, 33, 567–572. [Google Scholar] [CrossRef]
- Burke, C.P.; Jones, D.L. Global radiolocation in the lower ELF frequency band. J. Geophys. Res. 1995, 100, 26263–26272. [Google Scholar] [CrossRef]
- Nickolaenko, A.P. Modern aspects of Schumann resonance studies. J. Atoms. Terr. Phys. 1997, 59, 806–816. [Google Scholar] [CrossRef]
- Boccippio, D.J.; Wong, C.; Williams, E.; Boldi, R.; Christian, H.J.; Goodman, S.J. Global validation of single-station Schumann resonance lightning location. J. Atmos. Terr. Phys. 1998, 60, 701–712. [Google Scholar] [CrossRef]
- Greenberg, E.; Price, C. A global lightning location algorithm based on the electromagnetic signature in the Schumann resonance band. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Jones, D.L. The calculations of the Q-factors and frequencies of Earth-ionosphere cavity resonances for a two-layer ionosphere model. J. Geophys. Res. 1974, 69, 4037–4046. [Google Scholar] [CrossRef]
- Jones, D.L. Schumann resonances and ELF propagation for inhomogeneous, isotropic ionosphere profiles. J. Atmos. Terr. Phys. 1967, 29, 1037–1044. [Google Scholar] [CrossRef]
- Yamashita, M. Propagation of ELF radio waves to great distances below the unisotropic ionosphere. J. Atmos. Terr. Phys. 1967, 29, 937–948. [Google Scholar] [CrossRef]
- Yamashita, M. The propagation characteristics of ELF radio waves to great distances below the horizontally stratified ionosphere. J. Atmos. Terr. Phys. 1968, 30, 1943–1953. [Google Scholar] [CrossRef]
- Hynninen, E.M.; Galyuck, Y.P. The field of a vertical electric dipole over the spherical Earth’s surface below the vertically inhomogeneous ionosphere. Probl. Diffr. Wave Propag. 1972, 11, 109–115. (In Russian) [Google Scholar]
- Greifinger, C.; Greifinger, P. Approximate method for determining ELF eigenvalues in the Earth-ionosphere waveguide. Radio Sci. 1978, 13, 831–837. [Google Scholar] [CrossRef]
- Mushtak, V.C.; Williams, E.R. ELF propagation parameters for uniform models of the Earth-ionosphere waveguide. J. Atoms. Terr. Phys. 2002, 64, 1989–2001. [Google Scholar] [CrossRef]
- Toledo-Redondo, S.; Salinas, A.; Fornieles, J.; Portí, J.; Lichtenegger, H.I.M. Full 3-D TLM simulations of the Earth-ionosphere cavity: Effect of conductivity on the Schumann resonances. J. Geophys. Res. Space Phys. 2016, 121, 5579–5593. [Google Scholar] [CrossRef]
- Yang, H.; Pasko, V. Three-dimensional finite difference time domain modeling of the Earth-ionosphere cavity resonances. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Galuk, Y.P.; Hayakawa, M. Vertical profile of atmospheric conductivity that matches Schumann resonance observations. SpringerPlus 2016. [Google Scholar] [CrossRef] [PubMed]
- Galuk, Y.P.; Nickolaenko, A.P.; Hayakawa, M. Knee model: Comparison between heuristic and rigorous solutions for the Schumann resonance problem. J. Atoms. Terr. Phys. 2016, 135, 85–91. [Google Scholar] [CrossRef]
- Silber, I.; Price, C.; Galanti, E.; Shuval, A. Anomalously strong vertical magnetic fields from distant lightning. J. Geophys. Res. Space Phys. 2015, 120, 6036–6044. [Google Scholar] [CrossRef]
- Ogawa, T.; Tanka, Y.; Miura, T.; Yasuhara, M. Observations of natural ELF electromagnetic noises by using the ball antennas. J. Geomagn. Geoelectr. 1966, 18, 443–454. [Google Scholar] [CrossRef]
- Price, C.; Melnikov, M. Diurnal, seasonal and inter-annual variations of the Schumann resonance parameters. J. Atoms. Terr. Phys. 2004, 66, 1179–1185. [Google Scholar] [CrossRef]
- Christian, H.J.; Blakeslee, R.J.; Boccippio, D.J.; Boeck, W.L.; Buechler, D.E.; Driscoll, K.T.; Goodman, S.J.; Hall, J.M.; Koshak, W.J.; Mach, D.M.; et al. Global frequency and distribution of lightning as observed from space by the Optical Transient Detector. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
- Greenberg, E.; Price, C. Diurnal variations of ELF transients and background noise in the Schumann resonance band. Radio Sci. 2007, 42. [Google Scholar] [CrossRef]
- Sentman, D.D. Magnetic elliptical polarization of Schumann resonances. Radio Sci. 1987, 22, 595–606. [Google Scholar] [CrossRef]
- Mushtak, V.C.; Williams, E.R. An improved Lorentzian technique for evaluating resonance characteristics of the Earth-ionosphere cavity. Atmos. Res. 2009, 91, 188–193. [Google Scholar] [CrossRef]
- Satori, G.; Rycroft, M.; Bencze, P.; Marcz, F.; Bor, J.; Barta, V.; Nagy, T.; Kovacs, K. An overview of thunderstorm-related research on the atmospheric electric field, Schumann resonances, sprites, and the ionosphere at Sopron, Hungary. Surv. Geophys. 2013, 34, 255–292. [Google Scholar] [CrossRef]
- Yamashita, K.; Takahashi, Y.; Sato, M.; Kase, H. Improvement in lightning geolocation by time-of-arrival method using global ELF network data. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Kułak, A.; Młynarczyk, J.; Zięba, S.; Micek, S.; Nieckarz, Z. Studies of ELF propagation in the spherical shell cavity using a field decomposition method based on asymmetry of Schumann resonance curves. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- De, S.S.; De, B.K.; Bandyopadhyay, B.; Paul, S.; Haldar, D.K.; Barui, S. Studies on the shift in the frequency of the first Schumann resonance mode during a solar proton event. J. Atmos. Sol-Terr. Phys. 2010, 72, 829–836. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, H.; Cao, B.; Qiao, X. Diurnal and seasonal variations in the Schumann resonance parameters observed at Chinese observatories. J. Atmos. Sol-Terr. Phys. 2013, 98, 86–96. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Xiao, Z.; Hao, Y.Q.; Zhang, D.H. Variability of Schumann resonance parameters observed at low latitude stations in China. Adv. Space Res. 2015, 56, 1389–1399. [Google Scholar] [CrossRef]
- Tatsis, G.; Votis, C.; Christofilakis, V.; Kostarakis, P.; Tritakis, V.; Repapis, C. A prototype data acquisition and processing system for Schumann resonance measurements. J. Atmos. Sol-Terr. Phys. 2015, 135, 152–160. [Google Scholar] [CrossRef]
- Fornieles-Callejón, J.; Salinas, A.; Toledo-Redondo, S.; Portí, J.; Méndez, A.; Navarro, E.A.; Morente-Molinera, J.A.; Soto-Aranaz, C.; Ortega-Cayuela, J.S. Extremely low frequency band station for natural electromagnetic noise measurement. Radio Sci. 2015, 50, 191–201. [Google Scholar] [CrossRef]
- Clayton, M.; Polk, C. Diurnal validation and absolute intensity of worldwide lightning activity. In Electrical Processes in Atmospheres; Dolezalek, H., Reiter, R., Eds.; Springs: Darmstadt, Germany, 1977; pp. 440–449. [Google Scholar]
- Sentman, D.D.; Fraser, B.J. Simultaneous observation of Schumann resonances in California and Australia: Evidence for intensity modulation by local height of the D region. J. Geophys. Res. 1991, 96, 15973–15984. [Google Scholar] [CrossRef]
- Mezuman, K.; Price, C.; Galanti, E. On the spatial and temporal distribution of thunderstorm cells. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M.; Hobara, Y. Temporal variations of the global lightning activity deduced from the Schumann resonance data. J. Atmos. Terr. Phys. 1996, 58, 1699–1709. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Satori, G.; Zieger, B.; Rabinowicz, L.M.; Kudintseva, L.G. Parameters of global thunderstorm activity deduced from the long-term Schumann resonance records. J. Atoms. Terr. Phys. 1998, 60, 387–399. [Google Scholar] [CrossRef]
- Satori, G.; Szendroi, J.; Vero, J. Monitoring Schumann resonances—I. Methodology. J. Atmos. Terr. Phys. 1996, 58, 1475–1481. [Google Scholar] [CrossRef]
- Belyaev, G.G.; Schekotov, A.Y.; Shvets, A.V.; Nickolaenko, A.P. Schumann resonances observed using Poynting vector spectra. J. Atoms. Terr. Phys. 1999, 61, 751–763. [Google Scholar] [CrossRef]
- Shvets, A.V. Distance estimation to the world thunderstorm centers by measurement of the Schumann resonance background. In Proceedings of the XXVI General Assembly, Union Radio Science International, Union of Radio Science, Lille, France, 1999.
- Bliokh, P.V.; Nickolaenko, A.P.; Filippov, Y.F. Schumann Resonances in the Earth-Ionosphere Cavity; Peter Peregrinus: Oxford, UK, 1980. [Google Scholar]
- Yatsevich, E.I.; Shvets, A.V.; Rabinowicz, L.M.; Nickolaenko, A.P.; Belyaev, G.G.; Schekotov, A.Y. Results of comparing Schumann resonance observations with a model of the single world thunderstorm center. Izv. Vuzov Radiophys. 2005, 48, 283–298. [Google Scholar]
- Shvets, A.V. A technique for reconstruction of global lightning distance profile from background Schumann resonance signal. J. Atoms. Terr. Phys. 2001, 63, 1061–1074. [Google Scholar] [CrossRef]
- Shvets, A.V.; Hayakawa, M.; Sekiguchi, M.; Ando, Y. Reconstruction of the global lightning distribution from ELF electromagnetic background signals. J. Atmos. Solar Terr. Phys. 2009, 71, 1405–1412. [Google Scholar] [CrossRef]
- Raemer, H.R. On the extremely low frequency spectrum of the earth-ionosphere cavity response to electrical storms. J. Geophys. Res. 1961, 66, 1580–1583. [Google Scholar] [CrossRef]
- Polk, C.; Fitchen, F. Schumann resonances of the earth-ionosphere cavity—extremely low frequency reception at Kingston, R.I. J. Res. NBS 1962, 66, 313–318. [Google Scholar] [CrossRef]
- Rycroft, M.J. Low Frequency Disturbances of Natural Origin of The Electric and Magnetic Fields of the Earth. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1963. [Google Scholar]
- Madden, T.; Thompson, W. Low-frequency electromagnetic oscillations of the Earth-ionosphere cavity. Rev. Geophys. 1965, 3, 211–254. [Google Scholar] [CrossRef]
- Polk, C. Relation of ELF noise and Schumann resonances to thunderstorm activity. In Planetary Electrodynamics; Volland, H., Ed.; CRC Press: Boca Ration, FL, USA, 1968; pp. 55–83. [Google Scholar]
- Jones, D.L. ELF-VLF Radio Wave Propagation; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Fullekrug, M.; Fraser-Smith, A.C. Global lightning and climate variability inferred from ELF magnetic field variations. Geophys. Res. Lett. 1997, 24, 2411–2414. [Google Scholar] [CrossRef]
- Sátori, G.; Zieger, B. El Niño-related meridional oscillation of global lightning activity. Geophys. Res. Lett. 1999, 26, 1365–1368. [Google Scholar] [CrossRef]
- Price, C. Evidence for a link between global lightning activity and upper tropospheric water vapor. Nature 2000, 406, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Nickolaenko, A.P.; Hayakawa, M.; Hobara, Y. Q-bursts: Natural ELF radio transients. Surv. Geophys. 2010, 31, 409–425. [Google Scholar] [CrossRef]
- Ishaq, M.; Jones, D.L. Method of obtaining radiowave propagation parameters for the Earth–ionosphere duct at ELF. Electr. Lett. 1977, 13, 254–255. [Google Scholar] [CrossRef]
- Jones, D.L.; Burke, C.P. An experimental investigation of ELF attenuation rates in the Earth–ionosphere cavity. J. Atmos. Terr. Phys. 1992, 54, 243–250. [Google Scholar]
- Price, C.; Greenberg, E.; Yair, Y.; Sátori, G.; Bór, J.; Fukunishi, H.; Sato, M.; Israelevich, P.; Moalem, M.; Devir, A.; et al. Ground-based detection of TLE-producing intense lightning during the MEIDEX mission on board the Space Shuttle Columbia. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Nakamura, T.; Sekiguchi, M.; Hobara, Y.; Hayakawa, M. A comparison of different source location methods for ELF transients by using the parent lightning discharges with known positions. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Rafalsky, V.A.; Shvets, A.V.; Hayakawa, M. One-site distance-finding technique for locating lightning discharges. J. Atoms. Terr. Phys. 1995, 57, 1255–1261. [Google Scholar] [CrossRef]
- Burke, C.P.; Jones, D.L. An experimental investigation of ELF attenuation rates in the Earth-ionosphere duct. J. Atmos. Terr. Phys. 1992, 54, 243–254. [Google Scholar] [CrossRef]
- Schmidt, C.T. Detection of Distant Lightning Strikes from One Location Using Schumann Resonances. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 1993. [Google Scholar]
- Williams, E.R. Lightning and climate: A review. Atmos. Res. 2005, 76, 272–287. [Google Scholar] [CrossRef]
- Price, C. Global surface temperatures and the atmospheric global circuit. Geophys. Res. Lett. 1993, 20, 1363–1366. [Google Scholar] [CrossRef]
- Price, C.; Rind, D. Possible implications of global climate change on global lightning distributions and frequencies. J. Geophys. Res. 1994, 99, 10823–10831. [Google Scholar] [CrossRef]
- Jones, P.D.; Wigley, T.M.L.; Wright, P.B. Global Temperature-Variations between 1861 and 1984. Nature 1986, 322, 430–434. [Google Scholar] [CrossRef]
- Price, C.; Asfur, M. Can lightning observations be used as an indicator of upper-tropospheric water-vapor variability. Bull. Amer. Met. Soc. 2006, 34. [Google Scholar] [CrossRef]
- Physical Sciences Division. NCEP/NCAR Reanalysis 1: Summary. Available online: http://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.html (accessed on 13 September 2016).
- Hansen, J.; Lacis, A.; Rind, D.; Russel, G.; Stone, P.; Fung, I.; Ruedy, R.; Lerner, J. Climate sensitivity: Analysis of feedback mechanisms. In Climate Processes and Climate Sensitivity; Hansen, J.E., Takahashi, T., Eds.; American Geophysical Union: Washington, DC, USA, 1984; pp. 130–163. [Google Scholar]
- Lindzen, R.S. Some coolness concerning global warming. Bull. Am. Meteorol. Soc. 1990, 71, 288–299. [Google Scholar] [CrossRef]
- Rind, D.; Chiou, E.W.; Chu, W.; Larsen, J.; Oltmans, S.; Lerner, J.; McCormick, M.P.; McMaster, L. Positive water vapor feedback in climate models confirmed by satellite data. Nature 1991, 349, 500–502. [Google Scholar] [CrossRef]
- Del Genio, A.D.; Kovari, W.J.; Yao, N.S. Climatic implications of the seasonal variations of upper troposphere water vapour. Geophys. Res. Lett. 1994, 21, 2701–2704. [Google Scholar] [CrossRef]
- Sun, D.Z.; Held, I.M. A Comparison of modeled and observed relationships between interannual variations of water vapor and temperature. J. Clim. 1996, 9, 665–675. [Google Scholar] [CrossRef]
- Rind, D. Just add water vapor. Science 1998, 28, 1152–1153. [Google Scholar] [CrossRef]
- Satori, G.; Ziegler, B. El nino related meridional oscillation of global lightning activity. Geophys. Res. Let. 1999, 26, 1365–1368. [Google Scholar] [CrossRef]
- Satori, G.; Williams, E.R.; Lemperger, I. Variability of global lightning activity on the ENSO time scale. Atmos. Res. 2009, 91, 500–507. [Google Scholar] [CrossRef]
- Wilson, C.T.R. The electric field of a thundercloud and some of its effects. Proc. Phys. Soc. London 1924, 37. [Google Scholar] [CrossRef]
- Franz, R.C.; Nemzek, R.J.; Winckler, J.R. Television image of a large upward electrical discharge above a thunderstorm system. Science 1990, 249, 48–51. [Google Scholar] [CrossRef] [PubMed]
- Boeck, W.L.; Vaughan, O.H., Jr. Lightning observations from the STS-32 space shuttle mission. EOS Trans. AGU 1990, 71, 1241. [Google Scholar]
- Sentman, D.D.; Wescott, E.M. Observations of upper atmosphere optical flashes recorded from an aircraft. Geophys. Res. Lett. 1993, 20, 2857–2860. [Google Scholar] [CrossRef]
- Lyons, W.A. Characteristics of luminous structures in the stratosphere above thunderstorms as imaged by low-light video. Geophys. Res. Lett. 1994, 21, 875–878. [Google Scholar] [CrossRef]
- Boeck, W.L.; Vaughan, O.H., Jr.; Blakeslee, R.J.; Vonnegut, B.; Brook, M.; McKune, J. Observations of lightning in the stratosphere. J. Geophys. Res. 1995, 100, 1465–1475. [Google Scholar] [CrossRef]
- Heavner, M.J.; Hampton, D.L.; Sentman, D.D.; Wescott, E.M. Sprites over Central and South America (abstract). Eos Trans. AGU 1995, 76, 115. [Google Scholar]
- Sentman, D.D. Observations of red sprites and blue jets. In Proceedings of 25th General Assembly, Union Radio Science International, Union of Radio Science, Lille, France, 1996.
- Dowden, R.L.; Rodger, C.J. Decay of a vertical plasma column: A model to explain VLF sprites. Geophys. Res. Lett. 1997, 24, 2765–2768. [Google Scholar] [CrossRef]
- Fukunishi, H.; Takahashi, Y.; Uchida, A.; Sera, M.; Adachi, K.; Miyasato, R. Occurrences of sprites and elves above the Sea of Japan near Hokuriku in winter. Eos Trans. AGU 1999, 80, 217. [Google Scholar]
- Hardman, S.F.; Dowden, R.L.; Brundell, J.B.; Blahr, J.L.; Kawasaki, Z.I.; Rodger, C.J. Sprites observation in the northern territory of Australia. J. Geophys. Res. 2000, 105, 4689–4697. [Google Scholar] [CrossRef]
- Su, H.T.; Hsu, R.; Chen, A.B.C.; Lee, Y.J.; Lee, L.C. Observation of sprites over the Asian continent and over oceans around Taiwan. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Yair, Y.; Price, C.; Levin, Z.; Joseph, J.; Israelevitch, P.; Devir, A.; Moalem, M.; Ziv, B.; Asfur, M. Sprite observations from the space shuttle during the Mediterranean Israeli Dust Experiment (MEIDEX). J. Atoms. Terr. Phys. 2003, 65, 635–642. [Google Scholar] [CrossRef]
- Neubert, T.; Allin, T.; Blanc, E.; Farges, T.; Haldoupis, C.; Mika, A.; Soula, S.; Knutsson, L.; van der Velde, O.; Marshall, R.; et al. Co-ordinated observations of transient luminous events during the EuroSprite 2003 campaign. J. Atoms. Terr. Phys. 2005, 67, 807–820. [Google Scholar] [CrossRef]
- Chen, A.B.; Kuo, C.L.; Lee, Y.J.; Su, H.T.; Hsu, R.R.; Chern, J.L.; Frey, H.U.; Mende, S.B.; Takahashi, Y.; Fukunishi, H.; et al. Global distributions and occurrence rates of transient luminous events. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Williams, E.R. Sprites, elves, and glow discharge tubes. Phys. Today 2001, 41, 41–47. [Google Scholar] [CrossRef]
- Barrington-Leigh, C.P.; Inan, U.S. Elves triggered by positive and negative lightning discharges. Geophys. Res. Lett. 1999, 26, 683–686. [Google Scholar] [CrossRef]
- Pasko, V.P.; Inan, U.S.; Taranenko, Y.N.; Bell, T.F. Heating, ionization and upward discharges in the mesosphere due to intense quasi-electrostatic thundercloud fields. Geophys. Res. Lett. 1995, 22, 365–368. [Google Scholar] [CrossRef]
- Pasko, V.P.; Inan, U.S.; Bell, T.F.; Taranenko, Y.N. Sprites produced by quasi-electrostatic heating and ionization in the lower ionosphere. J. Geophys. Res. 1997, 102, 4529–4561. [Google Scholar] [CrossRef]
- Takahashi, Y.; Yoshida, A.; Sato, M.; Adachi, T.; Kondo, S.; Hsu, R.R.; Su, H.T.; Chen, A.B.; Mende, S.B.; Frey, H.U.; et al. Absolute optical energy of sprites and its relationship to charge moment of parent lightning discharge based on measurement by ISUAL/AP. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Williams, E.R.; Mushtak, V.C.; Boldi, R.; Dowden, R.L.; Kawasaki, Z. Sprite lightning heard round the world by Schumann resonance methods. Radio Sci. 2007, 42. [Google Scholar] [CrossRef]
- Bell, T.F.; Pasko, V.P.; Inan, U.S. Runaway electrons as a source of red sprites in the mesosphere. Geophys. Res. Lett. 1995, 22, 2127–2130. [Google Scholar] [CrossRef]
- Milikh, G.M.; Papadopoulos, K.; Chang, C.L. On the physics of high altitude lightning. Geophys. Res. Lett. 1995, 22, 85–88. [Google Scholar] [CrossRef]
- Roussel-Dupré, R.; Gurevich, A.V. On runaway breakdown and upward propagating lightning. J. Geophys. Res. 1996, 101, 2297–2311. [Google Scholar] [CrossRef]
- Valdivia, J.A.; Milikh, G.; Papadopoulos, K. Red sprites: Lightning as a fractal antenna. Geophys. Res. Lett. 1997, 24, 3169–3172. [Google Scholar] [CrossRef]
- Reising, S.C.; Inan, U.S.; Bell, T.F.; Lyons, W.A. Evidence for continuing current in sprite-producing cloud-to-ground lightning. Geophys. Res. Lett. 1996, 23, 3639–3642. [Google Scholar] [CrossRef]
- Williams, E.; Downes, E.; Boldi, R.; Lyons, W.; Heckman, S. Polarity asymmetry of sprite-producing lightning: A paradox? Radio Sci. 2007, 42. [Google Scholar] [CrossRef]
- Hobara, Y.; Iwasaki, N.; Hayashida, T.; Hayakawa, M.; Ohta, K.; Fukunishi, H. Interrelation between ELF transients and ionospheric disturbances in association with sprites and elves. Geophys. Res. Lett. 2001, 28, 935–938. [Google Scholar] [CrossRef]
- Ganot, M.; Yair, Y.; Price, C.; Ziv, B.; Sherez, Y.; Greenberg, E.; Devir, A.; Yaniv, R. First detection of transient luminous events associated with winter thunderstorms in the eastern Mediterranean. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Cummer, S.A.; Inan, U.S. Measurement of charge transfer in sprite-producing lightning using ELF radio atmospherics. Geophys. Res. Lett. 1997, 24, 1731–1734. [Google Scholar] [CrossRef]
- Bell, T.F.; Reising, S.C.; Inan, U.S. Continuing currents determined from broadband ELF/VLF magnetic fields radiated by positive cloud-to-ground discharges associated with red sprites. EOS Suppl. 1996, 77, 61. [Google Scholar]
- Nieckarz, Z.; Baranski, P.; Mlynarczyk, J.; Kulak, A.; Wiszniowski, J. Comparison of the charge moment change calculated from electrostatic analysis and from ELF radio observations. J. Geophys. Res. Atmos. 2015, 120, 63–72. [Google Scholar] [CrossRef]
- Yaniv, R.; Yair, Y.; Price, C.; Bór, J.; Sato, M.; Hobara, Y.; Cummer, S.; Li, J.; Devir, A. Ground-based observations of the relations between lightning charge-moment-change and the physical and optical properties of column sprites. J. Atmos. Sol-Terr. Phys. 2014, 107, 60–67. [Google Scholar] [CrossRef]
- Hu, W.; Cummer, S.A.; Lyons, W.A.; Nelson, T.E. Lightning charge moment changes for the initiation of sprites. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Greenberg, E.; Price, C.; Yair, Y.; Ganot, M.; Bór, J.; Sátori, G. ELF transients associated with sprites and elves in eastern Mediterranean winter thunderstorms. J. Atmos. Solar-Terr. Phys. 2007, 69, 1569–1586. [Google Scholar] [CrossRef]
- Greenberg, E.; Price, C.; Yair, Y.; Haldoupis, C.; Chanrion, O.; Neubert, T. On the ELF charge moment change, VLF bursts and subionospheric perturbations associated with sprites. J. Atmos. Terr.-Solar Phys. 2009. [Google Scholar] [CrossRef]
- Bór, J.; Ludván, B.; Attila, N.; Steinbach, P. Systematic deviations in source direction estimates of Q-bursts recorded at Nagycenk, Hungary. J. Geophys. Res. Atmos. 2016, 121, 5601–5619. [Google Scholar] [CrossRef]
- Yair, Y.; Fischer, G.; Simoes, F.; Renno, N.; Zarka, P. Updated review of planetary atmospheric electricity. Space Sci. Rev. 2008, 137, 29–49. [Google Scholar] [CrossRef]
- Ksanfomaliti, L.V. Lightning in the cloud layer of Venus. Kosm. Issled. 1979, 17, 747–762. (In Russian) [Google Scholar]
- Ksanfomaliti, L.V. Planet Venus; Nauka: Moscow, Russia, 1985. (In Russian) [Google Scholar]
- Taylor, W.; Scarf, F.L.; Russell, C.T.; Brace, L.H. Evidence for lightning on Venus. Nature 1979, 279, 614–616. [Google Scholar] [CrossRef]
- Scarf, F.L.; Russell, C.T. Lightning measurements from the Pioneer Venus Orbiter. Geophys. Res. Lett. 1983, 10, 1192–1195. [Google Scholar] [CrossRef]
- Eden, H.F.; Vonnegut, B. Electrical breakdown caused by dust motion in low-pressure atmospheres: Consideration for Mars. Science 1973, 180, 962–963. [Google Scholar] [CrossRef] [PubMed]
- Melnik, O.; Parrot, M. Electrostatic discharge in Martian dust storms. J. Geophys. Res. 1998, 103, 29107–29117. [Google Scholar] [CrossRef]
- Farrell, W.F.; Kaiser, M.L.; Desch, M.D.; Houser, J.G.; Cummer, S.A.; Wilt, D.M.; Landis, G.A. Detecting electrical activity from Martian dust storms. J. Geophys. Res. 1999, 104, 3795–3801. [Google Scholar] [CrossRef]
- Renno, N.O.; Wong, A.; Atreya, S.K.; de Pater, I.; Roos-Serote, M. Electrical discharges and broadband radio emission by Matian dust devils and dust storms. Geophys. Res. Lett. 2003, 30, 2140. [Google Scholar] [CrossRef]
- Bar-Nun, A. Thunderstorms on Jupiter. Icarus 1975, 24, 86–94. [Google Scholar] [CrossRef]
- Little, B.; Anger, C.D.; Ingersoll, A.P.; Vasavada, A.R.; Senske, D.A.; Breneman, H.H.; Borucki, W.J. Galileo Images of lightning on Jupiter. Icarus 1999, 142, 306–323. [Google Scholar] [CrossRef]
- Desch, S.J.; Borucki, W.J.; Russell, C.T.; Bar-Nun, A. Progress in planetary lightning. Rep. Prog. Phys. 2002, 65, 955–997. [Google Scholar] [CrossRef]
- Fischer, G.; Kurth, W.S.; Dyudina, U.A.; Kaiser, M.L.; Zarka, P.; Lecacheux, A.; Ingersoll, A.P.; Gurnett, D.A. Analysis of a giant lightning storm on Saturn. Icarus 2007, 190, 528–544. [Google Scholar] [CrossRef]
- Tokano, T.; Molina-Cuberos, G.J.; Lammer, H.; Stumptner, W. Modeling of thunderclouds and lightning on Titan. Planer. Space Sci. 2001, 49, 539–560. [Google Scholar] [CrossRef]
- Lammer, H.; Tokano, T.; Fischer, G.; Stumptner, W.; Molina-Cuberos, G.J.; Schwingenschuh, K.; Rucher, H.O. Lightning activity of Titan: Can Cassiny/Huygens detect it? Planet. Space Sci. 2001, 49, 561–574. [Google Scholar] [CrossRef]
- Fischer, G.; Gurnett, D.A.; Kurth, W.S.; Farrell, W.M.; Kaiser, M.L.; Zarka, P. Nondetection of Titan lightning radio emissions with Cassini/RPWS after 35 close Titan flybys. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Sentman, D.D. Electrical conductivity of Jupiter’s Shallow interior and the formation of a resonant planetary-ionosphere cavity. ICARUS 1990, 88, 73–86. [Google Scholar] [CrossRef]
- Yang, H.; Pasko, V.P.; Yair, Y. Three-dimensional finite difference time domain modeling of the Schumann resonance parameters on Titan, Venus, and Mars. Radio Sci. 2006, 41. [Google Scholar] [CrossRef]
- Simoes, F.; Hamelin, M.; Grard, R.; Aplin, K.L.; Béghin, C.; Berthelier, J.J.; Besser, B.P.; Lebreton, J.P.; López-Moreno, J.J.; Molina-Cuberos, G.J.; et al. Electromagnetic wave propagation in the surface-ionosphere cavity of Venus. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Sukhorukov, A.I. On the Schumann resonances on Mars. Planet. Space Sci. 1991, 39, 1673–1676. [Google Scholar] [CrossRef]
- Molina-Cuberos, G.J.; Morente, J.A.; Besser, B.P.; Porti, J.; Lichtenegger, H.; Schwingenschuh, K.; Salinas, A.; Margineda, J. Schumann resonances as a tool to study the lower ionosphere of Mars. Radio Sci. 2006, 41. [Google Scholar] [CrossRef]
- Morente, J.A.; Molina-Cuberos, G.J.; Porti, J.A.; Schwingenschuh, K.; Besser, B.P. A study of the propagation of electromagnetic waves in Titan’s atmosphere with the TLM numerical method. Icarus 2003, 162, 374–384. [Google Scholar] [CrossRef]
- Molina-Cuberos, G.J.; Porti, J.; Besser, B.P.; Morente, J.A.; Margineda, J.; Lichtenegger, H.I.M.; Salinas, A.; Schwingenschuh, K.; Eichelberger, H.U. Schumann resonances and electromagnetic transparence in the atmosphere of Titan. Adv. Space Res. 2004, 33, 2309–2313. [Google Scholar] [CrossRef]
- Navarro, E.A.; Soriano, A.; Morente, J.A.; Portí, J.A. A finite difference time domain model for the Titan ionosphere Schumann resonances. Radio Sci. 2007, 42. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Besser, B.P.; Schwingenschuh, K. Model computations of Schumann resonance on Titan. Planet. Space Sci. 2003, 51, 853–862. [Google Scholar] [CrossRef]
- Pechony, O.; Price, C. Schumann resonances: Interpretation of local diurnal intensity modulation. Radio Sci. 2006, 41. [Google Scholar] [CrossRef]
- Pechony, O.; Price, C.; Nickolaenko, A.P. Relative importance of the day–night asymmetry in Schumann resonance amplitude records. Radio Sci. 2007, 42. [Google Scholar] [CrossRef]
- Satori, G.; Mushtak, V.; Williams, E. Schumann resonance signatures of global lightning. In Lightning: Principles, Instruments and Applications; Springer: Berlin, Germany, 2009; pp. 347–386. [Google Scholar]
- Nickolaenko, A.; Hayakawa, M. Localize ionospheric disturbance over the earthquake epicenter and modifications of Schumann resonance electromagnetic fields. Geomat. Nat. Haz. Risk 2014. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, Z.; Qiao, X.; Yu, H. Anomalous phenomena in Schumann resonance band observed in China before the 2011 magnitude 9.0 Tohoku-Oki earthquake in Japan. J. Geophys. Res. Atmos. 2013, 118, 13338–13345. [Google Scholar] [CrossRef]
- Price, C.; Mushtak, V. The impact of the August 27, 1998, Gamma-ray burst on the Schumann resonances. J. Atoms. Terr. Phys. 2001, 63, 1043–1047. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Kudintseva, I.G.; Pechony, O.; Hayakawa, M.; Hobara, Y.; Tan, Y.T. The effect of a gamma ray flare on Schumann resonances. Ann. Geophys. 2012, 30, 1321–1329. [Google Scholar] [CrossRef]
- Singh, B.; Tyagi, R.; Hobara, Y.; Hayakawa, M. X-rays and solar proton event induced changes in the first mode Schumann resonance frequency observed at a low latitude station Agra, India. J. Atmos. Sol-Terr. Phys. 2014, 113, 1–9. [Google Scholar] [CrossRef]
- Dyrda, M.; Kulak, A.; Mlynarczyk, A.; Ostrowski, M. Novel analysis of a sudden ionospheric disturbance using Schumann resonance measurements. J. Geophys. Res. Space Phys. 2015, 120, 2255–2262. [Google Scholar] [CrossRef]
- Satori, G.; Williams, E.; Price, C.; Boldi, R.; Koloskov, A.; Yampolski, Y.; Guha, A.; Barta, V. Effects of energetic solar emissions on the Earth-ionosphere cavity of Schuman Resonances. Surv. Geophys. 2016. [CrossRef]
- Nickolaenko, A.P.; Koloskov, A.V.; Hayakawa, M.; Yampolski, Y.M.; Budanov, O.V.; Korepanov, V.E. 11-year solar cycle in Schumann resonance data as observed in Antarctica. Sun Geosph. 2015, 10, 39–49. [Google Scholar]
- Ondraskova, A.; Sevicik, S.; Kostecky, P. Decrease of Schumann resonance frequencies and changes in the effective lightning areas toward the solar cycle minimum of 2008–2009. J. Atmos. Sol-Terr. Phys. 2011, 73, 534–543. [Google Scholar] [CrossRef]


© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Price, C. ELF Electromagnetic Waves from Lightning: The Schumann Resonances. Atmosphere 2016, 7, 116. https://doi.org/10.3390/atmos7090116
Price C. ELF Electromagnetic Waves from Lightning: The Schumann Resonances. Atmosphere. 2016; 7(9):116. https://doi.org/10.3390/atmos7090116
Chicago/Turabian StylePrice, Colin. 2016. "ELF Electromagnetic Waves from Lightning: The Schumann Resonances" Atmosphere 7, no. 9: 116. https://doi.org/10.3390/atmos7090116
APA StylePrice, C. (2016). ELF Electromagnetic Waves from Lightning: The Schumann Resonances. Atmosphere, 7(9), 116. https://doi.org/10.3390/atmos7090116