1. Introduction
Electromagnetic radiation fields are associated not only with energy but also with a momentum [
1,
2]. Thus, any object that emits electromagnetic radiation will experience a momentum equal and opposite to the momentum transported by the electromagnetic radiation. The net momentum transported by the radiation depends on its directive properties. If the electromagnetic radiation is directed in one particular direction, then the electromagnetic radiation will transport a net momentum in that direction. If the spatial distribution of the emitted electromagnetic field has mirror symmetry with respect to the
x–
y,
x–
z, and
y–
z planes, the net momentum transported by the radiation is zero. Here we consider a transient dipole where a current is initiated at one end and propagates towards the other end where it is absorbed. The electromagnetic fields radiated by such transient dipoles are neither directed in one particular direction nor completely symmetric with respect to the three-spatial axis. In the case of dipoles, the net momentum transported by the radiation depends on the directivity of the radiation. The directivity of the radiation emitted by a transient dipole depends on the length of the dipole and the effective wavelength of the excitation current. The effective wavelength in turn depends on the duration of the current waveform.
The literature on the radiation produced by Hertizian dipoles is numerous, and it is sufficed to refer to several textbooks dealing with the subject such as Jackson [
1] and Panofsky and Philips [
2]. There is also a significant amount of literature on the radiation fields of oscillating long dipoles. A dipole working in frequency domain is called “long” because the wavelength associated with the current oscillations is either comparable or shorter than the length of the dipole [
3]. Even in the case of long transient dipoles, a certain amount of information on their radiation fields is available in the literature [
4]. In the case of transient dipoles, the adjective “long” shows that the effective wavelength of the current exciting the dipole is either comparable to or shorter than the length of the dipole, or the duration of the current is either comparable to or shorter than the travel time of the current along the dipole. The current evolution in these dipoles has to be described by current pulses that travel from one end of the dipole to the other. Theories on long dipoles are developed mainly in connection with lightning research, where currents are assumed to propagate along long lightning channels [
4]. Irrespective of these advances, however, the way in which the momentum transported by the radiation fields of a dipole varies with the duration of the excitation current and the length of the dipole has never been investigated in the literature. The goal of this paper is to fill this gap in our knowledge concerning dipole radiation.
In this paper we will consider the momentum transported by the radiation fields of a long transient dipole. We will consider the general case where the characteristic wavelength of the current pulse propagating along the dipole can take any value with respect to the length of the dipole.
3. The Energy and Momentum of the Radiation Field
The energy density generated by an electromagnetic field is given by the Poynting vector
which in turn is defined by [
1,
2]
This gives the power transmitted by the electromagnetic wave across a unit area located perpendicular to the direction of propagation of the wave. The momentum density associated with this electromagnetic field
is given by [
1,
2]
This expression gives the linear momentum transferred per unit time by the wave across a unit area located perpendicular to the direction of propagation of the wave. In the above equations, and are the electric flux density and magnetic field intensity, respectively.
3.1. Transient Hertzian Dipole
The Poynting vector and the momentum density vector associated with the Hertzian dipole is given by
The total energy radiated by the dipole is given by
where
One can easily show that, due to symmetry, net momentum transported by the radiation field in any given direction is zero. For example, the net momentum transported in the
z-direction by a Hertzian dipole is given by
Due to symmetry, the value of the above integral is zero. In other words, the ratio for a Hertzian dipole is zero. In the sections to follow, we will show that this ratio departs from zero as the dipole changes from a Hertzian to a long dipole.
3.2. Long Transient Dipole
Using the expressions for the electric radiation fields given in Equation (5), and noting that
for radiation fields, we obtain
and
The energy radiated across a unit area in any given direction
is given by
The total energy radiated by the system can be obtained by integrating the Poynting vector over a spherical region. That is, the total energy dissipated by the system is given by
The net momentum transported by the electromagnetic field through a unit area in the direction
is given by
Due to the angular symmetry of the emitted radiation, the
x and
y components of this momentum will add up to zero, leaving behind only the
z component. The net momentum transported in the
z- direction by the electromagnetic field is given by
Since this is the only component of the net momentum transported by the radiation, we will drop the subscript z and write it simply as .
Consider a transient electromagnetic field emitted in a direction
by a dipole. If the electromagnetic field is confined only to direction
, then the total energy radiated
and the total momentum
transported by the electromagnetic field are related through Equations (6) and (7) as
In the case of a normal dipole, the net momentum transported by the radiation field departs from this equation because the radiation is not directed in one particular direction. However, as we will show in this paper, as the effective wavelength of the current becomes comparable to or shorter than the length of the dipole (or the duration of the current pulse becomes comparable to or shorter than the travel time of the current pulse across the dipole), the radiation becomes more and more directional and the relationship between the momentum transfer and the total energy approaches (note that is the z-component of the transferred momentum). This will be investigated in the next section.
4. The Total Electromagnetic Energy Radiated and the Total Electromagnetic Momentum Transported by a Long Dipole—General Case
In order to take into account the radiation fields generated by long dipoles excited by current waveforms of different durations, let us define a parameter
as
In Equation (20), is the duration of the pulse and is the time taken by the current pulse to propagate the length of the dipole. In the case of the Gaussian pulse, and, therefore, and , are connected through the equation = . As decreases, the duration of the current pulse becomes shorter and shorter in comparison to the time given by .
The way in which the radiated energy of a dipole varies as a function of
and
has been studied previously by Cooray and Cooray [
8]. They showed that the total energy radiated by a long dipole excited by a Gaussian current pulse can be written as
In the above equation,
is a function that depends only on
, and
is the charge associated with the Gaussian current pulse. That is:
Since the time dependence of the current, which appeared in the expressions for both the energy and the momentum transfer, is the same except for a geometrical factor that arises due to the presence of
in the integration that appears in Equation (12), the net momentum transported by the radiation field can be written as
Thus, the ratio of the total momentum and the total energy (divided by the speed of light) transported by the dipole is given by
This ratio depends only on the parameter . In the case where one can derive an analytical expression for the above ratio. This is done in the next section.
5. The Total Electromagnetic Energy Dissipated by the Long Dipole and the Total Momentum Transported by the Radiation—Case When β ≪ 1
Observe that, as given by Equation (5c), the delay between the two radiation pulses generated by the dipole during current initiation and termination is equal to
. For very small angles, the two pulses overlap. As the angle
increases from zero, the separation between the radiation field pulses increases; when it reaches a critical value, say
, the two pulses separate from each other completely. This critical angle is given by
Substituting for
in terms of
, we obtain
As the value of
decreases, the angle
decreases; for very small values of
, it becomes almost equal to zero. In such cases, almost all the energy generated by the dipole is confined to the spatial region where
. As pointed out earlier, in this region of space the radiation field consists of two separate pulses, each with a signature identical to that of the current pulse. Thus, the total energy radiated by the dipole can be approximated by
The factor 2 in the above equation comes from the fact that there are two identical radiation pulses, each with a time signature identical to that of the current waveform. The expression for the total momentum transported by the radiation field is given similarly by the expression
The spatial integrals in Equations (27) and (28) can be evaluated without much difficulty. Furthermore, when one evaluates the ratio
, the time integral of the square of the current cancels off. Thus, the final result is given by
Note in the above equation that the ratio becomes 1 as goes to infinity.
6. The Relationship between the Total Energy Dissipated and the Total Momentum Transported by the Long Dipole Field
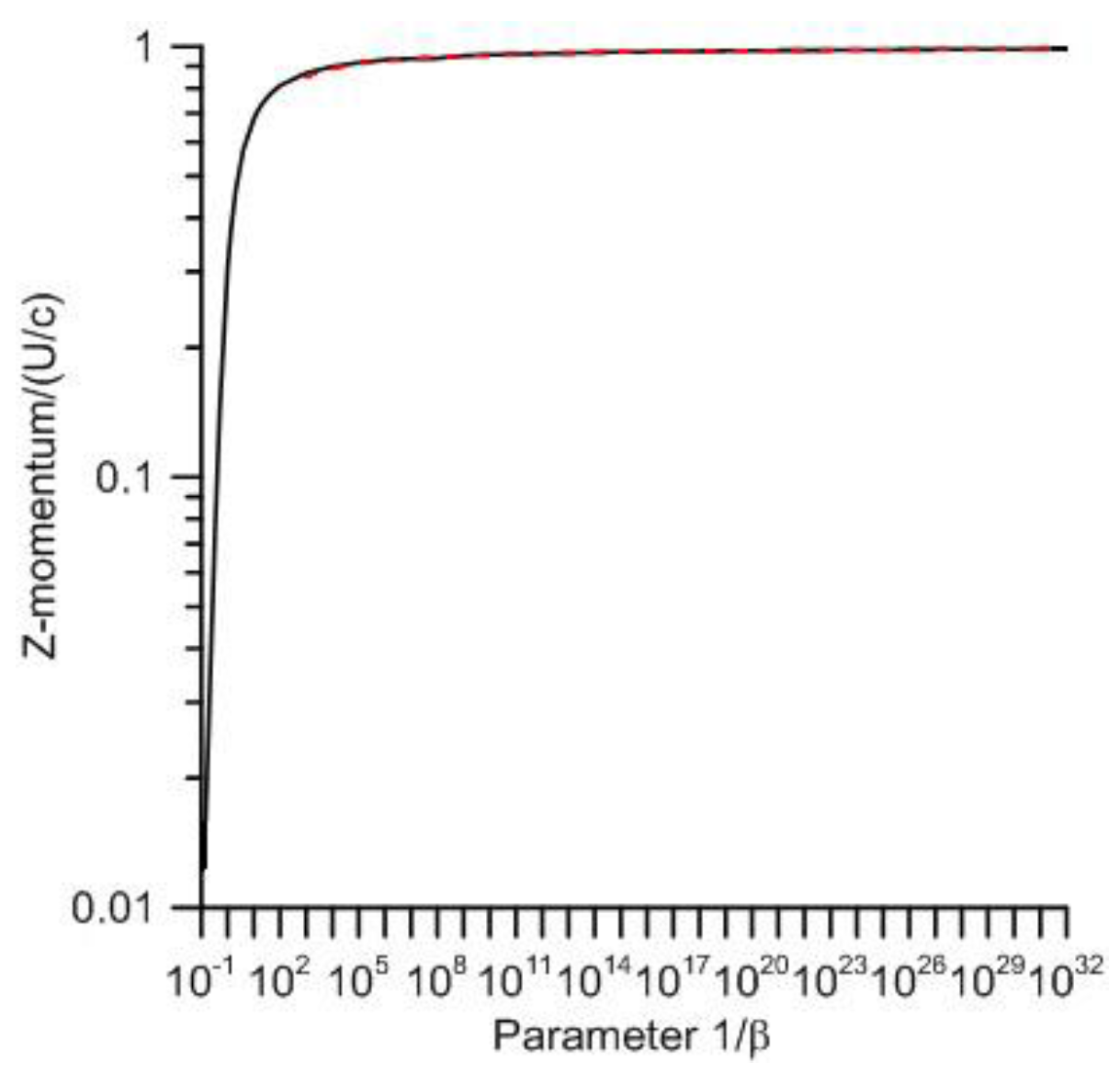
Let us consider the ratio
for a dipole. This ratio is given by Equation (24) and, for the case
, by Equation (29). Again, we remind the reader that
stands for the net momentum transferred by the radiation field in the
z-direction. A plot of
as a function of
is shown in
Figure 4. The ratio calculated using the approximate expression given by Equation (29) is shown in the same diagram by a dotted line. Observe that this ratio depends on the value of
. Let us study how this ratio varies with this parameter. For small values of
, the ratio
is significantly less than unity, and this indicates that the radiation is not strongly directional. Indeed, as seen earlier, for a Hertzian dipole
and the ratio
is equal to zero. However, as
increases, the ratio increases and its value asymptotically approaches unity. For values of
larger than about 10
5–10
6, this ratio is almost equal to unity. This shows that as
increases, the radiation becomes more and more directional and it aligns along the
z-axis (or along the axis of the dipole). When
, the total momentum transported by the field is almost equal to
, where
is the total energy radiated. In other words, for
the radiation emitted by the dipole can be treated as almost unidirectional.
The results presented here are obtained for a Gaussian current pulse. However, observe that the ratio
for large
is independent of the current. Thus, the results obtained above—which show that the radiation becomes more and more unidirectional as
increases—is valid also for other current waveforms. Actually, a similar effect can also be observed in dipole antennas where sinusoidal currents are oscillating. When the length of the antenna to the wavelength ratio (i.e.,
is very small), the radiation as a function of
has a broad peak, as in the case of sinusoidal Hertzian dipole [
3]. However, as the ratio
increases, the radiation becomes more and more directional; for an antenna located along the
z-axis, the radiation direction aligns along the
z-axis [
3,
8]. This is exactly what happens when
increases in the long dipole. Note that the equivalent wavelength,
, for a current pulse of duration
is about
. Thus, the ratio
is equal to
, and this in turn is equal to
. This shows that the reason for the increase in directivity of the radiation as
increases can also be understood by appealing to radiation generated by dipole antennas working in frequency domain.
7. Discussion
The results presented in this paper can be utilized in a hypothetical experiment to derive an interesting property associated with dipole radiation. Consider an electromagnetic dipole completely at rest. Its location is unknown. At a given time, the dipole emits a burst of electromagnetic radiation whose duration is
. The task is to measure the momentum and the location of the dipole by using the emitted electromagnetic radiation. Let us assume that the emission mechanism of radiation satisfies the condition that the total momentum transported by the dipole electromagnetic field is given by
where
is the total energy associated with the electromagnetic radiation (i.e.,
). The law of momentum conservation dictates that a momentum of equal magnitude but of opposite direction is transferred to the dipole by the outgoing radiation field. Let
represents the uncertainty in the emitted energy. Then, the uncertainty in the momentum of the dipole
is equal to
. This is the case because
. If the duration of the radiation emitted by the dipole is
, the effective wavelength associated with the radiation is
. Now, when an object is illuminated by electromagnetic radiation, the location of the object cannot be specified to an accuracy better than the wavelength of the radiation [
9]. Thus, the uncertainty in the position of the dipole in the
z-direction,
, is equal to
. Since the uncertainty in the position and the momentum of any object should satisfy the Heisenberg’s uncertainty principle we can write
In the above equation,
h is the Plank constant. Substituting
and
in Equation (30) we obtain
In our case, the condition
is approximately satisfied by the radiation fields when the value of
is larger than about 10
5. Thus, for dipoles working in time domain where the condition
is satisfied, the emitted radiation should satisfy approximately the condition given by Equation (31). This is an interesting result, which shows that dipole fields, when excited by fast current pulses, satisfy a time–energy uncertainty relationship as given by Equation (31). Indeed, Cooray and Cooray [
8] used this relationship to show that the smallest charge that can radiate in an antenna working in time domain is equal to the electronic charge.
In order to be treated as a Hertzian dipole, the effective wavelength associated with the radiation of the dipole should satisfy the conditions and , where and are the radius and length of the dipole, respectively. In the case of a long dipole, we relax the second condition, and this makes it necessary to consider the propagation effects of the current along the dipole. However, even in the case of a long dipole, we still have to satisfy the condition . Thus, the results obtained for a long dipole are valid, provided this condition is satisfied. This shows that the possible values of are bound on one side by the smallest radius of the conductor that can be realized in nature and on the other side by the longest dipole that can be realized in nature (i.e., where is the radius of the universe).
In this paper, we have considered an idealized situation in which current pulses are assumed to propagate along the long dipole with speed of light and without attenuation. This idealization was warranted here because the goal of the study reported in this paper was to understand the connection between the energy and momentum transported by the long dipole radiation. However, the application of this procedure in more practical situations needs further consideration. For example, dipole antennas are constructed in practice by locating vertical conductors over perfectly conducting ground. In this case, the long dipole acts as a vertical transmission line. Pulses propagating along vertical conductors located over a ground plane are affected by the finite conductivity of the material of the conductor and by the effects of radiation damping [
1]. The calculations conducted by Baba and Rakov [
10] show that the current pulses propagating along such conductors can attenuate as they propagate along them. Moreover, close to the ground end of the conductors, even the speed of propagation of the current pulses is slightly less than the speed of light. At present, we are investigating these effects to extract the conditions under which the ideal assumptions made in the present paper, namely propagation of current pulses without attenuation, are valid. The results obtained by us at present using the mathematical equations developed by Wu [
11] and Chen [
12] for pulse propagation along vertical conductors located over a ground plane, indicate that the ideal conditions assumed in the present paper are valid for values of
less than about 10
6–10
7. Further research work is necessary to confirm this result.
Another natural phenomenon that acts as a dipole located over a ground plane is the lightning return stroke. Experimental data show that the return stroke can be treated as a current pulse propagating along a more or less vertical channel with an average speed of propagation of about (1–2) × 10
8 m/s while undergoing attenuation. The actual front speed decreases with increasing height [
13]. In reality, the ground is finitely conducting and the radiation fields are affected by the propagation losses. Research work is underway to investigate the momentum transferred by radiation fields of lightning return strokes and how it is related to the total energy radiated by them. Furthermore, how the magnitude of the radiated momentum and its relationship to total radiated energy vary as a function of return stroke parameters—such as current amplitude, current signature, speed of propagation, and current attenuation along the channel—are under investigation. We hope to present the results of these investigations in the near future.