Abstract
The estimation of the lightning performance of a power distribution network is of great importance to design its protection system against lightning. An accurate evaluation of the number of lightning events that can create dangerous overvoltages requires a huge computational effort, as it implies the adoption of a Monte Carlo procedure. Such a procedure consists of generating many different random lightning events and calculating the corresponding overvoltages. The paper proposes a methodology to deal with the problem in two computationally efficient ways: (i) finding out the minimum number of Monte Carlo runs that lead to reliable results; and (ii) setting up a procedure that bypasses the lightning field-to-line coupling problem for each Monte Carlo run. The proposed approach is shown to provide results consistent with existing approaches while exhibiting superior Central Processing Unit (CPU) time performances.
1. Introduction
Interest in the assessment of the impact lightning has on power systems is increasing in terms of power quality problems [1]. In this respect, the evaluation of the lightning performance of distribution networks is a critical issue when dealing with the design of their lightning protection systems. The lightning performance typically consists of curves reporting how many lightning faults per year the system may experience as a function of its insulation level; thus, there is a probability that the line is subject to an overvoltage greater than its critical impulse flashover voltage (CFO). Lightning may cause flashovers on distribution lines from overvoltages resulting from direct strikes and induced voltages from nearby strikes. The first ones cause insulation flashover in great majority, but many of the lightning-related outages of low-insulation lines are due to indirect lightning flashes [2]. Moreover, considering the limited height of distribution lines of medium- and low-voltage distribution networks, indirect lightning strikes are more frequent than direct ones. As a consequence, the literature has been focused on the evaluation of the indirect lightning performance, which is, unfortunately, a very hard task from a computational point of view. The reason is that the problem of the field-to-line coupling needs to be solved a significant number of times in order to account for all of the possible values that the involved stochastic variables can assume. To face this problem, a first and simplified approach has been proposed in [2], which is based on the Rusck formula for the calculation of the maximum amplitude of the lightning-induced voltages on the line. This solution was then improved in order to account both for the finite length of multi-conductor lines and for the ground finite conductivity [3].
The complexity of the power distribution networks was accounted for in [4]. In this work, a heuristic technique was applied in order to reduce the number of calls to the coupling code (e.g., Lightning Induced Overvoltage Code—LIOV [5]) in a distribution network characterized by a number of lines (main feeder with laterals) and by the presence of several power components (e.g., transformers and surge arresters). This method is used in the recently released IEEE Std. 1410–2011 [6] for the evaluation of the induced-voltage flashover rate of overhead distribution lines.
This paper is part of this research line, since it aims to represent the lightning performance of a line as accurately as possible and, at the same time, reduce the required CPU time. This is done first by deriving a methodology that determines the optimal number of Monte Carlo runs. Such a method is based on the analysis of the evolution of the experimental error (Mean Square Pure Error, MSPE for short) and defines the confidence interval in which the obtained probability lays. Moreover, the proposed approach aims to bypasses the necessity of calling the coupling code for each Monte Carlo run; this is done by constructing a lookup table that reports the overvoltage values as a function of the stochastic variables (e.g., the lightning point of impact and current peak). When the statistical analysis is performed, overvoltages are obtained by interpolation rather than by executing all required calculations.
The paper is organized as follows: In Section 2, the procedure for the evaluation of the lightning performance is presented. In Section 3, the techniques used to improve the procedure performances are proposed. Section 4 presents numerical results on a realistic distribution network and relevant discussion. Finally, conclusive remarks are presented in Section 5.
2. Procedure for the Evaluation of the Lightning Performance of Distribution Networks
In the present section, the procedure proposed in [3,4] for the evaluation of the lightning performance of a Multiconductor Transmission Line (MTL) network is briefly summarized in the following steps:
- Random generation of a large number of lightning events N. Each event Sn (with n = 1,…,N) is characterized by the point of impact and the channel-base current peak I0,n. According to [7,8], the current is assumed to follow a log-normal Probability Density Function (PDF), while, for the point of impact coordinates, a uniform PDF is considered within a striking area that contains the power system of interest and all possible lightning events that can cause critical flashovers [3,4].
- Application of an attachment model (e.g., the electrogeometric model (EGM) [1]) that determines whether the selected event is a direct or indirect stroke. The direct lightning events can be simulated with the injection of a current source represented using Heidler’s function [9] in parallel with a suitable resistance accounting for the lightning channel. Otherwise, in case of an indirect strike, one has to resort to the equations describing the field-to-line coupling problem.
- For each event Sn, with n = 1,…,N, the obtained overvoltage is compared with the line CFO in order to define a Boolean variable:
- Computation of the probability of having a dangerous overvoltage as the following ratio:
The effectiveness and computational efficiency of the procedure strongly depends on the choice of the number of lightning events used in the code. From the effectiveness standpoint, it is necessary to choose a sufficiently large value for N in order to correctly reproduce the PDF of the resulting overvoltage. However, if such a value becomes too large, an unnecessarily high number of simulations is performed, and this becomes computationally cumbersome, especially for the case of indirect lightning events, as each run requires the solution of the field-to-line coupling problem.
3. A Methodology to Improve the Procedure Performances
In this section, the methodology to improve the computational efficiency of the lightning performance evaluation is presented. As outlined in the introduction, this will be done in two ways. The first consists of determining the optimal number of Monte Carlo extractions N in order to correctly reproduce the PDF of the resulting overvoltage without performing unnecessary calculations (Section 3.1). The second idea is based on the construction of a lookup table that provides the overvoltage values for a set of different lightning events characterized by an assigned current peak and point of impact; thus, for each Monte Carlo extraction, one can interpolate the values of such a table without calling the coupling code (Section 3.2).
3.1. Reduction of the Number of Monte Carlo Runs
In this subsection, the application of a methodology that identifies the minimum number of runs necessary to obtain correct outputs from the Monte Carlo model is presented. It has been proposed in [10] for a very simple system and will be here briefly recalled and then applied to a distribution network with a complex topology:
- Set a number K > 2 of Monte Carlo simulations, carried out in parallel, in which the independent model variables are maintained the same.
- Set .
- Build up a set of K random events SN,j, for any j = 1,…,K.
- Determine the probability pN,j according to Equation (2).
- Calculate the means for each j = 1,…, K:
- Calculate the means of the means:
- Calculate values of the MSPE of the mean (MSPEMEAN):
- Compute the confidence interval for the probability, , to a significance level 1−α aswhereand is the Student’s t- distribution with K−1 degrees of freedom.
- Define the Boolean quantity:where are two suitable threshold parameters and(note that BN = 1 if at least one of the two conditions is verified, otherwise it is equal to 0).
- If BN = 0, increase N of a unit, i.e., N = N + 1 and repeat all steps starting from Step 3, otherwise stop the Monte–Carlo procedure.
Let us observe that, for any choice of , there is a sufficiently large integer N such that BN = 1, as in [11] it is shown that , which means that . This guarantees that the stopping criterion introduced at Step 10 is well defined and effectively enables an exit out of the loop.
A few words on the physical interpretation of Equation (8) are in order. The condition on the relative error EN is posed to relate the amplitude of the interval δN to the mean probability value , but is likely to become ineffective for very small values of . This way, the condition on the absolute value of such interval 2δN prevents us from performing an unnecessarily high number of Monte–Carlo runs.
3.2. Reduction of the Number of Calls to the Field-to-Line Coupling Code
In this subsection, an efficient technique to reduce the number of calls to the coupling code is described.
Let us consider the situation depicted in Figure 1, where an MTL system consisting of M straight and parallel conductors of length L and diameter ai, each of them placed at a height hi (I = 1,…,M) over a lossy ground. In the reference frame depicted in Figure 1, a reference system Oxyz is placed with the x axis parallel to the direction of the line conductors, so that it is possible to define the position yi of each conductor. For the sake of simplicity and without losing generality, we can suppose that each line starts from the point (0, yi, hi) and ends at (L, yi, hi). Let us then suppose that a lightning strike occurs in a point PF at the ground level with coordinates (xF, yF,0).
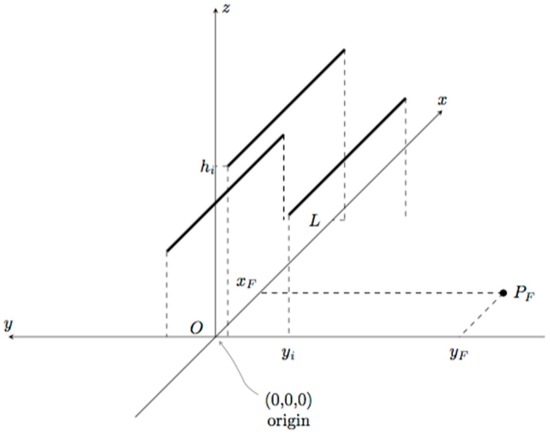
Figure 1.
Geometry of the Multiconductor Transmission Line (MTL) system.
First of all, a suitable area A containing the points of impact PF of all the possible events that can cause dangerous overvoltages has to be chosen. According to the geometry represented in Figure 1, such an area is here indicated as
where and (see [3,4]). The choice of ymin and ymax can be based on the following considerations:
- ymin can be chosen as the value under which, for any peak current, the power system will always experience a direct strike. Recalling the electrogeometric criterion described in [1], one can express the lateral distance as a function of the peak current. As can be expected, such function is monotonically increasing; thus, the value corresponding to the minimum current can be selected as ymin. In the following, ymin will be set as 15.00 m, which corresponds to about 2 kA (that has a probability smaller than 0.016% according to the current lognormal probability density function presented in Equation (1) in [1] by using the parameters of Table 1 in [1]);
- ymax can be chosen as the horizontal distance at which, no matter the peak current, the resulting overvoltage will always be smaller than the CFO. According to the Rusk–Darveniza formula [12], one can set
In the following, ymax is assumed to be 1500.0 m, corresponding to the most critical situation characterized by a peak current of 100.0 kA (that has a probability smaller than 0.0038% according to the current lognormal probability density function presented in Equation (1) in [1] by using the parameters of Table 1 in [1])), a ground conductivity of 0.001 S/m, and a CFO of 50 kV.
Let us observe that the domain can be reduced to whenever the symmetry conditions allow that.
The evaluation of the lightning performance requires the adoption of an algorithm that, for any lightning event S, characterized by peak current I0 and impact point PF in area A, calculates the resulting overvoltage, i.e., the quantity:
where [Ts, Te] is the duration of the lightning electromagnetic fields and is the voltage at point x of the conductor i at time t. In this work, this calculation is performed using the algorithm and the PSCAD interface presented in [13].
If one defines a grid of impact points , with s = 1,…, S and q = 1,…, Q, in the area A and a sequence I0r, r = 1,…,R of peak currents, a set of SxQxR events is available, named Ssqr, and it is possible to write the 3D matrix
Therefore, for any event selected by the statistical procedure, the overvoltage can be evaluated by means of a three-dimensional linear interpolation as follows:
where the function INTERP3 performs the 3D linear interpolation of the elements of matrix V when the impact point is PF and the channel-base current amplitude is I0.
The interpolation procedure allows us to call the coupling code only SxQxR times, which is much smaller than the number of Monte–Carlo simulations N (as will be detailed later on in the paper).
4. Numerical Results
The aim of the present section is to evaluate the lightning performance of the three Medium Voltage distribution networks represented in Figure 2 and characterized by the geometrical data reported in Table 1, more precisely:
- in Test1 (see Figure 2a), the network is fed by a 132 kV voltage source and contains an HV/MV transformer, a MV/LV transformer (both protected by surge arresters), and two laterals respectively at 250 m and 750 m from the HV/MV transformer and consisting of two MV/LV identical transformers with two 300-m-long LV cables.
- in Test2 (see Figure 2b), the same network of Test1 is considered, but without laterals.
- in Test3 (see Figure 2c), the same network of Test1 is considered, but without the surge arresters.
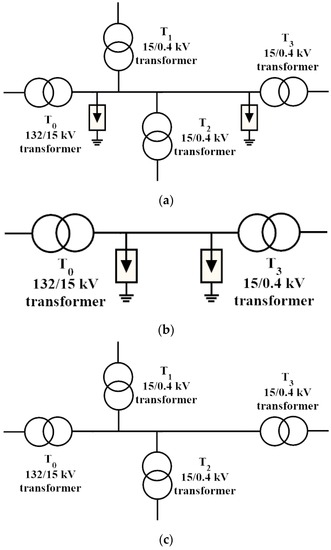
Figure 2.
Distribution network topology for the three considered tests. Panels (a–c) show the networks for Test1, Test2, and Test3, respectively.

Table 1.
Geometry of the MTL system.
Surge arresters have been modeled using typical ABB 15 kV arrester nonlinear V–I characteristics [14,15], while the HF behavior of the transformers has been accounted for combining a classical low-frequency model with suitable capacitors, following indications reported in [16].
The results of the proposed procedure, for different CFO values, are reported in the following subsections
- the number of parallel runs K is 5 (according to [10]);
- two significance levels, 90% and 95% (corresponding to and , respectively), are analyzed;
- the threshold constant values are and , which means that the mean probability value, for a selected CFO, will belong, at level , to the confidence interval with an amplitude smaller than 0.015 or, in any case, smaller than 15% of the computed mean probability .
The number of replications N is an output of the proposed procedure and depends on the network topology as well as the selected CFO. Obviously, the smaller and are, the larger N is; for this reason, the proposed values for and can be considered a right compromise between accuracy and computational time.
Table 2 shows the statistical analysis relevant to the first test case (Figure 2a): for the two chosen confidence levels and for the five selected values of CFO, the table contains the number of runs N obtained applying Equation (8) and, accordingly:
- the mean value of the probability
- the boundaries of the confidence strip and
- the absolute and relative errors and (in bold the leading stop condition)

Table 2.
Stopping criterion results for Test1.
Examining Table 2 leads to the conclusion that the maximum number of necessary replications is 1500.
The same results are reported in a graphical form for the case of CFO = 150 kV. Figure 3 reports the following:
- the evolution of as a function of the number of runs for and (Panels a and b);
- the evolution of as a function of the number of runs for and (Panels c and d) with an indication of the number of runs selected to construct Table 2;
- the evolution of the confidence strip and the mean probability as a function of the number of runs for and (Panels e and f).
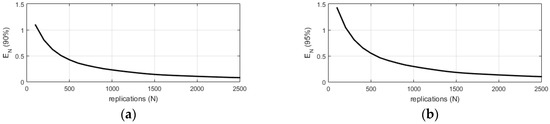
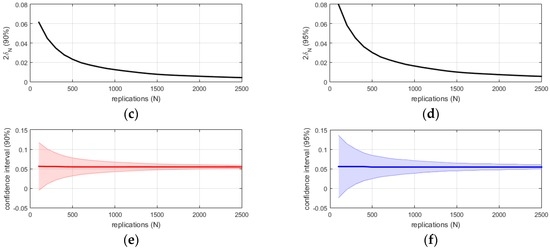
Figure 3.
Graphical evolution of (Panel (a) and (b)), (Panel (c) and (d)), confidence strip and (Panel (e) and (f)) as a function of N for CFO = 150 kV.
The same analysis has been performed for Tests2 and -3, leading to the results reported in Table 3 and Table 4.

Table 3.
Stopping criterion results for Test2.

Table 4.
Stopping criterion results for Test3.
Examining Table 3 and Table 4 leads to the conclusion that the maximum number of necessary replications is 2600 for Test2 and 3900 for Test3 with , and 1200 for Test2 and 1300 for Test3 with .
The next analysis is relevant to the validation of the procedure described in Section 3.2. The proposed approach was compared with those presented in [3,4], and a good agreement was found, as can be seen from Figure 4. Moreover, while the approach proposed in [3] requires calling the coupling code for any Monte–Carlo run (resulting in 120,000 calls [3]), the heuristic rule presented in [4] limits the number of coupling analysis to a quantity that depends on the CFO (see [4] for details).
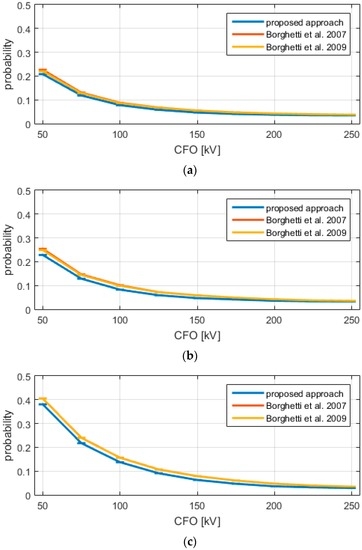
Figure 4.
Comparison of the proposed approach with the ones in [3,4] in the evaluation of the lightning performance of a complex distribution network. Panels (a–c) show the results for Test1, Test2, and Test3, respectively.
The only application that the MSPE technique requires, in the worst case, is 3900 × 5 runs; however, when the procedure described in Section 3.2 is applied with S = 9, Q = 21, and R = 4 (see [17] for this choice), the number of coupling-code calls is reduced to 756 to construct matrix in Equation (13). This reduction saves more than 40 min of computational time (based on a Windows PC equipped with an Intel i7-2600 CPU @ 3.40 GHz and 8 GB of RAM) in the best case (N = 400) and 640 min in the worst case (N = 3900).
Further, a sensitivity analysis has been conducted in order to assess the impact of the chosen area A on the final result. To do this, a variation of the aforementioned procedure has been set up, according to which, for a given Monte Carlo extraction, the overvoltages are calculated with Equation (14) only if the point of impact belongs to the following “reduced” domain D defined as (See Figure 5):
where
with γ0 and γL being two quarters of the circles centered respectively on (0, ymin) and (L, ymin) with a radius of d-ymin. As mentioned in the definition of the domain A, here, D can be reduced to D+ if a perfect symmetry of the MTL is exploited.
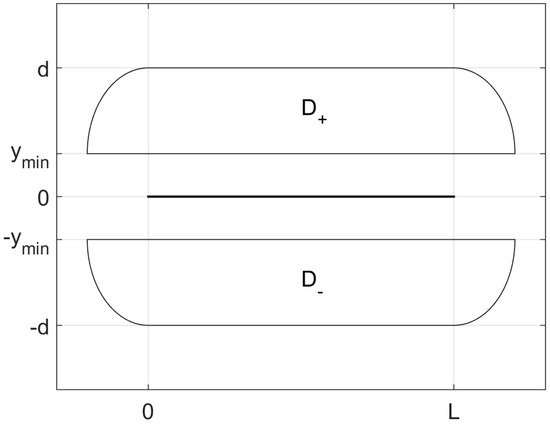
Figure 5.
Graphical representation of the domain D defined in Equations (15)–(17).
Alternatively, one supposes that the overvoltage will not exceed the CFO, and no calculation is thus required. Figure 6 reports the results of the comparison between the calculations performed on the original and reduced domains for d = 400 m, highlighting a good agreement for all CFO values in the networks characterized by the presence of the arresters. Some deviations appear for the third test case and low values of CFO. From a CPU effort standpoint, this last approach requires only 138 calls to the coupling code.
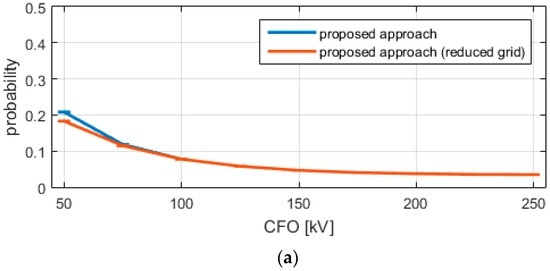
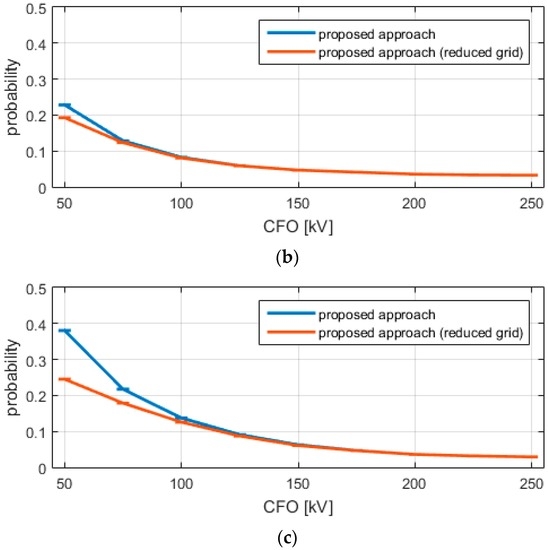
Figure 6.
Comparison of the proposed approach performed on the original domain (blue) and on the reduced one (red). Panels (a–c) show the results for Test1, Test2, and Test3, respectively.
5. Conclusions
This paper presents a methodology to reduce the computational effort necessary for evaluating the lightning performance of a distribution power network. First, the application of the MSPE algorithm determines the optimal number of Monte–Carlo extractions. Then, a procedure based on a 3D interpolation bypasses the necessity of running the field-to-line coupling code for each Monte–Carlo run.
Comparative results with existing methods highlight good performances in terms of both accuracy and computational efficiency. The defined methodology will be applied in the future to evaluate the lightning performance of realistic MV distribution networks equipped with different protection systems, in order to evaluate their effectiveness.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nucci, C.A. A Survey on Cigré and IEEE Procedures for the Estimation of the Lightning Performance of Overhead Transmission and Distribution Lines; X International Symposium on Lightning Protection: Curitiba, Brazil, 2009; pp. 151–165. [Google Scholar]
- Guide for Improving the Lightning Performance of Electric Power overhead Distribution Lines; IEEE Std. 1410; IEEE Working Group: Piscataway, NJ, USA, 2004.
- Borghetti, A.; Nucci, C.A.; Paolone, M. An improved procedure for the assessment of overhead line indirect lightning performance and its comparison with the IEEE Std. 1410 method. IEEE Trans. Power Del. 2007, 22, 684–692. [Google Scholar] [CrossRef]
- Borghetti, A.; Nucci, C.A.; Paolone, M. Indirect-lightning performance of overhead distribution networks with complex topology. IEEE Trans. Power Del. 2009, 24, 2206–2213. [Google Scholar] [CrossRef]
- Nucci, C.A.; Rachidi, F. Interaction of electromagnetic fields with electrical networks generated by lightning. In The Lightning Flash: Physical and Engineering Aspects; Series Power and Energy. 34; IEE Press: London, UK, 2003. [Google Scholar]
- Guide for Improving the Lightning Performance of Electric Power overhead Distribution Lines; IEEE Std. 1410; IEEE Working Group: Piscataway, NJ, USA, 2011.
- Berger, K.; Anderson, R.B.; Kröninger, H. Parameters of lightning flashes. Electra 1975, 41, 23–37. [Google Scholar]
- Guide to Procedures for Estimating the Lightning Performance of Transmission Lines. Available online: http://c4.cigre.org/WG-Area/WG-C4.23-Guide-to-Procedures-for-Estimating-the-Lightning-Performance-of-Transmission-Lines (accessed on 20 November 2016).
- Heidler, F. Analytische blitzstromfunktion zur EMP berechnung. In Proceedings of the 18th International Conference Lightning Protection, Munich, Germany, 16–20 September 1985.
- Brignone, M.; Delfino, F.; Procopio, R.; Rossi, M.; Bendato, I.; Mosca, R.; Rachidi, F. Evaluation of the lightning performance of an overhead multiconductor transmission line system. In Proceedings of the International Colloquium on Lightening and Power Systems, Bologna, Italy, 27–30 June 2016.
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley and Sons: New York, NY, USA, 1997. [Google Scholar]
- Darveniza, M. A practical extension of Rusk’s formula for maximum lightning induced voltages that accounts for ground resistivity. IEEE Trans. Power Del. 2007, 22, 605–612. [Google Scholar] [CrossRef]
- Brignone, M.; Delfino, F.; Procopio, R.; Rossi, M.; Rachidi, F. Evaluation of power system lightning performance, part I: Model and numerical solution using the PSCAD-EMTDC platform. IEEE Trans. Electromagnet. Compat. 2016, 59, 137–145. [Google Scholar] [CrossRef]
- Imece, A.F.; Durbak, D.W.; Elahi, H.; Kolluri, S.; Lux, A.; Mader, D.; McDemott, T.E.; Morched, A.; Mousa, A.M.; Natarajan, R.; et al. Modeling guidelines for fast front transients. IEEE Trans. Power Del. 1996, 11, 493–506. [Google Scholar]
- ABB Application Guidelines. Overvoltage Protection: Metal Oxide Surge Arresters Medium Voltage Systems. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0ahUKEwiZu8aik7bQAhXBv7wKHdWOD30QFggZMAA&url=https%3A%2F%2Flibrary.e.abb.com%2Fpublic%2F70e9fd6933c8c644c12578d200333cb5%2F952_abb_awr_mittelspannung_E_low.pdf&usg=AFQjCNEjfPL5DqsZHpROZyADDhcnQe_VuA&sig2=NX-6SnVuYA_MEwDHUdPHcw (accessed on 20 November 2016).
- Borghetti, A.; Morched, A.S.; Napolitano, F.; Nucci, C.A.; Paolone, M. Lightning induced overvoltages transferred through distribution power transformers. IEEE Trans. Power Del. 2009, 24, 360–372. [Google Scholar] [CrossRef]
- Brignone, M.; Delfino, F.; Procopio, R.; Rossi, M.; Rachidi, F. Evaluation of power system lightning performance, part II: Application to an overhead distribution network. IEEE Trans. Electromagnet. Compat. 2016, 59, 146–153. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).