Patterns of Dekadal Rainfall Variation Over a Selected Region in Lake Victoria Basin, Uganda
Abstract
:1. Introduction
2. Methods and Data Sources
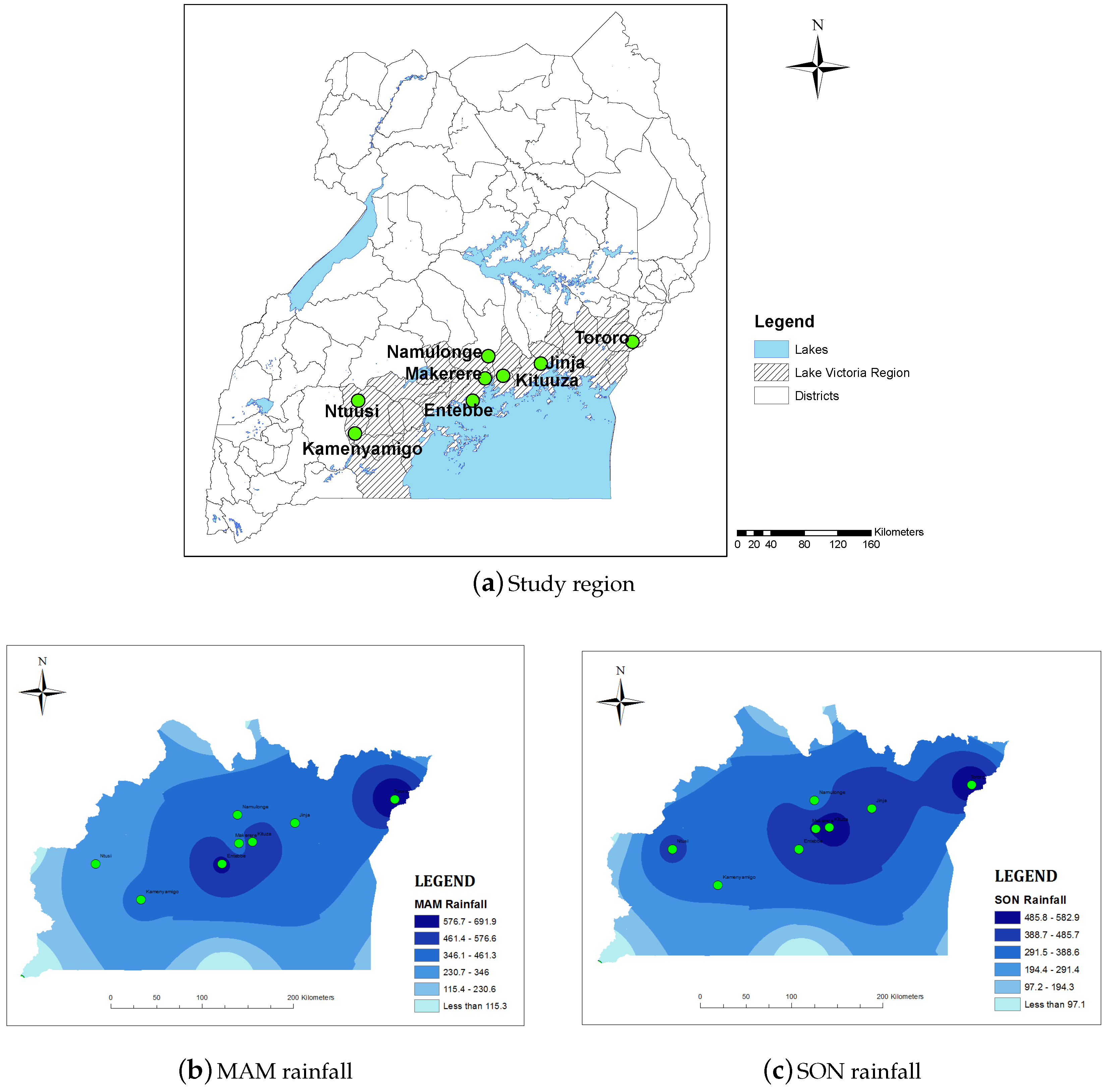
2.1. Study Area
2.2. Data
2.3. Data Analysis
3. Results and Discussion
3.1. Seasonal Rainfall Amount and Rain Days for the Period 2000–2015
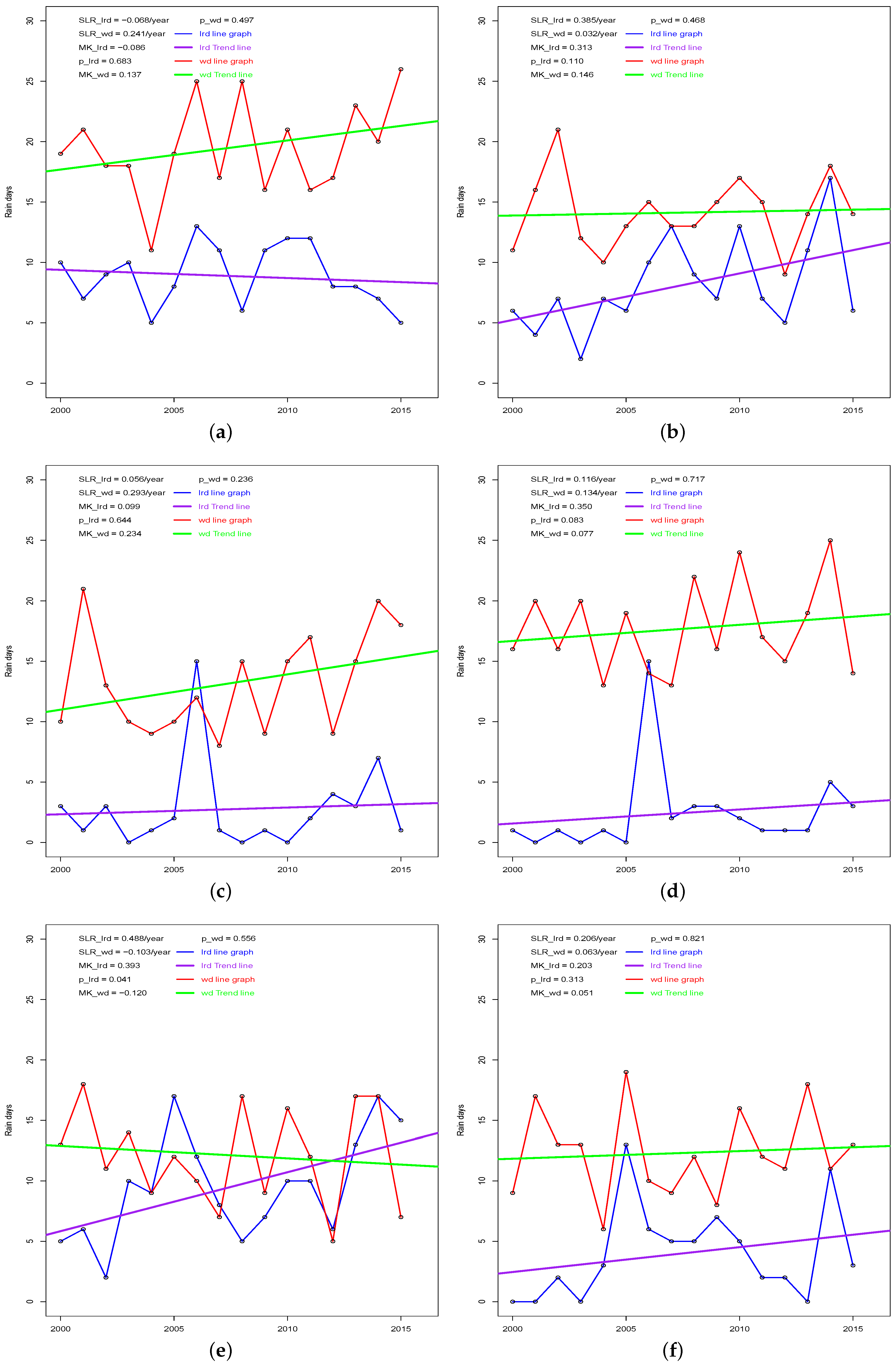
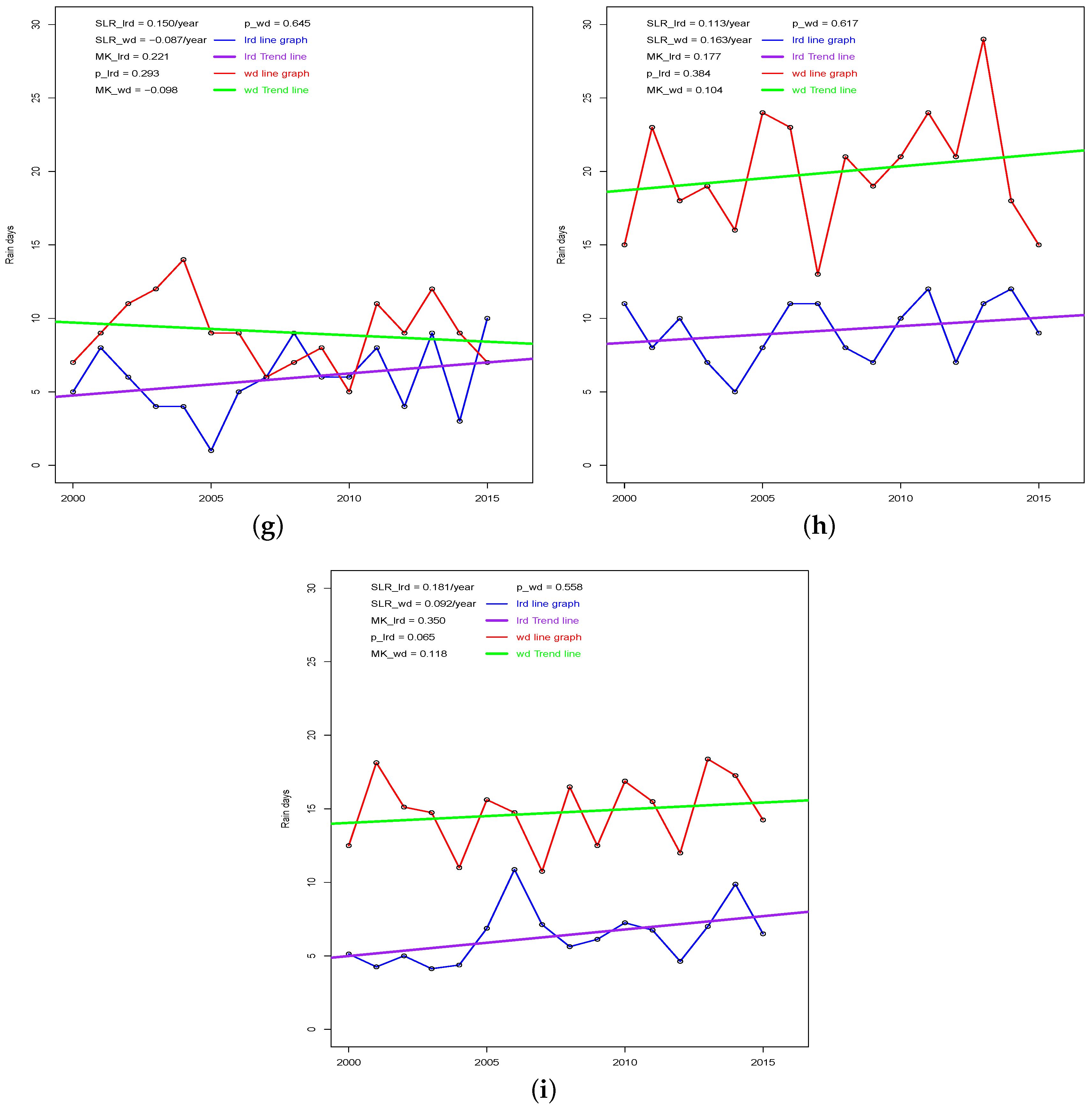
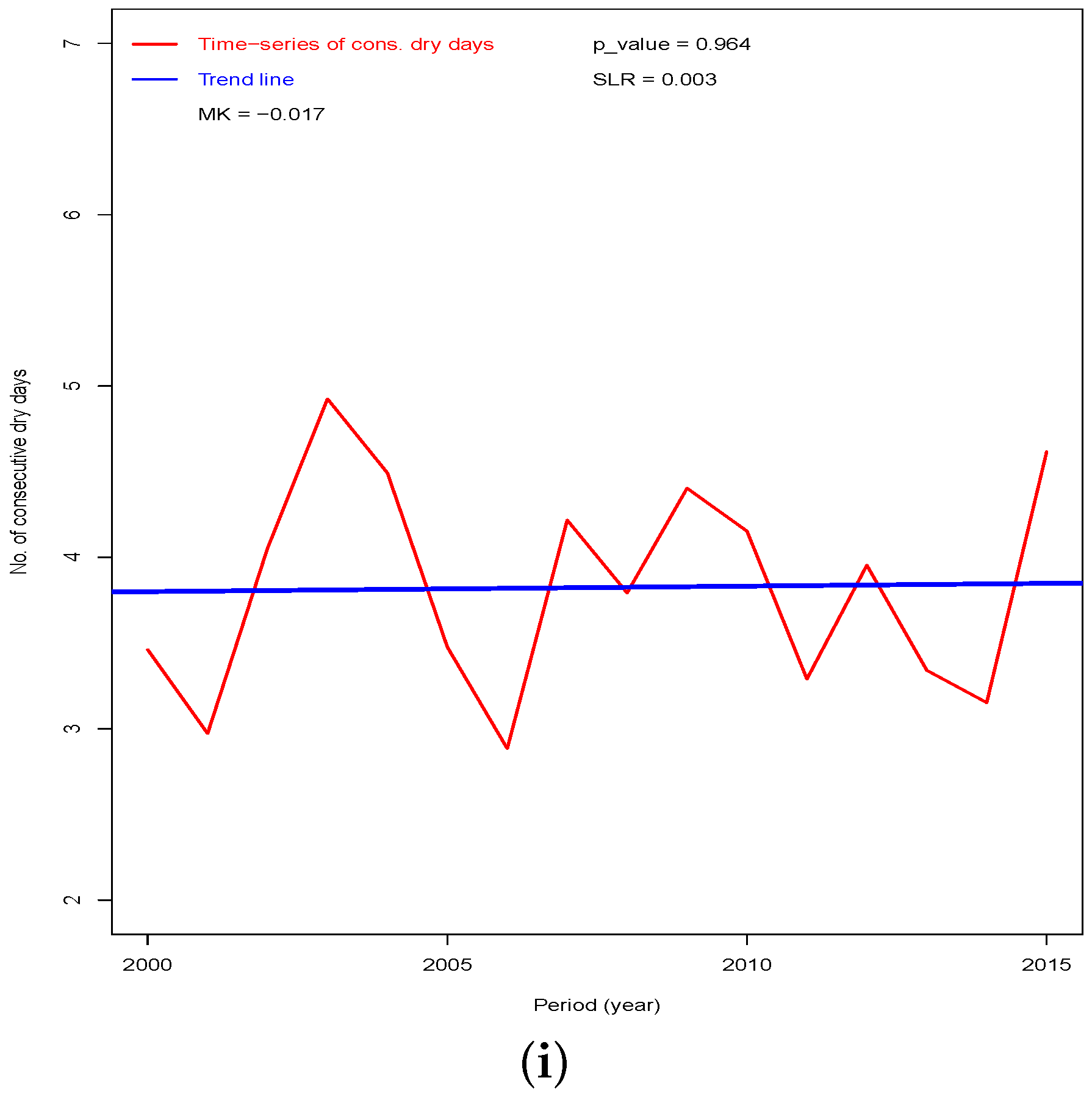
3.2. The Trend of Dekadal Rain Days
3.3. The Trend of the Dekadal Rainfall Amount
3.4. The Dekadal Rainfall Intensity
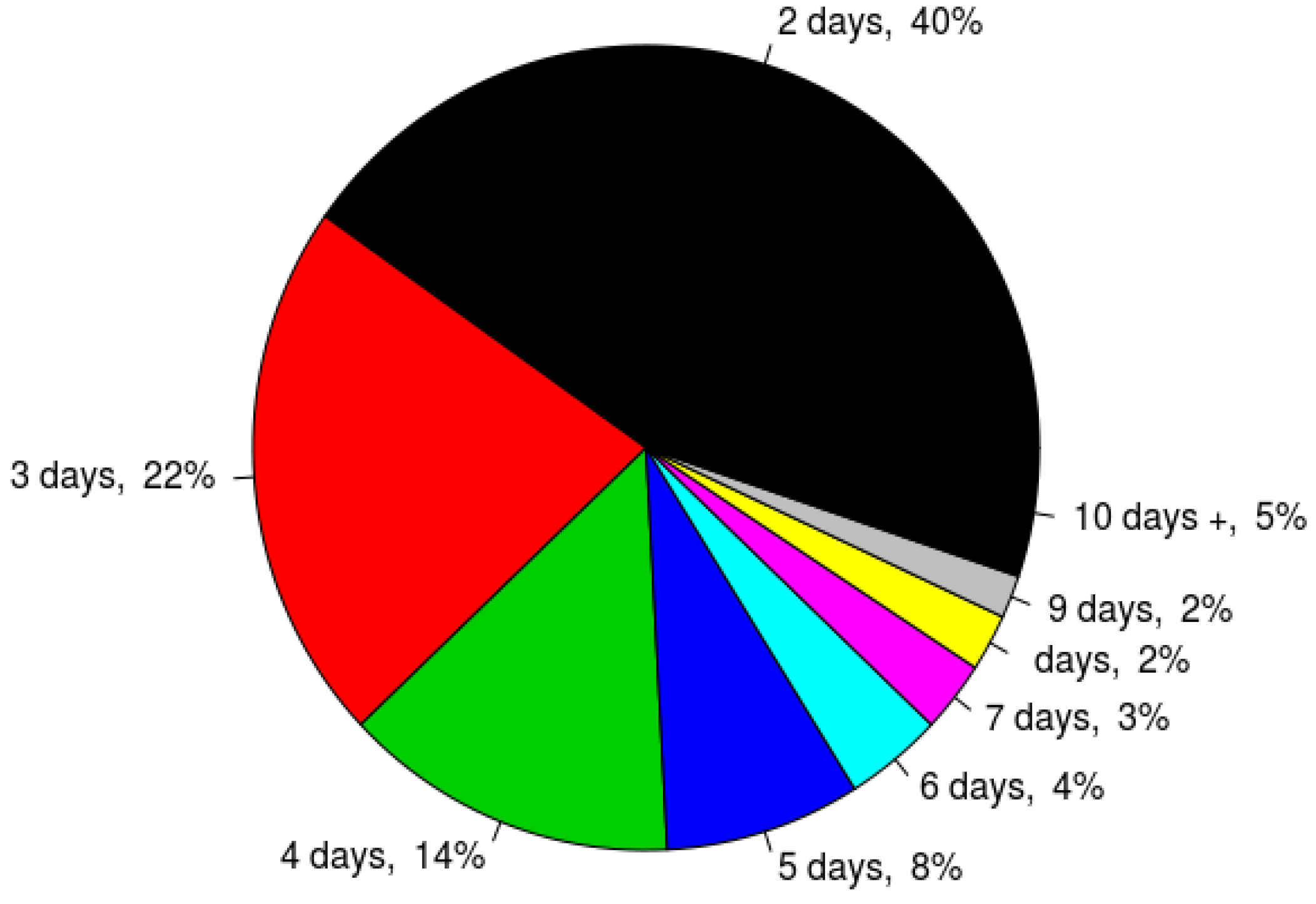
3.5. The Trend of Extreme Weather
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
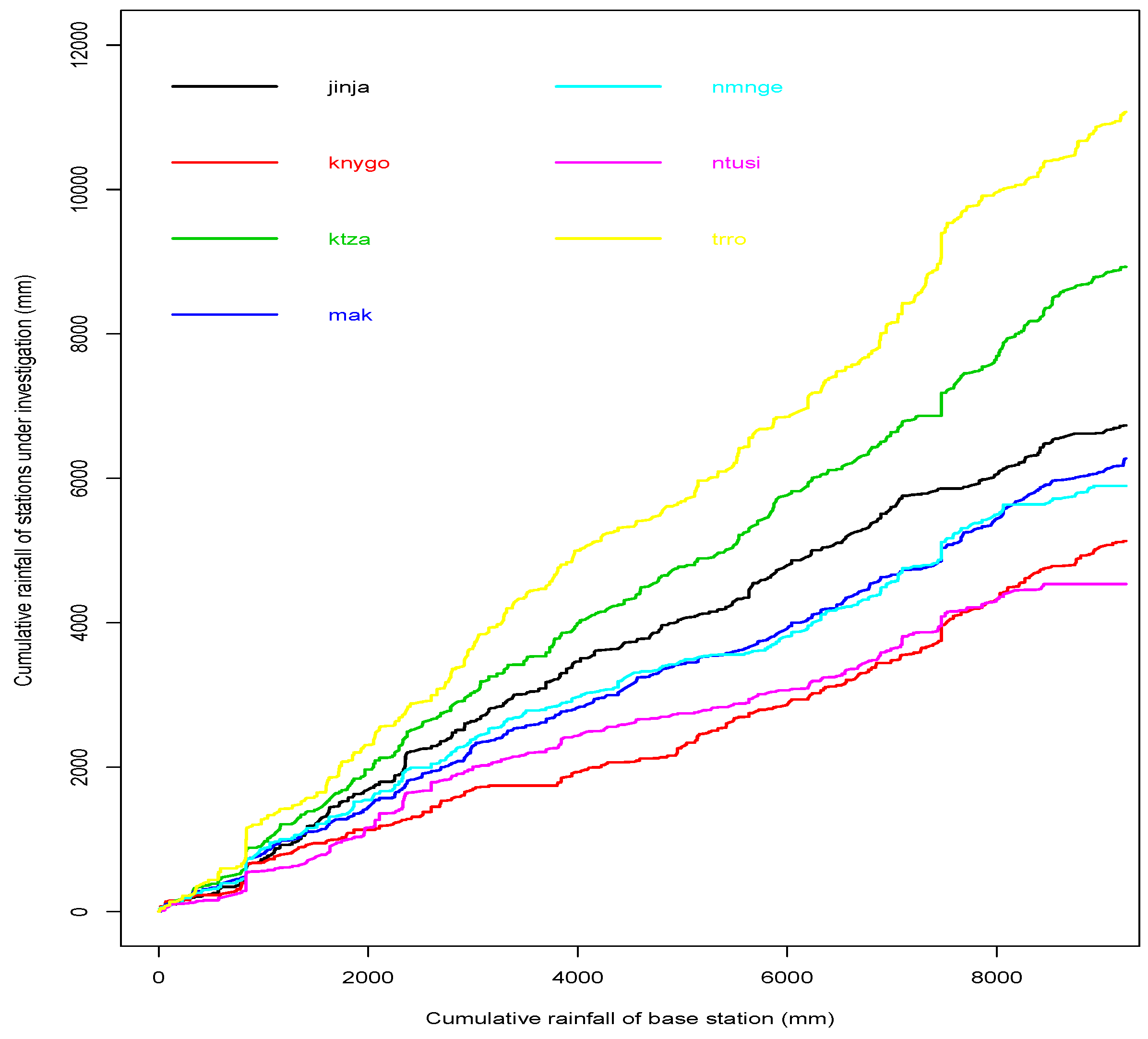
Appendix A.1. The Double-Mass Curve
Appendix A.2. Shapiro–Wilk’s Normality Test
Appendix A.3. The Normal Ratio Method
Appendix A.4. The Mann–Kendall Trend Test
Appendix A.5. Regression Analysis
References
- Ogwang, B.A.; Guirong, T.; Haishan, C. Diagnosis of September–November drought and the associated circulation anomalies over Uganda. Pak. J. Meteorol. 2012, 9, 11–24. [Google Scholar]
- Nsubuga, F.N.W.; Olwoch, J.M.; Rautenbach, C.J.; Botai, O.J. Analysis of mid-twentieth century rainfall trends and variability over southwestern Uganda. Theor. Appl. Climatol. 2014, 15, 53–71. [Google Scholar] [CrossRef]
- Ongoma, V.; Guirong, T.; Ogwang, B.A.; Ngarukiyimana, J.P. Diagnosis of seasonal rainfall variability over east africa: A case study of 2010–2011 drought over Kenya. Pak. J. Meteorol. 2015, 11, 13–21. [Google Scholar]
- Kizza, M.; Rodhe, A.; Xu, C.Y.; Ntale, H.K.; Halldin, S. Temporal rainfall variability in the lake victoria basin in east africa during the twentieth century. Theor. Appl. Climatol. 2009, 98, 119–135. [Google Scholar] [CrossRef]
- Anyah, R.O.; Semazzi, F.H.; Xie, L. Simulated physical mechanisms associated with climate variability over lake Victoria basin in East Africa. Mon. Weather Rev. 2006, 134, 3588–3609. [Google Scholar] [CrossRef]
- Awange, J.; Anyah, R.; Agola, N.; Forootan, E.; Omondi, P. Potential impacts of climate and environmental change on the stored water of lake Victoria basin and economic implications. Water Resour. Res. 2013, 49, 8160–8173. [Google Scholar] [CrossRef]
- Mailu, A.M. Biological and integrated control of water hyacinth, eichhornia crassipes. ACIAR Proc. 2001, 102, 130–139. [Google Scholar]
- Sabiiti, G.; Ininda, J.M.; Ogallo, L.; Opijah, F.; Nimusiima, A.; Otieno, G.; Ddumba, D.S.; Nanteza, J.; Basalirwa, C. Empirical relationships between banana yields and climate variability over Uganda. J. Environ. Agric. Sci. 2016, 7, 3–13. [Google Scholar]
- Mukwaya, P.I.; Sengendo, H.; Lwasa, S. Enhancing security and resilience of low-income communities to climate change in growing cities: An assessment of flood management and planning regimes in Kampala City, Uganda. In Climate Change, Human Security and Violent Conflict; Scheffran, J., Brzoska, M., Brauch, G., Link, M.P., Schilling, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 543–557. [Google Scholar]
- Williams, K.; Chamberlain, J.; Buontempo, C.; Bain, C. Regional climate model performance in the lake Victoria basin. Clim. Dynam. 2015, 44, 1699–1713. [Google Scholar] [CrossRef]
- Barron, J.; Rockström, J.; Gichuki, F.; Hatibu, N. Dry spell analysis and maize yields for two semi-arid locations in East Africa. Agric. For. Meteorol. 2003, 117, 23–37. [Google Scholar] [CrossRef]
- Goswami, B.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Cheung, W.H.; Senay, G.B.; Singh, A. Trends and spatial distribution of annual and seasonal rainfall in Ethiopia. Int. J. Climatol. 2008, 28, 1723–1734. [Google Scholar] [CrossRef]
- Nimusiima, A.; Basalirwa, C.; Majaliwa, J.; Mbogga, S.; Mwavu, E.; Namaalwa, J.; Okello-Onen, J. Analysis of future climate scenarios over central Uganda cattle corridor. J. Earth Sci. Clima. Chang. 2014, 2014, 1–13. [Google Scholar]
- Bowden, J.H.; Semazzi, F.H. Empirical analysis of intraseasonal climate variability over the Greater Horn of Africa. J. Clim. 2007, 20, 5715–5731. [Google Scholar] [CrossRef]
- Hartter, J.; Stampone, M.D.; Ryan, S.J.; Kirner, K.; Chapman, C.A.; Goldman, A. Patterns and perceptions of climate change in a biodiversity conservation hotspot. PLoS ONE 2012, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Nimusiima, A.; Basalirwa, C.; Majaliwa, J.; Otim-Nape, W.; Okello-Onen, J.; Rubaire-Akiiki, C.; Konde-Lule, J.; Ogwal-Byenek, S. Nature and dynamics of climate variability in the uganda cattle corridor. Afr. J. Environ. Sci. Technol. 2013, 7, 770–782. [Google Scholar] [CrossRef]
- Chaves, L.F.; Satake, A.; Hashizume, M.; Minakawa, N. Indian ocean dipole and rainfall drive a moran effect in east africa malaria transmission. J. Infect. Dis. 2012, 205, 1885–1891. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Shen, S.; Li, Y.; Wang, Q.; Gao, P.; Mugume, I. Projected crop production under regional climate change using scenario data and modeling: Sensitivity to chosen sowing date and cultivar. Sustainability 2016, 8, 214. [Google Scholar] [CrossRef]
- Odada, E.O.; Ochola, W.O.; Olago, D.O. Drivers of ecosystem change and their impacts on human well-being in Lake Victoria basin. Afr. J. Ecol. 2009, 47, 46–54. [Google Scholar] [CrossRef]
- Basalirwa, C. Delineation of uganda into climatological rainfall zones using the method of principal component analysis. Int. J. Climatol. 1995, 15, 1161–1177. [Google Scholar] [CrossRef]
- Searcy, J.K.; Hardison, C.H. Double-mass curves. In Manual of Hydrology: Part 1. General Surface-Water Techniques; Pecora, W.T., Ed.; USA Department of Interior: Washington, DC, USA, 1960; pp. 33–64. [Google Scholar]
- Wigbout, M. Limitations in the use of double-mass curves. J. Hydrol. 1973, 12, 132–138. [Google Scholar]
- Royston, J.P. Algorithm as 181: The w test for normality. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 176–180. [Google Scholar] [CrossRef]
- Royston, J.P. An extension of shapiro and wilk’s w test for normality to large samples. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Royston, J.P. Remark as R94: A remark on algorithm as 181: The w-test for normality. J. R. Stat. Soc. Ser. C Appl. Stat. 1995, 44, 547–551. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.B. Temporal pattern of aridity index in iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Sayemuzzaman, M.; Jha, M.K. Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos. Res. 2014, 137, 183–194. [Google Scholar] [CrossRef]
- Villazón, M.F.; Willems, P. Filling gaps and daily disaccumulation of precipitation data for rainfall-runoff model. In Proceedings of the 4th International Science Conference BALWOI 2010, Ohrid, Republic of Macedonia, 25–29 May 2010; pp. 25–29.
- Diem, J.E.; Hartter, J.; Ryan, S.J.; Palace, W.M. Validation of satellite rainfall products for western Uganda. J. Hydrometeorol. 2014, 15, 2030–2038. [Google Scholar] [CrossRef]
- Tennant, W.J.; Hewitson, B.C. Intra-seasonal rainfall characteristics and their importance to the seasonal prediction problem. Int. J. Climatol. 2002, 22, 1033–1048. [Google Scholar] [CrossRef]
- Uganda National Meteorological Authority (UNMA). The 2nd July 2016 dekad. In Dekadal Agromet-Hydrometeorological Bulletin; UNMA: Kabupaten Majalengka, Indonesia, 2016; Volume 7, pp. 1–3. [Google Scholar]
- Kiktev, D.; Sexton, D.M.H.; Alexander, L.; Folland, C.K. Comparison of modeled and observed trends in indices of daily climate extremes. J. Clim. 2003, 16, 3560–3571. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Marengo, J.; Marwan, N.; von Storch, J.-S.; Kurths, K. Extreme rainfall of the South American monsoon system: A dataset comparison using complex networks. J. Clim. 2015, 28, 1031–1056. [Google Scholar] [CrossRef]
- Ngailo, J.T.; Reuder, J.; Rutalebwa, E.; Nyimvua, S.; Mesquita, D.S.M. Modelling of extreme maximum rainfall using extreme value theory for Tanzania. Int. J. Sci. Innov. Math. Res. 2016, 4, 34–45. [Google Scholar]
- Mugume, I.; Shen, S.; Tao, S.; Mujuni, G. Analysis of temperature variability over desert and urban areas of Northern China. J. Climatol. Weather Forecast. 2016, 4, 1–9. [Google Scholar] [CrossRef]
- Zende, A.M.; Nagarajan, R.; Atal, R.K. Rainfall trends in semi arid region—Yerala river basin of western maharashtra, India. Int. J. Adv. Technol. 2012, 3, 137–145. [Google Scholar]
- Lacerda, F.; Nobre, P.; Sobral, M.; Lopes, G.; Chou, S.; Assad, E.; Brito, E. Long-term temperature and rainfall trends over Northeast Brazil and Cape Verde. J. Earth Sci. Clim. Chang. 2015, 6, 1–8. [Google Scholar]
- Zhai, P.; Xuebin, Z.; Hui, W.; Xiaohua, P. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Odekunle, T.O. Determining rainy season onset and retreat over Nigeria from precipitation amount and number of rainy days. Theor. Appl. Climatol. 2006, 83, 193–201. [Google Scholar] [CrossRef]
- Nyatuame, M.; Owusu-Gyimah, V.; Ampiaw, F. Statistical analysis of rainfall trend for volta region in Ghana. Int. J. Atmos. Sci. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Camberlin, P.; Moron, V.; Okoola, R.; Philippon, N.; Gitau, W. Components of rainy seasons’ variability in equatorial East Africa: Onset, cessation, rainfall frequency and intensity. Theor. Appl. Climatol. 2009, 98, 237–249. [Google Scholar] [CrossRef] [Green Version]
- Anjum, S.A.; Xie, X.Y.; Wang, L.C.; Saleem, M.F.; Man, C.; Lei, W. Morphological, physiological and biochemical responses of plants to drought stress. Afr. J. Agric. Res. 2011, 6, 2026–2032. [Google Scholar]
- Lipinski, B.; Hanson, C.; Lomax, J.; Kitinoja, L.; Waite, R.; Searchinger, T. Reducing food loss and waste. In World Resources Institute Working Paper; World Resources Institute: Washington, DC, USA, 2013. [Google Scholar]
- Camberlin, P.; Okoola, R.E. The onset and cessation of the “long rains” in Eastern Africa and their interannual variability. Theor. Appl. Climatol. 2003, 75, 43–54. [Google Scholar]
- Mugalavai, E.M.; Kipkorir, E.C.; Raes, D.; Rao, M.S. Analysis of rainfall onset, cessation and length of growing season for Western Kenya. Agric. For. Meteorol. 2008, 148, 1123–1135. [Google Scholar] [CrossRef]
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Subramanya, K. 2013 Estimation of missing data. In Engineering Hydrology; McGraw-Hill Education Private Limited: New Delhi, India, 2103; pp. 31–34. [Google Scholar]
- McLeod, A.I. Kendall rank correlation and Mann–Kendall trend test. Available online: http://btr0x2.rz.uni-bayreuth.de/math/statlib/R/CRAN/doc/packages/Kendall.pdf (accessed on 5 December 2015).
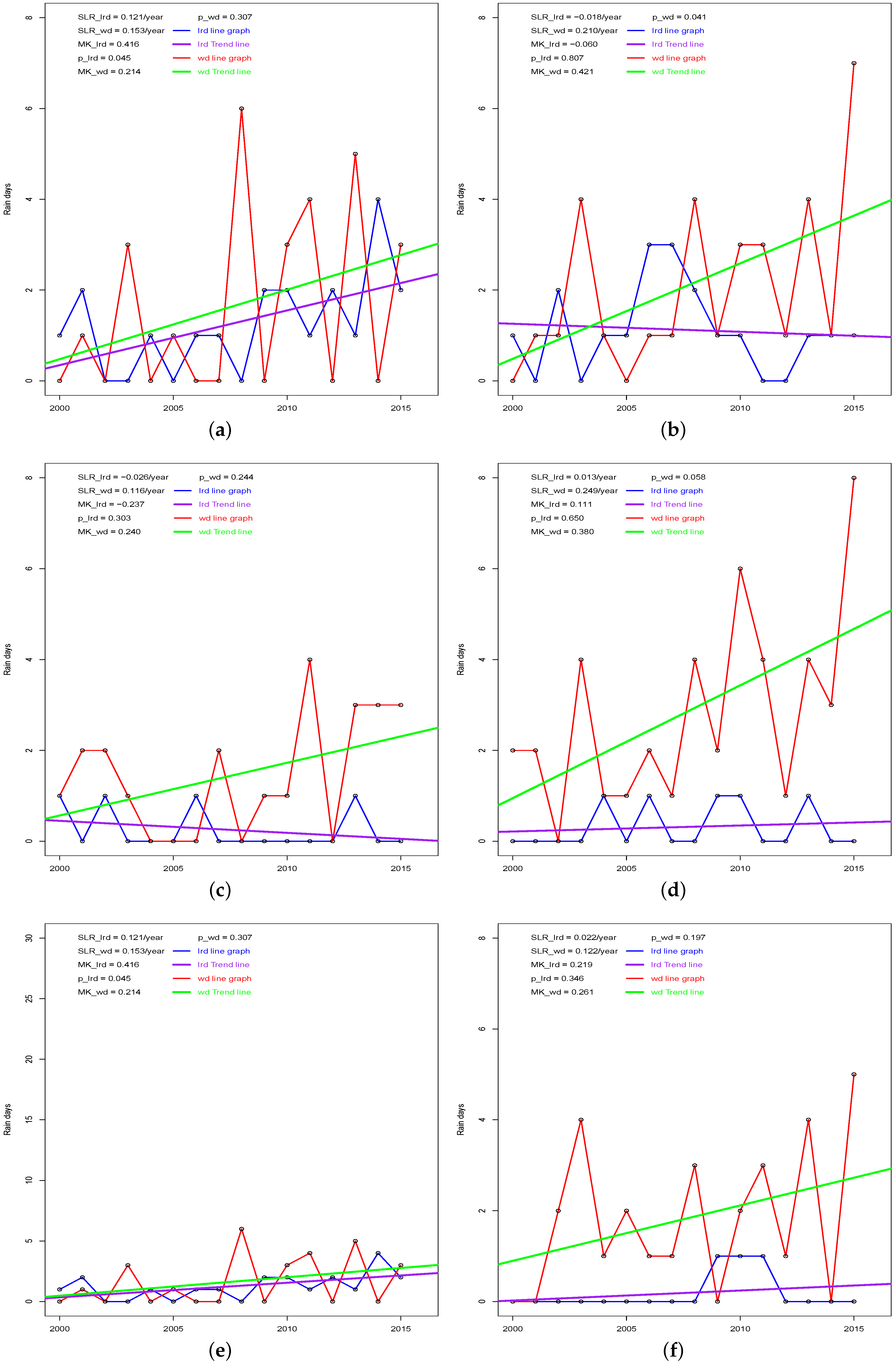
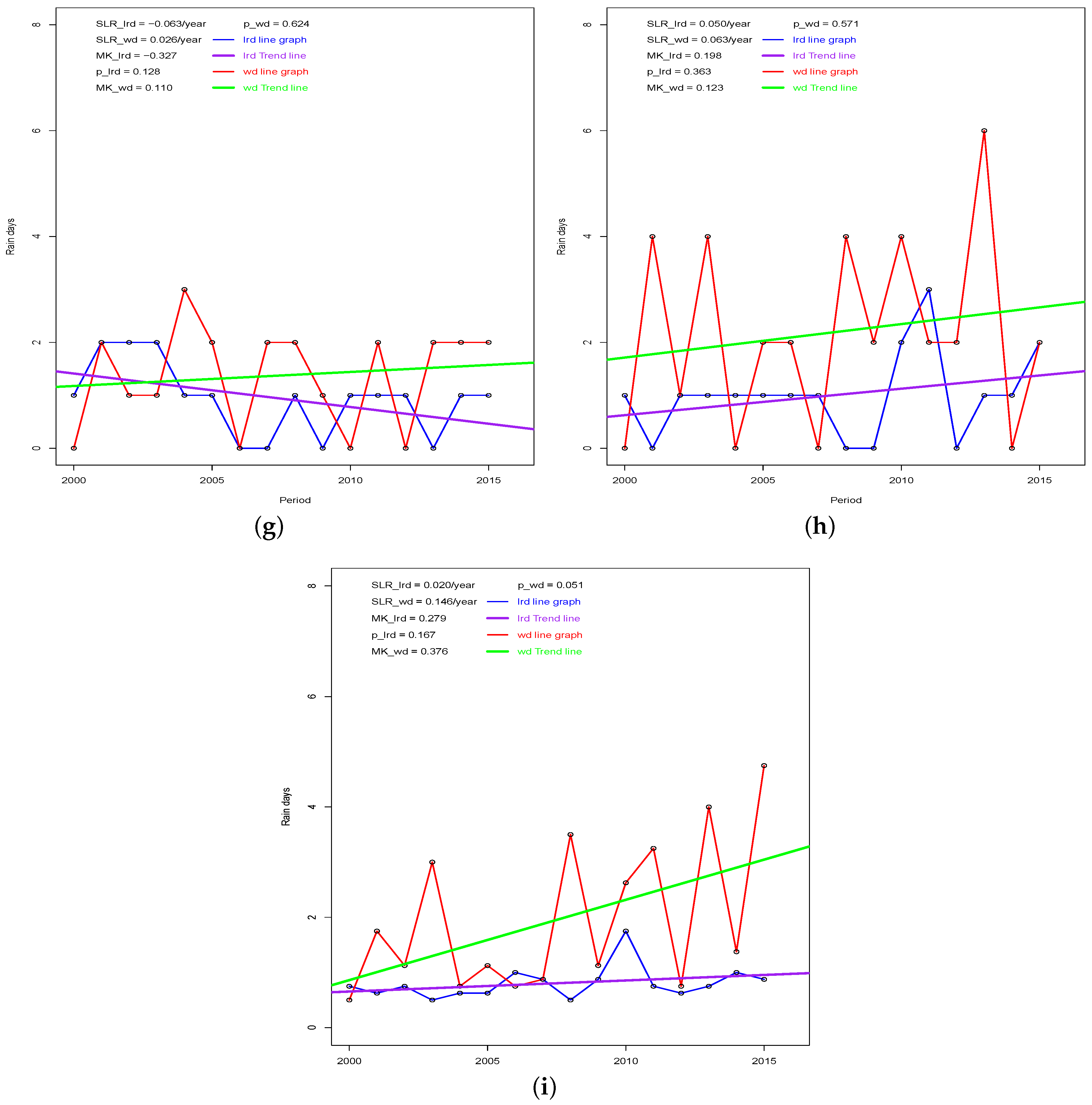
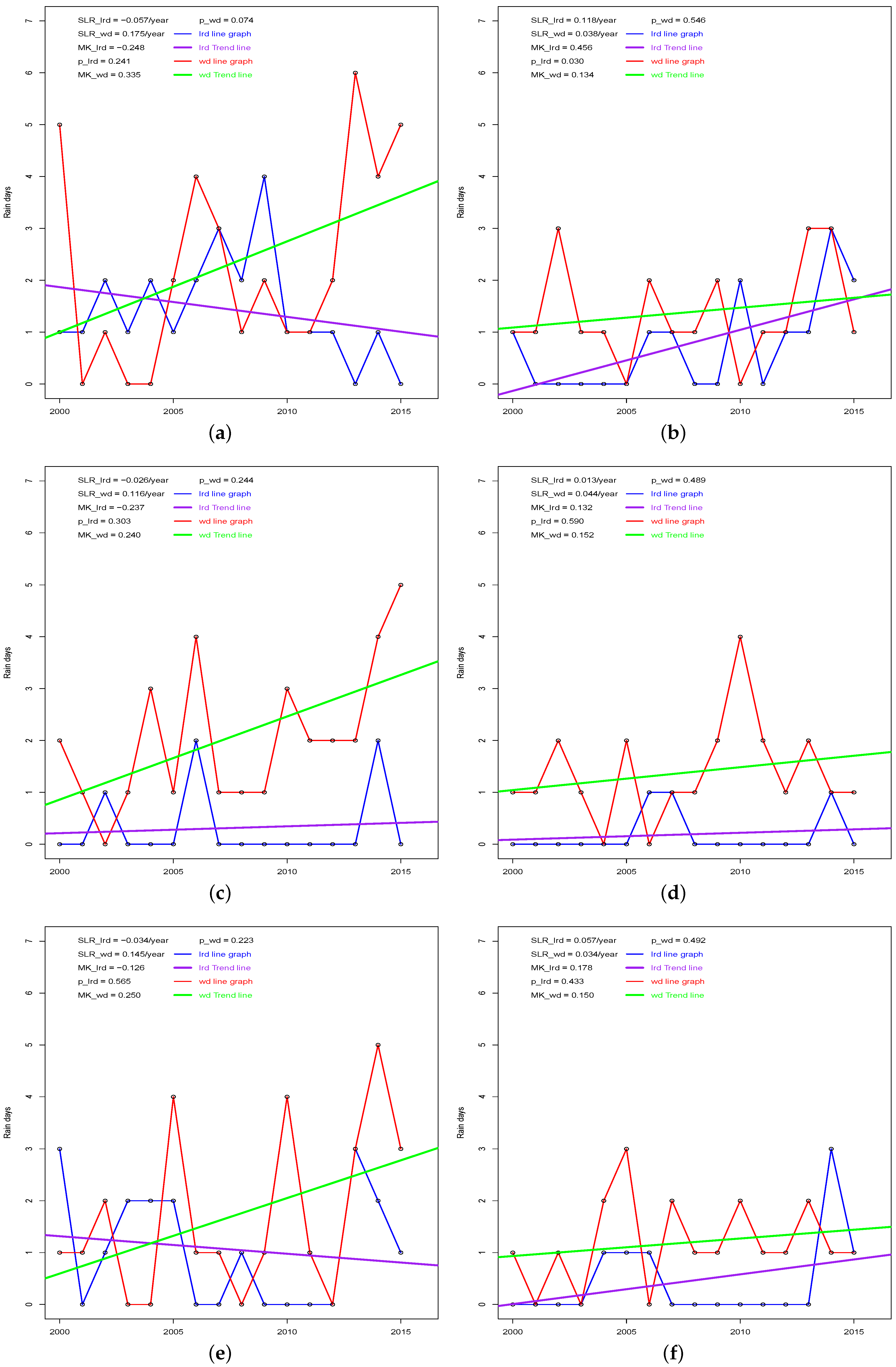
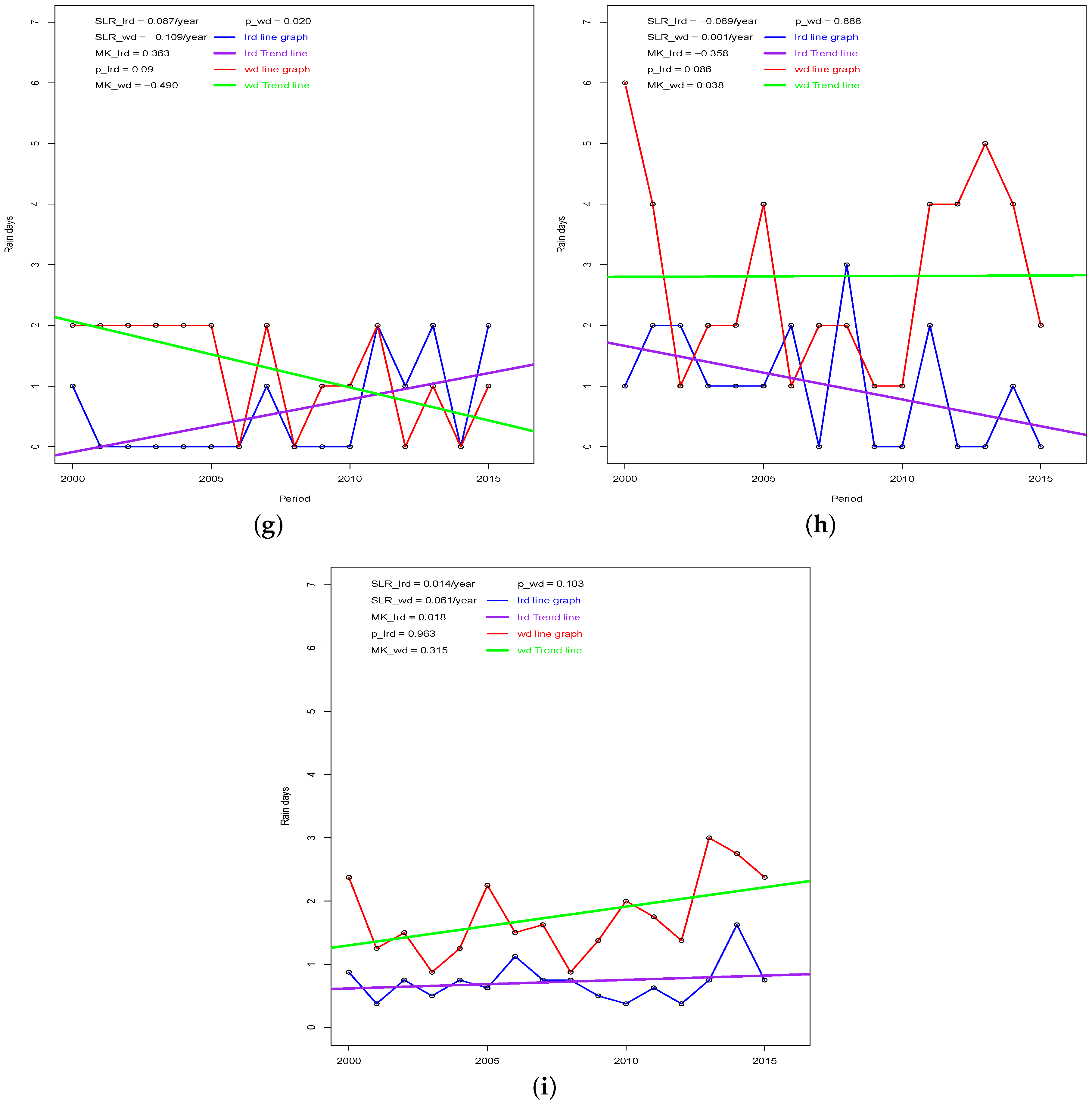
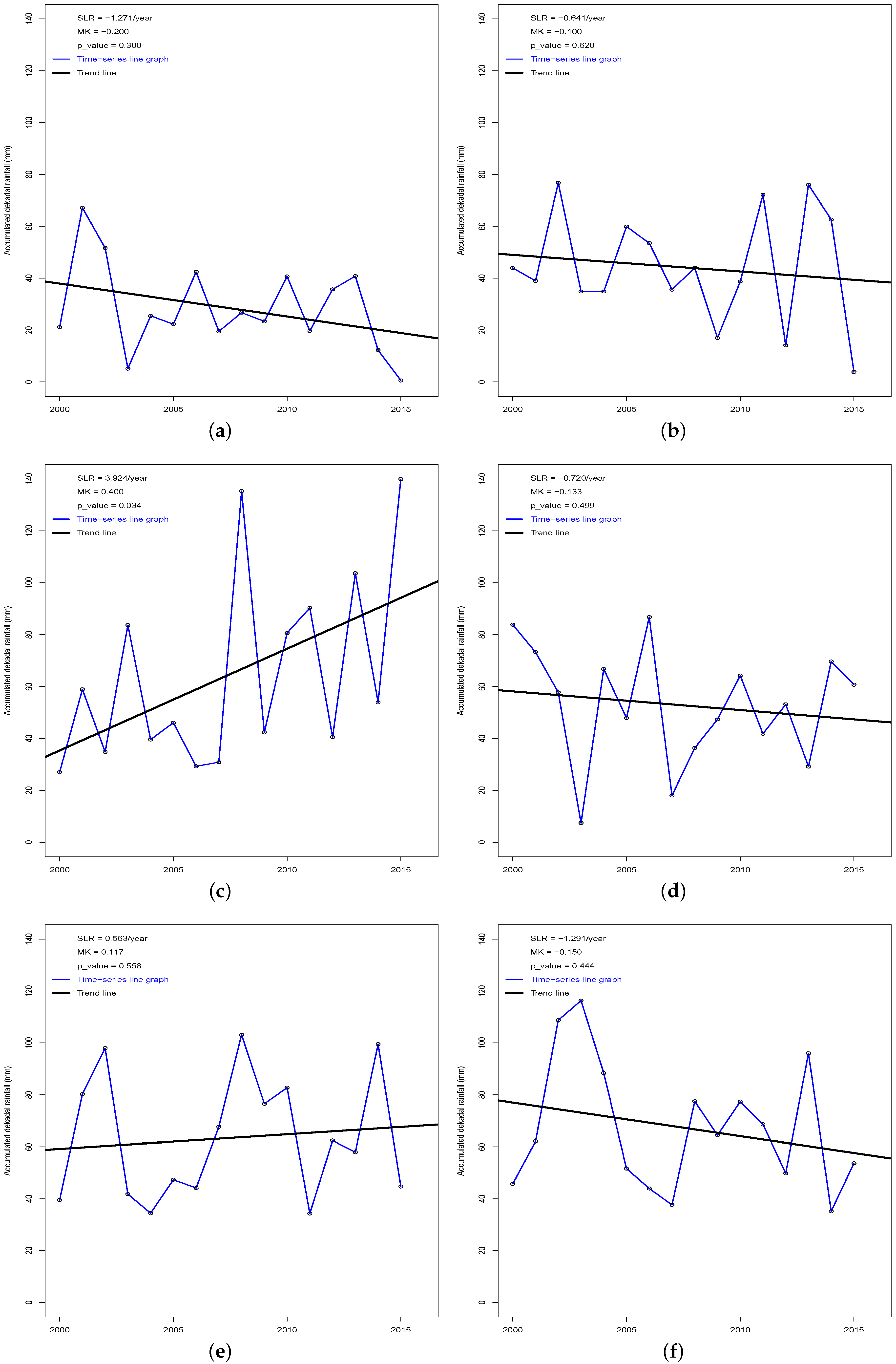
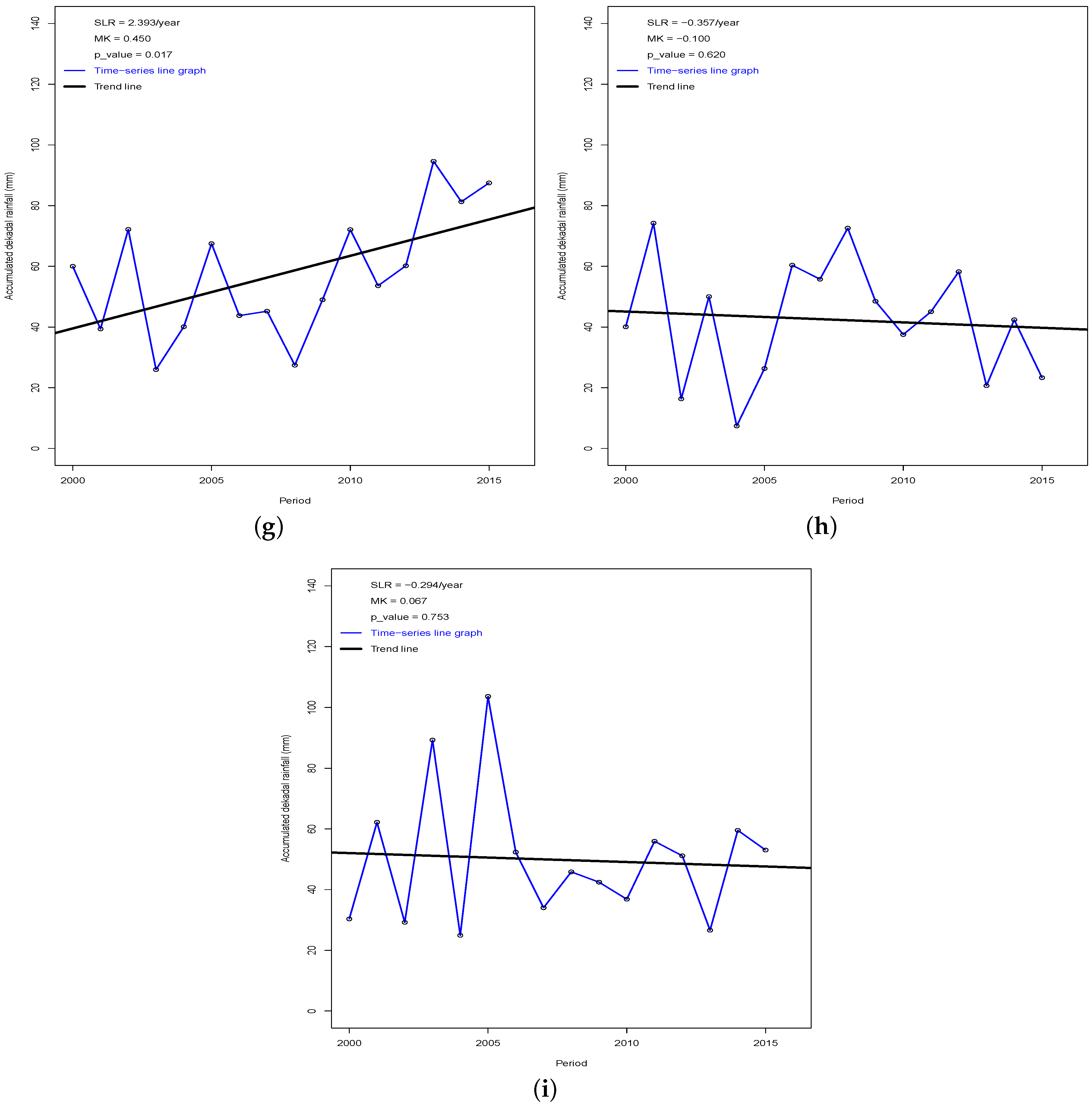
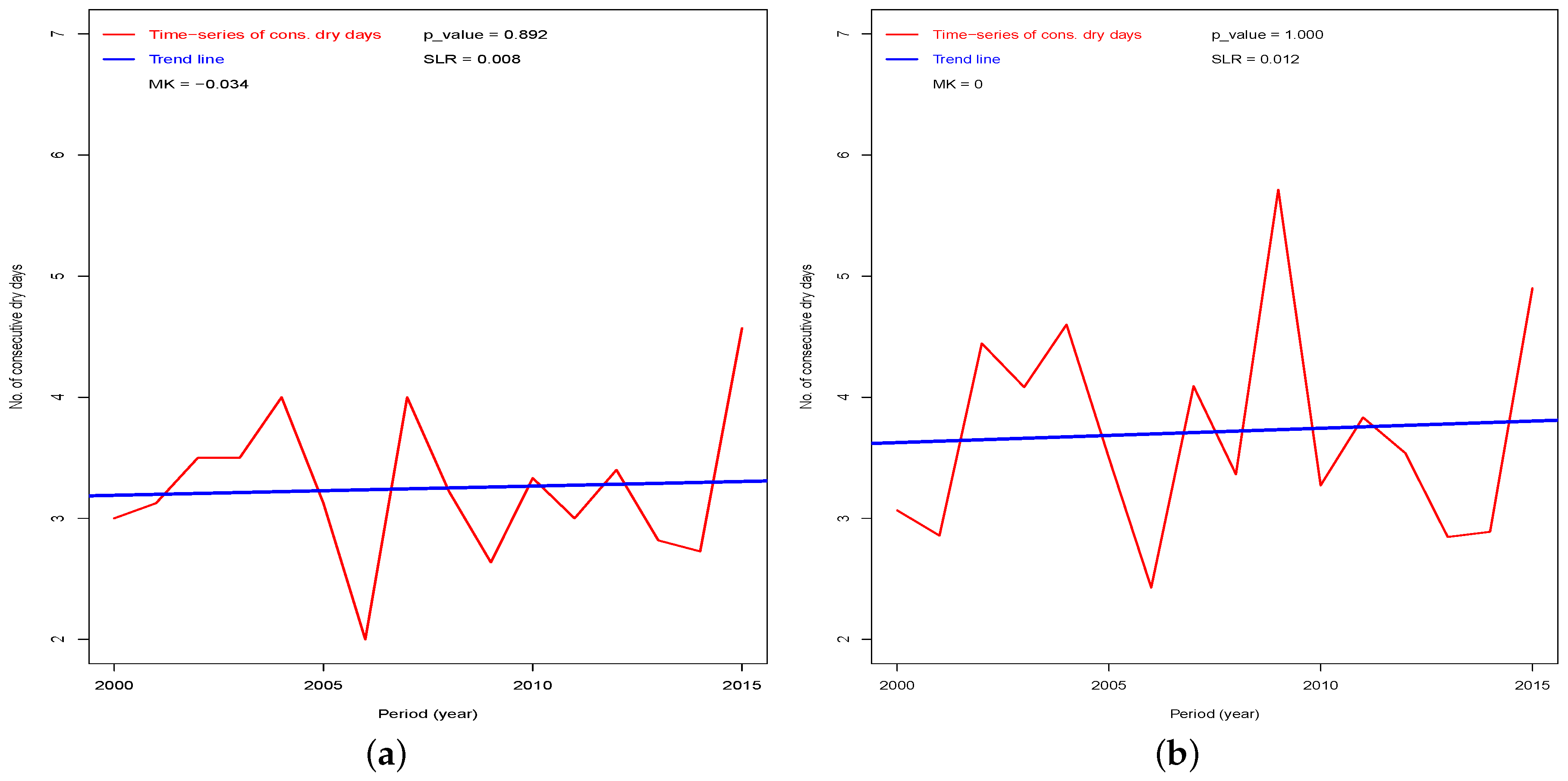
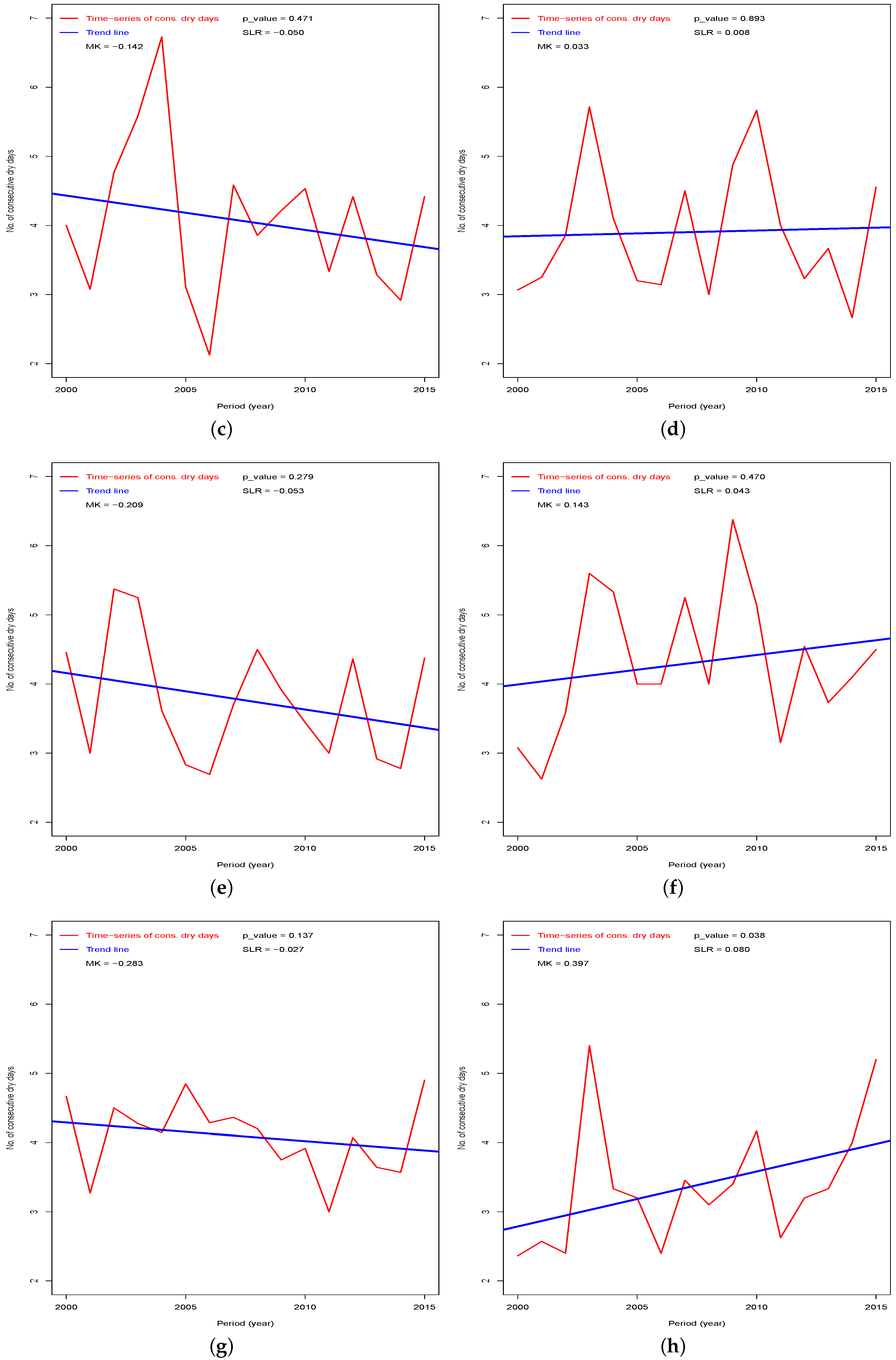
| Station | Rainfall Amount (mm) | Rainfall Days | Light Rain Days | Wet Days | ||||
|---|---|---|---|---|---|---|---|---|
| MAM (mm) | SON (mm) | MAM | SON | MAM | SON | MAM | SON | |
| Entebbe | 611 | 387 | 44 | 31 | 9 | 9 | 20 | 12 |
| Jinja | 443 | 446 | 33 | 36 | 8 | 10 | 14 | 14 |
| Kamenyamigo | 367 | 291 | 30 | 25 | 3 | 3 | 13 | 11 |
| Kituza | 564 | 583 | 42 | 43 | 2 | 3 | 18 | 18 |
| Makerere | 394 | 495 | 34 | 40 | 10 | 14 | 12 | 16 |
| Namulonge | 393 | 325 | 34 | 30 | 4 | 4 | 12 | 11 |
| Ntusi | 300 | 415 | 28 | 38 | 6 | 7 | 9 | 14 |
| Tororo | 692 | 557 | 45 | 44 | 9 | 10 | 20 | 17 |
| Average | 471 | 437 | 36 | 36 | 6 | 8 | 15 | 14 |
| Station | dk_01 | dk_02 | dk_03 | dk_04 | dk_05 | dk_06 | dk_07 | dk_08 | dk_09 |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | 0.88 | 0.95 | 0.79 * | 0.86 * | 0.87 * | 0.89 | 0.94 | 0.93 | 0.94 |
| Jinja | 0.89 | 0.90 | 0.90 | 0.85 * | 0.90 | 0.89 | 0.91 | 0.92 | 0.72 * |
| Kamenyamigo | 0.95 | 0.94 | 0.98 | 0.90 | 0.94 | 0.95 | 0.94 | 0.94 | 0.91 |
| Kituza | 0.86 * | 0.91 | 0.87 * | 0.93 | 0.86 * | 0.91 | 0.95 | 0.94 | 0.90 |
| Makerere | 0.85 * | 0.90 | 0.73 * | 0.91 | 0.88 * | 0.96 | 0.86 * | 0.97 | 0.85 * |
| Namulonge | 0.94 | 0.96 | 0.85 * | 0.95 | 0.99 | 0.85 * | 0.85 * | 0.74 * | 0.89 |
| Ntusi | 0.83 * | 0.83 * | 0.89 | 0.97 | 0.80 * | 0.78 * | 0.92 | 0.76 * | 0.82 * |
| Tororo | 0.90 | 0.89 | 0.88 * | 0.91 | 0.97 | 0.90 | 0.86 * | 0.94 | 0.92 |
| Station | dk_01 | dk_02 | dk_03 | dk_04 | dk_05 | dk_06 | dk_07 | dk_08 | dk_09 |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | 0.71 | 0.54 | 0.67 | 0.82 | 0.67 | 0.49 | 0.64 | 0.75 | 0.69 |
| Jinja | 0.65 | 0.66 | 0.61 | 0.57 | 0.82 | −0.57 | 0.50 | 0.91 | 0.66 |
| Kamenyamigo | 0.70 | 0.50 | 0.55 | 0.72 | 0.83 | 0.57 | 0.73 | 0.83 | 0.65 |
| Kituza | 0.67 | 0.74 | 0.72 | 0.52 | 0.60 | 0.22 | 0.70 | 0.91 | 0.60 |
| Makerere | 0.64 | 0.70 | 0.49 | 0.63 | 0.53 | 0.36 | 0.77 | 0.65 | 0.51 |
| Namulonge | 0.66 | 0.75 | 0.48 | 0.69 | 0.75 | 0.31 | 0.63 | 0.44 | 0.82 |
| Ntusi | 0.68 | 0.32 | 0.68 | 0.77 | 0.53 | 0.72 | 0.54 | 0.60 | 0.54 |
| Tororo | 0.32 | 0.74 | 0.69 | 0.67 | 0.26 | 0.37 | 0.21 | 0.63 | 0.35 |
| Average | 0.63 | 0.62 | 0.61 | 0.67 | 0.62 | 0.43 | 0.59 | 0.72 | 0.60 |
| Station | dk_01 | dk_02 | dk_03 | dk_04 | dk_05 | dk_06 | dk_07 | dk_08 | dk_09 |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | −0.219 | −0.518 | 0.330 | 0.054 | −0.087 | 0.037 | 0.559 | −0.221 | −0.044 |
| Jinja | −0.199 | −0.009 | 0.256 | −0.197 | −0.153 | 0.010 | 0.241 | −0.009 | −0.164 |
| Kamenyamigo | 0.159 | −0.107 | 0.179 | 0.223 | 0.113 | 0.161 | 0.452 | 0.322 | 0.183 |
| Kituza | 0.000 | −0.054 | 0.234 | 0.151 | 0.009 | −0.132 | 0.301 | −0.072 | 0.027 |
| Makerere | −0.067 | −0.127 | 0.299 | −0.009 | 0.019 | −0.073 | 0.251 | −0.052 | −0.009 |
| Namulonge | −0.235 | −0.284 | −0.080 | 0.093 | −0.328 | −0.071 | −0.337 | −0.286 | −0.279 |
| Ntusi | −0.081 | −0.311 | 0.000 | −0.139 | −0.097 | −0.135 | −0.366 | −0.063 | 0.000 |
| Tororo | −0.312 | −0.035 | 0.269 | 0.158 | 0.110 | −0.091 | 0.091 | 0.111 | 0.277 |
| Station | dk_01 | dk_02 | dk_03 | dk_04 | dk_05 | dk_06 | dk_07 | dk_08 | dk_09 |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | −0.019 | −0.086 | 0.295 | −0.124 | 0.219 | −0.162 | 0.333 | −0.067 | −0.159 |
| Jinja | −0.191 | −0.143 | 0.333 | −0.209 | 0.033 | −0.077 | 0.117 | 0.100 | −0.183 |
| Kamenyamigo | −0.135 | −0.295 | −0.033 | 0.253 | 0.165 | 0.077 | 0.641 | 0.077 | −0.271 |
| Kituza | −0.276 | 0.05 | 0.257 | −0.183 | 0.067 | −0.124 | 0.287 | −0.105 | 0.086 |
| Makerere | −0.219 | −0.083 | 0.167 | −0.150 | −0.067 | −0.219 | 0.283 | −0.057 | 0.133 |
| Namulonge | −0.387 | 0 | 0.050 | 0.105 | 0.029 | −0.143 | 0.055 | −0.066 | 0.165 |
| Ntusi | 0.153 | −0.096 | 0.221 | −0.086 | 0.086 | −0.121 | −0.390 | −0.048 | 0.209 |
| Tororo | −0.192 | −0.153 | 0.083 | 0.100 | 0.050 | −0.010 | 0.233 | 0.100 | −0.033 |
| Station | dk_01 | dk_02 | dk_03 | dk_04 | dk_05 | dk_06 | dk_07 | dk_08 | dk_09 |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | 0.154 | 0.238 | 0.162 | −0.010 | 0.257 | −0.219 | 0.317 | −0.200 | −0.067 |
| Jinja | −0.253 | −0.333 | 0.200 | −0.308 | −0.033 | −0.143 | 0.033 | −0.017 | −0.100 |
| Kamenyamigo | −0.364 | −0.390 | −0.205 | 0.265 | 0.077 | 0.205 | 0.179 | −0.026 | −0.244 |
| Kituza | −0.385 | −0.033 | 0.276 | −0.257 | 0.083 | −0.162 | −0.010 | −0.077 | 0.124 |
| Makerere | −0.238 | 0.033 | 0.150 | −0.183 | −0.117 | −0.314 | 0.067 | −0.121 | 0.117 |
| Namulonge | −0.319 | 0.183 | 0.150 | 0.319 | 0.276 | −0.077 | 0.282 | 0.055 | 0.308 |
| Ntusi | 0.087 | −0.077 | 0.243 | −0.162 | −0.124 | −0.143 | −0.314 | 0.077 | 0.143 |
| Tororo | −0.159 | −0.055 | 0 | 0.050 | 0.133 | −0.010 | 0.250 | −0.283 | −0.105 |
| Station | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | 8 Days | 9 Days | 10 Days+ |
|---|---|---|---|---|---|---|---|---|---|
| Entebbe | 68 | 34 | 19 | 11 | 2 | 3 | 1 | 2 | 3 |
| Jinja | 73 | 41 | 33 | 16 | 3 | 4 | 3 | 4 | 6 |
| Kamenyamigo | 75 | 42 | 38 | 16 | 12 | 3 | 9 | 2 | 12 |
| Kituza | 66 | 38 | 12 | 10 | 8 | 5 | 5 | 2 | 8 |
| Makerere | 74 | 38 | 17 | 12 | 8 | 4 | 5 | 3 | 6 |
| Namulonge | 66 | 27 | 23 | 14 | 9 | 3 | 4 | 2 | 15 |
| Ntusi | 64 | 42 | 31 | 24 | 8 | 10 | 2 | 5 | 11 |
| Tororo | 76 | 41 | 21 | 10 | 7 | 9 | 0 | 1 | 7 |
| Average | 70 | 38 | 24 | 14 | 7 | 5 | 4 | 3 | 9 |
| Station | dk_3 | dk_7 | MAM |
|---|---|---|---|
| Entebbe | 0.371 * | 0.502 ** | 0.036 |
| Jinja | 0.275 | 0.178 | −0.269 |
| Kamenyamigo | −0.011 | 0.472 ** | 0.168 |
| Kituza | 0.389 * | 0.259 | 0.184 |
| Makerere | 0.364 * | 0.179 | −0.009 |
| Namulonge | 0.182 | 0.228 | 0.052 |
| Ntusi | 0.225 | −0.254 | −0.127 |
| Tororo | −0.084 | 0.227 | −0.157 |
| Average | 0.363 * | 0.429 ** | 0.209 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mugume, I.; Mesquita, M.D.S.; Basalirwa, C.; Bamutaze, Y.; Reuder, J.; Nimusiima, A.; Waiswa, D.; Mujuni, G.; Tao, S.; Jacob Ngailo, T. Patterns of Dekadal Rainfall Variation Over a Selected Region in Lake Victoria Basin, Uganda. Atmosphere 2016, 7, 150. https://doi.org/10.3390/atmos7110150
Mugume I, Mesquita MDS, Basalirwa C, Bamutaze Y, Reuder J, Nimusiima A, Waiswa D, Mujuni G, Tao S, Jacob Ngailo T. Patterns of Dekadal Rainfall Variation Over a Selected Region in Lake Victoria Basin, Uganda. Atmosphere. 2016; 7(11):150. https://doi.org/10.3390/atmos7110150
Chicago/Turabian StyleMugume, Isaac, Michel D. S. Mesquita, Charles Basalirwa, Yazidhi Bamutaze, Joachim Reuder, Alex Nimusiima, Daniel Waiswa, Godfrey Mujuni, Sulin Tao, and Triphonia Jacob Ngailo. 2016. "Patterns of Dekadal Rainfall Variation Over a Selected Region in Lake Victoria Basin, Uganda" Atmosphere 7, no. 11: 150. https://doi.org/10.3390/atmos7110150
APA StyleMugume, I., Mesquita, M. D. S., Basalirwa, C., Bamutaze, Y., Reuder, J., Nimusiima, A., Waiswa, D., Mujuni, G., Tao, S., & Jacob Ngailo, T. (2016). Patterns of Dekadal Rainfall Variation Over a Selected Region in Lake Victoria Basin, Uganda. Atmosphere, 7(11), 150. https://doi.org/10.3390/atmos7110150







