Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation
Abstract
:1. Introduction
2. The Adaptive in Time and Space Estimation Technique (ATS)
2.1. Definition of the Time Domain
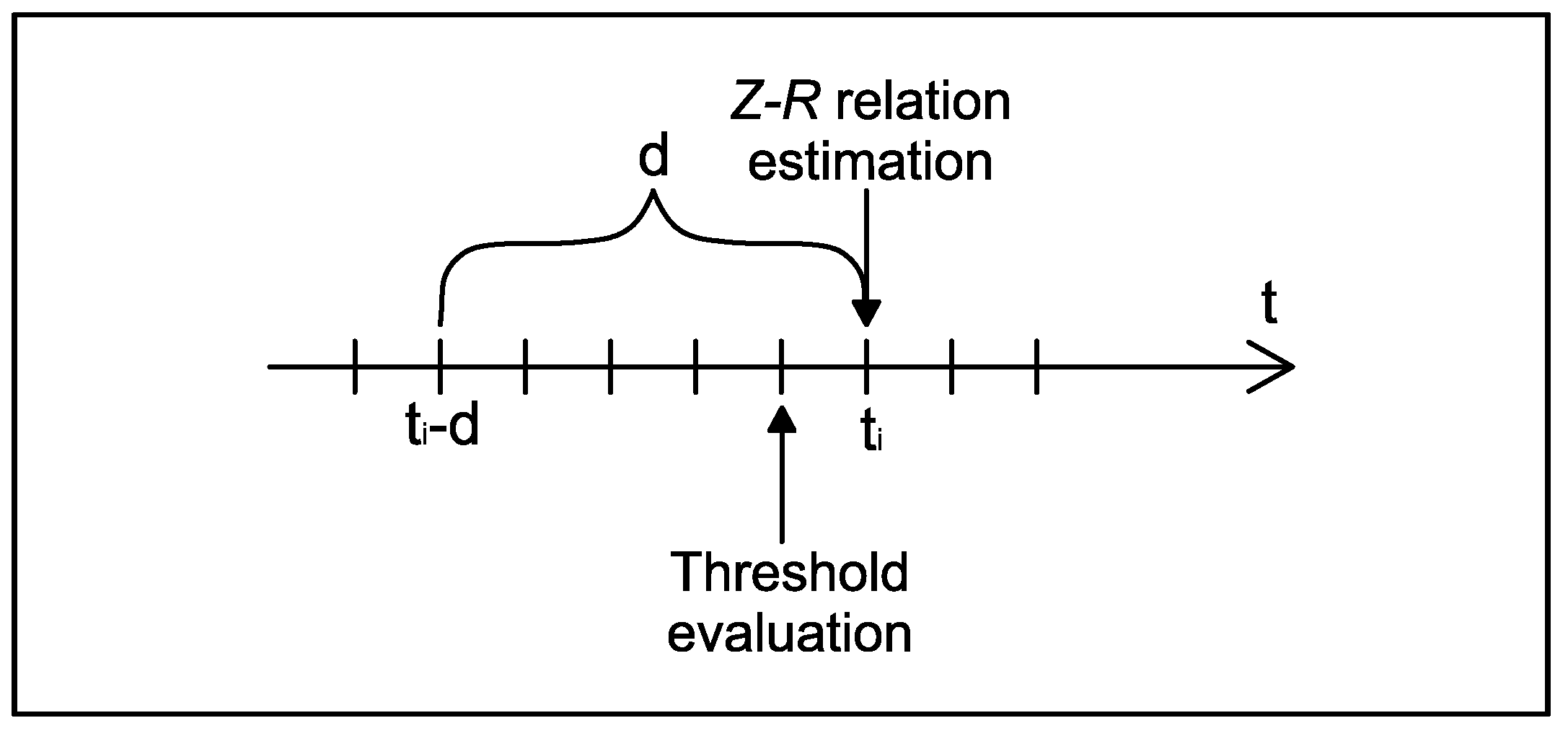
2.2. Definition of the Spatial Domains and Parameters Estimation
2.3. Calibration Procedure
3. Application
3.1. Case Study
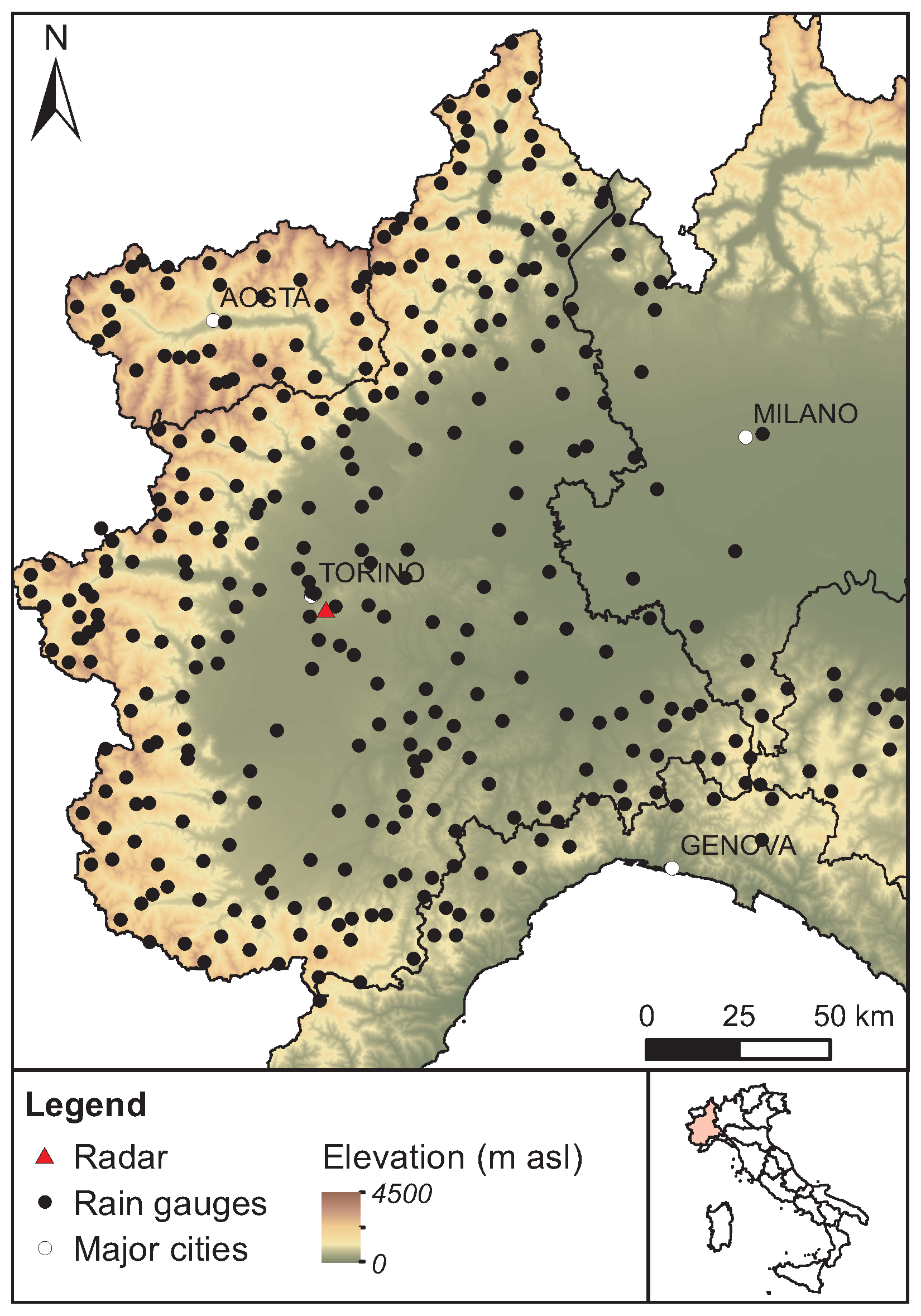
3.2. Definition of the Set of Events and Estimation of the Static Coefficients
| ID | Convective events | ID | Stratiform events |
|---|---|---|---|
| 1 | 27/07/2003 | 9 | 31/10-01/11/2003 |
| 2 | 02/08/2005 | 10 | 25/10-02/11/2004 |
| 3 | 20/08/2005 | 11 | 15/04-17/04/2004 |
| 4 | 06/07/2006 | 12 | 06/09-12/09/2005 |
| 5 | 12/07/2006 | 13 | 14/09-15/09/2006 |
| 6 | 08/08/2007 | 14 | 01/05-04/05/2007 |
| 7 | 30/08/2007 | 15 | 25/05-28/05/2007 |
| 8 | 29/05/2008 | 16 | 28/10-06/11/2008 |
| 17 | 01/12-04/12/2003 | ||
| 18 | 16/12-17/12/2008 |
| Event | ninv | Event | ninv |
|---|---|---|---|
| 1 | 0.254 | 9 | 0.001 |
| 2 | 0.003 | 10 | 0.004 |
| 3 | 0.003 | 11 | 0.005 |
| 4 | 0.004 | 12 | 0.051 |
| 5 | 0.003 | 13 | 0.003 |
| 6 | 0.461 | 14 | 0.003 |
| 7 | 0.002 | 15 | 0.073 |
| 8 | 0.050 | 16 | 0.011 |
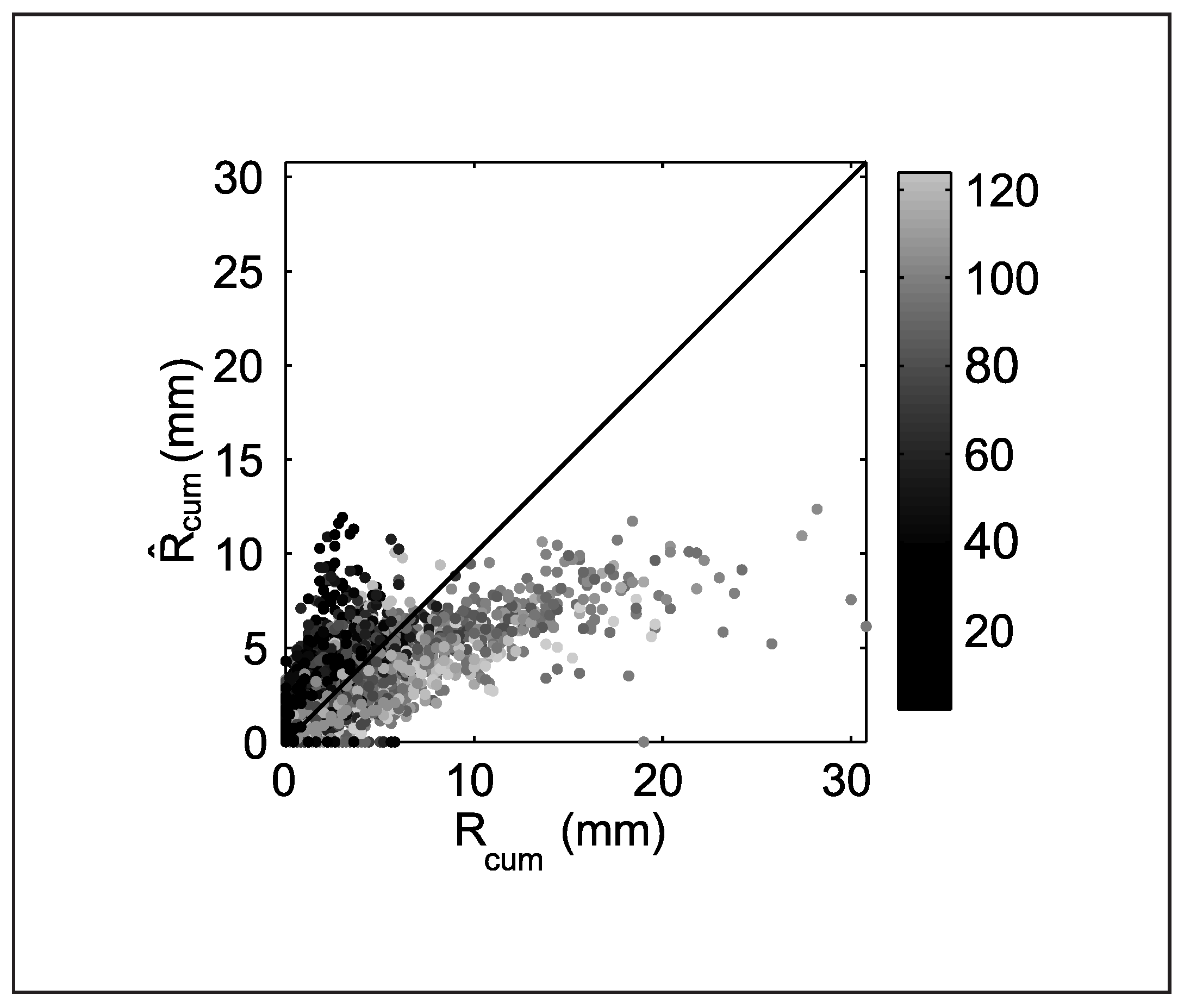
3.3. Calibration of the ATS Technique
| Event | Mean (dbZ) | Std (dbZ) | Event | Mean (dbZ) | Std (dbZ) |
|---|---|---|---|---|---|
| 1 | −2.06 | 6.51 | 9 | 20.94 | 6.96 |
| 2 | 14.94 | 7.52 | 10 | 11.77 | 10.74 |
| 3 | 9.55 | 10.70 | 11 | 11.88 | 9.85 |
| 4 | 5.17 | 11.51 | 12 | 5.59 | 9.55 |
| 5 | 2.16 | 8.66 | 13 | 16.73 | 7.99 |
| 6 | 2.58 | 9.97 | 14 | 9.78 | 10.38 |
| 7 | 4.45 | 9.54 | 15 | 9.71 | 8.36 |
| 8 | 19.73 | 8.17 | 16 | 17.70 | 6.30 |
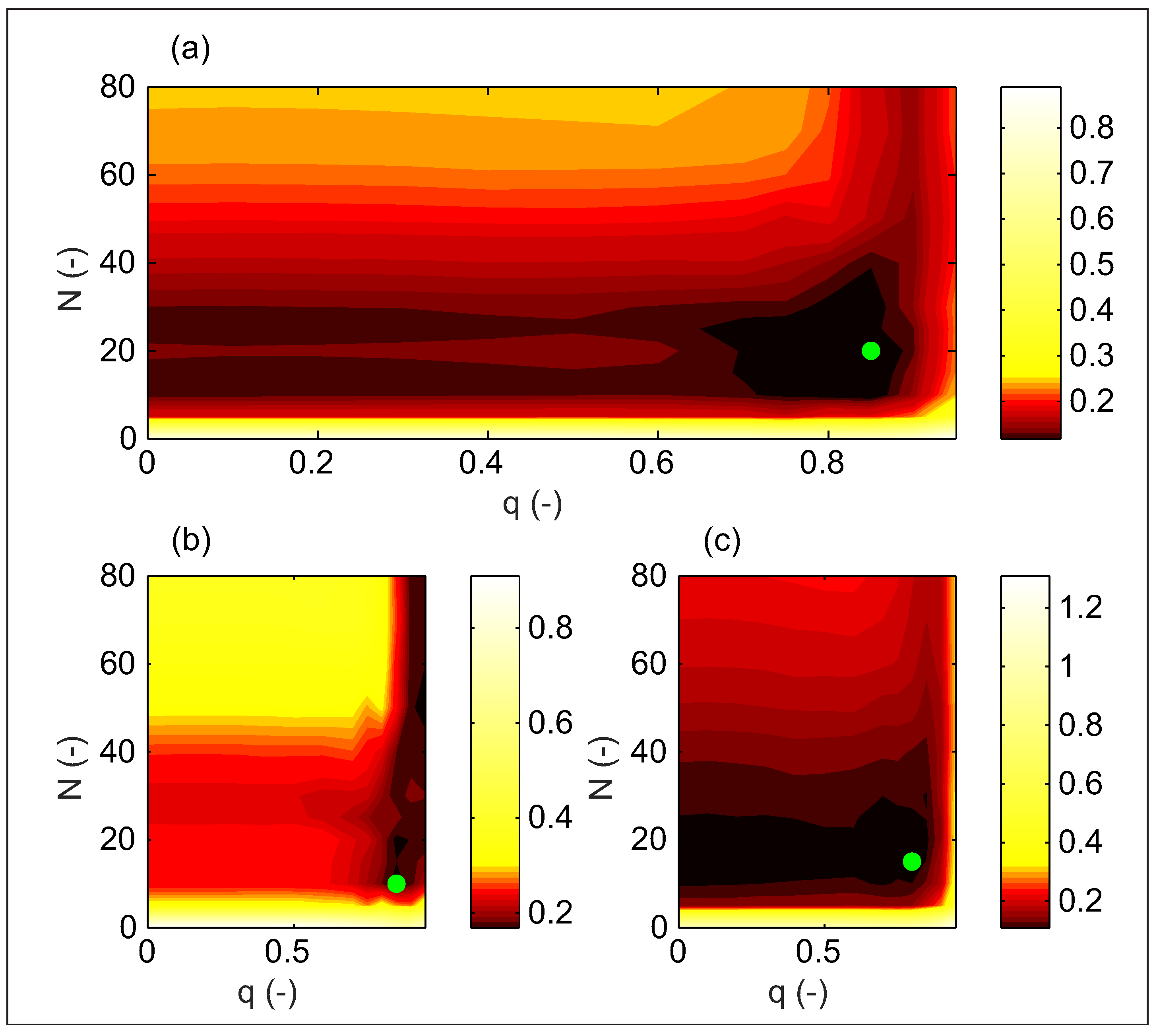
4. Results and Discussion
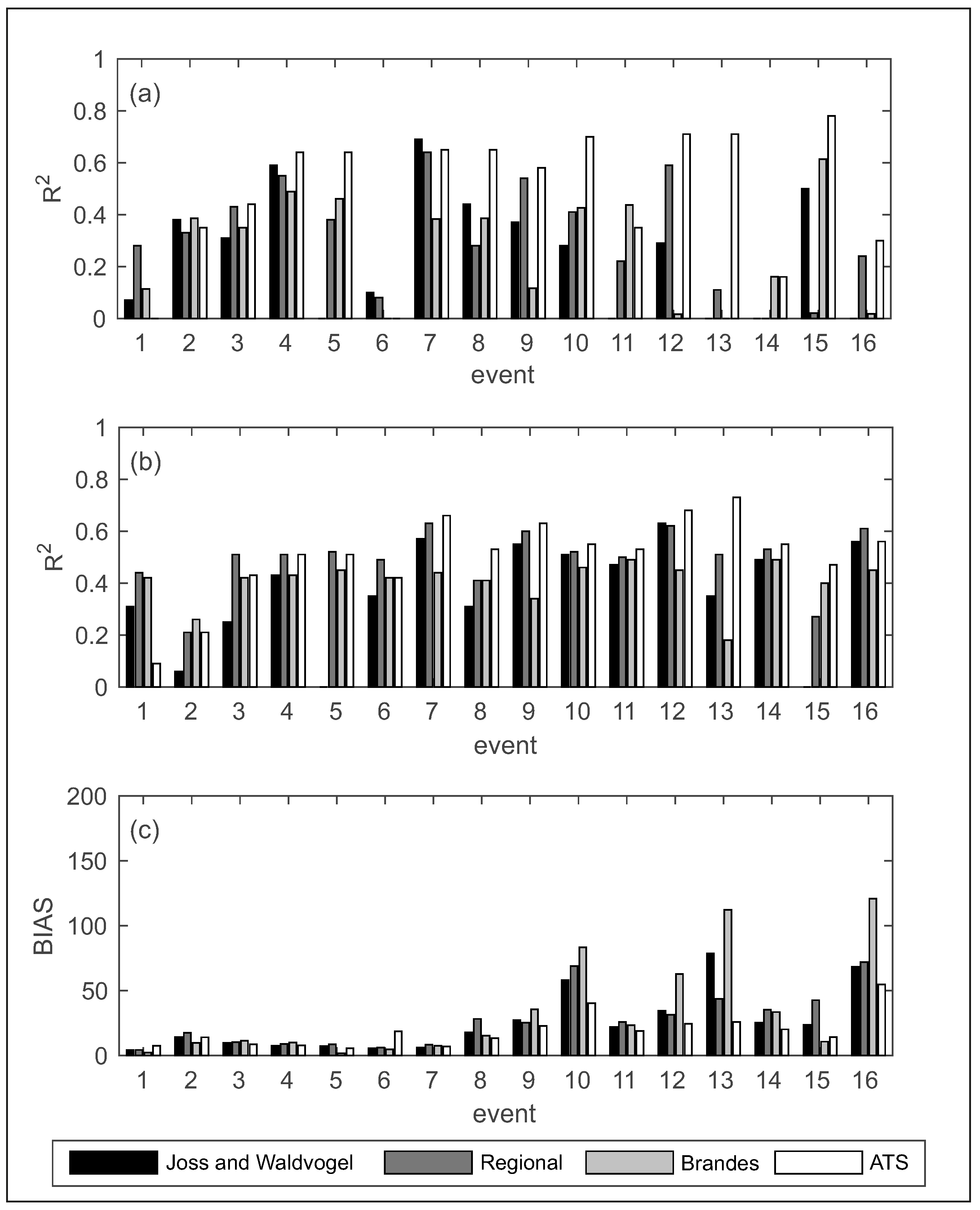

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
A. Determination of a regional Z-R static relationship

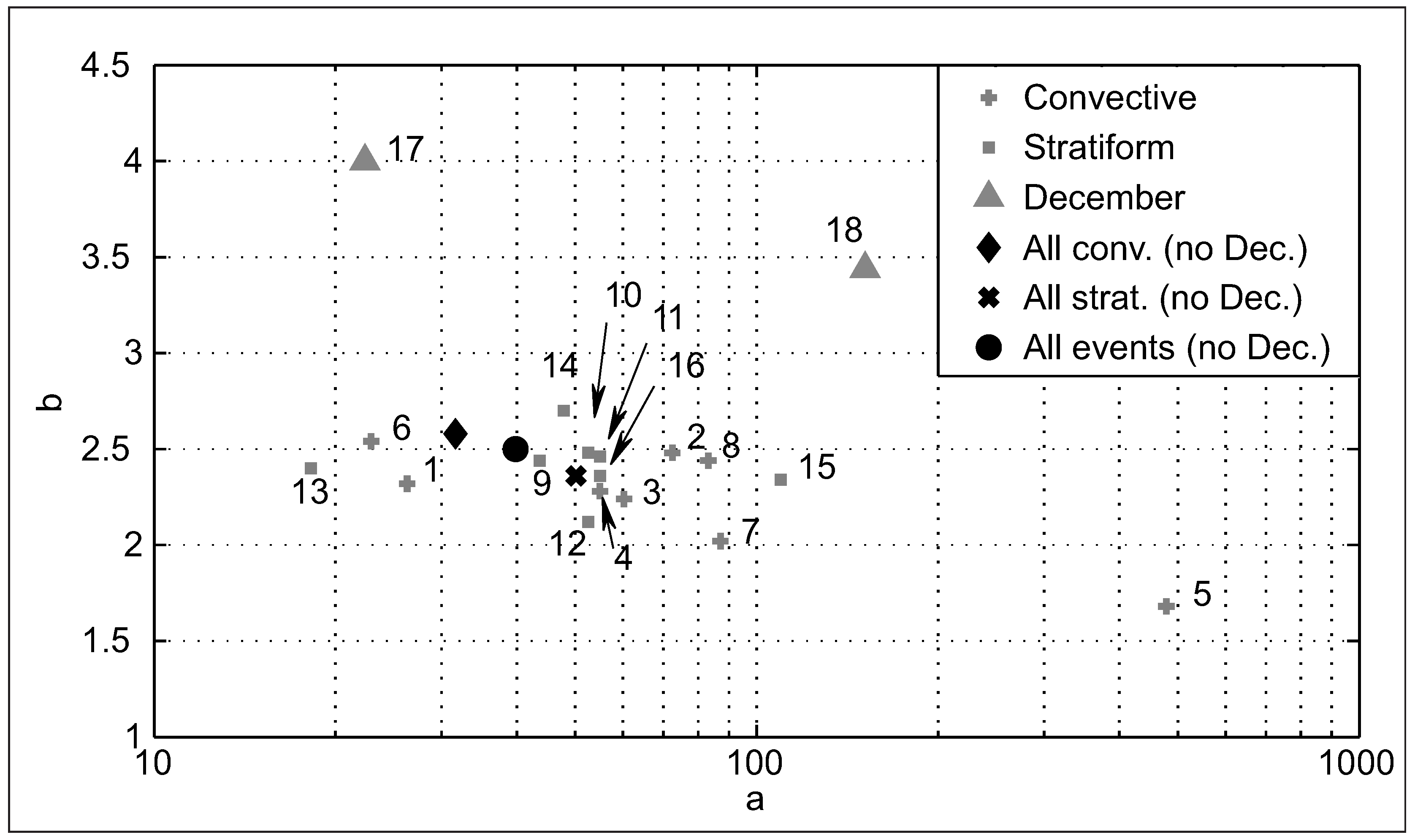
References
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Metorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Joss, J.; Waldwogel, A. A method to improve the accuracy of radar-measured amounts of precipitation. In Proceedings of 14th Conference of Radar Meteorology, Tucson, AZ, USA, 17–20 November 1970; pp. 237–238.
- Battan, L. Radar Observation of the Atmosphere; University of Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Raghavan, S.S. Radar Metorology; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Doviak, R.J.; Zrnic, D.S. Doppler Radar and Weather Observations, 2 ed.; Dover Publication: Dover, UK, 2006. [Google Scholar]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol. 1996, 35, 355–371. [Google Scholar] [CrossRef]
- Bringi, V.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Smith, J.A.; Krajewski, W.F. A modeling study of rainfall rate-reflectivity relationships. Water Resour. Res. 1993, 29, 2505–2514. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I. Variability of drop size distributions: Time-scale dependence of the variability and its effects on rain estimation. J. Appl. Meteorol. 2005, 44, 241–255. [Google Scholar] [CrossRef]
- Chapon, B.; Delrieu, G.; Gosset, M.; Boudevillain, B. Variability of rain drop size distribution and its effect on the Z-R relationship: A case study for intense Mediterranean rainfall. Atmos. Res. 2008, 87, 52–56. [Google Scholar]
- Cremonini, R.; Bechini, R. Heavy rainfall monitoring by polarimetric C-Band weather radars. Water 2010, 2, 838–848. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Villarini, G.; Smith, J.A. RADAR-rainfall uncertainties where are we after thirty years of effort? Bull. Amer. Meteor. Soc. 2010, 91, 87–94. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F. Radar-rain gauge comparisons under observational uncertainties. J. Appl. Meteorol. 1999, 38, 1519–1525. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F. Real-time radar rainfall estimation. Part I: Algorithm formulation. J. Atmos. Ocean. Technol. 1999, 16, 189–197. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F. Real-time radar rainfall estimation. Part II: Algorithm formulation. J. Atmos. Ocean. Technol. 1999, 16, 198–205. [Google Scholar] [CrossRef]
- Borga, M.; Anagnostou, E.N.; Frank, E. On the use of real-time radar rainfall estimates for flood prediction in mountainous basins. J. Geophys. Res.: Atmos. 2000, 105, 2269–2280. [Google Scholar] [CrossRef]
- Wood, S.; Jones, D.; Moore, R. Static and dynamic calibration of radar data for hydrological use. Hydrol. Earth Syst. Sci. Discuss. 2000, 4, 545–554. [Google Scholar] [CrossRef]
- Vieux, B.E.; Rendon, S.H. Derivation and Evaluation of Seasonally Specific Z-R Relationships; Final Report; South Florida Water Management District: West Palm Beach, FL, USA, 2009. [Google Scholar]
- Rendon, S.; Vieux, B.; Pathak, C. Estimation of regionally specific Z-R relationships for radar-based hydrologic prediction. In Proceedings of the World Environmental and Water Resources Congress, Providence, RI, USA, 16–20 May 2010; pp. 4668–4680.
- Pathak, C.; Teegavarapu, R. Utility of optimal reflectivity-rain rate (Z-R) relationships for improved precipitation estimates. In Proceedings of the World Environmental and Water Resources Congress, Providence, RI, USA, 16–20 May 2010; pp. 4681–4691.
- Seo, D.-J.; Breidenbacha, J.P.; Johnsonb, E.R. Real-time estimation of mean field bias in radar rainfall data. J. Hydrol. 1999, 223, 131–147. [Google Scholar] [CrossRef]
- Legates, D.R. Real-time calibration of radar precipitation estimates. Prof. Geogr. 2000, 52, 235–246. [Google Scholar] [CrossRef]
- Seo, D.J.; Breidenbach, J. Real-time correction of spatially nonuniform bias in radar rainfall data using rain gauge measurements. J. Hydrometeorol. 2002, 3, 93–111. [Google Scholar] [CrossRef]
- Rendon, S.; Vieux, B.; Pathak, C. Continuous forecasting and evaluation of derived Z-R relationships in a sparse rain gauge network using NEXRAD. J. Hydrol. Eng. 2013, 18, 175–182. [Google Scholar] [CrossRef]
- Brandes, E.A. Optimizing rainfall estimates with the aid of radar. J. Appl. Meteorol. 1975, 14, 1339–1345. [Google Scholar] [CrossRef]
- Nanding, N.; Rico-Ramirez, M.A.; Han, D. Comparison of different radar-raingauge rainfall merging techniques. J. Hydro. 2015, 17, 422–445. [Google Scholar] [CrossRef]
- Yufa, W.; Cuihong, W.; Hongxiang, J. Real-time synchronous integration of radar and raingauge measurements based on the quasi same-rain-volume sampling. Acta Meteor. Sinica 2010, 24, 340–353. [Google Scholar]
- Alfieri, L.; Claps, P.; Laio, F. Time-dependent ZR relationships for estimating rainfall fields from radar measurements. Nat. Hazard. Earth Syst. Sci. 2010, 10, 149–158. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Ding, Y. Improvement of radar quantitative precipitation estimation based on real-time adjustments to Z-R relationships and inverse distance weighting correction schemes. Adv. Atmos. Sci. 2012, 29, 575–584. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Jaime Gómez-Hernández, J. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar] [CrossRef]
- Pereira, F.; Augusto, J. Improving WSR-88D hourly rainfall estimates. Weather Forecast. 1998, 13, 1016–1028. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Chumchean, S.; Sharma, A.; Seed, A. An integrated approach to error correction for real-time radar-rainfall estimation. J. Atmos. Ocean. Technol. 2006, 23, 67–79. [Google Scholar] [CrossRef]
- Bruen, M.; O’Loughlin, F. Towards a nonlinear radar-gauge adjustment of radar via a piece-wise method. Meteorol. Appl. 2014, 21, 675–683. [Google Scholar] [CrossRef]
- Caracciolo, C.; Porcu, F.; Prodi, F. Precipitation classification at mid-latitudes in terms of drop size distribution parameters. Adv. Geosci. 2008, 16, 11–17. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Davini, P.; Bechini, R.; Cremonini, R.; Cassardo, C. Radar-based analysis of convective storms over Northwestern Italy. Atmosphere 2011, 3, 33–58. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.F.; Kruger, A. Sampling errors of tipping-bucket rain gauge measurements. J. Hydrol. Eng. 2001, 6, 159–166. [Google Scholar] [CrossRef]
- Ciach, G.J. Local random errors in tipping-bucket rain gauge measurements. J. Atmos. Ocean. Technol. 2003, 20, 752–759. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Libertino, A.; Allamano, P.; Claps, P.; Cremonini, R.; Laio, F. Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation. Atmosphere 2015, 6, 1559-1577. https://doi.org/10.3390/atmos6101559
Libertino A, Allamano P, Claps P, Cremonini R, Laio F. Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation. Atmosphere. 2015; 6(10):1559-1577. https://doi.org/10.3390/atmos6101559
Chicago/Turabian StyleLibertino, Andrea, Paola Allamano, Pierluigi Claps, Roberto Cremonini, and Francesco Laio. 2015. "Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation" Atmosphere 6, no. 10: 1559-1577. https://doi.org/10.3390/atmos6101559
APA StyleLibertino, A., Allamano, P., Claps, P., Cremonini, R., & Laio, F. (2015). Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation. Atmosphere, 6(10), 1559-1577. https://doi.org/10.3390/atmos6101559





