Vertical and Horizontal Polarization Observations of Slowly Varying Solar Emissions from Operational Swiss Weather Radars
Abstract
:1. Introduction
2. Operational Observations of Solar Spectral Power at the Antenna Feed
3. Description of Acquired Data and Instruments
4. Results and Discussion
4.1. Choice of the Reference Solar Signal and Scores for the Assessment of the Agreement
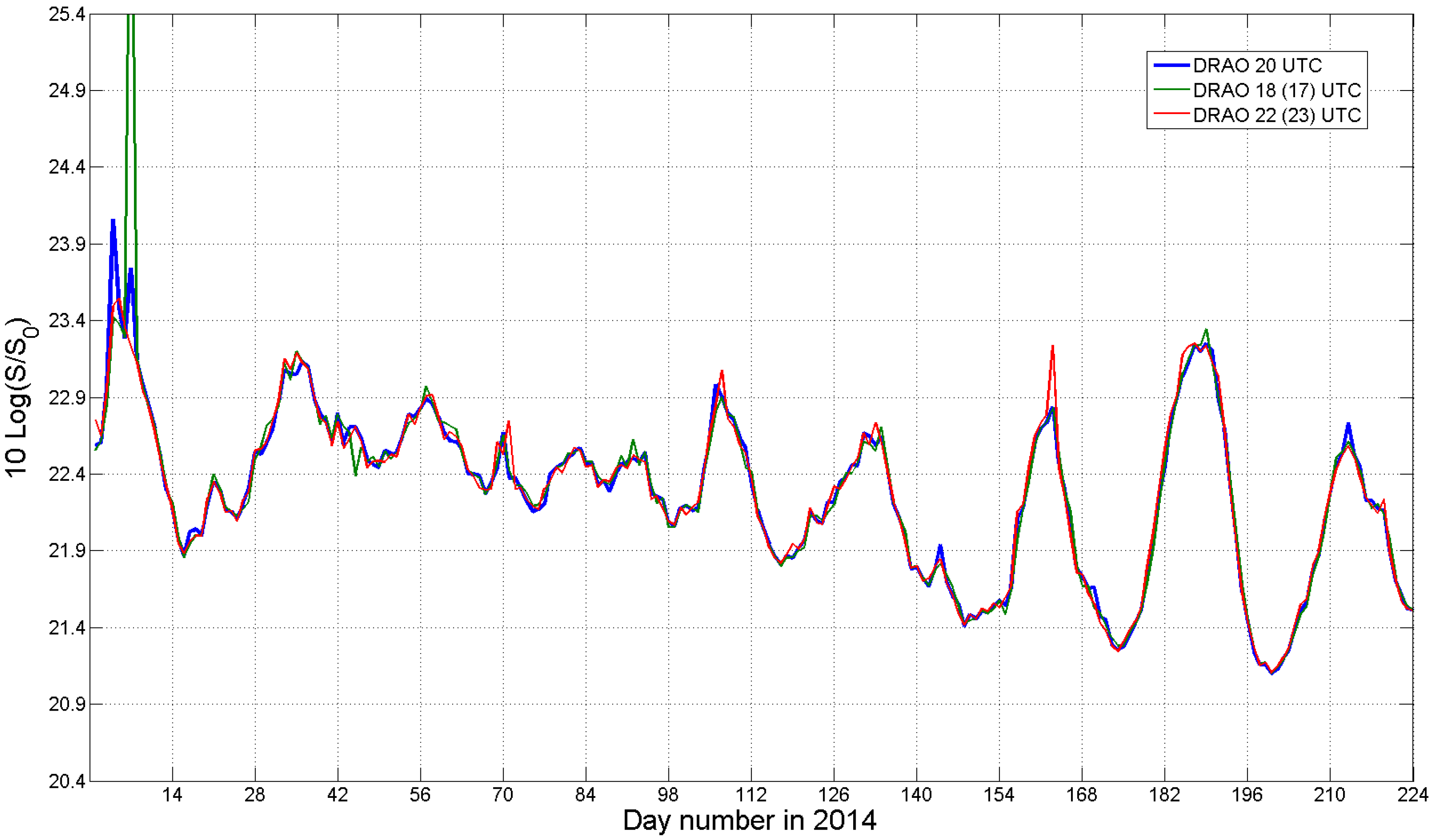
| DRAO 20 UTC | DRAO 18 (17) UTC | DRAO 22 (23) UTC | |
|---|---|---|---|
| DRAO 20 UTC | 0 dB | 0.041 dB | 0.044 dB |
| DRAO 18 (17) UTC | 0.040 dB | 0 dB | 0.056 dB |
| DRAO 22 (23) UTC | 0.044 dB | 0.057 dB | 0 dB |
4.2. Results of the Daily Online Analysis (Horizontal Polarization)
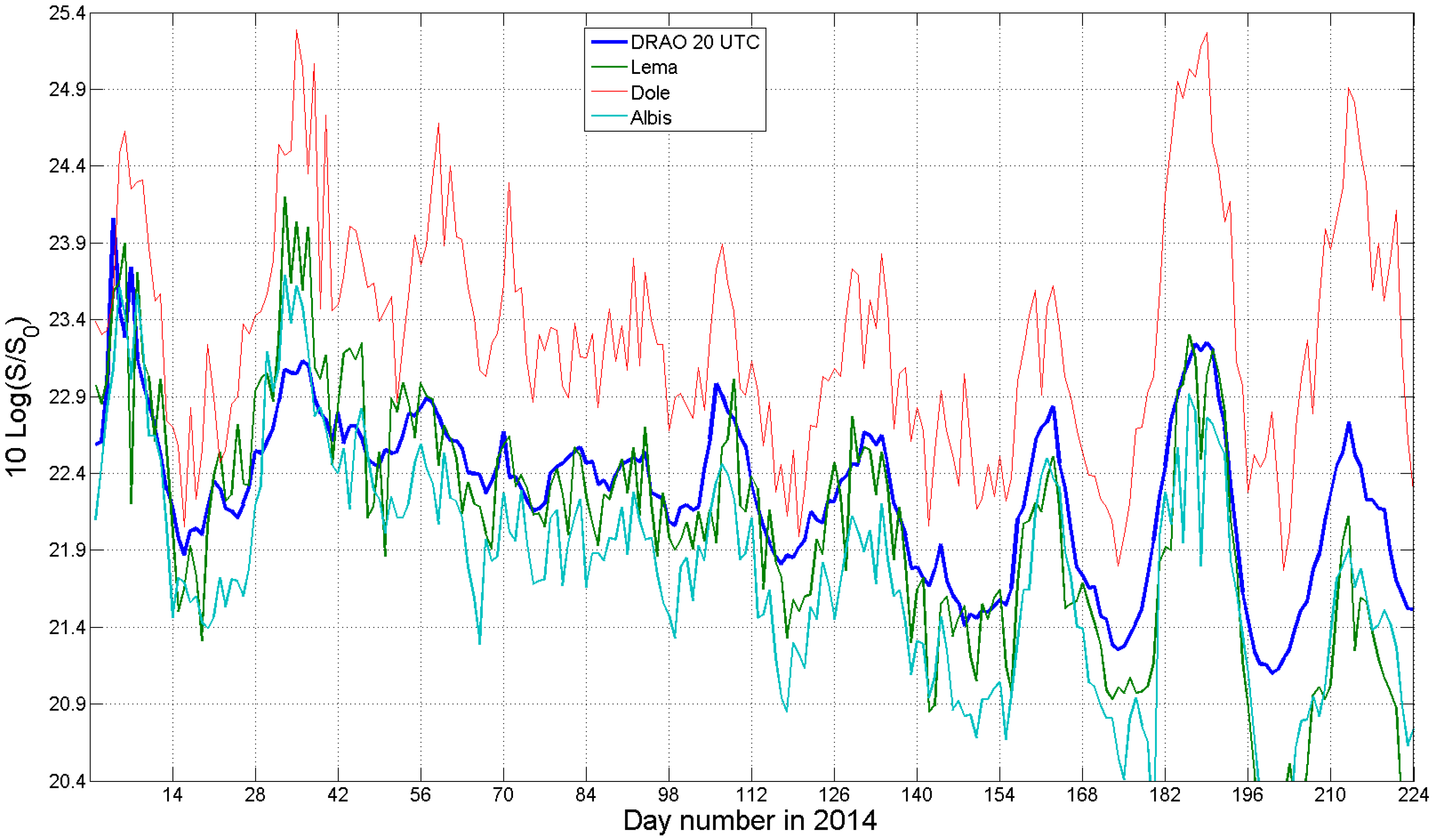
| Albis Radar | Lema Radar | Dole Radar | |
|---|---|---|---|
| Explained variance in % | 83% | 74% | 62% |
| Scatter in dB | 0.28 dB | 0.42 dB | 0.44 dB |
| Standard deviation in dB | 0.35 dB | 0.48 dB | 0.48 dB |
4.3. Improvement Obtained When the Random Error Component That Affects Radar Estimates Is Smoothed
| Albis Radar | Lema Radar | Dole Radar | |
|---|---|---|---|
| Explained variance in % | 88% | 80% | 66% |
| Scatter in dB | 0.05 dB | 0.07 dB | 0.07 dB |
| Standard deviation in dB | 0.29 dB | 0.41 dB | 0.43 dB |
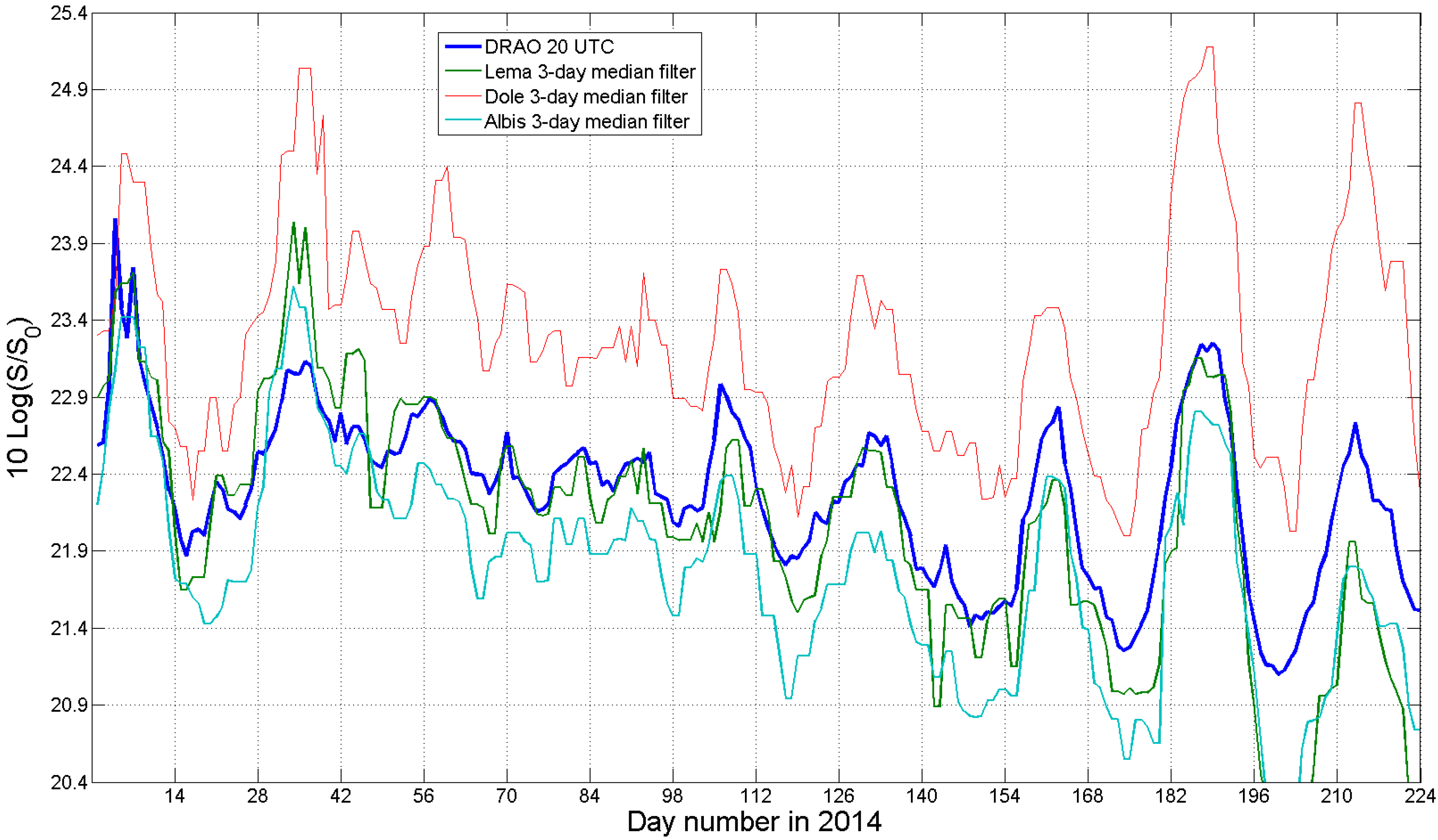
4.4. Operational Monitoring of Radar Differential Reflectivity Using the Sun
| Albis Radar | Lema Radar | Dole Radar | |
|---|---|---|---|
| Number of median daily values used | 220 | 204 | 203 |
| Median value in dB | −0.65 dB | 0.17 dB | −0.40 dB |
| Average value in dB | −0.66 dB | 0.18 dB | −0.40 dB |
| Standard deviation in dB | 0.05 dB | 0.06 dB | 0.06 dB |
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huuskonen, A.; Holleman, I. Determining weather radar antenna pointing using signals detected from the Sun at low antenna elevations. J. Atmos. Oceanic Technol. 2007, 24, 476–483. [Google Scholar] [CrossRef]
- Holleman, I.; Huuskonen, A.; Kurri, M.; Beekhuis, H. Operational monitoring of weather radar receiving chain using the Sun. J. Atmos. Oceanic Technol. 2010, 27, 159–166. [Google Scholar] [CrossRef]
- Holleman, I.; Huuskonen, A.; Gill, R.; Tabary, P. Operational monitoring of radar differential reflectivity using the Sun. J. Atmos. Oceanic Technol. 2010, 27, 881–887. [Google Scholar] [CrossRef]
- Huuskonen, A.; Kurri, M.; Hohti, H.; Beekhuis, H.; Leijnse, H.; Holleman, I. Radar performance monitoring using the angular width of the solar image. J. Atmos. Oceanic Technol. 2014, 31, 1704–1712. [Google Scholar] [CrossRef]
- Gabella, M.; Sartori, M.; Progin, O.; Germann, U.; Boscacci, M. An innovative instrumentation for checking electromagnetic performances of operational meteorological radar. In Proceedings of the Sixth European Conference on Radar in Meteorology and Hydrology (ERAD2010), Sibiu, Romania, 6–10 September 2010; pp. 263–269.
- Gabella, M.; Sartori, M.; Progin, O.; Germann, U. Acceptance tests and monitoring of the next generation polarimetric weather radar network in Switzerland. In Proceedings of the 2013 International Conference on Electromagnetics in Advanced Applications (ICEAA), Torino, Italy, 9–13 September 2013. ISBN: 978-1-4673-5678-9.
- Vollbracht, D.; Sartori, M.; Gabella, M. Absolute dual-polarization radar calibration: Temperature dependence and stability with focus on antenna-mounted receivers and noise source-generated reference signal. In Proceedings of the 8th European Conference on Radar in Meteorology and Hydrology (ERAD2014), Garmisch-Partenkirchen, Germany, 1–5 September 2014; pp. 91–102.
- Tapping, K. Antenna Calibration Using the 10.7 cm Solar Flux. Available online: http://www.k5so.com/RadCal_Paper.pdf (accessed on 25 September 2014).
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M.; Gabella, M. Quantitative precipitation estimation in the Alps: where do we stand? In Proceedings of the Third European Conference on Radar in Meteorology and Hydrology (ERAD2004), Visby, Sweden, 6–10 September 2004; pp. 2–6.
- Ryzhkov, A.V.; Giangrande, S.E.; Melnikov, V.M.; Schuur, T.J. Calibration issues of dual-polarization radar measurements. J. Atmos. Oceanic Technol. 2005, 22, 1138–1155. [Google Scholar] [CrossRef]
- Pratte, J.F.; Ferraro, D.G. Automated solar gain calibration. In Proceedings of the 24th Conference on Radar Meteorology, Tallahassee, FL, USA, 27–31 March 1989; pp. 619–622.
- Illingworth, A. Improved precipitation rates and data quality by using polarimetric measurements. In Advanced Applications of Weather Radar; Meischner, P., Ed.; Springer Verlag: Heidelberg, Germany, 2004; Chapter 5; pp. 130–166. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabella, M.; Sartori, M.; Boscacci, M.; Germann, U. Vertical and Horizontal Polarization Observations of Slowly Varying Solar Emissions from Operational Swiss Weather Radars. Atmosphere 2015, 6, 50-59. https://doi.org/10.3390/atmos6010050
Gabella M, Sartori M, Boscacci M, Germann U. Vertical and Horizontal Polarization Observations of Slowly Varying Solar Emissions from Operational Swiss Weather Radars. Atmosphere. 2015; 6(1):50-59. https://doi.org/10.3390/atmos6010050
Chicago/Turabian StyleGabella, Marco, Maurizio Sartori, Marco Boscacci, and Urs Germann. 2015. "Vertical and Horizontal Polarization Observations of Slowly Varying Solar Emissions from Operational Swiss Weather Radars" Atmosphere 6, no. 1: 50-59. https://doi.org/10.3390/atmos6010050
APA StyleGabella, M., Sartori, M., Boscacci, M., & Germann, U. (2015). Vertical and Horizontal Polarization Observations of Slowly Varying Solar Emissions from Operational Swiss Weather Radars. Atmosphere, 6(1), 50-59. https://doi.org/10.3390/atmos6010050






