Abstract
The Weather Research and Forecasting (WRF) model is used to investigate choice of land surface model (LSM) on the near surface wind profile, including heights reached by multi-megawatt (MW) wind turbines. Simulations of wind profiles and surface energy fluxes were made using five LSMs of varying degrees of sophistication in dealing with soil–plant–atmosphere feedbacks for the Department of Energy (DOE) Southern Great Plains (SGP) Atmospheric Radiation Measurement Program (ARM) Central Facility in Oklahoma, USA. Surface flux and wind profile measurements were available for validation. WRF was run for three, two-week periods covering varying canopy and meteorological conditions. The LSMs predicted a wide range of energy flux and wind shear magnitudes even during the cool autumn period when we expected less variability. Simulations of energy fluxes varied in accuracy by model sophistication, whereby LSMs with very simple or no soil–plant–atmosphere feedbacks were the least accurate; however, the most complex models did not consistently produce more accurate results. Errors in wind shear were also sensitive to LSM choice and were partially related to energy flux accuracy. The variability of LSM performance was relatively high suggesting that LSM representation of energy fluxes in WRF remains a large source of model uncertainty for simulating wind turbine inflow conditions.
Keywords:
WRF; land surface model; Southern Great Plains; ARM; surface energy fluxes; lidar; wind energy; wind shear 1. Introduction
Atmospheric models are not perfect predictors of incoming wind conditions or “inflow” at heights spanned by industrial-scale wind turbines (~40 to 200 m above ground level, a.g.l.). One way to optimize model accuracy is to identify areas in numerical models that may lead to a wind forecasting improvement. This is a warranted endeavor, as a wind forecasting improvement of as little as 10%–20% could result in hundreds of millions of dollars ($140M–$260M) in annual operating cost savings for the U.S. wind industry [1]. One candidate for optimization is the user’s choice of land surface model (LSM) employed in numerical weather prediction models. The LSM controls the exchange of energy between the surface and the atmosphere and may have a large effect on inflow in the lower boundary layer. We hypothesize that wind speeds simulated at heights equivalent to a turbine rotor disk are sensitive to LSM choice due to variations in the sophistication of each model’s characterization or parameterization of the soil–vegetation–atmosphere continuum. In this work, this theory is tested for northern Oklahoma using the Weather Research and Forecasting (WRF) model [2].
Oklahoma is currently ranked 6th in the nation for total megawatts installed (over 3300 MW) and is one of the leading states for percentage of electricity provided by wind (nearly 15%) [3]. As such, the Department of Energy (DOE) Southern Great Plains (SGP) Atmospheric Radiation Measurement Program (ARM) Central Facility in northern Oklahoma in recent years has become an ideal location for conducting wind energy research. Moreover, in 2013, a multi-MW wind farm began operation just to the west of the ARM Central Facility. At present, this farm has 140 General Electric (GE) 1.68 MW turbines, each with a hub-height of 80 m, and rotor diameter of 82.5 m. Each turbine blade tip has a minimum height of 39 m and a maximum height of 121 m and is located well within the lower PBL. The farm rotor diameters are typical of the average size (89 m) installed at present in the U.S. [4].
WRF is heavily utilized in the atmospheric community for weather prediction and more recently for wind forecasting, including its use in predicting hub-height wind speed and direction in the wind power industry. WRF has many physics options that are user defined, including options for choosing the planetary boundary layer (PBL) scheme, surface layer scheme, radiation scheme, microphysics and convective schemes, and LSM. Given the large number LSMs currently available in WRF, it remains a challenge for modelers to select and configure the appropriate land surface scheme to fit their needs [5]. These models range from those with a simplistic treatment of surface processes (e.g., no plant canopy) to sophisticated subsurface-vegetation-atmosphere transfer models. The LSM in WRF calculates heat and moisture fluxes over land to provide a lower boundary condition for vertical transport (i.e., atmospheric mixing) in the PBL scheme.
Energy exchange at the surface can strongly drive lower PBL flow features in the daytime, as thermally-generated, buoyant sensible heat fluxes, in combination with mesoscale forcing and drag across the surface roughness elements, largely determine the magnitude of wind shear (i.e., change in wind speed with height) and turbulence at heights encountered by a wind turbine rotor-disk. Previous studies have examined the role of surface and subsurface properties on near-surface meteorology and PBL development (e.g., [6,7,8,9,10,11,12,13]), the role of the PBL scheme in WRF for wind forecasting (e.g., [14,15]), and the impact of crop type and surface drag (via the aerodynamic roughness length, zo) on hub-height wind speed and shear [16]. However, few studies have specifically looked at the role of surface energy exchange and LSM choice on rotor-disk wind shear. This is a potential area for wind forecasting improvement as numerous studies have shown that wind shear characteristics are in part dependent on atmospheric stability and that shear has significant impacts on turbine power generation (e.g., [17,18,19,20,21,22,23]).
Surface energy exchange is described by the terrestrial radiation budget, defined in Equation (1), where Rn is net radiation flux (W·m−2) (i.e., the difference between incoming and outgoing radiation), H is sensible heat flux (W·m−2), LE is latent energy flux (W·m−2), G is ground heat flux (W·m−2) and S is biomass storage heat flux (W·m−2).
Rn = H − LE − G − S
While some of the available energy is absorbed by the ground and biomass, this is on average less than 15% of the net radiation flux for most plant canopies and the majority of available energy is transferred back into the atmosphere as sensible and latent heat [8]. Latent heat is the quantity of heat absorbed or released by water undergoing a change of state. Over a plant canopy, LE is the heat released by water as it changes from a liquid to gaseous state through evapotranspiration (ET). ET includes water evaporated from the canopy and ground surfaces plus water lost through gas exchange via the plant vascular system (transpiration).
The magnitudes of H, LE, G and S are dependent on many variables as well as the nature of the feedbacks between them. These variables include the amount of incoming radiation, soil moisture availability, groundwater availability and plant access, soil properties, canopy properties (e.g., species, albedo, biomass density, leaf area index (LAI), and rooting depth), air and soil temperature, relative humidity, and entrainment of dry air into the boundary layer from the free atmosphere. The ratio of sensible heat to latent energy transfer is called the Bowen ratio (β = H/LE) and is usually expressed as a midday average. A high β indicates that a larger portion of available energy is partitioned into sensible heat than latent heat.
Here we largely focus on the partitioning of incoming radiation into sensible and latent energy. Wind shear at heights encountered by wind turbines is hypothesized to be strongly correlated to β during the summer months when land-atmosphere interactions are the strongest. Large H fluxes produce strongly buoyant heat fluxes which increase thermally-driven mixing in the lower PBL and decrease wind shear. On the other hand, smaller H fluxes will lead to weaker thermally-driven mixing and an environment with possibly greater wind shear across the wind turbine rotor-disk. H fluxes can be attenuated for a number of reasons. For example, if they are relatively small during the warm summer months this is usually because a large amount of available energy is going into evaporation and transpiration of water from the crop canopy. Despite the significant influence of H and LE on the daytime PBL, uncertainty remains in the parameterization of surface heat and moisture fluxes in numerical weather prediction models [24].
Experimental studies such as CASES-97 and IHOP-2002 have shown that latent and sensible heat fluxes in the SGP region vary significantly in time and space due to land use, climatology, and soil type differences across the landscape [25,26,27]. However, a typical wind forecaster, such as a wind plant operator, usually runs WRF in a “standard mode” which does not capture fine-scale land use heterogeneity nor fine-scale temporal vegetation changes. LSMs in standard WRF use either a monthly or seasonally-adjusted or annually-fixed land use value from look-up tables to assign surface characteristics, but crop cover can change frequently and suddenly in this region; for example, rapid canopy changes would be caused by crop “greening” or senescence, flood or hail crop losses, or harvest or field tillage events. This coarse approach for incorporating land use and vegetation property changes in LSMs is likely a shortcoming in areas such as the SGP with high spatial and temporal surface variability. To improve modeling in heterogeneous areas, some research groups have incorporated high-resolution remote sensing surface data into their land surface model [28,29]. This “mosaic approach” of using satellite products for data assimilation has been incorporated into certain, research-geared applications of LSMs such as Noah, RUC and the Community Land Model (CLM).
While satellite data assimilation of near real-time surface properties would likely result in more accurate surface fluxes, and potentially more accurate simulations of turbine-relevant wind inflow conditions, this was not employed here. In brief, we wanted to evaluate the accuracy of each LSM in WRF by running WRF in a “standard” mode as a wind plant operator or forecaster would do. This is done for a number of reasons. First, wind plant operators are usually limited by their computational resources which restrict them to run WRF in mesoscale mode and not at finer resolution. Second, plant operators need to run forecasts quickly as the energy market relies on hourly and day ahead forecasts. The recent operation of a neighboring wind farm provided additional motivation for studying the importance of LSMs in a standard version of WRF.
Here we aim to answer the following questions for a wide range of LSMs and surface and meteorological conditions:
- (1)
- Is there a correlation between surface energy exchange and wind shear in the observations at this site? Is this correlation seasonal?
- (2)
- Is modeled energy flux and wind shear accuracy related to complexity in the LSM’s parameterization of soil–vegetation–atmosphere feedbacks?
2. Methods
2.1. Site Description and Instrumentation
All measurements were taken at the DOE SGP ARM Central Facility near Lamont, Oklahoma (36.605°N, 97.488°W, 317 m a.s.l.) (Figure 1). SGP ARM is set in a rural landscape dominated by pastureland and annually grown crops. The landscape is relatively flat with a local terrain slope less than three degrees. The species of annual crops planted in fields adjacent to the Central Facility vary across years and seasons depending on climatic conditions and market prices. Crops can include winter wheat and canola, typically grown from fall to early summer, and corn, sorghum, cowpeas, barley and soybeans grown during spring and summer. The region has fine scale spatial heterogeneity due to small land holdings and changing crop rotations. Regional heterogeneity is enhanced by climatic gradients resulting in a wide range of precipitation across the larger SGP ARM domain from the northwest (380 mm) to the southeast (1270 mm) [30]. The crops are not irrigated and crop losses, delayed plantings, and early or late harvests can result from anomalous climate conditions. Area soils are classified as well-drained silt loam, silty clay loam or clay loam and have permanent wilting points of ~0.13 m3·m−3. Permanent wilting point is defined as the water content of the soil when most plants will wilt and fail to recover their turgor even if the soil moisture is replenished.
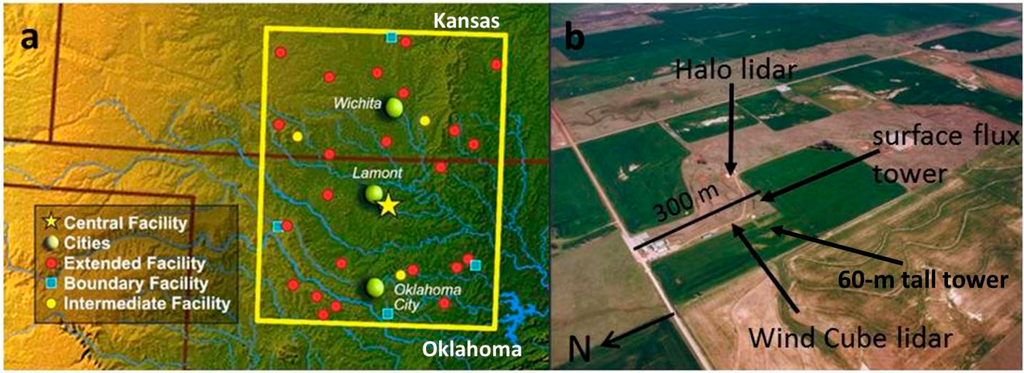
Figure 1.
(a) Map showing the boundaries of the greater Southern Great Plains (SGP) Atmospheric Radiation Measurement (ARM) Facility in Oklahoma and Kansas (yellow box) including the Central Facility near Lamont, Oklahoma; (b) Aerial photograph of the Central Facility depicting the fine-scale spatial heterogeneity in the area and locations of instruments used in this study. Live crops are indicated by dark green while pasturelands and fallow fields are light brown.
We utilized the surface energy flux measurements from the Central Facility’s 4 m tall AmeriFlux tower and mean wind speed from a co-located 60 m tall tower. Both towers are well described in [13,31,32,33]. In brief, the wind vectors are measured on the tall meteorological tower with two 3-D sonic anemometers (Gill-Solent WindMaster Pro, Gill, England) at heights of 25 and 60 m and are available as 30-min averages. The surface flux tower measures carbon dioxide, water vapor, and energy fluxes over an annual cropland with an estimated uncertainty of ±10% based on methods found in [34]. Homogenous fetch is approximately 200 m in length across a 180° arc centered pointing south. The surface flux tower has an open-path infrared gas analyzer (LICOR Li-7500, Li-Cor Biosciences, NE, USA) that measures atmospheric carbon dioxide and water vapor and a 3-D sonic anemometer (Gill-Solent WindMaster Pro) that measures the wind vectors and sonic temperature, from which the sensible heat flux is calculated. From these instruments the Obukhov length (L), a scaling parameter used to indicate atmospheric stability in the surface layer, is also calculated [35]. Other surface meteorology measurements include air temperature, relative humidity, net radiation, soil heat flux, root-zone (0–20 cm) soil moisture, soil temperature and precipitation. The energy fluxes were calculated using a 30-min averaging period and were post-processed using standard algorithms for spike removal, density corrections [36], spectral corrections [37], and coordinate rotation.
It is important to note that the energy flux measurements are taken with separate instruments and full energy budget closure (Rn = H − LE − G − S) can be difficult to achieve. Reasons for this may include different-size instrument footprints, random and systematic measurement errors, incorrect assumptions about instrument time lags for LE (due to sensor separation between the IRGA and sonic anemometer), and uncertainties in spectral corrections (for H and LE). In practice it is generally acceptable for flux towers to achieve only 75%–80% energy closure [38].
The SGP ARM Central Facility has a continuously running Halo scanning lidar (Halo Photonics, Worcestershire, UK) which provides measurements of horizontal wind speed and direction, taken once an hour in 2011, for heights ranging from 75 m to 10 km [39]. In the summer of 2011, the scanning strategy was frequently changed to optimize vertical wind speed retrieval during the middle of the day which further limited the availability of horizontal wind speed data, e.g., 45% of the midday measurements were missing for the second simulation period. Furthermore, the measurements taken close to the surface (<100 m) were deemed suspect due to their location in the near field of the lidar [40]. For these reasons we decided to use the wind speed profile system on the meteorological towers (4, 25, 60 m) in lieu of the lidar for the first two study periods. Wind speeds above the 60 m measurement height were estimated using the power-law expression in Equation (2) with a calculated wind shear exponent (α) from the available data at heights of 25 and 60 m. This was done to estimate the wind speeds at multiple heights above 60 m which represent inflow conditions across the area of a 1.68 MW wind turbine rotor disk (40–120 m).
In Equation (2) U is the mean horizontal wind speed (m/s) at height z (m), UR is the mean horizontal wind speed (m/s) at a reference height zR (m) (here we used the 25 m height), and α is a wind shear exponent used to describe the variations in the wind speed with height. For example, a well-mixed atmosphere will have an α value close to 0 while a strongly stable atmosphere will have α closer to 0.35 [22].
In November 2012, we installed a vertically-profiling Wind Cube v2 pulsed Doppler lidar system (Leosphere, Orsay, France) which measured the u, v and w wind components at 12 vertical levels from 50 m to 180 m above the surface at a ~1 Hz rate and wind speed accuracy of ±0.1 m/s. These data were averaged over 30-min periods to coincide with the energy fluxes. A wind shear exponent was calculated using the 50 m and 80 m heights to best coincide with the methodology used for the meteorological tower. It is important to note that the Wind Cube calculates the wind vectors using a spatial average across a scanned volume cone which increases in diameter with increasing height. This introduces some uncertainty into the measurements as the algorithms used to calculate mean wind speed assume horizontal homogeneity in the sampled flow; although, this source of uncertainty should be relatively low at the flat SGP ARM site. Further uncertainty is introduced by the fact that each measurement level is actually an average of wind flow conditions over a ±10 m probe depth. Even so, studies have shown high agreement between meteorological tower wind speed measurements and those taken by the Wind Cube in flat terrain sites [41,42].
2.2. Case Studies
To study the impact of LSM choice on WRF simulated near-surface wind profiles, we performed atmospheric simulations for three case studies. These cases were associated with a variety of land surface conditions that would affect the surface energy fluxes, including variability in crop cover, albedo, soil moisture, incoming radiation, relative humidity, and air and soil temperature (Table 1, Figure 2).

Table 1.
Brief description of Cases 1–3 highlighting canopy and surface meteorology differences.
| Variable of Interest | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Date | 10–24 June 2011 | 13–27 July 2011 | 23 November–7 December 2012 |
| Climate characteristics | very warm, wet | hot, dry | cool, dry |
| Mean air temperature | 27.2 °C | 32.1 °C | 10.2 °C |
| Precipitation, including the two weeks prior | 55.8 mm | 8.8 mm | 18.1 mm |
| Mean root-zone soil moisture | 24% | 6% | 12% |
| Crop | canola | none | none |
| Field conditions | peak LAI and active canopy in early June then rapid senescence | post-harvest, bare soil with small amounts of crop residue | bare soil with small amounts of crop residue and emerging wheat seedlings |
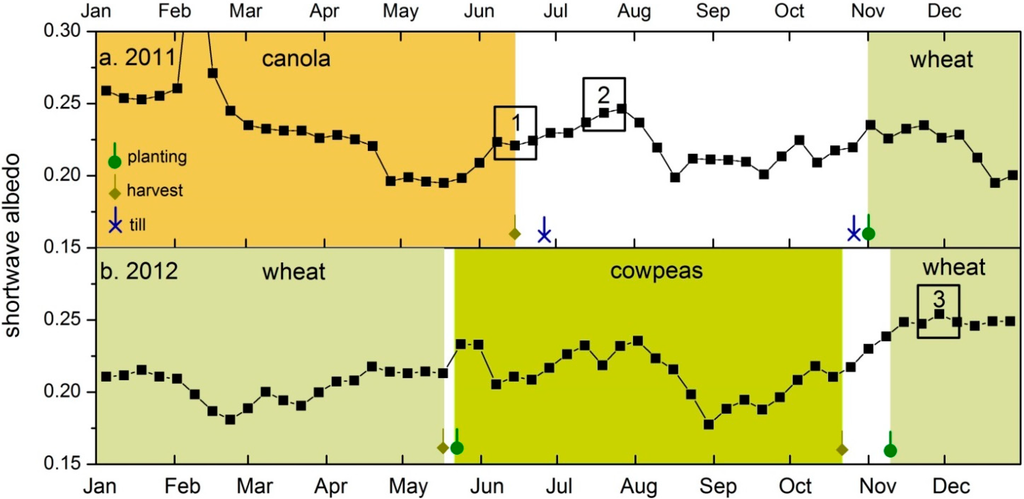
Figure 2.
Time series of measured mean weekly albedo at the SGP ARM Central Facility in (a) 2011 and (b) 2012. Variations in albedo indicate changes in the surface canopy. Each growing season is shaded with a color depending on crop species. Also shown is the timing of planting, harvest and till events. Boxes 1–3 indicate the timing of simulated case periods. Note the differences in albedo between the case studies. The spike in albedo in February 2011 is due to snow cover.
Conditions during Case 1 (10–24 June 2011) included a green canola canopy with peak LAI and adequate access to soil moisture in the root zone (θv = 24%) in early June followed by a rapid crop senescence and crop harvest on 16 June. The field was tilled on 30 June. Although only a month later, Case 2 (13–27 July 2011) conditions included a bare dirt field with some dead crop residue. At this time the field and the surrounding areas were covered with <5% photosynthesizing vegetation and root-zone soil moisture (θv = 6%) was below the wilting point. Case 3 was run to include the autumn (23 November–7 December) of 2012 when the local area was a mixture of <0.5 m tall senesced grasses in the pasturelands and bare ground in the agricultural fields with some dead cowpea residue (<1 cm tall) and a few emerging wheat seedlings (<5 cm tall). Case 3 also included cool temperatures and moderately dry soils (root zone θv = 12%) and was considered a “control” period as energy fluxes would be relatively low during this time of year and should not have a significant influence on PBL behavior and development.
Case 1 and Case 2 (2011) were chosen because they present an interesting test case due to the rapidly observed changes in soil moisture, soil temperature, and atmospheric moisture in comparison to nearly equal incoming radiation. It is not uncommon for such rapid changes to occur in the area due to weather extremes and the type of crop management practices used (e.g., no irrigation). Errors in our WRF runs may be highlighted in such cases since the LSMs did not include high resolution canopy information. Case 3 was chosen because it represents a nice comparison point to Case 2. These two periods differed significantly in meteorology (e.g., air temperature, incoming radiation, importance of synoptic meteorology versus local forcings) but both included no canopy.
2.3. WRF Domain Configuration
WRF is a non-hydrostatic, fully compressible atmospheric model that is maintained by the National Center for Atmospheric Research (NCAR) [2]. This study used the advanced research dynamical core version of the WRF 3.4.1 model release with a double nested domain configuration as shown in Figure 3. The outer WRF model domain (domain 1) had a horizontal grid spacing of 9 km and covered a large portion of the central United States. The second domain (domain 2) had a horizontal grid spacing of 3 km while the innermost domain (domain 3) had a grid spacing of 1 km. The model domain configuration was centered on the SGP ARM Central Facility. Given the absence of complex terrain in the innermost model domain, 1 km horizontal resolution was deemed sufficient to resolve fine-scale horizontal flow in the domain of primary interest. A total of 50 terrain-following vertical sigma levels were used for all of the WRF simulations. The 50 sigma level configuration resulted in a vertical resolution of roughly 20–30 meters in the lowest 200 meters of the atmosphere. The top of the model grid was at 50 hPa, which corresponds roughly to a height of 20 km above sea level.
2.4. Ensemble Description
An ensemble consisting of five common LSMs available in WRF 3.4.1 was used to study the impact of LSM choice and configuration on simulating surface energy fluxes and near-surface wind profiles. All runs used the Lin microphysics, Kain-Fritsch cumulus scheme, CAM shortwave and longwave radiation model, Mellor-Yamada-Janjic (MYJ) PBL scheme, and Monin-Obukhov (M-O) surface layer scheme. Surface property input data came from the default 24 USGS land use categories. In all members, land use was classified as “Dry Cropland and Pastureland”. The tested LSMs included: thermal diffusion [43], RUC [44], Pleim-Xiu (PX) [45,46], Noah [47], and Noah Multi-Physics (Noah-MP) [48]. Descriptions of each are provided in Section 2.7.
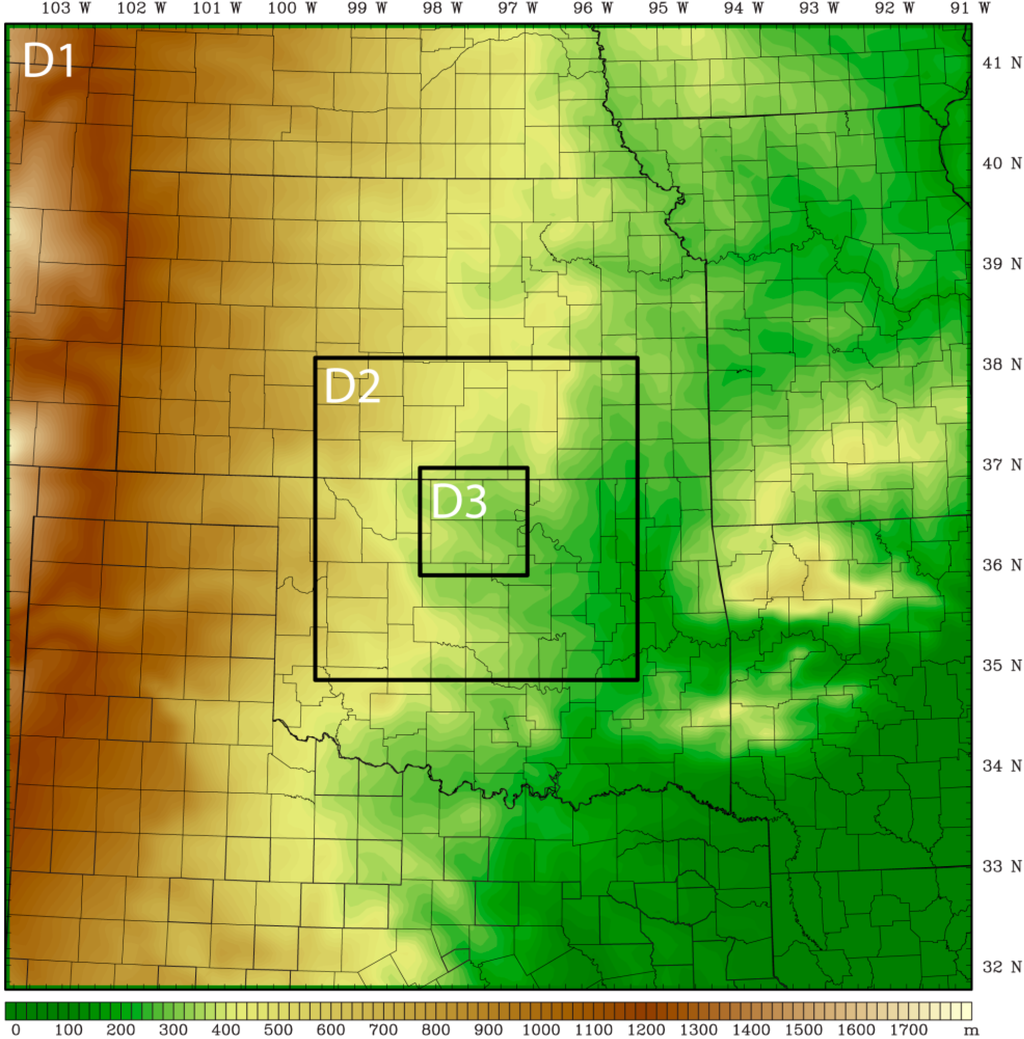
Figure 3.
Elevation map showing the WRF model double nested domains used in this study. The inner domain, D3, is centered on the SGP ARM Central Facility in northern Oklahoma, USA. The horizontal grid resolution of domain 1 (labeled D1), domain 2 (D2), and domain 3 (D3) is 9, 3, and 1 km, respectively.
2.5. Input Data
Initial and lateral boundary conditions for the WRF simulations were provided by gridded analysis fields from the North American Model (NAM). The NAM analysis fields are available every 6-h with a horizontal resolution of 12 km. Three-dimensional atmospheric data are provided on 40 pressure levels with a vertical resolution of 25 hPa in the NAM analysis data set. Meteorological variables provided by the NAM data include atmospheric pressure, geopotential height, horizontal wind components, air temperature, relative humidity, surface pressure, sea level pressure, and soil moisture and temperature at four sub-surface layers. NAM analysis data are available for public download from the National Climatic Data Center’s (NCDC) data website.
2.6. Four-Dimensional Data Assimilation
WRF has a 4-D data assimilation (FDDA) capability for both analysis (gridded) [49] and observational nudging [50]. The FDDA nudging approach has been demonstrated to reduce error by constraining large-scale atmospheric flow towards analysis fields while allowing smaller scale atmospheric features to develop in fine-scale domains [51,52,53,54,55]. Here we applied analysis nudging on model domains 1 and 2 to constrain the simulated large scale flow of the simulations. Model grid points within the planetary boundary layer were not nudged in either domain 1 and 2 to avoid conflicting with small-scale features that may develop. As an additional constraint to ensure that the nudging algorithm did not influence model results in the lower atmosphere, the FDDA analysis option was turned off below model level 10, which corresponded to a height of roughly 600 m above the surface. The additional FDDA constraint was needed for extremely stable nighttime periods when boundary layer heights of less than 100 m were plausible. Observational nudging was not utilized in any of the WRF domains so that the model solution was free to evolve near the surface where results were later compared with atmospheric observations.
We ran each case study for a spin up period of four days before the WRF output was compared with observations. A multi-day spin up was used to give the soil moisture and temperature initialization-induced LSM biases sufficient time to reach a reasonable balance with underlying atmospheric forcings. All of the model simulations were performed as a single continuous run with no restarts. Output was saved at 10 min intervals for comparison with observations.
2.7. Land Surface Models
Land surface models in WRF use atmospheric information from the surface layer scheme, radiative forcing information from the radiation scheme, and precipitation forcing from the microphysics and convective schemes, together with information about the land surface, to output heat and moisture fluxes. LSMs are described here in order of increasing complexity in regards to how they deal with thermal and moisture fluxes in the soil and vegetation. Additional details are listed in Table 2.
The most basic LSM used here is the thermal diffusion, or “slab”, model. Thermal diffusion calculates surface heat fluxes from a 1-dimensional equation and then assumes linear temperature profiles across five layers of soil. Soil moisture is fixed according to land use category and season. Latent energy is computed from the soil moisture availability only. There are no explicit vegetation processes.
The Rapid Update Cycle (RUC) model is largely focused on an accurate characterization of the soil with 6–9 soil levels (or more possible) with the default parameterization reaching down to a soil depth of 300 cm. The physics of snow and phase change in soil are well characterized [44]; however, RUC applies a basic approach to characterize evapotranspiration from the canopy. ET calculations are based on work of [56] wherein the same equations used to calculate the transfers of heat and moisture from the soil are adjusted to estimate the energy fluxes from the canopy. Canopy evapotranspiration is scaled by potential evapotranspiration, canopy moisture content, rooting depth, and the soil moisture relative to the plant wilting point.

Table 2.
Configuration of the WRF land surface model (LSM) ensemble. Also listed are the surface runoff and stomatal conductance parameterizations used in Noah-MP. LUC = land use category.
| LSM | Vegetation | Drivers of Soil Moisture | Soil Layers | Drivers of Water Flux Exchange |
|---|---|---|---|---|
| Thermal diffusion | None | LUC | 5 | Soil surface |
| RUC | Extension of soil | LUC + evap | 6 or 9; 3 m max | Air temperature, relative humidity |
| Pleim-Xiu (PX) | 1-layer from LUC | LUC+ evap+ roots | 2; 1 m max | Soil surface + plant transpiration |
| Noah | 1-layer from LUC | LUC+ evap+ roots+ drainage | 4; 2 m max | Soil surface + plant transpiration |
| Noah-MP 1—Ball-Berry/TOPMODEL | 2-layer from multiple LUC | LUC + evap + roots + drainage + runoff + storage | Variable; 8 m max | Complex soil–plant feedbacks |
| Noah-MP 2—Ball-Berry/BATS | 2-layer from multiple LUC | LUC + evap + roots + drainage + runoff + storage | Variable; 8 m max | Complex soil–plant feedbacks |
| Noah-MP 3—Jarvis/TOPMODEL | 2-layer from multiple LUC | LUC + evap + roots + drainage + runoff + storage | Variable; 8 m max | Complex soil–plant feedbacks |
| Noah-MP 4—Jarvis/BATS | 2-layer from multiple LUC | LUC + evap + roots + drainage + runoff + storage | Variable; 8 m max | Complex soil–plant feedbacks |
The Pleim-Xiu (PX) model [45] builds off of the Noilhan and Planton model [57]. PX only has two soil layers; a shallow layer (1 cm) at the surface interacting with the atmosphere, and a thick layer (99 cm) below interacting with the upper soil layer and the plants via the roots. Moisture fluxes are either from precipitation, dew formation, evaporation directly from the soil surface or vegetation, transpiration (ultimately controlled by soil moisture in the root zone via stomatal resistance), or vertical movement within the soil. Regardless of canopy cover or density, only a soil heat capacity is used to calculate soil heat flux.
The Noah model [47] is the most complex of the LSMs evaluated. Noah is the product of a large community of researchers combining previous iterations of multiple land surface models. The model has four soil layers reaching 2 m in which soil temperature and moisture are calculated. The first three layers form the root zone in non-forested areas. The shallow soil, “leaky” bottom (precipitation that infiltrates to the bottom of the soil column is lost from the system) and simple snow/melt/thaw dynamics are seen as areas where the model avoids complexity. Vegetation, however, is well defined using monthly estimates of albedo and fraction of green vegetation cover based on vegetation class. Vertical rooting depth for crops is also allowed to change from month to month. Evapotranspiration can be modeled by the Ball-Berry equation, taking both the physics of water flow through the soil and plants as well as the physiology of photosynthesis into account. Alternatively, a simpler Jarvis scheme based only on leaf area index and physics of water flow through the soil–vegetation–atmosphere continuum can be used. These advancements were implemented to improve parameterizations related to seasonal and diurnal simulations of water fluxes, energy fluxes and state variables [58].
Multiple physics parameterization options are available with the Noah model (Noah-MP) for users to tune the model in order to maximize complexity for dominant processes, while using simpler modeling approaches for other processes [48]. For example, Noah-MP includes three options for modeling the response of transpiration to changes in site water status: via soil moisture directly as in Noah and via two variations of the response of stomatal conductance to soil matric potential. Site hydrology can be modeled simply as in Noah with the “leaky” bottom either with the simplified calculations of surface runoff or with more complex calculation of surface runoff based on the BATS model [59]. Alternatively, the TOPMODEL-based [60] calculation of surface runoff and groundwater discharge can be used with varying levels of complexity in modeling groundwater. Here we ran four versions of Noah-MP, including two versions of a surface runoff model (BATS, TOPMODEL) and two versions of canopy stomatal resistance model (Ball-Berry, Jarvis) to assess any differences in simulated surface energy fluxes due to these parameterizations.
3. Results and Discussion
3.1. Land-Atmosphere Energy Exchange
3.1.1. Observations
Case 1 and Case 2 were chosen as they represented very different surface conditions across a relatively short time scale (e.g., <month) during a period with similar incoming radiation. The rapid changes in crop cover, albedo, and surface meteorology are evident in the soil moisture and energy flux measurements, the latter shown by the midday Bowen ratio (Figure 4). Average daily soil moisture during Case 1 was 24% in comparison to 6% in Case 2. Likewise, significant differences in midday β were apparent as the measured Bowen ratio in Case 2 was ten times higher (β = 10) than during Case 1 (β = 0.9). Mean midday latent energy fluxes reached just 50 W·m−2 during Case 2 leading to very high β values while the LE flux reached 250 W·m−2 in Case 1. These differences in LE are largely explained by the presence of a transpiring canopy, periods of evaporation from a wet canopy or wet ground, and soil moisture above the wilting point during much of Case 1 while Case 2 was characterized by post-harvest conditions including dry, bare ground. During Case 2, 75% of the available energy in the afternoon was re-emitted to the atmosphere in the form of sensible heat. In Case 3, we saw much lower H and LE fluxes due to less available net radiation during the autumn months. Average soil moisture during Case 3 was 12% and the midday average β was 4.5.
The storage of energy in the crop canopy is negligible at this site; however, storage of energy in the ground surface (G) is significant at times. During daylight hours in Case 1, G compromised 8% of available energy while in Cases 2 and 3, G was a larger portion at 13% due to the lack of canopy cover. Average midday energy budget closure was 83% in Case 1, 96% in Case 2, and 96% in Case 3. The “missing” or unaccounted energy during Case 1 is likely due to an underestimation of the LE flux. LE is more difficult to accurately measure than H, and LE was a significant component of the net energy balance during Case 1.
3.1.2. LSM Performance
The LSM runs were initialized with NAM soil moisture values close to observed values in Case 1 and Case 3 but with wetter than actual conditions in Case 2. In fact, the NAM data showed no dry down between Case 1 and 2 as the initialized soil moisture conditions were the same for both periods (θv = 15%). We also compared the LSM simulated soil moisture on days 4 and 14 of each simulation for all models except for thermal diffusion, as this LSM does not predict soil moisture. In Case 1, a couple of the LSMs (RUC, PX) overestimated the drying out of the soil over the two week period and simulated soil moisture values equal to 6%–7% by the end of the two weeks. This occurred even as significant precipitation fell during week 2. In contrast, average soil moisture simulated by the Noah-MP runs was 20%–24% at the end of the simulations and in agreement with the observations. In Case 2, most of the LSMs underestimated the drying out of the soil partially because the initial conditions were so much higher than those observed. For example, Noah and Noah-MP simulated soil moisture values (mean θv = 14%) above the wilting point (θv =10%) at the end of the period. Only two of the LSMs had declining soil moisture in agreement with the observations: RUC (θv = 7%) and PX (θv = 6%). In Case 3 there was very little difference in soil moisture between the LSMs by the end of the simulation period as the atmospheric conditions (low radiation, low temperature) limit evaporative water loss. The simulated θv values were in agreement with the observations for Case 3 for all LSMs.
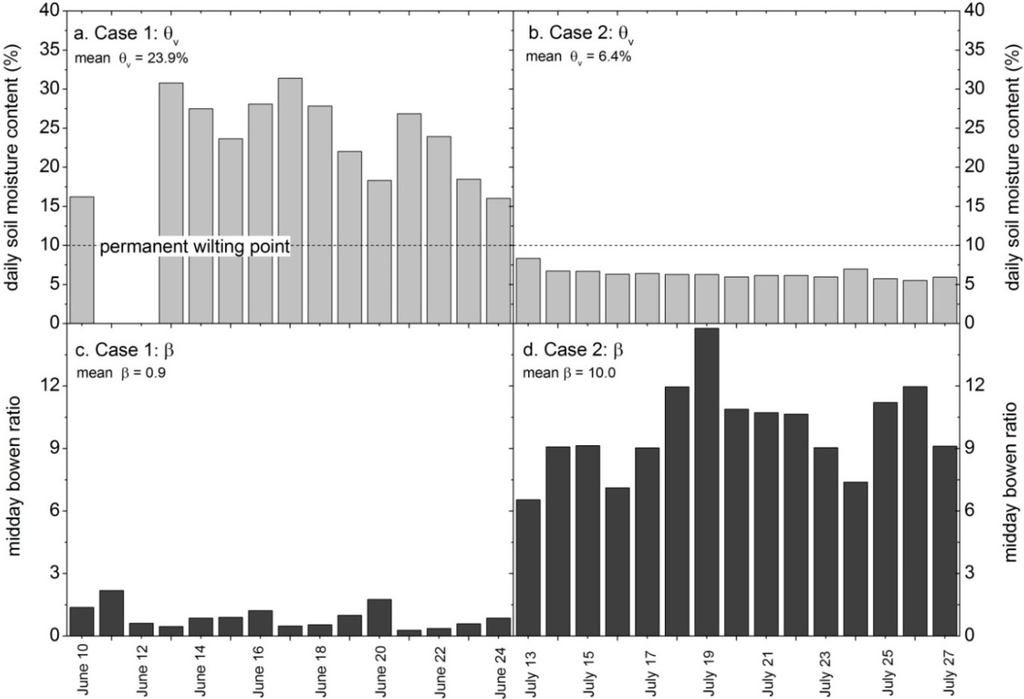
Figure 4.
Mean daily soil moisture content measurements in (a) June 2011/Case 1 and (b) July 2011/Case 2. Mean midday Bowen ratio (β) measurements from the surface flux tower are also plotted for (c) June 2011/Case 1 and (d) July 2011/Case 2. The permanent wilting point is for a well-drained Kirkland soil.
Mean measured and simulated Rn, H, LE and G fluxes are shown in Figure 5, Figure 6 and Figure 7 by time of day for each case period. Although Rn and G are not discussed in detail they are shown in the diurnal plots to illustrate how well each model simulated the full energy budget. Mean midday Bowen ratios are listed in Table 3 for each case period.

Table 3.
Mean (± standard deviation) midday Bowen ratios by case period show differences across LSMs and seasons.
| Observations/LSM | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Observations | 0.92 ± 0.62 | 9.90 ± 4.52 | 5.33 ± 2.30 |
| Thermal diffusion | 0.20 ± 0.12 | 0.23 ± 0.11 | 0.76 ± 0.27 |
| RUC | 4.43 ± 4.15 | 132.45 ± 237.36 | 2.47 ± 2.43 |
| PX | 1.12 ± 0.36 | 1.36 ± 1.02 | 1.29 ± 0.53 |
| Noah | 1.82 ± 0.26 | 4.40 ± 0.82 | 2.54 ± 1.58 |
| Noah-MP 1 | 1.55 ± 0.27 | 5.89 ± 2.37 | 9.01 ± 3.91 |
| Noah-MP 2 | 2.05 ± 0.38 | 5.47 ± 2.61 | 8.64 ± 3.98 |
| Noah-MP 3 | 1.97 ± 0.39 | 7.55 ± 3.34 | 8.34 ± 3.84 |
| Noah-MP 4 | 1.12 ± 0.38 | 7.41 ± 2.92 | 8.41 ± 3.86 |
| LSM Range | 0.20–4.43 | 0.23–132.45 | 0.76–9.01 |
For Case 1, mean midday β ranged from 0.2 (thermal diffusion) to 4.4 (RUC) while most simulations fell between β = 1–2, just slightly higher than the mean observed value (β = 0.9) (Table 3). Nearly all of the LSMs in Case 1 overestimated midday H fluxes (Figure 5). The greatest overestimation was by RUC as this model predicted a mean midday H equal to 500 W·m−2 while the mean observation peaked at 150 W·m−2. For comparison, RUC also simulated much drier soil moisture conditions than the observations. Although thermal diffusion was relatively accurate in predicting the buoyant heat flux, this model, which does not include plant dynamics or predictions of soil moisture, greatly overestimated LE which led to a very low Bowen ratio.
Small but noticeable differences in mean midday β were apparent in the Noah-MP runs as Noah-MP 4 predicted the lowest Bowen ratio (β = 1.1) of the Noah-MP group and Noah-MP 2 simulated the highest (β = 2.1). These models differed in the choice of stomatal conductance model but were run with the same soil hydrology model (BATS) (Table 2). Noah-MP 3 was slightly lower than Noah-MP 2, however not significantly, indicating that the choice of soil hydrology model also played a role. This suggests that LE fluxes in June were driven by evaporation fluxes in addition to transpiration as there were periods of precipitation during this case. The soil hydrology models used here in Noah-MP differ in the way they parameterize surface runoff, which was especially important during the second half of Case 1. Simulated soil moisture for the Noah MP runs was similar during the beginning of the simulations but deviated by the end (θv ranged from 18% to 22%). Prior studies have shown that differences in surface runoff characterization can be significant, for example, the study of [61] found that the TOPMODEL led to significant improvements in simulating surface runoff for sites in the Mississippi River Basin.
The results for Case 2 are found in Figure 6. Large errors were found in simulated H and LE fluxes for thermal diffusion (overestimated LE and underestimated H), in H for RUC (overestimated), and in LE for PX (overestimated). Exact reasons for these errors are unknown especially since RUC and PX were the most accurate of all the LSMs in simulating surface soil moisture. These errors are evident in the large range of simulated mean midday Bowen ratios: 0.2 (thermal diffusion) and 132 (RUC). The observed mean midday β was 10 (Table 3).
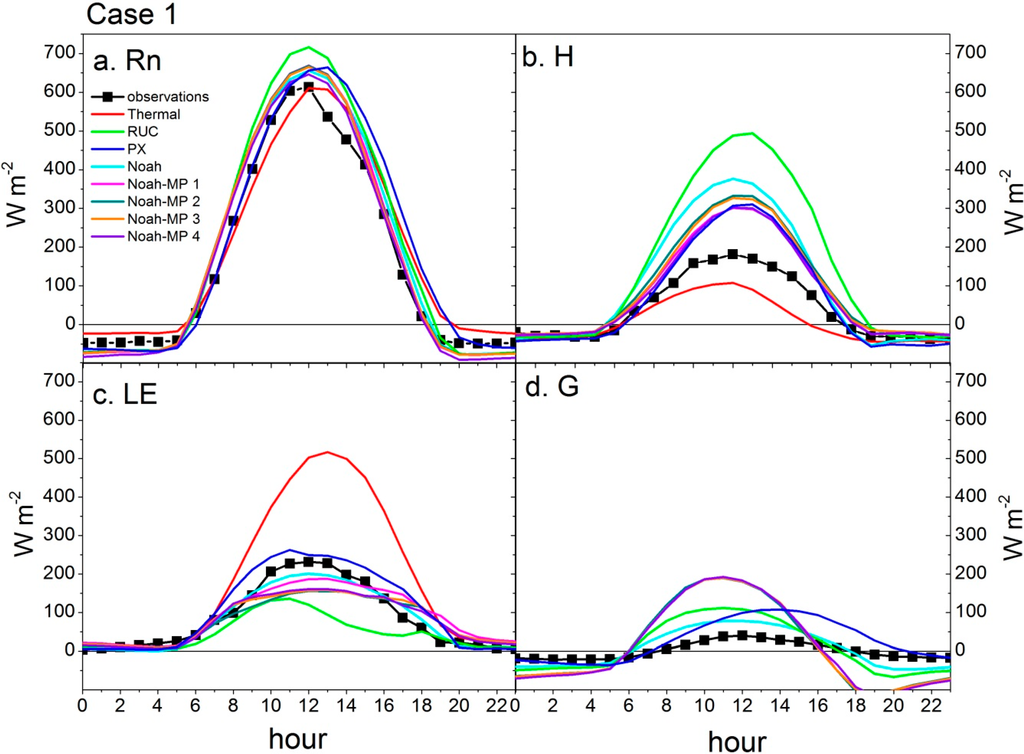
Figure 5.
Mean diurnal plots of measured and simulated (a) net available energy (Rn), (b) sensible heat (H), (c) latent energy (LE), and (d) ground heat (G) fluxes for each LSM during Case 1 (June 2011). Positive H and LE fluxes indicate net energy transfer to the atmosphere. Positive G fluxes indicate net energy transfer to the ground surface. Time is given in Local Standard Time.
Significant differences within the Noah-MP models were also apparent in Case 2. The Bowen ratios were similar between Noah-MP 1 and 2 (β ~ 5.5) and Noah-MP 3 and 4 (β ~ 7.5). These groups are divided by the parameterization of stomatal conductance whereby Noah-MP 1-2 used the more complex Ball-Berry equation. Noah-MP runs 1 and 2 simulated slightly wetter soil moisture values than Noah-MP 3 and 4. Since these Bowen ratio differences are divided by the choice of stomatal conductance parameterization it appears that the vegetative indices or LAI values used as input into the LSMs were not reflective of actual conditions as no vegetation was growing during this period at the site. Hence, the type of model used to parameterize photosynthesis and thus transpiration should have had no effect on the simulated Bowen ratios if the models had the correct vegetation cover information as input.
Noah and Noah-MP were the most accurate LSMs during the no-canopy, low soil moisture periods even as the actual plant–atmosphere feedbacks were negligible and these models overestimated soil moisture. We had expected RUC to perform well during Case 2 as this model has sophisticated soil layers and drivers that are based on atmospheric temperature and humidity instead of physiologically driven controls. RUC, however, overestimated H and predicted low LE fluxes leading to unrealistically high midday Bowen ratios (>100).
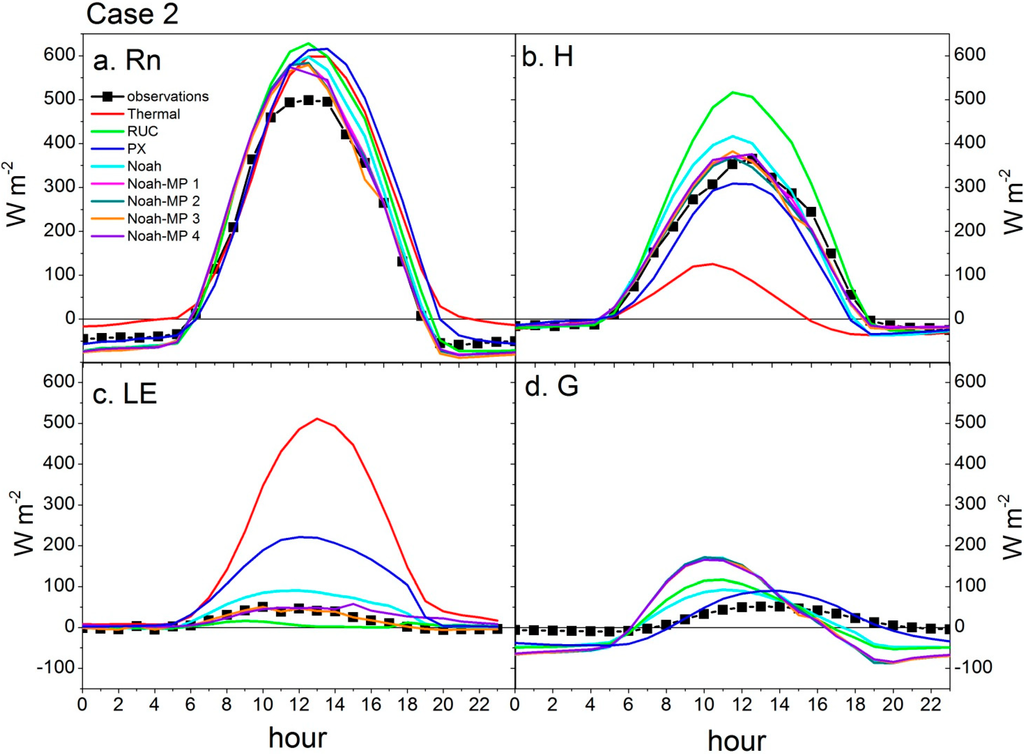
Figure 6.
Mean diurnal plots of measured and simulated (a) net available energy (Rn), (b) sensible heat (H), (c) latent energy (LE), and (d) ground heat (G) fluxes for each LSM during Case 2 (July 2011).
Both the simulated and observed energy fluxes during Case 3 were much lower in autumn than the summer months due to lower incoming radiation (Figure 7). The largest errors occurred for simulated sensible heat as the thermal diffusion, RUC and PX models all underestimated the midday daytime buoyant heat flux. Thermal diffusion and PX also largely overestimated the LE flux. Mean midday Bowen ratios for these two models were 0.76 and 1.3, respectively, while the observed mean midday β was 5.3 (Table 3). During Case 3 we saw the largest differences between Bowen ratios for Noah and Noah-MP whereby mean midday β was 2.5 for Noah and ranged from 8.3 to 9.0 for the Noah-MP group. However, even small LE and H differences, as was the case during Case 3, can create large Bowen ratio differences due to less available energy in the system. This is evident in the wide range of β magnitudes simulated by the LSMs (Table 3). Despite this instability in the Bowen ratio, Noah and Noah-MP both performed reasonably well in simulating the energy budget.
While the surface property and meteorology conditions were very different amongst the case periods, some of the LSMs produced a very narrow range of Bowen ratios. Mean midday β ranged from 0.2 (Case 1) to 0.8 (Case 3) for thermal diffusion, which had no plant dynamics and uses a fixed value for soil moisture, and from 1.1 (Case 1) to 1.4 (Case 2) for PX. In comparison, the range was 0.9 (Case 1) to 10 (Case 2) for the flux observations. LSMs with similar variance included the Noah-MP group which ranged from 1.5 (Case 1) to 9 (Case 3) although the highest Bowen ratio was found for the third case and not the second as we saw in the observations. It is interesting that the PX model had such a small range of Bowen ratios amongst the case studies since vegetation processes are relatively complex in this model.
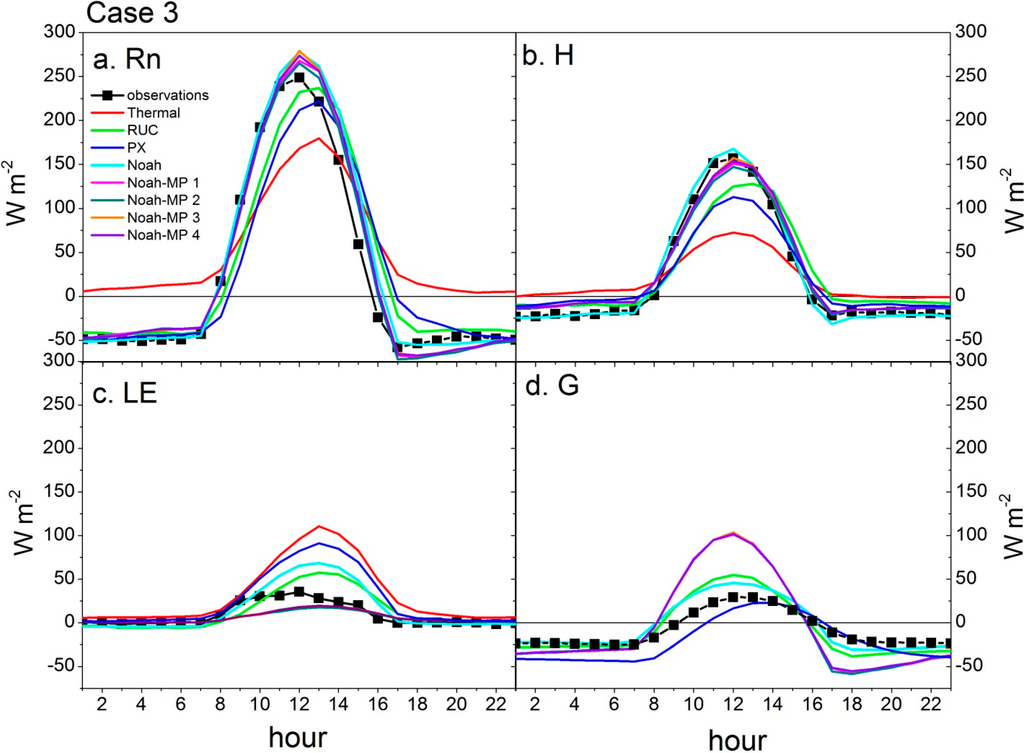
Figure 7.
Mean diurnal plots of measured and simulated (a) net available energy (Rn), (b) sensible heat (H), (c) latent energy (LE), and (d) ground heat (G) fluxes for each LSM during Case 3 (November-December 2012).
Vegetation plays a key role in the Noah-MP model. For example, stomatal conductance determines rates of photosynthesis and transpiration, the dynamic leaf model predicts leaf area index and green vegetation fraction, and the canopy water scheme simulates canopy water interception and evaporation. Even so, we saw little to no significant improvement of Noah-MP over Noah. We expected to see largest differences between Noah and Noah-MP as well as variability within the Noah-MP runs during Case 1 when the vegetation-atmosphere feedbacks were most important. However, the simulation results were not consistent with this theory. Work from other studies may explain this finding. While Noah-MP has shown improvement in natural ecosystems (forests, grasslands), no significant improvement over baseline Noah has been noted for Noah-MP simulations of LE in croplands as both models tend to overestimate LE fluxes for croplands [61,62]. This is likely due to the fact that neither the leaf dynamics in Noah-MP nor the monthly LAI estimates used by Noah can capture managed crop growth [61]. Simulating crops in Noah may require a dynamic leaf and root growth module to enhance performance as found in [63].
3.2. Rotor-Disk Wind Shear
Due to the change in surface meteorology and canopy characteristics from June to July 2011, Cases 1 and 2 had very different energy partitioning schemes (Figure 4, Figure 5 and Figure 6). As such, we expected to see less wind shear in Case 2 due to stronger daytime mixing as the buoyancy heat flux, or sensible heat flux, dominated the surface energy exchange. Atmospheric mixing or stability was described by the Obukhov length (L). Cases 1 and 2, as expected, showed differences in atmospheric mixing during the midday hours. Average midday L was −128 m during Case 1 and L = −12 m during Case 2. These magnitudes correspond to forced convective conditions in Case 1 and strongly convective in Case 2 [22,64].
Differences between Case 1 and Case 2 were also apparent in the measured mean midday wind shear exponent where α was 0.12 (higher shear) in June and 0.02 (lower shear) in July across heights equal to a wind turbine rotor disk. In June the wind speed at the top of the rotor disk was over 1 m/s faster than at the bottom of the rotor disk. Shear across the rotor disk not only changes the magnitude of the inflow or the rotor disk-equivalent wind speed (e.g., [20,22,65]), but can also put fatigue loads on turbine components which reduce turbine performance and lifetimes [66]. This is especially true if the shear is related to intense turbulence bursts (i.e., strong coherent structures) such as those experienced during a nocturnal low level jet (LLJ). At sites without LLJs, on the other hand, shear across the rotor-disk may increase the average wind speed in the inflow conditions (i.e., rotor disk wind speed > hub-height wind speed) leading to greater power generation than otherwise is produced during a well-mixed environment (i.e., rotor disk wind speed = hub-height wind speed) [23].
Wind speed profiles for the measurements as well as the simulations in all three cases are presented in Figure 8. Here, the wind speed at each height is plotted as the difference between the measured or simulated speed at height z and the measured or simulated speed at height 80 m. This was done to ease comparisons between the simulated and observed profiles, however, the shape of the profiles in these plots do not correspond directly to wind shear exponent magnitudes. For example, wind shear appears to be far greater during Case 1 than Case 3, however this is largely a function of higher wind speeds at all heights during Case 1 as the mean midday α values between each cases were nearly identical.
Simulated wind shear exponents ranged from 0.08 (RUC) to 0.15 (thermal diffusion) in June, 0.05 (RUC) to 0.10 (thermal diffusion) in July, and 0.09 (Noah-MP) to 0.15 (PX) in November–December in comparison to the observations of α = 0.12, 0.02, and 0.13 in those periods, respectively. For perspective, a study performed at a West Coast wind farm found that α values < 0 correspond to strongly convective conditions, 0 < α < 0.1 correspond to convective conditions, and 0.1 < α < 0.2 correspond to neutral conditions [22]. Near-neutral conditions in June may have been caused by frequent periods of high wind speeds, cloud cover and a weakened buoyant heat flux.
In Case 1, all of the models under-predicted wind shear in the top half of the turbine rotor disk, leading to underestimations of the total rotor disk wind speed (Figure 8a). In this case, underestimations of rotor disk wind speed from the models could lead to under-predictions of power produced by the wind turbines. Both the models and the observations indicated convective conditions in July although the models slightly under-predicted the strength of the midday mixing with the highest error occurring in the thermal model (Figure 8b). Greatest error is seen here in the lower half of the rotor-disk as the models over-estimated wind shear between 40 and 80 m a.g.l. as compared to the observations. Wind shear exponent magnitudes indicate near-neutral stability in Case 3. Agreement between the models and observations during the autumn period were overall high for the top half of the rotor-disk, with greatest accuracy occurring in the Noah and Noah-MP model runs (Figure 8c).
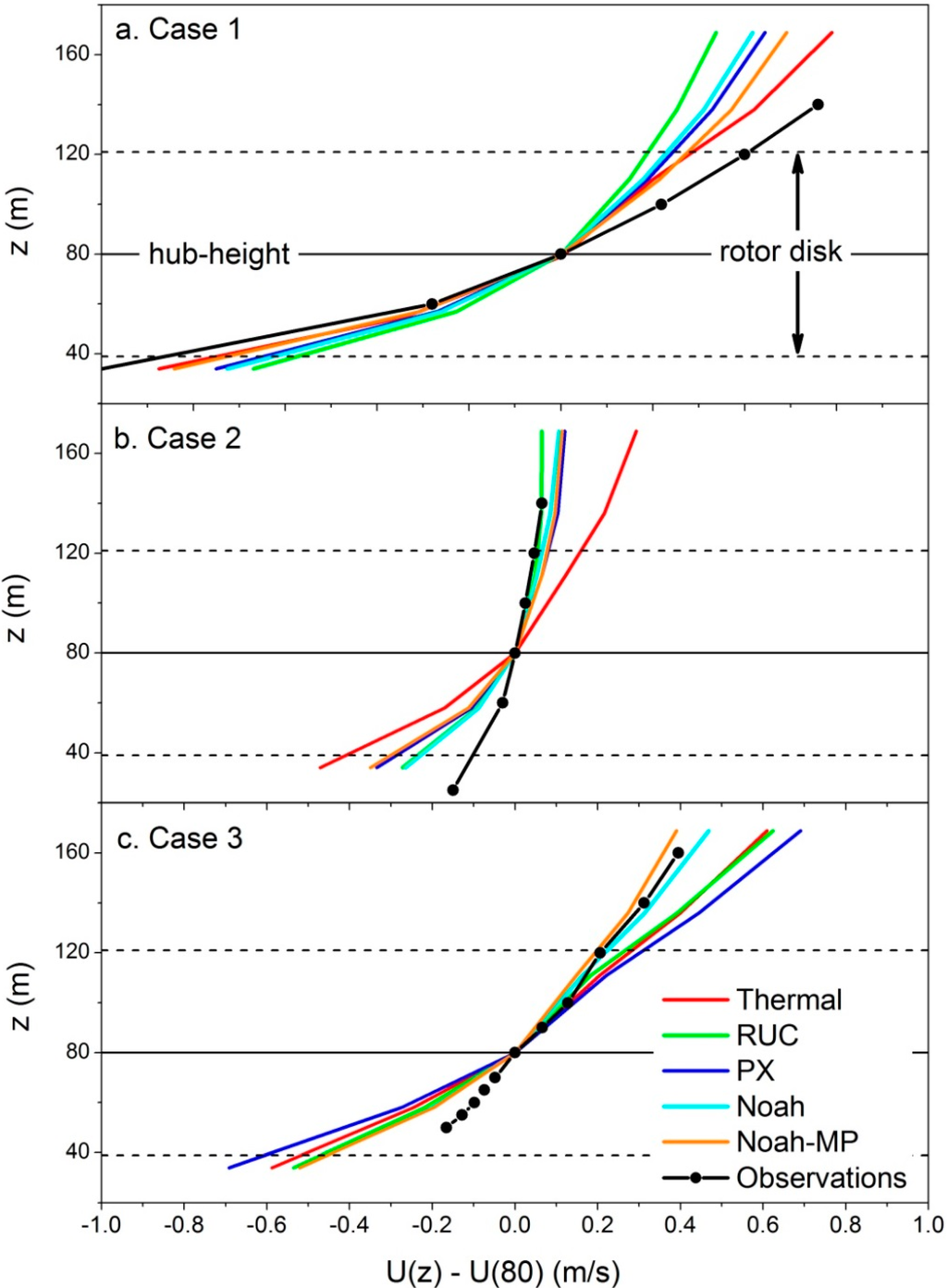
Figure 8.
Mean midday wind speed profiles during (a) Case 1, (b) Case 2, and (c) Case 3 for each LSM in comparison to the observations shown in black. The four Noah-MP runs are shown as a group average. The wind speeds are plotted as the difference between the wind speed at height (z) and the wind speed at 80 m (wind turbine hub-height). Blades on nearby turbines span from 40 to 120 m in the atmosphere. Differences in shear profiles represent differences in the mean wind speed across a turbine rotor-disk.
3.3. Relationship between Wind Shear and Surface Energy Exchange
The following analysis was done to identify periods of significant land surface-atmosphere feedbacks. A relationship between midday wind shear and midday Bowen ratio in June and July is seen in the observations. Cases 1 and 2 in Figure 9 show a decline in wind shear with increasing β; i.e., increased atmospheric mixing is associated with a higher portion of the available energy re-emitted as the buoyant heat flux. Slopes were −0.019 in June and −0.006 in July. As expected this trend was not seen in November–December (slope = +0.003) namely because land surface-atmosphere feedbacks are much weaker during the autumn months at this site.
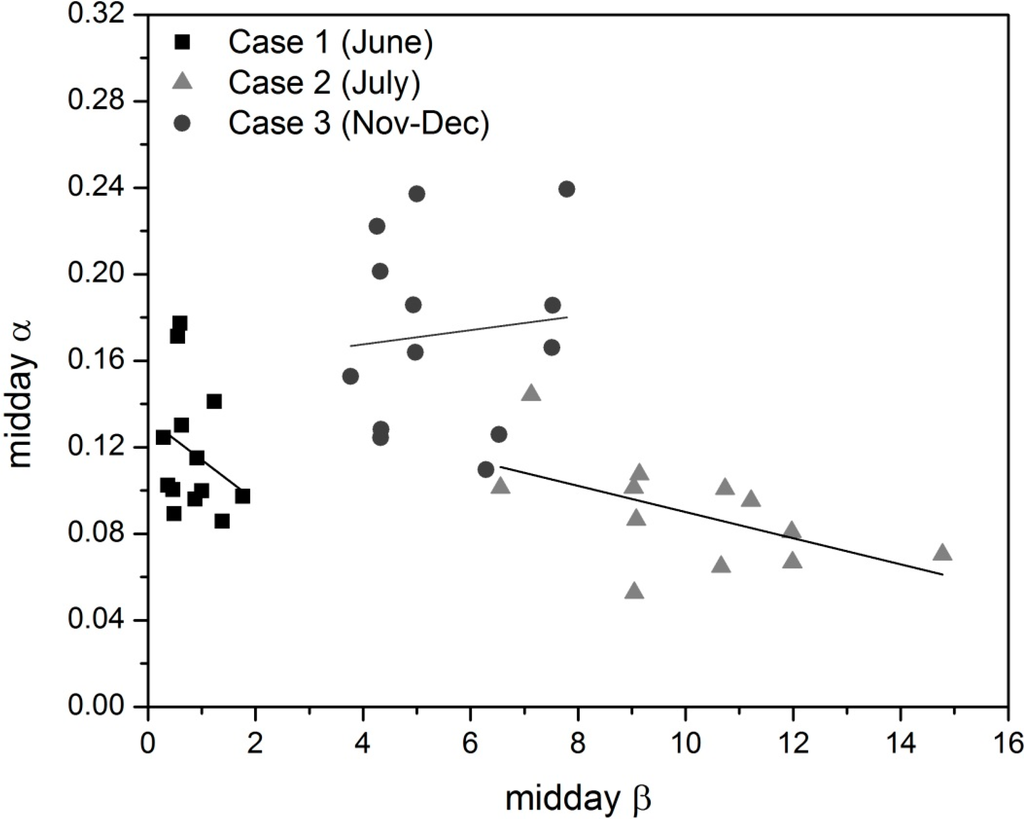
Figure 9.
Scatter plots of observed wind shear exponents (α) and observed Bowen ratios (β) for all three cases. Plotted are daily mean midday values. This plot shows a similar correlation between wind shear and surface energy exchange during the summer months. In Cases 1 and 2 higher β (sensible heat > latent heat) was correlated with less wind shear (lower α). This relationship is not seen during the cool, dry Case 3 period which indicates a weaker surface-atmosphere forcing in November–December.
Figure 10 shows the relationship between mean midday Bowen ratio and wind shear parameter for each LSM in comparison to the mean observation for each case period. As in Figure 9, Figure 10 also shows a relationship between simulated energy flux partitioning and simulated wind shear. For example, simulations of greater wind shear (higher α) were correlated to lower Bowen ratios, such as those predicted by the thermal diffusion and PX models. Simulations of lower wind shear or a well-mixed atmosphere were correlated to higher Bowen ratio predictions, such as RUC in Case 1 and Noah-MP in Case 3. One exception was the RUC performance in Case 2 whereby RUC simulated an outlier Bowen ratio that did not fit the pattern.
In Case 1 the LSMs closest to the observations included those with explicit vegetation-atmosphere processes (PX, Noah and Noah-MP); however, the complexity of these feedbacks (such as those found in Noah-MP) did not improve model performance. In Case 2 nearly all of the models predicted more shear and lower Bowen ratios than the observations with the exception of RUC which largely overestimated β. In Case 3 the LSMs predicted a wide range of Bowen ratios which is partially attributed to the sensitivity of β to small H and LE magnitudes (i.e., available energy was much lower during the autumn than during the summer months). These plots suggest a strong connection between the magnitude of simulated wind shear and the partitioning of surface energy fluxes in the model. These results also suggest that LSM choice in WRF via land-atmosphere connections has a significant impact on simulated wind flow at heights relevant to wind energy.
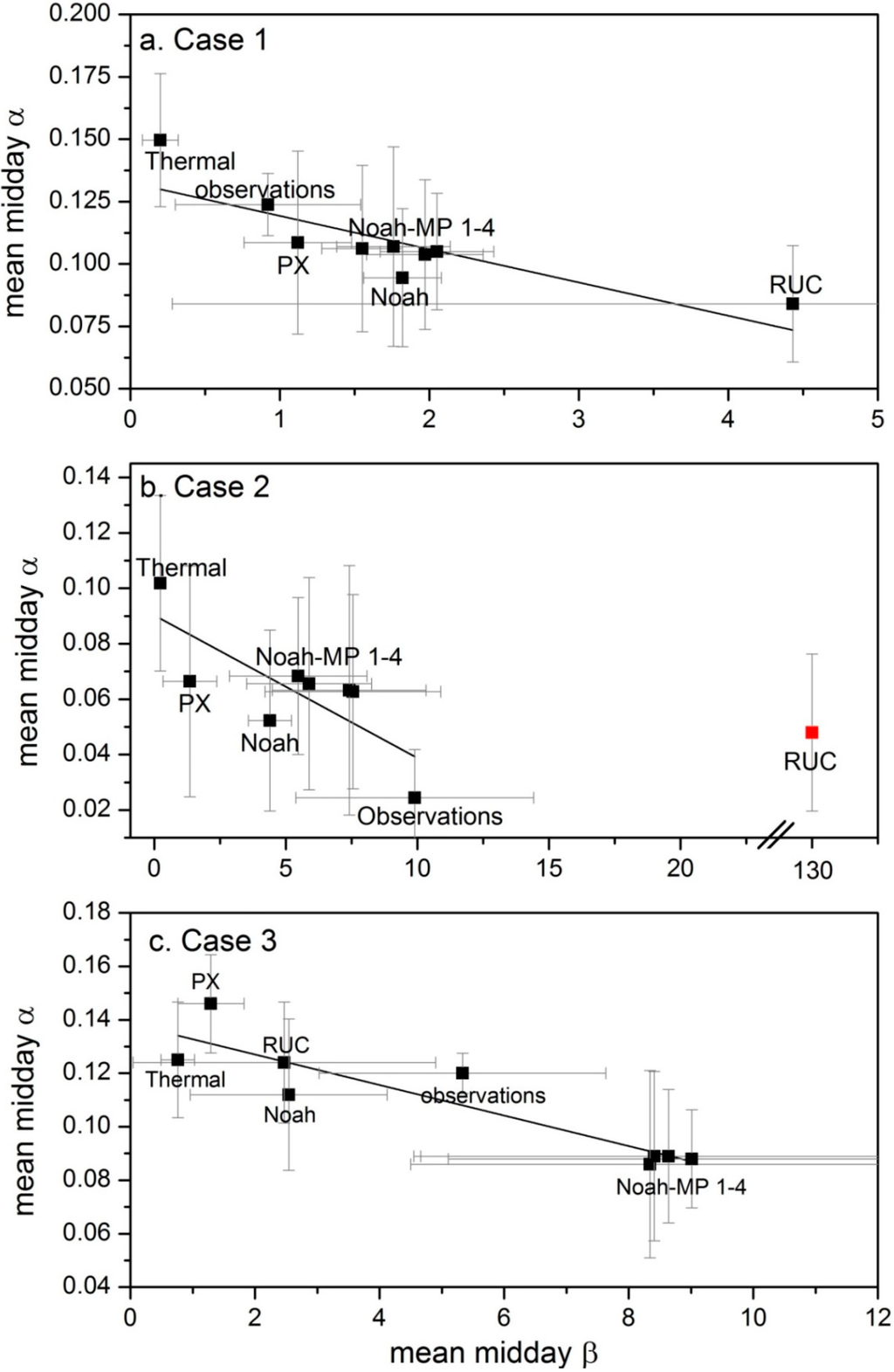
Figure 10.
Scatter plot of mean (± standard deviation) midday values of Bowen ratio and wind shear exponent for each LSM and the observations for (a) Case 1 (June 2011); (b) Case 2 (July 2011) and (c) Case 3 (November–December 2012). The data are fitted with a linear regression model (Case 1 slope = −0.013, R2 = 0.66; Case 2 slope = −0.005, R2 = 0.55; Case 3 slope = −0.006, R2 = 0.82). Models which simulated higher Bowen ratios (sensible heat > latent heat) tended to simulate less wind shear.
4. Conclusions
We conducted this study to look for relationships between observed wind shear and land surface energy exchange processes and to determine whether the choice of land surface model in WRF significantly influences the magnitudes of simulated wind inflow at rotor-disk height.
The flux tower and wind profile observations showed a relationship between energy partitioning at the surface and wind shear during the warm summer months when surface-atmosphere energy exchange coupling should be at its peak. As expected, stronger convection and less wind shear occurred during periods when buoyant heat fluxes dominated the surface energy exchange. This relationship was not found during the autumn “control” period; however, as surface energy forcing was relatively weak.
Overall, the simplest LSMs tended to have the poorest performance in estimating the surface energy budget and to a smaller extent with simulating wind shear. These models included the thermal diffusion model and the RUC model; however, the latter model had very inconsistent results across the three cases. These two models have either simple or no vegetative-atmosphere feedback processes. In addition, thermal diffusion uses a fixed soil moisture value based only on land use category. Making further conclusions based on model sophistication of soil–plant–atmosphere processes is however difficult as the PX, Noah, and Noah-MP performances were not consistently different from each other.
We had expected to see seasonal differences in model performance as the observed canopy and surface meteorological conditions varied greatly across the three cases. However, the range of LSM errors did not appear to differ dramatically from one period to another. Between Case 1 and Case 2, it is likely that the models are responding to atmospheric drivers (e.g., precip, temp, wind speed) from the boundary conditions as the land surface conditions (e.g., land-use category, zo) did not significantly change in the models. For example, in Case 1, Noah-MP predicted a higher Bowen ratio than observed (i.e., higher sensible heat flux, lower ET flux) possibly indicating that the model’s classification of the canopy was not as photosynthetically-active as observed in the field. This may be because canopy values are averaged across the whole life-span of crops whereas in Case 1 the crops were (for a time at least) at peak density and peak ET rates. While in Case 2, Noah-MP is using the same land surface conditions as in Case 1 and underestimates the Bowen ratio whereas the observations show higher Bowen ratios as is expected for bare soil.
Case 2 (summer) and Case 3 (winter) were dominated by differences in atmospheric drivers for the surface energy fluxes, e.g., temperature and precipitation, in addition to differences in the model’s interpretation of surface conditions. Despite Cases 2 and 3 having the same surface type (bare soil), the models that consider vegetation are interpreting both cases as having a crop canopy with varying surface roughness.
Generally we saw larger simulation errors in the wind speed profiles below hub-height (<80 m) than at heights above. This error affects the accuracy of the simulated rotor-disk wind speed. For example, in Cases 2 and 3 the simulated wind speeds in the bottom half of the rotor-disk were less than those observed. We also saw differences in the wind shear parameters amongst the LSM members even during the cool autumn Case 3 when land surface energy-atmosphere feedbacks should be negligible. This is because the wind speed profile is sensitive to other factors including the surface drag induced by canopy roughness. For example, in [16] the authors found that differences in the roughness length, z0, from changing the landscape from a corn canopy (zo = 0.25 m) to soybean (zo = 0.10 m) in the Noah LSM, increased hub-height wind speed and decreased wind shear in the U.S. Midwest. As changes in surface roughness affect surface drag, they also saw larger effects on wind shear in the bottom half of the rotor-disk. Although our study did not explicitly consider the impact of zo on the simulated wind profiles, we did see noticeable differences in zo of up to 0.10 m both across seasons and amongst LSMs. The largest differences between models occurred during Case 3 whereby values for PX (zo = 0.12 m) were higher than those found for thermal diffusion and RUC (zo = 0.05 m). The largest differences between seasons occurred within both thermal diffusion and RUC whereby summer values were 0.10 m greater than those in winter. These differences in zo may partially explain why we saw differences in wind shear during the winter “control” run in Case 3.
A portion of our simulation errors are also due to a mismatch between spatial and temporal scales. We ran WRF down to 1 km (mesoscale) resolution while the flux tower and wind profile instruments had a footprint closer to 200 m. Flow could have significant variability even across these scales with the existing sharp gradients of land use and soil moisture in this area. WRF was run with a land use category defined as Dry Cropland and Pastureland while in reality the canopy type varied across space and time during the simulation periods. The LSMs used here with the finest temporally adjusted land cover input were Noah and Noah-MP. A monthly time step may not have high enough precision. For example, the crop rapidly changed during two of our cases, Case 1 and 2. The crop quickly senesced over a period of a couple of weeks but this information was not in the standard versions of WRF. For example, WRF was reinitialized with new soil moisture conditions between the June and July 2011 simulations but it used the same land use based surface characteristics even though in reality the field was tilled during these four weeks in 2011. Further improvements to simulating the wind fields in this area could be done by using land use data with finer spatial and temporal resolution. For example, [33] found that the SGP region requires the characterization of vegetation properties in LSMs at a realistic spatial scale for accurately estimating surface energy fluxes. Thus, the SGP region may need LSMs with the capability of accurately specifying surface characteristics on a sub-grid scale, such as from satellite-derived products, to capture fine scale variability, including senescence, harvest and tillage events. Whether data assimilation of surface properties would also improve wind forecasting was beyond the scope of this paper but warrants exploration.
This study was conducted as an evaluation of running each LSM in WRF in “standard” mode as a wind farm operator might do without significantly fine-tuning each LSM to ensure the best performance. For example, some of the LSMs investigated here have options for remote sensing surface data assimilation (e.g., RUC, Noah-MP) which may have enhanced model performance. With these caveats in mind we showed that wind shear is sensitive to the choice of LSM. This is a significant finding, as wind shear across the rotor-disk has a significant impact on the power produced by the wind turbine [20,23]. Any improvement in short-term wind forecasting should drive down the cost of wind energy and further wind as a leading form of low cost renewable energy in the coming decade [67].
Lastly, we did not have available data to illustrate a link between surface energy exchange processes and turbine power production via the influence on the wind shear profiles. Although the SGP ARM site is located a few miles east of some of the turbines within a multi-MW wind farm, turbine measurements of power were not available during the case studies modeled here as the wind farm did not begin operations until 2013. New simulations should be done during periods of concurrent wind power data to assess the relationship between surface energy exchange, wind shear and power production at this wind farm.
Acknowledgments
This work was funded by the US Department of Energy, Wind and Water Power Technologies Office under agreement #WBS 02.07.00.01. The flux tower and surface meteorology observations were supported by the Office of Biological and Environmental Research of the US Department of Energy under contract No. DE-AC02-05CH11231 as part of the Atmospheric Radiation Measurement (ARM) and Atmospheric System Research programs. The authors would like to thank the staff at the SGP ARM Central Facility for their help with maintaining the Wind Cube lidar system and their support throughout our study. We’d also like to thank Marc Fischer and Margaret Torn (LBNL) for their support with the flux tower data and Rob Newsom (PNNL) for his support with the Halo lidar data. LLNL is operated by Lawrence Livermore National Security, LLC, for the DOE, National Nuclear Security Administration under contract DE-AC52-07NA27344. LLNL-JRNL-658967
Author Contributions
Sonia Wharton was responsible for project management and led the project design and data analysis. Matthew Simpson and Jessica Osuna ran the WRF simulations and provided discussion on the LSMs. Jennifer Newman helped with the lidar deployment and data analysis. Sebastien Biraud provided the surface flux and meteorological tower data and provided guidance on those datasets. All authors contributed to the writing of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lew, D.; Milligan, M.; Jordan, G.; Piwko, R. Value of Wind Power Forecasting; NREL Report No. CP-5500–50814; NREL: Golden, CO, USA, 2011. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3. NCAR Technical Report 2008. Available online: http://www.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf (accessed on 2 February 2014).
- American Wind Energy Association. Oklahoma Wind Energy Fact Sheet April 2014. Available online: http://awea.files.cms-plus.com/images/oklahoma.pdf (accessed on 21 May 2014).
- Wiser, R.; Bolinger, M.; Barbose, G.; Darghouth, N.; Hoen, B.; Mills, A.; Weaver, S.; Porter, K.; Buckley, M.; Fink, S.; Oteri, F.; Tegen, S. 2012 Wind Technologies Market Report; DOE/GO-102013–3948; U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy: Washington, DC, USA, 2013. [Google Scholar]
- Chen, F.; Bornstein, R.; Grimmond, S.; Li, J.; Liang, X.; Martilli, A.; Miao, S.; Voogt, J.; Wang, Y. Research priorities in observing and modeling urban weather and climate. Bull. Am. Meteorol. Soc. 2012, 93, 1725–1728. [Google Scholar] [CrossRef]
- Anderson, D.E.; Verma, S.B. Carbon-dioxide, water-vapor and sensible heat exchanges of a grain-sorghum canopy. Bound. Layer Meteor. 1986, 34, 317–331. [Google Scholar] [CrossRef]
- Baldocchi, D.D. A comparative study of mass and energy exchange rates over a closed C-3 (wheat) and an open C-4 (corn) crop. Part 2: CO2 exchange and water use efficiency. Agric. For. Meteorol. 1994, 67, 291–321. [Google Scholar] [CrossRef]
- Betts, A.K.; Ball, J.H.; Beljaars, A.C.M.; Miller, M.J.; Viterbo, P.A. The land surface-atmosphere interaction: A review based on observational and global model perspectives. J. Geophys. Res. 1996, 101, 7209–7225. [Google Scholar] [CrossRef]
- Raupach, M.R. Equilibrium evaporation and the convective boundary layer. Bound. Layer Meteor. 2000, 96, 107–141. [Google Scholar] [CrossRef]
- Patton, E.G.; Sullivan, P.P.; Moeng, C.-H. The influence of idealized heterogeneity on wet and dry planetary boundary layers coupled to the land surface. J. Atmos. Sci. 2004, 62, 2078–2097. [Google Scholar] [CrossRef]
- Desai, A.R.; Davis, K.J.; Senff, C.J.; Ismail, S.; Browell, E.V.; Stauffer, D.R.; Reen, B.P. A case study of the effects of heterogeneous soil moisture on mesoscale boundary-layer structure in the Southern Great Plains, U.S.A. Part 1: Simple prognostic model. Bound. Layer Meteorol. 2006, 119, 195–238. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The groundwater-land surface-atmosphere connection: Soil moisture effects on the atmospheric boundary layer in fully-coupled simulations. Adv. Water Resourc. 2007, 30, 2447–2466. [Google Scholar] [CrossRef]
- Fischer, M.L.; Billesbach, D.P.; Riley, W.J.; Berry, J.A.; Torn, M.S. Spatiotemporal variations in growing season exchanges of CO2, H2O, and sensible heat in agricultural fields of the Southern Great Plains. Earth Interact. 2007, 11, 1–21. [Google Scholar] [CrossRef]
- Storm, B.; Basu, S. The WRF model forecast-derived low-level wind shear climatology over the United States Great Plains. Energies 2010, 3, 258–276. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Vanderwende, B.J.; Lundquist, J.K. Could crop height impact the wind resource at agriculturally productive wind farms? In Proceedings of the 21st Symposium on Boundary Layers and Turbulence, Leeds, UK, 9–13 June 2014.
- Rohatgi, J.; Barbezier, G. Wind turbulence and atmospheric stability—Their effects on wind turbine output. Renew. Energy 1999, 16, 908–911. [Google Scholar] [CrossRef]
- Sumner, J.; Masson, C. Influence of atmospheric stability on wind turbine power performance curves. J. Sol. Energy Eng. 2006, 128, 531–537. [Google Scholar] [CrossRef]
- Van den Berg, G.P. Wind turbine power and sound in relation to atmospheric stability. Wind Energy 2008, 11, 151–169. [Google Scholar] [CrossRef]
- Wagner, R.; Antoniou, I.; Pedersen, S.M.; Courtney, M.S.; Jørgensen, H.E. The influence of the wind speed profile on wind turbine performance measurements. Wind Energy 2009, 12, 348–362. [Google Scholar] [CrossRef]
- Vanderwende, B.J.; Lundquist, J.K. The modification of wind turbine performance by statistically distinct atmospheric regimes. Environ. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Wharton, S.; Lundquist, J.K. Assessing atmospheric stability and its impact on rotor disk wind characteristics at an onshore wind farm. Wind Energy 2012, 15, 525–546. [Google Scholar] [CrossRef]
- Wharton, S.; Lundquist, J.K. Atmospheric stability affects wind turbine power collection. Environ. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Trier, S.B.; Davis, C.A.; Ahijevych, D. Environmental controls on the simulated diurnal cycle of warm-season precipitation in the Continental United States. J Atmos. Sci. 2010. [Google Scholar] [CrossRef]
- LeMone, M.A.; Grossman, R.L.; Coulter, R.L.; Wesley, M.L.; Klazura, G.E.; Poulos, G.S.; Blumen, W.; Lundquist, J.K.; Cuenca, R.H.; Kelly, S.F.; et al. Land–atmosphere interaction research and opportunities in the Walnut River watershed in Southeast Kansas: CASES and ABLE. Bull. Am. Meteorol. Soc. 2000, 81, 757–779. [Google Scholar]
- Weckwerth, T.; Parsons, D.B.; Koch, S.E.; Moore, J.A.; LeMone, M.A.; Demoz, B.B.; Flamant, C.; Geerts, B.; Wang, J.; Feltz, W.F. An overview of the International H2O Project (IHOP_2002) and some preliminary highlights. Bull. Am. Meteorol. Soc. 2004, 85, 253–277. [Google Scholar] [CrossRef]
- LeMone, M.A.; Chen, F.; Alfieri, J.G.; Tewari, M.; Geerts, B.; Miao, Q.; Grossman, R.L.; Coulter, R.L. Influence of land cover and soil moisture on the horizontal distribution of sensible and latent heat fluxes in Southeast Kansas during IHOP_2 and CASES-97. J. Hydrometeorol. 2007, 8, 68–87. [Google Scholar] [CrossRef]
- Miller, J.; Barlage, M.; Zeng, X.; Wei, H.; Mitchell, K.; Tarpley, D. Sensitivity of the NCEP/Noah land surface model to the MODIS green vegetation fraction data set. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Case, J.L.; LaFontaine, F.J.; Kumar, S.V.; Peters-Lidard, C.D. Using the NASA-Unified WRF to assess the impacts of real-time vegetation on simulations of severe weather. In Proceedings of the 13th Annual WRF User’s Workshop, Boulder, CO, USA, 26–29 June 2012; pp. 1–69.
- Torn, M.S.; Biraud, S.C.; Still, C.J.; Riley, W.J.; Berry, J.A. Seasonal and interannual variability in 13C composition of ecosystem carbon fluxes in the U.S. Southern Great Plains. Tellus 2011, 63B, 181–195. [Google Scholar] [CrossRef]
- Billesbach, D.P.; Fischer, M.L.; Torn, M.S.; Berry, J.A. A portable eddy covariance system for the measurement of ecosystem-atmosphere exchange of CO2, water vapor, and energy. J Atmos. Ocean. Technol. 2004, 21, 639–650. [Google Scholar] [CrossRef]
- Riley, W.J.; Biraud, S.C.; Torn, M.S.; Fischer, M.L.; Billesbach, D.P.; Berry, J.A. Regional CO2 and latent heat surface fluxes in the Southern Great Plains: Measurements, modeling, and scaling. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Raz-Yaseef, N.; Fischer, M.L.; Billesbach, D.P.; Biraud, S.C.; Gunter, S.A.; Bradford, J.A.; Torn, M.S. Drought sensitivity of three U.S. southern plains ecosystems. Environ. Res. Lett. submitted.
- Finkelstein, P.L.; Sims, P.F. Sampling error in eddy correlation flux measurements. J. Geophys. Res. 2001, 106, 3503–3509. [Google Scholar] [CrossRef]
- Obukhov, A.M. Turbulence in an atmosphere with a non-uniform temperature. Bound. Layer Meteorol. 1971, 2, 7–29. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Quart. J. Roy. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound. Layer Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar]
- Newsom, R.K. Doppler Lidar Handbook. Office of Biological and Environmental Research, Office of Science, U.S. Department of Energy: Washington, DC, USA. Available online: http://www.arm.gov/publications/tech_reports/handbooks/dl_handbook.pdf (accessed on 15 December 2014).
- Emeis, S. Measurement Methods in Atmospheric Sciences: In-Situ and Remote; Borntraeger Science Publishers: Stuttgart, Germany, 2010. [Google Scholar]
- Betancur, S.; Lemoine, R.; Boinne, R.; Mail, P.-A.; Dewilde, L. Reducing risk in resource assessment using lidar. In Proceedings of the WindExpo Conference, Guadalajara, Mexico, 5–7 November 2008.
- Cañadillas, B.; Westerhellweg, A.; Neumann, T. Testing the performance of a ground-based wind LiDAR system: One year intercomparison at the offshore platform FINO1. Dewi Mag. 2011, 38, 58–64. [Google Scholar]
- Blackadar, A.K. Modeling pollutant transfer during daytime convection. In Proceedings of the Fourth Symposium on Atmospheric Turbulence, Diffusion and Air Quality, Reno, NV, USA, 15–18 January 1979; pp. 443–447.
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G. Performance of different soil model configurations in simulating ground surface temperature and surface fluxes. Mon. Weather Rev. 1997, 125, 1870–1884. [Google Scholar] [CrossRef]
- Pleim, J.E.; Xiu, A. Development and testing of a surface flux and planetary boundary layer model for application in mesoscale models. J. Appl. Meteor. 1995, 34, 16–32. [Google Scholar] [CrossRef]
- Xiu, A.; Pleim, J.E. Development of a land surface model. Part I: Application in a mesoscale meteorological model. J. Appl. Meteor. 2001, 40, 192–209. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.-L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011. [Google Scholar] [CrossRef]
- Stauffer, D.R.; Seaman, N.L. On multi-scale four-dimensional data assimilation. J. Appl. Meteor. 1994, 33, 416–434. [Google Scholar] [CrossRef]
- Liu, Y.; Bourgeois, A.; Warner, T.; Swerdlin, S.; Hacker, J. An implementation of obs-nudging-based FDDA into WRF for supporting ATEC test operations. In Proceedings of the WRF User Workshop, Boulder, CO, USA, 27–30 June 2005. Paper 10.7.
- Stauffer, D.R.; Seaman, N.L. Use of four-dimensional data assimilation in a limited-area mesoscale model. Part I: Experiments with synoptic-scale data. Mon. Weather Rev. 1990, 118, 1250–1277. [Google Scholar] [CrossRef]
- Lo, J.C.F.; Yang, Z.L.; Pielke, R.A., Sr. Assessment of three dynamical climate downscaling methods using the Weather Research and Forecasting (WRF) model. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Otte, T.L. The impact of nudging in the meteorological model for retrospective air quality simulations. Part I: Evaluation against national observation networks. J. Appl. Meteorol. Climatol. 2008, 47, 1853–1867. [Google Scholar] [CrossRef]
- Salathé, E.P.; Steed, R.; Mass, C.F.; Zahn, P.H. A high-resolution climate model for the U.S. Pacific Northwest: Mesoscale feedbacks and local responses to climate change. J. Clim. 2008, 21, 5708–5726. [Google Scholar] [CrossRef]
- Bowden, J.H.; Otte, T.L.; Nolte, C.G.; Otte, M.J. Examining interior grid nudging techniques using two-way nesting in the WRF model for regional climate modeling. J. Clim. 2012, 25, 2805–2823. [Google Scholar] [CrossRef]
- Pan, H.-L.; Mahrt, L. Interaction between soil hydrology and boundary layer development. Bound. Layer Meteorol. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2(NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. 2012. [Google Scholar] [CrossRef]
- Yang, Z.L.; Dickinson, R.E. Description of the Biosphere-Atmosphere Transfer Scheme (BATS) for the Soil Moisture Workshop and evaluation of its performance. Glob. Planet. Chang. 1996, 13, 117–134. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Dickinson, R.E.; Gulden, L.E. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res. 2005. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.-L.; David, C.H.; Niu, G.-Y.; Rodell, M. Hydrological evaluation of the Noah-MP land surface model for the Mississippi River basin. J. Geophys. Res. 2014. [Google Scholar] [CrossRef]
- Blyth, E.; Gash, J.; Lloyd, A.; Pryor, M.; Weedon, G.P.; Shuttleworth, J. Evaluating the JULES land surface model energy fluxes using FLUXNET data. J. Hydrometeorol. 2010, 11, 509–519. [Google Scholar] [CrossRef]
- Gaylor, S.; Wohling, T.; Grzeschik, M.; Ingwersen, J.; Wizemann, H.D.; Warrach-Sagi, K.; Hogy, P.; Attinger, S.; Streck, T.; Wulfmeyer, R. Incorporating dynamic root growth enhances the performance of Noah-MP at two contrasting winter wheat field sites. Water Resourc. Res. 2014, 50, 1337–1356. [Google Scholar] [CrossRef]
- Van Wijk, A.J.M.; Beljaars, A.C.M.; Holtslag, A.A.M.; Turkenburg, W.C. Evaluation of stability corrections in wind speed profiles over the North Sea. J. Wind Eng. Ind. Aerodyn. 1990, 33, 551–566. [Google Scholar] [CrossRef]
- Elliott, D.L.; Cadogan, J.B. Effects of wind shear and turbulence on wind turbine power curves. In Proceedings of the European Community Wind Energy Conference and Exhibition, Madrid, Spain, 10–14 September 1990.
- Kelley, N.; Shirazi, M.; Jager, D.; Wilde, S.; Adams, J.; Buhl, M.; Sullivan, P.; Patton, E. Lamar Low-Level Jet Project Interim Report; NREL/TP-500–34593; NREL: Golden, CO, USA, 2004; pp. 1–216. [Google Scholar]
- Department of Energy, Energy Efficiency and Renewable Energy. Wind Program Complex Flow Workshop Report; Department of Energy, Energy Efficiency and Renewable Energy: Boulder, CO, USA, 2012; pp. 1–122. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).