Abstract
The thermally driven wind over mountainous terrains challenges the estimation of CO2 exchange between forests and the atmosphere when using the eddy covariance technique. In this study, the wind regimes were investigated in a temperate deciduous forested valley at the Maoershan site, Northeast China. The wind direction above the canopy was preferentially up-valley in the daytime and down-valley in the nighttime, corresponding to the diurnal patterns of above-canopy temperature gradient and stability parameter. In both leaf-on and -off nighttime, a down-valley flow with a maximum velocity of 1~3 m∙s−1 was often developed at 42 m above the ground (2.3-fold of the canopy height). However, the below-canopy prevailing wind was down-slope in the night, contrast to the below-canopy temperature lapse and unstable conditions. This substantial directional shear illustrated shallow slope winds were superimposed on larger-scale valley winds. As a consequence, the valley-wind component becomes stronger with increasing height, indicating a clear confluence of drainage flow to the valley center. In the daytime, the below-canopy wind was predominated down-slope due to the temperature inversion and stable conditions in the leaf-on season, and was mainly up-valley or down-slope in the leaf-off season. The isolation of momentum flux and radiation by the dense canopy played a key role in the formation of the below-canopy unaligned wind and inverse stability. Significant lateral kinematic momentum fluxes were detected due to the directional shear. These findings suggested a significant interaction between slope and valley winds at this site. The frequent vertical convergence / divergence above the canopy and horizontal divergence/convergence below the canopy in the nighttime / daytime is likely to induce significant advections of trace gases and energy flux.
1. Introduction
The eddy covariance technique (EC) has been widely used to calculate the long-term net CO2 exchange (NEE) between the atmosphere and terrestrial ecosystems in the last two decades [1]. However, the accuracy of EC measurements of NEE has been questioned particularly over tall vegetation in complex terrains [2,3,4,5,6,7] and even over various forests with relative flat terrains [7,8]. One of the key factors that results in uncertainties in measuring scalar exchanges between the atmosphere and forests is the complexity of airflow above and within the forest canopy [4,9,10,11]. Understanding mechanisms of airflow above and within a forest canopy provides a basis for interpreting nighttime CO2 fluxes above the forest canopy [10,12,13,14].
In mountainous regions, disproportionate heating and cooling between airs in the valley slopes and the surrounding area result in mountain-valley circulations [15]. The nocturnal flows are typically down-slope and/or down-valley due to a surface temperature inversion, while the daytime airflows are normally up-slope and/or up-valley resulting from radiative heating and temperature lapse conditions [15]. On relatively simple sloping topography, the strength of the drainage flows (down-slope and down-valley winds) depends on slope gradient, distance from the crest, atmospheric stability and canopy structure [9,16,17,18,19]; on complex topography, the strength may be influenced by interactions between slope winds and valley winds [20,21,22,23]. In typical valley terrains, as the air cools down due to a negative radiation budget on the slope, a temperature inversion layer near the ground is developed before sunset. The cool air at the sidewalls moves downward along the slope, and then these flows converge on the valley floor with the flows downward along the valley axis [21]. Because the down-slope and down-valley winds are typically in orthogonal directions in most valleys, there is often a considerable directional shear through the slope wind layer [20]. In the daytime after sunrise, the radiative heating gradually breaks down the temperature inversion and then reverses the down-slope (down-valley) wind to up-slope (up-valley) wind [15]. Such wind regimes result in the complex nature of scalar transport, and make EC measurements in hilly topography difficult [11,24,25].
Forests, with tall canopies, are often distributed in mountainous terrains, which lead to a more complex wind regime than short vegetations (e.g., grassland, cropland) [12,18,26]. When a slope is covered by high and dense forest, the radiating surface to the night sky turns upward to the canopy, rather than the ground [27], and even an opposite temperature gradient is formed below canopy compared with that above canopy [24,28,29]. These situations are quite different with those of open canopy forest or bare ground. Beneath such dense and high forest canopies, persistent subcanopy nighttime upward and daytime downward flow patterns are observed [10,30], which contradicts the typical thermally driven winds [15]. Another distinct feature of dense canopy wind is the core of drainage flow may be beyond the canopy height [29,31]. However, the effects of the density of the canopy on generating a decoupling subcanopy layer and elevating the airflow are still not well known.
Most studies on wind regimes focus on nocturnal flows particularly in the leaf-on season, and few account for seasonal variations in thermally driven flows at small scales [10,31,32]. Daytime coupling/decoupling of airflows above and below forest canopy was investigated for a few studies [10,13]. However, because of the site-specific wind regime, it needs more researches to gain a general perspective on canopy winds in a complex topography. The combination of slope flows on the sidewalls and boundary layer processes on and above the valley floor is likely to cause valley winds [15], but the interaction between slope and valley winds in a forested area is poorly understood [10,22,30,33].
At the Maoershan Forest Ecosystem Research Station, a site of ChinaFLUX in Chinese temperate forests, Jiao et al [34] previously found that the daytime up-valley and nocturnal down-valley winds above the canopy had a classic characteristics of thermally driven winds. Accumulation of CO2 under canopy at night was frequently observed during the summer. However, daytime temperature inversion under the dense forest canopy occurred frequently at this site [34]. Therefore, we are attempted to tackle the following questions: how do the wind regimes (i.e., wind directions and velocities) in this forested valley vary vertically during the daytime and nighttime in both leaf-on and leaf-off seasons? Are there significant interactions between slope and valley winds at this site? Are the wind regimes influenced by the buoyancy forcing and atmospheric stability? What implications are the wind systems above and within the forest canopy to the EC measurements of NEE in complex terrains? To address these questions, we used the wind and temperature data on the 48-m-high flux tower at the Maoershan site to explore the diurnal variations and vertical shears of the canopy air flows in both nighttime and daytime during leaf-on and leaf-off seasons.
2. Slope/Valley Wind Theory
The slope wind system is a diurnal thermally driven wind system that blows up or down the slopes of a valley sidewall or an isolated hill or mountain, with upslope flows during daytime and down-slope flows during nighttime [15]. Slope flows result from the cooling or heating of an air layer over the slope relative to air at the same elevation away from the slope. The velocity of such thermotopographic flows depends largely on the scales of the flow and the forcing [10]. The drivers of thermotopographic flows may be examined using the equations of motion and the heat equation following Mahrt [35] and Zardi and Whiteman [15]. Here, we cite the three equations to provide a framework for our arguments. These equations are expressed base on a coordinate system that is oriented along (s) and perpendicular (n) to an infinitely extended slope of uniform inclination angle α [35]. n is perpendicular to the slope and increases upwards; s is parallel to the slope and increases in the down-slope direction. Using the Boussinesq approximation, the along-slope and slope perpendicular equations of motion, the thermodynamic energy equation, and the continuity equation are then written as
where u and w are the velocity components parallel to s and n, respectively. ρ is air density, and P is barometric pressure. θ is a reference value for the virtual potential temperature at the ground in the absence of surface cooling or heating, g is the gravitational acceleration, cp is the specific heat of air at constant pressure, R is the upward radiative flux, and and are the kinematic turbulent Reynolds fluxes of momentum and heat. Variables with subscript “0” denote the mean conditions in the absence of slope flow, unsubscripted variables denote locally perturbed mean conditions associated with cooling/warming within the slope flow layer, and primes denote turbulent fluctuations around a local mean. The ambient pressure Pa is determined from hydrostatic balance. In this framework, it is assumed that the ambient air, in the absence of thermally driven flow, is at rest. Note that, consistent with the assumption of a shallow layer, equation (1) includes only the slope-normal turbulent fluxes, and lateral momentum fluxes are ignored. For simplicity, latent heat fluxes are not included here, although they can sometimes play a crucial role in the overall energy budgets. Accelerations normal to the slope are generally considered negligible so that the atmosphere normal to the slope is in quasi-hydrostatic balance and the RHS of Equation (2) is practically zero.
It is instructive to consider which terms in these equations are most important for understanding slope flow physics. Down-slope flows are not governed by slope angle (gravity) alone, but controlled synergistically by slope cooling, ambient stratification and vegetation structure [17]. Although the most important factor of optimal down-slope wind is slope angle [17], for a given site (the slope angle is fixed), the key term that drives slope flows is the buoyancy caused by the temperature excess or deficit that forms over the slope (second term on the right hand side of Equation (1)) [15].
Valleys, with geometries more complex than simple slopes, exhibit that the radiation patterns and thermally driven winds are consequently more complex. Unlike slope winds, diurnal valley winds are thermally driven that blow along the axis of a valley, with up-valley flows during daytime and down-valley flows during nighttime [15]. Valley winds are not primarily a function of the slope of the underlying valley floor. Instead, they depend on other geometrical factors, such as the shape and aspect of the valley cross-section and their along-valley variations [15]. The dynamics of diurnal valley winds results from the combination of slope flows on the sidewalls and boundary layer processes on and above the valley floor, including such factors as free convection, shear, and compensatory subsidence in the valley core atmosphere.
The evolution of real thermally driven winds is usually determined by the topographic setting and the flow and energy budget at a larger scale [22,36]. Highly complex terrain can be viewed as a series of valleys and slopes, with small slopes converging into small valleys or basins, which in turn merge to form larger and larger scale slopes or valleys [10,21]. In such topography, thermally driven winds may be generated at many different scales, with flow in the thin layer nearest to the ground responding to the local slope and local forcings and thicker flows responding to large-scale slopes and large-scale forcings [22,36]. Thermal and dynamical properties of flows at any scale influence flows on both larger and smaller scales [37]. Therefore, dynamic interactions between the slope and valley flows are typically observed on valley sidewalls [15].
Thermotopographic flows in vegetated terrain (particularly tall forested terrain) are likely more complex than flows in unvegetated topography. In forested complex terrain, we must consider not only radiative heating/cooling near the ground, but also at the top of the canopy [27]. There may be multiple layers of thermally driven flow, which are decoupled from each other [9,38,39]. In deciduous forests, the influences of canopy on drainage flow may be expected to be different in foliated and leaf-off seasons [10,39]. Here, we will explore the patterns of and the forcings of the wind systems at a valley sidewall site, in both leaf-on and leaf-off seasons.
3. Experimental Section
3.1. Site Description
This study was conducted at the Maoershan Forest Ecosystem Research Station of Northeast Forestry University, Heilongjiang Province, Northeast China (45°24′N, 127°40′E, 400 m a.s.l.). The climate is a continental monsoon climate with a windy and dry spring, a warm and humid summer, and a dry and cold winter. The mean (1989–2009) annual precipitation is 629 mm, of which ~50% falls between June and August. The mean annual air temperature is 3.1 °C, and mean January and July air temperature are −18.5 °C and +22.0 °C, respectively [40]. The frost-free period is between 120 and 140 days with early frosts in September and late frosts in May. The mean slope around the tower was ~9°, and the slope of the along-valley center was ~1°.
The vegetation is a naturally generated temperate deciduous broadleaved forest. The dominant tree species include Fraxinus mandshurica Rupr., Ulmus japonica Sarg., Betula platyphylla Suk., Populus davidiana Dode, Juglans mandshurica Maxim., etc. The stand was about 60-year-old, with a basal area of 26.7 m2∙ha−1 and a canopy height of 18 m. The maximum leaf area index (LAI) was 5.7 m2∙m−2 based on the litter fall collection method in eight permanent plots (Wang, unpublished data). Briefly, the LAI was calculated as the species- and time-specific leaf mass per area, and accumulated from August to October. A 1~8 m high and well-developed understory is dominated by Syinga reticulata var. mandshurica, which contributed 16% to 42% of the stand LAI (with a mean of 27%).
3.2. Measurements and Instrumentations
A 48-m-high eddy flux tower is set up at the toe of the sidewall (NW-facing) of a NE-SW towards-valley that is about 2 km wide and 240 m deep (Figure 1). The valley axis has an azimuth of 20° to north and 240° to southwest. An open path EC system (CSAT3, Campbell Scientific, USA and LI-7500, LI-COR, USA) was installed at 36 m height to measure the momentum, heat and CO2 fluxes between forest and the atmosphere. Horizontal wind velocities, wind directions, and vertical wind velocities were measured at seven, three, and two height levels of the tower, respectively (Table 1). The winds at 36 m and 2 m were measured by ultrasonic anemometer at high frequency (10 HZ), wind speed at other levels (all over canopy) were measured by cup anemometers, with the lower wind speed threshold of 0.22 m∙s−1. To calculate the profile of the virtual potential temperature, air temperature and humidity were measured at five heights. The barometric pressure was measured at 28 m above the ground.
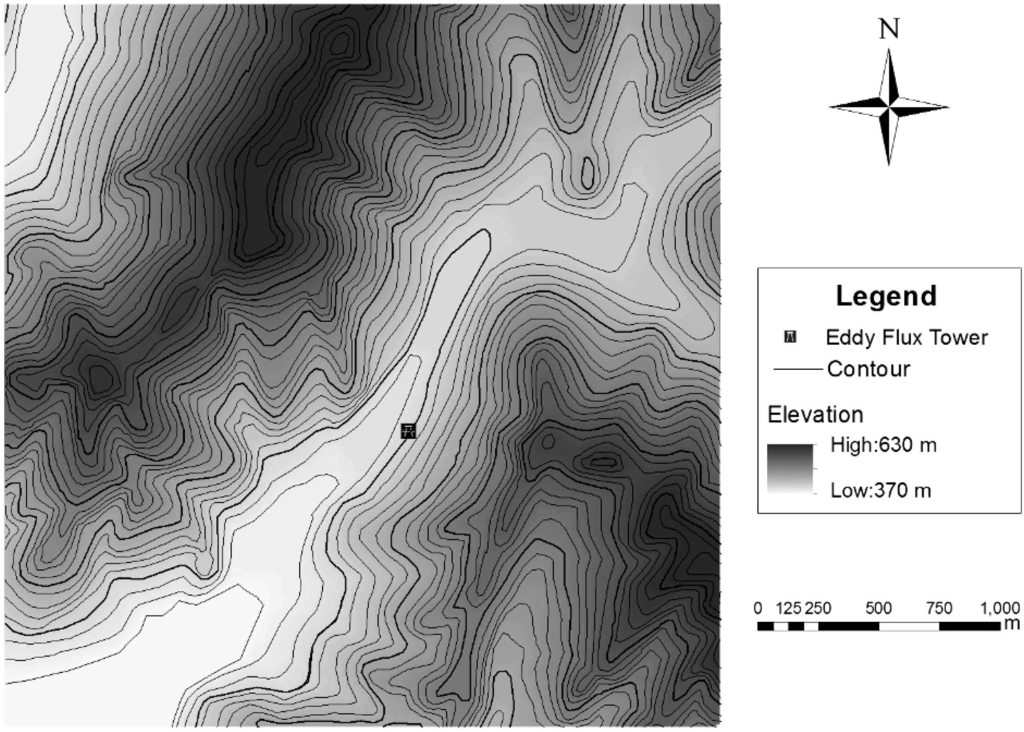
Figure 1.
Contour map of the site.

Table 1.
Instrumentation and measured variables at the flux tower.
| Variable | Height (m) | Anemometer Type | Instrument, Supplier |
|---|---|---|---|
| Horizontal wind velocity | 48, 42, 36, 28, 21, 16 | Cup | 010C, Met ONE |
| 2 | Sonic | 81,000, R.M. Yong | |
| Horizontal wind direction | 48 | Vane | 010C, Met ONE |
| 21 | Vane | 020C, Met ONE | |
| 2 | Sonic | R.M Young 81,000, R.M. Yong | |
| Vertical wind velocity | 36 | Sonic | CSAT3, Campbell Scientific |
| Net radiation | 48, 2 | - | CRN1, Kipp & Zone, |
| Air temperature and humidity | 48, 36, 28, 16, 2 | - | HMP45C with 076B, Vessla |
| Barometric pressure | 28 | - | CS100, Campbell Scientific |
3.3. Data Analysis
Four sectors of wind direction were divided: down-valley sector (from 350° to 50°), down-slope sector (from 50° to 210°), up-valley sector (from 210° to 270°) and up-slope sector (from 270° to 350°) according to the terrain. Then three conditions were considered as criteria of nocturnal above-canopy cold air drainage: (1) the wind direction must be within ±30° downward along the valley-axis (from 350° to 50°) [38]; (2) the horizontal wind-velocity profile must have a local maximum near the surface (usually at 42 m in this study) [15]; and (3) the nighttime was defined as that the global radiation measured at 48 m was less than 20 W∙m−2 [39].
Valley wind components were projected to the along-valley and cross-valley directions: the velocity components along the valley axis, consisted of down-valley component (negative value) and up-valley component (positive value); down-slope component (negative value) and up-slope component (positive value). The thermally driven flow intensity was expressed with the velocity components. The vertical shear of horizontal velocity just above the height of the drainage center (U48m − U42m)/(48 m − 42 m) was also a useful measure of the thermally driven wind flow, where U was the horizontal wind velocity. Moreover, the vertical velocity, corrected with the planar-fit method [41], was another measure of thermally driven wind [4,10].
The basic physical processes in the lowest atmospheric layers are the downward transport processes of momentum and the dissipative processes of turbulent energy cascades [42]. Drag, generated when a fluid moves over the ground or through vegetation, is essential in this process. Drag creates velocity gradients and eddies, characterized by the profiles of flow velocity and Reynolds stress, which lead to momentum loss of the fluid [42]. Drag coefficient (CD) related to friction velocity and wind velocity square [43,44],
where u*(z) is the friction velocity at height z and was related to the shear stress, U is the speed of the wind vector measured by sonic anemometer after tilt-correction by planar fit method. The physical meaning of cD(z) is the effectiveness of canopy drag elements in absorbing momentum from the airflow [42]. Unlike at simple slope of an isolated mountain, the air flow in the valley sidewall may have distinct directional shear [20,33], so we adopted the longitudinal and lateral shear stress in the u* [33,44,45] after planar fit correction [41],
where u, v and w were the along-wind, crosswind and vertical wind components, respectively. The prime indicated instantaneous deviation from the mean, over bar meant time average (half-hour).
The relations between the wind regime and the forcing was firstly through the buoyancy effect [15], which was expressed with difference in virtual potential temperature (θv) [24] between two height levels. A positive temperature gradient (Δθv/Δz) was indicative of a downward buoyancy force, and vice versa [24]. Because of the canopy isolation, we separately calculated the above canopy θv gradient ((θv48m − θv16m)/(48 m − 16 m)) and the subcanopy θv gradient ((θv16m − θv2m)/(16 m − 2 m)). We analyzed the relations of bin-averaged wind velocity to temperature gradients [9,41]. To gain further insight into the wind regime, the distributions of wind direction were plotted for various stability classes. The stability parameter ζ = − (z − d)/L was used in this study, where z was measurement height of EC (36 m), d was zero plane displacement (12.0 m for 36 m and 0.3 m for 2 m) and L was Monin-Obukhov length. The five stability regimes [28,46] have been defined as following: strongly unstable (ζ < −5), moderately unstable (−5 < ζ < −0.05), near-neutral (−0.05 < ζ < 0.05), moderately stable (0.05 < ζ < 5) and strongly stable (ζ > 5). The ζ was calculated for both above-canopy and below-canopy layers. To further explore the effect of canopy density on canopy wind flows, we divided the calendar year into two seasons: the leaf-on season (11 May to 5 October) and leaf-off season (the other times). The subcanopy decoupling with that above the canopy was defined as contrasting momentum fluxes, opposite stability conditions and thermal gradients between layers. Generally, all of the three aspects of subanopy decoupling were related to a misalignment on wind direction between layers [9,10,18,38,39].
It was worth noting that this study focused on the general patterns of and the common forcing on the air flow above and below the forest canopy, so the temporal intermittency [23,28] and horizontal variability [7,42,43,44] were not emphasized.
4. Results and Discussions
4.1. Variations in Wind Direction
4.1.1. Diurnal Variations in Wind Direction
For the whole year, the wind directions above canopy (48 m and 21 m) were along-valley in a relative frequency of 80% (Table 2). During the nighttime, the winds were predominantly down-valley, and during the daytime the winds were preferentially up-valley (Table 2). Down-valley winds occurred at 60% to 80% of the times at night and diminished to about 20% in the day, whereas the up-valley winds showed an opposite diurnal pattern. The regular changes in wind direction indicated that the wind above the canopy was a thermally driven wind system.

Table 2.
Frequency of down- and up-valley, and down- and up-slope winds under the canopy, just above canopy and above canopy in the daytime and nighttime during the leaf-on and leaf-off seasons of 2012. The data are calculated using 30-min average wind vectors. The dominant wind directions are bolded.
| Measuring Height | Wind Direction | All Season | Leaf-on Season | Leaf-off Season | ||
|---|---|---|---|---|---|---|
| Day | Night | Day | Night | |||
| (m) | sector | (%) | (%) | (%) | (%) | (%) |
| 48 (above-canopy) | Down-valley | 44.4 | 30.1 | 77.3 | 21.5 | 51.1 |
| Down-slope | 8.9 | 16.0 | 6.1 | 6.2 | 7.6 | |
| Up-valley | 41.2 | 47.7 | 14.7 | 62.4 | 37.1 | |
| Up-slope | 5.5 | 6.3 | 1.9 | 9.9 | 4.1 | |
| 21 (just above canopy) | Down-valley | 45.6 | 27.8 | 73.6 | 21.5 | 58.1 |
| Down-slope | 10.3 | 11.5 | 14.4 | 6.2 | 10.0 | |
| Up-valley | 38.9 | 50.2 | 11.0 | 63.8 | 30.0 | |
| Up-slope | 5.3 | 10.5 | 1.0 | 8.6 | 2.0 | |
| 2 (under-canopy) | Down-valley | 21.7 | 7.7 | 29.5 | 9.5 | 35.6 |
| Down-slope | 53.4 | 56.7 | 62.7 | 35.7 | 57.1 | |
| Up-valley | 14.3 | 15.2 | 2.3 | 37.3 | 5.4 | |
| Up-slope | 10.7 | 20.4 | 5.6 | 17.5 | 1.9 | |
The wind direction below the canopy (2 m) was quite different from that above canopy (Table 2). Subcanopy prevailing direction was down-slope at all times, with the exception of a slightly higher frequency of up-valley wind in the leaf-off afternoon. The frequency of the subcanopy down-valley winds was <30% and decreased to its minimum (<10%) in the daytime. In contrast, the frequency of the subcanopy up-valley and up-slope winds increased slightly in the daytime. These patterns of subcanopy winds suggested a frequent misalignment between above- and below-canopy winds (See Section 4.1.2. Vertical Shear of Wind Direction for details).
Although the diurnal patterns were overall similar in the leaf-on and leaf-off seasons, there were still some differences. At the 48 m level, nocturnal down-valley winds trended to have a higher frequency during the leaf-on season, whereas the up-valley winds were more frequent in both daytime and nighttime during the leaf-off season. At the 21 m level, the down slope-winds were more frequent during the leaf-on season than during the leaf-off season. At the 2 m level, the up-valley winds were more frequent during the leaf-on season than during the leaf-off season (Figure 2c,f). These findings were overall consistent with previous studies that accounted of the seasonal variability of thermally driven winds [9,28,31,38].
4.1.2. Vertical Shear of Wind Direction
Distinct vertical shears of wind direction were observed during both daytime and nighttime (Table 2). In the daytime, the wind direction at 21 m was in consistent with that at 48 m, yet that at 2 m shifted counter-clockwise to down-slope direction. In addition, the daytime counter-clockwise and nighttime clockwise shears of wind directions were more dramatic during the leaf-on season than the leaf-off season (Table 2). The frequencies of down-slope winds increased 40.7% and 29.5% from 48 m to 2 m in leaf-on and leaf-off seasons, respectively. The frequencies of up-valley winds correspondingly decreased from 48 m to 2 m by 32.5% and 25.1% in leaf-on and leaf-off seasons. At night, the dominating winds sheared clockwise to more than 40° from 48 m to 2 m. Compared with those at 48 m, the percentages of down-valley winds at 2 m decreased 47.8% during the leaf-on season, while decreased only 15.5% during the leaf-off season. The relative frequencies of down-slope winds increased 56.6% and 49.5% for the leaf-on and leaf-off seasons, correspondingly (Table 2).
The right (clockwise) shear of subcanopy flow at night was in qualitative agreement with previously observed and modeled horizontal mean wind directional shear in some forest sites [33,45,46,47,48], but conflicted to the left shift in other sites [32,43,49]. In fact, the subcanopy wind direction in calm night was highly dependent on the local longest slope direction [18,36], which is highly local site-dependent. However, the upper valley wind system was determined by the larger scale topography [14,32]. At our site, the clear down-slope direction shear from above-canopy layer towards the ground surface during the night indicated a confluence of down-slope flows to the valley center [19,20].
Using the 20° threshold of wind direction shear between height levels after Alekseychik et al. [8], we found the above canopy misalignment had a probability of 22% in the daytime and 39% in the nighttime. However, the below-canopy misalignment occurred much more frequent, 76% in the daytime and 71% in the nocturnal occasions. On one hand, the nocturnal misalignment of the subcanopy flow with that above canopy is a common feature of a site with a tall and dense canopy in complex terrain [8,9,12,18,43,47,50], and even at a old-growth tropical forest site with flat terrain (Santarém LBA-ECO site, ~1° slope) [8]. On the other hand, the frequent subcanopy down-slope winds during the day (Table 2) contradicts with the classical theory of diurnal mountain wind systems [15]. The daytime drainage flows under tall and dense canopies were also observed at other sites: down-slope at sites with flat terrain [8,30] or down-valley at complex sites [9,28,51]. Interestingly, the five sites with a daytime drainage flow below canopy (the MMSF site [10], the AEF site [29], the Manaus LBA site [30], the Xishuangbanna site [47] and the Maoershan site) had two common features: (1) a tall, dense canopy; (2) closed to the valley center or at the lower part of the sidewall with relative gentle slope. There is evidence that the radiative heating/cooling of dense canopy isolated the subcanopy layer with that above canopy [26,28], which plays a key role in the formation of these decoupled subcanopy flows. However, it is unclear why the five cases of daytime subcanopy drainage all occurred near the center of a valley. At our site, the daytime subcanopy down-slope wind may be a partial compensation for the up-valley wind above canopy. The frequent subcanopy drainage flow in both daytime and nighttime might question the one-point eddy flux observation above canopy.
4.2. Variations in Wind Velocity
4.2.1. Horizontal Wind Velocity
The mean diurnal courses of horizontal wind velocities over the canopy had roughly bimodal patterns in the leaf-on season but near unimodal in the leaf-off season (Figure 2). The above-canopy horizontal wind velocity was lowest in the morning and evening transition periods. The morning transition period occurred at two to three hours after sunrise and the evening transition started about one hour before sunset. In contrast, the horizontal wind velocity at 2 m was overall higher in the nighttime than in the daytime, although it was generally lower than that above the canopy.
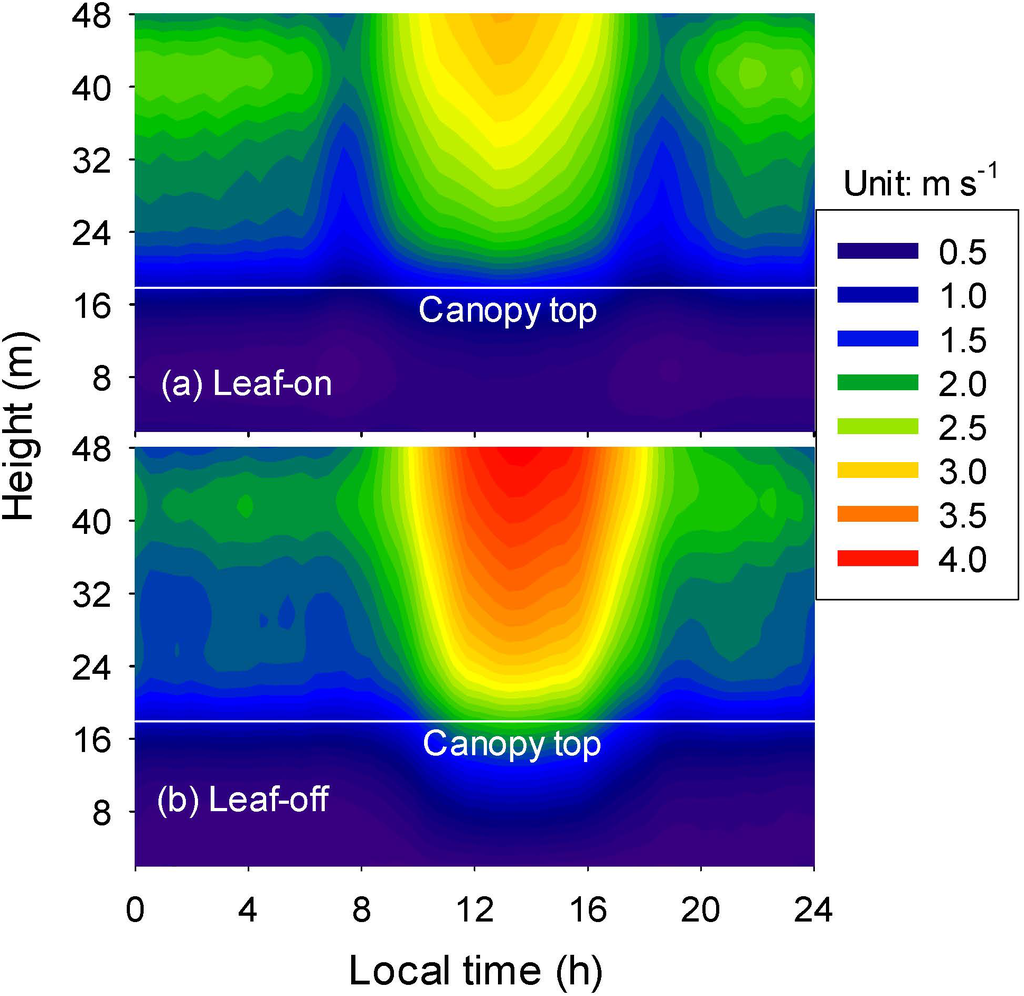
Figure 2.
Diurnal courses of horizontal wind velocity profile during the leaf-on (a) and leaf-off (b) seasons of 2012.
The vertical profiles of mean horizontal velocities varied with the time of the day, although that above canopy was always higher than that below canopy (Figure 2). The horizontal wind velocity had a distinct maximum at the height of 42 m (2.3-fold canopy height) during night, while it increased with height during the daytime. However, in contrast to the higher mean wind velocity in leaf-off season, the wind maximum was stronger in leaf-on season, indicating the drainage flow was stronger in the leaf-on season.
Other researches documented that the typical height of nocturnal drainage center is 10 to 100 s of meters [15]. For example, the height of wind velocity maximum on the low-angle (1.6°) side-wall of the floor of Utah’s Salt Lake Valley occurred at 10 to 15 m height [20], but could reach 40 m in another slope in the same valley [48]. Most studies in forest sites reported that the drainage flows were restricted in the subcanopy layer, which characterized with relative open canopy and insignificant understory vegetation [8,13,21], or at the upper part of a long slope [39,40], or very gentle slope [39]. We did not detect the possible subcanopy wind maximum as many previous studies [13,28,31,41,42] due to only one observation point below canopy.
The mean drainage maximum above canopy (42 m) at the Maoershan was relative high compared to other sites, which was likely the result of the valley terrain. In valley topography, significant interplays between the flows on side-wall and the flows along the valley axis, down-valley flows differ dramatically from down-slope flows on isolated mountains [15]. When the observation was conducted at upper slope, the depth of nocturnal drainage flow was often limited to the first few meters above the ground in the trunk-space e.g., [8,13,39,40]. On the side-wall of a valley, the down-slope flow often started before sunset [23,49], and then speeded up and increased in depth with down-slope distance before mid-night [18,19,23]. However, down-slope flows on valley sidewalls were routinely subject to the development of overlying valley flows [14,19]. In fact, down-slope flows typically converged onto the valley floor [20,45] or into the elevated portion of temperature inversion layer on the valley floor [20]. If the valley did not have major constrictions along its length or major changes in surface microclimates, the nighttime down-valley flows accelerated and increased in depth with down-valley distance [15]. So the main characteristic of the nighttime phase is the predominance of down-valley flows throughout the valley volume [15]. Unfortunately, most eddy flux towers were not tall enough to observe the jet-maximum of drainage flow above the canopy. Only a few studies (including this study) detected that the height of maximum wind velocity could occur over the canopy [21,28,30]. However, determining the whole profile of the valley-wind in any site needs high tower or other techniques (e.g., tethersonde balloon and sodar) [29]. The deep drainage in the night might question the mass and energy fluxes measured by EC above canopy [25].
4.2.2. Vertical Wind Velocity
The vertical wind velocity at 36 m (after planar-fit coordinate rotation) had a distinct diurnal pattern during the leaf-on season, with upward directions (positive values) in the daytime and downward directions (negative values) in the nighttime (Figure 3a). The vertical velocity at the 2 m was slightly downward at most times except for mid-morning and early-evening (Figure 3c). The nocturnal vertical velocity was in the order of −0.05 m∙s−1. The mean vertical velocities during the leaf-off season were near zero all day long (Figure 3b,d), although the variability between days was comparable with those during the leaf-on season.
The above-canopy diurnal pattern of daytime-upward and nighttime-downward vertical velocity, consistent with the diurnal course of wind direction, was a distinct feature of thermally driven wind system [3,4,18,24,45,52]. The leaf-on daily change in the above-canopy vertical velocity indicated that a convergence dominated in the nighttime and a divergence prevailed in the daytime [9,24,52]. This indicated positive vertical advection (removing CO2 from the control volume), ignoring which in the mass balance equation would underestimate the nocturnal respiration [25]. The nocturnal above-canopy convergence was likely compensated by the below-canopy horizontal divergence, in view of the systematic directional shear to down-slope from 48 to 2 m. In this situation, the sign and magnitude of horizontal advection could not be determined without knowing the horizontal CO2 gradient [25]. The positive vertical velocity in the daytime indicated a negative vertical advection, ignoring which would underestimate the CO2 uptake by the ecosystem. However, the contribution of total vertical and horizontal advection to the NEE depends on their signs and magnitudes, which are difficult to infer without direct horizontal advection measurements.
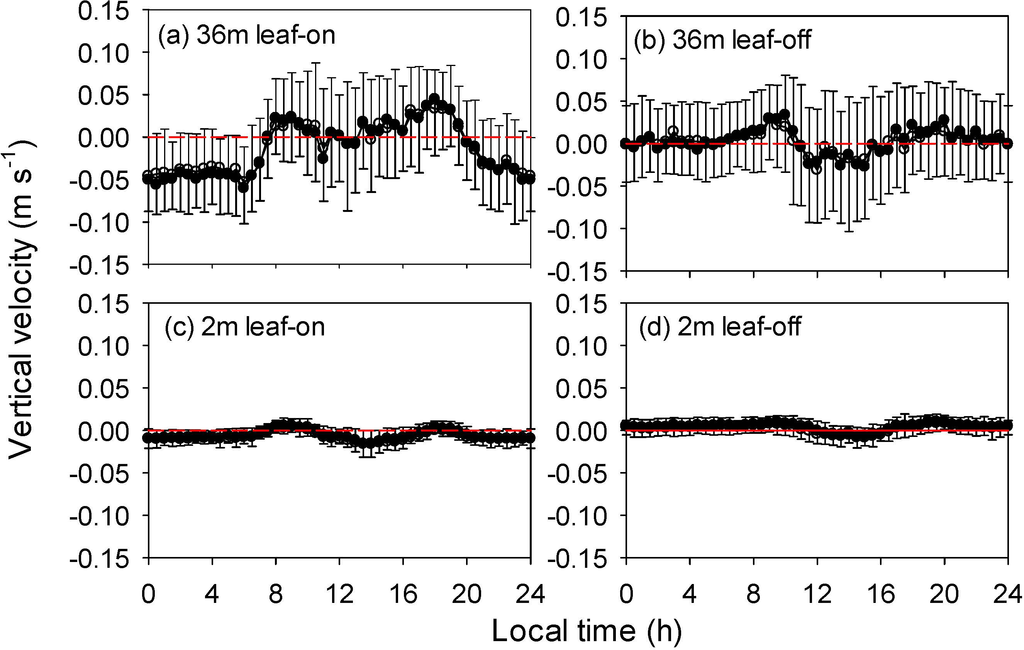
Figure 3.
Diurnal courses of vertical wind velocity above (36 m) and below (2 m) the canopy during the leaf-on and leaf-off seasons of 2012. (a) 36 m for leaf-on season, (b) 36 m for leaf-off season, (c) 2 m for leaf-on season, and (d) 2 m for leaf-off season. Open circles are mean values, filled circles are the median and error bars indicate the range between the 25 and 75 percentile, respectively. The dashed lines are zero velocities.
4.3. Variations in Thermal Gradient and Stability
During the leaf-on season, the mean subcanopy θv gradient was nearly opposite to that above canopy: negative in the daytime and positive in the nighttime above the canopy (Figure 4a), but positive or neutral in the daytime and negative in the nighttime below the canopy (Figure 4c). Interestingly, the below-canopy θv gradient was bimodal, with the small negative “saddle” at early-afternoon (~13:00). On the contrary, during the leaf-off season the below-canopy temperature gradient was generally consistent with that above canopy: negative from mid-morning to late-afternoon (Figure 4b,d). The above-canopy temperature gradient generally agreed with the classic diurnal course. However, the daytime temperature inversion and nighttime temperature lapse or isothermal conditions had been observed under tall and dense forests [10,29,30,39,50,51,53], which differed markedly from open canopies or the leaf-off season [9,33]. In the daytime with clear sky, the heating mainly occurred at the top of the canopy because the dense canopy absorbed much more solar radiation than the ground [28,46]. As illustrated in Figure 5, the net radiation was roughly mirrored the thermal gradient for the corresponding layer (Figure 4). Surprisingly, the below-canopy daytime net radiation peaked at the early-afternoon (~13:00) rather than at the noon, corresponding to the pattern of below-canopy thermal gradient (Figure 4c). This is caused by that on the northwest-facing slope, the solar elevation angle is still high at that time (high radiation above canopy), and meanwhile the shadow effect of canopy is relative small (the length of the pathway for radiation penetration in the canopy is relative small, which is largest when the sun is “behind” the slope and smallest when the sun is “facing” to the slope). However, quantification of this effect is beyond the scope of this paper.
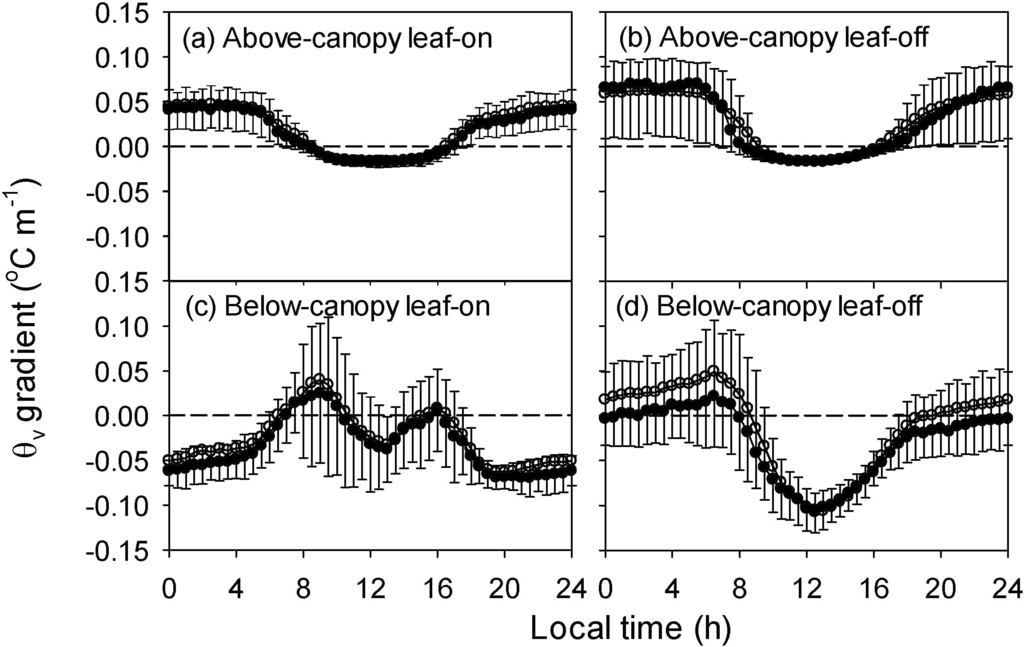
Figure 4.
Diurnal courses of the gradients of virtual potential air temperature (θv) above (16 m–48 m) and bellow (2 m–16 m) the canopy during the leaf-on and leaf-off seasons of 2012. (a) above-canopy for leaf-on season, (b) above-canopy for leaf-off season, (c) below-canopy for leaf-on season, and (d) below-canopy for leaf-off season. Open circles are mean values, filled circles are the median and error bars indicate the range between the 25 and 75 percentile, respectively. The dashed lines are zero gradients.
The mean below-canopy daytime net radiation was comparable for the leaf-on and leaf-off seasons, although the above-canopy net radiation was higher during the leaf-on season. The canopy layer on average net absorbed 199 W∙m−2 during the leaf-on daytime, whereas it decreased to 125 W∙m−2 during the leaf-off daytime. This resulted in an above-canopy unstable but subcanopy thermally stable or near neutral stratification under dense canopy as shown in Figure 4 [9,12,29,47]. On the other hand, in clear and calm nighttime, canopy elements (the surfaces of leaves, branches and boles) initially cool much more quickly than the canopy air space after the net radiative cooling starts [27], leading to a cool center often at the top of canopy, which in turn resulted in a stable above-canopy layer but unstable subcanopy layer [9,12,29,47]. At our site, it was clear that the net radiation absorbed by the canopy was much stronger in the leaf-on season than in the leaf-off season, indicating a heat isolation of dense canopy (Figure 4). Notably, in a short and very dense conifer canopy (9.5 m high with a LAI of 9 m2∙m−2), the temperature gradient within-canopy was positive [54]. It seemed that this short canopy had no sufficient space to form an unstable subcanopy layer because the foliage reached the ground. Therefore, a dense canopy and sufficient trunk space are indispensable requirements for a subcanopy inversion layer.
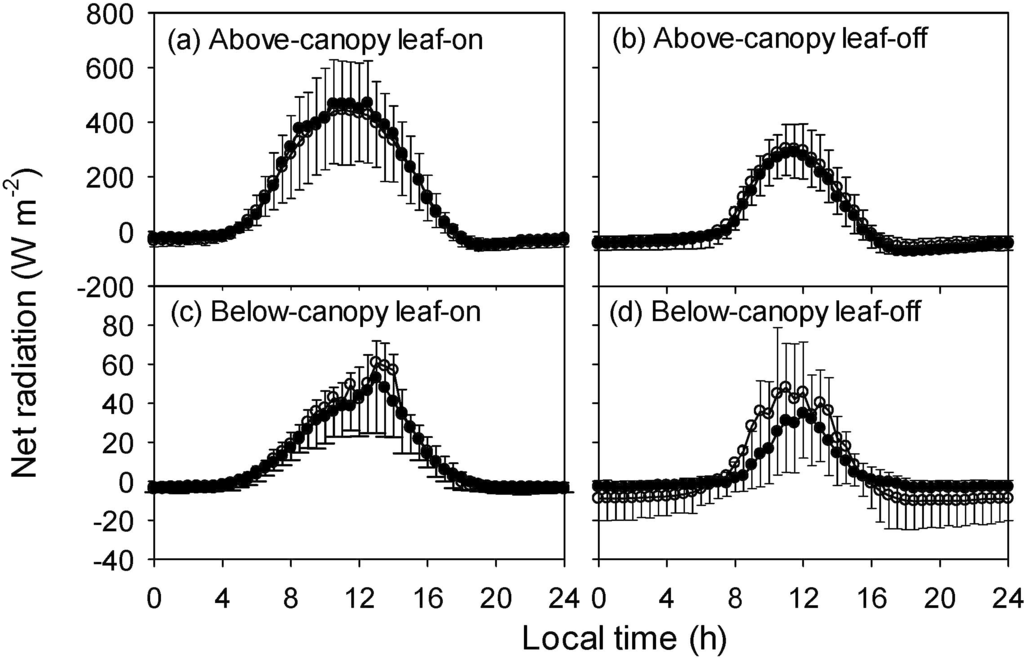
Figure 5.
Diurnal courses of the net radiation above (48 m) and bellow (2 m) the canopy during the leaf-on and leaf-off seasons from May of 2013 to April of 2014. (a) 48 m for leaf-on season, (b) 48 m for leaf-off season, (c) 2 m for leaf-on season, and (d) 2 m for leaf-off season. Open circles are mean values, filled circles are the median and error bars indicate the range between the 25 and 75 percentile, respectively. The dashed lines are zero radiations.
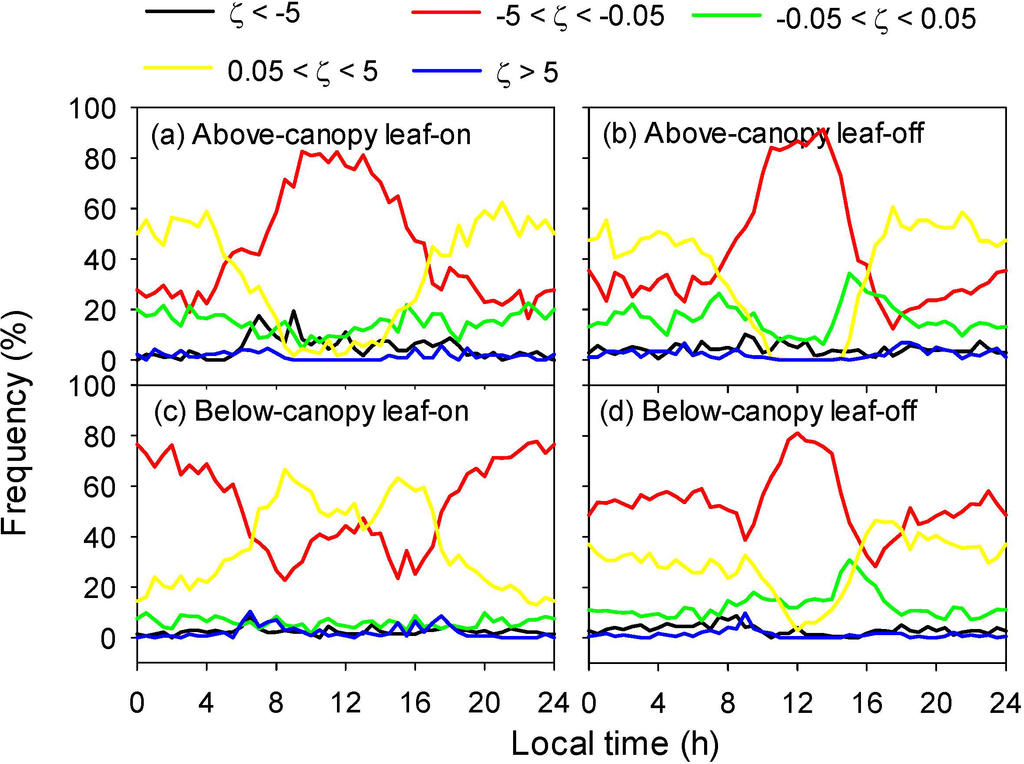
Figure 6.
Diurnal courses of relative frequency of stability regimes for above-canopy (36 m) and below-canopy (2 m) layer in the daytime and nighttime during the leaf-on and leaf-off seasons of 2012. (a) 36 m for leaf-on season, (b) 36 m for leaf-off season, (c) 2 m for leaf-on season, and (d) 2 m for leaf-off season.
The frequencies of stability regimes were shown in Figure 6. At the 36 m height, the moderate unstable conditions dominated in the daytime and moderate stable conditions were prevailed during the night for both seasons. However, at the 2 m height, these situations were reversed, except for the daytime during the leaf-off season. This suggested the local stability of below-canopy layer was often opposite to that of above-canopy layer, which was due to the canopy isolation of vertical momentum and heat transport. Decoupling of above-canopy unstable and sub-canopy stable layers was also observed in relative open forest canopy at night, which was due to quite different mechanisms with that in dense canopy [6].
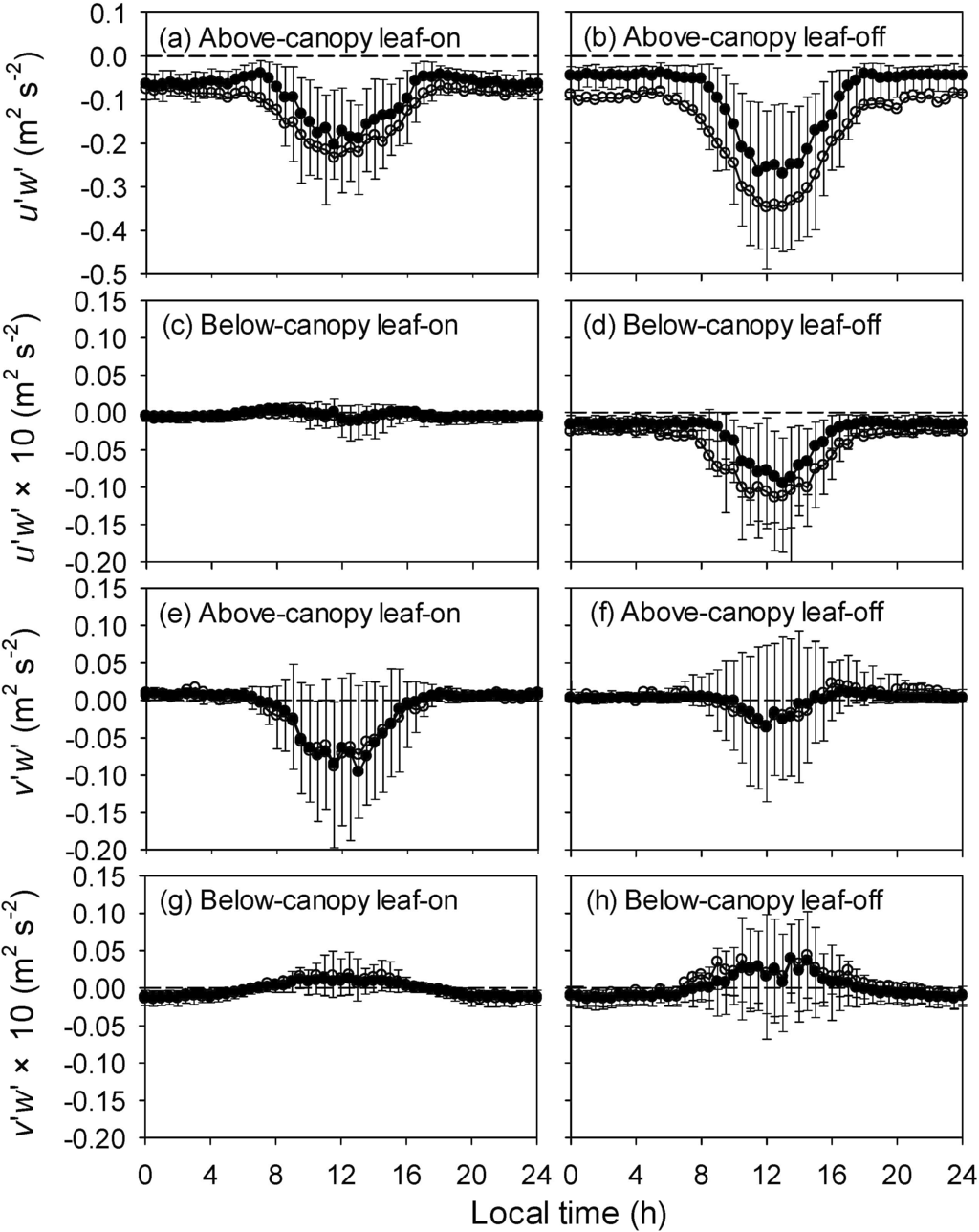
Figure 7.
Diurnal courses of Reynolds stress components above (48 m) and bellow (2 m) the canopy during the leaf-on and leaf-off seasons of 2012. (a)–(d): longitudinal Reynolds stress, (a) 36 m for leaf-on season, (b) 36 m for leaf-off season, (c) 2 m for leaf-on season, and (d) 2 m for leaf-off season, (e)–(h): lateral Reynolds stress, (e) 36 m for leaf-on season, (f) 36 m for leaf-off season, (g) 2 m for leaf-on season, and (h) 2 m for leaf-off season. Open circles are mean values, filled circles are the median and error bars indicate the range between the 25 and 75 percentile, respectively. The dashed lines are zero gradient. Note the different vertical axis in the upper-most row of the panels.
4.4. Variations in Reynolds Stress and Drag Coefficient
Turbulence data are usually analyzed in a coordination system with along-wind, crosswind and vertical components in order to distinguish between the different characteristics of longitudinal and lateral turbulence. For the vertical momentum transport components of the Reynolds stress tensor, this means that in homogeneous terrain the lateral component is actually zero and the non-alignment between the mean horizontal wind vector and the stress vector is purely statistical [55]. In situations where two wind systems of different (spatial and time) scale are interacting this can of course not be expected [22]. The mean diurnal variations of above- and below-canopy Reynolds stress components (kinematic momentum fluxes) were shown in Figure 7. The longitudinal stress was negative and reached its negative maximum around the noon, roughly opposite to the daily course of horizontal wind velocity (Figure 2). The below-canopy longitudinal stress was much small in magnitude, and could be positive during the leaf-on season. Three distinct features could be detected for the lateral stress (Figure 4): (1) the magnitude of lateral stress was in the same order at, or even larger than (below canopy during the leaf-on season) the longitudinal one; (2) the daily course of longitudinal stress was similar between above and below canopy, whereas the pattern of lateral stress above canopy was reversed from that below canopy; (3) the lateral stress fluxes were generally small and of varying sign especially in the daytime. These findings illustrated a significant interaction between slope and valley winds.
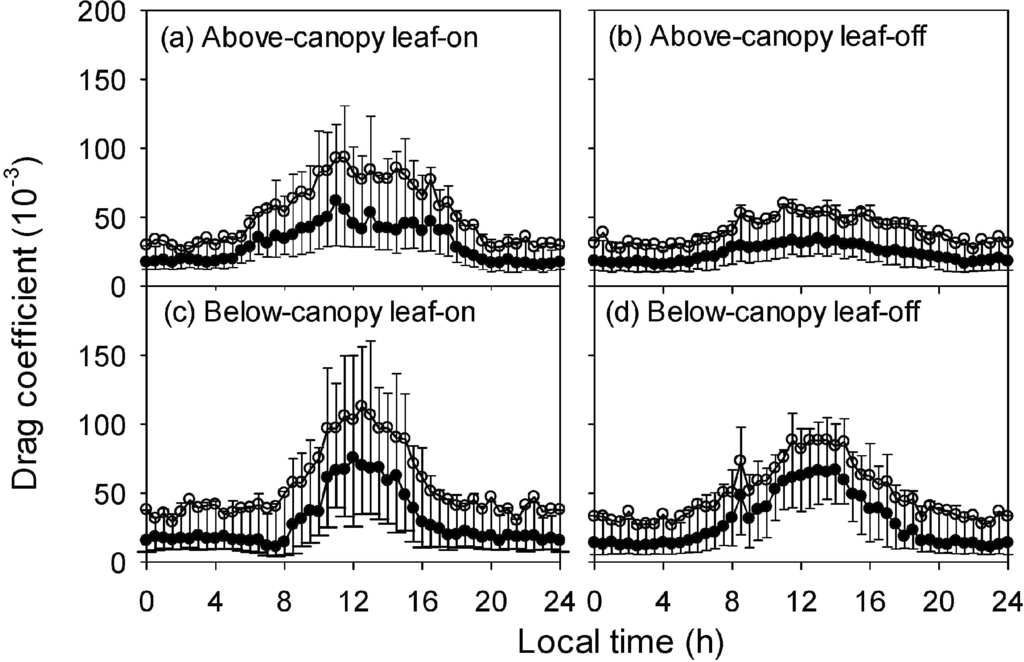
Figure 8.
Diurnal courses of drag coefficients above (36 m) and bellow (2 m) the canopy during the leaf-on and leaf-off seasons of 2012. (a) above-canopy for leaf-on season, (b) above-canopy for leaf-off season, (c) below-canopy for leaf-on season, and (d) below-canopy for leaf-off season. Open circles are mean values, filled circles are the median and error bars indicate the range between the 25 and 75 percentile, respectively.
Previous momentum transport in canopy often simplified to a 2-D condition, i.e., ignored the directional shear component of kinematic stress. Our results as well as the findings at other valley sites give the evidence that the lateral component of vertical momentum flux cannot be ignored. The opposite sign of below-canopy lateral stress with the above-canopy one at Maoershan site was in consistent with the findings above a steep forested slope in an alpine valley [22]. However, Rotach et al. [33] found that the lateral component of Reynolds stress exhibited a similar daily cycle in timing and magnitude as the component due to frictional (shear) stress at a valley sidewall, which was covered by meadow vegetation. It seems that the canopy layer played an essential role between the discrepancies. At our site, the upward moving fluctuations experienced a left, and the downward moving eddies a right turn, respectively. This situation seemed to be reversed at the 2 m height, indicating a decoupling subcanopy layer. However, detailed profile of stress measurement is necessary to give a whole picture of the momentum transport within the canopy and thus may help to interpret the site-specific regimes [22].
For the drag coefficient cD, the below-canopy ones were slightly larger than the above-canopy ones particularly during the leaf-off season (Figure 8). This is due to the maximum cD values are located around the maximum leaf area density levels for most forest canopies [42]. However, the cD had a distinct daily course, which kept at a low level at night although the wind was continuous (Figure 2) and peaked around the noon when the wind speed reached its maximum (Figure 2). In addition, the daily course of cD was similar to that of unstable condition (opposite to the stable condition), indicating a negative correlation between cD and stability as previous findings [44,56]. Moreover, the cD was larger in the leaf-on season than in the leaf-off season. These patterns of cD indicated a nocturnal decoupling at the tower site, which could suppress momentum transport and scalar mixing during this period.
4.5. Relations to Thermal Gradient and Stability
4.5.1. Above-Canopy
The wind directions were related to the above-canopy θv gradient (Figure 9). Overall, in the conditions of moderate to strong above-canopy inversion (positive θv gradient), the down-valley wind occurred more frequently during both daytime and nighttime, whereas the down-slope wind became more important only during the day. These patterns illustrated that negative buoyancy forced the occurrence of drainage flow. Similarly, the stability strongly influenced the wind direction distribution (Figure 10). At 48 m and 21 m, the situation that the wind was dominated by up-valley direction at unstable conditions gradually converted to down-valley wind when conditions became moderately stable (0.05 < ζ < 0.5). However, for strongly stable conditions, the wind changed to up-valley wind dominating again (Figure 10i). Interestingly, the down-slope wind prevailed at 2 m height level during the leaf-on season for all stability regimes, particular for strongly-unstable conditions (Figure 10a), whereas during the leaf-off season the down-slope wind became more frequent only when the conditions were stable (Figure 10h,j). The wind direction shift from down-valley at 48 m to down-slope at the 2 m was more dramatic at moderate stable conditions for both leaf-on and leaf-off seasons. The magnitude of directional shear was smallest for the near-neutral conditions, which was consistent with the situations at University of Michigan Biological Station site [55].
The velocities of the valley and slope winds were overall negatively correlated with the θv gradient (Figure 11). This suggested that the down-valley and down-slope winds were favored by the strong negative buoyancy (positive temperature inversion). However, there were distinct differences between valley and slope winds, between nighttime and daytime and between seasons. Compared with slope wind, the valley wind was more sensitive to the change of the above-canopy thermal gradient. At the same level of thermal inversion, the down-valley and down-slope winds were stronger in the nighttime than in the daytime. In addition, the down-valley wind was slightly stronger in the leaf-on season than in the leaf-off season.
The velocity shear between 42 and 48 m also responded strongly to the temperature gradient (Figure 12). During the nighttime, the negative velocity shear occurred when temperature inversion formed and reached the most negative values at moderate inversions, and then the velocity shear recovered to near zero when strong inversion formed (Figure 12a). This nonlinear response suggested that the strongest drainage flow occurred at moderate temperature inversion conditions, consistent with the response of the down-valley frequency (Figure 9a,d) and the along-valley velocity (Figure 11a). Country to the nighttime, the daytime velocity shear decreased gradually with the temperature gradient increasing (Figure 12b), roughly coincident with the trends of the down-valley frequency (Figure 9g) and the valley wind velocity (Figure 11b).
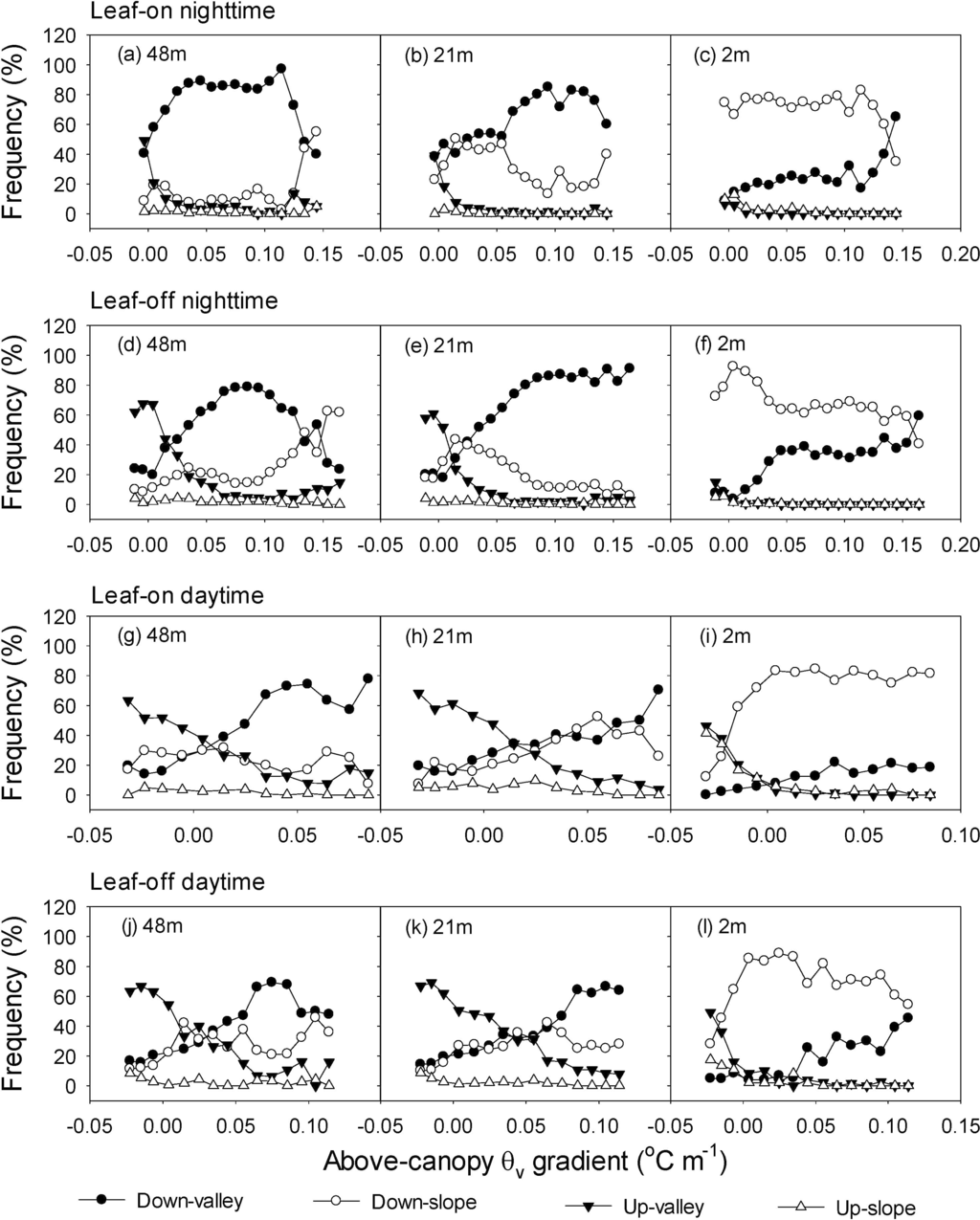
Figure 9.
Changes of the relative frequency of mean wind direction sector at the 48 m, 21 m and 2 m with the gradient of above-canopy virtual potential air temperature (θv) in 2012. (a), (b), (c) are in the nighttime for 48 m, 21 m and 2 m in the leaf-on season, respectively, and (d), (e), (f) are in the nighttime for 48 m, 21 m and 2 m in the leaf-off season, correspondingly, (g), (h), (i) are in the daytime for 48 m, 21 m and 2 m in the leaf-on season, respectively, and (j), (k), (l) are in the daytime for 48 m, 21 m and 2 m in the leaf-off season, correspondingly.
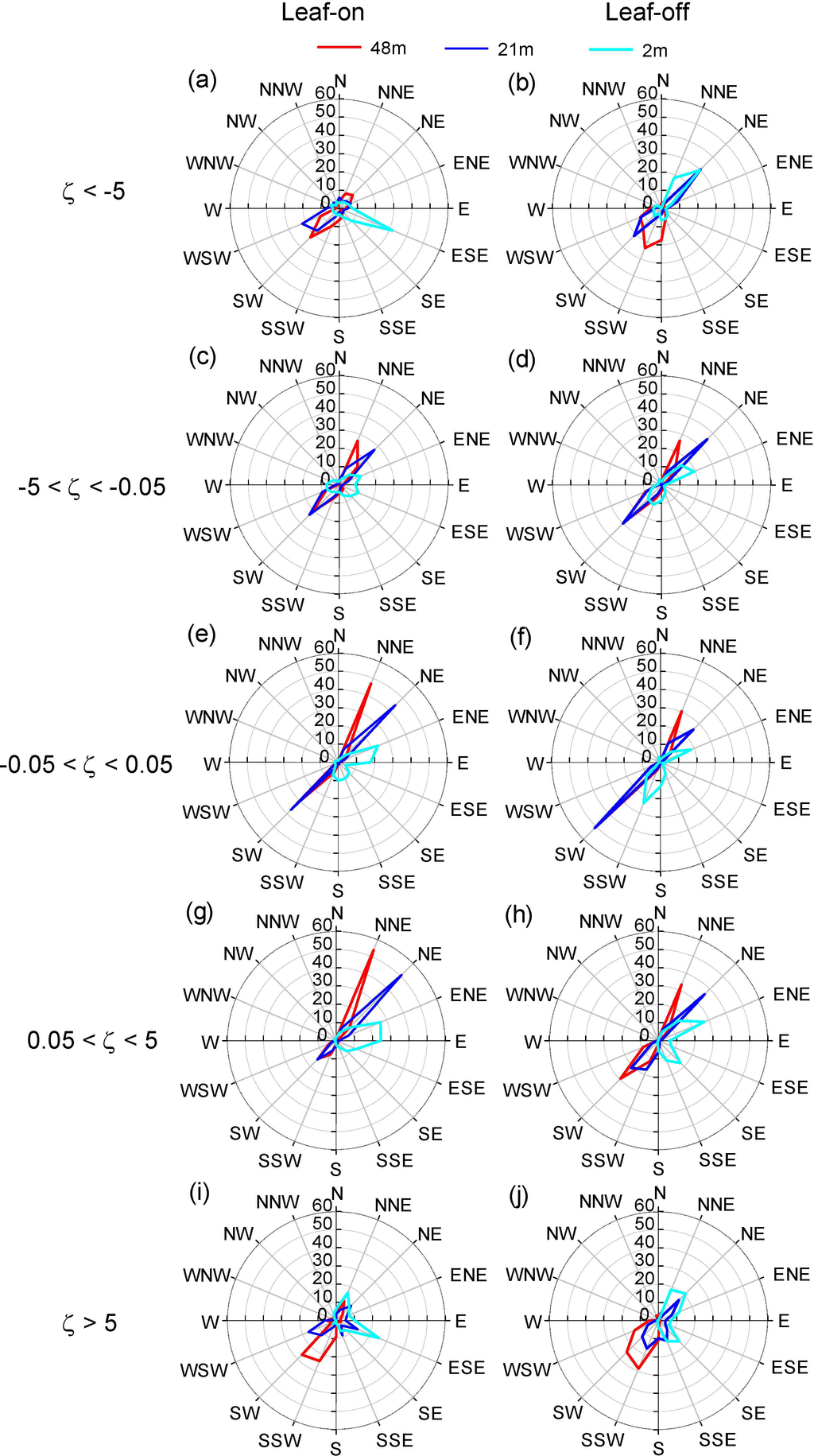
Figure 10.
Relative frequency distributions of wind direction at the 48 m, 21 m and 2 m for five stability regimes during the leaf-on and leaf-off seasons of 2012. (a) and (b) are for ζ< −5 in leaf-on and leaf-off seasons, correspondingly. (c) and (d) are for −5 < ζ < −0.05 in leaf-on and leaf-off seasons, respectively. (e) and (f) are for −0.05 < ζ < 0.05 in leaf-on and leaf-off seasons, respectively. (g) and (h) are for 0.05 < ζ < 5 in leaf-on and leaf-off seasons, respectively. (i) and (j) are for ζ > 5 in leaf-on and leaf-off seasons, correspondingly.
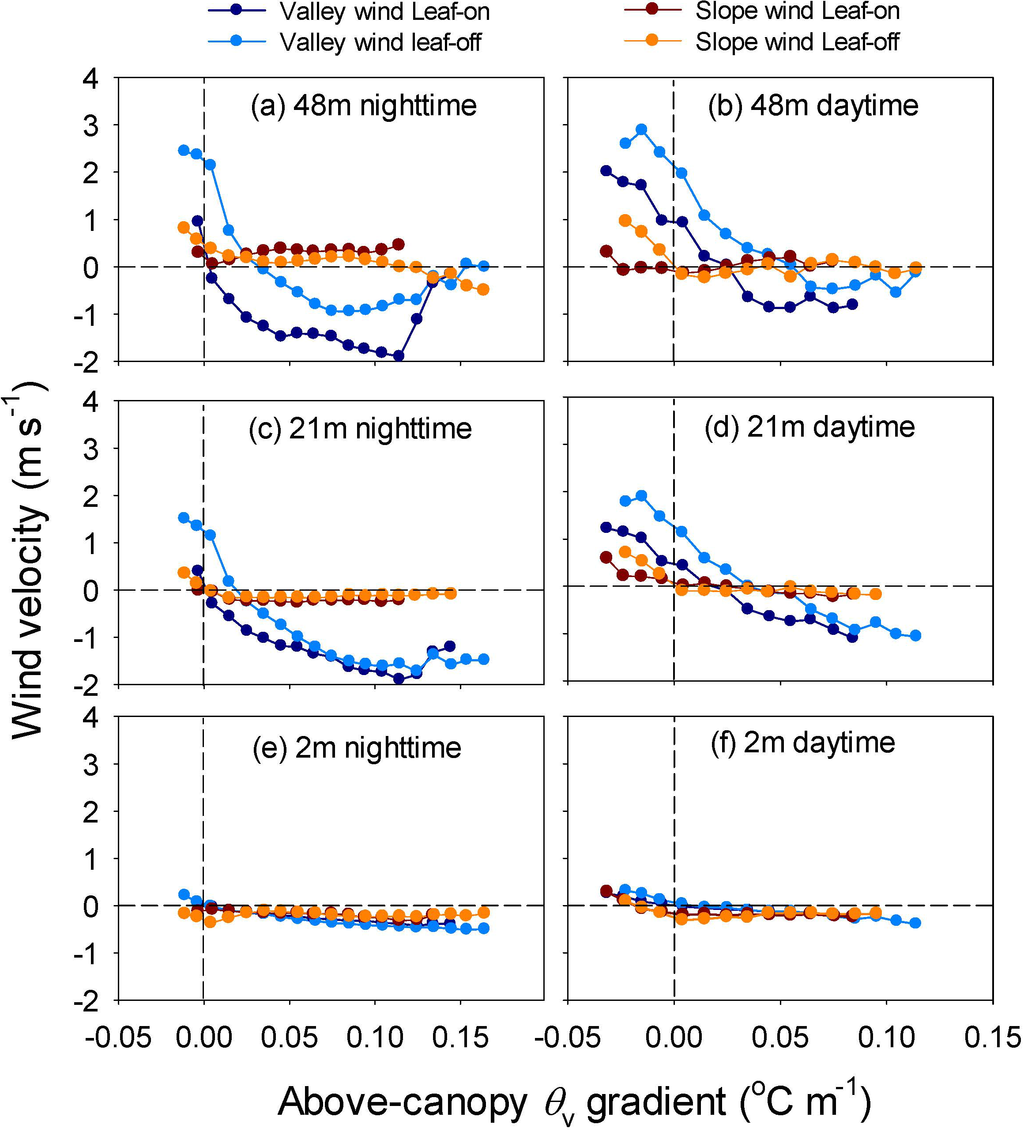
Figure 11.
Changes of mean along-valley and cross-valley wind velocities at the 48 m, 21 m and 2 m with the gradient of above-canopy virtual potential air temperature (θv) in 2012. (a) and (b) are at 48 m in the nighttime and daytime, respectively. (c) and (d) are at 21 m in the nighttime and daytime, correspondingly. (e) and (f) are at 2 m in the nighttime and daytime, respectively.
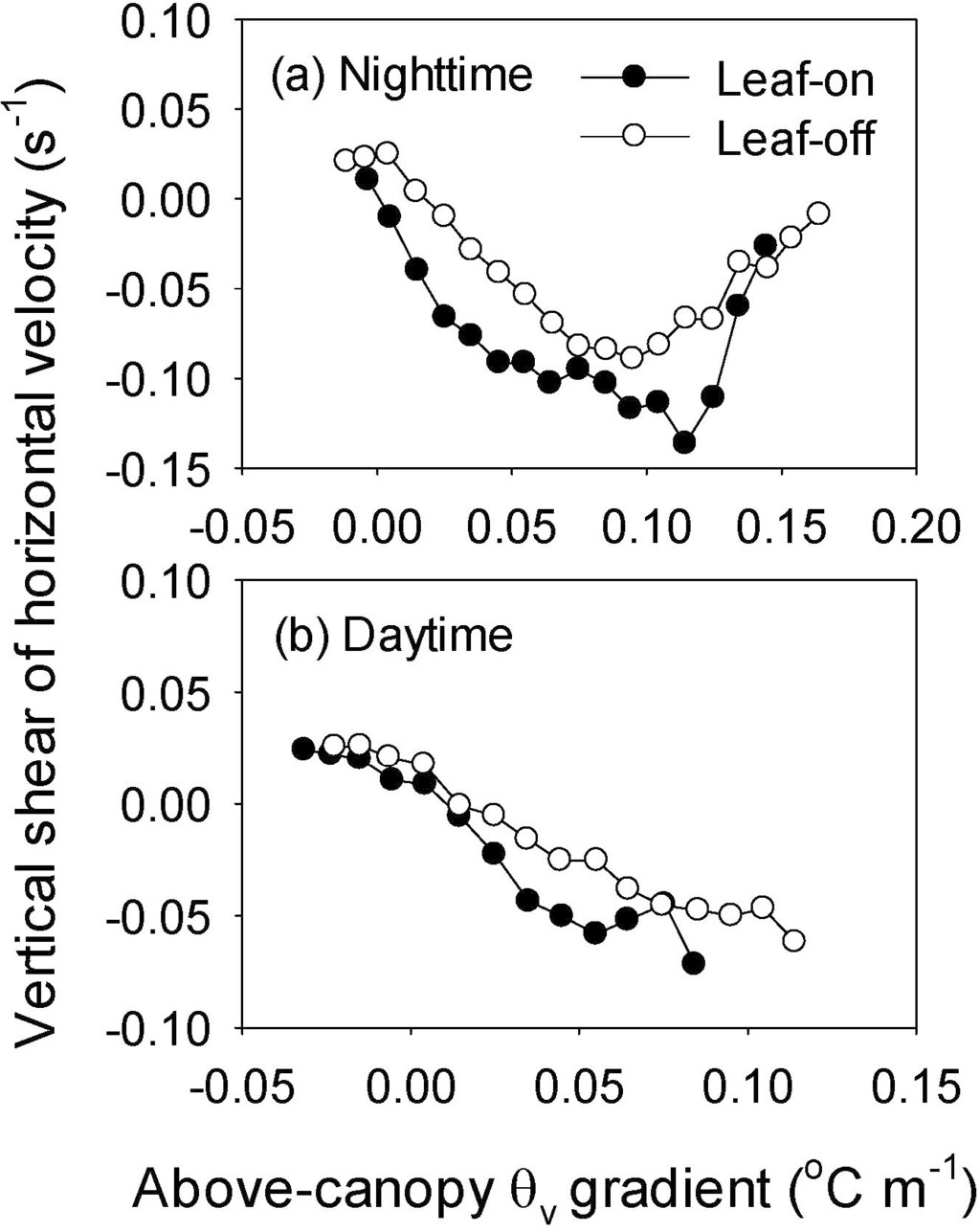
Figure 12.
Changes of the vertical shear of horizontal wind speed between 42 and 48 m with the gradient of above-canopy virtual potential air temperature (θv) in the nighttime (a) and daytime (b) in 2012.
4.5.2. Below-Canopy
As expected, wind direction responded to the change in the below-canopy θv gradient (Figure 13). During the nighttime, the frequency of down-valley flow increased with the below-canopy θv gradient before a threshold and then trended to level off (Figure 13a,c). Surprisingly, the percentage of down-slope wind decreased under inversion conditions. During the daytime, the wind mainly blew to up-valley direction when the θv gradient above −0.1 °C∙m−1, the wind turned to down-slope direction when θv gradients were less inversed or strongly lapsed (Figure 13b,d). These responses with thermal gradient were roughly consistent with those with the stability regime (Figure 14). The down-slope wind dominated for all stability classes even for strongly unstable conditions during the leaf-on season (Figure 14a), with the exception of the strongly unstable and near-neutral conditions in the leaf-off season. The dominance of down-slope wind was most dramatic for strongly stable conditions under the canopy.
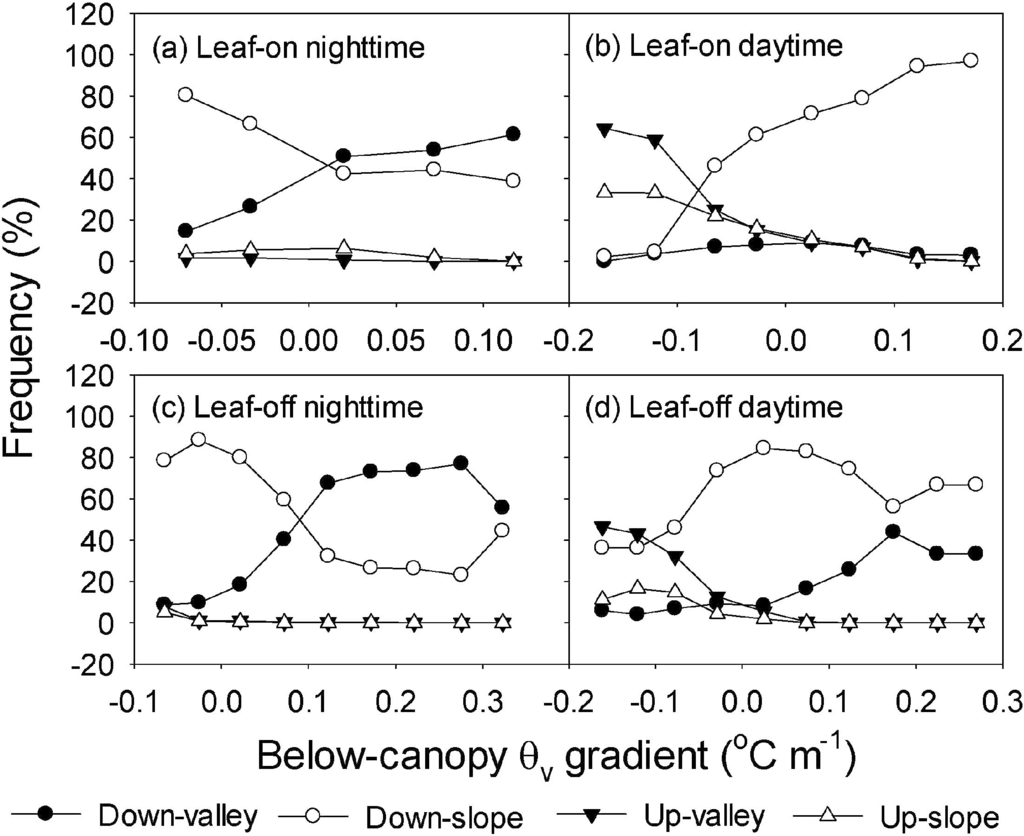
Figure 13.
Change of the relative frequency of mean wind direction sector at the 2 m with the gradient of below-canopy virtual potential air temperature (θv) in 2012. (a) nighttime for leaf-on season, (b) daytime leaf-on season, (c) nighttime for leaf-off season, and (d) daytime for leaf-off season.
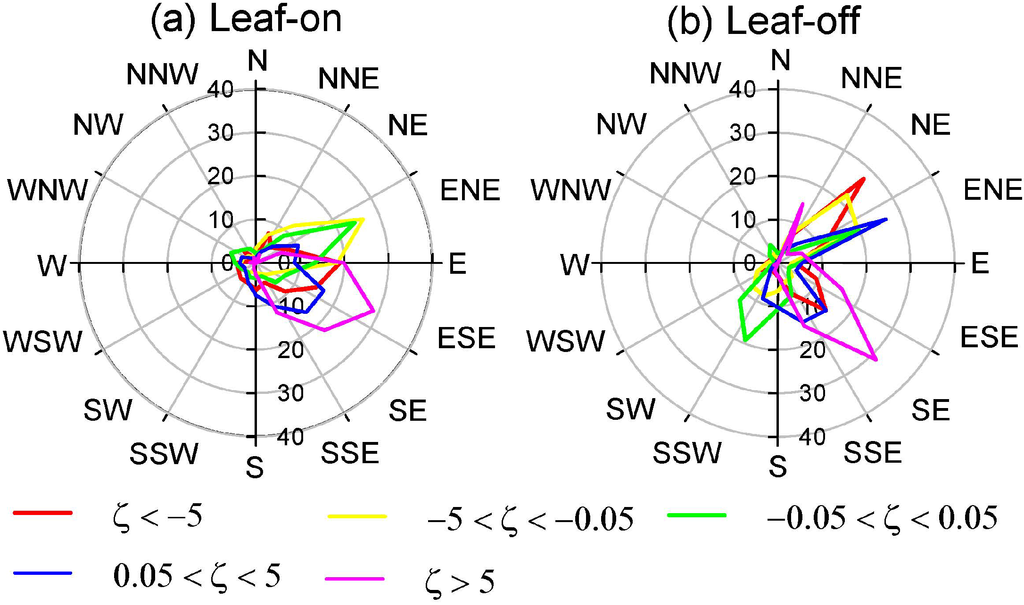
Figure 14.
Relative frequency distributions of wind direction at the 2 m for five stability regimes during the leaf-on (a) and leaf-off (b) seasons of 2012.
The below-canopy wind velocity also changed with subcanopy thermal gradient (Figure 15). During the night, the below-canopy valley wind velocity generally decreased with the below-canopy temperature inversion forming and increasing. Surprisingly again, the down-slope wind became weaker as inversion increasing. This indicated that the down-slope wind was suppressed by down-valley wind at situations with strong negative buoyancy force. During the daytime, however, the response of valley wind to temperature gradient was similar to that of the slope wind. However, the down-valley wind trended to be weakened by down-slope wind at conditions of strong negative buoyancy force in the leaf-on season.
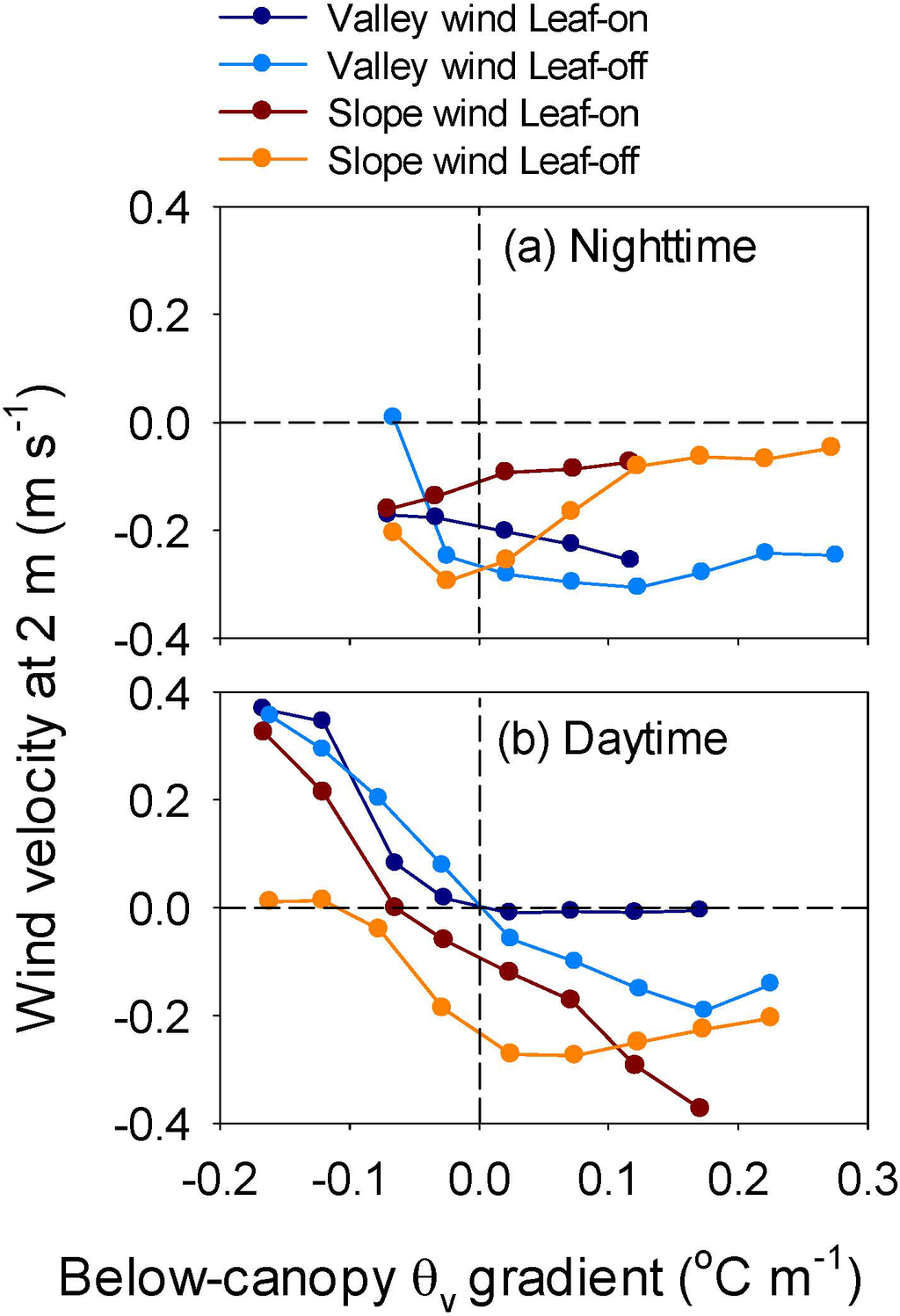
Figure 15.
Change of mean velocity of valley and slope winds at the 2 m with the gradient of below-canopy virtual potential air temperature (θv) in the nighttime (a) and daytime (b) in 2012.
5. Conclusions
We examined the airflows above and below a temperate deciduous forest canopy in a valley at the Maoershan site of ChinaFLUX. In general, the above-canopy airflow was a typical thermally driven valley wind system, with the wind preferable up-valley in the daytime and down-valley in the nighttime (Table 2), which was consistent with the daytime temperature lapse and nocturnal inversion above the canopy (Figure 4a,b). Notably, the below-canopy airflow was often not aligned with that above canopy, especially in the leaf-on season (Table 2) and for above-canopy stable conditions (Figure 10). During the night in both leaf-on and leaf-off seasons, the below-canopy wind significantly sheared to the slope direction compared with the down-valley wind above canopy, which indicated a clear confluence of drainage flow onto the valley center. This drainage flow contradicted the prevailing temperature lapse and unstable conditions. During the daytime of the leaf-on season, the below-canopy layer prevailing direction was down-slope because of the frequent temperature inversion and isothermal conditions (Figure 4c), while during the leaf-off daytimes the below-canopy layer up-valley wind became more important due to the strong temperature lapse conditions (Figure 4d). The mean daytime positive and nighttime negative vertical velocity above the canopy during the leaf-on season (Figure 7a) indicated a flow convergence at night and a divergence in the daytime. This partly compensated by the below-canopy horizontal convergence in the daytime, but not in the nighttime. Overall, the below-canopy misalignment occurred at more than 70% of the time. The directional shear leaded to considerable lateral kinematic momentum fluxes (Figure 7), indicating a significantly interaction between slope and valley winds.
Above canopy, the nocturnal drainage maximum often occurred at the 42 m above the ground level or at the 24 m above the canopy (Figure 3), which was relative high compared with previous studies [19,28,38]. The drainage flow intensity (measured by the down-valley velocity at the 48 m and the velocity shear between 42 and 48 m) and probability were optimized when the above-canopy θv gradient was about 0.11 °C∙m−1 during the leaf-on season and 0.08 °C∙m−1 during the leaf-off season, respectively (Figure 9 and Figure 11). In the daytime, the up-valley wind intensity and probability decreased as the θv gradient changed from lapse conditions to isothermal conditions. Below the canopy, the nocturnal drainage nearly persistently strengthened with above-canopy θv gradient increasing (Figure 9 and Figure 11).
We found that the wind around the tower had a distinct 3-dimensional nature, which had significant implications for the mass flux measurements by EC method. First, inference about drainage flow based on above-canopy measurement alone may be not enough, since the down-slope wind prevails under the dense canopy even for unstable conditions, independent of the above-canopy wind (Figure 10a,c). Second, we found significant directional shear of horizontal wind, suggesting it might be inappropriate to simplify the horizontal advection to a 2-dimensional design such as at the Vielsalm site in Belgium [56], the Hainich site in Germany [53] and the Lageren site in Switzerland [46]. It may be more accurate to estimate the horizontal advection layer by layer, with the horizontal gradient of CO2 concentration projected to the mean wind stream for each layer [57]. Third, the magnitude of vertical velocity at 36 m trended to vanish near ground, but the below-canopy vertical velocity could be opposite to that above canopy in the leaf-on mid-day (Figure 3a,c), which was due to the prevailing subcanopy down-slope wind but above-canopy up-valley wind (Table 2). This support the argument that the vertical advection based on one point vertical velocity measurement above canopy as a simplification are not generally applicable [58]. Thus, detailed profile of vertical velocity may be necessary to accurately estimate the total vertical advection by various layers with different vertical velocity and CO2 concentration measurements [58]. However, the profile of vertical velocity is particularly difficult to measure because of various factors such as coordinate system selection and sonic anemometer bias [11,59,60]. And there is another challenge to “continuously” monitor the horizontal and vertical gradients of CO2 concentration due to large temporal fluctuation, discrete temporal sampling and small magnitude gradients [6,60,61]. Fourth, the wind regime (and thus advection) at Maoershan site is different from those at the three sites in the Advection Experiment (ADVEX) [2,3], the Colorado site [5,14,18,57], the Morgan-Monroe State Forest site [10,62] and others [9,11,13,30], although there are some general patterns of thermally driven wind. These findings supported the advection regime is highly site-dependent [25]. The eddy flux measurements at valley sites are still a big challenge because of more complex wind regime than at slope sites. This inference was confirmed by the findings at two other valley sites [11,30]. Fifth, because direct advection measurements may be suffered from considerable errors [2], novel experiment design [13] and data processing strategies [11,38,63] may be helpful to gain robust annual fluxes of carbon and water vapor in complex terrain. On the other hand, comprehensive comparisons between the NEE by the EC technique with other independent measurements such as the ecosystem respiration by chamber-based up-scaling method and the biometric net ecosystem production [13,64,65] will be necessary to make a cross-validation of the carbon fluxes, which are ongoing at the Maoershan site.
In conclusion, we found a strong interaction between valley and slope winds at the Maoershan site. The relative high elevation of nocturnal drainage maximum (often 42 m) likely resulted from the unique terrain characteristics: the lower part of the sidewall of the valley and a long distance from the valley head. The above-canopy wind was a typical thermally driven valley wind system. However, below the canopy during the leaf-on season, down-slope wind predominated at night despite of a temperature lapse and unstable condition, whereas down-slope flow prevailed in the daytime due to frequent temperature inversion and isothermal conditions. The contrasting thermal gradients, stability regimes, and wind directions between below-canopy and above-canopy layers suggested a frequent decoupling of subcanopy layer. During the leaf-on season, the frequent directional shear and significant lateral kinematic momentum fluxes, above-canopy convergence in the nighttime and divergence in the daytime probably result in significant advective fluxes of trace gases and energy. A 3-dimensional design of wind vector and scalar concentration fields is essential to direct advection measurements in similar complex terrains.
Acknowledgments
The research was financially supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China (No. 2011BAD37B01), the Program for Changjiang Scholars and Innovative Research Team in University (IRT1054) and the National Natural Science Funds (No. 30625010) to C. K. Wang. Special thanks go to two anonymous reviewers for their constructive comments. We also appreciate Jiquan Chen and Christian Feigenwinter for their constructive suggestions on the manuscript. The Maoershan Forest Ecosystem Research Station provided field logistic support.
Author Contributions
The paper was written by Xingchang Wang with a significant contribution by Chuankuan Wang and Qinglin Li. Chuankuan Wang and Xingchang Wang are responsible for the research design. Xingchang Wang conducted most of the field work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baldocchi, D. Measuring fluxes of trace gases and energy between ecosystems and the atmosphere—The state and future of the eddy covariance method. Global. Change. Biol. 2014, 20, 3600–3609. [Google Scholar] [CrossRef]
- Aubinet, M.; Feigenwinter, C.; Heinesch, B.; Bernhofer, C.; Canepa, E.; Lindroth, A.; Montagnani, L.; Rebmann, C.; Sedlak, P.; van Gorsel, E. Direct advection measurements do not help to solve the night-time CO2 closure problem: Evidence from three different forests. Agric. For. Meteorol. 2010, 150, 655–664. [Google Scholar] [CrossRef]
- Feigenwinter, C.; Bernhofer, C.; Eichelmann, U.; Heinesch, B.; Hertel, M.; Janous, D.; Kolle, O.; Lagergren, F.; Lindroth, A.; Minerbi, S.; et al. Comparison of horizontal and vertical advective CO2 fluxes at three forest sites. Agric. For. Meteorol. 2008, 148, 12–24. [Google Scholar] [CrossRef]
- Lee, X. On micrometeorological observations of surface-air exchange over tall vegetation. Agric. For. Meteorol. 1998, 91, 39–49. [Google Scholar] [CrossRef]
- Sun, J.; Burns, S.P.; Delany, A.C.; Oncley, S.P.; Turnipseed, A.A.; Stephens, B.B.; Lenschow, D.H.; LeMone, M.A.; Monson, R.K.; Anderson, D.E. CO2 transport over complex terrain. Agric. For. Meteorol. 2007, 145, 1–21. [Google Scholar] [CrossRef]
- Van Gorsel, E.; Harman, I.N.; Finnigan, J.J.; Leuning, R. Decoupling of air flow above and in plant canopies and gravity waves affect micrometeorological estimates of net scalar exchange. Agric. For. Meteorol. 2011, 151, 927–933. [Google Scholar] [CrossRef]
- Staebler, R.M.; Fitzjarrald, D.R. Observing subcanopy CO2 advection. Agric. For. Meteorol. 2004, 122, 139–156. [Google Scholar] [CrossRef]
- Tóta, J.; Fitzjarrald, D.R.; Staebler, R.M.; Sakai, R.K.; Moraes, O.M.; Acevedo, O.C.; Wofsy, S.C.; Manzi, A.O. Amazon rain forest subcanopy flow and the carbon budget: Santarém lba-eco site. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Alekseychik, P.; Mammarella, I.; Launiainen, S.; Rannik, Ü.; Vesala, T. Evolution of the nocturnal decoupled layer in a pine forest canopy. Agric. For. Meteorol. 2013, 174–175, 15–27. [Google Scholar] [CrossRef]
- Froelich, N.; Schmid, H. Flow divergence and density flows above and below a deciduous forest: Part II. Below-canopy thermotopographic flows. Agric. For. Meteorol. 2006, 138, 29–43. [Google Scholar] [CrossRef]
- Novick, K.; Brantley, S.; Miniat, C.F.; Walker, J.; Vose, J.M. Inferring the contribution of advection to total ecosystem scalar fluxes over a tall forest in complex terrain. Agric. For. Meteorol. 2014, 185, 1–13. [Google Scholar] [CrossRef]
- Belcher, S.E.; Harman, I.N.; Finnigan, J.J. The wind in the willows: Flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 2012, 44, 479–504. [Google Scholar] [CrossRef]
- Thomas, C.K.; Martin, J.G.; Law, B.E.; Davis, K. Toward biologically meaningful net carbon exchange estimates for tall, dense canopies: Multi-level eddy covariance observations and canopy coupling regimes in a mature douglas-fir forest in oregon. Agric. For. Meteorol. 2013, 173, 14–27. [Google Scholar] [CrossRef]
- Yi, C.; Monson, R.K.; Zhai, Z.; Anderson, D.E.; Lamb, B.; Allwine, G.; Turnipseed, A.A.; Burns, S.P. Modeling and measuring the nocturnal drainage flow in a high-elevation, subalpine forest with complex terrain. J. Geophys. Res. 2005. [Google Scholar] [CrossRef]
- Zardi, D.; Whiteman, C.D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting: Recent Progress and Current Challenges; Chow, F., de Wekker, S., Snyder, B., Eds.; Springer: Berlin, Germany, 2013; pp. 35–119. [Google Scholar]
- Grisogono, B.; Axelsen, S.L. A note on the pure katabatic wind maximum over gentle slopes. Bound.-Layer Meteorol. 2012, 145, 527–538. [Google Scholar] [CrossRef]
- Chen, H.; Yi, C. Optimal control of katabatic flows within canopies. Q. J. R. Meteor. Soc. 2012, 138, 1676–1680. [Google Scholar] [CrossRef]
- Burns, S.P.; Sun, J.; Lenschow, D.H.; Oncley, S.P.; Stephens, B.B.; Yi, C.; Anderson, D.E.; Hu, J.; Monson, R.K. Atmospheric stability effects on wind fields and scalar mixing within and just above a subalpine forest in sloping terrain. Bound.-Layer Meteorol. 2011, 138, 231–262. [Google Scholar] [CrossRef]
- Aubinet, M.; Berbigier, P.; Bernhofer, C.; Cescatti, A.; Feigenwinter, C.; Granier, A.; Grünwald, T.; Havrankova, K.; Heinesch, B.; Longdoz, B. Comparing CO2 storage and advection conditions at night at different carboeuroflux sites. Bound.-Layer Meteorol. 2005, 116, 63–93. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Zhong, S. Downslope flows on a low-angle slope and their interactions with valley inversions. Part I: Observations. J. Appl. Meteorol. Climitol. 2008, 47, 2023–2038. [Google Scholar] [CrossRef]
- Trachte, K.; Nauss, T.; Bendix, J. The impact of different terrain configurations on the formation and dynamics of katabatic flows: Idealised case studies. Bound.-Layer Meteorol. 2010, 134, 307–325. [Google Scholar] [CrossRef]
- van Gorsel, E.; Christen, A.; Feigenwinter, C.; Parlow, E.; Vogt, R. Daytime turbulence statistics above a steep forested slope. Bound.-Layer Meteorol. 2003, 109, 311–329. [Google Scholar]
- Mahrt, L.; Richardson, S.; Seaman, N.; Stauffer, D. Non-stationary drainage flows and motions in the cold pool. Tellus A 2010, 62, 698–705. [Google Scholar]
- Belcher, S.; Finnigan, J.; Harman, I. Flows through forest canopies in complex terrain. Ecol. Appl. 2008, 18, 1436–1453. [Google Scholar] [CrossRef] [PubMed]
- Aubinet, M. Eddy covariance CO2 flux measurements in nocturnal conditions: An analysis of the problem. Ecol. Appl. 2008, 18, 1368–1378. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, M.T.; Zhong, S. The effect of sidewall forest canopies on the formation of cold-air pools: A numerical study. J. Geophys. Res. 2013, 118, 5965–5978. [Google Scholar] [CrossRef]
- Froelich, N.; Grimmond, C.; Schmid, H. Nocturnal cooling below a forest canopy: Model and evaluation. Agric. For. Meteorol. 2011, 151, 957–968. [Google Scholar] [CrossRef]
- Mahrt, L. Stratified atmospheric boundary layers. Bound.-Layer Meteorol. 1999, 90, 375–396. [Google Scholar] [CrossRef]
- Pypker, T.; Unsworth, M.; Lamb, B.; Allwine, E.; Edburg, S.; Sulzman, E.; Mix, A.; Bond, B. Cold air drainage in a forested valley: Investigating the feasibility of monitoring ecosystem metabolism. Agric. For. Meteorol. 2007, 145, 149–166. [Google Scholar] [CrossRef]
- Tóta, J.; Roy Fitzjarrald, D.; da Silva Dias, M.A. Amazon rainforest exchange of carbon and subcanopy air flow: Manaus lba site—A complex terrain condition. Sci. World J. 2012. [Google Scholar] [CrossRef]
- Komatsu, H.; Yoshida, N.; Takizawa, H.; Kosaka, I.; Tantasirin, C.; Suzuki, M. Seasonal trend in the occurrence of nocturnal drainage flow on a forested slope under a tropical monsoon climate. Bound.-Layer Meteorol. 2003, 106, 573–592. [Google Scholar] [CrossRef]
- Pypker, T.G.; Unsworth, M.H.; Mix, A.C.; Rugh, W.; Ocheltree, T.; Alstad, K.; Bond, B.J. Using nocturnal cold air drainage flow to monitor ecosystem processes in complex terrain. Ecol. Appl. 2007, 17, 702–714. [Google Scholar] [CrossRef] [PubMed]
- Rotach, M.; Andretta, M.; Calanca, P.; Weigel, A.; Weiss, A. Boundary layer characteristics and turbulent exchange mechanisms in highly complex terrain. Acta Geophys. 2008, 56, 194–219. [Google Scholar] [CrossRef]
- Jiao, Z.; Wang, C.-K.; Wang, X.-C. Spatio-temporal variations of CO2 concentration within the canopy in a temperate deciduous forest, northeast China. Chin. J. Plant Ecol. 2011, 35, 512–522. [Google Scholar] [CrossRef]
- Mahrt, L. Momentum balance of gravity flows. J. Atmos. Sci. 1982, 39, 2701–2711. [Google Scholar] [CrossRef]
- Mahrt, L.; Vickers, D.; Nakamura, R.; Soler, M.R.; Sun, J.; Burns, S.; Lenschow, D.H. Shallow drainage flows. Bound.-Layer Meteorol. 2001, 101, 243–260. [Google Scholar] [CrossRef]
- Rotach, M.W.; Zardi, D. On the boundary-layer structure over highly complex terrain: Key findings from map. Q. J. R. Meteor. Soc. 2007, 133, 937–948. [Google Scholar] [CrossRef]
- Rebmann, C.; Zeri, M.; Lasslop, G.; Mund, M.; Kolle, O.F.; Schulze, E.-D.; Feigenwinter, C. Treatment and assessment of the CO2-exchange at a complex forest site in thuringia, germany. Agric. For. Meteorol. 2010, 150, 684–691. [Google Scholar] [CrossRef]
- Staebler, R.M.; Fitzjarrald, D.R. Measuring canopy structure and the kinematics of subcanopy flows in two forests. J. Appl. Meteorol. 2005, 44, 1161–1179. [Google Scholar] [CrossRef]
- Wang, C.; Han, Y.; Chen, J.; Wang, X.; Zhang, Q.; Bond-Lamberty, B. Seasonality of soil CO2 efflux in a temperate forest: Biophysical effects of snowpack and spring freeze–thaw cycles. Agric. For. Meteorol. 2013, 177, 83–92. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound.-Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Yi, C. Momentum transfer within canopies. J. Appl. Meteorol. Climitol. 2008, 47, 262–275. [Google Scholar] [CrossRef]
- Mahrt, L.; Lee, X.; Black, A.; Neumann, H.; Staebler, R. Nocturnal mixing in a forest subcanopy. Agric. For. Meteorol. 2000, 101, 67–78. [Google Scholar] [CrossRef]
- Mahrt, L.; Vickers, D.; Sun, J.; Jensen, N.; Jørgensen, H.; Pardyjak, E.; Fernando, H. Determination of the surface drag coefficient. Bound.-Layer Meteorol. 2001, 99, 249–276. [Google Scholar] [CrossRef]
- Weber, R. Remarks on the definition and estimation of friction velocity. Bound.-Layer Meteorol. 1999, 93, 197–209. [Google Scholar] [CrossRef]
- Dupont, S.; Patton, E.G. Influence of stability and seasonal canopy changes on micrometeorology within and above an orchard canopy: The chats experiment. Agric. For. Meteorol. 2012, 157, 11–29. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Liang, N.; Tan, Z.; Yu, G.; Sha, L.; Song, Q. Pooling of CO2 within a small valley in a tropical seasonal rain forest. J. Forest. Res. 2012, 17, 241–252. [Google Scholar] [CrossRef]
- Monti, P.; Fernando, H.; Princevac, M.; Chan, W.; Kowalewski, T.; Pardyjak, E. Observations of flow and turbulence in the nocturnal boundary layer over a slope. J. Atmos. Sci. 2002, 59, 2513–2534. [Google Scholar] [CrossRef]
- Burns, P.; Chemel, C. Evolution of cold-air-pooling processes in complex terrain. Bound.-Layer Meteorol. 2014, 150, 423–447. [Google Scholar] [CrossRef]
- Thomas, C.K. Variability of sub-canopy flow, temperature, and horizontal advection in moderately complex terrain. Bound.-Layer Meteorol. 2011, 139, 61–81. [Google Scholar] [CrossRef]
- Wu, J.; Guan, D.; Yuan, F.; Yang, H.; Wang, A.; Jin, C. Evolution of atmospheric carbon dioxide concentration at different temporal scales recorded in a tall forest. Atmos. Environ. 2012, 61, 9–14. [Google Scholar] [CrossRef]
- Aubinet, M.; Heinesch, B.; Yernaux, M. Horizontal and vertical CO2 advection in a sloping forest. Bound.-Layer Meteorol. 2003, 108, 397–417. [Google Scholar] [CrossRef]
- Kruijt, B.; Malhi, Y.; Lloyd, J.; Norbre, A.; Miranda, A.; Pereira, M.; Culf, A.; Grace, J. Turbulence statistics above and within two amazon rain forest canopies. Bound.-Layer Meteorol. 2000, 94, 297–331. [Google Scholar] [CrossRef]
- Sedlák, P.; Aubinet, M.; Heinesch, B.; Janouš, D.; Pavelka, M.; Potužníková, K.; Yernaux, M. Night-time airflow in a forest canopy near a mountain crest. Agric. For. Meteorol. 2010, 150, 736–744. [Google Scholar] [CrossRef]
- Bernardes, M.; Dias, N.L. The alignment of the mean wind and stress vectors in the unstable surface layer. Bound.-Layer Meteorol. 2010, 134, 41–59. [Google Scholar] [CrossRef]
- Su, H.-B.; Schmid, H.; Vogel, C.; Curtis, P. Effects of canopy morphology and thermal stability on mean flow and turbulence statistics observed inside a mixed hardwood forest. Agric. For. Meteorol. 2008, 148, 862–882. [Google Scholar] [CrossRef]
- Yi, C.; Anderson, D.E.; Turnipseed, A.A.; Burns, S.P.; Sparks, J.P.; Stannard, D.I.; Monson, R.K. The contribution of advective fluxes to net ecosystem exchange in a high-elevation, subalpine forest. Ecol. Appl. 2008, 18, 1379–1390. [Google Scholar] [CrossRef] [PubMed]
- Feigenwinter, C.; Montagnani, L.; Aubinet, M. Plot-scale vertical and horizontal transport of CO2 modified by a persistent slope wind system in and above an alpine forest. Agric. For. Meteorol. 2010, 150, 665–673. [Google Scholar] [CrossRef]
- Queck, R.; Bernhofer, C. Constructing wind profiles in forests from limited measurements of wind and vegetation structure. Agric. For. Meteorol. 2010, 150, 724–735. [Google Scholar] [CrossRef]
- Siebicke, L.; Hunner, M.; Foken, T. Aspects of CO2 advection measurements. Theor. Appl. Climatol. 2012, 109, 109–131. [Google Scholar] [CrossRef]
- Marcolla, B.; Cobbe, I.; Minerbi, S.; Montagnani, L.; Cescatti, A. Methods and uncertainties in the experimental assessment of horizontal advection. Agric. For. Meteorol. 2014, 198–199, 62–71. [Google Scholar] [CrossRef]
- Froelich, N.; Schmid, H.; Grimmond, C.; Su, H.-B.; Oliphant, A. Flow divergence and density flows above and below a deciduous forest: Part I. Non-zero mean vertical wind above canopy. Agric. For. Meteorol. 2005, 133, 140–152. [Google Scholar] [CrossRef]
- van Gorsel, E.; Delpierre, N.; Leuning, R.; Black, A.; Munger, J.W.; Wofsy, S.; Aubinet, M.; Feigenwinter, C.; Beringer, J.; Bonal, D. Estimating nocturnal ecosystem respiration from the vertical turbulent flux and change in storage of CO2. Agric. For. Meteorol. 2009, 149, 1919–1930. [Google Scholar]
- Gielen, B.; de Vos, B.; Campioli, M.; Neirynck, J.; Papale, D.; Verstraeten, A.; Ceulemans, R.; Janssens, I. Biometric and eddy covariance-based assessment of decadal carbon sequestration of a temperate scots pine forest. Agric. For. Meteorol. 2013, 174, 135–143. [Google Scholar] [CrossRef]
- Wu, J.; Larsen, K.; van der Linden, L.; Beier, C.; Pilegaard, K.; Ibrom, A. Synthesis on the carbon budget and cycling in a danish, temperate deciduous forest. Agric. For. Meteorol. 2013, 181, 94–107. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).