1. Introduction
The most important property of the Earth’s atmosphere is the great variability of its parameters [
1,
2]. Scientists in the world are searching for theoretical and practical means to investigate these variations in order to conceive some models which are able to predict the evolution of climate. Taking advantage of the technological progress in several domains, meteorological instruments used for the measurement of these parameters are now very reliable while obtaining direct and punctual measurements. Nevertheless, the installation of this equipment in a given region, for a spatio-temporal survey, needs enormous human and financial means. This constitutes a handicap in mastering the spatio-temporal evolution of the atmospheric parameters in these regions, particularly in developing countries like the sub-Saharan ones.
The use of atmospheric remote sensing with the help of radars and satellites can be considered as a good alternative or complementary to the ground-based equipment. The characterization of the atmosphere can be realized everywhere, but the measurements are not direct. The determination of the indirectly measured physical parameter means that data, obtained
in situ, must be taken into account in the calibration process of the instrument [
3].
Remote sensing has paved the way for the development of powerful applications in the domain of atmospheric physics in order to understand the complexity of some atmospheric perturbations. However, the most important difficulty encountered lies in the different relationships issued from the calibration. That is the case when measurements are processed on convective systems with meteorological radars. In this example, the aim is to find a relationship between the radar reflectivity Z (dBZ) and the rain rate R (mm∙h
−1) (Z-R relationship). The observed precipitation’s variability is due to the raindrop size distribution whose instability is reliable for some factors like speed, collision or agglomeration of rain drops [
4,
5]
An automatic adjustment of the Z–R relationship dependent on the type of precipitation is extremely difficult to put in place in operational conditions [
6]. The raindrop size distribution diversity of precipitations and the different phases of the hydrometers, solid or liquid, have an influence on this relationship. There are a lot of relationships between Z and R [
7,
8,
9,
10,
11,
12]
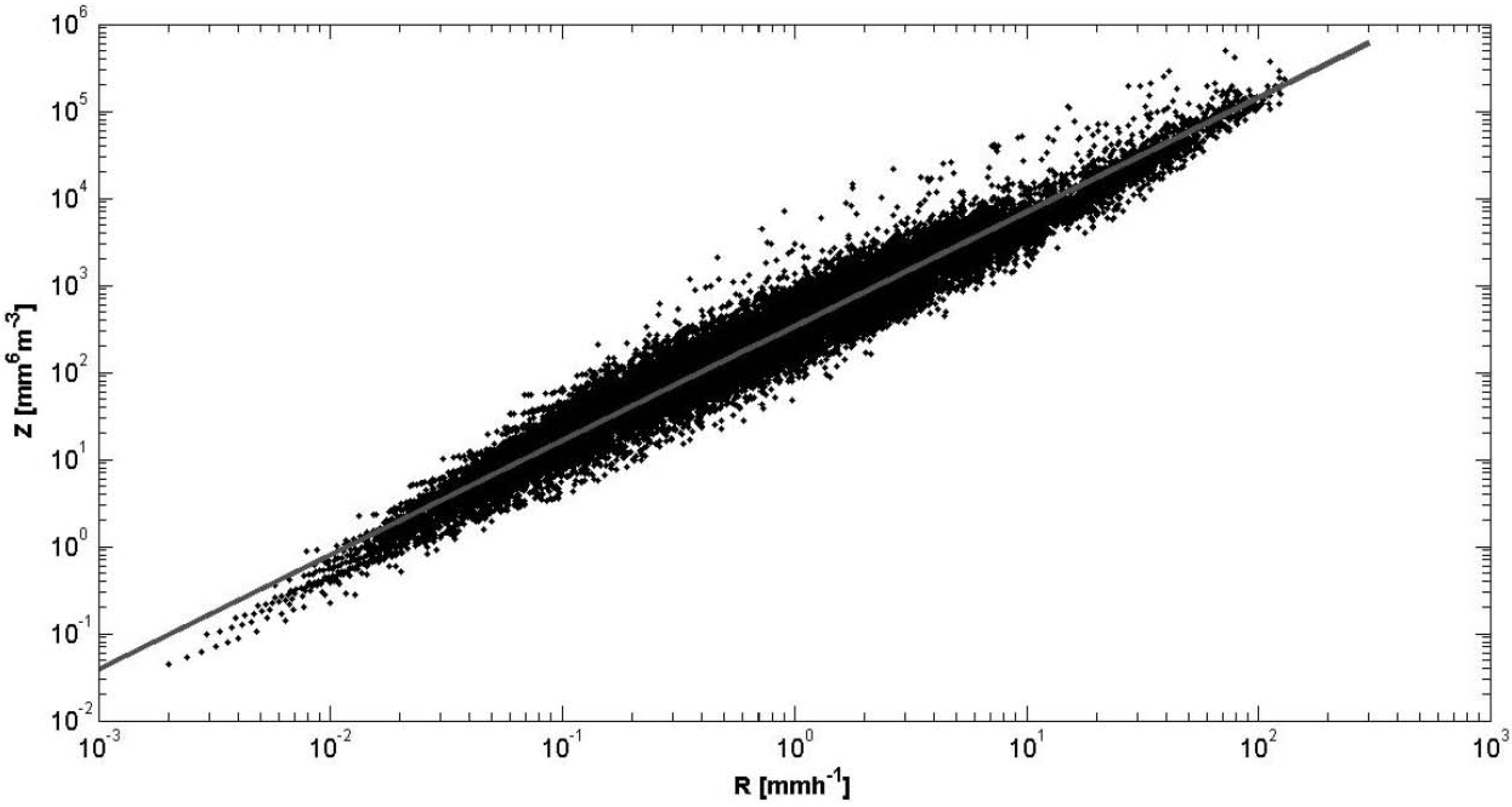
The use of only one relationship cannot generally represent the natural variability of precipitations. For example (see
Figure 1), for a value of R, one can get several values corresponding to Z and
vice versa.
Several studies have been conducted for the modelling of the size of rain drops under different latitudes [
13]. The theoretical distribution functions evaluated are many but likely are not easy to manipulate [
6]. The disdrometer allows measuring automatically and continuously the extent of rain drop distribution.
In this study, we want to adapt the neural network technique to the Rain Drop Size Distribution (RDSD) of precipitations in order to conceive a model which could take into account the distinct types of rain perturbations under different latitudes, with the RDSD. The liquid water content (M), the rain rate (R) and the radar reflectivity (Z) are considered as outputs.
The most important property of the neural networks is the nature of their adaptation, which may be deducted from samples. This characteristic provides some tools, which are able to solve high non-linear relationships [
14]. The neural network is an alternative tool for modelling and describing complex relationships between physical or technical parameters [
15]. It is considered as an “engine” delivering to its entries an “answer” which is inaccessible or not easily accessible with existing analytical methods. In the following work, we describe briefly the theory of neural networks, presenting the Feed Forward Back Propagation (FFBP) and the Cascade Forward Back Propagation (CFBP) models. We will then situate the five African localities which were subject to our experimental work and where the collection and the classification of the rain drops were realized, while using the disdrometer. Lastly, we will describe how the different neural network models have been constructed, trained and used for the estimation of the water content, the rain rate and the radar reflectivity. We present the results in the form of curve comparisons and calculated root means square errors (RMSE).
Figure 1.
Radar reflectivity factor Z vs. rain rate R as deduced from the 1-min rain RDSD (Rain Drop Size Distribution) observed with the JWD (Joss-Waldvogel Disdrometer) in Dakar (Senegal), during 1997–2002, and fitted curve.
Figure 1.
Radar reflectivity factor Z vs. rain rate R as deduced from the 1-min rain RDSD (Rain Drop Size Distribution) observed with the JWD (Joss-Waldvogel Disdrometer) in Dakar (Senegal), during 1997–2002, and fitted curve.
2. Theoretical Background on Artificial Neural Networks
2.1. Basic Principles
An artificial neural network is organized into several layers. One layer contains some neurons which are connected to those of the following layer. Each connection is weighed. A neuron is described with its own activation level, which is responsible for the propagation of the information from the input layer to the output layer. However, to obtain reliable weights, the neural network must, first of all, learn about the known input- and output-samples. During the learning process, an error between theoretical and experimental outputs is computed. Thus, the weight-values are modified through an error back propagation process which is executed on several sampling data, until achieving as small error as possible. After this last step, the neural network can be considered as trained and able to be used in calculating other responses to new entries that have never been presented to the network. It is important to emphasize that the learning speed of the neural network depends not only on the architecture but also on the algorithm used.
2.2. Model of a Neuron in a Neural Network
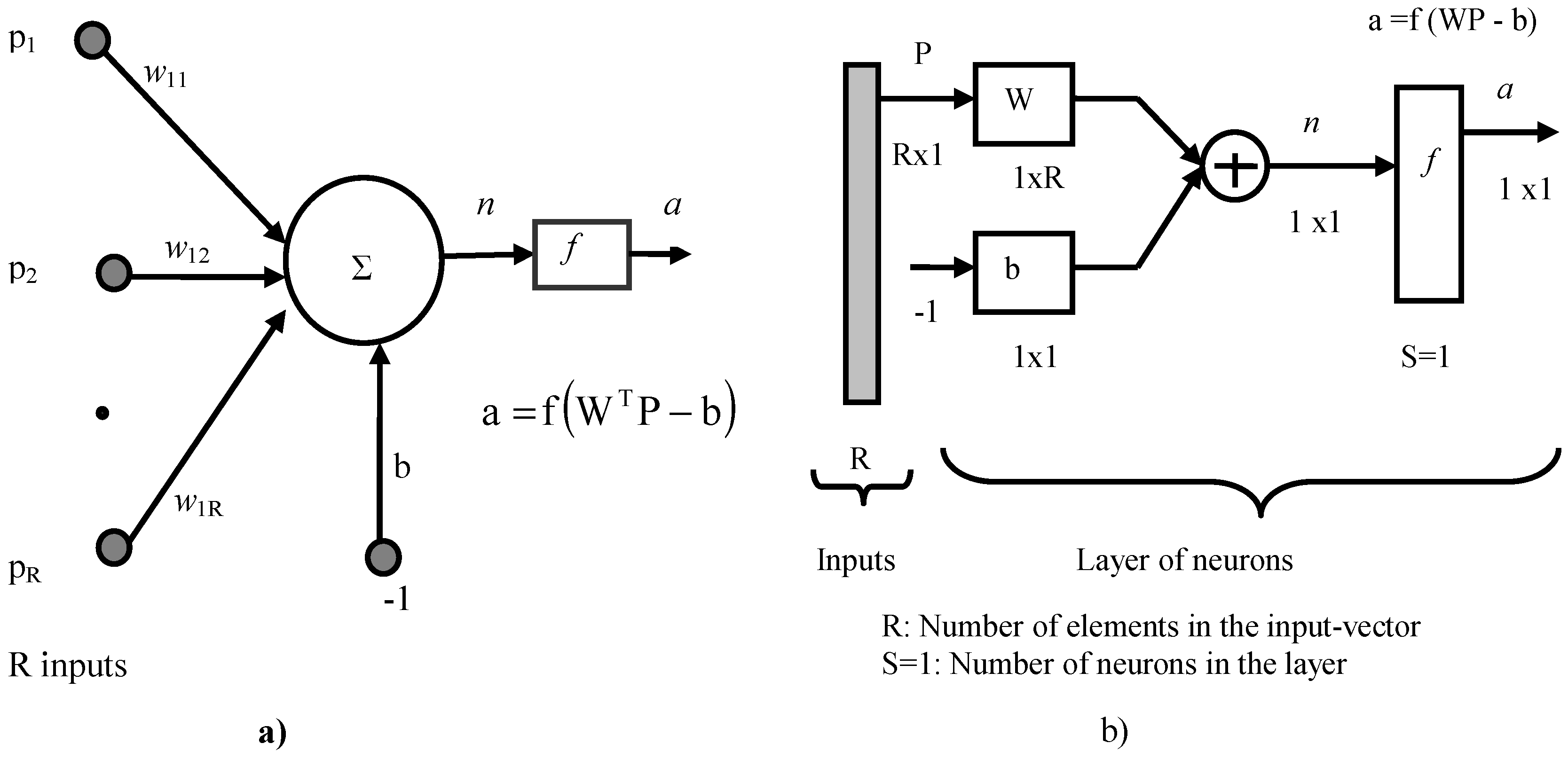
The neuron is considered as an elementary cell in which some computational operations are realized (see
Figure 2a). It is composed of an integrator (∑) which calculates the weighted sum of the entries. The activation level
n, with b as bias, of this integrator, is transformed by a transfer function
f in order to produce an output
a. The matrix representation of the neuron is shown on
Figure 2b, with S supposed to be equal to the unity, to signify that there is only one neuron [
16].
Figure 2.
Representation of a neuron: (a) model; (b) matrix representation for S = 1.
Figure 2.
Representation of a neuron: (a) model; (b) matrix representation for S = 1.
The
R entries of the neuron correspond to the vector
P = [
P1 P2 …
PR]
T while
W = [
W11 W12 …
W1R]
T represents the vector weights of the neuron. The output
n of the integrator is then described by Equation (1):
If the argument of the function
f becomes zero or positive, the activation level reaches or is superior to the bias
b, if not, it is negative [
16,
17].
The output of the neuron is given by the Equation (2):
2.3. Construction of a Neural Network and its Learning Process
To build a neural network, it is sufficient to combine the neural layers. Each layer has its own matrix weight
Wk, where
k designates the index of the layer. Thus, the vectors
bk,
nk and
ak are associated to the layer
k. To specify the neural network structure, the number of layers and the number of neurons in each layer must be chosen. The learning step is a dynamic and iterative process which consists in modifying the parameters of the network after receiving the inputs from its environment. The learning type is determined by the way the change of the parameters occurs [
14]. In almost all neural architectures encountered, the learning results in the synaptic modification of the weights connecting one neuron to the other. If
wij (
t) designates the weight connecting the neuron
i to its entry
j and at time
t, a change ∆
wij (
t) of the weights can simply be expressed by the Equation (3):
where
wij (
t + 1) represents the new entry value of the weight
wij.
A set of well-defined rules that allow realizing a weight adaptation process is designated by a learning algorithm of the neural network. There are a lot of rules that can be used. We can enumerate among others: the method of learning by error correction, the so-called Least Mean Square (LMS) method; the feed forward back propagation in a multilayer neural network; and the method of the back propagation of error sensitivities. In our study, we focalize on the method based on a small modification of the feed forward back propagation method.
2.4. The Feed Forward Back Propagation Method Used by a Multilayer Neural Network
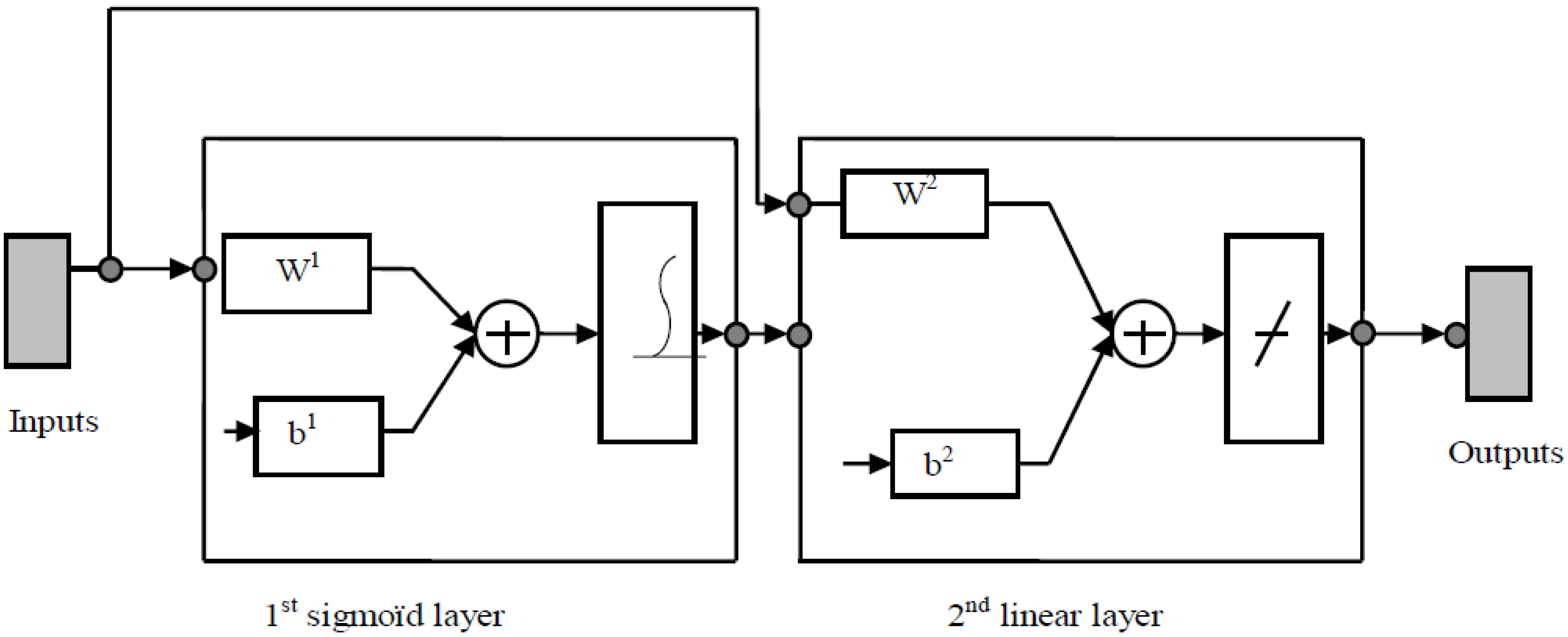
Let us now consider the multilayer neural network (composed of
M layers) whose synoptic graphical representation is given in
Figure 3 for three layers. The equation describing the outputs of the layer
k is:
In the presence of sample-data combinations entries/outputs{(Pq, dq)}, q = 1, …, Q, where Pq designates an entry-vector and dq a desired output-vectors, we can forward propagate at each instant t, an entry-vector P(t) through the neural network in order to get an output-vector a(t).
Figure 3.
An example of synoptic representation of a 3 layer-neural network in a feed forward back propagation form.
Figure 3.
An example of synoptic representation of a 3 layer-neural network in a feed forward back propagation form.
Given here are
e(
t), the error produced by the network calculation for an entry, and the corresponding desired output
d(
t):
The performance function
F that permits minimizing the root mean square error is defined by the following expression:
where
E[ ] and
X are respectively the mean and the vector grouping the set of the weights and the biases of the neural network.
F will be approximated on a layer with the instantaneous error:
The method of the steepest falling gradient is used to optimize
X with the help of the following equations:
where
η designates the learning rate of the neural network. To calculate the partial derivatives of
![Atmosphere 05 00454 i004]()
the rule of composition functions is used:
The activation levels
![Atmosphere 05 00454 i006]()
of the layer
k depend directly on the weights and biases on this layer, and can be expressed by the following relation:
Now, for the first terms of the Equation (9), we define the sensitivities
![Atmosphere 05 00454 i008]()
of
![Atmosphere 05 00454 i004]()
in relation with the changes of the activation level
![Atmosphere 05 00454 i006]()
of the neuron
i belonging to the layer
k by the equation:
The expressions of
![Atmosphere 05 00454 i010]()
and
![Atmosphere 05 00454 i011]()
become:
Equation (12) is responsible for the modification of the weight connections and biases and the different iteration learning steps of the neural network presented in
Section 4.
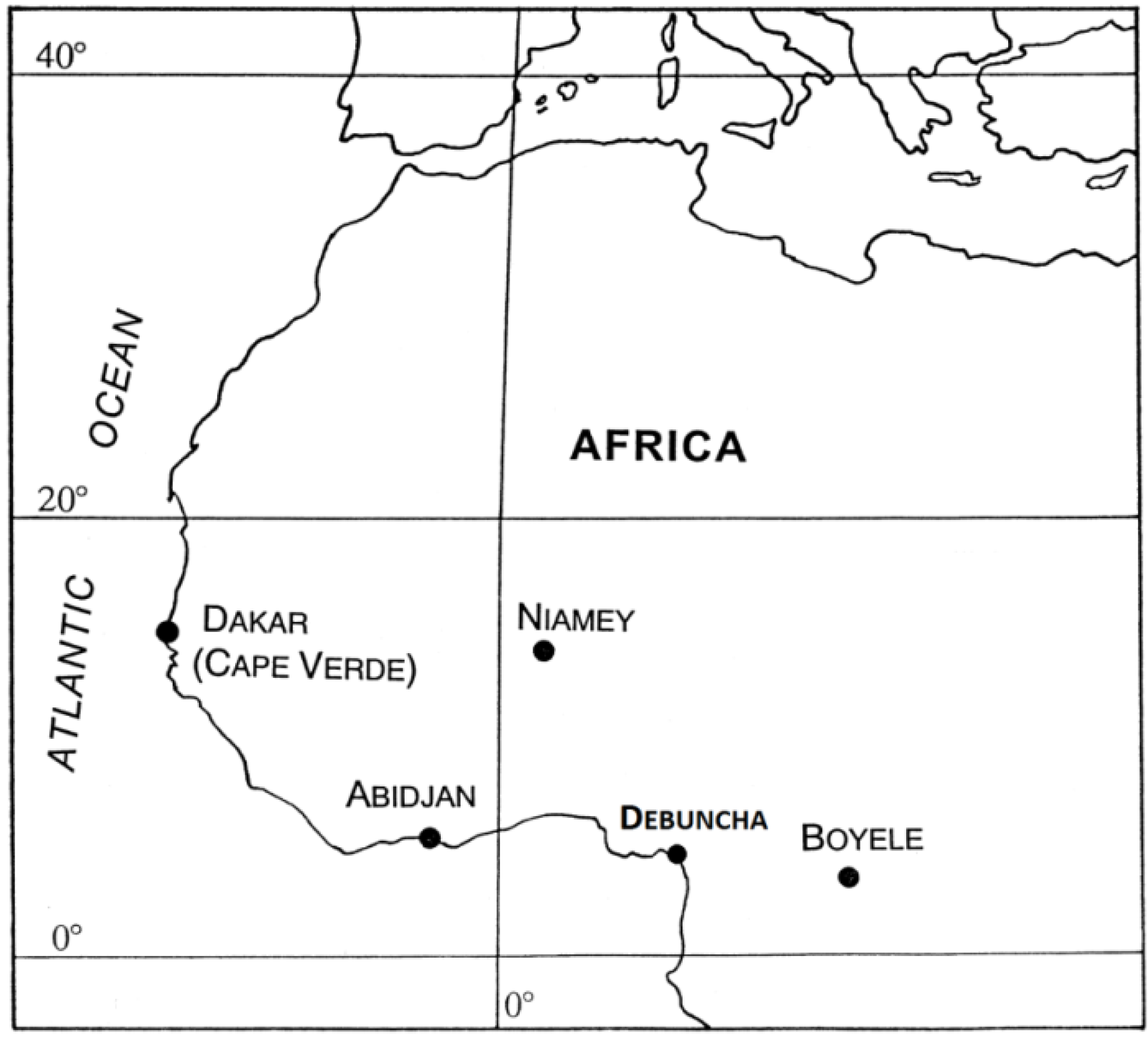
3. Localities and Data Used for the Study
The applications of our study have been realized after using the RDSD. These data have been collected under different latitudes in Sub-Saharan Africa (see
Figure 4). Their main characteristics are grouped in the
Table 1. The disdrometer used for the data collection is a mechanical one and was developed by Joss and Waldvogel [
18,
19]. This instrument produces the RDSD minute by minute. The technical description of its functions is given by [
18,
19,
20,
21].
The principle of data processing of the disdrometer consists in classifying repeatedly in an interval of one minute the rain drops according to their diameter. During the collection period, some values are computed with the data by minute in order to obtain the values of some rain parameters such as the total number of rain drops, the distribution of the rain drop size, the rain rate, the radar reflectivity, the liquid water content and the median volume diameter.
Figure 4.
Location of the data collection sites.
Figure 4.
Location of the data collection sites.
Table 1.
Database and localities studied in sub-Saharan Africa.
Table 1.
Database and localities studied in sub-Saharan Africa.
| Town (Country) | Collection Period of the RDSD | Total Number of the RDSD (min) |
|---|
| Abidjan (Ivory Coast) | June; September to December: 1986 | 23,126 |
| Boyele (Congo) | March to June: 1989 | 18,354 |
| Debuncha (Cameroon) | May to June 2004 | 39,113 |
| Dakar (Senegal) | July to September: 1997, 1998 et 2000 | 15,145 |
| Niamey (Niger) | July to September: 1989 | 4468 |
Table 2.
Values of the exponent factor
p and of the multiplicative factor
ap in relation to the parameter studied (
![Atmosphere 05 00454 i013]()
).
Table 2.
Values of the exponent factor p and of the multiplicative factor ap in relation to the parameter studied ( ![Atmosphere 05 00454 i013]() ).
).
| Parameter | Symbol P | Exponent Factor p | Unit | Multiplicative Factor ap |
|---|
| Rain rate | R | 3.67 | mm∙h−1 | 7.1 × 10−3 |
| Liquid water content | W | 3 | g∙m−3 | (π/6) × 10−3 |
| Radar reflectivity factor | Z | 6 | mm6∙m−3 | 1 |
The control parameters of the RDSD are calculated by different drop-diameter moments observed [
10] and changes with particular used moments [
22,
23,
24,
25,
26]. The parameters M, R and Z exploited in our study can be expressed in a generic form as follows:
where N(D) is the number of rain drops per unit height and per volume (mm
−1∙m
−3), D (mm) is the diameter of the equivalent sphere, and
aP a coefficient which depends on the type of parameter considered and on the chosen units, so as shown in t
Table 2. The stated disdrometer observation normally has large errors for small drop size and large drop size [
27]. The coefficient
p in Equation (13) is issued from the definition of the parameters; Z and R are respectively defined as the moment of order 6 and 3.67 of the diameter D [
28].
4. Methodology
The modelling process of a neural network requires the disposal of an entry’s number
R as well as the number of neurons in the output layer. These neural networks are defined by the specifications of the problem to be solved. The CFBP (Cascade Forward Back Propagation) model (see
Figure 5) is one of the artificial neural network types, which is used for the prediction of new output data [
29,
30,
31].
Figure 5.
Model of Cascade Forward Back Propagation (CFBP).
Figure 5.
Model of Cascade Forward Back Propagation (CFBP).
Taking into consideration the different analyses in, we will give an abstract of the methodology used in the learning process that we have implemented.
Initialize the weights with small random values;
For each combination (
pq,
dq) in the learning sample:
Propagate the entries
pq forward through the neural network layers:
Back propagate the sensitivities through the neural network layers:
Modify the weights and biases:
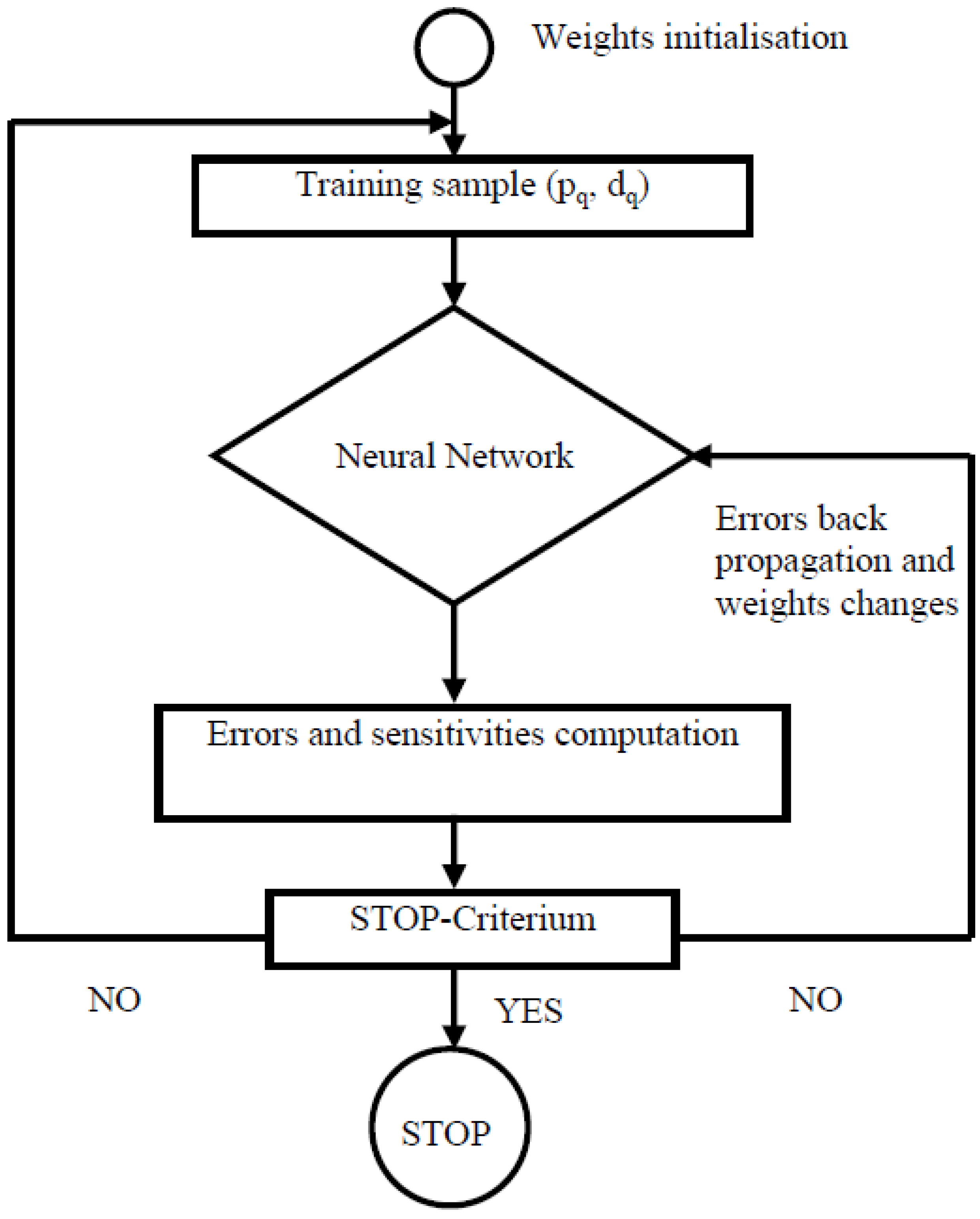
If the stopping criteria are reached, then stop; if not reached, they permute the presentation order of the combination built from the learning database, and begin again at Step 2.
The diagram describing the different steps of the learning process of the neural network is given by
Figure 6.
Figure 6.
Diagram of the learning process of the neural network.
Figure 6.
Diagram of the learning process of the neural network.
4.1. Description of the Databases and their Use in the Neural Models
The classes of diameters are used as entries of the neural network models in order to estimate the water content, the rain rate and the radar reflectivity factor. Thus, the neural networks will then be constituted of 25 entries corresponding to the 25 classes and of one output. The samples presented to the entry of the neural network correspond each to the one-minute values that were calculated by the disdrometer.
On the basis of the retrieval work, we then have two databases that we have named as “Base X” and “Base Y”. They are each made up of 23,126 samples. Each sample from the first database is a vector of 25 elements
X[
x1,
x2, …,
x25]
T. The base Y is a matrix of 23,126 × 3 dimensions whose three rows represent three different vectors, Y
1, Y
2 and Y
3. These three last vectors are known as the water content (M(g∙m
−3)), the rain rate (R(mm∙h
−1)) and the radar reflectivity (Z(mm
6∙m
−3)), each retrievable individually, from the X database. With each sample
j of the first database is then associated a real number
yij(
i = 1,2,3;
j = 1,2,…,23126). In this work, we have to retrieve these parameters. The different neural networks have as entries the parameters
xk (
k = 1,2,…,25) and as outputs the parameter
yi (
i = 1,2,3). The neural model is a cascade forward back propagation (CFBP) one, with a hidden layer of 20 neurons (
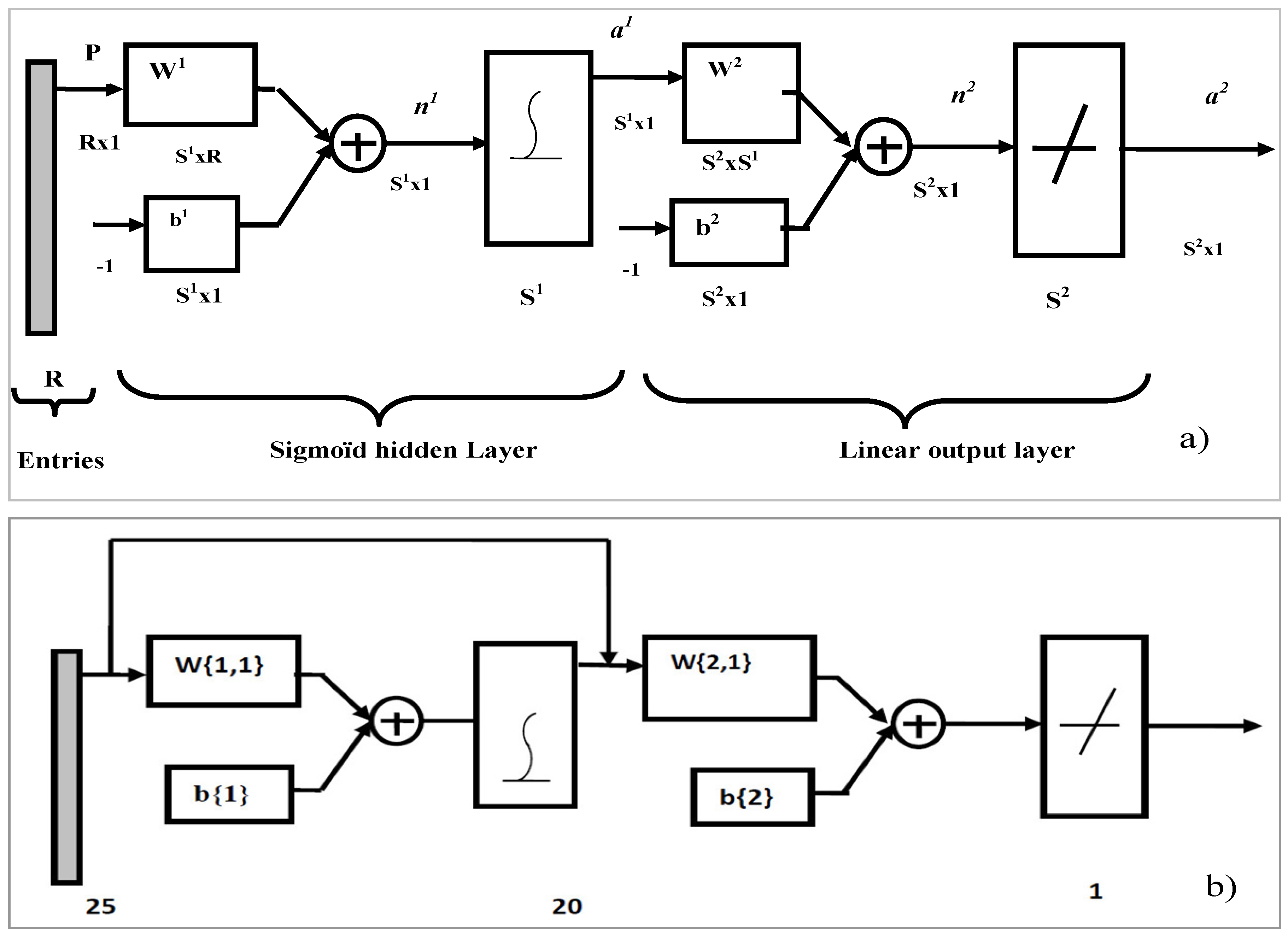
Figure 7a,b). We develop for each locality a model which will be applied to other localities before building another model, which will integrate all five localities. This last model will be applied on all five localities.
Figure 7.
ANN models: (a) description of the model; (b) the faster CFBP model, which was used for our simulations.
Figure 7.
ANN models: (a) description of the model; (b) the faster CFBP model, which was used for our simulations.
- -
R entry’s number (25 in our case)
- -
S1: Number of neurons in the first layer (hidden layer): 20 in our case
- -
S2: Number of neurons in the output layer: 1 in our case
- -
b1: Bias’ vector of the first layer with the dimension S1 × 1 (20 × 1 dimension in our case)
- -
b2: Bias’ vector of the output layer with the dimension S2 × 1 (1 × 1 in our case)
- -
W1: Matrix of weights according to the neurons of the first layer with the dimension S1 × R (20 × 25 dimension in our case);
- -
W2: Matrix of weights according to the neurons of output layer with the dimension S2 × S1 (1 × 20 dimension in our case)
4.2. Construction and Use of the Different Neural Networks
The databases are available for five studied localities, and two approaches are taken into consideration:
First, we create for each locality three LANN-models corresponding to the three parameters yi. The initial 5000 entries and the primary 5000 desired outputs, except Niamey with only 4468 sample data, are used for the training of the neural networks, and the 5000 following sample data (from the 5001st to 10,000th) have served as test data. After the training, we have obtained acceptable performance curves and have stored the LANN, that we designate by the indices, i, to confer them the role of retrieving the parameter yi. Each LANN i of a given locality is then invited to predict the parameters yi over the other localities. In this case, we have used as LANN inputs the entries obtained in the locality subjected to the predictive process. We estimate for the samples from the 5001st–10,000th the outputs that we compare with the available experiment present in this locality.
Secondly, we build for each parameter
Yi(M, R, Z) a polyvalent model (PANN): we extract from the databases of each locality the first 1200 sample data and constitute a training set composed of 6000 training data combinations. Each PANN
i (
i indicating its role of retrieval of parameter
Yi) is then used to predict the parameters
Yi over all localities. As follows, we use the designations from
Table 3 and the notations M, R and Z, respectively, for the variables Y1, Y2 and Y3.
Table 3.
Model designation for each locality.
Table 3.
Model designation for each locality.
| Locality | Neural Model Developed by Data from the Locality |
|---|
| Abidjan (Ivory Coast) | A |
| Boyele (Congo Brazzaville) | B |
| Debuncha (Cameroon) | C |
| Dakar (Senegal) | D |
| Niamey (Niger) | N |
| All localities | PANN |
5. Results and Discussions
5.1. Capability of a Neural Network to Estimate the Parameters in Various Other Localities
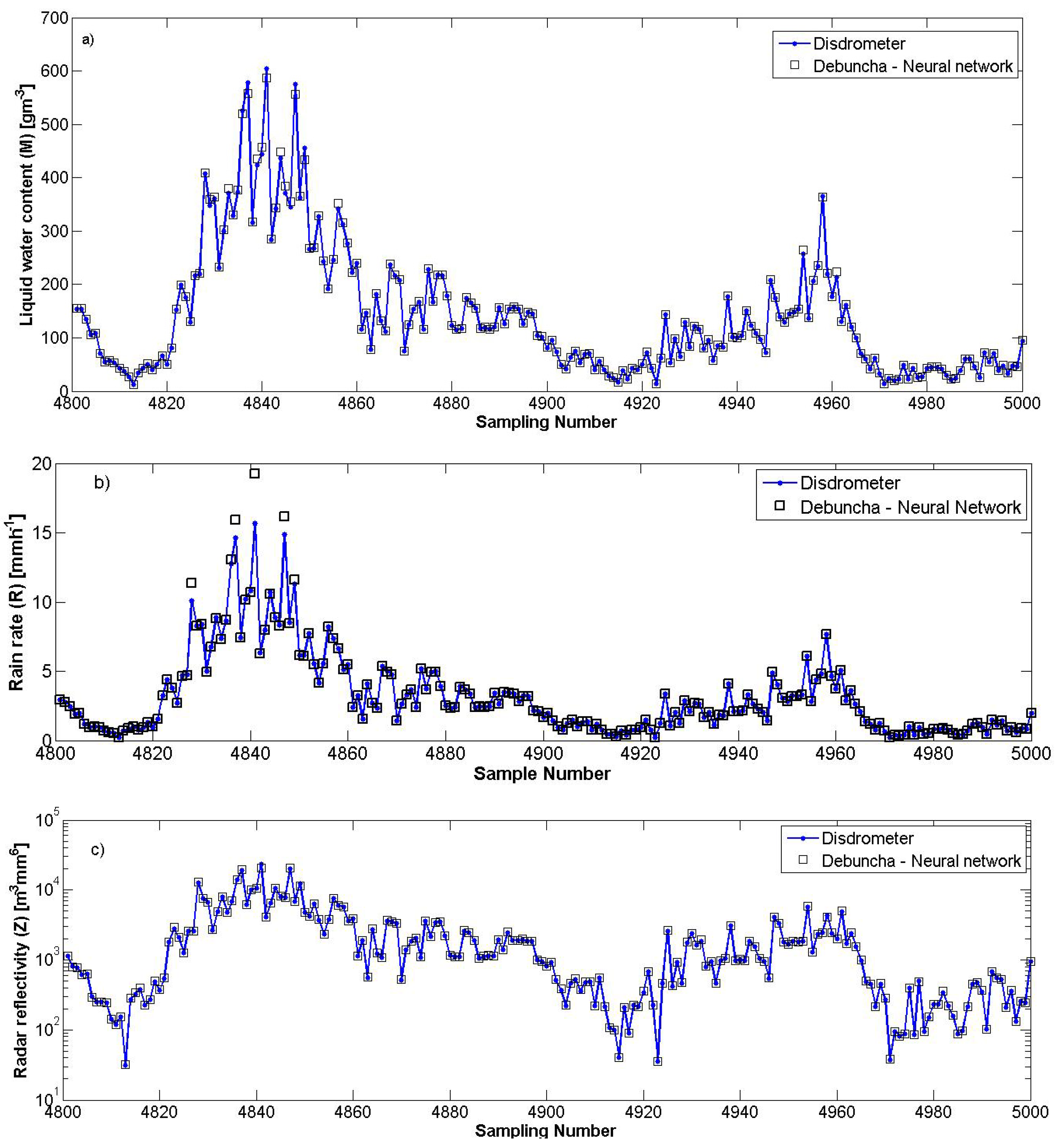
We have estimated the values of the three parameters (M, R and Z) over five localities with a LANN which has been trained only with the experimental RDSD values measured in Debuncha (Cameroon). For example, after using the first 500 training samples of this locality, we predicted in Abidjan (Côte d’Ivoire) 200 values for each parameter, corresponding to the sample data from the 4801st to the 5000th and have obtained the approximations presented in
Figure 8. The dots correspond to the experimental values and the squares to the estimated ones.
The different approximations can be considered as very good because the values measured by the disdrometer are practically the same as those estimated by the LANN.
5.2. Estimation of the Values of M, R and Z with the PANN
We have shown that a LANN which has been trained with disdrometer parameters issued only from a given locality, in order to estimate the parameters M, R and Z, was also able to estimate the same parameters in another locality, which is far different from the first. For ameliorating this type of estimation, we have created another ANN that we have qualified as a polyvalent one (PANN) and, which takes into account, while it is in development, data issued from all the localities where it will be used for prediction. For our concrete case, we have put together the first 1200 sampling data of each locality in order to obtain training values. The trained PANN has been used to estimate 5000 values of M, R and Z over all five localities, namely those from the 1201st to the 6200th.
Figure 8.
Neural prediction in Abidjan (Ivory Coast) of the liquid water content M (a), the rain rate R (b) and the radar reflectivity Z (c) by a LANN constructed with data issued only from Debuncha (Cameroon).
Figure 8.
Neural prediction in Abidjan (Ivory Coast) of the liquid water content M (a), the rain rate R (b) and the radar reflectivity Z (c) by a LANN constructed with data issued only from Debuncha (Cameroon).
5.3. Evaluation of the Root Mean Square Errors (RMSE)
We have evaluated the root mean square errors produced by the LANN and the PANN estimation, while comparing the estimates to the disdrometer measures. Equation (17) has been used:
where E
i: Error (observed value−Neural Network estimate); and N: Number of observed values.
5.3.1. RMSE between Measured Parameters in the Localities and Estimates Delivered by the LANN A, B, C, D and N
We present in
Table 4 the RMSE between values measured by the disdrometer and those estimated by the different LANN.
If the estimates over a given locality are delivered by a LANN trained with data issued from another locality, N is equal to 5000 (except the estimations realized in Niamey (Niger), only 4468 values were available). The estimations produced locally by the LANN concern the sample data from the 5001st to the 10,000th.
Table 4.
Comparisons between RMSE after use of the different LANN (A, B, C, D and N).
Table 4.
Comparisons between RMSE after use of the different LANN (A, B, C, D and N).
| LANN | Abidjan | Boyele | Debuncha |
| Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) |
| A | 0.01 | 0.01 | 0.58 | 4.87 | 0.35 | 870.16 | 17.60 | 1.25 | 3144.06 |
| B | 0.04 | 0.14 | 1.27 | 0.01 | 0.01 | 0.24 | 0.02 | 0.03 | 0.58 |
| C | 0.02 | 0.06 | 1.05 | 0.01 | 0.01 | 0.49 | 0.01 | 0.01 | 0.33 |
| D | 0.83 | 0.15 | 1.91 | 0.17 | 0.01 | 0.36 | 0.48 | 0.06 | 0.66 |
| N | 0.07 | 0.54 | 3.77 | 0.01 | 0.01 | 0.46 | 0.03 | 0.13 | 0.83 |
| LANN | Dakar | Niamey |
| Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) |
| A | 6.11 | 0.44 | 1091.45 | 3.57 | 0.26 | 638.14 |
| B | 0.01 | 0.01 | 0.35 | 0.01 | 0.01 | 0.25 |
| C | 0.01 | 0.01 | 0.62 | 0.01 | 0.01 | 0.45 |
| D | 0.01 | 0.01 | 0.15 | 0.13 | 0.01 | 0.22 |
| N | 0.02 | 0.02 | 0.38 | 0.01 | 0.01 | 0.13 |
Table 5 gives the two best LANN for the retrieval of the parameters M, R and Z.
Table 5.
Choice of the two best LANN for retrieval of the parameters in the different localities (A, B, C, D and N).
Table 5.
Choice of the two best LANN for retrieval of the parameters in the different localities (A, B, C, D and N).
| | Abidjan | Boyele | Debuncha | Dakar | Niamey |
|---|
| 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd |
|---|
| LANN | LANN | LANN | LANN | LANN | LANN | LANN | LANN | LANN | LANN |
|---|
| M | A | C | B | C | C | B | D | C | N | C |
| R | A | C | B | D | C | B | D | C | N | B |
| Z | A | C | B | D | C | B | D | B | N | D |
Considering the results obtained in
Table 4 and
Table 5, we observe that the best LANN for the estimation in a locality is logically the one which has been developed with data issued from that same locality and shows that the LANN of Debuncha (Cameroon) is in almost all cases able to predict the parameters in other localities.
5.3.2. RMSE between Values Measured by the Disdrometer and Estimates Delivered by the PANN
We have constructed a polyvalent ANN model (PANN) with data issued from the five localities and have chosen the data-gathering order: A+B+C+D+N. The training entries and the desired outputs are constituted by the first 1200 sampling data from A, the initial 1200 sampling data from B, the primary 1200 sampling data from C, the initial 1200 sampling data from D and lastly, the first 1200 sampling data from N. We have calculated and presented in
Table 6 the RMSE between values measured by the disdrometer and those estimated by the PANN.
Table 6.
RMSE between values measured by the disdrometer and those estimated by the PANN.
Table 6.
RMSE between values measured by the disdrometer and those estimated by the PANN.
| Abidjan | Boyele | Debuncha |
|---|
| M | R | Z | M | R | Z | M | R | Z |
| 0.02 | 0.01 | 0.66 | 0.01 | 0.01 | 0.24 | 0.02 | 0.01 | 0.52 |
| Dakar | Niamey |
| M | R | Z | M | R | Z |
| 0.01 | 0.01 | 0.25 | 0.01 | 0.01 | 0.15 |
Observing the results obtained, the use of the PANN allows obtaining the best RMSE-values (
Table 6). However, it is to be noted that while juxtaposing the training data, the order of the localities must be also respected in the fusion of the desired outputs.
Table 7.
Comparisons between RMSE after use of the different LANN: Case of stratiform rains.
Table 7.
Comparisons between RMSE after use of the different LANN: Case of stratiform rains.
| LANN | Abidjan | Boyele | Debuncha |
| Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) |
| A | 0.010 | 0.010 | 0.130 | 0.940 | 0.052 | 67.49 | 1.730 | 0.125 | 118.5 |
| B | 0.010 | 0.010 | 0.075 | 0.010 | 0.010 | 0.043 | 0.010 | 0.010 | 0.063 |
| C | 0.010 | 0.010 | 0.130 | 0.010 | 0.010 | 0.098 | 0.010 | 0.010 | 0.075 |
| D | 0.010 | 0.010 | 0.100 | 0.015 | 0.010 | 0.089 | 0.010 | 0.061 | 0.360 |
| N | 0.020 | 0.010 | 0.092 | 0.010 | 0.010 | 0.066 | 0.012 | 0.058 | 0.220 |
| LANN | Dakar | Niamey |
| Y1 (M) | Y2 (R) | Y3 (Z) | Y1 (M) | Y2 (R) | Y3 (Z) |
| A | 1.100 | 0.074 | 52.45 | 1.450 | 0.089 | 124.0 |
| B | 0.010 | 0.010 | 0.051 | 0.010 | 0.010 | 0.058 |
| C | 0.010 | 0.010 | 0.120 | 0.010 | 0.010 | 0.120 |
| D | 0.010 | 0.010 | 0.060 | 0.010 | 0.010 | 0.070 |
| N | 0.010 | 0.010 | 0.110 | 0.010 | 0.010 | 0.05 |
6. Conclusions
Our study concerns the estimation of water content (M), rain rate (R) and radar reflectivity (Z). For this purpose, we have used RDSD data measured by a disdrometer installed in five African sub-Saharan localities. We have developed and trained for each locality a LANN with the disdrometer data of the same locality and have used the trained LANN to estimate the parameters M, R and Z over all localities. We have also developed a polyvalent ANN model (PANN) whose training was realized with a combination of data issued from all the localities where it will be used for estimating the parameters over each locality.
We have, first of all, considered the precipitations generally before taking into account their stratiform and convective structures. For appreciating the capability of the developed and trained LANN and PANN to estimate the parameters, we have calculated the RMSE produced by them during their use over the distinct localities. Observing the different results and comparisons obtained, we have perceived that the PANN is very capable of predicting over all the localities the values of the parameter for which it has been developed.
The RMSE produced by the PANN, while considering stratiform structures, is generally lower than those induced while considering the convective ones. After our investigation, we can thus consider the LANN and the PANN as models, which are able to predict rainfall values under different latitudes.
In areas of low coverage measurement networks of meteorological parameters, as in our study area (sub-Saharan Africa), the implementation of a PANN in a chain of radar measurements for rainfall could provide better understanding and describe the precipitations independently of their form and locality of occurrence.
The neural network technique is known to be difficult to manipulate. However, the implementation of such a technique in modern data acquirement instruments like rain radars may constitute a very interesting method to be investigated. Putting in place such a technology could permit a simultaneous measurement of DSD and the computing of rain parameters.
In our future works, we will also conduct a sensitivity study that consists of evaluating the significance of the RMSE between disdrometer measurement, rain gauge observations and NN estimates taking into account the disdrometer errors caused by rain drop size limitation during the measurement process.
Acknowledgments
We thank the laboratory LPAO-SF in Dakar, Senegal and Laboratory of Aerology through Henri Sauvageot in Toulouse, France, for the data kindly put at our disposal. The authors thank the external editor and three reviewers for their valuable suggestions.
Author Contributions
Siddi Tengeleng prepared the manuscript, and developed the computational codes for all analyses. Nzeukou Armand contributed valuable scientific insight, ideas, direction and writing editing. All authors discussed the results and implications and commented on the manuscript.
Conflicts of Interest
I can state that neither, I nor my co-authors have a direct financial relation with the trademarks eventually mentioned in our paper that might lead to a conflict of interest among us.
References
- Aires, F.; Prigent, C.; Rossow, W.B.; Rothstein, M. A new neural network approach including first guess for retrieval of atmospheric water vapour, cloud liquid water path, surface temperature, and emissivities over land from satellite microwave observations. J. Geophys. Res. 2001, 106, 14887–14907. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrieval. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Bouzeboudja, O.; Haddad, B.; Ameur, S. Estimation radar des précipitations par la méthode des aires fractionnelles. Larhyss J. 2010, 8, 7–26. [Google Scholar]
- Kumar, L.S.; Lee, Y.H.; Yeo, J.X.; Ong, J.T. Tropical rain classification and estimation of rain from Z-R (reflectivity-rain rate relationships) relationships. Prog. Electromagn. Res. B 2011, 32, 107–127. [Google Scholar] [CrossRef]
- Anagnostou, M.N.; Kalogiros, J.; Anagnostou, E.N.; Tarolli, M.; Papadopoulos, A.; Borga, M. Performance evaluation of high-resolution rainfall estimation by X-band dual-polarization radar for flash flood applications in mountainous basins. J. Hydrol. 2010, 394, 4–16. [Google Scholar] [CrossRef]
- Alfieri, L.; Claps, P.; Laio, F. Time-dependent Z-R relationships for estimating rainfall fields from radar measurements. Nat. Hazard. Earth Syst. Sci. 2010, 10, 149–158. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar]
- Battan, L.J. Radar Observations of the Atmosphere; University of Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Atlas, D.; Ulbrich, C.W.; Marks, F.D.; Amitai, E.; Williams, C.R. Systematic variation of drop size and radar-rainfall relations. J. Geophys. Res. 1999, 104, 6155–6169. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol. 1996, 35, 355–371. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A.; Williams, C.R.; Ecklund, W.L.; Gage, K.S. Tropical rainfall associated with convective and stratiform clouds: Intercomparison of disdrometer and profiler measurements. J. Appl. Meteorol. 1999, 38, 302–320. [Google Scholar] [CrossRef]
- Maki, M.; Keenan, T.D.; Sasaki, Y.; Nakamura, K. Characteristics of the raindrop size distribution in tropical continental squall lines observed in Darwin, Australia. J. Appl. Meteorol. 2001, 40, 1393–1412. [Google Scholar] [CrossRef]
- Bumke, K.; Seltmann, J. Analysis of measured drop size spectra over land and sea. ISRN Meteorol. 2012. [Google Scholar] [CrossRef]
- Widrow, B.; Lehr, M.A. 30 years of adaptive neural networks: Perceptron, Madaline, and Backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Malkeil Burton, G. A Random Walk down Wall Street; Norton & Company: New York, NY, USA, 1996. [Google Scholar]
- Parizeau, M. Réseaux de neurones, GIF-21140 et GIF-64326; Université Laval: Laval, QC, Canada, 2004. [Google Scholar]
- Shiguemori, E.H.; Haroldo, F.; da Silva, J.D.S.; Carvalho, J.C. Neural Network Based Models in the Inversion of Temperature Vertical Profiles from Radiation Data. In Proceedings of the Inverse Problem Design and Optimization (IPDO-2004) Symposium, Rio de Janeiro, Brazil, 17–19 March 2004.
- Joss, J.; Waldvogel, A. Ein spectrograph für niederschagstropfen mit automatisher auswertung (A spectrograph for the automatic analysis of raindrops). Pure Appl. Geophys. 1967, 68, 240–246. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A. Raindrop size distribution and sampling size errors. J. Atmos. Sci. 1969, 26, 566–569. [Google Scholar] [CrossRef]
- Sheppard, B.E.; Joe, P.I. Comparison of raindrop size distribution measurements by a Joss–Waldvogel disdrometer, a PMS 2DG spectrometer, and a POSS Doppler radar. J. Atmos. Ocean. Technol. 1994, 11, 874–887. [Google Scholar] [CrossRef]
- Tokay, A.; Kruger, A.; Krajewski, W.F. Comparison of drop size distribution measurements by impact and optical disdrometers. J. Appl. Meteorol. 2001, 40, 2083–2097. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E.; Menegini, R.; Kozu, T. The shape–slope relation in observed gamma raindrop size distributions: Statistical error or useful information? J. Atmos. Ocean. Technol. 2003, 20, 1106–1119. [Google Scholar] [CrossRef]
- Nzeukou, A.; Sauvageot, H.; Ochou, A.D.; Kebe, C.M.F. Raindrop size distribution and radar parameters at cape verde. J. Appl. Meteorol. 2004, 43, 90–105. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V. The bias in moment estimators for parameters of drop size distribution functions: Sampling from exponential distributions. J. Appl. Meteorol. 2005, 44, 1195–1205. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G. Errors in estimating raindrop size distribution parameters employing disdrometer and simulated raindrop spectra. J. Appl. Meteor. Climatol. 2009, 48, 406–425. [Google Scholar] [CrossRef]
- Smith, P.L.; Liu, Z.; Joss, J. A study of sampling variability effects in raindrop size observations. J. Appl. Meteorol. 1993, 32, 1259–1269. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E.; Schuur, T.; Ryzhkov, A.; Ikeda, K. Analysis of video disdrometer and polarimetric radar data to characterize rain microphysics in Oklahoma. J. Appl. Meteorol. Climatol. 2008, 47, 2238–2255. [Google Scholar] [CrossRef]
- Adrot, G.; Gosset, M.; Boudevillain, B.; Flaus, J.M. Inversion du Model d’observation d’un radar météorologique par une méthode ensembliste. e-STA 2008, 5, 29–34. [Google Scholar]
- Khatib, T.; Mohamed, A.; Sopian, K.; Mahmoud, M. Assessment of artificial neural networks for hourly solar radiation prediction. Int. J. Photoenergy 2012. [Google Scholar] [CrossRef]
- Omaima, N.; Al-Allaf, A. Cascade-Forward vs. Function Fitting Neural Network for Improving Image Quality and Learning Time in Image Compression System. In Proceedings of the World Congress on Engineering 2012 Vol II WCE 2012, London, UK, 4–6 July 2012.
- Dheeraj Badde1, S.; Gupta Anil, K.; Patki Vinayak, K. Cascade and feed forward back propagation artificial neural network models for prediction of compressive strength of ready mix concrete. IOSR J. Mech. Civ. Eng. 2012, 3, 1–6. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).




 the rule of composition functions is used:
the rule of composition functions is used:

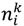 of the layer k depend directly on the weights and biases on this layer, and can be expressed by the following relation:
of the layer k depend directly on the weights and biases on this layer, and can be expressed by the following relation:

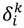 of
of  in relation with the changes of the activation level
in relation with the changes of the activation level 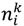 of the neuron i belonging to the layer k by the equation:
of the neuron i belonging to the layer k by the equation:

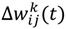 and
and  become:
become:

 ).
).