Abstract
Six meteorological drought indices including percent of normal (PN), standardized precipitation index (SPI), China-Z index (CZI), modified CZI (MCZI), Z-Score (Z), the aridity index of E. de Martonne (I) are compared and evaluated for assessing spatio-temporal dynamics of droughts in six climatic regions in Iran. Results indicated that by consideration of the advantages and disadvantages of the mentioned drought predictors in Iran, the Z-Score, CZI and MCZI could be used as a good meteorological drought predictor. Depending on the month, the length of drought and climatic conditions of the region, they are an alternative to the SPI that has limitations both because of only a few available long term data series in Iran and its complex structure.
1. Introduction
Drought is a natural local or regional phenomenon, its basic cause being the lack of precipitation over a time period. Drought may be studied from the environmental or the water resources point of view [1]. Environmental droughts can be classified into meteorological drought, hydrological drought and agricultural drought. This study focuses on meteorological drought. Meteorological droughts are temporary, recurring natural disasters, which originate from lack of precipitation and can bring significant economic losses. It is not possible to avoid meteorological droughts, but they can be predicted and monitored, and their adverse impacts can be alleviated [2].
Nowadays, many different drought indices are used as drought monitoring tools. The most popular indices include the Palmer Drought Severity Index (PDSI) [3], which is widely used in the United States, the Deciles Index [4], which is operational in Australia, the China-Z index (CZI), which is used by the National Metrological Center of China [5] and the standardized precipitation index (SPI) [6], which has gained world popularity. Most of these indices are calculated using climate data (rainfall, or temperature). An advantage of the SPI is that it can monitor dry and wet periods over a wide spectrum of time scales from one to 72 months [7]. Based on an analysis of the drought in the Southern Plains and the southwestern United States in the spring of 1996, the SPI has been shown to be a more reliable index of developing drought conditions than the PDSI [8]. This conclusion is based on the responsiveness of the SPI to emerging precipitation deficits at shorter time scales (e.g., three months). Thus, the SPI recognizes moisture deficits more rapidly than the PDSI, which has a response time scale of approximately 8–12 months [6,9]. The SPI is simpler than the PDSI in calculation and is more spatially consistent and it can be used, in risk and decision analyses [10].The choice of indices for drought monitoring in a specific area should eventually be based on the quantity of climate data available and on the ability of the index to consistently detect spatial and temporal variations during a drought event [11].
2. Study Area
Iran is situated in Southwest Asia, bordering the Gulf of Oman, the Persian Gulf, and the Caspian Sea, between Iraq and Pakistan. The mountains enclose several broad basins, or plateaus, on which major agricultural and urban settlements areas are located (Figure 1).
Iran's climate is mostly arid or semiarid, to wet along the Caspian coast. Iran was classified into six separate climatic areas according to climatological parameters as Desert, Semi Desert, Mountains, Semi Mountains, Coastal Wet and Coastal Desert (Figure 2) [12]. On the northern edge of the country (the Caspian coastal plain), temperatures nearly fall below freezing during winter and remain humid for the rest of the year. Summer temperatures rarely exceed 29 °C. Annual precipitation is 680 mm in the eastern part of the plain and more than 1,700 mm in the western part and the southern coasts of the Caspian Sea. To the west, settlements in the Zagros Mountains basin, experience lower temperatures, severe winters, sub-freezing average daily temperatures and heavy snowfall. The eastern and central basins are arid, with less than 200 mm (eight inches) of rain and have occasional desert. Average summer temperatures exceed 38 °C. The coastal plains of the Persian Gulf and Oman Sea in southern Iran have mild winters, and very humid and hot summers. The annual precipitation ranges from 135 to 355 mm [13].
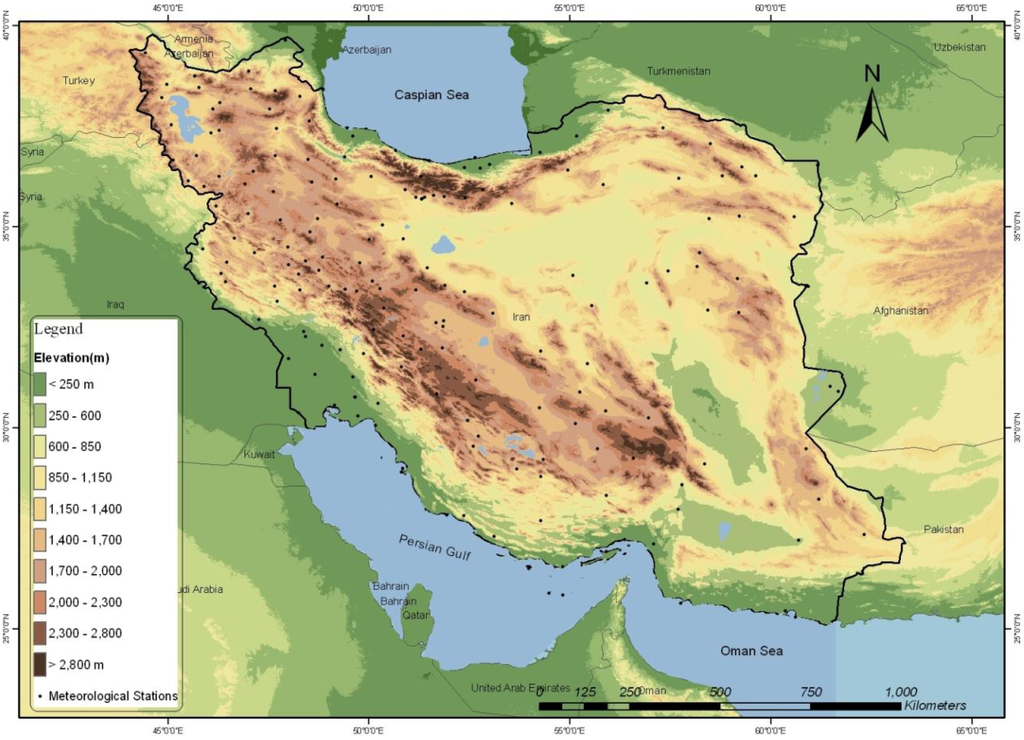
Figure 1.
Geographical location and topographic map of Iran and spatial distribution of meteorological stations.
Iran has experienced ever increasing droughts in recent years, e.g., from 2000 to 2005, possibly attributed to the redistribution of surface water budget as result of global and regional climate change [14]. According to the statistics reported by the OFDA/CRED International Disaster Database, drought is the major natural disaster that has affected Iran from 1900 to early 2008 (Table 1) [15]. Therefore accurate drought monitoring methods are of importance for short and long term regional drought forecasting and disaster management in Iran, especially for agricultural and food production.
Several studies on drought monitoring over Iran consider only limited areas of Iran where in this paper authors considered the whole country as a case study area including six separate climatological regions [11,16,17,18,19].
In order to contribute to improved drought monitoring in Iran, in this study we compared and evaluated six meteorological drought indices including percent of normal (PN), standardized precipitation index (SPI), China-Z index (CZI), modified CZI (MCZI), Z-Score (Z), the aridity index of E. de Martonne (I), for multiple time scales in six climate regions. The average monthly rainfall and temperature data of 180 meteorological stations (from Iran Meteorological Organization (IRIMO) that registered at the World Meteorological Organization (WMO) as standard types of synoptic station), which are distributed over the Iran territory and cover the 1950–2005 period, were used (Figure 1) [13]. However, only 40 stations could be finally selected in this study because the calculation of the SPI as the reference index requires that there is no missing data in the time series, which should cover at least 30 years and to compare other indices with SPI, we were able to calculate all of the mentioned indices only for 40 weather stations (Figure 2 and Table 2). Obviously use of interpolation methods for only 40 stations for assessing of the spatial pattern of different drought indices over the whole of Iran with an area of 1,648,000 square kilometers is not possible. Therefore, in this study the authors compared the results on a local (station) scale.

Table 1.
Summarized table of natural disasters in Iran from 1900 to 2008.
| Disaster | Killed | Total Affected | Damage US$(000’s) | |
|---|---|---|---|---|
| Drought | Drought | - | 37,625,000 | 3,300,000 |
| Earthquake | Earthquake | 147,100 | 2,579,024 | 10,518,628 |
| Epidemic | Diarrhoeal/Enteric | 372 | 2500 | - |
| Extreme Temperature | Heat wave | 158 | - | - |
| Flood | Unspecified | 1,281 | 1,374,034 | 6,002,028 |
| Flash Flood | 60 | 4453 | 28,000 | |
| Flood | 6,404 | 2,272,567 | 1,622,500 | |
| Slides | Avalanche | 73 | 44 | - |
| Landslide | 43 | 100 | - | |
| Wild Fires | Scrub | - | - | - |
| Wind Storm | Cyclone | 12 | 160,009 | - |
| Storm | 217 | 11,700 | 15,240 | |
| Winter | 91 | 8,085 | 13,300 |
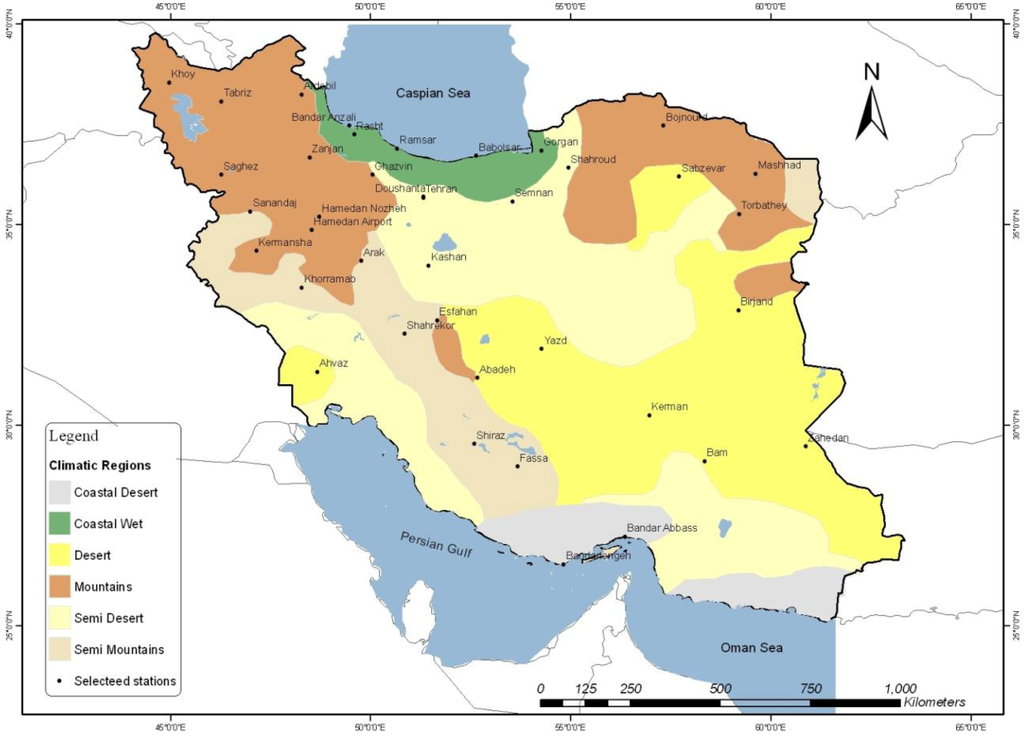
Figure 2.
The study area classified into six climatic regions with spatial distribution of selected meteorological stations.

Table 2.
List of selected meteorological stations.
| Name | Latitude (Decimal Degree) | Longitude (Decimal Degree) | Elevation (m) | WMO Code |
|---|---|---|---|---|
| Abadeh | 31.18 | 52.67 | 2,030 | 40818 |
| Ahwaz | 31.33 | 48.67 | 23 | 40811 |
| Arak | 34.10 | 49.77 | 1,708 | 40769 |
| Ardebil | 38.25 | 48.28 | 1,332 | 40708 |
| Babolsar | 36.72 | 52.65 | −21 | 40736 |
| Bam | 29.10 | 58.35 | 1,067 | 40854 |
| Bandar Abass | 27.22 | 56.37 | 10 | 40875 |
| Bandar Anzali | 37.47 | 49.47 | −26 | 40718 |
| Bandar Lengeh | 26.53 | 54.83 | 23 | 40883 |
| Birjand | 32.87 | 59.20 | 1,491 | 40809 |
| Bojnurd | 37.47 | 57.32 | 1,091 | 40723 |
| Doushan Tappeh | 35.70 | 51.33 | 1,209 | 40753 |
| Esfahan | 32.62 | 51.67 | 1,550 | 40800 |
| Fassa | 28.97 | 53.68 | 1,288 | 40859 |
| Ghazvin | 36.25 | 50.05 | 1,279 | 40731 |
| Gorgan | 36.85 | 54.27 | 13 | 40738 |
| Hamedan Noyheh | 35.20 | 48.72 | 1,680 | 40767 |
| Hamedan−Airport | 34.87 | 48.53 | 1,741 | 40768 |
| Kashan | 33.98 | 51.45 | 982 | 40785 |
| Kerman | 30.25 | 56.97 | 1,754 | 40841 |
| Kermanshah | 34.35 | 47.15 | 1,319 | 40766 |
| Khorramabad | 33.43 | 48.28 | 1,148 | 40782 |
| Khoy | 38.55 | 44.97 | 1,103 | 40703 |
| Mashhad | 36.27 | 59.63 | 999 | 40745 |
| Noushahr | 36.65 | 51.50 | −21 | 40734 |
| Ramsar | 36.90 | 50.67 | −20 | 40732 |
| Rasht | 37.25 | 49.60 | −7 | 40719 |
| Sabzevar | 36.20 | 57.72 | 978 | 40743 |
| Saghez | 36.25 | 46.27 | 1,523 | 40727 |
| Sanandaj | 35.33 | 47.00 | 1,373 | 40747 |
| Semnan | 35.58 | 53.55 | 1,131 | 40757 |
| Shahre Kord | 32.28 | 50.85 | 2,049 | 40798 |
| Shahroud | 36.42 | 54.95 | 1,345 | 40739 |
| Shiraz | 29.53 | 52.60 | 1,484 | 40848 |
| Tabriz | 38.08 | 46.28 | 1,361 | 40706 |
| Tehran Mehrabad | 35.68 | 51.32 | 1,191 | 40754 |
| TorbateHeydarieh | 35.27 | 59.22 | 1,451 | 40762 |
| Yazd | 31.90 | 54.28 | 1,237 | 40821 |
| Zahedan | 29.47 | 60.88 | 1,370 | 40856 |
| Zanjan | 36.68 | 48.48 | 1,663 | 40729 |
3. Drought Indices and Methods
3.1. Standardized Precipitation Index (SPI)
The SPI was defined as the number of standard deviations that the observed cumulative rainfall at a given time scale would deviate from the long-term mean for that same time scale over the entire length of the record [6]. As a single numeric value, the SPI can be compared across regions with markedly different climates. The Colorado Climate Center, the Western Regional Climate Center and the National Drought Mitigation Center use the SPI to monitor drought in the USA [7]. Since the cumulative precipitation may not be normally distributed, the data has been transformed approximately to the normal domain to standardize the drought index. The time scale of the SPI is also flexible, which is an attractive feature because it is possible to experience wet conditions at one time scale but dry conditions at another simultaneously [6].
The SPI may be computed with different time steps (e.g., one month, three months, and 24 months). It was shown that the use of SPI at longer time steps was not advisable as the sample size reduces even with originally long-term data sets. The use of different timescales allows the effects of a precipitation deficit on different water resource components (groundwater, reservoir storage, soil moisture, stream flow) to be assessed [10]. Positive SPI values indicate greater than mean precipitation and negative values indicate less than mean precipitation. The SPI may be used for monitoring both dry and wet conditions. The “drought” part of the SPI range is arbitrarily split into “near normal” (0.99 > SPI > −0.99), “moderately dry” (−1.0 > SPI > −1.49), “severely dry” (−1.5 > SPI > −1.99) and “extremely dry” (SPI < −2.0) conditions. A drought event starts when it becomes negative and ends when SPI becomes positive again. Calculation of the SPI requires that there is no missing data in the time series. The data record length is recommended to be at least 30 years [5], because the drought index classes are fitted to that period and are also intercomparable with other sites of different climates. This index has been used widely recently in different drought related studies for assessing climate change effects on water resource, agriculture, hydrology and ecosystems [20].
3.2. China-Z index (CZI), Modified CZI (MCZI) and Z-Score
The CZI is based on the Wilson–Hilferty cube-root transformation [21]. Assuming that precipitation data follow the Pearson Type III distribution, the index is calculated as:
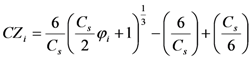
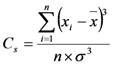
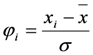 where i is the current month, Cs is the coefficient of skewness, n is the total number of months in the record, φi is the standard vitiate, also called the Z-Score and xi is the precipitation of i month(mm). To compute the MCZI, the median of precipitation (Med) is used instead of the mean of precipitation in the calculation of the CZI (i.e., Med is substituted for x in Equations (2) and (3) [5]).
where i is the current month, Cs is the coefficient of skewness, n is the total number of months in the record, φi is the standard vitiate, also called the Z-Score and xi is the precipitation of i month(mm). To compute the MCZI, the median of precipitation (Med) is used instead of the mean of precipitation in the calculation of the CZI (i.e., Med is substituted for x in Equations (2) and (3) [5]).
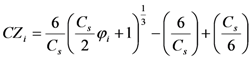
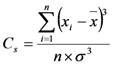
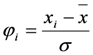
3.3. Aridity Index of E. de Martonne (I)
The aridity index, introduced by de Martonne, is one of the indices that is used for determination of irrigation demand [22,23]. Its monthly values are described by the following equation:
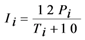 where, Pi is the monthly precipitation amount(mm) and Ti (°C) is the respective mean monthly air-temperature. The purpose of this index is to identify the months for which irrigation is necessary, which in turn depends both on rainfall and ambient temperature. Thus, irrigation according to this index becomes necessary when Ii < 20.
where, Pi is the monthly precipitation amount(mm) and Ti (°C) is the respective mean monthly air-temperature. The purpose of this index is to identify the months for which irrigation is necessary, which in turn depends both on rainfall and ambient temperature. Thus, irrigation according to this index becomes necessary when Ii < 20.
3.4. The Percent of Normal (PN)
The percent of normal is one of the simplest measurements of precipitation for a location. Analyses using the percent of normal are very effective when used for a single region or a single season. Percent of normal is also easily misunderstood and gives different indications of conditions, depending on the location and season. It is calculated by dividing actual precipitation (Pi) by normal precipitation ( 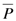 )—typically considered to be a 30-year mean—and multiplying by 100%.
)—typically considered to be a 30-year mean—and multiplying by 100%.
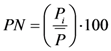
3.5. Data Processing
As mentioned previously, each of the drought indices has its own strengths and weaknesses. Concerning these strengths and weaknesses and considering the lack of available input data in Iran the SPI has been selected as a reference meteorological (statistical-based) index with a suitable performance to detect and to measure drought conditions in many studies. Therefore, in this chapter, five meteorological drought indices including percent of normal (PN), China-Z index (CZI), modified CZI (MCZI), Z-Score (Z) and the aridity index of E. de Martonne (I) are compared with the SPI for assessing spatio-temporal dynamics of droughts in Iran. Because of the recommendation that for the calculation of the SPI index a minimum of a 30 year precipitation record should be used (this is the condition for the given SPI drought index classes and for intercomparability between different climatic sites), only 40 weather stations over Iran could be used. To quantify the comparison results, the Pearson’s correlation coefficients (r-value) of regression line for the SPI versus the CZI, the SPI versus the MCZI, the SPI versus the Z-Score, the SPI versus the PN and the SPI versus the I, were computed for selected stations. To inspect the relationships between the six indices in different climatic regions, r-values were computed in three formats: monthly, seasonal and annual, respectively. Further the indices with the best performances over six climatic regions are identified as being suitable for monitoring of regional drought (e.g., as an alternative to SPI at sites with only short term weather records or where high quality long term precipitation records without gaps are not available).
4. Results and Discussion
4.1. Temporal Analysis of Drought Indices
4.1.1. Results of Monthly Analysis
Linear regressions between the monthly values of the SPI and Z-Score, CZI, MCZI, PN and I from 1950 to 2005 indicate that the SPI and Z-Score, CZI, MCZI, PN and I, respectively, in general show a good relationship for the time scale of one month. However, these relationships depend on the month and climatic region (Table 3). PN and I show the weakest relationship especially in dry months and for desert regions. The strongest relationship was found between SPI and MCZI especially in rainy months in the Coastal wet regions. For every station the index with the highest correlation to the SPI was selected as the best drought index and mapped over the whole region. The spatial patterns of these best indices are shown in Figure 3, Figure 4, Figure 5.

Table 3.
The best indices according to region and time scale with the number of included stations per region in monthly analysis*.
| Climatic Regions | |||||||
|---|---|---|---|---|---|---|---|
| Coastal Desert | Coastal Wet | Desert | Semi Desert | Mountain | Semi Mountain | ||
| Month | January | CZI (3/3) R = 98–99 | MCZI (2/5) R = 100 CZI (2/5) R = 100 Zscore (1/5) R = 97 | CZI (7/8) R = 99–100 MCZI (1/8) R = 99 | MCZI (3/5) R = 99–100 CZI (2/5) R = 98–99 | MCZI (11/13) R = 86–100 CZI (1/13) R = 99 Zscore (1/13) R = 98 | MCZI (3/6) R = 98–99 CZI (3/6) R = 98–99 |
| February | CZI (3/3) R = 99 | MCZI (3/5) R = 99–100 CZI (1/5) R = 99 Zscore·(1/5) R = 95 | CZI (7/8) R = 99–100 MCZI (1/8) R = 99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 97–99 | MCZI (10/13) R = 98–100 CZI (1/13) R = 99 Zscore (1/13) R = 95 | MCZI (3/6) R = 96–99 CZI (3/6) R = 98–100 | |
| March | CZI (3/3) R = 98–99 | MCZI (3/5) R = 94–100 CZI (1/5) R = 100 Zscore (1/5) R = 95 | CZI (6/8) R = 98–100 MCZI (2/8) R = 98–99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 98–99 | MCZI (11/13) R = 95–100 CZI (2/13) R = 95–99 | CZI (4/6) R = 98–100 MCZI (3/6) R = 98–99 | |
| April | CZI (3/3) R = 91–93 | MCZI (3/5) R = 99–100 Zscore (2/5) R = 96–97 | CZI (6/8) R = 97–100 MCZI (2/8) R = 98–99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 98–99 | MCZI (12/13) R = 98–100 Zscore (1/13) R = 96 | MCZI (4/6) R = 98–99 CZI (2/6) R = 99–100 | |
| May | CZI (2/3) R =99–100 Zscore (1/3) R = 96 | MCZI (2/5) R = 99–100 CZI (2/5) R = 98–99 Zscore (1/5) R = 97 | CZI (5/8) R = 99–100 MCZI (3/8) R = 98–99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 98–99 | MCZI (10/13) R = 91–96 CZI (2/13) R = 99–100 Zscore (1/13) R = 98 | MCZI (3/6) R = 94–99 CZI (3/6) R = 97–99 | |
| June | CZI (3/3) R = 99–100 | MCZI (4/5) R = 95–99 CZI (1/5) R = 98 | CZI (5/8) R = 99–100 MCZI (2/8) R = 98–100 Zscore (1/8) R = 99 | CZI (2/5) R = 99–100 MCZI (2/5) R = 98–99 Zscore (1/5) R = 99 | MCZI (12/13) R = 96–100 CZI (1/13) R = 99 | MCZI (3/6) R = 98–100 CZI (3/6) R = 99–100 | |
| July | CZI (2/3) R = 98–100 Zscore (1/3) R = 100 | MCZI (3/5) R = 94–99 CZI (2/5) R = 95–98 | CZI (4/8) R = 99–100 MCZI (3/8) R = 97–100 Zscore ( 1/8) R = 99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 99–100 | MCZI (9/13) R = 98–100 CZI (2/13) R = 98–99 Zscore (2/13) R = 95–97 | MCZI (3/6) R = 96–98 CZI (3/6) R = 98–99 | |
| August | CZI (2/3) R = 98–99 MCZI (1/3) R = 99 | MCZI (3/5) R = 94–99 CZI (2/5) R = 98–99 | Zscore( 4/8) R = 94–100 CZI (3/8) R = 99–100 MCZI (1/8) R = 99 | MCZI (3/5) R = 99–100 CZI (2/5) R = 99–100 | MCZI (10/13) R = 92–100 CZI (2/13) R = 95–100 Zscore (1/13) R = 96 | MCZI (3/6) R = 97–100 CZI (3/6) R = 98–100 | |
| September | CZI (3/3) R = 100 | MCZI (3/5) R = 96–100 CZI (2/5) R = 97–99 | CZI (3/8) R = 98–100 MCZI (3/8) R = 98–100 Zscore ( 2/8) R = 99–100 | CZI (2/5) R = 99–100 MCZI (2/5) R = 98–100 Zscore (1/5) R = 99 | MCZI (7/13) R = 97–100 CZI (5/13) R = 99–100 Zscore (1/13) R = 99 | MCZI (2/6) R = 98–99 CZI (2/6) R = 97–100 Zscore (2/6) R = 98–100 | |
| October | CZI (2/3) R = 98–99 MCZI (1/3) R = 99 | MCZI (3/5) R = 98–99 Zscore (2/5) R = 95–98 | CZI (5/8) R = 99–100 MCZI (3/8) R = 99–100 | CZI (3/5) R = 98–99 MCZI (2/5) R = 98 – 99 | MCZI (12/13) R = 97–100 CZI (1/13) R = 95 | MCZI (3/6) R = 97–99 CZI (3/6) R = 99–100 | |
| November | CZI (3/3) R = 96–97 | MCZI (4/5) R = 99–100 Zscore (1/5) R = 97 | CZI (6/8) R = 98–100 MCZI (2/8) R = 98–99 | CZI (3/5) R = 99–100 MCZI (2/5) R = 97–99 | MCZI (13/13) R = 97–100 | MCZI (3/6) R = 99–100 CZI (3/6) R = 98–99 | |
| December | CZI (3/3) R = 92–94 | MCZI (2/5) R = 100 CZI (2/5) R = 100 Zscore (1/5) R = 97 | CZI (6/8) R = 97–100 MCZI (2/8) R = 99–100 | MCZI (3/5) R = 99–100 MZI (2/5) R = 99–100 | MCZI (13/13) R = 96–100 | MCZI (3/6) R = 97–99 CZI (3/6) R = 96–100 | |
*Every cell contains drought indices which have the best correlation with the SPI index and Numbers in margins (X/Y) shows the number of stations where the index performed best (X) out of the total number of stations per region (Y). R shows the range of the Pearson’s correlation coefficients of the regression line for every index.
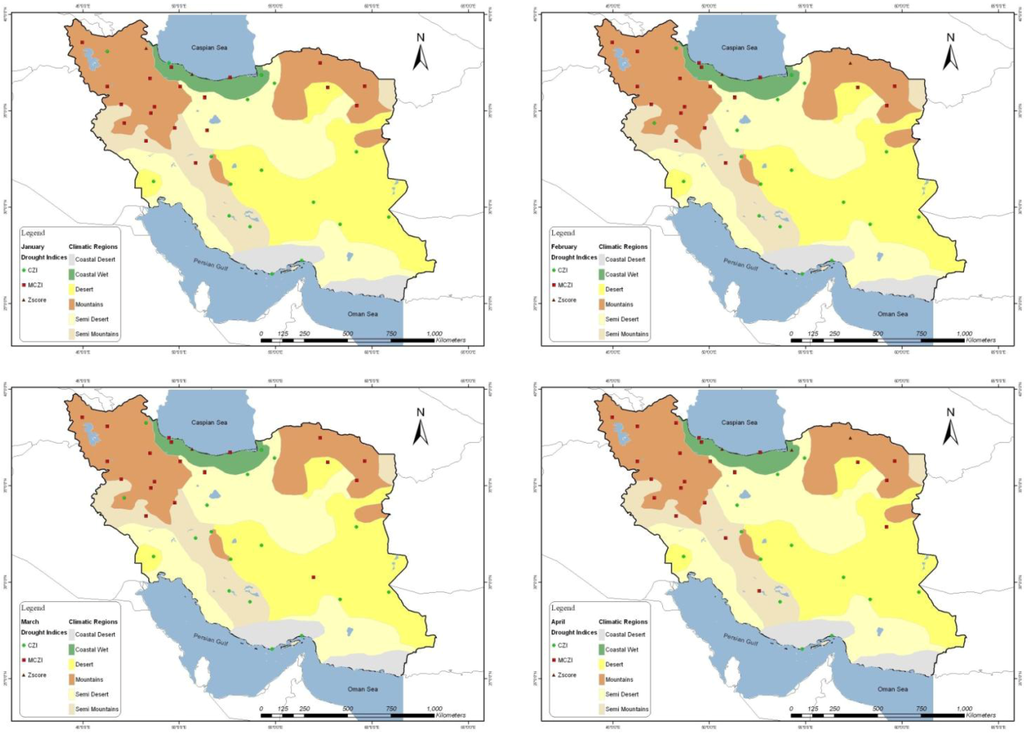
Figure 3.
Spatial distribution of monthly drought indices with the best correlation to standardized precipitation index (SPI) for January, February, March and April.
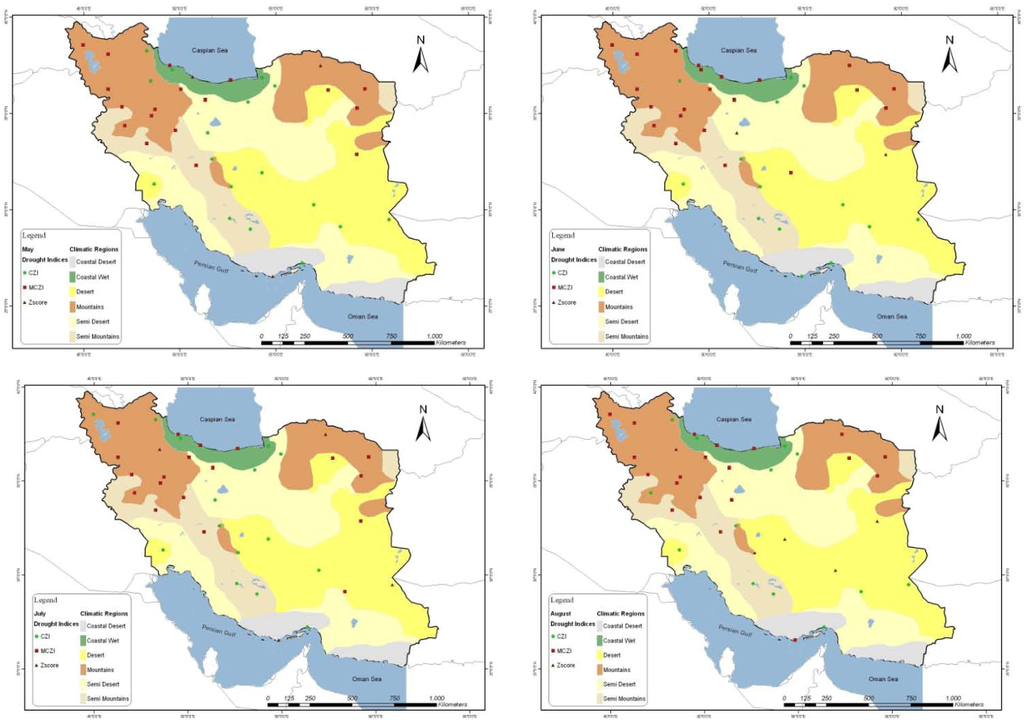
Figure 4.
Spatial distribution of monthly drought indices with the best correlation to standardized precipitation index (SPI) for May, June, July and August.
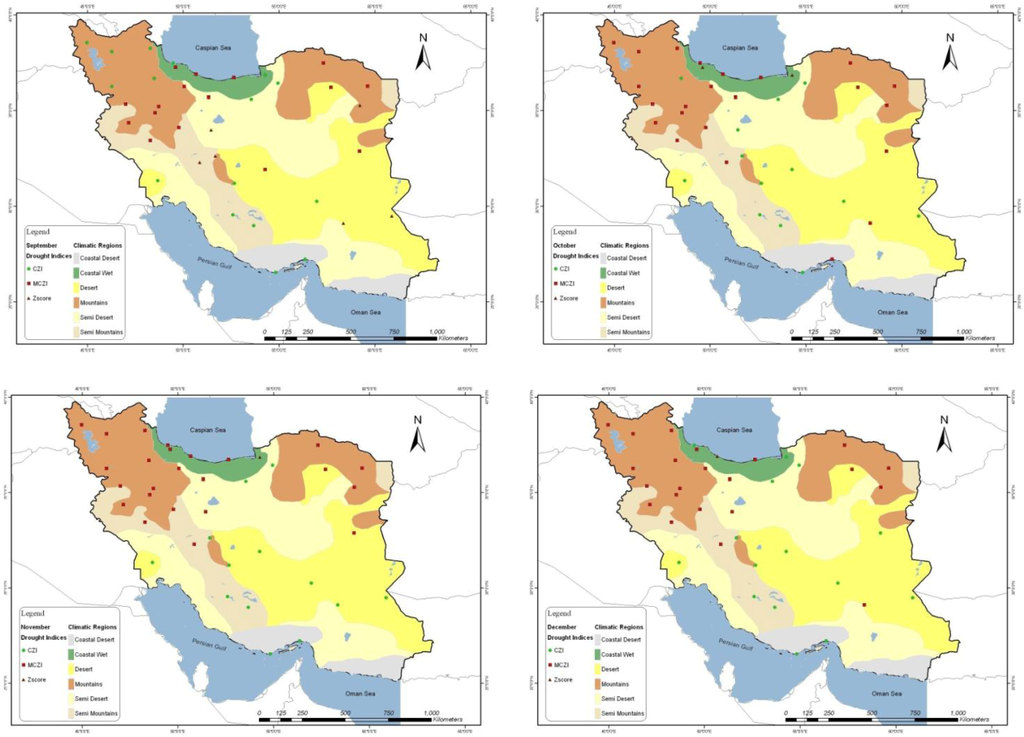
Figure 5.
Spatial distribution of monthly drought indices with the best correlation to standardized precipitation index (SPI) for September, October, November and December.
As shown in Figure 3, Figure 4, Figure 5, in Coastal wet, Mountains and Semi Mountain regions the strongest relationship was calculated between SPI and MCZI and in every month of the year. There is a similar spatial pattern of the MCZI in Coastal wet, Mountain and Semi Mountain regions. The CZI best performed in Coastal Desert, Desert and Semi Desert regions especially during dry months (May, June, July and August). However, the best performance of CZI is also obvious in some northern parts of Iran that include some parts of Coastal wet and Semi Mountain climatic regions. Referring to Equations (1) to (3), the median of precipitation (Med) is used instead of the mean of precipitation in the calculation of the CZI (i.e., Med is substituted for (x) in Equations (2) and (3)). This method was introduced in an attempt to reduce the differences between the SPI and the MCZI. Obviously, this modification also improved the result in our study [5]. In that research it was concluded that the differences between these two indices did not decline as significantly as they did between the SPI and the CZI.
The Z-Score performed well only in some parts of the driest regions of Iran that belong to Desert and Semi Desert regions where no rainfall or the lowest amount of rainfall months (June, July and August) occurred. In conclusion it can be argued that the MCZI has the strongest correlation with SPI under wet conditions but inversely in dry conditions. The CZI and Z-Score show the strongest relationship with SPI in dry environments and the other indices (PN and I) do not have strong correlations with SPI.
4.1.2. Results of Seasonal Analysis
The linear regressions between the seasonal values of the SPI and Z, CZI, MCZI, PN and I from 1950 to 2005 indicate that the SPI and Z, CZI, MCZI, PN and I in general show a good relationship for the time scales of three-months, but less significant than for the one-month time scale and depending on the season and climatic region (Table 4). In addition, here, the PN and I show the weakest correlation and SPI and MCZI perform best especially in rainy seasons and in Mountain and Semi Mountain regions.

Table 4.
The best indices according to region and time scale with the number of included stations per region in seasonal and annual analysis *.
| Climatic Regions | |||||||
|---|---|---|---|---|---|---|---|
| Coastal Desert | Coastal Wet | Desert | Semi Desert | Mountain | Semi Mountain | ||
| Season | Spring | CZI (3/3) R = 43–53 | CZI (3/5) R = 52–63 Zscore (2/5) R = 64–75 | CZI (4/8) R = 58–78 MCZI (2/8) R = 63–73 Zscore ( 2/8) R = 73–75 | CZI (2/5) R = 77–86 Zscore ( 2/5) R = 77–81 MCZI (1/5) R = 83 | Zscore (9/13) R = 77–82 MCZI (2/13) R = 50–73 CZI (2/13) R = 74–80 | CZI (4/6) R = 57–88 MCZI (1/6) R = 75 Zscore ( 1/5) R = 40 |
| Summer | CZI (2/3) R = 86–98 MCZI (1/3) R = 85 | MCZI (2/5) R = 52–67 CZI (2/5) R = 50–55 Zscore (1/5) R = 56 | CZI (4/8) R =76 – 90 MCZI (3/8) R = 51–76 N/A (1/8) | CZI (2/5) R = 67–77 Zscore (2/5) R = 58–78 MCZI (1/5) R = 52 | MCZI (6/13) R = 45–89 CZI (3/13) R = 43–65 Zscore (2/13) R = 44–52 N/A (2/13) | MCZI (3/6) R = 67–84 CZI (2/6) R = 88–94 N/A 81/6) | |
| Fall | CZI (2/3) R = 77–83 N/A (1/3) | Zscore (4/5) R = 69–87 CZI (1/5) R = 75 | CZI (6/8) R = 67–73 MCZI (2/8) R = 68–75 | MCZI (3/5) R = 75–83 CZI (2/5) R = 70–83 | MCZI (8/13) R = 63–84 Zscore (5/13) R = 75–86 | MCZI (3/6) R = 79–82 CZI (3/6) R = 62–84 | |
| Winter | Zscore (2/3) R = 63–83 N/A (1/3) | MCZI (1/5) R = 84 Zscore (2/5) R = 54 – 64 N/A ( 2/5) | CZI (3/8) R = 62–78 MCZI (1/8) R = 59 Zscore( 1/8) R = 84 N/A (3/8) | CZI (2/5) R = 62–68 MCZI (2/5) R = 64–68 Zscore ( 1/5) R = 72 | MCZI (10/13) R = 61- 78 CZI (2/13) R = 75–83 Zscore (1/13) R = 60 | MCZI (3/6) R = 53–71 Zscore (2/6) R = 65–67 N/A (1/6) | |
| Annual | Annual | MCZI (3/3) R = 91–96 | Zscore (5/5) R = 97–100 | Zscore (8/8) R = 97–99 | Zscore ( 5/5) R = 97–100 | Zscore (13/13) R = 95–100 | Zscore (2/6) R = 97–99 |
*Every cell contains drought indices which have the best correlation with the SPI index and Numbers in margins (X/Y) shows the number of stations where the index performed best (X) out of the total number of stations per region (Y). R shows the range of the Pearson’s correlation coefficients of the regression line for every index.
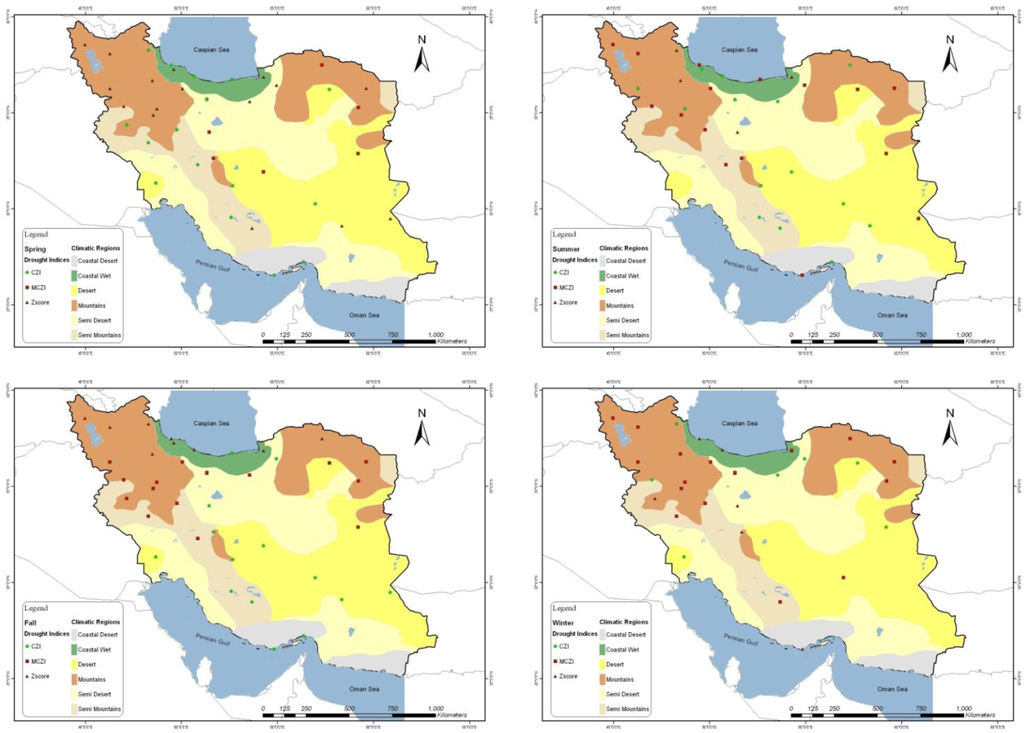
Figure 6.
Spatial distribution of seasonal drought indices with the best correlation to SPI for spring, summer, autumn and winter seasons.
As shown in Figure 6, there is no dominating spatial distribution pattern of drought indices that have the best correlation with SPI as was shown in the monthly analysis. However, in general the MCZI has the best correlation with SPI in Mountains and Semi Mountain regions and partly in the Costal wet region. In the other parts of Iran the highest correlation was calculated between SPI and CZI including Desert, Semi Desert and Costal desert regions. In some exceptions the Z-Score index performed best, for example in the spring and summer seasons in the northern parts of Iran that are covered by the high Albourz mountain chain and in parts of the south eastern regions that are covered by Desert and Semi Desert regions. In Table 4 the best indices according to region and time scale with the number of included stations are shown.
4.1.3. Results of Annual Analysis
The linear regressions between the annual values of the SPI and Z, CZI, MCZI, PN and I from 1950 to 2005 were calculated (Table 4). There is a big difference between the pattern of spatial distribution of the best performing indices with SPI and other patterns that were obtained in the monthly and seasonal analyses (Figure 7). On the annual time scale, the Z score has the strongest correlation with SPI at almost all of the selected stations located in a variety of climatic regions from Coastal wet to Desert regions except for some parts of Coastal desert region (Table 4). Additionally, in this stage there was no strong correlation between CZI, PN and I with SPI even in dry climatic regions.
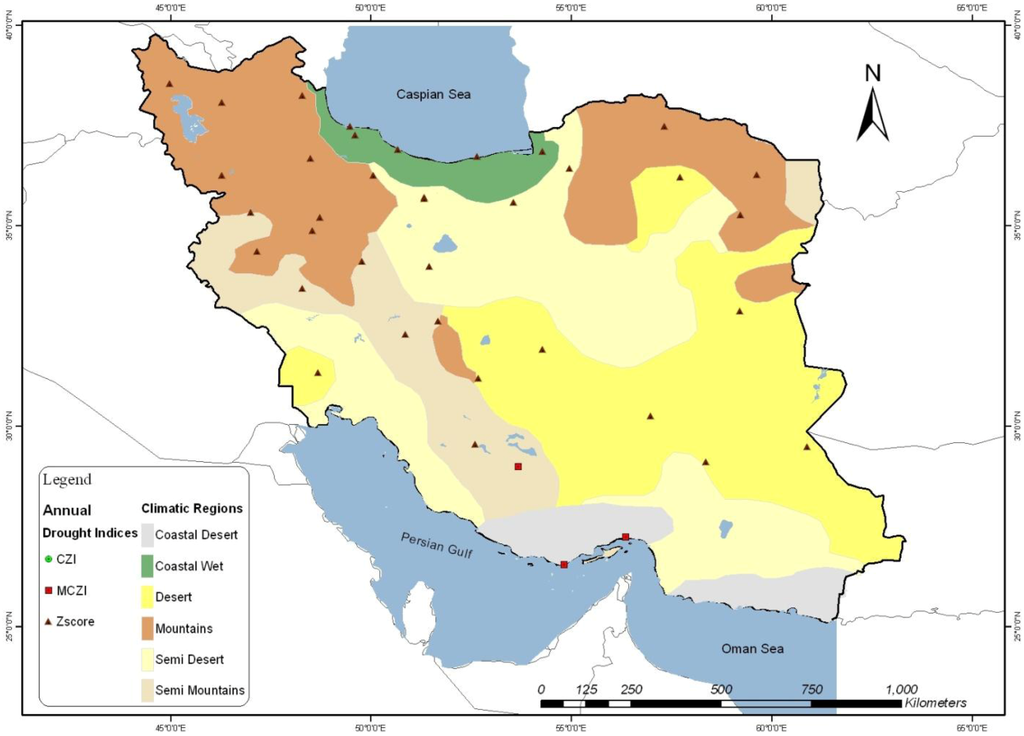
Figure 7.
Spatial distribution of annual drought indices with the best correlation to SPI.
4.2. Spatial Analysis of Droughts Indices
According to the recorded rainfall data by the Iranian Emergency Agency, the year of 1999 was one of the driest years in Iran. Therefore, all indices were calculated for the period of October1998 to September 1999—hydrological year 1999—and have been analyzed for their performance in objecting patterns of regional droughts. As shown in Figure 8(a–f) in the first half of these two year periods, which included rainy periods, the SPI showed the lowest minimum values of the mentioned drought indices in all of the climatic regions. Rainfall during this period was about 60% lower than normal. The SPI index showed an extreme dry condition that evolved at almost all of the stations, especially in April 1999, which was the worst dry month reported by the OFDA/CRED International Disaster Database (Table 1) [15].
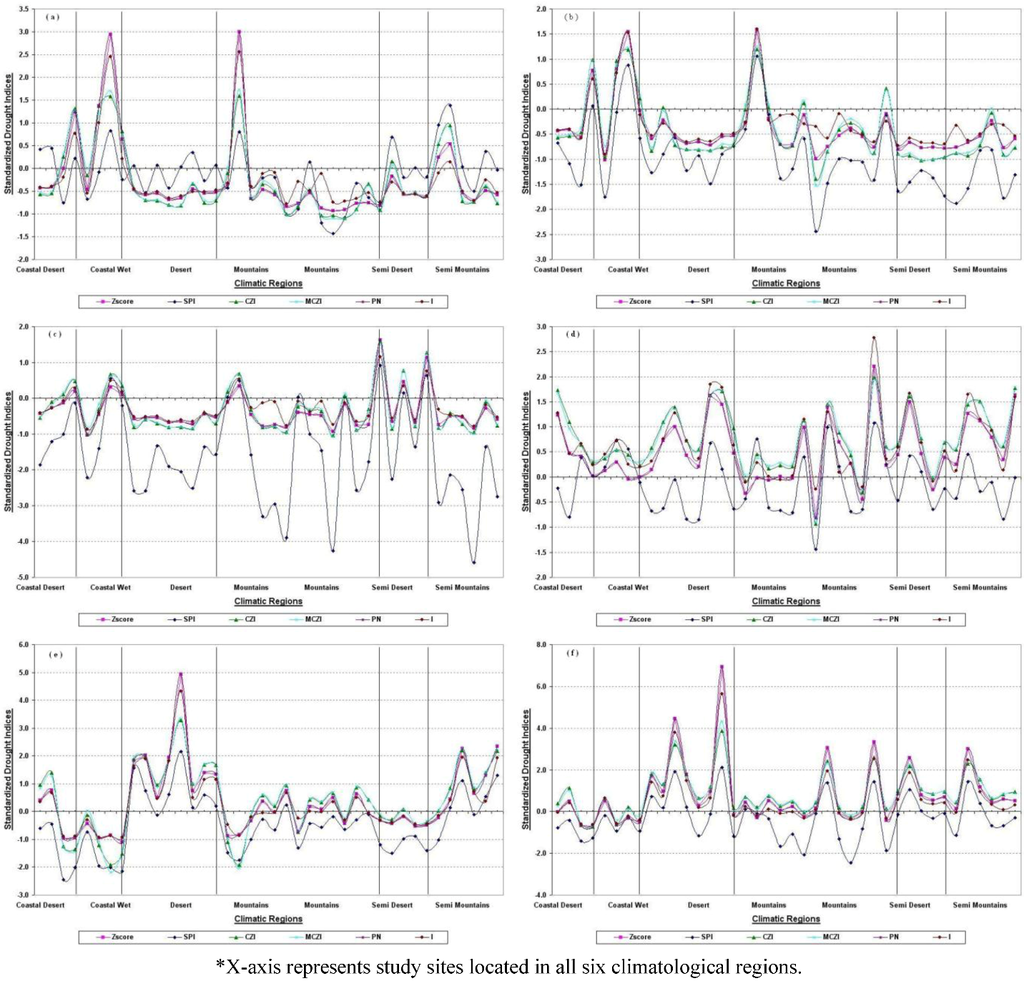
Figure 8.
Behavior of the standardized monthly drought indices over six climatic regions during October 1998 to March 1999 in Iran as: (a) October 1998, (b) November 1998, (c) December 1998, (d) January 1999, (e) February 1999, (f) March 1999 *.
In the second half of these two year periods from April until August 1998 and 1999 (Figure 9(a–f) that included the months without any rainfall, the SPI changed its behavior slowly and showed the highest positive as well as negative values—except in April and May where at some stations still little rainfall was recorded. In the second half of the period, CZI and MCZI showed a similar behavior to the SPI, where the amount of precipitation was however not lower than normal. Both CZI and MCZI showed extreme drought conditions during April until September 1999.
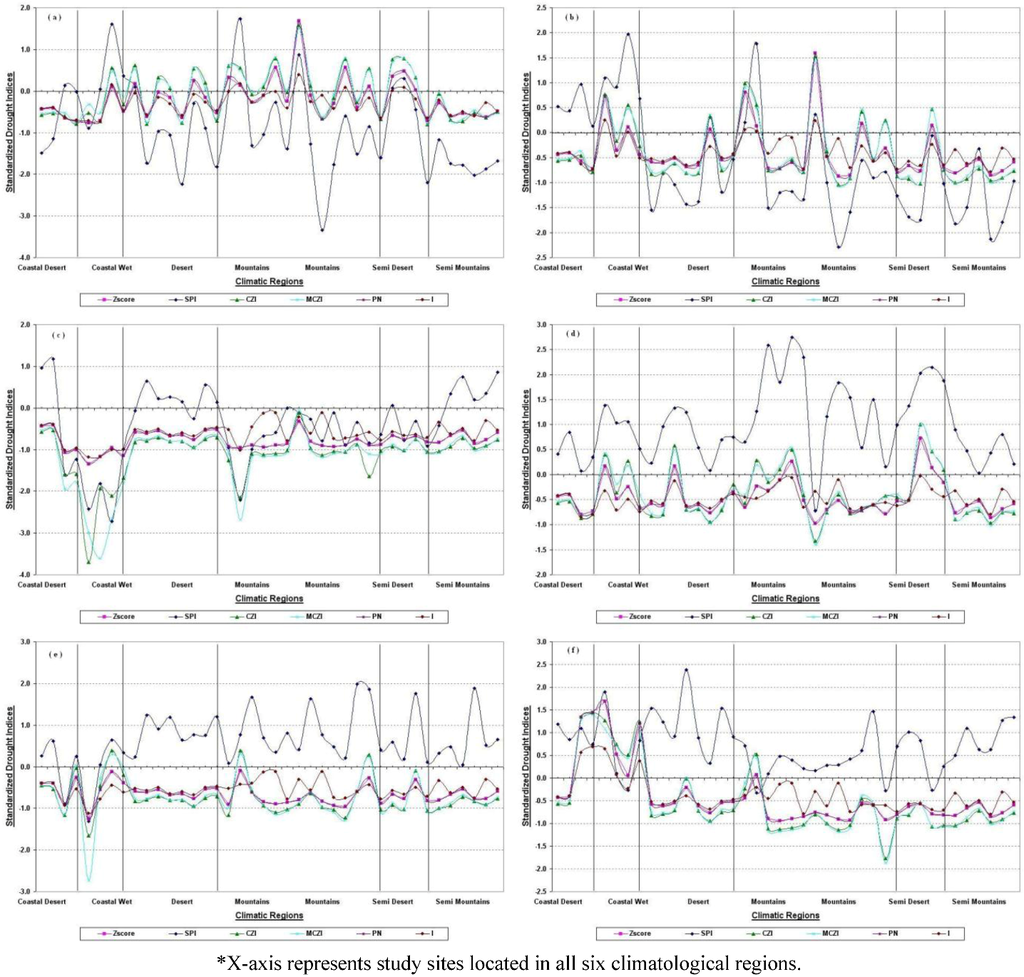
Figure 9.
Behavior of the standardized monthly drought indices over six climatic regions during April to September 1999 in Iran as: (a) April 1999, (b) May 1999, (c) June 1999, (d) July 1999, (e) August 1999, (f) September 1999*.
5. Conclusions
This work is a contribution to studies which focus on the applications of remote sensing based drought indices in the agricultural environment located in Iran and other neighboring countries in Central Asia [24,25,26]. In these researches authors have concluded that meteorological drought indices show high performance in detecting and measuring drought intensity compared with other remote sensing based drought indices. It was revealed that there is a strong significant correlation between remote sensing based and meteorological drought indices over the case study areas and the strength of these relationships is very dependent on the climatological conditions and vegetation coverage of the study points.
In this research, linear regressions between the monthly, seasonal and annual values of the SPI and Z, CZI, MCZI, PN and I from 1950 to 2005 in Iran show that the SPI and Z-Score, CZI, MCZI, PN and I show very different correlations related to the time scales of one, three and 12 months. However, the degree of these relationships is related to the season and the climatic region. For example, the strongest relationship was calculated between SPI and MCZI especially in rainy months and seasons in Coastal wet regions. In the annual analysis of drought indices, the Z-Score has the best spatial and temporal distribution over all climatic regions. The analysis of the dry spell 1998/1999 indicated that MCZI is more sensitive than SPI for detection of absolute drought conditions as a predictor for agro-meteorological drought whereas SPI is very sensitive to deviations from long term precipitation regimes.
5.1. Conclusions for Operational Applications
According to the results, by considering the advantages and disadvantages of the investigated drought indices in Iran, e.g., there is less limitation from available input data for calculation of the Z, CZI and MCZI drought indices, the mentioned indices can be used as good drought predictors depending on the season, the length of drought and climatic conditions. They could be used instead of SPI for operational applications which are limited by the availability of long term climatic data and low sensitivity to agro-meteorological drought conditions.
An operational example of the application of these drought indices in agriculture in Iran is for winter wheat which is one of the major rainfed crops in Iran. In general, the growing period of winter wheat starts in late October and lasts until July [27]. During this period, according to the results achieved, in Mountains, Semi Mountain and Coastal Desert regions, the MCZI could be used as a related drought predictor. In the Arid and Semi-Arid areas the CZI has a good performance in detecting and measuring drought conditions for winter wheat. Especially, in May and June, which includes three important and water stress sensitive stages of the growing period of winter wheat (booting, heading and ripening), this method could accurately monitor drought risk for agricultural stakeholders in Iran.
5.2. Conclusions for Research Applications
It is clear that to assess the results more accurately, the use of more climatic data including precipitation on a temporal and spatial scale is required. This is the main constraint for studying the behavior of drought phenomena over Iran and also in other developing countries. For example, the combination with remote sensing based methods seems to be a promising method.
Regarding the recent effects of climate change in increasing severe drought conditions in several parts of Asian countries, the validation and application of drought indices for the construction of dynamic drought monitoring systems is crucial. High temporal and spatial resolution (updating of drought maps every month or even every week) seems to be very useful for implementing local measures to reduce drought effects on food production risks.
Acknowledgements
This work was supported by the Austrian Agency for International Cooperation in Education and Research (OeAD). The authors would like to thank Abduwasit Ghulam for his constructive comments. Thanks are due to the Iran Meteorological Organization (IRIMO) who provided the data required for this study. The authors would like to extend their thanks to the anonymous reviewers for their valuable comments and suggestions.
References
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in Greece using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; US Department of Commerce Weather Bureau: Washington, DC, USA, 1965.
- Gibbs, W.J.; Maher, J.V. Rainfall Deciles as Drought Indicators; Bureau of Meteorology bulletin No. 48; Commonwealth of Australia: Melbourne, VIC, Australia, 1967.
- Wu, H.; Hayes, M.J.; Welss, A.; Hu, Q. An evaluation the standardized precipitation index, the China-z index and the statistical Z-Score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceeding of the 8th American Meteorological Society (AMS) Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184.
- Edwards, D.C.; Mckee, T.B. Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Climatology Report 97-2. Department of Atmospheric Science-Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Amer. Meteor. Soc. 1999, 80, 429–438. [Google Scholar]
- Alley, W.M. The Palmer Drought Severity Index: limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Guttmann, N.B. Comparing the palmer drought index and the standardized precipitation index. J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtinb, V.; Moghaddasi, M. Comparison of seven meteorological indices for drought monitoring in Iran. Int. J. Climatol. 2006, 26, 1149–1165. [Google Scholar] [CrossRef]
- Alijani, B.; Ghohroudi, M.N.; Arabi, N. Developing a climate model for Iran using GIS. Theor. Appl. Climatol. 2008, 92, 103–112. [Google Scholar] [CrossRef]
- Iran Meteorological Organization (IRIMO), The Climatological Normal of Synoptic Stations in Iran; IRIMO: Tehran, Iran, 2005.
- Dai, A. Drought under global warming: A review. WIRES Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef]
- OFDA/CRED. International Disaster Database; Université Catholique de Louvain: Brussels, Belgium, 2013. Available online: http://www.emdat.be (accessed on 5 February 2013).
- Raziei, T.; Saghafian, B.; Paulo, A.A.; Pereira, L.S.; Bordi, I. Spatial patterns and temporal variability of drought in western Iran. Water Resour. Manag. 2009, 23, 439–455. [Google Scholar] [CrossRef]
- Rahimzadeh, B.P.; Darvishsefatb, A.A.; Khalili, A.; Makhdoum, M.F. Using AVHRR-based vegetation indices for drought monitoring in the Northwest of Iran. J. Arid. Environ. 2009, 72, 1086–1096. [Google Scholar]
- Tabari, H.; Abghani, H.; Talaee, P.H. Temporal trends and spatial characteristics of drought and rainfall in arid and semi-arid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Rezaeian-Zadeh, M.; Tabari, H. MLP-based drought forecasting in different climatic regions. Theor. Appl. Climatol. 2012, 109, 407–414. [Google Scholar] [CrossRef]
- Capra, A.; Consoli, S.; Scicolone, B. Long-term climatic variability in Calabria and effects on drought and agrometeorological parameters. Water Resour. Manage. 2013, 27, 601–617. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Charles Griffin & Company-High Wycombe: London, UK, 1997; pp. 400–401. [Google Scholar]
- World Meteorological Organization (WMO), Drought and Agriculture; WMO Note 138 Pub. WMO-392; Geneva, Switzerland, 1975; p. 127.
- Nastos, P.T.; Politi, N.; Kapsomenakis, J. Spatial and temporal variability of the aridity index in Greece. Atmos. Res. 2013, 119, 140–152. [Google Scholar] [CrossRef]
- Shahabfar, A.; Ghulam, A.; Eitzinger, J. Drought monitoring in Iran using the perpendicular drought indices. Int. J. Appl. Earth Obs. 2012, 18, 119–127. [Google Scholar] [CrossRef]
- Shahabfar, A.; Eitzinger, J. Agricultural drought monitoring in semi-arid and arid areas using MODIS data. J. Agr. Sci. 2011, 149, 403–414. [Google Scholar] [CrossRef]
- Shahabfar, A.; Reinwand, M.; Conrad, C. A re-examination of perpendicular drought indices over Central and Southwest Asia. Proc. SPIE 2012, 8531, 24–27. [Google Scholar]
- Ziaei, A.N.; Sepaskhah, A.R. Model for simulation of winter wheat yield under dryland and irrigated conditions. Agr. Water Manage. 2003, 58, 1–17. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).