Impact of Spatial Resolution on River Flow Simulation Based on the Total Runoff Integrating Pathway (TRIP) Model
Abstract
1. Introduction
2. Materials and Methods
2.1. River Routing Model
2.2. Atmospheric Forcing Data
2.3. Experiment Design
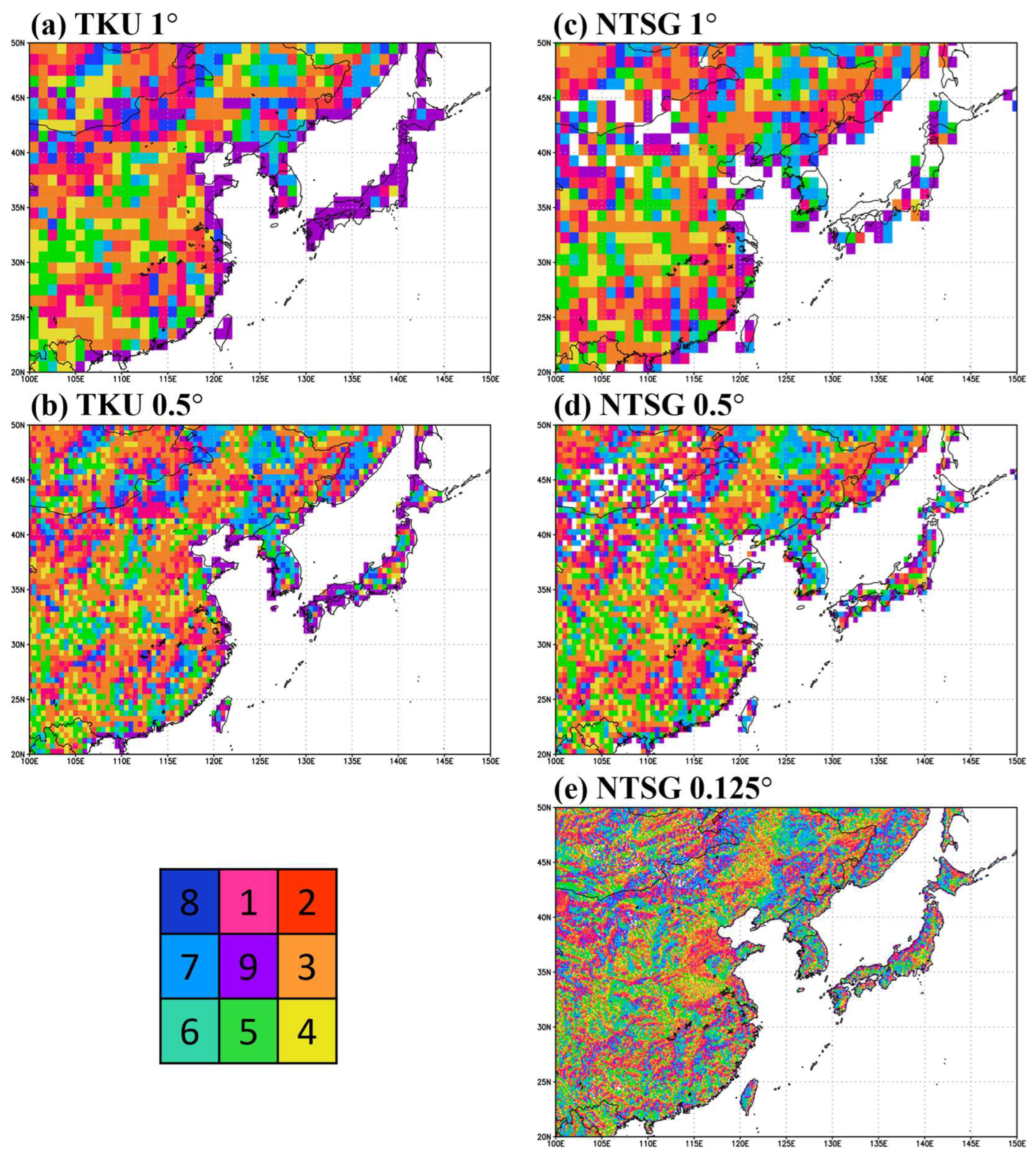
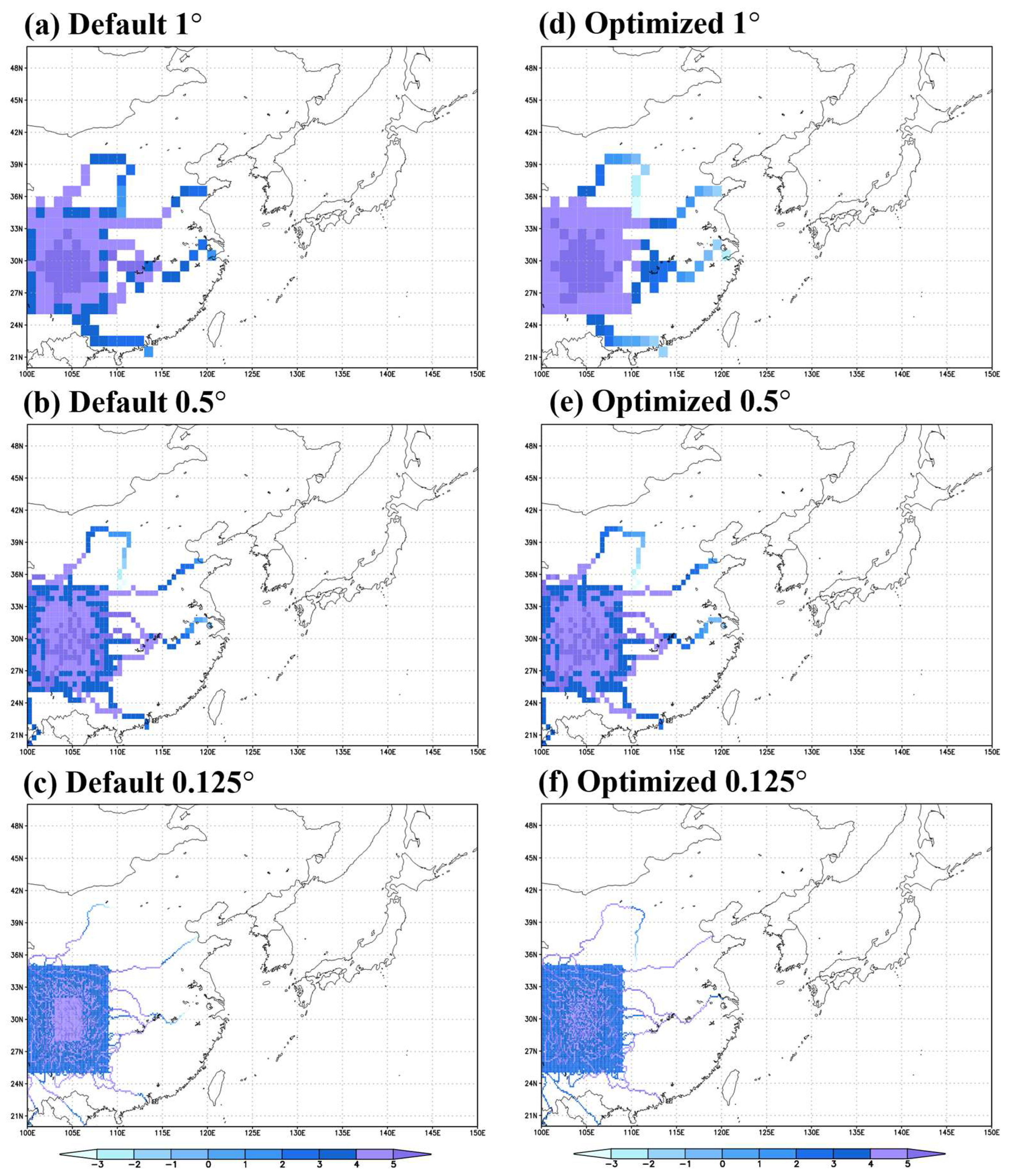
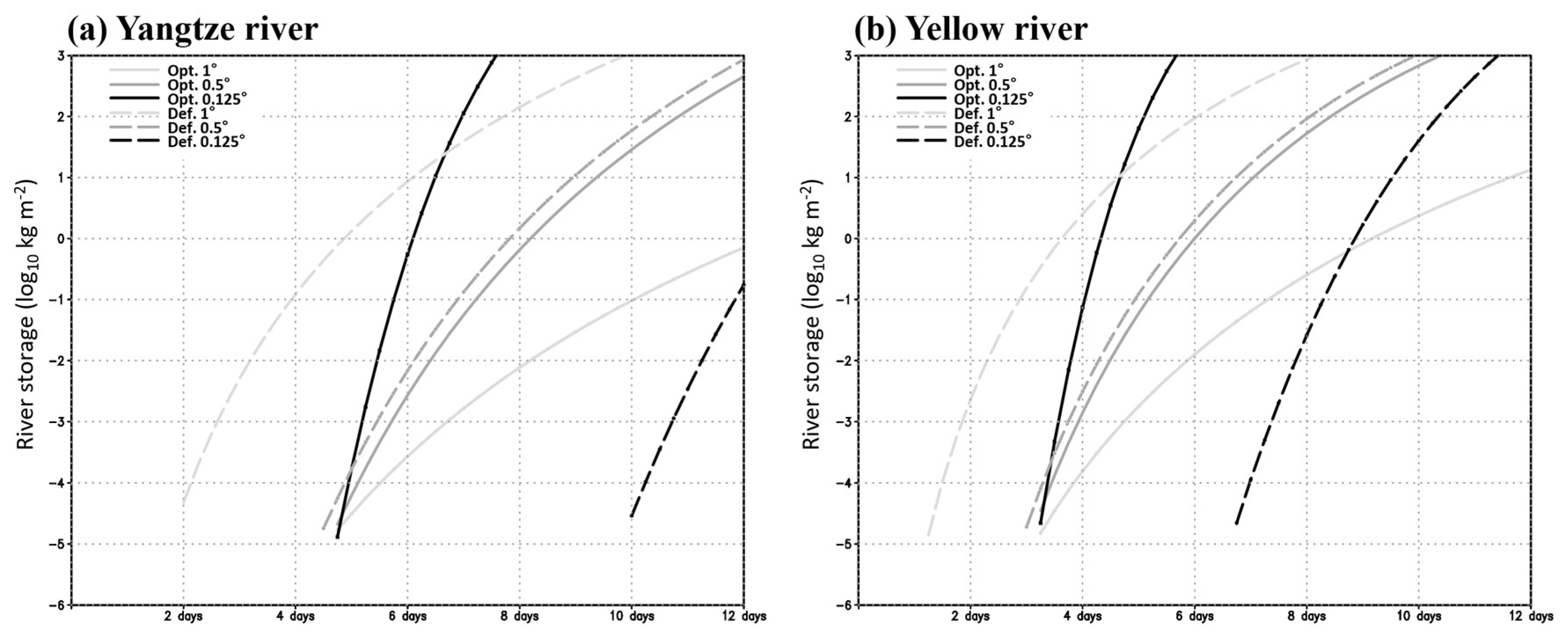
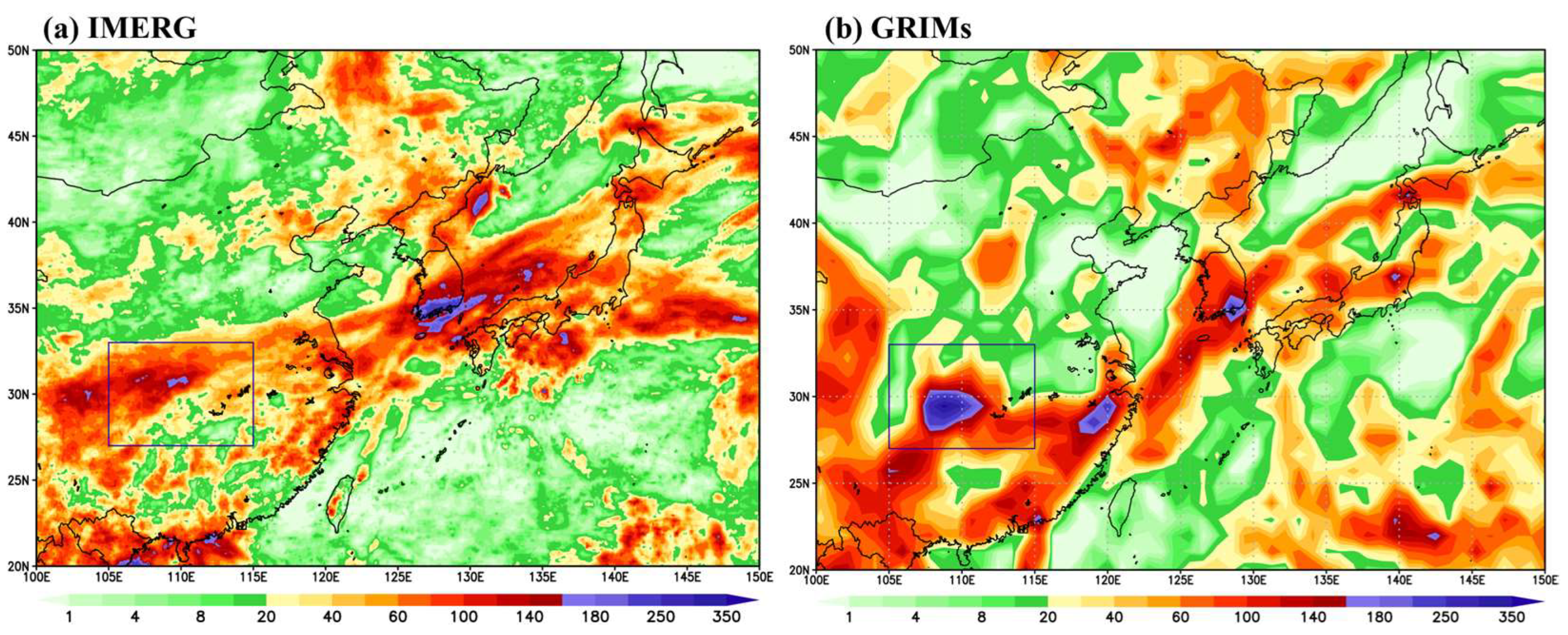
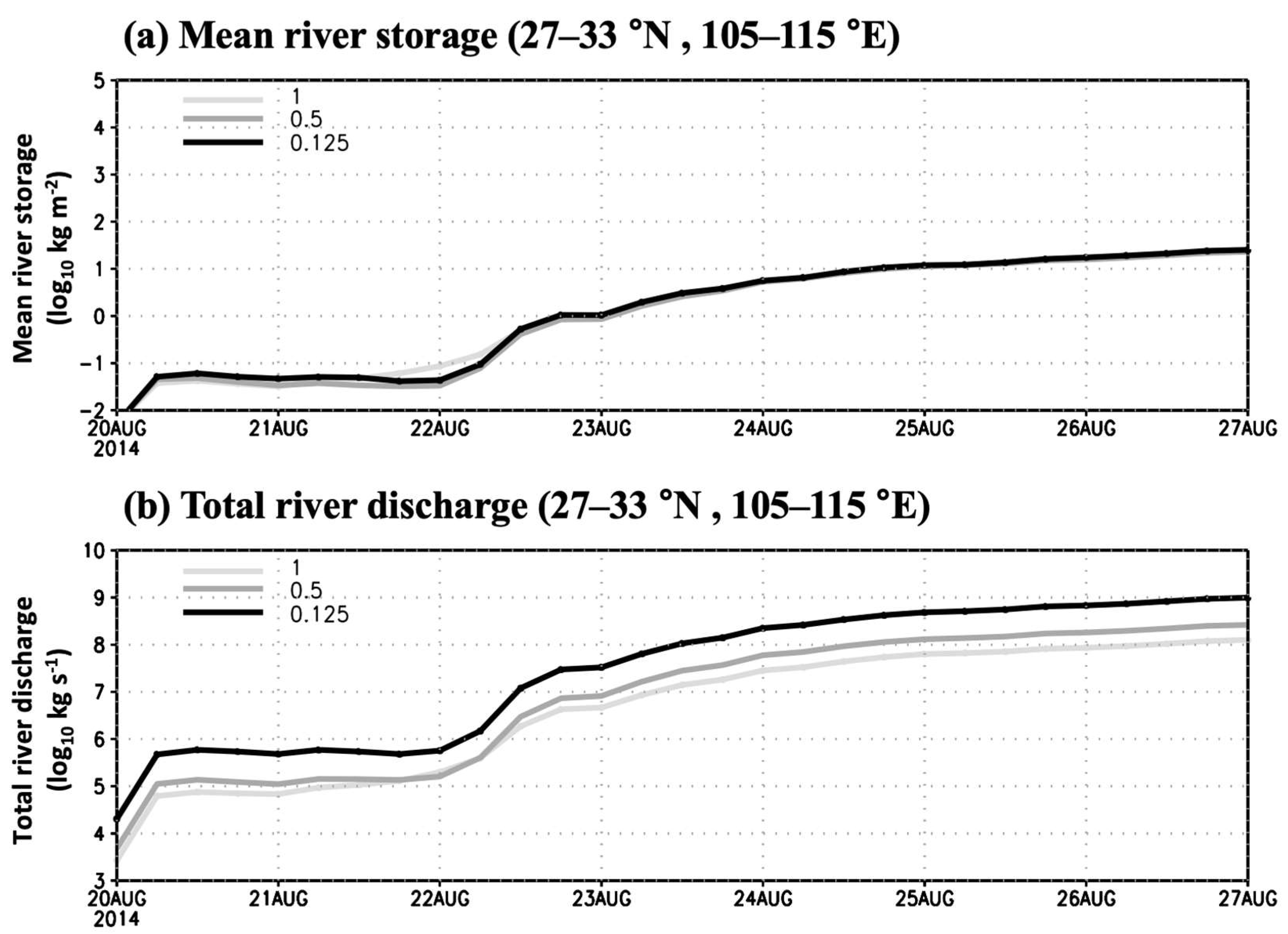
3. Results
3.1. Idealization Experiment
3.2. Real Case Experiment
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TRIP | Total runoff integrating pathways |
| JULES | Joint UK Land Environment Simulator |
| ESM | Earth system model |
| NTGS | Northwest Territories Geological Survey |
| IMERG | Integrated Multi-satellitE Retrievals for Global Precipitation Measurement |
| GRIMs | Global/Regional Integrated Model system |
| NCEP | National Centers for Environmental Prediction |
| DOE | Department of energy |
| ETOPO5 | Earth topography five-minute grid |
| DEM | Digital elevation map |
| UM | Met Office Unified Model |
References
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef]
- He, C.; Tian, J.; Zhang, Q.; Wu, J.; Li, J. Future global urban water scarcity and potential solutions. Nat. Commun. 2021, 12, 4667. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, S.; Kong, X.; Zheng, W.; Feng, W.; Zhang, X.; Yuan, R.; Song, X.; Sprenger, M. Interaction of surface water and groundwater influenced by groundwater over-extraction, waste water discharge and water transfer in Xiong’an New Area, China. Water 2019, 11, 539. [Google Scholar] [CrossRef]
- Li, Z.; Fang, Y.; Meng, B.; Guo, H.; Du, X. Identification of groundwater—Surface water interaction using combined hydraulic and hydrogeochemical methods. Water 2024, 16, 2777. [Google Scholar] [CrossRef]
- Pielke, R.A., Sr. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall. Rev. Geophys. 2001, 39, 151–177. [Google Scholar] [CrossRef]
- Boucher, O.; Myhre, G.; Myhre, A. Direct human influence of irrigation on atmospheric water vapour and climate. Clim. Dyn. 2004, 22, 597–603. [Google Scholar] [CrossRef]
- Koster, R.D.; Sud, Y.C.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oki, T.; Cox, P.; Davies, H.; Gordon, C.T.; Kanae, S.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Cook, B.I.; Bonan, G.B.; Levis, S. Soil moisture feedbacks to precipitation in southern Africa. J. Clim. 2006, 19, 4198–4206. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture—Climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015, 6, 6443. [Google Scholar] [CrossRef]
- Clark, M.P.; Fan, Y.; Lawrence, D.M.; Adam, J.C.; Bolster, D.; Gochis, D.J.; Hooper, R.P.; Kumar, M.; Leung, L.R.; Mackay, D.S.; et al. Improving the representation of hydrologic processes in Earth System Models. Water Resour. Res. 2015, 51, 5929–5956. [Google Scholar] [CrossRef]
- Wedi, N.P. Increasing horizontal resolution in numerical weather prediction and climate simulations: Illusion or panacea? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130289. [Google Scholar] [CrossRef]
- Kmoch, A.; Kanal, A.; Astovar, A.; Kull, A.; Virro, A.; Partel, M.; Sepp, K. EstSoil-EH: A high-resolution eco-hydrological modelling parameters dataset for Estonia. Earth Syst. Sci. Data 2021, 13, 83–97. [Google Scholar] [CrossRef]
- Towler, E.; Foks, S.S.; Dugger, A.L.; Dickinson, J.E.; Essaid, H.I.; Gochis, D.; Viger, R.J.; Zhang, Y. Benchmarking high resolution hydrologic model performance of long-term retrospective streamflow simulations in the contiguous United States. Hydrol. Earth Syst. Sci. 2023, 27, 1809–1825. [Google Scholar] [CrossRef]
- Boeing, F.; Rakovec, O.; Kumar, R.; Samaniego, L.; Schrön, M.; Hildebrandt, A.; Rebmann, C.; Thober, S.; Müller, S.; Zacharias, S.; et al. High resolution drought simulations and comparison to soil moisture observations in Germany. Hydrol. Earth Syst. Sci. 2022, 26, 5137–5161. [Google Scholar] [CrossRef]
- Hanasaki, N.; Matsuda, H.; Fujiwara, M.; Hirabayashi, Y.; Seto, S.; Kanae, S.; Oki, T. Toward hyper resolution global hydrological models including human activities: Application to Kyushu island, Japan. Hydrol. Earth Syst. Sci. 2022, 26, 1953–1975. [Google Scholar] [CrossRef]
- Oki, T.; Sud, Y.C. Design of Total Runoff Integrating Pathways (TRIP)—A global river channel network. Earth Interact. 1998, 2, 1–37. [Google Scholar] [CrossRef]
- Oki, T.; Nishimura, T.; Dirmeyer, P. Assessment of annual runoff from land surface models using Total Runoff Integrating Pathways (TRIP). J. Meteorol. Soc. Japan. Ser. II 1999, 77, 235–255. [Google Scholar] [CrossRef]
- Alkama, R.; Decharme, B.; Douville, H.; Becker, M.; Cazenave, A.; Sheffield, J.; Voldoire, A.; Tyteca, S.; Le Moigne, P. Global evaluation of the ISBA-TRIP continental hydrological system. Part I: Comparison to GRACE terrestrial water storage estimates and in situ river discharges. J. Hydrometeorol. 2010, 11, 583–600. [Google Scholar] [CrossRef]
- Mouri, G.; Minoshima, D.; Golosov, V.N.; Chalov, S.R.; Seto, S.; Yoshimura, K.; Nakamura, S.; Oki, T. Probability assessment of flood and sediment disasters in Japan using the Total Runoff-Integrating Pathways model. Int. J. Disaster Risk Reduct. 2013, 3, 31–43. [Google Scholar] [CrossRef]
- National Geophysical Data Center. Data Announcement 88-MGG-02, Digital Relief of the Surface of the Earth; NOAA, National Geophysical Data Center: Boulder, CO, USA, 1988. Available online: https://www.ngdc.noaa.gov/mgg/global/relief/ETOPO5/TOPO/ETOPO5 (accessed on 2 December 2024).
- Oki, T.; Agata, Y.; Kanae, S.; Saruhashi, T.; Yang, D.; Musiake, K. Global water resources assessment under climatic change in 2050 using TRIP. IAHS Publ. 2003, 280, 124–133. [Google Scholar]
- Kim, J.-E.; Hong, S.-Y. A global atmospheric analysis dataset downscaled from the NCEP–DOE reanalysis. J. Clim. 2012, 25, 2527–2534. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Park, H.; Cheong, H.C.; Kim, J.-E.; Koo, M.-S.; Jang, J.; Ham, S.; Hwang, S.O.; Park, B.K.; Chang, E.C.; et al. The Global/Regional Integrated Model System (GRIMs). Asia-Pac. J. Atmos. Sci. 2013, 49, 219–243. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Chang, E.-C.; Yeh, S.-W.; Hong, S.-Y.; Kim, J.-E.; Wu, R.; Yoshimura, K. Study on the changes in the East Asian precipitation in the mid-1990s using a high-resolution global downscaled atmospheric data set. J. Geophys. Res. Atmos. 2014, 119, 2279–2293. [Google Scholar] [CrossRef]
- Walters, D.N.; Boutle, I.A.; Brooks, M.E.; Melvin, T.; Stratton, R.A.; Vosper, S.B.; Wells, H.; Williams, K.D.; Wood, N.; Allen, T.; et al. The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations. Geosci. Model Dev. 2017, 10, 1487–1520. [Google Scholar] [CrossRef]
- Cortés-Salazar, N.; Vásquez, N.; Mizukami, N.; Mendoza, P.A.; Vargas, X. To what extent does river routing matter in hydrological modeling? Hydrol. Earth Syst. Sci. 2023, 27, 3505–3524. [Google Scholar] [CrossRef]
- Munier, S.; Decharme, B. River network and hydro-geomorphological parameters at 1/12° resolution for global hydrological and climate studies. Earth Syst. Sci. Data 2022, 14, 2239–2258. [Google Scholar] [CrossRef]
- Liu, X.; Kan, G.; Ding, L.; He, X.; Liu, R.; Liang, K. Improving the performance of hydrological model parameter uncertainty analysis using a constrained multi-objective intelligent optimization algorithm. Water 2023, 15, 2700. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Mathison, C.T.; Burke, E.J. River parametrisation of the JULES land surface model for improved runoff routing at the global scale. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar] [CrossRef]

| Factor | 1° | 0.5° | 0.125° | |
|---|---|---|---|---|
| Default value | River speed | 0.4 | 0.4 | 0.4 |
| Meandering | 0.4 | 0.4 | 0.4 | |
| Optimized value | River speed | 0.5 | 0.5 | 0.5 |
| Meandering | 1.5 | 0.525 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Byun, U.-Y.; Chang, E.-C.; Lim, Y.-J. Impact of Spatial Resolution on River Flow Simulation Based on the Total Runoff Integrating Pathway (TRIP) Model. Atmosphere 2025, 16, 1083. https://doi.org/10.3390/atmos16091083
Kim M, Byun U-Y, Chang E-C, Lim Y-J. Impact of Spatial Resolution on River Flow Simulation Based on the Total Runoff Integrating Pathway (TRIP) Model. Atmosphere. 2025; 16(9):1083. https://doi.org/10.3390/atmos16091083
Chicago/Turabian StyleKim, Minwoo, Ui-Yong Byun, Eun-Chul Chang, and Yoon-Jin Lim. 2025. "Impact of Spatial Resolution on River Flow Simulation Based on the Total Runoff Integrating Pathway (TRIP) Model" Atmosphere 16, no. 9: 1083. https://doi.org/10.3390/atmos16091083
APA StyleKim, M., Byun, U.-Y., Chang, E.-C., & Lim, Y.-J. (2025). Impact of Spatial Resolution on River Flow Simulation Based on the Total Runoff Integrating Pathway (TRIP) Model. Atmosphere, 16(9), 1083. https://doi.org/10.3390/atmos16091083






