Artificial Intelligence-Based Methods and Algorithms in Fog and Atmospheric Low-Visibility Forecasting
Abstract
1. Introduction
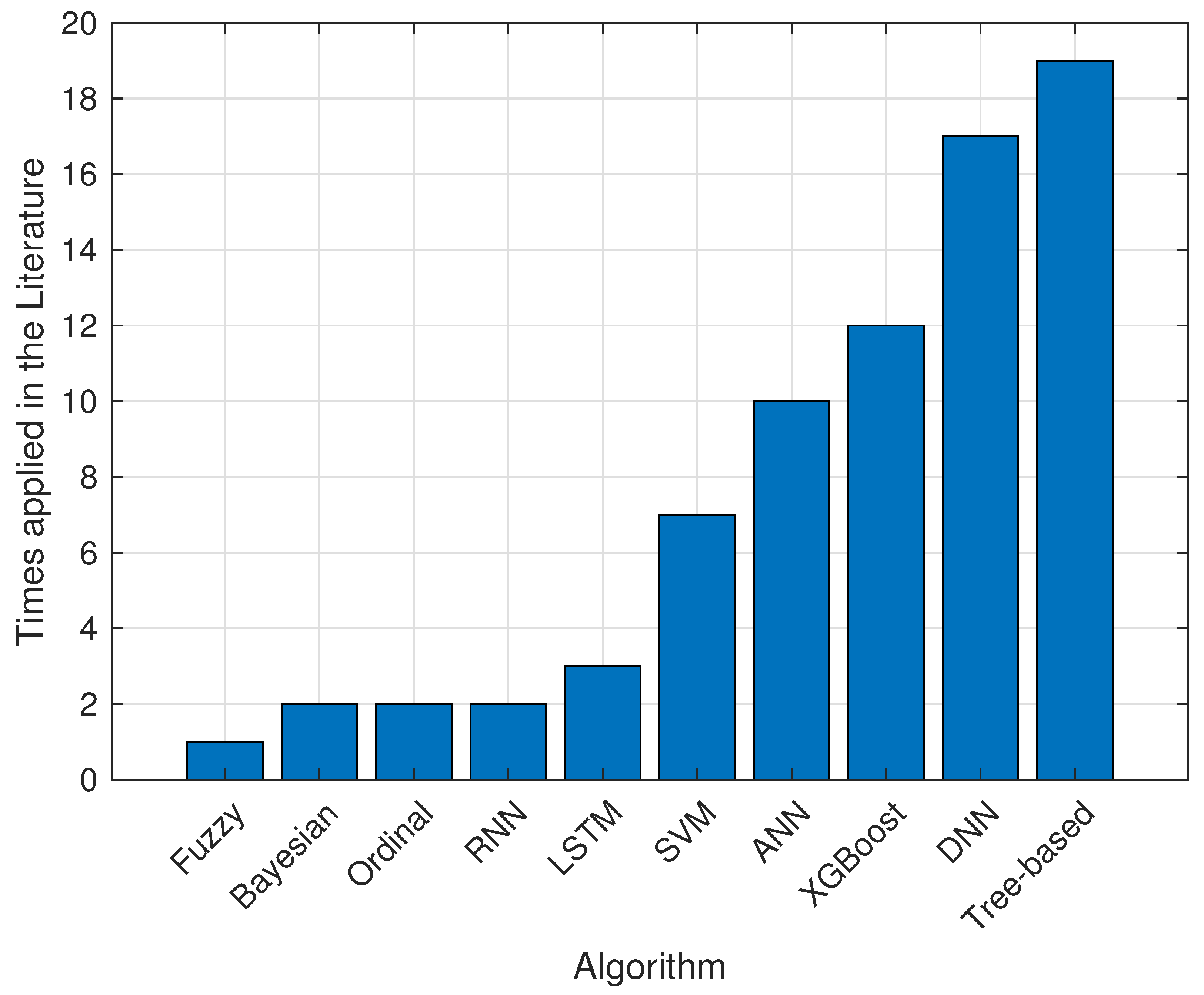
2. Literature Review
3. Discussion, Analysis and Challenges
3.1. Discussion and Analysis
3.2. Challenges
3.2.1. Imbalanced Data
3.2.2. Data and Quality of Observations
3.2.3. New Methodological Approaches
4. Computational Examples
4.1. Ordinal Classification
4.2. Data Description
- m,
- m m,
- m m,
- m .
4.3. Logistic All-Threshold (LAT)
4.4. Experimental Settings
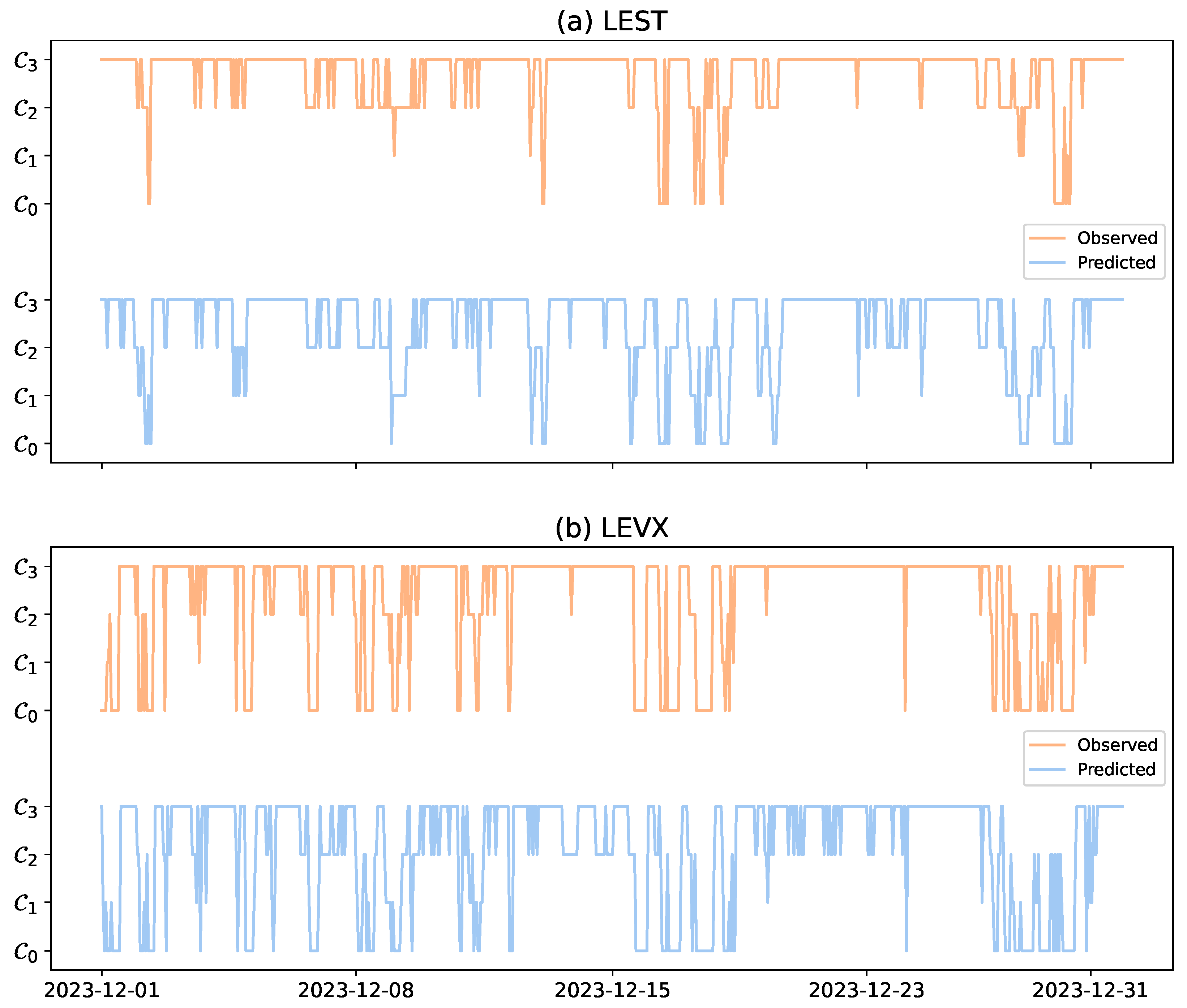
4.5. Results
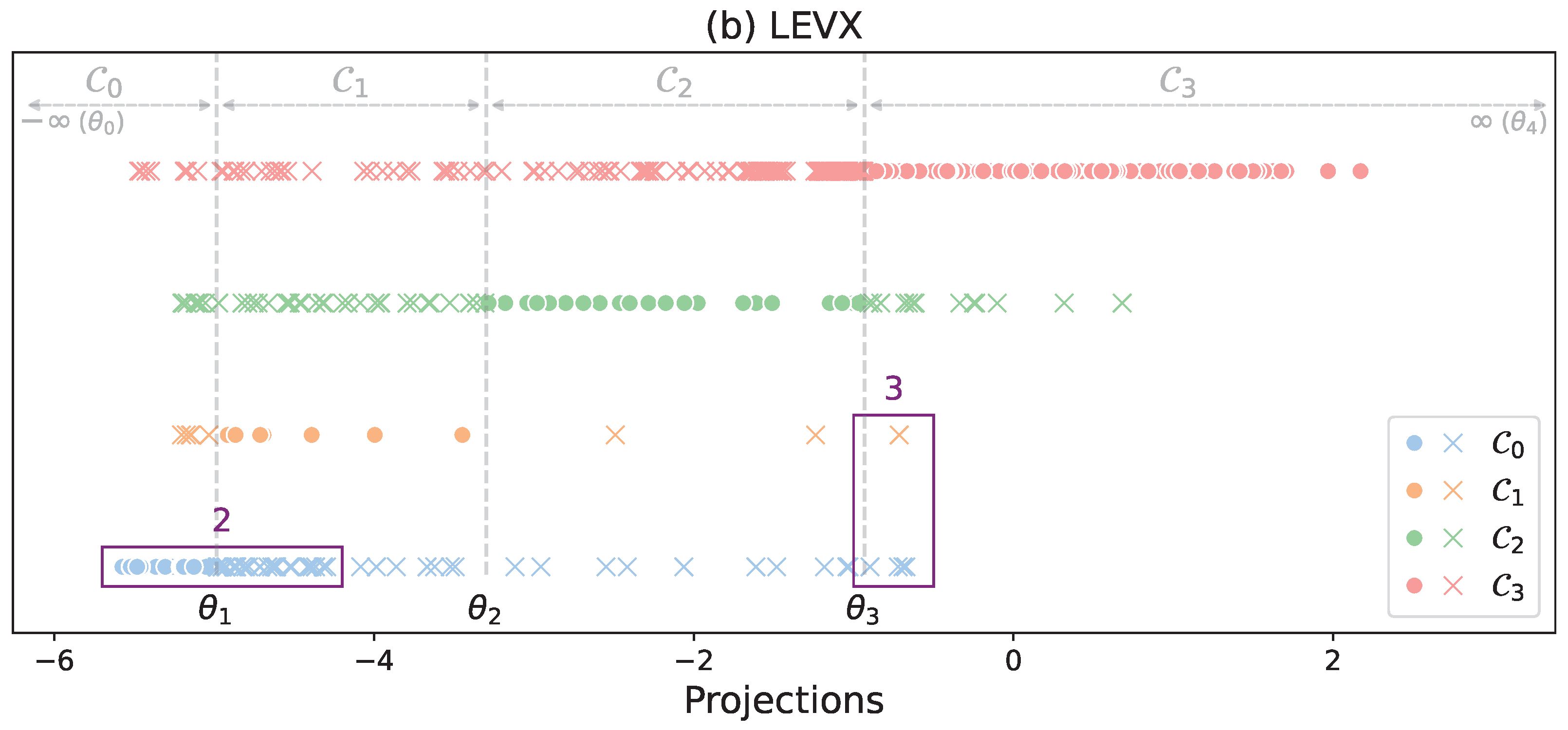
4.6. Explainability of LAT Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gultepe, I.; Tardif, R.; Michaelides, S.C.; Cermak, J.; Bott, A.; Bendix, J.; Müller, M.D.; Pagowski, M.; Hansen, B.; Ellrod, G.; et al. Fog research: A review of past achievements and future perspectives. Pure Appl. Geophys. 2007, 164, 1121–1159. [Google Scholar] [CrossRef]
- Koračin, D.; Dorman, C.E.; Lewis, J.M.; Hudson, J.G.; Wilcox, E.M.; Torregrosa, A. Marine fog: A review. Atmos. Res. 2014, 143, 142–175. [Google Scholar] [CrossRef]
- Lakra, K.; Avishek, K. A review on factors influencing fog formation, classification, forecasting, detection and impacts. Rend. Lincei. Sci. Fis. Nat. 2022, 33, 319–353. [Google Scholar] [CrossRef]
- Klemm, O.; Schemenauer, R.S.; Lummerich, A.; Cereceda, P.; Marzol, V.; Corell, D.; van Heerden, J.; Reinhard, D.; Gherezghiher, T.; Olivier, J.; et al. Fog as a fresh-water resource: Overview and perspectives. AMBIO 2012, 41, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Montecinos, S.; Carvajal, D.; Cereceda, P.; Concha, M. Collection efficiency of fog events. Atmos. Res. 2018, 209, 163–169. [Google Scholar] [CrossRef]
- Shrestha, S.; Moore, G.A.; Peel, M.C. Trends in winter fog events in the Terai region of Nepal. Agric. For. Meteorol. 2018, 259, 118–130. [Google Scholar] [CrossRef]
- Baldocchi, D.; Waller, E. Winter fog is decreasing in the fruit growing region of the Central Valley of California. Geophys. Res. Lett. 2014, 41, 3251–3256. [Google Scholar] [CrossRef]
- Anber, U.; Gentine, P.; Wang, S.; Sobel, A.H. Fog and rain in the Amazon. Proc. Natl. Acad. Sci. USA 2015, 112, 11473–11477. [Google Scholar] [CrossRef]
- Monga, S.; Taneja, A.; Saluja, N.; Garg, R.; Singh, N. Analyzing the impact of fog on wireless propagation using different attenuation models. Aip Conf. Proc. 2023, 2916, 110003. [Google Scholar]
- Wen, C.C.; Yeh, H.H. Comparative influences of airborne pollutants and meteorological parameters on atmospheric visibility and turbidity. Atmos. Res. 2010, 96, 496–509. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, H.; Liu, D.; Wang, H.; Zhou, L.; Zhu, C.; Zu, F.; Wu, H.; Lyu, Y.; Xia, Y.; et al. Observations and forecasts of urban transportation meteorology in China: A review. Atmosphere 2022, 13, 1823. [Google Scholar] [CrossRef]
- Cho, H.J.; Kim, K.S. Development of hazardous road fog index and its application. J. East. Asia Soc. Transp. Stud. 2005, 6, 3357–3371. [Google Scholar]
- Peng, Y.; Abdel-Aty, M.; Lee, J.; Zou, Y. Analysis of the impact of fog-related reduced visibility on traffic parameters. J. Transp. Eng. Part A Syst. 2018, 144, 04017077. [Google Scholar] [CrossRef]
- Praveen, M.; Sarika, M.; Anjani, N.; Yamini, M. Improving Pedestrian Detection in Low-Visibility Conditions: Fusing Visual and Infrared Data with Deep Learning. J. Comput. Anal. Appl. 2024, 33, 1465–1473. [Google Scholar]
- Bartok, J.; Bott, A.; Gera, M. Fog prediction for road traffic safety in a coastal desert region. Bound.-Layer Meteorol. 2012, 145, 485–506. [Google Scholar] [CrossRef]
- Wu, Y.; Abdel-Aty, M.; Park, J.; Zhu, J. Effects of crash warning systems on rear-end crash avoidance behavior under fog conditions. Transp. Res. Part C Emerg. Technol. 2018, 95, 481–492. [Google Scholar]
- Fernández-González, S.; Bolgiani, P.; Fernández-Villares, J.; González, P.; García-Gil, A.; Suárez, J.C.; Merino, A. Forecasting of poor visibility episodes in the vicinity of Tenerife Norte Airport. Atmos. Res. 2019, 223, 49–59. [Google Scholar]
- Guerreiro, P.M.; Soares, P.M.; Cardoso, R.M.; Ramos, A.M. An Analysis of Fog in the Mainland Portuguese International Airports. Atmosphere 2020, 11, 1239. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Pérez-Aracil, J.; Ascenso, G.; Del Ser, J.; Casillas-Pérez, D.; Kadow, C.; Fister, D.; Barriopedro, D.; García-Herrera, R.; Giuliani, M.; et al. Analysis, characterization, prediction, and attribution of extreme atmospheric events with machine learning and deep learning techniques: A review. Theor. Appl. Climatol. 2023, 155, 1–44. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Cracknell, A.P. Remote Sensing Letters contribution to the success of the Sustainable Development Goals-UN 2030 agenda. Remote Sens. Lett. 2020, 11, 715–719. [Google Scholar] [CrossRef]
- Shi, C.; Wang, L.; Zhang, H.; Zhang, S.; Deng, X.; Li, Y.; Qiu, M. Fog simulations based on multi-model system: A feasibility study. Pure Appl. Geophys. 2012, 169, 941–960. [Google Scholar] [CrossRef]
- Steeneveld, G.; Ronda, R.; Holtslag, A. The challenge of forecasting the onset and development of radiation fog using mesoscale atmospheric models. Bound.-Layer Meteorol. 2015, 154, 265–289. [Google Scholar] [CrossRef]
- Román-Cascón, C.; Steeneveld, G.; Yagüe, C.; Sastre, M.; Arrillaga, J.; Maqueda, G. Forecasting radiation fog at climatologically contrasting sites: Evaluation of statistical methods and WRF. Q. J. R. Meteorol. Soc. 2016, 142, 1048–1063. [Google Scholar] [CrossRef]
- Alaoui, B.; Bari, D.; Bergot, T.; Ghabbar, Y. Analog ensemble forecasting system for low-visibility conditions over the main airports of Morocco. Atmosphere 2022, 13, 1704. [Google Scholar] [CrossRef]
- Taylor, G. The Formation of Fog and Mist. Q. J. R. Meteorol. Soc. 2007, 43, 241–268. [Google Scholar] [CrossRef]
- Gultepe, I.; Milbrandt, J.A.; Zhou, B. Marine Fog: A Review on Microphysics and Visibility Prediction; Chapter Marine Fog: Challenges and Advancements in Observations, Modeling, and Forecasting; Springer: Berlin/Heidelberg, Germany, 2017; pp. 345–394. [Google Scholar]
- Pérez-Díaz, J.L.; Ivanov, O.; Peshev, Z.; Álvarez-Valenzuela, M.A.; Valiente-Blanco, I.; Evgenieva, T.; Dreischuh, T.; Gueorguiev, O.; Todorov, P.V.; Vaseashta, A. Fogs: Physical basis, characteristic properties, and impacts on the environment and human health. Water 2017, 9, 807. [Google Scholar] [CrossRef]
- Bari, D.; Bergot, T.; Tardif, R. Fog Decision Support Systems: A Review of the Current Perspectives. Atmosphere 2023, 14, 1314. [Google Scholar] [CrossRef]
- Ait Ouadil, K.; Idbraim, S.; Bouhsine, T.; Carla Bouaynaya, N.; Alfergani, H.; Cliff Johnson, C. Atmospheric visibility estimation: A review of deep learning approach. Multimed. Tools Appl. 2024, 83, 36261–36286. [Google Scholar] [CrossRef]
- Qu, Y.; Fang, Y.; Ji, S.; Cheng, Y.; Wu, H.; Zhu, S.; Qin, H.; Que, F. Deep Learning-Based Atmospheric Visibility Detection. Atmosphere 2024, 15, 1394. [Google Scholar] [CrossRef]
- Koziara, M.C.; Renard, R.J.; Thompson, W.J. Estimating marine fog probability using a model output statistics scheme. Mon. Weather Rev. 1983, 111, 2333–2340. [Google Scholar] [CrossRef]
- Tag, P.M.; Peak, J.E. Machine learning of maritime fog forecast rules. J. Appl. Meteorol. Climatol. 1996, 35, 714–724. [Google Scholar] [CrossRef]
- Fabbian, D.; Dear, R.; Lellyett, S. Application of Artificial Neural Network Forecasts to Predict Fog at Canberra International Airport. Weather Forecast. 2007, 22, 372–381. [Google Scholar] [CrossRef]
- Marzban, C.; Leyton, S.; Colman, B. Ceiling and visibility forecasts via neural networks. Weather Forecast. 2007, 22, 466–479. [Google Scholar] [CrossRef]
- Miao, Y.; Potts, R.; Huang, X.; Elliott, G.; Rivett, R. A fuzzy logic fog forecasting model for Perth Airport. Pure Appl. Geophys. 2012, 169, 1107–1119. [Google Scholar] [CrossRef]
- Dutta, D.; Chaudhuri, S. Nowcasting visibility during wintertime fog over the airport of a metropolis of India: Decision tree algorithm and artificial neural network approach. Nat. Hazards 2015, 75, 1349–1368. [Google Scholar] [CrossRef]
- Colabone, R.d.O.; Ferrari, A.L.; Vecchia, F.A.d.S.; Tech, A.R.B. Application of artificial neural networks for fog forecast. J. Aerosp. Technol. Manag. 2015, 7, 240–246. [Google Scholar] [CrossRef]
- Boneh, T.; Weymouth, G.T.; Newham, P.; Potts, R.; Bally, J.; Nicholson, A.E.; Korb, K.B. Fog forecasting for Melbourne Airport using a Bayesian decision network. Weather Forecast. 2015, 30, 1218–1233. [Google Scholar] [CrossRef]
- Bartoková, I.; Bott, A.; Bartok, J.; Gera, M. Fog prediction for road traffic safety in a coastal desert region: Improvement of nowcasting skills by the machine-learning approach. Bound.-Layer Meteorol. 2015, 157, 501–516. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Casanova-Mateo, C.; Sanz-Justo, J.; Cerro-Prada, E.; Salcedo-Sanz, S. Efficient prediction of low-visibility events at airports using machine-learning regression. Bound.-Layer Meteorol. 2017, 165, 349–370. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, G.; Han, L.; Wang, N. The Application of Deep Learning in Airport Visibility Forecast. Atmos. Clim. Sci. 2017, 7, 314. [Google Scholar] [CrossRef]
- Bari, D. Visibility Prediction Based on Kilometric NWP Model Outputs Using Machine-Learning Regression. In Proceedings of the 2018 IEEE 14th International Conference on E-Science (e-Science), Amsterdam, The Netherlands, 29 October–1 November 2018; IEEE: Piscataway, NJ, USA, 2018; p. 278. [Google Scholar]
- Durán-Rosal, A.M.; Fernández, J.C.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S.; Hervás-Martínez, C. Efficient Fog Prediction with Multi-Objective Evolutionary Neural Networks. Appl. Soft Comput. 2018, 70, 347–358. [Google Scholar] [CrossRef]
- Guijo-Rubio, D.; Gutiérrez, P.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S.; Hervás-Martínez, C. Prediction of low-visibility events due to fog using ordinal classification. Atmos. Res. 2018, 214, 64–73. [Google Scholar] [CrossRef]
- Palvanov, A.; Im Cho, Y. DHCNN for visibility estimation in foggy weather conditions. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 240–243. [Google Scholar]
- Dietz, S.J.; Kneringer, P.; Mayr, G.J.; Zeileis, A. Forecasting low-visibility procedure states with tree-based statistical methods. Pure Appl. Geophys. 2019, 176, 2631–2644. [Google Scholar] [CrossRef]
- Ortega, L.; Otero, L.D.; Otero, C. Application of Machine Learning Algorithms for Visibility Classification. In Proceedings of the 2019 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 8–11 April 2019; pp. 1–5. [Google Scholar]
- Zhang, C.; Wu, M.; Chen, J.; Chen, K.; Zhang, C.; Xie, C.; Huang, B.; He, Z. Weather Visibility Prediction Based on Multimodal Fusion. IEEE Access 2019, 7, 74776–74786. [Google Scholar] [CrossRef]
- Bari, D.; Ouagabi, A. Machine-Learning Regression Applied to Diagnose Horizontal Visibility from Mesoscale NWP Model Forecasts. SN Appl. Sci. 2020, 2, 556. [Google Scholar] [CrossRef]
- Jonnalagadda, J.; Hashemi, M. Forecasting atmospheric visibility using auto regressive recurrent neural network. In Proceedings of the 2020 IEEE 21st International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 11–13 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 209–215. [Google Scholar]
- Dewi, R.; Harsa, H. Fog prediction using artificial intelligence: A case study in Wamena Airport. J. Phys. Conf. Ser. 2020, 1528, 012021. [Google Scholar] [CrossRef]
- Cornejo-Bueno, S.; Casillas-Pérez, D.; Cornejo-Bueno, L.; Chidean, M.I.; Caamaño, A.J.; Sanz-Justo, J.; Casanova-Mateo, C.; Salcedo-Sanz, S. Persistence analysis and prediction of low-visibility events at Valladolid Airport, Spain. Symmetry 2020, 12, 1045. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Piles, M.; Cuadra, L.; Casanova-Mateo, C.; Caamano, A.J.; Cerro-Prada, E.; Camps-Valls, G. Long-Term Persistence, Invariant Time Scales and on-off Intermittency of Fog Events. Atmos. Res. 2021, 252, 105456. [Google Scholar] [CrossRef]
- Shankar, A.; Sahana, B.C.; Singh, S.P. Prediction of Low-Visibility Events by Integrating the Potential of Persistence and Machine Learning for Aviation Services. Mausam 2024, 75, 977–992. [Google Scholar]
- Miao, K.C.; Han, T.T.; Yao, Y.Q.; Lu, H.; Chen, P.; Wang, B.; Zhang, J. Application of LSTM for Short Term Fog Forecasting Based on Meteorological Elements. Neurocomputing 2020, 408, 285–291. [Google Scholar] [CrossRef]
- Cornejo-Bueno, S.; Casillas-Pérez, D.; Cornejo-Bueno, L.; Chidean, M.I.; Caamaño, A.J.; Cerro-Prada, E.; Casanova-Mateo, C.; Salcedo-Sanz, S. Statistical analysis and machine learning prediction of fog-caused low-visibility events at A-8 motor-road in Spain. Atmosphere 2021, 12, 679. [Google Scholar] [CrossRef]
- Kim, B.Y.; Cha, J.W.; Chang, K.H.; Lee, C. Visibility Prediction over South Korea Based on Random Forest. Atmosphere 2021, 12, 552. [Google Scholar] [CrossRef]
- Lee, H.B.; Heo, J.H.; Sohn, E.H. Korean fog probability retrieval using remote sensing combined with machine-learning. GIScience Remote Sens. 2021, 58, 1434–1457. [Google Scholar] [CrossRef]
- Outay, F.; Taha, B.; Chaabani, H.; Kamoun, F.; Werghi, N.; Yasar, A.U.H. Estimating ambient visibility in the presence of fog: A deep convolutional neural network approach. Pers. Ubiquitous Comput. 2021, 25, 51–62. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine Learning Based Visibility Estimation to Ensure Safer Navigation in Strait of Istanbul. Appl. Ocean Res. 2021, 112, 102693. [Google Scholar] [CrossRef]
- Yu, Z.; Qu, Y.; Wang, Y.; Ma, J.; Cao, Y. Application of machine-learning-based fusion model in visibility forecast: A case study of Shanghai, China. Remote Sens. 2021, 13, 2096. [Google Scholar] [CrossRef]
- Guo, X.; Wan, J.; Liu, S.; Xu, M.; Sheng, H.; Yasir, M. A scse-linknet deep learning model for daytime sea fog detection. Remote Sens. 2021, 13, 5163. [Google Scholar] [CrossRef]
- Bartok, J.; Šišan, P.; Ivica, L.; Bartoková, I.; Malkin Ondík, I.; Gaál, L. Machine learning-based fog nowcasting for aviation with the aid of camera observations. Atmosphere 2022, 13, 1684. [Google Scholar] [CrossRef]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Ghimire, S.; Cerro-Prada, E.; Gutierrez, P.; Deo, R.; Salcedo-Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhu, Y.; Yang, L.; Ge, L.; Luo, C. Visibility prediction based on machine learning algorithms. Atmosphere 2022, 13, 1125. [Google Scholar] [CrossRef]
- Kim, B.Y.; Belorid, M.; Cha, J.W. Short-Term Visibility Prediction Using Tree-Based Machine Learning Algorithms and Numerical Weather Prediction Data. Weather Forecast. 2022, 37, 2263–2274. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, G.; Yang, J.; Wang, S.; Xue, B.; Du, X.; Tian, Y.; Wang, K.; Jiang, R.; Gao, J. Temporal and Spatial Characteristics of Meteorological Elements in the Vertical Direction at Airports and Hourly Airport Visibility Prediction by Artificial Intelligence Methods. Sustainability 2022, 14, 12213. [Google Scholar] [CrossRef]
- Kim, B.Y.; Cha, J.W.; Chang, K.H.; Lee, C. Estimation of the Visibility in Seoul, South Korea, Based on Particulate Matter and Weather Data, Using Machine-Learning Algorithm. Aerosol Air Qual. Res. 2022, 22, 220125. [Google Scholar] [CrossRef]
- Choi, W.; Park, J.; Kim, D.; Park, J.; Kim, S.; Lee, H. Development of two-dimensional visibility estimation model using machine learning: Preliminary results for South Korea. Atmosphere 2022, 13, 1233. [Google Scholar] [CrossRef]
- Kim, S.; Rickard, C.; Hernandez-Vazquez, J.; Fernandez, D. Early night fog prediction using liquid water content measurement in the monterey bay area. Atmosphere 2022, 13, 1332. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.H.; Seo, H.W.; Wang, Y.V.; Lee, Y.G. Meteorological characteristics of fog events in Korean smart cities and machine learning based visibility estimation. Atmos. Res. 2022, 275, 106239. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, G.; Wang, S.; Xue, B.; Yang, J.; Gao, J.; Wang, K.; Jiang, R.; Zhu, X. Forecast of hourly airport visibility based on artificial intelligence methods. Atmosphere 2022, 13, 75. [Google Scholar] [CrossRef]
- Park, J.; Lee, Y.J.; Jo, Y.; Kim, J.; Han, J.H.; Kim, K.J.; Kim, Y.T.; Kim, S.B. Spatio-Temporal Network for Sea Fog Forecasting. Sustainability 2022, 14, 16163. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Gu, X.; Yeoh, J.K.; Zhang, Q. Visibility classification and influencing-factors analysis of airport: A deep learning approach. Atmos. Environ. 2022, 278, 119085. [Google Scholar] [CrossRef]
- Negishi, M.; Kusaka, H. Development of statistical and machine learning models to predict the occurrence of radiation fog in Japan. Meteorol. Appl. 2022, 29, e2048. [Google Scholar] [CrossRef]
- Bari, D.; Lasri, N.; Souri, R.; Lguensat, R. Machine Learning for Fog-and-Low-Stratus Nowcasting from Meteosat SEVIRI Satellite Images. Atmosphere 2023, 14, 953. [Google Scholar] [CrossRef]
- Wen, W.; Li, L.; Chan, P.W.; Liu, Y.Y.; Wei, M. Research on the Usability of Different Machine Learning Methods in Visibility Forecasting. Atmósfera 2023, 37. [Google Scholar]
- Liang, C.W.; Chang, C.C.; Hsiao, C.Y.; Liang, C.J. Prediction and analysis of atmospheric visibility in five terrain types with artificial intelligence. Heliyon 2023, 9, e19281. [Google Scholar] [CrossRef] [PubMed]
- Shankar, A.; Sahana, B. Early Warning of Low Visibility Using the Ensembling of Machine Learning Approaches for Aviation Services at Jay Prakash Narayan International (JPNI) Airport Patna. SN Appl. Sci. 2023, 5, 132. [Google Scholar] [CrossRef]
- Shankar, A.; Sahana, B. Efficient prediction of runway visual range by using a hybrid CNN-LSTM network architecture for aviation services. Theor. Appl. Climatol. 2023, 155, 2215–2232. [Google Scholar] [CrossRef]
- Ortega, L.C.; Otero, L.D.; Solomon, M.; Otero, C.E.; Fabregas, A. Deep Learning Models for Visibility Forecasting Using Climatological Data. Int. J. Forecast. 2023, 39, 992–1004. [Google Scholar] [CrossRef]
- Peláez-Rodríguez, C.; Pérez-Aracil, J.; de Lopez-Diz, A.; Casanova-Mateo, C.; Fister, D.; Jiménez-Fernández, S.; Salcedo-Sanz, S. Deep learning ensembles for accurate fog-related low-visibility events forecasting. Neurocomputing 2023, 549, 126435. [Google Scholar] [CrossRef]
- Peláez-Rodríguez, C.; Marina, C.M.; Pérez-Aracil, J.; Casanova-Mateo, C.; Salcedo-Sanz, S. Extreme Low-Visibility Events Prediction Based on Inductive and Evolutionary Decision Rules: An Explicability-Based Approach. Atmosphere 2023, 14, 542. [Google Scholar] [CrossRef]
- Zang, Z.; Bao, X.; Li, Y.; Qu, Y.; Niu, D.; Liu, N.; Chen, X. A modified RNN-based deep learning method for prediction of atmospheric visibility. Remote Sens. 2023, 15, 553. [Google Scholar] [CrossRef]
- Zhai, B.; Wang, Y.; Wu, B. An ensemble learning method for low visibility prediction on freeway using meteorological data. IET Intell. Transp. Syst. 2023, 17, 2237–2250. [Google Scholar] [CrossRef]
- Zhen, M.; Yi, M.; Luo, T.; Wang, F.; Yang, K.; Ma, X.; Cui, S.; Li, X. Application of a Fusion Model Based on Machine Learning in Visibility Prediction. Remote Sens. 2023, 15, 1450. [Google Scholar] [CrossRef]
- Penov, N.; Guerova, G. Sofia Airport Visibility Estimation with Two Machine-Learning Techniques. Remote Sens. 2023, 15, 4799. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, F.; Ren, J.; Li, Z.; Xu, W.; Sun, Y.; Liu, L.; Wang, X. Changes in wintertime visibility across China over 2013–2019 and the drivers: A comprehensive assessment using machine learning method. Sci. Total Environ. 2024, 912, 169516. [Google Scholar] [CrossRef]
- Son, D.H.; Chun, M.; Kim, Y.T.; Kang, B.; Kim, K.J.; Han, J.H. FogFusionNet: Coastal Sea Fog Prediction by Using a Multimodal Deep Learning Approach. IEEE Access 2024, 12, 137491–137503. [Google Scholar] [CrossRef]
- Gultepe, E.; Wang, S.; Blomquist, B.; Fernando, H.J.; Kreidl, O.P.; Delene, D.J.; Gultepe, I. Machine learning analysis and nowcasting of marine fog visibility using FATIMA Grand Banks campaign measurements. Front. Earth Sci. 2024, 11, 1321422. [Google Scholar] [CrossRef]
- Huang, Q.; Zeng, P.; Guo, X.; Lyu, J. Utilizing Machine Learning and Multi-Station Observations to Investigate the Visibility of Sea Fog in the Beibu Gulf. Remote Sens. 2024, 16, 3392. [Google Scholar] [CrossRef]
- Sim, S.; Im, J.; Jung, S.; Han, D. Improving Short-Term Prediction of Ocean Fog Using Numerical Weather Forecasts and Geostationary Satellite-Derived Ocean Fog Data Based on AutoML. Remote Sens. 2024, 16, 2348. [Google Scholar] [CrossRef]
- Schütz, M.; Schütz, A.; Bendix, J.; Thies, B. Improving classification-based nowcasting of radiation fog with machine learning based on filtered and preprocessed temporal data. Q. J. R. Meteorol. Soc. 2024, 150, 577–596. [Google Scholar] [CrossRef]
- Jahani, B.; Karalus, S.; Fuchs, J.; Zech, T.; Zara, M.; Cermak, J. Algorithm for continual monitoring of fog life cycles based on geostationary satellite imagery as a basis for solar energy forecasting. EGUsphere 2024, 2024, 1–22. [Google Scholar] [CrossRef]
- Chen, P.J.; Chen, W.T.; Wu, C.M.; Tsou, S.W.; Lo, M.H. Machine learning detection of fog top over eastern Taiwan mountains from Himawari-8 satellite true-color images. Remote Sens. Appl. Soc. Environ. 2024, 34, 101203. [Google Scholar] [CrossRef]
- Kim, J.; Cha, J.; Kim, T.; Lee, H.; Yu, H.Y.; Suh, M.S. VisNet: Spatiotemporal self-attention-based U-Net with multitask learning for joint visibility and fog occurrence forecasting. Eng. Appl. Artif. Intell. 2024, 136, 108967. [Google Scholar] [CrossRef]
- Yuan, C.; Li, L.; Xia, X.; Xiong, D.; Li, Y.; Hu, J.; Li, H.; Zuo, C. Enhancing Road Safety: Real-Time Classification of Low Visibility Foggy Weather Using ABNet Deep-Learning Model. J. Transp. Eng. Part A Syst. 2024, 150, 04024060. [Google Scholar] [CrossRef]
- He, D.; Wang, Y.; Tang, Y.; Kong, D.; Yang, J.; Zhou, W.; Li, H.; Wang, F. Improvement in the Forecasting of Low Visibility over Guizhou, China, Based on a Multi-Variable Deep Learning Model. Atmosphere 2024, 15, 752. [Google Scholar] [CrossRef]
- Alhathloul, S.H.; Mishra, A.K.; Khan, A.A. Low visibility event prediction using random forest and K-nearest neighbor methods. Theor. Appl. Climatol. 2024, 155, 1289–1300. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Gao, Z.; Kang, J.; Jiang, Y.; Li, Z.; Shen, H. Visibility forecast in Jiangsu province based on the GCN-GRU model. Sci. Rep. 2024, 14, 12599. [Google Scholar] [CrossRef]
- Aman, N.; Panyametheekul, S.; Sudhibrabha, S.; Pawarmart, I.; Xian, D.; Gao, L.; Tian, L.; Manomaiphiboon, K.; Wang, Y. Estimating visibility and understanding factors influencing its variations at Bangkok airport using machine learning and a game theory–based approach. Environ. Sci. Pollut. Res. 2024, 1–18. [Google Scholar] [CrossRef]
- Yang, L.; Li, R.; Qiu, X.; Bi, C. BLCM: A BP-LGBM-based atmospheric visibility forecasting model. J. Vis. 2024, 27, 997–1014. [Google Scholar] [CrossRef]
- Wang, F.; Liu, R.; Yan, H.; Liu, D.; Han, L.; Yuan, S. Ground visibility prediction using tree-based and random-forest machine learning algorithm: Comparative study based on atmospheric pollution and atmospheric boundary layer data. Atmos. Pollut. Res. 2024, 15, 102270. [Google Scholar] [CrossRef]
- Tian, W.; Lin, C.; Wu, Y.; Jin, C.; Li, X. Multi-site collaborative forecasting of regional visibility based on spatiotemporal convolutional network. Meteorol. Appl. 2024, 31, e2206. [Google Scholar] [CrossRef]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th international conference on information and communication systems (ICICS), Irbid, Jordan, 7–9 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 243–248. [Google Scholar]
- Peng, C.Y.; Park, Y.J. A new hybrid under-sampling approach to imbalanced classification problems. Appl. Artif. Intell. 2022, 36, 1975393. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Z.; Wang, D. RFCL: A new under-sampling method of reducing the degree of imbalance and overlap. Pattern Anal. Appl. 2021, 24, 641–654. [Google Scholar] [CrossRef]
- Bej, S.; Davtyan, N.; Wolfien, M.; Nassar, M.; Wolkenhauer, O. LoRAS: An oversampling approach for imbalanced datasets. Mach. Learn. 2021, 110, 279–301. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Rodríguez-Torres, F.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A. An oversampling method for class imbalance problems on large datasets. Appl. Sci. 2022, 12, 3424. [Google Scholar] [CrossRef]
- Alamri, M.; Ykhlef, M. Hybrid undersampling and oversampling for handling imbalanced credit card data. IEEE Access 2024, 12, 14050–14060. [Google Scholar] [CrossRef]
- Tomek, I. Two modifications of CNN. IEEE Trans. Syst. Man, Cybern. 1976, 6, 769–772. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Ningbo, China, 26–29 July 2025; Springe: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Yilmaz Eroglu, D.; Pir, M.S. Hybrid oversampling and undersampling method (houm) via safe-level smote and support vector machine. Appl. Sci. 2024, 14, 10438. [Google Scholar] [CrossRef]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. Safe-level-smote: Safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand, 27–30 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 475–482. [Google Scholar]
- Koçyiğit, F. The Effect of Meteorological Data on Energy Efficiency and Flight Performance in Sustainable Aviation. J. Aviat. 2025, 9, 295–302. [Google Scholar] [CrossRef]
- Teshiba, M.; Hashiguchi, H.; Uematsu, A.; Tanaka, H.; Ohmori, Y.; Fukao, S. Fog observations with a millimeter-wave scanning radar at Miyoshi basin, Japan. Earth Planets Space 2004, 56, 259–268. [Google Scholar] [CrossRef]
- Fernando, H.J.; Gultepe, I.; Dorman, C.; Pardyjak, E.; Wang, Q.; Hoch, S.; Richter, D.; Creegan, E.; Gaberšek, S.; Bullock, T.; et al. C-FOG: Life of coastal fog. Bull. Am. Meteorol. Soc. 2021, 102, E244–E272. [Google Scholar] [CrossRef]
- Gultepe, I.; Heymsfield, A.J.; Fernando, H.; Pardyjak, E.; Dorman, C.; Wang, Q.; Creegan, E.; Hoch, S.; Flagg, D.; Yamaguchi, R.; et al. A review of coastal fog microphysics during C-FOG. Bound.-Layer Meteorol. 2021, 181, 227–265. [Google Scholar] [CrossRef]
- Müller, M.D.; Masbou, M.; Bott, A. Three-dimensional fog forecasting in complex terrain. Q. J. R. Meteorol. Soc. 2010, 136, 2189–2202. [Google Scholar] [CrossRef]
- Willett, H.C. Synoptic Studies in Fog; Massachusetts Institute of Technology: Cambridge, MA, USA, 1930. [Google Scholar]
- Kim, C.K.; Yum, S.S. Local meteorological and synoptic characteristics of fogs formed over Incheon international airport in the west coast of Korea. Adv. Atmos. Sci. 2010, 27, 761–776. [Google Scholar] [CrossRef]
- Andersen, H.; Cermak, J.; Fuchs, J.; Knippertz, P.; Gaetani, M.; Quinting, J.; Sippel, S.; Vogt, R. Synoptic-scale controls of fog and low-cloud variability in the Namib Desert. Atmos. Chem. Phys. 2020, 20, 3415–3438. [Google Scholar] [CrossRef]
- Fonseca, R.; Francis, D.; Nelli, N.; Cherif, C. Regional atmospheric circulation patterns driving consecutive fog events in the United Arab Emirates. Atmos. Res. 2023, 282, 106506. [Google Scholar] [CrossRef]
- Corell, D.; Estrela, M.J.; Valiente, J.A.; Azorin-Molina, C.; Chen, D. Influences of synoptic situation and teleconnections on fog-water collection in the Mediterranean Iberian Peninsula, 2003–2012. Int. J. Climatol. 2019, 40, 3297–3317. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Peláez-Rodríguez, C.; Pérez-Aracil, J.; Casanova-Mateo, C.; Salcedo-Sanz, S. Efficient prediction of fog-related low-visibility events with Machine Learning and evolutionary algorithms. Atmos. Res. 2023, 295, 106991. [Google Scholar] [CrossRef]
- Gutiérrez, P.A.; Perez-Ortiz, M.; Sanchez-Monedero, J.; Fernandez-Navarro, F.; Hervas-Martinez, C. Ordinal regression methods: Survey and experimental study. IEEE Trans. Knowl. Data Eng. 2015, 28, 127–146. [Google Scholar] [CrossRef]
- Sánchez-Monedero, J.; Gutiérrez, P.A.; Pérez-Ortiz, M. Orca: A matlab/octave toolbox for ordinal regression. J. Mach. Learn. Res. 2019, 20, 1–5. [Google Scholar]
- Bérchez-Moreno, F.; Ayllón-Gavilán, R.; Vargas, V.M.; Guijo-Rubio, D.; Hervás-Martínez, C.; Fernández, J.C.; Gutiérrez, P.A. dlordinal: A Python package for deep ordinal classification. Neurocomputing 2024, 622, 129305. [Google Scholar] [CrossRef]
- Binotto, G.; Delgado, R. Adapting performance metrics for ordinal classification to interval scale: Length matters. Mach. Learn. 2025, 114, 41. [Google Scholar] [CrossRef]
- Rennie, J.D.; Srebro, N. Loss functions for preference levels: Regression with discrete ordered labels. In Proceedings of the IJCAI Multidisciplinary Workshop on Advances in Preference Handling, Edinburgh, UK, 31 July–1 August 2005; AAAI Press: Menlo Park, CA, USA, 2005; Volume 1, pp. 1–6. [Google Scholar]
- Pedregosa, F.; Bach, F.; Gramfort, A. On the consistency of ordinal regression methods. J. Mach. Learn. Res. 2017, 18, 1–35. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Applications to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Middlehurst, M.; Bagnall, A. The freshprince: A simple transformation based pipeline time series classifier. In Proceedings of the International Conference on Pattern Recognition and Artificial Intelligence, Xiamen China, 23–25 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 150–161. [Google Scholar]
- Peralez-González, C.; Pérez-Rodríguez, J.; Durán-Rosal, A.M. Boosting ridge for the extreme learning machine globally optimised for classification and regression problems. Sci. Rep. 2023, 13, 11809. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Cheng, Q. Discriminative ridge machine: A classifier for high-dimensional data or imbalanced data. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 2595–2609. [Google Scholar] [CrossRef] [PubMed]
- Vargas, V.M.; Gómez-Orellana, A.M.; Gutiérrez, P.A.; Hervás-Martínez, C.; Guijo-Rubio, D. EBANO: A novel Ensemble BAsed on uNimodal Ordinal classifiers for the prediction of significant wave height. Knowl.-Based Syst. 2024, 300, 112223. [Google Scholar] [CrossRef]
- Rosati, R.; Romeo, L.; Vargas, V.M.; Gutiérrez, P.A.; Hervás-Martínez, C.; Frontoni, E. A novel deep ordinal classification approach for aesthetic quality control classification. Neural Comput. Appl. 2022, 34, 11625–11639. [Google Scholar] [CrossRef]
- Fernández, J.C.; Martínez, F.J.; Hervás, C.; Gutiérrez, P.A. Sensitivity versus accuracy in multiclass problems using memetic pareto evolutionary neural networks. IEEE Trans. Neural Netw. 2010, 21, 750–770. [Google Scholar] [CrossRef]
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The balanced accuracy and its posterior distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3121–3124. [Google Scholar] [CrossRef]
- de La Torre, J.; Puig, D.; Valls, A. Weighted kappa loss function for multi-class classification of ordinal data in deep learning. Pattern Recognit. Lett. 2018, 105, 144–154. [Google Scholar] [CrossRef]
- Gómez-Orellana, A.M.; Guijo-Rubio, D.; Gutiérrez, P.A.; Hervás-Martínez, C.; Vargas, V.M. ORFEO: Ordinal classifier and Regressor Fusion for Estimating an Ordinal categorical target. Eng. Appl. Artif. Intell. 2024, 133, 108462. [Google Scholar] [CrossRef]



| Case Study | Class | Training Set | Testing Set |
|---|---|---|---|
| LEST | 1407 (1.53 %) | 386 (1.26 %) | |
| 939 (1.02 %) | 230 (0.75 %) | ||
| 9588 (10.42 %) | 2957 (9.64 %) | ||
| 80,099 (87.03 %) | 27,105 (88.35 %) | ||
| LEVX | 4506 (4.89 %) | 1853 (6.04 %) | |
| 1904 (2.07 %) | 634 (2.07 %) | ||
| 8979 (9.76 %) | 2128 (6.93 %) | ||
| 76,644 (83.28 %) | 26,063 (84.96 %) |
| Acronym | Description | Units |
|---|---|---|
| D | Wind direction | Degrees |
| S | Wind speed | m/s |
| T | Temperature | Celsius |
| De | Dew point | Celsius |
| P | Pressure | hPa |
| Visibility | m |
| Case Study | Classifier | CCR (↑) | MS (↑) | BA (↑) | QWK (↑) | AMAE (↓) | MMAE (↓) |
|---|---|---|---|---|---|---|---|
| LEST | LAT | 0.8372 | 0.2783 | 0.5696 | 0.6162 | 0.5263 | 0.8000 |
| Ridge | 0.8792 | 0.0174 | 0.5647 | 0.5969 | 0.6088 | 1.1478 | |
| LEVX | LAT | 0.8251 | 0.2571 | 0.5482 | 0.7327 | 0.5776 | 0.8297 |
| Ridge | 0.8712 | 0.2240 | 0.5295 | 0.7174 | 0.6586 | 1.0000 |
| LAT | Ridge | |||||||
|---|---|---|---|---|---|---|---|---|
| 247 | 74 | 42 | 23 | 308 | 10 | 22 | 46 | |
| 110 | 64 | 38 | 18 | 160 | 4 | 28 | 38 | |
| 180 | 728 | 1408 | 641 | 622 | 73 | 1526 | 736 | |
| 78 | 290 | 2771 | 23,966 | 287 | 46 | 1637 | 25,135 | |
| LAT | B | |||||||
|---|---|---|---|---|---|---|---|---|
| 1237 | 298 | 241 | 77 | 1268 | 284 | 83 | 218 | |
| 281 | 163 | 135 | 55 | 321 | 142 | 64 | 107 | |
| 358 | 530 | 813 | 427 | 552 | 318 | 552 | 706 | |
| 299 | 323 | 2342 | 23,099 | 473 | 197 | 629 | 24,764 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salcedo-Sanz, S.; Guijo-Rubio, D.; Pérez-Aracil, J.; Peláez-Rodríguez, C.; Gomez-Orellana, A.M.; Gutiérrez-Peña, P.A. Artificial Intelligence-Based Methods and Algorithms in Fog and Atmospheric Low-Visibility Forecasting. Atmosphere 2025, 16, 1073. https://doi.org/10.3390/atmos16091073
Salcedo-Sanz S, Guijo-Rubio D, Pérez-Aracil J, Peláez-Rodríguez C, Gomez-Orellana AM, Gutiérrez-Peña PA. Artificial Intelligence-Based Methods and Algorithms in Fog and Atmospheric Low-Visibility Forecasting. Atmosphere. 2025; 16(9):1073. https://doi.org/10.3390/atmos16091073
Chicago/Turabian StyleSalcedo-Sanz, Sancho, David Guijo-Rubio, Jorge Pérez-Aracil, César Peláez-Rodríguez, Antonio Manuel Gomez-Orellana, and Pedro Antonio Gutiérrez-Peña. 2025. "Artificial Intelligence-Based Methods and Algorithms in Fog and Atmospheric Low-Visibility Forecasting" Atmosphere 16, no. 9: 1073. https://doi.org/10.3390/atmos16091073
APA StyleSalcedo-Sanz, S., Guijo-Rubio, D., Pérez-Aracil, J., Peláez-Rodríguez, C., Gomez-Orellana, A. M., & Gutiérrez-Peña, P. A. (2025). Artificial Intelligence-Based Methods and Algorithms in Fog and Atmospheric Low-Visibility Forecasting. Atmosphere, 16(9), 1073. https://doi.org/10.3390/atmos16091073










