Abstract
Remote sensing image dehazing presents substantial challenges in balancing physical fidelity with generative flexibility, particularly under complex atmospheric conditions and sensor-specific degradation patterns. Traditional physics-based methods often struggle with nonlinear haze distributions, while purely data-driven approaches tend to lack interpretability and physical consistency. To bridge this gap, we propose the Atmospheric Scattering Prior embedded Diffusion Model (ASPDiff), a novel framework that seamlessly integrates atmospheric physics into the diffusion-based generative restoration process. ASPDiff establishes a closed-loop feedback mechanism by embedding the atmospheric scattering model as a physics-driven regularization throughout both the forward degradation simulation and the reverse denoising trajectory. The framework operates through the following three synergistic components: (1) an Atmospheric Prior Estimation Module that uses the Dark Channel Prior to generate initial estimates of the transmission map and global atmospheric light, which are then refined through learnable adjustment networks; (2) a Diffusion Process with Atmospheric Prior Embedding, where the refined priors serve as conditional guidance during the reverse diffusion sampling, ensuring physical plausibility; and (3) a Haze-Aware Refinement Module that adaptively enhances structural details and compensates for residual haze via frequency-aware decomposition and spatial attention. Extensive experiments on both synthetic and real-world remote sensing datasets demonstrate that ASPDiff significantly outperforms existing methods, achieving state-of-the-art performance while maintaining strong physical interpretability.
1. Introduction
Remote sensing imagery plays a vital role in a wide range of applications, including environmental monitoring, disaster response, precision agriculture, and urban planning. The reliability and effectiveness of these applications heavily rely on the clarity, structural integrity, and radiometric fidelity of the captured images. However, real-world remote sensing images are frequently degraded by atmospheric phenomena—particularly haze and fog—caused by the scattering and absorption of light by suspended particles in the air. These degradations not only reduce contrast and obscure fine details but also severely impair the performance of downstream vision tasks such as object detection [1], land cover classification [2], and change detection [3].
Early research in remote sensing image dehazing (RSID) was largely dominated by traditional physics-based models, most notably those derived from the Atmospheric Scattering Model (ASM) [4]. This model describes the observed hazy image as a linear combination of attenuated scene radiance and globally scattered airlight. Classical methods such as the Dark Channel Prior (DCP) [5], color attenuation prior [6], haze-line [7], and contrast enhancement [8] estimate the transmission map and atmospheric light from the input image, and then invert the ASM to recover the clean image. These approaches offer strong physical interpretability and can perform well under simplified conditions such as homogeneous haze and stable lighting. However, they suffer from fundamental limitations. Their underlying assumptions are often violated in remote sensing scenarios, where haze can vary dramatically with altitude, topography, and surface composition. These methods are also highly sensitive to estimation inaccuracies, which can result in artifacts such as halos, color shifts, and over-enhancement. Moreover, their lack of adaptability to sensor-specific properties—such as spatial resolution, noise distribution, and spectral variation—further limits their applicability in large-scale Earth observation tasks.
With the rapid advancement of deep learning, data-driven methods [9,10,11,12,13] have significantly improved single image dehazing by learning complex nonlinear mappings between hazy and clean images in an end-to-end manner. Early convolutional neural network (CNN) models, such as DehazeNet [14] and AOD-Net [15], replaced hand-crafted priors with learned features, enabling better generalization and robustness. Later developments incorporated architectural innovations, including dense connections, attention mechanisms, and multi-scale features. Transformer-based models like sdbadNet [9] and DehazeFormer [16] further pushed the frontier by capturing long-range dependencies and modeling global context. These approaches have demonstrated compelling perceptual performance on natural image datasets, delivering enhanced contrast and texture fidelity. However, despite these successes, their direct application to remote sensing image dehazing (RSID) remains suboptimal. Unlike natural images, remote sensing imagery [17,18] exhibits complex and non-uniform haze distributions caused by variations in altitude, terrain, and atmospheric composition. Additionally, the orthographic perspective and spectral diversity of aerial images reduce the efficacy of semantic priors, which are often implicitly exploited in natural image models. Moreover, many deep learning-based methods prioritize visual enhancement but lack physically grounded constraints. This often results in oversaturated colors, structural distortions, or loss of radiometric consistency issues that are particularly detrimental in downstream tasks such as land cover classification, object detection, and change analysis. Furthermore, most of these models follow a single-pass processing strategy, making it difficult to adaptively correct spatially varying haze patterns across large-scale scenes.
In this context, Denoising Diffusion Probabilistic Models (DDPMs) [19] have emerged as a promising alternative, especially for image restoration tasks. Unlike conventional feed-forward networks, diffusion models [20,21,22,23] progressively denoise a signal through a series of stochastic transitions, allowing them to better capture the data distribution and preserve intricate structures. Their iterative nature is well-aligned with haze removal, where gradual refinement can facilitate more accurate recovery of depth cues and luminance variations. Recent explorations have adapted diffusion models to low-level vision problems, including low-light enhancement [21], image inpainting [22], and dehazing [23]. For instance, FourierDiff [21] introduces frequency-domain guidance to jointly recover high-frequency structure and brightness, while Diff-Dehazer [23] leverages diffusion’s capacity for perceptual realism to generate clean outputs. Nevertheless, existing diffusion-based methods [21,23] typically treat dehazing as a pure data-driven generation process, and do not incorporate physical principles of atmospheric scattering. This becomes a critical limitation in the remote sensing domain, where haze formation is governed by physics-based processes such as light attenuation and airlight scattering. Ignoring these underlying mechanisms often leads to inconsistent or non-interpretable results, especially in regions with strong haze gradients or low visibility.
To address these challenges, we propose ASPDiff—an Atmospheric Scattering Prior embedded Diffusion Model—that seamlessly integrates physical modeling with a generative diffusion framework tailored for remote sensing image dehazing. ASPDiff introduces three interlinked components: the Atmospheric Prior Estimation Module (APEM), the Diffusion with Atmospheric Prior Embedding (DAPE), and the Haze-Aware Refinement Module (HARM). Specifically, APEM uses the dark channel prior to obtain initial estimates of the transmission map and global atmospheric light, which are then refined via learnable networks to correct common failure cases such as overestimation in bright or complex regions. These refined priors are supervised with physically consistent losses derived from the atmospheric scattering model. The DAPE component then embeds these priors as conditional inputs into the reverse diffusion process, guiding generation toward physically plausible and spatially coherent dehazed outputs. Finally, to restore high-frequency textures and mitigate haze-induced structural degradation, HARM leverages Discrete Cosine Transform (DCT)-based frequency decomposition and SimAM-based spatial attention, adaptively enhancing regions with dense haze or fine structural details. By establishing a closed-loop interaction between atmospheric physics and deep generative modeling, ASPDiff achieves both high restoration accuracy and strong physical interpretability. Extensive experiments on synthetic and real-world remote sensing datasets demonstrate that our method consistently outperforms state-of-the-art approaches across quantitative metrics and visual quality. Our main contributions are summarized as follows:
- We propose ASPDiff, a novel Atmospheric Scattering Prior embedded Diffusion Model for remote sensing image dehazing.
- We design an Atmospheric Prior Estimation Module (APEM) that leverages the dark channel prior for initial transmission and atmospheric light estimation, and introduces learnable refinement networks supervised by physical consistency loss, enabling robust and interpretable prior modeling in complex remote sensing scenes.
- We develop a prior-guided conditional diffusion mechanism (DAPE), where refined atmospheric priors are embedded into each denoising step to guide the generation trajectory, aligning the stochastic sampling process with physical degradation laws.
- We introduce a Haze-Aware Refinement Module (HARM) that enhances high-frequency textures and local contrast using DCT-based spectral decomposition and SimAM-based spatial attention, improving structural fidelity in severely degraded regions.
- We conduct extensive experiments on several remote sensing datasets. The results show that ASPDiff outperforms state-of-the-art methods both quantitatively and qualitatively, and ablation studies confirm the effectiveness of each proposed component.
The remainder of this paper is organized as follows. Section 2 reviews related work on physics-based dehazing, natural/remote-sensing single-image dehazing, and diffusion-based restoration, with emphasis on ASM-aware diffusion. Section 3 presents the proposed ASPDiff framework, detailing (i) the Atmospheric-Prior Estimation Module (APEM), (ii) the Diffusion with Atmospheric-Prior Embedding (DAPE), and (iii) the Haze-Aware Refinement Module (HARM). Section 4 describes datasets, evaluation metrics, and implementation details, including training and inference settings. Section 5 reports comprehensive experiments: quantitative/qualitative comparisons with state-of-the-art methods, ablation studies on prior estimation, reverse-step conditioning, and frequency refinement, and generalization to real remote-sensing scenes. Section 6 discusses conclusion and future directions.
2. Related Works
This section positions our work within the literature on physics-based dehazing, natural-image single-image dehazing, remote-sensing dehazing, and diffusion-based restoration. We pay particular attention to ASM-aware diffusion methods, which motivates our design choices and clarifies how ASPDiff differs from prior art.
2.1. Traditional Physics-Based Approaches
Traditional image dehazing methods are predominantly grounded in the Atmospheric Scattering Model (ASM), which models the formation of hazy images as the result of light attenuation and airlight accumulation caused by particles in the atmosphere. The widely adopted formulation is expressed as follows:
where denotes the observed hazy image, is the unknown scene radiance, represents the medium transmission describing the portion of light that reaches the camera, and refers to the global atmospheric light. Recovering a clean image thus requires accurate estimation of both and , which is inherently ill-posed.
One of the most influential priors for solving this inverse problem is the Dark Channel Prior (DCP) [5], which leverages the observation that in most haze-free outdoor images, at least one color channel in a local patch tends to have very low intensity. This assumption enables coarse yet effective estimation of dense haze regions and transmission maps. Several improvements and alternative priors have since been proposed, such as the Color Attenuation Prior (CAP) [6], which builds a linear model between depth and color attenuation; Boundary Constrained Context Regularization, which incorporates edge-aware smoothness; and Non-local Dehazing, which aggregates long-range dependencies to better preserve structures and semantics.
Despite their interpretability and low computational cost, these physics-based methods exhibit critical limitations when applied to remote sensing imagery. Firstly, their foundational assumptions—such as the existence of dark pixels in local patches or uniform atmospheric conditions—are often violated in overhead imagery. For example, rooftops, deserts, snowfields, and water bodies frequently exhibit high albedo or reflectance, which breaks the DCP assumption and results in inaccurate transmission estimation. Additionally, remote sensing images often feature complex terrain with significant elevation changes, leading to vertical variations in haze density that contradict the homogeneous medium assumption used in many traditional models. Moreover, remote sensing imagery brings unique challenges that these methods do not account for. These include the need to preserve radiometric fidelity for quantitative analysis, handle high spatial resolutions, and maintain spectral alignment across multiple bands. Traditional dehazing methods, designed primarily for natural photography, often fail to generalize in such contexts and can introduce artifacts that undermine the accuracy of downstream applications such as land cover classification, object detection, or environmental monitoring.
2.2. Natural Single-Image Dehazing
In recent years, deep learning-based dehazing methods have evolved significantly, moving beyond early CNN-based designs to incorporate advanced architectures and training strategies. Transformer-based models, frequency-aware frameworks, and multi-task learning approaches have all contributed to improved generalization and perceptual quality.
DehazeFormer [16] proposed one of the first transformer-based architectures tailored for image dehazing, introducing a hybrid CNN-transformer design that captures both local and global dependencies. It demonstrated state-of-the-art performance on synthetic datasets and established the transformer paradigm in low-level vision. Similarly, MITNet [24] introduced mutual interaction mechanisms between clean and hazy features to improve recovery fidelity and edge sharpness. These models benefit from enhanced long-range modeling, but still rely heavily on large-scale synthetic datasets like RESIDE. To address the limitations of spatial-domain-only processing, FSDGN [25] and PhDNet [26] incorporated frequency-domain information into the network, enabling the restoration of high-frequency textures typically suppressed by haze. PhDNet in particular proposed a progressive hybrid-domain strategy, jointly learning in both spatial and frequency representations. Other recent works [10] explored more compact or efficient designs. For example, DEA-Net [11] proposed a dual enhancement attention mechanism with lightweight complexity, while OneRestore [27] introduced a generalist restoration network capable of handling dehazing, deraining, and desnowing in a unified pipeline via weather-type conditioning.
Despite these advances, most of the aforementioned methods are developed and evaluated on natural image benchmarks with synthetic haze. Their generalizability to real-world remote sensing imagery remains limited due to fundamental domain gaps. Natural image dehazing models often exploit semantic priors (e.g., object contours, horizon lines) that are ineffective in overhead, orthographic views common to satellite or aerial platforms. Moreover, these models rarely consider radiometric consistency or the spectral integrity required in Earth observation tasks.
2.3. Remote Sensing Single-Image Dehazing
Recognizing the limitations of directly applying natural image dehazing models, recent works have tailored deep learning techniques specifically for remote sensing scenarios. The unique challenges in this domain include: Orthographic viewpoints lacking perspective depth cues; Large-scale scenes with heterogeneous haze distributions; Minimal semantic guidance, especially in low-resolution or texture-poor areas. To address these, several methods have been proposed. For example, Chen et al. [18] proposed a memory-oriented generative adversarial network (MO-GAN) that employs unpaired learning to capture hazy features. This method addresses the challenge of obtaining paired training data, which is often a limitation in RSID research. Bie et al. [28] explored a Gaussian and physics-guided dehazing network (GPD-Net) that enhances the generalization ability of dehazing methods in real-world conditions. Zhang et al. [17] focused on UAV remote sensing images, proposing a dehazing method based on a double-scale transmission optimization strategy. Zheng et al. [29] introduced Dehaze-AGGAN, an enhanced attention-guide generative adversarial network that operates without the need for paired training data. By incorporating a novel total variation loss alongside cycle consistency loss, their approach effectively reduces wave noise and enhances edge quality in dehazed images. Huang et al. [30] proposed an adaptive region-based diffusion dehazing net (ARDD-Net), which leverages a diffusion-based model for free-form RS dehazing. Li et al. [31] proposed a progressive self-refinement network (PSR-Net) to iteratively refine the initial deblurring result via the proposed restoration attention block to achieve lightweight dehazing. SFAN [13] utilized modulation experts (MoME) and decoupled frequency learning blocks (DFLB) to dynamically learn different contextual features of different granularities and to facilitate the removal of low-frequency global haze and the reconstruction of high-frequency local texture information.
2.4. Diffusion Models for Image Restoration
Denoising Diffusion Probabilistic Models (DDPMs) [19] have recently emerged as a powerful generative framework in low-level vision tasks, including image restoration, super-resolution, and inpainting. These models iteratively learn to reverse a predefined noising process and progressively sample clean data from Gaussian noise, offering strong capacity for generating fine-grained, perceptually convincing results.
In the field of image restoration, diffusion models have shown promising results across a range of degradations. For example, IDDPM [32] demonstrated the ability of conditional diffusion models to perform high-fidelity super-resolution. Similarly, RePaint [22] applied diffusion for diverse inpainting tasks by leveraging iterative re-sampling, and IR-SDE [33] introduced stochastic differential equation formulations for continuous restoration. More recently, several works have explored the use of diffusion models for more complex degradation scenarios such as blind denoising and weather-related restoration. Bansal et al. [20] explored the generative capabilities of diffusion models beyond standard Gaussian noise, proposing the Cold Diffusion framework. Their findings suggest that the generative behavior of diffusion models can be adapted to various image transformations, expanding the potential applications of these models in image restoration. Mardani et al. [34] approached the challenges of intractable posteriors in diffusion models through a variational perspective. Their work emphasizes the complexity of solving inverse problems with diffusion models and proposes strategies to approximate true posterior distributions, contributing to the theoretical understanding of these models.
However, most of these approaches treat the inverse task purely as a data-driven mapping, without incorporating any domain-specific physical knowledge. In particular, for haze removal, the majority of diffusion-based models do not leverage the well-established atmospheric scattering model, nor do they utilize structural constraints such as transmission maps or illumination priors. This often leads to unstable convergence or inconsistent reconstructions in scenes with complex haze patterns, especially in remote sensing contexts.
2.5. ASM-Aware Diffusion for Dehazing
Recent studies explicitly embed the Atmospheric Scattering Model (ASM) into diffusion frameworks. DehazeDDPM [35] adopts a two-stage pipeline: a physics modeling stage first estimates the transmission map , atmospheric light A, and a pseudo-clear image J under ASM; then a conditional DDPM refines details, with further used as a fog-aware confidence to guide refinement and frequency restoration. IDDM [36] formalizes physics-guided diffusion by injecting ASM into the forward process: at each step, a haze component is added together with Gaussian noise, and both are removed during sampling; a dedicated estimator (HtNet) is introduced to improve generalization to real images. Diff-Dehazer [23] leverages Stable Diffusion within an unpaired (CycleGAN-style) framework and introduces Physics-Aware Guidance (PAG)—combining ASM-based reconstruction with DCP/BCCR priors—and Text-Aware Guidance (TAG) to regularize restoration with multi-modal cues.
Our difference. Unlike two-stage post-physics refinement (DehazeDDPM), forward-only coupling (IDDM), or SD-based unpaired guidance (Diff-Dehazer), ASPDiff injects learned atmospheric priors into the reverse denoising process throughout sampling. APEM (DCP-initialized, physically supervised) robustly refines transmission and atmospheric light, mitigating failures in bright sky, reflective surfaces, and spatially non-uniform haze. DAPE conditions the denoiser at every step via feature-level concatenation and attention, enforcing step-wise physical plausibility rather than a single pre-/forward-stage constraint. HARM couples DCT-band enhancement with lightweight spatial attention to recover high-frequency structures, tailored for remote sensing with orthographic views, large scale variation, and strongly non-uniform haze.
3. Atmospheric Scattering Prior Embedded Diffusion Model
This section presents the proposed ASPDiff framework. We first describe the Atmospheric-Prior Estimation Module (APEM), then explain how the Diffusion with Atmospheric-Prior Embedding (DAPE) injects priors throughout reverse denoising, and finally introduce the Haze-Aware Refinement Module (HARM) for frequency-aware detail recovery in remote sensing imagery.
3.1. Preliminaries-Conditional Diffusion Models
Diffusion probabilistic models [19] have recently emerged as powerful generative frameworks that model complex data distributions through a gradual denoising process. These models define a Markovian forward process that progressively adds Gaussian noise to the input data, and a learned reverse process that reconstructs the original data by iteratively denoising. In image restoration tasks such as dehazing, conditional diffusion models extend this framework by incorporating a degraded observation as conditioning information, guiding the generative process towards task-specific goals.
Forward Process. Given a clean image , the forward process corrupts it through a sequence of latent variables using a fixed noise schedule as follows:
The full forward process is defined as follows:
This process gradually converts the data into a nearly isotropic Gaussian distribution as .
Using closed-form sampling, we can directly sample from as follows:
where and .
Reverse Process (Conditional). The reverse process aims to recover from a noisy latent , by learning a parameterized conditional distribution, as follows:
where denotes the conditioning information, such as a degraded observation (e.g., hazy remote sensing image). The model is trained to predict the noise added at each step t, rather than the clean image directly.
Training objective. A common training objective is the following simplified noise prediction loss:
where is a neural network that predicts the noise given the current noisy image, time step, and conditioning input. The estimated clean image can then be reconstructed from the denoised intermediate result as follows:
Through iterative denoising from to , the model gradually recovers a clean sample conditioned on .
3.2. Overview
While conditional diffusion models have shown impressive capability in image generation and restoration, their performance in remote sensing image dehazing remains limited by the lack of explicit physical constraints. In particular, the complex and spatially variant degradation patterns caused by atmospheric particles in large-scale Earth observation imagery cannot be sufficiently addressed by data-driven priors alone. Motivated by this gap, we propose ASPDiff, an Atmospheric Scattering Prior embedded Diffusion Model, which integrates domain-specific physical knowledge into the diffusion-based generation process, as shown in Figure 1.
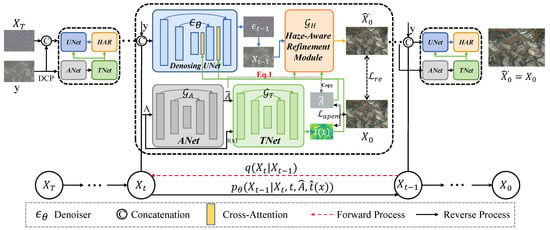
Figure 1.
Overall architecture of the proposed ASPDiff framework. Given an input hazy image , the Atmospheric Prior Estimation Module (APEM) leverages the Dark Channel Prior (DCP) to produce initial estimates of the transmission map and atmospheric light , which are then refined by two learnable sub-networks: TNet () and ANet (). These refined priors are injected as conditional guidance into the reverse denoising diffusion process via cross-attention. The denoising network generates an intermediate state , which is further enhanced by the Haze-Aware Refinement Module (HARM, ) using frequency-based and spatial-aware refinement. The full process ensures physically grounded and perceptually consistent dehazing, with a forward process and a reverse process driven by atmospheric priors.
The key insight behind ASPDiff is to establish a closed-loop interaction between atmospheric scattering physics and the stochastic refinement capability of diffusion models. Rather than treating the diffusion process as a purely statistical mapping, we explicitly embed priors derived from the atmospheric scattering model—such as the transmission map and global atmospheric light into the conditional generation process. These priors serve both as physical regularizers and structural conditions, guiding the model toward more interpretable and physically plausible reconstructions. ASPDiff is composed of the following three major components:
1. Atmospheric Prior Estimation Module: We utilize dark channel prior-based techniques to extract initial transmission maps and global atmospheric light from the input hazy image. These estimations are further refined via learnable networks to enhance reliability and adaptivity.
2. Diffusion with Atmospheric Prior Embedding (DAPE): Built upon a standard denoising diffusion probabilistic model, we incorporate the hazy image and the refined priors as conditioning inputs. This allows the reverse diffusion process to be guided by both data and physics.
3. Haze-Aware Refinement Module: To better capture the subtle structural degradations specific to remote sensing imagery, we introduce a haze perception module that injects fine-grained, haze-aware features into the denoising steps, ensuring high-frequency consistency and scene fidelity.
By harmonizing physical modeling and generative learning, ASPDiff bridges the long-standing gap between interpretability and performance in remote sensing image dehazing. The following subsections provide detailed descriptions of each module and the overall training strategy.
3.3. Atmospheric Prior Estimation Module
In remote sensing image dehazing, the ability to incorporate physically meaningful constraints is essential due to the complex and spatially heterogeneous atmospheric degradation that arises from diverse landscapes, varying altitudes, and changing environmental conditions. The atmospheric scattering model serves as a well-established physical framework to describe the formation of hazy images. However, directly inverting this model remains fundamentally ill-posed, as it requires the accurate estimation of the following two latent variables: the transmission map and the global atmospheric light . In practice, both are often ambiguous, spatially inconsistent, or affected by noise, especially in high-resolution satellite or aerial imagery.
The Dark Channel Prior (DCP) has long served as a heuristic method for estimating these variables. By assuming that, in haze-free images, the minimum value across RGB channels in a local patch tends to be low (i.e., the “dark channel” is near zero), DCP can produce coarse estimates of and . However, DCP is known to degrade under certain conditions, such as bright areas, white objects, reflective surfaces, and complex topography, all of which are common in remote sensing imagery.
To address these challenges, we propose the Atmospheric Prior Estimation Module (APEM). We exploit the interpretability of DCP to obtain a rough but physically meaningful initial estimate. A learnable refinement module is then introduced to correct biases and artifacts in the handcrafted priors. Finally, the refined priors are supervised in a physically consistent way. The APEM consists of two learnable networks: for adjusting the atmospheric light and for adjusting the transmittance.
Given a hazy remote sensing image , we first apply DCP to obtain coarse estimates of the transmission map and global atmospheric light . Let be a local patch centered at pixel x. The dark channel is defined as follows:
Assuming a constant global atmospheric light , the initial transmission map is as follows:
where is a weighting factor (typically set to 0.95), and is the value of atmospheric light in the channel c with the highest intensity. The global atmospheric light is estimated from the brightest pixels in the image, selected from the top darkest pixels in the dark channel as follows:
where denotes the selected pixel subset.
Although DCP offers physically meaningful estimates, they are often noisy or spatially biased. To improve upon these initial priors, APEM introduces two lightweight neural networks: for adjusting the atmospheric light and for adjusting the transmittance. These networks take the initial DCPs and the hazy image as input and output refined spatially coherent priors as follows:
where is the refined transmission map, and is the refined global atmospheric light.
To ensure the consistency of the refined priors with the physical formation model, we supervise and via reconstruction-based consistency loss using the corresponding clean ground-truth image . Specifically, we define a prior consistency loss as follows:
where is a small constant to prevent division instability. This encourages the refined priors to lead to accurate clean image recovery via inversion of the scattering model. An optional smoothness regularization may be applied to enforce spatial coherence as follows:
The final training objective for the APEM becomes as follows:
where is a balancing weight.
3.4. Diffusion with Atmospheric Prior Embedding
While the Atmospheric Prior Estimation Module (APEM) provides physically meaningful estimates of the transmission map and atmospheric light , these priors are further utilized to guide the generation process of the diffusion model. Rather than treating dehazing as a purely data-driven synthesis task, we embed the physical degradation model directly into the denoising diffusion process, forming a tightly coupled mechanism between physics and generative modeling.
Following conventional DDPM settings, we define the forward process as gradually adding Gaussian noise to a clean image :
where is a noise schedule and .
Physics-Guided Conditioning: Haze Injection. Given the refined priors and from APEM, we generate the corresponding hazy observation using the atmospheric scattering model:
This physically grounded hazy image is then used as the conditional input to the diffusion model. That is, we no longer denoise from pure noise alone, but from a haze-conditioned representation.
To generate the clean image from noise, we define a conditional denoising process guided by the atmospheric priors as follows:
where is the concatenated atmospheric condition embedding . In practice, and are broadcast or spatially encoded to match the dimensionality of image features, and injected either via concatenation and cross-attention.
During inference, we start from a noise sample , and iteratively denoise it using the reverse process conditioned on the atmospheric priors estimated from the input hazy image . This creates a physically consistent dehazed image as follows:
3.5. Haze-Aware Refinement Module
Remote sensing images often contain subtle and complex haze-induced degradations due to varying terrain, reflectance, and altitude conditions. These degradations tend to obscure high-frequency structures such as building contours, road edges, and vegetation textures, making their restoration particularly challenging. To address this, we design a Haze-Aware Refinement Module (HARM) that explicitly enhances feature representations by injecting frequency-domain haze prior and spatial attention derived from atmospheric estimates, as shown in Figure 2.
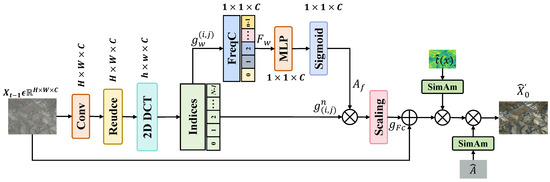
Figure 2.
Architecture of the proposed Haze-Aware Refinement Module (HARM). This module enables adaptive refinement of haze-affected regions by leveraging both frequency-domain and physically guided attention cues.
To restore high-frequency details, we first project the denoising state into the frequency domain using a channel-wise 2D Discrete Cosine Transform (DCT) as follows:
where and are normalization factors. We retain the top frequency coefficients that capture the dominant spectral energy and form a compact frequency representation . Each frequency sub-band is individually fed into a group of submodules , which modulate its contribution to the corresponding feature channels as follows:
All the modulated frequency responses are aggregated to form a composite spectral feature map . This frequency-aware representation is further passed through a lightweight MLP to generate channel-wise attention weights as follows:
where is the Sigmoid function and GAP denotes global average pooling. The resulting frequency-channel attention map is applied to enhance the original features as follows:
After scaling, the enhanced frequency-channel attention is output . This mechanism adaptively strengthens the recovery of frequency bands most affected by haze, enabling high-frequency consistency in restored images.
SimAM-based Spatial Attention Encoding. To transform the prior into differences in lighting conditions across the scene, we use Simple Attention Module (SimAM), a parameter-free attention mechanism based on a neuroscience-inspired energy function. Given an activation map t, SimAM computes attention weights based on the spatial contrast of each activation relative to its local statistics as follows:
Here, u and denote the mean and variance of activations within a local region, and is a small constant ensuring numerical stability. This formulation favors pixels that exhibit distinctive activations in their context—i.e., regions with meaningful contrast or anomalies, which in our case correspond to haze-affected areas.
We apply SimAM separately to the refined transmission map and refined atmospheric light , yielding two attention maps, as follows:
These maps capture spatial importance from both haze density and illumination bias. Finally, we use these attention maps to modulate the early frequency-enhanced features and obtain the following final clear image:
3.6. Training Objectives
To comprehensively guide the training of our proposed ASPDiff framework, we design a multi-component loss function that supervises both the atmospheric prior estimation and the diffusion-based image reconstruction. The overall objective is formulated as follows:
Specifically, the reconstruction los is defined as the pixel-wise distance between the restored image and the clean ground truth , encouraging accurate intensity restoration as follows:
The atmospheric prior estimation loss , as detailed in Section 3.3, supervises the refinement of the transmission map and atmospheric light from initial DCP priors.
To further enhance detail consistency, the frequency consistency loss aligns the spectral characteristics of the restored and ground truth images across 16 discrete cosine transform (DCT) sub-bands as follows:
where denotes the i-th frequency component extracted via DCT decomposition.
We also include a perceptual loss , which compares feature activations extracted from multiple layers of a pretrained VGG-19 network, thereby enforcing semantic consistency and visual realism, as follows:
where represents the feature maps from the l-th layer.
Lastly, the total variation loss serves as a regularizer to suppress minor artifacts and noise, encouraging local smoothness as follows:
We empirically set the weights as , , , , and . This composite loss function ensures that the model not only produces visually and quantitatively accurate dehazed images but also retains physical interpretability, spectral fidelity, and fine-grained structure—all of which are crucial for reliable remote sensing applications.
4. Experiments
This section outlines the experimental protocol employed to evaluate our ASPDiff. We begin by detailing the implementation settings, followed by quantitative and qualitative comparisons with recent state-of-the-art methods on both synthetic and real remote sensing datasets. Next, we assess the spectral fidelity of restored images through a spectral similarity analysis. We also perform ablation studies to isolate the contribution of individual modules, examine practical deployment scenarios within intelligent transport systems, and conclude with a discussion on the limitations and future research potential of our approach.
4.1. Datasets
To comprehensively evaluate model performance across diverse scenarios, we conduct experiments on the following six benchmark datasets with distinct characteristics:
SateHaze1K [37]: Contains three subsets (thin, moderate, thick haze) with 400 synthetic image pairs each, following a 320:35:45 split for training/validation/testing.
RSID [12]: Comprising 1000 authentic hazy/clean pairs, partitioned into 900 training and 100 testing samples through random selection.
LHID and DHID [38]: Light Haze Image Dataset (14,490 training/500 testing pairs) and Dense Haze Image Dataset (30,517 training/500 testing pairs), categorized by atmospheric opacity levels.
RICE [39]: Collected from Google Earth imagery, divided into two subsets: RICE1 (402 training/98 testing) and RICE2 (590 training/146 testing), covering urban, desert, mountainous, and oceanic terrains.
RRSD300 [40]: It provides a collection of 300 real-world aerial images affected by haze, selected from the Microsoft Bing platform and the DIOR dataset to reflect practical remote sensing conditions.
4.2. Quantitative Comparison
We compare our proposed ASPDiff with a comprehensive set of both natural scene image (NSI) dehazing methods and remote sensing image (RSI)-specific models across several challenging benchmark datasets. These datasets represent varying levels of haze density, geographical complexity, and imaging conditions. The results are summarized in Table 1, where the best and second-best scores are highlighted in red and blue, respectively.

Table 1.
Quantitative comparison of remote sensing image dehazing methods on five benchmark datasets. The 1st and 2nd best results are emphasized with red and blue color, respectively.
On the DHID dataset, which simulates heavy haze using real-world transmission maps and varying atmospheric light, ASPDiff achieves a PSNR of 29.24 dB and SSIM of 0.945, outperforming the top-performing RSI method SFAN [13] by +0.07 dB in PSNR and +0.3% in SSIM. Compared to leading NSI methods such as FSDGN [25] and DehazeFormer [16], ASPDiff offers a substantial improvement of up to +1.6 dB in PSNR and +1.2% in SSIM. This validates the importance of incorporating physically grounded priors in highly turbid atmospheric conditions. On LHID, which includes lighter haze, ASPDiff continues to deliver superior performance with 34.13 dB PSNR and 0.972 SSIM, leading SFAN by +0.10 dB and +0.2%, and surpassing OneRestore [27] by +0.18 dB in PSNR. The consistent gain across both light and dense haze scenarios indicates our model’s robustness to varying haze levels and its ability to adapt to subtle degradations often ignored by purely data-driven models. The visual comparison is in Figure 3.

Figure 3.
Visual comparisons of dehazing results on DHID and LHID datasets.
For RICE1 dataset, ASPDiff achieves 36.731 dB PSNR and 0.983 SSIM. Compared to SFAN, the closest competitor, our method achieves a +0.08 dB gain in PSNR, while maintaining parity in SSIM. Compared to recent NSI models (e.g., PhDNet-S [26]), ASPDiff shows a relative PSNR gain of +1.34%, suggesting its enhanced generalization in authentic satellite imagery. On RICE2, which presents more severe haze and varied lighting conditions, ASPDiff again leads with a PSNR of 34.172 dB and SSIM of 0.901, achieving a notable +1.4% increase in SSIM over SFAN. Interestingly, while several NSI models perform reasonably well in PSNR, their SSIM scores decline, implying that they tend to oversmooth fine details—an issue mitigated by our Haze-Aware Refinement Module. The visual comparison is in Figure 4.

Figure 4.
Visual comparisons among several state-of-the-art methods and our proposed ASPDiff on the RICE1 and RICE2 datasets.
The RSID dataset is particularly challenging as it combines haze with noise, illumination imbalance, and sensor distortions. ASPDiff achieves 26.153 dB PSNR and 0.953 SSIM, slightly outperforming the current state-of-the-art method OneRestore in PSNR and matching SFAN in SSIM. Compared to older RSI methods such as PSMBNet [48] and EMPFNet [47], ASPDiff demonstrates up to +13.3% improvement in PSNR and +2.8% in SSIM, confirming its robustness under multi-factor degradation. As shown in Figure 5, our method can remove more residual smog and is closest to the true ground.

Figure 5.
Comparison of dehazing results on RSID dataset, while existing approaches (e.g., DehazeFormer, DEA-Net, SFAN) may produce over-smoothed textures, color distortions, or incomplete haze removal, our method successfully recovers clearer structural boundaries and realistic color tones, especially in sky, vegetation, and building regions.
To further evaluate the robustness of different models under varying haze densities, we conduct experiments on three subsets of the synthetic dataset: S-thin, S-moderate, and S-thick, which simulate thin, moderate, and dense haze conditions, respectively. The quantitative results are reported in Table 2.

Table 2.
Quantitative comparison of remote sensing image dehazing methods on the StateHaze1K dataset. The 1st and 2nd best results are emphasized with red and blue color, respectively.
Thin Haze (S-thin). In the S-thin setting, where haze degradation is relatively mild, our ASPDiff achieves the best performance with a PSNR of 24.102 dB and SSIM of 0.979, narrowly outperforming OneRestore by +0.072 dB in PSNR. Compared to the best RSI method SFAN [13], ASPDiff yields a +0.41% increase in SSIM, suggesting that our method can retain more subtle high-frequency structures even under light haze.
Moderate Haze (S-moderate). Under moderate haze conditions, ASPDiff continues to outperform all competing methods, achieving a PSNR of 28.239 dB and SSIM of 0.978. This marks a +0.038 dB improvement in PSNR and a slight +0.1% boost in SSIM over SFAN, and a larger gain of +0.8 dB in PSNR compared to the best NSI method DEA-Net [11]. The results confirm that even under moderate scattering, physics-guided diffusion enables more faithful reconstruction of clean structures.
Thick Haze (S-thick). When haze becomes visually dominant, performance gaps between NSI and RSI methods widen. ASPDiff demonstrates strong resilience to severe degradation, reaching 23.101 dB PSNR and 0.944 SSIM, ranking first among all methods in PSNR and second in SSIM (slightly behind OneRestore’s 0.949). Compared to SFAN, ASPDiff offers a +0.095 dB gain in PSNR and a +0.2% improvement in SSIM, highlighting the benefits of prior-conditioned generation when restoring heavily obscured content. As shown in Figure 6, DehazeFormer, DEA-Net, and SFAN often produce over-enhanced areas with unnatural color shifts. In contrast, ASPDiff reconstructs clear scene radiance with improved global contrast and color fidelity. Particularly, edges of terrain boundaries, road networks, and rooftops appear sharper and more realistic, confirming the benefit of physical prior integration.

Figure 6.
Qualitative dehazing results on the StateHaze1K dataset, which includes large-scale, geographically diverse remote sensing scenes with synthetic haze.
Comparison Across Method Categories. Across all datasets, NSI dehazing models such as DehazeFormer [16], OneRestore [27], and FSDGN [25] though powerful on natural images, fail to generalize optimally to remote sensing domains due to their lack of physical reasoning and adaptation to large-scale spatial variation. Meanwhile, RSI-specific methods, such as SFAN and DCINet, although integrating advanced attention or fusion strategies, lack the ability of real physical modeling and fine-grained structural reasoning. In contrast, our ASPDiff benefits from a synergistic architecture that unifies physics-based estimation, conditional generative modeling, and fine-structure refinement, yielding consistent gains across both synthetic and real-world settings.
To assess the generalization capability of our method on real-world remote sensing haze, we evaluate ASPDiff and several recent dehazing baselines on the RRSD300 dataset using no-reference perceptual metrics: NIQE and FADE. As shown in Table 3, our ASPDiff achieves the lowest scores on both metrics (NIQE: 3.96, FADE: 0.4329), outperforming both natural image dehazing models (e.g., DeHamer, DehazeFormer) and remote sensing-specific methods (e.g., DCINet, SFAN). These results confirm the effectiveness of our physically guided design under real, complex atmospheric conditions. In particular, the substantial drop in NIQE compared to other methods indicates improved perceptual clarity and artifact suppression. The FADE reduction reflects more effective haze removal and contrast recovery. Notably, methods like DehazeFormer and SFAN still retain relatively high NIQE, suggesting limitations in their ability to generalize from synthetic training to remote sensing domains.

Table 3.
Quantitative comparison of dehazing methods on the RRSD300 dataset using no-reference metrics. Lower NIQE and FADE scores indicate better perceptual quality and reduced fog artifacts.
As shown in Figure 7, DEA-Net and OneRestore occasionally retaining residual haze in the sky or far distances. However, our ASPDiff demonstrates robust generalization by preserving radiometric balance and reducing haze uniformly across the image. The results are not only visually pleasing but also beneficial for downstream remote sensing applications such as object detection and land cover classification.

Figure 7.
Qualitative comparisons on the RRSD300 dataset, composed of real-world hazy satellite and aerial imagery. Our method produces natural and visually consistent results, showcasing its practical utility for remote sensing tasks.
5. Ablation Study
To evaluate the contribution of each core component in ASPDiff, we conduct a module-level ablation study on both the DHID and LHID datasets. Specifically, we remove one module at a time from the full model to assess its individual impact. The following model variants are compared:
- w/o APEM: Removes the Atmospheric Prior Estimation Module. The model operates without transmission map and global atmospheric light , relying solely on the degraded image for conditional diffusion.
- Ours w/o DAPE: Disables the diffusion-based generation. A conventional UNet is used directly to reconstruct the haze-free image without iterative denoising.
- w/o HARM: Excludes the Haze-Aware Refinement Module. The output of the diffusion process is used as the final prediction without frequency-aware enhancement or spatial attention.
- Full: The complete ASPDiff framework, integrating all three modules.
The results are reported in Table 4. We observe that removing any of the key modules leads to a clear performance drop. Excluding APEM causes a noticeable decline in SSIM, indicating that the incorporation of atmospheric priors is critical for structural fidelity. Removing DAPE results in a larger PSNR reduction, highlighting the role of the diffusion process in detailed image recovery. Although the performance drop from removing HARM is relatively modest, it still demonstrates the value of frequency-sensitive and spatially adaptive refinement in enhancing fine textures and scene contrast. These findings validate the complementary effects of all three modules and justify the design choices made in ASPDiff.

Table 4.
Module-level ablation study results on the DHID and LHID datasets. Bold numbers denote the best performance.
5.1. Ablation on Atmospheric Prior Estimation (APEM)
To evaluate the contribution of each component within the Atmospheric Prior Estimation Module (APEM), we perform targeted ablation experiments focused on three aspects: the effectiveness of DCP-based initialization, the impact of learnable refinement networks (, ), and the role of reconstruction-based supervision.
The tested model variants are as follows:
- w/DCP only: Uses only the raw transmission map and atmospheric light estimated by DCP, without refinement or supervision.
- w/o prior supervision: Employs the full APEM architecture but removes the loss supervision for and .
- Full APEM: The complete prior estimation module, including DCP initialization, learnable refinement, and physical consistency supervision.
As shown in Figure 8, directly using DCPs yields suboptimal results due to estimation noise and spatial inconsistency. Refinement via learnable networks improves performance, and the addition of physically consistent supervision further enhances both PSNR and SSIM. These results highlight the importance of combining heuristic priors with learnable correction and physical constraints in remote sensing image dehazing. As illustrated in Figure 9, DCP-based priors provide a physically interpretable starting point but often produce over-simplified or inaccurate estimates in bright regions or complex textures, leading to noticeable haze residues. Introducing learnable refinement improves structural fidelity but, without supervision, the network tends to produce suboptimal priors, resulting in visible haze remnants and artifacts. In contrast, the full APEM setup yields sharper, haze-free outputs with consistent global illumination and clearer boundaries.
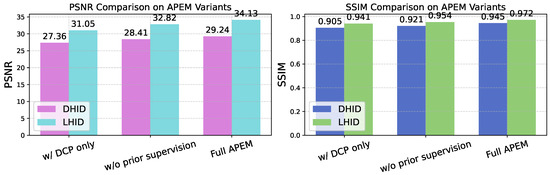
Figure 8.
Ablation results on APEM components on DHID and LHID.
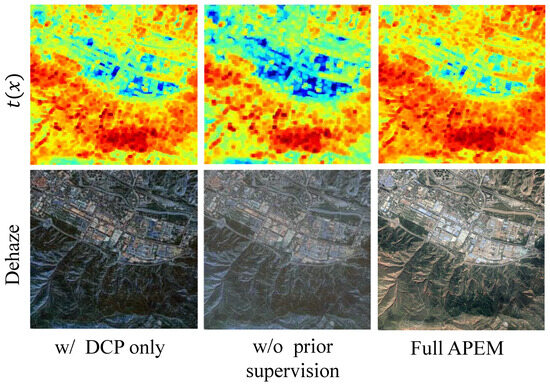
Figure 9.
Qualitative comparison of different configurations of the Atmospheric Prior Estimation Module (APEM). DCP-only results show haze residues. Without supervision, local artifacts and incomplete haze removal appear. Full APEM yields clean and visually consistent results.
5.2. Ablation on Frequency and Spatial Enhancement (HARM)
The Haze-Aware Refinement Module (HARM) is introduced to enhance the restoration of high-frequency structures and haze-dense regions in remote sensing imagery. It combines DCT-based frequency decomposition and SimAM-based spatial attention, aiming to improve both texture fidelity and semantic consistency. To evaluate their respective contributions and synergy, we conduct an ablation study with four configurations:
- w/o HARM: Removes the entire refinement module. The diffusion model outputs are directly used without any post-enhancement.
- w/DCT only: Applies frequency-channel modulation using DCT sub-bands and MLP-based weighting, omitting SimAM attention.
- w/SimAM only: Integrates only SimAM-based spatial attention derived from and , disabling DCT processing.
- Full HARM: Complete refinement pipeline with both frequency and spatial enhancement.
Table 5 presents the quantitative results on DHID and LHID. Compared with the baseline (w/o HARM), adding either frequency or spatial refinement improves the restoration quality. The DCT-only configuration shows enhanced edge sharpness and reduced spectral blur, particularly in urban and structural areas. This confirms the effectiveness of decomposing the image into sub-band representations, which allow the model to reweight critical frequency components suppressed by haze. On the other hand, the SimAM-only variant contributes to better scene-level consistency, as SimAM adaptively highlights haze-affected areas based on local activation contrast. This leads to more accurate color reconstruction in heavily obscured regions such as sky or shadows, and improves SSIM in low-texture regions. The Full HARM configuration, which integrates both mechanisms, achieves the best performance. Not only does it preserve building outlines and road boundaries with sharper textures, but it also reconstructs spatially consistent global illumination. This synergy results in a notable improvement of +0.33 dB PSNR and +0.011 SSIM on DHID, and +0.37 dB PSNR and +0.006 SSIM on LHID compared to the baseline.

Table 5.
Ablation study of the HARM on DHID and LHID datasets.
6. Conclusions
In this work, we present ASPDiff, an Atmospheric Scattering Prior embedded Diffusion Model tailored for remote sensing image dehazing. Unlike prior methods that rely solely on statistical learning or deterministic physical priors, ASPDiff establishes a tightly coupled interaction between atmospheric physics and conditional generative modeling. By embedding transmission maps and global atmospheric light, derived and refined via the proposed APEM, into the denoising diffusion process, ASPDiff offers both interpretability and high-fidelity restoration. Furthermore, our Haze-Aware Refinement Module (HARM) complements the generative backbone by injecting fine-grained frequency and spatial attention cues, significantly enhancing the recovery of high-frequency structures and contrast in haze-dense scenarios. Extensive experiments on synthetic and real-world remote sensing datasets validate the superiority of our method over both natural image dehazing networks and remote sensing-specific approaches. ASPDiff consistently achieves state-of-the-art results across multiple benchmarks, especially under heavy haze and complex terrain. In future work, we plan to extend ASPDiff to address more diverse atmospheric degradations such as smoke, thin clouds, or night haze, and to explore its integration with downstream remote sensing tasks including semantic segmentation and object detection under adverse conditions.
Author Contributions
Methodology, S.W.; software, S.W.; validation, M.Z.; writing—original draft, S.W.; writing—review and editing, M.Z.; supervision, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Anhui Provincial Quality Engineering Project for Higher Education Institutions (2022jnds043), Chuzhou Polytechnic Science and Technology Innovation Platform Project (YJP-2023-02), Anhui Provincial Natural Science Research Project for Higher Education Institutions (2023AH053088 and 2024AH051439), Chuzhou Polytechnic Natural Science Research Project (ZKZ-2022-02), Teacher’s Internship Program for Hanging Jobs in Industry and Enterprises (xjgz2024009), School level Quality Engineering Project “Teaching Resource Library for Software Technology Major” (2023jxzyk01), Anhui Vocational and Adult Education Association Planning Project (AZCJ2024208), and Anhui Province Mid-Career and Young Teachers Training Initiative—Outstanding Young Teacher Cultivation Project (YQYB2023163).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fang, W.; Zhang, G.; Zheng, Y.; Chen, Y. Multi-task learning for uav aerial object detection in foggy weather condition. Remote Sens. 2023, 15, 4617. [Google Scholar] [CrossRef]
- Roy, S.K.; Sukul, A.; Jamali, A.; Haut, J.M.; Ghamisi, P. Cross hyperspectral and LiDAR attention transformer: An extended self-attention for land use and land cover classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Wang, C.; Luo, L.; Fang, W.; Yang, J. Cross-modal Gaussian Localization Distillation for Optical Information guided SAR Object Detection. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; IEEE: New York, NY, USA, 2025; pp. 1–5. [Google Scholar]
- Narasimhan, S.G.; Nayar, S.K. Chromatic framework for vision in bad weather. In Proceedings of the Proceedings IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2000 (Cat. No. PR00662), Hilton Head, SC, USA, 15 June 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 598–605. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, J.; Shao, L. A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar] [CrossRef]
- Berman, D.; Treibitz, T.; Avidan, S. Single image dehazing using haze-lines. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 720–734. [Google Scholar] [CrossRef] [PubMed]
- Arici, T.; Dikbas, S.; Altunbasak, Y. A histogram modification framework and its application for image contrast enhancement. IEEE Trans. Image Process. 2009, 18, 1921–1935. [Google Scholar] [CrossRef]
- Fang, W.; Fan, J.; Zheng, Y.; Weng, J.; Tai, Y.; Li, J. Guided real image dehazing using ycbcr color space. arXiv 2024, arXiv:2412.17496. [Google Scholar] [CrossRef]
- Zhang, G.; Fang, W.; Zheng, Y.; Wang, R. SDBAD-Net: A spatial dual-branch attention dehazing network based on meta-former paradigm. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 60–70. [Google Scholar] [CrossRef]
- Chen, Z.; He, Z.; Lu, Z.M. DEA-Net: Single image dehazing based on detail-enhanced convolution and content-guided attention. IEEE Trans. Image Process. 2024, 33, 1002–1015. [Google Scholar] [CrossRef] [PubMed]
- Chi, K.; Yuan, Y.; Wang, Q. Trinity-Net: Gradient-guided Swin transformer-based remote sensing image dehazing and beyond. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Shen, H.; Ding, H.; Zhang, Y.; Cong, X.; Zhao, Z.Q.; Jiang, X. Spatial-frequency adaptive remote sensing image dehazing with mixture of experts. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. Dehazenet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef]
- Li, B.; Peng, X.; Wang, Z.; Xu, J.; Feng, D. Aod-net: All-in-one dehazing network. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4770–4778. [Google Scholar]
- Song, Y.; He, Z.; Qian, H.; Du, X. Vision transformers for single image dehazing. IEEE Trans. Image Process. 2023, 32, 1927–1941. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Ma, S.; Zheng, R.; Zhang, L. UAV remote sensing image dehazing based on double-scale transmission optimization strategy. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y. Memory-oriented unpaired learning for single remote sensing image dehazing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Bansal, A.; Borgnia, E.; Chu, H.M.; Li, J.; Kazemi, H.; Huang, F.; Goldblum, M.; Geiping, J.; Goldstein, T. Cold diffusion: Inverting arbitrary image transforms without noise. Adv. Neural Inf. Process. Syst. 2023, 36, 41259–41282. [Google Scholar]
- Lv, X.; Zhang, S.; Wang, C.; Zheng, Y.; Zhong, B.; Li, C.; Nie, L. Fourier priors-guided diffusion for zero-shot joint low-light enhancement and deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 25378–25388. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11461–11471. [Google Scholar]
- Lan, Y.; Cui, Z.; Liu, C.; Peng, J.; Wang, N.; Luo, X.; Liu, D. Exploiting diffusion prior for real-world image dehazing with unpaired training. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 4455–4463. [Google Scholar]
- Shen, H.; Zhao, Z.Q.; Zhang, Y.; Zhang, Z. Mutual information-driven triple interaction network for efficient image dehazing. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 7–16. [Google Scholar]
- Yu, H.; Zheng, N.; Zhou, M.; Huang, J.; Xiao, Z.; Zhao, F. Frequency and spatial dual guidance for image dehazing. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 181–198. [Google Scholar]
- Lihe, Z.; He, J.; Yuan, Q.; Jin, X.; Xiao, Y.; Zhang, L. Phdnet: A novel physic-aware dehazing network for remote sensing images. Inf. Fusion 2024, 106, 102277. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, Y.; Lu, Y.; Zhu, H.; Liu, R.W.; He, S. Onerestore: A universal restoration framework for composite degradation. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2024; pp. 255–272. [Google Scholar]
- Bie, Y.; Yang, S.; Huang, Y. Single remote sensing image dehazing using gaussian and physics-guided process. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zheng, Y.; Su, J.; Zhang, S.; Tao, M.; Wang, L. Dehaze-AGGAN: Unpaired remote sensing image dehazing using enhanced attention-guide generative adversarial networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Huang, Y.; Xiong, S. Remote sensing image dehazing using adaptive region-based diffusion models. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Y.; Kung, S.Y. PSRNet: A Progressive Self-refine Network for Lightweight Optical Remote Sensing Image Dehazing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
- Luo, Z.; Gustafsson, F.K.; Zhao, Z.; Sjölund, J.; Schön, T.B. Image restoration with mean-reverting stochastic differential equations. arXiv 2023, arXiv:2301.11699. [Google Scholar] [CrossRef]
- Mardani, M.; Song, J.; Kautz, J.; Vahdat, A. A variational perspective on solving inverse problems with diffusion models. arXiv 2023, arXiv:2305.04391. [Google Scholar] [CrossRef]
- Yu, H.; Huang, J.; Zheng, K.; Zhao, F. High-quality image dehazing with diffusion model. arXiv 2023, arXiv:2308.11949. [Google Scholar]
- Zhou, S.; Fan, B.; Tian, J. Physics-Guided Image Dehazing Diffusion. arXiv 2025, arXiv:2504.21385. [Google Scholar]
- Huang, B.; Zhi, L.; Yang, C.; Sun, F.; Song, Y. Single satellite optical imagery dehazing using SAR image prior based on conditional generative adversarial networks. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass, CO, USA, 1–5 March 2020; pp. 1806–1813. [Google Scholar]
- Zhang, L.; Wang, S. Dense haze removal based on dynamic collaborative inference learning for remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar] [CrossRef]
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Zheng, Z.; Ren, W.; Cao, X.; Hu, X.; Wang, T.; Song, F.; Jia, X. Ultra-high-definition image dehazing via multi-guided bilateral learning. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: New York, NY, USA, 2021; pp. 16180–16189. [Google Scholar]
- Wu, H.; Qu, Y.; Lin, S.; Zhou, J.; Qiao, R.; Zhang, Z.; Xie, Y.; Ma, L. Contrastive learning for compact single image dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10551–10560. [Google Scholar]
- Guo, C.L.; Yan, Q.; Anwar, S.; Cong, R.; Ren, W.; Li, C. Image dehazing transformer with transmission-aware 3D position embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5812–5820. [Google Scholar]
- Li, J.; Hu, Q.; Ai, M. Haze and thin cloud removal via sphere model improved dark channel prior. IEEE Geosci. Remote Sens. Lett. 2018, 16, 472–476. [Google Scholar] [CrossRef]
- Han, J.; Zhang, S.; Fan, N.; Ye, Z. Local patchwise minimal and maximal values prior for single optical remote sensing image dehazing. Inf. Sci. 2022, 606, 173–193. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X. A coarse-to-fine two-stage attentive network for haze removal of remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1751–1755. [Google Scholar] [CrossRef]
- Wen, Y.; Gao, T.; Zhang, J.; Li, Z.; Chen, T. Encoder-free multiaxis physics-aware fusion network for remote sensing image dehazing. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Sun, H.; Luo, Z.; Ren, D.; Hu, W.; Du, B.; Yang, W.; Wan, J.; Zhang, L. Partial siamese with multiscale bi-codec networks for remote sensing image haze removal. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).