Abstract
Our previous study examined the stratosphere-troposphere exchange (STE) of air mass and ozone using ERA5 and MERRA2 reanalysis data and observations for 2007–2010. Their analysis applied a lower stratosphere mass budget approach, with the 380 K isentropic surface serving as the upper boundary of the lowermost stratosphere. This study employs a dynamic isentropic surface fitted to the tropical tropopause, providing an update to the results using the static 380 K boundary. Additionally, we improve the numerical scheme for deriving the mass of the lowermost stratosphere. Under this new framework, the air mass upward flux at the isentropic surface in the tropics increases from 19.3 × 109, 19.3 × 109, and 22.0 × 109 kg s−1 in our previous study to 21.9 × 109, 20.9 × 109, and 26.3 × 109 kg s−1 in the present study for ERA5, MERRA2, and observations, respectively. The global ozone fluxes across the fitted isentrope become −347.6, −362.5 and −368.4 Tg yr−1 as compared to −345.7, −359.5 and −335.6 Tg yr−1 at the 380 K level from our previous study for ERA5, MERRA2 and observations, respectively. The corresponding extratropical ozone fluxes are −539.3, −541.3 and −565.5 Tg yr−1 versus previous estimates of −538.1, −542.5 and −527.8 Tg yr−1. The increased role of tropical cirrus clouds near the tropopause is also highlighted under the updated framework in observations. The contribution of cloud heating to tropical air mass flux increases from 2.0% in our previous study to 8.2% in the present analysis, while for ozone, the corresponding contribution increases from 1.8% to 8.1%. We further show that the improved estimate of the change rate of mass in the lowermost stratosphere has an impact on seasonal ozone STE results from chemistry climate models presented in another of our previous studies. These findings provide new insights into the processes governing stratosphere-troposphere exchange.
1. Introduction
The stratosphere–troposphere exchange (STE) of air mass and ozone modulates the composition, radiative balance, and dynamics of both atmospheric layers [1,2,3,4,5,6]. Previous studies have shown the impacts of STE on the tropospheric ozone budget, methane lifetime, and other chemicals [5,7,8,9,10,11,12,13]. Ozone in the stratosphere and troposphere has opposite effects on human health. In the stratosphere, ozone acts as a protective shield by absorbing harmful ultraviolet radiation. In contrast, ozone in the troposphere contributes to air pollution [13,14,15] and is a potent greenhouse gas [16]. With tropospheric ozone concentrations expected to increase in a warming climate, it is increasingly important to accurately quantify the upward and downward ozone fluxes between the troposphere and the stratosphere [13,15,17]. A widely used method for deriving the STE of air mass and ozone is the lowermost stratosphere mass budget approach, first introduced by Appenzeller et al. [18]. This method derives the STE of ozone and air mass across the tropopause by combining two components: the diabatic flux across an isentropic upper boundary of the lowermost stratosphere and the change rate of the mass in the lowermost stratosphere. Unlike earlier studies [17,19,20,21], Wang and Fu [22] considered both the downward ozone flux in the extratropics and the upward flux in the tropics to estimate global ozone STE. Using reanalysis data and observations, they reported a global ozone STE of 336–360 Tg/yr and an extratropical ozone STE of 528–543 Tg/yr for the period 2007–2010. However, all of these studies employ a fixed upper boundary for the lowermost stratosphere, namely the 380 K isentrope [18,20,22].
The use of a static 380 K isentropic surface introduces a gap between this surface and the tropical tropopause, which varies with season, interannual variability, and climate. The gap, along with its variability, would lead to uncertainties in estimating STE and its changes [22,23]. To address this issue, Wang et al. [24] proposed, for the first time, the use of dynamic isentropic surfaces fitted to monthly tropical tropopauses as the upper boundary of the lowermost stratosphere in a mass budget approach. This method is particularly well-suited for estimating air mass and ozone STEs across different climates, as it explicitly accounts for the variations and changes in the tropical tropopause [25,26,27]. This method has been applied to various studies, including air mass and ozone STEs during the Last Glacial Maximum, changes in air mass and ozone STEs projected by Chemistry-Climate Model Initiative (CCMI) data for 1960–2099, and climatology and seasonality and interannual variability of air mass and ozone STEs based on two renowned reanalysis products [23,24,28].
This study revisits the work of Wang and Fu [22] on the STEs of air mass and ozone for 2007 to 2010 based on observations and two reanalyses, using a dynamic isentrope as the upper boundary of the lowermost stratosphere. Another notable update is the implementation of a scheme for calculating lowermost stratosphere mass, replacing a built-in software function that fails when pressure is not monotonically decreasing in isentropic coordinate–a rare but possible occurrence. We thus also examine its impact on the results including those based on the CCMI simulations [23]. The observational and reanalysis datasets remain the same as those used in Wang and Fu [22]. Furthermore, we revisit the role of clouds in modulating diabatic heating at the dynamic isentrope levels. Wang and Fu [22] highlighted the significant impact of clouds, particularly cirrus clouds, on STE, noting opposing effects in reanalyses versus observations in the tropics. Given these findings, it is crucial to revisit the results using the dynamic isentrope method for this four-year time range.
2. Data and Methods
2.1. Observational Datasets
We use the same observational dataset as outlined in Wang and Fu [22] to derive fields of diabatic heating, isentropic density, and ozone mass mixing ratio, as well as tropopause height and isentropic surfaces. The dataset integrates radiative heating rates derived from CloudSat Level 2B-FLXHR-LIDAR, high-resolution temperature profiles from COSMIC I radio occultation (RO) measurements, and vertical ozone distribution fields retrieved from the Aura Microwave Limb Sounder (MLS) observations.
Radiative heating rates are derived from CloudSat Level 2B-FLXHR-LIDAR net fluxes and processed according to the protocols provided by the CloudSat Data Processing Center documentation. Shortwave radiative heating rates are then adjusted using the methodology described by L’Ecuyer et al. [29] and Henderson et al. [30], as adopted by Wang and Fu [22], to obtain daily mean shortwave radiative heating rates. Corrections are also applied to mitigate the known biases in clear-sky shortwave fluxes from the 2BFL dataset compared to CERES observations, following Henderson et al. [30] and Wang and Fu [22]. For the longwave radiative heating rates, all-sky values are computed as an average of daytime and nighttime clear-sky radiative heating rates plus nighttime cloud radiative heating rates, which excludes the effect of “solar background noise” inherent in CALIPSO measurements [31]. Cloud radiative heating rates are determined as the difference between all-sky and clear-sky rates. As in Wang and Fu [22], we focus on the period from January 2007 to December 2010 because the 2BFL product is only available from 7 July 2006 to 17 April 2011.
We use temperature profiles retrieved from COSMIC radio occultation measurements for the study period [22,32,33]. These RO data, characterized by their fine vertical resolution and high accuracy, are processed following the methods outlined by Pirscher et al. [34] and Sweeney and Fu [35]. The derived tropopause height, isentropic surface, and isentropic density serve as key parameters for quantifying stratosphere–troposphere exchange of air mass and ozone.
Ozone mass mixing ratio fields are obtained from Aura MLS v4.2x Level 2 retrievals [36]. These data provide the vertical structure of ozone concentrations essential for evaluating ozone exchange. The processing method is consistent with the approach detailed by Wang and Fu [22].
2.2. Reanalysis Datasets
This study uses two state-of-the-art reanalysis datasets: ERA5 and ERA5.1 from the European Centre for Medium-Range Weather Forecasts (ECMWF) [37], and MERRA2 from NASA’s Modern-Era Retrospective Analysis for Research and Applications, Version 2 [38].
Our analyses employ monthly data with a horizontal resolution of a 1.5° latitude by 1.5° longitude grid [22].
2.3. Modeling Data
CCMI simulations are used to document the impact of a code update in the calculation of lowermost stratosphere mass on the results shown in Wang and Fu [23]. In these simulations, the historic forcings and observed sea surface conditions are used for 1960–2010 while the 2010–2099 period follows the WMO (2011) A1 scenario for ODS and RCP 6.0 [39] for other GHGs, tropospheric ozone precursors, and aerosol and aerosol precursor emissions [40]. We use simulations from the first ensemble member of ten CCMI models [23].
2.4. Mass Budget Approach
We employ the mass budget approach first introduced by Appenzeller et al. [18] and subsequently refined by Schoeberl [20], Wang and Fu [22], Wang et al. [24], and Wang and Fu [23]. A brief description of the method is provided below. For full details, refer to Wang et al. [24] and Wang and Fu [23].
Wang et al. [24] refined the mass budget approach using a dynamic isentropic upper boundary of the lowermost stratosphere, determined monthly (Using daily rather than monthly data has little impact on the derived STEs [24], as near-tropopause small-scale dynamical processes on sub-monthly timescales play only a minimal role in global STE [1]) by minimizing the difference between an isentrope and the lapse-rate tropopause in the tropics (equatorward of the latitudes with zero diabatic heating) [41]. The fitted isentropic surface is then used to approximate the tropical tropopause, while the extratropical tropopause remains the lapse-rate definition. The zero diabatic heating latitude at the fitted isentrope defines the tropics-extratropics boundary: equatorward regions are tropical, poleward are extratropical. The extratropical flux is the sum of fluxes over the NH and SH extratropics, while the global flux is the sum of fluxes over the extratropics and tropics.
The net tropopause flux (i.e., STE) of an atmospheric constituent, denoted as , can be expressed as the sum of its flux across the fitted isentropic surface, , and the time change rate of its mass in the lowermost stratosphere (i.e., the region between the tropopause and fitted isentropic surface), .
Here, the subscript c refers to the specific atmospheric constituent being considered—in this study, air mass and ozone. In Equation (1), a positive flux indicates upwelling. Chemical sources and sinks are neglected in the lowermost stratosphere, which is exact for air and a good approximation for ozone [22,24]. In the tropics, the net tropopause flux simplifies to .
The flux across the fitted isentropic surface is computed for air and ozone, respectively, using the following expressions:
In these equations, Q denotes the diabatic heating rate, is the isentropic density, is ozone mass mixing ratio, and A is the area at the fitted isentropic surface in the NH extratropics, SH extratropics, and tropics. The diabatic heating rate is given by , where R is the radiative heating rate, θ is the potential temperature, and T is the temperature. The isentropic density is given by , where p is the pressure, and g is the gravitational acceleration.
The lowermost stratosphere mass is calculated for air and ozone using the following equations:
where Pt and Pi are pressures at the tropopause and fitted isentropic levels, respectively.
A notable update in this study involves implementing a calculation for the mass of the lowermost stratosphere, replacing a built-in software function that fails when pressure is not monotonically decreasing with potential temperature. The vertical integration of Equation (3) is performed using the following numerical schemes:
where j is the pressure level index, increasing with height. Ji corresponds to the index of the pressure level at the fitted isentrope, which defines the upper boundary of the lowermost stratosphere, while corresponds to the index at the tropopause, the lower boundary of the stratosphere.
In this study, instead of using the 3.5 (potential vorticity units (PVU) for the extratropical tropopause as in Wang and Fu [22], we employ the LRT for all latitudes and longitudes, following Wang et al. [24], Wang and Fu [23] and Wang et al. [28]. For observationally based estimates of STEs, we use COSMIC-derived temperature fields along with radiative heating rates to determine the tropical LRT (tLRT) and the fitted upper isentropic surface, different from Wang and Fu [22] who used the ECMWF ancillary temperature profiles in the CloudSat/CALIPSO product [29,30]. The final update concerns our definition of the tropical boundary. While Wang and Fu [22] define this boundary based on the zero diabatic heating points on the LRT, we instead define it using the zero diabatic heating points at the fitted isentropic surface [23].
3. Results
3.1. Ozone STEs from CCMI Models
We begin by updating the ozone STE estimates, averaged across the 10 CCMI models presented in Wang and Fu [23], using the improved mass calculation method. We note the availability of data from phase 2 of the CCMI, however, this study focuses on providing a direct comparison with Wang and Fu [23] by updating the phase 1 results using the improved methodology. Table 1 shows the updated ozone STEs, including annual and seasonal means averaged over 1980–2020, as well as trends for the periods 1960–2000 and 2000–2100, versus the corresponding values from Wang and Fu [23]. Notably, all decadal trends from the present study for 1960–2000 (except over the NH extratropics) and for 2000–2100 are statistically significant at a 95% confidence level.

Table 1.
Annual and seasonal mean tropopause net flux (i.e., STE) of ozone in Tg/yr from 1980 to 2020 for the multi-model mean computed from 10 CCMI models. The numbers in the parentheses correspond to trends in %/decade for 1960–2000 and 2000–2100, bolded values are significant at the 95% confidence level. The black and blue values are from the present study and Wang and Fu [23] (see their Table 1), respectively. The results are shown over Northen Hemisphere (NH) extratropics, Southern Hemisphere (SH) extratropics, tropics, extratropics, and globe.
The revised estimates show minimal differences from Wang and Fu [23] in terms of annual mean climatology and trends. However, substantial discrepancies emerge in the seasonal results, particularly over NH extratropics, for both the climatological mean and the trends. For example, during SON, the ozone STEs over the NH extratropics are −149.4 Tg/yr in this study versus −78.0 Tg/yr in Wang and Fu [23], and −254.4 Tg/yr versus −187.5 Tg/yr globally. Substantial differences are also observed in seasonal trends over the NH extratropics.
Discrepancies in ozone STE estimates shown in Table 1 are also due to methodological differences in computing the time derivative of mass within the lowermost stratosphere. Since the CCMI data is provided yearly, Wang and Fu [23] computed the monthly mass tendency () independently for each of the 140 calendar years, applying forward differencing in January, central differencing from February through November, and backward differencing in December. This year-by-year approach introduces discontinuities at calendar year boundaries and thus biases in the DJF seasonal averages. Our revised method applies forward differencing only at the initial time step (January 1960), central differencing from February 1960 through November 2099, and backward differencing only at the final time step (December 2099). This continuous treatment of the time derivative across the full 140-year period improves the accuracy and physical consistency of monthly and seasonal ozone flux estimates.
We find no differences in the annual means of air mass and ozone STEs after applying the improved mass calculations in ERA5 and MERRA2 for 1980–2020. Seasonal means in ERA5 remain unchanged for both air mass and ozone. MERRA2 exhibits small but noticeable discrepancies in ozone STE during JJA in the Southern Hemisphere, which also affects the global JJA means. Seasonal air mass estimates in MERRA2 are unaffected under the updated framework. Accordingly, the results reported by Wang et al. [28] show minimal change.
Wang and Fu [23] focused on the annual-mean air mass and ozone STEs, which remain unaffected by the revisions. The only results requiring revision are the seasonal STE values reported in their Table 1.
3.2. Fitted Isentropic Surface
We update the results of Wang and Fu [22] in the STEs based on observations and reanalyses by using the fitted isentropic surface to the tLRT. Figure 1 shows the monthly fitted isentropic surface and tropical tropopause pressure. It reveals clear seasonal cycles for all three datasets, consistent with the ERA5 and MERRA2 results shown in Wang et al. [28] (see their Figure 1a,c). Also, see Wang et al. [28] for an explanation of the August peak in the MERRA 2 fitted isentrope.
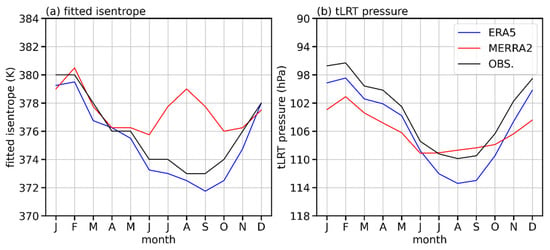
Figure 1.
(a) Seasonal variations of the fitted isentrope used as the upper boundary of the lowermost stratosphere, and (b) the seasonal cycle of the tropical lapse rate tropopause (tLRT) pressure, averaged over 2007–2010, as derived from COSMIC RO observations, ERA5, and MERRA2.
The fitted isentropic surfaces from COSMIC I observations and ERA5 closely track each other throughout the year, while MERRA2 consistently lies at higher potential temperatures (Figure 1a). The annual mean values of the fitted isentropic surface are 375.25 K for ERA5, 377.48 K for MERRA2, and 376.0 K for observations. Importantly, all monthly fitted isentropes remain below the commonly used 380 K throughout the year, except in January and February from the observations and in February from MERRA2. This highlights the need for updating previous STE estimates that used a static upper boundary. For tropical tropopause pressure (Figure 1b), observations exhibit lower values than both reanalyses throughout the year, except in August and September when they are higher than those from MERRA2. The annual means are 103.16 hPa for observations, compared to 105.53 hPa for ERA5 and 106.03 hPa for MERRA2. These differences suggest that the observationally derived tropopause lies slightly higher in altitude than in the reanalyses, potentially reflecting coarser vertical resolution in reanalyses.
3.3. STE of Air Mass and Ozone
We first present air mass and ozone fluxes across the fitted isentropic surface, derived from observational data as well as ERA5 and MERRA2 reanalyses. It is worth noting that the annual-mean climatology of diabatic fluxes across the fitted isentropic surfaces are equivalent to the annual mean net fluxes across the tropopause, provided that chemical sources in the lowermost stratosphere are negligible.
Table 2 presents air mass and ozone fluxes across the upper isentropic surface for 2007–2011, including values from Wang and Fu [22] (blue), updated estimates using a dynamic isentrope in place of the fixed 380 K level (red), and final values obtained by further modifying the tropical boundary definition (black). Replacing the fixed 380 K surface with a fitted isentrope increases the magnitude of annual mean air mass fluxes, as the fitted level generally lies at a lower altitude (Figure 1). Further enhancement in flux magnitudes is caused by defining the tropical boundary based on the zero diabatic heating on the fitted isentrope, which maximizes both upward and downward fluxes. For the observationally derived fluxes, differences between this study and Wang and Fu [22] also arise from the choice of the dataset to derive the tropopause. Wang and Fu [22] used the ECMWF ancillary temperature profiles in the CloudSat/CALIPSO product, while the present study used the COSMIC I RO temperatures, which results in a lower fitted isentrope. All these three factors enhance air mass flux magnitudes. As a result, tropical air mass fluxes increase from 19.3 × 109 kg/s, 19.3 × 109 kg/s, and 22.0 × 109 kg/s to 21.9 × 109 kg/s, 20.9 × 109 kg/s, and 26.3 × 109 kg/s, for ERA5, MERRA2, and the observational dataset, respectively.

Table 2.
Air mass and ozone fluxes across the upper isentrope for 2007–2011 from ERA5, MERRA2, and the observational data. Flux values in blue are from Wang and Fu [22] (see their Table 1) using the 380 K isentrope and tropical boundaries based on the zero diabatic heating latitudes at the tropopause. Red values are results using a fitted isentrope instead of the fixed 380 K level, while black values further modify the tropical boundary based on the zero diabatic heating at the fitted isentropic surface. The numbers in parentheses indicate the change for each step.
Unlike air mass fluxes, ozone fluxes have varied responses to updating the isentropic surface. This is because, at the fitted isentropic surface, air mass fluxes increase while ozone concentrations decrease, leading to net effects that can be either positive or negative. While the global ozone flux remains unaffected by the definition of the tropical boundary, ozone flux magnitudes across other regions increase with redefinition of the tropical boundary, consistent with the air mas flux changes. Considering the overall impact (comparing the black and blue values in Table 2) reanalyses see a slight reduction in tropical upward ozone flux, from 192.4 Tg yr−1 and 183.0 Tg yr−1 to 191.7 Tg yr−1 and 178.8 Tg yr−1 for ERA5 and MERRA2, respectively. In contrast, the observationally derived tropical upward ozone flux increases from 192.2 Tg yr−1 to 197.1 Tg yr−1. Across the extratropical regions, ERA5 and MERRA2 see enhanced downward fluxes in the northern hemisphere and reduced downward fluxes in the southern hemisphere. Observationally derived ozone flux magnitudes, however, increase across all regions. The global net flux magnitudes at the upper boundary of the lowermost stratosphere increase across all datasets, from 345.7 Tg yr−1, 359.5 Tg yr−1, and 335.6 Tg yr−1 to 347.6 Tg yr−1, 362.5 Tg yr−1, and 368.4 Tg yr−1, for ERA5, MERRA2, and observations, respectively.
Differences between the previous and updated flux estimates are attributed to changes in diabatic heating, isentropic density, and ozone mass mixing ratio at the isentropic surface in addition to the tropical boundary definition, each of which is influenced by the updated methodology. Figure 2 highlights these differences across datasets at the fitted isentropic level (solid lines) and at the 380 K isentropic level (dashed lines). Figure 2a shows the maximum tropical diabatic heating rate increases slightly from about 1.2 K day−1 to about 1.25 K day−1 in observations. Increased diabatic heating aligns with physical intuition, and lowering the isentropic surface enhances the influence of radiative heating. Figure 2b demonstrates that isentropic density increases across all latitudes and for all datasets. Figure 2c reveals decreased ozone mass mixing ratios across all latitudes, with the largest reductions in the extratropics. Figure 2 also provides insights into potential errors and uncertainties in the reanalyses. Comparisons between the solid lines, or between the dashed lines, highlight differences within each component. Relative differences in STEs between reanalyses and observations due to each component at the 380 K iesntrope are given in Figure 5 in Wang and Fu [22], with the largest differences caused by the diabatic heating component.
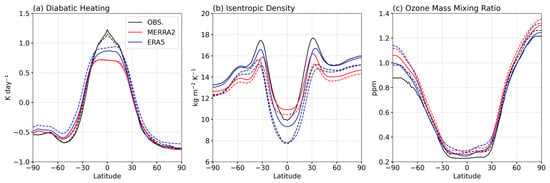
Figure 2.
The zonal-mean diabatic heating, isentropic density, and ozone mass mixing ratio for ERA5 (blue), MERRA2 (red), and observations (black) at the fitted (solid) and 380 K (dashed) isentropes, averaged for 2007–2010.
Wang and Fu [22] showed the net fluxes at the tropopause (i.e., STEs) for air mass and ozone and all relevant components based on MERRA2 for 2007–2010. Table 3 presents the comparison between the present study (black) and Wang and Fu [22] (blue) for these values. It is worth noting that the annual-mean climatology of net fluxes across the tropopause is approximately equal to the annual-mean diabatic fluxes across the isentropic surfaces, because the climatological mean of is zero and chemical sources in the lowermost stratosphere are negligible. Using the updated method, the magnitudes of the diabatic components at the tropopause for both air mass and ozone become smaller across all extratropical regions compared to results in Wang and Fu [22]. In the tropics, the adiabatic flux becomes zero. This is expected, as the fitted isentropic surface is used as the tropical tropopause. This mitigates any exchange that would have occurred through the gap between the static upper boundary and the tropopause.

Table 3.
Air mass (top) and ozone (bottom) fluxes and relevant components from MERRA2 for 2007–2010, including the flux across the isentropic surface, , the net tropopause flux, the diabatic tropopause flux, and adiabatic tropopause flux. The negative of ozone chemical sources in the lowermost stratosphere (−CTO3 is also shown. The values in black and blue are from the present study and Wang and Fu [22], respectively.
Figure 3 presents the seasonal cycle of the STE of air mass (left) and ozone (right) across all relevant components from MERRA2 for 1980–2020. The overall seasonal patterns remain consistent with those in Wang and Fu [22]. The small differences reflect the influence of improved vertical integration of mass, the use of a fitted isentropic surface, and tropopause definitions.
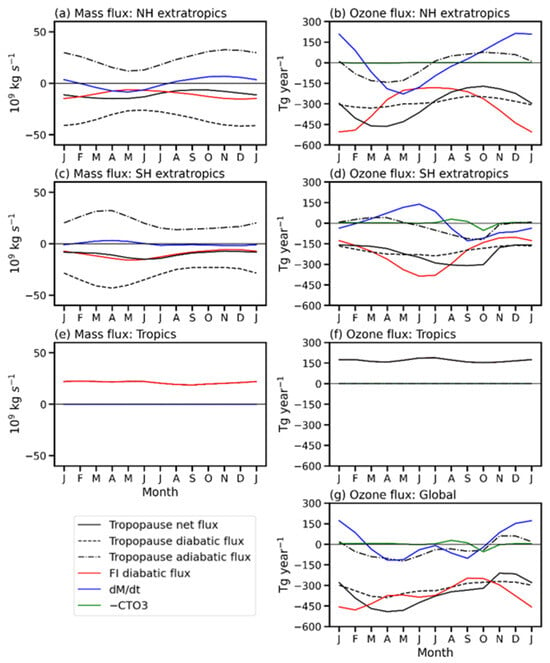
Figure 3.
Seasonal cycles of the tropopause net flux, the tropopause adiabatic and diabatic fluxes, the diabatic flux across the fitted isentrope, dM/dt, dO3/dt, and the chemical sinks (-CTO3) from MERRA2 for 1980–2020.
3.4. Cloud Heating at the Fitted Isentrope
This section details the effects of clouds on air mass and ozone fluxes across the fitted isentrope. Figure 4 illustrates longwave, shortwave, and total cloud heating latitudinal distributions. The results at the fitted isentrope (solid lines) present a similar structure to those at 380 K (dashed lines) [22]. Figure 4a highlights an increase in observationally derived longwave cloud heating relative to previous estimates. This increase primarily reflects the lowered isentropic surface intersecting more cirrus clouds [22,42,43]. Figure 4b shows negligible changes in shortwave heating, consistent with the low cirrus shortwave heating there.
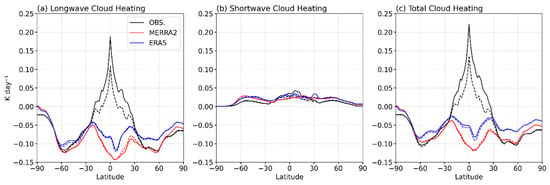
Figure 4.
Zonally and temporally averaged longwave, shortwave, and total cloud heating for ERA5 (blue), MERRA2 (red), and observations (black) for 2007–2010. The solid (dashed) lines are cloud heating at the fitted (380 K) isentrope.
The impact of cloud radiative effects on fluxes at the fitted isentropic surface and 380 K [22] is shown in Table 4. In the tropics, while negative cloud heating from reanalyses works to reduce the upward flux of ozone and air mass, the positive cloud heating based on observations enhances upward fluxes [22]. For reanalyses, the magnitude of cloud heating impacts on fluxes using the fitted isentrope remains similar to estimates at the 380 K level. In contrast, the observations show a marked increase in tropical upward flux due to cloud heating. The contribution of cloud heating to tropical air mass flux increases from 2.0% in Wang and Fu [22] to 8.2% in the present analysis. For ozone, the corresponding contribution increases from 1.8% to 8.1%.

Table 4.
The impact of cloud radiative heating on air mass (top) and ozone (bottom) fluxes across the fitted isentropic surface for 2007–2010. Percentages in parentheses represent the fraction of the flux affected. The values in black and blue are from the present study and Wang and Fu [22], respectively.
Figure 5 presents the spatial distribution of cloud radiative effects for the annual mean and four seasons. The observational results (left) highlight regions of positive cloud radiative heating in the tropics, associated with tropical cirrus clouds that are underrepresented in reanalyses (middle and right). These regions align with known patterns of persistent cirrus clouds [43]. While the spatial structure remains broadly consistent with Wang and Fu [22], the use of the fitted isentropic surface leads to a general increase in the magnitude of tropical cloud heating in observations. In reanalyses, the update results in only modest differences in the spatial structure of cloud radiative effects. One exception is an increase in longwave cloud heating over the Tibetan Plateau in ERA5 during boreal summer.
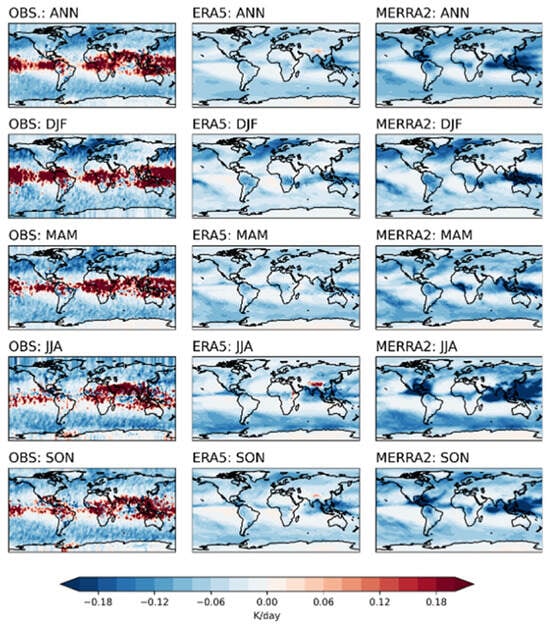
Figure 5.
Spatial distributions of cloud radiative heating at the fitted isentrope based on observations (left), ERA5 (middle) and MERRA2 (right) for annual mean and four seasons from 2007 to 2010.
4. Conclusions and Discussion
The updated method for deriving the change rate of mass in the lowermost stratosphere enables a more accurate estimation of the seasonal stratosphere-to-troposphere exchange (STE) of ozone in chemistry-climate models. Although the updated annual mean fluxes and trends remain consistent with earlier estimates, substantial seasonal discrepancies emerge in DJF and SON, particularly in the Northern Hemisphere. These improvements strengthen the foundation for evaluating seasonal STE fluxes and trends in chemistry-climate models.
Updated air mass and ozone fluxes across the fitted isentropic surface are shown based on ERA5, MERRA2 and observations for 2007–2010. The fitted isentrope lies consistently below the fixed 380 K surface, leading to a lower upper boundary for the lowermost stratosphere. Additionally, the tropopause used in the updated observational analysis is derived from COSMIC RO temperature profiles, rather than the ECMWF ancillary data included in the CloudSat product. The zero diabatic heating residing on the fitted isentrope, rather than on the tropopause, also shifts the tropical boundary. Under this new framework, the upward flux of air mass in the tropics increases from 19.3 × 109, 19.3 × 109, and 22.0 × 109 kg s−1 in Wang and Fu [22] to 21.9 × 109, 20.9 × 109, and 26.3 × 109 kg s−1 in the present study for ERA5, MERRA2, and observations, respectively. The global ozone fluxes across the fitted isentrope become −347.6, −362.5 and −368.4 Tg yr−1 as compared to −345.7, −359.5 and −335.6 Tg yr−1 at the 380 K level from Wang and Fu [22] for ERA5, MERRA2 and observations, respectively. The corresponding extratropical ozone fluxes are −539.3, −541.3 and −565.5 Tg yr−1 versus previous estimates of −538.1, −542.5 and −527.8 Tg yr−1.
The increased role of tropical cirrus clouds near the tropopause is also highlighted under the updated framework in observations. Longwave cloud radiative heating dominates the change in total cloud radiative effects. The contribution of cloud heating to tropical air mass flux increases from 2.0% in Wang and Fu [22] to 8.2% in the present analysis, while for ozone, the corresponding contribution increases from 1.8% to 8.1%.
This study represents updates to results shown in Wang and Fu [22], and therefore focuses on the time range from January 2007 to December 2010. To better understand the long-term role of clouds and improve comparisons with reanalysis products, future work should extend the observational time period. Additionally, as noted by Wang and Fu [22], the observational dataset still relies on ancillary analyses for temperature and humidity fields for clear-sky radiative heating rate calculations. A logical next step is to derive radiative heating rates entirely from observations using a radiative transfer model, eliminating dependence on reanalysis input.
Author Contributions
Conceptualization, A.H. and Q.F.; formal analysis, A.H., C.D. and Q.F.; investigation, A.H., C.D. and Q.F.; writing—original draft preparation, A.H.; writing—review and editing, A.H. and Q.F.; supervision, Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by NSF Grant AGS-2202812. Additional funding was provided by the Calvin Professorship in Atmospheric Sciences.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We thank Mingcheng Wang for valuable discussions and help regarding the analyses. We would also like to acknowledge high-performance computing support from Cheyenne (https://doi.org/10.5065/D6RX99HX, accessed on 31 August 2025) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation, for the analyses presented in this study and for data management, storage, and preservation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holton, J.R.; Haynes, P.H.; McIntyre, M.E.; Douglass, A.R.; Rood, R.B.; Pfister, L. Stratosphere-troposphere Exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
- Pan, L.L.; Honomichl, S.B.; Kinnison, D.E.; Abalos, M.; Randel, W.J.; Bergman, J.W.; Bian, J. Transport of Chemical Tracers from the Boundary Layer to Stratosphere Associated with the Dynamics of the Asian Summer Monsoon. J. Geophys. Res. Atmos. 2016, 121, 14–159. [Google Scholar] [CrossRef]
- Ramanathan, V.; Callis, L.; Cess, R.; Hansen, J.; Isaksen, I.; Kuhn, W.; Lacis, A.; Luther, F.; Mahlman, J.; Reck, R.; et al. Climate-chemical Interactions and Effects of Changing Atmospheric Trace Gases. Rev. Geophys. 1987, 25, 1441–1482. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Schwarzkopf, M.D.; Shine, K.P. Radiative Forcing of Climate from Halocarbon-Induced Global Stratospheric Ozone Loss. Nature 1992, 355, 810–812. [Google Scholar] [CrossRef][Green Version]
- Škerlak, B.; Sprenger, M.; Wernli, H. A Global Climatology of Stratosphere–Troposphere Exchange Using the ERA-Interim Data Set from 1979 to 2011. Atmos. Chem. Phys. 2014, 14, 913–937. [Google Scholar] [CrossRef]
- Stohl, A.; Bonasoni, P.; Cristofanelli, P.; Collins, W.; Feichter, J.; Frank, A.; Forster, C.; Gerasopoulos, E.; Gäggeler, H.; James, P.; et al. Stratosphere-troposphere Exchange: A Review, and What We Have Learned from STACCATO. J. Geophys. Res. Atmos. 2003, 108, 8516. [Google Scholar] [CrossRef]
- Bates, K.H.; Jacob, D.J. An Expanded Definition of the Odd Oxygen Family for Tropospheric Ozone Budgets: Implications for Ozone Lifetime and Stratospheric Influence. Geophys. Res. Lett. 2020, 47, e2019GL084486. [Google Scholar] [CrossRef]
- Fiore, A.M.; Jacob, D.J.; Field, B.D.; Streets, D.G.; Fernandes, S.D.; Jang, C. Linking Ozone Pollution and Climate Change: The Case for Controlling Methane. Geophys. Res. Lett. 2002, 29, 25-1–25-4. [Google Scholar] [CrossRef]
- Geng, L.; Murray, L.T.; Mickley, L.J.; Lin, P.; Fu, Q.; Schauer, A.J.; Alexander, B. Isotopic Evidence of Multiple Controls on Atmospheric Oxidants over Climate Transitions. Nature 2017, 546, 133–136. [Google Scholar] [CrossRef] [PubMed]
- Kentarchos, A.S.; Roelofs, G.J. A Model Study of Stratospheric Ozone in the Troposphere and Its Contribution to Tropospheric OH Formation. J. Geophys. Res. Atmos. 2003, 108, 8517. [Google Scholar] [CrossRef]
- Lin, M.; Fiore, A.M.; Horowitz, L.W.; Langford, A.O.; Oltmans, S.J.; Tarasick, D.; Rieder, H.E. Climate Variability Modulates Western US Ozone Air Quality in Spring via Deep Stratospheric Intrusions. Nat. Commun. 2015, 6, 7105. [Google Scholar] [CrossRef]
- Ordóñez, C.; Brunner, D.; Staehelin, J.; Hadjinicolaou, P.; Pyle, J.A.; Jonas, M.; Wernli, H.; Prévôt, A.S.H. Strong Influence of Lowermost Stratospheric Ozone on Lower Tropospheric Background Ozone Changes over Europe. Geophys. Res. Lett. 2007, 34, L07805. [Google Scholar] [CrossRef]
- Zeng, G.; Pyle, J.A.; Young, P.J. Impact of Climate Change on Tropospheric Ozone and Its Global Budgets. Atmos. Chem. Phys. 2008, 8, 369–387. [Google Scholar] [CrossRef]
- Levy, H. Global Transport of Ozone. In Tropospheric Ozone; Isaksen, I.S.A., Ed.; Springer: Dordrecht, The Netherlands, 1988; pp. 319–325. ISBN 978-94-010-7811-5. [Google Scholar]
- Xie, F.; Tian, W.; Chipperfield, M.P. Radiative Effect of Ozone Change on Stratosphere-troposphere Exchange. J. Geophys. Res. 2008, 113, D00B09. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (Ed.) Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-05799-9. [Google Scholar]
- Olsen, M.A.; Schoeberl, M.R.; Douglass, A.R. Stratosphere-troposphere Exchange of Mass and Ozone. J. Geophys. Res. Atmos. 2004, 109, D24114. [Google Scholar] [CrossRef]
- Appenzeller, C.; Holton, J.R.; Rosenlof, K.H. Seasonal Variation of Mass Transport across the Tropopause. J. Geophys. Res. Atmos. 1996, 101, 15071–15078. [Google Scholar] [CrossRef]
- Olsen, M.A.; Douglass, A.R.; Kaplan, T.B. Variability of Extratropical Ozone Stratosphere–Troposphere Exchange Using Microwave Limb Sounder Observations. J. Geophys. Res. Atmos. 2013, 118, 1090–1099. [Google Scholar] [CrossRef]
- Schoeberl, M.R. Extratropical Stratosphere-troposphere Mass Exchange. J. Geophys. Res. Atmos. 2004, 109, D13303. [Google Scholar] [CrossRef]
- Yang, H.; Chen, G.; Tang, Q.; Hess, P. Quantifying Isentropic Stratosphere-troposphere Exchange of Ozone. J. Geophys. Res. Atmos. 2016, 121, 3372–3387. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Q. Stratosphere-Troposphere Exchange of Air Masses and Ozone Concentrations Based on Reanalyses and Observations. J. Geophys. Res. Atmos. 2021, 126, e2021JD035159. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Q. Changes in Stratosphere-Troposphere Exchange of Air Mass and Ozone Concentration in CCMI Models From 1960 to 2099. J. Geophys. Res. Atmos. 2023, 128, e2023JD038487. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Q.; Solomon, S.; Alexander, B.; White, R.H. Stratosphere-Troposphere Exchanges of Air Mass and Ozone Concentration in the Last Glacial Maximum. J. Geophys. Res. Atmos. 2022, 127, e2021JD036327. [Google Scholar] [CrossRef]
- Gettelman, A.; Birner, T.; Eyring, V.; Akiyoshi, H.; Bekki, S.; Brühl, C.; Dameris, M.; Kinnison, D.E.; Lefevre, F.; Lott, F.; et al. The Tropical Tropopause Layer 1960–2100. Atmos. Chem. Phys. 2009, 9, 1621–1637. [Google Scholar] [CrossRef]
- Gettelman, A.; Forster, P.M.D.F. A Climatology of the Tropical Tropopause Layer. J. Meteorol. Soc. Jpn. 2002, 80, 911–924. [Google Scholar] [CrossRef]
- Reid, G.C.; Gage, K.S. On the Annual Variation in Height of the Tropical Tropopause. J. Atmos. Sci. 1981, 38, 1928–1938. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Q.; Hall, A.; Sweeney, A. Stratosphere-Troposphere Exchanges of Air Mass and Ozone Concentrations from ERA5 and MERRA2: Annual-Mean Climatology, Seasonal Cycle, and Interannual Variability. J. Geophys. Res. Atmos. 2023, 128, e2023JD039270. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; Wood, N.B.; Haladay, T.; Stephens, G.L.; Stackhouse, P.W. Impact of Clouds on Atmospheric Heating Based on the R04 CloudSat Fluxes and Heating Rates Data Set. J. Geophys. Res. 2008, 113, D00A15. [Google Scholar] [CrossRef]
- Henderson, D.S.; L’Ecuyer, T.; Stephens, G.; Partain, P.; Sekiguchi, M. A Multisensor Perspective on the Radiative Impacts of Clouds and Aerosols. J. Appl. Meteorol. Climatol. 2013, 52, 853–871. [Google Scholar] [CrossRef]
- McGill, M.J.; Vaughan, M.A.; Trepte, C.R.; Hart, W.D.; Hlavka, D.L.; Winker, D.M.; Kuehn, R. Airborne Validation of Spatial Properties Measured by the CALIPSO Lidar. J. Geophys. Res. 2007, 112, D20201. [Google Scholar] [CrossRef]
- Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.-P.; Hunt, D.C.; Kuo, Y.-H.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–334. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Wee, T.-K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and Error Estimation of GPS Radio Occultation Data. J. Meteorol. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef]
- Pirscher, B.; Foelsche, U.; Borsche, M.; Kirchengast, G.; Kuo, Y.-H. Analysis of Migrating Diurnal Tides Detected in FORMOSAT-3/COSMIC Temperature Data. J. Geophys. Res. 2010, 115, D14108. [Google Scholar] [CrossRef]
- Sweeney, A.J.; Fu, Q. Diurnal Cycles of Synthetic Microwave Sounding Lower-Stratospheric Temperatures from Radio Occultation Observations, Reanalysis, and Model Simulations. J. Atmos. Ocean. Technol. 2021, 38, 2045–2059. [Google Scholar] [CrossRef]
- Livesey, N.J.; Read, W.G.; Wagner, P.A.; Froidevaux, L.; Santee, M.L.; Schwartz, M.J.; Lambert, A.; Millán Valle, L.F.; Pumphrey, H.C.; Manney, G.L.; et al. Earth Observing System (EOS), Aura Microwave Limb Sounder (MLS), Version 4.2x Level 2 Data Quality and Description Document; Jet Propulsion Laboratory: La Cañada Flintridge, CA, USA, 2015. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K.; et al. The RCP Greenhouse Gas Concentrations and Their Extensions from 1765 to 2300. Clim. Change 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Morgenstern, O.; Hegglin, M.I.; Rozanov, E.; O’Connor, F.M.; Abraham, N.L.; Akiyoshi, H.; Archibald, A.T.; Bekki, S.; Butchart, N.; Chipperfield, M.P.; et al. Review of the Global Models Used within Phase 1 of the Chemistry–Climate Model Initiative (CCMI). Geosci. Model Dev. 2017, 10, 639–671. [Google Scholar] [CrossRef]
- Munchak, L.A.; Pan, L.L. Separation of the Lapse Rate and the Cold Point Tropopauses in the Tropics and the Resulting Impact on Cloud Top-Tropopause Relationships. J. Geophys. Res. Atmos. 2014, 119, 7963–7978. [Google Scholar] [CrossRef]
- Fu, Q.; Hu, Y.; Yang, Q. Identifying the Top of the Tropical Tropopause Layer from Vertical Mass Flux Analysis and CALIPSO Lidar Cloud Observations. Geophys. Res. Lett. 2007, 34, L14813. [Google Scholar] [CrossRef]
- Wang, T.; Dessler, A.E. Analysis of Cirrus in the Tropical Tropopause Layer from CALIPSO and MLS Data: A Water Perspective. J. Geophys. Res. 2012, 117, D04211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).