Abstract
The important role of neutral wind, its vertical shear, and external electric fields in the formation and localization of sporadic E (Es) are demonstrated analytically and numerically in equatorial and mid-latitude regions. The ion/electron density behavior, obtained analytically, indicates that their initial layer moves vertically at ion drift velocity. When the maximal total ion vertical convergence rate (MTotIVCR) (the minimal negative value of the ion drift velocity divergence), determined according to the wind velocity, wind shear, and electric field, exceeds ion/electron loss due to recombination and diffusive displacement, the initial layer peak density increases, and ion accumulation into narrow, high-density Es-type layers becomes possible. In this case, the Es layers formed localize either in the region surrounding ion drift velocity nodes or where they are frequently observed (around 100–105 km), where drift velocity disappears. Analysis and numerical simulations also show that an increase in the downward drift velocity and the total ion vertical convergence rate (TotIVCR), including the effects of westward or/and downward electric fields and westward or/and northward neutral wind, can also result in additional increases in the Es layer density as it descends to its localization region. The important contributions of the directions and magnitudes of meridional and zonal winds (using HWM14 data), wind shear, and electric field (using four different polarizations) to the vertical drift velocity of ions and, accordingly, the MTotIVCR (about 10−3–10−4 s−1), are evident during the formation of Es layers in typical equatorial regions (with magnetic inclination I = 0 and 0.5° N; 195° E) and between equatorial and mid-latitude (BEML) (I = 30°; 16° N; 195° E) and mid-latitudes (I = 60°; 45° N, 195° E) regions. For the zonal wind data and zonal and vertical components of the electric field considered, the importance of the electric field in the increase in the TotIVCR and the corresponding formation and localization of Es layers in the equatorial region is shown. If an electric field is present at mid-latitudes, it also can affect the increase or decrease in the TotIVCR and the localization of Es layers. It also has the ability to destroy these layers, which are formed under the combined effect of meridional and zonal wind velocities and vertical shear. In this case, the electric field also affects increases in the meridional wind factor with latitude in the formation and localization of high-density Es layers. This study shows that in addition to considering the vertical shear of neutral wind, it is necessary to take into account its magnitude and direction and the presence of electric fields to predict the possibility of sporadic E (Es) formation and localization.
1. Introduction
A complete theoretical mechanism for the formation of sporadic E (Es), capable of predicting its possible formation and localization region, is of increasing practical importance for modern continuous radio communications [1]. A complete mechanism of the formation and localization of Es layers is also important for studying the regional, global, vertical, and horizontal distribution of ionic composition, including metal ions, of the mesopause-lower thermosphere (MLT) [2,3,4,5]. Diurnal, seasonal, geomagnetic, and solar phase-dependent variations in ionic composition are related to corresponding changes in the formation of these irregular ionospheric structures [6,7,8].
Although many authors have considered that horizontal neutral wind with vertical shear (windshear mechanism) is the main mechanism of sporadic E (Es) formation [9] the formation and localization of Es layers observed in various regions around the globe indicate that sporadic E cannot be explained by the windshear factor alone [10,11,12,13,14,15,16]. An additional factor influencing ion vertical motion and, correspondingly, the formation of Es layers in the MLT is the presence of an external electric field [12,17], which becomes more important in equatorial regions [18,19,20,21]. Observational results also show that Es layers are not always localized to the region of wind polarization changes [16,22], which is in alignment with the windshear theory [23].
The influence of the meridional, zonal, and vertical components of neutral wind velocity and electric and geomagnetic fields on ion vertical drift [24,25], as well as their effect on the formation and localization of Es layers, are expected [26]. In this case, estimating the roles of all these factors in ion drift velocity, vertical changes in ion drift velocity, and, accordingly, ion/electron density behavior will increase the likelihood of predicting the formation and localization of these layers in the MLT.
The analytical form of the temporal evolution of an initial ion/electron Gauss-type layer, recently obtained by Didebulidze et al. [27,28] and Dalakishvili et al. [29], shows the possibility of its transformation into a narrow, high-density Es-type layer in the MLT. In this case, when the minimal negative value of ion drift velocity divergence (corresponding to the maximal total ion vertical convergence rate, MTotIVCR), determined according to the wind velocity and its shear, exceeds ion/electron loss due to recombination and diffusive displacement, the initial ion/electron layer peak density increases, and the accumulation of ions into narrow, high-density Es-type layers is possible. This Es layer, which has an increasing density, moves at ion drift velocity and localizes around its node (the region in which the ion drift velocity is equal to zero or a minimal value and where their upward and downward flux to this region increases) or descends to the region wherein which drift velocity disappears [30]. If only meridional or/and zonal winds are present, the latter region corresponds to the upper region of the bottom of the lower thermosphere (around 95–105 km), where Es layers are observed more frequently [12,22,31].
In this present study, differing from Didebulidze et al. [26], we estimate the fractions and corresponding roles of the neutral wind velocity (with meridional and zonal components), its vertical shear, and the electric field (with zonal and vertical components) in the TotIVCR. We also develop the conditions for the formation of higher density Es layers descending and localizing to the bottom of the MLT region, which occurs in the equatorial and mid-latitude regions. For these cases, we demonstrate the importance of the electric field in combination with wind velocity and shear for the TotIVCR and the formation of high-density Es layers.
Our numerical simulations include (1) the ion vertical drift velocity; (2) vertical changes in the ion vertical drift velocity; (3) ion/electron density; and (4) the corresponding fractions of wind velocity, wind shear, and electric field in the TotIVCR. These simulations were performed for a typical equatorial region (e.g., with magnetic inclination I = 0 and 0.5° N; 195° E), between equatorial and mid-latitude (BEML) regions with I = 30° (16° N; 195° E), and mid-latitude regions with I = 60° (45° N, 195° E). The presence of an electric field characteristic of equatorial regions [32,33,34] with four different polarizations is also assumed for mid-latitude regions. Horizontal wind model (HWM14) data were used for meridional and zonal wind height profiles [35].
As a result, we show that in addition to the important role of the vertical shear of horizontal wind in the TotIVCR and, accordingly, in the formation of Es layers, it is also important to consider the combined effect of the wind magnitude and direction and the electric field (if present) in both the formation of these layers and in determining their localization regions at equatorial and mid-latitudes.
Our analytical and numerical results show that the conditions required for the vertical convergence of ions and their accumulation into Es-type layers are irregular, and to predict the formation of these layers, it is important to know the experimental/model wind profile and near-real-time electric field data. Accordingly, under these conditions, the frequency and localization of Es-layer formation, as determined by the combined action of wind magnitude, direction, and shear and electric field factors depending on diurnal, seasonal, and geomagnetic disturbances and solar phases, are important for studying the features of the corresponding changes in the regional and global distribution of metal ions [2,36].
2. Theoretical Context for the Role of Wind Velocity, Wind Shear, and Electric Field Effects in the Formation of Sporadic E (Es)
The main parameters for estimating the vertical motion of ions/electrons, their convergence into a thin layer, and the corresponding formation of sporadic E (Es) are the height profiles of ion drift velocity and its vertical changes [22,29,37,38], which are determined by the effects of neutral wind velocity and shear and electric and geomagnetic fields. We assume that the horizontal changes in ion vertical drift velocity are smaller than its vertical changes; thus, in this study, ion drift velocity divergence is determined by the ion vertical drift velocity. In this case, the main condition for ion vertical convergence and the formation of an Es layer for a given region of the lower thermosphere (with arbitrary geomagnetic inclination I) is a minimal negative value of ion drift velocity divergence [29]:
In this case, for an ion density with a Gaussian-type initial layer , peak density at height (initial peak height), and characteristic ionic scale height ,
under condition (1), ions can accumulate into a thin layer and form an Es layer. Like in Didebulidze et al. [26,27,28], this layer can be described by an approximate analytical solution of the ion/electron density continuity equation (assuming quasi-neutrality and taking into account the rates of formation and loss ):
Here, small variations in the ion drift velocity , its divergence , and the vertical changes in production (Q) and loss (L) rates during time are assumed. is the ion vertical diffusion coefficient, which is taken into account in the ion total vertical drift velocity in addition to its drift velocity in the absence of diffusion, and has the following form:
Here, separating the diffusion displacement of ions () from the total vertical drift velocity in a given altitude range makes it possible to determine the conditions for the vertical convergence of ions, taking into account their production (Q) and loss (L) rates. In this case, according to Equation (3), describing the evolution of the initial ion/electron Gaussian-type layer that moved vertically at ion drift velocity , a more generalized condition for ion vertical convergence is
However, this mostly applies to the height region with because the impact of diffusion and production Q and loss L rates in the MLT for an ion initial layer with is negligibly small.
In this study, the ion vertical drift velocity in equatorial and mid-latitude regions is determined by the horizontal neutral wind velocity and electric field and has the following form [25,29]:
where
In this case, the coefficient of ion vertical diffusion in the ion total vertical drift velocity , Equation (4), is
and are the ionic and electronic temperatures, respectively. , where and are the ion-neutral collision frequency and ion gyrofrequency, respectively. is the Earth’s magnetic field vector.
According to the roles of neutral wind, wind shear, and electric field in ion/electron vertical convergence (), determined in Equations (1) and (5), and, correspondingly, in the formation of the Es layers, we estimate the ion vertical drift velocity , like in Didebulidze et al. [26], which has the following form:
where , , and are the parts/fractions of the vertical shear (,) of the meridional and zonal components of the horizontal wind velocity , the wind velocity magnitude and direction, and the external electric field , respectively, with effects of the zonal and vertical components on the total ion vertical convergence /divergence rate. Hereafter, the value of , which describes the rate of increase/convergence in ion/electron density , Equation (3), will be referred to more definitely as the total ion vertical convergence rate (TotIVCR).
The value of , which describes the rate of ion/electron density decrease , Equation (3), will be referred as the ion/electron divergence rate. Below we use the peak height of the maximal value of TotIVCR (MTotIVCR) , where
Using Equations (6)–(8) in Equation (10), we obtain equations for the contributions of wind shear, wind speed, and electric field to the total ion convergence/divergence rates:
Here,
Note that in equatorial region (I = 0), the fraction of the ion convergence rate caused by windshear in the TotIVCR, Equation (10), is significantly dependent on the vertical shear of the zonal component of wind velocity , while in mid-latitude regions, the windshear convergence rate is determined by the combined effect () of the vertical shear of the meridional () and zonal () winds, Equation (12).
The wind velocity convergence rate , Equation (13), in the TotIVCR, Equation (10), in an equatorial region (I = 0) caused by zonal wind velocity and at mid-latitudes () caused by both meridional and zonal wind velocities () is determined by vertical changes in ion-neutral collisional frequency (or ), resulting in and , Equations (15) and (16).
The fraction of the electric field , Equation (14), in the TotIVCR, Equation (10), also depends on the height profiles of the factors of , , , and , Equations (7), (8), (15) and (16), respectively. If there are small changes in the electric field , these factors have a significant effect on the height profiles of and, correspondingly, the maximal TotIVCR, Equation (11), in the formation of Es layers.
In the next section, unlike the previous consideration [26], we numerically show the important fraction (role) of each of the parameters , , and , determined by Equations (12)–(14), in the MTotIVCR , Equation (11), and, correspondingly, in the formation of Es layers, which are predicted using the analytical approach , Equation (3), for the evolution of a Gaussian-type initial layer.
On the basis of the numerical estimation, we also develop the TotIVCR condition, obtained from Equation (3), for an initial layer descending into the region in which and . This condition occurs at equatorial and mid-latitude regions and can be caused by an electric field or/and neutral wind velocity in case of an absence of (or decreased) windshear. In this case, Es layers with higher density () can form at the bottom of the MLT (around 95–105 km), where they are observed more frequently [12,22,31]. For simplicity, we assume the presence of only metallic ions, Fe+ and .
3. Results and Discussion
We demonstrate the time-varying parameters of the windshear (described by ), wind velocity (described by ), and electric field (described by ) in the MTotIVCR , Equations (10)–(16), during the formation of Es layers at equatorial (I = 0) and mid-latitude regions with I = 30 and I = 60. In this case, estimating the ion drift velocity height profile, Equations (6)–(8), allows us to identify the height region with or/and , where Es layer localization is expected. By the height profile the height profile of , Equations (10)–(14), and the corresponding height and MTotIVCR values are estimated, showing the possibility of Es layer formation (Equation (3)). The formation and localization of the Es layers predicted by Equation (3) are demonstrated for an initial ion/electron layer maximum at . In this case, at the height , the values of the windshear , wind velocity , and electric field factors, resulting in MTotVICR , are estimated.
This estimation uses an electric field with four different polarizations (e.g., , ) and possible values of its zonal and vertical components in the equatorial region [32,33,34,39]. The presence of an electric field with the same zonal and vertical components in regions between equatorial and mid-latitudes I = 30° (16° N; 195° E) and at mid-latitudes I = 60° (45° N, 195° E) is also considered. These electric field component values ( and ) are chosen in accordance with the model data [32,33] and taking into account that near these values, their influence on the vertical drift velocity of ions , Equation (6), is comparable to the effect caused by the meridional and zonal components of the horizontal neutral wind velocity . Here, we assume that the meridional and horizontal wind velocities are about 10–60 m/s, according to HWM14 data for the height region (about 90–150 km) of the lower thermosphere in equatorial and mid-latitudes [35]. We also note that different electric field directions may be characteristic for different heliogeophysical conditions, and considering opposing electric field directions may reveal a possible role of the known daily reversal of the E-region electric field in the formation or disruption of Es layers [17,19,34].
For the meridional and zonal wind velocities, we use a realistic altitude profile, according to HWM14 data [33], for a day around the September equinox (e.g., day 264). The neutral densities for the MLT region are chosen in accordance with the NRLMSISE00 model [40].
Figure 1 shows the HWM14 data of the horizontal neutral wind velocity’s meridional (left columns) and zonal (right columns) components at equatorial I = 0 (0.5° N; 195° E), between equatorial and mid-latitudes (BEML) I = 30° (16° N; 195° E) and mid-latitudes I = 60° (45° N, 195° E), for day 264.
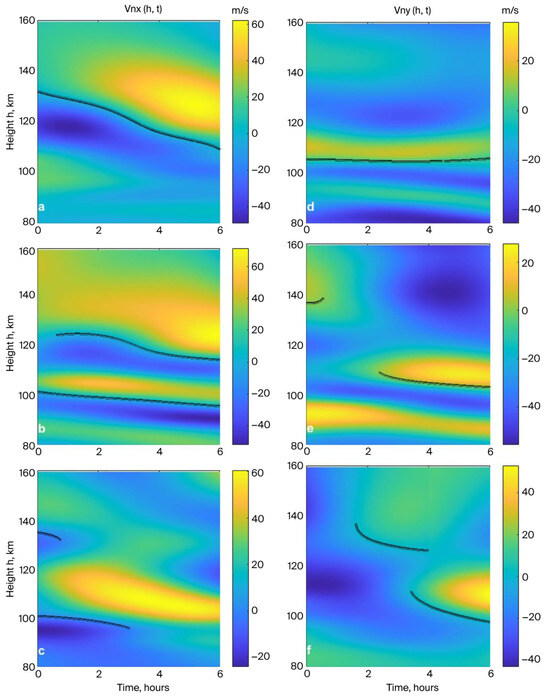
Figure 1.
The horizontal wind model data (HWM14) for the neutral wind velocity (a–c) meridional and (d–f) zonal components at (a,d) equatorial I = 0 (0.5° N; 195° E), (b,e) regions between equatorial and mid-latitudes (BEML) I = 30° (16° N; 195° E), and (c,f) mid-latitudes I = 60° (45° N, 195° E) for day 264 and time interval ( corresponds UT = 08:00 for day 264 in the considered regions). Full lines correspond to the meridional and zonal wind polarization changes with positive vertical shear values of (a–c) and (d–f).
Figure 1 shows that the wind profiles in the equatorial I = 0 region, as well as at BEML I = 30° and mid-latitudes I = 60° for the time interval , always have a region with polarization changes in the meridional and zonal winds at the height where (panels a, b, c) and (panels d, e, f), with important positive vertical shear values of and , respectively. The height of meridional and zonal changes in wind polarization differs between equatorial (see Figure 1a,d) and mid-latitudes (see Figure 1b,c,e,f). Accordingly, this meridional difference in the wind height profile reflects the difference in the altitude profile of the vertical drift velocity of ions and vertical changes in this vertical drift velocity; see Equation (6).
In these cases, in the equatorial region (I = 0), assuming the absence of an electric field E = 0, the node of the vertical drift velocity of ions (the height region with and an increase in vertical ion flux into this region) will be determined by the zonal wind and its shear, per Equation (12). In the same case (E = 0), in mid-latitudes, it will be determined by the combined action of the meridional and zonal wind velocities and their vertical shear ( and ) [41,42].
In accordance with the above consideration, a meridional effect on the formation and localization of Es layers under the influence of only horizontal wind is expected. Taking into account the presence of an electric field, which influences the ion vertical drift velocity , Equation (6), and vertical changes in ion vertical drift velocity (), Equation (10), differences in its influence on Es layer formation and localization at equatorial and mid-latitude regions are also expected.
Figure 2 shows that the ion vertical drift velocity (panels a, b, and c), determined by the horizontal wind meridional and zonal components, Equation (6), always has a region in which or . Around these regions, the total convergence/divergence rate (panels d, e, and f) has an MTotIVCR (see panels k, l, and j), and high-density Es layers form (panel g: ; panel h: ; panel i: ). These Es layers (see Figure 2g–i) localize at ion vertical drift velocity nodes and/or in regions in which . In these cases, in the absence of an electric field, the impacts of the vertical shear of the neutral wind velocity and the velocity magnitude and direction (see panels k, l, j) always occur for the considered time in equatorial (panel j), BEML (panel k), and mid-latitude (panels l) regions. In the case considered, using the HWM14 data (day 264) for equatorial (I = 0—upper panels), BEML (I = 30°—middle panels), and mid-latitude (I = 60°—bottom panels) regions, the height profile of the ion vertical drift velocity and its vertical changes determine the ion/electron density behavior. Here, the MTotIVCR (about ), the presence of which determines Es layer formation, is mostly determined by the windshear fraction , but the wind magnitude and direction fraction are also important in equatorial (Figure 2j), BEML (Figure 2k), and mid-latitude (Figure 2l) regions. For example, in the case of high-density Es layers formed at BEML and mid-latitudes for a time of (Figure 2k,l), the MTotIVCR (about ) is primarily determined by the wind velocity factor of (. Correspondingly, these layers are formed without the windshear effect.
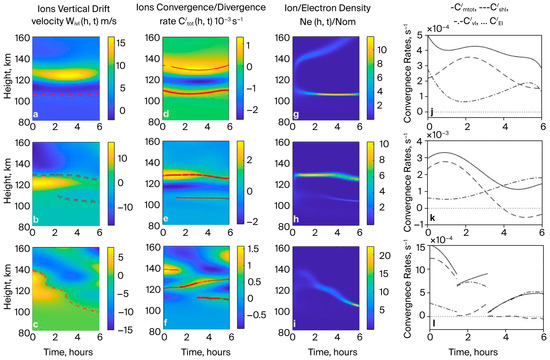
Figure 2.
(a–c) The ion vertical drift velocity , (d–f) its vertical convergence/divergence rate , (g–i) ion/electron density behavior , (j–l) (dashed lines), (dashed–dotted lines), and (dotted lines) at the height of MTotIVCR (full lines). Upper panels (a,d,g,j) correspond to the equatorial I = 0 (7° N; 195° E), middle panels (b,e,h,k) to BEML I = 30°, and bottom panels (c,f,i,l) to mid-latitude I = 60° (45° N, 195° E) regions in the case in which meridional () and zonal () wind is determined by the HWM14 data given in Figure 1 and the external electric field is absent (). The ion/electron density initial peak () is located at . (a–c) Red dashed lines correspond to the heights of ion drift velocity nodes with ; (d–f) red solid lines correspond to the peak heights of the MTotIVCR , where the values of , , and (j–l) are estimated for solid-line time intervals.
Here, in the equatorial region, the values of and, correspondingly, the MTotIVCR are determined by the zonal wind; however, at mid-latitudes, the values depend on the combined effect of the meridional and zonal winds. This combined effect results in different behavior of the Es layers at BEML and mid-latitude compared to in the equatorial region. In these cases, the wind velocity value (see Figure 1) at the equator and the height regions of its polarization changes (with ) differ from those at BENL and mid-latitudes (with or/and ). Thus, their combined effect influences ion vertical drift velocity and its vertical changes differently, resulting in different localization regions and behaviors.
Cases in which the formed Es layers descend to their more frequently observed height in the lower thermosphere (around 95–105 km) are noticeable for equatorial (see Figure 2h: Es layer formed at h < 110 km), BEML (See Figure 2g: Es layer formed at h < 110 km), and mid-latitudes (Figure 2i).
The electric field significantly affects the vertical drift velocity of ions , Equation (6). Accordingly, it is expected to influence the formation and behavior of the Es layers, in addition to the neutral wind velocity and its shear effect. We will demonstrate the case in which an external electric field with four different polarizations (e.g., , ; , ; , ; , ) is present.
This electric field can cause (1) additional upward or downward drift of ions, leading to a change in the region of the height of drift velocity node with (or regions in which ); (2) changes in the magnitude and height of the peak of the total ion/electron vertical convergence rate ; and (3) an effect on the formation of the Es layer and its localization and density, which differ from in the case in which only horizontal wind is present (see Figure 1). Thus, using Equations (10)–(14), it is possible to estimate the magnitude of and its fraction in the total vertical convergence rate of ions and, accordingly, its role in the formation of Es layers in combination with the wind velocity and shear fractions in equatorial (I = 0), BEML (I = 30°) and mid-latitudes (I = 60°), similar to that shown in Figure 2.
Figure 3, similar to Figure 2, shows the presence of an electric field with westward and upward components.
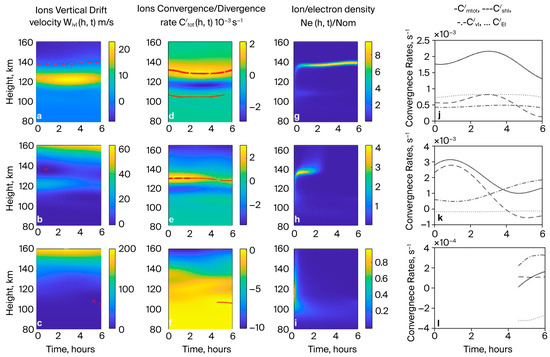
Figure 3.
The same as in Figure 2, with the presence of an electric field with westward and downward components.
Figure 3 shows that the additional combined effect of downward () and upward () ion drifts caused by the westward and upward electric field components leads to changes in the height profiles of the vertical ion drift velocity , Equation (6); its nodes (panels a, b, c); and their total convergence ()/divergence () rates (panels d, e, f), Equation (10), compared to the case of horizontal wind only (Figure 2a–f).
In the case with an electric field , the behavior of the ion/electron density (panels g, h, i), as well as the formation and localization of the Es layers (panels g and h), align with the nodes of the ion vertical drift velocity and the MTotIVCR , which, in addition to the wind velocity and its shear fraction, also includes the contribution of the electric field (Figure 3j–l).
In this case, this contribution of the electric field to the ion drift velocity , the total convergence rate, and its peak value during the formation of Es-type layers is different at equatorial I = 0 (Figure 3a,d,g,j), BEML I = 30° (Figure 3b,e,h,k) and mid-latitudes I = 60° (Figure 3c,f,i,l).
In the equatorial region (I = 0), the electric field and zonal wind (Figure 1d) result in the formation of an ion drift velocity node at about 140 km and at an altitude of about 135 km, and the Es layers form (see Figure 3g: ) at an altitude near the drift velocity node (140 km). In this case, the magnitude of the fraction of the electric field (about ) exceeds the fractions of the wind velocity and its shear, > and .
Thus, in the equatorial region, the electric field may play a dominant role in the formation and localization of the Es layer.
The presence of an electric field (with westward and upward components) in the region I = 30°, in combination with the meridional and zonal winds, causes an ion drift velocity node (at about 137 km in altitude, see Figure 3b) and (at about 127 km in altitude, see Figure 3e), leading to the formation of an Es layer (see Figure 3g: ) with a lower density than in the case in which only neutral wind is present (see Figure 2g).
In this case, the electric field causes a negative (see Figure 3l) value and a corresponding decrease in compared to the value in the absence of the electric field (see Figure 2l).
Figure 3c,f,i,l show that at mid-latitudes (I = 60), the electric field under consideration (with and ) causes a dominant upward drift of ions (Figure 3c) and a mostly negative value of . This causes ions/electrons to diverge from the initial layer, and a high-density Es-type layer does not form. In this case, for time , the presence of cannot cause a significant increase in the ion/electron density in the rarefied region (Equation (3)). Thus, the electric field ( and ) can result in the disappearance of the Es layer that formed in the presence of horizontal wind.
The above consideration shows that the electric field’s influence on the behavior of the ion/electron density and the formation of Es layers can differ according to its polarization.
In Figure 4, similar to Figure 2, the outcomes in the presence of an electric field with westward and downward components are shown.
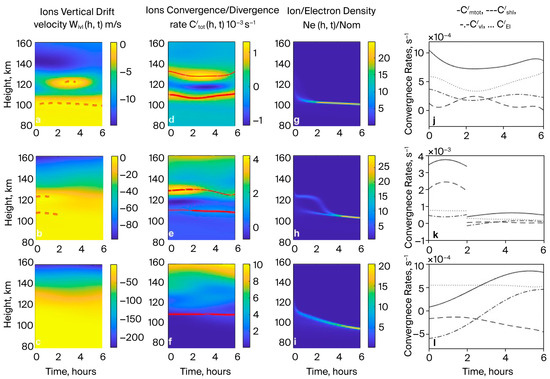
Figure 4.
Similar to Figure 2, showing the presence of an electric field with eastward and downward components.
Figure 4 shows that the ion drift caused by the electric field, with the considered westward and downward components, is predominantly downward (see Figure 4a–c), Equation (6), and the total convergence/divergence rates (see Figure 4d–f), Equation (10), also contain values (see Figure 4j–l). In these cases, the Es layers (see Figure 4g–i) descend to the height in which (Figure 4g,h) or (Figure 4i).
Figure 4a,d,g,j show that in the equatorial region (I = 0), the electric field results in an increase in the vertical convergence of ions, > and , and causes a corresponding increase in the total convergence rate (see Figure 4j) at the altitude of the main convergence peak (about 115 km, see Figure 2d and Figure 4d). In this case, the Es layer’s descent to the height region within which , where , results in the formation of a higher-density Es layer (about ) than the layer that formed when zonal wind alone was present (see Figure 2g: ). Based on Equation (17), the latter outcome is expected.
Figure 4b,e,h,k show that at BEML (I = 30°), although the electric field influences the peak MTotIVCR value (see Figure 4e,k), its contribution is relatively smaller than that of the wind and its shear.
In this case, the increase in the speed of descent (Figure 4b) of the Es layers to the region around h = 100 km (Figure 4h), with and TotIVCR (Figure 4e), caused by the westward and downward components of the electric field, Equations (6) and (14), leads to the formation of a higher density Es layer () than the layer that formed under the influence of only neutral wind (see Figure 2h: ).
Note that descent of the ion/electron layer at a drift velocity in the case of the TotIVCR causes an additional increase in their densities during the descent (e.g., for time , see Figure 4b,e,h) and localization to the region with (see Figure 4h). This can be predicted using Equation (3) under the following conditions:
Here, is some lower height at the bottom of the MLT, below which the vertical drift velocity of ions changes insignificantly, and the diffusion displacement and recombination of ions lead to a decrease in their density. According to Equation (3) and condition (17), the increase in the density of the Es layer (convergence instability) during its descent to the bottom of the lower thermosphere (about 100–105 km), where , will be mainly compensated by an increase in the ion recombination rate (the diffusion displacement of ion/electrons is relatively small). Taking into account ion production (), this can result in an additional increase in the Es layer density.
For time (see Figure 4k), the electric field fraction () exceeds the wind velocity () and its shear fraction () in the MTotIVCR . Equation (17) corresponds to the condition under which Es layers can form without windshear.
Figure 4h also shows that for the time interval , the upper layer (formed mostly due to the windshear effect for time at about 120 km) descends at a higher velocity and localizes in the region of the lower Es layer (which is formed by dominance of electric field factor about 100 km), which descends at a slower speed. This results in the formation of single-layer sporadic E.
Figure 4c,f,i,l also show an important increase in the downward drift velocity of (see Figure 4c) at mid-latitudes (I = 60°). In this case, the TotIVCR is (Figure 4f), where the effect of the electric field is greater than the wind shear effect for the whole time interval considered (Figure 4l). This means that the formation of an Es layer with increased density () during its descent into the region with (see Figure 4i) occurs without the windshear effect and can be predicted from Equation (3) and condition (17). In this case, the density of the formed Es layer is greater () and approximately the same as when it forms due to the wind effect only (see Figure 2i). The possibility Es layers forming under the influence of horizontal wind without the windshear effect in regions h < 110 km, where they are observed more frequently, also is noted by Dalakishvili et al. [29] and Tang et al. [13].
Thus, for the considered electric field polarization and the HWM14 data for (Figure 1), Es layers form at equatorial, BEML, and mid-latitudes (see Figure 4g–i) at higher densities than in the presence of horizontal wind only (see Figure 2g,h). Next, we consider the case of an electric field with polarization opposite to that in Figure 4, .
In Figure 5, similar to Figure 2, the outcomes in the presence of an electric field with eastward and upward components are shown.
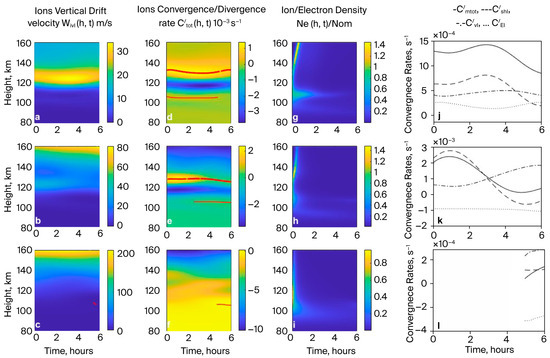
Figure 5.
Similar to Figure 2, showing the presence of an electric field with eastward and upward components.
Figure 5 shows that the upward drift of ions caused by the eastward and upward components of the electric field, Equation (6), causes an increase in the upward drift of ions/electrons (see Figure 5a–c) and in the total convergence/divergence rates (see Figure 5d–f), Equation (10). Values of (see Figure 5j–l) also occur for a short time interval of . In this case, the Es layers formed with relatively low density (about 1.4) (see Figure 5g,h) flow upward above an altitude of 140 km with an ion/electron drift velocity (see Figure 5a,b).
This upward drift of the initial ion/electron density layer leads to its disappearance at greater heights, h > 130 km, and to an increase in the diffusion effect to the mid-latitudes (see Figure 5h), Equation (9). However, Es layers do not form at the mid-latitudes (I = 60°) (see Figure 5i) due to the upward drift of ions/electrons (see Figure 5c) and an increase in diffusion displacement at these upper heights. This rarefaction of ions/electrons in the upper heights (h > 130 km) of the lower thermosphere does not allow for the formation of a high-density Es-type layer in the time interval , where the conditions and (see Figure 5i,l) necessary for its formation are fulfilled at a height of about h = 105 km.
Thus, Figure 5 shows that the electric field under consideration causes an increase in the vertical convergence of ions and only for equatorial regions (see Figure 5j), while for mid-latitudes, it causes a divergence (see Figure 5k,l) and, accordingly, a decrease in (see Figure 5e,f). In these cases, a decrease in the Es layer density (Figure 5h) or its disappearance (Figure 5i) occurs compared to the cases in which only neutral wind is present at mid-latitudes (see Figure 2h,i).
We also consider the case of an electric field with polarization opposite to that in Figure 3, .
In Figure 6, similar to Figure 2, the outcomes in the presence of an electric field with eastward and downward components are shown.
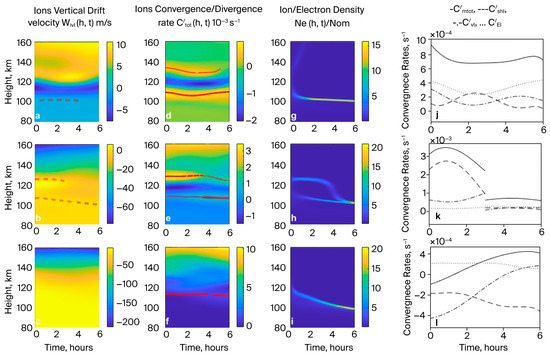
Figure 6.
Similar to Figure 2, in the presence of an electric field with eastward and downward components.
Figure 6 shows that the additional combined effect of the ions’ upward (caused by eastward ) and downward (caused by downward ) electric field components results in an increase in the downward drift velocity , Equation (6), and, correspondingly, a lower location (about 100 km) of nodes (Figure 6a,b) compared to the case without an electric field (see Figure 2a–c). The electric field causes an important increase in the MTotIVCR at equatorial, I = 0 (Figure 6d,j), and mid-latitude, I = 60°, regions, but its increase at BEML, I = 30°, is smaller (Figure 6e,k).
The increased MTotIVCR in the equatorial region with I = 0 results in higher-density Es layers (Figure 6g: ) relative to the case in which only horizontal wind velocity and its shear effect are considered (see Figure 2g,h).
Note that despite the small contribution of the electric field to the MTotIVCR at BEML with I = 30 (Figure 6k), the increase in the downward drift velocity of ions it causes (Figure 6b) results in the convergence of two relatively high-density Es layers, which formed in upper (about h = 125 km) and lower (about h = 110 km) height regions, into a single high-density layer (Figure 6h: ) toward the lower (about h = 100 km) region. This process, which would not be observed in the presence of wind alone (see Figure 2h), can be predicted using Equation (17).
The electric field fraction also has an important effect on the MTotIVCR (Figure 6l) at mid-latitude and the increase in the downward drift velocity of ions/electrons (Figure 6c) descending to the region with , resulting in the formation of higher-density Es layers (Figure 6g,i) without the windshear factor. This is also expected from condition (17).
Thus, to study the role of wind velocity, wind shear, and electric field in the formation and localization of sporadic E (Es), we numerically demonstrate the behavior of the vertical drift velocity of ions (Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels a–c), their total convergence (>0)/divergence (<0) rates (Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels d–f), the ion/electron density (Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels g, h, i), and the fractions of wind velocity (), wind shear (), and electric field () in the MTotIVCR (see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels j, k, l).
Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (panels j, k, l) show that the horizontal neutral wind velocity, its shear, and the electric field are important for formation and localization of sporadic E (Es) at equatorial and mid-latitudes. We used HWM14 data to select the height profiles of the meridional and zonal components, and the values of the electric field’s zonal and vertical components are characteristic of the equatorial region [32,33,34]. To study the importance of the electric field in these processes, we also assumed its presence at BEML and mid-latitudes.
Using approximately the same order of electric field (including a value of about 0.5–1.2 mV/m) demonstrated its importance in the formation/destruption of Es layers in the equatorial region [17,19]. The influence of its daily reversal (mainly on the zonal component) on the development of these processes also is demonstrated when various directions/polarizations of the electric field are considered [34]. Unlike previous considerations [17,19,34], in this study, the conditions for the formation of Es layers, Equations (5) and (17); the electric field, Equation (14); and the vertical shear of the zonal and meridional components of the horizontal wind velocity, Equation (12) also include the influence of the direction and magnitude of its velocity, Equation (13). The integration of these convergence factors into the total ion convergence/divergence rate (Equation (11)) allowed us to consider for the first time, to the best of our knowledge, the role of the electric field, horizontal wind velocity, and its vertical shear in the formation of Es layers. It is also possible to distinguish the roles of these parameters in the sublayers (e.g., see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) of the sporadic E.
This theoretical study demonstrates the possibility of using arbitrary modeled/observed wind velocity and electric field data to estimate the ion vertical drift velocity and its vertical variations and, accordingly, the behavior of the ion/electron density in the MLT region. The theoretical conditions for TotIVCR, Equations (5) and (17), required for the formation of Es layers and their localization in the regions of ion drift velocity nodes or regions with and obtained from the analytical ion/electron density height profile, Equation (3), can be used for various parameters characteristic of the MLT region, including ion production and loss rates. The condition (17) and numerical simulations also show the possibility of the formation of higher density Es layers without the windshear effect in equatorial and mid-latitude regions, which can also be predicted from Equation (3). In this case, the use of near-real-time neutral wind velocity, shear, and electric field data is more convenient for predicting the possibility of Es layer formation and localization for a given region.
The actual wind velocity also includes its vertical component, which can influence the formation and localization of Es layers and has been theoretically demonstrated in the absence of an electric field [28]. The influence of vertical wind on the formation of Es layers was also observed using a method based on the creation of artificial periodic inhomogeneities in the ionospheric plasma [43]. Our future research will take into account the role of the electric field and the magnitude of the actual wind velocity, its direction, and vertical changes in all its components in the vertical convergence of ions and the formation of Es layers. Such a study, including an analytical approach to the formation of the Es layer, similar to Equation (3), will be developed by including the effect of the vertical component of the neutral wind velocity (e.g., see [28]) in the vertical drift velocity of ions, Equations (4) and (6), and its vertical changes to describe the TotIVCR, which, in turn, would include the vertical wind factor.
The initial distribution of charged particles, the neutral wind velocity, and the electric field undergo daily, inter-annual, and solar- and geomagnetic-activity-dependent variations [1,36]. We can use the peak height of the initial ion layer, Equation (2), at different altitudes, which can influence the formation of Es layers [26,29] and, accordingly, the role of wind velocity, its shear, and the regional electric field. For brevity, a peak height , which is close to the most frequently observed electron density, was chosen as it is convenient for demonstrating the most important properties of the formation of Es layers (see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6). The use of thermosphere–ionosphere parameters in accordance with model data [32,44,45] is important in studying the formation of sporadic E [2,4,5,46,47] and for the development of models to describe the formation and localization of Es layers globally. It is also important to consider the role of the actual neutral wind velocity magnitude, direction, and shear and the role of the electric field in vertical ion convergence/divergence processes [26,46,47]. Using near-real-time data for these parameters increases the possibility of predicting the probability Es layer formation and localization for a given region of the globe. It also benefits the study of the specifications of their formation frequency, which are associated with the features of the regional and global distribution of metal ions in the MLT [2,3,5]. Note that the condition required for the development of ion vertical convergence, which is necessary for the formation of Es layers, Equation (5), was obtained from the ion continuity equation, assuming the dominance of metallic Fe+ ions. Condition (5) can be derived similarly for any ion species in the MLT, including molecular ions (e.g., O2+, NO+) and metallic ions (e.g., Mg+, K+, Ca+, Na+) [3,5], using their continuity equations and taking into account the downward drift velocities; ion-neutral collision frequencies; and diffusion, production and loss rates of each ion species. This approach can be the subject of future modeling studies.
4. Conclusions
The important role of the neutral wind velocity (e.g., using the HWM14 data), its meridional and zonal components, vertical shear ( and ), and the external electric field (e.g., with zonal and vertical components close to the modeled data [32,33]) in the formation and localization of sporadic E (Es) has been shown analytically and numerically. These parameters significantly affect the ion vertical drift velocity ; vertical changes in this value; and, correspondingly, ion/electron density behavior in the MLT.
The conditions required for ion vertical convergence and the formation of high-density Es layers, , Equations (5) and (17), were obtained from the analytical solution (3) of the evolution of the initial Gaussian-type distribution of ion/electron density at the lower thermosphere. The MTotIVCR , Equation (11), includes the fractions of the neutral wind velocity, Equation (12); its shear, Equation (13); and the electric field, Equation (14). The fractions/shares of the wind velocity, wind shear, and electric field in the MTotIVCR during Es layer formation (see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels g, h, i) were estimated for a typical equatorial I = 0° (0.5° N; 195° E), between equatorial and mid-latitude (BEML) I = 30° (16° N; 195° E), and mid-latitude I = 60° (45° N, 195° E) regions (see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, panels j, k, l) of the north hemisphere. Here, the combined effect of only zonal wind and its shear (assuming ) in equatorial regions, as well as the influence of only meridional and zonal winds and their shear values in regions with I = 30° and I = 60°, influence the height profile of the total ion vertical convergence ()/divergence () rates and the location of ion drift velocity nodes or regions with , where the Es layers localize (see Figure 2). The electric field , in addition to the neutral wind velocity and its shear, affects the ion vertical drift velocity and its vertical changes () in the considered regions, Equations (6) and (10). In this case, the ion/electron vertical drift caused by the electric field influences the formation and localization of Es layers at equatorial I = 0, BEML I = 30°, and mid-latitude I = 60° regions. It also results in additional meridional differences (see Figure 3, Figure 4, Figure 5 and Figure 6) compared to the case in which only neutral wind is present (see Figure 2).
In the considered case of four different directions (two opposite polarizations) of the electric field, its contribution (up to about ) to the MTotIVCR (up to about ) is mostly important; however, its presence at mid-latitude can also cause an additional increase in the density of the Es layers, as well as their destruction.
It is also noticeable that the descent of the initial ion/electron layer or formed Es layer at the downward drift velocity , in the case of the TotIVCR (), results in additional increase in the Es layer density, which localizes at the region with .
Such phenomena of increasing descending Es layer density, which can occur without the windshear factor, can be predicted using the analytical approach to Es layer formation, Equation (3), under condition (17). In this case, the increase in the TotIVCR caused by the westward and/or northward wind, as well as the drift caused by the westerly and/or downward electric field components, exceeds ion/electron losses due to recombination and diffusion displacement, and a higher density Es layer is formed (see Figure 2i, Figure 4h,i and Figure 6i) at around top of the MLT (about 95–105 km), where Es layers are observed more frequently.
These results show that to study the predictability of sporadic E (Es) forming and localizing, the role of the neutral wind velocity’s magnitude and direction, its shear, and electric fields must be taken into account. Correspondingly, it is important to use realistic models to investigate the regional and global distribution of metallic ions. The importance of taking into account the vertical component of the actual wind velocity for creating such a realistic model of the global distribution of metallic ions and, accordingly, its role in the vertical convergence of ions and the formation of Es layers is also noted.
Author Contributions
G.G.D.: conceptualization, investigation, methodology, and writing—original draft. G.D.: formal analyses, methodology, validation, visualization, and funding acquisition. M.T.: investigation, validation, visualization, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Georgian Shota Rustaveli National Science Foundation, grant no. FR-21-22825.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in: https://osf.io/search/?q=Dalakishvili&page=1 (accessed on 12 April 2025).
Acknowledgments
We used the NRLMSISE-00 model. Data are available at https://ccmc.gsfc.nasa.gov/modelweb/models/nrlmsise00.php (accessed on 19 July 2025). We used the public domain database open science framework (https://osf.io/search/?q=Dalakishvili&page=1 (accessed on 19 July 2025)) for dissemination of our numerical code, the data given by the horizontal wind model HWM14, which ran with MATLAB 2020, and the data of the observed profile.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ishiia, M.; Berdermann, J.; Forte, B.; Hapgoodd, M.; Bisi, M.M.; Romanoe, M. Space weather impact on radio communication and navigation. Adv.Space Res. 2024; in press. [Google Scholar] [CrossRef]
- Huba, J.D.; Krall, J.; Drob, D. Global ionospheric metal ion transport with SAMI3. Geophys. Res. Lett. 2019, 46, 7937–7944. [Google Scholar] [CrossRef]
- Plane, J.M.C.; Gumbel, J.; Kalogerakis, K.S.; Marsh, D.R.; Savigny, C.V. Opinion: Recent developments and future directions in studying the mesosphere and lower thermosphere. Atmos. Chem. Phys. 2023, 23, 13255–13282. [Google Scholar] [CrossRef]
- Parsch, E.V.; Franz, A.L.; Dao, E.V.; Wu, D.L.; Swarnalingam, N.; Salinas, C.C.J.H.; Emmons, D.J. Global Empirical Model of Sporadic-E Occurrence Rates. Front. Astron. Space Sci. 2024, 11, 1434367. [Google Scholar] [CrossRef]
- Aylett, T.; Feng, W.; Marsh, D.R.; Themens, D.R.; Plane, J.M.C. Characteristics of sporadic E layer occurrence in a global chemistry-climate model: A comparison with COSMIC derived data. J. Geophys. Res. Space Phys. 2025, 130, e2024JA033044. [Google Scholar] [CrossRef]
- Haldoupis, C.; Pancheva, D.; Singer, W.; Meek, C.; MacDougall, J. An explanation for the seasonal dependence of midlatitude sporadic E layers. J. Geophys. Res. Space Phys. 2007, 112, A06315. [Google Scholar] [CrossRef]
- Yiğit, E.; Koucká Knízová, P.; Georgieva, K.; Ward, W. A review of vertical coupling in the Atmosphere–Ionosphere system: Effects of waves, sudden stratospheric warmings, space weather, and of solar activity. J. Atmos. Sol.-Terr. Phys. 2016, 141, 1–12. [Google Scholar] [CrossRef]
- Resende, L.C.A.; Zhu, Y.; Santos, A.M.; Chagas, R.A.J.; Denardini, C.M.; Arras, C.; Da Silva, L.A.; Nogueira, P.A.B.; Chen, S.S.; Andrioli, V.F.; et al. Nocturnal sporadic cusp type layer (Esc) resulting from anomalous excess ionization over the SAMA region during the extreme magnetic storm on May 11, 2024. J. Geophys. Res. Space Phys. 2024, 129, e2024JA033167. [Google Scholar] [CrossRef]
- Haldoupis, C.; Midlatitude Sporadic, E. A Typical Paradigm of Atmosphere-Ionosphere Coupling. Space Sci. Rev. 2012, 168, 441–461. [Google Scholar] [CrossRef]
- Wakabayashi, M.; Ono, T. Multi-layer structure of mid-latitude sporadic-E observed during the SEEK-2 campaign. Ann. Geophys. 2005, 23, 2347–2355. [Google Scholar] [CrossRef]
- Hysell, D.L. From instability to irregularities. In The Dynamical Ionosphere—A Systems Approach to Ionospheric Irregularity; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 11; pp. 137–167. [Google Scholar]
- Luo, J.; Liu, H.; Xu, X. Sporadic E morphology based on COSMIC radio occultation data and its relationship with wind shear theory. Earth Planets Space 2021, 73, 212. [Google Scholar] [CrossRef]
- Tang, Q.; Zhou, C.; Liu, H.; Liu, Y.; Zhao, J.; Yu, Z.; Zhao, Z.; Feng, X. The possible role of turbopause on sporadic-E layer formation at middle and low latitudes. Space Weather 2021, 19, e2021SW002883. [Google Scholar] [CrossRef]
- Tang, Q.; Zhou, C.; Liu, H.; Liu, Y.; Zhao, J.; Yu, Z.; Hu, L.; Zhao, Z.; Feng, X. Low altitude tailing Es (LATTE): Analysis of sporadic-E layer height at different latitudes of middle and low region. Space Weather 2023, 21, e2022SW003323. [Google Scholar] [CrossRef]
- Qiu, L.; Yamazaki, Y.; Yu, T.; Miyoshi, Y.; Zuo, X. Numerical investigation on the height and intensity variations of sporadic E layers at mid-latitude. J. Geophy. Res. Space Phys. 2023, 128, e2023JA031508. [Google Scholar] [CrossRef]
- Kunduri, B.S.R.; Erickson, P.J.; Baker, J.B.H.; Ruohoniemi, J.M.; Galkin, I.A.; Sterne, K.T. Dynamics of mid-latitude sporadic-E and its impact on HF propagation in the North American sector. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031455. [Google Scholar] [CrossRef]
- Abdu, M.A.; MacDougall, J.W.; Batista, I.S.; Sobral, J.H.A.; Jayachandran, P.T. Equatorial evening prereversal electric field enhancement and sporadic E layer disruption: A manifestation of E and F region coupling. J. Geophys. Res. 2003, 108, 1254. [Google Scholar] [CrossRef]
- Arras, C.; Resende, L.C.A.; Kepkar, A.; Senevirathna, G.; Wickert, J. Sporadic E layer characteristics at equatorial latitudes as observed by GNSS radio occultation measurements. Earth Planets Space 2010, 74, 163. [Google Scholar] [CrossRef]
- Abdu, M.A.; de Souza, J.R.; Batista, I.S.; Santos, A.M.; Sobral, J.H.A.; Rastogi, R.G.; Chandra, H. The role of electric fields in sporadic E layer formation over low latitudes under quiet and magnetic storm conditions. J. Atmos. Sol.-Terr. Phys. 2014, 115–116, 95–105. [Google Scholar] [CrossRef]
- Moro, J.; Resende, L.C.A.; Denardini, C.M.; Xu, J.; Batista, I.S.; Andrioli, V.F.; Schuch, N.J. Equatorial E region electric fields and sporadic E layer responses to the recovery phase of the November 2004 geomagnetic storm. J. Geophys. Res. Space Phys. 2017, 122, 12517–12533. [Google Scholar] [CrossRef]
- Resende, L.C.A.; Shi, J.K.; Denardini, C.M.; Batista, I.S.; Nogueira, P.A.B.; Arras, C.; Andrioli, V.F.; Moro, J.; Da Silva, L.A.; Carrasco, A.J.; et al. The influence of disturbance dynamo electric field in the formation of strong sporadic E layers over Boa Vista, a low-latitude station in the American sector. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027519. [Google Scholar] [CrossRef]
- Qiu, L.; Yu, T.; Yan, X.; Sun, Y.-Y.; Zuo, X.; Yang, N.; Wang, J.; Qi, Y. Altitudinal and latitudinal variations in ionospheric sporadic-E layer obtained from FORMOSAT-3/COSMIC radio occultation. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029454. [Google Scholar] [CrossRef]
- Whitehead, J.D. Recent work on mid-latitude and equatorial sporadic-E. J. Atmos. Terr. Phys. 1989, 51, 401–424. [Google Scholar] [CrossRef]
- Yokoyama, T.; Yamamoto, M.; Fukao, S. Computer simulation of polarization electric fields as a source of midlatitude field-aligned irregularities. J. Geophys. Res. 2003, 108, 1054. [Google Scholar] [CrossRef]
- Chu, X.; Yu, Z. Formation mechanisms of neutral Fe layers in the thermosphere at Antarctica studied with a thermosphere-ionosphere Fe/Fe+ (TIFe) model. J. Geophys. Res. Space Phys. 2017, 122, 6812–6848. [Google Scholar] [CrossRef]
- Didebulidze, G.G.; Dalakishvili, G.; Todua, M.; Toriashvili, L. The importance of electric field or/and neutral wind in formation and prediction of sporadic E(Es) at the equatorial and mid-latitude regions. J. Atmos. Sol.-Terr. Phys. 2025, 272, 106540. [Google Scholar] [CrossRef]
- Didebulidze, G.G.; Dalakishvili, G.; Todua, M. Formation of Multilayered Sporadic E under an Influence of Atmospheric Gravity Waves (AGWs). Atmosphere 2020, 11, 653. [Google Scholar] [CrossRef]
- Didebulidze, G.G.; Dalakishvili, G.; Todua, M.; Toriashvili, L. The Role of Neutral Wind Velocity and Its Vertical Component on Predictability of Formation and Localization of Sporadic E (Es). Atmosphere 2023, 14, 1008. [Google Scholar] [CrossRef]
- Dalakishvili, G.; Didebulidze, G.G.; Todua, M. Formation of sporadic E (Es) layer by homogeneous and inhomogeneous horizontal winds. J. Atmos. Sol. Terr. Phys. 2020, 209, 105403. [Google Scholar] [CrossRef]
- Oikonomou, C.; Haralambous, H.; Leontiou, T.; Tsagouri, I.; Buresova, D.; Mosna, Z. Intermediate descending layer and sporadic E tidelike variability observed over three mid-latitude ionospheric stations. Adv. Space Res. 2022, 69, 96–110. [Google Scholar] [CrossRef]
- Jacobi, C.; Kandieva, K.; Arras, C. Migrating and nonmigrating tidal signatures in sporadic E layer occurrence rates. Adv. Radio Sci. 2023, 20, 85–92. [Google Scholar] [CrossRef]
- Alken, P.; Maus, S. Electric fields in the equatorial ionosphere derived from CHAMP satellite magnetic field measurements. J. Atmos. Sol.-Terr. Phys. 2010, 72, 319–326. [Google Scholar] [CrossRef]
- Alken, P.; Maus, S.; Chulliat, A.; Vigneron, P.; Sirol, O.; Hulot, G. Swarm equatorial electric field chain: First results. Geophys. Res. Lett. 2015, 42, 673–680. [Google Scholar] [CrossRef]
- Resende, L.C.A.; Shi, J.; Denardini, C.M.; Batista, I.S.; Picanco, G.A.S.; Moro, J.; Chagas, R.A.J.; Barros, D.; Chen, S.S.; Nogueira, P.A.B.; et al. The impact of the disturbed electric field in the sporadic E (Es) layer development over Brazilian region. J. Geophys. Res. 2021, 126, e2020JA028598. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Ma, J.; Fu, H.; Huba, J.D.; Jin, Y. A novel ionospheric inversion model: PINN-SAMI3 (physics informed neural network based on SAMI3). Space Weather 2024, 22, e2023SW003823. [Google Scholar] [CrossRef]
- Shinagawa, H.; Tao, C.; Jin, H.; Miyoshi, Y.; Fujiwara, H. Numerical prediction of sporadic E layer occurrence using GAIA. Earth Planets Space 2021, 73, 28. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, Y.; Wang, J.; Tian, Y.; Wu, J.; Zhao, H.; Peng, H.; Wu, J.; Sun, S.; Li, X.; et al. The observation and simulation of descending sporadic E layers over different mid-latitude stations. Adv. Space Res. 2025, 75, 5559–5568. [Google Scholar] [CrossRef]
- Kikuchi, T.; Hashimoto, K.K.; Tanaka, T.; Nishimura, Y.; Nagatsuma, T. Middle latitude geomagnetic disturbances caused by hall and Pedersen Current circuits driven by prompt penetration electric fields. Atmosphere 2022, 13, 580. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar]
- Didebulidze, G.G.; Lomidze, L. The formation of sporadic E layers by a vortical perturbation excited in the horizontal wind shear flow. Ann. Geophys. 2008, 26, 1741–1749. [Google Scholar] [CrossRef]
- Didebulidze, G.G.; Dalakishvili, G.; Lomidze, L.; Matiashvili, G. Formation of sporadic-E (Es) layers under the influence of AGWs evolving in a horizontal shear flow. J. Atmos. Sol.-Terr. Phys. 2015, 136, 163–173. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigoriev, G.I. Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere 2022, 13, 1346. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Liu, H.; Bardeen, C.G.; Foster, B.T.; Lauritzen, P.; Liu, J.; Lu, G.; Marsh, D.R.; Maute, A.; McInerney, J.M.; Pedatella, N.M.; et al. Development and Validation of the Whole Atmosphere Community Climate Model with Thermosphere and Ionosphere Extension (WACCM-X 2.0). J. Adv. Model Earth Syst. 2018, 10, 381–402. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Z.Z.; Yue, X.A.; Liu, L.B. Effects of mesoscale gravity waves on sporadic E simulated by a one dimensional dynamic model. Earth Planet. Phys. 2025, 9, 1–9. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, T.; Qiu, L.; Yan, X.; Wang, J.; Liang, Y.; Liu, S.; Qi, Y. Comparison of the Heights of Sporadic E Layers and Vertical Ion Convergence Parameters. Remote Sens. 2023, 15, 5674. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).