A Spatiotemporal Multimodal Framework for Air Pollution Prediction Based on Bayesian Optimization—Evidence from Sichuan, China
Abstract
1. Introduction
- (1)
- The Local Moran’s Index (LMI) is introduced to quantify the spatial autocorrelation of pollutant concentrations between each monitoring station and its neighboring sites. Combined with pollutant concentration sequences, LMI features are incorporated into the CNN module to provide localized spatial structural information and to support the characterization of current pollution dispersion patterns.
- (2)
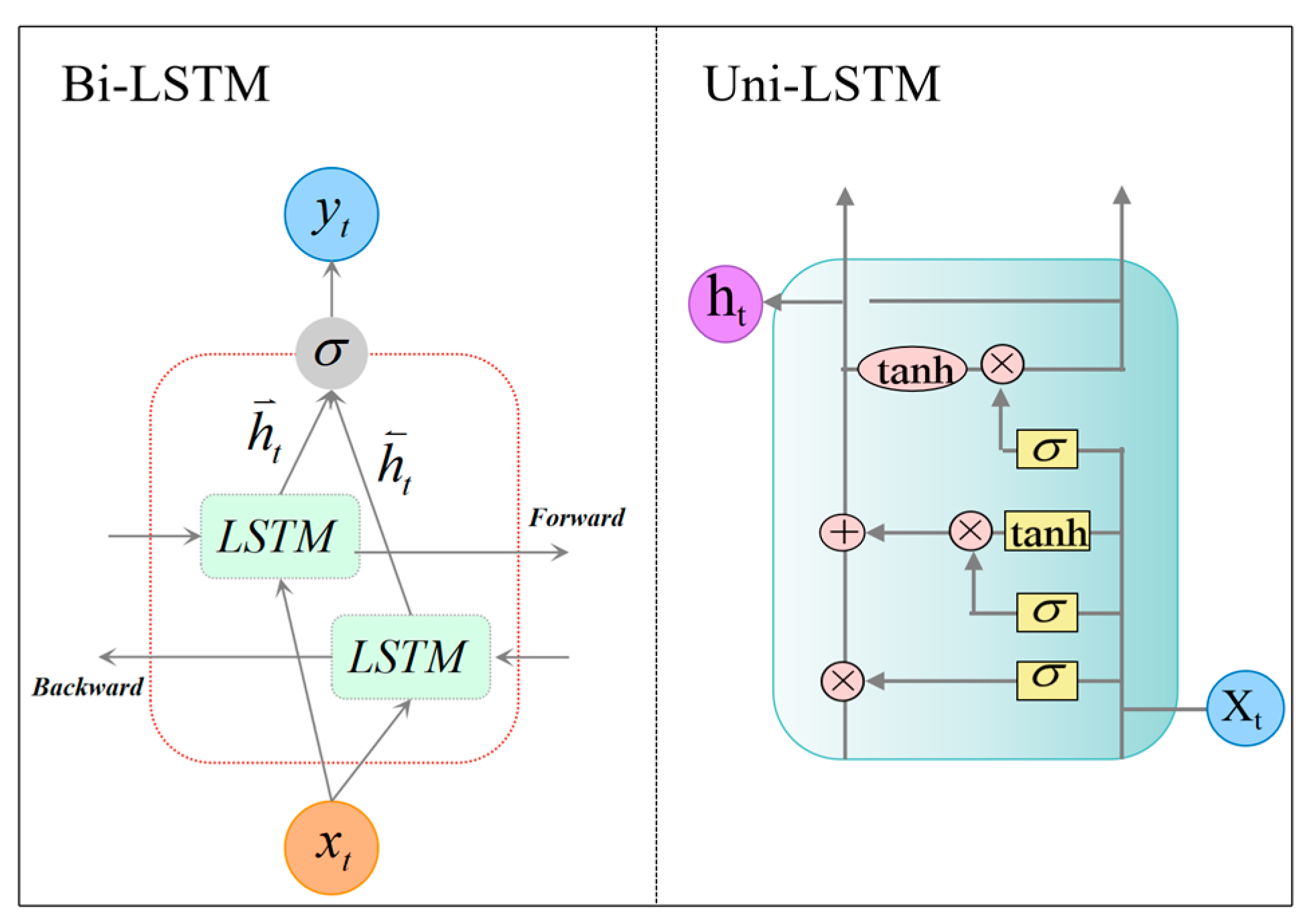
- Build a two-channel LSTM architecture in which Bi–LSTM is used in the main channel to model the two-way dependence of time series, and three-layer unidirectional LSTM is used in the auxiliary channel to enhance the ability to extract the one-way evolution trend of pollutant concentration, so as to realize the deep decoupling modeling of multi-scale time dynamics.
- (3)
- Combined with the multi-head self-attention mechanism of the Transformer encoder, the global dynamic modeling among pollutants, meteorological factors and spatial characteristics is realized.
- (4)
- The Bayesian optimization algorithm is introduced to adaptively adjust the key super-parameters such as learning rate, LSTM layer number and Dropout rate, so as to comprehensively improve the prediction accuracy, stability and generalization ability of the model.
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Preprocessing
2.2.1. Main Features
2.2.2. Data Processing
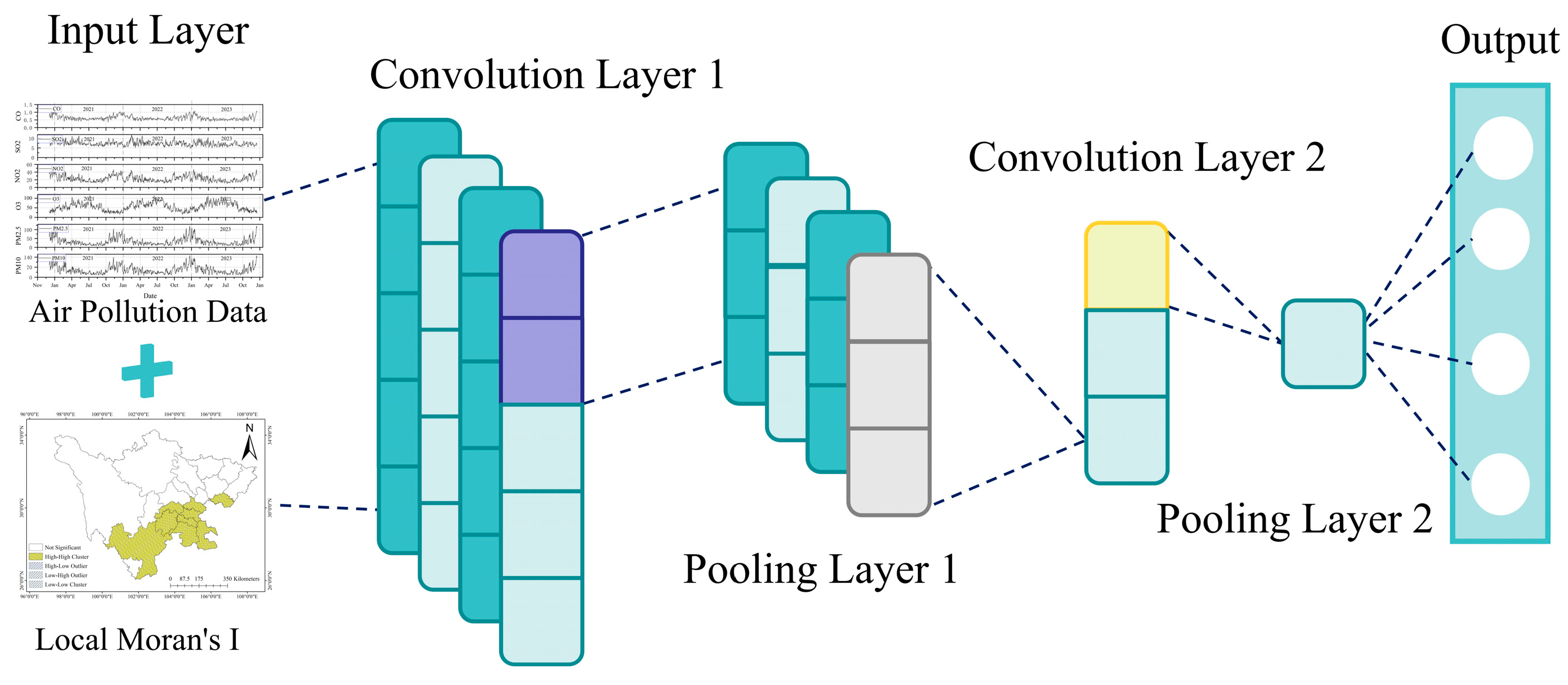
2.2.3. Local Moran’s Index Feature Modeling
2.3. Methodology
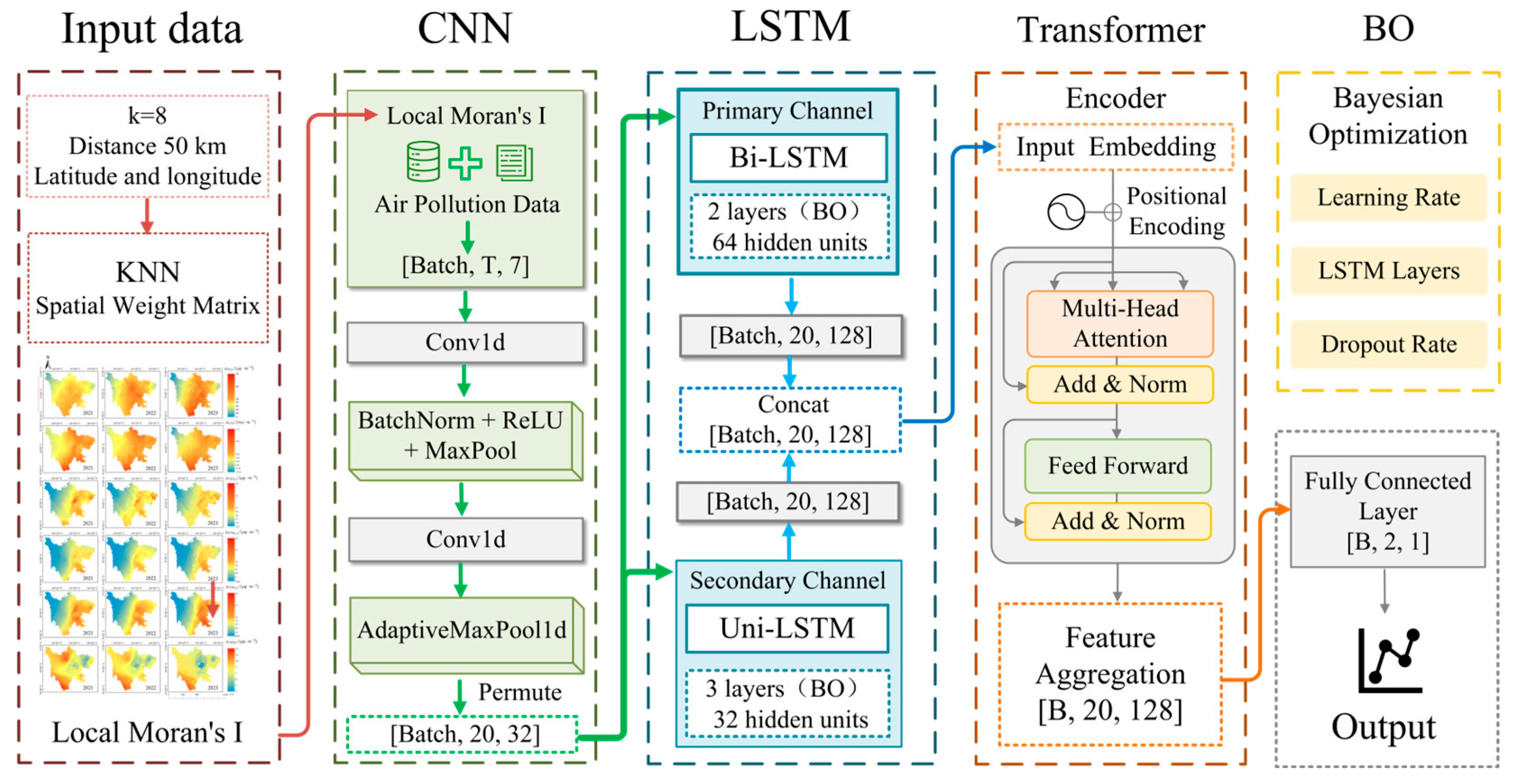
2.3.1. Framework Overview
2.3.2. Dual-Channel LSTM Architecture
2.3.3. Convolutional Neural Network
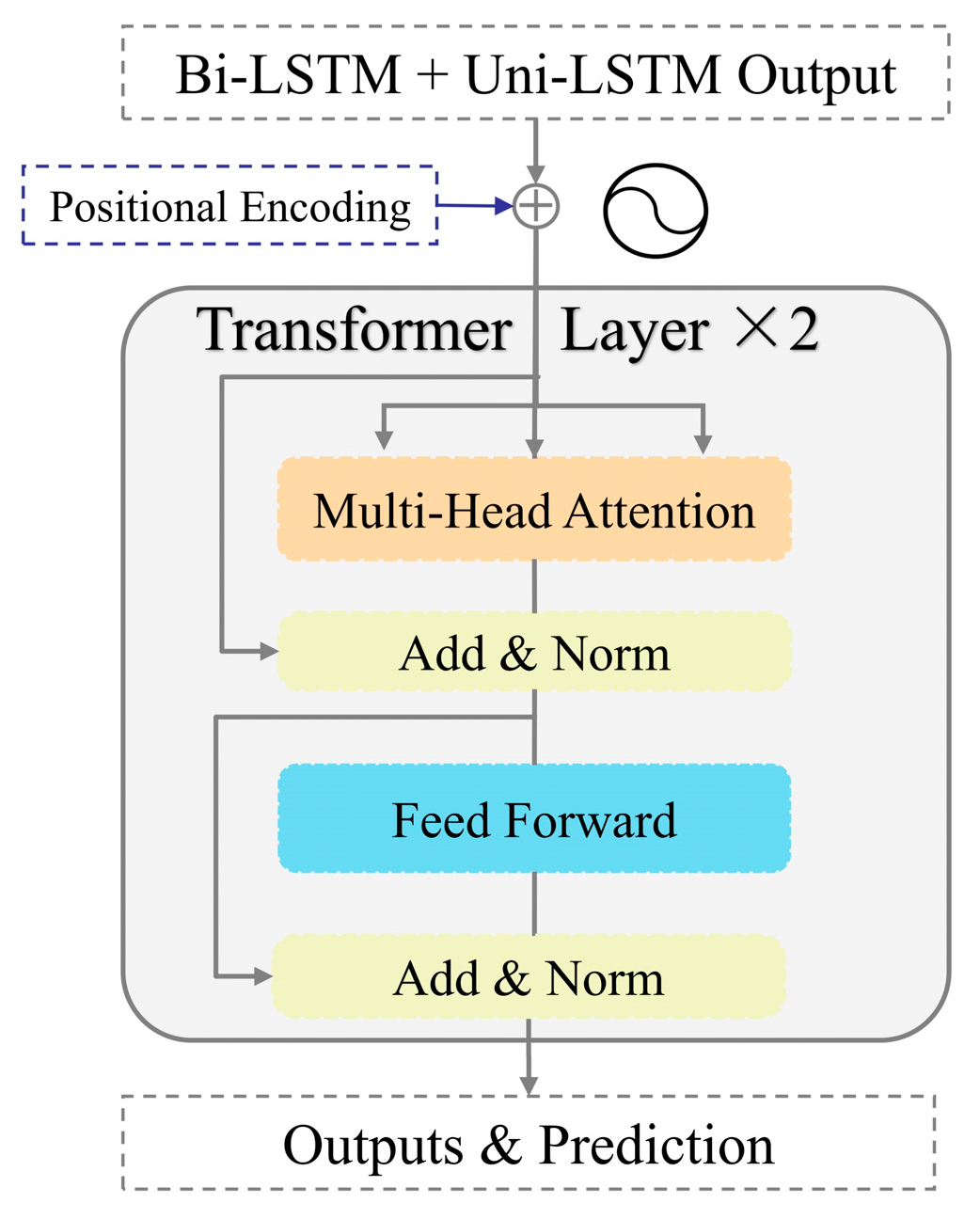
2.3.4. Transformer Encoder
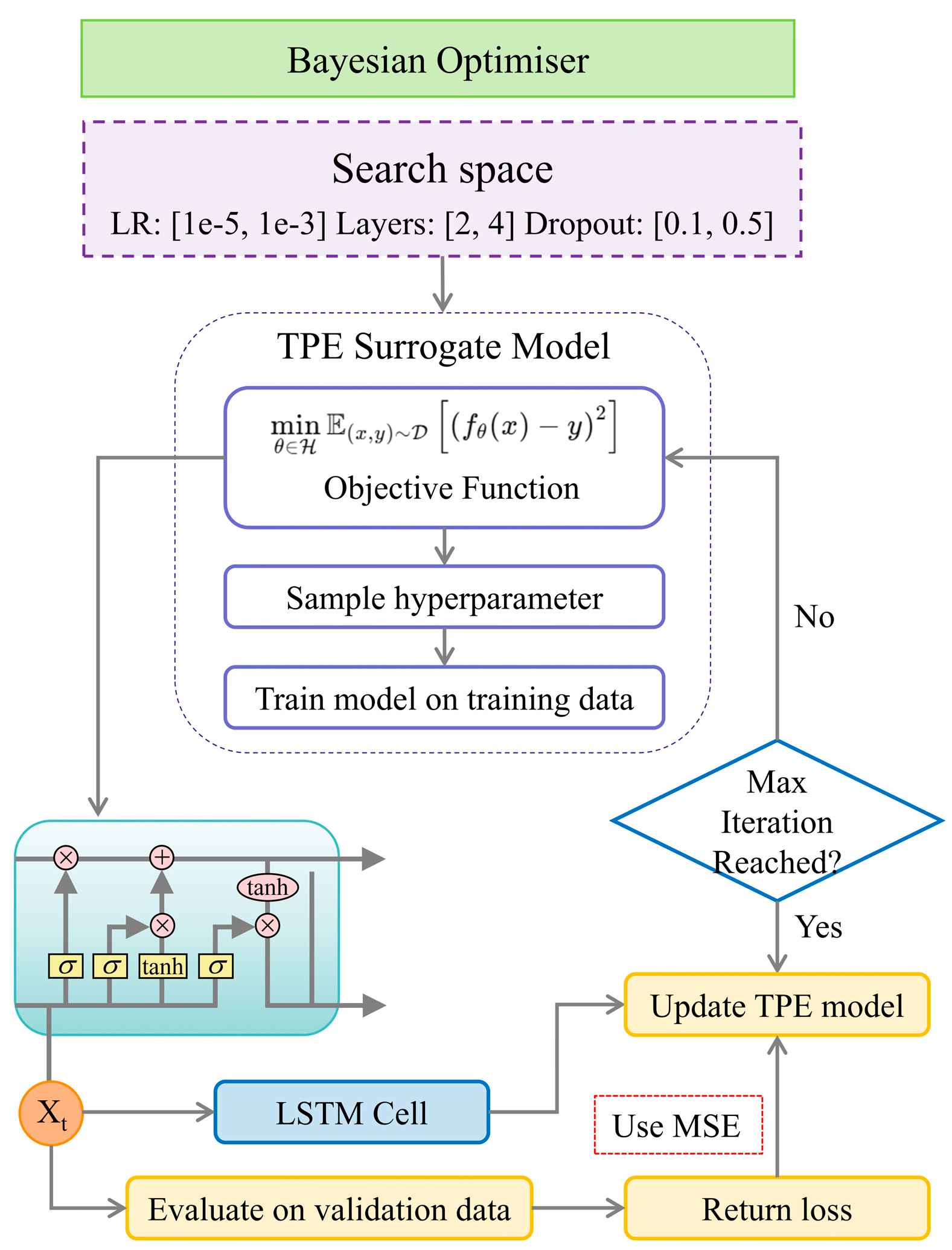
2.3.5. Bayesian Optimization
3. Data Visualization Processing and Analysis
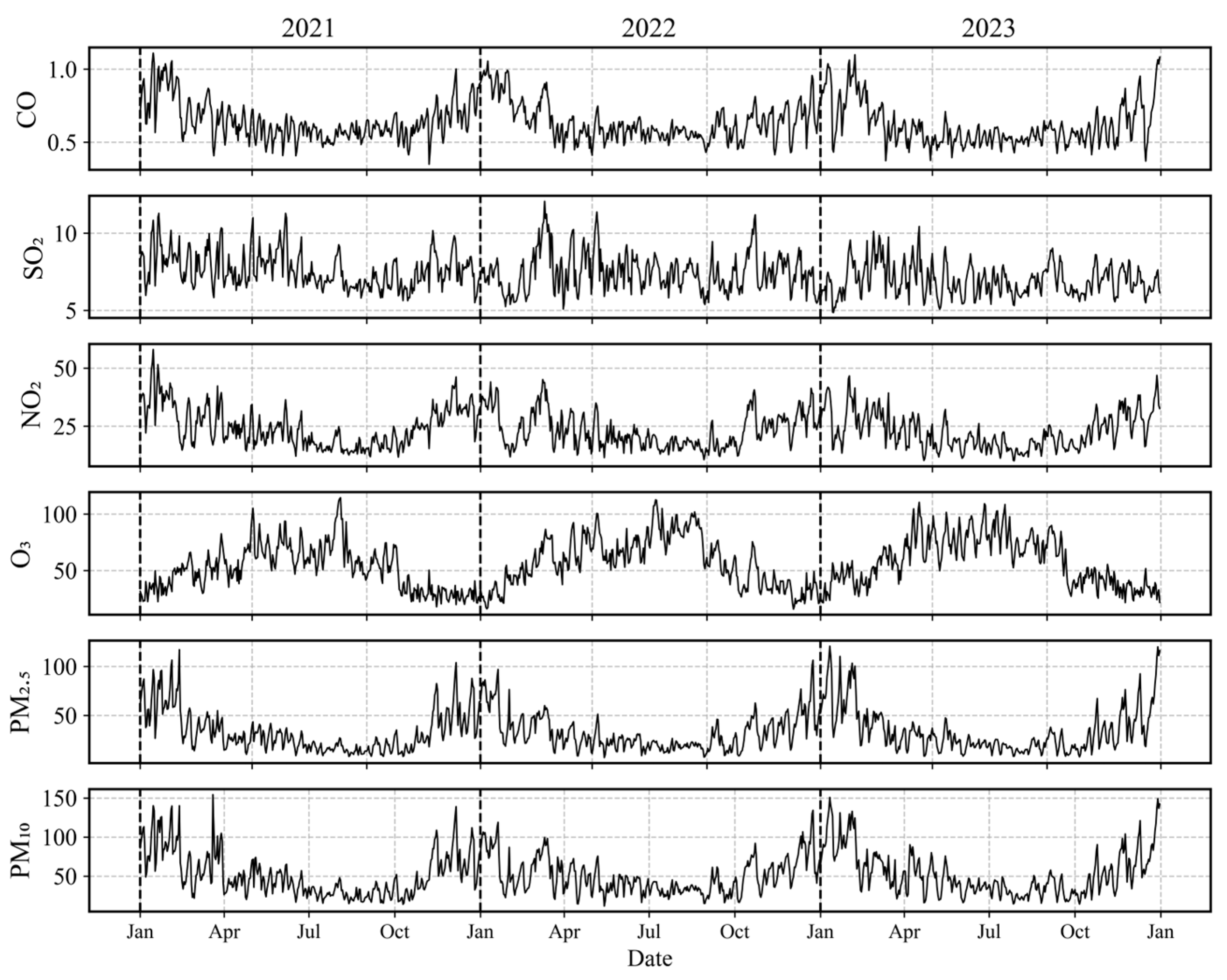
3.1. Time Evolution Characteristics Analysis
3.2. Spatial Differentiation Analysis
3.2.1. Spatial Interpolation Method
3.2.2. Result
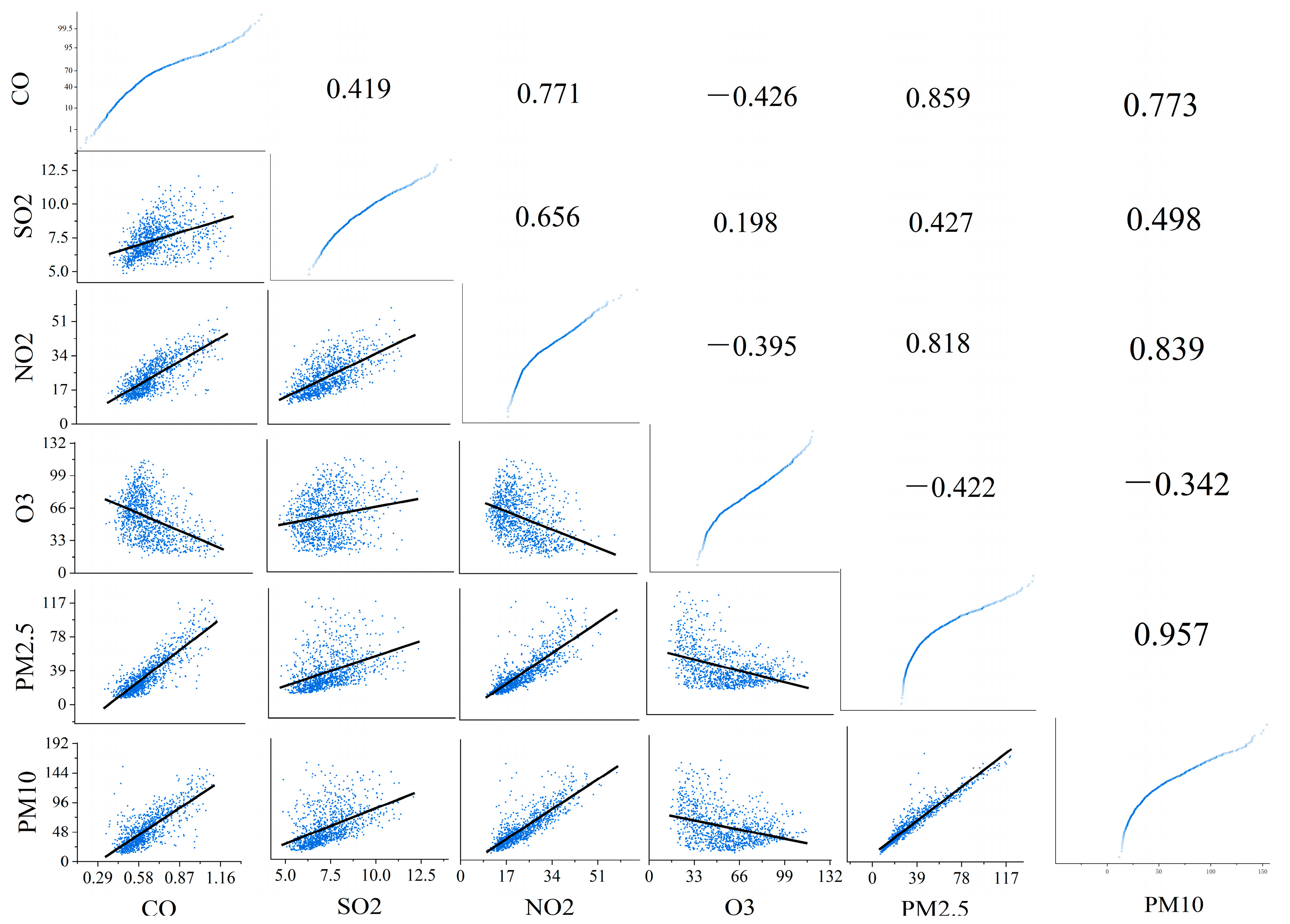
3.3. Analysis of Interrelationships Among Pollutants
- (1)
- Strong synergistic effect of homologous pollutants:
- (2)
- Compound action chain of sulfur-containing pollutants:
- (3)
- Dynamic Antagonism Between Ozone and Primary Pollutants:
4. Experiments
4.1. Evaluation Metrics and Training Strategy
4.1.1. Evaluation Metrics
4.1.2. Training Strategy
4.2. Experimental Results
4.2.1. Selection of Benchmark Cities
4.2.2. Comparative Experiments
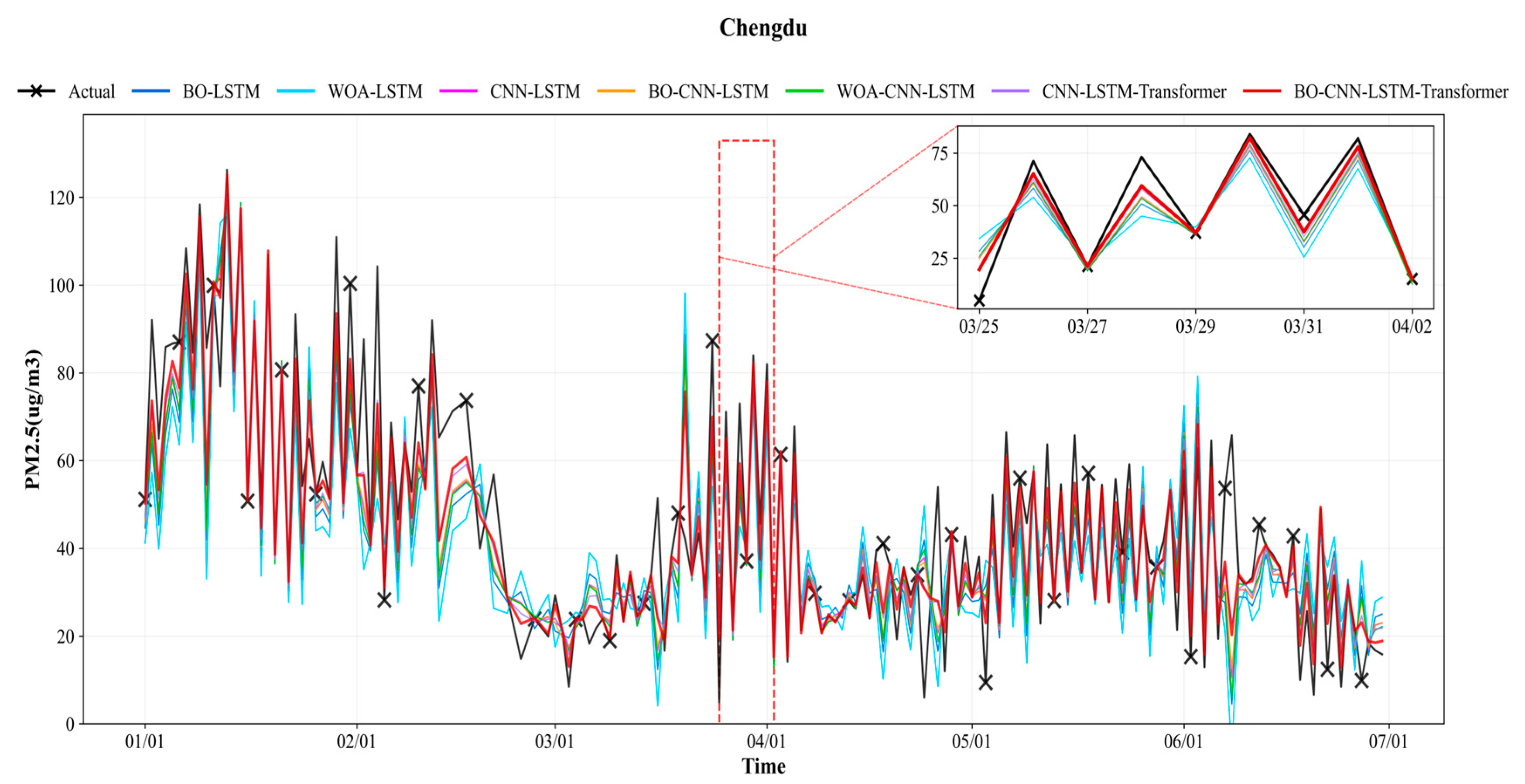
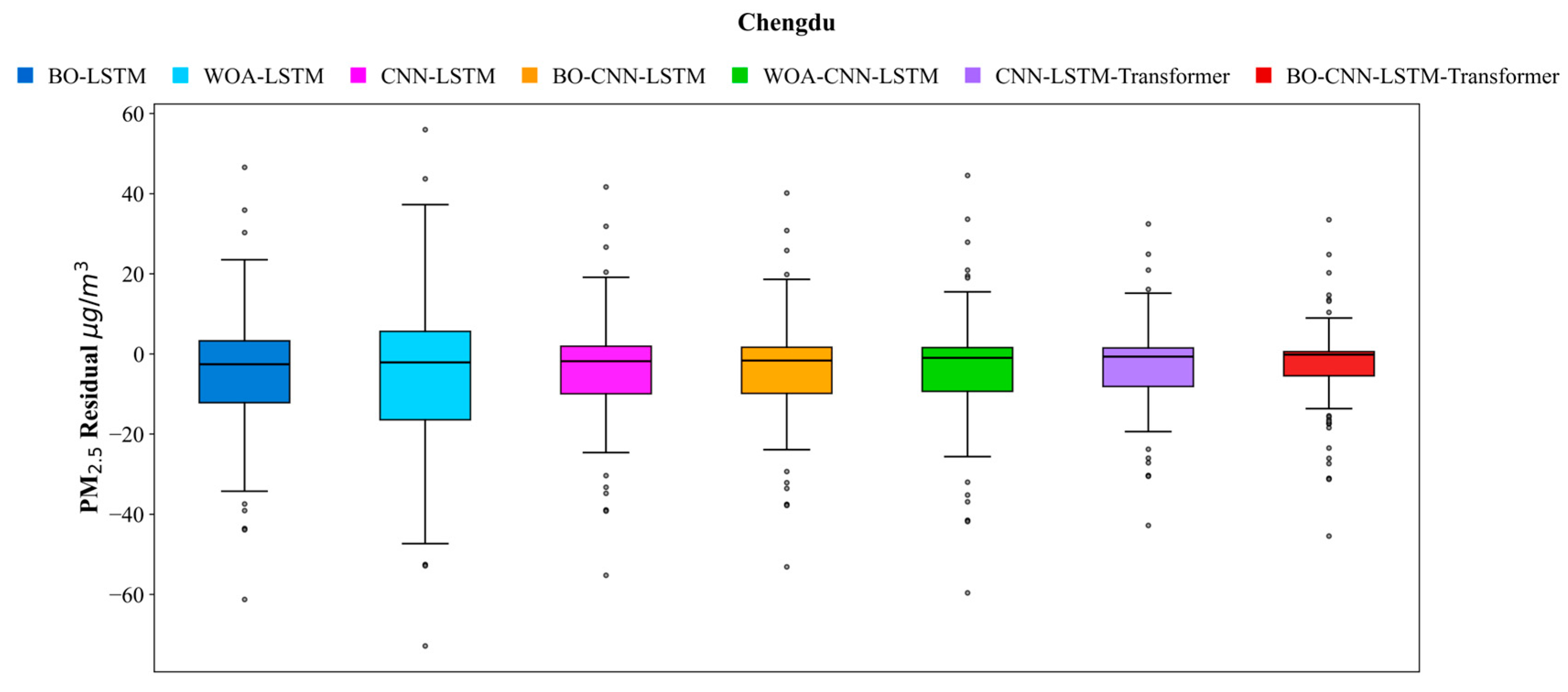
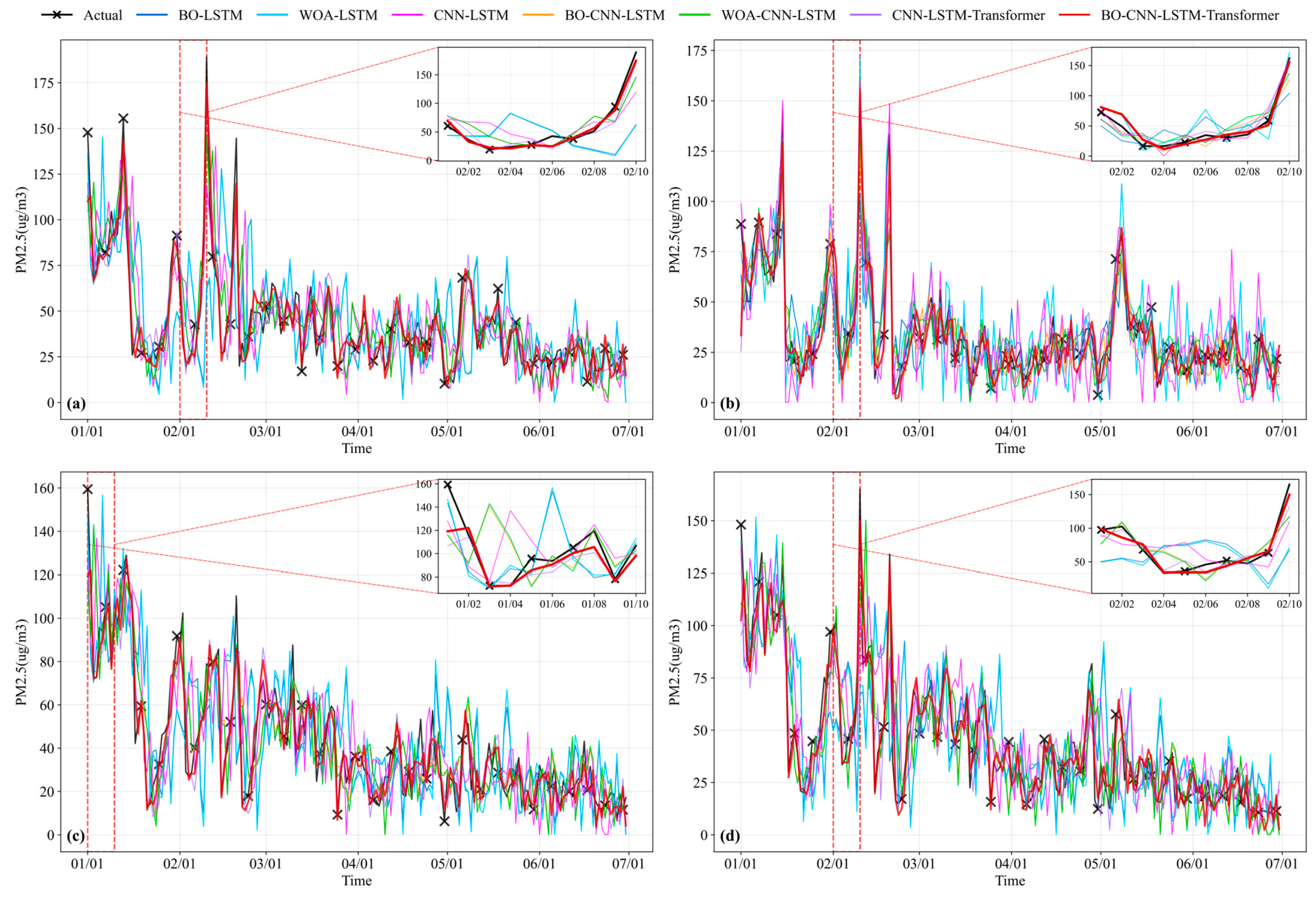
4.2.3. Comparison and Error Analysis of PM2.5 Prediction Models
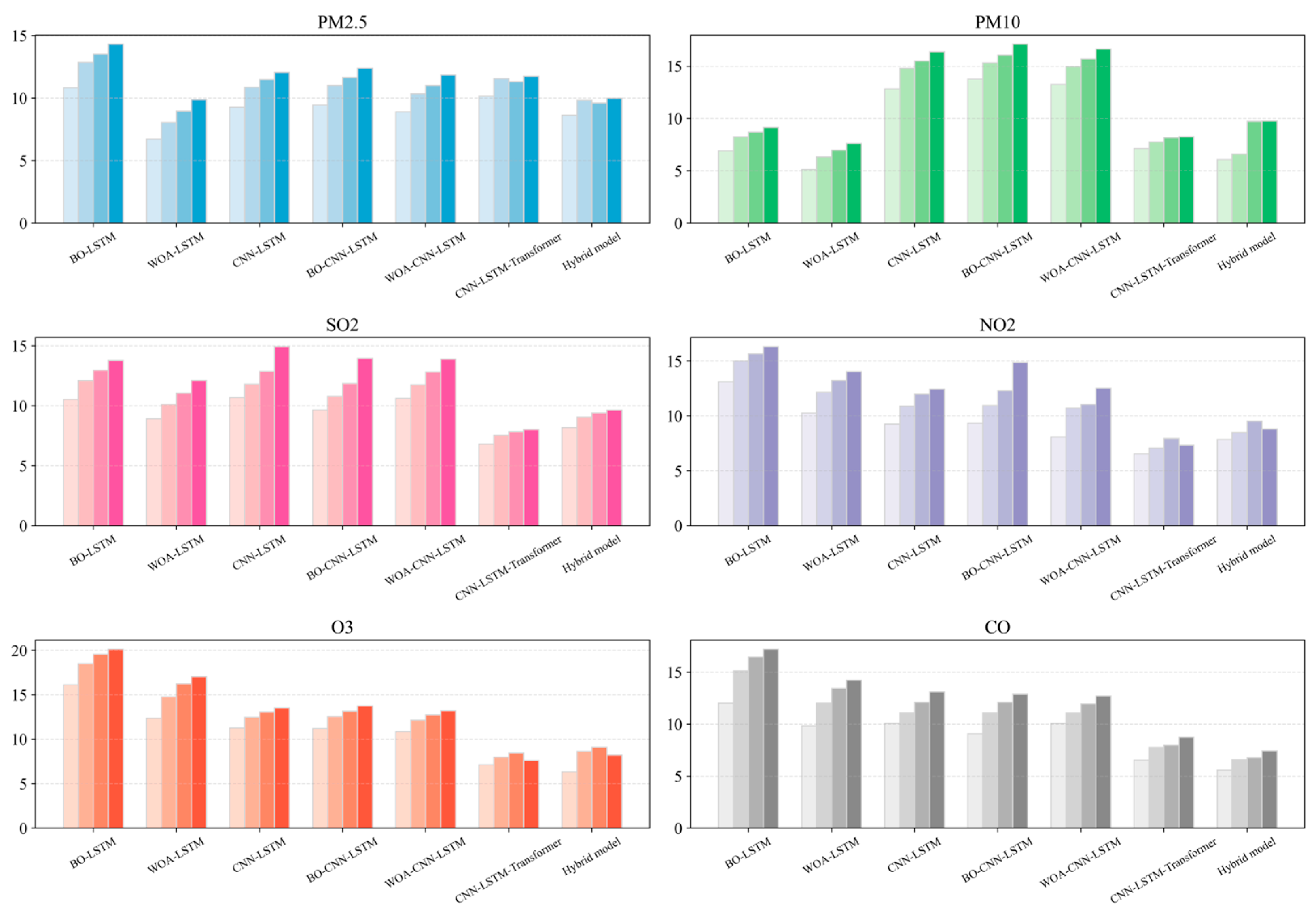
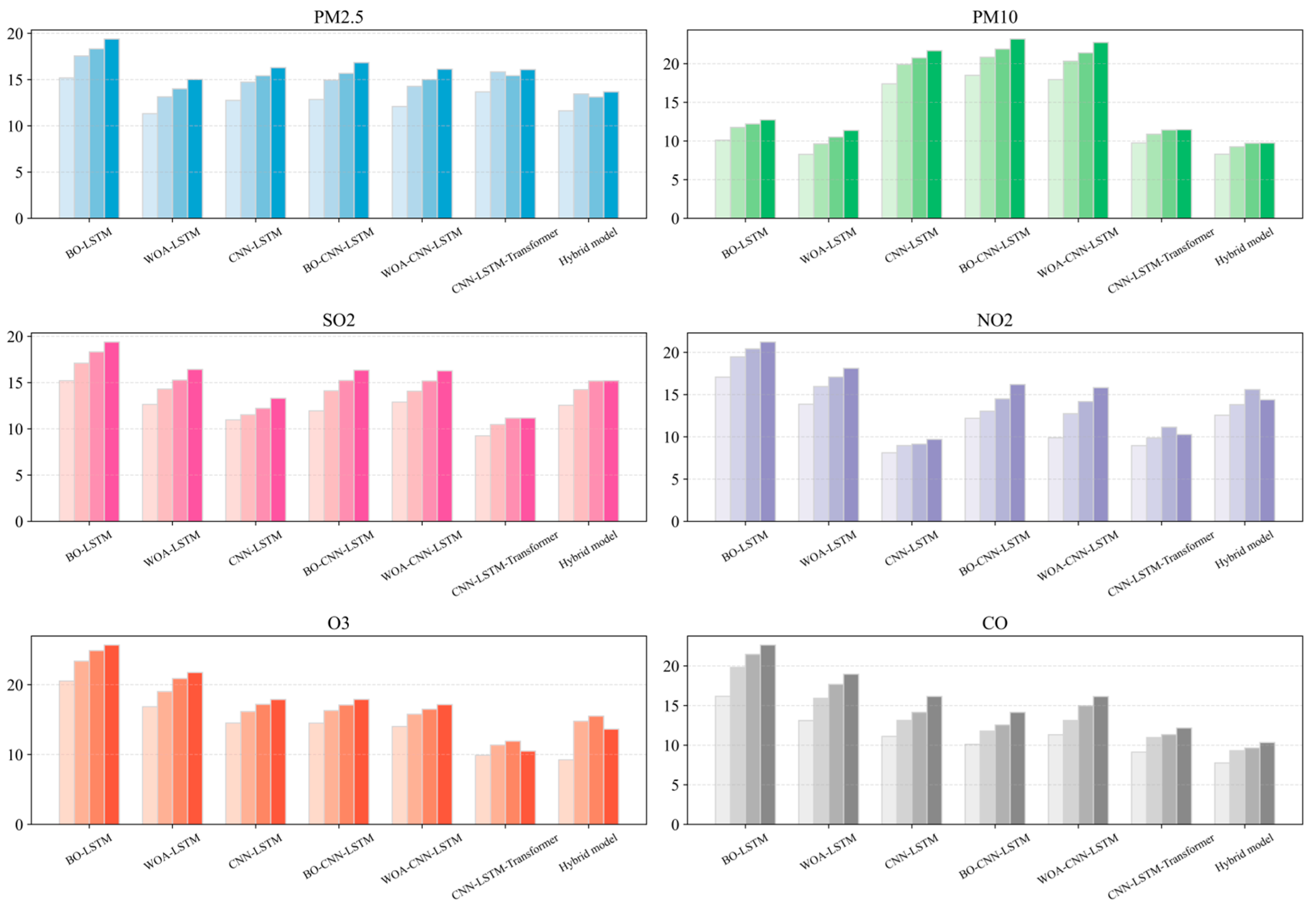
4.2.4. Multi-Step Forecasting Evaluation
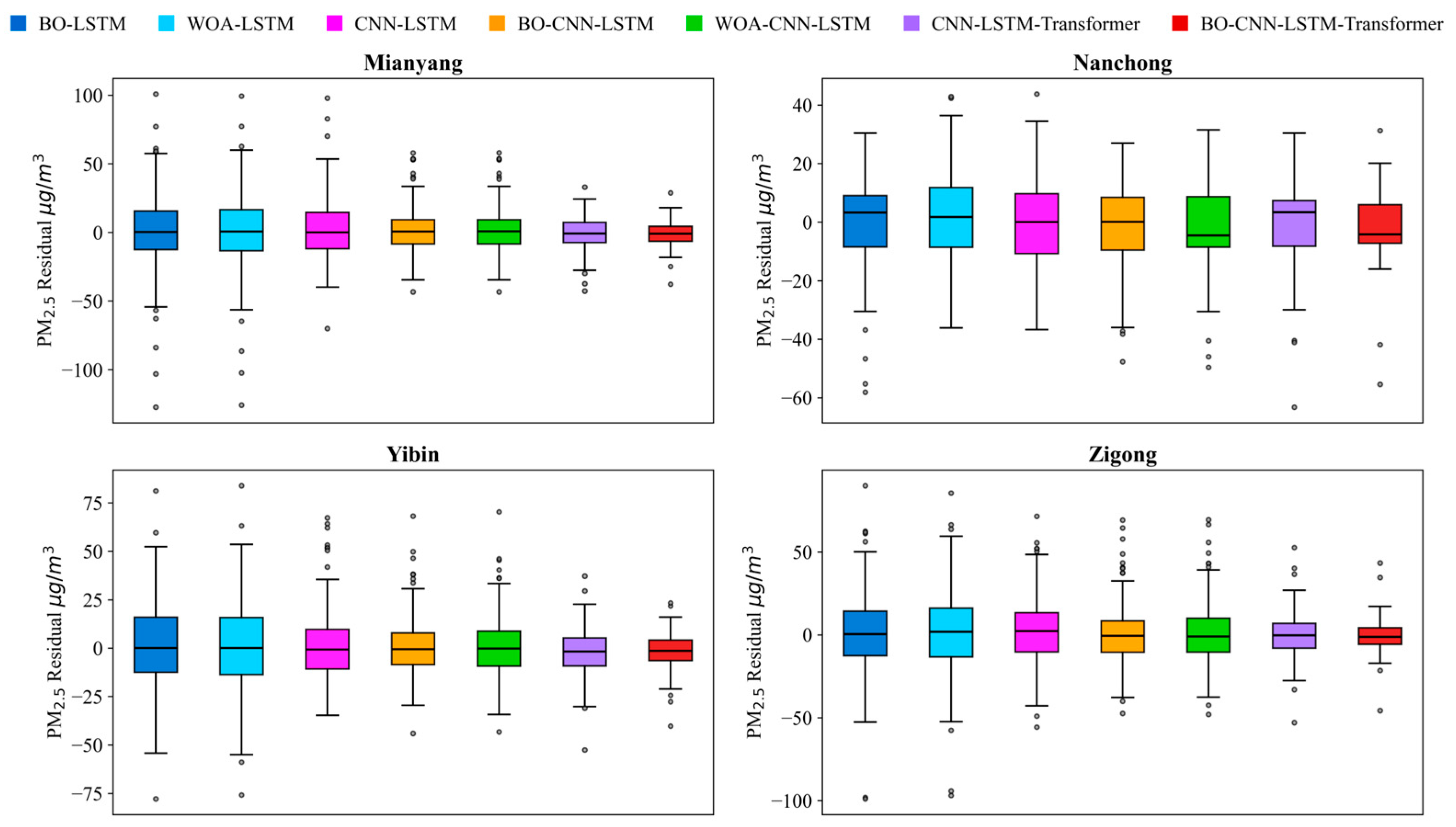
4.2.5. Regional Generalization Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maji, K.J.; Dikshit, A.K.; Arora, M.; Deshpande, A. Estimating premature mortality attributable to PM2.5 exposure and benefit of air pollution control policies in China for 2020. Sci. Total Environ. 2017, 612, 683. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, J.; Wang, Q.Y.; Qi, L.; Manousakas, M.I.; Han, Y.M.; Ran, W.K.; Sun, Y.L.; Liu, H.K.; Zhang, R.J.; et al. High-time-resolution chemical composition and source apportionment of PM2.5 in northern Chinese cities: Implications for policy. Atmos. Chem. Phys. 2023, 23, 9455–9471. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.L.; Qin, W.N.; Guo, L.M. Sustainable Policy Evaluation of Vehicle Exhaust Control-Empirical Data from China’s Air Pollution Control. Sustainability 2020, 12, 125. [Google Scholar] [CrossRef]
- Niu, Y.Y.; Yan, Y.L.; Dong, J.Q.; Yue, K.; Duan, X.L.; Hu, D.M.; Li, J.J.; Peng, L. Evidence for sustainably reducing secondary pollutants in a typical industrial city in China: Co-benefit from controlling sources with high reduction potential beyond industrial process. J. Hazard. Mater. 2024, 478, 10. [Google Scholar] [CrossRef] [PubMed]
- Thangavel, P.; Park, D.; Lee, Y.C. Recent Insights into Particulate Matter (PM2.5)-Mediated Toxicity in Humans: An Overview. Int. J. Environ. Res. Public Health 2022, 19, 7511. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.H.; Zhang, H.S.; Zhang, X.Y.; Cai, X.H.; Jin, X.P.; Zhang, L.; Song, Y.; Kang, L.; Hu, F.; Zhu, T. COATS: Comprehensive observation on the atmospheric boundary layer three-dimensional structure during haze pollution in the North China Plain. Sci. China-Earth Sci. 2023, 66, 939–958. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.Z.; Xiao, Z.S.; Tang, G.G.; Li, H.; Gao, R.; Dao, X.; Wang, Y.Y.; Wang, W.X. Heavy haze pollution during the COVID-19 lockdown in the Beijing-Tianjin-Hebei region, China. J. Environ. Sci. 2022, 114, 170–178. [Google Scholar] [CrossRef]
- Spiric, V.T.; Jankovic, S.; Vranes, A.J.; Maksimovic, J.; Maksimovic, N. The impact of air pollution on chronic respiratory diseases. Pol. J. Environ. Stud. 2012, 21, 481–490. [Google Scholar]
- Gao, Z.Q.; Zhou, X.H. A review of the CAMx, CMAQ, WRF-Chem and NAQPMS models: Application, evaluation and uncertainty factors. Environ. Pollut. 2024, 343, 14. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Jiang, N.B.; Ahmed, A.A.M.; Prasad, S.S.; Casillas-Pérez, D.; Salcedo-Sanz, S.; Yaseen, Z.M. Explainable deep learning hybrid modeling framework for total suspended particles concentrations prediction. Atmos. Environ. 2025, 347, 17. [Google Scholar] [CrossRef]
- Singh, S.; Suthar, G. Machine learning and deep learning approaches for PM2.5 prediction: A study on urban air quality in Jaipur, India. Earth Sci. Inform. 2025, 18, 97. [Google Scholar] [CrossRef]
- Gao, W.; Xiao, T.; Zou, L.; Li, H.; Gu, S. Analysis and Prediction of Atmospheric Environmental Quality Based on the Autoregressive Integrated Moving Average Model (ARIMA) Model in Hunan Province, China. Sustainability 2024, 16, 8471. [Google Scholar] [CrossRef]
- Xing, Y.F.; Xu, Y.H.; Shi, M.H.; Lian, Y.X. The impact of PM2.5 on the human respiratory system. J. Thorac. Dis. 2016, 8, E69–E74. [Google Scholar] [PubMed]
- Zendehboudi, A.; Baseer, M.A.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Talepour, N.; Birgani, Y.T.; Kelly, F.J.; Jaafarzadeh, N.; Goudarzi, G. Analyzing meteorological factors for forecasting PM10and PM2.5 levels: A comparison between MLR and MLP models. Earth Sci. Inform. 2024, 17, 5603–5623. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Chen, S.Y.; Kuo, C.M.; Tseng, H.W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Chan, K.; Matthews, P.; Munir, K. Time Series Forecasting for Air Quality with Structured and Unstructured Data Using Artificial Neural Networks. Atmosphere 2025, 16, 320. [Google Scholar] [CrossRef]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A Deep Neural Network Model for Short-Term Load Forecast Based on Long Short-Term Memory Network and Convolutional Neural Network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B. Monthly rainfall forecasting using one-dimensional deep convolutional neural network. IEEE Access 2018, 6, 69053–69063. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, F.; Du, Z. PM2.5 hourly concentration prediction based on RNN-CNN ensemble deep learning model. J. Zhejiang Univ. Sci. Ed. 2019, 46, 370–379. [Google Scholar]
- Shi, L.; Zhang, H.; Xu, X.; Han, M.; Zuo, P. A balanced social LSTM for PM2.5 concentration prediction based on local spatiotemporal correlation. Chemosphere 2022, 291, 133124. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shi, G.; Yang, F. Air pollution deterioration prior to dissipation induced by complex topography: A case study in the Sichuan Basin, southwestern China. Atmos. Res. 2025, 320, 108071. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, H.; Yang, J.; Niu, B.; Xu, Z. PM2.5 concentration prediction using a whale optimization algorithm based hybrid deep learning model in Beijing, China. Environ. Pollut. 2025, 371, 125953. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, S. Air quality index forecast in Beijing based on CNN-LSTM multi-model. Chemosphere 2022, 308, 136180. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Liu, H.Z.; Chen, J. Prediction of harmful gas concentration in air based on VMD-Transformer-ECM model. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2024, 51, 102–111. [Google Scholar]
- Tang, X.M.; Wu, N. PM2.5 concentration prediction model based on frequency domain information and BiLSTM. Radio Commun. Technol. 2023, 49, 1134–1141. [Google Scholar]
- Jia, Y.X.; Guo, N.; Qiao, J.F. Atmospheric pollutant prediction model of GRU neural network with intelligent tuning mechanism. Control Eng. 2025. Advance online publication. [Google Scholar]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Luo, J.; Gong, Y. Air pollutant prediction based on ARIMA-WOA-LSTM model. Atmos. Pollut. Res. 2023, 14, 101761. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Yang, X.; Ma, Y.K.; Sun, Y.H.; Wang, T.L. Integrating explainable AI and causal inference to unveil regional air quality drivers in China. J. Environ. Manag. 2025, 390, 18. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574–591. [Google Scholar] [CrossRef]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for Simplicity: The All Convolutional Net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kushwah, V.; Agrawal, P. Hybrid model for air quality prediction based on LSTM with random search and Bayesian optimization techniques. Earth Sci. Inform. 2025, 18, 17. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, Z.; Liu, D.; Chen, J.; Jin, J.; Qin, Q.; Shi, H. Transient simulation of SO2 absorption into water in a bubbling reactor. J. Environ. Sci. Health Part A 2023, 58, 811–824. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhou, W.; Gao, Q.; Zhao, D.; Liu, X.; Wang, Y. Effects of Air Pollutants on Summer Precipitation in Different Regions of Beijing. Atmosphere 2022, 13, 141. [Google Scholar] [CrossRef]
- Gupta, A.; Kamble, T.; Machiwal, D. Comparison of ordinary and Bayesian kriging techniques in depicting rainfall variability in arid and semi-arid regions of north-west India. Environ. Earth Ences 2017, 76, 512. [Google Scholar] [CrossRef]
- Xian, Y.; Zhang, Y.; Liu, Z.; Wang, H.; Wang, J.; Tang, C. Source apportionment and formation of warm season ozone pollution in Chengdu based on CMAQ-ISAM. Urban Clim. 2024, 56, 102017. [Google Scholar] [CrossRef]
- Tan, H.; Chen, Y.; Mao, F.; Wilson, J.P.; Zhang, T.; Cui, X.; Li, Z. PM2.5 estimation and its relationship with NO2 and SO2 in China from 2016 to 2020. Int. J. Digit. Earth 2024, 17, 1–20. [Google Scholar] [CrossRef]
- Liao, T.; Gui, K.; Jiang, W.; Wang, S.; Wang, B.; Zeng, Z.; Sun, Y. Air stagnation and its impact on air quality during winter in Sichuan and Chongqing, southwestern China. Sci. Total Environ. 2018, 635, 576–585. [Google Scholar] [CrossRef]
- Ormanova, G.; Hopke, P.K.; Dhammapala, R.; Ozturk, F.; Shah, D.; Torkmahalleh, M.A. Chemical characterization and source apportionment of atmospheric fine particulate matter (PM2.5) at an urban site in Astana, Kazakhstan. Atmos. Pollut. Res. 2025, 16, 102324. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Liu, G.; Zhang, X.; Gong, C.; Zhou, X.; Ma, Z. Characteristics of NO/SO2 generation during coal/steel dust co-firing under multi-factor synergies. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 1853–1871. [Google Scholar]
- Li, J. The Characteristics of PM2.5 and O3 Synergistic Pollution in the Sichuan Basin Urban Agglomeration. Atmosphere 2025, 16, 329. [Google Scholar] [CrossRef]
- Zhou, H.; Mao, Y.; Li, X.; Rong, Y.; Chen, L.; Yin, C. TKSTAGNet: A Top-K Spatio-Temporal Attention Gating Network for air pollution prediction. Expert Syst. Appl. 2025, 260, 125409. [Google Scholar] [CrossRef]
- Xiang, S.; Huang, X.; Lin, N.; Yi, Z. Synergistic reduction of air pollutants and carbon emissions in Chengdu-Chongqing urban agglomeration, China: Spatial-temporal characteristics, regional differences, and dynamic evolution. J. Clean. Prod. 2025, 493, 144929. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Kong, Q.; Gao, J. High-precision concentration detection of CO2 in flue gas based on BO-LSTM and variational mode decomposition. Meas. Sci. Technol. 2024, 35, 095202. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Jiang, Z.; Lin, X. Deep learning models for multi-step prediction of water levels incorporating meteorological variables and historical data. Stoch. Environ. Res. Risk Assess. 2024, 1–23. [Google Scholar] [CrossRef]
- Liu, R.; Vakharia, V. Optimizing Supply Chain Management Through BO-CNN-LSTM for Demand Forecasting and Inventory Management. J. Organ. End User Comput. 2024, 36, 1–25. [Google Scholar] [CrossRef]
- GB 3095-2012; Ambient Air Quality Standards. Ministry of Environmental Protection: Beijing, China, 2012.
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]


| Model | Spatial Feature | Temporal Feature | Global Model | Hyperparameter Optimization |
|---|---|---|---|---|
| MLR [11]/ARIMA [12] | ✔ | |||
| SVM [14]/MLP [15]/RF [16] | ✔ | |||
| LSTM [18] | ✔ | |||
| CNN [19] | ✔ | |||
| FD–BiLSTM [26] | ✔ | |||
| CNN–LSTM [24] | ✔ | ✔ | ||
| BO–GRU [27] | ✔ | ✔ | ||
| ARIMA–WOA–LSTM [29] | ✔ | ✔ | ||
| VMD–Transformer [25] | ✔ | ✔ | ||
| BO–CNN–BiLSTM–Transformer (This Study) | ✔ (Local Moran’s I) | ✔ (BiLSTM + Uni-LSTM) | ✔ | ✔ |
| Item | Raw Data | Cleaned Data |
|---|---|---|
| Number of Stations (sites) | 123 | 104 |
| Total Data Volume (records) | 924,198 | 794,664 |
| Number of Missing Values (records) | 27,269 | 0 |
| Missing Rate (%) | 17.70% | 0.00% |
| Outlier Proportion (3σ, %) | 0.27% | <After 3σ rule interpolation |
| Outlier Proportion (IQR, %) | 1.09% | <After IQR-based interpolation |
| Pollutants | Unit | 2021 | 2022 | 2023 | |||
|---|---|---|---|---|---|---|---|
| Average | Average | Change from 2021 | Average | Change from 2021 | Change from 2022 | ||
| CO | mg/m3 | 0.65 | 0.64 | −1.22% | 0.61 | −6.15% | −4.01% |
| SO2 | µg/m3 | 7.65 | 7.48 | −2.18% | 6.95 | −9.15% | −7.10% |
| NO2 | µg/m3 | 24.55 | 22.99 | −6.36% | 22.62 | −7.86% | −1.61% |
| O3 | µg/m3 | 127 | 140 | 10.24% | 136 | 7.09% | −2.86% |
| PM2.5 | µg/m3 | 33.14 | 32.20 | −2.84% | 33.98 | 2.53% | 5.54% |
| PM10 | µg/m3 | 51.54 | 49.82 | −3.33% | 53.13 | 3.08% | 6.65% |
| Parameters | Number |
|---|---|
| Input nodes | 7 |
| Output node | 1 |
| Activation function | ReLU |
| Optimizer | Adam |
| Iterations | 100 |
| Time step size | 7(9) |
| batch | 32 |
| Loss function | MAE |
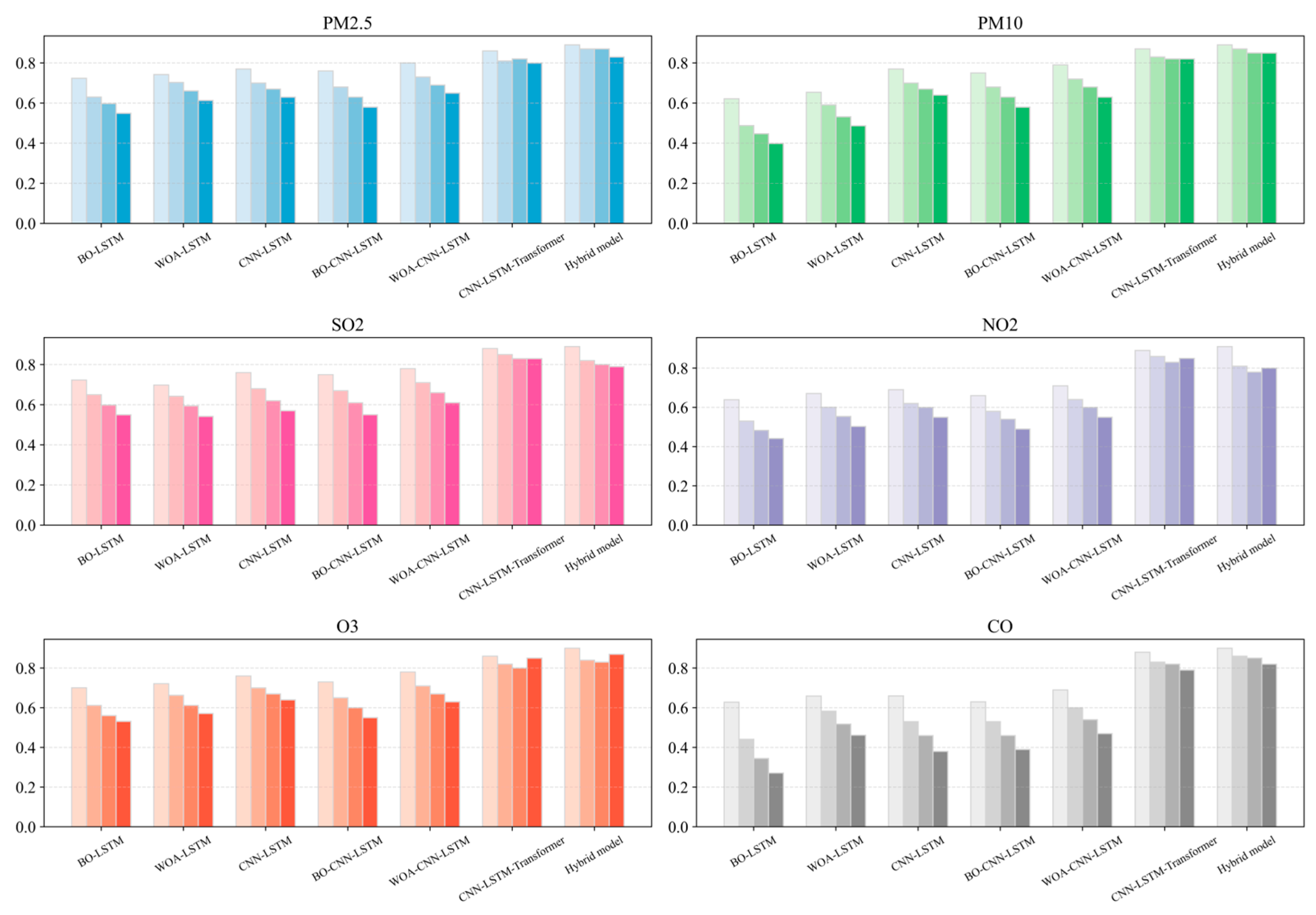
| Model | Metrics | Pollutants | |||||
|---|---|---|---|---|---|---|---|
| CO | PM10 | PM2.5 | NO2 | SO2 | O3 | ||
| BO–LSTM [47] | MAE | 15.90 | 13.10 | 10.40 | 13.69 | 14.11 | 14.00 |
| RMSE | 23.40 | 16.14 | 15.95 | 17.53 | 21.14 | 21.74 | |
| R2 | 0.60 | 0.69 | 0.792 | 0.749 | 0.641 | 0.649 | |
| WOA–LSTM [48] | MAE | 15.25 | 16.98 | 14.10 | 12.90 | 15.51 | 14.63 |
| RMSE | 21.19 | 24.41 | 18.98 | 16.90 | 22.75 | 20.06 | |
| R2 | 0.613 | 0.516 | 0.652 | 0.709 | 0.608 | 0.619 | |
| CNN–LSTM [24] | MAE | 11.13 | 11.23 | 11.16 | 11.52 | 10.73 | 10.22 |
| RMSE | 12.72 | 12.83 | 12.75 | 13.04 | 12.79 | 12.59 | |
| R2 | 0.774 | 0.771 | 0.773 | 0.765 | 0.777 | 0.782 | |
| BO–CNN–LSTM [49], | MAE | 11.02 | 11.20 | 10.75 | 8.80 | 9.10 | 9.50 |
| RMSE | 13.30 | 13.50 | 12.90 | 12.20 | 12.90 | 12.30 | |
| R2 | 0.791 | 0.784 | 0.803 | 0.851 | 0.832 | 0.841 | |
| WOA–CNN–LSTM [23] | MAE | 8.90 | 11.20 | 10.40 | 8.30 | 8.51 | 8.20 |
| RMSE | 12.24 | 14.10 | 13.20 | 11.80 | 11.30 | 10.80 | |
| R2 | 0.803 | 0.752 | 0.784 | 0.842 | 0.841 | 0.851 | |
| CNN–LSTM–Transformer | MAE | 9.67 | 8.63 | 8.54 | 8.13 | 8.28 | 8.80 |
| RMSE | 13.25 | 11.46 | 12.43 | 10.78 | 10.84 | 9.54 | |
| R2 | 0.831 | 0.862 | 0.844 | 0.875 | 0.874 | 0.872 | |
| BO–LSTM–Transformer | MAE | 9.59 | 8.93 | 9.27 | 10.15 | 7.32 | 10.96 |
| RMSE | 12.47 | 12.12 | 12.94 | 13.42 | 10.76 | 14.89 | |
| R2 | 0.804 | 0.834 | 0.815 | 0.807 | 0.863 | 0.798 | |
| BO–CNN–LSTM–Transformer without LMI | MAE | 10.09 | 7.19 | 8.23 | 8.47 | 8.17 | 7.74 |
| RMSE | 11.22 | 9.57 | 13.99 | 10.03 | 9.97 | 10.88 | |
| R2 | 0.829 | 0.871 | 0.853 | 0.863 | 0.865 | 0.842 | |
| BO–CNN–LSTM–Transformer | MAE | 7.38 | 6.15 | 6.98 | 6.67 | 7.15 | 7.33 |
| RMSE | 9.89 | 8.47 | 9.52 | 9.57 | 10.29 | 9.45 | |
| R2 | 0.878 | 0.884 | 0.873 | 0.894 | 0.874 | 0.883 | |
| Cities | Year | PM2.5 | PM10 | NO2 | O3 | SO2 | CO |
|---|---|---|---|---|---|---|---|
| Chengdu | 2021 | 67 | 32 | 8 | 0 | 0 | 0 |
| Chengdu | 2022 | 61 | 7 | 3 | 2 | 0 | 0 |
| Chengdu | 2023 | 52 | 22 | 2 | 2 | 0 | 0 |
| Pollution | Year | Chengdu | Zigong | Yibin | Mianyang | Nanchong |
|---|---|---|---|---|---|---|
| PM2.5 | 2021 | 67 | 54 | 51 | 22 | 28 |
| 2022 | 61 | 38 | 43 | 14 | 18 | |
| 2023 | 52 | 56 | 45 | 36 | 35 |
| Model | Metrics | City | |||
|---|---|---|---|---|---|
| Zigong | Yibin | Mianyang | Nanchong | ||
| BO–LSTM | MAE | 13.4 | 12.84 | 12.54 | 11.25 |
| RMSE | 15.59 | 14.96 | 16.20 | 16.74 | |
| R2 | 0.753 | 0.758 | 0.734 | 0.721 | |
| WOA–LSTM | MAE | 13.10 | 12.20 | 12.03 | 13.53 |
| RMSE | 19.37 | 18.61 | 17.68 | 17.12 | |
| R2 | 0.647 | 0.695 | 0.706 | 0.643 | |
| CNN–LSTM | MAE | 11.92 | 11.79 | 12.42 | 12.20 |
| RMSE | 15.80 | 13.41 | 14.57 | 15.87 | |
| R2 | 0.735 | 0.764 | 0.769 | 0.728 | |
| BO–CNN–LSTM | MAE | 10.21 | 10.50 | 10.51 | 10.54 |
| RMSE | 14.62 | 12.83 | 12.62 | 12.46 | |
| R2 | 0.794 | 0.816 | 0.793 | 0.799 | |
| WOA–CNN–LSTM | MAE | 11.46 | 11.17 | 10.41 | 10.66 |
| RMSE | 16.75 | 15.71 | 12.32 | 13.02 | |
| R2 | 0.752 | 0.771 | 0.795 | 0.764 | |
| CNN–LSTM–Transformer | MAE | 10.95 | 10.90 | 9.64 | 9.30 |
| RMSE | 13.66 | 12.30 | 11.29 | 11.86 | |
| R2 | 0.817 | 0.843 | 0.801 | 0.814 | |
| BO–CNN–LSTM–Transformer | MAE | 6.92 | 7.34 | 7.56 | 7.74 |
| RMSE | 9.67 | 9.01 | 9.31 | 9.55 | |
| R2 | 0.871 | 0.883 | 0.884 | 0.856 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Hu, J.; Zeng, M. A Spatiotemporal Multimodal Framework for Air Pollution Prediction Based on Bayesian Optimization—Evidence from Sichuan, China. Atmosphere 2025, 16, 958. https://doi.org/10.3390/atmos16080958
Zhang F, Hu J, Zeng M. A Spatiotemporal Multimodal Framework for Air Pollution Prediction Based on Bayesian Optimization—Evidence from Sichuan, China. Atmosphere. 2025; 16(8):958. https://doi.org/10.3390/atmos16080958
Chicago/Turabian StyleZhang, Fengfan, Jiabei Hu, and Ming Zeng. 2025. "A Spatiotemporal Multimodal Framework for Air Pollution Prediction Based on Bayesian Optimization—Evidence from Sichuan, China" Atmosphere 16, no. 8: 958. https://doi.org/10.3390/atmos16080958
APA StyleZhang, F., Hu, J., & Zeng, M. (2025). A Spatiotemporal Multimodal Framework for Air Pollution Prediction Based on Bayesian Optimization—Evidence from Sichuan, China. Atmosphere, 16(8), 958. https://doi.org/10.3390/atmos16080958





