Abstract
The article is focused on the quantitative assessment of the thermal impact of polar mesospheric clouds (PMCs) on the mesopause caused by the emission of absorbed solar and terrestrial infrared (IR) radiation by cloud particles. For this purpose, a parameterization of mesopause heating by PMC crystals has been developed, the main feature of which is to incorporate the thermal properties of ice and the interaction of cloud particles with the environment. Parametrization is based on PMCs zero-dimensional (0-D) model and uses temperature, pressure, and water vapor data in the 80–90 km altitude range retrieved from Solar Occultation for Ice Experiment (SOFIE) measurements. The calculations are made for 14 PMC seasons in both hemispheres with the summer solstice as the central date. The obtained results show that PMCs can make a significant contribution to the heat balance of the upper atmosphere, comparable to the heating caused, for example, by the dissipation of atmospheric gravity waves (GWs). The interhemispheric differences in heating are manifested mainly in the altitude structure: in the Southern Hemisphere (SH), the area of maximum heating values is 1–2 km higher than in the Northern Hemisphere (NH), while quantitatively they are of the same order. The most intensive heating is observed at the lower boundary of the minimum temperature layer (below 150 K) and gradually weakens with altitude. The NH heating median value is 5.86 K/day, while in the SH it is 5.24 K/day. The lowest values of heating are located above the maximum of cloud ice concentration in both hemispheres. The calculated heating rates are also examined in the context of the various factors of temperature variation in the observed atmospheric layers. It is shown in particular that the thermal impact of PMC is commensurate with the influence of dissipating gravity waves at heights of the mesosphere and lower thermosphere (MLT), which parameterizations are included in all modern numerical models of atmospheric circulation. Hence, the developed parameterization can be used in global atmospheric circulation models for further study of the peculiarities of the thermodynamic regime of the MLT.
1. Introduction
The MLT (60–110 km) dynamics are affected by a complex combination of meridional advection and wave processes of different scales (e.g., [1]). The modulation of planetary waves (PWs) by thermal tides occurs in the MLT, providing an opportunity for penetration of the first ones into the thermosphere [2]. Here, the orographic gravity waves [3] and most of the spectrum of internal gravity waves (IGWs) are finally dissipated [4]. Among other things, the MLT has a unique feature during the summer season: in the polar mesopause, the air temperature drops to the lowest values (below 150 K). One of the important sources of objective information on the dynamic processes in the upper atmosphere are the PMCs formed in the 80–85 km layer during summer at the mentioned temperatures and relatively low concentrations of water vapor (3–6 ppmv). PMCs exist from May to August in the NH and from November to February in the SH. Observation of cloud fields allows studying atmospheric perturbations of different spatial and temporal scales: both GWs [5], PWs (e.g., [6]), and atmospheric tides.
Residual meridional circulation features [7], leading to MLTs adiabatic cooling [8] and meteoric smoke (Fe, Mg, etc.), serving as condensation nuclei, presented in the upper atmosphere lead to heterogeneous formation of 20–80 nm ice particles. The PMC fields usually cover almost the entire polar cap and are observed from the Earth, as a rule, at high latitudes (65–70°). Information on the microphysical characteristics of clouds has been repeatedly confirmed by satellite measurements (e.g., [9,10]). The so-called noctilucent clouds (NLCs) and PMC differ somewhat in their optical characteristics and the way they are observed. Registered from the ground, NLCs exist from July to August in the NH in the latitudinal band of 60–80° N and are visible against the background of the twilight sky, illuminated by the light of the setting/rising sun. PMCs are traditionally observed in the entire polar region during the summer season from space by various spacecraft in a wide range of the solar radiation spectrum.
When discussing the PMC/NLC, their connection with the 11-year solar cycle, in particular with the solar flux at a wavelength of 10.7 cm (F10.7), is usually considered. Romejko et al. [11] analyzed various NLC characteristics obtained from ground-based observations over a 40-year period (1962–2001). Based on the results of statistical analysis, the authors stated that the period of variation of the NLC brightness is 1–1.5 years shorter than the 11-year variation of the F10.7 flux. At the same time, they emphasize fluctuations with a period of 2–5 years, which may be due to interactions between atmospheric layers and interhemispheric inhomogeneities. In addition, PMC observations from space also allow us to analyze the long-term variability of their characteristics. UV radiation with wavelengths of 250–300 nm, fully absorbed by O3 molecules in the stratosphere, is backscattered in the presence of PMC from the cloud layer and can be detected by a spacecraft sensor and converted into a hydrodynamic characteristic. Using such a technique, DeLand and Thomas [12] derived and analyzed ice water content (IWC) time series from 1979 to 2013 from limb measurements by the Solar Backscattered Ultraviolet (SBUV) sensors. Until the end of the last century (1979–1997), the IWC value in bright clouds slowly increased but has remained almost constant since 1998 [12]. The response of solar activity over its 24th cycle in the PMC signal of the NH is much weaker than in previous cycles. However, in the SH, clouds are more strongly affected by variations in the solar radiation fluxes. Similar results were also obtained using SBUV data and numerical modeling [13]: the observed changes in PMC parameters are accompanied by a cooling of the mesopause (−0.5 ± 0.2 K/decade at 77° N) and an increase in water vapor concentration (0.07 ± 0.03 ppmv/decade).
The variations in GW energy density, IWC, particle radius, and cloud albedo were also investigated [14]. It was shown that GWs activity affects the formation of PMCs. In the NH, the increase in GW is associated with an increase in IWC and occurs about 0–23 days before the summer solstice. In the SH, the peak of GW activity occurs about 55 days after the solstice, and the increase in IWC begins about 20 days before the solstice. These results demonstrate a close connection between the dynamics of GWs and PMC formation in both hemispheres.
Further study of the PMCs impact on the environment is important for understanding the circulation features and chemistry of the upper atmosphere. Despite already known patterns, new details about the properties of the summer mesopause of both hemispheres are constantly being discovered by various authors. For example, Siskind et al. [15] described the relationship of mesopause dehydration, driven by water vapor sublimation, with the depletion of atomic hydrogen (H) at 95 km at mid and high latitudes. The authors suggest that PMC may play a key role in the transport of H to the upper atmosphere. Also, they found that the same sublimation of water vapor leads to an increase in mesospheric O3 above the cloud layer, as far as O3 anti-correlates with H2O [16]. The ongoing global warming caused by anthropogenic emissions of greenhouse gases (H2O, CH4, and CO2) into the troposphere also affects the upper atmosphere. According to numerical projections, the temperature in the MLT will gradually decrease until the end of the 21st century [17]. An increase in stratospheric and mesospheric water vapor concentrations accompanied by a positive trend [18] will lead to changes in PMC characteristics such as their extent [19]. In addition, PMC occurrence is predicted to increase at midlatitudes (55–60°). Lower temperatures cause downwelling of cloud crystals, which affects the decreasing of the PMC layer [20]. PMCs are capable of making a significant contribution to the thermodynamic regime of the MLT area, for example, both through the release of latent heat during water vapor sublimation and through the absorption of IR radiation.
The purpose of this article is to quantify the thermal impact of PMCs on the environment caused by the re-emission by cloud particles of the absorbed fluxes of incoming and outgoing IR radiation. To achieve the mentioned goal, a parameterization of the mesopause heating by PMC crystals due to the aforementioned absorption, described in Section 2.1, was developed. The calculations, as described in Section 2.2, are performed using background temperature, pressure, and water vapor data from SOFIE measurements for 7 cloud seasons in the NH and 7 in the SH. Section 3 and Section 4 are dedicated to a discussion of the results and relations with other possible sources of MLT heating. Final remarks and conclusions are presented in Section 5.
2. Methodology
2.1. Parameterization of PMC Thermal Impact
To calculate the thermal impact of PMC, we use a numerical scheme (parameterization) based on the PMC 0-D model developed by Hervig et al. [21], whose input information is the vertical profiles of temperature (T), water vapor (QV), and pressure (p). PMCs are modeled using T and QV, in the first instance assuming that ice exists in local thermodynamic equilibrium (LTE). To determine the atmospheric regions where PMC can exist, the condition is used that for H2O sublimation into ice, the partial pressure of water vapor must exceed the saturation pressure over ice at a given temperature [16]. The critical temperature, also called the “frost point” (Ts), depends on p and QV at a given altitude [22]:
Ts = 6077.4/(25.548 − lnQV − lnp).
If there are regions at mesopause heights where the atmospheric temperature is below the frost point temperature (T < Ts), it is assumed that PMCs are formed under such conditions. The volume mixing ratio of the supersaturated water vapor (Qs) is related to the volume mixing ratio of the sublimated vapor (Qice) by the following equation:
where Qs depends on saturation pressure—ps. In supercooled water, ps can be approximated by an exponential law as a function of T [23]:
where ps is in Pa. Then Qs = ps/p.
Qice = Qs − QV,
ps = exp(9.550426 − 5723.265/T + 3.53968 lnT − 0.00728332 T)
After sublimation of water vapor, PMC crystals begin to exchange heat with the environment. Based on the ice’s thermal properties, the equation of the radiation budget of a cloud particle can be written in the following form (e.g., [24,25]):
where the last two terms are responsible for the heat sinks due to emission of the particle’s radiation (Prad) and collisions with other molecules (Pcol). At the same time, PMC crystals also absorb radiation at some parts of the spectrum: short-wave infrared (SWIR) solar radiation (Psol; ~3 μm) and outgoing long-wave (thermal) infrared radiation (Pterr; 10–14 μm). The Pterr term depends mainly on the type of emitting surface and, consequently, its temperature. Table 1 [26] lists the different types of surfaces, their average temperatures, and emission rates.
Pterr + Psol − Prad − Pcol = 0,

Table 1.
Intensity of Pterr fluxes from different emitting surfaces.
Despite the fact that variations in the albedo of the radiating surface can vary significantly in time and space, the thermal radiation flux can be simplified and assumed to be Pterr = 24 W/cm3 [26]. The SWIR flux, in turn, experiences insignificant diurnal variations at high latitudes of the summer MLT region (due to the polar day and, consequently, close to uniform distribution of incoming radiation). This allows us to consider it constant: Psol = 16 W/cm3. Thus, the heating of the environment by cloud particles due to absorption of IR radiation and its re-emission will depend only on the concentration of ice crystals:
where εPMC is in K/s, α = 0.68 cm3/(J/K), and Qice is in ppmv. In Equation (5), Ptot = Pterr + Psol. The formula is proposed by Siskind et al. [26] and is an adaptation of the results obtained by Espy and Jutt [25]. This form of the equation of thermal impact on the environment takes place in the approach that all sublimated H2O absorbs incoming radiation in the corresponding parts of the spectrum, and the flux of latent heat during sublimation is not considered.
εPMC = dT/dt = 0.68 Ptot Qice,
2.2. Solar Occultation Data
Spatiotemporal distributions of T, QV, and p in the mesopause, used in parameterization (see Section 2.1), are taken from the measurements of the Solar Occultation for Ice Experiment (SOFIE; [27]) onboard the sun-synchronous satellite of the Aeronomy of Ice in the Mesosphere (AIM; [28]), which started to operate in 2007, on April 25. The sensor measures solar radiation flux, attenuated by passing through the atmospheric limb, both at the rising and setting of the star above the horizon relative to the satellite position. Based on the collected information, vertical profiles of T, p, and five gas components (H2O, O3, CH4, NO, and CO2) are retrieved, such as aerosol extinction coefficients at several wavelengths. SOFIE has 8 channels, each tuned to a pair of spectral bands, and covers a wide wavelength range from 0.3 to 5 µm. The sensor performs 15 sunrise and 15 sunset scans per day in the latitude band 65–85° in both hemispheres (except for 2016–2018, when AIM orbit changes were performed and measurements did not extend beyond midlatitudes; see Figure 1). Each vertical profile covers an altitude range of 20–95 km and has a 0.2 km vertical resolution.
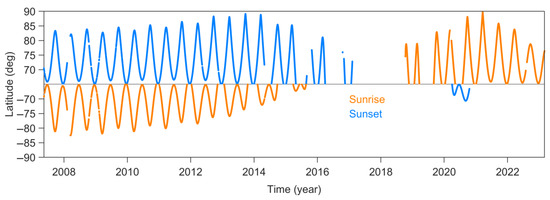
Figure 1.
SOFIE measurements of latitudes (in polar caps) during 2007–2023.
The main measured parameter serving as a basis for reconstructing the geophysical characteristics of the atmosphere is the atmospheric transmittance, which is the ratio between the intensity of radiation that has passed through the atmosphere (V) and external (outside the atmosphere) radiation (V0): V/V0. The main advantage of the sensor is the ability to retrieve PMC characteristics (ice crystal radius, ice mass density, mesopause height, etc.) from the measured spectra. The sensor was operational throughout the entire AIM lifetime from 2007 to 2023, except when the satellite′s solar array failure occurred. After 2021, measurements on Sunrise were terminated. In 2023, AIM′s battery completely failed, and contact with the satellite was lost. In August 2024, after drifting in near-Earth space and constantly losing altitude, the satellite entered the dense layers of the Earth′s atmosphere. The SOFIE Level 2 version v1.3 data used in this study is freely available at http://sofie.gats-inc.com. SOFIE measurements for 7 summer seasons in the NH (2007–2013) and 7 seasons in the SH (2007/2008–2013/2014) were analyzed. The use of other satellite sensors imposes significant limitations within the context of our research for several reasons: (1) the need for high vertical resolution to study the altitudinal structure of the observed process; (2) the availability of continuous measurements throughout the PMC season. For example, the Microwave Limb Sounder (MLS) on board the Aura satellite has only 3 vertical levels in the 80–90 km layer: 0.01, 0.005, and 0.002 hPa [29], making it unsuitable for studying the vertical distribution of parameterized heating. The Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) [30] on the Envisat (Environmental Satellite) and the Submillimeter Radiometer (SMR) onboard the Odin satellite [31] have limited spatiotemporal data sampling in the polar region where PMCs are formed. The Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS) on Canadian SciSat-1 (Scientific Satellite) scans the atmosphere at latitudes > 60° in both hemispheres for short periods of time every few months [32], as does the Sounding of the Atmosphere Using Broadband Emission Radiometry (SABER) [33]. Therefore, it is appropriate to use such a sensor that provides high vertical resolution of the retrieved atmospheric parameters as well as a continuous series of measurements at high latitudes during the PMC season.
3. Results
3.1. Parameterization Sensitivity to Temperature and Water Vapor
To understand the effect of external factors on heating variability, the sensitivity of the parameterization to variations in background conditions (T and p) was calculated. The 0-D model allows us to automate the search for areas where PMC formation is possible using the frost point and different QV concentrations. Ts values were calculated for five different QV concentrations (1, 3, 5, 7, and 9 ppmv) and a range of p values equivalent to altitudes of 75–95 km. Depending on p and QV, the frost point can vary over a wide range, but as can be seen in Figure 2a, for values of QV > 7 ppmv, Ts changes are relatively small. Moreover, starting from the level of 0.01 hPa (equivalent to an altitude of about 80 km), the bottom of the cloud formation layer, all Ts values are overestimated relative to the actually observed temperatures in the mesopause (e.g., [34]), which is a favorable condition for sublimation of water vapor into ice.
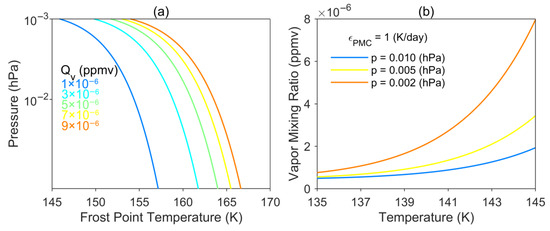
Figure 2.
Vertical profiles of the Ts as a function of QV and p (a), and εPMC sensitivity to T and p variations (b).
One can conclude that the smaller the QV and the lower the p, the lower the real temperature must be for PMCs to form. Moreover, such calculations allow us to estimate the necessary values of water vapor and temperature concentration necessary for induction of heating of the environment by 1 degree. Figure 2b shows the necessary water vapor concentrations at different values of T and 3 levels of p (0.01, 0.005, and 0.002 hPa) required for 1 K/day heating. Figure 2b shows that at temperatures below 138 K, εPMC is virtually insensitive to water vapor variations. Similarly, heating is also virtually insensitive to variations in QV at p = 0.01 hPa. The situation changes if the real temperature is above 139 K. Then, the lower the atmospheric pressure, the more QV is needed to achieve a given value of εPMC.
3.2. Heating Quantifying
The PMC season lasts from May to August in the NH and from November to February in the SH. Complete dissipation of the PMC occurs due to the change of the thermodynamic regime of the polar MLT. The central date of each cloud season is the summer solstice. Vertical profiles of T, QV, and p were selected for the Ts calculation. Further, all values of temperature when T > Ts were excluded from the subsequent calculations, as far as the conditions necessary for cloud formation were not achieved. After calculating and other related variables, heating rates (εPMC, K/s) were calculated for each remaining vertical profile. Then these heating rates were averaged for each day and converted to daily rates (K/day). Figure 3 and Figure 4 show the altitudinal and temporal structures of daily mean εPMC values for the 14 seasons considered. It can be seen that the maximum εPMC values are concentrated in the bottom part of the low-temperature region; the 150 K isotherm is drawn in these figures to indicate its boundaries.
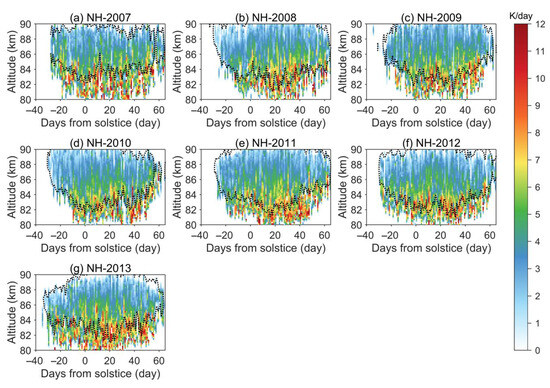
Figure 3.
Altitude versus time plot of daily mean εPMC in NH with 150 K isotherm (dotted).
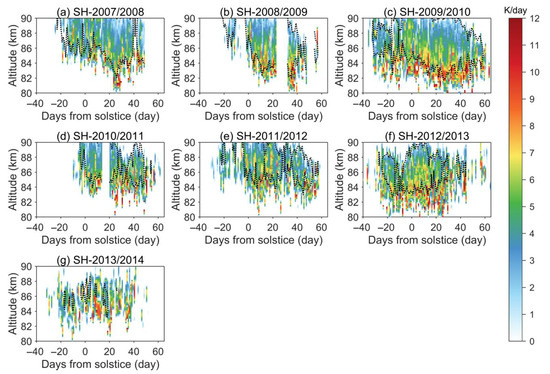
Figure 4.
Same as Figure 3, but for SH.
The minimum temperatures, which are also commonly referred to as the mesopause temperature, Tmes (e.g., [20]), are usually located in the central part of the above-mentioned region, and the maximum εPMC is located at altitudes of 81–82 km in the NH and 82–83 km in the SH, i.e., below the Tmes. Three conclusions follow from these results. First, since the only varying term in Equation (5) is Qice, the variations of εPMC will depend on the distribution of sublimated H2O in time and space. Sublimating above Tmes, ice crystals under the gravity force begin to descend as their concentration and radius increase. This process continues till the lower boundary of the low temperature level, then cloud particles begin to melt due to the increase in T and lose their thermophysical properties. Consequently, the maximum concentrations of Qice and hence εPMC are located there (i.e., at the lower boundary of the low temperature level). Second, the interhemispheric differences in εPMC maximum heights are due to inhomogeneities in the structure of the mesopause of both hemispheres: as a rule, PMCs are 1–2 km higher in the SH compared to the NH (e.g., [35]). Third, interannual variability, diurnal variations, and any fluctuations in εPMC values are due to local thermodynamic and chemical processes affecting the mesopause and, consequently, the PMC ice crystal fields. For example, the presence of GWs leads to both the appearance and complete destruction of cloud fields due to temperature perturbations reaching several degrees, which can play a significant role in the processes of sublimation or evaporation of ice crystals [36]. On the other hand, solar activity, manifested in changes in the mesopause temperature, may be responsible for the multiyear variability of PMC parameters, which also affects, for example, the start of the PMC season [11,12,19].
Figure 5 shows histograms of the distribution of εPMC values for all seasons in both hemispheres. For quantitative assessment, the εPMC was divided into layers: layers above and below the Tmes level. The histograms in Figure 5a,b correspond to the area of maximum Qice values (where the maximum heating is concentrated). The median values for NH and SH are 5.86 and 5.24 K/day, respectively, i.e., the differences are about 11%. It should be noted that the distribution in both hemispheres is symmetric with respect to each other. Maximum εPMC values > 10 K/day occur in the same zone. Above the Tmes level (Figure 5c,d), small εPMC values are concentrated, and the interhemispheric differences are ~7%. The shape of the distribution in the NH is also different, which is probably due to the large number of measurement gaps. Overall, the heating patterns both above and below Tmes in both hemispheres are similar. That is, PMCs affect the mesopause heat balance equally in both the NH and SH. At the same time, according to the calculations, an increase in QV is expected to enhance the formation of PMCs and, consequently, to strengthen the parameterized heating.
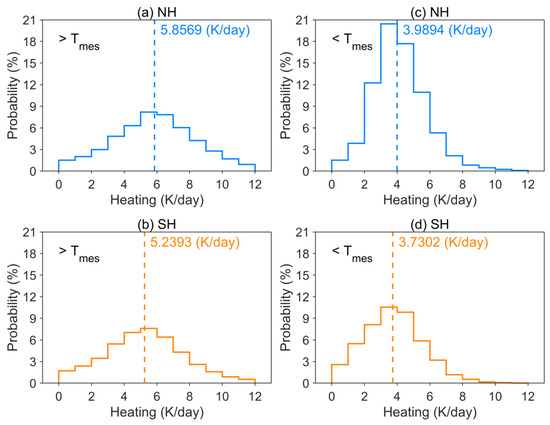
Figure 5.
Histogram of εPMC in NH (blue) and SH (orange) below Tmes (a,b) and above (c,d).
4. Discussion
Calculated in the present study, heating rates due to absorption of IR radiation by PMC ice particles are additions to other heating/cooling rates caused by different atmospheric gases and dynamical processes. It is therefore particularly important to examine the results obtained in the context of the various factors of temperature variation at these altitudes.
At altitudes of 80–85 km, the heating rate of the atmosphere due to absorption of solar energy is εs~4–10 K/day (e.g., [37]). Near the mesopause, this solar heating is mainly compensated by atmospheric IR cooling, having the rate εIR comparable in magnitude to εs but having the negative sign [37]. Important dynamical processes in the region of PMC formation are IGWs, which create wave structures of the cloud fields.
Traveling IGW structures in the PMC were widely observed (e.g., [38,39]). A statistical analysis of IGW structures in PMC observed in Norway during the years of 2007–2010 was made by [40]. Using a Fourier transform technique, they found the IGW horizontal wavelength, λh, phase speed, ch, period, τ, and the amplitude of PMC relative intensity variations, which are proportional to the relative density variations, |ρ′/ρ|. For latitudes 64–72° N, ref. [40] found broad distributions of the above parameters within the following ranges: λh~3–40 km, ch~10–60 m/s, τ~6–50 min, and |ρ′/ρ|~2–10%. These ranges correspond to other observations of IGW structures in PMC (see [38,39]).
IGWs propagating from below produce upward momentum and heat fluxes. Dissipation of waves leads to a decrease in those fluxes with altitudes. IGW mode becomes convectively unstable at the breaking level, at which the amplitude of horizontal velocity variations becomes U = |u0 − ch|, where u0 is the projection of the mean wind on the direction of wave propagation. Above the breaking level, IGWs produce turbulence and become saturated. The conception of IGW saturation supposes that the transport of wave energy to turbulence totally balances the IGW amplitude growth due to decreasing the atmospheric density with height [41]. The heating rate (wave heat flux divergence) produced by saturated IGWs can be estimated using the following expression [37,41]:
where σ is the IGW observable frequency, U is the amplitude of wave variations of horizontal velocity, and N is the Brunt-Vaisala frequency. The IGW dispersion equation and polarization relations for low-frequency short IGW [42] give U ≈ g |ρ′/ρ0|/N, where g is the acceleration due to gravity. After this substitution, Equation (6) takes the following form:
εGW = σU3/(2NH),
εGW = σg3/(2N4H) |ρ′/ρ0|3.
Near the mesopause at the mean temperature T0 = 145–150 K typical for PMC events [43] N2 ≈ g2/(T0cp), where cp is the atmospheric air heat capacity at constant pressure. Assuming that smaller IGW periods correspond to smaller amplitudes in the above-mentioned ranges of periods, τ, and amplitudes |ρ′/ρ| of IGWs observed in PMC by [40], we can estimate εGW~3–40 K/day. These values can be comparable with the additional heating by PMC εPMC shown in Figure 3 and Figure 4. Studies of turbulence near the mesopause with sounding rockets showed that atmospheric heating caused by dissipation of turbulence produced by breaking IGWs can reach 10–20 K/day [43]. This generally corresponds to obtained εGW values; however, Equation (7) may give overestimated values for low-frequency IGWs with large amplitudes. This may show that not all IGWs observed in PMC might be saturated.
Ref. [40] found that most relatively short IGWs observed in PMC are subject to strong dissipation and cannot be explained with models of wave propagation from the lower atmosphere. Ref. [44] simulated IGWs at altitudes from the lower to the upper atmosphere. They found that primary IGWs propagating from the troposphere can dissipate and deposit energy and momentum in the stratosphere and lower mesosphere. Inhomogeneities of these depositions can generate secondary wave modes. This process can reiterate, producing higher-order IGWs in the thermosphere having larger scales than those of the primary IGWs. Generation of secondary IGWs near critical levels was also demonstrated with high-resolution numerical IGW simulations [45].
Except for heating due to dissipation of wave and turbulent energy, the background and wave-induced turbulence can produce a heat outflow and cooling of the atmosphere. The rate of turbulent heating/cooling of the atmosphere is described as follows [37,46]:
where Kteff is the mean over wave period effective coefficient of turbulent heat conduction. Cooling (εt0 < 0) occurs when ∂T0/∂z > −g/cp. Ref. [37] made a simulation of solar and IR heat influxes as well as GW heating and turbulent cooling at altitudes of 60–130 km. They found that approximately heating εs is balanced by cooling εIR, and heating εGW is balanced by cooling εt0 at a wide range of IGW intensities. Therefore, the heat balance near the mesopause involves many different heating/cooling impacts, and inclusion of the additional comparable heating rate due to PMC ice particles may produce substantial effects, which require further studies.
εt0 = 1/ρ0 ∂/∂z [ρ0 cp Kteff (∂T0/∂z + g/cp)],
Despite the fact that calculations of the PMC thermal impact on the environment were made only for a small number of years out of the entire period of satellite observations of the PMC, the obtained εPMC values also allow us to make the following assumption. Heating due to absorption of infrared (SWIR and thermal) radiation fluxes by PMC particles increases the vertical temperature gradient, which, in turn, increases the value of the vertical wind component and, as a consequence, may cause additional adiabatic cooling of the overlying atmosphere. Such an effect was demonstrated, for example, by [26]: an increase in the temperature of the polar mesopause at altitudes of 80–90 km is accompanied by cooling of the overlying layers. Thus, the predicted decrease in the mesopause temperature caused by climate change, as well as the increase in water vapor concentration and, as a consequence, the increase in the PMC area and their spreading toward the middle latitudes, lead to the strengthening of the εPMC. This triggers a series of positive feedback through the amplification of the vertical wind, which causes additional adiabatic cooling of the mesopause above the PMC layer. To further analyze this process, we plan to implement this parameterization of heating from the PMC into a general atmospheric circulation model.
When discussing the various factors influencing the thermodynamic regime of the mesopause, it is also necessary to mention the PWs. For instance, the 2- and 5-day PWs, which play an important role in the dynamics of the summer polar MLT. Dalin et al. studied the NH polar mesopause in the summer of 2007 and 2008 and found that the temperature variations caused by these PWs reached values of 2.5–3 K, and their maximum occurred at the 80–110 km layer [47]. By analyzing 16 years of Aura Microwave Limb Sounder (MLS) measurements in the NH (2007–2022), it was found that if a westward 5-day PW with a wave number of 1 intensifies at the start of the PMC season (~15–28 May), the first cloud fields will form in its cold trough [6]. Stationary planetary waves are also capable of causing significant variations in hydrodynamic parameters in the MLT [48]. Their impact is concentrated mainly in the polar latitudes during the winter season. However, the contribution of these waves to the PMC/NLC variability is not comparable to the contribution made by IGWs, having horizontal scales of 10–100 km. These waves can lead to temperature perturbations from several to tens of degrees (see also [40]). Atmospheric thermal tides (especially migrating ones) also play a significant role in the MLT [1]. The amplitudes of temperature variations due to tides increase in low latitudes and are of the order of several degrees in the lower thermosphere. Their influence increases in the higher layers of the atmosphere. The heating of the mesosphere-lower thermosphere is also significantly affected by variations in incoming solar radiation within the 11-year solar cycle [49,50]. However, these studies will remain outside the scope of our article.
5. Conclusions
This article describes the calculation of the thermal impact of polar mesospheric clouds on the environment caused by the emission of absorbed incoming and outgoing IR radiation fluxes by cloud particles. To calculate this effect, a parameterization of mesopause heating due to the absorption of IR radiation flows by PMC crystals was developed, the main feature of which is the consideration of the thermophysical properties of ice and the interaction of cloud particles with the environment. Fluxes of solar radiation in a narrow band near 3 μm and terrestrial radiation in the wavelength range of 10–14 μm, absorbed by cloud particles, are re-emitted back into the atmosphere, causing its heating, contributing to the change of the thermodynamic conditions of the mesopause. The parameterization is based on T, QV, and p data retrieved from the solar radiation spectra measured by the SOFIE sensor. We present the results of heating calculations for 14 PMC seasons: 2007–2013 in NH and from 2007/2008 to 2013/2014 in SH.
Based on the results obtained, the following conclusions are derived:
- Since the parameterization depends solely on Qice, the most intense εPMC heating values are concentrated at the altitudes of maximum ice crystal concentrations: 81–82 km in NH and 82–83 km in SH.
- Any variations of atmospheric parameters, caused, for example, by IGWs, and perturbing the Qice distribution in time and space, lead to perturbations in the heating intensity. An increase in water vapor concentration is expected to enhance the formation of PMC and, as a consequence, enhance radiative heating.
- The median εPMC values centered below the Tmes heights are 5.86 and 5.24 K/day in NH and SH, respectively, and their distribution is symmetric in both hemispheres.
- The lowest values of heating are located above the maximum of cloud ice concentration in both hemispheres. The maximum values of the calculated heat influx are concentrated at the lower boundary of the cloud layer, which is due to the behavior of sublimated crystals: appearing above 85 km, small cloud particles settle, shifting to the zone of low temperatures, where the radius of the crystals increases.
Thus, it is shown that PMCs can make a significant contribution to the heat budget of the upper atmosphere, comparable to the heating caused, e.g., by the dissipation of IGWs, the parameterization of which is included in all global atmospheric circulation models (e.g., [51,52,53]). The results obtained are comparable with the calculations by [26].
The integration of the developed parameterization into climate and atmospheric general circulation models will improve the accuracy of describing and predicting changes in the condition of the upper atmosphere. In particular, in the future, in order to study in detail the feedback that can cause cooling of the MLT region above the PMC/NLC layer, it is planned to implement the developed parameterization into the global atmospheric circulation models, including the Model of the Middle and Upper Atmosphere (MUAM).
Author Contributions
Conceptualization, A.S.; ice properties explanation, K.K.; providing the solar occultation data, A.S.; analysis of gravity wave activity, N.G.; the calculation of the heating rates, and the analysis of its changes, A.S., A.K. and E.S.; writing—review and editing, K.D. and T.E. All authors have read and agreed to the published version of the manuscript.
Funding
Developing the new parameterization of PMC heating/cooling rates is supported by Saint Petersburg State University (project 124032000025-1); estimations of IGW thermal effects are supported by the Russian Science Foundation (grant #25-17-00166).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Smith, A.K. Global Dynamics of the MLT. Surv. Geophys. 2012, 33, 1177–1230. [Google Scholar] [CrossRef]
- Laštovicka, J. Forcing of the ionosphere by waves from below. J. Atmos. Sol.-Terr. Phys. 2006, 68, 479–497. [Google Scholar] [CrossRef]
- Koval, A.V.; Gavrilov, N.M.; Zubov, V.A.; Rozanov, E.V.; Golovko, A.G. Modified Parameterization Scheme of Orographic Gravity Waves in the SOCOL Chemistry-Climate Model. Pure Appl. Geophys. 2025, 182, 255–270. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Baumgarten, G.; Fritts, D.C. Quantifying Kelvin-Helmholtz instability dynamics observed in noctilucent clouds: 1. Methods and observations. J. Geophys. Res. Atmos. 2014, 119, 9324–9337. [Google Scholar] [CrossRef]
- Thurairajah, B.; Bailey, S.M.; Harvey, V.L.; Randall, C.E.; France, J.A. The role of the quasi 5-day wave on the onset of polar mesospheric cloud seasons in the northern hemisphere. J. Geophys. Res. Atmos. 2023, 128, e2022JD037982. [Google Scholar] [CrossRef]
- Koval, A.V.; Chen, W.; Didenko, K.A.; Ermakova, T.S.; Gavrilov, N.M.; Pogoreltsev, A.I.; Toptunova, O.N.; Wei, K.; Yarusova, A.N.; Zarubin, A.S. Modelling the residual mean meridional circulation at different stages of sudden stratospheric warming events. Ann. Geophys. 2021, 39, 357–368. [Google Scholar] [CrossRef]
- Karlsson, B.; Kuilman, M. On how the middle atmospheric residual circulation responds to the solar cycle close to the solstices. J. Clim. 2018, 31, 401–421. [Google Scholar] [CrossRef]
- Christensen, O.M.; Benze, S.; Eriksson, P.; Gumbel, J.; Megner, L.; Murtagh, D.P. The relationship between polar mesospheric clouds and their background atmosphere as observed by Odin-SMR and Odin-OSIRIS. Atmos. Chem. Phys. 2016, 16, 12587–12600. [Google Scholar] [CrossRef]
- García-Comas, M.; López-Puertas, M.; Funke, B.; Jurado-Navarro, Á.A.; Gardini, A.; Stiller, G.P.; von Clarmann, T.; Höpfner, M. Measurements of global distributions of polar mesospheric clouds during 2005–2012 by MIPAS/Envisat. Atmos. Chem. Phys. 2016, 16, 6701–6719. [Google Scholar] [CrossRef]
- Romejko, V.A.; Dalin, P.A.; Pertsev, N.N. Forty years of noctilucent cloud observations near Moscow: Database and simple statistics. J. Geophys. Res. 2003, 108, 8443. [Google Scholar] [CrossRef]
- DeLand, M.T.; Thomas, G.E. Updated PMC trends derived from SBUV data. J. Geophys. Res. Atmos. 2015, 120, 2140–2166. [Google Scholar] [CrossRef]
- Hervig, M.E.; Berger, U.; Siskind, D.E. Decadal variability in PMCs and implications for changing temperature and water vapor in the upper mesosphere. J. Geophys. Res. Atmos. 2016, 121, 2383–2392. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, N.; Soon, W.; Herrera, V.M.V.; Yang, C.; Dou, X. The Hemispheric Asymmetry of Gravity Wave Impact on the Polar Mesospheric Cloud, Based on the Aeronomy of Ice in the Mesosphere Satellite. Atmosphere 2023, 14, 419. [Google Scholar] [CrossRef]
- Siskind, D.E.; Merkel, A.W.; Marsh, D.R.; Randall, C.E.; Hervig, M.E.; Mlynczak, M.G.; Russell, J.M., III. Understanding the effects of polar mesospheric clouds on the environment of the upper mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 2018, 123, 11705–11719. [Google Scholar] [CrossRef]
- Siskind, D.E.; Stevens, M.H. A radiative feedback from an interactive polar mesospheric cloud parameterization in a two dimensional model. Adv. Space Res. 2006, 38, 2383–2387. [Google Scholar] [CrossRef]
- Vargin, P.; Kostrykin, S.; Koval, A.; Rozanov, E.; Egorova, T.; Smyshlyaev, S.; Tsvetkova, N. Arctic stratosphere changes in the 21st century in the Earth system model SOCOLv4. Front. Earth Sci. 2023, 11, 1214418. [Google Scholar] [CrossRef]
- Yue, J.; Russell, J., III; Gan, Q.; Wang, T.; Rong, P.; Garcia, R.; Mlynczak, M. Increasing water vapor in the stratosphere and mesosphere after 2002. Geophys. Res. Lett. 2019, 46, 13452–13460. [Google Scholar] [CrossRef]
- Yu, W.; Yue, J.; Garcia, R.; Mlynczak, M.; Russell, J., III. WACCM6 projections of polar mesospheric cloud abundance over the 21st century. J. Geophys. Res. Atmos. 2023, 128, e2023JD038985. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Sun, S.; Li, X. Correlation between Peak Height of Polar Mesospheric Clouds and Mesopause Temperature. Atmosphere 2024, 15, 1149. [Google Scholar] [CrossRef]
- Hervig, M.E.; Stevens, M.H.; Gordley, L.L.; Deaver, L.E.; Russell, J.M., III; Bailey, S.M. Relationships between polar mesospheric clouds, temperature, and water vapor from Solar Occultation for Ice Experiment (SOFIE) observations. J. Geophys. Res. 2009, 114, D20203. [Google Scholar] [CrossRef]
- Thomas, G.E. Mesospheric clouds and the physics of the mesopause region. Rev. Geophys. 1991, 29, 553–575. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapor pressure of ice and super-cooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef]
- Asmus, H.; Wilms, H.; Strelnikov, B.; Rapp, M. On the heterogeneous nucleation of mesospheric ice on meteoric smoke particles: Microphysical modeling. J. Atmos. Sol.-Terr. Phys. 2014, 118, 180–189. [Google Scholar] [CrossRef][Green Version]
- Espy, P.J.; Jutt, H. Equilibrium temperature of water-ice aerosols in the high-latitude summer mesosphere. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1823–1832. [Google Scholar] [CrossRef]
- Siskind, D.E.; Hervig, M.; Gumbel, J.; Stevens, M.H. Polar mesospheric cloud mass and the ice budget: 3. Application of a coupled ice-chemistry-dynamics model and comparison with observations. J. Geophys. Res. 2007, 112, D08303. [Google Scholar] [CrossRef]
- Gordley, L.L.; Hervig, M.E.; Fish, C.; Russell, J.M., III; Bailey, S.; Cook, J.; Hansen, S.; Shumway, A.; Paxton, G.; Deaver, L.; et al. The solar occultation for ice experiment. J. Atmos. Sol.-Terr. Phys. 2008, 71, 300–315. [Google Scholar] [CrossRef]
- Russell, J.M.; Bailey, S.M.; Gordley, L.L.; Rush, D.W.; Horányi, M.; Hervig, M.E.; Thomas, G.E.; Randall, C.E.; Siskind, D.E.; Stevens, M.H.; et al. The Aeronomy of Ice in the Mesosphere (AIM) mission: Overview and early science results. J. Atmos. Sol.-Terr. Phys. 2009, 71, 289–299. [Google Scholar] [CrossRef]
- Waters, J.W.; Froidevaux, L.; Harwood, R.S.; Jarnot, R.F.; Pickett, H.M.; Read, W.G.; Siegel, P.H.; Cofield, R.E.; Filipiak, M.J.; Flower, D.A.; et al. The Earth observing system microwave limb sounder (EOS MLS) on the Aura Satellite. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1075–1092. [Google Scholar] [CrossRef]
- Fischer, H.; Birk, M.; Blom, C.; Carli, B.; Carlotti, M.; von Clarmann, T.; Delbouille, L.; Dudhia, A.; Ehhalt, D.; Endemann, M.; et al. MIPAS: An instrument for atmospheric and climate research. Atmos. Chem. Phys. 2008, 8, 2151–2188. [Google Scholar] [CrossRef]
- Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jiménez, C.; Megie, G.; et al. An overview of the Odin atmospheric mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
- Bernath, P.F.; McElroy, C.T.; Abrams, M.C.; Boone, C.D.; Butler, M.; Camy-Peyret, C.; Carleer, M.; Clerbaux, C.; Coheur, P.-F.; Colin, R.; et al. Atmospheric Chemistry Experiment (ACE): Mission overview. Geophys. Res. Lett. 2005, 32, L15S01. [Google Scholar] [CrossRef]
- Russell, J.M., III; Mlynczak, M.G.; Gordley, L.L.; Tansock, J.J., Jr.; Esplin, R.W. Overview of the SABER experiment and preliminary calibration results. Proc. SPIE 1999, 3756, 277. [Google Scholar] [CrossRef]
- Pertsev, N.; Dalin, P.; Perminov, V.; Romejko, V.; Dubietis, A.; Balčiunas, R.; Černis, K.; Noctilucent, M.Z. clouds observed from the ground: Sensitivity to mesospheric parameters and long-term time series. Earth Planets Space 2014, 66, 98. [Google Scholar] [CrossRef]
- Kuilman, M.; Karlsson, B.; Benze, S.; Megner, L. Exploring noctilucent cloud variability using the nudged and extended version of the Canadian middle atmosphere model. J. Atmos. Sol.-Terr. Phys. 2017, 164, 276–288. [Google Scholar] [CrossRef]
- Dalin, P.; Pogoreltsev, A.; Pertsev, N.; Perminov, V.; Shevchuk, N.; Dubietis, A.; Zalcik, M.; Kulikov, S.; Zadorozhny, A.; Kudabayeva, D.; et al. Evidence of the formation of noctilucent clouds due to propagation of an isolated gravity wave caused by a tropospheric occluded front. Geophys. Res. Lett. 2015, 42, 2037–2046. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Roble, R.G. The effect of gravity waves on the global mean temperature and composition structure of the upper atmosphere. J. Geophys. Res. 1994, 99, 25773–25780. [Google Scholar] [CrossRef]
- Pautet, P.-D.; Stegman, J.; Wrasse, C.M.; Nielsen, K.; Takahashi, H.; Taylor, M.J.; Hoppel, K.W.; Eckermann, S.D. Analysis of gravity waves structures visible in noctilucent cloud images. J. Atmos. Sol.-Terr. Phys. 2011, 73, 2082–2090. [Google Scholar] [CrossRef]
- Taylor, M.J.; Pautet, P.-D.; Zhao, Y.; Randall, C.E.; Lumpe, J.; Bailey, S.M.; Carstens, J.; Nielsen, K.; Russell, J.M., III; Stegman, J. High-latitude gravity wave measurements in noctilucent clouds and polar mesospheric clouds. In Aeronomy of the Earth’s Atmosphere and Ionosphere; IAGA Special Sopron Book Series; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2, pp. 93–105. [Google Scholar] [CrossRef]
- Demissie, T.D.; Espy, P.J.; Kleinknecht, N.H.; Halten, M.; Kaifler, N.; Baumgarten, G. Characteristics and sources of gravity waves observed in noctilucent cloud over Norway. Atmos. Chem. Phys. 2014, 14, 12133–12142. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Gossard, E.E.; Hooke, W.H. Waves in the Atmosphere, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Lübken, F.-J. Physics in the mesosphere/lower thermosphere: A personal perspective. Front. Astron. Space Sci. 2022, 9, 1000766. [Google Scholar] [CrossRef]
- Vadas, S.L.; Becker, E.; Bossert, K.; Hozumi, Y.; Stober, G.; Harvey, V.L.; Baumgarten, G.; Hoffmann, L. The role of the polar vortex jet for secondary and higher-order gravity waves in the northern mesosphere and thermosphere during 11–14 January 2016. J. Geophys. Res. Space Phys. 2024, 129, e2024JA032521. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Kshevetskii, S.P.; Koval, A.V.; Kurdyaeva, Y.A. Tunneling of acoustic-gravity waves through critical levels to the upper atmosphere. Adv. Space Res. 2025, 75, 3661–3670. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Yudin, V.A. Model for coefficients of turbulence and effective Prandtl number produced by breaking gravity waves in the upper atmosphere. J. Geophys. Res. 1992, 97, 7619–7624. [Google Scholar] [CrossRef]
- Dalin, P.; Pertsev, N.; Dubietis, A.; Zalcik, M.; Zadorozhny, A.; Connors, M.; Schofield, I.; McEwan, T.; McEachran, I.; Frandsen, S.; et al. A comparison between ground-based observations of noctilucent clouds and Aura satellite data. J. Atmos. Sol.-Terr. Phys. 2011, 73, 2097–2109. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D.; Andonov, B. Climatology of the stationary planetary waves seen in the SABER/TIMED temperatures (2002–2007). J. Geophys. Res. 2010, 115, A06315. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Koval, A.V.; Didenko, K.A.; Ermakova, T.S.; Gavrilov, N.M.; Golovko, A.G. Diagnostics of the solar activity influence on the global atmospheric circulation in the thermosphere and MLT area: Wave—Mean flow interaction effects. Clim. Dyn. 2025, 63, 19. [Google Scholar] [CrossRef]
- Garcia, R.R.; Smith, A.K.; Kinnison, D.E.; de la Cámara, Á.; Murphy, D.J. Modification of the Gravity Wave Parameterization in the Whole Atmosphere Community Climate Model: Motivation and Results. J. Atmos. Sci. 2017, 74, 275–291. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Klaassen, P. Thermal effects of saturating gravity waves in the atmosphere. J. Geophys. Res. 2003, 108, 4040. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Heating and cooling of the thermosphere by internal gravity waves. Geophys. Res. Lett. 2009, 36, L14807. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).