Abstract
Apiculture is among the most weather-dependent sectors of agriculture; however, quantifying the impact of meteorological factors remains challenging. Beehive weight has long been recognized as an important indicator of colony health, strength, and food availability, as well as foraging activity. Atmospheric influences on hive weight dynamics have been a subject of research since the early 20th century. This study aims to estimate hourly hive weight variation by applying linear time-series models to hive weight data collected from active apiaries during intensive foraging periods, considering atmospheric predictors. We employed a rolling 24 h forward ARIMAX and SARIMAX model, incorporating meteorological variables as exogenous factors. The median estimates for the study period resulted in model RMSE values of 0.1 and 0.3 kg/h. From numerous meteorological variables, the hourly maximum temperature was found to be the most significant predictor. ARIMAX model results also exhibited a strong diurnal cycle, pointing out the weather-driven seasonality of hive weight variations.
Keywords:
honey bees; ARIMAX; SARIMAX; hive weight; black locust; Robinia; precision beekeeping; forecasting 1. Introduction
Apis mellifera L., commonly known as the Western honey bee, is considered to be one of the most important pollinator species in the care of beekeepers. Their activity significantly influences ecological and economic stability as well as biodiversity, crop production, food security, and overall human well-being [1,2].
Thanks to their complex plant–pollinator interaction, the bees contribute to the pollination of approximately 75% of food crops, which collectively contribute to 35% of human nutrition [1]. Honey bees are also indicators of the pollinator population, such as bumblebees or other wild bee types, or the condition of the environment [3]. Beyond their role in pollination, they produce a range of valuable products [4], including honey, bee bread, pollen, propolis, royal jelly, venom, apilarnil, and wax, which have a significant global economic value [5]. The EU represents 16% of the global annual honey production, ranking as the world’s second-largest producer, with an estimated output of ~280,000 tons per year [6]. If we consider the density of the managed beehives, Hungary and Greece stand out from the European countries [7]. Within the EU, approximately 700,000 beekeepers manage 20 million beehives, with Hungary accounting for around 6% of the total hive population. Acacia honey originating from the black locust tree (Robinia pseudoacacia L.) constitutes around 30–50% of honey production in Hungary [8] and is exported in large quantities [9].
Monitoring the hive weight is advantageous because it predicts honey flow and allows one to investigate the honey bee’s health status, swarming periods, or possible thefts [10]. Hive weight dynamics has been the subject of study since the early 20th century [11]. The expansion of digital hive monitoring sensors as IoT-based monitoring systems has significantly enhanced the understanding of colony responses to environmental changes, optimized pollination management, and reduced reaction times to weather-related risks [12].
Nowadays, various devices are available for monitoring colony health and productivity remotely, thanks to the development of precision beekeeping [13], including temperature, humidity, air quality, vibration, acoustic, capacitance, and infrared sensors, as well as radio-frequency identification (RFID), harmonic radar, and cameras. However, among these, hive scales remain the most widely used tool for both beekeepers and researchers [3,10,13,14,15,16,17]. A comprehensive review of hive sensor technologies was presented by Zaman and Dorin [12], Meikle and Holst [18], Marchal et al. [19], while relevant research on weather impact on honey production has been collected in our previous review [20]. Despite the technological development in this field, there is limited research using real field data on the relationship between the honey bee behavior and weather conditions [21].
The objective of the present study is to forecast the bees’ foraging behavior during periods of heavy nectar flow in active apiaries, incorporating meteorological factors as exogenous variables. To the best of our knowledge, this is the first study to apply and compare the ARIMA model to beehive data during the black locust foraging season. Beyond the development of the model, the objective is twofold: first, to quantify the influence of weather conditions on hive weight fluctuations and, second, to gain a better understanding of the biological responses of honey bees to environmental changes. These insights are crucial for advancing modern precision apiculture, optimizing hive management strategies and adapting to climate change.
2. Materials and Methods
2.1. Hive Weight Data
The hive weight database was obtained from the Hungarian Apiarists’ Network. Measurements were performed using GSM stainless steel electronic hive scales manufactured in Hungary (500 mm × 400 mm × 80 mm, max. capacity 150 kg, precision ±0.1 kg, net weight 8 kg, operating temperature −20~60 °C) under 24 colonies at 15 different locations within Hungary between 2021 and 2024. The selected apiaries were continuously monitored at intervals of 10, 30, and 60 min depending on the beekeeper’s measurement setup, and the colonies remained in the same location during the foraging season. For consistency and comparability across all time series, the data were aggregated into hourly averages for analysis.
The metadata included the nearest meteorological monitoring site to the respective apiary (Figure S1) as well as the flowering species from which they harvested the honey in a given period. Two of the twenty-four time series were measured at our own apiary (Hive 1 and Hive 2), where we also tracked key beekeeping interventions (see in File S1). The minimum distance between any two apiaries was 2 km, the median distance was 160 km, and the maximum distance was 424 km.
These hives housed the Apis mellifera carnica Pollmann (also known as ‘Krajnai’), a subspecies of honey bee of the ‘Pannonian’, a unique ecotype in Hungary [22]. Due to their controlled data quality and continuous time series, Hive 1 and Hive 2 were used to test and optimize the prediction model. Forecasts were created and validated for all 24 hives available in the apiarist network.
In this study, we focused on the period of Robinia pseudoacacia (black locust) nectar collection, from 15 April to 15 June. However, for modeling purposes, we only included days when bees were actively foraging, and the characteristic nectar flow pattern had already emerged. Missing data points were interpolated, and all the hive weight data were standardized and aggregated to a 1 h resolution. To ensure data quality, we applied filtering based on the 1st and 99th percentiles, and each time series was visually inspected before numerical processing.
Significant beekeeping interventions were recorded in our own apiary (Hives 1 and 2), the colonies’ development was monitored throughout the year by the same beekeeper, and similar colonies were selected. During this period, we calculated the daily hive weight changes, considering values within a ±2 kg/h range as valid. This simple method could filter major beekeeping interventions (harvesting or feeding) and is a common practice in agricultural applications. A similar filtering technique can be found in Arias-Kalluari et al. [23], who defined a ±20 g/2 min threshold for maximum hive weight change—however, this would be a very low value for Robinia foraging. Lecocq et al. [24] applied a ±3 kg/2 h threshold. These simple-but-objective conditions are suitable for the filtering of interventions, while more detailed breakpoint detections methods are often applied to detect and predict swarming, e.g., in Davidson et al. [25].
The colonies were kept strong and healthy throughout the years. On average, the monitored colonies in our apiary had 7 to 9 frames of brood and the beekeeper kept moderately strong colonies throughout the observation period. Varroa mite control was applied with oxalic acid sublimation, glycerol strip trapping, and maintaining strong colonies. Cleaning harvest was carried out before the observation period. The colonies were provided with a permanent water source. The colonies were prepared for intensive foraging, leaving sufficient space for the arrival of fresh nectar, and the reproduction was timed to ensure the most forager bees. The hives were one of the Hungarian NB (‘Nagy Boconádi’, 420 mm × 360 mm, virgin honeycomb weight 0.4 kg) ten-frame BOROVI pine wooden Tamási type deep boxes (61.2 L capacity, 16.9 kg), featuring an expandable ½ honey box system with ½ NB frames as needed for a separate honey collection and a well-isolated nest, which enhances colony protection from external impacts.
2.2. Meteorological Data
Hourly meteorological data was provided by the nearest HungaroMet meteorological station, located within 18 km of the respective apiaries (Figure S1). In total, data from six different weather stations were used to characterize the environmental conditions relevant to each apiary. The mean distance between the apiaries and their associated weather stations was 9 km, with the minimum distance being 1.4 km.
In this study, the following meteorological variables were used: 2 m actual temperature (t), 1 h minimum temperature (tn), 1 h maximum temperature (tx), surface temperature (tsn), radiation (sr), wind speed (fs), wind gust (fx), precipitation (r), and relative humidity (u).
Hungary is characterized by a continental climate, marked by hot, dry summers and moderately cold winters. For the 1991–2020 climate period, the country’s annual mean temperature was 10.8 °C, while the annual average precipitation was around 617 mm. The spring (March, April, May) mean temperature ranged between 5.9 °C and 16.1 °C. During the study years (2021–2024), the spring temperature anomaly varied between −1.9 and +2.3 °C, while the monthly mean precipitation anomaly was between 71 and 116% (Table 1). The largest differences in spring weather occurred between 2021 and 2024 (HungaroMet, Hungarian Meteorological Service, homogenized data).

Table 1.
Average anomaly of the spring (MAM) weather of the study period compared to the 1991–2020 climatological means in Hungary. Source: HungaroMet (Hungarian Meteorological Service).
2.3. Time Series Prediction Methods
We aimed to predict the change in hive weight using meteorological factors as external variables during the intensive foraging period of the R. pseudoacacia flowering phase. For this purpose, a linear statistical model was employed to gain a better understanding of how honey bees forage and to identify any natural variations in their behavior for other reasons or environmental changes.
The statistical analysis and modeling were implemented using R version 4.3.2. (2023-10-31 ucrt) [26]. Time series forecasting was performed using ARIMA (AutoRegressive Integrated Moving Average) models [27,28,29,30,31,32,33,34,35], which were generalized by G. Box and G. Jenkins [36,37], as referred by Siami-Namini et al. [38]. The ARIMAX (ARIMA with eXogenous variables) model algorithm was applied in the R programming environment using the ‘forecast’ package with maximum likelihood estimation [39,40]. The X in ARIMAX refers to the exogenous variable. In our study, these exogenous variables were meteorological factors (e.g., hourly maximum temperature) and diurnal pattern, which we hypothesized to have a direct effect on beehive weight changes.
The combination of differencing (d) with autoregression (p) and the moving average component (q) results in a non-seasonal ARIMA (p, d, q) model. The autoregressive (AR) component can be interpreted as a multiple regression, where lagged values of y serve as predictors, capturing the relationship between the current value and its past values. Meanwhile, the moving average (MA) component incorporates past forecast errors in the regression. In the case d ≥ 1, differencing is applied to both the predicted and the exogenous variables in the regression model [41]. The general non-seasonal ARIMA model can be expressed mathematically using backshift notation ( as follows in Equations (1) and (2):
where is the fitted coefficient of the autoregressive part (AR), is the observed value (hive weight), B is the backshift (lag) operator, d is the order of differencing, is the fitted coefficient of exogenous variables, is the vector of exogenous (meteorological) variables, c is a constant term, is the fitted coefficient of the moving average part (MA), and is the error term, which is considered to have zero mean and normally distributed [42,43].
Initially, a correlation analysis was performed on the selected external variables. The residuals of the regression were tested to ensure they followed a stationary or trend-stationary time series. A 12-lag Augmented Dickey–Fuller (ADF) test [44] was conducted to assess stationarity, rejecting the null hypothesis of non-stationarity at a significance level of p < 0.01. Additionally, the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test [45] was employed to evaluate trend stationarity. Another way to ensure the relationship between the study variables is using Pearson correlation [46,47] in cross-correlation analysis, which is widely used in colony weight studies [20]. Therefore, the model coefficients contribution, or their deviation from zero, was analyzed using the ‘coeftest’ function from the ‘lmtest’ R package, which performs a Wald z-test [48] for the corresponding model parameters [49].
To measure our model performance, we calculated the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Square Error (MSE), Mean Absolute Percentage Error (MAPE), Akaike’s Information Criterion (AIC), corrected AIC (AICc), and the Bayesian Information Criterium (BIC) evaluation metrics, which are commonly used in time-series modeling. The metrics’ formulae [42,50] are listed in the Appendix A.
For the time series modeling, four settings were tried: (1) without exogenous variables; (2) with meteorological variables; (3) with diurnal pattern; and (4) using both the diurnal pattern and one of the meteorological variables. The best p, q degrees were calculated based on the AIC and RMSE evaluation metrics during the iterations. The following parameter values were investigated: p = 0, 1, 3, 6, 9, 12; d = 0, 1; q = 0, 1, 3, 6.
Hive weight time series experience significant diurnal cycles, marked by a two-peak maximum during the day and minimum at night (Figure 1). Two approaches were used to assess this seasonality in the model. In the ARIMA modeling, the regression factors (XREGs) were the meteorological variables and the mean diurnal pattern (Figure 1), which was also provided for the model as a predictor variable (i.e., trend variable).
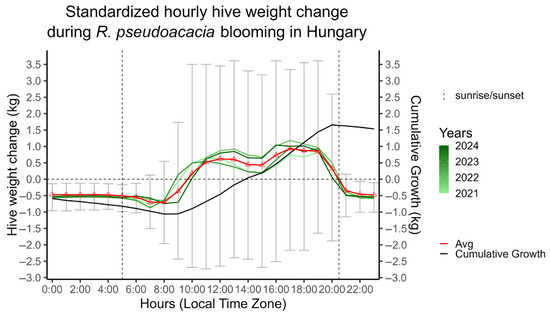
Figure 1.
Standardized hourly changes in the hive weight from 2021 to 2024 during R. pseudoacacia blooming. The green colors represent the annual averages of 24 individual hives, while the average over the whole period is colored red. The black line denotes the daily standardized cumulative growth, while the vertical dashed lines indicate the average sunrise and sunset time. Grey error bars extend to 1.5 times the interquartile range.
In the other approach, a seasonal component was introduced in the model, and Seasonal ARIMAX (SARIMAX) models were evaluated. The previously selected p, d, q values and meteorological variables were held constant, while seasonal parameters were explored with the following values: P = 0, 1, 3, 6, 9, 12; D = 0; Q = 0, 1, 3, 6. The seasonal period was set to S = 24, replacing the explicit diurnal pattern as a model component. With the SARIMAX approach, we introduced the values and forecast errors lagging P and Q days behind the predicted timestep as predictors.
A wide range of rolling forecast approaches is available [50]. During our analysis, we used a multistep 24 h rolling forecast with re-estimation. The first training dataset consisted of 3 days. For each consecutive 24 h prediction, the training dataset contained one more day of hive weight measurements, simulating the daily re-training of the model throughout the foraging season. The 24 h “future” meteorological variables were assumed to be known, according to the perfect prognostic approach [51]. Validation was performed on the time series created from consecutive 24 h hive weight predictions. A grid search was used to evaluate all possible model combinations, with the optimal model selected based on RMSE sensitivity, AICc, Pearson’s correlation, and the significance of model coefficients.
3. Results
3.1. Variation of the Hive Weight
The hourly weight changes exhibited a range from −1.32 to 1.2 kg, while the daily mean accumulated gain was 1.82 ± 1.87 kg for the specified period. The daily maximum accumulated gain was observed to be 9.27 kg/day. The mean weight accumulation per hive throughout the season was found to be 30.4 ± 14.1 kg. The most productive hives exhibited a mean weight yield of 79.8 kg per season, although some colonies had lower yields, with a minimum of 8.69 kg per season. This large variation between colonies is not an uncommon occurrence.
The daily cyclical nature closely mirrors the bees’ biological rhythm along with the plant’s diurnal variability, an observation that has been documented by numerous researchers [10,14,15,20,52] (Figure 1). The morning decrease, also known as ‘morning loss’, specified by Hambleton [11], can be interpreted as the departure of worker bees after sunrise if environmental conditions are permitting and the temperature is above 10 °C [20,53]. In our case, this characteristic was observed between 6 and 8 a.m. in local time. As these bees return to the hive carrying nectar, propolis, pollen, and water, the weight loss slows down, and the hive’s overall weight steadily increases. In certain cases, foraging follows a bimodal daily pattern, characterized by distinct noon and afternoon peak nectar collection periods. The net gain continues until sunset (after 8 p.m.), when a gradual decline occurs. The hive weight slowly declines at nighttime, which Hambleton [11] and Meikle et al. [15] identified as ‘nocturnal loss,’ attributing it primarily to respiration and evaporation processes. This average diurnal pattern (red line in Figure 1) was also used as a regression factor during ARIMAX modeling to forecast the short-term hive weight change.
3.2. Relationship with the Meteorological Variables
The correlation analysis between hourly hive weight change and meteorological parameters revealed a negative correlation with humidity (R = −0.5) while radiation, surface temperature, and the 2 m temperature (minimum, maximum, average, and actual values) exhibited a positive correlation with hive weight change (R = 0.57–0.59), at a significance level exceeding 99.9%. Among these factors, radiation in the three hours preceding weight measurements emerged as the primary driver of hive weight changes, but this parameter was not recorded at all stations. The observed relationships confirm that meteorological factors have a significant impact on hourly hive weight fluctuations. The lagged correlation coefficients are presented in Figure 2.
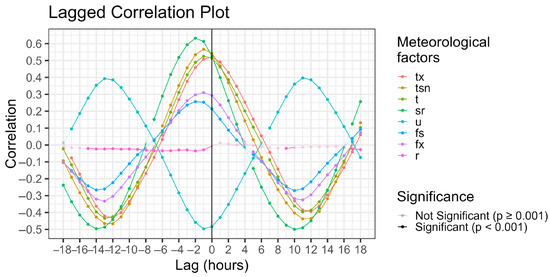
Figure 2.
Lagged correlation plot between the hive weight change and the external variables. The colors show the meteorological values (tx = maximum temperature, tsn = near-surface temperature minimum, t = actual temperature, sr = solar radiation, u = relative humidity, fs = wind speed, fx = wind gust, r = precipitation). The transparency denotes the significance at p = 0.001 level.
Although we considered many exogenous variables during the ARIMAX modeling, the model performed better if the diurnal pattern and univariate meteorological values were included. As illustrated in Figure 2, all possible parameter combinations of p, d, and q were evaluated for model fitting (Fit), averaged over time and validated using hives 1 and 2 for the period 2021–2024. The analysis indicated that the hourly maximum temperature emerges as the most favorable variable for the model fitting and prediction (Figure 3).
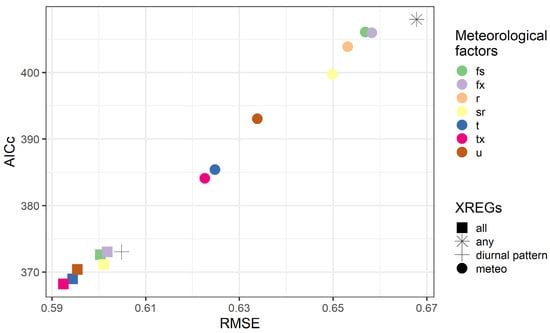
Figure 3.
Results of ARIMA model fit with or without regression errors for all possible model parameter variations. The colors show the meteorological values (fs = wind speed, fx = wind gust, r = precipitation, sr = radiation, t = actual temperature, tx = maximum temperature, u = relative humidity), while the shape of the points set the type of the regression factors (XREGs) (all = meteorological factor and diurnal pattern, any = without any XREGs, meteo = meteorological factors). RMSE values are in standardized units.
However, the combination of meteorological variables for selecting the optimal model proved to be non-significant, and adding too many variables caused overfitting. While the model RMSE and AICc metrics have been improved, this observation was inconsistent with the forecast results. This finding aligns with our observation that not all external variables were significant during the testing of coefficient combinations with the Wald z-test; only the hourly maximum temperature and in some cases the solar radiation proved to be a contributing factor. Our assumption is that the high collinearity among meteorological variables may have contributed to the decrease in significance. These results are presented in Figure 4, where the strength of opacity illustrates the significance.
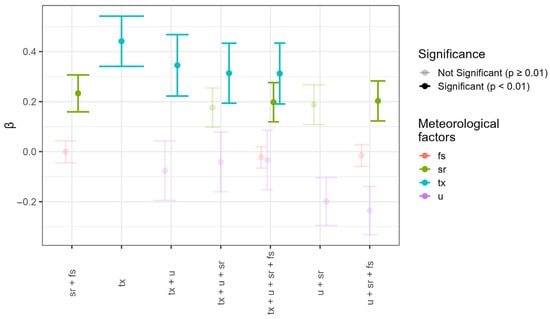
Figure 4.
Increasing the number of external variables and their possible combinations for the best model parameter selection. The colors and the x-axis show the meteorological values and their combinations (fs = wind speed, sr = solar radiation, tx = maximum temperature, u = relative humidity), while the y-axis represents the fitted coefficient of the external variable and its standard error. The transparency denotes the critical significance level at p = 0.01.
3.3. Time Series Model Selection
To select the most accurate model, we estimated the hive weight change for all possible variations. We have run through our model for all p, d, and q variations, as detailed in Section 2.3. Both the model fit and forecast were improved by selecting a higher degree model (see Figure 5). The evaluation metrics indicated the optimal parameter selection to be the ARIMAX (0, 0, 1), incorporating the hourly maximum temperature and the diurnal pattern of external variables. While the model fit improved with more parameters, like p = 9, d = 0, q = 6, the correlation (R) decreased for the forecast. The simplest model configuration could reveal the strongest and most consistent effect of temperature (tx). As the number of model parameters increased, the significance of tx became more variable. The model also failed to converge in some cases when using higher-order parameters (e.g., p = 12 or p = 24). These observations indicate that the weight of the hive exhibits a general diurnal pattern, characterized by a strong weather-driven variability among the days. This finding is consistent with general beekeeping observations. It was observed that differencing the dataset (d = 1) caused inconsistent results in model fitting and unsignificant external variables. Note that the predicted variable, the hive weight change (d = 0), is already the first differential of the hive weight. Model testing and stationarity tests revealed that further differencing was not necessary.
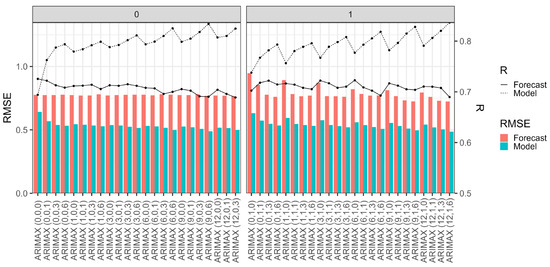
Figure 5.
Sensitivity testing: Evaluation metrics over all the p, d, q model combinations, RMSE (in standardized units), and R (Pearson correlation) for the fit and the forecast. The lines indicate the R values, while the colored bars show the RMSE. The blue color and the dotted lines denote the fit residuals, while the red color and the solid line are the forecast errors. The x-axis represents all the model combinations.
The model RMSE changes over the foraging season are illustrated in Figure 6, while Figure 7 presents the rolling forecast for Hive 1, along with the significance of the hourly maximum temperature. The model RMSE has increased near the middle of the foraging season (around 8 days), which can be attributed to the peak of flowering with the highest daily weight gains. The initial and final days of the season were more challenging to predict due to their irregular diurnal pattern. The RMSE for the best ARIMAX (0, 0, 1) model was consistently lower than that of the other models for most of the season (Figure 6).
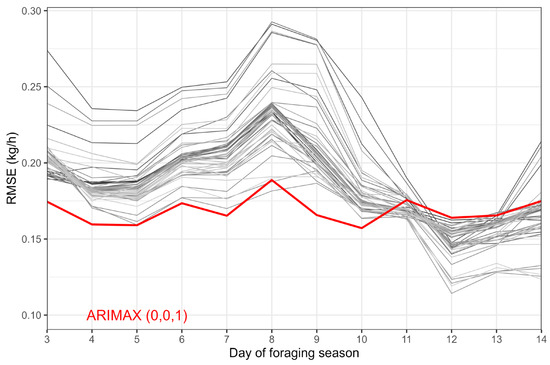
Figure 6.
ARIMAX 24 h rolling forecast RMSE (mean of all hives). The figure shows all the model variations with gray, while the best model combination ARIMAX (0, 0, 1) is highlighted with red.
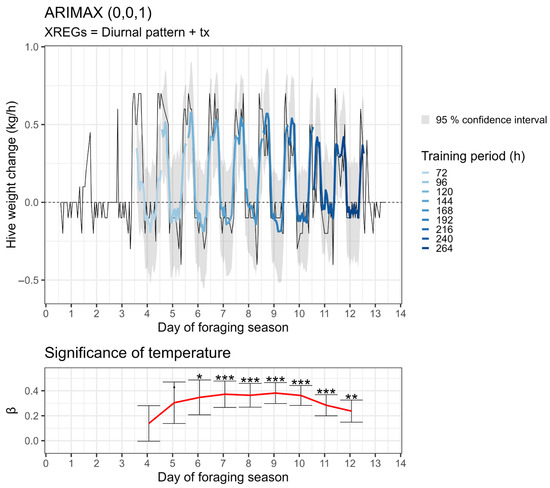
Figure 7.
Predicted hive weight change for one selected colony (Hive 1) and period (2024). The upper part of the figure illustrates the estimated weight change, colored blue, while the measured weight changes are shown in black. The blue color depth denotes the length of the training period of the 24 h rolling forecast. The lower part of the figure shows the significance of the hourly maximum temperature in the model over time. The red line indicates the mean, while the error bars represent the standard error. The stars *, **, and *** are used to determine statistical significance at the level of 95%, 99%, and 99.9%, respectively.
The temperature as an exogenous variable maintained its significant impact in the ARIMA model throughout the season. However, the fitted β coefficient of the temperature and its significance varied considerably both in time and among different hives (Figure 7). The significance of temperature was largest near the peak of season when foraging was most efficient, and nectar production was largely impacted by cold or warm weather.
The ARIMAX (0, 0, 1) time series model with hourly maximum temperature (tx) and diurnal pattern regression errors and the SARIMAX (0, 0, 1) (1, 0, 1) [24] time series model solely with tx external variable were fitted on all the 24 hives. The median evaluation metrics (MAE, MAPE, RMSE) are reported in Table 2 and Table 3. The temperature as an external variable was a significant predictor of the hive weight for all the hives in both cases. The ARIMAX model with predefined daily pattern as an external variable provided similar results to that of the SARIMAX model with a 1-day period (Table 2 and Table 3). For the ARIMAX and SARIMAX models, the average RMSE was 0.18 kg/h and 0.17 kg/h, while the average correlation coefficient was 0.742 and 0.743, respectively.

Table 2.
ARIMAX (0, 0, 1) model parameters for 24 h hive weight change estimation. The regression factors were the diurnal pattern and the hourly maximum temperature (tx). The medians of the evaluation metrics (MAE, MAPE, RMSE) quantify the difference between the forecast and the observed values. Parameter superscript *** is used to denote statistical significance at the 99.9% level. The highlighted rows show the results obtained for Hives 1 and 2 where the model was optimized.

Table 3.
SARIMAX (0, 0, 1) (1, 0, 1) [24] model parameters for 24 h hive weight change estimation. The regression factor was the hourly maximum temperature (tx). The medians of the evaluation metrics (MAE, MAPE, RMSE) quantify the difference between the forecast and the observed values. Parameter superscripts ** and *** are used to denote statistical significance at the level of 99% and 99.9%, respectively. The highlighted rows show the results obtained for Hives 1 and 2 where the model was optimized.
Temperature was a significant predictor of hive weight for all the investigated hives and models (Table 2). ARIMAX and SARIMAX 24 h prediction RMSE ranged between 0.1 and 0.3 kg/h and the Pearson correlation values were between 0.6 and 0.9 between predicted and observed hive weight time series.
4. Discussion
The relationship between honey bees and meteorological variables is a challenging field of biometeorological research [20]. Their activity and behavior are closely linked to environmental factors and the bee pastures’ phenological cycles, responding rapidly to even minor changes. The result of this study showed that the temperature was the most significant predictor the hive weight change among the meteorological variables, along with the diurnal pattern of the hive weight, an observation that is consistent with the results of other studies [3,14,21,54,55].
The research focused specifically on Robinia pseudoacacia (black locust), a melliferous tree species native to North America. Widely considered invasive in Europe, black locust is nonetheless prized for its abundant nectar production [56,57,58,59]. In Hungary, it is the most important bee pasture and serves as the primary nectar source for honey bees during its flowering period. The resulting acacia honey is of high commercial value and constitutes a key source of income for Hungarian beekeepers [9,60].
To investigate the relationship between hive activity and environmental variables during the black locust blooming period, feature selection and model parameter tuning was performed on hourly hive weight time series from two hives located near Debrecen, Hungary between 2021 and 2024. Predictions were made and validated for a total of 24 hives throughout Hungary.
Due to the strong daily cycle of foraging, the mean diurnal pattern of hive weight change was also incorporated as a predictor in the model. The model effectively captured daily hive weight fluctuations, although its performance declined during peak activity, highlighting the influence of nonlinear biological and environmental factors.
After extensive testing, we determined the optimal parameter selection to be the most optimal for capturing these relationships. In this model, the p = 0 (autoregressive order) and the q = 1 (moving average order) indicates that the current hive weight change is not directly influenced by its own past values, but rather by contemporaneous external variables and past forecast errors. The d = 0 (differencing order) signifies that the weight changes were found to be stationary, thus requiring no additional differencing. With this parameter setup, the mean runtime for a 24 h forecast was 0.32 s.
Our results further underline the fact that bees have a strong relationship with temperature. According to the literature, bees initiate foraging above 9–10 °C, and optimal foraging occurs between 20 °C and 27 °C, although it varies by the foraged species and season. The upper flight limit is 46 °C [20,53]. Another study showed that flight activity increases when the air temperature is 17 °C in spring and 26 °C in summer, while the optimal range is between 14 and 28 °C [21]. In alignment with these findings, our data show that the most intensive nectar collection occurred when daily maximum temperatures exceeded 25 °C. Due to the seasonal timing of Robinia pseudoacacia flowering, data for higher temperatures were limited; nevertheless, the observed trend supports a strong positive relationship between temperature and foraging intensity within the studied range (Figure S2).
Additional meteorological variables have decreased the model’s performance and remained non-significant, due to their multicollinearity with temperature. As the complexity of the model increased, the significance of the hourly maximum temperature had become more emphasized.
Several studies have tried to forecast the hive weight (Table 4); however, none of them concerned the vegetation type and most of them focused on extreme events such as swarming or hive health conditions, and less of them concerned with the effect of the external meteorological variables. Some studies discussed the challenges in the modeling of the nonlinear relationship between air temperature and beehive daily productivity [3]. However, in the study of Kulyukin et al. [61], the ARIMA models performed similarly to nonlinear Machine Learning (ML) models like Convolutional Neural Networks (CNN), Artificial Neural Networks (ANN), and Long Short-Term Memory (LSTM) networks. However, their model was developed primarily to achieve sensitivity in predicting swarming. On the contrary, Robustillo et al. [62] found Vector AutoRegression (VAR) and Vector Error Correction (VEC) models better than the linear models in predicting the hive weight, in-hive temperature, and humidity. This finding implies that a nonlinear or hybrid model may improve our results for the hive weight prediction of the intensive foraging period. However, Kulyukin et al. [61] recommended the application of cost-efficient ARIMA models for real-world agricultural applications where computational capacities are limited.

Table 4.
Recent studies in the context of hive weight forecasting.
In the time series preprocessing for hive weight forecasting, breakpoint analysis or anomaly detection can help filter out unwanted occurrences such as extreme weather events, harvesting, migrating, or other hive interventions made by beekeepers, which are frequent in hive weight time series [25,71,72]. In our case, however, we were aware of these events in the registered hives and only those with an undisturbed foraging period were selected for analysis, allowing for a simpler data cleaning approach. Once extraneous events were accounted for, the remaining hive weight fluctuations primarily reflected colony activity. Hive weight fluctuations within the range of 0.0 to 0.3 kg per day are primarily associated with colony activity, including brood rearing, adult bee population dynamics, nest construction, and the collection of water and propolis. This variability is in the range of the RMSE of our ARIMAX (0,0,1) model, 0.133 to 0.273 kg/h. Weight increases of more than 0.3 kg are typically linked to nectar, bee bread, and honey accumulation. Notably, strong colonies could forage up to 3 kg of pollen and nectar within a single day [10]. The hive weight follows a strong daily cyclic behavior for which the addition of a seasonal component to the model is recommended. Therefore, after the parameter setup, we incorporated the SARIMAX (Seasonal ARIMAX) model, relying only on the hourly maximum temperature as an external variable.
Limitations of Hive Weight Forecasting
This study proposes an application to predict hive weight in an intensive foraging period to understand the external effects on the collection. However, it should be noted that there are key limitations associated with the hive weight estimation:
- The unrepresented biological and environmental factors causing large fluctuations in foraging, as well as the nonlinear relationship between temperature and hive weight. Additional parameters, such as colony health, developmental stage, nectar-producing vegetation yield, and beekeeper knowledge, may significantly influence outcomes, but these are difficult to measure.
- The distance of the meteorological station, such as radiation, cloud cover, and precipitation measurements, may not fully represent conditions near the hives. While radiation played a minor role compared to temperature in comparisons, previous research highlights its significant influence on honey bee behavior.
- More complex data-cleaning methods risk filtering out genuine variations inherent to general honey bee behavior.
- The low-cost hive scales used may lack sufficient accuracy (dkg- or g-level precision) for such studies, though they are widely adopted in the beekeeping community.
- Hive weight reflects not only nectar collection but also colony reproduction, water, propolis, pollen, and wax production, making it difficult to isolate nectar yield. These minor anomalies cannot be filtered with time series methods and require beekeeper observations to account for.
- The worker bees could also change their colonies during nectar flow, called ‘drifting’, if the hives are near each other and some hives are easier to approach. However, this behavior depends on various factors like the hive color, painted shapes on the hive, environmental factors, and the orientation or arrangement of the hives [73,74,75].
- Weight sensors can be affected by outdoor temperature fluctuations [17] or the humidity could affect the weight of the wood hives.
Further improvements in hive weight prediction could be achieved with nonlinear time series models (e.g., recurrent neural networks) and more advanced in-hive sensors. However, our model targets real-world applications and scalability with its very low computational cost, limited data requirement (only hive weight and temperature), easily interpretable regression coefficients of temperature, and the focus on Robinia, the most important bee pasture in the study region. By quantifying how weather conditions influence nectar intake during the Robinia pseudoacacia honey flow period, beekeepers can optimize hive placement and migration strategies based on expected foraging conditions, adjust harvesting times to maximize honey yields, and improve risk management by anticipating poor foraging conditions.
5. Conclusions
Time series models are efficient tools for the prediction of weather-driven biometeorological processes where the complexity of the underlying physical and biological system requires a statistical approach. In this study, 24 h hive weight rolling prediction was performed using a linear time series regression model with exogenous meteorological variables (ARIMAX and SARIMAX) during a heavy nectar flow episode, the black locust blooming. Our choice was determined by the fact that this specific plant is one of the most important bee pastures in Hungary. Our findings confirm that temperature is a primary meteorological driver of short-range hive weight changes. Other meteorological variables showed limited predictive power due to their multicollinearity with temperature. Due to the strong daily cycle, the daily hive fluctuations also played an important role in the model.
Our study aimed to develop a model that relies on affordable and easily accessible data, such as basic meteorological information and low-cost hive scales. The presented model provides a computationally efficient time series model for the prediction of weather-driven hive weight changes, without the need for specialized or expensive equipment, providing an efficient tool for data-driven beekeeping practices and the environmental management of pollination services.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16080918/s1, Figure S1: The locations of meteorological stations and associated hives applied in the study; Figure S2: The relationship between daily maximum temperature and daily hive weight change. File S1: Measured hive weight time series of Hives 1 and 2.
Author Contributions
Conceptualization, C.I.-V., Á.L. and R.M.; methodology, C.I.-V. and Á.L.; software, C.I.-V.; validation, C.I.-V.; investigation, C.I.-V., Á.L. and R.M.; resources: C.I.-V. and R.M.; data curation, C.I.-V.; writing—original draft preparation, C.I.-V. and Á.L.; writing—review and editing, C.I.-V., Á.L. and R.M.; visualization, C.I.-V.; supervision, Á.L. and R.M.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been implemented by the National Multidisciplinary Laboratory for Climate Change (RRF-2.3.1-21-2022-00014) project within the framework of Hungary’s National Recovery and Resilience Plan supported by the Recovery and Resilience Facility of the European Union.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the meteorological data were downloaded from the website of the HungaroMet (https://odp.met.hu/ (accessed on 25 January 2025)), which is a free, open platform. The beekeeper notes from our primary apiary site (Hive 1 and Hive 2) are provided in the Supplementary Materials (File S1). The raw scale measurements used in this study for this site are openly available in Mendeley Data at the following DOI: https://doi.org/10.17632/3v3hhkddmz.1. Other hive weight data is the courtesy of the respective apiarists.
Acknowledgments
We express our gratitude to the Hungarian beekeepers who participated in the research and provided valuable data from their apiaries. We would also like to thank Ferenc Vincze from Debrecen for valuable assistance in the field.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Formulae of the applied validation metrics:
where represents the predicted values, and denotes the actual values for n data points. The likelihood of the data is given by L, with k = 1 if c ≠ 0 and k = 0 if c = 0. Here, T represents the number of observations used for estimation, and k corresponds to the number of predictors in the model [42,50].
References
- Klein, A.-M.; Vaissière, B.E.; Cane, J.H.; Steffan-Dewenter, I.; Cunningham, S.A.; Kremen, C.; Tscharntke, T. Importance of Pollinators in Changing Landscapes for World Crops. Proc. R. Soc. B Biol. Sci. 2007, 274, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Potts, S.G.; Biesmeijer, J.C.; Kremen, C.; Neumann, P.; Schweiger, O.; Kunin, W.E. Global Pollinator Declines: Trends, Impacts and Drivers. Trends Ecol. Evol. 2010, 25, 345–353. [Google Scholar] [CrossRef]
- Czekońska, K.; Łopuch, S.; Miścicki, S.; Bańkowski, J.; Szabla, K. Monitoring of Hive Weight Changes in Various Landscapes. Apidologie 2023, 54, 30. [Google Scholar] [CrossRef]
- Krell, R. Value-Added Products from Beekeeping. In FAO Agricultural Services Bulletin, 1st ed.; FAO: Rome, Italy, 1996. [Google Scholar]
- Kebede, I.A.; Gebremeskel, H.F.; Ahmed, A.D.; Dule, G. Bee Products and Their Processing: A Review. Pharm. Pharmacol. Int. J. 2024, 12, 5–12. [Google Scholar] [CrossRef]
- European Commission Honey. Available online: https://agriculture.ec.europa.eu/farming/animal-products/honey_en (accessed on 25 February 2025).
- De la Rúa, P.; Jaffé, R.; Dall’Olio, R.; Muñoz, I.; Serrano, J. Biodiversity, Conservation and Current Threats to European Honeybees. Apidologie 2009, 40, 263–284. [Google Scholar] [CrossRef]
- OMME. National Program of Beekeeping 2021–2022; Országos Magyar Méhészeti Egyesület (OMME): Budapest, Hungary, 2022; Volume 50, ISSN 2062-9915. [Google Scholar]
- Feketéné, F.A.; Szűcs, I.; Vida, V. A hazai méhészeti ágazat helyzetének elemzése (termelés, kereskedelem). Hung. J. Nutr. Mark. 2021, 8, 21–34. [Google Scholar] [CrossRef]
- Meikle, W.G.; Rector, B.G.; Mercadier, G.; Holst, N. Within-Day Variation in Continuous Hive Weight Data as a Measure of Honey Bee Colony Activity. Apidologie 2008, 39, 694–707. [Google Scholar] [CrossRef]
- Hambleton, J.I. The Effect of Weather Upon the Change in Weight of a Colony of Bees During the Honey Flow; U.S. Department of Agriculture: Washington, DC, USA, 1925.
- Zaman, A.; Dorin, A. A Framework for Better Sensor-Based Beehive Health Monitoring. Comput. Electron. Agric. 2023, 210, 107906. [Google Scholar] [CrossRef]
- Zacepins, A.; Ozols, N.; Kviesis, A.; Gailis, J.; Komasilovs, V.; Komasilova, O.; Zagorska, V. Evaluation of the Honey Bee Colonies Weight Gain during the Intensive Foraging Period. Agron. Res. 2022, 20, 457–468. [Google Scholar] [CrossRef]
- Meikle, W.G.; Weiss, M.; Stilwell, A.R. Monitoring Colony Phenology Using Within-Day Variability in Continuous Weight and Temperature of Honey Bee Hives. Apidologie 2016, 47, 1–14. [Google Scholar] [CrossRef]
- Meikle, W.G.; Holst, N.; Colin, T.; Weiss, M.; Carroll, M.J.; McFrederick, Q.S.; Barron, A.B. Using Within-Day Hive Weight Changes to Measure Environmental Effects on Honey Bee Colonies. PLoS ONE 2018, 13, e0197589. [Google Scholar] [CrossRef]
- Atanasov, A.Z.; Hristakov, I.S.; Koszel, M.; Przywara, A. Monitoring Agrometeorological Factors and Weight of the Bee Hive During Black Locust (Robinia pseudoacacia) Flowering. In Proceedings of the Farm Machinery and Processes Management in Sustainable Agriculture; Pascuzzi, S., Santoro, F., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 239–251. [Google Scholar]
- Stalidzans, E.; Zacepins, A.; Kviesis, A.; Brusbardis, V.; Meitalovs, J.; Paura, L.; Bulipopa, N.; Liepniece, M. Dynamics of Weight Change and Temperature of Apis mellifera (Hymenoptera: Apidae) Colonies in a Wintering Building With Controlled Temperature. J. Econ. Entomol. 2017, 110, 13–23. [Google Scholar] [CrossRef]
- Meikle, W.G.; Holst, N. Application of Continuous Monitoring of Honeybee Colonies. Apidologie 2015, 46, 10–22. [Google Scholar] [CrossRef]
- Marchal, P.; Buatois, A.; Kraus, S.; Klein, S.; Gomez-Moracho, T.; Lihoreau, M. Automated Monitoring of Bee Behaviour Using Connected Hives: Towards a Computational Apidology. Apidologie 2020, 51, 356–368. [Google Scholar] [CrossRef]
- Vincze, C.; Leelőssy, Á.; Zajácz, E.; Mészáros, R. A Review of Short-Term Weather Impacts on Honey Production. Int. J. Biometeorol. 2025, 69, 303–317. [Google Scholar] [CrossRef] [PubMed]
- Gounari, S.; Proutsos, N.; Goras, G. How Does Weather Impact on Beehive Productivity in a Mediterranean Island? Ital. J. Agrometeorol. 2022, 1, 65–81. [Google Scholar] [CrossRef]
- Péntek-Zakar, E.; Oleksa, A.; Borowik, T.; Kusza, S. Population Structure of Honey Bees in the Carpathian Basin (Hungary) Confirms Introgression from Surrounding Subspecies. Ecol. Evol. 2015, 5, 5456–5467. [Google Scholar] [CrossRef]
- Arias-Calluari, K.; Colin, T.; Latty, T.; Myerscough, M.; Altmann, E.G. Modelling Daily Weight Variation in Honey Bee Hives. PLoS Comput. Biol. 2023, 19, e1010880. [Google Scholar] [CrossRef]
- Lecocq, A.; Kryger, P.; Vejsnæs, F.; Jensen, A.B. Weight Watching and the Effect of Landscape on Honeybee Colony Productivity: Investigating the Value of Colony Weight Monitoring for the Beekeeping Industry. PLoS ONE 2015, 10, e0132473. [Google Scholar] [CrossRef]
- Davidson, P.; Steininger, M.; Lautenschlager, F.; Kobs, K.; Krause, A.; Hotho, A. Anomaly Detection in Beehives Using Deep Recurrent Autoencoders; SciTePress: Valletta, Malta, 2020; Volume 1, pp. 142–149. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- László, E.; Palcsu, L.; Leelőssy, Á. Estimation of the Solar-Induced Natural Variability of the Tritium Concentration of Precipitation in the Northern and Southern Hemisphere. Atmos. Environ. 2020, 233, 117605. [Google Scholar] [CrossRef]
- Mahmudimanesh, M.; Mirzaee, M.; Dehghan, A.; Bahrampour, A. Forecasts of Cardiac and Respiratory Mortality in Tehran, Iran, Using ARIMAX and CNN-LSTM Models. Environ. Sci. Pollut. Res. 2022, 29, 28469–28479. [Google Scholar] [CrossRef]
- Saranj, A.; Zolfaghari, M. The Electricity Consumption Forecast: Adopting a Hybrid Approach by Deep Learning and ARIMAX-GARCH Models. Energy Rep. 2022, 8, 7657–7679. [Google Scholar] [CrossRef]
- Sheng, F.; Jia, L. Short-Term Load Forecasting Based on SARIMAX-LSTM. In Proceedings of the 2020 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 90–94. [Google Scholar]
- Supriya, A. Study on the Performance of the ARIMAX-ANN Hybrid Forecasting Model over the Other Time Series Forecasting Models ARIMAX and ANN in Forecasting the Rice Yield. Int. J. Curr. Microbiol. App. Sci. 2021, 10, 3421–3428. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, Z.; Meng, Y.; Wang, S.; Li, S.; Niu, R.; Wang, Y.; Guo, Q.; Li, Y. Comparison of ARIMA and LSTM in Forecasting the Incidence of HFMD Combined and Uncombined with Exogenous Meteorological Variables in Ningbo, China. Int. J. Environ. Res. Public Health 2021, 18, 6174. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Zhang, R.; Zhang, H.; He, S. Prediction of Global Omicron Pandemic Using ARIMA, MLR, and Prophet Models. Sci. Rep. 2022, 12, 18138. [Google Scholar] [CrossRef]
- Zhou, Y. Regional Energy Consumption Prediction Based on SARIMAX-LSTM Model. Acad. J. Comput. Inf. Sci. 2021, 4, 41–51. [Google Scholar] [CrossRef]
- Ospina, R.; Gondim, J.A.M.; Leiva, V.; Castro, C. An Overview of Forecast Analysis with ARIMA Models during the COVID-19 Pandemic: Methodology and Case Study in Brazil. Mathematics 2023, 11, 3069. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-67492-5. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Siami Namin, A. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; Kuroptev, K.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; et al. Forecast: Forecasting Functions for Time Series and Linear Models. 2024. Available online: https://cran.r-project.org/web/packages/forecast/forecast.pdf (accessed on 25 February 2025).
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The Forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; Monash University: Melbourne, Australia, 2018. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; Monash University: Melbourne, Australia, 2021. [Google Scholar]
- Pandit, P.; Sagar, A.; Ghose, B.; Dey, P.; Paul, M.; Alqadhi, S.; Mallick, J.; Almohamad, H.; Abdo, H.G. Hybrid Time Series Models with Exogenous Variable for Improved Yield Forecasting of Major Rabi Crops in India. Sci. Rep. 2023, 13, 22240. [Google Scholar] [CrossRef]
- Said, S.E.; Dickey, D.A. Testing for Unit Roots in Autoregressive-Moving Average Models of Unknown Order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root: How Sure Are We That Economic Time Series Have a Unit Root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Chok, N.S. Pearson’s Versus Spearman’s and Kendall’s Correlation Coefficients for Continuous Data. Master’s Thesis, Winona State University, Winona, MN, USA, 2008. [Google Scholar]
- Pearson, K. Notes on the History of Correlation. Biometrika 1920, 13, 25–45. [Google Scholar] [CrossRef]
- Wald, A. Tests of Statistical Hypotheses Concerning Several Parameters When the Number of Observations Is Large. Trans. Am. Math. Soc. 1943, 54, 426–482. [Google Scholar] [CrossRef]
- Zeileis, A.; Hothorn, T. Diagnostic Checking in Regression Relationships. R News 2002, 2, 7–10. [Google Scholar]
- Dissanayake, B.; Hemachandra, O.; Lakshitha, N.; Haputhanthri, D.; Wijayasiri, A. A Comparison of ARIMAX, VAR and LSTM on Multivariate Short-Term Traffic Volume Forecasting. In Proceedings of the Conference of Open Innovations Association, Fruct, Moscow, Russia, 27–29 January 2021; pp. 564–570. [Google Scholar]
- Marzban, C.; Sandgathe, S.; Kalnay, E. MOS, Perfect Prog, and Reanalysis. Mon. Weather. Rev. 2006, 134, 657–663. [Google Scholar] [CrossRef]
- Holst, N.; Meikle, W.G. Breakfast Canyon Discovered in Honeybee Hive Weight Curves. Insects 2018, 9, 176. [Google Scholar] [CrossRef]
- Abou-Shaara, H.F.; Owayss, A.A.; Ibrahim, Y.Y.; Basuny, N.K. A Review of Impacts of Temperature and Relative Humidity on Various Activities of Honey Bees. Insect. Soc. 2017, 64, 455–463. [Google Scholar] [CrossRef]
- Clarke, D.; Robert, D. Predictive Modelling of Honey Bee Foraging Activity Using Local Weather Conditions. Apidologie 2018, 49, 386–396. [Google Scholar] [CrossRef]
- Brini, A.; Giovannini, E.; Smaniotto, E. A Machine Learning Approach to Forecasting Honey Production with Tree-Based Methods. arXiv 2023, arXiv:2304.01215. [Google Scholar]
- Vadas, J. Az Ákácfa Monografiája, Különös Tekintettel Erdőgazdasági Jelentőségére; Országos Erdészeti Egyesület: Budapest, Hungary, 1911. [Google Scholar]
- Vítková, M.; Müllerová, J.; Sádlo, J.; Pergl, J.; Pyšek, P. Black Locust (Robinia pseudoacacia) Beloved and Despised: A Story of an Invasive Tree in Central Europe. For. Ecol. Manag. 2017, 384, 287–302. [Google Scholar] [CrossRef]
- Vítková, M.; Sádlo, J.; Roleček, J.; Petřík, P.; Sitzia, T.; Müllerová, J.; Pyšek, P. Robinia pseudoacacia-Dominated Vegetation Types of Southern Europe: Species Composition, History, Distribution and Management. Sci. Total Environ. 2020, 707, 134857. [Google Scholar] [CrossRef]
- Samsonova, I.; Mannapov, A.; Khisamov, R.; Plakhova, A.; Sattarov, V. Analysis of Honey Productivity of Robinia (Robinia pseudoacacia L.) Plantations in Forest Vegetation Conditions of the Steppe Don Region. IOP Conf. Ser. Earth Environ. Sci. 2020, 574, 012071. [Google Scholar] [CrossRef]
- Mezőné, T.É.O. A Hazai Mézpiac Fogyasztói és Szervezeti Sajátosságainak Marketing Szemléletű Összefüggései. Doktori Értekezés; Szent István Egyetem: Gödöllő, Hungary, 2020. [Google Scholar]
- Kulyukin, V.A.; Coster, D.; Kulyukin, A.V.; Meikle, W.; Weiss, M. Discrete Time Series Forecasting of Hive Weight, In-Hive Temperature, and Hive Entrance Traffic in Non-Invasive Monitoring of Managed Honey Bee Colonies: Part I. Sensors 2024, 24, 6433. [Google Scholar] [CrossRef]
- Robustillo, M.C.; Naranjo, L.; Parra, M.I.; Pérez, C.J. Addressing Multidimensional Highly Correlated Data for Forecasting in Precision Beekeeping. Comput. Electron. Agric. 2024, 226, 109390. [Google Scholar] [CrossRef]
- Braga, A.R.; GGomes, D.; Rogers, R.; EHassler, E.; MFreitas, B.; ACazier, J. A Method for Mining Combined Data from In-Hive Sensors, Weather and Apiary Inspections to Forecast the Health Status of Honey Bee Colonies. Comput. Electron. Agric. 2020, 169, 105161. [Google Scholar] [CrossRef]
- Braga, A.R.; Freitas, B.M.; Gomes, D.G.; Bezerra, A.D.M.; Cazier, J.A. Forecasting Sudden Drops of Temperature in Pre-Overwintering Honeybee Colonies. Biosyst. Eng. 2021, 209, 315–321. [Google Scholar] [CrossRef]
- Komasilova, O.; Komasilovs, V.; Kviesis, A.; Zacepins, A. Modeling of the Potential Honey Bee Colony Foraging Activity Based on the Agrometeorological Factors. Balt. J. Mod. Comput. 2021, 9, 280–289. [Google Scholar] [CrossRef]
- Anwar, O.; Keating, A.; Cardell-Oliver, R.; Datta, A.; Putrino, G. WE-Bee: Weight Estimator for Beehives Using Deep Learning. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022. [Google Scholar]
- Anwar, O.; Keating, A.; Cardell-Oliver, R.; Datta, A.; Putrino, G. Design and Development of Low-Power, Long-Range Data Acquisition System for Beehives—BeeDAS. Comput. Electron. Agric. 2022, 201, 107281. [Google Scholar] [CrossRef]
- Robustillo, M.C.; Pérez, C.J.; Parra, M.I. Predicting Internal Conditions of Beehives Using Precision Beekeeping. Biosyst. Eng. 2022, 221, 19–29. [Google Scholar] [CrossRef]
- Anwar, O.; Keating, A.; Cardell-Oliver, R.; Datta, A.; Putrino, G. Apis-Prime: A Deep Learning Model to Optimize Beehive Monitoring System for the Task of Daily Weight Estimation. Appl. Soft Comput. 2023, 144, 110546. [Google Scholar] [CrossRef]
- Rigakis, I.; Potamitis, I.; Tatlas, N.-A.; Psirofonia, G.; Tzagaraki, E.; Alissandrakis, E. A Low-Cost, Low-Power, Multisensory Device and Multivariable Time Series Prediction for Beehive Health Monitoring. Sensors 2023, 23, 1407. [Google Scholar] [CrossRef]
- Degenfellner, J.; Templ, M. Modeling Bee Hive Dynamics: Assessing Colony Health Using Hive Weight and Environmental Parameters. Comput. Electron. Agric. 2024, 218, 108742. [Google Scholar] [CrossRef]
- Davidson, P.; Steininger, M.; Lautenschlager, F.; Krause, A.; Hotho, A. Anomaly Detection in Beehives: An Algorithm Comparison. In Sensor Networks: 9th International Conference, SENSORNETS 2020, Valletta, Malta, 28–29 February 2020, and 10th International Conference, SENSORNETS 2021, Virtual Event, 9–10 February 2021, Revised Selected Papers; Ahrens, A., Prasad, R.V., Benavente-Peces, C., Ansari, N., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–20. [Google Scholar]
- Free, J.B. The Drifting of Honey-Bees. J. Agric. Sci. 1958, 51, 294–306. [Google Scholar] [CrossRef]
- Pfeiffer, K.J.; Crailsheim, K. Drifting of Honeybees. Insectes Sociaux 1998, 45, 151–167. [Google Scholar] [CrossRef]
- Šekulja, D.; Pechhacker, H.; Licek, E. Drifting Behavior of Honey Bees (Apis mellifera carnica Pollmann, 1879) in the Epidemiology of American Foulbrood. Zb. Veleučilišta Rijeci 2014, 2, 345–358. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).