Abstract
Source inversion optimization using sensor observations is a key method for rapidly and accurately identifying unknown source parameters (source strength and location) in abrupt hazardous gas leaks. Sensor number and location distribution both play important roles in source inversion; however, their combined impacts on source inversion optimization remain poorly understood. In our study, the optimization inversion method is established based on the Gaussian plume model and the generation algorithm. A research strategy combining random sampling and coefficient of variation methods was proposed to simultaneously quantify their combined impacts in the case of a single emission source. The sensor layout impact difference was analyzed under varying atmospheric conditions (unstable, neutral, and stable) and source location information (known or unknown) using the Prairie Grass experiments. The results indicated that adding sensors improved the source strength estimation accuracy more when the source location was known than when it was unknown. The impacts of sensor location distribution were strongly negatively correlated (r ≤ −0.985) with the number of sensors across scenarios. For source strength estimation, the impacts of the sensor location distribution difference decreased non-linearly with more sensors for known locations but linearly for unknown ones. The impacts of sensor number and location distribution on source strength estimation were amplified under stable atmospheric conditions compared to unstable and neutral conditions. The minimum number of randomly scattered sensors required for stable source strength inversion accuracy was 11, 12, and 17 for known locations under unstable, neutral, and stable atmospheric conditions, respectively, and 24, 9, and 21 for unknown locations. The multi-layer arc distribution outperformed rectangular, single-layer arc, and downwind-axis distributions in source strength estimation. This study enhances the understanding of factors influencing source inversion optimization and provides valuable insights for optimizing sensor layouts.
1. Introduction
Ambient air pollution in small-scale areas caused by the release of hazardous materials during abrupt accidents poses risks to human health and ecosystems. The rapid and accurate determination of source parameters, such as source strength and location, is crucial for effective emergency response to accidents [1]. However, the direct measurement of these parameters is often challenging due to emission concealment or the toxicity of pollutants. Source inversion using ground-based static sensor observations is a feasible approach for estimating source parameters [2], and it can be categorized into four types [3,4]: optimization, Bayesian inference, data-driven (e.g., machine learning), and direct inverse-dispersion (e.g., backward Lagrangian stochastic model) models. Among them, optimization methods such as swarm intelligence algorithms (e.g., genetic algorithm, GA; particle swarm optimization, PSO) do not require differentiable objective functions, are less dependent on strictly defined initial values, and enable global search, making them widely applicable in accident emergency scenarios [5,6,7,8,9]. In this approach, the source inverse problem is converted to a multimodal function optimizing tasks with typically ill-posed and non-linear features, where source parameters are independent variables [10].
The performance of the source inversion optimization is usually affected by three key factors, namely forward dispersion simulation, cost functions, and sensor observations. A forward dispersion simulation is typically conducted using the atmospheric dispersion model—most commonly the Gaussian plume model or the CFD method [11]. The Gaussian dispersion model offers rapid response times [2] and is mainly applied to source inversion problems in flat and open areas. The CFD method can obtain a more accurate concentration field in urban neighborhoods. However, it requires substantial calculations, and its modeling process is complex [12]. Past studies have proposed diverse cost functions for source inversion optimization models, with Dong et al. [13] systematically reviewing and comparing common objective functions such as squared deviation sums and absolute deviation values, identifying squared deviation sums as relatively more excellent. Source inversion depends on downwind pollution concentration data. When the measurement accuracy of the sensor is certain, the sensor layout, as a necessary working link for obtaining monitoring data, is bound to affect inversion outcomes. Understanding this impact is crucial for optimizing sensor placement and ensuring reliable inversion results. It should be noted that the impact of the sensor layout may be complex. First, the sensor layout involves both quantity and location distributions, with location distribution effects likely being quantity-dependent. Therefore, the number and distribution of sensors should both be considered, and the combined influence of quantity and location distributions should be investigated when assessing the impact of a sensor layout. Second, the complexity between quantity and location distribution impact requires moving beyond traditional single-factor comparative methods toward a research strategy to simultaneously consider the quantity and location of sensors and quantify their combined impacts.
Over recent decades, sensor layout impacts on source inversion have remained a focal research topic. Existing studies have predominantly focused on two methodological frameworks of source inversion: Bayesian inference and optimization theory. Liu and Li [14] conducted a comprehensive review of the Bayesian inference inversion method. They revealed that current research primarily determines the optimal sensor position for source parameter estimation when the number of sensors is given; furthermore, the influence of the number of sensors on estimation results in complex urban neighborhoods is investigated. Compared to the Bayesian inference inversion method, a relatively more extensive research outcome was obtained from source inversion optimization. Some key findings include the following: (1) Increasing the number of sensors generally improves the accuracy of source inversion [15,16], with recommendations to exceed the count of unknown parameters in source inversion [17,18]. (2) Sufficient inter-sensor spacing is required to obtain the effective concentration gradient information [17]. (3) Inversion accuracy is more sensitive to the angle between source–receptor lines and dominant wind directions than to source-monitoring distances [19]. However, the above studies on source inversion optimization mainly focused on one dimension of complex issues (i.e., the limited sensor number or the location distribution under a relatively sufficient sensor quantity was considered alone). Additionally, some scholars also focused on sensor layout optimization, and three typical research ideas are proposed: (1) determining the relative best layout scheme by comparing various location distribution modes when the number of sensors is given or relatively sufficient (dozens or hundreds) [20,21]; (2) deriving the optimal sensor layout through optimized cost functions [22,23]; and (3) sequential deployment strategies combining redundancy detection with risk maximization [24]. However, these studies simplify the complexity of sensor layout impacts.
In summary, current research lacks a research strategy for simultaneously identifying the combined influence of quantity and location distributions on source inversion optimization. The sensitivity of inversion optimization results in variations in sensor distribution, and the relationship between sensor distribution influence and sensor quantity remains unclear. While previous studies [15,25] have highlighted the influence of prior knowledge of the source location (known or unknown) and atmospheric dispersion conditions on inversion outcomes, the combined impact of sensor quantity and location distributions across diverse application scenarios remains unaddressed. Furthermore, source strength is a key parameter for hazardous distance predictions during emergency response to accidents [26]. However, most existing studies have emphasized sensor layout effects on the overall estimation performance of source strength and locations, with limited attention solely focused on source strength parameters. To fill the above research gap, this study investigated the combined influence of sensor quantity and distribution on optimization-based source inversion, employing a research strategy based on a random sampling combined with the coefficient of variation. Sensor layout impacts on the estimation results of source strength and location were analyzed under six application scenarios: three atmospheric dispersion conditions (unstable, neutral, and stable) and two prior pieces of information about the source location (known and unknown). To reflect the real world, the Prairie Grass experimental dataset [27], comprising 68 single-point source gas release experiments in small-scale areas, was utilized in this study. The results of this study are expected to enhance our understanding of the factors that influence source inversion optimization.
2. Methodology
2.1. Experimental Field Data
The dataset used for evaluating sensor layout impact was obtained from the 1956 Prairie Grass field experiments conducted in O’Neill, Nebraska, USA (42°29.6′ North, 98°34.3′ West) [27]. The dataset is one of the few publicly available datasets of classic dispersion experiments conducted at the microscale and has been widely used in previous studies [5,10] for various research purposes. It consists of 68 release experiments covering various atmospheric dispersion conditions and is well suited to our research purposes. Thus, this classical dataset was also selected in our study. A detailed introduction to the dataset is provided as follows. The Prairie Grass dataset includes 68 single-point SO2 releases, each lasting 10 min. Approximately 600 sensors at 1.5 m height were arranged along five semi-circular arcs with radii of 50, 100, 200, 400, and 800 m around the release point to measure 10 min average concentrations. Sensors were placed at 2° intervals along arcs at 50, 100, 200, and 400 m and at 1° intervals at 800 m in a semi-circular downwind arrangement (Figure S1). Our statistical analysis showed that 51 out of 68 experiments had over 70 usable sensors, while a few experiments had fewer but still contained more than 41 sensors. Wind speeds and directions at 2 m were recorded using cup anemometers and airfoil-type vanes. The dataset covers various atmospheric dispersion conditions—unstable (classes A, B, and C), neutral (class D), and stable (classes E and F)—as per the Pasquill criteria, with 20, 31, and 17 experiments under each condition, respectively [5].
2.2. Inversion Model
The source inverse method uses a forward model to calculate concentrations based on given source parameters. The Gaussian plume model was chosen for this study. The refined model (e.g., CFD) is not adopted in the present investigation, as it requires more source details; otherwise, the refined model would not necessarily provide better simulation than a simple model [28]. In recent years, data-driven models [4] emerged to address rapid, accurate simulation challenges in complex environments. However, these methods demand extensive training data and often lack sufficient generalization for random accident scenarios. While Gaussian dispersion models exhibit limited adaptability to intricate environments, their computational efficiency and straightforward framework remain advantageous for practical applications, particularly rapid emergency response to sudden incidents. Notably, the Gaussian plume model has been widely applied in source inversion studies for gas leakages [5,24,29,30] and industrial air pollutant discharges [31]. Meanwhile, the purpose of this study is to present a research strategy that reveals the combined impacts of quantity and location distribution and to investigate the changing characteristics of the combined impacts across diverse scenarios with varying atmospheric conditions and prior source location information. Therefore, on the premise of meeting the requirements of this study, we chose the simple and efficient Gaussian plume model as the forward dispersion model. According to the assumptions of the Gaussian plume model, the representation of spatial position is mainly described in Cartesian coordinates. The positive direction of the x-axis in coordinates is consistent with the wind speed direction. The y-axis is perpendicular to the x-axis on the horizontal plane, and the positive direction left of the x-axis. The z-axis is perpendicular to the horizontal plane, and the upward direction is defined as positive. The model is expressed as follows:
where Q0 is the source strength (g/s); u is the mean wind speed (m/s) near the ground; C(x, y, z) is the concentration (g/m3) at a location (x, y, z), where x, y, and z represent the downwind, crosswind, and height location coordinates of the receptor; x0, y0, and z0 are the location coordinates of the source; and are dispersion coefficients for horizontal crosswind and vertical directions, respectively, with both being functions of the downwind distance (x − x0). The formulas for these coefficients are as follows [25]:
where a1, a2, b1, b2, r1, and r2 are the constants used to calculate the dispersion coefficients. Table S1 provides a detailed description of these constants.
The inversion method was used to estimate the unknown source parameters by optimizing the fit between the simulation data of the dispersion model and sensor monitoring data. Referring to a previous study [13], the squared deviation sum is selected as the objective function for constructing the source inversion model. The expression is as follows:
where n is the number of monitoring sensors, and and are the observed and simulated concentrations at downwind site i, respectively. For the two scenarios with different source location prior information, the inversion model combines Equations (1) and (4) as follows:
Scenario 1. Known source location (only estimating source strength):
Scenario 2. Unknown source location (estimating source strength and locations):
where , , , and are the unknown source parameters to be estimated. Due to forward model limitations, this inversion method applies to the constant release of hazardous gas under conditions of a stable wind field and flat terrain in small-scale areas. In practice, the Gaussian model can be replaced with a more suitable model based on application requirements.
Based on Equations (5) and (6), the source inversion model is formulated as a minimization optimization problem. Genetic algorithms, known for their robustness and global search capabilities, are widely used in source inversion [20,25,32]. GAs perform iterative evaluations, selections, crossovers, and mutations to find the optimal solutions without requiring derivative information, rendering them suitable for complex non-linear problems. Figure S2 shows the GA flowchart. This study used MATLAB (R2015b)’s GA toolbox to solve optimization problems. Haupt et al. [33] pointed out that the crossover rate, population size, and mutation rate are the most commonly tuned parameters in source inversion optimization based on a GA, and the population size and mutation rate, in particular, can significantly impact the number of cost function evaluations required, and consequently, the CPU time. In their studies, a population size of 8, a mutation rate of 0.20, and a crossover rate of 0.5 were used. Mao et al. [34] further tested the impact of the population size of a GA with a mutation rate of 0.20 and a crossover rate of 0.5 on source inversion and found that the population size could affect the source inversion’s accuracy; moreover, the population size for a stable source inversion was larger than 30. Referring to prior experience, the parameters of the mutation and crossover rates for the GA’s operation were set as 0.2 and 0.5 in this study, and the population size was set as 100, which is greater than 30. The maximum number of iterations, 1000, was set as the termination criterion for the GA’s optimization iterations in this study. To minimize randomness, 100 independent trials were conducted for each calculation, and the mean results were analyzed. We note that since Q0 represents source strength, a negative optimization result is invalid. Therefore, a judgment condition was set for the calculation results to solve this problem in our study. That is, if a negative value of Q0 appears in the optimization result of a certain trial, it will be judged as an invalid calculation. In this case, the result will not be retained, and a new random trial needs to be conducted to ensure that it meets the requirements of the total number of random trials in our research scheme.
2.3. Evaluation Indicators
The absolute relative deviation (ARD) and absolute deviation (AD) are separately calculated to assess the inversion accuracy of source strength and location using the following formulas [13]:
where e and r are the estimated and real values, respectively; Q and L represent the source strength Q0 and locations (i.e., x0, y0, z0); I is the test experiment’s serial number.
The coefficient of variation (CV) is a normalized measure of the dispersion degree of the probability distribution and is defined as the ratio of the standard deviation to the mean. This indicator was used to evaluate the robustness of inversion results. A higher CV indicates greater data fluctuation. The formula is as follows:
where is the standard deviation of ARD for source strength Q0 or AD for locations x0, y0, and z0, and is the mean of ARDs or ADs.
The ARDs, ADs, and CVs of all random trials for each field experiment for each sensor number were calculated. The mean ARD, AD, and CV for all experiments represent the results of this study. Ideal values of ARD, AD and CV are zero, with lower values indicating better estimation performance.
2.4. Research Strategy
This study proposes a research strategy combining random sampling and coefficient of variation (CV) methods to assess the combined impacts of sensor quantity and distribution on source inversion. The random sampling method used in this study was based pm a previous study [16,35]. Random sampling involves selecting a given number of sensors, N, from all available sensors, U, with each selection representing a unique sensor location combination. The total number of combinations is given by the binomial coefficient . A large number of random samples ensures reliable conclusions about the influence of sensor quantity. The CV, calculated from source inversion results across all random combinations, quantifies the impact of sensor distribution. Further analysis under different sensor numbers helps identify the relationship between sensor distribution effects and sensor quantity. We note that the research strategy can serve as a reference for other similar studies, with specific methods (e.g., the random method, inversion model, and optimization algorithm) adaptable to different scenarios.
As noted in Section 2.1, each experiment used in this study has more than 41 available sensors (U); thus, the upper limit for testing is set below 41. Following previous recommendations [17,18], the number of sensors should exceed the number of unknown parameters for source inversion. Thus, for known locations, N ranges from 1 to 40, and for unknown locations, it ranges from 4 to 40. Using the scenario of only estimating the source strength in 68 Prairie Grass experiments as an example, a flowchart of the research methodology is presented in Figure 1. The main steps of the research strategy are as follows:
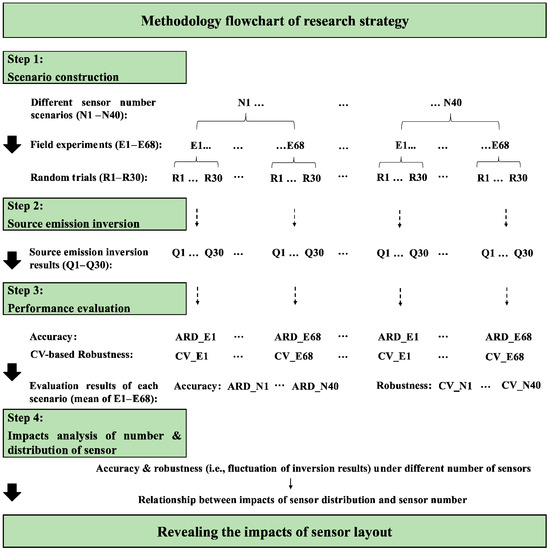
Figure 1.
Methodological flowchart of the research strategy. “N1–N40,” “E1–E68,” “R1–R30,” and “Q1–Q30” represent the source inversion scenarios by sensor number, the serial numbers of field experiments, and the serial number of random trials, respectively. “ARD” (absolute relative deviation) and “CV” (coefficient of variation) represent the accuracy and robustness of source inversion performance, respectively.
- (i)
- Scenario construction: Inversion scenarios (N1 to N40) for sensor numbers 1–40 were constructed using 68 field experiments (E1–E68) from the Prairie Grass dataset. For each scenario, sensors were randomly selected from all monitoring sensors in each experiment, with 30 random trials (R1 to R30) conducted to ensure that the results accurately reflected the statistical relationship between inversion performance and sensor number.
- (ii)
- Source strength inversion: Source strengths were estimated for all random trials across 68 experiments using the source inversion method detailed in Section 2.2.
- (iii)
- Performance evaluation: The performance of source strength inversion for each field experiment in each scenario was evaluated using ARD and CV as indicators, as described in Section 2.3. ARDs and CVs were calculated for each experiment under each scenario to assess inversion accuracy and robustness (i.e., the fluctuation of the inversion results) based on all random trials. This yielded evaluation results (ARD_E1 to ARD_E68 and CV_E1 to CV_E68) from each field experiment under each scenario. Finally, the mean of these evaluation results provided the overall inversion performance for each sensor number scenario.
- (iv)
- Analysis of sensor layout impact: This step analyzed the impacts of sensor number and location distribution on source inversion by examining how ARD and CV indicators vary with different sensor numbers. The variation characteristics of ARD and CV under different numbers of sensors reveal the impact of the sensor number on inversion accuracy and robustness. The CV values indicate how much sensor location distributions affect inversion performance. A large CV suggests that sensor location differences significantly influence the inversion results for the given number of sensors. The relationship between the impacts of the sensor distribution and sensor number can be revealed by analyzing the CV under different sensor numbers.
2.5. Curve Fitting and Correlation Analysis
Curve fitting uses continuous functions to represent discrete data, revealing data trends through mathematical functions [36]. In this study, it was employed to describe how inversion performance indicators vary with the number of sensors. The decision coefficient R2 indicates the model’s goodness of fit, where values closer to 1 indicate a better fit. IBM SPSS software (Version 22.0)was used to calculate the Pearson and Spearman correlation coefficients (r) to separately measure linear and non-linear relationships between the sensor numbers and evaluation indicators. An r value that is closer to −1 or 1 signifies a stronger negative or positive correlation, respectively.
3. Results
3.1. In Cases with Known Source Locations
This section assesses the inversion performance for estimating a single unknown parameter (i.e., Q0) using different numbers (1–40) of sensors across 68 experiments. The evaluation indicators (i.e., ARD and CV) with a 95% confidence limit (C.L.) were calculated for all trials. The variation trends of the evaluation indicators with the number of sensors were analyzed based on the curve-fitting method, and the corresponding mathematical models were established. The correlation coefficients (r) between the evaluation indicators and the number of sensors were calculated. Detailed results are shown in Figure 2 and Table 1.
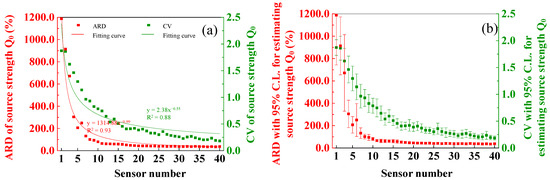
Figure 2.
(a) Inversion performance (ARD and CV) of different numbers of sensors for the estimation of source strength (Q0) when the source location is known; (b) the results of ARDs and CVs with 95% confidence limits for estimating Q0.

Table 1.
Correlation coefficient (r) between the number of sensors and the evaluation indicators.
In terms of accuracy, ARD exhibited a non-linear decrease that finally stabilized as the number of sensors increased (Figure 2a). The power function fit the data well with a high goodness of fit (R2 = 0.93). The large |r| (0.986) in Table 1 indicates a strong correlation between the two variables. Combined with Figure 2b and compared to situations with a relatively large number of sensors, the estimation accuracy with a small number of sensors was worse due to the larger ARD and C.L. values, and ARD fluctuated significantly with respect to a change in the number of sensors. To facilitate a better quantitative description of the results, this study used six sensors to represent the “small number of sensors” mentioned above. The mean ARD of the inversion scenarios based on 1 to 6 sensors reached 589.4%. For the ARD fluctuation with changes in sensor quantity, the maximum ARD gap between different sensor numbers reached 981.4%. The C.L. of ARD (mean value = 232.0%) for a small number of sensors is also remarkably large. These results indicate poor estimation accuracy. To characterize the sensor quantity required for stable source inversion, this study defined a concept of “inflection point” for the estimation accuracy of source strength. In this section, a deviation gap of <30.0% between the maximum and minimum ARD from the current number to the maximum number of sensors was set as the judgment standard of the inflection point, which refers to a stable state of inversion accuracy. The mean ARD of all inversion scenarios from the number of sensors at the inflection point to the maximum number (i.e., 40) of sensors was calculated to represent the estimation accuracy at the stable state of the source inversion. According to the above definitions, the number of sensors in the inflection point was 12, with an ARD of (44.2 ± 3.2)%. In terms of robustness, similarly to the estimation accuracy, CV exhibited a non-linearly decrease and finally stabilized with an increase in the number of sensors (Figure 2a). A strong correlation between the CV and the number of sensors was observed because of the high value of |r| (0.993) (Table 1). Meanwhile, compared to the number of available sensors, when a small number of sensors was used, a distinctly large CV and large confidence limits occurred under different numbers of sensors, and the CV also fluctuated significantly with the number of sensors (Figure 2b). Consistent with the previous discussion, we define a small number of sensors as six. When a small number of sensors were available, the mean CV reached 1.54, and the maximum gap value of CV under different numbers of sensors was 0.73. As introduced in Section 2.4, the CV indicator quantifies the effect of the sensor distribution difference. Thus, it was determined that the smaller the number of sensors, the greater the sensor distribution’s impact on the source strength inversion; however, this influence was not significant when the number of sensors reached a certain value.
3.2. In Cases with Unknown Source Locations
In this section, the inversion results for estimating multiple unknown parameters (Q0, x0, y0, and z0) were obtained using the Prairie Grass dataset. The evaluation indicators (ARD, AD, and CV) and their C.L. values were calculated for all trials. The detailed results for different numbers (4–40) of sensors are shown in Figure 3 and Table 1.
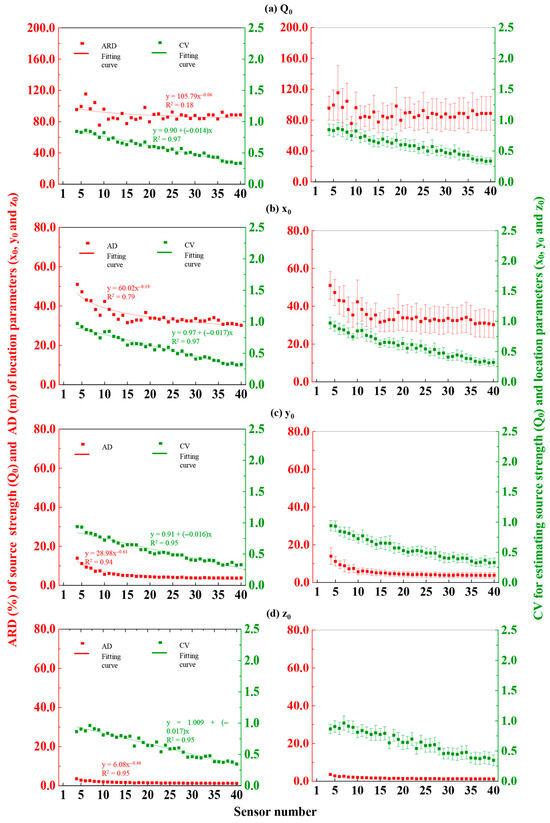
Figure 3.
Inversion performance (ARD, AD, and CV) for estimating source parameters with varying sensor numbers when the location is unknown: (a–d) the estimation results for Q0, x0, y0, and z0, respectively. The left side of Figure 3 displays the curve-fitting graphs showing the variation trend of the inversion accuracy index with the number of sensors, while the right side shows the scatter plots showing the inversion accuracy indicators with a 95% confidence limit under different sensor quantities.
The left side of Figure 3a shows the variation characteristics of the ARD and CV of parameter Q0 with respect to the number of sensors used. Overall, as the number of sensors increased, the ARD gradually decreased and finally stabilized, although the poor performance in curve fitting (R2 = 0.18) and a weak correlation (r = −0.179) (Table 1) between the ARD and sensor quantity were easily observed. The right side of Figure 3a shows that using a low number of sensors (1–6) resulted in a relatively large mean ARD (103.4%) and high confidence limit (19.9%) compared to using a larger number of sensors. Based on the “inflection point” definition in Section 3.1, an inflection occurred at seven sensors, where the inversion deviation stabilized at (84.4 ± 2.0)%. For robustness, the CV exhibited a distinct linear decrease with increasing sensor numbers, showing a strong negative correlation (r = −0.983) (Table 1) and high R2 (0.97) for the linear fitting model. Notably, the mean CV was remarkably high (0.85) when using a low number of sensors (1–6). Figure 3b–d show the results for estimating locations x0, y0, and z0. For accuracy, the ADs of all parameters showed a non-linear decrease and eventual stabilization with increasing sensor numbers, with R2 > 0.79 for the non-linear fitting model of each location parameter. Table 1 shows strong negative correlations between the estimation error and sensor quantity, with r values of −0.771, −0.980, and −0.967 for x0, y0, and z0, respectively. Simultaneously, the majority of the estimation deviation lies in location parameter x0 (AD > 30.2 m), whereas there were small errors in estimating y0 (AD < 13.9 m) and z0 (AD < 3.6 m). Additionally, the C.L. values for estimating x0 were remarkably larger (mean C.L. = 7.0 m) than y0 (mean C.L. = 1.6 m) and z0 (mean C.L. = 0.3 m). For robustness, similarly to the results of Q0, the CVs for all location parameters decreased linearly with the number of sensors. A strong correlation between the impact of sensor distribution and sensor quantity was evident from the high |r| values, which were 0.983, 0.975, and 0.976 for parameters x0, y0, and z0, respectively (Table 1).
3.3. Influence of Atmospheric Stability Conditions
3.3.1. Estimation Results When the Source Location Is Known
Figure 4 shows the inversion results of Q0 under different atmospheric conditions with a known source location.
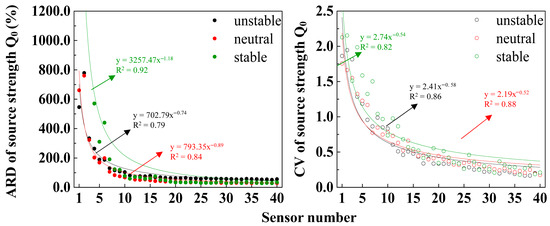
Figure 4.
Inversion performance (ARD and CV) of different numbers of sensors for estimating source strength Q0 when the location is known.
The left panel shows that the ARDs decreased non-linearly with increasing sensor numbers across all atmospheric conditions and eventually stabilized. The high R2 values (0.79, 0.84, and 0.92 for unstable, neutral, and stable conditions, respectively) indicated the good fit of the mathematical models. Table 1 shows strong negative correlations between sensor quantity and ARD, with r values of −0.981, −0.988, and −0.913 for unstable, neutral, and stable conditions, respectively. Inflection points occurred at 11, 12, and 17 sensors for unstable, neutral, and stable conditions, achieving accuracies of (61.8 ± 2.9)%, (35.6 ± 2.8)%, and (34.1 ± 2.3)%, respectively. Based on the property that the growth rate of a power function is related to its exponent, the change in amplitude of the function value is positively correlated with the absolute value of the exponent (ABE) as the independent variable changes. In other words, for this study, a greater ABE indicates that changes in the number of sensors have a larger impact on the accuracy of source inversion. The ABEs of 1.18 (stable), 0.74 (unstable), and 0.89 (neutral) indicated that sensor quantity most significantly affected inversion accuracy under stable conditions. Regarding robustness (Figure 4, right), similarly to accuracy, the relationship between CVs and the number of sensors exhibited a good fit using non-linear decline functions under different atmospheric conditions. The CV and sensor quantity showed significant correlations with |r| > 0.90 under each atmospheric condition (Table 1). The largest CV in all sensor quantity inversion scenarios occurred most frequently (28 out of 40) under stable conditions, indicating that the sensor distribution had a larger influence on source inversion in stable conditions.
3.3.2. Estimation Results When the Source Location Is Unknown
Figure 5a–d separately display the inversion results of Q0, x0, y0, and z0 under different atmospheric conditions. Figure 5a shows that the ARD of Q0 was affected by the number of sensors under all atmospheric conditions. Under unstable conditions, ARD initially increased slightly before stabilizing, whereas under neutral and stable conditions, ARD decreased non-linearly with increasing sensor numbers, eventually stabilizing. The relationships between ARD and sensor quantity were well described by power functions with R2 values of 0.62 (unstable), 0.53 (neutral), and 0.71 (stable) conditions. Table 1 shows a strong positive correlation between sensor number and estimation accuracy under unstable conditions (r = 0.809) and strong negative correlations under neutral (r = −0.618) and stable (r = −0.754) conditions. The inflection points varied for different atmospheric conditions: 24 sensors for unstable conditions with the highest ARD (146.5 ± 3.7%), 21 sensors for stable conditions with a lower ARD (46.2 ± 1.4%), and only 9 sensors for neutral conditions with an ARD of 71.7 ± 2.2%. The absolute value of the exponent (ABE) in power functions indicates that sensor quantity had the greatest impact on inversion accuracy under stable conditions (ABE = 0.42) compared to unstable (0.14) and neutral (0.17) conditions. For robustness, the CV under each atmospheric condition showed a clear linear decrease with the number of sensors. The R2 values of the fitting model for the unstable, neutral, and stable conditions were 0.88, 0.94, and 0.81, respectively. Table 1 shows strong negative correlations between CV and sensor numbers, with r values of −0.941, −0.971, and −0.904 for unstable, neutral, and stable conditions, respectively. The largest CV value in all sensor quantity inversion scenarios occurred most frequently (29 out of 37) under stable conditions. For location parameter x0 (Figure 5b, left), AD exhibited a non-linear downward trend with respect to the number of sensors and finally stabilized. The best fit between the number of sensors and AD was obtained under neutral conditions, with the highest R2 of 0.87, followed by unstable conditions (R2 = 0.33), and the worst fit was obtained under stable conditions, with the lowest R2 of 0.13. Correlation coefficients (Table 1) revealed a significantly strong correlation between the number of sensors and AD under unstable (r = −0.919) and neutral (r = −0.932) conditions and a weak correlation under stable (r = −0.172) conditions. For parameters y0 (Figure 5c, left) and z0 (Figure 5d, left), the ADs showed a non-linear downward trend with respect to the number of sensors and finally tended to stabilize. The relationships between the number of sensors and inversion deviation for y0 and z0 were well fitted by power functions, with high R2 (≥0.80) values under all atmospheric conditions. Significantly strong correlations between the ADs of y0 and z0 and the number of sensors are observed in Table 1. Regarding robustness (Figure 5b–d, right), the CVs of x0, y0, and z0 decreased linearly with an increase in the number of sensors, exhibiting strong correlations (|r| ≥ 0.847) under different atmospheric conditions. Comparing the CVs under different atmospheric conditions, we found that atmospheric conditions showed a distinct impact on the sensor distribution effect, and the impact varied with the location’s parameter types. Specifically, under neutral atmospheric conditions, the CVs for the horizontal location x0 were higher in most sensor quantity scenarios (30 out of 37) compared to unstable and stable conditions, indicating that the estimation of x0 is more sensitive to sensor distribution variation in neutral conditions. However, for the horizontal location y0, the largest CV value in all inversion scenarios appeared most frequently (30 out of 37) in unstable conditions. Regarding the vertical location z0, the number of scenarios with the largest CV was similar between unstable (16 out of 37) and neutral (17 out of 37) conditions, both significantly exceeding those in stable conditions.
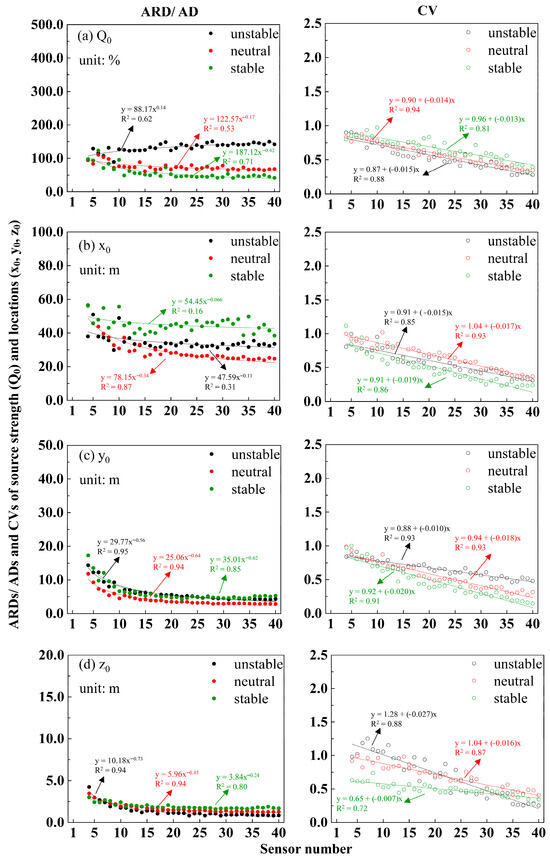
Figure 5.
Inversion performance (ARD, AD, and CV) of different numbers of sensors for estimating multiple source parameters. (a–d) represent the results for the estimation of Q0, x0, y0, and z0, respectively.
4. Discussion
This study investigated the combined influence of sensor quantity and location distribution on source inversion optimization by employing a new research strategy combining random sampling and coefficient of variation methods. The combined impacts were analyzed under multiple scenarios with different atmospheric conditions (unstable, neutral, and stable) and prior source location information (known and unknown).
Overall, the estimation error of each source parameter in the case of simultaneously estimating Q0, x0, y0, and z0 non-linearly decreased with the number of sensors. This finding is consistent with that of [16], where another optimization approach consisting of two steps (i.e., separating the estimation of the source strength and location) was utilized. This indicated that the influence of sensor quantity for different solution strategies changed little within the optimization inversion framework. Section 3.1 showed that the ARD of Q0 also decreased non-linearly with increasing sensor numbers for known source locations, but the correlation and regression fit were notably weaker for unknown locations (R2 = 0.18, r = −0.179) compared to known locations (R2 = 0.93, r = −0.986). This might be attributed to differences in the decision variables of inversion models resulting from varying prior source location information. Section 3.1 and Section 3.2 mention that the CV showed a non-linear decreasing trend with respect to the number of sensors when only estimating Q0, whereas a remarkable linear descent trend was observed for estimating Q0, x0, y0, and z0. Simultaneously, the large correlation coefficients (|r| ≥ 0.847) between CV and the number of sensors can be observed in all study cases (Table 1). These results indicated that the impact of sensor location distribution was significantly related to the number of sensors; moreover, the decreasing trend revealed that the lower the sensor quantity, the greater the impact of sensor distribution on source inversion. The difference in the CV fitting curves for Q0 can be attributed to the fact that the variation in the decision variables (i.e., unknown parameters) of the inversion model changes the complexity of the optimization problem. Section 3.3 demonstrated that, compared to unstable and neutral conditions, a significantly larger number of sensors was required for stable atmospheric conditions, and sensor quantity and location distribution had greater impacts on source strength inversion. This may result from the poor fit between the monitoring and forward model simulation data under stable atmospheric conditions [15,37].
This study evaluated the minimum number of randomly scattered sensors (inflection points) required for stable source strength inversion across multiple scenarios. The sensor distribution based on random sensitive points (residential areas, schools, etc.) is commonly used in emergency monitoring [38]. Thus, conclusions regarding the inflection points can serve as a reference for successfully estimating source strength using a random sensitive point monitoring scheme in emergencies. To facilitate application, detailed results are summarized in Table 2. The relationship between the “goal” (i.e., source strength estimation accuracy) and the “criterion” (i.e., number of sensors scattered randomly) is revealed in the table. Of particular note is that, in the case of unknown locations, the ARD of Q0 under unstable atmospheric conditions is positively correlated with the number of sensors (r = 0.809). However, we still provided the minimum number of sensors required for a stable source inversion accuracy. This is mainly because the extremely small exponent (0.14) of the fitted curve power function (left side of Figure 5a) indicated that, when the number of sensors reaches a certain value, further increasing the number of sensors results in very little change in the inversion deviation. In order to facilitate the practical application of the source inversion methods, in this study, we assumed that under unstable atmospheric conditions, if the ARD under the number of tested sensors reached the “inflection point” standard, it was determined as the minimum number of sensors required for the stable inversion accuracy. However, it should be pointed out that the evaluation results hold only under the same source inversion method and the same criterion for judging the “inflection point”. Moreover, this study found that the location distribution’s impact is a function of sensor quantity, suggesting the inflection point marks the critical number of sensors below which the sensor distribution can cause significant impacts on source strength inversion when the number of sensors is lower than the inflection point. When sensor quantity was below the inflection point, optimizing sensor layouts under limited resources can be achieved by further evaluating the inversion accuracy of potential candidate distribution schemes. Building on Ma et al. [20], who evaluated arc and square distributions for multi-parameter inversion, this study focuses on a scenario where only the source strength is unknown in order to demonstrate its significance in optimizing sensor layouts. According to Section 3.1, as the inflection point occurred at 12 sensors, a smaller sensor number (6) was randomly selected in this study. Typical sensor distributions including rectangular, arc (single-layer and multi-layer), and downwind axes were designed (Figure S3). The inversion accuracy of various distributions was evaluated using virtual experiments from a Gaussian model. In the simulation, an emission rate Q of 50 g/s was used, and concentrations at a 1.5 m height for downwind sensors were calculated. To mimic real-world data uncertainty, Gaussian white noise was added to the simulation results at infinite, 20, 2, and 0.1 SNRs, with ten trials conducted for each SNR level. The results indicated the relatively better inversion accuracy of multilayer arc distributions under the limited monitoring source. Detailed results are shown in Figure S4 and Table S2.

Table 2.
Evaluation results of source strength (Q0) inversion for multiple scenarios with different atmospheric conditions and prior source location information.
The above analysis shows that the proposed strategy combining random sampling and coefficient of variation methods can effectively identify the combined impacts of sensor quantity and location distribution and assist in sensor layout optimization. We note that the concept of this research strategy holds reference value for similar studies in other specific source inversion cases. The novel findings of this study can improve our understanding of sensor layout impacts on source inversion optimization in real-world applications. The conclusions on the sensor quantity inflection point and evaluations of typical distributions can support sensor layout optimization for source strength inversion in real applications—such as small-scale industrial parks in flat rural areas or during emergencies. However, there are also some limitations in the present study. Firstly, the objective function of the squared deviation sum used in our study ignores the dependence of the observational and model errors on the magnitude of concentration. This might limit the applicability of the conclusions to scenarios where optimization models are constructed using the sum of squared deviations. Therefore, in the future, it is necessary to conduct further tests, using an objective function (e.g., weighted quadratic function) that takes into account the above dependencies, and to compare the results with those of this study for verification. Secondly, the Bayesian inference approach is another key method for identifying unknown source parameters. Although this study did not test this method, given that it shares similarities with the optimization approach—both relying on a forward model for which its performance is influenced by atmospheric conditions—we can preliminarily infer that the impact of sensor layouts under extremely stable atmospheric conditions may also be amplified. However, whether this hypothesis is valid and how sensor distribution and quantity specifically affect the estimation of different parameters (e.g., source strength and location) remain to be verified through future research. Thirdly, this study was performed using a simple Gaussian model and a small-scale grassland dataset, limiting its applicability to urban or long-distance air pollution. Additionally, the relatively simple scenarios—including a single emission source, constant wind field, and random sensor placement ignoring site restrictions—further limit the applicability of the conclusions in the real world. Thus, future research on more complex scenarios—such as urban terrains, multiple emission sources, large distances, dynamic gas release rates, and changing wind fields—should also be considered.
5. Conclusions
Source inversion optimization using downwind sensor observations is a key method for estimating source strength (Q0) and locations (x0, y0, and z0) in hazardous gas leakages. This study applied a research strategy that combines random sampling and coefficient of variation methods to investigate the combined impacts of sensor quantity and location distribution on source parameter inversion using the Prairie Grass experiments. The differences in the combined impacts under multiple scenarios with different atmospheric conditions (unstable, neutral, and stable) and prior source location information (known and unknown) were analyzed and discussed. The following conclusions were drawn:
- (1)
- The impact of sensor quantity on estimating Q0 varied depending on the prior source location information. The correlation between estimation deviations and sensor quantity was weak (r = −0.179) for unknown locations but strong (r = −0.986) for known locations. Under the condition of limited monitoring resources, adding the same number of sensors will yield greater improvement in the accuracy of source strength estimation for known locations than for unknown locations.
- (2)
- The impact of sensor distributions was affected by the number of sensors. For known source locations, the impact on source strength inversion decreased non-linearly with more sensors. For unknown locations, the impact on all source parameters decreased linearly as the number of sensors increased.
- (3)
- The impacts of sensor quantity and location distribution on Q0 estimation would be amplified under stable atmospheric conditions. For x0 and y0, the influence of sensor distribution was most pronounced under neutral and unstable conditions, respectively. For z0, the influence was comparable under both unstable and neutral conditions and greater than under stable conditions.
- (4)
- For random sensor distributions on flat terrains, achieving stable source strength inversion required 11, 12, and 17 sensors for known locations under unstable, neutral, and stable conditions, respectively; for unknown locations, it required 24, 9, and 21 sensors, respectively. In source strength inversion applications with known locations, the multi-layer arc distribution for sensor placement outperformed rectangular, single-layer, and downwind axis distributions in estimation accuracy.
The results of this study can enhance our understanding of the impact of sensor layouts on source inversion optimization. The proposed research strategy can provide valuable guidance for similar studies aiming to determine the required number of sensors and optimal sensor layouts in other particular cases of source inversion.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16070850/s1, Table S1: Constants of BRIGGS formula for dispersion parameter (Briggs 1973, [39]); Figure S1: Graph of source-sensor distribution; Figure S2: Flowchart for the Genetic algorithm; Figure S3: Different sensor location distributions under the limited number of sensors. The release source was marked by full solid red circles. The symbols of dark green circles and black crosses represent the monitoring sensors; Table S2: Evaluation results of source strength (Q0) inversion for different sensor distributions under different levels of monitoring data quality (i.e., SNRs); Figure S4: Inversion deviations of source strength Q0 under different sensor distribution forms. “inf” is short for “infinite”.
Author Contributions
Conceptualization, J.L.; Methodology, S.M.; Software, F.H.; Validation, F.H., X.W. and K.W.; Formal analysis, X.W.; Investigation, S.M. and K.W.; Resources, T.C. and S.C.; Writing—original draft, S.M.; Writing—review & editing, J.L., G.Z. and F.C.; Visualization, F.H.; Supervision, J.L.; Funding acquisition, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by the National Key R&D Program of China (No. 2017YFC0209905), Beijing Nova Program (20220484209) from the Beijing Municipal Science & Technology Commission, Innovation Ability Improvement Project of Science and Technology for SMEs in Shandong Province (NO. 2023TSGC0911) from Department of Science & Technology of Shandong Province, Doctoral research fund project in Shandong Jianzhu University (X25161), and Shandong Jianzhu University Graduate Education Quality Improvement Program (NO. YZKC202214). In addition, we greatly appreciate the Beijing Municipal Commission of Education and the Beijing Municipal Commission of Science and Technology for supporting this work.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, Y.; Yang, T.; Gui, H.; Li, X.; Wang, W.; Duan, J.; Mao, S.; Yin, H.; Zhou, B.; Lang, J. Atmospheric environment monitoring technology and equipment in China: A review and outlook. J. Environ. Sci. 2023, 123, 41–53. [Google Scholar] [CrossRef]
- Hutchinson, M.; Oh, H.; Chen, W. A review of source term estimation methods for atmospheric dispersion events using static or mobile sensors. Inf. Fusion 2017, 36, 130–148. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, X.; Kikumoto, H. Source term estimation in the unsteady flow with dynamic mode decomposition. Sustain. Cities Soc. 2024, 115, 105843. [Google Scholar] [CrossRef]
- Ni, C.; Lang, Z.; Wang, B.; Li, A.; Cao, C.; Du, W.; Qian, F. Data-driven source term estimation of hazardous gas leakages under variable meteorological conditions. J. Loss Prev. Process Ind. 2025, 94, 105506. [Google Scholar] [CrossRef]
- Cui, J.; Lang, J.; Chen, T.; Cheng, S.; Shen, Z.; Mao, S. Investigating the impacts of atmospheric diffusion conditions on source parameter identification based on an optimized inverse modelling method. Atmos. Environ. 2019, 205, 19–29. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, B.; Zhu, Z.; Wang, R.; Chen, F.; Zhao, Y.; Zhang, L. A hybrid strategy on combining different optimization algorithms for hazardous gas source term estimation in field cases. Process Saf. Environ. Prot. 2020, 138, 27–38. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, R.; Su, T.; Jang, J. Gas diffusion model based on an improved Gaussian plume model for inverse calculations of the source strength. J. Loss Prev. Process Ind. 2022, 75, 104677. [Google Scholar] [CrossRef]
- Lu, J.; Huang, M.; Wu, W.; Wei, Y.; Liu, C. Application and Improvement of the Particle Swarm Optimization Algorithm in Source-Term Estimations for Hazardous Release. Atmosphere 2023, 14, 1168. [Google Scholar] [CrossRef]
- Jang, S.; Park, J.; Lee, H.; Jin, C.; Kim, E. Comparative study on gradient-free optimization methods for inverse source-term estimation of radioactive dispersion from nuclear accidents. J. Hazard. Mater. 2024, 461, 132519. [Google Scholar] [CrossRef]
- Ma, D.; Tan, W.; Wang, Q.; Zhang, Z.; Gao, J.; Zeng, Q.; Wang, X.; Xia, F.; Shi, X. Application and improvement of swarm intelligence optimization algorithm in gas emission source identification in atmosphere. J. Loss Prev. Process Ind. 2018, 56, 262–271. [Google Scholar] [CrossRef]
- Jia, H.; Kikumoto, H. Sensor configuration optimization based on the entropy of adjoint concentration distribution for stochastic source term estimation in urban environment. Sustain. Cities Soc. 2022, 79, 103726. [Google Scholar] [CrossRef]
- Duan, J.; Mao, S.; Xie, P.; Lang, J.; Li, A.; Tong, J.; Qin, M.; Xu, J.; Shen, Z. Key emergency response technologies for abrupt air pollution accidents in China. J. Environ. Sci. 2023, 123, 235–254. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Du, W.; Wang, B.; Xu, Q. Investigating impacts of cost functions to atmospheric dispersion modeling and source term estimation in turbulent condition. CIESC J. 2020, 71, 1163–1173. (In Chinese) [Google Scholar]
- Liu, Z.; Li, X. Influence of number of sensors on source term estimation performance in complex urban neighborhood. Sustain. Cities Soc. 2025, 121, 106174. [Google Scholar] [CrossRef]
- Cervone, G.; Franzese, P. Non-Darwinian evolution for the source detection of atmospheric releases. Atmos. Environ. 2011, 45, 4497–4506. [Google Scholar] [CrossRef]
- Efthimiou, G.; Kovalets, I.; Venetsanos, A.; Andronopoulos, S.; Argyropoulos, C.; Kakosimos, K. An optimized inverse modelling method for determining the location and strength of a point source releasing airborne material in urban environment. Atmos. Environ. 2017, 170, 118–129. [Google Scholar] [CrossRef]
- Singh, S.; Rani, R. A least-squares inversion technique for identification of a point release: Application to Fusion Field Trials 2007. Atmos. Environ. 2014, 92, 104–117. [Google Scholar] [CrossRef]
- Singh, S.; Sharan, M.; Issartel, J. Inverse modelling methods for identifying unknown releases in emergency scenarios: An overview. Int. J. Environ. Pollut. 2015, 57, 68–91. [Google Scholar] [CrossRef]
- Sun, S.; Li, H.; Fang, S. A forward-backward coupled source term estimation for nuclear power plant accident: A case study of loss of coolant accident scenario. Ann. Nucl. Energy 2017, 104, 64–74. [Google Scholar] [CrossRef]
- Ma, D.; Deng, J.; Zhang, Z. Comparison and improvements of optimization methods for gas emission source identification. Atmos. Environ. 2013, 81, 188–198. [Google Scholar] [CrossRef]
- Dong, J.; Du, W.; Wang, B.; Cao, C.; Chen, S.; Xu, Q. Impact analysis of multi-sensor layout on the source term estimation of hazardous gas leakage. J. Loss Prev. Process Ind. 2021, 73, 104579. [Google Scholar] [CrossRef]
- Ngae, P.; Kouichi, H.; Kumar, P.; Feiz, A.A.; Chpoun, A. Optimization of an urban monitoring network for emergency response applications: An approach for characterizing the source of hazardous releases. Q. J. R. Meteorol. Soc. 2019, 145, 967–981. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, X.; Kikumoto, H. Detector configuration optimization method considering response time for spatial source parameter estimation in complex urban wind environment. Build. Environ. 2024, 265, 111997. [Google Scholar] [CrossRef]
- Dong, J.; Wang, B.; Wang, X.; Cao, C.; Chen, S.; Du, W. Optimization of sensor deployment sequences for hazardous gas leakage monitoring and source term estimation. Chin. J. Chem. Eng. 2023, 56, 169–179. [Google Scholar] [CrossRef]
- Mao, S.; Lang, J.; Chen, T.; Cheng, S.; Wang, C.; Zhang, J.; Hu, F. Impacts of typical atmospheric dispersion schemes on source inversion. Atmos. Environ. 2020, 232, 117572. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, P.; Wen, H.; Wang, Y.; Liu, C.; Du, X.; Liu, L. Effect of source strength on the simulation of jet dispersion and hazard distances during accidental release of liquid CO2. Process Saf. Environ. Prot. 2024, 183, 1152–1169. [Google Scholar] [CrossRef]
- Barad, M. Project Prairie Grass, A Field Program in Diffusion; Air Force Cambridge Research Center: Bedford, MA, USA, 1958; p. 300. [Google Scholar]
- Huang, Z.; Wang, Y.; Yu, Q.; Ma, W.; Zhang, Y.; Chen, L. Source area identification with observation from limited monitor sites for air pollution episodes in industrial parks. Atmos. Environ. 2015, 122, 1–9. [Google Scholar] [CrossRef]
- Cao, B.; Cui, W.; Chen, C.; Chen, Y. Development and uncertainty analysis of radionuclide atmospheric dispersion modeling codes based on Gaussian plume model. Energy 2020, 194, 116925. [Google Scholar] [CrossRef]
- Blackmore, D.; Hickey, J.; Wigle, A.; Osadetz, K.; Daun, K. A Bayesian technique for quantifying methane emissions using vehicle-mounted sensors with a Gaussian plume model. Atmos. Environ. 2025, 344, 121002. [Google Scholar] [CrossRef]
- Guo, W.; Shi, Y.; Liu, Y.; Su, M. CO2 emissions retrieval from coal-fired power plants based on OCO-2/3satellite observations and a Gaussian plume model. J. Clean. Prod. 2023, 397, 136525. [Google Scholar] [CrossRef]
- Haupt, S. A demonstration of coupled receptor/dispersion modeling with a genetic algorithm. Atmos. Environ. 2005, 39, 7181–7189. [Google Scholar] [CrossRef]
- Haupt, S.; Young, G.S.; Allen, C.T. Validation of a Receptor–Dispersion Model Coupled with a Genetic Algorithm Using Synthetic Data. J. Appl. Meteorol. Climatol. 2006, 45, 476–490. [Google Scholar] [CrossRef]
- Mao, S.; Hu, F.; Lang, J.; Chen, T.; Cheng, S. Comparative Study of Impacts of Typical Bio-Inspired Optimization Algorithms on Source Inversion Performance. Front. Environ. Sci. 2022, 10, 894255. [Google Scholar] [CrossRef]
- Kovalets, I.; Andronopoulos, S.; Venetsanos, A.; Bartzis, J. Identification of strength and location of stationary point source of atmospheric pollutant in urban conditions using computational fluid dynamics model. Math. Comput. Simul. 2011, 82, 244–257. [Google Scholar] [CrossRef]
- Li, P.; Duan, S.; Wang, K.; Wang, L. Grey model and curve fitting settlement prediction and correlation analysis. J. Undergr. Space Eng. 2014, 10, 109–115. (In Chinese) [Google Scholar]
- Finn, D.; Clawson, K.; Eckman, R.; Liu, H.; Russell, E.; Gao, Z.; Brooks, S. Project Sagebrush: Revisiting the value of the horizontal plume spread parameter σy. J. Appl. Meteorol. Climatol. 2016, 55, 1305–1322. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Y.; Zhang, X.; Liu, Z. Research on emergency monitoring sampling spots of sudden air Environmental Pollution Accident. Environ. Monit. China 2007, 4, 9–13. (In Chinese) [Google Scholar]
- Briggs, G.A. Diffusion Estimation for Small Emission. In U.S. National Oceanic and Atmospheric Administration E.R.L Report; ATDL-106; U.S. National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1973. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).