New Insights into Meteorological and Hydrological Drought Modeling: A Comparative Analysis of Parametric and Non-Parametric Distributions

Abstract

Accurate drought monitoring depends on selecting an appropriate cumulative distribution function (CDF) to model the original data, resulting in the standardized drought indices. In the numerous research studies, while rigorous validation was not made by scrutinizing the model assumptions and uncertainties in identifying theoretical drought CDF models, such oversights lead to biased representations of drought evaluation and characteristics. This research compares the parametric theoretical and empirical CDFs for a comprehensive evaluation of standardized Drought Indices. Additionally, it examines the advantages, disadvantages, and limitations of both empirical and theoretical distribution functions in drought assessment. Three drought indices, Standardized Precipitation Index (SPI), Streamflow Drought Index (SDI), and Standardized Precipitation Evapotranspiration Index (SPEI), cover meteorological and hydrological droughts. The assessment spans diverse applications, covering different climates and regions: Durham, United Kingdom (SPEI, 1868–2021); Konya, Türkiye (SPI, 1964–2022); and Lüleburgaz, Türkiye (SDI, 1957–2015). The findings reveal that theoretical and empirical CDFs demonstrated notable discrepancies, particularly in long-term hydrological drought assessments, where underestimations reached up to 50%, posing risks of misinformed conclusions that may impact critical drought-related decisions and policymaking. Root Mean Squared Error (RMSE) for SPI3 between empirical and best-fitted CDF was 0.087, and between empirical and Gamma it was 0.152. For SDI, it ranged between 0.09 and 0.143. The Mean Absolute Error (MAE) for SPEI was approximately 0.05 for all timescales. Additionally, it concludes that empirical CDFs provide more reliable and conservative drought assessments and are free from the constraints of model assumptions. Both approaches gave approximately the same drought duration with different intensities regarding drought characteristics. Due to the complex process of drought events and different definitions of drought events, each drought event must be studied separately, considering its effects on different sectors.

1. Introduction

Natural catastrophes like droughts have become increasingly frequent, with higher records reported in recent years [1,2]. Climate change, coupled with drought, significantly drives global natural disasters [3,4]. Drought poses a significant threat to sustainability by undermining water security, agricultural productivity, and ecosystem stability, especially in climate-vulnerable regions. According to the 2015 Paris Agreement under the United Nations Framework Convention on Climate Change (UNFCCC), addressing drought impacts is essential for achieving long-term resilience and adaptation goals [4]. Droughts typically involve significant reductions in rainfall for a prolonged period below the average precipitation, which results in a water shortage affecting various sectors, which is crucial for sustaining the hydrological cycle [5,6]. Rainfall is a critical indicator for evaluating the effects of climate change and especially drought [7,8]. The decrease in rainfall due to drought limits water availability, influencing supply and demand. It also adversely affects several sectors, including the economy, agriculture, and industry [9,10]. Furthermore, droughts are considered among the most destructive natural disasters [11], causing extensive global and local damage [12,13].

Various standardized indices have been developed to quantify and analyze drought conditions in the field of drought monitoring. Examples of the most commonly used indices are the Standardized Precipitation Index (SPI) [14], the Standardized Precipitation Evapotranspiration Index (SPEI) [15], the Streamflow Drought Index (SDI) [16], and the Reconnaissance Drought Index (RDI) [17]. Short-term scales are related to meteorological and agricultural droughts, and longer timescales are related to hydrological droughts [18]. Among these indices, the SPI is one of the most universally recognized and applied indices. According to the World Meteorological Organization [18], the SPI’s popularity stems from its reliance on precipitation data only, simplifying its application compared to other multi-variable indices. This simplicity allows straightforward implementation across different regions and climates [19,20]. Another important index, SPEI, considers precipitation and potential evapotranspiration, providing a more in-depth view of drought, taking into account the water balance [15]. Both SPI and SPEI are widely used for evaluating meteorological droughts, while the SDI is commonly employed for assessing hydrological droughts. These indices incorporate the concept of standardization, transforming the original data into dimensionless measures that facilitate comparative analysis across diverse climatic datasets [21,22,23]. As such, the accurate computation of these indices is fundamental to reliable assessment and the development of effective drought management strategies [24].

Standardized drought indices (DIs) fundamentally depend on fitting the original data records for each index into an optimal/suitable theoretical distribution function (Theoretical PDF) [14,25]. This function is then probabilistically standardized into a normal distribution with a mean of zero and a standard deviation of one. As noted by Laimighofer and Laaha [26], this approach encompasses several uncertainties and shortcomings, including the choice of distribution, sample size, the method of parameter calculation, and the application of various goodness-of-fit tests. Numerous studies have explored the effects of using different distributions for SDIs, as highlighted by comprehensive analyses in various research [27,28,29,30,31,32]. However, several studies (Chong et al. [33] (gamma for SPI in Malaysia); Sobral et al. [34] (Brazil); Gumus [35] (Türkiye); Ortiz-Gómez et al. [36] (Mexico); Merabti et al. [37] (Algeria); Paulo et al. [38] (Portugal)) have applied arbitrary PDFs without adequately verifying their applicability or suitability to the original data, originally proposed for DIs like SPI (Gamma) and SPEI (Lognormal), which were deemed specific and suitable for the region under study. These studies employed specific parametric distributions without conducting goodness-of-fit tests to verify their appropriateness, revealing a significant gap in the literature. This oversight underscores the necessity to discuss this limitation and explore alternative solutions and methodologies for computing DIs to enhance the robustness and reliability of drought assessments.

Due to the uncertainties involved in selecting the optimal PDF, Farahmand and AghaKouchak [39] introduced the Standardized Drought Analysis Toolbox (SDAT). This approach provides a general framework for deriving non-parametric univariate and multivariate standardized indices. It can be applied to different climates and variables without assuming any specific parametric distributions. Instead of using any parametric PDF, Farahmand and AghaKouchak [39] proposed the use of the empirical Gringorten plotting position [40] to calculate the cumulative probabilities. However, this article did not compare the DIs results based on the empirical and theoretical PDFs using statistical metrics and their effects on the drought characteristics, which represents a significant gap in fully understanding the performance and applicability of these indices under different conditions.

Several studies in the existing literature have evaluated different functions and approaches for calculating drought indices. For example, Cheval [41] provides an overview, highlighting the advantages of SPI and the most commonly used parametric PDFs for SPI. Stagge et al. [42], similarly based on goodness-of-fit analyses, assessed different distribution functions for SPI and SPEI over Europe, recommending the Gamma for SPI, and the Generalized Extreme Value (GEV) distribution function for SPEI. Additionally, Raziei [43] tested different distribution functions for SPI in Iran, finding that the Gamma distribution fits well at longer (6–12-month) time scales, which is aligned with the original article on SPI [14], while Pearson Type III and GEV functions give more accurate results at shorter time scales. In their comparison of parametric approaches (like the Gamma) and non-parametric methods (like the Weibull), Soláková et al. [44] and Mallenahalli [45] concluded that non-parametric methods frequently represent drought and wetness conditions better, especially when dealing with non-normal data distributions. Recently, Vangelis and Kourtis [46] confirmed these findings in Greece by only using the Gamma function without considering other functions and only for SPI, pointing out that although non-parametric approaches can make the SPI calculation easier, they might understate the severity of drought in severe situations, which would support the continued applicability of parametric approaches in some climates.

Despite the importance and contributions of these studies, there are still several research gaps. One key gap is adopting a specific PDF without evaluating its suitability. Moreover, few studies simultaneously analyze meteorological and hydrological droughts in different climates using several indices, such as SPI, SPEI, and SDI. An additional gap exists: the non-inclusion of drought characteristics, such as duration and intensity, alongside statistical performance metrics in the comparison process. Lastly, despite significant advancements in the subject, the detailed comparison between theoretical and empirical approaches with an expanded discussion remains fully underexplored.

Considering these gaps and uncertainties, the selection of PDFs without considering model criteria can lead to significant errors in drought assessments and the characterization of drought conditions, ultimately impacting the reliability of the results derived from these indices and all corresponding applications. This research aims to (1) address and discuss these common mistakes in selecting PDFs by exploring the use of non-parametric indices/empirical drought indices that employ the empirical cumulative distribution function without fitting the data to any predetermined function, (2) highlight the benefits of a more data-driven approach in accurately assessing drought conditions. This discussion will provide a critical examination of the traditional methodologies and propose alternatives that might better reflect the variability in climatic data, (3) conduct a comprehensive comparison between drought indices derived from both theoretical and empirical approaches, utilizing well-established meteorological and hydrological indices across various time scales for meteorological and hydrological droughts, and (4) explore and discuss the advantages and disadvantages of theoretical versus empirical functions in drought analysis, considering a new framework and concepts. This research critically evaluates their contributions and limitations, providing a nuanced understanding of how each approach affects drought characterization and the implications for water resource management. To address and fulfill the main objectives of this research, three different meteorological and hydrological DIs were utilized across various climates. The first is SPI using precipitation data from Karapınar in Konya, Türkiye, from 1964 to 2022. The second involves SPEI calculated from data at Durham station in the UK, covering the period from 1868 to 2021. Lastly, the SDI was determined using streamflow data from Lüleburgaz, Türkiye, from 1957 to 2015.

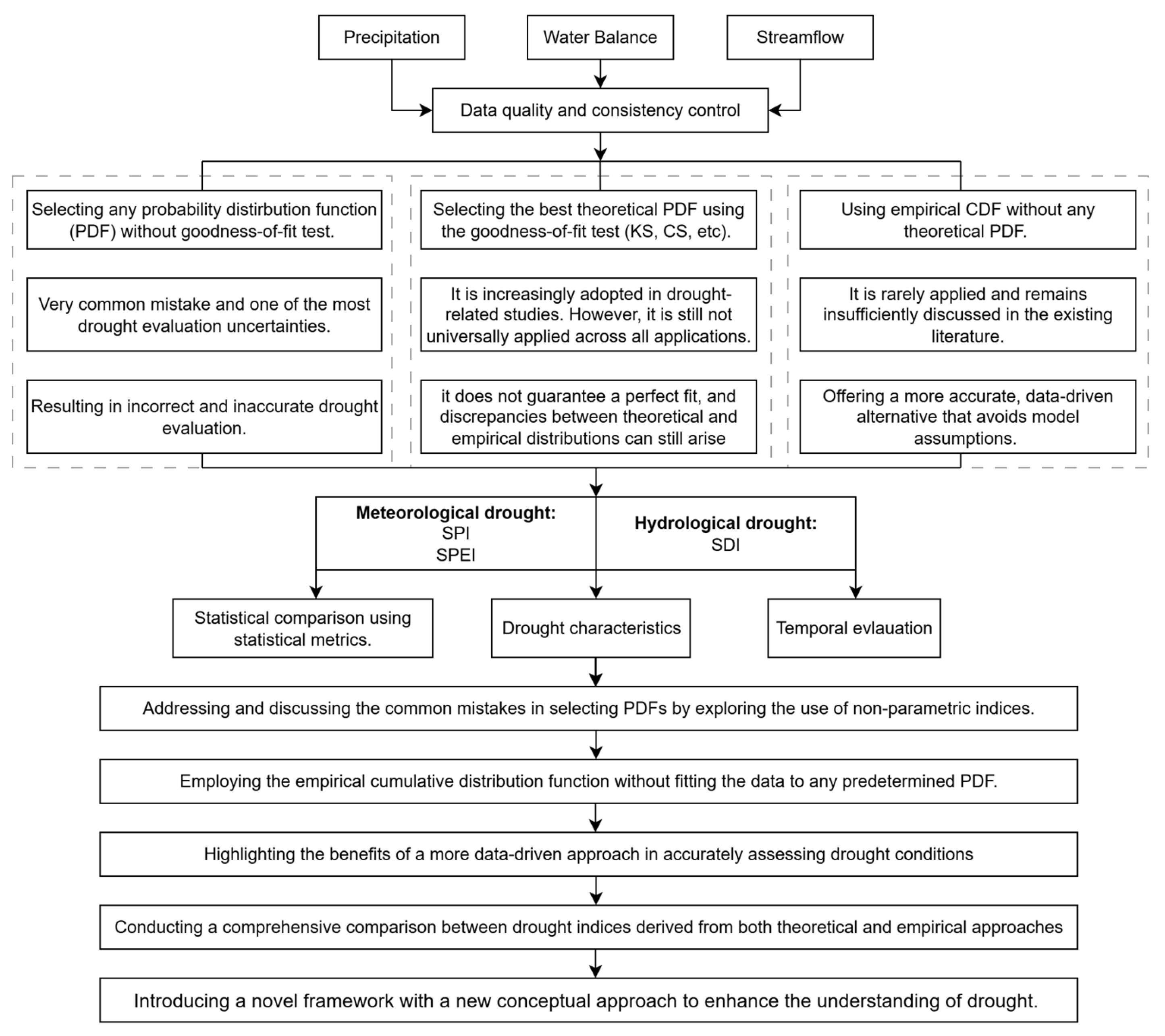
2. Methodology

The methodology section of this research is structured into four distinct sub-sections to address the calculation and comparison of DIs thoroughly. The first sub-section focuses on the DIs, covering meteorological and hydrological drought using SPI, SPEI, and SDI at various time scales. Additionally, these DIs are used to determine both dry and wet periods based on the DIs values. The second sub-section discusses the theoretical cumulative distribution functions (CDFs), which are recognized as the classical approach for DIs. The third sub-section covers the empirical CDF for DIs. Finally, the fourth sub-section presents a comprehensive comparison scheme, employing well-known statistical metrics and drought characteristics to compare the outputs derived from theoretical and empirical approaches. This structured framework ensures a holistic analysis of DIs, enhancing our understanding of their certainties, advantages, and disadvantages, as well as their implications and effectiveness.

2.1. Standardized Drought Indices (DIs)

2.1.1. Standardized Precipitation Index (SPI)

The SPI, introduced by McKee et al. [14], depends on the probability of precipitation over various time scales, including 1, 3, 6, and 12 months, and it is used for both drought and wet events. The initial step in computing the SPI involves selecting a PDF that best fits the original precipitation data for these time scales. In their seminal work, McKee et al. [14] chose the Gamma distribution for its appropriateness for their dataset. Subsequent research, such as that by Wang et al. [31], has confirmed the Gamma distribution as the most fitting PDF for SPI calculations across different studies. Selecting the right PDF requires using goodness-of-fit tests, like the Kolmogorov-Smirnov and Chi-Square tests, to validate the fit to the actual precipitation data [47]. The resulting probabilities from the various timescale monthly precipitation data are then transformed into a standardized normal distribution with a mean of zero and a standard deviation of one. The process of standardization, often confused between statistical and probabilistic approaches, was further explained and detailed by Şen and Şişman [25] to address existing gaps.

2.1.2. Standardized Precipitation Evapotranspiration Index (SPEI)

The SPEI, developed by Vicente-Serrano et al. [15], is based on both precipitation and potential evapotranspiration (PET) and operates across diverse time scales similar to the SPI. The main concept of the SPEI is similar to the SPI, but it modifies the approach by using the water balance, calculated as precipitation minus PET. The computation of SPEI begins with selecting a PDF that fits the water balance datasets. Unlike the SPI, which predominantly uses the Gamma distribution, the SPEI often involves the Log-Logistic distribution due to its ability to better model differences that may include negative values [15]. The selection of the appropriate PDF for SPEI calculations is critical and involves rigorous goodness-of-fit tests to ensure accuracy in fitting the water balance datasets [47,48]. While similar to SPI, the methodological approach to standardization in SPEI also considers the additional complexity introduced by PET, thereby addressing more comprehensive aspects of drought conditions.

2.1.3. Streamflow Drought Index (SDI)

The SDI was developed to assess hydrological droughts by considering streamflow data. Similar to the SPI and SPEI, the SDI operates across various time scales to provide a comprehensive view of drought impacts on streamflow. The main concept behind the SDI is to quantify deviations in streamflow from historical data, which are critical for managing water resources effectively [16]. The computation of the SDI starts with selecting a PDF that best fits the streamflow data. Unlike the SPI and the SPEI, the SDI frequently employs the Pearson Type III distribution [15]. This distribution is particularly selected for streamflow data due to its flexibility in modeling skewed data and its ability to handle zero values, which are common in streamflow records, especially in summer months [49]. Choosing the most suitable PDF for the SDI is a crucial step similar to other DIs calculations that requires conducting rigorous goodness-of-fit tests to validate the fit of the data [47]. This ensures that the computed SDI accurately reflects the actual behavior of stream flows. Once the appropriate PDF has been identified, the streamflow data are transformed into a standardized normal distribution.

Table 1. Drought classifications based on SPI theory [14].

Drought Index_DI	Drought Classification	Probability (%)
2.0 ≤ DI	Extreme wet (EW)	2.31%
1.5 ≤ DI < 2.0	Severe wet (SW)	4.42%
1.0 ≤ DI < 1.5	Moderate wet (MW)	9.22%
−1.0 ≤ DI < 1.0	Normal (N)	68.1%
−1.5 ≤ DI < −1.0	Moderate drought (MD)	9.22%
−2.0 ≤ DI < −1.5	Severe drought (SD)	4.42%
−2.0 > DI	Extreme drought (ED)	2.31%

summarizes the drought classification with the corresponding probabilities.

2.2. Theoretical Probability Distribution Function (PDFs)

Theoretical or parametric PDFs play a pivotal role in various fields of statistics, data analysis, and hydrology by providing a framework to describe the behavior of datasets through known mathematical functions. These distributions are defined by formulas that depend on certain parameters, hence the name ‘parametric’ [48,50]. Common examples include the Normal, Exponential, Gamma, General Extreme Value (GEV), Weibull, Generalized Pareto (GP), and Log-Normal distributions [51,52,53]. Each of these distributions has specific properties that make them suitable for modeling different data types based on characteristics such as skewness, kurtosis, and the presence of a lower bound [54].

In hydrology and drought analysis, theoretical PDFs are essential for transforming raw data into a format that can be universally understood and compared. This transformation helps standardize data for identifying anomalies and assessing their statistical significance [55]. Selecting an appropriate theoretical distribution requires understanding the data’s underlying behavior, which is typically validated using goodness-of-fit tests [48]. These tests assess how well the chosen distribution matches the empirical data, allowing researchers to ensure that their analyses are based on a solid statistical foundation [47]. Theoretically, PDFs are crucial in DIs such as the SPI, SPEI, and SDI. They allow for the standardized assessment of drought conditions across different timescales and geographical locations. By transforming diverse hydro-meteorological datasets into standardized indices, researchers and decision-makers can better compare drought severity, analyze drought trends, and implement effective water management and mitigation strategies.

This research used Normal, Gamma, Weibull, General Extreme Value (GEV), and Generalized Pareto (GP) distribution functions for DIs calculations. CDFs for these distributions are given in

Table 2. Probability Density Functions (PDFs) and their parameters.

Probability Distributions Type	Probability Density Function (PDF)	Parameters
Weibull	$f\left(x\right)={\displaystyle \frac{k}{\alpha }}{({\displaystyle \frac{x}{\alpha }})}^{k-1}exp\left[-{({\displaystyle \frac{x}{\alpha }})}^k\right]$	$k=shape parameter (k>0$) $\alpha =scale parameter (\alpha >0)$
Normal	$f\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}exp\left[-{\displaystyle \frac{1}{2}}{({\displaystyle \frac{x-\mu }{\sigma }})}^2\right]$	$\mu =mean \left(location parameter\right)$ $\sigma =standard deviation$ $\left(scale parameter\right) \sigma >0$
Gama	$f\left(x\right)={\displaystyle \frac{x^{k-1}}{{\alpha }^k\left(\Gamma \right)k}}exp\left[{\displaystyle \frac{-\left(x\right)}{\alpha }}\right]$	$k=shape parameter (k>0$) $\alpha =scale parameter (\alpha >0)$ $\Gamma =Gamma function$
General Extreme Value (GEV)	$f\left(x\right)=\left({\displaystyle \frac{1}{\sigma }}\right)e^{-(1+k{({\displaystyle \frac{x-\mu }{\sigma }})}^{-{\displaystyle \frac{1}{k}}}}(1+k{({\displaystyle \frac{x-\mu }{\sigma }})}^{-1-{\displaystyle \frac{1}{k}}}$	$\mu =Location parameter$ $\sigma =Scale parameter$ $k=shape parameter (k\ne 0$)
Generalized Pareto (GP)	$f\left(x\right)=\left({\displaystyle \frac{1}{\sigma }}\right)(1+k{({\displaystyle \frac{x-\theta }{\sigma }})}^{-1-{\displaystyle \frac{1}{k}}}$	$\theta =Threshold parameter$ $\sigma =Scale parameter$ $k=shape parameter (k\ne 0$)

. The Kolmogorov–Smirnov (KS) test determines the most appropriate distribution function. The KS test statistic is given below in Equation (1).

$$KS=mak\left|F{x}_i-F{x}_i^{\ast }\right|$$

(1)

Fx_i is the CDF value obtained according to the selected theoretical probability distribution function. Fx_i^* is the empirical CDF value.

2.3. Empirical Probability Distribution Function

The empirical (ECDF) is a fundamental tool in statistical analysis, offering a non-parametric approach to calculate a dataset’s CDF. Unlike theoretical or parametric distributions that assume a specific form and parameters for the distribution, the ECDF relies solely on the data to provide a stepwise approximation of the CDF. Several variations of the ECDF exist, each using different plotting positions to adjust how the empirical probabilities are calculated slightly, tailoring the ECDF for specific applications. Common types include the standard ECDF, Weibull Plotting Position, Gringorten Plotting Position, and others, summarized with their equations and references in

Table 3. Types of empirical cumulative distribution functions (ECDF) and their equations and references.

ECDF Type	Equation	Reference
Standard ECDF	$F\left(X_i\right)={\displaystyle \frac{i}{n}}$	Stedinger et al. [49]
Weibull Plotting Position ECDF	$\mathit{F}\left({\mathit{X}}_{\mathit{i}}\right)={\displaystyle \frac{\mathit{i}}{\mathit{n}+\mathbf{1}}}$	Cunnane [56]
Gringorten Plotting Position ECDF	$F\left(X_i\right)={\displaystyle \frac{i-0.44}{n+0.12}}$	Gringorten [40]
Hazen Plotting Position ECDF	$F\left(X_i\right)={\displaystyle \frac{i-0.5}{n}}$	Hazen [57]
Tukey Plotting Position ECDF	$F\left(X_i\right)={\displaystyle \frac{i-0.33}{n+0.33}}$	Tukey [58]
Blom Plotting Position ECDF	$F\left(X_i\right)={\displaystyle \frac{i-0.375}{n+0.25}}$	Blom [59]

n: the sample size, i: the rank data from the smallest, and F(Xi): the corresponding empirical probability.

.

Farahmand and AghaKouchak [39] extended the application of the ECDF in drought analysis by proposing the SDAT, which uses the non-parametric approach to develop generalized standardized drought indices. They employed the empirical Gringorten plotting position to calculate cumulative probabilities. However, for hydrological and drought studies, the Weibull Plotting Position ECDF is often preferred for several reasons. It offers a balanced approach to plotting positions, reducing bias and the probabilities of extreme events. The Weibull position is better at handling both lower and upper extremes in hydrological data, providing a more reliable fit for the entire range of data and especially improving the assessment of droughts and floods. Additionally, it adapts well to different sample sizes and data distributions, making it robust for various datasets commonly encountered in hydrological studies [49,56]. For these reasons, the Weibull position is used in this research to calculate the empirical Cumulative Distribution Functions (CDFs). Table 3 below summarizes the types of empirical CDFs with their equations and references.

2.4. Comparison Scheme

In this study, the comparison between drought indices calculated using theoretical/parametric CDFs and those derived from empirical CDFs is rigorously conducted using a set of statistical metrics. Here’s an overview of each metric and its significance in the analysis:

• R² measures the ratio of the variation in the dependent variable that may be forecasted from the independent variable(s). In the context of this study, it indicates how well the empirical or theoretical CDF-based drought indices explain the variance in the observed data. The ideal value of R² is 1, which would indicate a strong relationship.
• Pearson’s Correlation Coefficient (CC) assesses the linear relationship between two datasets. This research measures the degree of linear correlation between drought indices derived from theoretical and empirical CDFs. A CC of +1 indicates a strong positive linear relationship, 0 indicates no linear correlation, and −1 indicates a strong negative linear relationship.
• Mean Squared Error (MSE) measures the average of the squares of the errors, specifically the average squared deviation between the theoretical and empirical CDF values. A lower MSE indicates a better fit, showing that the data points are closer to the fitted line. The ideal value of MSE is 0.
• Root Mean Squared Error (RMSE) is the square root of the mean of the squared errors and provides a measure of the magnitude of the error. Like MSE, it measures how close empirical CDF values are to the model’s values. RMSE is particularly useful because it gives a relatively high weight to large errors. The ideal RMSE value is 0, indicating no error.
• Mean Absolute Error (MAE) is the average of the absolute differences between theoretical and empirical CDF values. Unlike MSE or RMSE, MAE provides a linear error scale, allowing for an easier interpretation. A MAE of 0 indicates no error.
• Mean Bias Error (MBE) measures the average bias in the model predictions, the average difference between the theoretical and empirical CDF values. A positive MBE indicates a model’s tendency to overpredict, whereas a negative MBE indicates underprediction. The ideal MBE value is 0, which signifies no bias.

This research aims to explain and discuss the differences between DIs based on theoretical and empirical CDFs, providing a comprehensive understanding of their accuracy, reliability, and potential biases in drought assessment and evaluation.

Table 4. Statistical metrics used for comparing DIs.

Statistic Metric	Equation	Value Range	Ideal Value
Correlation Coefficient (CC)	$CC={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left(E_i-\overline{E}\right)\left(T_i-\overline{T}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(E_i-\overline{E}\right)}^2} \sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(T_i-\overline{T}\right)}^2}}}$	(−1)–(1)	1
Coefficient of determination (R2)	$R^2={\left[{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left(E_i-\overline{E}\right)\left(T_i-\overline{T}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(E_i-\overline{E}\right)}^2} \sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(T_i-\overline{T}\right)}^2}}}\right]}^2$	(0)–(1)	1
Mean Square Error (MSE)	$MSE={\displaystyle \frac{1}{n}} {{\displaystyle \sum }}_{i=1}^n{\left(E_i-T_i\right)}^2$	(0)–(∞)	0
Root Mean Square Error (RMSE)	$RMSE=\sqrt{{\displaystyle \frac{1}{n}} {{\displaystyle \sum }}_{i=1}^n{\left(E_i-T_i\right)}^2}$	(0)–(∞)	0
Mean Absolute Error (MAE)	$MAE={\displaystyle \frac{1}{n}} {{\displaystyle \sum }}_{i=1}^n\left|E_i-T_i\right|$	(0)–(∞)	0
Mean Bias Error (MBE)	$MBE={\displaystyle \frac{1}{n}} {{\displaystyle \sum }}_{i=1}^n\left(E_i-T_i\right)$	(−∞)–(∞)	0

E = DI value based on empirical CDF, T = DI value based on theoretical CDF, n = number of months/samples, $\overline{E}$ = mean DI value based on empirical CDF, $\overline{T}$ = mean DI value based on theoretical CDF.

below summarizes the statistical metrics, equations, and ideal values. Figure 1 below shows the methodological approach of this research.

3. Application

This research selected stations from diverse climates and spanning different periods for analysis to ensure a broad and comprehensive application. These varying locations and historical records provide a robust framework for evaluating the effectiveness of the drought indices under different climatic conditions. The first station, Karapınar in Konya, is located in the heartland of Türkiye and is known for being the country’s largest city by land area. This district experiences a semi-arid climate, with an average annual precipitation of about 298 mm. Due to the combination of low rainfall and high temperatures during the summer, Konya faces significant hydrological and environmental challenges, ranking it among the driest cities in Türkiye. The monthly precipitation (P) data from 1964 to 2022 (58 years) were obtained from the Turkish State Meteorological Service (TSMS). The Karapınar station data were utilized for calculating the SPI in this study.

Secondly, Durham, situated northeast of the UK, features a temperate maritime climate that blends mild summers and cool winters. This hybrid climate results in an average annual precipitation of 652.50 mm. The Durham University meteorological station provided the monthly precipitation (P) and temperature data from 1868 to 2021, covering 154 years [60]. The precipitation and temperature data from the Durham station were employed to calculate the SPEI. The third application involves the Lüleburgaz station in Türkiye, located on the Ergene River, where monthly streamflow records span from 1957 to 2015 (59 years). These data were used to calculate the hydrological drought using SDI, with an average annual streamflow of 114.84 m³/s. 

Table 5. Climatic characteristics of the annual total precipitation, average temperature, and monthly streamflow of the stations used in this study.

Station	Latitude	Longitude	Variable	Average	Standard Deviation	Time Period
Karapınar station	37.71 (N)	33.52 (E)	Annual precipitation (mm)	297.5	21.57	1964–2022
Durham station	54.77 (N)	1.59 (W)	Annual precipitation (mm)	652.5	31.74	1868–2021
			Monthly Temperature (°C)	8.59	4.46	1868–2021
Lüleburgaz station	41.35 (N)	27.35 (E)	Annual streamflow (m3/s)	114.84	13.2	1957–2015

summarizes each station’s name, latitude, longitude, annual precipitation, annual temperature, and annual streamflow, along with the standard deviation and the relevant time periods for all utilized stations. All data have been thoroughly processed and checked for consistency and continuity to ensure accuracy.

4. Results

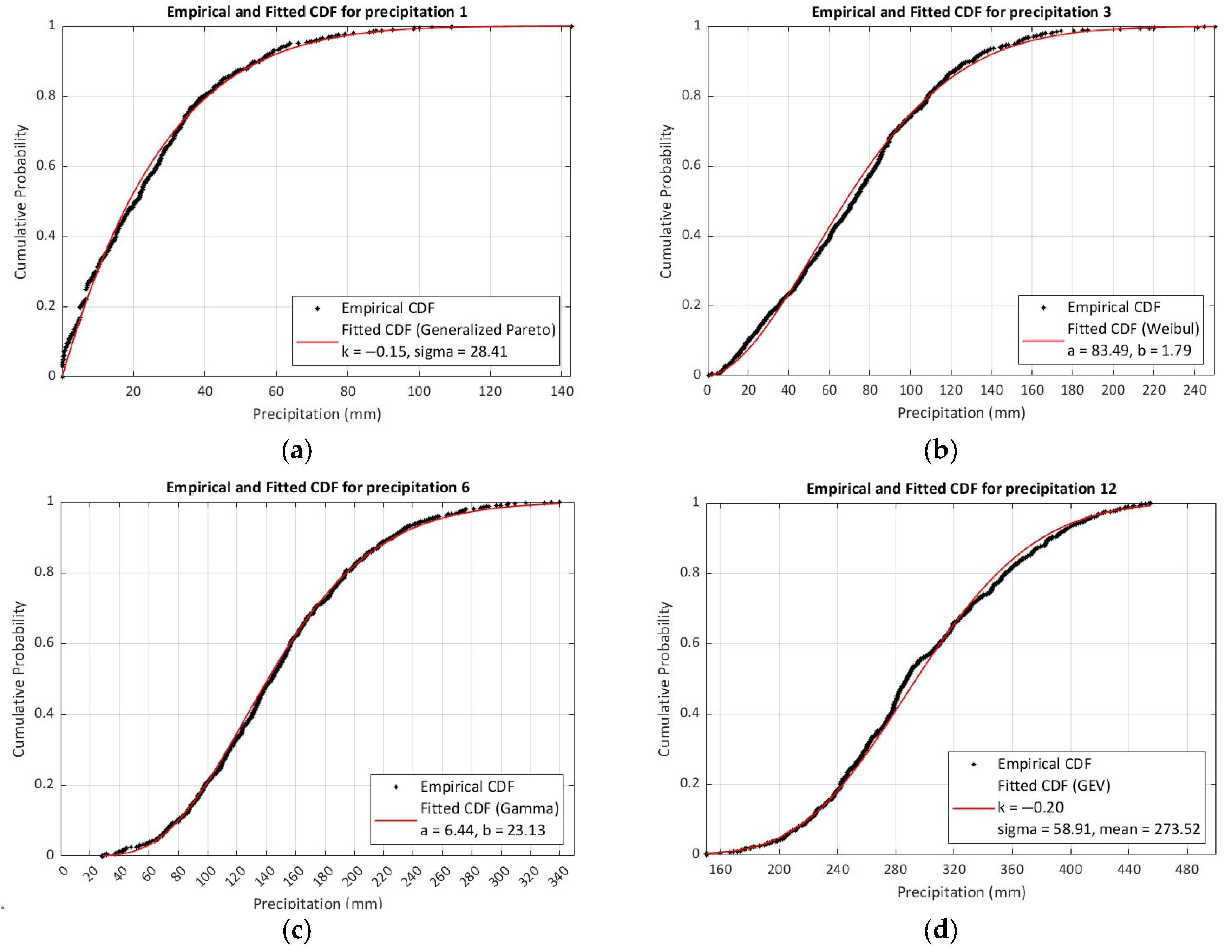
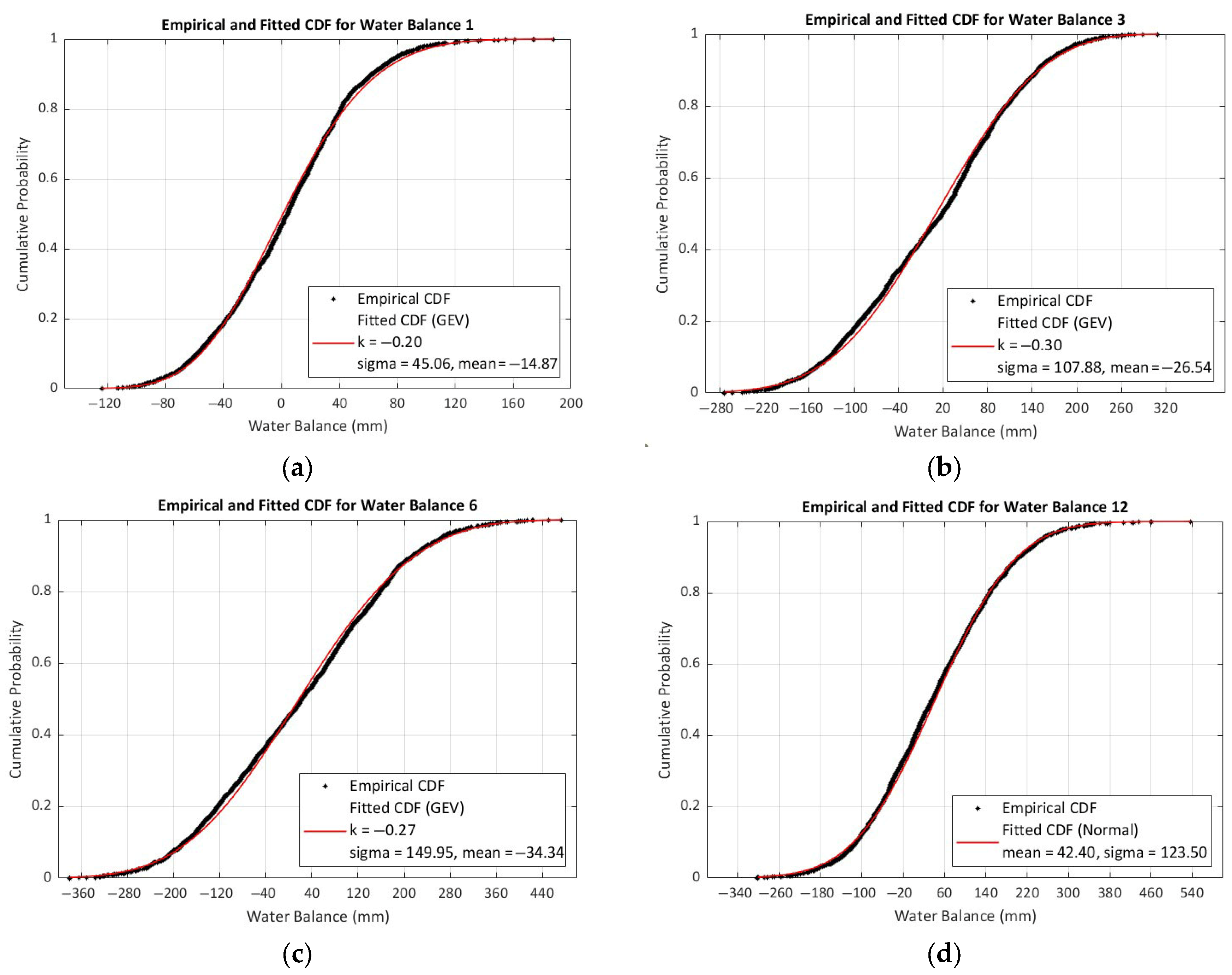
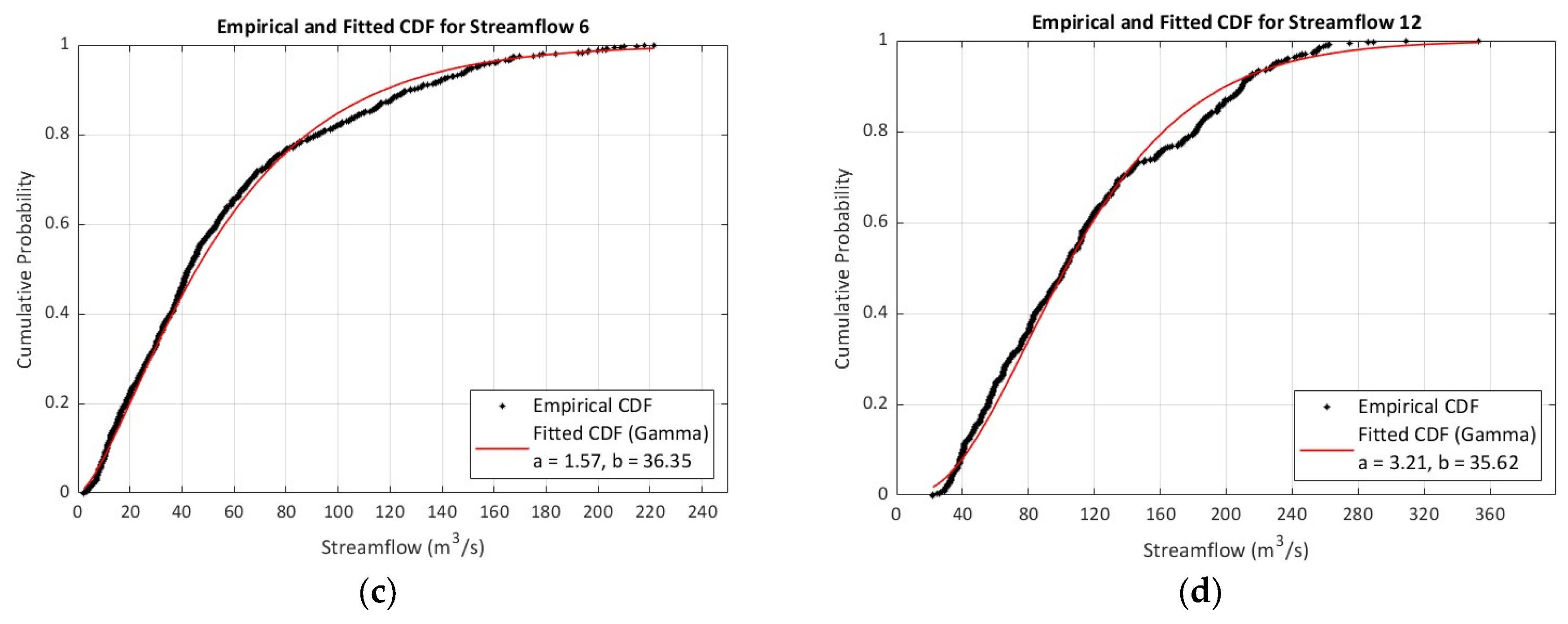
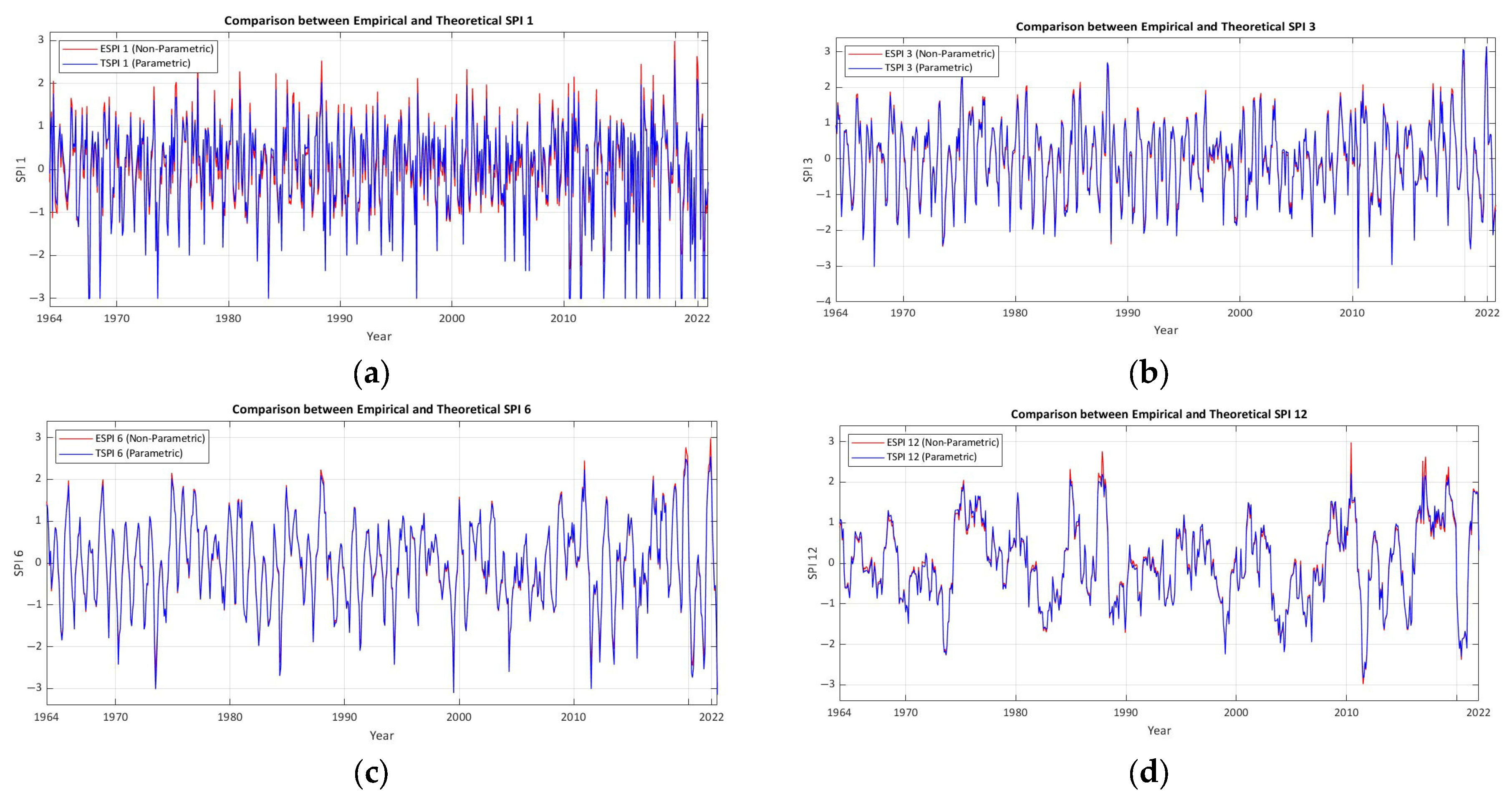
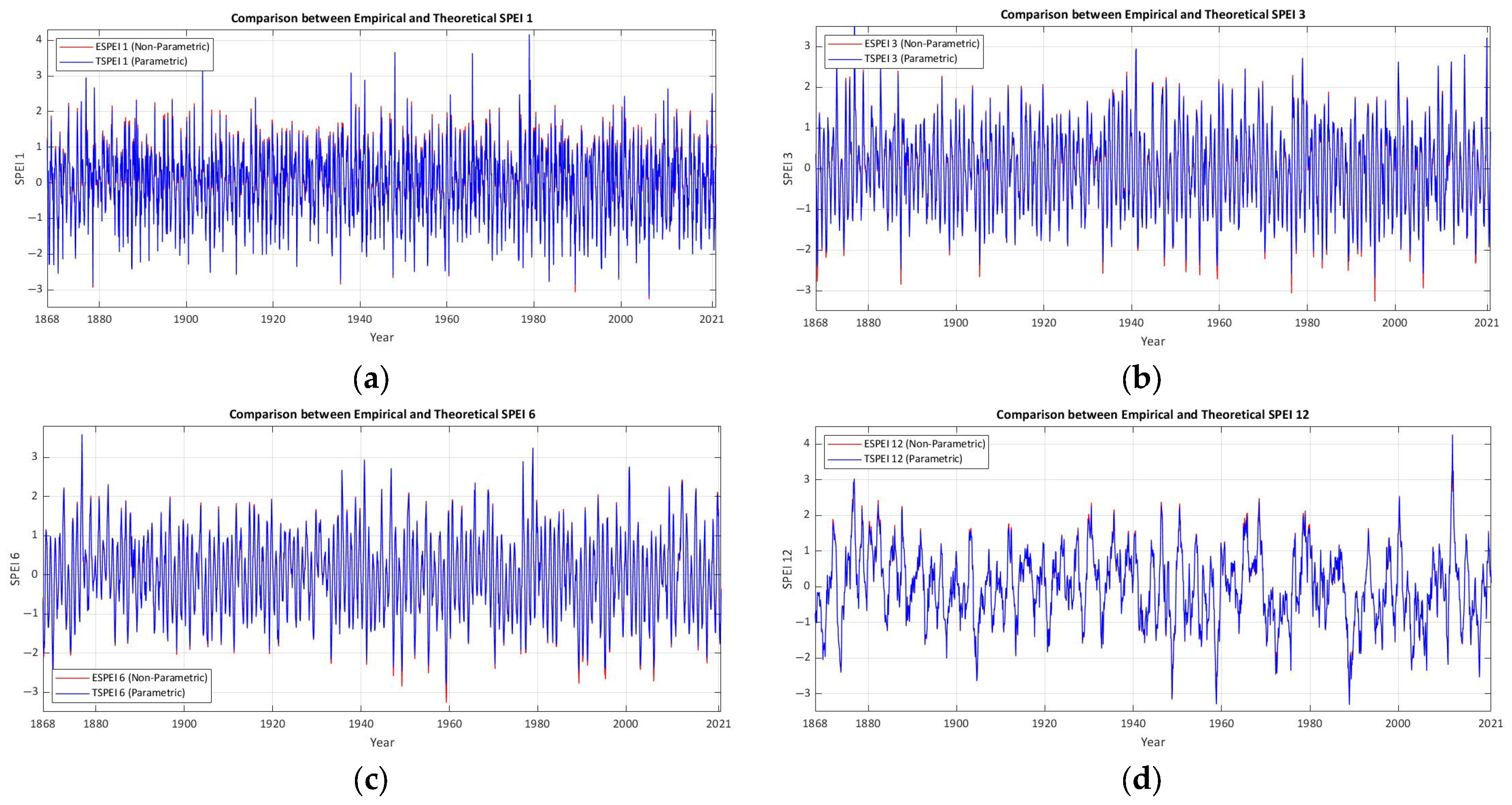
4.1. Empirical and Theoretical Cumulative Distribution Functions

The appropriate CDF for precipitation data at Karapınar station in Türkiye between 1964 and 2022 varies across different timescales. For the 1, 3, 6, and 12-month scales, the chosen theoretical CDFs are Generalized Pareto, Weibull, Gamma, and Generalized Extreme Value (GEV), respectively (Figure 2a). The empirical and fitted cumulative distribution functions for precipitation data on a monthly scale exhibit a strong correspondence, employing a Generalized Pareto distribution. The juxtaposition of the empirical data points and the fitted curve demonstrates that the Generalized Pareto distribution offers an adequate fit for short-term precipitation variability. However, in the empirical CDF representations, there are notable gaps or discontinuities, particularly noticeable in the precipitation ranges between 8 and 12 mm and beyond 80 mm, where the data points fail to form a continuous line. Additionally, a discrepancy between the empirical and theoretical CDFs is evident in the 15–38 mm precipitation range, as illustrated in Figure 2a. This variation highlights areas where the empirical CDF diverges substantially from the fitted theoretical CDF. The Weibull distribution was employed throughout a three-month period. This distribution accurately reflects the empirical cumulative distribution function, illustrating its suitability for modeling cumulative precipitation probability over a quarterly timeframe. For the 3-month precipitation data, a notable difference between the theoretical and empirical CDFs is observed, particularly between 55 and 85 mm (Figure 2b). This discrepancy highlights the potential limitations of the theoretical model in accurately representing the empirical data within this range.

For the 6-month timescale, the Gamma distribution was selected. The close alignment between the empirical CDF and the fitted Gamma CDF underscores its effectiveness in modeling medium-term precipitation patterns and their impacts on drought assessment. The primary difference between the theoretical and empirical CDFs occurs within the 40 to 60-mm precipitation range, often corresponding to extreme and severe drought classifications (Figure 2c). This gap suggests a need for careful consideration of how theoretical assumptions influence the main results and the potential implications for drought assessment. On an annual scale, the Generalized Extreme Value (GEV) distribution was employed. The fit is notably robust, emphasizing the GEV distribution’s ability to manage extremes and variability in yearly precipitation data. In a general assessment of the 12-month timescale precipitation, noticeable differences are observed between the theoretical and empirical CDFs. Specifically, this difference appears after 280 mm (corresponding to a cumulative probability of 0.4), as shown in Figure 2d, which is not typically associated with drought conditions according to SPI classifications. However, despite careful selection of the most suitable theoretical CDF, there remains a notable difference between the theoretical and empirical CDFs, underscoring potential limitations in the theoretical approach when applied to drought analysis.

The examination of the empirical and fitted cumulative distribution functions for water balance data at Durham station from 1868 to 2021, over several time scales, similarly underscores the disparities between actual observations and theoretical predictions. For the 1-month scale, the GEV distribution provides a good alignment with the empirical data, as depicted in Figure 3a. Despite the close match, minor deviations are evident, especially in ranges where the data lead to gaps in the empirical CDF curve, notably below −80 mm and beyond 120 mm. These disparities, while small, underscore the limitations of the theoretical CDF in capturing the extreme lower-tail behaviors in monthly water balance data. Moving to the 3-month water balance data, the GEV distribution again serves as the chosen theoretical CDF, reflecting its robustness in modeling quarterly variations (Figure 3b). However, the difference becomes more pronounced between −120 mm and 50 mm. Additionally, at a water balance of less than −250 mm, there is a difference between the empirical and theoretical CDFs. For the 6-month water balance, the GEV distribution continues to illustrate a good fit, effectively representing the cumulative probabilities across a semi-annual period (Figure 3c). The major discrepancies between −160 mm and 160 mm indicate the theoretical model’s potential overestimation and underestimation of extreme values. On an annual scale, the Normal distribution is utilized to model the water balance data (Figure 3d). This choice reflects a strong fit, the best fit in water balance data.

The streamflow data at Lüleburgaz station in Türkiye, analyzed through the application of both empirical and theoretical CDFs at various time scales, exhibit varying levels of fit and disparity. The results for the streamflow data, displayed across 1, 3, 6, and 12-month scales, show the selection of different theoretical CDFs to best match the empirical CDFs. For the 1-month streamflow, the GEV distribution was applied, showing a strong correspondence with the empirical data, except for streamflow data exceeding 30 m³/s (corresponding to a cumulative probability of 0.9) (Figure 4a). The accuracy of the theoretical cumulative distribution function for arid events is elevated. The Weibull distribution was used for the three-month time frame. The correspondence between the Weibull model and the empirical cumulative distribution function is satisfactory, particularly up to 20 m³/s (corresponding to a cumulative probability of 0.5) for dry events within the SPI definition. However, for streamflow data exceeding 20 m³/s, there is a noticeable difference between the theoretical and empirical CDFs (Figure 4b).

The 6-month data utilized the Gamma distribution, chosen for its flexibility in fitting diverse data shapes. The empirical and Gamma CDFs exhibit a near-perfect match throughout dry events, but significant discrepancies exist between 40 m³/s and 150 m³/s (Figure 4c). These differences point to the theoretical distribution’s inadequacy in modeling extreme events within the semi-annual streamflow records, indicating the need for empirical CDFs. In the analysis of the 12-month timescale, the selection of the best theoretical CDF showed significant discrepancies when compared to the empirical CDF, particularly for dry events significantly at streamflow levels ≤ 30 m³/s, indicative of extreme and severe drought conditions. The theoretical cumulative distribution function significantly underestimated the drought index values. This underestimation was evident in the range up to 90 m³/s, where differences between the theoretical and empirical CDFs persisted, although less pronounced than in the extremely dry range. The most substantial discrepancy was observed in the interval between 150 m³/s and 210 m³/s, as illustrated in Figure 4d. These observations underscore that the empirical CDF provides a more conservative and accurate approach to calculating drought indices.

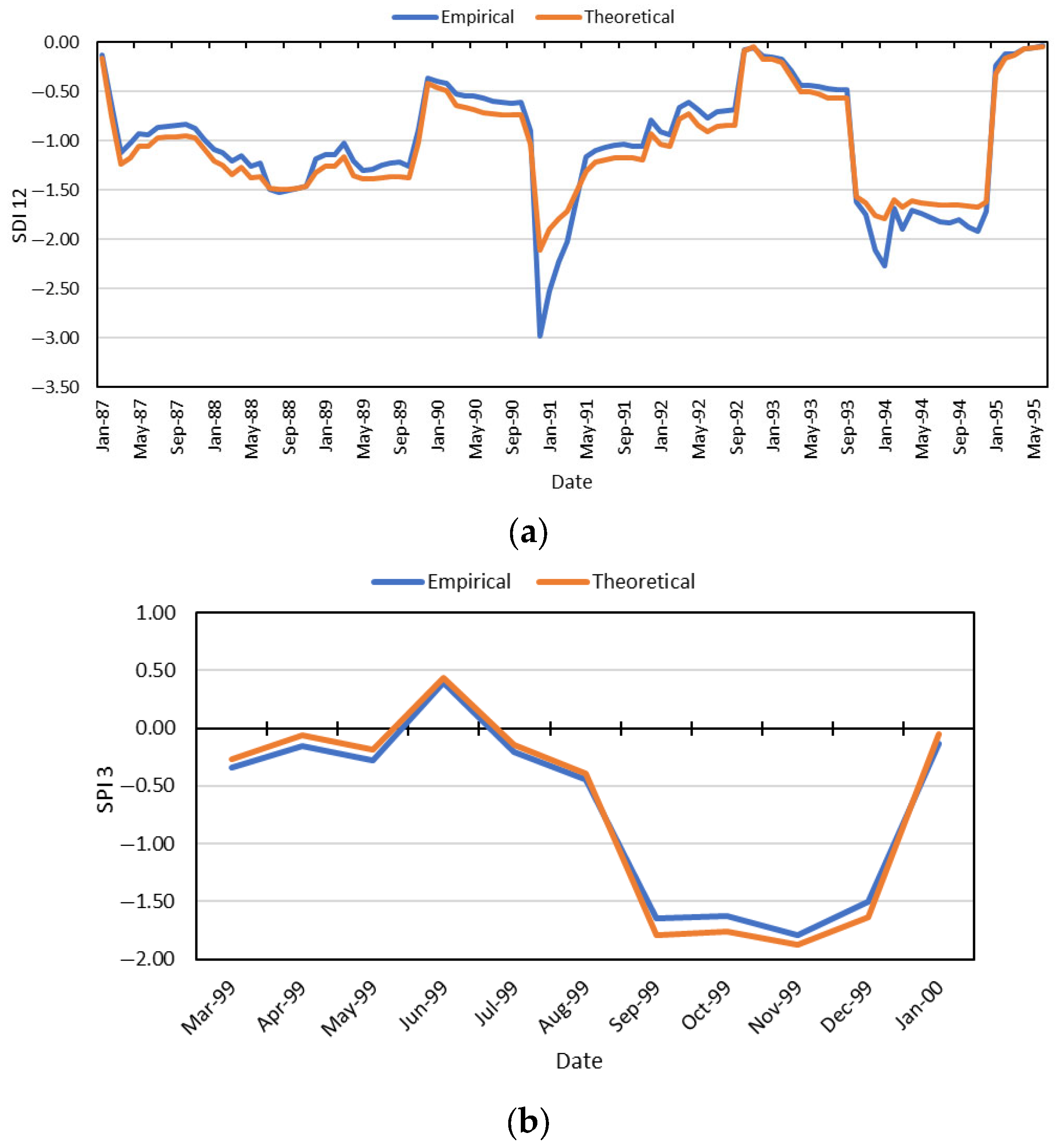
4.2. Temporal Evaluation of Empirical and Theoretical CDFs

The temporal evaluation of the SPI across different timescales (1, 3, 6, and 12 months) highlights quite significant differences between empirical (E) and theoretical (T) calculations. For SPI 1, in general, the theoretical and empirical CDFs exhibit remarkably similar drought index values across various timescales (Figure 5a). However, the empirical CDFs tend to record more extreme values, particularly noticeable in the long-term analyses, such as the 12-month timescale (Figure 5d). When comparing shorter durations like SPI 3 and SPI 6 (Figure 5b,c), the discrepancies between the theoretical and empirical data are less pronounced than those observed in SPI 1. The fundamental distinctions become increasingly apparent over extended durations, wherein empirical evidence can document more severe drought situations. For instance, in the 12-month SPI, the empirical CDFs have recorded extreme drought index values reaching as low as −3, highlighting its sensitivity in detecting significant drought events that the theoretical models might understate.

At Durham station, with a record extending over 150 years, the SPEI calculated for a 1-month scale shows minimal variation between the empirical and theoretical CDFs, suggesting a strong alignment in short-term drought assessment (Figure 6a). However, the situation changes with longer timescales: SPEI 3 and SPEI 6, as evidenced by empirical CDFs, indicate more extreme values (illustrated in red in Figure 6b,c). This divergence underscores the empirical CDF’s superior capability to adapt and respond to the diverse conditions specific to the study area, capturing more severe drought scenarios effectively. Conversely, for SPEI 12, the comparison reveals no significant differences between the empirical and theoretical CDFs, indicating that both CDFs converge well in reflecting long-term drought conditions at this station (Figure 6d). The maximum drought index for SPEI 12 is −3.0.

For the streamflow-related SDI at various timescales, significant discrepancies exist between the empirical and theoretical CDFs. Across all examined time scales, empirical CDFs consistently show more severe drought indices (Figure 7). Notably, at the SDI12 timescale, the empirical CDF records a drought index of −3.0, while the theoretical CDF only reaches −2.0, representing a substantial 50% difference in the severity of drought conditions (Figure 7d). This pattern also exists across other timescales, where the empirical CDF generally shows drought indices values approximately 25% higher than those calculated by the theoretical CDF (Figure 7a–c). This consistent difference highlights the empirical CDF’s enhanced sensitivity and accuracy in capturing the extremities of drought conditions across various time scales.

4.3. Statistical Metrics Results

Analyzing statistical metrics comparing empirical and theoretical CDFs across various drought indices and time scales reveals significant insights.

Table 6. Statistical metrics for comparing empirical and theoretical CDFs of DIs (SPI, SPEI, SDI) across different time scales.

SPI	R2	CC	MSE	RMSE	MAE	MBE	KS Test p-value	PDF
1-month	0.932	0.984	0.067	0.260	0.122	0.069	0.312	GP
3-month	0.992	0.997	0.008	0.087	0.071	0.003	0.538	Weibull
6-month	0.995	0.997	0.005	0.072	0.042	−0.001	0.935	Gamma
12-month	0.994	0.997	0.006	0.077	0.054	0.000	0.487	GEV
SPEI	R2	CC	MSE	RMSE	MAE	MBE	KS Test p-value	PDF
1-month	0.996	0.998	0.004	0.066	0.052	0.003	0.359	GEV
3-month	0.996	0.998	0.004	0.065	0.051	−0.002	0.148	GEV
6-month	0.996	0.998	0.004	0.060	0.051	−0.002	0.426	GEV
12-month	0.998	0.999	0.002	0.043	0.023	0.001	0.999	Normal
SDI	R2	CC	MSE	RMSE	MAE	MBE	KS Test p-value	PDF
1-month	0.984	0.992	0.015	0.124	0.081	−0.001	0.125	GEV
3-month	0.992	0.996	0.008	0.090	0.064	−0.003	0.343	Weibull
6-month	0.990	0.995	0.010	0.101	0.077	0.004	0.535	Gamma
12-month	0.979	0.990	0.021	0.143	0.100	0.001	0.105	Gamma

below summarizes the statistical metrics results for all drought indices and time scales used in this research. For SPI, results show high R² and correlation coefficients (CC), indicating strong agreement between the empirical and theoretical distributions across all considered time scales, with the best fit being Gamma for 6-month and Weibull for 3-month durations. The Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) values are minimal, further substantiating the closeness of these distributions. However, the KS test p-values suggest varying degrees of fit across different time scales. The SPI-1 exhibits an R² of 0.932 and a CC of 0.984, with an MSE of 0.067 and an RMSE of 0.260.

Similarly, for SPEI and SDI, the statistical metrics consistently exhibit strong correlations and high R² values, with the R² for the 12-month time scale reaching as high as 0.998 and the CC at 0.999, with the Normal distribution showing a strong relationship. The SPEI generally demonstrates lower RMSE and MAE values than the SPI, suggesting a more precise fit for the theoretical models, particularly the GEV model for shorter time scales. The SDI metrics, especially for the 12-month duration, showed some variability yet maintained high conformity between empirical and theoretical CDFs, with 6-month and 12-month scales showing slight deviations in MBE, indicating minor biases in the model fits. These results underline the effectiveness of selected parametric distributions in capturing the behavior of drought-related data and emphasize the nuanced differences between various indices and time scales in drought characterization.

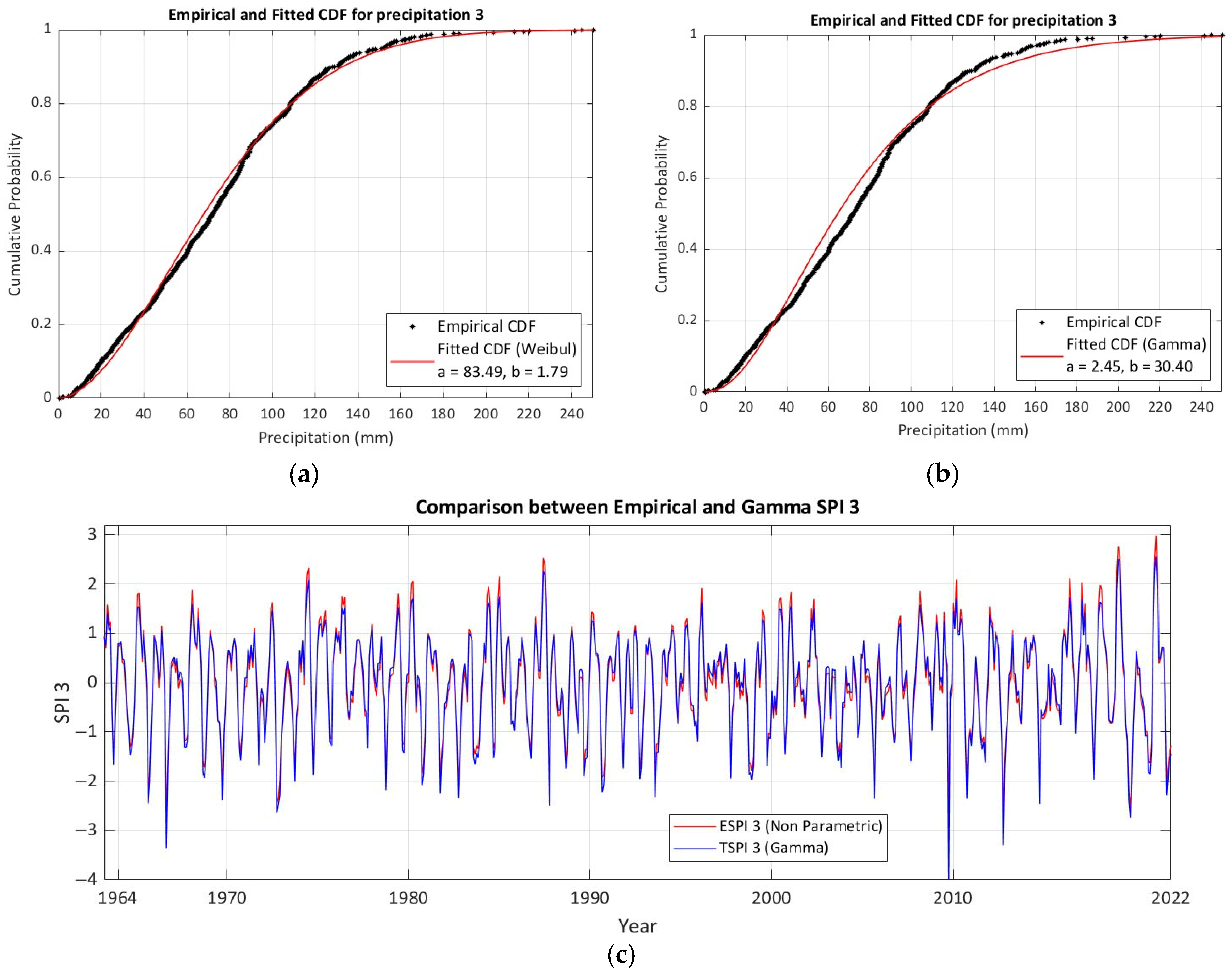
4.4. Evaluating Theoretical CDFs: An Example for SPI-3

In evaluating theoretical CDFs for the SPI-3, it is commonly observed that the Gamma function is used for SPI calculation without verifying its suitability using goodness-of-fit tests. However, when we used similar tests in this study, we discovered that the Weibull function fits SPI-3 better than the Gamma function. As illustrated in Figure 8a, the Empirical CDF and the fitted CDF using the Weibull function show a much closer alignment compared to the fitted CDF using the Gamma function (Figure 8b). Specifically, between 40 mm and 90 mm of precipitation, the Gamma function significantly underestimates the drought index values, resulting in wetter values. This discrepancy highlights the importance of selecting the correct theoretical CDF for DIs’ calculations or relying on empirical CDFs, which can be simpler and more accurate.

Figure 8c compares the SPI 3 using empirical and Gamma functions for Karapinar Station from 1964 to 2022. The first method uses an empirical/non-parametric approach, represented in red, while the second method uses a Gamma distribution, represented in blue. Figure 8c shows that both methods have followed similar temporal behavior over the past six decades, except for the very dry and wet periods, and in representing the SPI’s peaks (maximum and minimum values). These general similarities and differences in peak values reflect the need to consider empirical methods instead of using any CDF to check its suitability. Additionally, subtle differences can be observed between the two approaches, especially at extreme peaks, where the empirical method sometimes tends to give higher or lower maximum values than the Gamma method. This suggests that the empirical method may be more responsive to sudden or extreme changes in data, which could be useful in some early drought monitoring applications.

Table 7. Statistical metrics for comparing empirical and theoretical CDFs of SPI across the Karapinar station.

	R2	CC	MSE	RMSE	MAE	MBE
Empirical vs. Weibull	0.992	0.997	0.008	0.087	0.071	0.003
Gamma vs. Weibull	0.992	0.996	0.008	0.091	0.067	0.010
Empirical vs. Gamma	0.977	0.989	0.023	0.152	0.127	−0.007

summarizes a set of statistical indices used to compare the empirical and theoretical CDF of the SPI 3 at Karapinar Station, using the Weibull (best-fitted CDF) and Gamma (most commonly used) distributions as theoretical models. The high R² values (0.992 for both Empirical vs. Weibull and Gamma vs. Weibull) indicate a strong fit, while the slightly lower R² values (0.977) for Empirical vs. Gamma support this finding. In terms of error indices such as MSE and RMSE, the lowest values were always in favor of the Weibull (0.008 and 0.087, respectively), while the Gamma distribution increased significantly, especially when compared to the Empirical distribution (0.023 and 0.152). The MAE value also increased from 0.067 to 0.127, indicating a significant increase in error when using the Gamma distribution.

4.5. Drought Characteristics

Figure 9a shows a specific drought event for the Lüleburgaz station, which shows the evolution of the SDI 12 from January 1987 to May 1995, with a detailed analysis of the consequences of this significant drought event. This Figure compares experimental values calculated directly from monthly streamflow data with theoretical values derived from a best-fitting CDF. The intersection and convergence of the ESDI 12 and TSDI 12 reflect the similarity between the experimental and theoretical behaviors. Drought characteristics were calculated based on Run theory [61]. A clear convergence in the identification of dry periods, especially during the peak years between 1990 and 1995, was noticed, when the SDI decreased significantly in both series, indicating a prolonged and highly impactful drought in the region. Regarding the drought characteristics extracted from this temporal evaluation, it was found that the total drought duration was relatively long, reaching about 8.5 years for both empirical and theoretical approaches. This demonstrates the agreement between the two methods in monitoring the onset and end of the drought. This agreement is an important indicator of the effectiveness of the theoretical method adopted. Drought severity was also calculated by summing the negative values of the SDI during the drought period. The empirical approach was −103.64 and the theoretical approach −106.44, demonstrating a close convergence between the two methods, with the difference between them not exceeding 2.8 standard deviations. Additionally, drought intensity was calculated at −1.026 using the empirical approach and −1.054 for the theoretical approach. In terms of the general shape of the two curves, it is noted that the experimental values are characterized by sharp fluctuations in some periods, especially during the beginning or end of drought. This natural feature results from direct changes in monthly data without any statistical processing. The theoretical approach, on the other hand, reflects the behavior of a complex probability distribution. It is worth noting that this type of dual analysis (empirical vs. theoretical) is an important tool in verifying the quality of the statistical models used to estimate DIs. It also helps understand potential differences between actual behavior and theoretical representations.

On the other hand, Figure 9b shows the evolution of the SPI 3 for the Karapinar station for a specific drought event from March 1999 to January 2000 using both empirical and theoretical approaches. The figure shows an agreement between the two approaches in determining the drought characteristics with a little difference. The drought began in mid-1999 and continued until the end of December of the same year, before improving in January 2000. The drought duration in both approaches was 11 months, indicating the accuracy of the theoretical model in representing the onset and end of the drought event. The drought severity was also very close between the two approaches, with the empirical being −7.72 and the theoretical being −7.71. In terms of drought intensity, a uniform value of −0.70 was recorded. In summary, there was a slight difference between them, but the general performance is the same.

These results reinforce the importance of using the most appropriate probability distribution when calculating the DIs or using the empirical approach without any complex calculations, as it not only provides theoretical values that are close to the empirical ones, but also helps clarify some of the dynamic characteristics of drought more consistently and objectively. The convergence of results in terms of severity, duration, and intensity reflects the effectiveness of this approach in predicting drought characteristics, making it an effective tool in water resource management studies, especially in light of increasing climate change, which is impacting water availability. Therefore, it can be recommended that an empirical approach be used at other monitoring stations, with similar analyses being conducted, to build a knowledge base that will help decision-makers better plan to address the impacts of drought on various vital sectors, such as agriculture, energy, and human consumption.

5. Discussion

5.1. Importance of the Selected Theoretical Function

As highlighted in the introduction, the improper use of DIs such as SPI, SPEI, and SDI underscores the critical importance of these indices as the initial step in drought evaluation and assessment. The accurate computation of DIs is crucial due to their pivotal role in informing drought management and mitigation strategies. Despite this, several articles published after 2021 [33,36] have adopted the theoretical CDF without verifying its appropriateness or suitability for the original data. Furthermore, according to Laimighofer and Laaha [26], the choice of distribution is the second most important source of uncertainty. Consequently, this research addresses these concerns by comparing the theoretical and empirical CDFs. Stagge et al. [42] conducted goodness-of-fit evaluations for SPI and SPEI across Europe and concluded that the Gamma distribution is most suitable for SPI, while the Generalized Extreme Value (GEV) distribution performs best for SPEI. Similarly, Raziei [43] examined various distribution functions for SPI in Iran and found that the Gamma distribution is well-suited for longer time scales (6–12 months), consistent with the original SPI formulation by McKee et al. [14]. In contrast, the Pearson Type III and GEV distributions provided more accurate results at shorter time scales. Additionally, Şen and Şişman [25] examined the importance of selecting the best-suited CDF. This research and the difference between results obtained using empirical, best-fitted theoretical, and Gamma functions align with the existing literature. However, many articles use the Gamma function as the first option without checking its suitability, raising a need to provide more practical and easier solutions [46].

5.2. Comparison with the Existing Empirical Approaches

As Farahmand and AghaKouchak [39] proposed, utilizing the empirical CDF over the parametric approach is a powerful tool for calculating DIs, with their study employing the Gringorten positioning plot. In contrast, this current study adopts the well-known Weibull position plot for empirical CDF calculations, a method recommended by Cunnane [56] and Stedinger et al. [49], which is particularly effective for hydrological studies. This choice underscores the empirical CDF’s superiority in capturing the complexities and extremities of hydrological data. Both this research and Farahmand and AghaKouchak [39] corroborate the benefits of using non-parametric empirical CDFs for DIs, demonstrating their more conservative approach in evaluating drought severity and frequency of dry events, as illustrated in Figure 7. This methodology ensures a more accurate and sensitive assessment of drought conditions, essential for effective water resource management.

Considering other related research, Soláková et al. [44] and Mallenahalli [45] concluded that the empirical method often assesses drought and wetness conditions better, particularly when addressing non-normal data distributions. Vangelis and Kourtis [46] recently validated these findings in Greece by exclusively employing only the Gamma function for the SPI, neglecting alternative functions. They noted that, while non-parametric methods may simplify SPI calculations, they could underestimate drought severity in extreme cases, reinforcing the relevance of parametric approaches in certain climates.

5.3. Comparison Between Empirical and Theoretical Approaches

In the context of analyzing dry events, the theoretical CDF approach uses the whole original dataset, encompassing both minimum and maximum values. However, this method permits discrepancies in certain segments of the fitted curve, often noticeable within the drier events of the curve (at a probability less than 0.5). In contrast, the empirical CDF method accurately treats each data point according to its order or ranking, assigning an exact probability to each value. These significant differences between the theoretical and empirical approaches underscore the superiority of the empirical CDF. By accurately reflecting the distribution of each data point, the empirical CDF ensures a more precise analysis of drought conditions, making it a preferable choice for detailed and context-specific drought assessments. This advantage is critical for effective drought management and policymaking, where precision in early-stage evaluation can significantly influence outcomes.

While the macro-scale assessment of these statistical metrics, summarized in Table 6 and Table 7, suggests a strong alignment between theoretical and empirical CDFs, this apparent agreement largely stems from carefully selecting and validating theoretical CDFs using the Kolmogorov-Smirnov (KS) test. This alignment is observed at a macro scale; however, a detailed examination of each CDF for individual indices and time scales reveals more pronounced discrepancies. Additionally, these differences become noticeable compared to the most commonly used function for each DI (Table 7 and Figure 8). Therefore, based on these findings, employing empirical CDFs could be considered a more conservative approach, potentially minimizing errors arising from assumptions inherent in theoretical models and not selecting the best model. This method could provide a more robust framework for understanding and assessing drought conditions, ensuring more accurate and reliable assessment and evaluation. This research demonstrated that the empirical approach offers advantages, such as simplicity, reliability, and ease of implementation. Moreover, it effectively minimizes error and bias compared to parametric methods, making it a robust choice for drought index calculation.

5.4. Meteorological and Hydrological Droughts

Meteorological and hydrological droughts are both critical components of drought assessment; however, they differ in their origins, temporal scales, and impacts. Meteorological drought is characterized by a significant deficit in precipitation over a given period, often assessed using indices such as the SPI and SPEI. These indices capture precipitation anomalies and, in the case of SPEI, also incorporate evapotranspiration effects, making it a more comprehensive measure of atmospheric drought conditions. On the other hand, hydrological drought refers to deficits in surface and subsurface water resources, typically measured using indices like the SDI. While meteorological droughts develop rapidly and can be short-term (e.g., a few months), hydrological droughts often manifest more slowly, with long-term effects on river flows, groundwater levels, and reservoirs.

The results presented in Table 6 provide insight into the performance of various PDFs in modeling empirical CDFs for SPI, SPEI, and SDI at different time scales. The statistical metrics suggest that meteorological DIs (SPI and SPEI) exhibit stronger correlations (CC > 0.98) and higher coefficients of determination (R² > 0.99 for SPEI) compared to hydrological drought indices (SDI), which show slightly lower correlations and increased errors (MSE and RMSE). This difference can be attributed to SPI and SPEI responding directly to precipitation patterns. In contrast, SDI reflects delayed responses to precipitation deficits due to hydrological processes, such as infiltration, runoff, and groundwater recharge. For instance, the 12-month SDI shows the highest RMSE (0.143) and MAE (0.10) values, indicating larger deviations from the empirical CDF, likely due to the cumulative impact of prolonged precipitation deficits on streamflow and groundwater storage.

5.5. Drought Characteristics

In terms of drought characteristics, the results indicate that there is no consistent or specific relationship between the empirical and theoretical approaches. While both methods generally produced the same drought duration, notable differences were observed in severity and intensity. In some events, the empirical approach yielded higher severity and intensity values, whereas the theoretical method produced more extreme results in other cases. However, the empirical method proved more reliable and accurate overall, making it more suitable for practical applications such as planning and design. This is particularly important because relying on overly extreme estimates can lead to unnecessarily high costs and may result in solutions that are not feasible. Therefore, while both approaches can assess worst-case scenarios, the empirical method is preferable when accurate, consistent, and practical outcomes are needed. This aligns with previous research, which emphasizes the importance of comparing different drought indices and types [62].

5.6. Applications, Limitations, and Future Implications

The correct and accurate calculation of DIs is essential for drought assessment and evaluation, which is crucial for water resource management, drought mitigation plans, and the agricultural sector. Abu Arra and Şişman [63] emphasized that drought indices are a significant component of drought risk assessment, highlighting their importance in identifying and managing drought-related risks. Additionally, Bouabdelli et al. [64] demonstrated in their study the critical role of accurate drought indices calculations in the agricultural sector, underscoring the need for precision in these indices to support effective agricultural planning and response. The findings of this study highlight the significant influence of distribution function selection on land-related drought assessments. Specifically, the comparison between empirical and theoretical distribution functions revealed that the empirical approach consistently provided more conservative and realistic estimates of drought. This is particularly important for land and water resource management, as over- or underestimation of drought conditions can lead to inappropriate mitigation strategies. By directly reflecting observed data without assuming a predefined form, the empirical distribution proved more adaptable to drought events’ variability and complexity. Consequently, this approach may offer more reliable insights for land-based drought monitoring and decision-making processes, especially in regions with non-normal or skewed precipitation patterns. This can help several research studies related to meteorological drought [65,66], drought propagation [67,68], and drought forecasting [69,70,71,72]. Thus, ensuring the accuracy of drought indices is vital for academic research and practical applications in various sectors. With its key findings, this article contributes significantly to the academic field and provides valuable insights for water management, drought mitigation, and agriculture practitioners.

Several limitations can be considered in this research. First, this research focused on a specific number of DIs, covering the most commonly used indices; however, more indices can be used and compared. Second, a more in-depth analysis is necessary for the drought characteristics, covering more drought events, drought event definitions, and other characteristics like frequency. Another important point is that the empirical approach relies on the quality and completeness of the data, which may be an uncertainty or critical issue in data-scarce regions. Additionally, empirical/non-parametric approaches often have lower statistical efficiency compared to parametric approaches. The extrapolation between the observed data is challenging when the data is limited, raising another limitation to the empirical approach. Empirical approaches can be more sensitive to the outliers, as the empirical ranking and the cumulative distribution of observed values directly influence them. Finally, this research did not consider the effect of the empirical and theoretical approaches on the drought trend using classical and innovative approaches, which can be a very important point for climate change adaptation strategies.

6. Conclusions

Given the critical role of DIs in drought assessment and other sectors, the accurate calculation and application of these indices are of utmost importance. The available literature indicates that theoretical and parametric approaches are commonly employed to calculate DIs. However, there are uncertainties and instances of improper use of theoretical CDFs without verifying their suitability, resulting in significant errors in drought assessment and its corresponding applications. The key findings can be summarized as follows:

• Choosing the best theoretical CDF through goodness-of-fit tests is essential for precise drought assessment.
• Despite selecting suitable theoretical CDFs, there were notable differences between theoretical and empirical CDFs, particularly for hydrological drought at long time scales (12-month).
• The assessment process must be conducted at a micro-scale rather than a macro-scale to understand the differences between theoretical and empirical CDFs.
• In certain drought events, theoretical CDFs may underestimate drought by as much as 50%. The RMSE may be up to 0.15, which is about 100% more than the empirical approach.
• In terms of simplicity and reliability, empirical CDFs provide more accurate results and minimize errors. For example, in SPI-3, the RMSE was 0.087, the MAE was 0.071, and the MBE was 0.003.
• Many previous studies used the Gamma distribution for SPI without testing its suitability, which can lead to inaccurate drought analysis. In contrast, the empirical distribution offers a more realistic and less biased representation, making it a better choice, especially when theoretical distributions fall short.
• There is no consistent or specific relationship between the empirical and theoretical approaches for drought characteristics. However, the empirical/non-parametric approach gives more reliable and actual results.
• The empirical distribution function proved more effective and reliable for drought assessment, offering valuable insights for water resource management and related fields.

These findings underscore the importance of employing empirical CDFs for a more accurate and realistic evaluation of drought conditions, ultimately enhancing the effectiveness of drought management and mitigation strategies.