The Beneficial Spatial Spillover Effects of China’s Carbon Emissions Trading System on Air Quality

Abstract

Between 2013 and 2020, China had implemented a pilot cap-and-trade carbon emissions trading system (ETS) in some cities. Previous research has reported that this policy significantly reduces air pollution in the policy-implementing districts. However, whether and to what extent there are spatial spillover effects of this policy on air pollution in other regions has not been sufficiently analyzed. The research objective of this study is to quantitatively assess the spatial spillover effects of China’s carbon ETS on air pollution. Based on data from 288 Chinese cities between 2005 and 2020, this study employs a multiple linear regression approach to estimate the policy effects. Our study finds that the policy significantly reduces the concentrations of black carbon (BC), nitrogen dioxide (NO₂), organic carbon (OC), particulate matter less than 1 micron in size (PM₁), fine particulate matter (PM_2.5), and particulate matter less than 10 microns in size (PM₁₀) in non-ETS regions. This indicates that the carbon ETS has beneficial impacts on air quality beyond the areas where the policy was implemented. The heterogeneity tests reveal that the beneficial spatial spillover effects of the ETS can be observed across cities with different levels of industrialization, population density, economic development, resource endowments, and geographical locations. Further mechanism analyses show that although the policy does not affect the degree of environmental regulation in other regions, it promotes green innovation, low-carbon energy transition, and industrial structure upgrading there, which explains the observed spatial spillover effects.

1. Introduction

1.1. Research Background

Global climate change threatens humanity’s sustainable future. To reduce carbon emissions and mitigate climate change, some countries have implemented cap-and-trade carbon emissions trading systems (ETS). Since carbon emissions and air pollution emissions often occur concomitantly, the implementation of ETS also influences air pollution. Previous research has examined the effects of carbon ETS policies on air pollution in the districts where these policies are implemented. These studies generally reported that ETS reduces local air pollution [1,2,3,4,5]. However, whether ETS affects air quality in regions without ETS implementation remains underexplored in the literature.

China is currently the largest carbon emitter in the world. In order to reduce the emissions of greenhouse gases, China had implemented carbon ETS in selected pilot regions between 2013 and 2020. This policy has attracted significant attention and spurred numerous studies. Although the previous literature has explored the spatial spillover effects of the Chinese carbon ETS, these studies have primarily focused on the spillover impacts on carbon emissions, such as the research by Dai et al. [6], Li et al. [7], and Li and Wang [8]. Existing research rarely analyzed the spatial spillover effects of China’s carbon ETS on air pollution.

Studying the spatial spillover effects of carbon ETS on air pollution holds practical value.

(1)

Investigating the spillover effects of ETS on air pollution helps us understand the environmental impacts of ETS more comprehensively. This is important for accurately assessing the environmental benefits of ETS. Causal inference methods are crucial for evaluating the effects of carbon ETS and other environmental policies, as researchers need to accurately identify the causal impacts of these policies on environmental or socioeconomic variables. Typical causal inference methods include difference-in-differences, instrumental variables regression, randomized controlled trials, regression discontinuity design, and synthetic control, among others, each relying on distinct identification strategies. Previous ex-post evaluation studies of ETS predominantly employed the difference-in-differences (DID) regression model [9,10,11,12,13]. A fundamental premise of the DID approach is the absence of spatial spillover effects; otherwise, the Stable Unit Treatment Value Assumption (SUTVA) would be violated [14,15]. If spatial spillover effects of ETS exist, the conclusions drawn from previous studies using the DID method to evaluate the impacts of ETS are likely to be biased. If ETS improves (decreases) air quality in other regions, neglecting such spillover effects would lead to an underestimation (overestimation) of ETS’s role in improving air quality. The presence of spatial spillover effects implies that solely considering the direct local impacts of ETS is insufficient; instead, more sophisticated spatial economic analysis models are required for a comprehensive cost–benefit assessment of ETS. Typical spatial economic analysis models include spatial econometric models and computable general equilibrium (CGE) models. Spatial econometric models, such as the spatial Durbin model (SDM), account for interdependence between neighboring units by incorporating spatial lags of dependent and independent variables. Computable general equilibrium models further extend this by simulating economy-wide spatial linkages.

(2)

Analyzing the spillover effects of ETS on air pollution aids in understanding China’s air pollution problems. Numerous past studies have investigated the influence of certain environmental policies on air pollution. For example, the study by Jiang et al. [16] found that the Chinese government’s Three-Year Action Plan to Fight Air Pollution effectively reduced concentrations of PM_2.5 and PM₁₀ in Chinese cities. Cui et al. [17] and Li et al. [18], respectively, reported that the Air Pollution Prevention and Control Action Plan significantly improved air quality in Jinan City and Beijing City. Yang and Teng [19] demonstrated that China’s coal control policies were significant for carbon emission reduction and local pollutant control. Beyond the scope of China’s environmental policies, the research by Greenstone and Hanna [20] using Indian data suggested that air pollution regulations in developing economies are able to effectively improve air quality, although the findings by Majumdar et al. [21] indicated that existing Indian policies were insufficient to substantially reduce PM_2.5 emissions in the Kolkata Metropolitan City before 2030. Shahbazi et al. [22] investigated the effects of the Tehran Comprehensive Clean Air Action Plan, and found that this policy reduced pollutant emissions in Tehran, Iran. These studies generally found that environmental policies significantly affected urban air pollution. However, most of them treated each region as an independent unit, seldom considering the spatial spillover effects of environmental policies. Our analysis suggests that environmental policies may have significant spatial spillover effects, which should be accounted for in the analysis of air pollution problems. The existence of spatial spillover effects implies that addressing China’s air pollution requires coordinated and collaborative policies across different regions. Methodologically, research on spatial spillover effects can benefit from interdisciplinary insights. For example, the study by Lupo et al. [23] on the discrete element method (DEM) simulation of cohesive particles demonstrated calibration strategies for particle interactions within complex systems, offering conceptual and computational insights relevant to spatial spillover dynamics in environmental modeling.

Theoretically, it is uncertain whether ETS’s spatial spillover effects on air pollution in other regions are positive or negative. ETS may either increase or reduce air pollution in other regions. On the one hand, ETS may increase the economic costs of polluting firms in areas where ETS is implemented, causing some polluting firms to move to areas where ETS is not implemented. This would increase pollution emissions in non-ETS regions, i.e., there is emission leakage. On the other hand, the implementation of the ETS policy has the potential to promote public awareness of environmental protection, low-carbon energy transition, green innovation, and technological advancement, which will benefit other regions as well. Thereby, in order to understand the possible spatial spillover effects of ETS, we need to conduct ex-post empirical analysis using actual data.

Before we proceed to a formal empirical analysis, let us first observe the preliminary visual evidence. Figure 1 is a binned scatter plot that displays the negative correlation between local atmospheric pollution levels and the “density of carbon ETS in neighboring regions”. This binned scatter plot is drawn by using data of 288 Chinese cities during 2005–2020, after controlling for region- and time-fixed effects. For a particular region i, the “density of ETS in neighboring regions” is a weighted average of the status of ETS implementation in all districts j other than region i, using the inverse of the distance between regions i and j as weights. (The detailed definition of this variable is explained in Section 2.2.) Given that the geographical distances remain constant, the value of the density will become larger when more neighboring regions implement ETS. The eight subfigures in the graph, respectively, demonstrate the circumstances of eight types of atmospheric pollutants, including black carbon (BC), nitrogen dioxide (NO₂), ozone (O₃), organic carbon (OC), particulate matter less than 1 micron in size (PM₁), fine particulate matter (PM_2.5), particulate matter less than 10 microns in size (PM₁₀), and sulfur dioxide (SO₂). From the figure, it can be observed that the degree of atmospheric pollution is lower when the density of carbon ETS in neighboring regions is greater. Based on this figure, it is reasonable to conjecture that there is a spatial spillover impact of carbon ETS that reduces air pollution in neighboring regions. To verify this conjecture, this study will utilize statistical methods for quantitative evaluation.

1.2. Research Purpose, Outline, and Contributions

The research purpose of the current study is to examine whether China’s carbon ETS has spatial spillover effects on air pollution. To achieve this purpose, we employ a multiple linear regression approach to analyze panel data from 288 Chinese cities between 2005 and 2020. Unlike previous studies that focused on a limited number of air pollution indicators—particularly PM_2.5 and SO₂—this research examines eight air pollution metrics: BC, NO₂, O₃, OC, PM₁, PM_2.5, PM₁₀, and SO₂. To control for potential confounding factors, we follow the prior literature by incorporating a range of meteorological (e.g., precipitation, wind speed, temperature), socioeconomic (e.g., GDP per capita, population, industrial structure), and policy variables (e.g., the air pollution prevention and control action plan, low-carbon city pilot policies) as control variables in the regression models. We adopt conventional robustness testing methods, including using the one-period-lagged explanatory variable and alternative spatial weighting matrices, to verify the reliability of our empirical findings. Previous studies have extensively confirmed that environmental regulation, green innovation, energy transition, and industrial structure upgrading can effectively mitigate air pollution. Therefore, our mechanism analyses investigate whether the ETS influences these mediating variables in non-ETS regions.

The contributions of the current study lie in two aspects. (1) Whether the ETS policy has spatial spillover influences on air pollution has not been sufficiently studied in the existing research. Our study addresses this research gap. Previous studies on the spatial spillover impacts of ETS have focused on carbon leakage, i.e., the spillover effects on CO₂. Our study will demonstrate that ETS generates significant beneficial impacts on air quality in non-ETS regions. This contributes to a better and deeper understanding of the environmental benefits of ETS. (2) Compared to the previous literature, this study analyzes multiple indicators of air pollution, providing a more comprehensive picture of the influences of ETS on atmospheric pollution. This offers novel empirical evidence for understanding the Chinese air pollution issues and the dynamic changes in air quality.

2. Materials and Methods

2.1. Regression Model

The current study employs the following multiple linear regression equation to estimate the spatial spillover effects of carbon ETS on air quality.

$$\begin{gathered} {\mathit{AirPollution}}_{\mathit{it}}=\mathsf{\alpha }\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)+\beta {\mathit{ControlVariables}}_{\mathit{it}}+ \\ \gamma {\mathit{OtherPolicies}}_{\mathit{it}}+u_i+v_t+{\epsilon }_{\mathit{it}} \end{gathered}$$

(1)

In Equation (1), the explanatory variable AirPollution_it denotes the degree of air pollution in region i in year t. The core explanatory variable in the equation is ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$. It represents the density of carbon ETS implementation in the neighboring areas of region i. W_ij is an element of a spatial weights matrix. CarbonETS_jt is a binary dummy variable used to indicate whether region j executes a carbon ETS in period t or not. The covariates are grouped in two vectors, represented by ControlVariables_it and OtherPolicies_it. We will describe the meanings of these variables in detail in Section 2.2. u_i, v_t, and ε_it represent the region-fixed effect, time-fixed effect, and residual term, respectively.

The values of the regression coefficients α, β, and γ in the equation will be estimated using econometric regression methods. We employ t-tests to examine whether the regression coefficient of each individual explanatory variable is statistically significant. All analyses are conducted using Stata 15 statistical software, which computes the t-statistics and their corresponding p-values automatically. We report the t-statistic values in our results. To assess the overall significance of the regression models, we perform F-tests to determine whether all explanatory variables jointly exert statistically significant influences on the dependent variables. Since all regression models in this study pass the F-test, we omit reporting the specific F-statistic values to conserve space in the article.

The coefficient of interest in this study is α, which captures the aggregate impact of ETS implemented in all other regions j ≠ i on the air pollution in local region i. A significantly negative value of coefficient α means that ETS generates a beneficial spatial spillover impact on air quality. In this case, the ETS implemented in region j decreases air pollution in region i by |α × W_ij|. In contrast, a significantly positive value of coefficient α indicates that ETS has an adverse spatial spillover effect on air quality. In this case, the ETS implemented in region j increases air pollution in region i by |α × W_ij|.

It is notable that, the coefficient α also captures the impact of ETS implemented in local region i on air pollution in other regions j ≠ i. A significant value of coefficient α indicates that the ETS implemented in region i would cause air pollution in region j to change by α × W_ji.

2.2. Variables

2.2.1. Dependent Variables

The explained variable in the current study is AirPollution_it, the level of air pollution. Air pollution is caused by multiple kinds of pollutants. In this study, we inspect the spillover impacts of carbon ETS on each of the eight air pollutants: BC, NO₂, O₃, OC, PM₁, PM_2.5, PM₁₀, and SO₂, respectively. The unit of pollution concentration is µg/m³.

2.2.2. Core Explanatory Variable of Interest

The core explanatory variable of interest in this study is ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$. It represents the density of carbon ETS implementation in the neighboring areas of region i. This variable is a weighted average of the status of ETS implementation in all districts j other than region i, with the inverse of the distance between regions i and j as weights. W_ij is an element in a spatial weights matrix commonly used in the spatial econometrics literature, defined as follows:

$$W_{ij}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{{Distance}_{ij}}},\hfill & \hfill if i\ne j\\ 0,\hfill & \hfill if i=j\end{array}\right.$$

(2)

In Equation (2), Distance_ij is the geographic distance (in units of 100 km) between region i and region j. We calculate the distance between two cities on the basis of the latitude and longitude coordinates of the center of each city. CarbonETS_jt is a binary dummy variable used to indicate whether region j implements a carbon ETS in period t or not.

The assumption behind Equation (2) is that the implementation of the ETS in region j may have an impact on region i, and this impact is inversely proportional to the distance between regions i and j. After summing up the impacts of all other regions j ≠ i on the local region i, which is expressed by ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$, we measure the aggregate impact of the ETS implemented in all other regions on the local region.

To more clearly explain the spatial spillover impacts of ETS on other regions that the current study aims to measure, we use Figure 2 for illustration. Suppose there are three regions, i, j, and k, where region j has implemented ETS while regions i and k have not. We assume the distance between regions i and j is Distance_ij = 2, and the distance between regions k and j is Distance_kj = 1. The ETS implemented in region j generates spillover effects, influencing air pollution levels in regions i and k. For region i, the spillover effect from region j is $\alpha W_{ij}{CarbonETS}_j=\alpha {\displaystyle \frac{1}{{Distance}_{ij}}}{CarbonETS}_j=\alpha {\displaystyle \frac{1}{2}}1={\displaystyle \frac{1}{2}}\alpha$; for region k, the spillover effect from region j is $\alpha W_{kj}{CarbonETS}_j=\alpha {\displaystyle \frac{1}{{Distance}_{kj}}}{CarbonETS}_j=\alpha {\displaystyle \frac{1}{1}}1=\alpha$.

2.2.3. Covariates

Following the previous literature, we use a set of covariates to control for potential confounding factors. Covariates are included in two groups: ControlVariables_it and OtherPolicies_it. ControlVariables_it contains twelve meteorological and socioeconomic factors: precipitation (Precipitation_it), sunlight duration (Sunlight_it), wind speed (WindSpeed_it), temperature (Temperature_it), GDP per capita (GDPPerCapita_it), population density (PopulationDensity_it), share of tertiary industry in the economy (TertiaryIndustry_it), financial development (FinancialDevelopment_it), trade openness (TradeOpenness_it), high-speed railway (HighSpeedRailway_it), road density (RoadDensity_it), and medical infrastructure (MedicalInfrastructure_it). OtherPolicies_it contains thirty binary dummy variables representing some place-based public policies relevant to environmental and economic issues. To save space, we put the detailed explanations on these covariates in Appendix A.

2.3. Data Source and Sample

The data were from several sources. (1) The data source of BC, OC, and PM₁ pollution data was NASA’s MERRA-2 M2T1NXAER product. The data source of NO₂, O₃, and PM₁₀ was the GlobalHighAirPollutants (GHAP) dataset [24,25,26]. The data source of PM_2.5 was the Satellite-derived PM2.5 V6.GL.02.02 dataset [27]. The data source of SO₂ was The Reports on the State of the Environment of China written by China’s Ministry of Ecology and Environment. The original data provided by these data sources were processed to calculate the annual average values of various pollutants for each Chinese city. With the exception of SO₂ data, which were initially provided by official Chinese ground monitoring stations, all other air pollutant data are derived from remote sensing datasets processed in previous studies. The specific technical details can be found in the relevant literature. (2) The data source of meteorological variables was the ERA5-Land dataset of the European Union’s Copernicus Climate Change Service. (3) The source of high-speed railway data was the CNRDS (Chinese Research Data Services Platform). (4) The information about different public policies was manually collected from relevant governmental websites. (5) The other variables such as GDP per capita and population were downloaded from the EPS China Data.

Our analysis is on the basis of the data for 288 Chinese cities between 2005 and 2020. The data are at annual frequency. In order to focus on analyzing the spatial spillover impacts of carbon ETS, we excluded from our study sample cities that have implemented the ETS policy locally, which are located within seven province-level administrative units (Beijing, Chongqing, Fujian, Guangdong, Hubei, Shanghai, and Tianjin). In the sample period, all the sample cities did not implement carbon ETS locally and, thus, the impacts of ETS on these cities were from spatial spillovers. China has over 330 prefecture-level and province-level cities in total. After excluding all ETS-implementing cities and those with missing data, we finally retained 288 non-ETS cities for the empirical analysis. China’s cap-and-trade carbon ETS pilot project was rolled out in three batches, implemented in 2013, 2014, and 2016, respectively. Our research sample covers 8 years before the policy (from 2005 to 2012) and 8 years after the policy (from 2013 to 2020). Since China began to implement a nationwide carbon ETS policy in 2021, which affected all regions, our analysis does not include data after 2021. Figure 3 shows the geographical distribution of cities with and without ETS implementation. We did not perform special treatment for missing values. If a variable had missing data for a certain city-year observation, that particular data point was simply dropped. Consequently, our data are unbalanced panel data.

Table 1. Descriptive statistics of main variables.

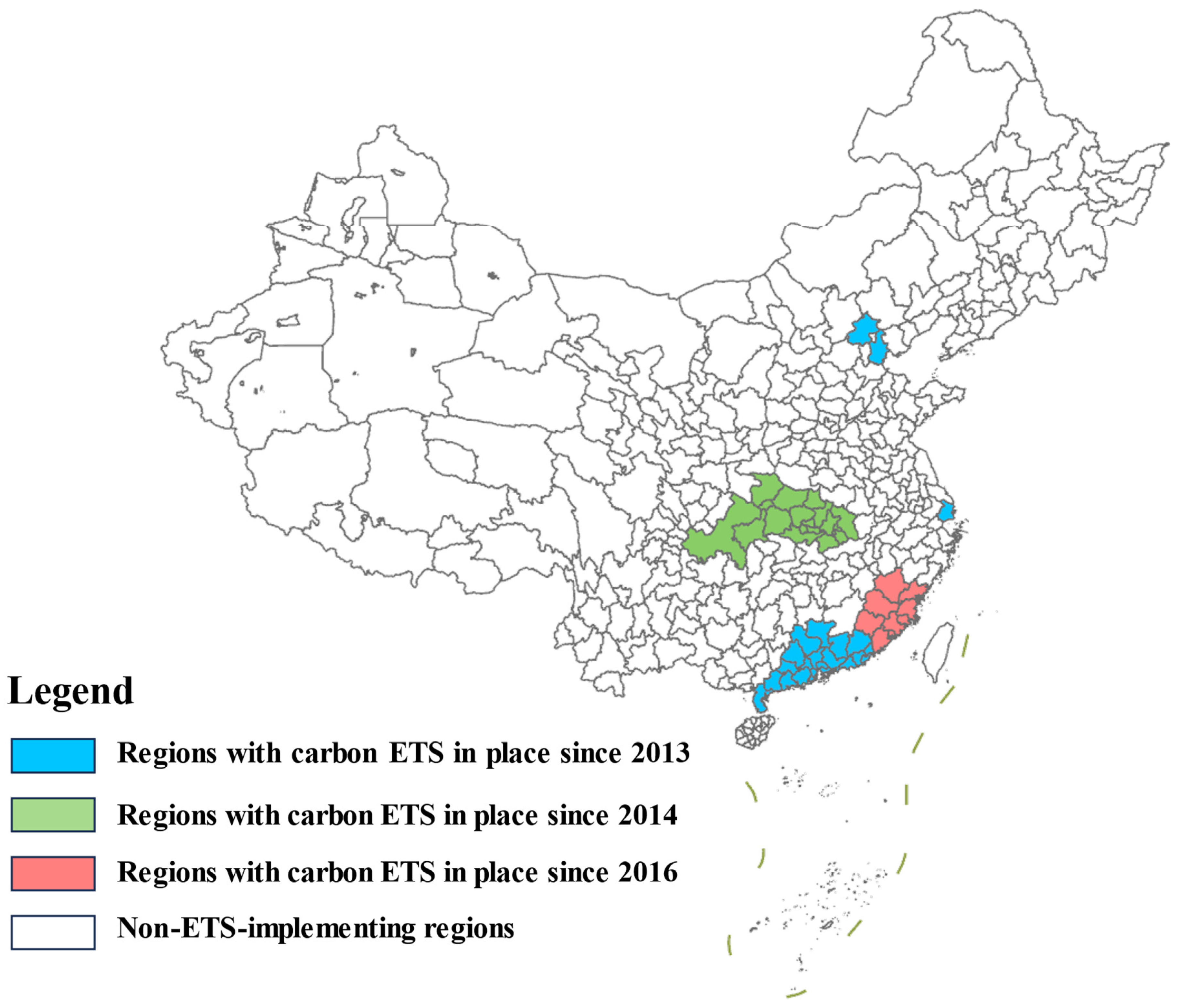
Variables	Number of Observations	Mean	Standard Deviation	Minimum	Maximum
BC	4561	2.815	1.943	0.050	8.733
NO2	3698	26.226	9.325	9.125	54.265
O3	4561	87.132	10.571	57.195	122.407
OC	4561	6.544	3.715	0.213	28.131
PM1	4561	26.319	9.721	4.670	60.922
PM2.5	4561	40.735	17.032	3.661	92.888
PM10	4561	87.860	34.913	21.865	295.404
SO2	3033	29.007	18.778	2.000	148.000
∑W × CarbonETS	4561	2.161	2.714	0.000	11.658
Precipitation	4561	6.575	0.708	3.290	7.923
Sunlight	4561	7.607	0.283	6.623	8.129
WindSpeed	4561	0.725	0.236	−0.021	1.480
Temperature	4561	11.923	6.068	−7.822	25.726
GDPPerCapita	4561	9.812	0.682	7.622	11.723
PopulationDensity	4561	5.205	1.477	−1.311	7.338
TertiaryIndustry	4561	0.396	0.100	0.086	0.805
FinancialDevelopment	4561	0.885	0.553	0.075	5.748
TradeOpenness	4561	0.173	0.561	0.000	17.176
HighSpeedRailway	4561	0.322	0.467	0.000	1.000
RoadDensity	4561	−0.473	0.947	−5.818	1.650
MedicalInfrastructure	4561	1.395	0.433	−0.088	2.704

Note: To save space, the descriptive statistics of variables contained in OtherPolicies are not reported in the table.

reports the descriptive statistics of main variables.

2.4. Methods of Robustness Tests

In order to ensure that the regression results based on Equation (1) are robust, we conduct three robustness checks. First, we consider that there may be a time lag in the policy effect of the ETS. Therefore, in the first robustness test, we use the one-year-lagged explanatory variable, ${\sum }_j{W}_{ij}\times {CarbonETS}_{j,t-1}$, for the regression analysis. We also consider that the regression results are dependent on the spatial weights matrix we choose. Therefore, in the second and third robustness tests, we use alternative spatial weights matrices: W^0.5 and W². The elements in these two matrices are defined as follows:

$$W_{ij}^{0.5}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{{Distance}_{ij}^{0.5}}},\hfill & \hfill if i\ne j\\ 0,\hfill & \hfill if i=j\end{array}\right.$$

(3)

$$W_{ij}^2=\left\{\begin{array}{cc}{\displaystyle \frac{1}{{Distance}_{ij}^2}},\hfill & if i\ne j\hfill \\ 0,\hfill & \hfill if i=j\end{array}\right.$$

(4)

2.5. Methods of Mechanism Analyses

To explore how the spillover effects of carbon ETS occur, we examine four possible mechanisms. Existing studies have confirmed that environmental regulation, green innovation, low-carbon energy transition, and industrial structure upgrading can effectively mitigate atmospheric pollution. If ETS promotes these mechanism variables in non-ETS regions, air pollution in non-ETS regions is likely to decrease. In the mechanism analyses, we replace the dependent variable in Equation (1) with these mechanism variables to estimate the effects of ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$. Statistically significant coefficients indicate that the tested mechanisms hold, thereby providing explanations for the spatial spillover influences of the carbon ETS.

3. Results

3.1. Main Results

Table 2. Estimated spillover effects of carbon ETS on air pollution.

Variables	BC	NO2	O3	OC
	(i)	(ii)	(iii)	(iv)
∑W × CarbonETS	−0.0384 ***	−0.168 ***	−0.161	−0.178 ***
	[0.004]	[0.058]	[0.166]	[0.024]
Precipitation	0.0250 **	−0.697 ***	−3.284 ***	0.00553
	[0.011]	[0.183]	[0.428]	[0.058]
Sunlight	−0.137 ***	0.396	12.82 ***	−0.401 *
	[0.027]	[0.463]	[1.441]	[0.230]
WindSpeed	−0.0708 **	−0.981	−1.268	−0.178
	[0.033]	[0.664]	[1.837]	[0.168]
Temperature	0.0131 **	0.0356	0.244	0.419 ***
	[0.005]	[0.070]	[0.185]	[0.056]
GDPPerCapita	−0.0730 ***	1.361 ***	2.136 **	−0.286 **
	[0.016]	[0.405]	[1.082]	[0.124]
PopulationDensity	−0.0224	0.196	1.323	−0.219 *
	[0.014]	[0.274]	[1.105]	[0.129]
TertiaryIndustry	−0.217 ***	−0.849	1.035	−1.081 *
	[0.066]	[1.490]	[3.423]	[0.646]
FinancialDevelopment	0.00401	−0.623 ***	0.583	0.0209
	[0.010]	[0.187]	[0.796]	[0.094]
TradeOpenness	0.00341 *	0.0698	−1.119 ***	0.0570 ***
	[0.002]	[0.054]	[0.249]	[0.014]
HighSpeedRailway	−0.0205 **	−0.031	−0.627	0.00854
	[0.008]	[0.146]	[0.384]	[0.041]
RoadDensity	−0.00739	−0.180	−0.714 *	−0.0195
	[0.014]	[0.287]	[0.419]	[0.126]
MedicalInfrastructure	−0.130 ***	−0.705	−0.230	−0.132
	[0.021]	[0.452]	[1.052]	[0.171]
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	288
Number of observations	4561	3698	4561	4561
Within R2	0.647	0.655	0.734	0.378
Variables	PM1	PM2.5	PM10	SO2
	(v)	(vi)	(vii)	(viii)
∑W × CarbonETS	−0.633 ***	−1.172 ***	−1.399 ***	−0.544
	[0.056]	[0.102]	[0.187]	[0.426]
Precipitation	−1.200 ***	−2.298 ***	−2.859 ***	−2.089 *
	[0.156]	[0.337]	[0.620]	[1.238]
Sunlight	−0.494	−5.809 ***	−4.032 **	−4.088
	[0.454]	[0.921]	[1.630]	[3.789]
WindSpeed	−2.077 ***	−3.617 **	−3.635	−4.731
	[0.638]	[1.434]	[2.219]	[4.314]
Temperature	0.126 *	1.032 ***	2.859 ***	1.153 *
	[0.073]	[0.173]	[0.290]	[0.651]
GDPPerCapita	−0.113	−1.978 ***	−1.408	−1.260
	[0.312]	[0.513]	[1.023]	[2.829]
PopulationDensity	−0.262 *	−0.692 **	−1.165 **	−2.615
	[0.157]	[0.320]	[0.561]	[1.719]
TertiaryIndustry	−3.359 ***	−8.908 ***	−14.18 ***	−0.960
	[0.918]	[1.785]	[3.735]	[8.732]
FinancialDevelopment	−0.494 ***	−0.0128	−0.539	1.390
	[0.191]	[0.421]	[0.603]	[1.702]
TradeOpenness	0.102 **	−0.0454	0.784 ***	1.000 *
	[0.050]	[0.072]	[0.225]	[0.527]
HighSpeedRailway	−0.0623	−0.615 **	0.473	−0.0493
	[0.144]	[0.255]	[0.472]	[1.091]
RoadDensity	0.157	0.827 **	1.012 **	0.722
	[0.141]	[0.320]	[0.463]	[2.168]
MedicalInfrastructure	−1.581 ***	−2.779 ***	−3.492 ***	−7.857 **
	[0.348]	[0.608]	[1.230]	[3.802]
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	287
Number of observations	4561	4561	4561	3033
Within R2	0.896	0.739	0.871	0.601

Note: *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively. Robust standard errors are clustered at the city level and reported in brackets under the coefficient estimates. To save space, the coefficients of covariates in OtherPolicies are not reported in the table.

provides the coefficient estimates for Equation (1). When the explained variables are BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀, the estimated coefficients of ∑W × CarbonETS are all negative and statistically significant at the 1% level. This indicates that when the density of ETS policies in neighboring areas increases, the pollution concentrations of BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀ in local area would decrease. When the explained variables are O₃ and SO₂, the estimated coefficients of ∑W × CarbonETS are not statistically significant, although the coefficients are also negative. This suggests that local O₃ and SO₂ pollution levels are not significantly affected by ETS policies in other regions. Overall, the results provided in Table 2 indicate that carbon ETS generates a significant spatial spillover effect on air pollution. The execution of carbon ETS improves air quality in non-ETS regions.

The coefficients of some covariates in Table 2 are also statistically significant. This implies that air pollution is also affected by the covariates. Since we focus on the spillover influences of ETS in this study, we do not discuss the coefficients of the covariates in detail.

Based on our empirical findings, we can reasonably draw the following two inferences. (1) Starting from 2013, as the ETS pilot policy was implemented in certain regions and generated beneficial spatial spillover effects, the concentrations of BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀ in non-ETS regions also experienced a significant decline. (2) The higher the “density of carbon ETS in neighboring regions” (i.e., ∑W × CarbonETS), the greater the reduction in air pollutant concentrations.

These inferences align with the actual trends in China’s air pollution. We illustrate this point using a figure. Based on whether a city’s average “density of carbon ETS in neighboring regions” (i.e., ∑W × CarbonETS) during the sample period was above the sample median, we divide the sample cities in this study into two groups: the group of large ∑W × CarbonETS and the group of small ∑W × CarbonETS. Figure 4 presents the trends in BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀ for these two groups from 2005 to 2020. Before 2013, air pollution levels in both groups remained relatively stable or even increased slightly. However, starting in 2013, both groups exhibited a significant decline in atmospheric pollution, with the group of large ∑W × CarbonETS showing a more pronounced decrease in pollutant concentrations. The patterns displayed in Figure 4 explicitly support the empirical results reported in Table 2: the ETS policy has generated significant spatial spillover effects, leading to reduced air pollution in non-ETS regions.

3.2. Robustness Tests

In order to ensure that the previous regression results are robust, we conduct three robustness checks. In the first robustness test, we use the one-year-lagged explanatory variable, ${\sum }_j{W}_{ij}\times {CarbonETS}_{j,t-1}$, for the regression analysis. In the second and third robustness tests, we use alternative spatial weights matrices: W^0.5 and W².

The results of these three robustness tests are provided in Panels A, B, and C of

Table 3. Coefficient estimates for robustness tests.

Variables	BC	NO2	O3	OC
	(i)	(ii)	(iii)	(iv)
Panel A
∑W × CarbonETSt-1	−0.0384 ***	−0.219 ***	−0.0627	−0.192 ***
	[0.003]	[0.063]	[0.185]	[0.022]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	288
Number of observations	4561	3698	4561	4561
Within R2	0.646	0.657	0.73	0.374
Panel B
∑W0.5 × CarbonETS	−0.0295 ***	−0.125 ***	−0.102	−0.141 ***
	[0.002]	[0.041]	[0.111]	[0.017]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	288
Number of observations	4561	3698	4561	4561
Within R2	0.653	0.655	0.730	0.377
Panel C
∑W2 × CarbonETS	−0.0506 ***	−0.217 *	−0.532	−0.221 ***
	[0.016]	[0.120]	[0.389]	[0.072]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	288
Number of observations	4561	3698	4561	4561
Within R2	0.629	0.653	0.731	0.354
Variables	PM1	PM2.5	PM10	SO2
	(v)	(vi)	(vii)	(viii)
Panel A
∑W × CarbonETSt-1	−0.735 ***	−1.275 ***	−1.496 ***	−0.553
	[0.069]	[0.107]	[0.227]	[0.419]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	287
Number of observations	4561	4561	4561	3033
Within R2	0.900	0.745	0.872	0.602
Panel B
∑W0.5 × CarbonETS	−0.446 ***	−0.924 ***	−1.006 ***	−0.510
	[0.033]	[0.060]	[0.121]	[0.313]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	287
Number of observations	4561	4561	4561	3033
Within R2	0.897	0.747	0.872	0.602
Panel C
∑W2 × CarbonETS	−1.053 ***	−1.541 ***	−2.331 ***	−0.413
	[0.245]	[0.456]	[0.546]	[0.773]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	288	287
Number of observations	4561	4561	4561	3033
Within R2	0.892	0.727	0.869	0.601

Note: * and *** represent significance levels of 10% and 1%, respectively. Robust standard errors are clustered at the city level and reported in brackets under the coefficient estimates. To save space, the coefficients of covariates are not reported in the table.

. These results are well consistent with the previous results reported in Table 2. We detect that ETS has a beneficial spatial spillover impact on air quality. The ETS significantly reduces the local BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀ pollution in non-ETS regions.

3.3. Heterogeneity Tests

In previous analyses, we treated all cities in the sample as homogeneous units and evaluated the “average” spillover effects of carbon ETS on all cities. However, it is possible that the spillover effects vary by city characteristics. For instance, highly industrialized regions and cities with high population density may be more sensitive to environmental policies, leading to stronger ETS spillover effects in these areas. We now conduct heterogeneity tests to assess whether the spillover impacts of ETS differ across regions.

We employ the following empirical strategy. We select a specific city characteristic and divide the sample cities into two groups: Group 1 and Group 2. We then construct two binary dummy variables, D_i^Group1 and D_i^Group2, to indicate which group city i belongs to. If city i is in Group 1, then D_i^Group1 = 1 and D_i^Group2 = 0; if it belongs to Group 2, then D_i^Group1 = 0 and D_i^Group2 = 1. We multiply these two dummy variables by ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$ to obtain two interaction terms: $\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times D_i^{Group1}$ and $\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times D_i^{Group2}$. We then replace ${\sum }_j{W}_{ij}\times {CarbonETS}_{jt}$ in Equation (1) with these two interaction terms to derive Equation (5). The coefficients ${\alpha }_1$ and ${\alpha }_2$ in Equation (5) measure the spatial spillover impacts of carbon ETS on cities in Group 1 and Group 2, respectively.

$$\begin{gathered} {\mathrm{AirPollution}}_{\mathrm{it}}={\alpha }_1\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times D_i^{Group1}+{\alpha }_2\left({\sum }_j{W}_{ij}\times \\ {CarbonETS}_{jt}\right)\times D_i^{Group2}+\beta {\mathit{ControlVariables}}_{\mathit{it}}+\gamma {\mathit{OtherPolicies}}_{\mathit{it}}+u_i+v_t+{\epsilon }_{\mathit{it}} \end{gathered}$$

(5)

We conducted five types of grouping based on the city’s industrialization level, population density, economic development level, resource endowment, and geographical location. (1) Based on the average share of secondary industry in GDP during the sample period, we classified cities into the group with high industrialization level and the group with low industrialization level. The heterogeneity test results are presented in Panel A of

Table 4. Coefficient estimates for heterogeneity tests.

Variables	BC	NO2	O3	OC
	(i)	(ii)	(iii)	(iv)
Panel A: different industrialization levels
(∑W × CarbonETS) × DGroup1 (high industrialization level)	−0.0384 ***	−0.189 ***	−0.0521	−0.182 ***
	[0.003]	[0.060]	[0.177]	[0.025]
(∑W × CarbonETS) × DGroup2 (low industrialization level)	−0.0383 ***	−0.133 **	−0.333 *	−0.171 ***
	[0.004]	[0.066]	[0.185]	[0.023]
Panel B: different population density
(∑W × CarbonETS) × DGroup1 (high population density)	−0.0389 ***	−0.187 ***	−0.0908	−0.180 ***
	[0.004]	[0.059]	[0.171]	[0.024]
(∑W × CarbonETS) × DGroup2 (low population density)	−0.0357 ***	−0.0484	−0.522 ***	−0.169 ***
	[0.004]	[0.070]	[0.192]	[0.024]
Panel C: different economic development levels
(∑W × CarbonETS) × DGroup1 (high economic development level)	−0.0383 ***	−0.203 ***	−0.180	−0.182 ***
	[0.003]	[0.058]	[0.178]	[0.025]
(∑W × CarbonETS) × DGroup2 (low economic development level)	−0.0384 ***	−0.137 **	−0.145	−0.175 ***
	[0.004]	[0.064]	[0.182]	[0.024]
Panel D: different resource endowment
(∑W × CarbonETS) × DGroup1 (resource-based cities)	−0.0381 ***	−0.0889	0.210	−0.199 ***
	[0.005]	[0.077]	[0.241]	[0.031]
(∑W × CarbonETS) × DGroup2 (non-resource-based cities)	−0.0385 ***	−0.209 ***	−0.363 *	−0.167 ***
	[0.004]	[0.061]	[0.194]	[0.025]
Panel E: different geographical locations
(∑W × CarbonETS) × DGroup1 (eastern region)	−0.0400 ***	−0.623 ***	−1.059 ***	−0.198 ***
	[0.005]	[0.105]	[0.279]	[0.031]
(∑W × CarbonETS) × DGroup2 (central and western regions)	−0.0383 ***	−0.160 ***	−0.151	−0.178 ***
	[0.003]	[0.058]	[0.163]	[0.024]
Variables	PM1	PM2.5	PM10	SO2
	(v)	(vi)	(vii)	(viii)
Panel A: different industrialization levels
(∑W × CarbonETS) × DGroup1 (high industrialization level)	−0.657 ***	−1.213 ***	−1.537 ***	−0.651
	[0.058]	[0.099]	[0.199]	[0.429]
(∑W × CarbonETS) × DGroup2 (low industrialization level)	−0.593 ***	−1.107 ***	−1.180 ***	−0.343
	[0.064]	[0.124]	[0.205]	[0.472]
Panel B: different population density
(∑W × CarbonETS) × DGroup1 (high population density)	−0.657 ***	−1.197 ***	−1.467 ***	−0.563
	[0.058]	[0.100]	[0.193]	[0.418]
(∑W × CarbonETS) × DGroup2 (low population density)	−0.504 ***	−1.042 ***	−1.046 ***	−0.411
	[0.068]	[0.139]	[0.214]	[0.597]
Panel C: different economic development levels
(∑W × CarbonETS) × DGroup1 (high economic development level)	−0.635 ***	−1.137 ***	−1.444 ***	−0.776 *
	[0.055]	[0.104]	[0.191]	[0.454]
(∑W × CarbonETS) × DGroup2 (low economic development level)	−0.630 ***	−1.201 ***	−1.360 ***	−0.283
	[0.063]	[0.117]	[0.200]	[0.443]
Panel D: different resource endowment
(∑W × CarbonETS) × DGroup1 (resource-based cities)	−0.549 ***	−1.055 ***	−1.216 ***	−0.140
	[0.072]	[0.130]	[0.220]	[0.505]
(∑W × CarbonETS) × DGroup2 (non-resource-based cities)	−0.678 ***	−1.235 ***	−1.498 ***	−0.743
	[0.063]	[0.111]	[0.216]	[0.497]
Panel E: different geographical locations
(∑W × CarbonETS) × DGroup1 (eastern region)	−0.713 ***	−1.179 ***	−1.248 ***	−0.655
	[0.088]	[0.163]	[0.299]	[0.577]
(∑W × CarbonETS) × DGroup2 (central and western regions)	−0.632 ***	−1.171 ***	−1.401 ***	−0.539
	[0.056]	[0.102]	[0.187]	[0.426]

Note: *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively. Robust standard errors are clustered at the city level and reported in brackets under the coefficient estimates. To save space, the coefficients of covariates are not reported in the table.

. (2) Based on population density, we divided cities into the group with high population density and the group with low population density. The regression results are shown in Panel B. (3) Using per capita GDP, we categorized cities into the group with high economic development level and the group with low economic development level. The results are reported in Panel C. (4) Following the official list from the “National Sustainable Development Plan for Resource-Based Cities (2013–2020)” published by China’s central government in 2013, we separated cities into the group of resource-based cities and the group of non-resource-based cities. The results appear in Panel D. (5) By geographic location, we distinguished between the group of cities in eastern region and the group of cities in central and western regions. Panel E displays the regression results.

As shown in Panels A–E of Table 4, the coefficients for both interaction terms—$\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times D_i^{Group1}$ and $\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times D_i^{Group2}$—are mostly significantly negative across different city groups, except in a few cases where they are statistically nonsignificant. In other words, the beneficial spatial spillover effects of ETS on air quality can be observed across different groups of cities. Moreover, it is important to note that the regression coefficients are generally similar among different groups. Therefore, we actually did not detect significant heterogeneity. These results also indicate that the core findings of this study are highly robust.

3.4. Mechanism Analyses

In previous analyses, we have already detected that carbon ETS has significant spatial spillover impacts, reducing air pollution in other regions. Next, we explore how the effects occur. We examine four possible mechanisms: environmental regulation, green innovation, low-carbon energy transition, and industrial structure upgrading. If ETS promotes environmental regulation, green innovation, energy transition, and industrial upgrading in other regions, air pollution in other regions is likely to decrease. Below, we analyze, respectively, whether the ETS changes these four variables in neighboring regions.

First, we inspect the spillover influence of carbon ETS on the degree of environmental regulation. We need to construct an environmental regulation indicator. Following the previous literature [28,29], we measure the stringency of environmental regulation within a city by the proportion of environment-related words in the text of the local government’s annual work reports. The higher value of this indicator represents that the local government pays more attention to ecological protection and the environmental regulation is stricter. We replace the dependent variable in Equation (1) with this environmental regulation indicator and estimate the impact of ∑W × CarbonETS. As indicated by the coefficient reported in column (i) of

Table 5. Coefficient estimates for mechanism analyses.

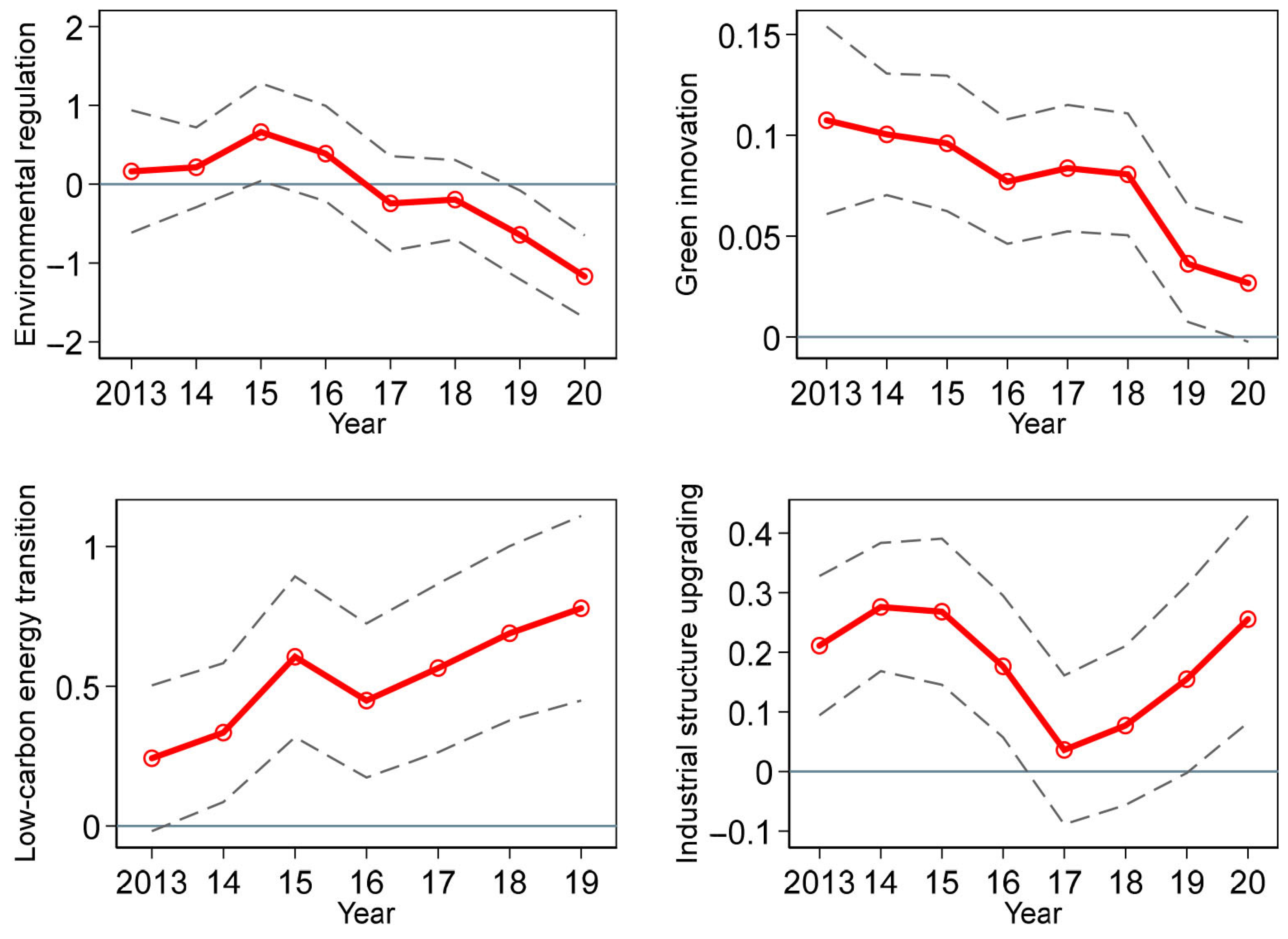
Variables	Environmental Regulation	Green Innovation	Low-Carbon Energy Transition	Industrial Structure Upgrading
	(i)	(ii)	(iii)	(iv)
∑W × CarbonETS	−0.108	0.0743 ***	0.546 ***	0.168 **
	[0.252]	[0.016]	[0.165]	[0.071]
ControlVariables	Yes	Yes	Yes	Yes
OtherPolicies	Yes	Yes	Yes	Yes
City-fixed effects	Yes	Yes	Yes	Yes
Year-fixed effects	Yes	Yes	Yes	Yes
Number of cities	288	288	236	288
Number of observations	4561	4561	3540	4561
Within R2	0.281	0.853	0.795	0.935

Note: ** and *** represent significance levels of 5% and 1%, respectively. Robust standard errors are clustered at the city level and reported in brackets under the coefficient estimates. To save space, the coefficients of covariates are not reported in the table.

, we do not find a significant impact of ETS on the environmental regulation stringency in other regions.

Second, we analyze the spillover effects of ETS on green innovation. To measure green innovation, we add 1 to the number of green patent applications in a city during one corresponding year and then take the logarithm. The data of green patent applications were available in the CNRDS database. We estimate the impact of ∑W × CarbonETS using green innovation as the explained variable. The estimated coefficient of ∑W × CarbonETS is provided in column (ii) of Table 5. The coefficient is significantly positive, indicating that ETS significantly encourages green innovation in the neighboring areas.

Third, we analyze the low-carbon energy transition. We choose the low-carbon energy transition index constructed by Shen et al. [30] to measure a city’s performance toward low-carbon energy transition. The larger value of this index represents better performance on the energy transition path. We use this index to replace the dependent variables in Equation (1). The regression results displayed in column (iii) of Table 5 suggest that ∑W × CarbonETS significantly promotes low-carbon energy transition.

Fourth, we investigate the industrial structure upgrading. Referring to the previous literature [31,32,33], we utilize an index (ISU) to track the progress of industrial structure upgrading. ISU = I₁ + I₂ × 2 + I₃ × 3 where I₁, I₂, and I₃ represent the proportion of value added of the primary industry, secondary industry, and tertiary industry in GDP, respectively. The larger the value of ISU, the higher the degree of industrial structure upgrading. We use ISU as the explained variable. The regression result displayed in column (iv) of Table 5 shows that ∑W × CarbonETS substantially contributes to industrial structure upgrading.

To further analyze the temporal dynamics of mechanism effects, we adopt the following model to estimate the influence of the ETS across different years:

$$\begin{gathered} Y_{\mathrm{it}}={\sum }_{k=2013}^{2020}\left[{\alpha }_k\left({\sum }_j{W}_{ij}\times {CarbonETS}_{jt}\right)\times I\left(t=k\right)\right]+\beta {\mathit{ControlVariables}}_{\mathit{it}}+ \\ \gamma {\mathit{OtherPolicies}}_{\mathit{it}}+u_i+v_t+{\epsilon }_{\mathit{it}} \end{gathered}$$

(6)

Here, Y_it represents the mechanism variables under study, including environmental regulation, green innovation, low-carbon energy transition, and industrial structure upgrading. I(t = k) is an indicator function that equals 1 if t = k, and equals 0 otherwise. For example, when k = 2013, if the observation is from the year of 2013 (i.e., t = 2013), then I(t = k) = 1; otherwise, I(t = k) = 0. The coefficient α_k captures the spatial spillover impact of the carbon ETS in year k. Using Equation (6), we are able to estimate the spillover impacts of the carbon ETS on the mechanism variables in each year from 2013 to 2020.

To visualize the dynamic effects of the ETS on these mechanism variables, we present the regression results in Figure 5. The four subplots depict the annual impacts of the ETS on environmental regulation, green innovation, low-carbon energy transition, and industrial structure upgrading, corresponding to the estimated coefficients α_k for each year. The graph reveals several key findings. (1) The spillover effects of ETS on environmental regulation are generally statistically nonsignificant. (2) The spillover effect on green innovation exhibits temporal decay: the effect peaked in 2013 and gradually diminished over time. (3) The effect on low-carbon energy transition demonstrates temporal strengthening: the effect started from the smallest magnitude in 2013 and progressively increased in subsequent years. (4) The impact on industrial structure upgrading shows fluctuation dynamics: the impact reached its maximum in 2014, declined to a trough in 2017, then rebounded in subsequent years to form an approximate U-shaped pattern.

In short, the mechanism analyses indicate that carbon ETS promotes green innovation, low-carbon energy transition, and industrial structure upgrading in non-ETS regions. The magnitude of ETS’s effects on these mechanism variables exhibits distinct temporal patterns across years. While its spillover effect on green innovation demonstrates a diminishing trend over time, the impact on low-carbon energy transition shows progressive strengthening, and the influence on industrial structure upgrading displays cyclical fluctuations.

4. Discussion

This study reveals that the implementation of the carbon ETS can significantly reduce air pollution concentrations in non-ETS regions, thereby improving air quality. We conducted a series of robustness tests, experimenting with different model specifications with alternative temporal windows and spatial neighborhood definitions. We also performed heterogeneity tests, considering various ways to group sample cities. These tests consistently support our core findings regarding the beneficial spatial spillover influences of the ETS.

Although the effects estimated in this study are indirect effects arising through spatial spillovers, the magnitude of these indirect effects is of practical significance. Based on our coefficient estimates and the variable values in the sample, we can calculate the marginal effects of the ETS on specific pollutants. For example, let us consider the scenario in 2020. In our sample, in 2020, the mean value of the implementation density of ETS, i.e., ∑W × CarbonETS, was 4.895. On average, if the number of cities implementing the ETS were to double (assuming these cities are uniformly and randomly distributed across China’s territory), this would double ∑W × CarbonETS, increasing its mean value by 4.895. This would lead to an additional reduction in air pollutant concentrations in a typical non-ETS city by |α × Δ(∑W × CarbonETS)|, where α is the coefficient value reported in Table 2 and Δ(∑W × CarbonETS) is the change in the implementation density of ETS. For instance, the concentration of BC would decrease by 0.0384 × 4.895 = 0.188 µg/m³. Similarly, we can calculate that the concentrations of NO₂, OC, PM₁, PM_2.5, and PM₁₀ would decrease by 0.822, 0.871, 3.099, 5.737, and 6.848 µg/m³, respectively. These environmental benefits carry substantial public health and economic gains. The findings of the current study have valuable academic and practical implications, which we elaborate on below.

4.1. Academic Implications

From the perspective of academic research, first, the findings in this study demonstrate that, when evaluating the impacts of ETS, its spatial spillover effect on the environment cannot be overlooked. The previous literature primarily used the DID method to ex-post evaluate the pros and cons of ETS. A core assumption of the traditional DID method is the absence of spatial spillover effects [14,15]. Our study reveals that the spatial spillover effects of ETS on air quality are significant and ETS can improve air quality in other regions. Therefore, conclusions drawn from past studies using the traditional DID method may be biased. Ignoring the beneficial spatial spillover influences of ETS on air quality would lead to an underestimation of its benefits.

Second, our study uncovers a crucial co-benefit: reducing greenhouse gas emissions often brings additional benefits in reducing other air pollutants, because they share common emission sources. This finding is consistent with some prior studies. For instance, Basaglia et al. [34] estimated that the EU ETS significantly reduced toxic air pollutants, such as SO₂, PM_2.5, and NO_x, and these pollution reductions would translate into substantial health gains, potentially amounting to hundreds of billions of Euros. Similarly, Zhang et al. [35] found that cooperative international efforts to reduce greenhouse gases could bring substantial air quality co-benefits to the United States. Therefore, beyond greenhouse gas reduction, ETS has significant environmental co-benefits, which should be fully recognized when evaluating the benefits of ETS.

4.2. Practical Implications

First, this study emphasizes the existence of spatial spillover effects from ETS. This suggests that implementing ETS may play a crucial role in countries with serious atmospheric pollution problems, such as China, India, and Pakistan. Since ETS generates positive externalities, governments should support enterprises across regions to actively participate in carbon emissions trading. Our findings indicate that the environmental benefits of ETS extend beyond administrative boundaries, significantly improving air quality in other areas by reducing BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀. However, these benefits diminish with increasing geographic distance. Thus, the development of carbon trading markets should persistently advance regional integration of policies [6,36,37]. Governments should strongly promote regionally coordinated carbon markets or gradually expanding ETS coverage on various economic sectors, to encourage firms across regions to take advantage of the carbon market, to leverage these spatial synergistic effects. When more regions participate in ETS, greater collective benefits can be achieved [38,39], thereby maximizing the spatial effectiveness of carbon markets design and environmental policies. It is worth noting that due to these positive externalities, some regions may have incentives to free ride by benefiting from others’ efforts without reducing their own emissions. Therefore, when designing carbon markets and various environmental policies, governments should pay attention to their potential spatial spillover effects and address possible free-riding problems through cooperation and coordination mechanisms among regions, such as cross-regional consultation, benefit compensation mechanisms, and regional joint emission reduction agreements.

Second, we also emphasize that China’s ETS should not be viewed as an isolated climate policy tool, but rather as part of an integrated climate–air quality policy portfolio. In practice, ETS can work alongside other environmental policies in China such as the “Blue Sky Defense War”, regional carbon neutrality plans, and the “Air Pollution Prevention and Control Action Plan”, to jointly achieve the dual goals of mitigating climate change and improving air quality.

Finally, our study scores the need to integrate ETS into the government’s long-term environmental protection strategy system to maximize its co-benefits. First, the government should promote technological innovation and low-carbon energy transition as key complementary policies to carbon ETS. Local governments can leverage the national carbon market platform to accelerate the cultivation of green industries, improve the green financial system, and foster a virtuous cycle of green development. Second, ETS can serve as a crucial policy tool for implementing the long-term strategy of “Beautiful China 2035”, supporting China’s transition towards a sustainable, low-carbon future. “Beautiful China 2035” emphasizes not only to reduce greenhouse gas emissions and improve air quality, but also to seek comprehensive improvements across various ecological aspects such as water quality, land, and forests [40]. Since carbon ETS can promote green innovation, low-carbon energy transition, and industrial structure upgrading, it has the potential to generate benefits for other aspects of the ecosystem.

5. Conclusions and Limitations

5.1. Conclusions

This study investigates the spatial spillover impacts of carbon ETS on air pollution in areas where the policy is not implemented. By analyzing data for 288 Chinese cities from 2005 to 2020, this study finds that the carbon ETS policy significantly reduces BC, NO₂, OC, PM₁, PM_2.5, and PM₁₀ concentrations in non-ETS regions. This result suggests that the beneficial effects of the ETS on air quality exist not only in the ETS-implementing areas, as already noted by the previous literature, but also extend to the areas where ETS is not implemented. The heterogeneity tests reveal consistent evidence of the ETS’s beneficial spatial spillover effects, which remain statistically significant across cities characterized by different levels of industrialization, population density, economic development, resource endowments, and geographical locations. Further mechanism analyses show that although the policy does not significantly change the level of environmental regulation in other regions, it promotes green innovation, low-carbon energy transition, and industrial structure upgrading in neighboring regions. These phenomena provide plausible explanations for the observed spatial spillover effects of policy.

5.2. Limitations and Future Research Directions

Our study contains several limitations that point to valuable avenues for future research.

(1)

Since our analysis relies on Chinese data, it remains unclear whether the conclusions regarding the spillover effects of ETS could be generalizable to other countries. Future studies could apply our methodology to examine the ETS programs in other countries, such as the EU ETS, US ETS, or Canadian ETS, to investigate whether similar spatial spillovers exist.

(2)

Our data coverage ended in 2020, precluding analysis of post-2021 developments. This cutoff was necessary because China launched its national carbon market in 2021, resulting in universal ETS coverage across all cities. There were no non-ETS cities after 2021. Consequently, our regression model (which captures the impact of ETS on non-ETS cities) became inapplicable. Future researchers could employ more sophisticated models coupled with granular data on policy intensity or trading volumes to analyze the national market’s effects after 2021.

(3)

This study focuses exclusively on the spillovers of carbon ETS without accounting for potential spillovers from other policies. China has implemented numerous environmental and regional development policies. Certain policies may also generate spatial spillover effects on air pollution. Future research could examine other critical policies, such as the Air Pollution Prevention and Control Action Plan, the Low-carbon City Pilot Project, and the Three-year Action Plan to Fight Air Pollution, to investigate their potential cross-regional spillover effects.