Machine Learning Model Optimization for Antarctic Blowing Snow Height and Optical Depth Diagnosis
Abstract
1. Introduction
2. Data, Input, and Model Selection
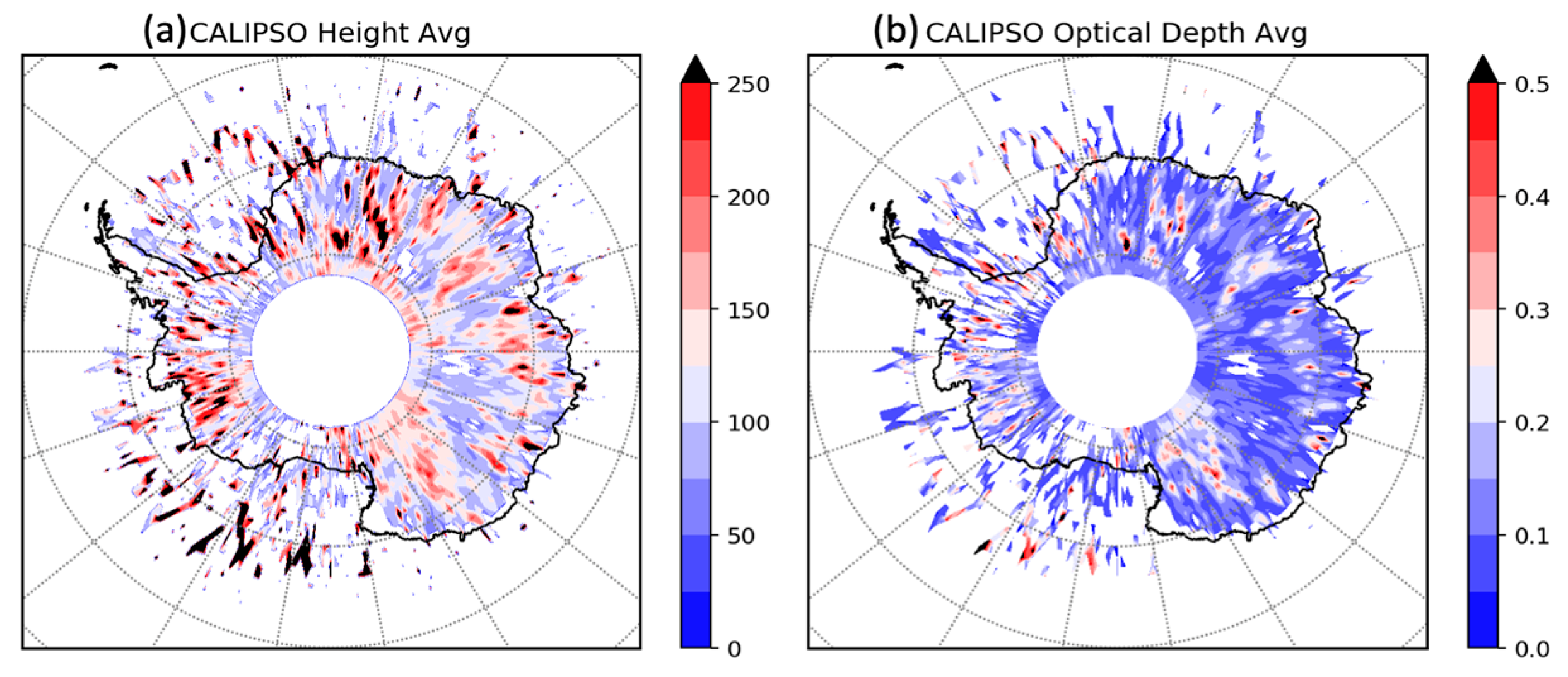
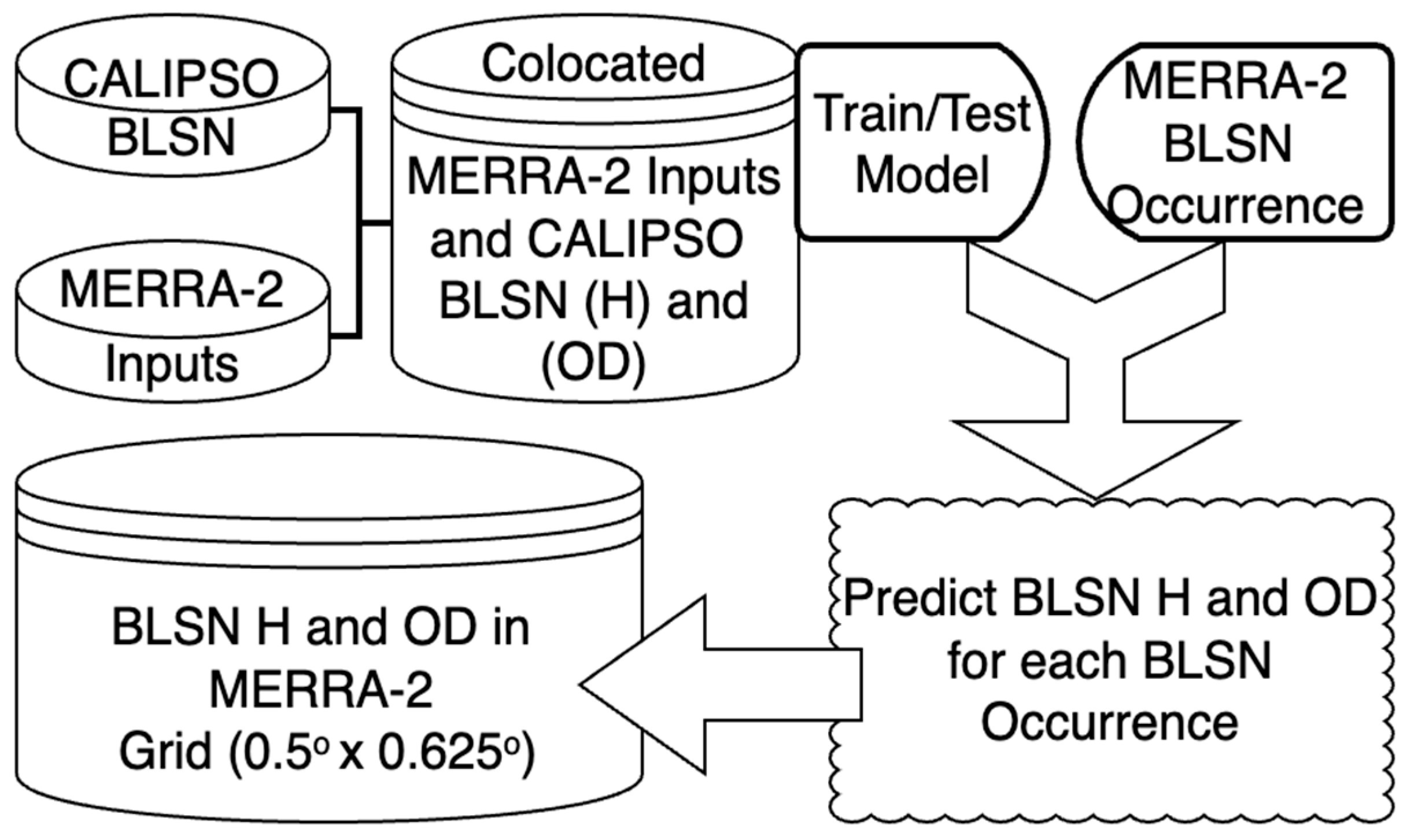
2.1. Input Features and Truth Data Fusion
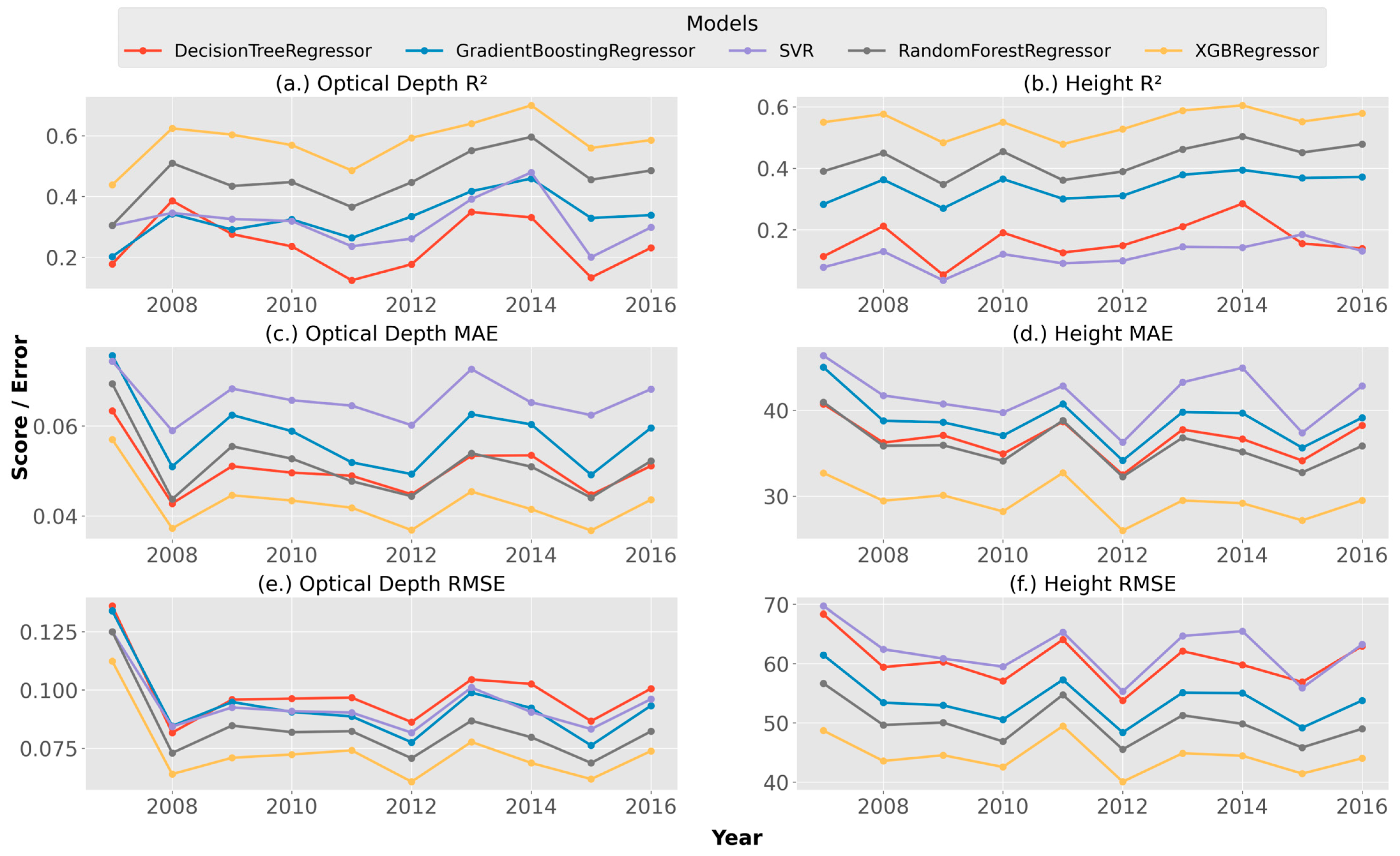
2.2. Model Selection
2.3. XGBoost Model
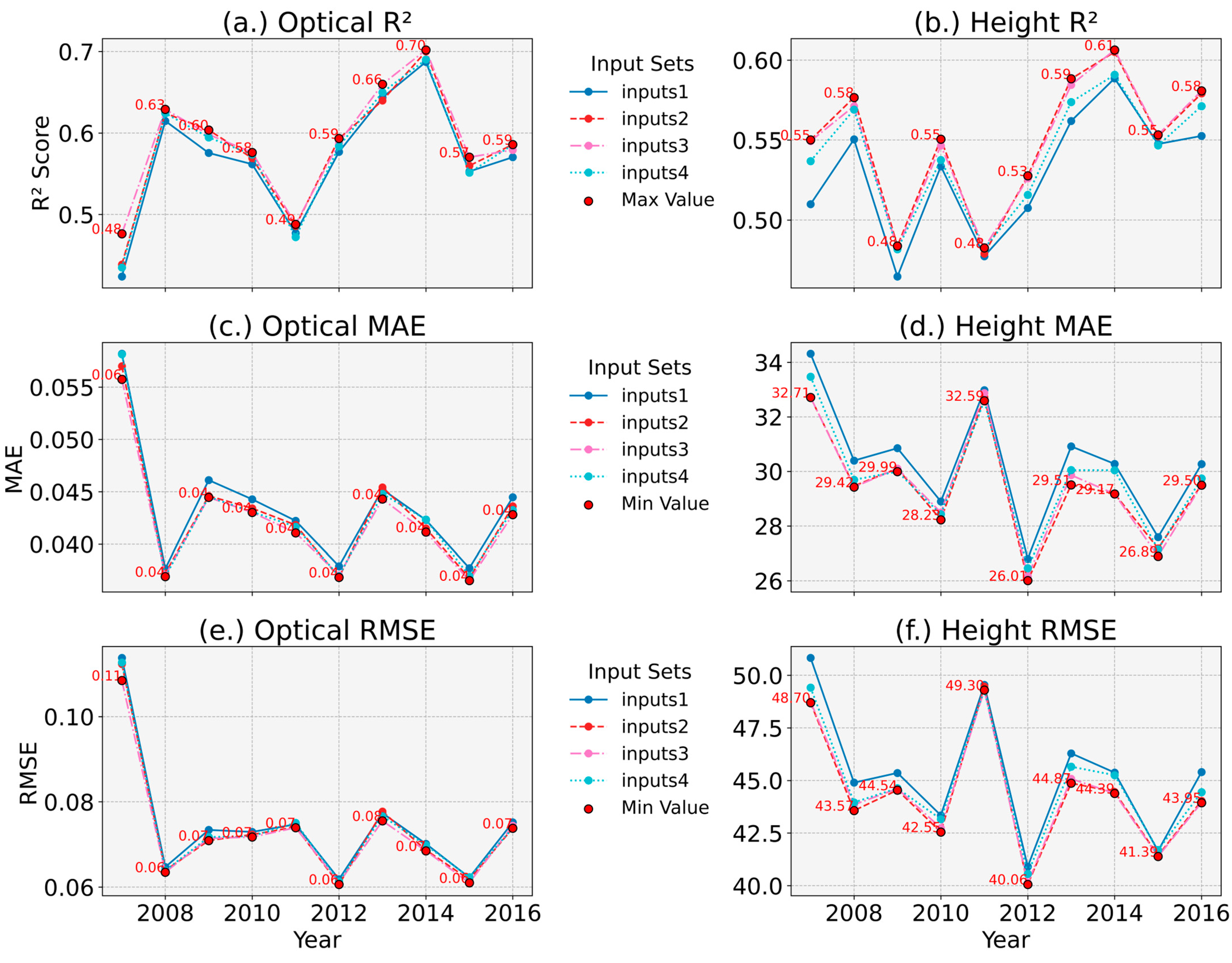
2.4. Input Feature Selection
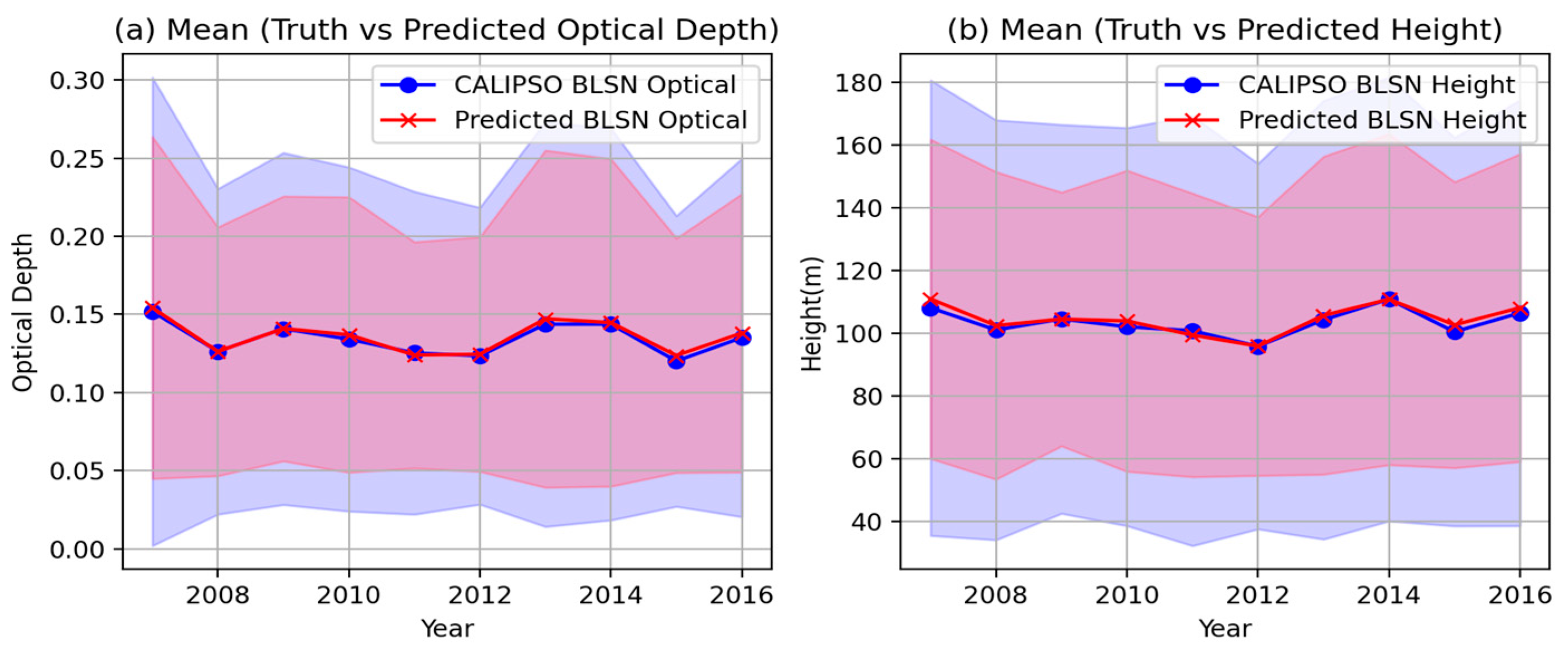
3. Results
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palm, S.P.; Yang, Y.; Spinhirne, J.D.; Marshak, A. Satellite Remote Sensing of Blowing Snow Properties over Antarctica. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Loeb, N.A.; Kennedy, A. Blowing Snow at McMurdo Station, Antarctica During the AWARE Field Campaign: Surface and Ceilometer Observations. J. Geophys. Res. Atmos. 2021, 126, e2020JD033935. [Google Scholar] [CrossRef]
- Xiao, J.; Bintanja, R.; Déry, S.J.; Mann, G.W.; Taylor, P.A. An Intercomparison Among Four Models Of Blowing Snow. Bound.-Layer Meteorol. 2000, 97, 109–135. [Google Scholar] [CrossRef]
- Mellor, M. Blowing Snow; CRREL Monograph, Part III, Section A3c; U.S. Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1965; 79p. [Google Scholar]
- Sigmund, A.; Melo, D.B.; Dujardin, J.; Nishimura, K.; Lehning, M. Parameterizing Snow Sublimation in Conditions of Drifting and Blowing Snow. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004332. [Google Scholar] [CrossRef]
- Palm, S.P.; Kayetha, V.; Yang, Y.; Pauly, R. Blowing Snow Sublimation and Transport over Antarctica from 11 Years of CALIPSO Observations. Cryosphere 2017, 11, 2555–2569. [Google Scholar] [CrossRef]
- Das, I.; Bell, R.E.; Scambos, T.A.; Wolovick, M.; Creyts, T.T.; Studinger, M.; Frearson, N.; Nicolas, J.P.; Lenaerts, J.T.M.; van den Broeke, M.R. Influence of Persistent Wind Scour on the Surface Mass Balance of Antarctica. Nat. Geosci 2013, 6, 367–371. [Google Scholar] [CrossRef]
- Gadde, S.; van de Berg, W.J. Contribution of Blowing-Snow Sublimation to the Surface Mass Balance of Antarctica. Cryosphere 2024, 18, 4933–4953. [Google Scholar] [CrossRef]
- Bintanja, R. Snowdrift Sublimation in a Katabatic Wind Region of the Antarctic Ice Sheet. J. Appl. Meteorol. 2001, 40, 1952–1966. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; van den Broeke, M.R.; Déry, S.J.; van Meijgaard, E.; van de Berg, W.J.; Palm, S.P.; Sanz Rodrigo, J. Modeling Drifting Snow in Antarctica with a Regional Climate Model: 1. Methods and Model Evaluation. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Déry, S.J.; Tremblay, L.-B. Modeling the Effects of Wind Redistribution on the Snow Mass Budget of Polar Sea Ice. J. Phys. Oceanogr. 2004, 34, 258–271. [Google Scholar] [CrossRef]
- Gossart, A.; Palm, S.P.; Souverijns, N.; Lenaerts, J.T.M.; Gorodetskaya, I.V.; Lhermitte, S.; van Lipzig, N.P.M. Importance of Blowing Snow During Cloudy Conditions in East Antarctica: Comparison of Ground-Based and Space-Borne Retrievals Over Ice-Shelf and Mountain Regions. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Palm, S.P.; Kayetha, V.; Yang, Y. Toward a Satellite-Derived Climatology of Blowing Snow Over Antarctica. J. Geophys. Res. Atmos. 2018, 123, 10301–10313. [Google Scholar] [CrossRef]
- Lesins, G.; Bourdages, L.; Duck, T.J.; Drummond, J.R.; Eloranta, E.W.; Walden, V.P. Large Surface Radiative Forcing from Topographic Blowing Snow Residuals Measured in the High Arctic at Eureka. Atmos. Chem. Phys. 2009, 9, 1847–1862. [Google Scholar] [CrossRef]
- Mann, G.W.; Anderson, P.S.; Mobbs, S.D. Profile Measurements of Blowing Snow at Halley, Antarctica. J. Geophys. Res. Atmos. 2000, 105, 24491–24508. [Google Scholar] [CrossRef]
- Li, L.; Pomeroy, J.W. Probability of Occurrence of Blowing Snow. J. Geophys. Res. Atmos. 1997, 102, 21955–21964. [Google Scholar] [CrossRef]
- Huang, J.; Jaeglé, L. Wintertime Enhancements of Sea Salt Aerosol in Polar Regions Consistent with a Sea Ice Source from Blowing Snow. Atmos. Chem. Phys. 2017, 17, 3699–3712. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s Laser Measurements of Polar Ice, Atmosphere, Ocean, and Land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Walden, V.P.; Warren, S.G.; Tuttle, E. Atmospheric Ice Crystals over the Antarctic Plateau in Winter. J. Appl. Meteorol. Climatol. 2003, 42, 1391–1405. [Google Scholar] [CrossRef]
- Taylor, P. The Thermodynamic Effects of Sublimating, Blowing Snow in the Atmospheric Boundary Layer. Bound.-Layer Meteorol. 1998, 89, 251–283. [Google Scholar] [CrossRef]
- Schmidt, R.A. Sublimation of Wind-Transported Snow: A Model; Rocky Mountain Forest and Range Experiment Station, Forest Service: Fort Collins, CO, USA; U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Déry, S.J.; Yau, M.K. Large-Scale Mass Balance Effects of Blowing Snow and Surface Sublimation. J. Geophys. Res. Atmos. 2002, 107, ACL 8-1–ACL 8-17. [Google Scholar] [CrossRef]
- Frezzotti, M.; Scarchilli, C.; Becagli, S.; Proposito, M.; Urbini, S. A Synthesis of the Antarctic Surface Mass Balance during the Last 800 Yr. Cryosphere 2013, 7, 303–319. [Google Scholar] [CrossRef]
- Déry, S.J.; Yau, M.K. A Bulk Blowing Snow Model. Bound.-Layer Meteorol. 1999, 93, 237–251. [Google Scholar] [CrossRef]
- Gallée, H.; Guyomarc’h, G.; Brun, E. Impact Of Snow Drift On The Antarctic Ice Sheet Surface Mass Balance: Possible Sensitivity To Snow-Surface Properties. Bound.-Layer Meteorol. 2001, 99, 1–19. [Google Scholar] [CrossRef]
- Essery, R.; Li, L.; Pomeroy, J. A Distributed Model of Blowing Snow over Complex Terrain. Hydrol. Process. 1999, 13, 2423–2438. [Google Scholar] [CrossRef]
- Scarchilli, C.; Frezzotti, M.; Grigioni, P.; De Silvestri, L.; Agnoletto, L.; Dolci, S. Extraordinary Blowing Snow Transport Events in East Antarctica. Clim. Dyn. 2010, 34, 1195–1206. [Google Scholar] [CrossRef]
- Pomeroy, J.; Jones, H. Wind-Blown Snow: Sublimation, Transport and Changes to Polar Snow. In Chemical Exchange Between the Atmosphere and Polar Snow; Springer: Berlin/Heidelberg, Germany, 1996; pp. 453–489. [Google Scholar]
- Mott, R.; Vionnet, V.; Grünewald, T. The Seasonal Snow Cover Dynamics: Review on Wind-Driven Coupling Processes. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef]
- Palm, S.P.; Yang, Y.; Herzfeld, U.; Hancock, D.; Hayes, A.; Selmer, P.; Hart, W.; Hlavka, D. ICESat-2 Atmospheric Channel Description, Data Processing and First Results. Earth Space Sci. 2021, 8, e2020EA001470. [Google Scholar] [CrossRef]
- Yang, Y.; Kiv, D.; Bhatta, S.; Ganeshan, M.; Lu, X.; Palm, S. Diagnosis of Antarctic Blowing Snow Properties Using MERRA-2 Reanalysis with a Machine Learning Model. J. Appl. Meteorol. Climatol. 2023, 62, 1055–1068. [Google Scholar] [CrossRef]
- Chung, Y.-C.; Bélair, S.; Mailhot, J. Blowing Snow on Arctic Sea Ice: Results from an Improved Sea Ice–Snow–Blowing Snow Coupled System. J. Hydrometeorol. 2011, 12, 678–689. [Google Scholar] [CrossRef]
- Leonard, K.C.; Maksym, T. The Importance of Wind-Blown Snow Redistribution to Snow Accumulation on Bellingshausen Sea Ice. Ann. Glaciol. 2011, 52, 271–278. [Google Scholar] [CrossRef]
- Bhatta, S.; Yang, Y. Selection and Optimization of a Machine Learning Algorithm for Antarctic Blowing Snow Diagnosis Using MERRA-2 Reanalysis. Artif. Intell. Earth Syst. 2025, 4. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Lucchesi, R.; Suarez, M. MERRA-2: File Specification 2015. Available online: https://ntrs.nasa.gov/citations/20150019760 (accessed on 25 February 2025).
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Mahesh, A.; Eager, R.; Campbell, J.R.; Spinhirne, J.D. Observations of Blowing Snow at the South Pole. J. Geophys. Res. Atmos. 2003, 108, 785–794. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Shapley, L.S. A Value for N-Person Games; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent Individualized Feature Attribution for Tree Ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Barral, H.; Genthon, C.; Trouvilliez, A.; Brun, C.; Amory, C. Blowing Snow in Coastal Adélie Land, Antarctica: Three Atmospheric-Moisture Issues. Cryosphere 2014, 8, 1905–1919. [Google Scholar] [CrossRef]
- Kodama, Y.; Wendler, G.; Gosink, J. The Effect of Blowing Snow on Katabatic Winds in Antarctica. Ann. Glaciol. 1985, 6, 59–62. [Google Scholar] [CrossRef]
- Parish, T.R. A Numerical Study of Strong Katabatic Winds over Antarctica. Mon. Weather Rev. 1984, 112, 545–554. [Google Scholar] [CrossRef]

| Bottom 4 Layers | Surface |
|---|---|
| Pressure (PL) | Pressure (PS) |
| Temperature (T) | Temperature (T2M) |
| Specific Humidity (Qv) | Eastward wind (U10M) |
| Eastward Wind (U) | Northward wind (V10M) |
| Northward Wind (V) | Specific Humidity (Qv2M) |
| Total Latent Energy Flux (EFLUX) | Temperature Gradient (2M) (Tg) |
| Sensible Heat Flux From Turbulence (HFLUX) | Geo. Potential Height |
| Variable Group | Inputs1 | Inputs2 | Inputs3 | Inputs4 |
|---|---|---|---|---|
| PS | PS | PS | PS | PS |
| HFLUX | HFLUX | HFLUX | HFLUX | HFLUX |
| EFLUX | EFLUX | EFLUX | EFLUX | EFLUX |
| PHIS | PHIS | PHIS | PHIS | PHIS |
| Temp Gradient | Temp_GR | Temp_GR | Temp_GR | Temp_GR |
| U10M | U10M | U10M | U10M | U10M |
| V10M | V10M | V10M | V10M | V10M |
| QV2M | QV2M | QV2M | QV2M | QV2M |
| T2M | T2M | T2M | T2M | T2M |
| U Levels | U71 | U71, U70 | U71, U70, U69 | U71, U70, U69, U68 |
| V Levels | V71 | V71, V70 | V71, V70, V69 | V71, V70, V69, V68 |
| T Levels | T71 | T71, T70 | T71, T70, T69 | T71, T70, T69, T68 |
| QV Levels | QV71 | QV71, QV70 | QV71, QV70, QV69 | QV71, QV70, QV69, QV68 |
| PL Levels | PL71 | PL71, PL70 | PL71, PL70, PL69 | PL71, PL70, PL69, PL68 |
| OMEGA Levels | OMEGA71 | OMEGA71, OMEGA70 | OMEGA71, OMEGA70, OMEGA69 | OMEGA71, OMEGA70, OMEGA69, OMEGA68 |
| Model Trained on October 2007–2016, Holdout: | Height R2 Score | Optical Depth R2 Score |
|---|---|---|
| 2008 October | 0.34 | 0.23 |
| 2014 October | 0.30 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatta, S.; Yang, Y. Machine Learning Model Optimization for Antarctic Blowing Snow Height and Optical Depth Diagnosis. Atmosphere 2025, 16, 760. https://doi.org/10.3390/atmos16070760
Bhatta S, Yang Y. Machine Learning Model Optimization for Antarctic Blowing Snow Height and Optical Depth Diagnosis. Atmosphere. 2025; 16(7):760. https://doi.org/10.3390/atmos16070760
Chicago/Turabian StyleBhatta, Surendra, and Yuekui Yang. 2025. "Machine Learning Model Optimization for Antarctic Blowing Snow Height and Optical Depth Diagnosis" Atmosphere 16, no. 7: 760. https://doi.org/10.3390/atmos16070760
APA StyleBhatta, S., & Yang, Y. (2025). Machine Learning Model Optimization for Antarctic Blowing Snow Height and Optical Depth Diagnosis. Atmosphere, 16(7), 760. https://doi.org/10.3390/atmos16070760








