The Southern Hemisphere Blocking Index in the ERA5 and the NCEP/NCAR Datasets: A Comparative Climatology for the Period 1940–2022

Abstract

Blocking anticyclones are important atmospheric phenomena generally associated with extreme weather (e.g., droughts and cold air surges). Blockings also constitute large-scale indicators of climate change. The study of blockings in the Southern Hemisphere (SH) has been traditionally carried out utilizing reanalysis products. This paper is aimed at presenting an updated, comprehensive climatology of blockings in the SH as extracted from the ERA5 and the NCEP/NCAR reanalysis datasets in the 1940–2022 and 1948–2022 periods, respectively. Blockings were located by means of a unidimensional index at 500 hPa. The results were stratified by season, longitude, region, persistence, and intensity, and the climatology from both datasets was compared. The primary location of blockings was close to the Date Line in every season. Additionally, depending on the season, up to fourth-rank maxima could be located. Generally, the secondary maxima were found in the south Atlantic; lower-order maxima were located in the south-eastern Pacific, west of South America, and in the south-western Indian Ocean east of South Africa. The most intense blockings were concentrated in the Pacific and in the south Atlantic in both datasets, and they were also located in the Indian Ocean, but in the ERA5 reanalysis only. The longest-lived blockings occurred in the south Pacific and in the south Atlantic during southern winter.

1. Introduction

The World Meteorological Organization (WMO) defines a blocking anticyclone as a “slow-moving anticyclone of middle latitudes which has the appearance on a synoptic chart of an obstacle blocking the normal west-to-east movement of migratory extra-tropical depressions” [1] (p. 86). Moreover, following the WMO parlance, blocking action is the “atmospheric process which leads, for an appreciable period, to meridional interruptions of the normal zonal, middle latitude current of the general circulation” [1] (p. 86). From a kineto-dynamic standpoint, nonlinear interactions between waves involving barotropic and baroclinic processes lead to a cascade of energy from synoptic-scale waves, whose wavelengths are at maximum growth upstream of the blocking, to stationary planetary-scale waves [2] (p. 335). The continuous influx of anticyclonic potential vorticity aloft that is provided by the foregoing small-scale waves approaching the blocking systems on their upstream flank supports their stationarity and persistence; their dissolution by convective mixing is prevented by the anticyclone’s inherent strong static stability [3] (p. 145). Simultaneously, downward motions within the anticyclonic static-stable environment enhance adiabatic warming, which contributes to the maintenance of a deep, warm anticyclonic system [3] (p. 145). The normal westerly flow is reversed equatorward for these particular anticyclones [3] (p. 145).

Blocking anticyclones, or blockings for short, are hence long-lived, stationary, warm high-pressure systems wherein the zonal movement of short waves is halted for extended periods [4] (p. 79). They are commonly associated with poleward shifts of the jet and are situated in the westerly wind belt [5] (p. 309) [6] (p. 463). Even though blockings are tied to dull weather for their recognizable clear skies and subsidizing air [3] (p. 145), they may also lead to extremes [7] (p. 607), including heat or cold waves [8,9,10], droughts or intense to torrential rains [11] (p. 14) [12,13,14], and pollution [6] (p. 145). Blockings capable of penetrating into the stratosphere can cause a westerly-to-easterly reversal of the flow there and, eventually, evolve into sudden stratospheric warmings [3] (p. 145) [15] (and references therein).

Blockings are subjectively classified into three different types according to the shape of their spatial patterns. In the Northern Hemisphere (NH), these types are (a) high-over-low block, (b) omega block, and (c) long-lasting high-amplitude ridge [4] (p. 79). In type (a), a cut-off low (COL) is located equatorward of a high-latitude blocking. The structure is characterized by a splitting of the jet whose branches surround the pattern; the westerlies’ disturbances are typically deflected poleward of the blocking [4] (p. 79) [5] (p. 309). As for type (b), it is a zonally oriented configuration consisting of a high-latitude anticyclone flanked on either equatorward side by a cyclone; the entire pattern resembles the shape of the Greek letter Ω, thereby its name [3] (p. 309) [4] (p. 79). Considering the Coriolis Effect sign reversal in the Southern Hemisphere (SH), the naming conventions for the aforementioned blocking types should be changed to (a) the low-over-high block and (b) the inverted omega block, whereas (c) remains unchanged. Type (a) is otherwise known as the “dipole pattern”, the “Rex blocking”, and the “split flow” [4] (p. 79). Additionally, in a study carried out in the SH [16], the terms “diffluent blocking” and “meridional blocking” were introduced for (a) and (b), respectively, yet all these names are hemisphere-independent. Having an equivalent barotropic structure, blockings frequently exhibit closed structures in the lower levels of the atmosphere, whereas ridges are present in the upper levels [5] (p. 309). In type (c), ridges with a diverse amplitude span the troposphere.

Blockings can objectively be located by requiring the pressure at the Earth’s surface, or the geopotential height at any pressure level (e.g., 500 hPa), to exceed a threshold for a given time span [17,18]. Another objective way to detect blockings is by means of the so-called blocking indices (BIs), whose definition can be unidimensional or bidimensional [19] (and references therein). These definitions were typically employed on gridded data [19], yet data from other sources, such as radiosondes, could also be used [20]. Both the frequency of occurrence and the spatial location of blockings are expected to depend upon the methodology and the dataset used. In either hemisphere, blockings can occur anywhere, but they are more prone to take place in the cold season and over the oceans, downstream of the storm tracks [2] (p. 145). Broadly speaking, in the SH, there was only one contiguous region where their occurrence was most favored, namely the South Pacific, whereas their frequency minimized in the Indian Ocean [6] (p. 464 and references therein). More precisely, studies that were carried out employing different datasets and definitions found that the regions where blockings had a noticeable frequency took place in the Southern Pacific (SP) around the Date Line (DL), in south-eastern South America (SESA), south-east of South Africa, and in the south-western Indian Ocean [20,21,22,23,24,25]. Even though the physical mechanisms that lead to the formation and maintenance of blockings were presented above, it is not the intention of this work to further discuss the reasons for the existence of preferred locations in the SH that are more prone to blockings.

Owing to a lack of in situ observations in the SH, remotely sensed data and reanalysis products have been widely employed in the last decades to carry out studies of the atmosphere. This paper focuses on the differences in the location of blockings using the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 [26] and the National Centers for Environmental Prediction (NCEP)-National Center for Atmospheric Research (NCAR) Reanalysis [27], to date the two most widely used reanalysis datasets, to evaluate the blocking index (BI) in the SH. In particular, these two reanalyses are suitable for calculating the BI at 500 hPa―the level that was traditionally used to study blockings in both hemispheres [28,29,30,31,32,33,34,35,36,37,38,39,40]―within a homogeneous grid.

The importance of blockings relies on the associated extreme weather mentioned in the preceding lines. They also have the potential of predicting tropical storms: the unprecedented hurricane Catarina, the first one to occur in the south Atlantic, was related to blocking conditions in SESA in the previous days [41]. Furthermore, blockings are instrumental as large-scale indicators of climate change, yet they are sensitive to the choice of the dataset [42]. Following this, comparisons between datasets are warranted, especially in the SH, which generally attracts less attention than the NH. Research efforts on the subject are scant. In [43], the NCEP/NCAR and ECMWF datasets encompassed the 1973–1997 and 1980–1993 periods, respectively, but proper comparisons between the two datasets were restricted to the average annual frequencies as a function of latitude since the work was more inclined towards analyzing the energetics in selected years. In a later study that covered the period 1960–2000, the results were presented in detail, as the frequencies of blockings were stratified by region and by season [44]. The goals of the present work are to provide a comprehensive and updated climatology of blockings in the SH, extending the analysis to 83 years (1940–2022) and 75 years (1948–2022) for the ECMWF and the NCEP/NCAR reanalysis, respectively, and to highlight the differences between both datasets. Additionally, these differences were statistically tested, which constitutes a novel approach to the topic.

2. Materials and Methods

2.1. Datasets

Daily 500 hPa geopotential height (GH) fields were obtained from two different reanalysis datasets. Data from the NCEP/NCAR Reanalysis Project (the NCEP dataset from now on) [45] consisted of yearly archives, each one including the gridded daily mean heights of the 6-hourly available runs in a resolution of 2.5° × 2.5° (latitude × longitude, 73 × 144 points) with global coverage. This data was retrieved from the dedicated webpage hosted by the National Oceanic and Atmospheric Administration’s Physical Science Laboratory [46]. The dataset spanned the 75-year period 1948–2022 and comprised 27,394 daily fields. The ERA5 reanalysis, an initiative from the European Union’s Copernicus [47] that was implemented by the ECMWF, had the longest timespan (stretching as far back as 1940), covered the entire globe with a maximum resolution of 0.25° × 0.25°, and was available on an hourly basis [48]. The retrieved information for this dataset (the ERA5 dataset hereafter) consisted of monthly files, including the daily data of potential energy by unit mass. These files were generated using the Copernicus Climate Change Service’s Daily Statistics Application [49] by aggregating all the available hourly data. In order to match the NCEP dataset’s spatial resolution, a tile selection of 2.5° × 2.5° was made (this selection was no longer available as of September 2024). The heights were calculated after dividing the fetched data by the constant of gravity $g=9.80665 m{s}^{-2}$ [50]. The resulting dataset encompassed the 83-year period 1940–2022 and totaled 30,316 daily fields. The working variable in both datasets was expressed in meters.

On each day and for every latitude, the set of 144 GH values was Fourier-analyzed using the accurate expansion

$$z_i\left(\phi \right)=\left[z\left(\phi \right)\right]+\sum _{n=1}^{72}\left[a_n\cos \left({\displaystyle \frac{2\pi n{z}_i}{{\lambda }_0}}\right)+b_n\sin \left({\displaystyle \frac{2\pi {nz}_i}{{\lambda }_0}}\right)\right]$$

(1)

In the above equation, $z_i\left(\phi \right)$ represents the zonal GH (ZGH) at longitude $i\left(1\le i\le 144\right)$ and at latitude $\phi$, $\left[z\left(\phi \right)\right]$ is the zonal mean value of the variable over the circle of latitude $\phi$, $n$ represents the contribution of the $n$-th harmonic that oscillated around the mean value and was associated with the wavenumber $2\pi n/{\lambda }_0$, with ${\lambda }_0$ being the fundamental wavelength $\left(n=1\right)$ that spanned an entire circle of latitude and had opposite longitudes in antiphase. The expansion coefficients $a_n$ and $b_n$ could be calculated by projecting the values of $z_i$ onto $\cos \left(2\pi n{z}_i/{\lambda }_0\right)$ and $\sin \left(2\pi n{z}_i/{\lambda }_0\right)$, respectively, and by summing up over $1\le i\le 144$ [51]. The contribution of the $n$-th wavenumber to the total variance of the series in (1) was proportional to $a_n^2+b_n^2$ [51]. From now on, the $n$-th wavenumber will be denoted as Wn (e.g., W1 for wavenumber 1).

Shown in Figure 1 is the average seasonal contribution from W1 to W10 to the ZGH’s total variance at 35° S and 50° S in the southern summer (December-January-February, DJF) and winter (June-July-August, JJA) in both reanalyses. The uppermost wavenumber in the abscissa of Figure 1’s panels corresponds to the upper limit of the baroclinic synoptic waves, which typically span W7–W10 [52] (p. 481). In DJF, the contribution to the total variance of the first ten wavenumbers in the ERA5 dataset ranged from 15.58% (W4) to 1.68% (W10) at 35° S and from 27.01% (W1) to 0.36% (W10) at 50° S (Figure 1a). When Figure 1a,b were compared, the differences between the two datasets in DJF were negligible. In both cases, the represented variance of W1, W3, and W4 was greater at 50° S, and the converse occurred for the rest of the wavenumbers at 35° S. The most notable differences between JJA and DJF was an increase in W1’s activity at the expense of the shorter waves (with the exception of W3) at 35° S, whereas W2, W3, and W4 increased their represented variance at 50° S (Figure 1c,d). In DJF, the ten wavenumbers altogether accounted for 96.49% and 99.47% of the total variance at 35° S and at 50° S, respectively, in the ERA5 dataset, versus 97.04% and 99.56%, respectively, in the NCEP dataset. In JJA, the shortest ten waves represented 98.03% (35° S) and 99.41% (50° S) of the total variance in the ERA5 dataset, against 98.33% (35° S) and 99.55% (50° S) in the NCEP dataset. The overall figures at 35° S reflected an increase in the activity of shorter (i.e., baroclinic) waves during JJA in both reanalyses. In the extratropics and in mid-latitudes, jets were often associated with frontal activity and cyclogenesis [53], among other phenomena. In the SH, there was an increase in baroclinicity during the cold season owing to a combination of the strengthening of the jets and double-jet structures [54,55], which had an impact on the observed activity of shorter waves that could be seen in the highest variability at 500 hPa during the season, a well-established result [56] (p. 62).

According to Figure 1, during the solstices, W1, W3, and W4 had the largest contributions to the variance at both 35° S and 50° S. This is not an unexpected result, for it was found that these wavenumbers drove, to a greater or lesser degree, the four leading Empirical Orthogonal Functions (EOFs) of the 500 hPa height anomalies in the SH with periods longer than 50 days filtered [57]. Specifically, at 50° S, the wavenumbers’ variances in Figure 1 did not quantitatively match those presented in [58], yet their distributions as extracted from the daily values were in qualitative resemblance with each other. Numerically, the discrepancies could arise from a number of factors, among them that the analyses were carried out on quite different datasets, with the one in [58] spanning the 1957–1958 period and having large regions deemed as not reliable [59].

Even though the BI defined further down seemed to encompass the middle troposphere between 35° S and 50° S only (and hence to bound a finite area), the existing literature stated that blocking action in both hemispheres could actually be linked to anomalous conditions located far away from the blockings themselves [60,61,62,63], therefore constituting hemispherical phenomena. Both the interaction of waves with the zonal flow and with each other supported the presence of blockings [64]. In the NH winter, the tracking of the ridges’ positions in W1, W2, and W3 associated with Rex blockings located in two disjoint areas led to the conclusion that the constructive interference between W2 and W3 in the 50° N–60° N range coincided with the presence of maxima frequency of these blockings in one of the areas, and the like occurred for the interference between W1 and W3 in the other region [65] (p. 163) (and references therein), evidencing the pivotal role of W3 to blockings. On the other hand, ref. [29] stressed the preponderance of westward-moving W1s at 500 hPa during blockings in the NH, whereas W2 was relegated to a secondary role. As for the SH, W1, W3, and W4 were associated with three major regimes of persistent anomalies [66]; in particular, W3 played a key part in blockings [18]. Bearing in mind the preceding considerations, the seasonal mean contribution of W1, W3, and W4 to the ZGH’s variance south of 20° S in the study period is illustrated in Figure 2, Figure A1 and Figure A2, respectively (the latter two are presented in Appendix A). The region of interest was extended beyond the 35° S–50° S band, which was formally associated with the BI, so that the wave activity that had the potential to contribute to the formation and maintenance of blockings both within the band and outside of it could be captured. A detailed analysis of the distribution of these variances across the study period is beyond the scope of the present work, and only the salient features will be described.

W1’s variance generally increases southwards [67]. In this study, W1’s variance in both reanalysis datasets was in very good agreement with each other (Figure 2). The minimum values were found at mid-latitudes across the seasons, stretching from 35° S to 45° S in DJF (Figure 2a,e) and spanning approximately the 35° S–50° S belt in JJA (Figure 2c,g), in both cases depending on the year. In general, it was in DJF that W1’s minimum variance was less dispersed latitudinally and confined to the 30° S–50° S band. During autumn (March-April-May, MAM), the minimum variance encompassed a broader latitudinal band (Figure 2b,c,f). It was in JJA and in spring (September-October-November, SON) (Figure 2d,h) that a strengthening of W1’s presence south of 20° S occurred. On the other hand, the dominance of W1 took place south of approximately 75° S, regardless of the season, with maxima variance found over Antarctica, close to the South Pole.

As with W1, the resemblance between W3’s representativeness across the years in the different seasons was also apparent (Figure A1). An outstanding difference between the evolution of W1 and W3 was that, generally speaking, the latter wave had its larger activity between 40° S and 80° S most of the time during all seasons, with spikes of lesser activity at lower latitudes that are more notorious during DJF (Figure A1a,e). Unlike with W1, whose variance was near 100% at high latitudes, W3’s variances barely reached 36%, and the overall maxima took place in JJA in specific years and at particular latitudes, e.g., close to 50° S in 1940 (NCEP) and in a region centered at 60° S in the mid-2000s (both datasets) (Figure A1c,g). Figure A1 also evidences an increase in the latitudinal extension of W3’s activity when DJF is compared to JJA, stretching from 50° S–70° S in the former season to 40° S–70° S in the latter one. Additionally, the maximum variance experienced a seasonal migration, reaching its northernmost position during JJA, in concomitance with the northward advance of the baroclinic zone mentioned in the preceding lines. When W4 is considered, its variance was capped at 30%, slightly below W3’s top values, and it was generally prominent between 40° S and 50° S in both datasets and in all seasons, yet maximum activity took place in MAM (Figure A2). These results were in consonance with earlier outcomes, as it was found that W4 dominated the 300 hPa field near 50° S on intra-seasonal scales [68]. In contrast with W1 and W3, W4 had a poor contribution to the total variance beyond 70° S, accounting for less than 10%.

2.2. The Blocking Index

Despite the first ten terms in (1) generally taking on the largest fraction of the total variance, in order to isolate the contribution of different wavelengths to the ZGH values at 35° S and 50° S, these were reconstructed using (1) with the inclusion of those waves whose explained variance was greater or equal to 1%, so that the activity of any wavelength shorter than ${\lambda }_0/10$, i.e., the uppermost limit in Figure 1, was individualized as well. It is worth noting that the greater the wavenumber, the more distorted the ZGH field was. The reconstructed ZGH field ${\tilde{z}}_i\left(\phi \right)$ was employed to identify blockings at each of the 144 longitudes by means of the BI defined in [22] as

$${\left(BI\right)}_i={\tilde{z}}_i\left(35°S\right)-{\tilde{z}}_i\left(50°S\right)<0$$

(2)

with $1\le i\le 144$. The negative values in (2) implied reversions of the meridional gradient in ZGH, and hence, the potential locations of blockings. Along with ${\left(BI\right)}_i<0,$ the following condition was required:

$${\displaystyle \frac{{\left(BI\right)}_{i-4}+{\left(BI\right)}_i+{\left(BI\right)}_{i+4}}{3}}<0$$

(3)

The above requisite ensured that the average value of the BI at three contiguous longitudes that were separated from each other by 10° was also negative. In other words, condition (3) required that the longitudinal span of the potential blockings was at least 30°, therefore excluding gradient reversions of the ZGH with local origin. Expression (3) could have been used as the value of the BI itself at longitude $i$; nonetheless, it was simply set as ${\left(BI\right)}_i$ in this paper, so the division by 3 in (3) was irrelevant to our study. Hence, the simultaneous fulfillment of (2) and (3) located a blocking case at longitude $i$ with an intensity value ${\left(BI\right)}_i$. The resulting blocking climatology was given for every 2.5° of longitude. In order to make our outcome comparable to previous research efforts, all the located blocking cases for each reanalysis were aggregated into pre-conditioned longitudinal bands of width 10°. These pre-conditioned longitudes were defined as $lon\left(i\right)=10°\times \left(i-1\right)\left(1\le i\le 36\right)$, and the correction $360°-lon\left(i\right)\to lon\left(i\right)$ was applied if $lon\left(i\right)>180°$ (as in the case of the NCEP database) so that positive (negative) longitudes were associated with the Eastern (Western) Hemisphere. For every longitude $LON,$ the counting condition $lon\left(i\right)\le LON<lon\left(i+1\right)$ was applied.

3. Results

3.1. An Introductory Example

The 500 hPa fields associated with the greatest absolute value of the BI in the period 1948–2021 were introduced in [20]. We present here an alternative approach not related to intensities but to persistence. The example relied upon the fields tied to the occurrence of 12 consecutive days of blocking cases (i.e., a blocking event, BE) between 18 and 29 August 2001 that were located at the three adjoining longitudes 145° W, 142.50° W, and 140° W in the ERA5 dataset, and 147.50° W, 145° W, and 142.50° W in the NCEP dataset. This example consisted of the longest-lived BE that was located in both datasets. Figure 3 shows the evolution of the absolute value of the BI in the 18–29 August 2001 time span at the corresponding longitudes. It was at these longitudes that the BI was strictly negative for 12 days, yet the BI was also negative beyond these longitudes for shorter periods. For instance, in the ERA5 dataset, between 18 and 29 August 2001, there were other regions fulfilling the blocking conditions (2) and (3) in the 167.50° W–132.50° W area. More specifically, on 18 August 2001, the conditions were satisfied in the 167.50° W–140° W area, and on 29 August 2001, the region shrank in extension and shifted to the east (145° W–132.50° W). Therefore, and in accordance with (3) this BE had a much greater spatial extension than just 5°, as Figure 3 might suggest. The presented BE was the one with the most number of longitudes exhibiting blockings in both datasets. There was just another BE that lasted 12 days, but it was located in the ERA5 dataset only: it was positioned further east, stretching across 107.50° W–102.50° W, and encompassed the 5–16 July 1987 period.

With values of the BI below −100 m at two of the three longitudes for six consecutive days, from 19 to 24 August, this BE seemed to have intensified in the ERA5 dataset (Figure 3a) earlier than in the NCEP counterpart (Figure 3b) in which, between 22 and 24 August, lower values of the BI were reached at the three longitudes. Actually, considering days and longitudes altogether, the event was, on average, slightly more intense in the ERA5 dataset (−82.22 m) than in the NCEP dataset (−80 m).

Figure S1 shows an animation of the 500 hPa field south of 20° S, between 18 and 29 August 2001. The wind field at 200 hPa was also included in the case of the NCEP dataset. On 22 and 23 August, the 500 hPa field attained a clear split flow pattern in which the split jet centered just east of 150° W; simultaneously, a reversal from westerlies to easterlies around 40° S persisted for at least four days, between 21 and 24 August. On 22 August, the most representative wavenumbers in 500 hPa at 35° S were W1 (51.46%), W6 (11.23%), and W2 (10.52%) in the ERA5 dataset; and W1, W6, and W2 took on 48.40%, 14.51%, and 10.80% of the variance, respectively, in the NCEP dataset. On the other hand, at 50° S, the most dominant waves were W3 and W1, representing 63.24% and 12.67% of the variance, respectively, in the ERA5 dataset; and 72.84% and 10.07%, respectively, in the NCEP dataset.

3.2. Climatic Characteristics Regardless of Duration

The total number of blocking cases that were located by the blocking-finding algorithm in the 1940–2022 period was 37,477 (ERA5) and 26,564 (NCEP), irrespective of the longitude. The greater number of cases in the ERA5 dataset was partly related to their series spanning 83 years versus 75 years in the NCEP counterpart. However, these figures led to annual averages of approximately 452 and 354 cases per year (CPY) for the ERA5 and the NCEP datasets, respectively, clearly indicating the presence of a greater relative number of blockings in the former reanalysis. If the common period 1948–2022 was considered, the grand total in the ERA5 dataset was 33,889; it still represented 452 CPY. Figure 4 shows the annual total number of blocking cases that were located in the analyzed period for the ERA5 and the NCEP datasets consolidated for every 10° of longitude, the differences in the annual totals, and the seasonal breakdown of these differences.

According to Figure 4a, the counting of blocking cases in the ERA5 dataset expectedly exceeded that in the NCEP counterpart at all the longitudes. A restriction of the ERA5 dataset to the 1948–2022 period did not exhibit noticeable differences regarding the location of blockings (Figure 4b). The maximum number of cases occurred just west of the DL in both reanalyses, and there seemed to be a second-rank maximum to the west of the Greenwich Meridian (GM). It can also be seen that the distribution of both the counting of blocking cases, as well as the differences between the two reanalyses (ERA5 minus NCEP), were not homogeneous across the globe (Figure 4c). The annual totals show that there were three distinct regions in which the differences maximized. The first-rank maximum was located just west of the DL, and second- and third-rank maxima occurred in the south-eastern Pacific (SEP), west of South America (SA); and the south-western Atlantic (SWA), east of SA, respectively. It is also worth noting that the seasonal differences did not follow the annual pattern and had an uneven distribution. In DJF, the west of the DL sector had a prominent maximum when compared to the rest of the longitudes (Figure 4d). DJF had the peculiarity of having the only negative value in the differences: a blocking case was located at 50° E in the NCEP dataset only. This is not reflected in Figure 4d, as it shows positive values only. During MAM, there was an increase in the differences in the west of the DL, along with a more noticeable rise in the SEP area (Figure 4e). It was in JJA that the differences in these two regions were nearly head-to-head (Figure 4f). As for SON, it was the season with the overall lower differences (Figure 4g). On the other hand, a noticeable growth in the differences within the 40° W–10° W sector took place during JJA and SON.

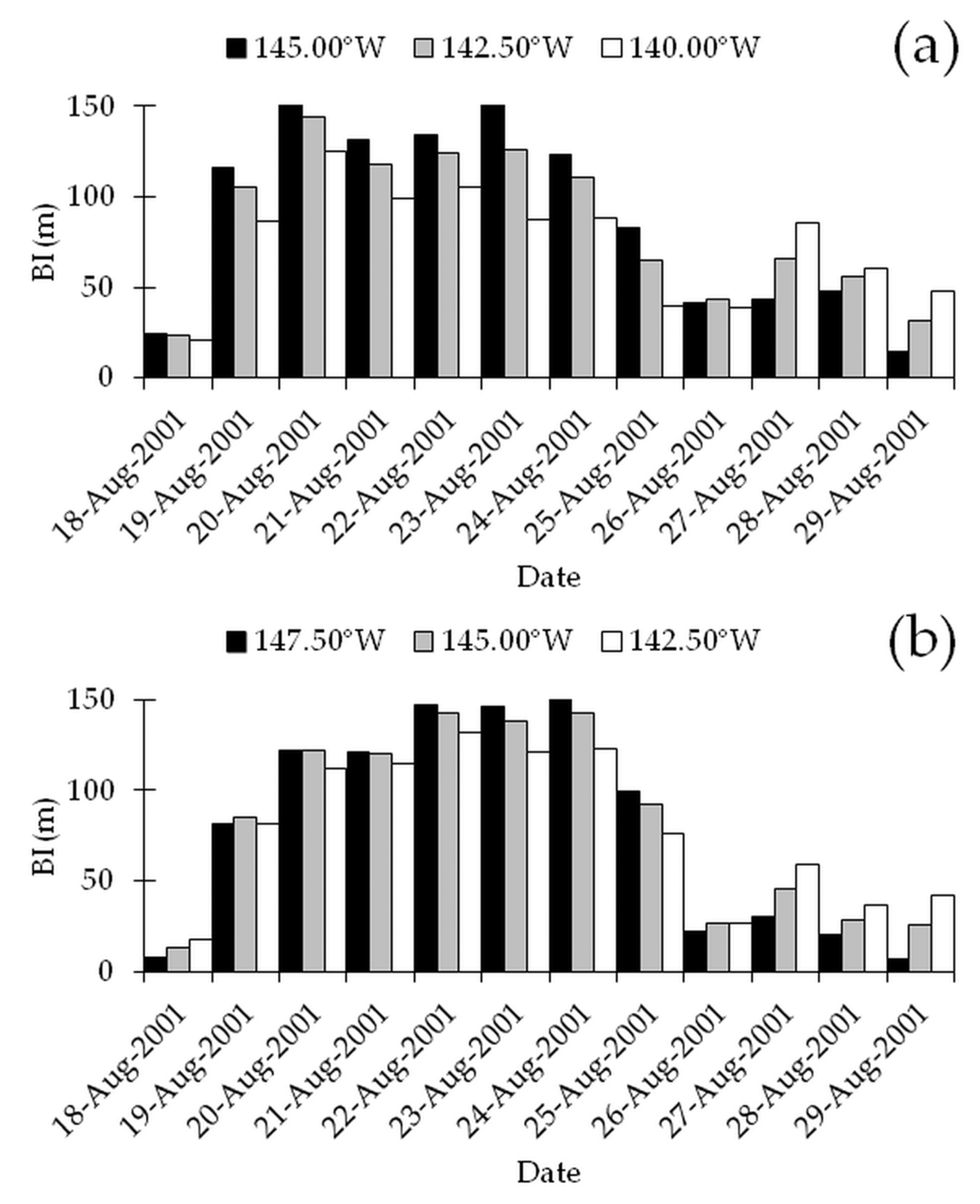
3.2.1. Comparative Distributions Across the Longitudes

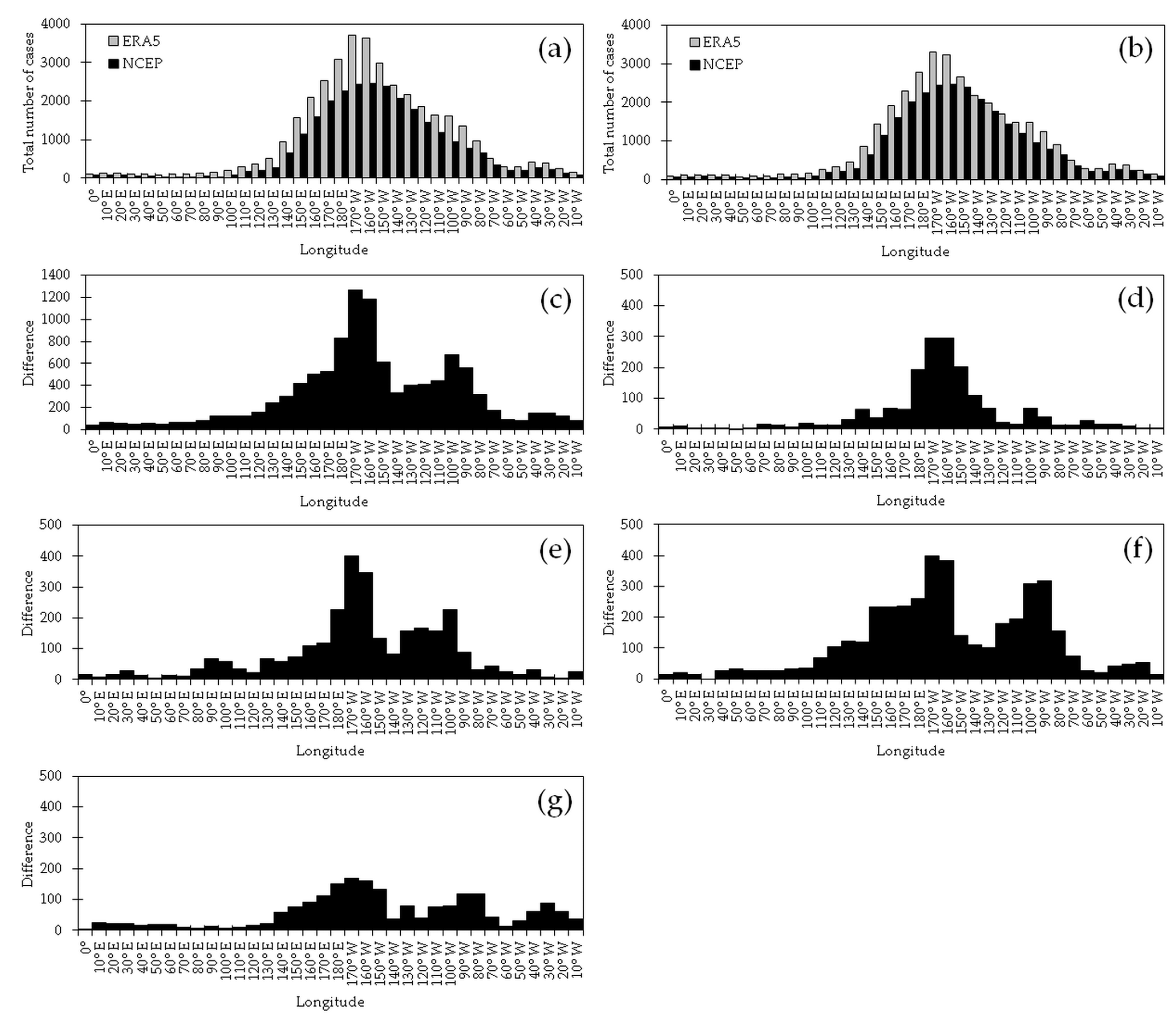
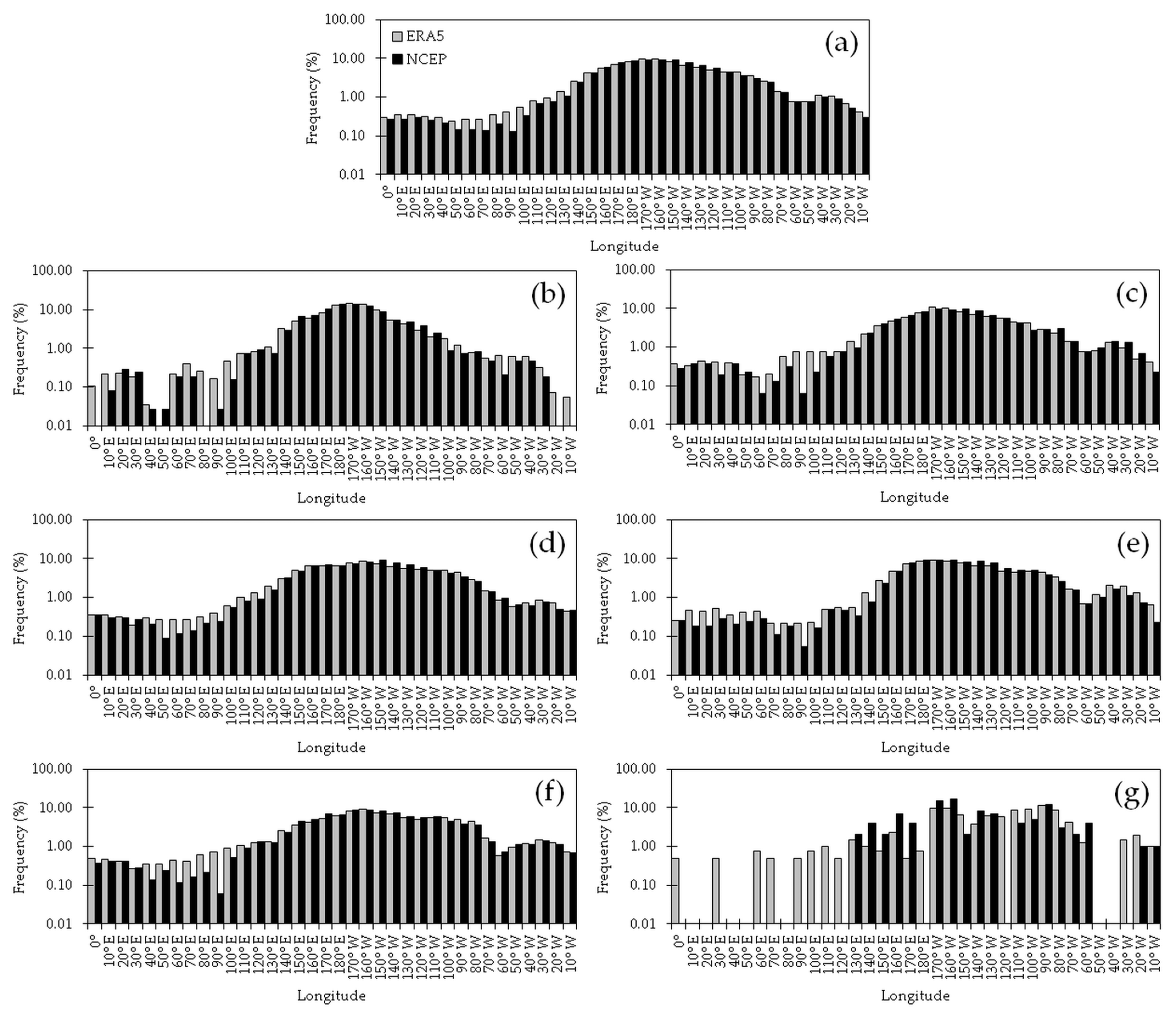
Figure 4 presents an overview of the climatology of blocking cases in both datasets, but given that each entire dataset spanned different periods, the absolute values were not appropriate for making comparisons. Following this, Figure 5 shows the annual and seasonal distributions in the frequency of blockings for every 10° of longitude in the two datasets. Unlike with the absolute values, the frequencies were normalized, and hence, they were comparable to each other, despite one of the records being longer. As in Figure 4a, the annual averages showed that the entire Pacific basin was the preferred region for the occurrence of blockings, and apparent secondary and tertiary maxima, as enhanced by the logarithmic vertical scale, occurred to the west and to the east of the GM, respectively (Figure 5a). The overall maximum took place at 170° W (9.86%) and 160° W (9.26%) in the ERA5 and in the NCEP datasets, respectively. These maxima shifted to the east of the one found in [22], in which the Australian dataset (ADS) encompassing less than 10 years was used, and the maximum, west of the DL, represented less than 5% of the total blocking cases. The secondary maxima were located at 40° W in both the ERA5 (1.11%) and the NCEP (1.01%) datasets; the tertiary maxima took place at 20° E in both datasets too, representing 0.35% (ERA5) and 0.30% (NCEP). Second- and third-rank maxima were also found in [22] the west and east of the GM, respectively. Our results were also in agreement with those presented in [18], whose calculations were carried out using the ADS, too, but the approach of persistent anomalies for the location of blockings was taken. Their overall maximum was vaguely described as taking place in the New Zealand sector within a longitudinal region stretching across 60°, and the secondary and tertiary maxima were situated in SWA and in the Southern Indian Ocean, respectively.

On a longitude-by-longitude analysis, the frequencies in the ERA5 and the NCEP datasets generally matched well across the SH; the exception was the 50° E–90° E area, where the values were quite lower in the latter reanalysis. For the distributions in Figure 5a, the asymmetry coefficients, measured through the skewness coefficients [69] (p. 28), were 1.01 (ERA5) and 0.94 (NCEP). This implied the presence of more blocking cases in the WH than in the EH in both reanalyses, something that is obscured in Figure 5a owing to the smoothing created by the logarithmic scale but can be easily identified in Figure 4a. A simpler support for these asymmetry values could be given by the number of blocking cases in the two hemispheres, which accounted for 25.93% (ERA5) and 25.18% (NCEP) in the EH, versus 74.07% (ERA5) and 74.82% (NCEP) in the WH. The skewnesses for the rest of the distributions in Figure 5 could also be exploited as a measurement of the seasonal adjustment in the frequency of blocking cases across the longitudes and the hemispheres.

Let us label the percentual frequencies introduced in Figure 5 as $f_{ERA5}$ and $f_{NCEP}$ for the ERA5 and the NCEP datasets, respectively. The difference $f_{ERA5}-f_{NCEP}$ is illustrated in Figure 6. The subtraction of the NCEP figures from the ERA5 ones is in agreement with the results presented in Figure 4. Nevertheless, for the assessment of the difference, a reversion in the foregoing subtraction leads to the same results, as explained below. The difference $f_{ERA5}-f_{NCEP}$ can be written as $100\times \left(p_{ERA5}-p_{NCEP}\right)$, where $p_{ERA5}=n_{ERA5}/N_{ERA5}$ and $p_{NCEP}=n_{NCEP}/N_{NCEP}$ are the proportion of located blockings at any given longitude for the ERA5 and the NCEP datasets, respectively, estimated using the number of cases at that longitude, $n_{ERA5}$ and $n_{NCEP}$, over the total number of located blockings, $N_{ERA5}$ and $N_{NCEP}$, either in the annual average or in the corresponding season. At every longitude, in order to establish whether $p_{ERA5}$ and $p_{NCEP}$ differed statistically from zero, the pooled z-test for independent proportions was employed. To address the difference, and following [70], the statistic below, which includes the correction for continuity, was compared against the critical value $z_c$ of the normal distribution having a mean equal to 0 and a standard deviation equal to 1:

$$z={\displaystyle \frac{|p_{ERA5}-p_{NCEP}|-\frac{1}{2}\left(\frac{1}{n_{ERA5}}+\frac{1}{n_{NCEP}}\right)}{\sqrt{\widehat{p}\widehat{q}\left(\frac{1}{n_{ERA5}}+\frac{1}{n_{NCEP}}\right)}}}$$

(4)

In the above equation, $\widehat{p}$ stands for the pooled proportion $\widehat{p}=\left(n_{ERA5}{p}_{ERA5}+n_{NCEP}{p}_{NCEP}\right)/\left(n_{ERA5}+n_{NCEP}\right)$ and $\widehat{q}=1-\widehat{p}$. If $p_{ERA5}=p_{NCEP}$, by taking into account the number of cases in each sample, the second term in the numerator of (4) prevents us from erroneously considering the two proportions as statistically equal unless the values of both $n_{ERA5}$ and $n_{NCEP}$ are sufficiently large. As expected, switching the variables in (4) yields the same outcome, and, hence, the order of the proportions in the subtraction $p_{ERA5}-p_{NCEP}$ is irrelevant to the test. Setting the level of significance at 95%, at every longitude, there was a statistical difference between the corresponding proportions $p_{ERA5}$ and $p_{NCEP}$ if $\left|z\right|>1.96$. Figure 6 also accounts for the outcome of the test.

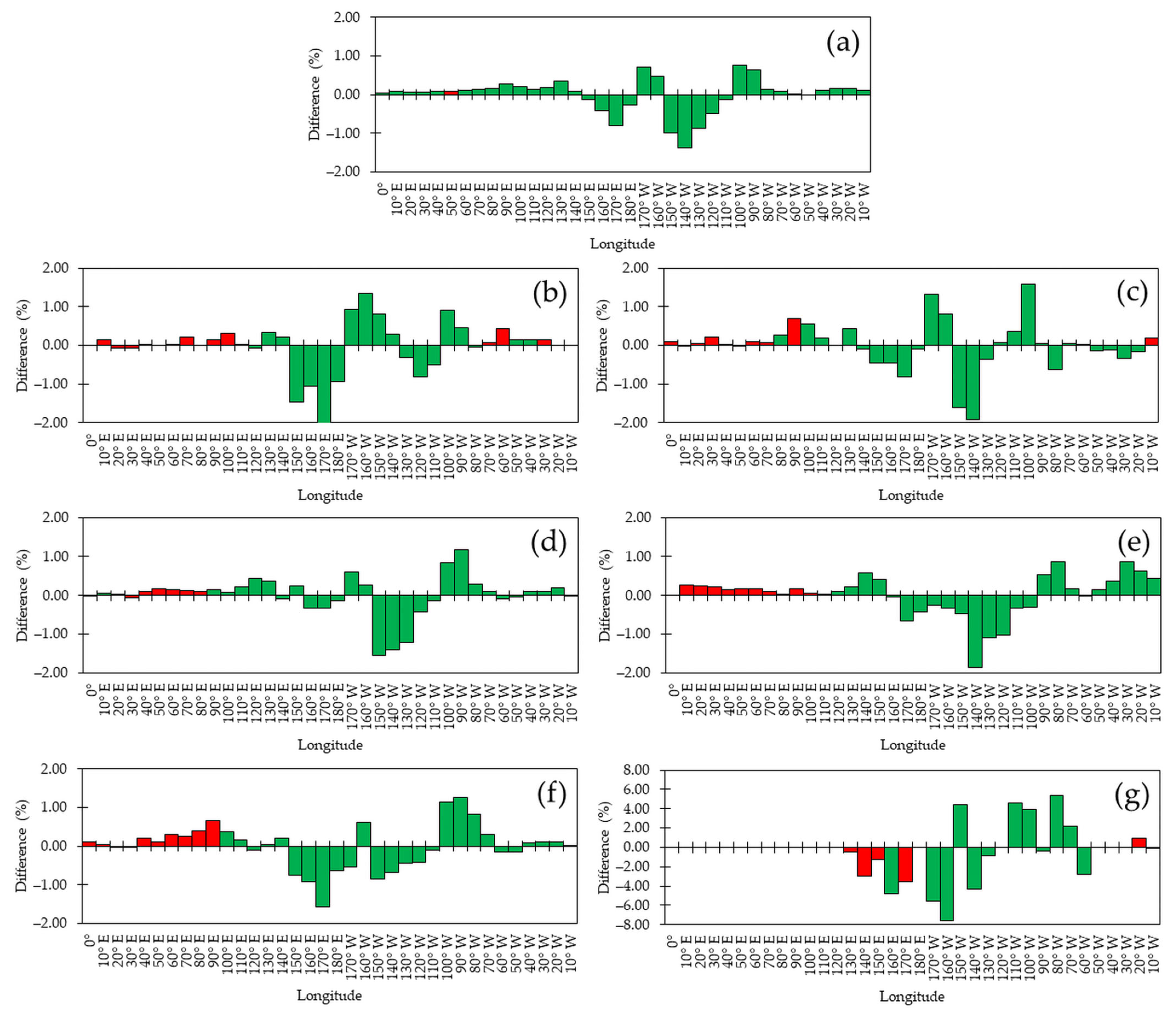
Figure 6. Difference $f_{ERA5}-f_{NCEP}$ in correspondence to the values presented in Figure 5: (a) annual; (b) DJF; (c) MAM; (d) JJA; (e) SON. Panels (f) and (g) show the annual distribution of $f_{ERA5}-f_{NCEP}$ for the blocking index restricted to values less than –100 m and –200 m, respectively. The vertical scales are the same in all the panels, with the exception of (g). Red bars indicate a statistical difference that was significant at a 95% level of confidence, green bars indicate no statistical difference, and blanks indicate that significance could not be assessed due to missing data in either dataset.

Figure 6. Difference $f_{ERA5}-f_{NCEP}$ in correspondence to the values presented in Figure 5: (a) annual; (b) DJF; (c) MAM; (d) JJA; (e) SON. Panels (f) and (g) show the annual distribution of $f_{ERA5}-f_{NCEP}$ for the blocking index restricted to values less than –100 m and –200 m, respectively. The vertical scales are the same in all the panels, with the exception of (g). Red bars indicate a statistical difference that was significant at a 95% level of confidence, green bars indicate no statistical difference, and blanks indicate that significance could not be assessed due to missing data in either dataset.

On an annual basis, the two datasets were indistinguishable from one another at all the longitudes, with the exception of 50° E (Figure 6a). Furthermore, the datasets differed by 2% at most (the ordinate’s top and bottom values), and the largest discrepancies were recorded in the Pacific, east of the DL, between 150° W and 130° W. Actually, the extreme value occurred at 140° E, where the number of blockings in the NCEP dataset exceeded that in the ERA5 counterpart by 1.38%. It is also worth stressing that the differences were positive between 100° W and 140° E, negative in the 150° E–180° E range, positive in the 170° W–160° W region (where the greater counting of blockings was recorded in both datasets, cf. Figure 5a), and negative between 150° W and 110° W.

In order to focus the analysis of the frequency distributions in Figure 5 across the seasons in just three different regions covering the SH, for comparison purposes, we followed [22] and defined the Pacific (PAC, 110° E–80° W), the Atlantic (ATL, 70° W–0°), and the Indian Ocean (IND, 10° E–100° E) regions.

Table 1. Frequencies of blocking cases in the Pacific (PAC, 110° E–80° W), the Atlantic (ATL, 70° W–0°), and the Indian Ocean (IND, 10° E–100° E) regions. Values expressed in percentages based on the corresponding annual or seasonal totals.

Region	Annual		Season
			DJF		MAM		JJA		SON
	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP
PAC	90.11	92.09	94.82	96.96	89.12	90.69	90.66	91.82	86.69	90.85
ATL	6.48	5.80	3.02	1.83	6.57	6.97	6.05	5.77	9.84	7.26
IND	3.41	2.12	2.16	1.22	4.31	2.34	3.29	2.41	3.48	1.88

shows the annual and seasonal frequencies at these regions. On an annual basis, the frequency of blocking cases in the PAC accounted for 90.11% (ERA5) and 92.09% (NCEP) of the totals, 6.48% (ERA5) and 5.80% (NCEP) in the ATL, and 3.41% (ERA5) and 2.12% (NCEP) in the IND.

In DJF (Figure 5b), the maximum frequency occurred at 170° W in the ERA5 dataset (14.65%) and at 180° E and 170° W (13.71% each) in the NCEP dataset; a secondary maximum was found at 60° W in the ERA5 (0.65%) and at 50° W and 40° W in the NCEP (0.48% each). In the ERA5 dataset, a tertiary maximum took place at 70° E (0.40%), and there was also a quaternary maximum that peaked at 20° E (0.23%). There were third- and fourth-rank maxima in the NCEP dataset too: the former took place at 20° E (0.29%), while the latter was circumscribed to just two longitudes, at 60° E and 70° E, accounting for 0.19% each. Generally speaking, the differences between the two datasets were not significant in the region that stretched between 110° E and 70° W, and they were significant elsewhere (Figure 6b). As in the annual case, the largest values took place in the region of maximum counting, between 150° E and 90° W; clusters enclosing up to four adjoining longitudes with differences of the same sign alternated with each other within this area. The difference exceeded the 2% threshold at 170° E (2.28%), where more blockings were located in the NCEP dataset.

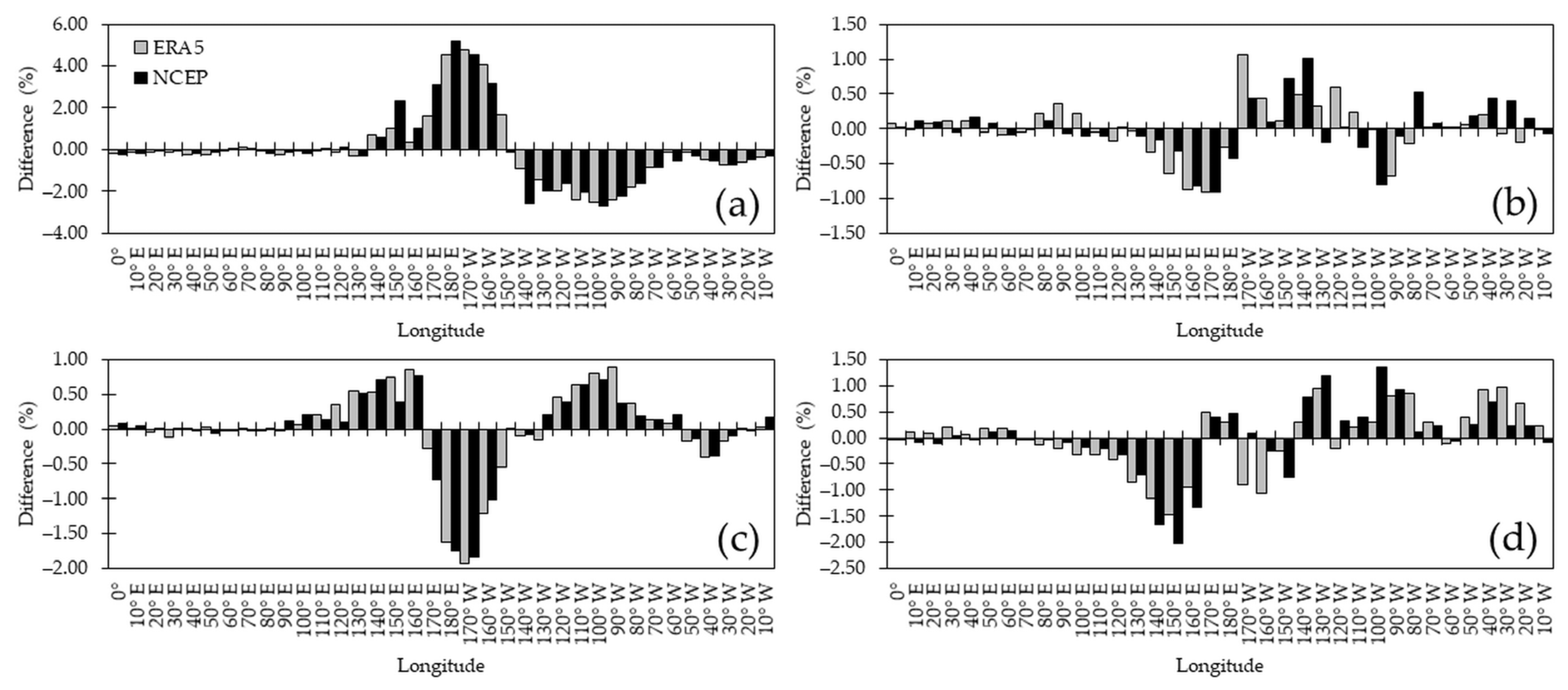
Further details could be extracted from the comparisons with the annual frequencies. Figure 7 shows the deviations of the seasonal distributions with respect to the annual average. The first thing worth noting is that DJF had the largest deviations of all seasons (Figure 7a). Aside from this, the most outstanding feature during DJF was the noticeable reduction in the number of blocking cases east of 150° W in both reanalyses, and that there was an even more notable increase—up to 5.21% in the NCEP case, in the 140° E–160° W sector. As drawn by a visual inspection of Figure 5a, in general terms, the excesses and deficits in the DJF frequencies were in apparent concordance across the longitudes in both datasets. We used Spearman’s correlation coefficient $\left(\rho \right)$, which relates the ranks of the data pairs rather than the raw values as the Pearson’s correlation coefficient does [69,71], as a single parameter to quantify this. The greater the absolute value of $\rho ,$ the more likely the correlated variables were related by a monotonous, yet undetermined, increasing $\left(\rho >0\right)$ or decreasing $\left(\rho <0\right)$ function. The calculations of $\rho$ were carried out using the subroutine spear included in [72]. The value of $\rho =0.91$ for DJF indicated that the deviations in both datasets were actually in very good agreement with each other.

The concentration of more blockings around the DL in DJF led to an imbalance in the frequencies (as seen in Figure 7a) that was consistent with larger skewnesses of the corresponding distributions in Figure 5b, namely 1.68 (ERA5) and 1.37 (NCEP). Alternatively, this was backed by an increase in the counting of blockings in the EH to 27.63% (ERA5) and to 30.87% (NCEP) of the total number of recorded cases in the season.

In a regional fashion, the frequencies during this season decreased with respect to the annual average to 3.02% (ERA5) and 1.83% (NCEP) in the ATL and to 2.16% (ERA5) and 1.22% (NCEP) in the IND, in favor of an increase to 94.82% (ERA5) and 96.96% (NCEP) in the PAC (Table 1).

Four different regions where blockings were more prone to occur during MAM could be located in the ERA5 dataset from Figure 5c: the maximum frequency took place at 170° W (10.92%) and second-, third-, and fourth-rank maxima occurred at 40° W (1.32%), 90° E (0.77%), and 20° E (0.44%), respectively. A spread in the frequencies across the longitudes was more apparent in the NCEP dataset, as the absolute maximum occurred at 150° W (9.69%), and local maxima could be spotted at 80° W (2.98%), 40° W (1.43%), 20° E and 40° E (0.38% each), and 80° E (0.32%). Yet with alternating signs in the differences, the counts of blockings in both datasets were in overall statistical agreement between 100° E and 20° W (Figure 6c) and in disagreement elsewhere. The larger difference, slightly below 2%, occurred at 140° W, with fewer blockings located in the ERA5 dataset. Moreover, it is worth pointing out that there was a local increase in the differences in the 50° W–20° W band in the region that exhibited an autumnal rise in the number of blockings; in this area, the counting in the NCEP dataset outnumbered the ERA5’s by as much as 0.33% at 30° W.

At first sight, and opposite to DJF, there seemed to be an overall decrease (increase) in the frequency of blockings in the EH (WH), yet with values that did not exceed 1.50%, both in the positive and in the negative deviations (Figure 7b). This was actually the case, as the percentages of detected blockings in the EH decreased to 23.86% (ERA5) and to 22.99% (NCEP). With exceptions, at longitudes beyond the vicinities of the DL, the frequencies were discrepant; the low value $\rho =0.40$ captured this mismatch well. According to Table 1, the big picture shows that blockings were less frequent than in the annual average in the PAC―and hence, more frequent in the two remaining sectors in both datasets. More specifically, the frequencies in the PAC constituted 89.12% (ERA5) and 90.69% (NCEP) of the total number of cases in the season, they were 6.57% (ERA5) and 6.97% (NCEP) in the ATL, and in the IND, they reached 4.31% (ERA5) and 2.34% (NCEP).

The low value of $\rho$ warrants a deeper analysis of the discrepancies. The literature’s usual assumption that any pixel in either the ERA5 or the NCEP datasets could be used as a proxy for an observation (e.g., [73]) might, within the scope of the present work, have entered into conflict in MAM. Aside from the statistical indistinguishability in the 100° E–20° W range (Figure 6c), both datasets were discordant at several longitudes regarding the departures from the corresponding annual averages (Figure 7b), so the selection of a third dataset was in order for the evaluations. As for the ERA5 dataset, in the NH, the occurrence of blockings was overestimated in the 0–30° E region when compared with the Coupled Model Intercomparison Project (CMIP) multimodel dataset in their Phases 5 (CMIP5) [74] and 6, which included 29 and 32 datasets, respectively [6] (p. 465). Unfortunately, to the best of our knowledge, no such comparisons were presented for the SH. Notwithstanding, annual and seasonal climatologies for the occurrence of blockings were introduced in [75] using the ERA-Interim (ERA-I) [76,77] and the CMIP5 datasets. Despite using a different methodology than the one used here for the detection of blockings (the authors in [75] based their definition of a blocking on persistent anomalies of surface pressure above a threshold), comparisons with their outcome are of interest to interpret our results, given the general barotropic nature of blockings (e.g., [2] (pp. 334–335), [78] and references therein). Also worth considering is that only four different models belonging to the CMIP5 dataset were used in [75]. In spite of this, it could be seen that this CMIP5 subset showed an increase in the frequencies of blocking occurrences along 45° W, north of 45° S, during MAM ([75]; see their Figure 2), something that was, to a greater or lesser degree, in accordance with the differences shown in Figure 7b for both datasets. In contrast, according to [75], there was a slight decrease in the frequency of blockings between 135° W and 90° W during MAM in the CMIP5 dataset; this was unmatched in the ERA5 dataset, but the decrease in the blocking counting seemed to be properly reproduced in the NCEP dataset within the area (Figure 7b). These disparate results could be tied to the location of blockings being sensitive to the chosen dataset [42].

Skewness minima were recorded during JJA (Figure 5d), which meant that the number of blockings in the EH and in the WH had the least difference of all seasons. Blockings in the former hemisphere accounted for 28.84% of the season’s total, the greatest of all seasons in the ERA5 dataset, while in the NCEP dataset, this percentage was 27.45%, only exceeded by the one in DJF (30.87%). The skewness represented this situation well, as it was lower for the ERA5 distribution than for the NCEP counterpart. The frequencies, as estimated from both datasets, were statistically different between 20° E and 80° E, whereas they were alike elsewhere (Figure 6d). Again, the maximum absolute difference in the frequencies, 1.55% at 150° E, took place in or close to the region where the most number of blockings were located (Figure 5d). It was also embedded in a cluster of longitudes where the NCEP figures outnumbered the ERA5 ones, 150° W–110° W, with the difference decreasing eastwards, ultimately shifting to positive values in the 100° W–70° W band. Besides significance, Figure 6 also shows that JJA was the season that had the overall lower difference.

Regarding the deviations with respect to the annual average, the results in both reanalyses agreed reasonably well, with $\rho =0.86$ (Figure 7c). The maximum frequencies still occurred in the surroundings of the DL, at 160° W (8.51%) and at 150° W (8.98%) for the ERA5 and the NCEP datasets, respectively (Figure 5d). The two distinct maxima that were located on both sides of the GM in DJF merged into a single lobe of secondary maxima in JJA. In the ERA5 dataset, it spanned approximately the 50° W–30° E longitudes with a peak (0.87%) in the SWA at 30° W; in the case of the NCEP dataset, this single lobe also had its peak at 30° W (0.78%), but it stretched from 40° W to 50° E. A remarkable contrast with respect to DJF was the reduction in the number of blockings within the 170° E–130° W range when compared to the annual average, which resulted in an increase in the frequencies just east and west of this range (Figure 7c).

Regionally, when compared with the annual figures, there was an increase in blocking cases in the PAC in the ERA5 dataset (90.66%), whereas a decrease in the NCEP dataset occurred (91.82%); a decrease to 3.29% and an increase to 2.41% were recorded in the IND in the ERA5 and in the NCEP datasets, respectively. On the other hand, the behavior in both reanalyses was the same in the ATL, with decreases to 6.05% (ERA5) and to 5.77% (NCEP) (Table 1).

As for SON, the primary location of blockings was just east of the DL, at 170° W in both reanalyses, accounting for 8.97% (ERA5) and 9.24% (NCEP) of the total number of the seasons’ cases (Figure 5e). The frequencies were in statistical disagreement between the GM and 100° E, and concordant elsewhere (Figure 6e). The maximum absolute difference took place at 140° W (1.87%). Moreover, blockings in the ERA5 dataset outnumbered those in the NCEP counterpart between 90° W and 160° E, and the opposite occurred beyond these longitudes.

Overall, the EH had an apparent reduction in frequencies when compared with the annual averages, whereas in the WH east of 150° W, the opposite took place (Figure 7d). This was confirmed by the counting of blocking cases, which, in the EH, reached the lowest value in both reanalyses, accounting for 21.26% (ERA5) and 19.09% (NCEP), and resulted in more symmetric distributions than in the annual case, as supported by the skewness values of 0.89 (ERA5) and 0.93 (NCEP). In addition, according to Figure 7d, the negative deviations were stronger than the positive ones. Indeed, the frequencies around 150° E went down to just below –2%, whereas the largest excesses, at 100° W, were slightly below 1.5%, with the anomalies in both cases being stronger in the NCEP dataset. The correlation between the anomalies in both datasets resulted in $\rho =0.82$; this aligned with the deterioration in the longitudinal jointness when compared with the solstices (Figure 7a,c). On the other hand, only second- and third-rank maxima could, at first glance, be devised from Figure 5e, but Figure 7d aids with splitting the 110° W–10° W sector with positive frequency anomalies into two separate areas, namely 120° W–70° W in the SEP and 50° W–20° W in the SWA, with negative anomalies in between. Following this, the second-rank maximum occurred at 100° W, representing 4.63% (ERA5) and 4.93% (NCEP) of the total number of cases, and the third-rank maxima took place at 40° W in both the ERA5 (2.04%) and the NCEP (1.68%) datasets. The fourth-rank maximum was at 30° E (0.51%) in the ERA5 dataset, and in the NCEP dataset, there was a lobe of relative maximum frequencies that spanned the 0–90° E range and peaked at 30° E and at 60° E (0.28% each).

When compared to the regional annual figures, there was a decrease in the counting of blockings in the PAC to 86.69% (ERA5) and to 90.85% (NCEP) at the expense of a rise in the other two sectors (ERA5) (Table 1). Regarding the NCEP dataset, the frequency reshuffling entailed a decrease in both the PAC and the IND (1.88% versus 2.12%) and an increase in the ATL (7.26% versus 5.80%).

The annual distributions of blocking cases restricted to $BI<-100m$ and $BI<-200m$ are concisely discussed for the sake of completeness. It can be seen from Figure 5f that the distribution for $BI<-100m$ followed a pattern that was similar to the one for the entire sample of blockings (Figure 5a). The skewnesses revealed that these blockings were more symmetrically distributed around the DL. The frequency differences in Figure 6a,f generally resembled each other, but with magnified values in the latter case. A noteworthy feature was that in the area stretching from the GM to 90° E, the differences were significant and reached their maximum value (0.66%) in the latter longitude. When compared with Figure 6a, the overall maximum is positioned at 170° E, where these mid-intense blockings were more frequent in the NCEP database by 1.58%. Actually, when compared with Figure 6a, greater negative differences were found in the area encompassing the 150° E–180° E band. The opposite occurred in the region between 100° W and 70° W, where positive differences were magnified when compared with Figure 6a. In contrast, the area between the two foregoing regions that saw an amplification of the differences exhibited smaller values, and the difference at 170° W changed from positive to negative.

The most intense blockings, i.e., $BI<-200m$, were more frequent at 90° W in the ERA5 dataset, accounting for 11.60% of the cases, and at 160° W (17%) in the NCEP dataset (Figure 5g). Moreover, in the NCEP dataset, there were no extreme cases within the IND basin; therefore, the associated skewness was relatively large when compared with the ERA5’s counterpart. The frequency difference in these blockings was, in general, greater than the ones discussed so far. The location of the maximum absolute values took place at 170° W (7.62%) and 160° W (5.62%) (Figure 6g). Although statistically indistinguishable, as with the majority of the differences shown in Figure 6g, the counting at the latter two longitudes in the NCEP dataset outnumbered the ERA5 counterpart. Conversely, there existed statistical discordance in the 130° E–150° E range, at 170° E, and in the 20° W–10° W band, with the counting of these particular blockings being greater in the ERA5 dataset than in the NCEP counterpart in the latter case only.

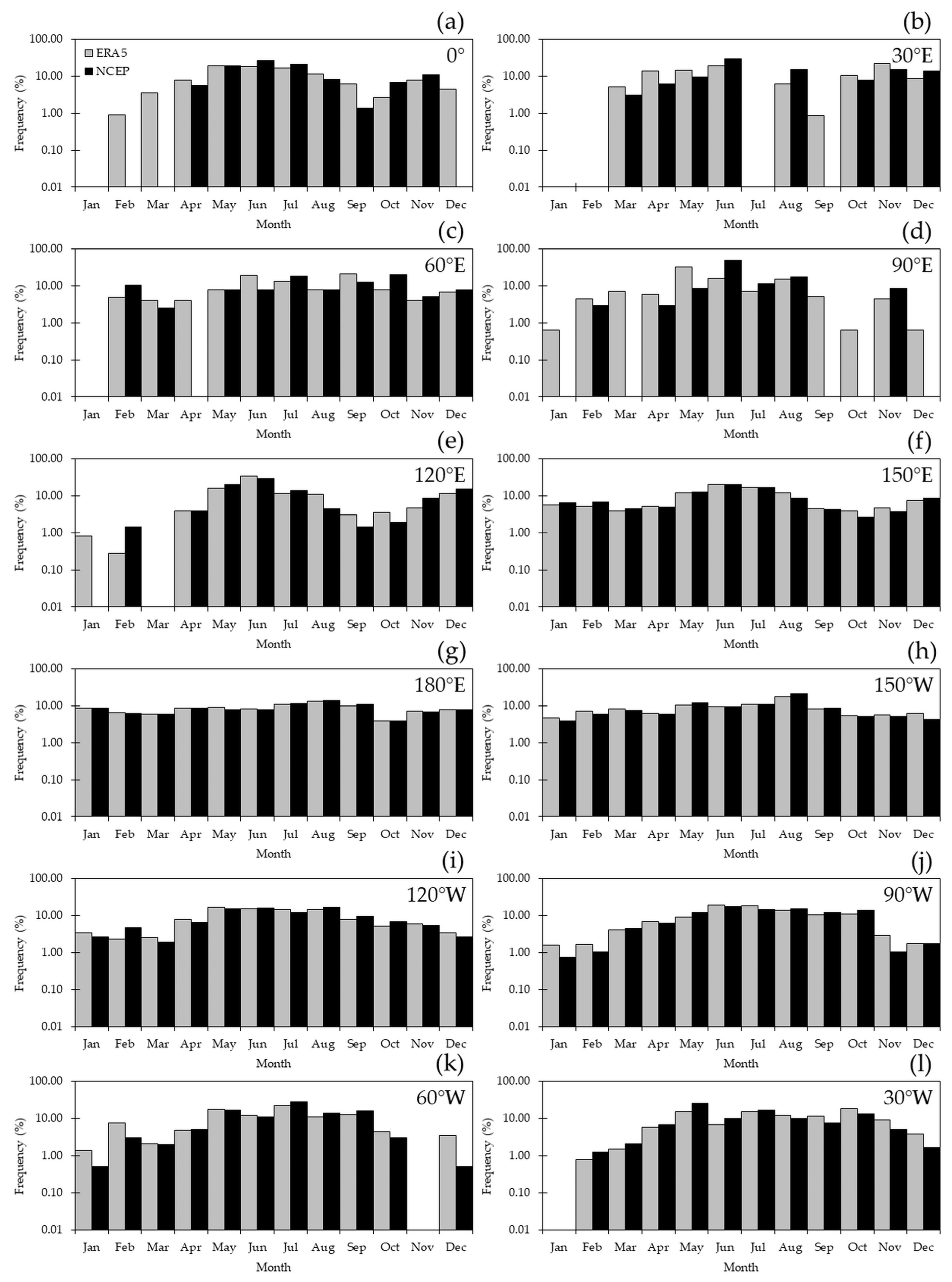
3.2.2. Comparative Distributions Across the Year at Selected Longitudes

Illustrated in Figure 8 is the annual cycle in the frequency of blocking cases for every 30°of longitude. At the GM (Figure 8a), there were no detected blockings in January in both reanalyses. Besides this month, the ERA5 dataset had blockings in the rest of the year, with loci of primary and secondary maxima peaking in May (19.47%) and in November (7.96%), respectively, whereas the location of blockings in the NCEP dataset was restricted to the April–November span, with maxima in June (26.39%) and in November (11.11%). The analysis of this longitude is in concordance with the aforementioned fact that blockings were more prone to occur in the cool season and over the oceans. At 30° E (Figure 8b), there were no blockings in January, February, and July. The latter month marked a discontinuity in the presence of blockings in this particular area. Actually, the quarter March–June registered cases in both datasets, with the maximum frequency peaking at 18.97% (ERA5) and 29.23% (NCEP), there were no cases at all in mid-winter, and blockings re-emerged in the area from August to December in a continuous fashion in the ERA5 dataset, ranging from 0.86% (September) to 21.55% (November), and with a gap in September in the NCEP dataset. Not considering September, the frequencies in the NCEP dataset ranged from 7.69% (October) to 15.38% (August and November). As with the two previous longitudes, there were no blockings located at 60° E in January (Figure 8c). The occurrence of blockings in the other months had a match in both reanalyses, with the exception of April, in which no blockings were found in the NCEP dataset. The distinction of different loci at this longitude was not as clear as it was in the previous two cases. The frequencies varied from 3.96% (March, April, and November) and 20.79% (September) in the ERA5 dataset, and from 2.56% (March) to 20.51% (October) in the NCEP dataset. There was a continuous presence of blockings in the ERA5 dataset across the year at 90° E, with a maximum in May (32.69%) and a minimum in January and in October (0.64% each) (Figure 8d). On the other hand, the monthly NCEP time series had breaks in January, March, September, October, and December. Aside from these months, the minimum frequency was 2.86% in February and in April, and the maximum frequency occurred in June (48.57%). As seen in Figure 8, the easternmost longitude in the EH that exhibited alterations no occurrence of blockings was 120° E (Figure 8e): it had no observed cases in March (ERA5) and in January and March (NCEP). In spite of these missing values, the frequency time series seemed to be modulated by a strong semi-annual wave that maximized in the solstices, with frequencies accounting for 33.52% (June) and 11.63% (December) in the ERA5 dataset and 29.61% (June) and 15.05% (December) in the NCEP counterpart. The presence of the semi-annual cycle is not unexpected, as it is one of the main forcings of the whole troposphere ([79] and references therein). More specifically, [80] analyzed the semi-annual wave in the frequency of COLs, whose interplay with the low-over-high blocking was described in the Introduction. Nonetheless, it is worth noting that the annual evolution of the frequency of blockings in Figure 8e was not expected to follow the one for COLs in a close fashion since the other two types of 500 hPa patterns that fit into the definition of Equations (2) and (3), i.e., omega blockings and large-amplitudes ridges, presumably were unaccounted for in [80].

There was a region spanning at least 120°, between 150° E and 90° W (Figure 8f–j), in which the frequency time series had no interruptions throughout the year in both reanalyses. At 150° E (Figure 8f), the frequencies ranged between 3.84% and 19.85% in the ERA5 reanalysis and between 2.71% and 20.14% in the NCEP counterpart, with the maxima (minima) taking place in June (October) in both cases. At 180° E (Figure 8g), the minima also occurred in October in both datasets, with frequencies of 3.79% (ERA5) and 3.90% (NCEP). However, the maxima shifted to August: 13.40% (ERA5) and 14.08% (NCEP). It is worth noting that the maximum frequencies were smaller than those at 150° E because of a more even distribution of blockings at 180° E than at 150° E, something that is visible from Figure 7. The unevenness increased to the east of the DL at 150° W (Figure 8h), with minima of 4.58% (ERA5) and 3.90% (NCEP), both in January, and maxima of 17.12% (ERA5) and 21.32% (NCEP), both in August. At 120° W (Figure 8i), the minimum frequencies were 2.27% in February (ERA5) and 1.87% in March (NCEP), while the maximum values were 17.02% in May (ERA5) and 16.98% in August (NCEP). Such behavior marked, on average, a steeper minimum-to-maximum transition in the NCEP dataset that was unseen in the three foregoing latitudes. The remaining longitude with an uninterrupted record across the year, i.e., 90° W (Figure 8j), showed minima of 1.55% (ERA5) and 0.76% (NCEP), both in January, and maxima of 19.30% (ERA5) and 17.13% (NCEP), both in June.

There was a single month with missing blockings at 60° W and at 30° W (Figure 8k,l, respectively), in November and January, respectively. For the rest of the year, the frequencies at 60° W were in the 1.39–22.22% range in the ERA5 dataset, with the minimum (maximum) occurring in January (July), and were between 0.51% and 28.28% in the NCEP dataset, with a double minimum in December–January and a maximum in July. As for 30° W (Figure 8l), the maximum was 18.04% in October (ERA5) and 25.42% in May (NCEP); from another perspective, these particular results replicated the local maxima found in the ATL during the equinoxes (cf. Figure 5c,e). If the longitudes were not restrained to those presented in Figure 8, the absolute maximum frequency reached 34.09% at 80° E in July in the ERA5 dataset and 48.57% at 90° E in June in the NCEP dataset (Figure 8d).

3.2.3. Comparative Wave Analysis

In the example provided at the beginning of Section 3 (cf. Figure 3 and Figure S1), the contributions of the most representative wavenumbers at 35° S and 50° S were presented. In this sub-section, we introduce the contribution of the most representative wavenumbers at the foregoing two latitudes for the entire blocking dataset that was extracted from the two databases. The most representative wave was estimated by identifying the largest single contribution to the variance of the ZGH field, i.e., the largest value of $a_n^2+b_n^2$ in (1) (or the largest amplitude).

Table 2. Counting of the most representative waves at 35° S and 50° S for blocked days across the entire year. All single individual dates at which the blocking condition was fulfilled in at least one longitude were considered.

ERA5
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	769	234	550	354	90	11	–	2008
	2	258	105	153	122	42	2	1	683
	3	206	64	94	85	21	1	–	471
	4	281	67	161	166	30	1	–	706
	5	283	82	180	98	55	5	–	703
	6	174	29	114	58	18	–	–	393
	7	78	14	56	27	5	1	–	181
	8	17	5	8	10	3	–	–	43
	9	2	1	–	–	–	–	–	3
	Total	2068	601	1316	920	264	21	1	5191
NCEP
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	668	159	363	252	57	9	–	1508
	2	217	76	112	86	19	2	–	512
	3	143	49	77	43	8	2	–	322
	4	221	61	109	114	9	–	–	514
	5	235	69	109	59	32	1	–	505
	6	146	20	81	41	14	–	–	302
	7	52	11	40	13	4	–	–	120
	8	12	4	8	5	3	–	–	32
	9	1	1	1	–	–	–	–	3
	Total	1695	450	900	613	146	14	–	3818

shows a consolidated picture of the combined contribution, on an annual basis, of the wavenumber that accounted for most of the variance at each of the latitudes on the individual dates on which the blocking condition was fulfilled at least once (i.e., a blocked day). Similarly,

Table 3. As in Table 2, but for DJF alone.

ERA5
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	150	23	36	20	16	–	–	245
	2	72	17	32	18	7	1	–	147
	3	40	4	14	9	3	1	–	71
	4	65	12	20	24	7	–	–	128
	5	71	10	28	15	9	1	–	134
	6	41	2	10	15	2	–	–	70
	7	12	2	5	5	2	1	–	27
	8	3	–	2	2	–	–	–	7
	9	–	–	–	–	–	–	–	–
	Total	454	70	147	108	46	4	–	829
NCEP
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	90	17	22	20	9	–	–	158
	2	49	16	27	12	6	–	–	110
	3	23	4	6	4	–	–	–	37
	4	53	9	13	24	4	–	–	103
	5	53	9	16	9	4	–	–	91
	6	45	1	8	9	2	–	–	65
	7	7	1	4	1	–	–	–	13
	8	3	–	2	1	–	–	–	6
	9	–	–	–	–	–	–	–	–
	Total	323	57	98	80	25	–	–	583

and

Table 4. As in Table 2, but for JJA alone.

ERA5
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	311	126	305	184	41	6	–	973
	2	71	33	39	33	8	–	–	184
	3	59	26	35	28	7	–	–	155
	4	69	28	62	58	6	1	–	224
	5	85	21	68	25	10	1	–	210
	6	43	14	53	16	5	–	–	131
	7	23	8	20	7	–	–	–	58
	8	4	–	3	2	1	–	–	10
	9	1	1	–	–	–	–	–	2
	Total	666	257	585	353	78	8	–	1947
NCEP
		50° S							Total
	Wavenumber	1	2	3	4	5	6	7
35° S	1	295	73	204	129	32	6	–	739
	2	64	18	33	21	3	–	–	139
	3	53	20	36	19	4	–	–	132
	4	53	24	35	47	1	–	–	160
	5	67	21	46	14	11	–	–	159
	6	36	6	39	6	5	–	–	92
	7	19	6	9	6	–	–	–	40
	8	–	–	1	1	1	–	–	3
	9	–	–	–	–	–	–	–	–
	Total	587	168	403	243	57	6	–	1464

show the contributions in DJF and JJA, respectively.

Out of 5191 blocked days in the annual case in the ERA5 dataset (Table 2), W1 took on the variance’s largest proportion, both at 35° S and at 50° S, with 2008 (38.68%) and 2068 (39.83%) days, respectively. It was followed by W4 (706 days, 13.60%) and W5 (703 days, 13.54%) at 35° S, and by W3 (1316 days, 25.35%) and W4 (703 days, 17.72%) at 50° S. Denoting the pair of dominant wavenumbers at the foregoing latitudes as $\left({\mathrm{W}}_{35°\mathrm{S}},{\mathrm{W}}_{50°\mathrm{S}}\right)$, the most frequent combination was (W1,W1), associated with 769 days (14.81%), followed by (W1,W3) (550 days, 10.60%) and (W1,W4) (354 days, 6.82%). The longest wavenumbers that took on the variance’s maximum percentage were W9 at 35° S (3 days) and W7 at 50° S (1 day).

Regarding the NCEP dataset, there were 3818 blocked days. The three most representative waves at 35° S were W1 (39.50%, 1508 days), W4 (13.36%, 514 days), and W2 (13.41%, 512 days), while at 50° S, they were W1 (44.39%, 1695 days), W3 (23.57%, 900 days), and W4 (16.06%, 613 days). In this case, the (W1,W1) pair was also the most frequent, tallying 17.50% of the days (668), and it was also followed by the (W1,W3) and the (W1,W4) pairs, with 363 days (9.51%) and 252 days (6.60%), respectively. The percentage represented by the (W1,W1) pair was higher in the NCEP dataset, whereas the opposite occurred for the other two pairs. The longest wavenumbers that exhibited the variance’s maximum fraction were W9 at 35° S (3 days) and W6 at 50° S (14 days).

From a wave standpoint, the exclusion of W2 from the analysis presented in Section 2.1 is further supported by the following considerations. Out of 5191 blocked days in the ERA5 dataset, W2 was the most prominent wave in 683 and 601 days, at 35° S and 50° S, respectively, taking on 13.16% and 11.58% of the total. In the NCEP dataset, out of 3818 blocked days, W2 was the most prominent wave on 512 (13.41%) and 450 (11.79%) days at 35° S and 50° S, respectively. The similarities in the importance of W2 to blockings at these two latitudes in both datasets are worth noting. Additionally, in terms of represented days, W2 came behind W1, W4, and W5 at 35° S, and behind W1, W3, and W4 at 50° S in the ERA5 dataset. In the NCEP counterpart, W2 came behind W1 and W4 at 35° S, and behind W1, W3, and W4 at 50° S. The dominance of W1, W3, and W4 over W2 was also in conformity with the findings in [66] using an EOF approach, in which W1 and W3 had a prevalence for EOF1, whereas EOF2 was driven by W4 and was tied to winter. Despite the differences between the NH and the SH regarding blockings [30,81], our results are also in agreement with those presented in [29] for the NH, for it was found that the preponderance of W1 during blockings more than quintupled that of W2.

The number of blocked days in DJF totaled 829 (ERA5) and 583 (NCEP), and they constituted 15.97% and 15.27% of the corresponding totals presented in Table 2. This made a difference of less than 1% between the two datasets. Considering 35° S alone, in the ERA5 dataset, W1 made up 61.22% (245 days) of the total (versus 38.68% in the annual figures). As for the NCEP dataset, it represented 56.96% (158 days) of the total (compared to 39.50% in the annual case). At 50° S, the figures for W1 were at 33.03% (454 days) (ERA5) and 27.86% (323 days) (NCEP), versus 39.83% (ERA5) and 44.39% (NCEP) in the annual case. Following these results, with respect to the annual figures, W1 had a remarkable increase in its occurrence during blocked days at 35° S, whereas there was a fall in its contribution at 50° S. As for the second and third most representative waves at 35° S, they were W2 and W5 in the ERA5 dataset, accounting for 17.73% (147 days) and 16.16% (134 days), respectively, while in the NCEP dataset, these waves were W2 (18.87%, 110 days) and W4 (17.67%, 103 days). The counterparts at 50° S were W3 and W4 in both datasets, with the relative contributions being 147 days (17.73%) and 108 days (13.03%), respectively, in the ERA5 dataset, and 98 days (16.81%) and 80 days (13.72%) in the NCEP dataset, respectively. Considering the two latitudes altogether, (W1,W1) was, as in the annual case, the more frequent combination, representing 16.82% (150 days) (ERA5) and 15.43% (90 days) (NCEP). Furthermore, (W2,W1) and (W5,W1) were the second and third most representative pairs in the ERA5 dataset, with 8.69% (72 days) and 8.56% (71 days), respectively, whereas in the NCEP dataset, (W4,W1) and (W5,W1) were second to (W1,W1), with 53 days each (9.09%).

The number of blocked days in JJA was 1947 (ERA5) and 1464 (NCEP) (Table 4). These figures accounted for 37.51% and 38.34%, respectively, of the corresponding annual totals in Table 2. Aside from the tiny difference between these two percentages, they show that more than a third of the blockings occurred in the cold season. At 35° S, W1 had the most explained variance in 973 days (49.97%) (ERA5) and 739 days (50.48%) (NCEP). The waves that followed W1 were W4 and W5 in both reanalyses: W4 took most of the variance in 224 days (11.50%) (ERA5) and in 160 days (10.93%) (NCEP), while for W5, these figures were 210 days (10.79%) (ERA5) and 159 (10.86%) (NCEP). Regarding 50° S, in both datasets, W1 also took on most of the variance, followed by W3 and W4. In the case of the ERA5 dataset, the number of days on which these waves had most of the variance were 666 (34.21%), 585 (30.05%), and 353 (18.13%), respectively, and in the NCEP dataset, these figures were 587 (40.10%), 403 (27.52%), and 243 (16.60%), respectively. With the two latitudes combined, (W1,W1), (W1,W3), and (W1,W4) were the pairs that had the most occurrence in both reanalyses, in 311 (15.97%), 305 (15.67%), and 184 days (9.45%), respectively, in the ERA5 dataset, and in 295 (20.15%), 204 (13.93%), and 129 (8.81%), respectively, in the NCEP dataset. A noticeable difference that arises from the comparison of Table 3 and Table 4 is that about half of the total number of blocked days in the cold season—973 out of 1947 (ERA5) and 739 out of 1464 (NCEP)— relied on the superposition of W1 at 35° S with longer waves at 50° S. Conversely, approximately the same fraction of blocked days in the hot season—454 out of 829 (ERA5) and 323 out of 583 (NCEP)—relied on the coexistence of W1 at 50° S with longer waves at 35° S.

3.3. Comparative Climatic Characteristics Considering Duration

The case study presented in Figure 3 and Figure S1 consisted of successive blocking cases that lasted up to 12 days at some longitudes. Persistence in the entire dataset is considered in this sub-section. Any set of consecutive individual blocking cases at the same longitude was regarded as a single BE at that longitude. The BE’s start date was assigned to the first date the set was located on.

Table 5. Breakdown of the total number of located blocking events by persistence and by region.

ERA5
Persistence (days)		Region		Total
	PAC	ATL	IND
1	8046	1032	748	9826
2	4884	535	255	5674
3	2265	159	54	2478
4	1041	40	12	1093
5	375	9	1	385
6	221	1	–	222
7	77	–	–	77
8	35	–	–	35
9	27	–	–	27
10	4	–	–	4
11	6	–	–	6
12	6	–	–	6
Total	16,987	1776	1070	19,833
NCEP
Persistence (days)		Region		Total
	PAC	ATL	IND
1	5952	725	374	7051
2	3623	369	94	4086
3	1657	70	30	1757
4	705	23	5	733
5	292	3	–	295
6	117	3	–	120
7	57	–	–	57
8	32	–	–	32
9	20	–	–	20
10	5	–	–	5
11	2	–	–	2
12	3	–	–	3
Total	12,465	1193	503	14,161

presents a breakdown of the total number of BEs that were detected by persistence (in days) and by region (cf. Table 1). Disregarding duration, the PAC accounted for the largest number of BEs in both datasets, totaling 16,987 (85.65%) and 12,465 (88.02%) in the ERA5 and in the NCEP datasets, respectively, followed by the ATL with 1776 (8.95%, ERA5) and 1193 (8.42%, NCEP) matches and the IND with 1070 (5.40%, ERA5) and 503 (3.55%, NCEP) hits. If duration was taken into account, the number of located BEs decreased as persistence increased. In order to align our analysis with the existing literature, it is convenient to bin the BEs into three different groups based on their duration, as in [22]: single-day events, two- to four-day events, and five-day events or longer. The rationale for the inclusion of single-day events relied upon the fact that once blockings were established, they tended to persist [82], so the primary location of long-lived events would coincide with those of single-day BEs. Irrespective of the region, the total number of located single-day blockings was 9826, or 49.54% (ERA5), and 7051, or 49.79% (NCEP). A regionalization of these results shows that single-day blockings made up 81.88% (ERA5) and 84.41% (NCEP) of the total in the PAC, 10.50% (ERA5) and 10.28% (NCEP) in the ATL, and 7.61% (ERA5) and 5.30% (NCEP) in the IND. When it comes to the two- to four-day group, regardless of the region, the matches were 9245, or 46.64% (ERA5), and 6576, or 46.43% (NCEP). Of all these BEs, those located in the PAC represented 88.59% (ERA5) and 91.01% (NCEP) of the total, the ones in the ATL took on 7.94% (ERA5) and 7.03% (NCEP), and those in the IND were left with the remaining 3.47% (ERA5) and 1.96% (NCEP). Similar analyses could be carried out for the rest of Table 5. A feature worth noting is that BEs lasting 7 days or more were present in the PAC only, with 155 events located over 83 years (ERA5) and 119 matches over 75 years (NCEP). The longest-lived recorded BEs encompassed 12 days in both datasets and occurred during JJA (cf. Section 3.1). Expectedly, the blocking definition had an impact on persistence. For instance, in [18] (and references therein), a BE was considered as such if positive anomalies exceeded a pre-specified threshold for 5 days or more, whereas a 10-day threshold was mentioned in [2] (p. 79). With the same blocking criteria used here but employing a different database, it was found in [22] that the longest-lived BEs lasted 13 days and that the only region with BEs lasting 7 days or longer was the PAC. Our findings are in agreement with these results. On the other hand, BEs lasting up to 26 days were found in [25] by allowing the BI not to be strictly negative.

Shown in Figure S2 are the annual and seasonal distributions of BEs in the aforesaid three duration groups presented every 10° of longitude. The panel’s ordinate scale is linear in this case in order to ease the comparisons between groups. All panels in Figure S2 have the concentration of longer-lived BEs to the east of the DL in common. On an annual basis, in the ERA5 dataset, the maximum (minimum) number of single-day BEs took place at 70° E (170° W), accounting for 79.22% (41.97%) of the total BEs that took place at the corresponding longitude. As for two- to four-day BEs, they were complementary to the single-day group, more (less) frequent at 170° W (70° E) and peaking (bottoming) at 52.49% (20.78%) of the total BEs recorded at these particular longitudes. In the case of five-day or longer BEs, the maximum occurred at 160° W (6.90%). These longest-lived events took place from 140° E through 80° W without breaks and exhibited the largest frequencies there, yet they also occurred in 100° E–110° E and in 30° W–20° W, but with a less prominent contribution. As for the NCEP dataset, the maximum (minimum) frequency in the occurrence of single-day events was 90.57% (40.98%) at 40° E (140° W). The maximum, somewhat higher than in the ERA5 counterpart, shifted 30° to the west with respect to this dataset. On the other hand, the minimum, which differed by 1% when compared with the corresponding ERA5 frequency, also shifted 30°, but to the east. As with the ERA5 dataset, the maximum and minimum frequencies for two- to four-day BEs were complementary to the single-day BEs’ ones, as they reached 52.70% at 140° W and 9.43% at 40° E, respectively. Finally, five-day or longer BEs maximized at 150° W (7.85%). These longest-lived events shrank spatially in the PAC/ATL regions with respect to the ERA5 dataset, as they stretched in a continuous fashion from 150° E to 70° W, and also took place at 20° W. A zonal average resulted in 57.76% (ERA5) and 60.09% (NCEP) of single-day BEs, 40.32% (ERA5) and 38.20% (NCEP) of two- to four-day BEs, and 1.92% (ERA5) and 1.71% (NCEP) of five-day or longer BEs. The foregoing annual figures provided a broad view of the occurrence of BEs across the SH; finer details could be extracted from the assessment of the seasonal distributions.

A feature common to all the seasons was the concentration of a greater number of events standing for two days or more in and around the DL. Frequencies there actually exceeded the single-day blockings and encompassed several adjoining longitudes, e.g., 150° E–160° W (ERA5) and 170° E–120° W (NCEP) in DJF, 170° W–100° W (ERA5) and 150° W–90° E (NCEP) in MAM, 140° E–90° W (ERA5) and 150° E–100° W (NCEP) in JJA, and 160° W–90° W (NCEP) in SON. In contrast with the preceding examples, the ERA5 dataset during SON saw single-day events accounting for more than 50% of the located blockings in some longitudes neighbored by longitudes at which they represented less than 50% of the blocks (e.g., 50% at 180° E, <50% at 170° W, >50% from 160° W through 140° W, and again, <50% at 130° W), meaning that there was no spatial continuity in either group’s preponderance in the surroundings of the DL.

Over the course of the years, DJF was the only season in which there were longitudes with no recorded blockings at all in the ERA5 dataset (50° E) and in the NCEP dataset (the 20° W–0° range and 80° E) (cf. Figure 5). Focusing on the longest-lasting BEs, particularly in DJF, the difference was that they spanned a larger region in the NCEP dataset, i.e., 150° E–110° W (excepting 160° E and 140° W, which had no cases), than in the ERA5 dataset, in which they only stretched from 160° E to 140° W. In MAM, there was an increase in these BEs, and they overall shifted to the east in both datasets, with their occurrence being continuous between 170° E and 70° W (ERA5) and 180° E and 80° W (NCEP). The frequencies peaked at 140° W (or 9.06% of this longitude totals) in the ERA5 dataset and at 130° W (12.14%) in the NCEP counterpart. Actually, the latter frequency reached the maximum value encompassing the NCEP dataset. In JJA, these BEs reached their maximum extent, spanning the 150° E–80° W (ERA5) and 150° E–90° W (NCEP) ranges in a continuous fashion, with additional occurrences at 100° E–110° E and 20° W (ERA5) and at 70° W and 20° W (NCEP). The overall maximum frequency in the ERA5 dataset (11.45% at 160° W) was also reached in JJA. The frequencies and the spatial extent were reduced in SON. The most notable difference between the two datasets was the counting of BEs at 110° E (7.69%) in the ERA5 reanalysis that had no pairing either at this longitude or its surroundings in the NCEP dataset. Nevertheless, these BEs did take place at 100° E and at 110° E during JJA, so their occurrence at 110° E in SON was, based on continuity grounds, genuine in appearance.

In the ERA5 dataset, the zonal average frequency for single-day BEs was 57.29%, 59.80%, 55.31%, and 60.43% in DJF, MAM, JJA, and SON, respectively. For two- to four-day BEs, these figures were 39.35% (DJF), 38.36% (MAM), 41.99% (JJA), and 38.15% (SON); for five-day or longer BEs, they were 0.58% (DJF), 1.84% (MAM), 2.70% (JJA), and 1.43% (SON). Correspondingly, the frequencies for the NCEP dataset were 55.41% (DJF), 61.26% (MAM), 56.81% (JJA), and 65.78% (SON) for single-day Bes; 32.79% (DJF), 36.81% (MAM), 40.74% (JJA), and 33.37% (SON) for two- to four-day Bes; and 0.69% (DJF), 1.93% (MAM), 2.45% (JJA), and 0.85% (SON) for five-day or longer BEs. According to these figures, the largest number of longest BEs occurred in JJA in both datasets.

3.4. Alternative Latitude-Dependent Definitions of the Blocking Index

We briefly discuss in this sub-section the outcome of altering the BI in (2) so that its latitudinal dependence was shifted by up to 10 degrees equatorward. In particular, we addressed whether

$${\left(BI\right)}_i={\tilde{z}}_i\left(30°S\right)-{\tilde{z}}_i\left(45°S\right)<0$$

(5)

and

$${\left(BI\right)}_i={\tilde{z}}_i\left(25°S\right)-{\tilde{z}}_i\left(40°S\right)<0$$

(6)

led to the correct definition of a blocking in the SH. Each of Equations (5) and (6) was combined with (3). It is worth noting that this procedure was presented in [22], where (5) and (6) were ruled out for not representing blockings. Nevertheless, we carried out the calculations for the ERA5 and NCEP databases in order to analyze the outcome. Shown in

Table 6. Same as Table 1, but computing the BI using Equations (3) and (5).

Region	Annual		Season
			DJF		MAM		JJA		SON
	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP
PAC	86.73	89.61	93.10	95.67	84.88	88.72	83.14	84.98	83.52	86.95
ATL	6.55	6.15	3.07	2.24	6.18	5.81	8.97	9.83	9.65	8.16
IND	6.72	4.24	3.83	2.09	8.95	5.47	7.90	5.19	6.84	4.90

and

Table 7. Same as Table 1, but computing the BI using Equations (3) and (6).

Region	Annual		Season
			DJF		MAM		JJA		SON
	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP	ERA5	NCEP
PAC	76.23	80.20	82.96	84.81	68.58	75.01	64.94	71.89	73.58	74.73
ATL	5.93	5.77	3.89	3.34	5.53	5.19	11.64	15.98	11.37	11.45
IND	17.84	14.03	13.15	11.85	25.88	19.80	23.43	12.12	15.05	13.82

are the annual and seasonal distributions of the located cases employing (5) and (6), respectively. The results were stratified using the same regions introduced for Table 1.

When using (5) and comparing to the values presented in Table 1, the frequency of cases in the PAC decreased during all the seasons in both datasets, with an immediate impact on the annual average (Table 6). The opposite occurred in the IND, with the new figures approximately doubling their counterparts in Table 1. On the other hand, mixed results were seen in the ATL: there was an increase in the seasonal figures during the solstices in both datasets, most remarkably in JJA, a decrease in the MAM figures in both datasets too, and the SON figures showed a decrease in the ERA5 dataset and an increase in the NCEP counterpart. Overall, there was a rise in the annual averages in the ATL in both datasets.

Let us focus on the ATL region. According to Table 1, the frequencies of blockings for this region were maxima in the equinoxes. In the case of Table 6, the frequencies were maxima in JJA and SON. This coincided with the northernmost reach of the baroclinic region. Separately, a climatological study showed that there were notable interseasonal variations in the shape of the subtropical high’s (STH) spatial pattern, but its centroid’s latitudinal or longitudinal migration was negligible [83]. Put another way, a more appropriate STH variable to be taken into account was its “pulsation”, i.e., the variation of its strength at 30° S across the longitudes. Piecing together the foregoing considerations, along with the fact that 45° S was included in (5), suggests that this expression was a measurement of the relative 500 hPa height between the STH and that of the mid-latitude eddies. An increase in the counting using (5) was thus expected when the baroclinic waves were closer to the Equator. This is exactly what is shown in Table 6. Following this reasoning, (5) did not represent blockings.

The STH pressure belt lying between 20° S and 40° S is a long-standing fact [84,85], yet other studies found that it stretched over the 25° S–42° S latitudinal band [23]. In any case, the calculation using (6) evaluated the relative 500 hPa height at opposite positions of the STHs at the same longitude. The latitudes involved in (6) are, hence, close to those limiting the STH pressure belt. So, the statistics presented in Table 7 are not a measurement of blockings but some sort of STH metrics. The disparately large frequencies in the IND, even larger than those in Table 6, are a noteworthy feature. Actually, given that the STHs laid over the oceans [84], Table 7 rather accounted, in a simultaneous fashion, for the relative extension of the three ocean basins and for the distribution of mass evaluated at 500 hPa within these particular anticyclones, which constituted centers of action at the corresponding longitudes [84]. Equation (6) did not represent blockings, either.

4. Discussion and Concluding Remarks

This paper was aimed at presenting an updated, comprehensive climatology of blockings in the SH using the ERA5 and NCEP reanalysis datasets, encompassing the periods 1940–2022 and 1948–2022, respectively. Blockings were located by means of the BI. The one employed here evaluated the difference between 35° S and 50° S at 500 hPa. Hence, some blockings that occurred beyond the latter latitude, particularly those taking place over East Antarctica [86,87,88], were unaccounted for in the current climatology. Locating these blockings requires the use of alternative methodologies.

The long-term annual and seasonal features of blockings were introduced for every 10° of longitude, and the discrepancies between the two datasets were raised. Moreover, the frequency differences were statistically tested; to the best of our knowledge, this was never done before, and hence, it constitutes a novel approach to the subject. The results were also stratified by the persistence of the blockings and by their intensity in the annual case only. The main findings of our study can be summarized in the following points:

• On an annual basis, the maximum frequency of blocking cases (approximately 10%) occurred at 170° W and 160° W in the ERA5 and NCEP datasets, with the difference between the two reanalyses being less than 0.60%. This outcome was in contrast with earlier findings using the same methodology, e.g., ref. [22], who found the peak west of the DL. As stressed in [42] (p. 339 and references therein), this peculiarity highlighted the fact that the spatial location of blockings had a dependence on the employed dataset. Second- and third-rank maxima took place at 40° W and 20° E, respectively, in both datasets, with the frequencies differing by 0.10% and 0.05%, respectively. As for the frequency difference, it did not exceed 2% at any longitude, and the two datasets were statistically indistinguishable from one another at all longitudes, with the exception of 50° E. Approximately 75% of the blocking cases occurred in the WH in both datasets. If regions were considered, the PAC (110° E–80° W) concentrated more than 90% of the cases, followed by the ATL (70° W–0°) and the IND (10° E–100° E). The distribution pattern for $BI<-100m$ was similar to the one for $BI<0$, but these blockings were more symmetrically located around the DL. The most intense blockings $\left(BI<-200m\right)$ were more frequent at 90° W (ERA5) and at 160° W (NCEP), and they did not occur in the IND basin.
• In DJF, up to fourth-rank maxima could be located in both reanalyses. As in the annual case, 170° W exhibited the maximum frequency in the ERA5 dataset, reaching almost 15% of the total number of located blocking cases in the season, while in the NCEP dataset, the maximum was just below 14% at both 180° E and 170° W. Second-rank maxima took place at 60° W (ERA5) and at 50° W and 40° W (NCEP). Third- and fourth-rank maxima were also found in both datasets but with a swap in location: third-rank maxima occurred at 70° E (ERA5) and at 20° E (NCEP), whereas fourth-rank maxima took place at 20° E (ERA5) and at 60° E and 70° E (NCEP). The two datasets were statistically indistinguishable in the 110° E–70° W band; the maximum difference was accounted for at 170° E, with more blocking cases located in the NCEP dataset. The deviations with respect to the annual frequencies across the longitudes in both datasets were in agreement with each other. On the other hand, the two reanalyses showed that the PAC saw an increase in the counting of blockings that was detrimental to the presence of blockings in both the ATL and the IND.
• In MAM, up to fourth-rank maxima were located in both datasets, too. The maximum frequency accounted for approximately 11% at 170° W (ERA5) and approximately 10% at 150° W (NCEP). The location of the lesser order maxima coincided in both datasets in a qualitative fashion (e.g., 20° E, 40° W), yet, comparatively, the NCEP dataset seemed to show, so to speak, a more even distribution of blockings across the longitudes. Regarding the differences, both datasets were in statistical agreement within the 100° E–20° W range. When compared to the annual averages, blockings were less frequent in the PAC sector in favor of an increased presence in the ATL and the IND.
• During JJA, the absolute maximum was recorded at 160° W and 150° W in the ERA5 and the NCEP datasets, respectively, accounting for approximately 9% in both cases. In contrast with the behavior described in the preceding points, the lower-rank maxima were restricted to secondary ones in both reanalyses: they occurred at 30° W within a frequency lobe that spanned the 50° W–30° E and the 40° W–50° E sectors in the ERA5 and the NCEP datasets, respectively. Both reanalyses were statistically indistinguishable in locating blockings beyond the 20° E–80° E range. When compared to the annual averages, the PAC and the IND registered opposing figures regarding the number of detected blockings. In the PAC, there was an increase in the frequencies in the ERA5 dataset and a decrease in the NCEP counterpart; the other way around took place in the IND. On the other hand, the ATL saw decreased frequencies in both datasets.
• The primary location of blockings in SON was at 170° W in both datasets, taking on approximately 9% of the total number of cases during the season. Secondary maxima, slightly below 5%, were found at 100° W, and tertiary maxima of around 2% were found at 40° W; fourth-rank maxima (less than 1%) were located in the IND. This took place in both datasets. The frequencies were statistically distinguishable in the IND and in agreement elsewhere. When compared to the annual figures, a decrease in the number of blockings was observed in the PAC in both reanalyses. A decrease was also seen in the IND in the NCEP reanalysis. In contrast, the ATL exhibited an increase in the counting of blockings in both datasets.
• The annual cycle in the frequency of blocking cases as presented for every 30° of longitude showed that the 150° E–90° W range exhibited the occurrence of blockings across the entire year, and that beyond this range, the absence of blockings took place, with the exception of 30° E, outside the winter months. Moreover, the distribution at the DL was the most even one.
• An analysis of the waves that took on most of the variance on each blocked day at 35° S and 50° S showed that on an annual average, the most frequent combination took place when W1 was most prominent at both longitudes, followed by W1 at 35° S and W3 at 50° S. These figures were found in both datasets. During DJF, the most frequent situation coincided with that of the annual average and was followed by different combinations that had W1 as the most prominent wave at 50° S and waves of different lengths at 35° S. Again, the same behavior was found in both datasets. As for JJA, the most frequent combination of waves had W1 as the most representative at both latitudes, closely followed by W1 at 35° S and W3 at 50° S, paralleling the behavior found in the annual case. This was observed in either dataset, too.
• A stratification of the frequency distributions by taking persistence into account showed that, on an annual average and regardless of the region, single-day blockings accounted for approximately half of the cases in both datasets. Furthermore, BEs lasting up to 4 days were present across the entire SH but with maxima occurrence in the PAC in both datasets. On the other hand, the longest-lived BEs (five days or longer) were primarily concentrated in the PAC, but they were also present in the ATL in both datasets and in the eastern IND in the ERA5 dataset only. On a seasonal basis, there were longitudes that had no blockings only in DJF in both datasets; the longest-lasting BEs were more frequent in JJA.

The objective of this paper was not to dig into the operational differences in the utilized reanalysis datasets. However, their resolution and their data assimilation are worth noting. Those interested in the technical details are referred to [45,89]. Additionally, a thorough assessment in the comparisons of several reanalyses was presented in [90]; although the ERA5 dataset was not included, its immediate predecessor―the ERA-Interim―was. In order to evaluate whether either of the datasets that were employed here reproduced the blocking conditions in the SH well, a reliable third-party dataset must be taken as data. In this respect, radiosondes proved to be good candidates, as shown in [20]. Actually, there is literature that confronted the reanalyses of radiosonde data in blocking- [20] and no blocking-related [91] applications. The main shortcoming with radiosondes is that launching sites in the SH are scant, and hence, the comparisons could only be carried out at restricted locations, e.g., 58.50° W [20]. Other alternatives consider the inclusion of remotely sensed data, e.g., satellite data, with which the two reanalyses were also compared (e.g., [92]). A caveat regarding the comparisons with these alternative datasets is that radiosonde and satellite data are ingested during the ERA5 and the NCEP runs on a routine basis, so they may render spurious.

Unlike other studies [23,93,94], no particular states of the general circulation were considered for carrying out this research effort. Rather, the encompassed period was long enough so that it included all the possible phases of the different general circulation indices, e.g., positive, neutral, and negative conditions of the El Niño-Southern Oscillation (ENSO) were evenly weighted. Notwithstanding, the existing literature shows that the frequency of some mid-latitude blockings in both hemispheres was modulated by wave propagation sourced in the subtropics, depending on the ENSO phase [33] (and references therein). More recently, sub-divisions of the ENSO led to finer classifications on the impact on the frequency of blockings in the NH [95]; to the best of our knowledge, no attempts at such categorizations were made for the SH, so this is a matter for future investigation. Overall, updating the impact of the different states of the general circulation on the frequency of blockings in the SH is a pending task.

Finally, the presented climatology led to a number of byproducts that could be studied in the future. In particular, time series of blocking metrics, such as the number of blocking cases or their intensity, were not analyzed here. As a step forward, an assessment of trends, inhomogeneities, and shifts in the annual and seasonal mean time series of the foregoing metrics will be included in a separate paper.