Abstract
To understand if machine learning algorithms could be employed in agricultural landscapes to estimate N2O emissions, multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR) and artificial neural network (ANN) algorithms are tested on an agricultural site in Ontario, Canada. Two scenarios, High Input (HI) and Low Input (LI), were used to check the performance of these algorithms’ using R2, RMSE, VE, p-factor, r-factor and visual inspection indicators. The HI consisted of discrete measurements of N2O, rainfall, temperature, fertilizer application dates, soil nitrate, ammonium content and pH values, whereas the LI scenario did not use the latter three. The results indicated that MLR was inapplicable as the data did not satisfy its fundamental assumptions. RFR, SVR and ANN under HI were able to capture 64% (66%), 59% (63%) and 94% (43%) of the variability of emissions within the training (testing) datasets. Subsequently, these models were able to capture 92%, 29% and 75% of high emissions (>10 gm/ha/day) within their predictive intervals of 95% confidence. RFR, SVR and ANN under the LI scenario captured 72% (68%), 61% (66%) and 81% (68%) of the variability in N2O emissions within the training (testing) datasets. While these models were found to have comparable performance in both HI and LI scenarios, HI was found to be better at capturing high emissions. Based on the computational cost, ease in finetuning, capture of peak emissions and stable model performance, RFR and ANN are recommended to estimate N2O emissions in the study area and similar agricultural landscapes in future studies.
1. Introduction
The Intergovernmental Panel on Climate Change (IPCC) sixth assessment report (AR6) concludes with high confidence that anthropogenic GHGs have been the dominant driver of observed global warming since the mid-20th century [1]. Of the key GHGs, N2O is the third major gas in terms of volume, yet remains highly important due to its significant ozone depletion and global warming potential [2]. It is also reported that there is emerging N2O–climate feedback due to the addition of nitrogen in the atmosphere and subsequent climate change, thereby highlighting the urgency to mitigate these emissions more than ever [3]. Thus, unless we understand and estimate N2O emissions from different landscapes, we cannot mitigate relevant actions to reduce them.
Measuring N2O emissions is possibly the only way to accurately quantify its release to the atmosphere. However, measurements can be tedious, cumbersome and resource consuming. Discrete measurements of N2O are generally taken with manual static chambers (~1 m2 coverage area) and then analyzed with gas chromatography techniques [4,5]. Despite relatively simple operating principles, minimal field requirements and low cost, chamber measurements have their own limitations. Potential leaks, the influence of disturbance of soil surface, the influence of concentrated built-up of gases and missing coverage of the spatial and temporal variability of gas fluxes are the most common issues with chamber measurements [6]. Automatic chambers can measure the fluxes continuously for longer periods but the issue of spatial coverage and other limitations still persist [7]. Also, while the static closed chambers are low cost and do not require power in the field to operate, the automatic chambers are still expensive and need power to operate continuously thus increasing the risk of power outages and instrument failures.
If the N2O fluxes need estimation over a larger geographical domain, micrometeorological (MM) techniques like eddy covariance, eddy accumulation, relaxed eddy accumulation, flux gradient and Bowen ratio methods can be used [8]. The basic assumptions for MM techniques are that the atmospheric turbulence is stationary in nature, the terrain is flat and homogenous and there are negligible mean vertical wind velocities. While MM increases the probability to detect hot spots and hot moments of N2O, the majority of the above stated requirements are seldom met, which leads to data quality issues along with risk of instrument failure and data acquisition. It is also computationally expensive to process the data acquired from MM and installation and operation costs are high. When field measurements are not realistic or possible over macro-scales, modeling techniques may be employed that simulate the relevant biogeochemical cycles pertaining to N2O emissions under different environment and management conditions.
Giltrap, et al. [9] discussed that different process-based and empirical models may be employed to extrapolate the GHG field measurements to macro scales, simulate long-term emissions and run mitigation scenarios to reduce them. There have been multiple developments of N2O emission routines in process-based models like NGAS [10], DNDC [11], APSIM [12,13], EPIC [14], DayCENT [15] and SWAT [16,17]. However, process-based models are relatively complex to understand [18,19,20], have complex algorithm and parametrization needing many and long-term data [21,22] and have their own representation on how different environmental processes affect N2O emissions [23]. Similarly, there is still a lot of ground to cover to make these models highly efficient in capturing N2O emissions [15,24,25,26]. Compared to the process-based models, site-specific empirical models have been found to perform better to estimate N2O emissions [26,27,28]. Accordingly, machine learning algorithms are gaining popularity these days in N2O estimation studies. The ability of machine learning algorithms to identify important variables, process the data and information in a shorter time than process-based models and a reduced requirement to understand the complex details of the N2O emissions process boosts its usage in N2O related studies [29]. Based on the input data provided to the machine learning algorithms, decisions can be made by understanding the relationship among data variables without any explicit process equations and pathways identification [23], which have often been reported in the literature with encouraging results.
Saha, Basso and Robertson [26] employed random forest regression techniques to estimate daily flux variance of N2O in the US Midwest and found it superior to a process-based model with an explanation of 65–89% of daily fluxes on the calibrated site and around 38% of weekly and biweekly fluxes in an untested site. Once coupled with the outputs from process-based models, the revised algorithm could explain 51% of the variability of fluxes in the test sites. The random forest technique was applied by Saha, et al. [30] to estimate efficient N2O sampling strategies. Taki, et al. [31] evaluated linear interpolation and artificial neural networks (ANNs) to fill the gaps in sub-daily N2O emissions estimated using MM techniques in Elora research station from 2001 to 2006 and reported the outperformance of the latter. Bigaignon et al. [32] evaluated linear interpolation and ANNs to fill the gaps in daily N2O fluxes measured using automated chambers during 2012–2016 in the southwestern part of France and recommended that the combination of both an ANN and linear interpolation yielded the best results compared to the individual ones. Goodrich, et al. [33] tested ANN and K-nearest neighbor (KNN) regression in the cattle farms of Waharoa, New Zealand, and reported the outperformance of the latter in filling the gaps of N2O measured using the MM method. Philibert, Loyce and Makowski [29] used a random forest regression technique on the global N2O database of Stehfest and Bouwman [34], with local environment and management variables, and reported its outperformance of several other regression models. Similarly, Maier, et al. [35] applied a marginal distribution sampling technique and RF to fill the gaps in N2O along with other GHGs. Mehmandoost Kotlar, et al. [36] compared multiple linear regression, support vector machine and random forest regression to predict N2O fluxes under the presence and absence of cover crops. Similarly, different machine learning algorithms are increasingly being used to estimate atmospheric [37,38] and environmental variables [39,40,41], which can support in the estimation of N2O fluxes.
While the gap-filling technique for N2O has not been standardized [42], several steps are currently being taken to recommend the best approach. Following the increasing usage of machine leaning algorithms in the estimation of N2O, Dorich, et al. [43] outlined and discussed the potential strengths and challenges of five techniques of gap filling, viz., linear interpolation, random forest regression, artificial neural networks, generalized additive models and autoregressive integrated moving average models. Accordingly, this study aims to (a) evaluate the effectiveness of multiple algorithms (linear regression, random forest regression, support vector regression and artificial neural networks) in predicting N2O emissions and (b) evaluate scenarios when readily available data is used to train the machine learning algorithms compared to the scenario when they are not. While the findings have implications for agricultural decision making, the primary focus was methodological—identifying which models perform best under different data constraints—rather than developing a directly deployable decision-support tool. The results from this study are expected to guide further studies to apply a readily available dataset for a more detailed estimate of direct N2O emissions from agricultural farms.
2. Materials and Methods
2.1. Data
In this study, discrete measurements of N2O (g/ha/day) were collected along with corresponding measurements of soil temperature (°C), soil volumetric moisture (%), pH, soil ammonium content (mg/kg of dry soil), soil nitrate content (mg/kg of dry soil), rainfall (mm) and average air temperature (°C) from “Baggs Farm” and the “Research North” agricultural farm in Ontario, Canada. The location of Baggs farm is 43.459° N, 80.309° W, and Research North is 43.440° N, 80.345° W. A total of 628 observations were taken during the years 2019 and 2020. In addition to the above-mentioned variables, three variables were derived, namely, days after rainfall (Daysrain), days after fertilizer application (Daysfert) and 2-day accumulation rainfall (Srain2D) from the local meteorological and management data. Similar variables are used by Saha, Kemanian, Rau, Adler and Montes [30], Saha, Basso and Robertson [26] and Taki, Wagner-Riddle, Parkin, Gordon and VanderZaag [31] in their N2O emission estimation studies. The summary of collected data is presented in Table 1.

Table 1.
Summary of collected data.
For more detailed information on the collected data and field information, please refer to Ashiq, et al. [44] and Ashiq, et al. [45]. To detect whether the N2O data had any temporal autocorrelation, the measurement intervals were calculated at each site. As these intervals were highly variable (Supplementary Table S1), a generalized least squares model with a continuous time (AR1) structure was used to check the autocorrelation. For this purpose, the corCAR1 model, which inherently accounted for irregular spacing, was used with the “nlme” package [46].
For covariates, continuous data on soil moisture, soil temperature and climate data and discrete information on crop yield and onsite mineral nitrogen are recommended for collection [43]. While the crop yield information was available [44], it was not used due to its non-differentiation at the test sites. Practically, information like Ph, NH4 and NO3 are not available from secondary data sources and need site specific measurements, whereas other predictor variables may be collected or estimated through external sources. For example, soil moisture and temperature may be estimated using techniques employing satellite images like SMAP [47] and Landsat [48]. Acknowledging the difficulty in estimating the data variables required to run the models, two scenarios, viz., High Input (HI), including all variables, and Low Input (LI), excluding Ph, NH4 and NO3 are formulated; all four algorithms were tested for both scenarios.
2.2. Training and Testing Data Sampling
Multiple studies have recommended different minimal sizes to perform statistical learning algorithms. A rule of thumb for sample size selection is based on a ratio of the number of observations to the independent predictors of 30:1 [49]. Alternatively, it can be estimated as 50 + 8 × n, where n is the number of independent variables [50]. Bujang, et al. [51] reported that for more than 10 variables, a minimum sample size of 300 should be used as a realistic approximation of estimates for the population. In other studies pertaining to N2O emission estimation using machine learning algorithms, various sample sizes have been used. Philibert, Loyce and Makowski [29] used 594 observations from the global N2O database [34] to train the random forest regression. Similarly, Zhuang, et al. [52] had 209 observations to apply an artificial neural network. Abbasi, et al. [53] used 26 datasets to predict N2O emissions from paddy wetlands using artificial neural networks. As both data collection sites were in geographical proximity and the management practices were alike, the data was merged into a single dataset. It is worth noting that some researchers, like Korkiakoski, et al. [54], trained these algorithms separately for each measurement site.
To ensure that all algorithms selected in this study were using the same data instances for training and testing, we fixed the seed for a random number generator (set.seed variable) in R and identified the unique and non-duplicated random rows of the dataset to split the data for training and testing purposes in a 70:30 ratio [53]. By doing this, it is ensured that the testing data is excluded before the commencement of model training and when the validation is performed, it is performed on completely independent data. Some studies split the data into an additional bin of training, testing and validation sets to avoid duplication of data during training and testing and to avoid possible overfitting. Many other studies also use K-fold cross-validation to generalize the model and reduce the risk of overfitting. However, for this study, we have kept the simple approach of a single split into two independent datasets, but for individual algorithms like RFR, we have employed bootstrapping techniques to avoid overfitting.
The seed number that was able to split the entire data into training and testing datasets of similar data statistics was finalized to ensure that the characteristics (values) of N2O during the training period were not too different than those in the testing period. A similar approach of fixing the random number generator to reproduce the results is followed in other N2O studies [35].
2.3. Multiple Linear Regression (MLR)
Regression analysis is a statistical technique that estimates the relationship among variables with a reason and result relation [55]. In MLR, a linear relationship is estimated between a dependent variable (predictand: Y in Equation (1)) and multiple independent variables (predictors: X1, X2, … Xn in Equation (1)).
where is the intercept, … are the parametric coefficients and is the residue error.
This best fit linear relationship is used to predict the observed instances and the error of MLR () is expected to follow a Gaussian distribution [56]. There are some pre-requisites of applying MLR to predict a variable of interest, of which, no multi-collinearity among predictors, no autocorrelation among the observed values, no random predictors (each predictor follows a distribution) and homoscedasticity of residuals are the key ones. If there is no linear relationship among the predictors and predictand, the predictor variables may need transformation. In this study, the assumptions needed to apply MLR on the study dataset were tested and only when they were deemed satisfactory was the appropriate MLR technique applied. If the majority of the assumptions were unmet, MLR was still applied to check if there was any merit to its application in N2O estimation in the study sites.
To test multicollinearity among predictor variables, the R package “car” [57] was used. The package estimates the Variance Inflation Factor (VIF) to detect the multi-collinearity of model parameters by estimating the correlation and its strength between the independent predictor variables. VIF values of 1 or less imply no correlation, values of 1-5 imply moderate correlation and values above 5 imply strong multicollinearity, meaning the variables are recommended to be removed from the model as they are expected to bring in redundancy in model performance [58]. As the N2O variables were measured in discrete intervals and not continuous ones in our study, the autocorrelation criterion was not considered. To check the linear relationship between the predictors, a diagnostic plot of residual errors and fitted values was inspected. If the line is horizontal in nature and without a distinct pattern, it is an indication of linear relationship. Similarly, the quantile plots of residuals can be inspected to check if the residuals are normally distributed and nominally follow a 1:1 line. For the homoscedasticity (homogeneity of variance of residuals), residuals are inspected in a scale-location plot. If a relatively horizontal line is seen in this plot with equally spread plots, it indicates that there is no problem of homoscedasticity and MLR can be applied. All these analyses were performed in R software, version 4.2. For MLR, four scenarios of model building are assumed:
- (1)
- HILMo: N2O is influenced by all independent predictors of Table 1. There is no interaction among the independent predictors.
- (2)
- HILM: N2O is influenced by all independent predictors of Table 1. There is interaction among ST, VM, Ph and NO3.
- (3)
- LILMo: N2O is influenced by independent variables under LI. No Ph, NO3 or NH4 data values are used to train the model. There is no interaction among the independent predictors.
- (4)
- LILM: N2O is influenced by independent variables under LI. Interaction among the ST, VM and Srain2D was permitted.
The ordinary least squares method is used to estimate the parameters of the MLR, which used mean square error as the model objective function.
2.4. Random Forest Regression (RFR)
RFR is a supervised machine learning algorithm that uses the results from multiple random decision trees predicting a continous variable [59]. Accordingly, it can be expected that the output of an RFR is more accurate than a single decision tree. For a better understanding of RFR, refer to Supplementary Figure S1.
RFR creates a set of decision rules based on the predictor input, then these trees run parallely and independently to provide their individual predictions. The random seed selected at the start of study was used to generate training and testing datasets at a 70:30 ratio. Then, this former data is used to create a bootstrap sample of observations (“in-bag”) and some data is left out as “out-of-bag”. Secondly, the explanatory variables and their number (mtry) are randomly selected for each tree. A tree is built using the “in-bag” data and “mtry” variables by recursively partitioning the initial data into smaller groups called nodes via binary splits based on a single predictor. Each split is finalized by comparing the splits with all predictor variables. Tree growth generally ends when the number of observations in the terminal node reaches five or fewer for regression. This process is repeated for a number of trees (ntree) to bootstrap samples and trees.
To finalize the number of trees in the forest and the variables in each tree to best estimate the N2O, we ran a permutation of 1–9 variables and 1–400 trees. The R package “randomForest” [59] was used to fit random forest regression on our dataset. The mean square error is used to identify the variables of importance in the RFR algorithm and the number of variables in each tree and numer of trees are finalized for the best R2 value between different simulated and observed N2O values during both the training and testing of the datatsets. Unlike MLR, which has multiple pre-requisites on predictor-predictand relationships, RFR does not need any prior relationship between them, thus making it one of the most powerful and easy to apply machine learning algorithms for both classification and regression problems.
2.5. Support Vector Regression (SVR)
Initially proposed by Vapnik [60], support vector machine (SVM) is an effective multi-purpose analytical tool that is mostly employed for classification problems. Recently, it has been advanced to use in regression problems (hence support vector regression (SVR)). It is an algorithm that can handle linear and non-linear data and also has an outlier detection ability [61]. In this supervised algorithm, each data point is plotted in a multi-dimensional space, and the correspinding value of each predictor variable represents a coordinate. A best fitting hyperplane is then estimated, i.e., the one that has maximum number of data points. Contrary to the MLR, where the objective was to minimize the error between the predicted and the observed values, SVR tries to fit an optimal plane within a pre-defined threshold (epsilon). This threshold is the distance between the hyperplane and the boundary line. This concept of maximal margin thus allows SVR to be viewed as a convex optimization problem that is penalized with a cost parameter to avoid overfitting. Additionally, there is no pre-requisite in SVR that the explanatory variables follow a particular distribution.
To construct a model in SVR, we need to specify an appropriate kernel function, which could be either linear, polynomial, sigmoid or radial. A radial basis kernel function was selected in this study, which transformed our data from the non-linear relationship to a linear plane where SVR was fitted and then the data was back-mapped to the original non-linear space [62]. SVR with radial basis function is reported to perform better for N2O emission estimation by Mehmandoost Kotlar, Singh and Kumar [36]. The SVR is fine-tuned by varying the error and penalty cost parameters. We defined the range of error from 0 to 1 (increments of 0.1) and cost parameter from 1 to 250 (increments of 0.5). The advantage of SVR is that it is robust to outliers and there is no pre-requirement for scaling or physcially transforming the variables. Also, the hyperplane that is close to the training data points is ignored and optimally placed to prevent it from overfitting on training data [63]. In this study, the R package “e1071” [64] was used to perform SVR.
A non-linear SVR function F(x) is presented in Equation (2).
2.6. Artifical Neural Networks (ANNs)
An ANN is a model mimicking the workflow process of neurons in a human brain by continuously learning with each data instance of the training data. It is a multi-layer perceptron (MLP) with at least three layers: input, hidden and output [67]. Represented as nodes and links, each layer receives input from the previous layer’s output. Generally, the number of neurons in the first layer is the same as the number of predictors available in our dataset. Thus, each node in the first layer receives data values of corresponding variables for an instance, then passes it to the second round with corresponding weights in each link and a bias value. In the second layer (or subsequent layers), a hidden layer exists, which receives a summation of weights and corresponding data values with an individual activation function. Similarly, these values are then passed to the next layer, if any, and this procedure is followed. By the end of hidden layer, the output is then generated at the output node. Based on the prediction made and actual value at the output node for this instance, the corresponding biases are adjusted and another data instance is passed through the model. In this study, we used R package “neuralnet” [68] to fit ANNs to the data. When the ANN was used on original data, the models did not converge. So, the data was scaled before using the ANN.
Since it was likely that we were dealing with the outliers in the predictor and predictand variables in our study, an appropriate scaling technique was required. Thus, we used a robust scaling technique that used the median and interquartile range of each variable to maintain the relative distances between non-outlier datapoints. This is a technique frequently used by researchers in N2O emissions studies [69]. The equation used to scale the data is presented in Equation (3).
2.7. Comparison Metrics
While each algorithm discussed above uses mean square error as the objective function in our study, we have identified Coefficient of Determination (R2), root mean square error (RMSE) and volumetric efficiency (VE) metrices to evaluate the performance of the algorithms to predict the best estimate of the N2O.
R2, ranging from 0 (poor model) to 1 (perfect fit), explains how well the input features explain the variability in emissions. Technically, it reflects how well the model fits but not the accuracy of the individual predictions. From a decision-making perspective, a high value (>0.7) would indicate a model capturing the overall emission patterns, which would be useful for exploring key drivers and informing high-level policies regarding those drivers. RMSE is expressed in the same units as the variable and ranges from 0 (perfect prediction) to infinity. It quantifies the average magnitude of prediction errors and helps to assess how closely the model predicts actual emission values, supporting applications like emission forecasting, compliance monitoring or planning emission abatement strategies. For multiple models with a comparable capture in the variance of observed values (similar R2 values), RMSE provides information regarding which model to select based on their lowest RMSE estimates. However, RMSE is sensitive to outliers and deviation from bigger observed values can distinctly increase it, thus warranting a careful scrutinization before finalizing the selection of best model. However, since N2O values are desired to be captured for their peak emission periods, RMSE remains a relevant comparison metric to evaluate the performance of models estimating N2O values. Similarly, VE, ranging from 0 (no efficiency) to 1 (perfect volumetric match), evaluates model’s ability to replicate cumulative emissions and thus emphasizes aggregate accuracy over individual predictions. Thus, for applications like total emission accounting or long-term nutrient management, a high VE would indicate dependable cumulative estimates. As well as these indices revealing the performance of each model to estimate the best possible estimate of N2O, we also identified the associated uncertainty in each prediction from the models using prediction intervals (PIs) [70].
For each algorithm, the best estimates of predicted values are associated with the prediction interval (PI), which is a quantification of the possible observed values for a given instance of input variables. For data with low variability, these PIs are relatively narrow, whereas for variables like N2O, which is known to have lot of variation, we can expect a wider prediction band. For MLR, we used the inherent prediction intervals using the standard Gaussian technique. Each band is generated at 95% probability, which indicates that for any given large database of measured N2O values and their respective co-variates, there is a 95% probability that any measurement of N2O will fall within the generated band. For RFR, SVR and ANN, the bootstrapping technique is used to generate the predicted values of N2O for a given data instance and then later summarized with the standard Gaussian technique. The bootstrapping technique has been tested and verified on RFR [71,72], SVR [73,74] and ANNs [75,76]. Two additional statistical factors, viz., the p-factor and r-factor, are also calculated to quantify these uncertainties. The p-factor, ranging from 0 to 1, indicates the fraction of observed values captured within model’s 95% prediction uncertainty bounds. Thus, a p-factor closer to 1 would mean that the model is favorable for uncertainty-aware decision making, especially in N2O modeling where capturing variability is critical. Similarly, the r-factor can range from 0 (tight band) to values >2 (very wide band) and is recommended when the values are less than 1 [77] for precise predictions. It is computed as average width of the uncertainty band divided by the standard deviation of measured variable [78]. This is important for high-resolution decisions such as site-specific management and needs to be balanced with the p-factor to avoid overconfidence. All these metrics form a robust evaluation framework, as R2 and VE assess model adequacy, RMSE ensures quantitative reliability and the p and r factors support decisions under uncertainty. Thus, it is recommended to analyze all metrices before interpreting the models for environmental and agricultural decision making. All metrics were calculated using the “hydroGOF” package in R [79].
3. Results
3.1. Testing Autocorrelation
While the data used in this study is treated as discrete measurements, it should be checked whether temporal autocorrelation exists among the measurement sites, which would affect the applicability of the models. This can easily cause overfitting and biased evaluation and uncertainties may be underestimated. Since the dates between measurements were highly variable across the measurement sites, a continuous time model (AR1) was used in conjunction with a model that inherently used irregular intervals [80]. The results suggested that within each site and across the dates of measurement the estimated AR1 autocorrelation parameter (Phi) was 0.024, which is very close to zero, indicating very weak or negligible autocorrelation. Conversely, if it were close to 1, it would have indicated a strong temporal autocorrelation. With this test, it was concluded that the N2O levels at the measurement sites (Figure 1) were almost uncorrelated with the next date and autocorrelation will not bring any bias to the further testing of the models.
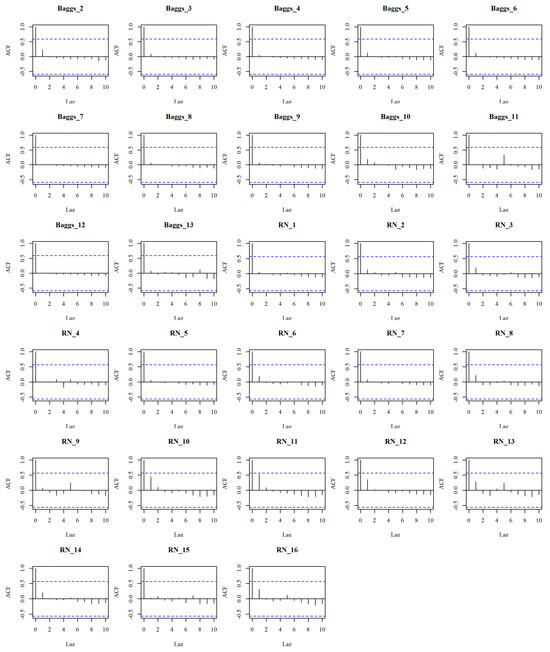
Figure 1.
Autocorrelation plots of N2O across multiple sites in Baggs and Research North (RN) farms. The x-axis shows the time lag (up to lag 10), y axis shows value of autocorrelation at each lag and the blue dashed lines show 95% confidence bounds, exceedance of which at any lag would mean statistically significant autocorrelation.
3.2. Training and Testing Data Sampling
To demonstrate that a bias starts from as early as selecting a random seed to split the training and testing data for similar analysis, we performed a bootstrap of the simple linear regression of N2O with all variables used in this study. The seed number to split the entire dataset into random subsets of training and testing data (in 70:30 ratio) increased by 1, from 1 to 1000. It was observed that there could be a significant bias arising from the selection of a seed number in the algorithm applied later (Supplementary Figure S2). To ensure that all algorithms selected in this study are applied on same dataset, which is reflected properly in both training and testing samples, a seed number of 16 was selected to ensure similar data characteristics (Figure 2). It is to be noted that selecting the best performing seed here could induce an additional bias, so the seed yielding close to median performance yet capturing the range of N2O data and its statistical characteristics was selected.
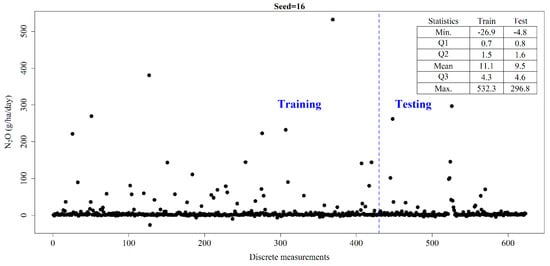
Figure 2.
Splitting training and testing datasets.
With seed number finalized as 16, it was observed that N2O values are distributed proportionately during the training and testing periods. The first quartile of N2O values during the training (testing) periods were 0.7 (0.8), the medians were 1.5 (1.6), the means were 11.1 (9.5) and the third quartiles were 4.3 (4.6) gm/ha/day. This makes our technique similar to a stratified sampling technique where the continuous target variable is binned into quartiles and the training/testing split is performed proportionately. Similarly, it was ensured that both training and testing data had their peak emissions and sinks of N2O values.
3.3. MLR
When the training data was subjected to MLR without any scaling or transformation of its predictor variables, it was observed that multiple predictors were heavily influenced by multicollinearity (Table 2).

Table 2.
Variance Inflation Factor of different linear regression models selected in the study.
Generally, it is recommended to remove the variables with high multicollinearity (>5) from the analysis, as they are expected to bring in redundancy to the model and their omission would not significantly alter the model performance. However, when we omitted the variables with multicollinearity, the performance of the model dropped significantly (Supplementary Table S1).
Similarly, when the plots of residuals were inspected for homoscedasticity, it was found that the residuals were not spread equally along the range of predictors that indicated heteroscedasticity and thus the violation of the assumption for MLR (Supplementary Figure S3). The assumption of linearity among variables and the output was also inspected (Supplementary Figure S4), which showed that there was a pattern in the residuals indicating a non-linear relationship between the predictors and predictand. Thus, it was summarized that MLR cannot be applied to the study site to predict N2O emissions without further intervention of data. Since the N2O emission values had negative numbers as well (indicating sinking of N2O into the soil), log-transformation could not be performed, which could have been an alternative in scenarios where data variables are not linearly related [81]. The results are quite expected, as it is well known that N2O generation is a highly non-linear process and depends on a multitude of environmental variables [16,82].
Even if all these assumptions are ignored and MLR is applied on the given data, it is observed that the technique does not explain more than 30% of the variability of the N2O fluxes during the training and 33% of the fluxes during the testing (Supplementary Table S2). A relatively old study by Ciarlo, et al. [83], which fitted MLR on soil moisture to explain the variations in N2O, also reported that none of the MLR models were able to satisfactorily explain the N2O emissions properly. Similarly, an even older study by Clayton, et al. [84] reported that MLR was explaining about 28% of the variability in N2O fluxes from a fertilized grassland. With site-specific variables, MLR may be able to explain more variability in the N2O fluxes than for a mixed dataset [85]; however, this explanation is still much lower. Mehmandoost Kotlar, Singh and Kumar [36] also reported that MLR was not able to estimate N2O emissions with satisfactory accuracy. For a coarse time-scale (e.g., yearly), MLR may still explain more than 70% of the variability in N2O fluxes in a similar study to ours [86].
It is also observed that none of the MLR techniques selected in this study could capture the hot moments of N2O, as indicated by the predictive intervals shown as red error bars in Figure 3 for the HILM and LILM scenarios.
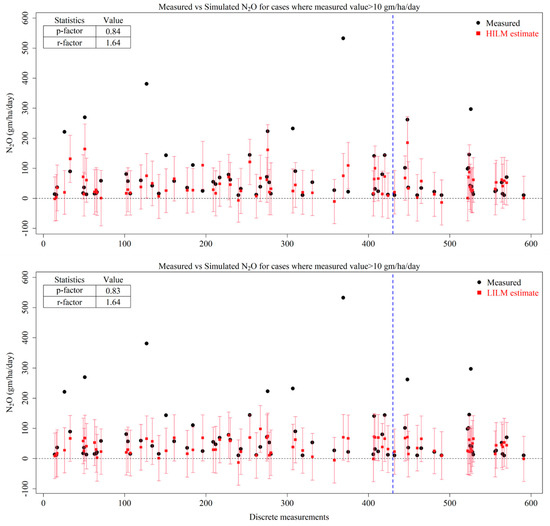
Figure 3.
Measured N2O values (black dots), predicted mean estimates of N2O (red squares) by High-Input linear model (HILM) and Low-Input linear model (LILM) and the prediction interval of models at 95% confidence (red error bars) formatting. The blue dotted line represents the split between training (left side) and testing (right side) datasets.
While in MLR models the predictive intervals were able to capture the emissions within 100 gm/ha/day and thereby have a p-factor of 0.84, the bigger values were left out, which is not desired from a N2O emission simulation model. Accordingly, it was concluded that MLR is not the right algorithm to estimate N2O emissions in our study area.
3.4. RFR
Compared to the MLR models, RFR was observed to have a distinct outperformance in the simulation of the N2O emissions in the study area. It is also observed that RFR can easily overfit (Figure 4). The combination of “mtry” and “ntree” variables in RFR for HI revealed very high R2 values (~0.9–0.97) during the training period and yielded very poor performance during the testing period (~0.1–0.4). For HI, it was observed that if the number of variables to include in a tree was kept as a lower number (2–4) and the number of trees was increased, a more favorable performance could be seen during both the training and testing periods.
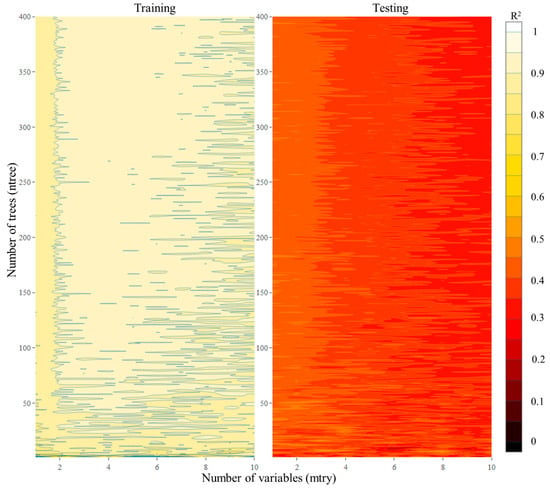
Figure 4.
Performance of RFR under HI scenario showing its possible overfitting.
While inclusion of multiple trees in an RFR increases its computational cost, it was not found to be significant in our study (training the data with multiple trees took a few extra minutes). For the LI scenario, the performance of RFR for different numbers of trees and variables is presented in Supplementary Figure S5. It is observed that for LI, in contrast to HI, the inclusion of more variables was found to have better performing models. However, for an optimal number of four variables in a tree and with a higher number of trees, the performance of the model for both the training and testing datasets was better. It is also observed that as the number of trees exceeded 40, the decrease in RMSE was not significant (Supplementary Figure S6), thereby prompting the number of trees to be limited to 50 for both models. Thus, an RFR algorithm with the architecture of variable/number of trees as 2:48 (4:40) was selected for the HI (LI) scenario in this study.
The HI RFR model was able to explain 65% of the variability in the measured N2O fluxes with an RMSE of 27.9 (20.0) gm/ha/day of the training (testing) datasets. Similarly, it was found to have 43% (35%) volumetric matches to the observed measurements for the training (testing) datasets. Interestingly, the LI RFR model was found to have better performance in estimating N2O emissions during both the training and testing periods. LI RFR was able to explain 72% (68%) of the variability of measured fluxes, with lower errors of 23.9 (19.2) g/ha/day and better volumetric matches of 52% (46%) during the training (testing) periods.
The model performance statistics for these two scenarios are quite interesting, as the LI RFR model is found to perform better than the HI RFR model, despite using fewer predictors, and can be described as a classic example of the “less is more” principle in machine learning. The reason for this could be the collinear variables (air temperature and soil temperature) or possible noise from NH4 and NO3 measurements. The higher number of covariates means more competition for split importance (evident from variable importance plots prepared in Figure 5), as opposed to the LI model where fewer features allowed the model to focus more clearly on highly relevant predictors. These performance metrices, along with a visual plot of HI and LI RFR, are presented in Supplementary Figure S7.
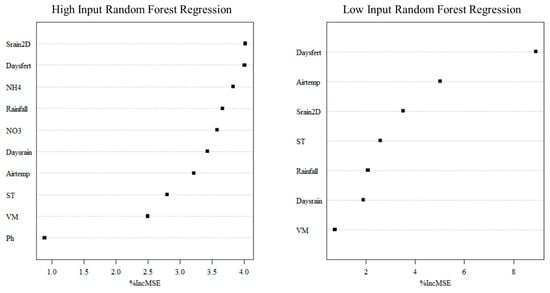
Figure 5.
Variable importance plots of HI-RFR and LI-RFR models based on the training dataset.
In the HI RFR, the five most important variables in terms of their influence on increasing the mean square error (MSE) are Srain2D, Daysfert, NH4, Rainfall and NO3. The gradual decline in importance indicates that the model drew from many variables. Similarly, under the LI RFR scenario, Daysfert was the most important variable, followed by air temperature and Srain2D. The overall shape also has a steep drop-off, indicating a heavy reliance on a few key features. Since Daysfert, Srain2D and Airtemp were consistently among the important predictors in both scenarios, this suggests that the timing of fertilization and recent rainfall events are the key drivers of N2O emissions. This aligns well with the established fertilizer-driven N2O emission hypothesis, especially when favorable environmental conditions persist (seen through the importance of rainfall and temperature in the plots).
The predictive intervals of both the HI and LI RFR models are presented for higher N2O emissions (for instance where the observed N2O values were > 10 gm/ha/day) in Figure 6. It is observed that both HI and LI RFR have the capability to capture 90% of the emissions within their 95% predictive intervals. Similarly, the average width of the uncertainty band was found to be 1.5 for HI and 1.3 for LI, indicating a slightly better performance for the LI scenario. However, it is observed that the peak emissions (for, e.g., 300–400 gm/ha/day) were not encapsulated within the predictive intervals of these models. The reasons for this could be that the number of samples with relatively lower N2O values is significantly higher than the samples with higher values and have been used to train the models. This also means that more peak emissions need to be included in the training dataset.
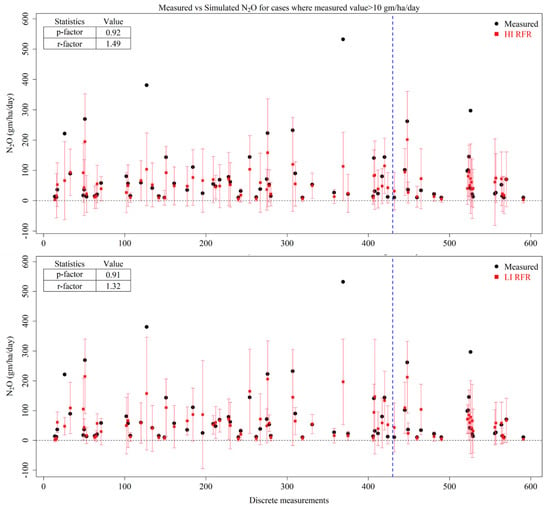
Figure 6.
Measured N2O values (black dots), predicted mean estimates of N2O (red squares) by High-Input Random Forest Regression (HI RFR) and Low-Input Random Forest Regression (LI RFR) and the prediction interval of models at 95% confidence (red error bars). The blue dotted line represents the split between training (left side) and testing (right side) datasets.
While these results were for the best estimate of N2O values, it is equally important to understand the uncertainty arising from the model itself. These uncertainties are quantified through the band of predicted data by different trees of each scenario. However, there could be an additional uncertainty stemming from the model itself, which is not represented through such analysis. For this purpose, techniques like Bayesian models [87] may be employed.
RFR was reported to explain nearly 90% of the variability of yearly N2O fluxes over the LUCAS points in Europe [88]. Similarly, Villa-Vialaneix, et al. [89] reported that as number of data instances in the training data increases, RFR performs better in N2O estimation. For a training data of 500 instances, it was reported to explain 70% of the variability of fluxes. A different application of RFR for N2O emissions due to biochar was reported to explain 24% of the variability [90]. Thus, it could be summarized that RFR had a much better overall performance compared to MLR in the study area; moreover, the data indicate that even the LI scenario could perform as well as or even better than HI in regions with limited data. One of the key disadvantages of techniques like RF could be that, with respect to a MLR, they cannot precisely analyze the impacts of changes in different input variables in N2O emissions [29]. For example, even if the soil moisture is changed to 100%, with the RFR model we selected, most of the trees might not use the soil moisture as a variable, so the aggregated results might not show the anticipated change in N2O values.
3.5. SVR
It is observed that the SVR algorithms trained in this study were not sensitive to the epsilon parameter. Only the changes in the cost value of model changed the RMSE computed by comparing the measured and model-simulated values. Villa-Vialaneix, Follador, Ratto and Leip [89] fixed the value of epsilon to 1 and only fine-tuned the SVR based on the kernel and cost parameters in a similar study. Figure 7 presents the calibration summary of the HI scenario; similar performance was observed for the LI scenario, as shown in Supplementary Figure S8.
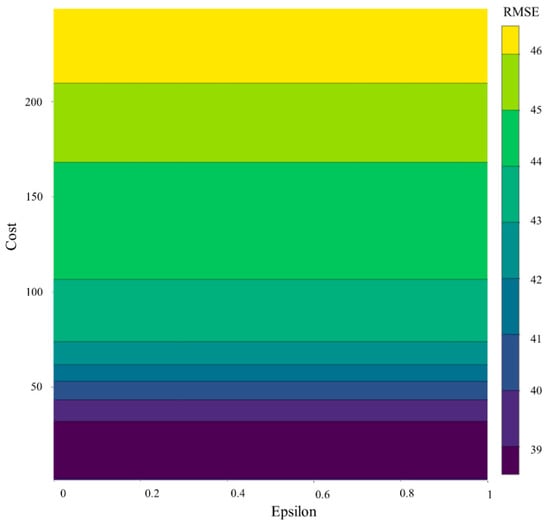
Figure 7.
Fine tuning of SVR under HI scenario using RMSE as objective function.
The performance summary of SVR in predicting N2O values under the HI and LI scenarios is presented in Supplementary Figure S9. The R2 value of the SVR model under the HI scenario was found to be 0.59 (0.63) for the training (testing) data. Similarly, the average deviations in terms of RMSE values were found to be 28.6 (26.0) g/ha/day for the training (testing) datasets. The volumetric match in terms of VE explained that SVR under the HI scenario was unable to capture the volume of N2O during the testing period, despite it capturing 38% of the volumetric efficiency during training period. Like RFR, the LI scenario was found to have a comparable performance to that of the HI scenario. It is observed that under LI, the R2 values estimated from the SVR are 0.61 (0.66), the RMSE values are 28.3 (23.4) gm/ha/day and the VE values are 0.34 (0.19) during the training (testing) periods. While the deterministic best estimates from the SVR are found to be comparable for both scenarios, the uncertainty in N2O emissions are better reflected in the HI scenario (Figure 8). However, it was observed that the prediction interval of SVR had poor coverage and underestimated the uncertainty. The narrow predictive intervals relative to the variability of observations also mean that the model was overconfident and not a good fit to estimate N2O emissions and the uncertainty in them in the study area.
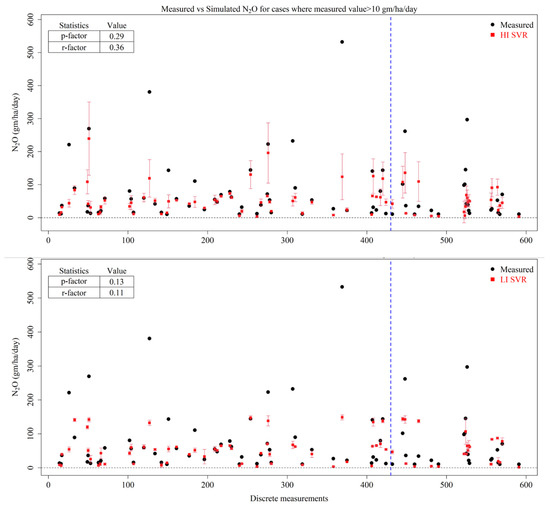
Figure 8.
Measured N2O values (black dots), predicted mean estimates of N2O (red squares) by High-Input Support Vector Regression (HI SVR) and Low-Input Support Vector Regression (LI SVR) and the prediction interval of models at 95% confidence (red error bars). The blue dotted line represents the split between training (left side) and testing (right side) datasets.
Villa-Vialaneix, Follador, Ratto and Leip [89] reported that SVM (or SVR) could explain nearly 85% of the variation in the N2O fluxes for a sample size of 500. Mehmandoost Kotlar, Singh and Kumar [36] also reported that SVR had better performance in estimating N2O emissions compared to other models. However, in our study, we found that SVR was comparable to RFR in predicting a deterministic value for N2O emissions. Also, compared to other algorithms, it was found that SVR is the most time consuming, as it essentially converts the entire data into a kernel matrix and takes a long time to fine-tune [89]. SVR had a better performance than RFR in estimating soil organic carbon stocks, explaining 60% of the variability in the study by Were, et al. [91]. However, owing to the higher computational expense, a similar accuracy to that of RFR to estimate the N2O emissions and the relatively low predictive intervals in this study, it was inferred that SVR was inferior to RFR in the study area for N2O emissions estimation.
3.6. ANN
Since there is no structured methodology to construct an ANN, it can have multiple hidden layers and nodes [92]. Thus, a thumb rule is followed in this study to construct a feed-forward ANN. Since the architecture was allowed to expand to two hidden layers, multiple ANN models were constructed with the number of nodes in each hidden layer ranging from 1to 10 for HI and from 1 to 7 for LI. Thus, a total of 100 ANNs were evaluated for the HI scenario and 49 ANNs were evaluated for the LI scenario. Accordingly, it was observed that for a HI ANN, the model was prone to overfitting (observed from high R2 values during training and low R2 values during testing). Accordingly, a few pockets of optimal performance were identified that had relatively similar performance during both the training and testing periods. It was observed that during testing under the HI scenario, three pockets (5,8; 5,4; 8,8) had good performance; we selected the latter one (Figure 9).
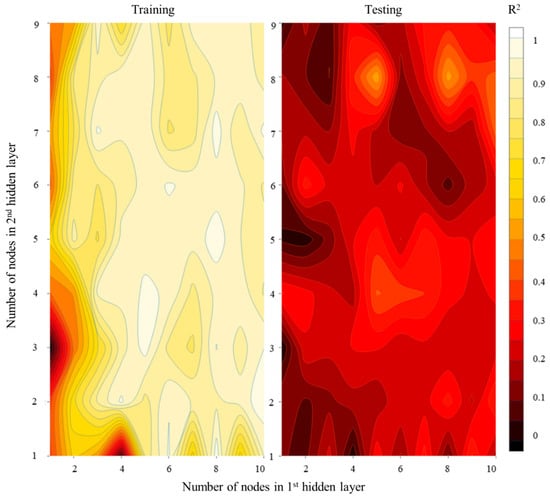
Figure 9.
Summary of model performance of ANN model for HI scenario showing R2 values for different parameters.
Similar calibration statistics for the LI scenario are presented in Supplementary Figure S10, where we finalized an ANN with 5:4 nodes in the two hidden layers. While it is generally recommended to have fewer nodes in hidden layer to prevent the overfitting of ANNs, other studies pertaining to N2O estimation have used higher numbers of nodes in their hidden layers [23]. In general, it was observed that the ANN had high accuracy in capturing the measured N2O emissions in the study area (Supplementary Figure S11). The HI ANN could explain 94% (44%) of variability of measured N2O, the RMSE values were 10.8 (35.2) gm/ha/day and the volumetric efficiencies were 0.59 (−0.1) for training (testing) periods. It was again observed that for the LI scenario, the results are more favorable, explaining 81% (68%) of the variability and having RMSE values of 18.9 (21.7) gm/ha/day and volumetric efficiencies of 0.41 (0.26) during training (testing) periods. Villa-Vialaneix, Follador, Ratto and Leip [89] reported similar performances for an ANN and RFR for a sample size of 500.
Accordingly, the uncertainty was estimated for values of more than 10 gm/ha/day and showed that the HI ANN was able to capture the N2O emissions with good accuracy (Figure 10). The model captures 75% of all high emissions within its prediction intervals of 1.25 times the observed variability, reflecting a balanced uncertainty range. The LI ANN had a slightly lower coverage (p = 0.64) but narrower uncertainty levels (1.07), showing slightly higher confidence with narrow spread. It exhibited a good fit for the majority of peak emissions, but a few extreme errors persisted, giving a slight edge to HI ANN.
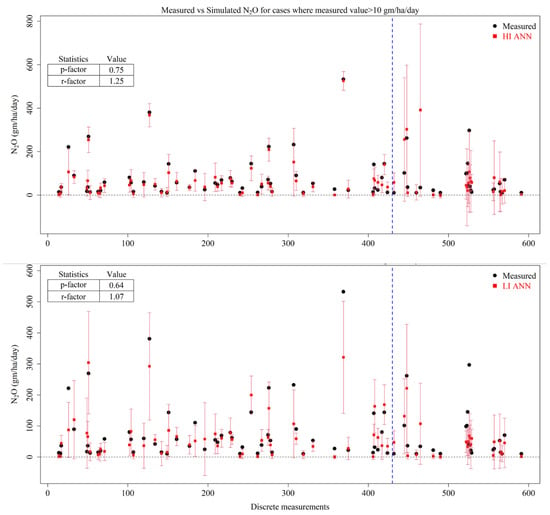
Figure 10.
Measured N2O values (black dots), predicted mean estimates of N2O (red squares) by High-Input Artificial Neural Networks (HI ANNs) and Low-Input Artificial Neural Networks (LI ANNs) and the prediction interval of models at 95% confidence (red error bars). The blue dotted line represents the split between training (left side) and testing (right side) datasets.
Taki, Wagner-Riddle, Parkin, Gordon and VanderZaag [31] used ANNs and a linear interpolation technique to fill the gaps in sub-daily N2O emissions and reported that the ANNs constructed for each year were able to explain 41% of the variability in fluxes. Abbasi, Luithui and Abbasi [53] used an ANN to estimate the N2O from paddy fields using predictors like soil characteristics, fertilizer inputs and rice cultivar yields and reported excellent performance (R2~0.99) for the testing period. It can be argued that the number of data instances used to train and test the ANN in the study of Abbasi, Luithui and Abbasi [53] was very low compared to ours (only 26 in total), which could be the reason for better performance. However, it can still be argued that, for a relatively smaller data size, having more layers and hidden nodes in each ANN can easily lead to overfitting.
The ANN frequently encountered problems while training the algorithms with the training dataset. Without scaling the data, none of the algorithms converged to a final value and thus the model could not be trained. Even when scaled, one had to be quite careful about the local minima values and the model thus needed multiple initializations of weights and repetition of runs. It was also highly sensitive to the number of predictor variables selected in the first input layer, as all the weights had to be initialized and trained accordingly [89]. Also, it was very prone to overfitting, as observed in Figure 9 and Figure S10.
4. Discussion
Measurement of N2O emissions from fields in their natural settings using standard techniques may be the best way to really understand their spatio-temporal characteristics. Despite this knowledge, for several reasons, it may not be feasible to employ such techniques over a large area or a long period. With emerging research and the accessibility of data, data readily available from secondary sources can be used in estimating the N2O emissions from an agricultural landscape. Some ML techniques have used readily available data like soil moisture, temperature and electrical conductivity to explain up to 64% of the variability in methane emissions from paddy fields [88]. This study also shows that ML algorithms like ANN, RFR and SVR could potentially capture trends in N2O emissions using data like rainfall, temperature, number of days after application of nitrogenous fertilizer, soil moisture and soil temperature. Information on in situ rainfall and temperature can be easily accessed from local weather stations and fertilizer application days can be approximated by talking with local farmers. Similarly, during the past decade, ML techniques have used satellite images to approximate soil moisture [93,94,95], pH [93], temperature [96,97] and, if needed, other atmospheric variables [37,38]. Thus, the novelty of this study is the demonstration that ML techniques can make use of such readily available secondary information to estimate N2O emissions, which are a product of a very complex biogeochemical process. These techniques can be also used to fill the gaps in the existing time-series of measured N2O emissions [31,43].
While evaluating the applicability of models, a single performance metric cannot explain the model’s ability for capturing the trends, magnitude and uncertainty of highly variable N2O fluxes. Thus, in this study, multiple performance indicators were used to robustly evaluate model performance; R2 and VE assess model adequacy, RMSE ensures the quantitative reliability and applicability for total emissions accounting and the p-factor and r-factor quantify the uncertainty. These metrices also have relevancy from a decision-making perspective, as models with higher uncertainty (e.g., SVR in our study) could not provide sufficient confidence for fine-tuning decisions, while models with more reliable performance (like RFR and ANN) enable risk-aware decision making. Thus, different models provide value in making decisions pertaining to nitrogen application timing, emissions accounting, climate smart farming initiatives, etc., where both accuracy and uncertainty are important.
It should also be highlighted that several improvements can be made to future studies on similar applications. The common issue of potential overfitting, which was identified across all algorithms, can be addressed through several procedures. If the data size is not large, it is better to reduce the number of variables (avoiding redundancy), which means simpler models (like fewer hidden layers in an ANN) can be built with fewer parameters. Similarly, penalty parameters can be specified in the loss function to discourage the complexity. Future studies are recommended to adopt a K-fold cross-validation technique to generalize the models. Similarly, the bootstrapping techniques employed to quantify the uncertainty in the N2O emissions estimations are likely to capture the aleatoric uncertainty but might not be enough to handle the epistemic uncertainty arising from the models themselves. Thus, for future studies, it is recommended to further explore the use of Bayesian techniques. Many studies have used the hierarchical Bayesian model for N2O, assuming lognormal probability distribution [87], or used these techniques to calibrate the existing model parameters, with great improvement [98,99]. It should also be acknowledged that the peak emissions were not captured with great accuracy in our case, the reason for which is likely the small number of peak emissions instances available to train the models. Additionally, covariates known to influence the peak N2O emissions should be identified from the literature and included in such modeling experiments.
5. Conclusions
Four generic machine learning algorithms, viz., multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR) and artificial neural networks (ANNs), were tested for their applicability to predicting N2O emissions from agricultural lands in Kitchener, Ontario, Canada. A set of readily available weather and management variables like rainfall, temperature, number of days after rainfall, 2-day accumulated rainfall, soil moisture, soil temperature and number of days after nitrogenous fertilizer application were collected, along with soil measurements of ammonium, nitrate, and pH on the days when discrete measurements of N2O were taken from the study site. Two scenarios, viz., High Input (HI) and Low Input (LI), were devised with the inclusion and exclusion of the last three variables (soil nitrate, soil ammonium and pH values) from the dataset. A total of 628 observations were then split into training and testing datasets in a 70:30 ratio in such a way that both datasets included similar statistical characteristics and non-duplicate data. Temporal autocorrelation was tested before any of the models were fitted with the data. To eliminate biases from the selection of training data, it was ensured that all algorithms used consistent training and testing datasets that were independent and representative in nature. The mean square error was used as an objective function to fine-tune each algorithm. Additionally, R2, RMSE, VE, p-factor and r-factor metrices were estimated for each algorithm to compare their ability to predict N2O emissions in the study area. Based on the analysis, the following conclusion were drawn.
- There is a need to appropriately split the data into training and testing datasets in such a way that the basic characteristics of the dataset are preserved. There is a considerable band of uncertainty in the results predicted by algorithms trained on different sets of training data.
- The dataset violated the basic assumptions of the MLR application, such as high multicollinearity, heteroscedasticity and no linear relationship between the predictors and predictand N2O variable, thereby rendering the application of MLR invalid. Despite the violation of these assumptions, MLR could not explain more than 30% of the variability of N2O emissions.
- RFR, SVR and ANN could subsequently explain more than 66%, 63% and 43% of the variability of an unseen test dataset when the models were trained for the HI scenario.
- The RFR, SVR and ANN models trained under the LI scenario were found to have comparable performance with models trained under the HI scenario, with subsequent explanations of 68%, 66% and 68% of the variability of the unseen test dataset.
- The peak emissions were better captured by an ANN under the HI scenario, followed by an ANN under the LI scenario, RFR under the HI scenario and RFR under the LI scenario. However, none of the models were able to capture all of the peak emissions within their uncertainty bands.
- Prediction uncertainties were best captured by the RFR and ANN algorithms, with SVM performing very poorly.
- All algorithms were prone to overfitting, thus demanding the careful selection of model parameters and representative training and testing datasets.
- Considering the computational cost, ease in fine-tuning the model, stability of the model results for bootstrapped datasets and a relatively easier interpretation, RFR followed by ANN is recommended for N2O estimation in future studies in the study area.
- There is a merit in using machine learning algorithms trained with local data to estimate N2O emissions in conjunction with readily measurable weather and management variables. However, additional variables known to influence peak emissions need to be included, along with more instances of peak emissions.
- Future studies are recommended to use K-fold cross-validation to generalize the model and avoid biased performance metrices. Similarly, techniques capable of handling epistemic uncertainty in addition to the aleatoric uncertainties stemming from data are recommended.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16060703/s1. Table S1. Dates when the N2O and relevant soil parameters were measured from Baggs and research north farm; Table S2. Performance of linear regression model when multicollinearity is removed to estimate N2O emission; Figure S1. Schematic of Random Forest Regression; Figure S2. Variability in coefficient of determination estimated for training and testing dataset selected using different seed numbers; Figure S3. Spread-location plot of the residues of HILM model set for N2O emission modeling; Figure S4. Testing the linearity of data variables and N2O in the study; Figure S5. Calibration of Random Forest regression for the LI scenario with respect to R2 values; Figure S6. Objective function optimization with respect to RMSE of simulated and measured N2O variables for HI RFR for the identified best model; Figure S7. Performance of HI RFR and LI RFR models to estimate the N2O emissions in study area during training and testing phases; Figure S8. Finetuning of parameters for SVR under LI scenario using RMSE as objective function; Figure S9. Performance of HI SVR and LI SVR models to estimate the N2O emissions in study area during training and testing phases; Figure S10. Calibration of the ANN for LI scenario for a 2 hidden layer architecture using R2 as an objective function; Figure S11. Performance of HI ANN and LI ANN models to estimate the N2O emissions in study area during training and testing phases.
Author Contributions
Conceptualization, U.G.; methodology, U.G.; software, U.G.; validation, P.D. and A.B.; formal analysis, U.G.; investigation, U.G.; resources, W.A.; data curation, W.A.; writing—original draft preparation, U.G.; writing—review and editing, P.D., A.B. and W.Y.; visualization, U.G.; supervision, P.D., A.B. and W.Y.; project administration, P.D.; funding acquisition, P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the Ontario Ministry for Agriculture Food and Rural Affairs (OMAFRA) University of Guelph project UofG 22017-2889 and NSERC Discovery grant RGPIN-2017-04400.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M. Climate change 2021: The physical science basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2021; Volume 2, p. 2391. [Google Scholar]
- Ravishankara, A.; Daniel, J.S.; Portmann, R.W. Nitrous oxide (N2O): The dominant ozone-depleting substance emitted in the 21st century. Science 2009, 326, 123–125. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Xu, R.; Canadell, J.G.; Thompson, R.L.; Winiwarter, W.; Suntharalingam, P.; Davidson, E.A.; Ciais, P.; Jackson, R.B.; Janssens-Maenhout, G.; et al. A comprehensive quantification of global nitrous oxide sources and sinks. Nature 2020, 586, 248–256. [Google Scholar] [CrossRef] [PubMed]
- Wohlfahrt, G.; Anfang, C.; Bahn, M.; Haslwanter, A.; Newesely, C.; Schmitt, M.; Drösler, M.; Pfadenhauer, J.; Cernusca, A. Quantifying nighttime ecosystem respiration of a meadow using eddy covariance, chambers and modelling. Agric. For. Meteorol. 2005, 128, 141–162. [Google Scholar] [CrossRef]
- Pavelka, M.; Acosta, M.; Kiese, R.; Altimir, N.; Brümmer, C.; Crill, P.; Darenova, E.; Fuß, R.; Gielen, B.; Graf, A. Standardisation of chamber technique for CO2, N2O and CH4 fluxes measurements from terrestrial ecosystems. Int. Agrophysics 2018, 32, 569–587. [Google Scholar] [CrossRef]
- Denmead, O. Approaches to measuring fluxes of methane and nitrous oxide between landscapes and the atmosphere. Plant Soil 2008, 309, 5–24. [Google Scholar] [CrossRef]
- Korkiakoski, M.; Tuovinen, J.-P.; Aurela, M.; Koskinen, M.; Minkkinen, K.; Ojanen, P.; Penttilä, T.; Rainne, J.; Laurila, T.; Lohila, A. Methane exchange at the peatland forest floor–automatic chamber system exposes the dynamics of small fluxes. Biogeosciences 2017, 14, 1947–1967. [Google Scholar] [CrossRef]
- Nicolini, G.; Castaldi, S.; Fratini, G.; Valentini, R. A literature overview of micrometeorological CH4 and N2O flux measurements in terrestrial ecosystems. Atmos. Environ. 2013, 81, 311–319. [Google Scholar] [CrossRef]
- Giltrap, D.; Yeluripati, J.; Smith, P.; Fitton, N.; Smith, W.; Grant, B.; Dorich, C.D.; Deng, J.; Topp, C.F.; Abdalla, M.; et al. Global Research Alliance N2O chamber methodology guidelines: Summary of modeling approaches. J. Environ. Qual. 2020, 49, 1168–1185. [Google Scholar] [CrossRef]
- Hergoualc’h, K.; Harmand, J.-M.; Cannavo, P.; Skiba, U.; Oliver, R.; Hénault, C. The utility of process-based models for simulating N2O emissions from soils: A case study based on Costa Rican coffee plantations. Soil Biol. Biochem. 2009, 41, 2343–2355. [Google Scholar] [CrossRef]
- Leip, A.; Busto, M.; Corazza, M.; Bergamaschi, P.; Koeble, R.; Dechow, R.; Monni, S.; De Vries, W. Estimation of N2O fluxes at the regional scale: Data, models, challenges. Curr. Opin. Environ. Sustain. 2011, 3, 328–338. [Google Scholar] [CrossRef]
- Fuchs, K.; Merbold, L.; Buchmann, N.; Bellocchi, G.; Bindi, M.; Brilli, L.; Conant, R.T.; Dorich, C.D.; Ehrhardt, F.; Fitton, N.; et al. Evaluating the potential of legumes to mitigate N2O emissions from permanent grassland using process-based models. Glob. Biogeochem. Cycles 2020, 34, e2020GB006561. [Google Scholar] [CrossRef]
- Vogeler, I.; Cichota, R. Effect of variability in soil properties plus model complexity on predicting topsoil water content and nitrous oxide emissions. Soil Res. 2018, 56, 810–819. [Google Scholar] [CrossRef]
- Gaillard, R.K.; Jones, C.D.; Ingraham, P.; Collier, S.; Izaurralde, R.C.; Jokela, W.; Osterholz, W.; Salas, W.; Vadas, P.; Ruark, M.D. Underestimation of N2O emissions in a comparison of the DayCent, DNDC, and EPIC models. Ecol. Appl. 2018, 28, 694–708. [Google Scholar] [CrossRef]
- Yue, Q.; Cheng, K.; Ogle, S.; Hillier, J.; Smith, P.; Abdalla, M.; Ledo, A.; Sun, J.; Pan, G. Evaluation of four modelling approaches to estimate nitrous oxide emissions in China’s cropland. Sci. Total Environ. 2019, 652, 1279–1289. [Google Scholar] [CrossRef]
- Ghimire, U.; Shrestha, N.K.; Biswas, A.; Wagner-Riddle, C.; Yang, W.; Prasher, S.; Rudra, R.; Daggupati, P. A Review of Ongoing Advancements in Soil and Water Assessment Tool (SWAT) for Nitrous Oxide (N2O) Modeling. Atmosphere 2020, 11, 450. [Google Scholar] [CrossRef]
- Wang, C.; Amon, B.; Schulz, K.; Mehdi, B. Factors that influence nitrous oxide emissions from agricultural soils as well as their representation in simulation models: A review. Agronomy 2021, 11, 770. [Google Scholar] [CrossRef]
- Fisher, R.A.; Koven, C.D. Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001453. [Google Scholar] [CrossRef]
- Berardi, D.; Brzostek, E.; Blanc-Betes, E.; Davison, B.; DeLucia, E.H.; Hartman, M.D.; Kent, J.; Parton, W.J.; Saha, D.; Hudiburg, T.W. 21st-century biogeochemical modeling: Challenges for Century-based models and where do we go from here? GCB Bioenergy 2020, 12, 774–788. [Google Scholar] [CrossRef]
- Vasilaki, V.; Massara, T.; Stanchev, P.; Fatone, F.; Katsou, E. A decade of nitrous oxide (N2O) monitoring in full-scale wastewater treatment processes: A critical review. Water Res. 2019, 161, 392–412. [Google Scholar] [CrossRef]
- Gao, X.; Ouyang, W.; Hao, Z.; Xie, X.; Lian, Z.; Hao, X.; Wang, X. SWAT-N2O coupler: An integration tool for soil N2O emission modeling. Environ. Model. Softw. 2019, 115, 86–97. [Google Scholar] [CrossRef]
- Wagena, M.B.; Bock, E.M.; Sommerlot, A.R.; Fuka, D.R.; Easton, Z.M. Development of a nitrous oxide routine for the SWAT model to assess greenhouse gas emissions from agroecosystems. Environ. Model. Softw. 2017, 89, 131–143. [Google Scholar] [CrossRef]
- Mehrani, M.-J.; Bagherzadeh, F.; Zheng, M.; Kowal, P.; Sobotka, D.; Mąkinia, J. Application of a hybrid mechanistic/machine learning model for prediction of nitrous oxide (N2O) production in a nitrifying sequencing batch reactor. Process Saf. Environ. Prot. 2022, 162, 1015–1024. [Google Scholar] [CrossRef]
- Wang, C.; Schürz, C.; Zoboli, O.; Zessner, M.; Schulz, K.; Watzinger, A.; Bodner, G.; Mehdi-Schulz, B. N2O Emissions from Two Austrian Agricultural Catchments Simulated with an N2O Submodule Developed for the SWAT Model. Atmosphere 2021, 13, 50. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Thomas, B.W.; Du, X.; Hao, X.; Wang, J. Modeling nitrous oxide emissions from rough fescue grassland soils subjected to long-term grazing of different intensities using the Soil and Water Assessment Tool (SWAT). Environ. Sci. Pollut. Res. 2018, 25, 27362–27377. [Google Scholar] [CrossRef]
- Saha, D.; Basso, B.; Robertson, G.P. Machine learning improves predictions of agricultural nitrous oxide (N2O) emissions from intensively managed cropping systems. Environ. Res. Lett. 2021, 16, 024004. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, W.; Luo, Y.; Yu, H.; Xu, Y.; Müller, C.; Xu, X.; Zhu, T. Nitrous oxide emissions from cultivated black soil: A case study in Northeast China and global estimates using empirical model. Glob. Biogeochem. Cycles 2014, 28, 1311–1326. [Google Scholar] [CrossRef]
- Song, K.; Park, Y.-S.; Zheng, F.; Kang, H. The application of Artificial Neural Network (ANN) model to the simulation of denitrification rates in mesocosm-scale wetlands. Ecol. Inform. 2013, 16, 10–16. [Google Scholar] [CrossRef]
- Philibert, A.; Loyce, C.; Makowski, D. Prediction of N2O emission from local information with Random Forest. Environ. Pollut. 2013, 177, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Saha, D.; Kemanian, A.R.; Rau, B.M.; Adler, P.R.; Montes, F. Designing efficient nitrous oxide sampling strategies in agroecosystems using simulation models. Atmos. Environ. 2017, 155, 189–198. [Google Scholar] [CrossRef]
- Taki, R.; Wagner-Riddle, C.; Parkin, G.; Gordon, R.; VanderZaag, A. Comparison of two gap-filling techniques for nitrous oxide fluxes from agricultural soil. Can. J. Soil Sci. 2018, 99, 12–24. [Google Scholar] [CrossRef]
- Bigaignon, L.; Fieuzal, R.; Delon, C.; Tallec, T. Combination of two methodologies, artificial neural network and linear interpolation, to gap-fill daily nitrous oxide flux measurements. Agric. For. Meteorol. 2020, 291, 108037. [Google Scholar] [CrossRef]
- Goodrich, J.; Wall, A.; Campbell, D.; Fletcher, D.; Wecking, A.; Schipper, L.J.A.; Meteorology, F. Improved gap filling approach and uncertainty estimation for eddy covariance N2O fluxes. Agric. For. Meteorol. 2021, 297, 108280. [Google Scholar] [CrossRef]
- Stehfest, E.; Bouwman, L. N2O and NO emission from agricultural fields and soils under natural vegetation: Summarizing available measurement data and modeling of global annual emissions. Nutr. Cycl. Agroecosystems 2006, 74, 207–228. [Google Scholar] [CrossRef]
- Maier, R.; Hörtnagl, L.; Buchmann, N. Greenhouse gas fluxes (CO2, N2O and CH4) of pea and maize during two cropping seasons: Drivers, budgets, and emission factors for nitrous oxide. Sci. Total Environ. 2022, 849, 157541. [Google Scholar] [CrossRef]
- Mehmandoost Kotlar, A.; Singh, J.; Kumar, S. Prediction of greenhouse gas emissions from agricultural fields with and without cover crops. Soil Sci. Soc. Am. J. 2022, 86, 1227–1240. [Google Scholar] [CrossRef]
- Wang, Y.; Basu, S. Using an artificial neural network approach to estimate surface-layer optical turbulence at Mauna Loa, Hawaii. Opt. Lett. 2016, 41, 2334–2337. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kovadlo, P.G.; Kiselev, A.V.; Eselevich, M.V.; Lukin, V.P. Application of Neural Networks to Estimation and Prediction of Seeing at the Large Solar Telescope Site. Publ. Astron. Soc. Pac. 2023, 135, 014503. [Google Scholar] [CrossRef]
- Carranza, C.; Nolet, C.; Pezij, M.; van der Ploeg, M. Root zone soil moisture estimation with Random Forest. J. Hydrol. 2021, 593, 125840. [Google Scholar] [CrossRef]
- Zhao, W.; Sánchez, N.; Lu, H.; Li, A. A spatial downscaling approach for the SMAP passive surface soil moisture product using random forest regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Hao, W.; Gao, L.; Gong, D. Estimation of soil temperature from meteorological data using different machine learning models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Nemitz, E.; Mammarella, I.; Ibrom, A.; Aurela, M.; Burba, G.G.; Dengel, S.; Gielen, B.; Grelle, A.; Heinesch, B.; Herbst, M.; et al. Standardisation of eddy-covariance flux measurements of methane and nitrous oxide. Int. Agrophysics 2018, 32, 517–549. [Google Scholar] [CrossRef]
- Dorich, C.D.; De Rosa, D.; Barton, L.; Grace, P.; Rowlings, D.; Migliorati, M.D.A.; Wagner-Riddle, C.; Key, C.; Wang, D.; Fehr, B.; et al. Global Research Alliance N2O chamber methodology guidelines: Guidelines for gap-filling missing measurements. J. Environ. Qual. 2020, 49, 1186–1202. [Google Scholar] [CrossRef]
- Ashiq, W.; Ghimire, U.; Vasava, H.; Dunfield, K.; Wagner-Riddle, C.; Daggupati, P.; Biswas, A. Identifying hotspots and representative monitoring locations of field scale N2O emissions from agricultural soils: A time stability analysis. Sci. Total Environ. 2021, 788, 147955. [Google Scholar] [CrossRef] [PubMed]
- Ashiq, W.; Vasava, H.; Ghimire, U.; Dunfield, K.; Daggupati, P.; Biswas, A. Seasonal agricultural wetlands act as potential source of N2O and CH4 emissions. CATENA 2022, 213, 106184. [Google Scholar] [CrossRef]
- Pinheiro, J. Nlme: Linear and Nonlinear Mixed Effects Models, Version 3.1-164. 2011. Available online: https://cran.r-project.org/web/packages/nlme/index.html (accessed on 25 February 2024).
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Pedhazur, E.J.; Schmelkin, L.P. Measurement, Design, and Analysis: An Integrated Approach; Psychology Press: London, UK, 2013. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S.; Ullman, J.B. Using Multivariate Statistics; Pearson: Boston, MA, USA, 2007; Volume 5. [Google Scholar]
- Bujang, M.A.; Sa’at, N.; Bakar, T.M.I.T.A. Determination of minimum sample size requirement for multiple linear regression and analysis of covariance based on experimental and non-experimental studies. Epidemiol. Biostat. Public Health 2017, 14. [Google Scholar] [CrossRef]
- Zhuang, Q.; Lu, Y.; Chen, M. An inventory of global N2O emissions from the soils of natural terrestrial ecosystems. Atmos. Environ. 2012, 47, 66–75. [Google Scholar] [CrossRef]
- Abbasi, T.; Luithui, C.; Abbasi, S.A. Modelling methane and nitrous oxide emissions from rice paddy wetlands in India using artificial neural networks (ANNs). Water 2019, 11, 2169. [Google Scholar] [CrossRef]
- Korkiakoski, M.; Ojanen, P.; Penttilä, T.; Minkkinen, K.; Sarkkola, S.; Rainne, J.; Laurila, T.; Lohila, A. Impact of partial harvest on CH4 and N2O balances of a drained boreal peatland forest. Agric. For. Meteorol. 2020, 295, 108168. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A study on multiple linear regression analysis. Procedia-Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Grégoire, G. Multiple linear regression. Eur. Astron. Soc. Publ. Ser. 2014, 66, 45–72. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S.; Adler, D.; Bates, D.; Baud-Bovy, G.; Ellison, S.; Firth, D.; Friendly, M.; Gorjanc, G.; Graves, S. Package ‘car’. R Foundation for Statistical Computing. 2012. Available online: https://cran.r-project.org/web/packages/car/index.html (accessed on 25 February 2024).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Breiman, L.; Cutler, A. randomForest: Breiman and Cutler’s random forests for classification and regression. CRAN Contrib. Packages 2018, 4, 6–14. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022. [Google Scholar]
- Seok, K.; Hwang, C.; Cho, D. Prediction intervals for support vector machine regression. Commun. Stat.-Theory Methods 2002, 31, 1887–1898. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.-C.; Lin, C.-C.; Meyer, M.D. Package ‘e1071’. 2019. Available online: https://cran.r-project.org/web/packages/e1071/index.html (accessed on 25 February 2024).
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar]
- Shaahmadi, F.; Anbaz, M.A.; Bazooyar, B. Analysis of intelligent models in prediction nitrous oxide (N2O) solubility in ionic liquids (ILs). J. Mol. Liq. 2017, 246, 48–57. [Google Scholar] [CrossRef]
- Kazemi, P.; Bengoa, C.; Steyer, J.-P.; Giralt, J. Data-driven techniques for fault detection in anaerobic digestion process. Process Saf. Environ. Prot. 2021, 146, 905–915. [Google Scholar] [CrossRef]
- Fritsch, S.; Guenther, F.; Guenther, M.F. Package ‘neuralnet’. The Comprehensive R Archive Network. 2016. Available online: https://cran.r-project.org/web/packages/neuralnet/neuralnet.pdf (accessed on 15 March 2024).
- Lin, C. Analysis of Complex Dynamical Systems by Combining Recurrent Neural Networks and Mechanistic Models. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2024. [Google Scholar]
- Nourani, V.; Paknezhad, N.J.; Tanaka, H. Prediction Interval Estimation Methods for Artificial Neural Network (ANN)-based modeling of the hydro-climatic processes, a review. Sustainability 2021, 13, 1633. [Google Scholar] [CrossRef]
- Lu, B.; Hardin, J. Constructing Prediction Intervals for Random Forests. Ph.D. Thesis, Pomona College, Claremont, CA, USA, 2017. [Google Scholar]
- Coulston, J.W.; Blinn, C.E.; Thomas, V.A.; Wynne, R.H. Approximating prediction uncertainty for random forest regression models. Photogramm. Eng. Remote Sens. 2016, 82, 189–197. [Google Scholar] [CrossRef]
- Lins, I.D.; Droguett, E.L.; das Chagas Moura, M.; Zio, E.; Jacinto, C.M. Computing confidence and prediction intervals of industrial equipment degradation by bootstrapped support vector regression. Reliab. Eng. Syst. Saf. 2015, 137, 120–128. [Google Scholar] [CrossRef]
- Xu, Y.; Mi, C.; Zhu, Q.-X.; Gao, J.-Y.; He, Y.-L. An effective high-quality prediction intervals construction method based on parallel bootstrapped RVM for complex chemical processes. Chemom. Intell. Lab. Syst. 2017, 171, 161–169. [Google Scholar] [CrossRef]
- Lian, C.; Chen, C.P.; Zeng, Z.; Yao, W.; Tang, H. Prediction intervals for landslide displacement based on switched neural networks. IEEE Trans. Reliab. 2016, 65, 1483–1495. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.; Cibin, R.; Sudheer, K.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Esmali, A.; Golshan, M.; Kavian, A. Investigating the performance of SWAT and IHACRES in simulation streamflow under different climatic regions in Iran. Atmósfera 2021, 34, 79–96. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. “Package ‘hydroGOF’.” Goodness-of-fit Functions for Comparison of Simulated and Observed (2017). 2017. Available online: https://cran.r-project.org/web/packages/hydroGOF/index.html (accessed on 7 January 2024).
- Batra, R.; Johal, S.K.; Chen, M.; Ferrer, E. Consequences of sampling frequency on the estimated dynamics of AR processes using continuous-time models. Psychol. Methods 2023. [Google Scholar] [CrossRef]
- Chirinda, N.; Carter, M.S.; Albert, K.R.; Ambus, P.; Olesen, J.E.; Porter, J.R.; Petersen, S.O. Emissions of nitrous oxide from arable organic and conventional cropping systems on two soil types. Agric. Ecosyst. Environ. 2010, 136, 199–208. [Google Scholar] [CrossRef]
- Butterbach-Bahl, K.; Baggs, E.M.; Dannenmann, M.; Kiese, R.; Zechmeister-Boltenstern, S. Nitrous oxide emissions from soils: How well do we understand the processes and their controls? Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130122. [Google Scholar] [CrossRef]
- Ciarlo, E.; Conti, M.; Bartoloni, N.; Rubio, G. The effect of moisture on nitrous oxide emissions from soil and the N2O/(N2O+ N2) ratio under laboratory conditions. Biol. Fertil. Soils 2007, 43, 675–681. [Google Scholar] [CrossRef]
- Clayton, H.; McTaggart, I.; Parker, J.; Swan, L.; Smith, K. Nitrous oxide emissions from fertilised grassland: A 2-year study of the effects of N fertiliser form and environmental conditions. Biol. Fertil. Soils 1997, 25, 252–260. [Google Scholar] [CrossRef]
- Van Haren, J.L.; de Oliveira, R.C., Jr.; Restrepo-Coupe, N.; Hutyra, L.; De Camargo, P.B.; Keller, M.; Saleska, S.R. Do plant species influence soil CO2 and N2O fluxes in a diverse tropical forest? J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Li, Y.; Barton, L.; Chen, D. Simulating response of N2O emissions to fertiliser N application and climatic variability from a rain-fed and wheat-cropped soil in Western Australia. J. Sci. Food Agric. 2012, 92, 1130–1143. [Google Scholar] [CrossRef] [PubMed]
- Nishina, K.; Akiyama, H.; Nishimura, S.; Sudo, S.; Yagi, K. Evaluation of uncertainties in N2O and NO fluxes from agricultural soil using a hierarchical Bayesian model. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Lugato, E.; Paniagua, L.; Jones, A.; de Vries, W.; Leip, A. Complementing the topsoil information of the Land Use/Land Cover Area Frame Survey (LUCAS) with modelled N2O emissions. PLoS ONE 2017, 12, e0176111. [Google Scholar] [CrossRef]
- Villa-Vialaneix, N.; Follador, M.; Ratto, M.; Leip, A. A comparison of eight metamodeling techniques for the simulation of N2O fluxes and N leaching from corn crops. Environ. Model. Softw. 2012, 34, 51–66. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, B.; Zhang, Y.; Hu, T.; Lin, Z.; Liu, G.; Wang, X.; Ma, J.; Wang, H.; Jin, H.; et al. Biochar application as a tool to decrease soil nitrogen losses (NH3 volatilization, N2O emissions, and N leaching) from croplands: Options and mitigation strength in a global perspective. Glob. Change Biol. 2019, 25, 2077–2093. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Kohli, S.; Miglani, S.; Rapariya, R. Basics of artificial neural network. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 745–751. [Google Scholar]
- Ghazali, M.F.; Wikantika, K.; Harto, A.B.; Kondoh, A. Generating soil salinity, soil moisture, soil pH from satellite imagery and its analysis. Inf. Process. Agric. 2020, 7, 294–306. [Google Scholar] [CrossRef]
- Li, B.; Ti, C.; Zhao, Y.; Yan, X. Estimating soil moisture with Landsat data and its application in extracting the spatial distribution of winter flooded paddies. Remote Sens. 2016, 8, 38. [Google Scholar] [CrossRef]
- Mobasheri, M.R.; Amani, M. Soil moisture content assessment based on Landsat 8 red, near-infrared, and thermal channels. J. Appl. Remote Sens. 2016, 10, 026011. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A practical split-window algorithm for estimating land surface temperature from Landsat 8 data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Zhao, S.; Liu, S.; Yao, Y. Estimating land surface temperature from Landsat-8 data using the NOAA JPSS enterprise algorithm. Remote Sens. 2019, 11, 155. [Google Scholar] [CrossRef]
- Myrgiotis, V.; Williams, M.; Topp, C.F.; Rees, R.M. Improving model prediction of soil N2O emissions through Bayesian calibration. Sci. Total Environ. 2018, 624, 1467–1477. [Google Scholar] [CrossRef]
- Hashimoto, S.; Morishita, T.; Sakata, T.; Ishizuka, S.; Kaneko, S.; Takahashi, M. Simple models for soil CO2, CH4, and N2O fluxes calibrated using a Bayesian approach and multi-site data. Ecol. Model. 2011, 222, 1283–1292. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).