Next Article in Journal
Reconstructing and Projecting 2012-like Drought in Serbia Using the Max Planck Institute Grand Ensemble
Previous Article in Journal
Summer Thermal Comfort in Urban Squares: The Case of Human Tower Exhibitions in Catalonia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 16
Issue 6
10.3390/atmos16060667
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Testing the Performance of Large-Scale Atmospheric Indices in Estimating Precipitation in the Danube Basin

by
Constantin Mares
,
Venera Dobrica
*,
Ileana Mares
* and
Crisan Demetrescu
Institute of Geodynamics, Romanian Academy, 020032 Bucharest, Romania
*
Authors to whom correspondence should be addressed.
Atmosphere 2025, 16(6), 667; https://doi.org/10.3390/atmos16060667
Submission received: 25 March 2025 / Revised: 23 May 2025 / Accepted: 24 May 2025 / Published: 1 June 2025
(This article belongs to the Section Climatology)
Browse Figures
Versions Notes

Abstract

The objective of this study was to analyse the influence of two large-scale climate indices on precipitation in the Danube basin, both separately and in combination. The evolution of the hydroclimatic regime in this area is of particular importance but has received limited attention. One of the indices for these data is the well-known the North Atlantic Oscillation (NAOI) climate index, which has been used in numerous investigations; the aim of using this index is to determine its influence on various hydroclimatic variables in many regions of the globe. The other index, the Greenland–Balkan Oscillation index (GBOI), has been demonstrated to have a greater influence on various hydroclimatic variables in Southeastern Europe compared to the NAOI. First, through different bivariate methods, such as estimating wavelet total coherence (WTC) in the time–frequency domain and applying partial wavelet coherence (PWC), the performance of the GBOI contributing to precipitation in the Danube basin was compared with that of the NAOI in the winter season. Then, by using relatively simple multivariate methods such as multiple linear regression (MLR) and a variant thereof called ridge regression (RR), notable results were obtained regarding the prediction of overall precipitation in the Danube basin in the winter season. The training period was 90 years (1901–1990), and the testing period was 30 years (1991–2020). The used Nash–Sutcliffe (NS) performance criterion varied between 0.65 and 0.94, depending on the preprocessing approach applied for the input data, proving that statistical modelling for the winter season is both simple and powerful compared to modern deep learning methods.

1. Introduction

The Danube River, the largest hydrographic basin in Europe [1] and the second longest after the Volga, through its water regime, is an integrator of the rainfall regime; this, in turn, is determined by the atmospheric processes of the climate system, which is a particularly complex environment [2,3]. The atmospheric factors that are associated with or determinants of the rainfall regime inherently lead to the determination of the hydroclimatic regime in the respective basin.
It is now known that parts of the climate system, such as the climate of Europe, are influenced by variabilities in an atmospheric factor called the North Atlantic Oscillation (NAO) [4,5,6]. The NAO, first defined by the British climatologist Sir. Gilbert Walker in 1930, is linked to the Permanent Centres of Action, the Icelandic depression, and the Azorean Anticyclone. The quantification of the NAO’s impact on the rainfall regime at the European level is described in [7]. Accordingly, the NAO has been linked to European droughts, given its predominant control over winter rainfall in the North Atlantic [8] and Western Mediterranean regions [9,10]. The NAO affects the climates of both Western Europe and the Mediterranean basin in summer.
The hydroclimatic regime in Europe, under the NAO’s impact, exhibits notable spatiotemporal differentiations, especially in the winter season. Important details regarding the spatiotemporal distribution of the NAO’s impact and its association with other planetary oscillations are provided in [11,12]. Many recent studies have focused on the local/regional effects of NAO on the rainfall regime in Central and Southeastern Europe, more precisely in the Danube basin. Some of them are summarized in the following paragraphs.
For instance, Tošić et al. (2014) [13] investigated annual and seasonal precipitation variability in relation to the NAO index, based on correlation analysis; this was achieved through the use of the first principal component (PC1) of the decomposition into empirical orthogonal functions (EOFs) of precipitation from 92 stations in the Vojvodina (Serbia) region. Their results showed that the correlation coefficients had the highest statistical significance, at a confidence level greater than 99%, for the winter season. The relationship between the NAO index and precipitation in Serbia was analysed by Luković et al. (2015) [14]; their analysis was conducted on various types of averages data (monthly, seasonal, annual), and they additionally identified the correlation with the highest statistical significance level in the winter season. The influence of atmospheric circulation patterns on the variability in annual and seasonal precipitation in Slovenia was addressed by Milošević et al. (2016) [15], revealing that the strongest correlations between NAOI and seasonal precipitation were found in the winter season. Furthermore, Malinović-Milićević et al. (2018) [16] examined the evolution of daily extreme precipitation in the Vojvodina region, taking into account the influence of the NAO; they obtained the most significant correlations in the case of total precipitation (amount of precipitation cumulated on wet days) for the winter season.
In the present study, we demonstrate that the individual imprint of the large-scale atmospheric index associated with the North Atlantic Oscillation on the Southeastern European rainfall regime is of relatively small importance; a certain contribution can be achieved only when it is used in tandem with another complementary large-scale atmospheric index, i.e., one associated with the Greenland–Balkan Oscillation (GBO).
The GBO was introduced by [17] to reflect the baric contrast between the Balkan and Greenland zones; the GBO is similar to the NAO in terms of its baric dipolarity on the Earth’s surface, but the direction of the GBO’s dipole is almost perpendicular to that of the NAO. The large-scale atmospheric index associated with the GBO was calculated using the difference between the normalised sea level pressures at Nuuk and Novi Sad. Many studies have reported on the contribution of the GBOI, separately or in comparison with the NAOI, to the climatic aspects regarding the moisture content and precipitation regime in Southeastern Europe primarily; here, we will mention only a few of these studies [18,19].
Deciphering the complexity of how a climate system can be affected to greater or lesser extents by changes over time has been the subject of multiple deterministic or stochastic–dynamic approaches [20].
However, it is possible to use high-level statistical procedures (special downscaling) by employing predictors that represent multiple conditions on a large scale to determine probabilistic parameters that describe the frequency and intensity of climatic variables that are difficult to assess, such as precipitation [21].
Consequently, the most sensitive climate indices have been identified from a large set of potentially available indices that are signal carriers for the hydroclimate regime of Southeastern Europe. These are the GBOI and the NAOI, which are robust predictors for the local/regional hydroclimate in Southeastern Europe.
Overall, different pros and cons are evident for the different statistical methods; thus, we should select those that are most suitable for the phenomena that are of interest here. Accordingly, we focus on the relationship between the predictand (precipitation) and the two predictors (GBOI and NAOI) being tested, and we assess them using bivariate and multivariate statistical methods. The bivariate relationships present here were found to consist of simple Pearson correlations and time–frequency analyses using wavelet analysis. The importance of signal analysis with wavelet representation in the time–frequency domain is, in fact, a reflection of the complexity and, at the same time, the essence of the signal structure through its information content [22].
The analyses of multiple relationships between the predictand and the predictor consisted of applying multivariate regressions with testing and the elimination of redundancy. Although the NAOI and GBOI predictors can be considered to be almost orthogonal by construction, orthogonalization was also performed using simple procedures. It is entirely justifiable to use an alternative approach for finding the state in which a single climate index is insufficient for explaining rainfall variability across some territory; however, a combination of specific climate indices provides a more comprehensive explanation for variability [23]. We share this idea and have applied it in our previous studies [19,24]. In addition, by considering a set of variables according to their provided synergistic effect, the possibility for redundancy is eliminated [25].
However, the two large-scale atmospheric indices, GBOI and NAOI, cannot distinguish between regional/global climate changes due to anthropogenic and natural factors, recorded through different climatic parameters such as the temperature and amount of precipitation for any season. Investigations using bivariate and multivariate wavelet analyses were also carried out in a recent publication [26] to analyse the combined effect of atmospheric and extra-atmospheric natural factors on certain terrestrial variables that can be used to describe the hydroclimate in Southeastern Europe.
Therefore, in the following text, the influence of the two large-scale atmospheric indices, mentioned above, on the precipitation regime in the Danube basin is going to be studied by using bivariate and multivariate statistical approaches. The structure of the paper is as follows: Section 2 describes the data used and the applied methods; Section 3 contains the results and their discussion; the conclusions are presented in Section 4.

2. Data and Methods

2.1. Data

At the regional scale, precipitation data from 15 meteorological stations in the Danube basin were considered. The spatial distribution of these stations is shown in Table 1 and their geographical information is shown in Figure 1.
The daily precipitation values from the 15 stations were extracted from the European Climate Assessment & Dataset (ECA&D) [27] (through the website www.ecad.eu (accessed on 5 February 2025)), for a period of 120 years (1901–2020). From the daily values, the monthly and then seasonal value for the respective stations were obtained.
For the two large-scale atmospheric indices, we used the following:
-
The NAOI, obtained from the Hurrell-Station-Based Monthly NAO Index [28].
Accessed at https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based (accessed on 5 February 2025).
-
The GBOI, introduced by [17]; supplied monthly values for the period 1901–2020 are presented in the Supplementary Materials.
For the analysed period (1901–2020), the seasonal values of the GBOI and NAOI were calculated as averages over three corresponding calendar months. For the winter season, the months of January and February of the respective year and December of the previous year were considered; meanwhile, for the remaining seasons, the averages were calculated from three months corresponding to the spring, summer, and autumn seasons of the respective year.

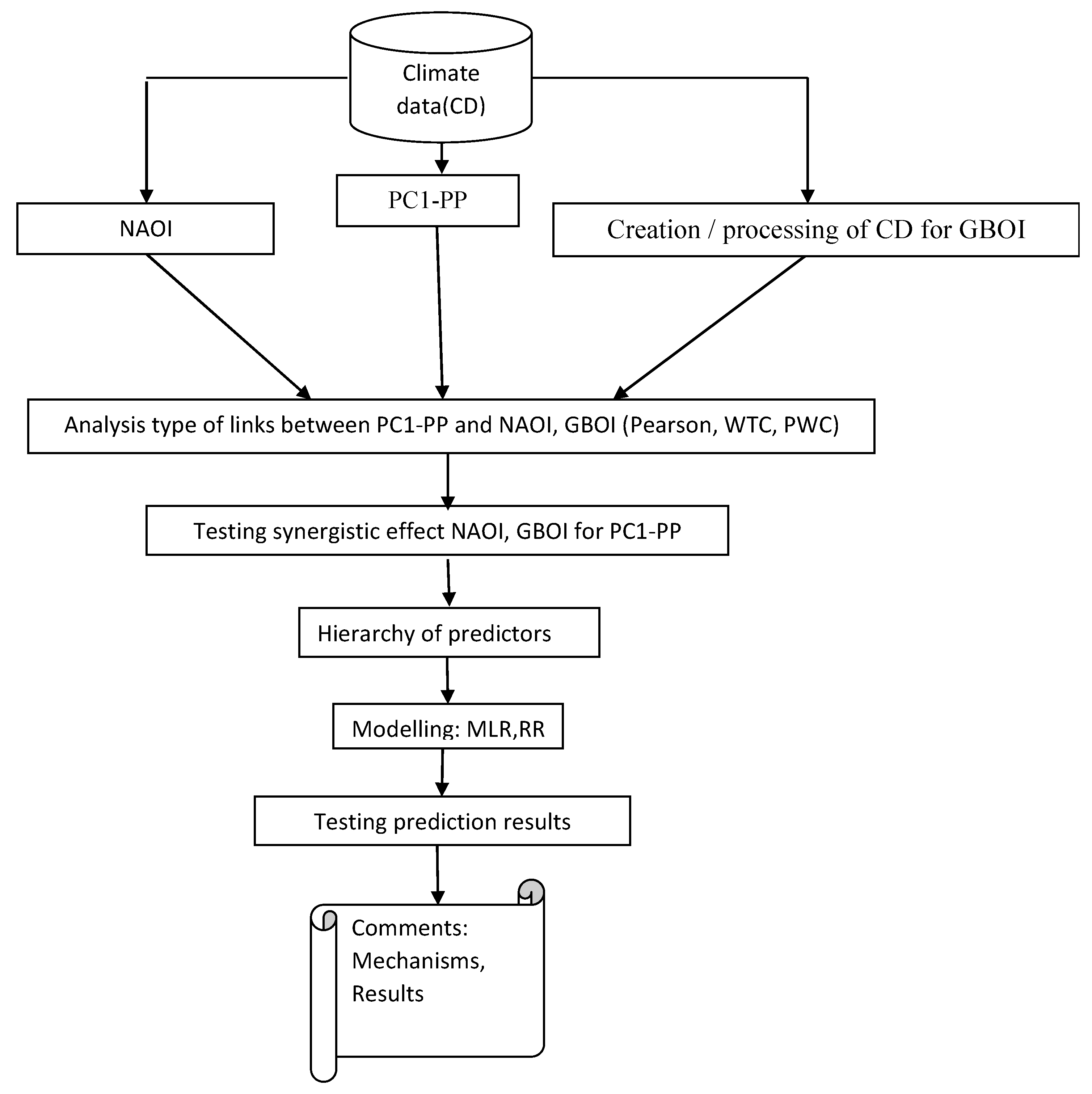
2.2. Methods

In this study, the variability in precipitation was analysed mainly by considering the first principal component (PC1) of the empirical orthogonal function (EOF) developments of the total seasonal values from the 15 stations considered. Figure S1, in the Supplementary Materials, shows the map of correlations between the PC1 of precipitation in the Danube basin and sea level pressure (SLP) during winter.
Simple tests were also performed regarding the influence of large-scale atmospheric factors on the precipitation field, considering the time–series data at each station, and more robust tests were performed regarding three representative stations corresponding to the three Danube basins.
The roles of the teleconnections represented by the two large-scale atmospheric indices, the NAOI and GBOI (which are considered as predictors for the precipitation field, i.e., the predictand), were highlighted using both linear and nonlinear methods. First, simultaneous and seasonal links between the two climate indices and precipitation were tested using Pearson correlations.
In order to find the coherence between the predictand and the two predictors in the time–frequency domain, bivariate wavelet analyses were performed. Thus, both the distribution of wavelet coherence in the time–frequency domain (WTC) [29] and the averages of coherences corresponding to certain periodicities, i.e., global coherence (GC) [30] (accessed 9 February 2025), were determined (Schulte, MATLAB R2023b) [31].
Multivariate analyses were then performed by applying partial wavelet coherence (PWC) [28] in order to reveal the contribution of one of the predictors when the other was eliminated. We performed all the experiments related to partial coherence with the routine provided by Hu and Si (2021) [32]. The above analyses were performed for the entire 120-year period (1901–2020).
Further, in the present study, in order to determine the predictive potential of the two predictors NAOI and GBOI, multiple linear regression (MLR) was applied by using the fitlm function in MATLAB. In order to determine the response of the model, that is, of the dependent variable for predictors considered on independent data, the predict function, also in MATLAB, was used.
For the training period, 75% of the data were considered (those covering the period 1901–1990), and 25% were used for testing (those covering the period 1991–2020).
As a metric for testing the model’s performance, the Nash–Sutcliffe (NS) index [33] was used, defined as follows:
N S = 1 − ∑ i = 1 N ( Y i o b s − Y i e s t ) 2 ∑ i = 1 N ( Y i o b s − Y m e a n ) 2
where Y i o b s is the ith observation, Y i e s t is the ith value estimated by regression in our case, Y m e a n is the mean of the observed data, and N is the total number of observations.
In the case of the present study, N = 30 represents the number of years over which the performance of the prediction model was tested.
According to Moriasi et al. (2007) [34] and Alfieri et al. (2014) [35], the Nash–Sutcliffe index ranges between −∞ and 1.0. A value of 1.0 is associated with the optimal estimation. In general, practical results can only be accepted if the NS value is greater than 0.5.
A schematic diagram of the workflow is presented in Figure 2.

3. Results and Discussion

3.1. Bivariate Analyses

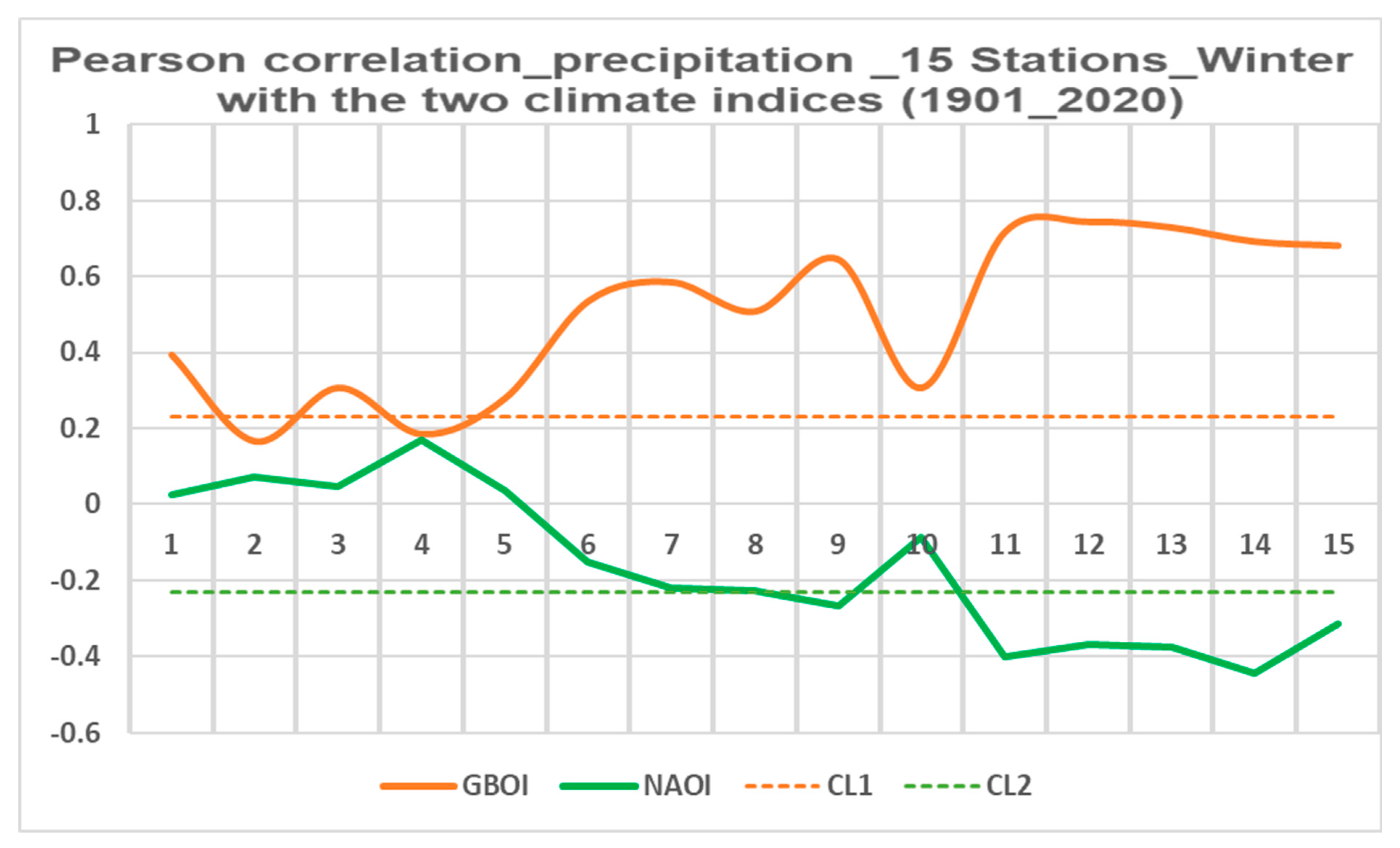
3.1.1. Testing the Links Through Pearson Correlation Coefficients

In the present study, considering the overall state of precipitation at the 15 stations, represented by the first principal component of the development in EOFs of precipitation (PC1-PP), the connection with the two climate indices for each season from 1901 to 2020 was analysed. First, the influence of each of the two climate indices (CIs), GBOI and NAOI, on precipitation was tested by determining the Pearson correlations (R), both simultaneously in the same season and with certain lags (season). Following the tests for both correlations and other correlative analyses, the most significant results were obtained for the simultaneous links between precipitation and CIs in the winter season. The results are shown in Table 2.
From Table 2, it can be seen that the GBOI has an impact with high statistical significance in all seasons, with the highest values in the winter season. In the winter season, the NAOI presents the most important significant influence. As already shown by [13,14,15,16] for the eastern part of the middle Danube basin, this influence can also be observed in the autumn season. By contrast, in the spring and summer seasons, it has no influence that can be taken into consideration. The R values between the precipitation and the GBOI and NAOI for the winter season at each of the 15 stations are shown in Figure 3. The R value of 0.232 for CL = 99%, corresponding to a size of 120 values, was also plotted. The value of 0.178 corresponds to CL = 95%.
As can be seen from Figure 3, the precipitation from stations located in the eastern part of the middle basin and in the lower Danube basin are correlated with the GBOI with a CL higher than 99%; meanwhile, for the NAOI, there are only five stations for which the CL is clearly > 99%.
In terms of the results regarding the influences of the two climate indices considered simultaneously in the same season with precipitation (and for the other seasons), we can mention the autumn season, in which the correlations with the GBOI are statistically significant with a CL > 99% for all the stations considered; meanwhile, for the NAOI’s influence, CL > 99% was obtained only for a few stations located in the transition area from the middle to the lower Danube basin.
For the spring season, except for two stations in the upper basin, the influence of the GBOI was significant, with CL ≥ 99%, and for the NAOI, only precipitation at the Arad station indicates a significant relationship. During the summer, weak links between the NAOI and precipitation were obtained at the analysed stations; in this season, the link with the GBOI was found to be significant only at a few stations.
Regarding the links between the two climate indices, in the presence of certain lags (from one to three seasons), compared to the precipitation at the stations, the statistical significance of these links was generally low.
In analyses performed at the level of months, not seasons, by Mares et al. (2002) [36], it was found that the NAO signal was evident in wintertime, but its influence on the precipitation and drought indices was not simultaneous in the same month––it showed some lags.
In the present seasonal analysis, the influences of both the NAOI and GBOI in the winter season on spring precipitation were statistically insignificant.
From the seasonal analyses presented in this paragraph, it became clear that the most significant links between climate indices and PC1-PP or precipitation series at individual stations were found for the winter season. Therefore, we will present only the results for this winter season in the following subsections.

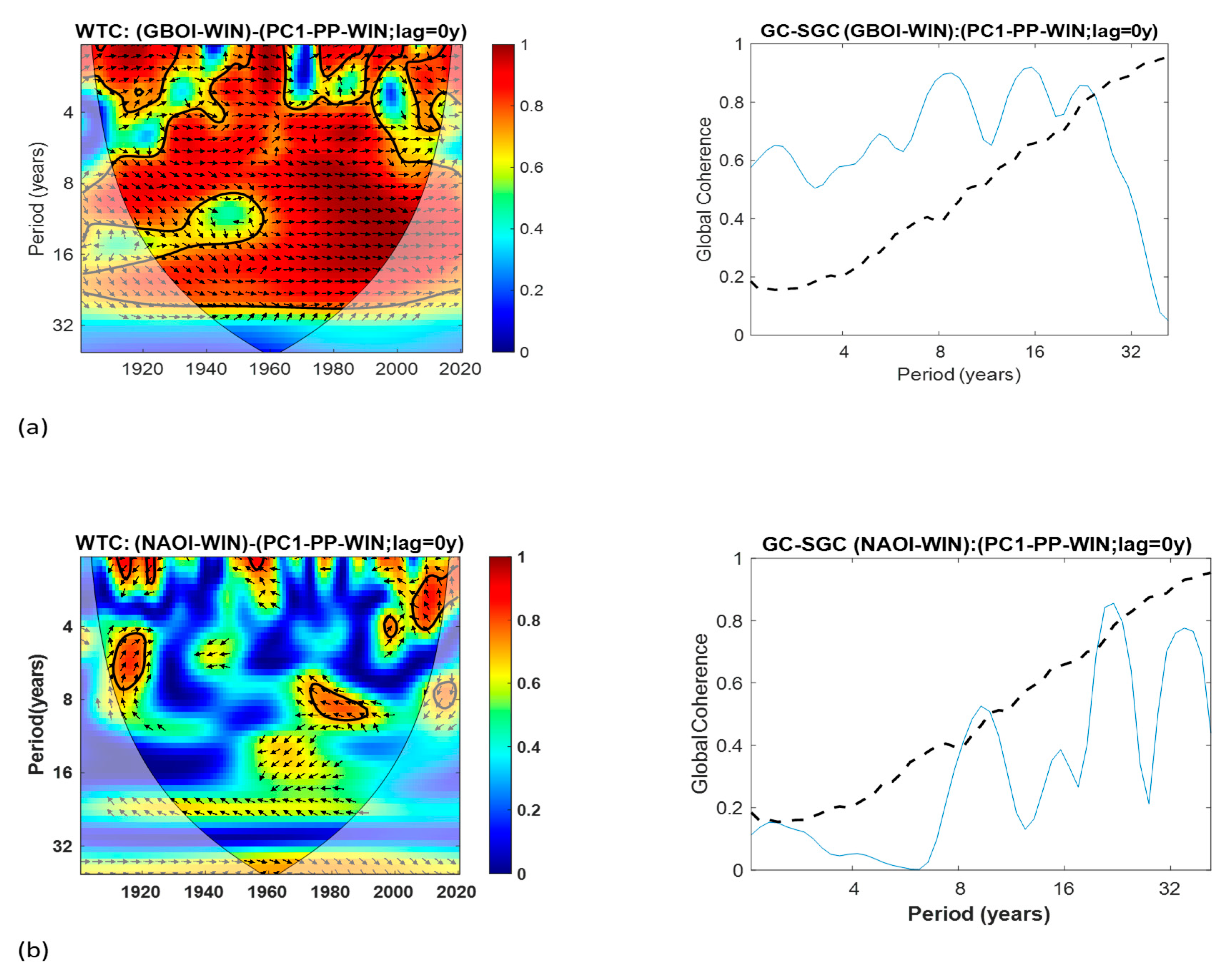
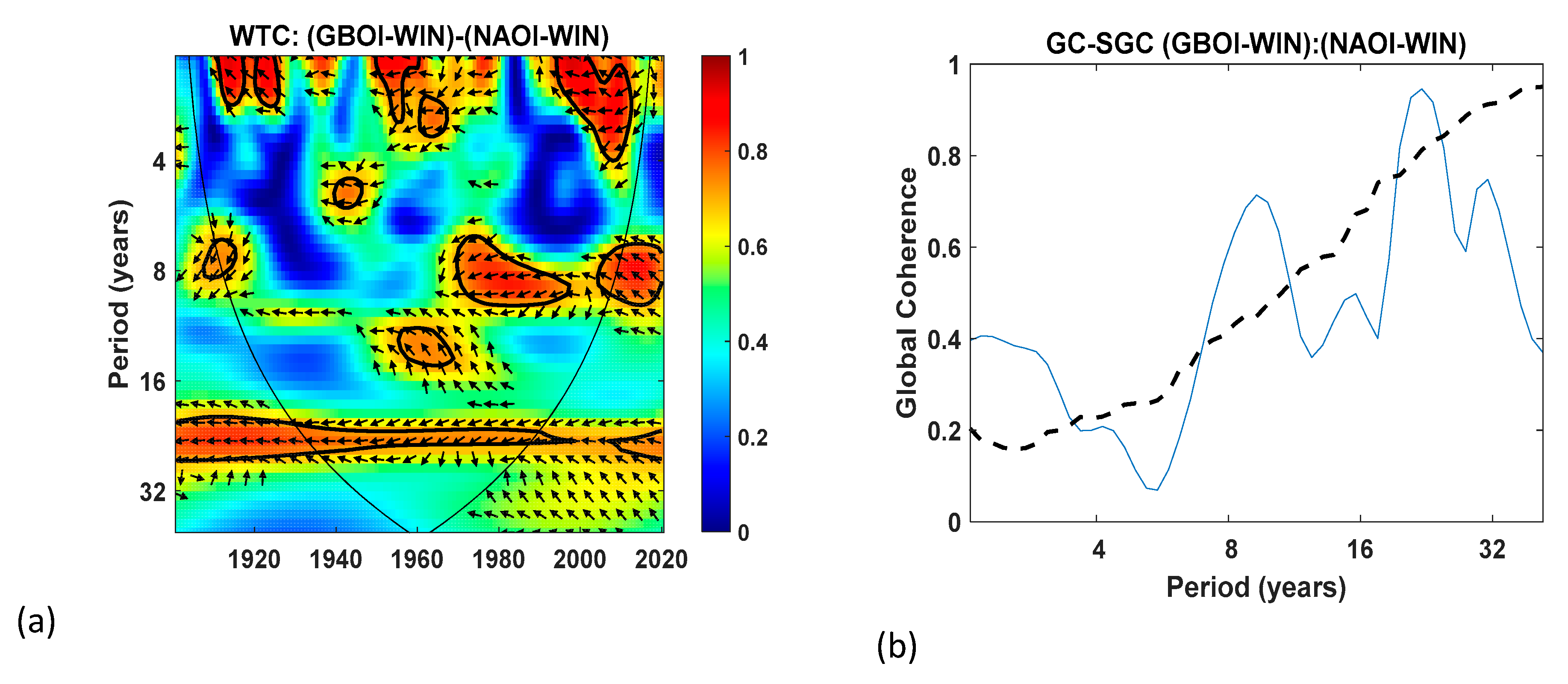
3.1.2. Time–Frequency Domain Analysis

In the following text, we first present the results obtained by applying wavelet coherence to determine the time–frequency relationship between PC1-PP and the GBOI and NAOI in the winter season, at a regional (Danube basin) scale. These distributions were associated with global coherence to observe the significant periodicities averaged over the studied time interval (Figure 4a,b). Thus, in Figure 4a, the results obtained for the relationship between PC1-PP and the GBOI are presented in the form of a frequency–time distribution in the left panel, and in terms of GC in the right panel. In the WTC distribution, the left panels’ thin solid lines demarcate the cones of influence, and the thick solid lines show the 95% CL; in the right panels, the 95% CL is indicated by a dashed line. A significant coherence between PC1-PP and the GBOI during winter can be observed, except for periodicities greater than 30 years, where the coherence is no longer significant. It is observed that precipitation is in phase with the GBOI, i.e., positive values of the GBOI determine precipitation above normal values. Regarding the relationship between precipitation expressed by PC1 and the NAOI (Figure 4b), both the WTC and GC indicate a significant relationship only for limited parts in terms of both time and frequency and according to the shape of the GC; these periodicities might be associated with the solar activity cycles (Schwabe, 11-year interval, and Hale, 22-year interval).
The WTC is a powerful tool in determining regions in a time–frequency domain where the two time–series covary. Phase is indicated by arrows on the wavelet coherence plots. Arrows pointing to the right (left) when the time–series are in-phase (anti-phase), i.e., positively (negatively) correlated. However, for the case when the series are neither phase nor antiphase, interpretation is more complex (Grinsted et al., 2004) [29].
In order to determine the influence of the two climate indices on precipitation at the local scale, we chose three representative stations for the three Danube basins. The Regensburg (Germany) station was selected for the upper basin, the Novi Sad (Serbia) station was selected for the middle basin, and the Arad (Romania) station was selected for the lower basin.
Figure 5 presents the results of the winter season links obtained for the WTC and GC between the precipitation at each of these stations and the GBOI, compared to those for the NAOI. It is observed that, for the upper basin, the difference in the influences of the two climate indices is not significant. For the middle and lower basins, as can be seen from Figure 5, the GBOI has a much more significant influence in both the time and frequency domains compared to the precipitation coherences with the NAOI. The differences are more evident for Arad, a station located in the lower basin.
From the analysis of the above results, it can be seen that there are certain time intervals and certain periodicities where the influences of the two climate indices complement each other; for example, as can be seen from Figure 4, the NAOI makes a certain contribution for periodicities greater than 32 years, areas for which the contribution of the GBOI is negligible, with the coherence being insignificant.
Such situations can also be found in the analysis by station (Figure 5); here, at the Novi Sad station, a significant coherence between precipitation and the NAOI is observed for periods between 20 and 33 years.
There are also cases (time intervals and period bands) where both the GBOI and NAOI have a significant coherence with precipitation, such as at the Regensburg station (Figure 5), for periods between 16 and 32 years. In this case, it is very difficult to conclude which of the two climate indices has greater significance. This situation occurs due to the fact that the predictor variables are intercorrelated during winter for certain time intervals and certain periodicities (Figure 6). Although the Pearson correlation coefficient between the GBOI and NAOI is −0.58 during winter, the detailing of the relationship between the two variables in the time–frequency domain presented in Figure 6 indicates that the coherence is significant only between certain time intervals and certain periodicities.
A significant coherence for the entire analysed interval (1901–2020) is observed for a short band of periods, accounting for around 24 years. For relatively short time intervals, especially after the 1960s, significant coherences also appear in the band of periods around 11 years. We can link these significant periods to natural external atmospheric factors such as the 11- and 22-year solar cycles (Schwabe and Hale). Significant coherences for shorter periods (up to 4 years) may be due to the internal variability in the atmosphere.
To eliminate the interdependence between the two predictor variables acting on precipitation, the partial wavelet coherence analysis was applied.

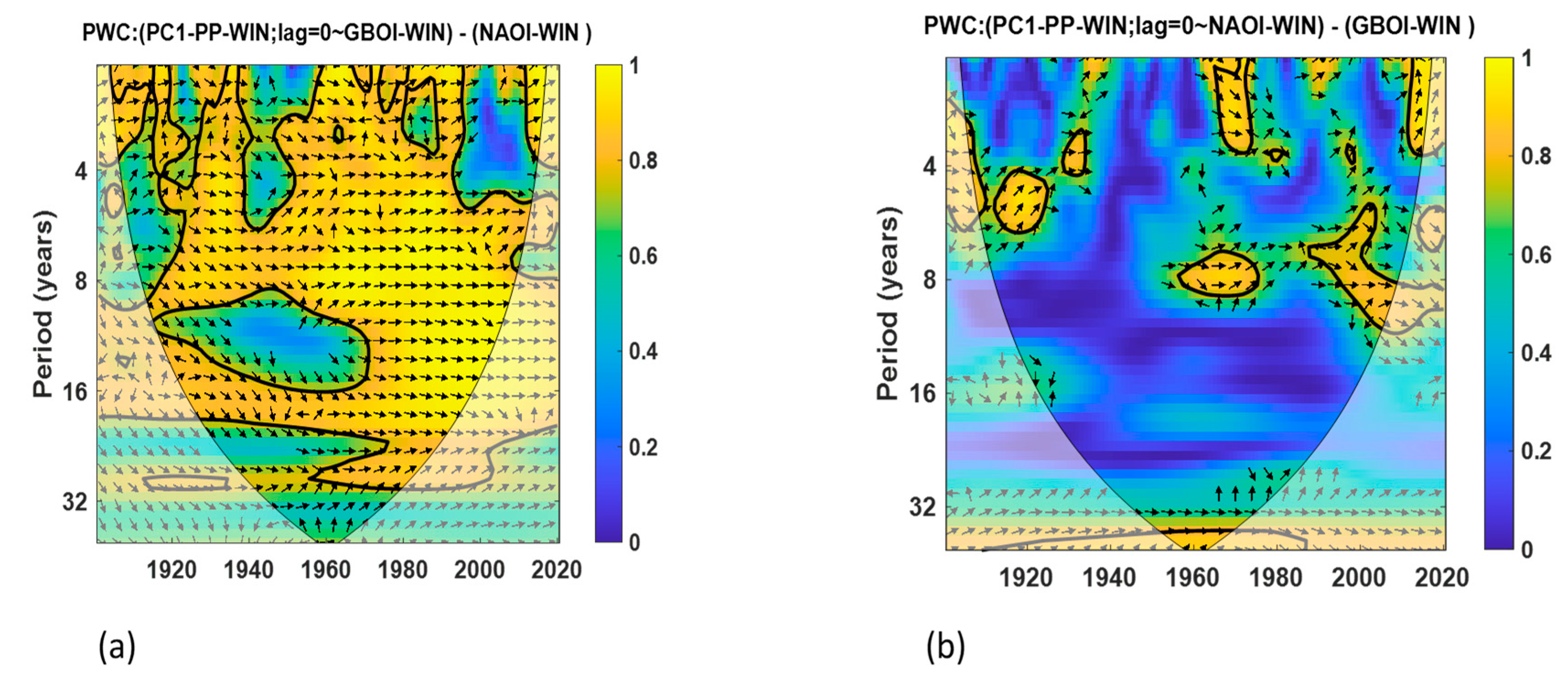
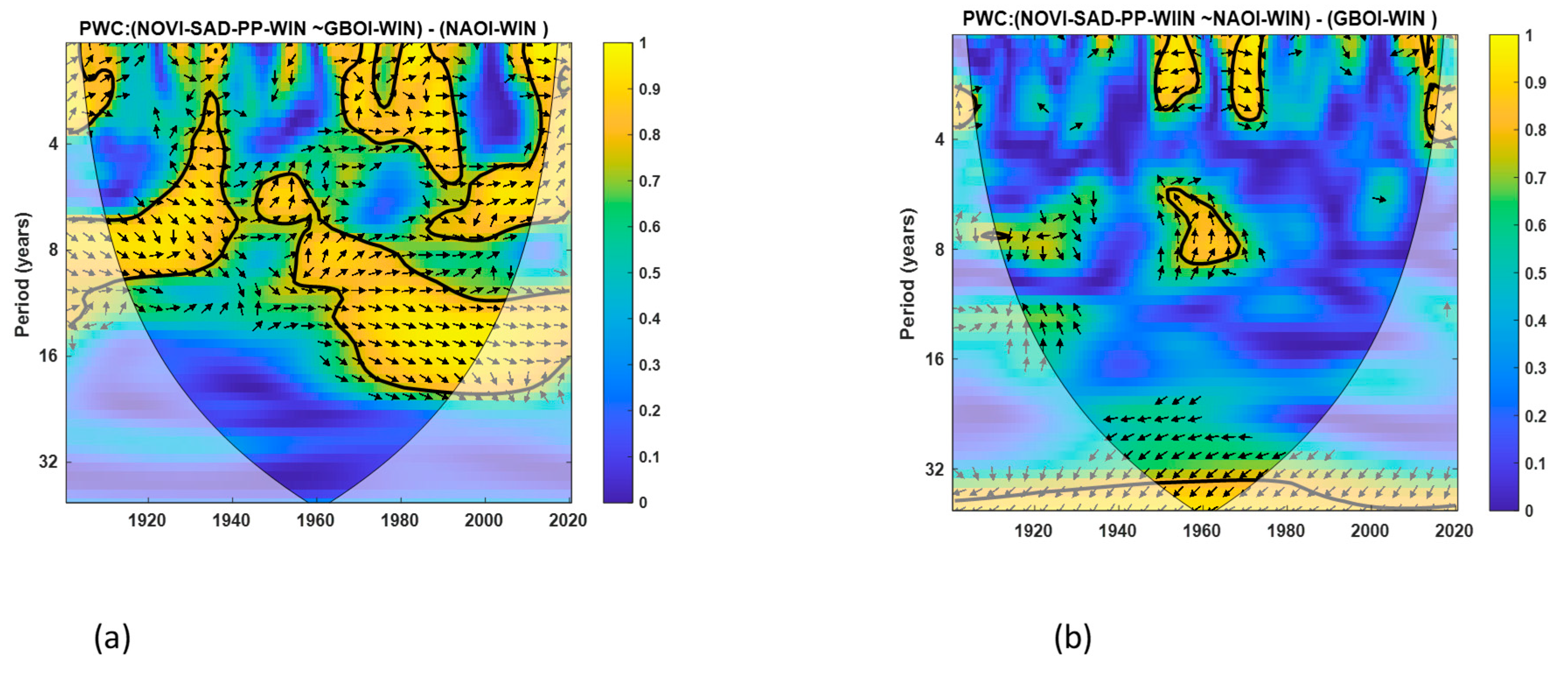
3.2. Partial Wavelet Coherence (PWC) Analyses

Through the partial coherence analysis, the coherence between the predictand and one of the predictors was determined, eliminating the effect of the other predictor.
As shown by Sreedevi et al. (2022) [37], when there is an interaction between variables that are considered as predictors, a bivariate relationship can be clearly explained only by untangling the role of other contributory variables. This can be carried out by including only one predictand and one predictor in the analysis of the partial wavelet coherence and by excluding the effect of the other predictor variables. The PWC method was suggested by Mihanović et al. (2009) [38] and then used in many studies, but in many of these studies, only two predictors were used, and only the effect of one of the predictors was excluded.
Hu and Si (2021) [32] improved the PWC method so that the improved PWC could reveal the relation of two variables after removing the influence of multiple variables. Their improved partial wavelet coherence method has been successfully used in many fields, including climate and hydrology [24,39,40,41].
In Mares et al. (2022) [24], based on information theory and partial wavelet coherence analysis, optimal predictors were selected from several Palmer-type drought indices, leading to an improvement in the estimation of discharge in the Danube lower basin.
Figure 7 presents the results obtained using PWC. Figure 7a shows the relationship between PC1-PP and the GBOI, eliminating the NAOI, while Figure 7b shows the relationship between PC1-PP and the NAOI, eliminating the GBOI. It is observed that, upon eliminating the NAOI, comparing Figure 7a with Figure 4a, the influence of the GBOI is diminished very little, only for the frequencies corresponding to the periods of 18–28 years for the first half of the 20th century.
This may be due to the fact that, for this time interval and for this frequency band, the coherence between the GBOI and NAOI is significant, according to Figure 6. Removing the GBOI from the PC1-PP relationship with the NAOI (Figure 7b) produces some changes in the coherence with PC1-PP, compared to Figure 4b; i.e., the significant coherences corresponding to the 8–24-year period bands, which are located in the time interval between 1940 and 1990, disappear. It can be assumed that these significant periodicities (Figure 4b) appear in the WTC between PC1-PP and the NAOI due to the influence of the GBOI. Therefore, upon removing the GBOI from the NAOI coherence with precipitation, the area of the influence of the NAOI on precipitation is narrowed (Figure 7b). It is worth mentioning that, in the coherence field between PC1-PP and the NAOI, a relatively significant coherence appears inside the cone of influence, in both Figure 4 and Figure 7, around periods greater than 32 years, which can be associated with the 33-year solar cycle (Brüuckner cycle).
In a recent work [19], by using WTC, the influence of solar activity on several climate variables was analysed, emphasizing the presence of a period associated with the Brüuckner cycle with a significance of 95% during winter in the Palmer hydrological drought index (PHDI). For the GBOI and NAOI, the coherence with the solar activity during winter indicated a relatively significant coherence at a CL slightly lower than 95%.
The PWC analysis was also performed for precipitation at the three selected stations for the three Danube River basins. The most significant result is presented in Figure 8 for the Novi Sad station. The partial wavelet coherence between precipitation at Novi Sad and the GBOI and NAOI, eliminating the influence of the NAOI, and, respectively, of the GBOI, is shown in Figure 8a,b. Comparing the results obtained by PWC and WTC between precipitation and the GBOI, it can be seen that PWC removed the influence of the NAOI, which was present in the bands with higher periodicities, where relatively significant coherences appear. In cases of coherence between precipitation and the NAOI, upon eliminating the GBOI, only significant coherences for periods related to the solar cycle of about 30 years are kept; meanwhile, those that appeared significant (inside the cone of influence and limited by solid lines) for the band of periods between 8 and 16 years, i.e., between the years 1960 and 1990, disappeared.
Thus, PWC analysis helps us gain knowledge of the influence of a predictor on the predictand by eliminating each predictor in turn.
The investigations carried out so far showed that, for the eastern part of the middle basin and for the lower Danube basin, the GBOI can be used alone as a predictor for estimating winter precipitation. For the other parts of the Danube, in addition to the GBOI’s influence, the NAOI’s influence must also be taken into account, where the synergistic effect of the two predictors can be observed.

3.3. Testing the Combined Influence of GBOI and NAOI on Precipitation in the Danube Basin Through Multiple Linear Regression (MLR)

Going further, the general state of precipitation in the upper and middle basin (rendered evident by PC1-PP) is very important for the state of the Danube discharge at the entrance to Romania; we will focus on an estimate of PC1-PP based on the two considered large-scale atmospheric indices.
The analyses performed with WTC and PWC revealed that, although the GBOI’s influence on precipitation in the Danube basin is predominant and significant, especially for the middle and lower basin, there are period bands in which the NAOI can also make a significant contribution. For this reason, we tested for the winter season the combined influences of the GBOI and NAOI on precipitation using MLR.
We also calculated the variance inflation factor (VIF), which is one of the methods for detecting multicollinearity. There are several views regarding the VIF values for predictors that are optimal for inclusion in regression equations, some of which are indicated in Mares et al. (2020) [18]. However, in the majority of studies, as mentioned in Shrestha (2021) [42], it has been concluded that if 1 < VIF < 5, the variables are moderately correlated and their use in regression is accepted, a VIF between 5 and 10 indicates a problematic correlation, and VIF > 10 indicates a major multicollinearity that must be eliminated. In the present investigation, the value of VIF was found to be 1.51 for the GBOI and NAOI as predictors. Given the above, we assumed that the two climate indices in this case were not redundant or that the redundancy was very low and therefore could be used together in a multiple linear regression equation.
The multiple linear regression model was applied for a training period of 90 years (1901–1990), representing 75% of the data volume, and a testing period of 30 years (1991–2020). As a metric to measure the performance of the MLR modelling, the Nash–Sutcliffe (NS) index was used. The tests were performed during winter both for the PC1-PP and for the total precipitation at each of the three stations considered in this study. As previously mentioned, to be statistically significant, the NS index should be greater than 0.5. Because no case with NS > 0.5 was found in the tests performed for precipitation at the three selected stations, these results have not been detailed here. Figure 9 shows the result for the testing period on independent data (1991–2020), obtained by MLR, with the two predictors GBOI and NAOI and having PC1-PP as predictand for the winter season. Figure 9a shows the observed and predicted time–series for the 30 years, and Figure 9b represents the scatter plot of these variables. In this case, NS = 0.6232, and, for the Pearson correlation coefficient, R = 0.835. Regarding the R value, it has a very high statistical significance, taking into account the critical R values corresponding to the 30 years of the testing period. To obtain the regression coefficients for the training period 1901–1990, the fitlm routine from MATLAB was used, with the ‘RobustOpts’ option, meaning that the data are fitted using a robust linear regression model. This model is less sensitive to outliers than standard linear regression. The p-values associated with the regression coefficients for the predictor variables were 3.8441 × 10−18 for GBOI and 0.012034 for NAOI, respectively. Thus, even after the p-values, in this case, considering the NAOI in combination with GBOI brings additional information to the response of the variable predictand PC1-PP. As previously mentioned, the predict routine from MATLAB was also used to test the model for the period 1991–2020.

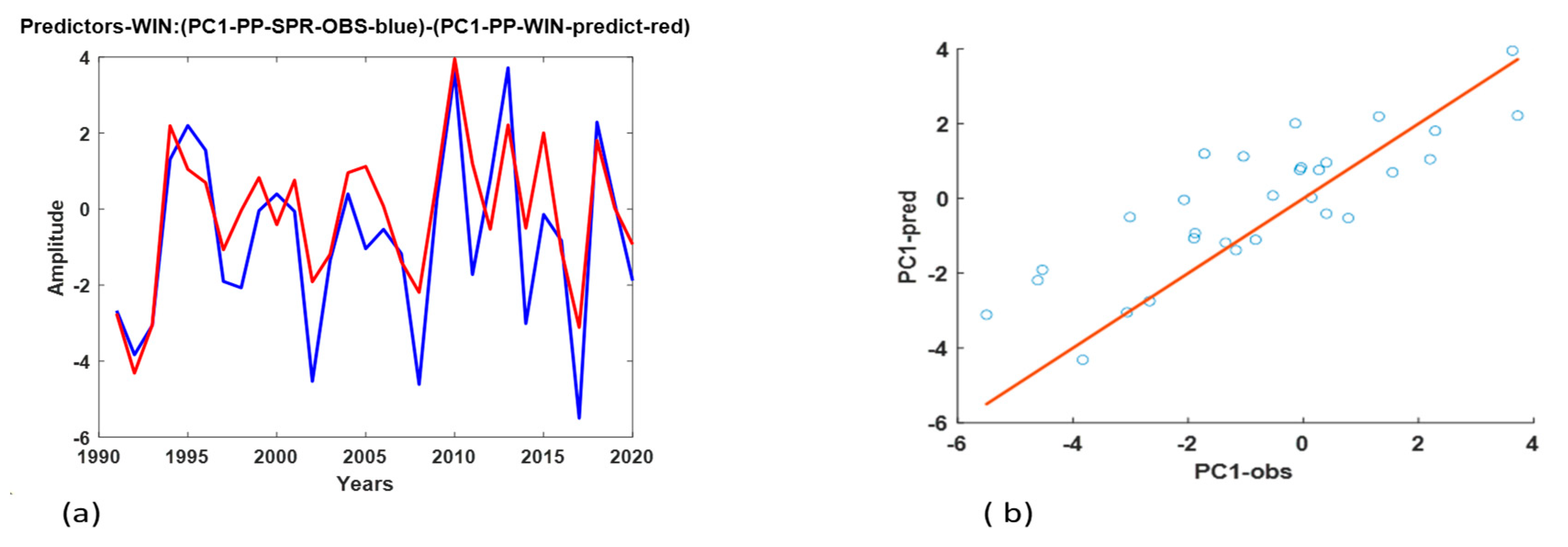
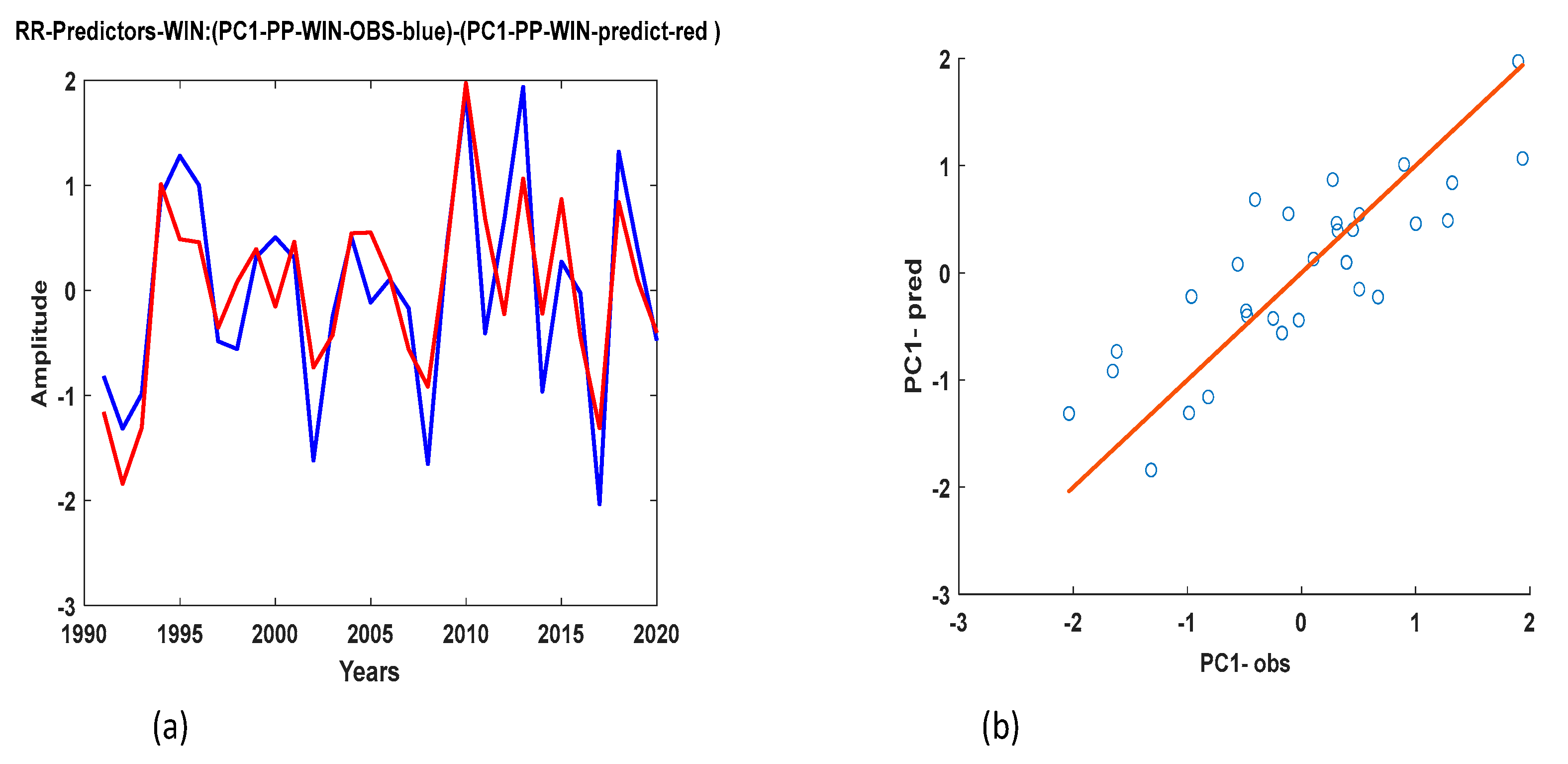
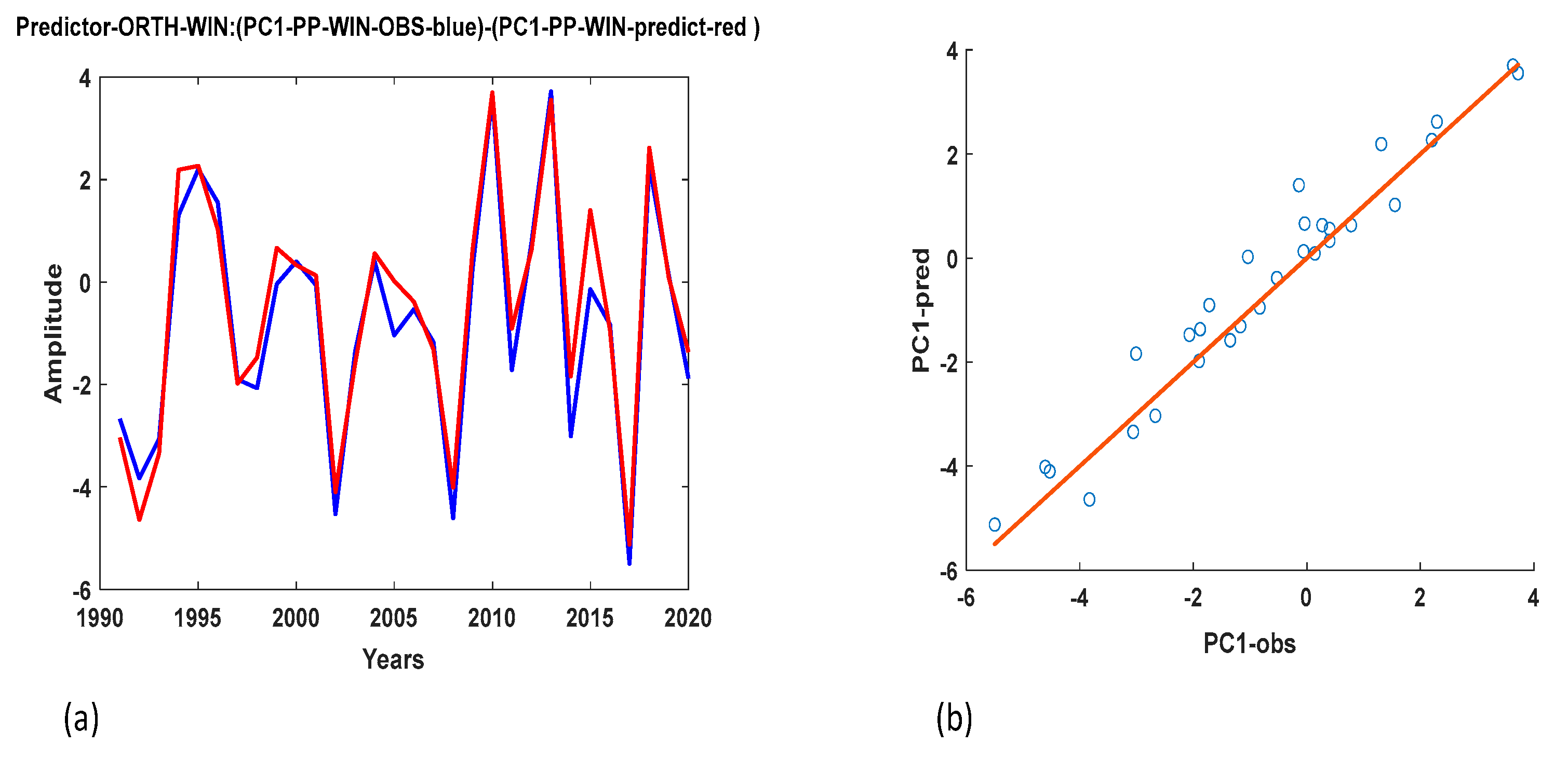
3.4. Experiments to Eliminate Collinearity Between Predictors

The WCT and PWC analyses, as well as the VIF value, showed that the two predictors have a low degree of collinearity; however, in order to eliminate certain suspicions related to negative effects related to the relationship between these predictors, i.e., the production of instability in the estimates of the regression coefficients, we further applied a ridge regression (RR).
Before applying this type of regression, both the predictors and the predictand were standardised for both the training and testing periods. The predicted values for the 30-year testing period compared to the observed values are presented in Figure 10a, and the scatter plot for the respective time–series is shown in Figure 10b.
The results were obtained using the ridge routine in MATLAB [43,44,45]. By varying the ridge parameter k and taking into account the values of NS, the performance of the ridge regression is slightly better than that obtained in the MLR case, with an NS = 0.6908. The Pearson correlation coefficient did not change substantially.
Details on the application of ridge regression to estimate the Danube discharge in the lower basin are given in the study by Mares et al., 2020 [18]. Applications in the field of hydrology of RR can also be found in a recent paper (Yin and Pena, 2024) [46].
Ridge regressions and other types of multiple linear regressions are used in machine learning (ML) predictions (Varentsov et al., 2023; Hoffman et al., 2025; Faye et al., 2025) [47,48,49].
The last experiment in the present study was to test an MLR with orthogonalized data. Thus, before applying the MLR, the climate indices GBOI and NAOI, considered as predictors, as well as the PC1-PP predictand, were orthogonalized using the orth routine in MATLAB. The results of the MLR application for the test period are presented in Figure 11a, where the amplitudes of the two observed and predicted time–series are shown, and the corresponding scatter plot is shown in Figure 11b.
The MLR performance in this case was very good, obtaining an NS = 0.9376 and R = 0.974. The VIF value of the orthogonalized predictors in this case is equal to 1.

4. Conclusions

The influence of large-scale atmospheric indices, NAOI and GBOI, on precipitation prediction in the Danube basin was tested in this study; their influences were described using both the PC1 of the development in EOF for precipitation at a group of stations and the total precipitation amount for specific stations. The measures used here were wavelet total coherence, partial wavelet coherence, and multiple linear regression analysis. The investigations revealed that the dependence of precipitation on the GBOI or NAOI differs from one station to another depending on its positioning (location) in the Danube basin. For the selected stations from the middle and lower Danube basin (Novi Sad and Arad, respectively), the influence of the GBOI is clearly superior to the influence of the NAOI.
Therefore, for the eastern part of the middle and lower Danube basins, the GBOI can be used alone as a predictor for estimating winter precipitation. For the other parts of the Danube basin, in addition to the GBOI influence, the influence of the NAOI must be taken into account as well.
Regarding the precipitation filtered by PC1 of the development in EOFs, a multiple linear regression (MLR) model with the inclusion of both large-scale climate indices is a good estimator of the overall precipitation in the Danube basin during winter.
In the present study, an overall index such as PC1 of the development in EOF of precipitation from a group of stations could be influenced by variations in the GBO and NAO climatic factors; their synergistic effects had particular practical importance. Thus, the two climate indices can be forecasted using climate models that simulate sea level pressure (SLP) values with sufficient accuracy, but the same principle does not apply to the direct simulation of precipitation. Therefore, we can estimate the general state of winter precipitation in the Danube basin based on the GBOI and NAOI estimated from the simulated SLP from climate models. Knowing the amounts of precipitation between certain limits in winter is very important for estimating the Danube discharge in the spring months, with increased risk of floods or prolonged droughts leading to possible socio-economic impacts. It is also necessary to perform an analysis using the approximate and detailed components of the wavelet decomposition, both for the predictand (precipitation at a station) and predictors (GBOI and NAOI); then, we must determine the connections between certain wavelet components. These will be the subjects of our investigations in the future.
A recommendation for investigators studying the effects of the NAOI on the European climate is to account for the effect of the GBOI on climate variability in the southeastern part of Europe.
A shortcoming of the present study is that it cannot achieve satisfactory predictions for the spring, summer, and autumn seasons. The reason for this could be that, although the meridional and zonal mass flux mechanisms through the GBO and NAO are considered by definition, in these seasons, the convective factor is not taken into account.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16060667/s1, Figure S1: Map of correlations between PC1 precipitation for the 15 stations in the Danube basin and SLP during winter. The arrow starts from the highest positive correlation (Nuuk, Greenland) and proceeds to the highest negative correlation (Novi Sad, Serbia); Table S1: The monthly GBOI values for the period 1901–2020.

Author Contributions

Conceptualization, C.M. and I.M.; Methodology, C.M., V.D. and I.M.; Software, C.M. and I.M.; Validation, V.D. and C.D.; Investigation, C.M.; Writing—original draft, C.M. and I.M.; Writing—review & editing, V.D.; Supervision, C.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Castellarin, A.; Persiano, S.; Pugliese, A.; Aloe, A.; Skøien, J.O.; Pistocchi, A. Prediction of streamflow regimes over large geographical areas: Interpolated flow–duration curves for the Danube region. Hydrol. Sci. J. 2018, 63, 845–861. [Google Scholar] [CrossRef]
  2. Tsonis, A.A.; Elsner, J.B. Chaos, strange attractors, and weather. Bull. Am. Meteor. Soc. 1989, 70, 14–23. [Google Scholar] [CrossRef]
  3. Nicolis, C. Long-term climatic variability and chaotic dynamics. Tellus A Dyn. Met. and Ocean. 1987, 39, 1–9. [Google Scholar] [CrossRef]
  4. Tang, X.; Li, J. Synergistic effect of boreal autumn SST over the tropical and South Pacific and winter NAO on winter precipitation in the southern Europe. npj Clim. Atmos. Sci. 2024, 7, 78. [Google Scholar] [CrossRef]
  5. Beniston, M.; Jungo, P. Shifts in the distributions of pressure, temperature and moisture and changes in the typical weather patterns in the Alpine region in response to the behavior of the North Atlantic Oscillation. Theor. Appl. Clim. 2002, 71, 29–42. [Google Scholar] [CrossRef]
  6. Beniston, M.; Stephenson, D.B.; Christensen, O.B.; Ferro, C.A.; Frei, C.; Goyette, S.; Halsnaes, K.; Holt, T.; Jylhä, K.; Koffi, B.; et al. Future extreme events in European climate: An exploration of regional climate model projections. Clim. Change 2007, 81, 71–95. [Google Scholar] [CrossRef]
  7. McKenna, C.M.; Maycock, A.C. The role of the North Atlantic Oscillation for projections of winter mean precipitation in Europe. Geophys. Res. Lett. 2022, 49, e2022GL099083. [Google Scholar] [CrossRef]
  8. Diodato, N.; Seim, A.; Ljungqvist, F.C.; Bellocchi, G. A millennium-long perspective on recent groundwater changes in the Iberian Peninsula. Commun. Earth Environ. 2024, 5, 257. [Google Scholar] [CrossRef]
  9. Mathbout, S.; Lopez-Bustins, J.A.; Royé, D.; Martin-Vide, J.; Benhamrouche, A. Spatiotemporal Variability of Daily Precipitation Concentration and Its Relationship to Teleconnection Patterns over the Mediterranean during 1975–2015. Int. J. Climatol. 2019, 40, 1435–1455. [Google Scholar] [CrossRef]
  10. Boughdadi, S.; Ait Brahim, Y.; El Alaoui El Fels, A.; Saidi, M.E. Rainfall Variability and Teleconnections with Large-Scale Atmospheric Circulation Patterns in West-Central Morocco. Atmosphere 2023, 14, 1293. [Google Scholar] [CrossRef]
  11. Christensen, J.H.; Kanikicharla, K.K.; Aldrian, E.; An, S.I.; Albuquerque Cavalcanti, I.F.; de Castro, M.; Dong, W.; Goswami, P.; Hall, A.; Kanyanga, J.K.; et al. Climate phenomena and their relevance for future regional climate change. In Climate Change 2013—The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013; Volume 9781107057999, pp. 1217–1308. [Google Scholar] [CrossRef]
  12. Cohen, J.; Zhang, X.; Francis, J.; Jung, T.; Kwok, R.; Overland, J.; Taylor, P.C.; Lee, S.; Coumou, D.; Handorf, D.; et al. Arctic Change and Possible Influence on Mid-Latitude Climate and Weather: A US CLIVAR White Paper; Uhlenbrock, K., Ed.; U.S. CLIVAR Project Office: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
  13. Tošić, I.; Hrnjak, I.; Gavrilov, M.B.; Unkašević, M.; Marković, S.B.; Lukić, T. Annual and seasonal variability of precipitation in Vojvodina, Serbia. Theor. Appl. Climatol. 2014, 117, 331–341. [Google Scholar] [CrossRef]
  14. Luković, J.; Blagojevć, D.; Kilibarda, M.; Bajat, B. Spatial pattern of North Atlantic Oscillation impact on rainfall in Serbia. Spat. Stat. 2015, 14, 39–52. [Google Scholar] [CrossRef]
  15. Milošević, D.; Savić, S.; Pantelić, M.; Stankov, U.; Žiberna, I.; Dolinaj, D.; Leščešen, I. Variability of seasonal and annual precipitation in Slovenia and its correlation with large-scale atmospheric circulation. Open Geosci. 2016, 8, 593–605. [Google Scholar] [CrossRef]
  16. Malinović-Milićević, S.; Mihailović, D.T.; Radovanović, M.M.; Drešković, N. Extreme precipitation indices in Vojvodina region (Serbia). J. Geogr. Inst. Jovan C 2018, 68, 1–15. [Google Scholar] [CrossRef]
  17. Mares, I.; Mares, C.; Mihailescu, M. Stochastic modeling of the connection between sea level pressure and discharge in the Danube lower basin by means of Hidden Markov Model. EGU Gen. Assem. Conf. Abstr. 2013, 15, 7606. [Google Scholar]
  18. Mares, I.; Mares, C.; Dobrica, V.; Demetrescu, C. Comparative study of statistical methods to identify a predictor for discharge at Orsova in the Lower Danube Basin. Hydrol. Sci. J. 2020, 65, 371–386. [Google Scholar] [CrossRef]
  19. Mares, C.; Mares, I.; Dobrica, V.; Demetrescu, C. Discriminant Analysis of the Solar Input on the Danube’s Discharge in the Lower Basin. Atmosphere 2023, 14, 1281. [Google Scholar] [CrossRef]
  20. Stosic, B.; Stosic, T.; Tosic, I.A.; Djurdjevic, V. Multifractal Analysis of Temperature in Europe: Climate Change Effect. Chaos Solitons Fractals 2025, 196, 116386. [Google Scholar] [CrossRef]
  21. Benestad, R.E.; Parding, K.M.; Dobler, A. Downscaling the probability of heavy rainfall over the Nordic countries. Hydrol. Earth Syst. Sci. 2025, 29, 45–65. [Google Scholar] [CrossRef]
  22. Jam-Jalloh, S.U.; Liu, J.; Wang, Y.; Li, Z.; Jabati, N.-M.S. Wavelet Analysis and the Information Cost Function Index for Selection of Calibration Events for Flood. Water 2023, 15, 2035. [Google Scholar] [CrossRef]
  23. Fadhel, S.; Han, D. On the connection between large-scale climate indices and rainfall variability in Iraq. Dyn. Atmos. Ocean. 2025, 110, 101540. [Google Scholar] [CrossRef]
  24. Mares, I.; Mares, C.; Dobrica, V.; Demetrescu, C. Selection of Optimal Palmer Predictors for Increasing the Predictability of the Danube Discharge: New Findings Based on Information Theory and Partial Wavelet Coherence Analysis. Entropy 2022, 24, 1375. [Google Scholar] [CrossRef]
  25. Mares, I.; Dobrica, V.; Mares, C.; Demetrescu, C. Assessing the solar variability signature in climate variables by information theory and wavelet coherence. Sci. Rep. 2021, 11, 11337. [Google Scholar] [CrossRef]
  26. Mares, I.; Dobrica, V.; Demetrescu, C.; Mares, C. The Combined Effect of Atmospheric and Solar Activity Forcings on the Hydroclimate in Southeastern Europe. Atmosphere 2023, 14, 1622. [Google Scholar] [CrossRef]
  27. Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demaree, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
  28. Hurrell, J.; Phillips, A. National Center for Atmospheric Research Staff (Eds). Last Modified 2023-07-10 “The Climate Data Guide: Hurrell North Atlantic Oscillation (NAO) Index (Station-Based)”. Available online: https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based (accessed on 5 February 2025).
  29. Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
  30. Schulte, J.; Najjar, R.G.; Li, M. The influence of climate modes on streamflow in the Mid-Atlantic region of the United States. J. Hydrol. Reg. Stud. 2016, 5, 80–99. [Google Scholar] [CrossRef]
  31. Schulte, J. Global Wavelet Coherence, MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/54682-global-wavelet-coherence (accessed on 9 February 2025).
  32. Hu, W.; Si, B.C. Technical Note: Improved partial wavelet coherency for understanding scale- specific and localized bivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2021, 25, 321–331. [Google Scholar] [CrossRef]
  33. Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
  34. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
  35. Alfieri, L.; Pappenberger, F.; Wetterhall, F.; Haiden, T.; Richardson, D.; Salamon, P. Evaluation of ensemble streamflow predictions in Europe. J. Hydrol. 2014, 517, 913–922. [Google Scholar] [CrossRef]
  36. Mares, I.; Mares, C.; Mihailescu, M. NAO impact on the summer moisture variability across Europe. Phys. Chem. Earth Parts A/B/C 2002, 27, 1013–1017. [Google Scholar] [CrossRef]
  37. Sreedevi, V.; Adarsh, S.; Nourani, V. Multiscale coherence analysis of reference evapotranspiration of north-western Iran using wavelet transform. J. Water Clim. Change 2022, 13, 505–521. [Google Scholar] [CrossRef]
  38. Mihanović, H.; Orlie, M.; Pasaria, Z. Diurnal thermocline oscillations driven by tidal flow around an island in the Middle Adriatic. J. Mar. Syst. 2009, 78, S157–S168. [Google Scholar] [CrossRef]
  39. Gu, X.; Sun, H.; Zhang, Y.; Zhang, S.; Lu, C. Partial Wavelet Coherence to Evaluate Scale-dependent Relationships Between Precipitation/Surface Water and Groundwater Levels in a Groundwater System. Water Resour. Manag. 2022, 36, 2509–2522. [Google Scholar] [CrossRef]
  40. Zhou, Z.; Liu, S.; Ding, Y.; Fu, Q.; Wang, Y.; Cai, H.; Shi, H. Assessing the responses of vegetation to meteorological drought and its influencing factors with partial wavelet coherence analysis. J. Environ. Manag. 2022, 311, 114879. [Google Scholar] [CrossRef]
  41. Mohan, M.G.; Fathima, S.; Adarsh, S.; Baiju, N.; Nair, G.A.; Meenakshi, S.; Krishnan, M.S. Analyzing the streamflow teleconnections of greater Pampa basin, Kerala, India using wavelet coherence. Phys. Chem. Earth Parts A/B/C 2023, 131, 103446. [Google Scholar] [CrossRef]
  42. Shrestha, N. Factor analysis as a tool for survey analysis. Am. J. Appl. Math. Stat. 2021, 9, 4–11. [Google Scholar] [CrossRef]
  43. Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
  44. Hoerl, A.E.; Kennard, R.W. Ridge Regression: Applications to Nonorthogonal Problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
  45. Marquardt, D.W.; Snee, R.D. Ridge Regression in Practice. Am. Stat. 1975, 29, 3–20. [Google Scholar] [CrossRef]
  46. Yin, Y.; Pena, M. An Imputing Technique for Surface Water Extent Timeseries with Streamflow Discharges. Water 2024, 16, 250. [Google Scholar] [CrossRef]
  47. Varentsov, M.; Krinitskiy, M.; Stepanenko, V. Machine Learning for Simulation of Urban Heat Island Dynamics Based on Large-Scale Meteorological Conditions. Climate 2023, 11, 200. [Google Scholar] [CrossRef]
  48. Hoffman, L.; Mazloff, M.R.; Gille, S.T.; Giglio, D.; Heimbach, P. Evaluating the Trustworthiness of Explainable Artificial Intelligence (XAI) Methods Applied to Regression Predictions of Arctic Sea Ice Motion. Artif. Intell. Earth Syst. 2025, 4, e240027. [Google Scholar] [CrossRef]
  49. Faye, D.; de Andrade, F.M.; Suárez-Moreno, R.; Wane, D.; Hegglin, M.I.; Dieng, A.L.; Kaly, F.; Lguensat, R.; Gaye, A.T. Assessment of machine learning-based approaches to improve sub-seasonal to seasonal forecasting of precipitation in Senegal, EGUsphere. Preprint 2025. [Google Scholar] [CrossRef]
Atmosphere 16 00667 g001
Figure 1. The distribution of 15 precipitation stations in the Danube basin.
Figure 1. The distribution of 15 precipitation stations in the Danube basin.
Atmosphere 16 00667 g001
Atmosphere 16 00667 g002
Figure 2. Framework of the proposed methodology.
Figure 2. Framework of the proposed methodology.
Atmosphere 16 00667 g002
Atmosphere 16 00667 g003
Figure 3. The winter season correlations coefficients between precipitation and GBOI and NAOI, at the 15 stations in the Danube basin, for the period 1901–2020 (solid lines). The 99% CL (dotted lines).
Figure 3. The winter season correlations coefficients between precipitation and GBOI and NAOI, at the 15 stations in the Danube basin, for the period 1901–2020 (solid lines). The 99% CL (dotted lines).
Atmosphere 16 00667 g003
Atmosphere 16 00667 g004
Figure 4. The relationship between the PC1-PP and GBOI (a) compared with the relationship with NAOI (b) during winter. The wavelet coherence (WTC) (left); the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line) (right).
Figure 4. The relationship between the PC1-PP and GBOI (a) compared with the relationship with NAOI (b) during winter. The wavelet coherence (WTC) (left); the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line) (right).
Atmosphere 16 00667 g004
Atmosphere 16 00667 g005
Figure 5. The relationship between the precipitation and GBOI and NAOI at the three stations in the Danube basin (Regensburg, Novi Sad and Arad) during winter. The wavelet coherence (WTC) (left); the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line) (right).
Figure 5. The relationship between the precipitation and GBOI and NAOI at the three stations in the Danube basin (Regensburg, Novi Sad and Arad) during winter. The wavelet coherence (WTC) (left); the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line) (right).
Atmosphere 16 00667 g005
Atmosphere 16 00667 g006
Figure 6. The relationship between GBOI and NAOI during winter. (a) The wavelet coherence (WTC); (b) the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line).
Figure 6. The relationship between GBOI and NAOI during winter. (a) The wavelet coherence (WTC); (b) the global coherence (GC) (solid line) and its significance (SGC) at a 95% confidence level (CL) (dashed line).
Atmosphere 16 00667 g006
Atmosphere 16 00667 g007
Figure 7. Partial wavelet coherence (PWC) for PC1-PP winter with (a) GBOI, excluding NAOI, and (b) NAOI, excluding GBOI.
Figure 7. Partial wavelet coherence (PWC) for PC1-PP winter with (a) GBOI, excluding NAOI, and (b) NAOI, excluding GBOI.
Atmosphere 16 00667 g007
Atmosphere 16 00667 g008
Figure 8. Partial wavelet coherence between the precipitation at the Novi Sad station during winter and (a) GBOI, excluding NAOI, and (b) NAOI, excluding GBOI.
Figure 8. Partial wavelet coherence between the precipitation at the Novi Sad station during winter and (a) GBOI, excluding NAOI, and (b) NAOI, excluding GBOI.
Atmosphere 16 00667 g008
Atmosphere 16 00667 g009
Figure 9. (a) Amplitude of PC1–PP prediction using MLR with predictors GBOI and NAOI (red), in comparison with the PC1–PP for observations (blue) in the period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Figure 9. (a) Amplitude of PC1–PP prediction using MLR with predictors GBOI and NAOI (red), in comparison with the PC1–PP for observations (blue) in the period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Atmosphere 16 00667 g009
Atmosphere 16 00667 g010
Figure 10. (a) Amplitude of PC1–PP prediction using ridge regression (RR) with predictors GBOI and NAOI (red), in comparison with the PC1–PP for observations (blue) in the testing period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Figure 10. (a) Amplitude of PC1–PP prediction using ridge regression (RR) with predictors GBOI and NAOI (red), in comparison with the PC1–PP for observations (blue) in the testing period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Atmosphere 16 00667 g010
Atmosphere 16 00667 g011
Figure 11. (a) Amplitude of PC1–PP prediction using MLR with predictors GBOI and NAOI orthogonalized (red), in comparison with the PC1–PP for observations (blue) in the period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Figure 11. (a) Amplitude of PC1–PP prediction using MLR with predictors GBOI and NAOI orthogonalized (red), in comparison with the PC1–PP for observations (blue) in the period 1991–2020; (b) scatter plot of two time–series values (blue circles) and the best fit (red line).
Atmosphere 16 00667 g011
Table 1. Geographical information about the analysed stations.
Table 1. Geographical information about the analysed stations.
No. St.StationCNLONGLATHeight (m)
1.AUGSBURGGE10.5648.26463
2.INNSBRUCKAT11.2447.16577
3.REGENSBURGGE12.0649.02365
4.SONNBLICKAT12.5747.033106
5.SALZBURGAT13.0047.48437
6KREDARICASI13.5146.222514
7.LJUBLJANASI14.3146.04299
8.GRAZAT15.2747.05366
9.ZAGREBHR15.5845.49156
10.WIENAT16.2148.14198
11.SARAJEVOBA18.2343.51577
12.OSIJEKHR18.3845.3288
13.NOVI-SADRS19.5145.2084
14.BEOGRADRS20.2844.48132
15.ARADRO21.2146.08117
Table 2. The correlations coefficients (R) between PC1-PP in the Danube basin and the two climate indices (CIs), GBOI and NAOI, for each season (1901–2020). The 99% confidence levels (CLs) correspond to R ≥ 0.232, marked in bold, and CL = 95% for R = 0.178.
Table 2. The correlations coefficients (R) between PC1-PP in the Danube basin and the two climate indices (CIs), GBOI and NAOI, for each season (1901–2020). The 99% confidence levels (CLs) correspond to R ≥ 0.232, marked in bold, and CL = 95% for R = 0.178.
CIs/SeasonWINSPRSUMAUTUMN
GBOI0.78680.49840.31490.5859
NAOI−0.2997−0.06800.0201−0.2332
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mares, C.; Dobrica, V.; Mares, I.; Demetrescu, C. Testing the Performance of Large-Scale Atmospheric Indices in Estimating Precipitation in the Danube Basin. Atmosphere 2025, 16, 667. https://doi.org/10.3390/atmos16060667

AMA Style

Mares C, Dobrica V, Mares I, Demetrescu C. Testing the Performance of Large-Scale Atmospheric Indices in Estimating Precipitation in the Danube Basin. Atmosphere. 2025; 16(6):667. https://doi.org/10.3390/atmos16060667

Chicago/Turabian Style

Mares, Constantin, Venera Dobrica, Ileana Mares, and Crisan Demetrescu. 2025. "Testing the Performance of Large-Scale Atmospheric Indices in Estimating Precipitation in the Danube Basin" Atmosphere 16, no. 6: 667. https://doi.org/10.3390/atmos16060667

APA Style

Mares, C., Dobrica, V., Mares, I., & Demetrescu, C. (2025). Testing the Performance of Large-Scale Atmospheric Indices in Estimating Precipitation in the Danube Basin. Atmosphere, 16(6), 667. https://doi.org/10.3390/atmos16060667

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop