Abstract
Using Schumann resonance (SR) records from the Antarctic, we evaluate the impact of the solar activity on the global ionosphere over the period from 2002 to 2024. The updated vertical profile of the middle atmosphere conductivity is applied. The pivoted upper part of profiles above the knee altitude is adjusted to represent different levels of solar activity. The electric (lower) hC and the magnetic (upper) hL characteristic heights, the propagation constant ν(f) of the extremely low frequency (ELF) radio waves, and the basic resonance frequency f1 are computed for the profiles corresponding to the solar maximum, moderate, and minimum activity conditions by using the full-wave solution in the form of the Riccati differential equation. Model data are compared with experimental observations at the Ukrainian Antarctic Station of “Akademik Vernadsky” (geographic coordinates: 65.25° S and 64.25° W). The following results are discussed: (i) Solar activity modifies the upper characteristic height hL of the ionosphere by ±1 km over the 11-year cycle; (ii) Equations were obtained linking the current level of solar activity with the basic SR frequency, with the magnetic characteristic height, and with the ELF propagation constant; (iii) Based on SR monitoring within two complete solar cycles, a practical rule is proposed: an increase in the index of solar activity I10.7 by ~150 units raises the first SR frequency by ~0.1 Hz and elevates the magnetic characteristic height by ~2.5 km.
1. Introduction
In the present paper, we address an impact of solar activity on the fundamental (first) frequency of the global electromagnetic resonance. This phenomenon is termed Schumann resonance (SR) after W.O. Schumann [1], who predicted this phenomenon and derived his classical formula for eigen-frequencies of the perfect Earth–ionosphere cavity in 1952. A comprehensive overview of the history of SR investigations is described in a review paper [2]. SR is observed in the shallow dielectric layer of air between the ground surface and the lower boundary of the ionosphere [3,4,5]. A detailed description of the phenomenon, experimental observations, and a formal description can be found in the extensive literature on the subject (see, e.g., [6,7,8,9,10,11,12,13] and references therein). The results of early investigations in the 1960s–1970s have been summarized in review papers and chapters in textbooks [6,7,8,9]. Monographs [10,11,12] present updated achievements in SR studies.
If we assume that the Earth is a large round apple with the radius of 6 cm, the Earth–ionosphere cavity would correspond to the peel of this apple, with a thickness of 0.6 mm. Lightning strokes are a natural sources of radio waves in such a thin spherical shell. Resonance frequencies are found near 8, 14, 20 Hz, etc., i.e., in the extremely low frequency (ELF) band. The global propagation of radio waves in the spherical Earth–ionosphere cavity takes place in the following way. In this description, the vertical lightning stroke is placed on the North Pole for convenience. Then, this stroke will generate a radio pulse propagating away from the Pole in the form of an expanding circular wave front. The wave propagation is similar to concentric circles formed on water when a stone is dropped into a pond. At each time moment, the diverging front coincides with a certain parallel, and the pulse amplitude gradually decreases. The wave front reaches the equator in about 41 ms and then it converges toward the antipode of the source (the South Pole). The pulse amplitude starts to gradually increase. Approximately 82 ms after the lightning stroke, the pulsed wave front arrives at the South Pole where it focuses into a point. Here, the pulse amplitude reaches its maximum, and afterwards, the front reappears again, expanding from the source antipode. The radio pulse returns to its starting point at the North Pole in ~165 ms, and then a new wave front resumes traveling toward the South Pole.
Thus, circular waves arise in the spherical cavity, travelling from the source to its antipode and backward. The amplitude of the pulse gradually decreases, while its width increases; this process is caused by geometrical expansion, wave dispersion in the waveguide, and losses in the ionospheric plasma. The electromagnetic losses are rather small at the ELF, and several propagation cycles might be observed experimentally. Thus, an observer on the ground surface detects the pulses from every lightning stroke of the planet, and the latter occur at a rate of 50–100 events per second. A formal description, physical properties, measurements and their interpretations have been described in numerous published studies [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. There are different approaches to the interpretation of observational data. Some studies [14,15,16] apply the diffusive upper boundary of the cavity and derive the radio propagation constant ν(f) using the exact full wave solution. Simplified approaches [17,18,19] have been elaborated and widely used in engineering computations. Direct digital procedures have been developed for the SR problem, including 2D telegraph equations (2DTE) or finite elements in the time domain (FDTD) [14,20,25,31,34]. Schumann resonance and ELF radio signals have been recorded continuously and globally on different time scales [22,23,25,26,27,30,33,38], simultaneously at both hemispheres [24,31,32,35,39] or on board satellites [28,29].
Electric properties of the cavity resonator depend on the height profile σ(h) of the atmospheric conductivity from the ground level to 100–110 km. In our calculations, we use the advanced profile model [40] presented in Appendix A. In computations, it provides the typical SR power spectra and fits to the properties of the global electrical circuit. The profile is plotted in Figure 1, and the table of σ(h) data is given in Appendix A at 1 km resolution. We note that, owing to the 40 Mm wavelength of the fundamental SR oscillation (equal to Earth’s circumference), our conductivity profile is “automatically” averaged over the entire planet. Thus, the data below correspond to the impact of solar activity on the globally averaged characteristics of the lower ionosphere.
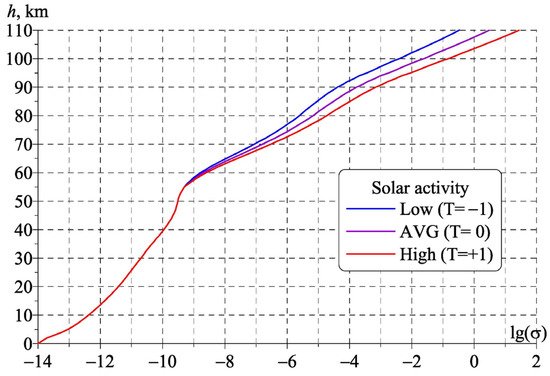
Figure 1.
Basic conductivity profile (purple curve) and profiles with the upper parts ‘pivoted’ by ±1° (red and blue curves, respectively).
We use the following approach. The level of solar activity controls the hard electromagnetic emission from the Sun and the averaged conductivity profile σ(h). Therefore, the solar activity is able to drive inter-annual trends in the parameters of the SR; see e.g., [26,27,32,35,38,39].
Alto summarize the above information, we find that the cavity resonator is formed by the Earth’s surface on the lower side and by the atmosphere conducting layers on the upper side. The radio wave length matches the circumference of the Earth. The sources of oscillations are the random lightning strokes of global thunderstorms. The detected signal is a white noise passed through the resonance system; see e.g., [33]. The control of such a signal is impossible, and therefore experimental studies consist of passive observation with a subsequent recording of data.
The objectives of our study are to determine the interannual trends in basic SR frequency and their connection with solar activity. The remainder of the paper proceeds as follows. We discuss the SR phenomenon and introduce the Earth–ionosphere cavity model that has been applied. Then, we compare the computed data with the long-term observations of first resonance frequency at the Ukrainian Antarctic Station “Akademik Vernadsky” (geographic coordinates: 65.25° S and 64.25° W). The experimental data span the period from 2002 to 2024, thus extending the dataset beyond that used in [39]. A comparison of model data with observations allows us to quantitatively estimate alterations in the height of the ionosphere region that are significant for ELF radio propagation. Finally, we estimate the impact of the solar cycle on the complex ELF radio propagation constant.
2. The Model Solution
One of the key aspects of the SR theory is postulating the frequency dependence ν(f) of the complex propagation constant in formulas for the ELF fields of the Earth–ionosphere cavity. The real part of this value determines the phase velocity of radio waves at a given frequency, and the imaginary part defines the attenuation rate. Different models are used in ELF–ULF computations [40,41,42,43]. Firstly, heuristic dependencies ν(f) are very popular [41,42] with the parameters settled in such a way that the computed power spectra agree with the observations. Such models are particularly prevalent in the “engineering” computations of ELF radio propagation. However, they have a poor relationship with the actual properties of ionosphere. Models based on geophysical data allow parameters of the Earth–ionosphere cavity resonator to be obtained, and these are commonly used for deriving the propagation constant. Although this approach is more complicated, it enables direct comparison with observational data and facilitates the extraction of valuable information on the global environment from SR records.
In the following text, we use the model of the spherical cavity formed by a perfectly conducting Earth surrounded by a horizontally uniform stratified atmosphere. The air conductivity σ(h) increases with the height h above the ground surface, so that the imaginary part increases the complex permittivity of the atmosphere: . Here ω = 2πf denotes the circular frequency, and ε0 = 8.858·10−12 F/m is the permittivity of the free space. Changes of ε(h) with height control the dispersion dependence ν(f). The full-wave solution is used for obtaining this dependence. The solution exploits the relationship between the longitudinal and the transverse components of the wave vector in a waveguide. A description of the full-wave solution procedure can be found in previous publications [14,15,16,17,18,19,20]. Here, we outline only the major steps of this solution.
The horizontally homogeneous atmosphere is divided into flat layers, each characterized by a definite dielectric constant. The solution of the electromagnetic problem within a layer involves a pair of radio waves: one is propagating upward and the other downward. The condition of continuity of the tangential components of the fields is applied at the boundaries of the slabs. The perfect boundary condition is commonly used at the ground surface. The conducting atmosphere above a certain sufficiently large height (100–110 km) is considered to be a vertically homogeneous medium, where the radiation boundary condition is imposed. Physically, this upper height is the altitude to which the magnetic field component of ELF radio waves can penetrate.
It is obvious that, after dividing the atmosphere into N horizontal layers, the system of 2 N linear equations is obtained for the wave amplitudes within each slab. The compatibility of these equations provides the transverse wave number at a given frequency. The desired longitudinal wave number is obtained by subtracting the square of the transverse wave number from the square of the total wave number and taking the square root of this difference.
Unfortunately, this clear procedure sometimes encounters difficulties in its practical applications. A problem may arise when the complex permittivity of different layers becomes equal. In particular, this might occur due to excessively small changes in the air conductivity when the step along the height is insufficient. In this case, the system of linear equations becomes degenerate, making a solution unattainable. To avoid this difficulty, layers of greater thickness could be used, especially at the lower altitudes above the ground. For example, Madden and Thompson [14] had to use the first layer of 27 km thickness in their calculations. This problem is rarer in modern computers operating with 64 precision; nevertheless, it may still occasionally occur.
The situation improves significantly when the problem is reformulated from the system of linear equations to the differential (difference) Riccati equation; see e.g., [15,20,44]. This necessitates transit from the horizontal components of the electric and magnetic field inside a layer to their ratio, i.e., to the surface impedance. In this case, the algebraic system of equations can be transformed into the Riccati differential equation. This equation is solved by the Newton’s iterations, resulting in the ELF propagation constant ν(f). The Riccati equation allows the realistic conductivity profile to be divided into slabs of 1 km height in the altitude range from 0 to 110 km.
We apply the ‘average’ conductivity profile in our calculations, which is the updated profile suggested in [40]. This profile corresponds to a median solar activity, as shown by the purple line in Figure 1. Profiles are also shown for the periods of active and quiet Sun. Low solar activity corresponds to the elevated (pivoted) upper part (blue line) and high activity results in the lowered upper part of profile (red line). These modified profiles are obtained from the average plot by rotating the purple curve above the 55 altitude by the angle of T = ±1°. The relevant numerical σ(h) data are given in Table A1 of Appendix A. It is observed that the conductivity profile varies with solar activity by ±4 km at the level where the conductivity σ(h) ≅ 10–3 S/m, i.e., in the altitude range 90–98 km. By default, all profiles converge below the knee altitude of 55 km.
In engineering ELF computations, the following standard heuristic frequency dependence is often used for obtaining the dimensionless propagation constant ν(f); see [41]:
Here, is the wave number, a = 6.37 Mm is the Earth’s radius, is the complex parameter with the and . The frequency f is measured in Hertz. This reference dependence ν(f) in the form (1) was obtained as a result of processing of a large amount of observational data collected by global observatories in support of the US Navy project ‘Sanguine-Seafarer’. Equation (1) provides the first SR mode peak frequency of 7.85 Hz.
In our modeling, we use the full-wave solution in the form of the Riccati equation and obtain the complex radio propagation constant [44]. Three functions ν(f) were computed, corresponding to conductivity profiles shown in Figure 1. Then, the model SR power spectra were computed in the vertical electric field component relevant to the uniform distribution of lightning strokes over the globe [10,12,20]. These spectra are shown in Figure 2.
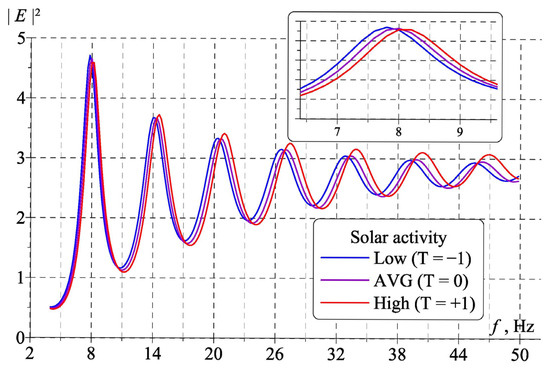
Figure 2.
Model SR power spectra in the vertical electric field component for the uniform distribution of lightning discharges over the globe when the solar activity is high, median or low (red, purple, and blue curves, respectively).
In this figure, the signal frequency is shown in Hertz along the abscissa, while the spectral power density of vertical electric field |E(f)|2 is presented along the ordinate in relative units. It is observed that modifications of atmosphere conductivity driven by solar activity result in changes of all SR peak frequencies and in the resonance intensity. The inset in Figure 2 shows in detail the vicinity of the first SR model, which is exclusively discussed in the following text.
Using three profiles of atmosphere conductivity, we computed three ν(f) functions around the first SR mode. We also calculated the lower characteristic (electric) hC(f) height and the upper (magnetic) height hL(f) [14,17,20,39,44]. Physically, the electric characteristic height hC(f) is the altitude where the conductivity current becomes equal to the displacement current of a given frequency. Therefore, the vertical electric field rapidly attenuates above the electric height. Similarly, a somewhat higher magnetic height hL(f) is the level from where the horizontal magnetic field starts to rapidly decrease with altitude. The results of full-wave solutions are presented in Figure 3.

Figure 3.
Results of full-wave solution in the vicinity of the first SR mode: (a)—characteristic heights of the Earth–ionosphere cavity; (b)—complex radio propagation constants.
The plots in Figure 3a depict the frequency variations of the magnetic (top panel) and the electric (bottom panel) characteristic heights. The frequency in Hertz is shown along the horizontal axis in the neighborhood of the first SR mode. Similarly to Figure 1 and Figure 2, the purple curves in Figure 3 correspond to the basic profile (median solar activity), while the blue and the red lines depict the results for the quiet and active Sun respectively. The electric characteristic height is almost independent of the solar activity in the entire frequency band. Its alterations from the quiet to active Sun conditions do not exceed ±50 m. Deviations of the magnetic characteristic height are more pronounced, reaching up to ±4 km. This value is rather close to deviations visible in Figure 1 around the lg[σ(h)] ≅ −3 in the 90–98 km altitude. Thus, our model of solar impact suggests that the atmosphere conductivity undergoes minor modifications in the stratosphere altitudes and below. Simultaneously, the model profiles support the long-term interannual changes in characteristic heights driven by the solar activity [35,39].
We next examine to what extent the complex ELF radio propagation constant ν(f) from our model matches the reference dependence [41] defined by Equation (1). The reference data are plotted in Figure 3b by the thin black line with the open circles. We observe that our propagation constants are rather close to the classical reference dependence.
By using the upper graph in Figure 3a, one may estimate the first SR peak frequency. This frequency is found from the condition Re[ν(f)] = 1. As might be observed, these values are close to 7.9; 8 and 8.1 Hz for the profiles corresponding to the quiet (pivot angle T = −1°), median (T = 0°) and active Sun (T = +1°), respectively. More exact values are shown in Figure 4. The peak frequency corresponding to the reference dispersion Equation (1) [41] is estimated as 7.85 Hz. This is shown in Figure 3b by the line with open circles.
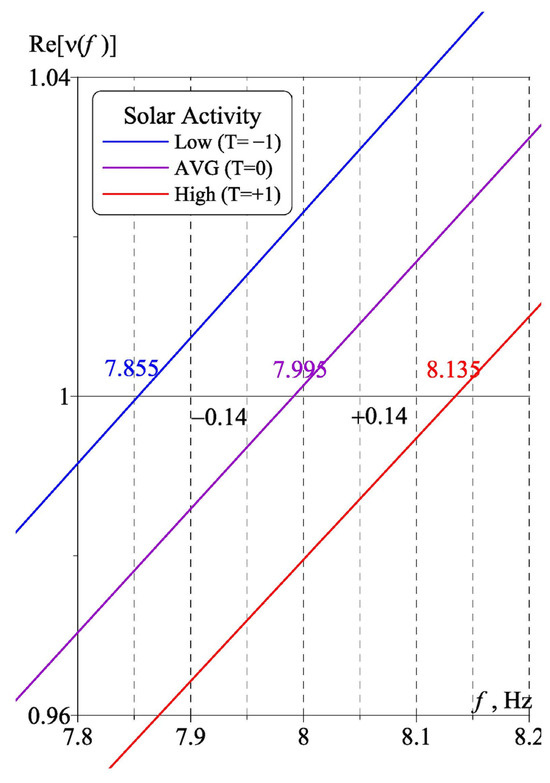
Figure 4.
Peak frequencies of the first SR mode for different levels of solar activity.
The plots in Figure 3a indicate that frequency variations of the characteristic heights and of the propagation constant are close to linear functions, at least in the vicinity of the first resonance mode. The plots in Figure 3b show that alterations in the rotation angle T of the profile upper part lead to an upward or downward shift of the ν (f). Using the computational data, we obtain the approximating dependence on T in the resonance condition and for the real parts of magnetic and electric characteristic heights Re[hL(f)] and Re[hC(f)] shown in Table 1.

Table 1.
Links between the pivot angle T, the peak frequency of the first SR mode, and characteristic heights pertinent to the model profile of atmosphere conductivity.
As one may observe, the pivot angle T of the upper part of the conductivity profile is related to the noticeable height change dhL in the magnetic characteristic height. Variations of electric characteristic height dhC are much smaller. This feature could be used to link the observed annually averaged changes in the SR peak frequency with the shifts of the upper characteristic height dhL driven by variations in solar activity.
The plots in Figure 4 show the frequency dependence Re[ν(f)] in a close vicinity of the first SR mode. Three colored lines correspond to different levels of solar activity and relevant tilt angles T of the upper parts of conductivity profiles. The colored numbers in this figure show the particular frequencies where Re[ν(f)] = 1, while the black numbers indicate the distance of 0.14 Hz between these crossings.
Table 1 summarizes the characteristic quantities of our model relevant to different pivot angles T. Using Figure 4 and Table 1 allows the following equations to be obtained for the annually averaged frequency of the first SR mode and the rotation angle T:
Additional equations are valid for the frequency variations of average characteristic heights in the vicinity of the basic SR mode:
3. Comparison with Observations
Table 1 and Equation (3) allow us to compute the interannual variations of the upper characteristic height of ionosphere Re[hL], shown by the thin stepped lines in the top panel of Figure 5. Similar data for the electric height Re[hC] were not plotted, as its alterations are much smaller than those of magnetic height. The bottom panel in Figure 5 demonstrates the interannual variations of the solar activity estimated by using the solar radio emission at 10.7 cm wavelength.
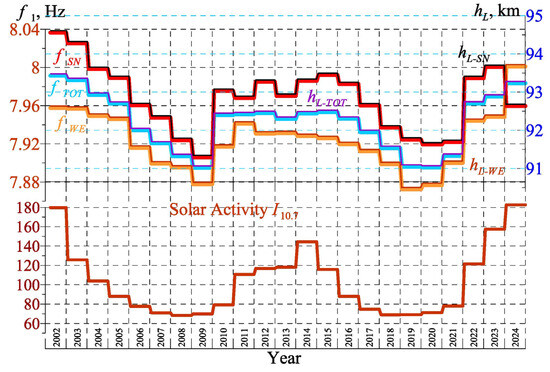
Figure 5.
Interannual variations of SR basic frequency and solar activity. The top panel shows the basic SR peak frequencies in Antarctica shown against the left ordinate (HSN is shown by the bold red line, HWE is the bold yellow line, and HTOT is the bold blue line). The relevant changes of the characteristic hL height are shown by thin lines plotted on the right ordinate. The bottom panel shows the solar activity in radiation at λ = 10.7 cm and in Wolf numbers (red and black curves).
The common abscissa in Figure 5 shows the years of observations from 2002 to 2024. The bold color lines in the top panel demonstrate the interannual variations of the first SR frequency in different field components combined with relevant changes of the upper characteristic height of the ionosphere shown by narrow lines. The annually averaged frequencies are shown by bold color stepped lines plotted against the left ordinate; their standard deviation was estimated as STD = 0.012 Hz. The estimated magnetic heights (narrow lines) are shown along the right ordinate. The labels at the plots indicate the particular field components used in observations and computations: the HSN and HWE horizontal magnetic fields and the total field. Systematic deviations of individual curves could be explained by the regular departures in the observed peak frequencies of the field components arising from the non-uniform spatial distribution of the field sources [32,35,39]. The peak frequencies averaged over the whole period of observations SR are: fSN = 7.968 Hz and fWE = 7.924. If we use the calibration curve from Figure 2 of [32], we obtain DSN = 14.2 Mm and DWE = 12.9 Mm. Departures in the median source—observer distances could be explained by the spatial distribution of thunderstorms. The HSN field component is sensitive to the sources located along the parallel relative to the observer, whereas the orthogonal component HWE is influenced by the sources positioned along the observer’s meridian. Obviously, this result should be linked to the position of the particular observatory against the three global thunderstorm centers. Such “effective” source—observer distances will alter in accordance with the observer location. Unfortunately, we cannot check this assumption by using concurrent whole term records of SR magnetic field components at some other observatory. However, the curves in Figure 5 are rather similar and demonstrate almost equal interannual height variations of ±1.6 km against the slightly different mean ionosphere heights that are close to 92.5 km.
The bottom panel in Figure 5 demonstrates the interannual variations of solar activity estimated using the solar radio emission at 10.7 cm wavelength. To facilitate the comparison, we show in this figure the annually averaged levels of the solar radio emission. There is an obvious similarity between variations in solar activity and in estimated ionosphere height. In Figure 6, the relevant phasors are plotted, which reveal this connection.

Figure 6.
Phasors f1 versus I10.7 (top plots) and phasors hL versus I10.7.
Figure 6 summarizes the results obtained for the peak frequency of the first SR mode (upper plots) and for magnetic characteristic height (lower plots). The black lines in the top plots depict the phasors f1 versus the index of solar activity I10.7. The color lines here show the linear fits for the observed variations. The solar index is estimated using solar radio emission at the 10.7 cm wavelength. The black lines in the lower plots depict the phasors Re[hL] versus I10.7. The straight color lines also show the linear fitting for the original phasors. The results of linear fitting are listed in Table 2. Table 2 contains valuable quantitative information on the geophysical characteristics of the Earth–ionosphere cavity: variations with the solar activity of SR frequency f1 and of the globally averaged magnetic characteristic height hL.

Table 2.
Peak frequency f1 and characteristic magnetic height hL as functions of solar activity I10.7.
It is also interesting to derive the related dependence for the ELF radio propagation constant. For this purpose, we apply the following steps. We linearly fit the model ν(f) dependence pertinent to the minimum and to the maximum solar activity, and then we interpolate these two functions for intermediate values of pivot angle T. We confine ourselves to the records of HSN magnetic field where the solar impact is the most pronounced. The following linear dispersion equation is obtained incorporating the rotation angle T:
The monitoring of the SR peak frequency f1 provides the following values for the HSN field component. The maximum and the minimum values of the peak frequency were equal to 8.04 and to 7.91 Hz. The mean value was 7.97 Hz and its standard deviation was equal to 0.034 Hz. The relevant index I10.7 of the solar activity varied from 182.7 to 68.3. The following relation follows from the long-term experimental observations:
The model data have the maximum and the minimum peak frequencies of 8.14 and 7.86 Hz. The relevant pivot angle T of conductivity profiles varies from −1° to +1°, and we obtain the equation:
By equalizing the frequencies from Equations (6) and (7), we obtain:
hence
or the pivot angle T varies with the solar activity as:
Now, we return to Equation (5) and substitute there the parameter T from Equation (10). As a result, we arrive at the following relation:
Equation (11) describes the ELF radio wave propagation constant, taking solar activity into account. It could be used as the ‘engineering’ formula when computing the expected ELF fields in the Earth–ionosphere cavity for different levels of solar activity. In the linear approximation, the annual mean basic SR frequency and the magnetic characteristic height vary with the solar activity in the following way:
Equations (12a) and (12b) could be used for interpreting and predicting long-term SR monitoring data. These equations are based on linear fitting of the observed long-term experimental data. They allow formulation of the following simple mnemonic rule: an increase in the index of the solar activity I10.7 by ~150 units may raise the first SR frequency by 0.1 Hz, and the increase in the I10.7 by 61 units elevates the magnetic characteristic height by 1 km.
4. Discussion
By using a realistic model of Earth–ionosphere cavity and the long-term Antarctic records of SR basic frequency, we quantitatively evaluated the impact of solar activity on the resonance parameters and the upper characteristic height of the atmospheric conductivity profile. A set of simple linear formulas was obtained evaluating the ‘solar modulations’ of the basic SR frequency, dispersion equations ν(f, I10.7), and the ionosphere characteristic height hL(f, I10.7).
The results obtained seem to be quite realistic. Changes in the characteristic heights of the lower ionosphere may reach ~2.5 km during the complete solar cycle.
In addition, the magnitude of the modulations obtained is in good agreement with published studies [32,35,39], where alternative models were used. In the paper [35], a heuristic knee model was applied, as suggested in [42]. The “knee height” of this model has been shifted vertically in accordance with the level of solar activity. In reference [39], the realistic σ(h) profile was used, which was pivoted as a whole around the central point at the 55 km altitude. The rotation angle was a function of contemporary solar activity.
The model we apply here uses an improved conductivity profile [40], shown in Figure 1. Only the upper part of this profile is pivoted above the 55 km altitude. Comparison of observational data with all of these models leads to similar results: the magnetic characteristic height of the ionosphere varies by approximately by 1–2 km relative to its average value.
These model variations in the magnetic characteristic altitude seem to be more realistic, especially when considering the following factors. First, the ionosphere region important for the ELF radio propagation and for the global resonance is located significantly lower than the maximum of ionosphere ionization, at ~(250–300) km. Therefore, the impact of variable solar activity becomes substantially reduced at the altitude of magnetic characteristic height hL~(90–100) km.
The small amplitude of interannual variations in the planetary averaged magnetic height hL is also explained by averaging of the observational data over annual periods of time. Contributions of substantial but short-term modulations (e.g., solar X-ray or galactic gamma-ray flares) are greatly reduced through averaging. The maximum height disturbances caused by these short-term events may reach tens of kilometers; see Section 6.4 in [12].
Additional decrease is linked to the global nature of the SR phenomenon: the evaluated altitude changes are related to the whole planet. Particular fast events, like the Bastille Day Solar Proton Event (SPE), also are able to cause a reduction in the polar ionosphere height by a factor of two, and their effect is detected worldwide; see Section 6.4.3 in [10] or Section 6.3 in [12]. However, the short-term impact of such events is noticeably reduced in temporal and spatial averaging. Finally, it is clear that the variable solar activity modifies only the dayside ionosphere, so that the global change of 1 km turns into the altitude variation of 2 km at the sunlit hemisphere, as it are absent on the night side of the Earth.
A number of significant details are caused by the random nature of the SR signals generated by global thunderstorm activity. The distribution of casual lightning strokes in time and space is, strictly speaking, unknown. Attempts to apply the data from global lightning location networks like the WWLLN [45] have generally encountered problems.
When modeling the dynamics of the observed SR spectra, of course, we suggest that the comprehensive averaging of the experimental data over a year has completely eliminated the random factors linked to field sources. Fortunately, we are able to quantitatively assess the validity of this assumption. We can obtain estimates using the synchronous records of the HSN and HWE field components and compare them. Such records are formed by thunderstorms positioned at different areas of the planet. If our assumption was correct, the final results based on these records will be completely coincident, because the source factor will have been totally eliminated. As shown in Figure 5, this is not so, since the individual curves in the upper panel of this figure are:
- (1)
- Shifted vertically relative to one another, however,
- (2)
- Their interannual patterns are remarkably similar.
It should be emphasized that the obtained estimates of the height trends characterize the average changes over the whole planet and therefore they are universal. This follows from the global nature of the SR phenomenon and the annually averaged observational data used. These expectations should be verified using similar long-term SR records from sites positioned at other latitudes and longitudes.
5. Conclusions
We conclude that SR data allow the reliable evaluation of the interannual variations in the global ionospheric height hL driven by the solar activity, whereas the average height may contain a systematic error reaching several kilometers. We also note that the normalized systematic deviation is rather small, at about 1%.
The long-term experimental observations allow us to formulate a simple mnemonic rule: an increase in the index of the solar activity I10.7 by 150 units raises the first SR frequency by 0.1 Hz and it will elevate the magnetic characteristic height by 2.5 km.
We utilize in this work the SR monitoring at the single Ukrainian Antarctic station of “Akademik Vernadsky”, and the results obtained agree with those of previous publications [32,35,39]. The advantage of the present work is in obtaining closed analytical expressions for the first peak frequency, complex propagation constant, and magnetic characteristic height of the lower ionosphere as functions of contemporary solar activity and in formulating the above ‘rule of thumb’.
However, this study has some limitations. We expect that concurrent records from the other sites or of the vertical electric field component will show essentially the same peak frequencies and their interannual variations. Of course, deviations will be present, demanding definite corrections in the above formulas. This kind of research activity is strongly desirable, especially, observations covering more than two solar cycles.
Author Contributions
Conceptualization, A.P.N.; observations and data processing, O.K.; validation, A.P.N., M.H. and O.K.; writing, review, and editing, A.P.N., M.H. and O.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data in this paper are available from the corresponding author upon request.
Acknowledgments
The authors express their sincere appreciation to the winterers of the Ukrainian Antarctic expeditions who have continuously ensured the reliable operation of receiving equipment under the harsh conditions of Antarctica for more than twenty years. The authors also acknowledge the State Institution National Antarctic Scientific Center for its logistical and financial support of the ELF research conducted by the Institute of Radio Astronomy and the Institute of Radiophysics and Electronics of the National Academy of Sciences of Ukraine, including STCU Project P775. We are deeply grateful to the reviewers and the editorial board for their diligent work in reviewing our manuscript and for their important and valuable comments and suggestions, which have undoubtedly contributed to its significant improvement. These investigations were carried out within the State Target Scientific and Technical Programs for Antarctic Research framework for 2002–2010 and 2011–2025.
Conflicts of Interest
M.H. is an employee of Hayakawa Institute of Seismo Electromagnetics, Co., Ltd. (Hi-SEM), but this paper reflects the views of the scientists and not the company.
Appendix A
This appendix presents numerical data on the applied conductivity profiles with a vertical step of 1 km.

Table A1.
Conductivity profiles of the mesosphere applied in model computations.
Table A1.
Conductivity profiles of the mesosphere applied in model computations.
| z, km | Quiet, T = −1 | AVG, T = 0 | Active T = +1 | z, km | Quiet, T = −1 | AVG, T = 0 | Active T = +1 | z, km | Quiet, T = −1 | AVG, T = 0 | Active T = +1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | −14 | −14 | −14 | 37 | −10.19 | −10.19 | −10.19 | 74 | −6.404 | −6.07 | −5.73 |
| 1 | −13.86 | −13.86 | −13.86 | 38 | −10.1 | −10.1 | −10.1 | 75 | −6.26 | −5.91 | −5.56 |
| 2 | −13.71 | −13.71 | −13.71 | 39 | −10.03 | −10.03 | −10.03 | 76 | −6.13 | −5.76 | −5.39 |
| 3 | −13.47 | −13.47 | −13.47 | 40 | −9.96 | −9.96 | −9.96 | 77 | −5.99 | −5.61 | −5.22 |
| 4 | −13.23 | −13.23 | −13.23 | 41 | −9.89 | −9.89 | −9.89 | 78 | −5.86 | −5.46 | −5.05 |
| 5 | −13.04 | −13.04 | −13.04 | 42 | −9.83 | −9.83 | −9.83 | 79 | −5.72 | −5.3 | −4.88 |
| 6 | −12.88 | −12.88 | −12.88 | 43 | −9.77 | −9.77 | −9.77 | 80 | −5.61 | −5.17 | −4.73 |
| 7 | −12.74 | −12.74 | −12.74 | 44 | −9.71 | −9.71 | −9.71 | 81 | −5.51 | −5.05 | −4.59 |
| 8 | −12.61 | −12.61 | −12.61 | 45 | −9.67 | −9.67 | −9.67 | 82 | −5.4 | −4.93 | −4.45 |
| 9 | −12.49 | −12.49 | −12.49 | 46 | −9.62 | −9.62 | −9.62 | 83 | −5.28 | −4.79 | −4.3 |
| 10 | −12.38 | −12.38 | −12.38 | 47 | −9.58 | −9.58 | −9.58 | 84 | −5.17 | −4.66 | −4.15 |
| 11 | −12.27 | −12.27 | −12.27 | 48 | −9.56 | −9.56 | −9.56 | 85 | −5.04 | −4.52 | −3.99 |
| 12 | −12.16 | −12.16 | −12.16 | 49 | −9.53 | −9.53 | −9.53 | 86 | −4.93 | −4.38 | −3.84 |
| 13 | −12.06 | −12.06 | −12.06 | 50 | −9.51 | −9.51 | −9.51 | 87 | −4.80 | −4.24 | −3.68 |
| 14 | −11.96 | −11.96 | −11.96 | 51 | −9.49 | −9.49 | −9.49 | 88 | −4.68 | −4.1 | −3.52 |
| 15 | −11.86 | −11.86 | −11.86 | 52 | −9.46 | −9.46 | −9.46 | 89 | −4.53 | −3.93 | −3.33 |
| 16 | −11.77 | −11.77 | −11.77 | 53 | −9.41 | −9.41 | −9.41 | 90 | −4.39 | −3.78 | −3.16 |
| 17 | −11.67 | −11.67 | −11.67 | 54 | −9.36 | −9.36 | −9.36 | 91 | −4.21 | −3.58 | −2.95 |
| 18 | −11.59 | −11.59 | −11.59 | 55 | −9.3 | −9.3 | −9.3 | 92 | −4.06 | −3.42 | −2.77 |
| 19 | −11.5 | −11.5 | −11.5 | 56 | −9.23 | −9.20 | −9.18 | 93 | −3.86 | −3.19 | −2.53 |
| 20 | −11.42 | −11.42 | −11.42 | 57 | −9.12 | −9.08 | −9.04 | 94 | −3.7 | −3.01 | −2.33 |
| 21 | −11.34 | −11.34 | −11.34 | 58 | −9.04 | −8.98 | −8.92 | 95 | −3.44 | −2.74 | −2.04 |
| 22 | −11.26 | −11.26 | −11.26 | 59 | −8.9 | −8.83 | −8.75 | 96 | −3.24 | −2.52 | −1.8 |
| 23 | −11.19 | −11.19 | −11.19 | 60 | −8.79 | −8.7 | −8.61 | 97 | −3.05 | −2.32 | −1.58 |
| 24 | −11.12 | −11.12 | −11.12 | 61 | −8.63 | −8.52 | −8.41 | 98 | −2.85 | −2.1 | −1.35 |
| 25 | −11.05 | −11.05 | −11.05 | 62 | −8.48 | −8.36 | −8.23 | 99 | −2.65 | −1.88 | −1.11 |
| 26 | −10.98 | −10.98 | −10.98 | 63 | −8.31 | −8.17 | −8.02 | 100 | −2.4 | −1.62 | −0.83 |
| 27 | −10.91 | −10.91 | −10.91 | 64 | −8.14 | −7.98 | −7.82 | 101 | −2.21 | −1.4 | −0.6 |
| 28 | −10.84 | −10.84 | −10.84 | 65 | −7.95 | −7.77 | −7.59 | 102 | −2.024 | −1.2 | −0.38 |
| 29 | −10.77 | −10.77 | −10.77 | 66 | −7.78 | −7.58 | −7.38 | 103 | −1.81 | −0.97 | −0.13 |
| 30 | −10.69 | −10.69 | −10.69 | 67 | −7.58 | −7.37 | −7.16 | 104 | −1.606 | −0.75 | 0.11 |
| 31 | −10.62 | −10.62 | −10.62 | 68 | −7.42 | −7.19 | −6.96 | 105 | −1.412 | −0.54 | 0.34 |
| 32 | −10.56 | −10.56 | −10.56 | 69 | −7.22 | −6.98 | −6.73 | 106 | −1.218 | −0.33 | 0.56 |
| 33 | −10.49 | −10.49 | −10.49 | 70 | −7.06 | −6.8 | −6.53 | 107 | −1.024 | −0.12 | 0.79 |
| 34 | −10.42 | −10.42 | −10.42 | 71 | −6.9 | −6.61 | −6.33 | 108 | −0.84 | 0.09 | 1.01 |
| 35 | −10.34 | −10.34 | −10.34 | 72 | −6.71 | −6.41 | −6.11 | 109 | −0.656 | 0.29 | 1.23 |
| 36 | −10.26 | −10.26 | −10.26 | 73 | −6.56 | −6.24 | −5.92 | 110 | −0.482 | 0.48 | 1.44 |
References
- Schumann, W.O. Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphäre Hülle umgeben ist. Z. Naturforschung 1952, 7a, 149–154. [Google Scholar] [CrossRef]
- Besser, B.P. Synopsis of the historical development of Schumann resonances. Radio Sci. 2007, 42, RS2S02. [Google Scholar] [CrossRef]
- Watt, A.D. VLF Radio Engineering; Pergamon Press: Oxford, UK; New York, NY, USA; Paris, France, 1967; 878p. [Google Scholar]
- Wait, J.R. Electromagnetic Waves in Stratified Media; Pergamon Press: Oxford, UK; New York, NY, USA; Toronto, ON, Canada, 1970; 608p. [Google Scholar]
- Galejs, J. Terrestrial Propagation of Long Electromagnetic Waves; Pergamon Press: New York, NY, USA, 1972; 362p. [Google Scholar]
- Jones, D.L. ELF propagation theory. In ELF−VLF Radio Wave Propagation; Holtet, J.A., Ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1974; pp. 207–223. [Google Scholar]
- Polk, C. Schumann resonances. In Handbook of Atmospherics; Volland, H., Ed.; CRC Press: Bocca Raton, FL, USA, 1982; Volume 1. [Google Scholar]
- Sentman, D.D. Schumann resonances. In Handbook of Atmospheric Electrodynamics; Volland, H., Ed.; CRC Press: Boca Raton, FL, USA; London, UK; Tokyo, Japan, 1995; Volume 1, pp. 267–298. [Google Scholar]
- Barr, R.; Jones, D.L.; Rodger, C.J. ELF and VLF radio waves. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1689–1718. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth-Ionosphere Cavity; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2002; 380p. [Google Scholar]
- Füllekrug, M.; Mareev, E.A.; Rycroft, M.J. (Eds.) Sprites, Elves and Intense Lightning Discharges; NATO Science Series; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Nickolaenko, A.P.; Hayakawa, M. Schumann Resonance for Tyros (Essentials of Global Electromagnetic Resonance in the Earth–Ionosphere Cavity); Springer: Tokyo, Japan, 2014; 348p. [Google Scholar] [CrossRef]
- Price, C. ELF Electromagnetic Waves from Lightning: The Schumann Resonances. Atmosphere 2016, 7, 116. [Google Scholar] [CrossRef]
- Madden, T.; Thompson, W. Low frequency electromagnetic oscillations of the earth−ionosphere cavity. Rev. Geophys. 1965, 3, 211–254. [Google Scholar] [CrossRef]
- Hynninen, E.M.; Galuk, Y.P. Field of vertical electric dipole over spherical Earth with non-uniform along the height atmosphere. In Problems of Diffraction and Radio Propagation; Leningrad University Press: Leningrad, Russia, 1972; pp. 100–120. (In Russian) [Google Scholar]
- Jones, D.L. Schumann resonances and E.L.F. propagation for inhomogeneous isotropic ionospheric profiles. J. Atmos. Terr. Phys. 1976, 29, 1037–1044. [Google Scholar] [CrossRef]
- Greifinger, C.; Greifinger, P. Approximate method for determining ELF eigen-values in the Earth-ionosphere waveguide. Radio Sci. 1978, 13, 831–837. [Google Scholar] [CrossRef]
- Jones, D.L.; Knott, M. Comparison of simplified and full-wave ELF propagation models. In Proceedings of the URSI General Assembly, Session E6, Toronto, ON, Canada, 13–21 August 1999. [Google Scholar]
- Greifinger, P.S.; Mushtak, V.C.; Williams, E.R. On modeling the lower characteristic ELF altitude from aeronomical data. Radio Sci. 2007, 42, RS2S12. [Google Scholar] [CrossRef]
- Galuk, Y.P. Schumann resonance in the model of thunderstorm activity uniformly distributed over the globe. Telecommun. Radio Eng. 2016, 75, 923–935. [Google Scholar] [CrossRef]
- Galejs, J. Frequency variations of Schumann resonances. J. Geophys. Res. 1970, 75, 3237–3251. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; McGill, P.R.; Bernardi, A.; Helliwell, R.A.; Ladd, M.E. Global measurements of the low frequency radio noise. In Environmental and Space Electromagnetics; Kikuchi, H., Ed.; Springer: Tokyo, Japan, 1991; pp. 191–200. [Google Scholar]
- Fraser-Smith, A.C.; Bannister, P.R. Reception of ELF signals at antipodal distances. Radio Sci. 1998, 33, 83–88. [Google Scholar] [CrossRef]
- Schlegel, K.; Füllekrug, M. Diurnal harmonics in Schumann resonance parameters observed on both hemispheres. Geophys. Res. Lett. 2000, 27, 2805–2808. [Google Scholar] [CrossRef]
- Pechony, O.; Price, C. Schumann resonance parameters calculated with a partially uniform knee model on Earth, Venus, Mars, and Titan. Radio Sci. 2004, 39, RS5007. [Google Scholar] [CrossRef]
- Sàtori, G.; Williams, E.; Mushtak, V. Response of the Earth-Ionosphere Cavity Resonator to the 11-year Solar Cycle in X-Radiation. J. Atmos. Sol.-Terr. Phys. 2005, 67, 553–562. [Google Scholar] [CrossRef]
- Williams, E.R.; Sàtori, G. Solar radiation-induced changes in ionospheric height and the Schumann resonance waveguide on different timescales. Radio Sci. 2007, 42, 1–8. [Google Scholar] [CrossRef]
- Simões, F.; Rycroft, M.; Renno, N.; Yair, Y.; Aplin, K.L.; Takahashi, Y. Schumann resonances as a means of investigating the electromagnetic environment in the solar system. Space Sci. Rev. 2008, 137, 455–471. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Li, Z.; Zhao, Z.; Zeren, Z.; Shen, X.; Wang, Q. Recent Advances and Challenges in Schumann Resonance Observations and Research. Remote Sens. 2023, 15, 3557. [Google Scholar] [CrossRef]
- Ondrášková, A.; Sevcík, S.; Kostecký, P. A significant decrease of the fundamental Schumann resonance frequency during the solar cycle minimum of 2008-9 as observed at Modra Observatory. Contrib. Geophys. Geod. 2009, 39, 345–354. [Google Scholar] [CrossRef]
- Toledo-Redondo, S.; Salinas, A.; Porti, J.; Morente, J.A.; Fornieles, J.; Méndez, A.; Galindo-Zaldívar, J.; Pedrera, A.; Ruiz-Constán, A.; Anahnah, F. Study of Schumann resonances based on magnetotelluric records from the western Mediterranean and Antarctica. J. Geophys. Res. 2010, 115, 114–124. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Koloskov, A.V.; Hayakawa, M.; Yampolski, Y.M.; Budanov, O.V.; Korepanov, V.E. 11-year solar cycle in Schumann resonance data as observed in Antarctica. Sun Geosph. 2015, 10, 39–49. [Google Scholar]
- Ayurov, D.; Bashkuev, Y.B. Schumann Resonances in high latitudes. In Proceedings of the International Kharkov Symposium on Physics and Engineering of Microwaves, Millimeter, and Submillimeter Waves (MSMW), Kharkov, Ukraine, 26–29 June 2016. [Google Scholar]
- Gołkowski, M.; Sarker, S.R.; Renick, C.; Moore, R.C.; Cohen, M.B.; Kułak, A.; Młynarczyk, J.; Kubisz, J. Ionospheric D region remote sensing using ELF sferic group velocity. Geophys. Res. Lett. 2018, 45, 12739–12748. [Google Scholar] [CrossRef]
- Koloskov, A.V.; Nickolaenko, A.P.; Yampolsky, Y.M.; Hall, C.S.; Budanov, O.V. Variations of global thunderstorm activity derived from the long-term Schumann resonance monitoring in the Antarctic and in the Arctic. J. Atmos. Sol.-Terr. Phys. 2020, 201, 105231. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Galuk, Y.P.; Hayakawa, M.; Kudintseva, I.G. Model sub-ionospheric ELF—VLF pulses. J. Atmos. Sol.-Terr. Phys. 2021, 223, 105726. [Google Scholar] [CrossRef]
- Füllekrug, M. Simulation of Earth-ionosphere cavity resonances with lightning flashes reported by OTD/LIS. J. Geophys. Res. Atmos. 2021, 126, e2021JD035721. [Google Scholar] [CrossRef]
- Sàtori, G.; Bozoki, T.; Williams, E.; Pracser, E.; Herein, M.; Albrecht, R.I.; Beltran, R.P. How do Schumann resonance frequency changes in the vertical electric field component reflect global lightning dynamics at different time scales? J. Geophys. Res. Atmos. 2024, 129, e2024JD041455. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M.; Koloskov, O.V. Schumann resonance as a remote sensor of lower ionosphere and global thunderstorms as based on the long-term observations at Antarctic and Arctic stations. J. Atmos. Sol.-Terr. Phys 2025, 269, 106465. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Nickolaenko, A.P.; Harrison, R.G.; Odzimek, A. The global circuit capacitor and two new ways of deriving the time constant of the global atmospheric electric circuit. J. Atmos. Sol.-Terr. Phys 2025. to be published. [Google Scholar] [CrossRef]
- Ishaq, M.; Jones, D.L. Method of obtaining radiowave propagation parameters for the Earth-ionosphere duct at ELF. Electron. Lett. 1977, 13, 254–255. [Google Scholar] [CrossRef]
- Mushtak, V.C.; Williams, E.R. ELF propagation parameters for uniform models of the Earth-ionosphere waveguide. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1989–2001. [Google Scholar] [CrossRef]
- Bozoki, T.; Sàtori, G.; Williams, E.; Mironova, I.; Steinbach, P.; Bland, E.C.; Koloskov, A.; Yampolski, Y.M.; Budanov, O.V.; Neska, M.; et al. Solar Cycle-Modulated Deformation of the Earth–Ionosphere Cavity. Front. Earth Sci. 2021, 9, 689127. [Google Scholar] [CrossRef]
- Galuk, Y.P.; Kudintseva, I.G.; Nickolaenko, A.P.; Hayakawa, M. Scattering of ELF radio waves by a localized non-uniformity in the lower ionosphere. J. Atmos. Sol.-Terr. Phys. 2019, 194, 105093. [Google Scholar] [CrossRef]
- Rodger, C.J.; Brundell, J.B.; Hutchins, M.; Holzworth, R.H. The world wide lightning location network (WWLLN): Update of status and applications. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).