Abstract
The climate of the Hungarian lowland (Central European region, Pannonian Plain area) can be characterized by Köppen’s Cfb climate formula (C—warm temperate, f—no seasonality in the annual course of precipitation, b—warm summer). This characterization does not provide information about the human thermal load and thermal perception. The aim of this work is to fill this gap. We focused on the morning, clear-sky periods of the day, when the heat supply provided by the weather is the lowest. The human thermal load of clear-sky mornings was estimated using the new clothing thermal resistance–operative temperature (rcl–To) model. In contrast to IREQ-type (Required Clothing Insulation) models, this model parametrizes the total metabolic heat flux density (M) as a function of anthropometric data (body mass, height, sex, age). In the simulations, the selected persons walk (M values range between 135 and 170 W m−2) or stand (M values range between 84 and 96 W m−2), while their body mass index (BMI) varies between 25 and 37 kg m−2. The following main results should be highlighted: (1) Human activity has a significant impact on rcl; it ranges between 0 and 3.5 clo during walking and between 0 and 6.7 clo during standing. (2) The interpersonal variability of rcl increases with increasing heat deficit accordingly; in the case of a walking person, it is around 1 clo in the largest heat deficits and around 0 clo in the smallest heat deficits. Since, in general, anticyclones increase the heat deficit while cyclones reduce it, extreme thermal loads are associated with anticyclones. It should be mentioned that the interpersonal variability of the human thermal load cannot be analyzed without databases containing people’s anthropometric data.
1. Introduction
The weather must be analyzed to understand (1) its processes [1] and (2) its impacts on human life. Agrometeorological information is intended to enhance the efficiency of crop production [2]. Meteorology can also provide information to the livestock industry [3], while human biometeorology deals with the study of human comfort or discomfort [4]. The popularity of human biometeorological studies is growing [5]. The most frequently discussed human biometeorological topics in Hungary [6] are UV radiation, air pollution, pollen forecasts, and medical meteorological assessment. Note that there is no mention of human thermal load caused by the weather or climate in the available analyses and data.
The Hungarian lowland is part of the Pannonian Plain, located between the Carpathians, the Alps, and the Dinaric Mountains in Central Europe. The climate of this area can be characterized by Köppen’s Cfb (C—warm temperate, f—no seasonality in the annual course of precipitation, b—warm summer) climate formula [7]. The first letter refers to the spatial distribution of biomes; the second and third letters express a physical characteristic independent of the biome. The Köppen climate classification is biome-based, reflecting the response of biomes to environmental heat and water loads. Since we are dealing with biomes, this characterization of climate is crude and only appropriate at a macroscale. This highlights the need for human bioclimatological studies to gain a better understanding of the climate in the Hungarian lowland.
The human bioclimate of the Hungarian lowland has been studied mostly using the PET (Physiologically Equivalent Temperature) and UTCI (Universal Thermal Climate Index) human thermal indices [8]. This study used a climatological approach. The multiannual variation of UTCI and PET was analyzed at four Hungarian stations. The studies examine either average [9,10,11], extreme [12,13], or specific urban microclimate [14,15,16,17,18,19] conditions. When studying urban microclimates, the issue of human comfort was the focus. A correlation between severe heat waves and increased mortality has also been observed [20]. The topic of subjective thermal sensation was also investigated [21,22]. These studies did not analyze the effects of human variability on the human thermal load.
It should be mentioned that the applications of human biometeorological studies and climate classification methods have developed independently of each other [7,23]. The two approaches were rarely linked [24]. These studies analyzed the frequency of human biometeorological information occurring in climate types [25,26] or compared the spatial distribution of climate types and human thermal loads [10,11]. These studies did not use data characterizing selected weather types, but measured time series [8].
The weather in the Cfb climate type, including the Hungarian lowland, is determined by the movement and frequency of cyclones and anticyclones. Extreme thermal loads caused by the weather are associated with anticyclones [27], either with large heat surpluses in summer [13] or with large heat deficits in winter [28]. In this study, we focus on the weather during anticyclonic conditions, regardless of the season, in order to estimate the thermal load in the early morning hours when the heat deficit is usually the greatest. To the best of our knowledge, there have been no studies estimating the magnitude of human thermal loads during the morning hours of anticyclonic situations in the Köppen climate type Cfb. This is relevant weather/climate information from both a global (mornings in a Cfb climate) and local (mornings in the Hungarian lowland) perspective. Based on the above, the objectives of the study are as follows: (1) to provide information on the thermal load of clear-sky mornings, and (2) to investigate how human characteristics (e.g., activity and body data) affect this information.
The study is structured as follows: in Section 2 basic information (Section 2.4 and Section 2.5), definitions (Section 2.1), and equations (Section 2.2 and Section 2.3) are presented. Section 3 describes the location where the observation took place. In Section 4, we discuss the data used in the study. The main results are presented in Section 5.2 (thermal load), Section 5.3 (sensitivity to human activity), and Section 5.4 (sensitivity to body data). Discussion and conclusions can be found in Section 6 and Section 7, respectively.
2. Materials and Methods
In this study, the rcl–To (clothing thermal resistance–operative temperature) model was used [28]. The rcl model follows Holmér’s concept [29] but it differs in its calculation method. Furthermore, a new module for calculating total metabolic heat flux density (M) was incorporated. To is also an energy balance-based parameter for the human thermal load. The calculation of M requires anthropometric data, which are taken from the Hungarian anthropometric database. This model has mainly been used in climate tests [10,22] and only a few times to analyze the weather [28,30].
In the following, we briefly present the BMI (body mass index) parameter for characterizing the human body, the rcl–To model used, the parameterization of M, the human thermal sensation scale used, and basic information for documenting clear-sky mornings.
2.1. Body Mass Index
Body mass index (BMI) is one of the most important and well-known parameters for distinguishing individuals based on body composition. It is defined as follows,
where Mbo is body mass (kg) and Lbo is body length (cm).
2.2. The Clothing Thermal Resistance–Operative Temperature Model
Both parameters, clothing thermal resistance (rcl) and operative temperature (To), are energy balance-based indicators of thermal load. The main difference between them is that rcl uses metabolic heat flux density (M) as a variable, whereas To does not. As a result, rcl depends on human anthropometric data, while To does not.
Clothing thermal resistance is modeled on the basis of Holmér’s concept [29], therefore it is an IREQ-type (Required Clothing Insulation) model. However, instead of iteratively calculating the clothing surface temperature (TS), we present an analytical solution [31]. Furthermore, in our model, M is not constant as in Holmér’s model, but is parameterized. This allows us to simulate persons rather than using the concept of a “standard human”.
The basic equations of rcl and To are as follows,
where ρ is air density [kg·m−3], cp is specific heat at constant pressure [J·kg−1·°C−1], TS is skin temperature (34 °C), rHr is combined resistance for expressing thermal radiative and convective heat exchange effect [s·m−1], and M is metabolic heat flux density [W·m−2], which refers to either a standing person or a person walking at a speed of 1.1 ms−1. λEsd is the latent heat flux density of dry skin [W·m−2], λEr is respiratory latent heat flux density [W·m−2], Hr is respiratory sensible heat flux density [W·m−2], W is mechanical work flux density [W·m−2], Ta is air temperature at a height of 2 m [°C], and Rni is isothermal net radiation [W·m−2]. It should be mentioned that rcl is usually expressed in units of [clo], where 1 [clo] = 0.155 m2·K·W−1. If rcl/(ρ· cp) = 1 [clo], then rcl = 1.2 [kg·m−3] · 1004 [J·kg−1·K−1] · 0.155 [m2·K·W−1] = 186.74 [s·m−1]. The parameterization of rHr, Rni, λEsd, λEr, Hr, and W can be found in work [28].
2.3. Parameterization of Metabolic Heat Flux Density
In the model, the person is either standing or walking. The speed of a walking person is 1.1 ms−1. The human’s total metabolic heat flux density is as follows,
where Mb is the basal metabolic heat flux density [W·m−2] and Ma is the metabolic heat flux density [W·m−2] associated with activity (such as walking or standing in our model). Mb is parameterized according to [32] separately for men and women as follows,
where age is expressed in years. In Equations (5) and (6), the unit of Mb is W and to obtain it in Wm−2, it must be divided by human body surface area A (m2). The well-known Dubois and Dubois formula [33] is applied,
In the case of a walking human, Ma = Mw. Mw is parameterized according to [34] as follows,
The coefficient 1.1 is added because of the chosen walking speed.
In the case of the standing human, Ma = Mst. According to the results of Amaro-Gahete et al. [35] and Júdice et al. [36], the metabolic heat flux density used up during standing is only slightly higher than the metabolic heat flux density used up while lying down. Based on this, we parameterized Mst as follows,
2.4. Human Thermal Sensation Scale
A 7-grade scale is used for characterizing human thermal sensation types. The thermal sensation categories are named as follows: “very warm”, “warm”, “slightly warm”, “neutral”, “cool”, “cold”, and “very cold”. These category names do not match the category names used in the work of Fanger [23], but the key point is that it is also a 7-grade scale. Thermal perception was performed by a man and a woman in a longitudinal experiment. Both persons were born in the Hungarian lowland. The results of these observations were described in detail in the work of Ács et al. [22]. Person 1 in the work of Ács et al. [22] is identical with person 1 in Table 1.

Table 1.
The anthropometric data of the three selected persons involved in the study and the metabolic heat flux density values of walking at a speed of 1.1 m s−1.
2.5. Basic Information Related to Clear-Sky Mornings
Observations were made between 23 January 2020 and 3 April 2024. The total number of observations was 161. In a huge proportion of the observations (about 90%), the surface air pressure was above 1020 hPa; that is, it was an anticyclonic weather situation. We conducted observations every month. The number of observations in the 6-month period from April to September was 56. The morning period was from 5 a.m. to 9:30 a.m. We registered 7 observations at night or at dawn. The vast majority of the observations took place between 6 a.m. and 8 a.m. There were also observations (though not during all of them) when, in addition to the atmospheric conditions, we also recorded the presence of microprecipitation (dew, hoar frost) forming on the grass surface.
3. Locations
The country and the locations of the observations can be seen in Figure 1.
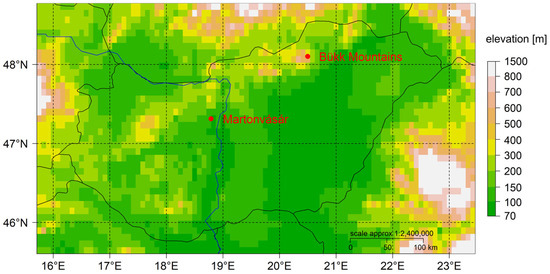
Figure 1.
Topographical map of Hungary (the arrow ↑ points north), Martonvásár (47.3° N, 18.8° E), and Bükk Mountains (48.1° N, 20.5° E), the locations of weather observations during clear-sky mornings.
All observations were conducted in Martonvásár—which is a small lowland town in the Central Transdanubian region of Hungary, about 30 km southwest of Budapest, Hungary—except one observation which was taken in the Bükk Mountains. According to Köppen [7,10], the climate of Martonvásár in the period 1971–2000 is Cfb (C—warm temperate, f—no seasonality in the annual course of precipitation, b—warm summer). In the same period, this climate is characterized by Feddema as “cool, dry, with extreme temperature fluctuations”. Regarding clothing thermal resistance, this climate requires an annual clothing thermal insulation value of 0.4–1 clo [11]. However, the range of rcl values during clear-sky mornings can be much larger than the magnitude of the average annual rcl value.
4. Data
We used anthropometric and weather data. These are briefly described below.
4.1. Anthropometric Data
To parametrize M, we need to know the anthropometric data of the person (body mass, body length, sex, and age). These data are contained in the anthropometric databases. Hungary has such a database, which has continuously been developed for the past decade [37]. It contains anthropometric data of more than 2000 children and more than 1000 adults. The dataset is a product of the Department of Biological Anthropology, Eötvös Loránd University, Budapest, Hungary.
We selected three people from the database, whose anthropometric data were also used in the simulations. Sex was not a consideration when selecting individuals. Our only consideration was that the M and BMI values should be as different as possible. We aimed to ensure that the M and BMI values cover the adult value range of the database as much as possible. The anthropometric data of these persons and the metabolic heat flux density values of walking at a speed of 1.1 m s−1 can be seen in Table 1.
4.2. Weather Data
We used the following meteorological elements for characterizing the thermal load of weather: air temperature, relative sunshine duration, cloud cover, wind gust speed, average wind speed, relative humidity of air, and air pressure. The values of those variables, with the exception of relative sunshine duration and cloudiness, were taken from the HungaroMet website (https://www.met.hu/en/idojaras/aktualis_idojaras/megfigyeles/, accessed on 20 May 2025) and transcribed into the database. We did this immediately after the observation. The observations were carried out randomly without prior preparation. The beeline distance between the station and the observer’s location (the garden of a family house) was shorter than 3 km. Relative sunshine duration and cloudiness were observed. Cloudiness was estimated visually in tenths. These values refer to the same 10 min period as the HungaroMet data. The radiation parameter (Equation (15) in [28]) values are hourly values and refer to the hour in which the observation took place.
The observed elements varied within the following range: the air temperature varied between −12.7 and 22.0 °C (except on 9 August 2020 at 6:45 a.m., when it reached 26 °C). 46% of the temperature values were less than 0 °C. Global radiation varied between 0 and 250 W m−2 but it was greater than 200 W m−2 in 23 cases. The global radiation was equal to 0 in 46 cases (33% of the cases). Cloud cover varied between 0 and 0.2. It was 0.2 in eleven cases and 0.1 in seven cases. The relative humidity of the air was usually between 70 and 100%, a few times between 60 and 70% and only once 54%. In the vast majority of the cases, the wind speed was low (less than 1.5 m s−1). The average wind speed was greater than 1.5 m s−1 in approximately 20% of the cases and it was greater than 3 m s−1 in only four cases. The observed data along with the simulated meteorological variables and thermal loads are included in Table S1.
5. Results
5.1. The M–BMI Relationship
The M–BMI pair of values characterizing a person’s state is human-specific. Therefore, M–BMI value pairs can be used to analyze the interpersonal variability among people. The point cloud of M–BMI relationship for walking (walking speed is 1.1 m·s−1) men and women, based on the use of data from the Hungarian anthropometric database [37], is shown in Figure 2.
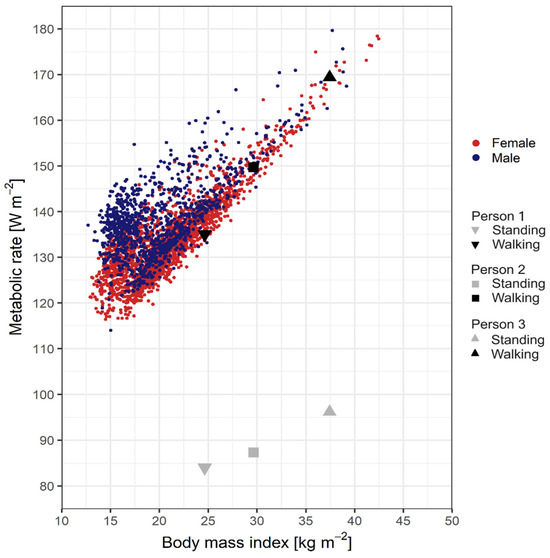
Figure 2.
The M–BMI point cloud for walking men (blue) and women (red). The three black (for walking) and grey (for standing) points represent the persons (males) whose anthropometric data are used in the model simulations. Sources of the data: [37].
The following relationships and basic information can be seen: (1) The M–BMI point clouds of walking men and women overlap, but men’s M values are somewhat larger than women’s M values. (2) For pedestrians, M increases with increasing BMI. (3) The rate of increase is maximum (30 W m−2/15 kg m−2), which is 2 W kg−1. Person 1 is represented with a triangle directed downwards in Figure 2. His M value during walking at a speed of 1.1 m s−1 is 135 W m−2. Person 1 was chosen because his M–BMI point (M = 135 W m−2, BMI = 24.4 kgm−2) is about in the middle of the M–BMI point cloud. It should also be noted that the M value of person 1 while walking is very close to the M value of the “standard human” while walking used in the PET (Physiologically Equivalent Temperature) and UTCI (Universal Thermal Climate Index) indices. These M values are 135, 141.3, and 144.2 Wm−2 for person 1, PET, and UTCI indices, respectively.
5.2. Thermal Load of the Weather During Cloud-Free Mornings
The rcl–To point cloud for cloud-free mornings for person 1 walking at a speed of 1.1 m s−1 can be seen in Figure 3.
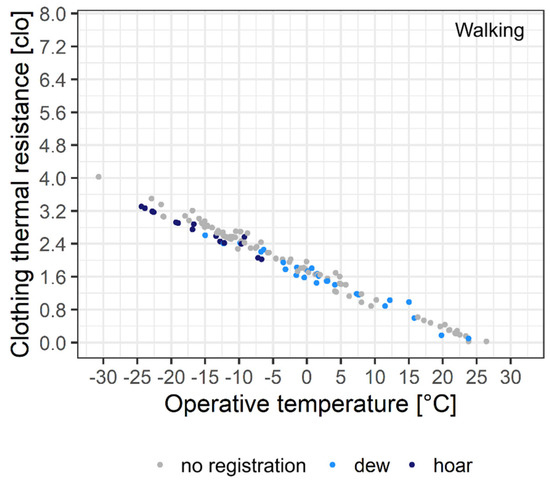
Figure 3.
rcl–To point cloud for clear–sky mornings for person 1 walking at a speed of 1.1 m s−1. No registration means that no microprecipitation was observed.
The rcl values varied between 0 and 3.5 clo, the corresponding To variation is between 27 and −25 °C. The annual value of the rcl in the lowlands is 0.6–0.8 clo, so the annual fluctuation of the rcl values of mornings with clear skies is five times the average annual value. In cases of the smallest heat deficit (near 0 clo), the thermal sensation is “neutral”, while in cases of the greatest heat deficit, the thermal sensation is “very cold” [22]. It should be emphasized that the thermal sensation type “slightly warm” does not occur even in cases of the smallest heat deficits. We cannot say anything for certain about the frequency distribution of rcl values, since the number of registered cases is smaller than the number of realized cases. We also have a point with a value of 4.1 clo (the associated To value is −30.7 °C), which refers to the Bükk Mountains and not to Martonvásár. We will refer to this point later in Section 6. It can be observed that the mornings with the formation of dew and hoar frost are separate, although we also had cases of dew in the case of To < 0 °C. In cases involving the formation of hoar frost, the smallest observed heat deficit was around 1.8 clo. This lack of heat causes people to feel either “cold” or “very cold” [22].
5.3. Sensitivity of the rcl–To Relationship to Human Activity
The sensitivity of the rcl–To point cloud to human activity will be estimated based on the comparison of the rcl–To point clouds of standing (less M value) and walking (greater M value) people. The rcl–To point cloud for standing person 1 can be seen in Figure 4.
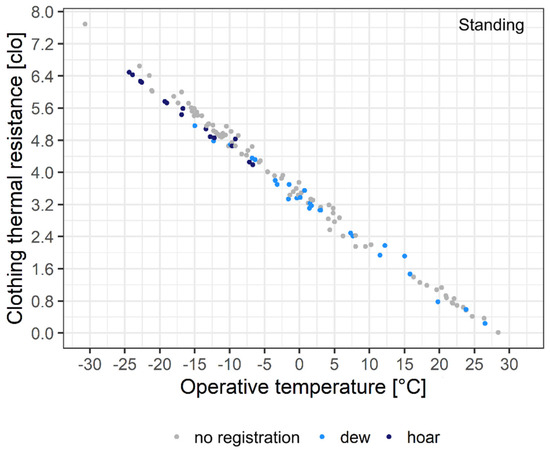
Figure 4.
rcl–To point cloud for clear–sky mornings for standing person 1.
Comparing Figure 3 and Figure 4, we can see that the marked difference between the two figures is in the slope of the point arrangement. In the case of standing person 1, the rcl values varied between 0 and 6.8 clo, and the corresponding To values between 28 and −25 °C (this is the same as the To limits shown in Figure 2). The rcl differences between a standing and a walking person increase linearly with increasing heat deficit. In cases of the smallest heat deficits (close to 0 clo), this difference is only a few tenths of a clo, in cases of the largest heat deficits (thermal sensation type “very cold”) the difference is around 3 clo; that is, approximately as big as the annual fluctuation of the rcl values of person 1. From this point of view, rcl sensitivity to activity is very high.
5.4. Sensitivity of rcl to Interpersonal Variability of M
Each rcl–To point cloud is human-specific; since people have different M values, the faster they walk, the better. The slope of the rcl–To point clouds is different; the smaller the value of M, the higher the slope, and conversely, the larger the value of M, the smaller the slope. Based on the Hungarian anthropometric database, the maximum change in M per 1 kg is 2 W. The sensitivity of rcl to personal changes in M was also analyzed by comparing the rcl values of the three persons. This comparison can be seen in Figure 5.
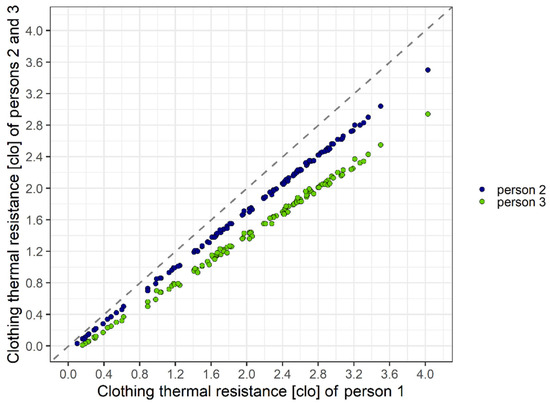
Figure 5.
Comparison of clothing thermal resistance values referring to persons 2 and 1 (blue) and persons 3 and 1 (green). The humans are walking at a speed of 1.1 m s−1.
The largest rcl differences are between persons 3 and 1 (31 kg difference in body mass); they reach 0.8–1 clo values. Note that these rcl differences are much less than the rcl differences between the standing and walking humans. In the case of small heat deficits (“neutral” thermal sensation [22]), the rcl differences are small (a few tenths of a clo value). They grow as the lack of heat increases.
6. Discussion
To the best of our knowledge, there has been no human thermal load study of the morning hours of the day when anticyclonic weather conditions prevailed in the Köppen climate type Cfb. We conducted our observations in the morning and during anticyclonic weather conditions because this is when the greatest environmental heat deficits occur, regardless of the season. We characterized the types of thermal sensation based on the thermal perception of person 1, who is native to the Cfb climate of Central Europe and has a near mesomorphic body type. It should be noted that the body type of a “standard human” is closest to the mesomorphic body type [38]. More information about the thermal perception data of person 1 can be found in the work of Ács et al. [22]. The thermal load of the Cfb climate is determined by its cyclonic and anticyclonic events. Anticyclonic weather increases the heat deficit on winter nights and the heat surplus on summer days. In contrast, cyclonic weather reduces the heat deficit on winter nights and the heat surplus on summer days. Extreme thermal loads are associated with anticyclones. The human thermal load values associated with cyclonic and anticyclonic weather conditions in the Cfb climate are still unknown; this topic is unexplored and new. This work is intended to partially fill this gap [28,30].
It is not an easy task to estimate the human thermal load, because we need to have both meteorological and human data. Among the meteorological data, radiation and wind show the greatest variability. Their estimation is also much more complicated than that of other weather elements. At the same time, their role in the environmental thermal load is very significant [30]. The variability of the human data (activity, clothing, anthropometric data) is greater than that of the meteorological data, and they are important in the changes in the value of M and the rate of sweating. In this work, by definition, we focus on the sensitivity of M to activity and personal variability. The dependence of M on activity is significant (the difference between the M values of standing and walking persons is around 60 W m−2, see Figure 2), so the related rcl changes are also significant (in the largest recorded heat deficit, it is around 3 clo, see Figure 3 and Figure 4). The interpersonal changes of M, even in the case of a walking person, are much smaller than the M-difference values between walking and standing people (see Figure 2). In the BMI range of 15–30 kg m−2, the largest M differences are around 30 W m−2; if we divide this by the mean of M (it is around 135 W m−2), then the variability of M can be estimated at 20 percent. We can say that this variability of M is half the size (25 W m−2) of the difference between the M values of the selected walking and standing persons (50–60 Wm−2). The rcl changes caused by the mentioned interpersonal M changes are around 1 clo, when the heat deficit is greatest (operative temperature is around −24 °C). That is, in the case of the largest heat deficits, the individual rcl values vary between 3 and 4 clo in the clear-sky morning for a person walking at a speed of 1.1 ms−1. Note that the value of 4 clo already approaches the heat deficit values occurring in the Hungarian mountains (Bükk Mountains) in the case of a walking person (Figure 3). We also emphasize that interpersonal rcl differences decrease with decreasing heat deficit and become practically negligible when the heat deficit is small [31]. It should also be mentioned that the most popular human thermal load models use the concept of the “standard human”, and therefore do not even simulate or analyze the sensitivity of thermal load to interpersonal changes [39,40,41,42,43,44].
As has been mentioned, anticyclonic weather conditions are associated with extreme human thermal loads [27]. The main cause of extreme thermal loads is a cloudless sky. It enables high insolation during midday hours and less downward atmospheric radiation at night, so large heat deficits develop in the morning. Based on our results, in the case of a person walking at a speed of 1.1 ms−1, the largest heat deficits are between 3 and 4 clo, and in the case of a standing person, they can be greater than 6 clo. Based on the results of Ács et al. [22], in cases of such a large heat deficit, the thermal sensation type is “very cold”. In the case of the smallest heat deficits, the rcl values are around 0–0.7 clo, which causes a “neutral” thermal sensation in people. It is to be underlined that there is no “warm” type among the types of human thermal sensations in cloudless morning hours during the year. This fact also proves that the climate of the lowland areas of the Carpathian region can be characterized as a “cool”/”cold” climate.
The rcl model is new, and the idea is taken from Holmér’s work [29]. It differs from Holmér’s IREQ-type model [29] in two fundamental ways: (1) rcl does not depend on the surface temperature of the clothing (Tcl), but on environmental factors, (2) the value of metabolic heat flux density (M) is not constant, but human-specific. The model used is simple, since it determines rcl in a non-iterative way, but at the same time, since it parametrizes M, it is also suitable for simulating interpersonal thermal load changes. Since we examined a cloudless sky, we also analyzed the sensitivity of the rcl values to different parametrizations of the clear-sky emissivity. The tested sensitivity is small, so we decided not to present the results. We will use this model to characterize the thermal load of other typical weather situations as well.
7. Conclusions
The human thermal load of cloudless mornings observed in the Cfb climate of the Hungarian lowland was characterized using the rcl–To model. The model simulates personal M values as a function of the person’s anthropometric data (body mass, body length, sex, and age) for standing or walking humans. The main conclusions of the study are as follows: (1) The morning weather of Cfb climates, when the sky is clear, causes a lack of heat even in the summer. (2) Human variability has a smaller impact on the variability of rcl values than the type of activity. (3) As the heat deficit increases, the interpersonal variability of rcl increases, too, and conversely, as the heat deficit decreases, the interpersonal variability of rcl decreases. (4) Customized individual models are not so complex that they should not be preferred over models that use the concept of a “standard human”.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16060647/s1, Table S1. Model input data, simulated meteorological variables and thermal load values estimated by the model.
Author Contributions
Conceptualization, F.Á.; methodology, F.Á. and A.Z.; software, F.Á. and E.K.; validation, F.Á.; formal analysis, F.Á.; investigation, F.Á., E.K. and A.Z.; resources, F.Á., E.K. and A.Z.; data curation, F.Á. and A.Z.; writing—original draft preparation, F.Á.; writing—review and editing, E.K. and A.Z.; visualization, E.K.; supervision, F.Á.; project administration, F.Á.; funding acquisition, F.Á. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Inquiries concerning data can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Radinović, D. Weather Analysis; Institute for Publishing Textbooks of the Socialist Republic of Serbia: Belgrade, Serbia, 1968; 367p. (In Serbian) [Google Scholar]
- Szász, G. Agrometeorological research and its results in Hungary (1870–2010). Időjárás 2013, 117, 315–358. [Google Scholar]
- Bianca, W. The significance of meteorology in animal production. Int. J. Biometeorol. 1976, 20, 139–156. [Google Scholar] [CrossRef]
- Mohan, M.; Gupta, A.; Bhati, S. A Modified Approach to Analyze Thermal Comfort Classification. ACS 2014, 4, 7–19. [Google Scholar] [CrossRef][Green Version]
- de Freitas, C.R.; Grigorieva, E.A. A comprehensive catalogue and classification of human thermal climate indices. Int. J. Biometeorol. 2015, 59, 109–120. [Google Scholar] [CrossRef]
- HungaroMet. 2024. Available online: https://www.met.hu/idojaras/humanmeteorologia/ (accessed on 5 September 2024). (In Hungarian).
- Köppen, W. The geographic system of climates (original: Das geographische system der Klimate). In Handbuch der Klimatologie, Bd.1, Teil C; Köppen, W., Geiger, R., Eds.; Borntraeger: Berlin, Germany, 1936; 44p. [Google Scholar]
- Németh, Á. Changing thermal bioclimate in some Hungarian cities. Acta Climatol. et Chorol. Univ. Szeged. 2011, 44–45, 93–101. [Google Scholar]
- Gulyás, Á.; Matzarakis, A. Seasonal and spatial distribution of physiologically equivalent temperature (PET) index in Hungary. Időjárás 2009, 113, 221–231. [Google Scholar]
- Ács, F.; Zsákai, A.; Kristóf, E.; Szabó, A.I.; Breuer, H. Carpathian Basin climate according to Köppen and a clothing resistance scheme. Theor. Appl. Climatol. 2020, 141, 299–307. [Google Scholar] [CrossRef]
- Ács, F.; Zsákai, A.; Kristóf, E.; Szabó, A.I.; Feddema, J.; Breuer, H. Clothing Resistance and Potential Evapotranspiration as Thermal Climate Indicators—The Example of the Carpathian Region. Int. J. Climatol. 2021, 41, 3107–3120. [Google Scholar] [CrossRef]
- Bašarin, B.; Lukić, T.; Matzarakis, A. Quantification and assessment of heat and cold waves in Novi Sad, Nothern Serbia. Int. J. Biometeorol. 2016, 60, 139–150. [Google Scholar] [CrossRef]
- Bašarin, B.; Lukić, T.; Matzarakis, A. Review of Biometeorology of Heatwaves and Warm Extremes in Europe. Atmosphere 2020, 11, 1276. [Google Scholar] [CrossRef]
- Lukić, M.; Filipović, D.; Pecelj, M.; Crnogorac, L.; Lukić, B.; Divjak, L.; Lukić, A.; Vučićević, A. Assessment of Outdoor Thermal Comfort in Serbia’s Urban Environments during Different Seasons. Atmosphere 2021, 12, 1084. [Google Scholar] [CrossRef]
- Unger, J.; Skarbit, N.; Kovács, A.; Gál, T. Comparison of regional and urban outdoor thermal stress conditions in heatwave and normal summer periods: A case study. Urban Clim. 2020, 32, 100619. [Google Scholar] [CrossRef]
- Kovács, A.; Németh, Á. Tendencies and differences in human thermal comfort in distinct urban areas in Budapest, Hungary. Acta Climatol. Chorol. Univ. Szeged. 2012, 46, 115–124. [Google Scholar]
- Gulyás, Á.; Matzarakis, A.; Unger, J. Differences in the thermal bioclimatic conditions on the urban and rural areas in a Southern Hungarian city (Szeged). Ber. Des Meteorol. Inst. Der Albert Ludwigs Univ. Freiburg. 2009, 18, 229–234. [Google Scholar]
- Unger, J.; Gulyás, Á.; Matzarakis, A. Effects of the different inner city micro-environments on the human bioclimatological comfort sensation. Légkör 2005, 50, 9–14. (In Hungarian) [Google Scholar]
- Kántor, N.; Gulyás, Á.; Égerházi, L.; Unger, J. Complex human comfort studies in urban environment—Part II. Légkör 2010, 55, 115–126. (In Hungarian) [Google Scholar]
- Páldy, A.; Bobvos, J.; Vámos, A.; Kováts, R.S.; Hajat, S. The effect of temperature and heat waves on daily mortality in Budapest, Hungary, 1970–2000. In Extreme Weather Events and Public Health Responses; Kirch, W., Menne, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 99–107. [Google Scholar]
- Kántor, N.; Égerházi, L.; Unger, J. Subjective estimation of thermal environment in recreational urban spaces–Part 1: Investigations in Szeged, Hungary. Int. J. Biometeorol. 2012, 56, 1089–1101. [Google Scholar] [CrossRef]
- Ács, F.; Kristóf, E.; Zsákai, A. Individual local human thermal climates in the Hungarian lowland: Estimations by a simple clothing resistance-operative temperature model. Int. J. Climatol. 2023, 43, 1273–1292. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970; 244p. [Google Scholar]
- Yang, S.Q.; Matzarakis, A. Implementation of human thermal comfort and air humidity in Köppen-Geiger climate classification and importance towards the achievement of Sustainable Development Goals. Theor. Appl. Climatol. 2019, 138, 981–998. [Google Scholar] [CrossRef]
- Yang, S.Q.; Matzarakis, A. Implementation of human thermal comfort information in Köppen-Geiger climate classification— the example of China. Int. J. Biometeorol. 2016, 60, 1801–1805. [Google Scholar] [CrossRef]
- Błażejczyk, K.; Baranowski, J.; Jendritzky, G.; Błażejczyk, A.; Bröde, P.; Fiala, D. Regional features of the bioclimate of Central and Southern Europe against the background of the Köppen-Geiger climate classification. Geographia Polonia 2015, 88, 439–453. [Google Scholar] [CrossRef]
- Ustrnul, Z.; Czekierda, D.; Wypych, A. Extreme values of air temperature in Poland according to different atmospheric circulation classifications. Phys. Chem. Earth Pt A/B/C 2010, 35, 429–436. [Google Scholar] [CrossRef]
- Kristóf, E.; Ács, F.; Zsákai, A. On the Human Thermal Load in Fog. Meteorology 2024, 3, 83–96. [Google Scholar] [CrossRef]
- Holmér, I. Assessment of cold stress in terms of required clothing insulation—IREQ. Int. J. Ind. Ergon. 1988, 3, 159–166. [Google Scholar] [CrossRef]
- Ács, F.; Szalkai, Z.; Kristóf, E.; Zsákai, A. Thermal Resistance of Clothing in Human Biometeorological Models. Geogr. Pannonica 2023, 27, 83–90. [Google Scholar] [CrossRef]
- Ács, F.; Zsákai, A.; Kristóf, E.; Szabó, A.; Breuer, H. Human thermal climate of the Carpathian Basin. Int. J. Climatol. 2021, 41, E1846–E1859. [Google Scholar] [CrossRef]
- Mifflin, M.D.; St Jeor, S.T.; Hill, L.A.; Scott, B.J.; Daugherty, S.A.; Koh, Y.O. A new predictive equation for resting energy expenditure in healthy individuals. Am. J. Clin. 1990, 51, 241–247. [Google Scholar] [CrossRef]
- Dubois, D.; Dubois, E.F. The measurement of the surface area of man. Arch. Intern. Med. 1915, 15, 868–881. [Google Scholar] [CrossRef]
- Weyand, P.G.; Smith, B.R.; Puyau, M.R.; Butte, N.F. The mass-specific energy cost of human walking is set by stature. J. Exp. Biol. 2010, 213, 3972–3979. [Google Scholar] [CrossRef]
- Amaro-Gahete, F.J.; Sanchez-Delgado, G.; Alcantara, J.M.A.; Martinez-Tellez, B.; Acosta, F.M.; Merchan-Ramirez, E.; Löf, M.; Labayen, I.; Ruiz, J.R. Energy expenditure differences across lying, sitting, and standing positions in young healthy adults. PLoS ONE 2019, 14, e0217029. [Google Scholar] [CrossRef]
- Júdice, P.B.; Hamilton, M.T.; Sardinha, L.B.; Zderic, T.W.; Silva, A.M. What is the metabolic and energy cost of sitting, standing and sit/stand transitions? Eur. J. Appl. Physiol. 2016, 116, 263–273. [Google Scholar] [CrossRef] [PubMed]
- Fehér, V.P.; Annár, D.; Zsákai, A.; Bodzsár, É. The determinants of psychosomatic health complaints in 18–90 year-old women. Anthr. Közlemények 2019, 60, 65–77. (In Hungarian) [Google Scholar] [CrossRef]
- Bröde, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar]
- Matzarakis, A.; Mayer, H.; Iziomon, M.G. Application of a universal thermal index: Physiological equivalent temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Bröde, P.; Fiala, D.; Błażejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the operational procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef]
- Blazejczyk, K.; Krawczyk, B. Bioclimatic Research of the Human Heat Balance; Institute of Geography & Spatial Organisation, Polish Academy of Science: Warsaw, Poland, 1994; p. 28. [Google Scholar]
- Matzarakis, A.; Mayer, H. Another kind of environmental stress: Thermal stress. WHO Newsl. 1996, 18, 7–10. [Google Scholar]
- Fiala, D.; Havenith, G.; Bröde, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala multi-node model of human heat transfer and temperature regulation. Int. J. Biometeorol. 2011, 56, 429–441. [Google Scholar] [CrossRef]
- Lin, T.P.; Matzarakis, A. Tourism climate and thermal comfort in Sun Moon Lake, Taiwan. Int. J. Biometeorol. 2008, 52, 281–290. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).