Abstract
A cyclonic ocean eddy (COE) exhibited an extraordinarily prolonged response to sequential typhoons Hinnamnor (1 September 2022) and Muifa (11 September 2022), reaching its peak strength 20 days post-typhoon (1 October 2022), almost double the typical 7–14-day latency for mesoscale eddies. In this study, we use a functional analysis apparatus, namely the multiscale window transform (MWT) and the MWT-based theory of canonical transfer and multiscale energetics analysis, to investigate the dynamics underlying this phenomenon. The original fields, which are obtained from HYCOM reanalysis data, are initially decomposed into three parts in three different scale windows, respectively, with the eddy-scale window (or COE window) lying in between. By examining the evolution of eddy kinetic energy (EKE), the response can be divided into two stages. From the energetic diagnosis, the COE’s response is not only visible at the surface but was even strengthened through interactions between the subsurface and surface, with vertical transport playing a crucial role. This response can be categorized into two stages: The energetics of the long-delayed response is in the first stage due to the storage of the eddy-scale available potential energy (EAPE) from the high-frequency scale window, where the typhoon injects energy through an inverse canonical transfer. The resulting EAPE is transported downward to the sub-surface. In the second stage, the subsurface EKE is carried upward to the surface via pressure work, leading to an explosive growth of the COE. These findings illuminate the significance of subsurface–surface interactions in modulating long-delayed eddy responses.
1. Introduction
It is well known that the upper ocean is influenced by tropical cyclones (TCs). As one of the most devastating meteorological systems [1], tropical cyclones can trigger violent disturbances in the upper ocean. The most notable phenomenon is the subsequent drop in sea surface temperature (SST) along a TC track. This kind of surface cooling is asymmetric and intense on the right-hand side following the track [2,3,4,5]. The primary mechanism for cooling is ocean vertical mixing associated with entrainment and upwelling, which can be induced by Ekman pumping caused by wind stresses [6,7,8,9].
Besides SST cooling, another well-known influence of TCs is their impact on the oceanic eddies in the upper ocean [10,11,12]. As expected, the cyclonic ocean eddy (COE) might be amplified and intensified, deformed into an ellipse, and subsequently readjusted to be circular, while the anticyclonic ocean eddy component (AOE) might be weakened or dissipated [13,14,15]. Specifically, typhoons usually affect COEs at the inertial frequency by inducing and breaking near-inertial internal waves, subsequently enhancing vertical mixing [16,17,18,19]. Secondly, the geostrophic response induced by a typhoon can inject positive relative vorticity into the thermocline to enhance the COE, and the ocean reacts directly to the input of vorticity [14,19,20]. In addition, both baroclinic and barotropic instability influence the COE’s variability [21,22]. All the processes essentially occur as soon as a TC passes; they form the instantaneous response mechanism of the ocean.
However, in September 2022, a COE in the northwestern Pacific was observed to reach its maximum energy after a very long time since the TC’s passage. This counterintuitive phenomenon has been identified for counterparts with much shorter delays. Typhoons Hagibis and Mitag caused substantial increases in the diameter and area of pre-existing COEs, which peaked 7 days after the typhoon event [10]. The maximum drop in the sea surface height anomaly (SSHA) of the COE was about 8 cm after 2 weeks compared with the pre-typhoon condition [11]. The SSHA of the COE decreased immediately after the arrival of Typhoon Namtheun and reached its maximum 8 days later via remote sensing and Argo floats [23]. However, how they are generated is still unclear. Particularly, their generation dynamics have not been investigated.
In this study, we aim to address this problem using a newly developed multiscale analysis tool, namely the multiscale window transform (MWT), and the MWT-based energetics analysis methodology. This investigation concerns the passage of the super typhoons Hinnamnor and Muifa in September 2022 and a pre-existing COE located along their trajectory. We first briefly introduce the MWT and the MWT-based methodology and the data used for this study in Section 2. In Section 3, a multiscale analysis of the related fields and the response of the designated COE to the passage of the typhoons is studied, and the underlying mechanism is explained. This study is summarized in Section 4.
2. Materials and Methods
2.1. Methods
In this study, we used a new functional analysis tool, the multiscale window transform [24], the MWT-based theory of canonical transfer, and the associated multiscale energy and vorticity analysis, or MS-EVA for short [25], to explore the dynamical processes underlying the delayed ocean response to the passage of Typhoons Hinnamnor and Muifa. The theory and methodology have successfully been applied to the studies of many important atmospheric and oceanic processes [26,27]. Here, we briefly introduce the concepts and list a few of the mathematical expressions needed. The details can be seen in many publications, such as [25,27,28,29], to name but a few.
Traditionally, filters have been used to decompose a field by scale. One of the problems is that the output of a classical filter (i.e., the filtered field) is only a reconstruction in functional analysis; it does not output something like the transform coefficient in Fourier analysis or the Fourier coefficient. So, classical filters cannot be used to study multiscale energetics, which are essentially the product of two Fourier coefficients. This problem has not been fixed until Liang and Anderson, who found that there exists a type of specially devised “filter”, or multiscale window transform (MWT), as they called it, which will output both reconstructions and transform coefficients [24]. With the MWT, a function space can be decomposed into a direct sum of the orthogonal subspaces in the frequency domain, termed the “scale window” or simply, the window.
For instance, given a time series u(t), if we consider a three-scale window decomposition, it can be reconstructed as follows:
with the notations = 0, 1, and 2, respectively, signifying the background flow window, the mesoscale window, and the high-frequency submesoscale window. is the reconstruction of u on window , which is defined by
where
The is a localized scaling basis, j is the wavelet scale level, and n is the discrete time step in the sampling space. Equations (2) and (3) are the multiscale window reconstruction (MWR) and its peer, MWT, respectively. The former can be considered as the filtering field in the traditional sense, while the latter is the corresponding transform coefficient, denoted as (in MSEVA, the subscript n is usually omitted, ). The time-dependent energy on window proves to be the square of the transform coefficients, i.e., [24]. Note that it is by no means trivially the square of the reconstructed (filtered) field, i.e., , as commonly used in the literature. For more details on the multiscale energy presentation, please refer to [24].
Within the MWT framework, the multiscale KE and APE on window ( = 0,1,2) can be expressed as
where is the two-dimensional horizontal velocity vector, denotes the MWT of on scale window (similar for ). Among the other symbols, g is the acceleration due to gravity, is the constant reference density (=1025 kg/m3), ρ denotes the density anomaly, calculated as the instantaneous density minus the horizontally and temporally averaged reference density state, denotes the MWT of ρ on scale window , and N is the buoyancy frequency.
The equations of KE and APE on window have been derived [25]. Here they are symbolically written as
The term () on the right side of Equations (6) and (7) represents the nonlocal transport of () induced by advection while represents the rate of work done by the pressure fluctuations. The vertical nonlocal processes (, and ) have been previously found to be essential to couple the eddy energetics between the upper and deep layer in the ocean [21,26,30]. has long been recognized as an important mechanism for the spatial redistribution of eddy KE both in the atmosphere [31,32] and the ocean [33,34,35]. The term is the buoyancy conversion from to . The () term represents all the effects of external forcing (such as wind/bottom stress) and frictional dissipation. All the definitions and meanings for the above terms are listed in Table 1. A detailed derivation of the formulas is referred to in detail [25].

Table 1.
Expressions of the MS-EVA terms in Equations (6) and (7). (:) is the colon (double dot) product of two dyads [25]. The other notations are conventional.
In the above, the terms represent the cross-scale transfer processes. In this framework, they satisfy an important conversation law [25]:
where and are the summation over all the sampling time steps n and scale windows , respectively. This equation states that the transfer process is a redistribution of energy among the scale windows, without generating or losing energy as a whole. This property does not hold in traditional energetics formalisms. To distinguish this, Γ has hence been termed “canonical transfer” [25].
The terms and in Equations (6) and (7) represent the canonical transfer of KE and APE to the window , respectively. They can be further decomposed to select out the transfer from a specific the window, say, , to the window in the three-scale window framework. Here we just write it symbolically as and , respectively [30,31]. For instance, we use superscript like 0→1 to signify such interactions; the canonical transfer of KE (APE) from the background flow window ( = 0) to the mesoscale eddy window ( = 1) is denoted as (). A positive () means a release of the background flow KE (APE), which is associated with barotropic (baroclinic) instability [24]. Similarly, the scale interaction between the submesoscale eddy and the mesoscale eddy is quantified by and . A positive () means an inverse temporal cascade of KE (APE) from the submesoscale eddies to the mesoscale eddies.
2.2. Data
We use the West North Pacific Ocean Best Track Data of six-hourly derived from the China Meteorological Administration (CMA) to obtain the best track for Typhoons Hinnamnor and Muifa. The CMA Tropical Cyclone Best Track Data were obtained from https://tcdata.typhoon.org.cn/ accessed on 1 April 2025 [36,37]. Typhoon Hinnamnor was generated at 0600 UTC on 28 August 2022 and began to enter the study area on 1 September 2022. Typhoon Muifa was generated at 0000 UTC on 8 September 2022 and began to enter the COE area on 11 September 2022.
The model outputs from the Hybrid Coordinate Ocean Model (HYCOM) are used for the ocean response study. They can be downloaded from the website https://hycom.org accessed on 1 April 2025. In this study, the daily outputs from 3 January 2022 to 29 May 2023 are used, which have a time span of 512 days in total, meeting the requirement for MWT analysis that the number of time steps should be a power of 2.
To validate that the response of the COE can be captured by the HYCOM reanalysis output in the study region, we also use the altimetry data from Archiving, Validation, and Interpretation of Satellite Oceanographic data (AVISO) with the same duration. By our result, the dataset with a daily time interval on a 1/4° × 1/4° grid is capable of detecting most of the mesoscale eddies in the ocean [38].
3. Results
3.1. MS-EVA Setup and Multiscale Window Reconstruction
The study area, i.e., the COE area, lies within 15–30° N, 114–130° E, on the track of Typhoon Hinnamnor, which was generated at 0600 UTC 28 August 2022 and began to enter the study area on 1 September 2022, and that of Typhoon Muifa, which was generated at 0000 UTC 8 September 2022 and entered the area on 11 September 2022.
The demarcation of the three scale windows is about the time domain. Previous studies have shown that the COEs in the Northwestern Pacific Ocean generally have an average lifetime of 11 weeks [22]. To determine the cutoff frequency for the COE activity, we plot in Figure 1a the surface geostrophic kinetic energy (KE) power spectra averaged over the study area (114–130° E, 15–30° N). Notable concentrations of elevated kinetic energy spectra are observed in two distinct ranges: below 16 days and between 16–256 days. This distribution pattern aligns with findings from MSEVA studies on mesoscale eddies in regions like the Kuroshio and Luzon Strait [39,40]. Consequently, we adopt the same scale separation scheme. The processes with periods longer than 256 days are defined as the background flow, which includes the Kuroshio and other large-scale processes. The mesoscale eddy window is chosen to be bounded by the cutoff periods of 16 and 256 days. This is the COE window. Processes with periods shorter than 16 days are taken as the submesoscale window. It includes those with time scales of the typhoon and other high-frequency processes. To examine the KE evolution of the COE based on two data sets, we compared the surface COE kinetic energy time evolutions after the Typhoons Hinnamnor and Muifa passed. Figure 1b shows the time series of surface COE kinetic energy averaged over the study area based on AVISO (red line) and HYCOM (blue line) data sets. The two sets have similar trends and get to peak at the same time, suggesting that the HYCOM output is reliable for our purpose, albeit with a slightly stronger amplitude.
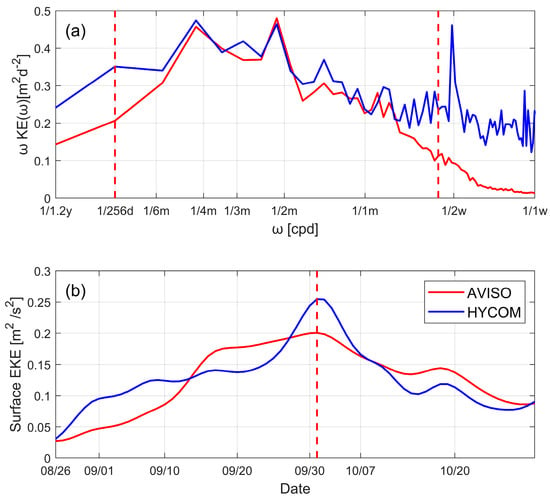
Figure 1.
(a) Variance-preserving frequency spectra of KE averaged over the whole area (15–30° N, 114–130° E) based on AVISO (solid red line) and HYCOM (solid blue line). Symbols d, m, and w at the x-axis are day, month, and week, respectively. The dashed red lines denote the periods of 16 and 256 days, respectively. (b) Surface EKE time series averaged over the region as marked within 15–30° N, 114–130° E from AVISO (solid red line) and HYCOM (solid blue line).
Figure 2 shows the original sea surface height anomalies (SSHA) fields on 1 September (left column) and 11 September (right column), and their reconstructions on the mesoscale window and submesoscale window, respectively. The features generally agree with what one would expect. In the following, we focus on the mesoscale eddy evolution.
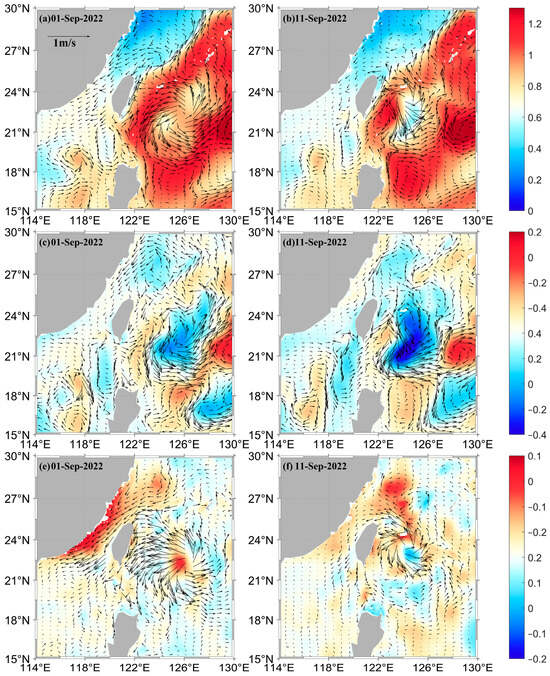
Figure 2.
The snapshots of SSHA (m) on 1 September 2022 (left column) and 11 September 2022 (right column). The first row represents the original SSHA field and the surface current velocity (arrows; m/s) simulated by HYCOM; the second and third columns represent the SSHA fields and the surface current vectors reconstructed by MWT on the mesoscale window and submesoscale window, respectively.
Figure 3 displays the evolution of the COE in response to Typhoons Hinnamnor and Muifa. From it, we can see that the COE located at 22.5° N, 125.5° E (shown in the closed contour in Figure 3) encountered Typhoons Hinnamnor and Muifa on 1 September 2022 and 11 September 2022, respectively, in the Western Pacific Ocean (Figure 3b,c). The Typhoon Hinnamnor and Muifa left the COE on 3 September 2022 and 12 September 2022, respectively. The best tracks of the two typhoons are shown in Figure 3b,c. The COE was enhanced and enlarged, and its amplitude increased after the typhoons passed. Moreover, it was through a deformation to an ellipse and was then readjusted to a circular form (Figure 3h), consistent with previous studies [15]. These processes are defined as elliptical deformation and reaxisymmetrization, and they are caused by horizontal current shear or strain and geostrophic adjustment [41]. The spatial evolution of the COE in Figure 3 also shows that its position almost stayed invariant during the deformation process within the region from 21° N to 24° N and 122° E to 126° E (Figure 3c–f), but gradually moved towards northwest after being transformed into a circular and more stable form (Figure 3g–i).
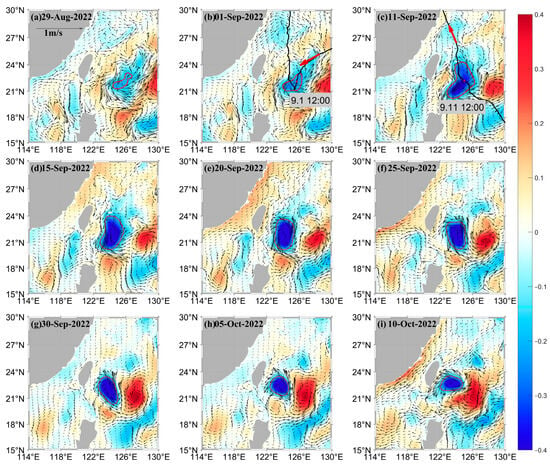
Figure 3.
The evolution of the COE maps of surface currents (arrows; m/s) and sea surface height anomalies (SSHA; shadings; m), calculated from HYCOM, is shown in images (a–i), which correspond to the following dates: (a) 29 August 2022, (b) 1 September 2022, (c) 11 September 2022, (d) 15 September 2022, (e) 20 September 2022, (f) 25 September 2022, (g) 30 September 2022, (h) 5 October 2022, and (i) 10 October 2022. The tracks of Typhoons Hinnamnor and Muifa are shown in panels (b) and (c), respectively. Red lines indicate closed contours where SSHA is less than −0.2 m, and red arrows represent the direction of typhoon movement.
One observation is that the COE did not cease to grow after the typhoon passed. Its amplitude had kept increasing, reaching its maximum 20–30 days later after the passage of the typhoon. This is counterintuitive, as usually the delay does not exceed two weeks. In the following, we will focus on this phenomenon.
First, take a look at the energy evolution on the COE window. We average the eddy-scale KE and APE, or EKE and EAPE for short, over the COE area, where the SSHA is less than −0.2 m. Figure 4a shows the vertical structure of the averaged EAPE after the passage of the two typhoons. The surface EAPE is through a significant growth, and extending to a depth as deep as 40 m and 60 m, respectively, after each typhoon’s passage, indicating that the typhoons inject energy into the upper layer of the ocean, leading to an increase in the potential energy of the surface layer (Figure 4a) as the mixed layer deepens. This is generally in agreement with previous studies, in which the surface APE increases with the TC-induced upwelling and vertical mixing [42,43,44]. Another observation is that, in the meantime, the sub-surface layer EAPE intensified gradually, while the surface layer EAPE was diminishing (Figure 4a,c; in blue dashed line).
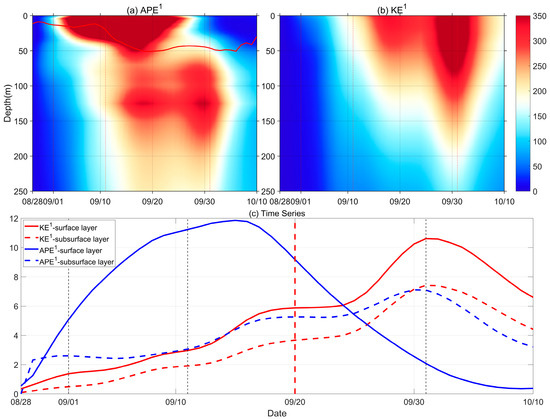
Figure 4.
(a,b) Vertical distribution of the COE area-averaged EAPE (a) and EKE (b) (shadings, units:). The red line represents the mixed layer depth (MLD). (c) Time series of volume-integrated EKE and EAPE averaged over the COE of the surface layer (0–40 m) (solid lines) and sub-surface layer (40–200 m) (dashed lines) based on HYCOM (units:). The red and blue lines are for KE and APE, respectively.
For the KE on the COE window, called EKE henceforth, Figure 4b shows that it began to strengthen slightly after the typhoons passed. It reached its maximum on 1 October and extended to about a depth of 200 m on the 20th day since excited by the typhoons.
According to the different vertical EAPE distributions over time, we divide the profile into two layers, the surface layer (0–40 m) and the sub-surface layer (40–200 m). We integrate the EAPE and EKE, respectively, vertically over the two sublayers and horizontally over the COE, obtaining two time series of the volume-integrated EAPE and EKE for the two sublayers. The series of the surface layer and sub-surface layer is shown in Figure 4c in solid and dashed lines. The EKE of the entire surface layer (0–200 m) undergoes a consistent intensification following the passage of the typhoons (in red) and reaches its peak approximately 20 days after the second typhoon Muifa passed. The results indicate that the EKE peak had been delayed concerning the atmospheric excitation. The surface EAPE exhibits a notable enhancement immediately after the passage of the two typhoons. Subsequently, it rapidly diminished upon the typhoon’s departure, while the EAPE in the sub-surface intensified. However, the total EKE of the surface layer shows no signs of reduction; instead, it continually grows. At the same time, it is seen that the EAPE of the sub-surface layer reached its peak and started to decrease almost simultaneously as the EKE peaked (October 1).
The above conspicuous phenomenon has not been identified in the other two scale windows. One would wonder what causes it and why it occurs on the COE scale window. The following is a dynamic study.
3.2. The Dynamics Study of the COE Evolution
Generally, the surface ocean’s response duration to typhoons correlates with mixed layer depth (MLD) restoration dynamics [1]. However, despite the MLD recovery observed around September 20 (Figure 4a), the kinetic energy of the COE reached its maximum on 1 October 2022. This temporal discrepancy prompts us to demarcate the COE’s evolutionary period at the September 20 threshold, partitioning its development into two distinct stages. The first is from 1 September 2022 to 20 September 2022, and the second is from 21 September 2022 to 30 September 2022. The first stage corresponds to the rapid increase of surface EAPE after the two typhoons just passed. The second stage corresponds to the rapid growth of EKE more than ten days after the typhoons left. These stages have different underlying dynamical processes, as shown in the following.
The variation of the COE can be well characterized by its EKE. Figure 4c shows that the surface EAPE experiences a rapid increase; it then weakens when the subsurface EAPE and the whole surface EKE undergo their first growth. To see the vertical structure more clearly, we present the COE area-integrated energetics budget, as introduced before.
From Figure 4c, we see that the surface EAPE immediately exhibits a rapid growth after the passage of two typhoons. Subsequently, it rapidly diminishes, and the EAPE in the sub-surface layer intensifies. We first examine how the mesoscale eddies are influenced by the submesoscale disturbances caused by the typhoons.
The positive indicates an inverse cascade of the APE from the high-frequency submesoscale processes to the lower-frequency mesoscale eddies. From Figure 5a, shows the short-lived period of positive value through a shallow depth, indicating that APE is transferred from the submesoscale processes to the mesoscale eddy scale, when the COE was disturbed by the two typhoons. The strong mixing generated by the typhoons facilitates the process of baroclinic instability and contributes to the strength of the APE [7,23]. However, the presence of negative values of in the sub-surface, as well as that in the surface a few days after the typhoons passed, indicates that APE is transferred downscale from the mesoscale to the submesoscale processes without the influence from the typhoons. Figure 5b shows that the pattern exhibited positive values in the surface when the COE was disturbed by the typhoons on 1 September 2022 and 11 September 2022. It can be seen that the duration and vertical extension of are greater than those of , indicating that the background flow loses energy to the mesoscale eddy through baroclinic instability. After the passage of the typhoons, becomes negative. That is to say, the baroclinic instability ceases, and the EAPE is now backward to strengthen the basic flow.
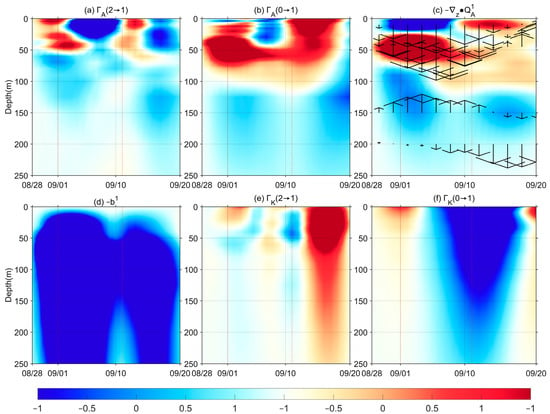
Figure 5.
Time series of the vertical distribution (units: m) of (a) and (b) is canonical transfer of APE, (c) is nonlocal transport of induced by advection, (d) is buoyancy conversion, (e) and (f) is canonical transfer of KE (shadings, units: *10−4 ) integrated over the COE area. The red dotted lines indicate the days when the typhoons passed. The superimposed vectors in (c) is the vertical component of the EAPE flux. The definitions of these variables are referred to in Equations (6) and (7).
Figure 5a,b show that both the transfer of APE from the submesoscale processes and the background flow impact the rapid increase in the surface EAPE. The atmospheric effect is felt predominantly near the surface, while, as shown in Figure 4c, the subsurface EAPE gradually increases. Therefore, the vertical energy process plays a role in influencing the entire surface layer. Next, we examine the vertical transport of EAPE over the COE.
As revealed in Figure 4c, the variation of the EAPE would extend to a greater depth after the typhoons passed, so we first look at the nonlocal processes referred to as in Equation (6), which can further be decomposed into its horizontal () and vertical () components. Because the vertical processes are mainly considered here, we analyze in the subsurface layer (40–200 m) and the surface layer (above 40 m) over the period of 1 September 2022 to 20 September 2022. To see how this process redistributes energy in the vertical direction, we additionally draw in the vertical component of the EAPE flux as arrows in Figure 5c. It can be seen that is dominantly downward from 1 September 2022 to 20 September 2022, leading to a divergence near the surface and a convergence around 100 m, consistent with the vertical change in Figure 4c. In addition to the above processes, buoyancy conversion also contributes to the variation of the EAPE. We can see that the buoyancy conversion is persistently negative, indicating that the EKE would convert into the EAPE over the COE during this period, contributing to the EAPE’s enhancement.
The COE also obtains EAPE from both the submesoscale processes and the background flow. A part of the surface-intensified EAPE is transported downward and hence has an impact on the strengthening of the sub-surface EAPE, which is also influenced by the conversion from EKE. At the same time, the EKE is also slowly increasing, as shown in Figure 4c. As shown in the KE budget equation (Equation (3)), when the transfer is positive, it represents that KE is transferred from the submesoscale processes to the COE, indicating that the canonical KE transfer is upscale. A negative means that the COE releases KE to the background flow via an inverse KE cascade. As can be seen, exhibits substantial positive values but only several days after the second typhoon left, indicating that the high-frequency eddies transfer KE to the COE with a delay of several days, in contrast to the instantaneous response of APE transfer from high-frequency eddies. This can partly explain why the increase in KE is delayed by a few days after 10 September 2022. However, exhibits a negative value during this period, indicating the KE transfer from the COE to the background flow. The whole scenario is hence as follows: during the period, the COE gains energy from the submesoscale processes and releases KE to the background flow through a strong inverse canonical KE transfer.
To attribute the rapid increase of the whole surface EKE 10–20 days after Typhoon Muifa left, we look again at the vertical distribution of the mesoscale energetics in the MS-EVA budget. Recall that represents nonlocal transport induced by advection and pressure work. From Figure 6, we see that below 50 m is negative while positive above 50 m, indicating that the EKE of the subsurface layer is transported upwards via vertical pressure work. It is worth noting that the value of is positive during this period, which is contrary to that observed during the previous period. That is to say, the enhanced sub-surface EAPE introduced in the last section is converted into EKE. Averaging over the period of 21 September 2022–30 September 2022,the vertical integrations of COE area-averaged eddy-scale energetics through the surface layer (0–40 m) and the sub-surface layer (40–200 m), we obtain the respective bulk energetic values in Table 2.
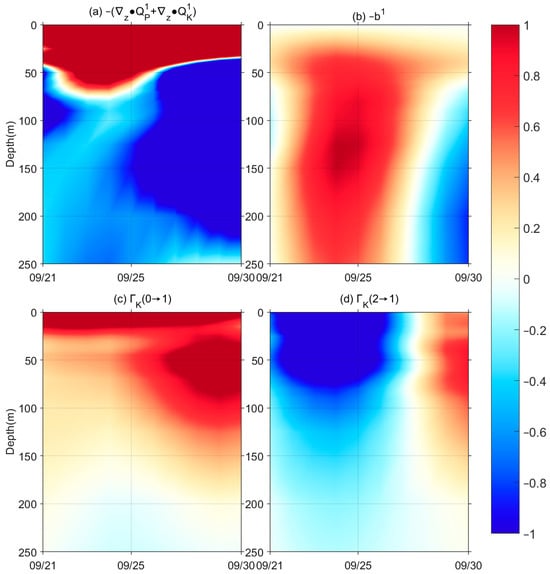
Figure 6.
Time series of the vertical distributions (units: m) of (a) is vertical nonlocal processes of K1; (b) , (c) and (d) (shadings, units: *10−4 ) integrated over the COE area. The definitions of these variables are referred to in Equation (6).

Table 2.
The values of the EKE associated terms within the surface layer (0–40 m) and sub-surface layer (40–200 m) integrated over the COE area (units: 10−4). They have been averaged over the ten-day period from 09/21 to 09/30.
From the table, is larger in magnitude than the other terms before the EKE reaches its peak, indicating that the vertical pressure work accounts mainly for the EKE production during this period within the surface layer. Meanwhile, the sub-surface is negative, with a value similar to the surface layer one, but for a negative sign. This clarifies that, at this stage, the sub-surface EKE can be transported upward to the surface through a nonlocal process.
Recall that, a positive barotropic canonical transfer indicates a barotropic instability of the basic flow, and a positive barotropic canonical transfer (or negative ) indicates a barotropic instability of the vortex, i.e., the COE. From Figure 6, is positive while exhibits a negative value with a larger absolute value compared to at this stage, indicating that the COE gains KE from the basic flow, and then release KE to the high-frequency processes via barotropic instability. The energy cascade is opposite to that in the first stage when the COE first encountered the typhoons.
Horizontally, the energetics distributions also yield clues to how the EAPE contributes to the production of the EKE of the COE. Figure 7 displays the composite maps of the EKE, EAPE, and associated terms vertically integrated from 40 to 200 m (Figure 7a–d) and 0 to 40 m (Figure 7e). Also, we calculate the time-averaged values over the 10-day period from 21 September 2022 to 30 September 2022. Figure 7a,b illustrate the spatial distributions of the sub-surface-integrated EKE and EAPE. The EKE is maximized along the outer periphery of the COE, while the EAPE is concentrated in the central region. The on the right side of Equation (7) represents the nonlocal transport of EAPE induced by advection. The is negative in the center, which aligns with the distribution of EAPE (Figure 7b), and positive in the southwest and northeast regions, indicating that the EAPE located at the center is transported towards the outer regions during the specified time period. The positive buoyancy conversion represents a conversion from the EAPE to the EKE, revealing that the sub-surface EAPE stored in the inner region is transported to both sides, and subsequently converted to EKE, effectively contributing to the increase of the sub-surface EKE. Note, the buoyancy conversion is relatively weak, implying that a part of the EAPE transported from the center is not converted into EKE in the sub-surface layer. In order to further investigate the role of the sub-surface EKE on that of the surface layer, Figure 7e depicts the surface distribution of the vertical components of the non-local processes. Considering the small magnitude of , we examine here the combined effect of the non-local spatial transport term () and the pressure work () term. The exhibits positive values on the distribution map in both the northeast and southwest regions of the COE, consistent with , indicating that a portion of the converted sub-surface layer EKE is transported upward to the surface.
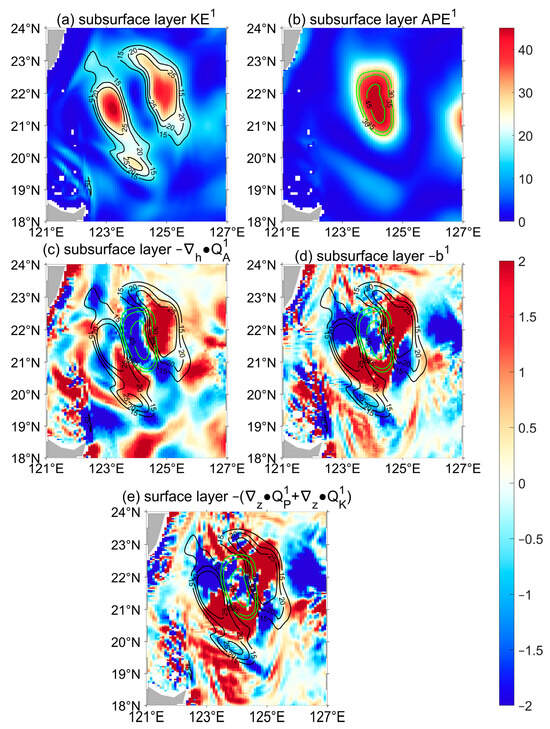
Figure 7.
Spatial distributions of the depth-integrated (a) subsurface EKE, (b) subsurface EAPE (shadings, units: ), (c) subsurface , (d) subsurface , and (e) surface (shadings, units: *10−4 ). The subsurface EKE (black) and EAPE (green) are superimposed (contours; ) in (c–e).
It is conventionally considered that the surface ocean response to the typhoon terminates upon mixed layer restratification [1]. However, this case study reveals a distinct second-stage enhancement of KE following mixed layer recovery. Notably, Typhoon Hinnamnor—which stagnated in this region with an unusually slow translation speed—induced intense vertical mixing that subsequently even attenuated its own intensity through the ocean feedback mechanisms [45]. Observational evidence confirms that during such extreme mixing events, sub-surface layers retain mixing-induced density anomalies even after surface layer restratification is complete [46]. This phenomenon is clearly discernible through available potential energy (APE) dynamics: Stage 1 exhibits downward transport of surface EAPE to subsurface layers, followed by rapid surface EAPE dissipation in Stage 2 while subsurface APE anomalies persist (Figure 4a). This subsurface EAPE demonstrates that mixing-induced subsurface EAPE accumulation serves as a critical mechanism delaying the peak energy response.
4. Discussion and Conclusions
We identified an extremely long delay in the response of a cyclonic ocean eddy (COE) in the northwest Pacific to the passage of two typhoons, namely Hinnamnor and Muifa, on 1 and 11 September 2022. Based on the HYCOM data, the dynamical processes underlying this unusual phenomenon have been diagnosed using the functional analysis apparatus, multiscale window transform (MWT), and MTW-based energetics analysis. Using the MWT, the original fields were reconstructed onto three scale windows, namely a nonstationary background flow window (periods of 256–512 days), a mesoscale window (periods of 16–256 days), and a high-frequency submesoscale window (periods <16 days).
Dynamically, we found that the evolution of the COE after the typhoon excitation can be divided into two stages, with 20 September 2022 (10 days after the second typhoon, Muifa, left) serving as the boundary. In the first stage, the eddy kinetic energy (EKE) of the COE grows rather slowly, but the surface eddy available potential energy (EAPE) grows much more rapidly. The COE obtained the APE from the submesoscale processes and the background flow, resulting in a rapid increase in the EAPE in the surface layer. At the same time, the obtained EAPE was transported downward, leading to an increase in the sub-surface APE.
The second stage is characterized by explosive growth in EKE (both surface and subsurface). There are two primary EKE sources in the subsurface layer. One is from the background flow (3.50 × 10−4) through barotropic instability, while the other is from the conversion (2.80 × 10−4) from EAPE. The EKE is transported upward via pressure work (1.02 × 10−4). Together with the component from the background flow through barotropic instability (2.20 × 10−4), it generates surface EKE. The dominant energy processes are illustrated in Figure 8.
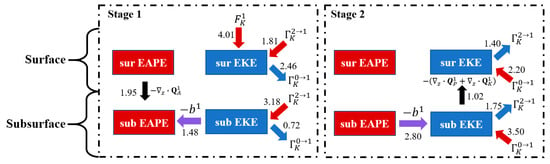
Figure 8.
A schematic diagram showing the dominant energy processes of the COE at two stages. The red/blue arrows indicate energy gain/loss from canonical transfer, the black ones are vertical energy transports between 20–60 m depth (between surface and subsurface layer), and the purple ones the conversion between the KE and APE. The energy flows are all in units of 10−4.
Essentially, the lengthy delay in the COE’s response to typhoon excitation occurs due to the storage of eddy-scale available potential energy (EAPE), which is followed by its release into the eddy-scale kinetic energy needed for the COE to grow. The whole scenario is as follows: High-frequency energy from the typhoon is transferred to the COE scale APE, or EAPE, at the surface through an inverse canonical transfer. The resulting EAPE is transported downward to the sub-surface, where it is converted into EKE; part of the EKE is then carried upward to the surface via pressure work, and subsequently, the COE grows explosively.
It should be noted that the present HYCOM reanalysis data only partially resolve the submesoscale processes. As a result, the submesoscale processes in the present study could be underestimated. Statistical analysis still needs to be further explored in future studies. The long-delayed response of the COE in this study may also be influenced by the number of typhoons (two passed successively), typhoon intensity (super typhoon Hinnamnor), and the western boundary current. Moreover, unresolved submesoscale eddies could attenuate energy cascades, impacting biogeochemical pathways such as nutrient upwelling. Future studies should employ ensemble simulations to isolate the roles of typhoon intensity, frequency, and background currents and evaluate the importance of biological processes.
Author Contributions
Conceptualization, J.W.; methodology, J.W. and Y.R.; software, Y.R.; validation, J.W.; formal analysis, J.W. and Y.R.; investigation, J.W.; resources, Y.R.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, Y.R.; visualization, J.W.; supervision, Y.R.; project administration, Y.R.; funding acquisition, Y.R. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China under grants 42305157 and 42230105.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The AVISO dataset is available at Centre national d’études spatiales (CNES, https://www.aviso.altimetry.fr/en/data/data-access/aviso-cnes-data-center.html), accessed on 9 November 2023. The HYCOM reanalysis dataset is available at https://data.marine.copernicus.eu/product/GLOBAL_MULTIYEAR_PHY_001_030/description, accessed on 19 September 2023. The typhoon track dataset is available at https://www.ncei.noaa.gov/products/international-best-track-archive, accessed on 6 November 2023. The MS-EVA software is available online (http://www.ncoads.cn/).
Acknowledgments
J.W. thanks Fen Xu, Weiyu Lu, Yang Yang, and X. San Liang for their suggestions and support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef]
- Vincent, E.M.; Lengaigne, M.; Madec, G.; Vialard, J.; Samson, G.; Jourdain, N.C.; Menkes, C.E.; Jullien, S. Processes Setting the Characteristics of Sea Surface Cooling Induced by Tropical Cyclones. J. Geophys. Res. Ocean. 2012, 117, C02020. [Google Scholar] [CrossRef]
- Potter, H.; Drennan, W.M.; Graber, H.C. Upper Ocean Cooling and Air-sea Fluxes under Typhoons: A Case Study. J. Geophys. Res. 2017, 122, 7237–7252. [Google Scholar] [CrossRef]
- Pei, Y.; Zhang, R.-H.; Chen, D. Roles of Different Physical Processes in Upper Ocean Responses to Typhoon Rammasun (2008)-Induced Wind Forcing. Sci. China Earth Sci. 2019, 62, 684–692. [Google Scholar] [CrossRef]
- Jacob, S.D.; Shay, L.K.; Mariano, A.J.; Black, P.G. The 3D Oceanic Mixed Layer Response to Hurricane Gilbert. J. Phys. Oceanogr. 2000, 30, 1407–1429. [Google Scholar] [CrossRef]
- Shay, L.; Goñi, G.; Black, P. Effects of a Warm Oceanic Feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic Mass Transport by Mesoscale Eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, R.; Chen, D.; Liu, X.; He, H.; Tang, Y.; Ke, D.; Shen, Z.; Li, J.; Xie, J.; et al. Net Modulation of Upper Ocean Thermal Structure by Typhoon Kalmaegi (2014). J. Geophys. Res. Ocean. 2018, 123, 7154–7171. [Google Scholar] [CrossRef]
- Yang, Y.J.; Sun, L.; Duan, A.M.; Li, Y.B.; Fu, Y.F.; Yan, Y.F.; Wang, Z.Q.; Xian, T. Impacts of the Binary Typhoons on Upper Ocean Environments in November 2007. J. Appl. Remote Sens. 2012, 6, 3583. [Google Scholar] [CrossRef]
- Sun, L.; Li, Y.X.; Yang, Y.J.; Wu, Q.; Chen, X.T.; Li, Q.Y.; Li, Y.B.; Xian, T. Effects of Super Typhoons on Cyclonic Ocean Eddies in the Western North Pacific: A Satellite Data-based Evaluation between 2000 and 2008. J. Geophys. Res. Ocean. 2014, 119, 5585–5598. [Google Scholar] [CrossRef]
- Shang, X.D.; Zhu, H.B.; Chen, G.Y.; Xu, C.; Yang, Q. Research on Cold Core Eddy Change and Phytoplankton Bloom Induced by Typhoons: Case Studies in the South China Sea. Adv. Meteorol. 2015, 2015, 340432. [Google Scholar] [CrossRef]
- Gordon, A.L.; Shroyer, E.; Murty, V.S.N. An Intrathermocline Eddy and A Tropical Cyclone in the Bay of Bengal. Sci. Rep. 2017, 7, 46218. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wang, G. Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling. Remote Sens. 2022, 14, 2865. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, G.; Shang, X. Response of a Preexisting Cyclonic Ocean Eddy to a Typhoon. J. Phys. Oceanogr. 2016, 46, 2403–2410. [Google Scholar] [CrossRef]
- Lee, D.K.; Niiler, P.P. The Inertial Chimney: The Near-inertial Energy Drainage from the Ocean Surface to the Deep Layer. Geophys. Res. Ocean. 1998, 103, 7579–7591. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean Circulation Kinetic Energy: Reservoirs, Sources, and Sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- Polzin, K.L. Mesoscale Eddy–Internal Wave Coupling. Part II: Energetics and Results from PolyMode. J. Phys. Oceanogr. 2010, 40, 789–801. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Zhou, L.; Liu, X.; Ding, T.; Zhou, B. Upper Ocean Response to Typhoon Kalmaegi (2014). J. Geophys. Res. Ocean. 2016, 121, 6520–6535. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, G.; Shang, X. Strength and Spatial Structure of the Perturbation Induced by a Tropical Cyclone to the Underlying Eddies. J. Geophys. Res. Ocean. 2020, 125, e2020JC016097. [Google Scholar] [CrossRef]
- Zhai, X.; Marshall, D.P. Vertical Eddy Energy Fluxes in the North Atlantic Subtropical and Subpolar Gyres. J. Phys. Oceanogr. 2013, 43, 95–103. [Google Scholar] [CrossRef]
- Yang, G.; Wang, F.; Li, Y.; Lin, P. Mesoscale Eddies in the Northwestern Subtropical Pacific Ocean: Statistical Characteristics and Three-dimensional Structures. J. Geophys. Res. Ocean. 2013, 118, 1906–1925. [Google Scholar] [CrossRef]
- Sun, L.; Yang, Y.J.; Xian, T.; Wang, Y.; Fu, Y.F. Ocean Responses to Typhoon Namtheun Explored with Argo Floats and Multiplatform Satellites. Atmos.-Ocean. 2012, 50, 15–26. [Google Scholar] [CrossRef]
- Liang, X.S.; Anderson, D.G.M. Multiscale Window Transform. Multiscale Model. Simul. 2007, 6, 437–467. [Google Scholar] [CrossRef]
- Liang, X.S. Canonical Transfer and Multiscale Energetics for Primitive and Quasigeostrophic Atmospheres. J. Atmos. Sci. 2016, 73, 4439–4468. [Google Scholar] [CrossRef]
- Yang, Y.; Weisberg, R.H.; Liu, Y.; Liang, X.S. Instabilities and Multiscale Interactions Underlying the Loop Current Eddy Shedding in the Gulf of Mexico. J. Phys. Oceanogr. 2020, 50, 1289–1317. [Google Scholar] [CrossRef]
- Xu, F.; Liang, X.S. The Synchronization between the Zonal Jet Stream and Temperature Anomalies Leads to an Extremely Freezing North America in January 2019. Geophys. Res. Lett. 2020, 47, e2020GL089689. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S.; He, W.B. On the Formation and Maintenance of the Interannual Variability of the North Atlantic Oscillation. J. Atmos. Sci. 2024, 81, 177–208. [Google Scholar] [CrossRef]
- Ma, J.; Liang, X.S.; Chen, D. The Role of Multiscale Interaction in the Maintenance and Propagation of MJO in Boreal Winter. J. Clim. 2023, 36, 7827–7846. [Google Scholar] [CrossRef]
- Maslo, A.; Azevedo Correia de Souza, J.M.; Pardo, J.S. Energetics of the Deep Gulf of Mexico. J. Phys. Oceanogr. 2020, 50, 1655–1675. [Google Scholar] [CrossRef]
- Mak, M.; Cai, M. Local barotropic instability. J. Atmos. Sci. 1988, 46, 3289–3311. [Google Scholar] [CrossRef]
- Holmes, R.M.; Thomas, L.N. Modulation of tropical instability wave intensity by equatorial Kelvin waves. J. Phys. Oceanogr. 2016, 46, 2623–2643. [Google Scholar] [CrossRef]
- Dewar, W.K.; Bane, J.M. Gulf stream dynamics. Pad II: Eddy Energetics at 73°W. J. Phys. Oceanogr. 1989, 19, 1574–1587. [Google Scholar] [CrossRef]
- Chapman, C.C.; McC Hogg, A.; Kiss, E.; Rintoul, S.R. The dynamics of southern ocean storm tracks. J. Phys. Oceanogr. 2015, 45, 884–903. [Google Scholar] [CrossRef]
- Yang, H.; Wu, L.; Chang, P.; Qiu, B.; Jing, Z.; Zhang, Q.; Chen, Z. Mesoscale energy balance and air–sea interaction in the Kuroshio Extension: Low-frequency versus high-frequency variability. J. Phys. Oceanogr. 2021, 51, 895–910. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Chaigneau, A.; Eldin, G.; Dewitte, B. Eddy Activity in the Four Major Upwelling Systems from Satellite Altimetry (1992–2007). Prog. Oceanogr. 2009, 83, 117–123. [Google Scholar] [CrossRef]
- Yang, Y.; Lia, X.S. New Perspectives on the Generation and Maintenance of the Kuroshio Large Meander. J. Phys. Oceanogr. 2019, 49, 2095–2113. [Google Scholar] [CrossRef]
- Zhao, Y.-B.; Liang, X.S.; Gan, J. Nonlinear multiscale interactions and internal dynamics underlying a typical eddy-shedding event at Luzon Strait. J. Geophys. Res. Ocean. 2016, 121, 8208–8229. [Google Scholar] [CrossRef]
- Carton, X. Hydrodynamical Modeling of Oceanic Vortices. Surv. Geophys. 2001, 22, 179–263. [Google Scholar] [CrossRef]
- Sun, J.; Oey, L.Y.; Chang, R.; Xu, F.; Huang, S.M. Ocean Response to Typhoon Nuri (2008) in Western Pacific and South China Sea. Ocean. Dyn. 2015, 65, 735–749. [Google Scholar] [CrossRef]
- Tseng, Y.H.; Jan, S.; Dietrich, D.E.; Lin, I.I.; Chang, Y.T.; Tang, T.Y. Modeled Oceanic Response and Sea Surface Cooling to Typhoon Kai-Tak. Terr. Atmos. Ocean. Sci. 2010, 21, 85–98. [Google Scholar] [CrossRef]
- Kuo, Y.C.; Chern, C.S.; Wang, J.; Tsai, Y.L. Numerical Study of Upper Ocean Response to a Typhoon Moving Zonally across the Luzon Strait. Ocean. Dyn. 2011, 61, 1783–1795. [Google Scholar] [CrossRef]
- Sriver, R.; Huber, M. Observational evidence for an ocean heat pump induced by tropical cyclones. Nature 2007, 447, 577–580. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Song, J.; Leng, H.; Wang, H.; Zhang, Z.; Zhang, H.; Zheng, M.; Yang, X.; Wang, C. The abnormal track of super typhoon Hinnamnor (2022) and its interaction with the upper ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2023, 201, 104160. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).