Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows
Abstract
1. Introduction
2. Dataset
3. Radiative Transfer Model
3.1. Cloud Layer Model
3.2. Numerical Model for Solving the Radiative Transfer Equation
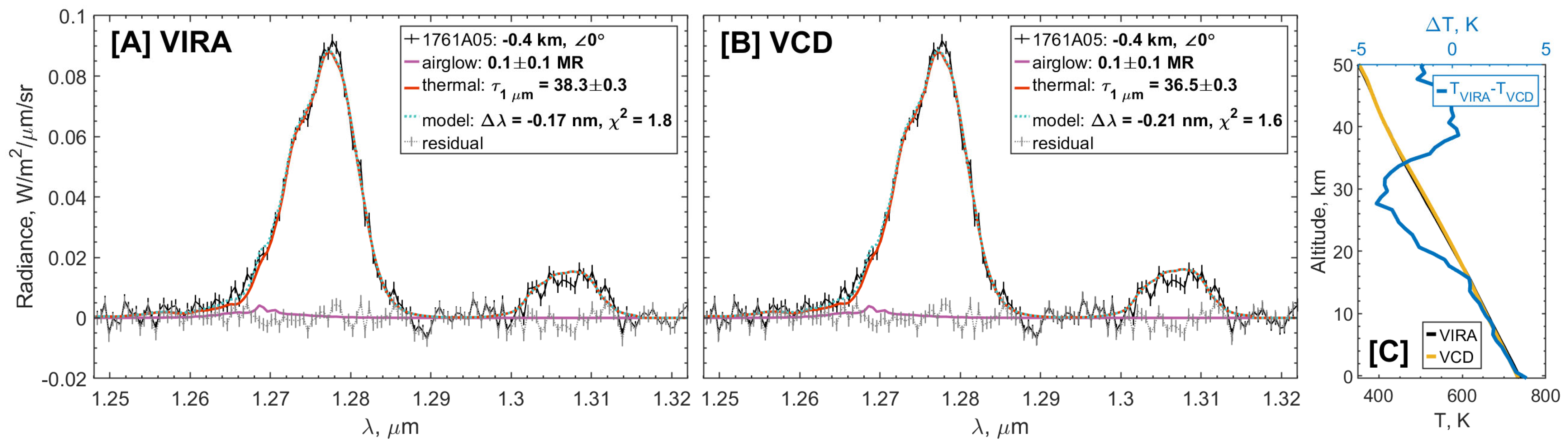
- The scaling factor of the vertical profiles of the mode 2, 2′ and 3 particle number densities;
- The column number density of O2* molecules;
- The scalar wavelength shift of the wavelength calibration.
4. Result
4.1. Venus Cloud Optical Depth Spatial Distribution and Temporal Behavior
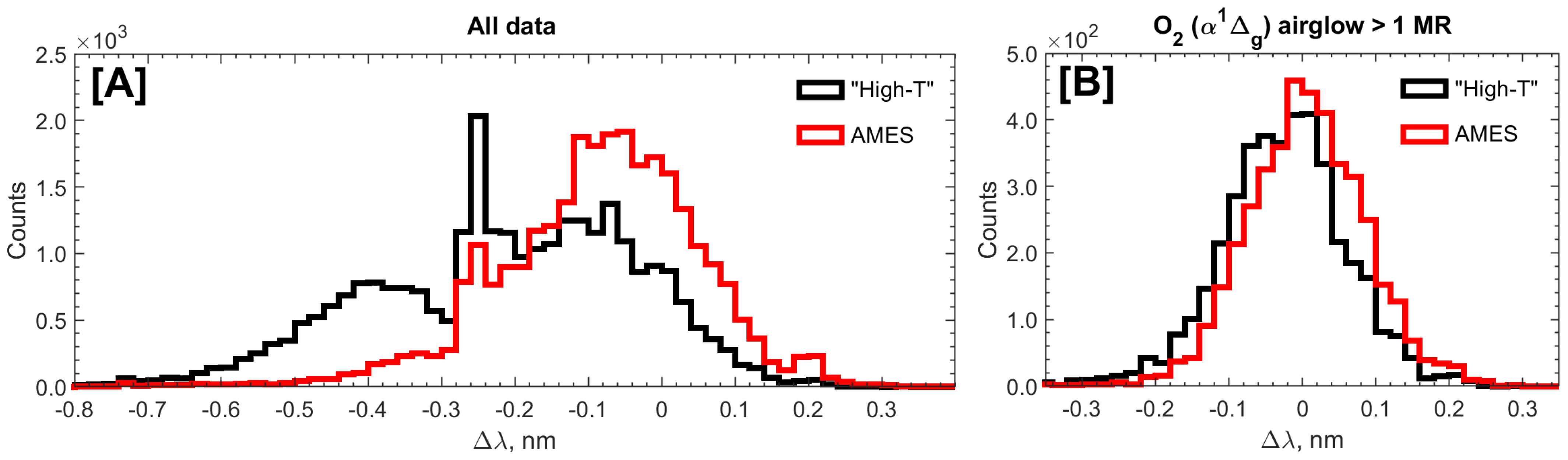
4.2. Investigation of Result Uncertainty
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IR | Infrared |
| SPICAV | SPectroscopy for the Investigation of the Characteristics of the Atmosphere of Venus |
| VIRTIS | Visible and Infrared Thermal Imaging Spectrometer |
| AOTF | Acousto-optical tunable filter |
| VIRA | Venus International Reference Atmosphere |
| VCD | Venus Climate Database |
| VMR | Volume mixing ratio |
| FAP | False-alarm probability |
References
- Esposito, L.W.; Knollenberg, R.G.; Marov, M.Y.A.; Toon, O.B.; Turco, R. The clouds and hazes of Venus. In Venus; Hunten, D.M., Colin, L., Donahue, T.M., Moroz, V.I., Eds.; The University of Arizona Press: Tucson, AZ, USA, 1983; pp. 484–564. [Google Scholar]
- Titov, D.V.; Ignatiev, N.I.; McGouldrick, K.; Wilquet, V.; Wilson, C.F. Clouds and hazes of Venus. Space Sci. Rev. 2018, 214, 126. [Google Scholar] [CrossRef]
- Sill, G.T. Sulfuric acid in the Venus clouds. CoLPL 1972, 9, 191–198. [Google Scholar]
- Young, A.T. Are the Clouds of Venus Sulfuric Acid? Icarus 1973, 18, 564–582. [Google Scholar] [CrossRef]
- Hansen, J.E.; Hovenier, J.W. Interpretation of the polarization of Venus. J. Atmos. Sci. 1974, 31, 1137–1160. [Google Scholar] [CrossRef]
- Pollack, J.B.; Erickson, E.F.; Witteborn, F.C.; Chackerian, C.; Summers, A.L.; van Camp, W.; Baldwin, B.J.; Augason, G.C.; Caroff, L.J. Aircraft Observations of Venus’ Near-Infrared Reflection Spectrum: Implications for Cloud Composition. Icarus 1974, 23, 8–26. [Google Scholar] [CrossRef]
- Dollfus, A.; Auriere, M.; Santer, R. Wavelength dependence of polarization. XXXVII. Regional observations of Venus. Astron. J. 1979, 84, 1419–1436. [Google Scholar] [CrossRef]
- Sato, M.; Travis, L.D.; Kawabata, K. Photopolarimetry Analysis of the Venus Atmosphere in Polar Regions. Icarus 1996, 124, 569–585. [Google Scholar] [CrossRef]
- Luginin, M.; Fedorova, A.; Belyaev, D.; Montmessin, F.; Wilquet, V.; Korablev, O.; Bertaux, J.-L.; Vandaele, A.C. Aerosol properties in the upper haze of Venus from SPICAV IR data. Icarus 2016, 277, 154–170. [Google Scholar] [CrossRef]
- Luginin, M.; Fedorova, A.; Belyaev, D.; Montmessin, F.; Korablev, O.; Bertaux, J.-L. Scale heights and detached haze layers in the mesosphere of Venus from SPICAV IR data. Icarus 2018, 311, 87–104. [Google Scholar] [CrossRef]
- Knollenberg, R.G.; Hunten, D.M. The microphysics of the clouds of Venus—Results of the Pioneer Venus particle size spectrometer experiment. J. Geophys. Res. 1980, 85, 8039–8058. [Google Scholar] [CrossRef]
- Toon, O.B.; Ragent, B.; Colburn, D.; Blamont, J.; Cot, C. Large, solid particles in the clouds of Venus: Do they exist? Icarus 1984, 57, 143–160. [Google Scholar] [CrossRef]
- Andreichikov, B.M.; Akhmetshin, I.K.; Korchuganov, B.N.; Mukhin, L.M.; Ogorodnikov, B.I.; Petryanov, I.V.; Skitovich, V.I. Chemical composition and structure of Venus clouds from results of X-ray radiometric experiments made with the Vega 1 and Vega 2 automatic interplanetary stations. Kosm. Issled. 1987, 25, 737–743. [Google Scholar]
- Mills, F.P.; Allen, M. A review of selected issues concerning the chemistry in Venus’ middle atmosphere. Planet. Space Sci. 2007, 55, 1729–1740. [Google Scholar] [CrossRef]
- Markiewicz, W.J.; Petrova, E.; Shalygina, O.; Almeida, M.; Titov, D.V.; Limaye, S.S.; Ignatiev, N.; Roatsch, T.; Matz, K.D. Glory on Venus cloud tops and the unknown UV absorber. Icarus 2014, 234, 200–203. [Google Scholar] [CrossRef]
- Petrova, E.V. Glory on Venus and selection among the unknown UV absorbers. Icarus 2018, 306, 163–170. [Google Scholar] [CrossRef]
- Tomasko, M.G.; Doose, L.R.; Smith, P.H. Absorption of Sunlight in the Atmosphere of Venus. Science 1979, 205, 80–82. [Google Scholar] [CrossRef]
- Esposito, L.W. Ultraviolet contrasts and the absorbers near the Venus cloud tops. J. Geophys. Res. 1980, 85, 8151–8157. [Google Scholar] [CrossRef]
- Ekonomov, A.P.; Moroz, V.I.; Moshkin, B.E.; Gnedykh, V.I.; Golovin Yu, M.; Crigoryev, A.V. Scattered UV solar radiation within the clouds of Venus. Nature 1984, 307, 345–347. [Google Scholar] [CrossRef]
- Marov, M.I.; Lystsev, V.E.; Lebedev, V.N.; Lukashevich, N.L.; Shari, V.P. The structure and microphysical properties of the Venus clouds: Venera 9, 10, and 11 data. Icarus 1980, 44, 608–639. [Google Scholar] [CrossRef]
- Zasova, L.V.; Moroz, V.I.; Linkin, V.M. Venera-15, 16 and VEGA mission results as sources for improvements of the Venus reference atmosphere. Adv. Space Res. 1996, 17, 171–180. [Google Scholar] [CrossRef]
- Gierasch, P.J.; Goody, R.M.; Young, R.E.; Crisp, D.; Edwards, C.; Kahn, R.; McCleese, D.; Rider, D.; Del Genio, A.; Greeley, R.; et al. The general circulation of the Venus atmosphere: An assessment. In Venus II—Geology, Geophysics, Atmosphere, and Solar Wind Environment; Bucher, J.W., Hunten, D.M., Phillips, R.J., Eds.; University of Arizona Press: Tucson, AZ, USA, 1997; pp. 459–500. [Google Scholar]
- Gorinov, D.A.; Zasova, L.V.; Khatuntsev, I.V.; Patsaeva, M.V.; Turin, A.V. Winds in the Lower Cloud Level on the Nightside of Venus from VIRTIS-M (Venus Express) 1.74 μm Images. Atmosphere 2021, 12, 186. [Google Scholar] [CrossRef]
- Sánchez-Lavega, A.; Lebonnois, S.; Imamura, T.; Read, P.; Luz, D. The Atmospheric Dynamics of Venus. Space Sci. Rev. 2017, 212, 1541–1616. [Google Scholar] [CrossRef]
- Svedhem, H.; Titov, D.V.; McCoy, D.; Lebreton, J.-P.; Barabash, S.; Bertaux, J.-L.; Drossart, P.; Formisano, V.; Häusler, B.; Korablev, O.; et al. Venus Express—The first European mission to Venus. Planet. Space Sci. 2007, 55, 1636–1652. [Google Scholar] [CrossRef]
- Nakamura, M.; Imamura, T.; Ishii, N.; Abe, T.; Kawakatsu, Y.; Hirose, C.; Satoh, T.; Suzuki, M.; Ueno, M.; Yamazaki, A.; et al. AKATSUKI returns to Venus. Earth Planets Space 2016, 68, 75. [Google Scholar] [CrossRef]
- Titov, D.V.; Taylor, F.W.; Svedhem, H.; Ignatiev, N.I.; Markiewicz, W.J.; Piccioni, G.; Drossart, P. Atmospheric structure and dynamics as the cause of ultraviolet markings in the clouds of Venus. Nature 2008, 456, 620–623. [Google Scholar] [CrossRef] [PubMed]
- Ignatiev, N.I.; Titov, D.V.; Piccioni, G.; Drossart, P.; Markiewicz, W.J.; Cottini, V.; Roatsch, T.; Almeida, M.; Manoel, N. Altimetry of the Venus cloud tops from the Venus Express observations. J. Geophys. Res. Planets 2009, 114, E00B43. [Google Scholar] [CrossRef]
- Fedorova, A.; Marcq, E.; Luginin, M.; Korablev, O.; Bertaux, J.-L.; Montmessin, F. Variations of water vapor and cloud top altitude in the Venus’ mesosphere from SPICAV/VEx observations. Icarus 2016, 275, 143–162. [Google Scholar] [CrossRef]
- Zasova, L.V.; Ignatiev, N.; Khatuntsev, I.; Linkin, V. Structure of the Venus atmosphere. Planet. Space Sci. 2007, 55, 1712–1728. [Google Scholar] [CrossRef]
- Lee, Y.J.; Titov, D.V.; Tellmann, S.; Piccialli, A.; Ignatiev, N.; Pätzold, M.; Häusler, B.; Piccioni, G.; Drossart, P. Vertical structure of the Venus cloud top from the VeRa and VIRTIS observations onboard Venus Express. Icarus 2012, 217, 599–609. [Google Scholar] [CrossRef]
- Haus, R.; Kappel, D.; Arnold, G. Self-consistent retrieval of temperature profiles and cloud structure in the northern hemisphere of Venus using VIRTIS/VEX and PMV/VENERA-15 radiation measurements. Planet. Space Sci. 2013, 89, 77–101. [Google Scholar] [CrossRef]
- Haus, R.; Kappel, D.; Arnold, G. Atmospheric thermal structure and cloud features in the southern hemisphere of Venus as retrieved from VIRTIS/VEX radiation measurements. Icarus 2014, 232, 232–248. [Google Scholar] [CrossRef]
- Wilson, C.F.; Guerlet, S.; Irwin, P.G.J.; Tsang, C.C.C.; Taylor, F.W.; Carlson, R.W.; Drossart, P.; Piccioni, G. Evidence for anomalous cloud particles at the poles of Venus. J. Geophys. Res. Planets 2008, 113, E00B13. [Google Scholar] [CrossRef]
- Tellmann, S.; Pätzold, M.; Häusler, B.; Bird, M.K.; Tyler, G.L. Structure of the Venus neutral atmosphere as observed by the Radio Science experiment VeRa on Venus Express. J. Geophys. Res. Planets 2009, 114, E00B36. [Google Scholar] [CrossRef]
- Limaye, S.S.; Grassi, D.; Mahieux, A.; Migliorini, A.; Tellmann, S.; Titov, D. Venus Atmospheric Thermal Structure and Radiative Balance. Space Sci. Rev. 2018, 214, 102. [Google Scholar] [CrossRef]
- Allen, D.A.; Crawford, J.W. Cloud structure on the dark side of Venus. Nature 1984, 307, 222–224. [Google Scholar] [CrossRef]
- Crisp, D.; McMuldroch, S.; Stephens, S.K.; Sinton, W.M.; Ragent, B.; Hodapp, K.-W.; Probst, R.G.; Doyle, L.R.; Allen, D.A.; Elias, J. Ground-Based Near-Infrared Imaging Observations of Venus During the Galileo Encounter. Science 1991, 253, 1538–1541. [Google Scholar] [CrossRef]
- Pollack, J.B.; Dalton, J.B.; Grinspoon, D.; Wattson, R.B.; Freedman, R.; Crisp, D.; Allen, D.A.; Bezard, B.; de Bergh, C.; Giver, L.P.; et al. Near-Infrared Light from Venus’ Nightside: A Spectroscopic Analysis. Icarus 1993, 103, 1–42. [Google Scholar] [CrossRef]
- Meadows, V.S.; Crisp, D. Ground-based near-infrared observations of the Venus nightside: The thermal structure and water abundance near the surface. J. Geophys. Res. Planets 1996, 101, 4595–4622. [Google Scholar] [CrossRef]
- Bézard, B.; De Bergh, C. Composition of the atmosphere of Venus below the clouds. J. Geophys. Res. Planets 2007, 112, E04S07. [Google Scholar] [CrossRef]
- Taylor, F.W.; Crisp, D.; Bézard, B. Near-infrared sounding of the lower atmosphere of Venus. In Venus II—Geology, Geophysics, Atmosphere, and Solar Wind Environment; Bucher, J.W., Hunten, D.M., Phillips, R.J., Eds.; University of Arizona Press: Tucson, AZ, USA, 1997; pp. 325–351. [Google Scholar]
- Crisp, D.; Sinton, W.M.; Hodapp, K.-W.; Ragent, B.; Gerbault, F.; Goebel, J.H.; Probst, R.G.; Allen, D.A.; Pierce, K.; Stapelfeldt, K.R. The Nature of the Near-Infrared Features on the Venus Night Side. Science 1989, 246, 506–509. [Google Scholar] [CrossRef]
- Grinspoon, D.H.; Pollack, J.B.; Sitton, B.R.; Carlson, R.W.; Kamp, L.W.; Baines, K.H.; Encrenaz, T.; Taylor, F.W. Probing Venus’s cloud structure with Galileo NIMS. Planet. Space Sci. 1993, 41, 515–542. [Google Scholar] [CrossRef]
- Drossart, P.; Piccioni, G.; Adriani, A.; Angrilli, F.; Arnold, G.; Baines, K.H.; Bellucci, G.; Benkhoff, J.; Bézard, B.; Bibring, J.-P.; et al. Scientific goals for the observation of Venus by VIRTIS on ESA/Venus express mission. Planet. Space Sci. 2007, 55, 1653–1672. [Google Scholar] [CrossRef]
- Haus, R.; Kappel, D.; Tellmann, S.; Arnold, G.; Piccioni, G.; Drossart, P.; Häusler, B. Radiative energy balance of Venus based on improved models of the middle and lower atmosphere. Icarus 2016, 272, 178–205. [Google Scholar] [CrossRef]
- Arney, G.; Meadows, V.; Crisp, D.; Schmidt, S.J.; Bailey, J.; Robinson, T. Spatially resolved measurements of H2O, HCl, CO, OCS, SO2, cloud opacity, and acid concentration in the Venus near-infrared spectral windows. J. Geophys. Res. Planets 2014, 119, 1860–1891. [Google Scholar] [CrossRef]
- Barstow, J.K.; Tsang, C.C.C.; Wilson, C.F.; Irwin, P.G.J.; Taylor, F.W.; McGouldrick, K.; Drossart, P.; Piccioni, G.; Tellmann, S. Models of the global cloud structure on Venus derived from Venus Express observations. Icarus 2012, 217, 542–560. [Google Scholar] [CrossRef]
- Bertaux, J.-L.; Nevejans, D.; Korablev, O.; Villard, E.; Quémerais, E.; Neefs, E.; Montmessin, F.; Leblanc, F.; Dubois, J.P.; Dimarellis, E.; et al. SPICAV on Venus Express: Three spectrometers to study the global structure and composition of the Venus atmosphere. Planet. Space Sci. 2007, 55, 1673–1700. [Google Scholar] [CrossRef]
- Korablev, O.; Fedorova, A.; Bertaux, J.-L.; Stepanov, A.V.; Kiselev, A.; Kalinnikov, Y.K.; Titov, A.Y.; Montmessin, F.; Dubois, J.P.; Villard, E.; et al. SPICAV IR acousto-optic spectrometer experiment on Venus Express. Planet. Space Sci. 2012, 65, 38–57. [Google Scholar] [CrossRef]
- Saunders, R.S.; Spear, A.J.; Allin, P.C.; Austin, R.S.; Berman, A.L.; Chandlee, R.C.; Clark, J.; deCharon, A.V.; De Jong, E.M.; Griffith, D.G.; et al. Magellan mission summary. J. Geophys. Res. 1992, 97, 13067–13090. [Google Scholar] [CrossRef]
- Palmer, K.F.; Williams, D. Optical constants of sulfuric acid; application to the clouds of Venus? Appl. Opt. 1975, 14, 208–219. [Google Scholar] [CrossRef]
- Seiff, A.; Schofield, J.T.; Kliore, A.J.; Taylor, F.W.; Limaye, S.S.; Revercomb, H.E.; Sromovsky, L.A.; Kerzhanovich, V.V.; Moroz, V.I.; Marov, M.Y. Models of the structure of the atmosphere of Venus from the surface to 100 kilometers altitude. Adv. Space Res. 1985, 5, 3–58. [Google Scholar] [CrossRef]
- Crisp, D. Radiative forcing of the Venus mesosphere I. Solar fluxes and heating rates. Icarus 1986, 67, 484–514. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Lin, Z.; Stamnes, S.; Jin, Z.; Laszlo, I.; Tsay, S.-C.; Wiscombe, W.J.; Stamnes, K. Improved discrete ordinate solutions in the presence of an anisotropically reflecting lower boundary: Upgrades of the DISORT computational tool. J. Quant. Spectrosc. Radiat. Transf. 2015, 157, 119–134. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.-C.; Jayaweera, K.; Wiscombe, W. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Evans, K.F. SHDOMPPDA: A Radiative Transfer Model for Cloudy Sky Data Assimilation. J. Atmos. Sci. 2007, 64, 3854–3864. [Google Scholar] [CrossRef]
- Fedorova, A.; Bézard, B.; Bertaux, J.-L.; Korablev, O.; Wilson, C. The CO2 continuum absorption in the 1.10- and 1.18-μm windows on Venus from Maxwell Montes transits by SPICAV IR onboard Venus express. Planet. Space Sci. 2015, 113, 66–77. [Google Scholar] [CrossRef]
- Martinez, A.; Lebonnois, S.; Millour, E.; Pierron, T.; Moisan, E.; Gilli, G.; Lefèvre, F. Exploring the variability of the venusian thermosphere with the IPSL Venus GCM. Icarus 2023, 389, 115272. [Google Scholar] [CrossRef]
- Huang, X.; Schwenke, D.W.; Tashkun, S.A.; Lee, T.J. An isotopic-independent highly accurate potential energy surface for CO2 isotopologues and an initial 12C16O2 infrared line list. J. Chem. Phys. 2012, 136, 124311. [Google Scholar] [CrossRef]
- Huang, X.; Freedman, R.S.; Tashkun, S.A.; Schwenke, D.W.; Lee, T.J. Semi-empirical 12C16O2 IR line lists for simulations up to 1500 K and 20,000 cm−1. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 134–146. [Google Scholar] [CrossRef]
- Huang, X.; Gamache, R.R.; Freedman, R.S.; Schwenke, D.W.; Lee, T.J. Reliable infrared line lists for 13 CO2 isotopologues up to E′ = 18,000 cm−1 and 1500 K, with line shape parameters. J. Quant. Spectrosc. Radiat. Transf. 2014, 147, 134–144. [Google Scholar] [CrossRef]
- Bézard, B.; Fedorova, A.; Bertaux, J.-L.; Rodin, A.; Korablev, O. The 1.10- and 1.18-μm nightside windows of Venus observed by SPICAV-IR aboard Venus Express. Icarus 2011, 216, 173–183. [Google Scholar] [CrossRef]
- Sneep, M.; Ubachs, W. Direct measurement of the Rayleigh scattering cross section in various gases. J. Quant. Spectrosc. Radiat. Transf. 2005, 92, 293–310. [Google Scholar] [CrossRef]
- Barber, R.J.; Tennyson, J.; Harris, G.J.; Tolchenov, R.N. A high-accuracy computed water line list. Mon. Not. R. Astron. Soc. 2006, 368, 1087–1094. [Google Scholar] [CrossRef]
- Bertaux, J.-L.; Hauchecorne, A.; Lefèvre, F.; Bréon, F.-M.; Blanot, L.; Jouglet, D.; Lafrique, P.; Akaev, P. The use of the 1.27 µm O2 absorption band for greenhouse gas monitoring from space and application to MicroCarb. Atmos. Meas. Tech. 2020, 13, 3329–3374. [Google Scholar] [CrossRef]
- Evdokimova, D.; Fedorova, A.; Zharikova, M.; Montmessin, F.; Korablev, O.; Soret, L.; Gorinov, D.; Belyaev, D.; Bertaux, J.-L. Night O2 (a1Δg) airglow spatial distribution and temporal behavior on Venus based on SPICAV IR/VEx nadir dataset. Icarus 2025, 429, 116417. [Google Scholar] [CrossRef]
- Bailey, J.; Meadows, V.S.; Chamberlain, S.; Crisp, D. The temperature of the Venus mesosphere from O2 (a1Δg) airglow observations. Icarus 2008, 197, 247–259. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Kopparla, P.; Lee, Y.J.; Imamura, T.; Yamazaki, A. Principal components of short-term variability in the ultraviolet albedo of Venus. Astron. Astrophys. 2019, 626, A30. [Google Scholar] [CrossRef]
- Lee, Y.J.; Kopparla, P.; Peralta, J.; Schröder, S.E.; Imamura, T.; Kouyama, T.; Watanabe, S. Spatial and Temporal Variability of the 365-nm Albedo of Venus Observed by the Camera on Board Venus Express. J. Geophys. Res. Planets 2020, 125, e06271. [Google Scholar] [CrossRef]
- Gilman, D.L.; Fuglister, F.J.; Mitchell, J.M. On the Power Spectrum of ‘Red Noise’. J. Atmos. Sci. 1963, 20, 182–184. [Google Scholar] [CrossRef]
- Schulz, M.; Mudelsee, M. REDFIT: Estimating red-noise spectra directly from unevenly spaced paleoclimatic time series. Comput. Geosci. 2002, 28, 421–426. [Google Scholar] [CrossRef]
- Snels, M.; Stefani, S.; Piccioni, G.; Bèzard, B. Carbon dioxide absorption at high densities in the 1.18 μm nightside transparency window of Venus. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 464–471. [Google Scholar] [CrossRef]
- Wilson, C.F.; Marcq, E.; Gillmann, C.; Widemann, T.; Korablev, O.; Mueller, N.T.; Lefèvre, M.; Rimmer, P.B.; Robert, S.; Zolotov, M.Y. Possible Effects of Volcanic Eruptions on the Modern Atmosphere of Venus. Space Sci. Rev. 2024, 220, 31. [Google Scholar] [CrossRef]
- Imamura, T.; Hashimoto, G.L. Venus cloud formation in the meridional circulation. J. Geophys. Res. 1998, 103, 31349–31366. [Google Scholar] [CrossRef]
- Marcq, E.; Lea Jessup, K.; Baggio, L.; Encrenaz, T.; Lee, Y.J.; Montmessin, F.; Belyaev, D.; Korablev, O.; Bertaux, J.-L. Climatology of SO2 and UV absorber at Venus’ cloud top from SPICAV-UV nadir dataset. Icarus 2020, 335, 113368. [Google Scholar] [CrossRef]
- Oschlisniok, J.; Häusler, B.; Pätzold, M.; Tellmann, S.; Bird, M.K.; Peter, K.; Andert, T.P. Sulfuric acid vapor and sulfur dioxide in the atmosphere of Venus as observed by the Venus Express radio science experiment VeRa. Icarus 2021, 362, 114405. [Google Scholar] [CrossRef]
- Cottini, V.; Ignatiev, N.I.; Piccioni, G.; Drossart, P.; Grassi, D.; Markiewicz, W.J. Water vapor near the cloud tops of Venus from Venus Express/VIRTIS dayside data. Icarus 2012, 217, 561–569. [Google Scholar] [CrossRef]
- Bertaux, J.-L.; Khatuntsev, I.V.; Hauchecorne, A.; Markiewicz, W.J.; Marcq, E.; Lebonnois, S.; Patsaeva, M.; Turin, A.; Fedorova, A. Influence of Venus topography on the zonal wind and UV albedo at cloud top level: The role of stationary gravity waves. J. Geophys. Res. Planets 2016, 121, 1087–1101. [Google Scholar] [CrossRef]
- Kouyama, T.; Imamura, T.; Nakamura, M.; Satoh, T.; Futaana, Y. Long-term variation in the cloud-tracked zonal velocities at the cloud top of Venus deduced from Venus Express VMC images. J. Geophys. Res. Planets 2013, 118, 37–46. [Google Scholar] [CrossRef]
- Khatuntsev, I.V.; Patsaeva, M.V.; Titov, D.V.; Zasova, L.V.; Ignatiev, N.I.; Gorinov, D.A. Twelve-Year Cycle in the Cloud Top Winds Derived from VMC/Venus Express and UVI/Akatsuki Imaging. Atmosphere 2022, 13, 2023. [Google Scholar] [CrossRef]
- Lee, Y.J.; Jessup, K.-L.; Perez-Hoyos, S.; Titov, D.V.; Lebonnois, S.; Peralta, J.; Horinouchi, T.; Imamura, T.; Limaye, S.; Marcq, E.; et al. Long-term variations of Venus’s 365 nm albedo observed by Venus Express, Akatsuki, MESSENGER, and the Hubble Space Telescope. Astron. J. 2019, 158, 126. [Google Scholar] [CrossRef]
- McGouldrick, K.; Tsang, C.C.C. Discovery of a 150 day period in the Venus condensational clouds. Icarus 2017, 286, 118–133. [Google Scholar] [CrossRef]
- McGouldrick, K.; Barth, E.L. The Influence of Cloud Condensation Nucleus Coagulation on the Venus Cloud Structure. Planet. Sci. J. 2023, 4, 50. [Google Scholar] [CrossRef]
- Evdokimova, D. Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows. Mendeley Data, V1. 2025. Available online: https://data.mendeley.com/datasets/8pvyvvn43h/1 (accessed on 6 May 2025).

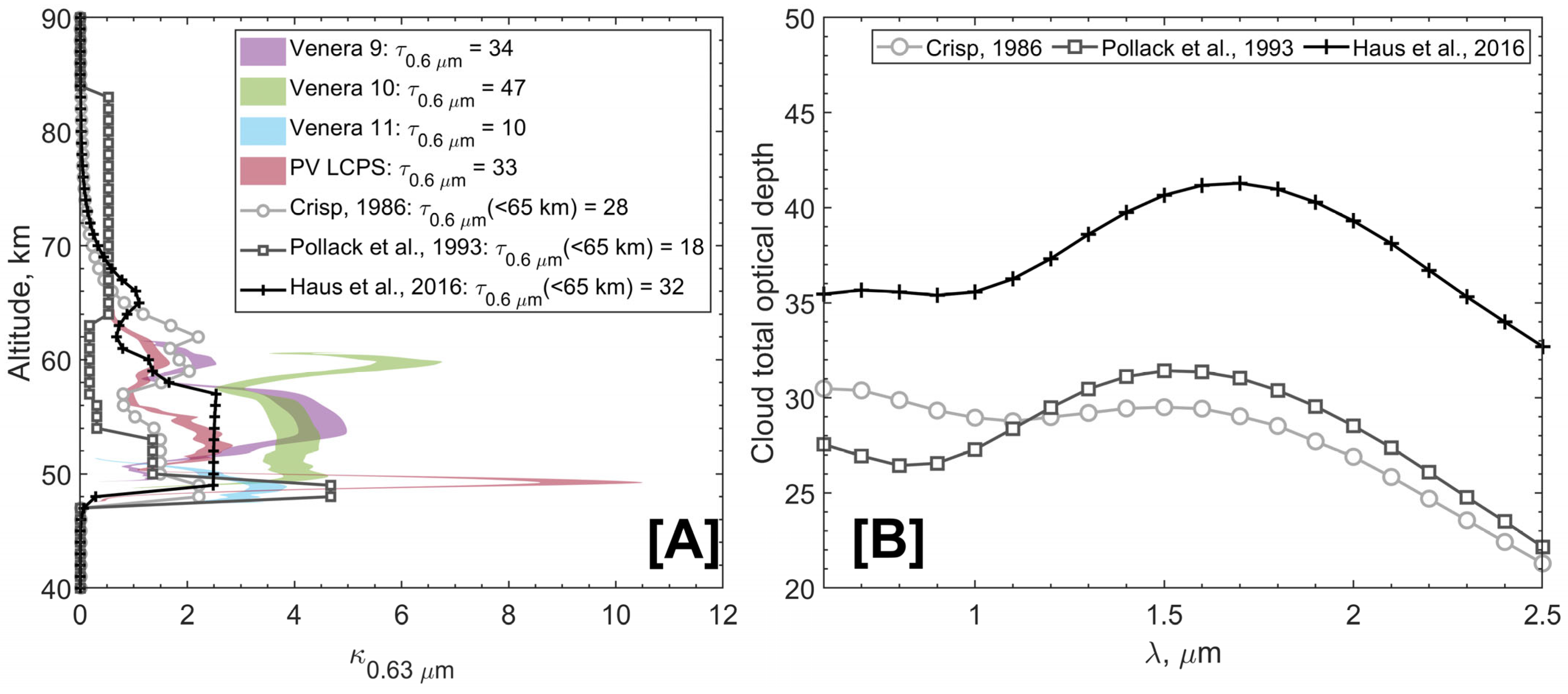
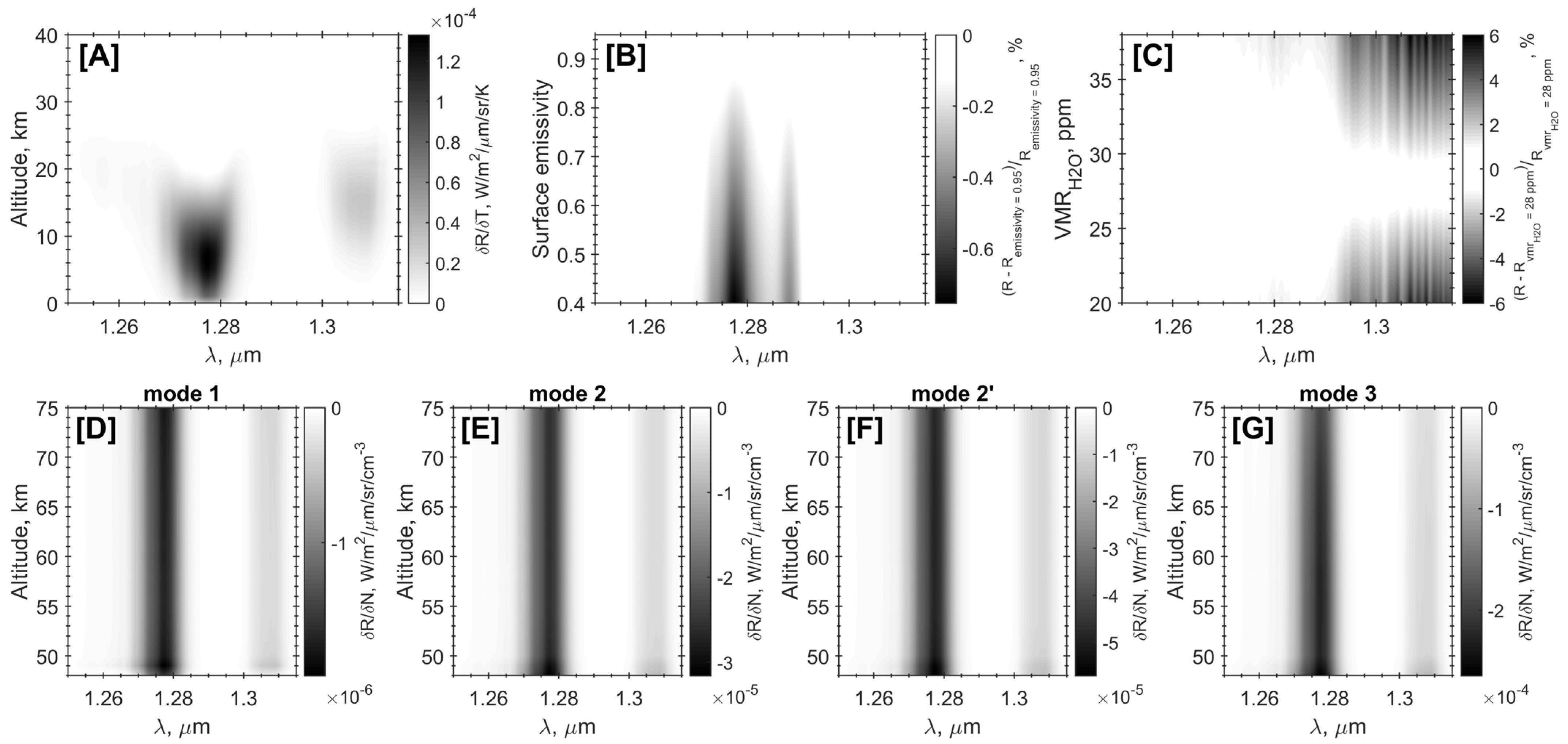


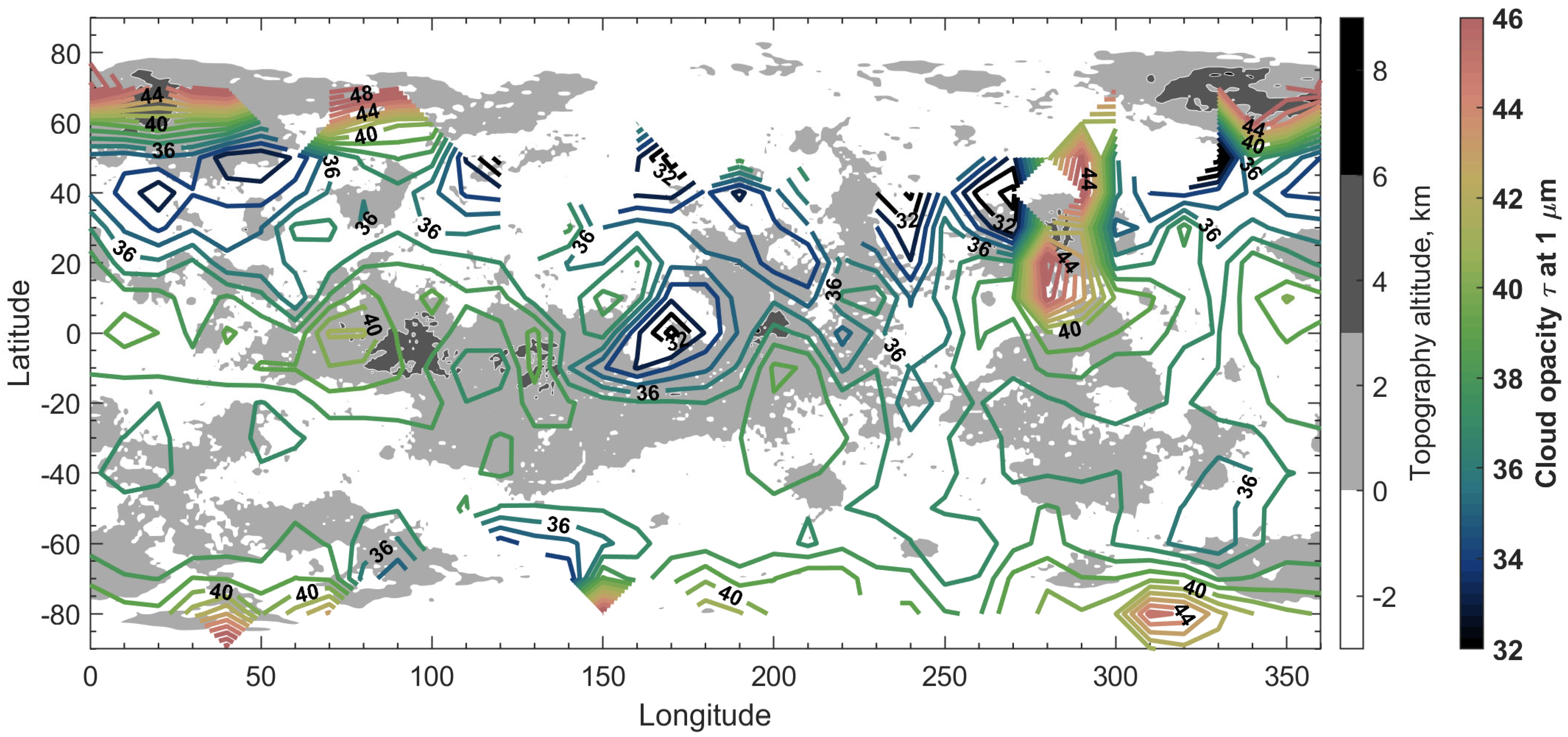
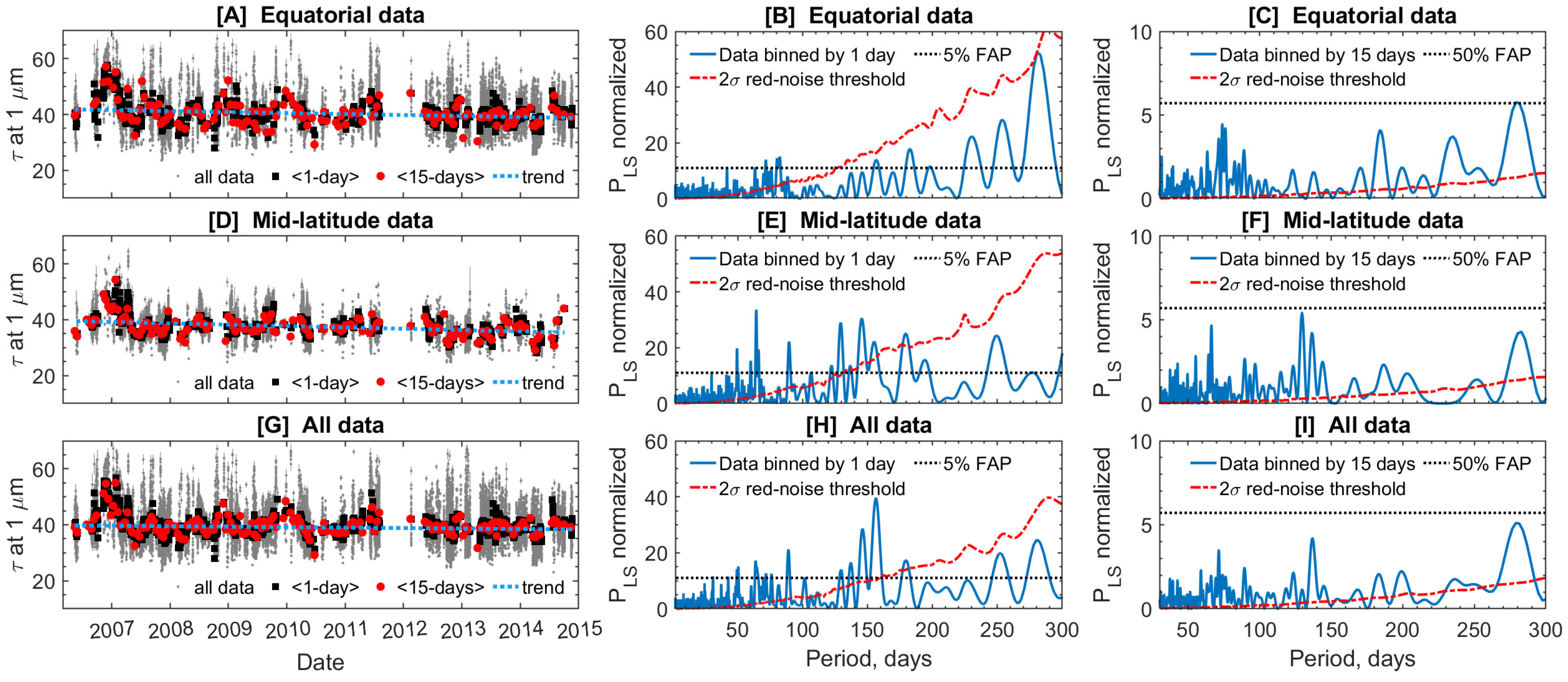

| Aerosol Particle Mode | 1 | 2 | 2′ | 3 |
|---|---|---|---|---|
| Lower base of peak altitude zb, km | 49.0 | 65.0 | 49.0 | 49.0 |
| Layer thickness of constant peak particle number zc, km | 16.0 | 1.0 | 11.0 | 8.0 |
| Upper scale height Hup, km | 3.5 | 3.5 | 1.0 | 1.0 |
| Lower scale height Hlo, km | 1.0 | 3.0 | 0.1 | 0.5 |
| Particle number density N0 at zb, cm−3 | 193.5 | 100 | 50 | 14 |
| Radiative transfer solver | DISORT4 [56,57] in pseudo-spherical geometry with 16 streams Line-by-line computation on wavelength grid with a step of 0.1 cm−1 |
| Atmosphere structure | (1) Venus International Reference Atmosphere (VIRA) [53] (2) Venus Climate Database (VCD) [60] |
| Cloud model | Aerosol number density set by Equation (1) and Table 1 [46] Effective radius of aerosol modes 1, 2, 2′ and 3: 0.3, 1.0, 1.4, and 3.65 μm [39,46] Dispersion of aerosol modes 1, 2, 2′ and 3: 1.56, 1.29, 1.23, and 1.28 [39,46] Aerosol composition: water solution of H2SO4 with concentration of 75% Aerosol particle shape: spherical H2SO4 refractive index [52] Optical depth, single scattering albedo and Legendre series expansion of particle scattering phase function are calculated using Mie theory |
| CO2 absorption and molecular scattering | Line list: AMES [61,62,63] Line shape: sub-Lorentzian profile [64] Line cut-off: 250 cm−1 CO2 continuum: <2 × 10−9 cm−1amagat−2 CO2 volume mixing ratio: 0.965 Rayleigh scattering [9,10,65] |
| H2O absorption | Line list: BT2 [66] Line shape: Voigt profile Line cut-off: 180 cm−1 H2O volume mixing ratio: 28 × 10−6 (28 ppm) |
| Surface emissivity | 0.95 |
| Surface topography | Magellan data [51] |
| O2 (a1Δg) airglow | Line-by-line model [67,68] |
| Model free parameters | (1) Scaling factor applied on particle number density vertical profiles of modes 2, 2′ and 3 (2) Column density of O2* molecules (3) Scalar wavelength shift |
| CO2 Continuum Coefficient, α | Weighted Mean with STD | Weighted Mean with STD at 50° N | Percentage of Retrieved τ in Range of 25–50 |
|---|---|---|---|
| 0.2 × 10−9 cm−1amagat−2 | 41.7 ± 6.5 | 39.0 ± 5.2 | 83% |
| 0.6 × 10−9 cm−1amagat−2 | 36.7 ± 6.1 | 32.7 ± 5.4 | 96% |
| 1 × 10−9 cm−1amagat−2 | 31.8 ± 6.1 | 28.8 ± 4.5 | 98% |
| Total Cloud Opacity | Instrument and Reference |
|---|---|
| τ = 25–40 | Descend probes [1] |
| τ = 25–50 | NIMS/Galileo spacecraft [39,44] |
| τ = 32–42 with <τ> = 36.5 at 1 μm | VIRTIS-M/Venus Express [33,46] |
| τ = 17–22 of lower cloud layer that corresponds to total τ = 35–40 | TripleSpec/Apache Point Observatory [47] |
| <τ> = 36.7 ± 6.1 at 1 μm for α = 0.6 × 10−9 cm−1amagat−2 <τ> = 31.8 ± 6.1 at 1 μm for α = 1.0 × 10−9 cm−1amagat−2 | SPICAV IR/Venus Express [33,46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evdokimova, D.; Fedorova, A.; Ignatiev, N.; Zharikova, M.; Korablev, O.; Montmessin, F.; Bertaux, J.-L. Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows. Atmosphere 2025, 16, 572. https://doi.org/10.3390/atmos16050572
Evdokimova D, Fedorova A, Ignatiev N, Zharikova M, Korablev O, Montmessin F, Bertaux J-L. Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows. Atmosphere. 2025; 16(5):572. https://doi.org/10.3390/atmos16050572
Chicago/Turabian StyleEvdokimova, Daria, Anna Fedorova, Nikolay Ignatiev, Mariya Zharikova, Oleg Korablev, Franck Montmessin, and Jean-Loup Bertaux. 2025. "Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows" Atmosphere 16, no. 5: 572. https://doi.org/10.3390/atmos16050572
APA StyleEvdokimova, D., Fedorova, A., Ignatiev, N., Zharikova, M., Korablev, O., Montmessin, F., & Bertaux, J.-L. (2025). Cloud Opacity Variations from Nighttime Observations in Venus Transparency Windows. Atmosphere, 16(5), 572. https://doi.org/10.3390/atmos16050572





