Abstract
Human populations are scattered worldwide and live under widely different climates. Like other mammals, humans respond to climatic influences through various processes involving behavior, physiology, and various forms of adaptation. Human populations can be explored in investigating patterns of adaptation because many of their biological attributes have been monitored for over a century. Here, we evaluated the association between several thermal indices and human birth weight (BW) and offered some initial observations on the temporal integration of thermal cues associated with pregnancy outcomes. We compiled three datasets: (1) a dataset with global coverage of recent BWs; (2) an extended time series for seven European countries; and (3) a time series for four countries in equatorial Africa. Each dataset was analyzed for associations between BW and mean annual temperature, as well as seasonal and daily amplitudes. Mean annual temperatures, as well as seasonal and daily amplitudes, delivered consistent and comparable impacts in our analyses. The thermal indices can explain approx. 80% of the global variation in BW and 25–50% of the BW variation in time series covering the last 70 to 120 years. Mean BW in larger aggregates of humans (i.e., millions) is associated with several thermal indices, likely associated with systematic differences in proximate factors (e.g., maternal height, weight, food intake) between populations. This study underlines the diverse impact of the thermal environment on human reproduction, but it also underscores that this impact is less pronounced for differences in mean BW with respect to different communities, and it is possibly undetectable and/or irrelevant with respect to differences between individuals.
1. Introduction
Climate change and the associated temperature increase will directly and indirectly affect ecosystems and human societies worldwide [1]. Many of the indirect effects are becoming more apparent as extreme weather conditions damage infrastructure [2], affect agricultural production [3], facilitate the spread of infectious diseases [4], and accelerate the loss of biodiversity and ecosystem services [5]. These marked impacts appear concurrently with subtle processes of adaptation that allow plants and animals to alter or appropriate ecological traits.
Living organisms respond to climate change by altering their behavior (avoidance), by phenotypic plasticity or genetic change (adaptation), by changing their range (relocation), or by going extinct if they are unable to ensure their long-term survival and reproduction [6]. However, our insight into adaptation patterns is limited due to a lack of understanding of how multiple concurrent changes supposedly contribute to individual and population fitness [7]. Humans are likely the only species for which we have adequate information with which to assess subtle changes in responses to climate change, the resulting patterns of adaptation, and their consequences. Studies on human adaptation are thus not only relevant for assessing current public health impacts [8] but can also contribute to identifying relevant meteorological indices and mechanisms of adaptation. In this paper, we investigate temporal and spatial variation in human birth weight and assess whether global differences in birth weight can be accurately assessed from thermal indices.
Neonate birth weight (BW) is recognized as a key human attribute, with robust associations with diminished cognitive skills [9], changes in metabolism [10], and an array of other health-related aspects [11,12]. BW is negatively affected by environmental variables such as altitude and elevated temperatures, which affect pregnancies and maternal phenotypes [13,14,15]. Elevated temperatures influence pregnancies through heat stress and heat acclimation [16], which may reduce the delivery of nutrients and oxygen to the placenta and fetus [17,18]. It is conceivable that temperature-dependent food intake in mothers contributes to global differences in BWs [19]. Possibly, intermittently occurring reduced temperatures may permit added food intake [19], improved intestinal function, and improved nitrogen retention [20], which augment fetal growth [21]. The importance of temperature-dependent hypophagia is, however, difficult to assess, as mothers in warmer climates are also shorter [22,23], have lower BMI [22,24], are affected by infectious diseases [25,26], and often perform strenuous physical labor [27]. Similar concerns can be raised about the effect of altitude and the associated effect on pregnancies and fetal growth through hypoxia [28]. The effect of altitude can be explained by other mechanisms, such as high daily temperature variation and/or poorer socioeconomic conditions [29,30].
However, a century of studies in human reproduction have only sporadically emphasized the importance of environmental factors on human reproduction. Most studies on BW have stressed that low BW is linked to adverse socioeconomic conditions [30,31], which affects mothers and unborn children. BW increments are viewed as slow but progressive as they increase due to gradual socioeconomic development over multiple decades [32]. Gradual socioeconomic development contributes to maternal height and weight increments, which compound socioeconomic effects, leading to higher BW [30,32,33]. Concurrent fertility rate declines diminish infectious diseases’ impact [34], which stabilizes the temporal variation in BWs. The underlying mechanisms are primarily linked to the maternal phenotype, namely, height, weight [33], nuptial status, parity, and maternal age [35]; but nutritional status, such as macronutrient intake (calories, protein, fat, carbohydrates [36]) and micronutrient supplements (iron, folic acid, etc. [37]), can also be important. The temporal variation in nutrition and infectious diseases can lead to considerable year-by-year variation in BW, and the direct dependency on nutritional conditions underlines that BWs also in the 21st century remain vulnerable to economic and social disruption [38,39,40,41,42].
Records on BW are also influenced by fetal death [43] as only live-born neonates are considered in BW studies. The risk of fetal (perinatal) death will disproportionally affect low- and high-weight fetuses, while fetuses of intermediate size have the lowest perinatal mortality [44,45]. The BW associated with the lowest perinatal mortality varies in terms of both time [45,46] and place [47], suggesting a variability that compares to that of BW itself. Studies on perinatal mortality across the world clearly show that low-weight neonates have elevated mortality in all human populations. It can also be surmised that the intermediate BW, which is associated with the lowest mortality, is often lower than reported for Northern Europe [47,48,49,50,51]. Whether fetal mortality patterns contribute to systematic global differences in the mean weight of live-born neonates among different populations is unknown, just as we remain ignorant of other population-thinning processes (self-thinning [52]) that may favor juveniles (follicles, embryos, fetuses, and neonates [53,54]) with a given intrauterine growth potential.
Extended BW time series show that the mean annual BWs in given countries fall within a relatively narrow range (±100 g). This is readily appreciated for Japanese neonates, as BWs are the same today as at the beginning of the 20th century (3000 g [55,56,57], but it also applies where BW shows increments. Figure 1 illustrates that Norwegian, French, and British neonates increased in weight from 1860 to the mid-20th century, but it is also clear that Norwegian BWs were rarely reduced to less than 3350 g, which is the typical BW in France and the United Kingdom (Figure 1 [56]). Compilations of historical BWs from a range of other countries also support the notion that past geographical differences in BW between nations/latitudes were much the same as today [55,56,58], and it is conceivable that they existed for centuries, perhaps even millennia. Consistently, Wells’ [59] projection of the Mediterranean’s BWs over the past 5000 years provides BW estimates that compare well with current BWs in the region [56]. These geographical differences can possibly be predicted from thermal environmental indices.
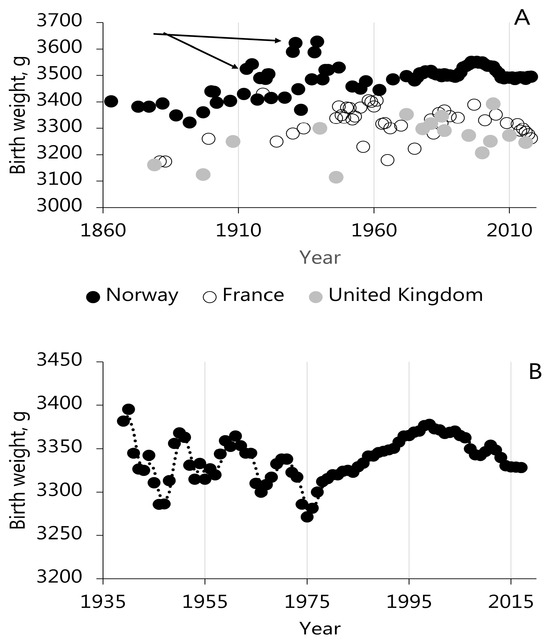
Figure 1.
(A) Birth weights in Norway, France, and the United Kingdom in the period 1860 to 2020. The data originate from multiple published papers and illustrate a limited variation in birth weight (±100 g) during marked socioeconomic and demographic developments. Arrows point to isolated records of elevated BW, which could emerge as the result of short-lived elevated perinatal mortality. (B) Mean annual BW for seven European countries from 1935 to 2022 adjusted by the effect of country. The regional estimate assumes synchronous variation in time for the given countries and that the differences in BW were fixed in this period.
1.1. Thermal Indices Relevant for the Assessment of Differences in Birth Weight
Recent studies on BW variation reflect the growing interest in climate change and its potential impact on human reproduction [18,60]. There has been increased interest in whether short-term seasonal exposure to temperature extremes increases the risk of preterm birth and whether fetal growth rates are affected [61,62]. Not all epidemiological studies on seasonal variation in BW have been conclusive [63], and it has been challenging to establish a relationship between BW, physiological stress, and specific thermal indices [60]. This lack of clarity is likely linked to the multifaceted relationship between BW and the thermal environment, which encompasses both short- and long-term effects of temperatures and temperature variation.
It has been argued that the long-term effect of temperatures influences human body size (Bergman’s rule [64], but see [23,65]) and the length of the legs and arms (Allan’s rule [66,67,68]; hence, individuals who live in cooler climates have been argued to be larger, but to have shorter body extremities [22,69]. As BW is associated with maternal height and weight [33], we can expect that BW will also be associated with temperatures, as has been noted in several studies [13,14,15].
There is less support for the idea that temperature variation influences BW. However, it is conceivable that seasonal resource intake/availability affects reproduction [70,71]. Seasonal differences in BWs [72,73] could thus result from an adaptation to local weather patterns. It could also be speculated that daily temperature amplitude either informs the risk of acute heat stress and prematurity [61] or functions as an environmental cue with respect to aridity and general food scarcity [74,75]. A reduction in BW due to daily temperature amplitudes could be interpreted as an adaptation that facilitates the development of phenotypes/genotypes with enhanced aptitude to survive and reproduce under permanent food scarcity [76,77].
Disentangling the impact of weather and climate while adequately controlling for proximate contributors such as maternal height is problematic due to the inter-relatedness of these contributors. It is not difficult to acknowledge that unfavorable weather conditions induce altered behavior, which allows mothers to avoid phenomena (stress or injury) that negatively impact pregnancy (Table 1). Less intuitively, climates shape maternal anthropometrics [22,69], which counters that mothers would deliver “substandard” neonates.

Table 1.
Overview of possible remote and proximate biometeorological associations with human birth weight. A lack of behavioral avoidance is associated with stress/injury, which affects pregnancies, while a lack of adaptation by altered anthropometrics will be associated with substandard maternal phenotypes.
Standard assessments of the biological impact of temperatures typically accommodate proximate factors that characterize pregnancies and maternal phenotypes, but this approach is likely to underestimate the impact of temperatures. It is safe to assume that short-term elevated temperatures can diminish fetal growth and cause prematurity [16,61,62], but much uncertainty shrouds other putative contributions from the thermal environment. It seems likely that long-term adaptations are tied to energy conservation [78], and/or the integration of other environmental cues, which manifest as changes in anthropometrics [64,69,79] (Table 1), and/or the fact that other epigenetic effects modulate physiological responses [80]. The process of adaptation is undoubtedly slow and only permits a gradual integration of environmental impacts/cues over multiple decades/generations (for intergenerational inertia, see [79,81]; for predictive adaptive responses, see [82,83]).
Current evidence documents the short-term impacts of nutritional perturbations, while multiple studies on war-induced famines have provided evidence of long-term/later life responses to in utero nutritional deficits [38,39,40,41]. The impact of nutritional deficits on development trajectories will, however, diminish with age, and even severe nutritional deficits will not alter physiological targets in adulthood [84,85]. Other studies have linked fetal deficiencies to maternal mental health and socioeconomic status [11,12], but few studies specifically investigate how the physical environment affects mothers and their future children. The period of integration/inertia of thermal cues is unknown, and therefore, there is little evidence to guide such analyses. However, when we contemplate that passive, non-evolving environmental traits function as “cues”, we must expect that these cues are adopted and have an effect before the relevant biological events take place. In respect to BW, we would refer to a “period of integration”, which is completed before the reproductive period ends. It is, however, also possible that this period of integration is completed before reproduction begins.
1.2. Objectives
We conducted the following analyses to gain further insight into the relationship between BW and meteorologically measured outdoor temperatures. We chose to assess remote associations (Table 1), which allowed for the assessment of all of the ensuing short- and long-term contributions of temperatures. The primary aims were (1) to determine which thermal indices were relevant to consider; (2) to assess which period of integration would allow us to predict the temporal variation in BW; and (3) to determine whether monitoring of BW can inform the biological impacts of changes in weather and/or climate with fair accuracy.
2. Materials and Methods
Our assessment is based on three data compilations. The first has global coverage, while the other two were restricted to seven European countries (Denmark, Finland, France, Germany, Norway, Sweden, and The United Kingdom) and four countries in equatorial Africa (Kenya, Ethiopia, Nigeria, and Gambia), respectively.
2.1. Global Data for BW
We identified prior compilations of BW records and searched Google Scholar and PubMed for recent publications that reported on BW. The search string was [birth weight] AND [name of relevant countries]. The data were selected for high spatiotemporal resolution, including information on BW from hospitals, cities, and municipalities, while all “National” surveys were excluded. The variation in BW reflects both marked socioeconomic differences and seasonal variation because the records often represent the community data for a single month or a season. A large part of the data originated from the WHO [56] (n = 575) and Meredith [86] (n = 22), which were supplemented with more recent records (n = 173). The total sample included 770 observations from 407 different geographic locations. The observations were distributed across the world and included multiple records from North America (38), Central America (17), Caribbean (12), South America (85), Oceania (20), East Asia (33), South-East Asia (85), South Asia (139), West Asia (43), Europe (89), North Africa (19), East Africa (94), West Africa (71), and South Africa (25). We aggregated the observations by even-integer latitudes (e.g., 0–2° N, 2–4° N, etc.) and generated 54 “populations of populations” (Figure 2A,B).
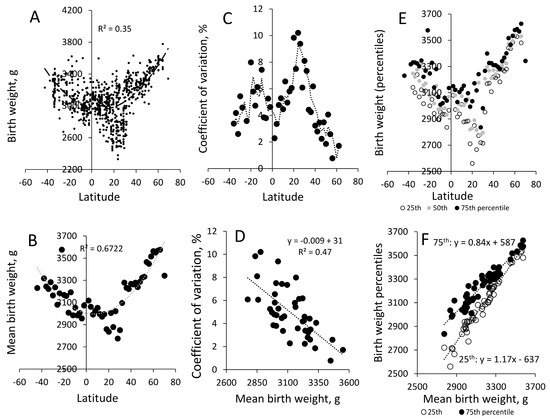
Figure 2.
Birth weight (BW) and birth weight variation for 770 observations: (A) birth weight (g) vs. latitude; (B) mean BW for even-integer latitudes; (C) coefficient of variation (×100) aggregated for even-integer latitudes; (D) the relationship between the coefficient of variation and birth weight for even-integer latitude records; (E) 25th, 50th, and 75th percentiles for even-integer latitudes, with R2 for a second-order function for the 50th percentile; (F) scatterplot of 25th and 75th percentiles vs. mean birth weight.
By aggregating the data by latitude (Figure 2), we removed most of the impact of socioeconomic factors [30,31], which cloud the association with global thermal indices by influencing BW for individuals and communities. The mean number of observations within the even-integer latitude was 14, sd 11 (range: 1 to 47). We calculated the 25th, 50th, and 75th percentiles within even latitudes for 49 even latitudes with more than one observation (Figure 2E, Supplemental Table S1). The mean year of the sample was 1981, sd 15.
2.2. Global Thermal Indices
We retrieved information on temperatures for each of the 407 locations. We first searched for thermal indices in the online record of the World Meteorological Organization [87]. We searched the World Weather Online [88] when the data were unavailable in the WMO database. If unavailable in either of these, temperatures were retrieved from Time and Date climate records [89]. A total of 63% (488/770) originated from WMO, 27% (261/770) from WWO, and 2% (21/770) from TAD. We incorporated four temperatures for all locations, representing the 30-year mean temperatures associated with daily temperature extremes (Table 2, Figure 3 and Figure S1).

Table 2.
Thermal indices as observed and calculated. The data are based on the mean for 54 locations defined by even-integer latitude.
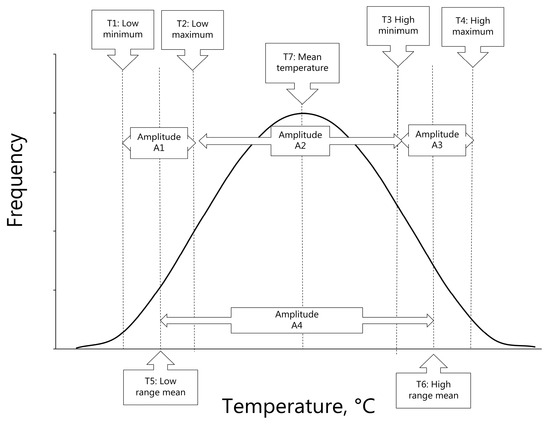
Figure 3.
Illustration of temperature range and frequency of given temperatures over the year for a given location. The notations (T1 to T7 and A1 to A4) refer to the observations and calculations provided in Table 2.
These included the following: T1—the lowest daily minimum temperature in any month; T2—the corresponding daily maximum monthly temperature with the lowest minimum temperature; T4—the highest daily maximum temperature in any month; and T3—the corresponding daily minimum monthly temperature in the month with the highest maximum temperature. The mean annual temperature (T7) was defined as the mean of the four temperatures, i.e., T1 to T4 (Table 2, Figure 3). Seasonal lows were defined as the mean of T1 and T2 (T5), and seasonal highs were defined as the mean of T3 and T4 (T6), which was associated with the amplitude A4, given as the difference between T5 and T6.
2.3. Statistical Models for the Global Dataset
The even-latitude BW percentiles were examined for their association with the means of various thermal indices [90]. To make the relevant comparisons, we first analyzed BW percentiles for their association with annual mean temperature (T7), seasonal amplitude (A4), and mean daily amplitude (A1–3). The pre-analysis assessment revealed an unexpectedly strong association between the within-sample coefficient of variation and BW; therefore, we also included this measure in the models. The analysis showed that interactions between daily amplitudes and the other two temperatures were irrelevant, and here, we present the outcome that only includes the interaction between annual mean temperatures and seasonal amplitudes. The model statement was as follows:
BWpercentile = a × CVBW + b × A1–3 + c × A4 + d × T7 + e × T7 ×A4 + err.
We continued by investigating alternative thermal indices, i.e., indices other than mean temperature, seasonal amplitudes, and daily amplitudes, which supported the identification of relevant thermal indices.
2.4. Models of Temporal Change in Annual Mean Birth Weight
Ecologists often apply space-for-time substitutions to infer slow ecological processes [91]. However, it is difficult to accept simple multivariate models on cross-sectional records as reliable predictors of temporal change [92]. The reason for this is that the underlying assumptions, transformations, omissions, and cross-correlations can lead to erroneous or misleading outcomes. Moreover, confounding between known (and unknown) factors limits our ability to provide an unambiguous interpretation. We compiled two additional datasets, which allowed us to determine whether the outcome of the global cross-sectional analyses corresponded to the association between seven European countries and four countries in equatorial Africa. In compiling these datasets, we made special efforts to secure BW observations for multiple decades (Figure 4).
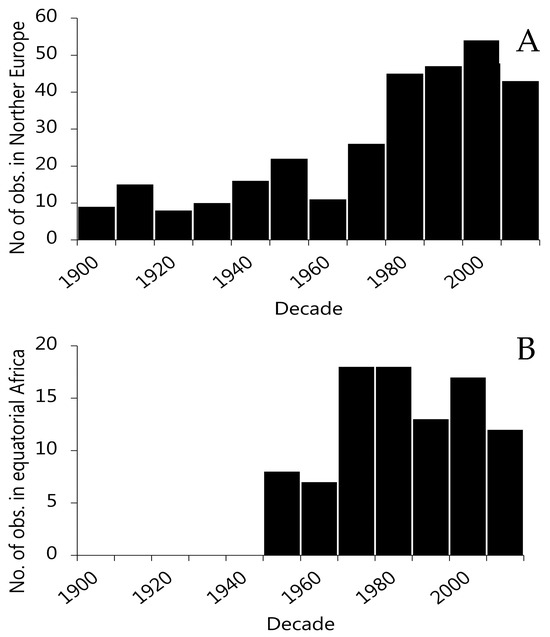
Figure 4.
Overview of the temporal distribution of BW records in (A) Europe and (B) equatorial Africa by decade.
To compile the records, we searched Google Scholar and PubMed for recent normative studies reporting mean BWs in specific countries. The search string was [birth weight] AND [name of relevant countries]. For Europe, relevant countries included Denmark, Finland, France, Germany, Norway, Sweden, and the United Kingdom. For equatorial Africa, the relevant countries included Kenya, Ethiopia, Nigeria, and Gambia. We retrieved a total of 305 observations for the years 1901 to 2019 for Europe, and 93 in the years 1952 to 2020 for equatorial Africa (Figure 4, Supplemental Table S3 and Table S4). Mean BW was, in many cases, and especially before 1970, drawn from small sample sizes (<500). The year of sampling was not always provided, and we had to assign the given BW to the year of publication. Hence, early records were likely biased (late) by 2–4 years, which undermines our ability to assess the association between a given year’s weather and BW.
Information on temperatures was obtained from The World Bank Climate Knowledge Portal [93]. Datasets providing the mean minimum and maximum daily temperatures, by month, for the years 1901 to 2022 were downloaded for each country. We calculated the mean temperatures (T7:1–12: the mean of 12 monthly means), temperature amplitudes (A4: the maximum minus the minimum monthly mean temperature), and mean daily amplitudes (A1–12: the mean difference between maximum and minimum monthly temperatures for 12 months) for each year for the given countries. We then calculated thermal indices with six different running means to compare the association for the current year, the average of the past 5 years (running mean for the current year to four years previously), and similarly for the running means of 10, 20, 30, and 35 years. The calculation of the 35-year running mean was based on the years 1901 to 1935 and only included 88 years of observation (1935–2022). Before analysis, all observations earlier than 1935 were deleted to ensure that all analyses had the same number of observations and that the statistical outcomes were comparable by the Akaike information criterion (AIC) and the level of explanation (R2). We began our analysis by retrieving the AIC and R2 for the association between BW and location (country), which revealed systematic differences between the countries (Figure 1). We then added thermal indices and executed the model without location information. Goodness-of-fit indices, namely, the AIC value (lower is better) and R2 (higher is better), were used to assess which models provided more information than the location, i.e., which models explain part of the temporal variation in BWs.
All statistics were executed in SAS 9.4 (SAS Institute, Cary, NC, USA), using PROC GENMOD to retrieve the AIC values and PROC GLM to retrieve the R2 values.
3. Results
Differences in BWs were associated with latitudes, allowing for higher BW at high latitudes in both hemispheres (Figure 2). Countries located at 20–30° N latitude depart clearly from a general second-order association (Figure 2A,B and Figure S1A,B), which is less apparent in the southern hemisphere. However, 20–30° S latitudes also show very high BW variation (Figure 2C), which, in unambiguous terms, sets the latitudes close to the Tropic of Capricorn and Tropic of Cancer apart from other latitudes. The mean 25th percentile was 3091, sd 246, i.e., approx. 100 and 250 g lower than the 50th percentile, i.e., 3173, sd 212; and the 75th percentile, i.e., 3252, sd 180, respectively. The global variation was substantially higher for the 25th percentile (8%: 246/3091 × 100) than for the 75th percentile (5%: 180/3252 × 100) (Figure 2F, Supplemental Table S1 and Table S2). The 25th percentile had a minimum at 20–30 degrees northern latitude, while the 75th percentile had a minimum closer to the equator (Figure 2E), indicating that the 25th percentile was more closely associated with maximum temperatures than the 75th percentile (Supplemental Figure S1).
The basic thermic environment model explained 91% (R2 = 0.91) of the variation in the 25th percentile and 75–80% in the 50th and 75th percentiles (Table 3, Models 1–5). The coefficient of variation within the even latitude was significantly associated with the 25th and 50th percentile but not the 75th percentile. However, the coefficient of variation was also strongly correlated with the given thermal indices (Table 3, Model 6), and its removal from the model only led to a marginal reduction in the level of explanation (R2).

Table 3.
Outcome of analysis of birth weight by percentiles and coefficients of variation (CVs) for even latitudes (n = 49) with respect to their association with mean temperature, seasonal amplitudes, daily amplitudes. R2* is the R2 value for models that do not include the coefficient of variation.
Mean temperatures, seasonal amplitudes, and daily amplitudes have a negative association with BWs, while the interaction between mean temperatures and seasonal amplitudes has a positive association (Table 3). The interaction between mean temperatures and seasonal amplitudes is only significant for the 75th BW percentiles. Various other models, which include alternative thermal indices, have a slightly lower ability to explain the global variation in the 75th percentiles (when the coefficient of variation is included, Table 4). Model 8, which includes a reference to the minimum temperature (T1) and three amplitudes (A1 to A3), shows significant effects for all the thermal indices. By replacing T1 with T4, only amplitude A2 is shown to be significant. Hence, the maximum temperature T4 would be a key index (Figure 3), which would challenge the three-split perception (Models 1 to 3). The three-split models will, however, also serve to identify the daily maximum temperature (T4) because the mean (T7) plus half the seasonal amplitude (A4/2) plus the daily amplitude in the warmest month (approx. equal to A1–3) equals T4. The importance of T4 was also indicated by the diminishing levels of explanation when the temporal resolution (using seasonal or annual indices) was used (Table 4, Models 7 to 11).

Annual Variation in Birth Weights
The selected European countries had mean daily amplitudes in the range of 6.4 to 8.5 °C (Supplemental Table S3). Seasonal amplitudes and mean annual temperatures were in the range of 12.7 to 28.4 °C and 1.7 to 11.0 °C, respectively. The association between the current thermal indices (running mean = 0) was significant for several thermal indices. However, the AIC value was higher than observed in the model that only included the country as a variable (2901 vs. 2786). When location (i.e., the country) was added to the model, no thermal indices were found to have a significant effect. Thus, current indices were only relevant as they served as an alternative expression of location/country.
All indices were significant after adding a location at a running mean of 20 years or higher. At these running means, the thermal indices explain more of the BW variation than location alone; i.e., a part of the temporal variation in BW from 1935 to 2019 was explained (Figure 1B). The highest level of explanation and lowest AIC value was reached for running means greater than 30 years, which offered a level of explanation (74%, Table 5) that compared to the level of explanation in the global cross-sectional model (Table 3, Model 2).

Table 5.
Outcomes of analyses of BW in European countries (Denmark, Finland, France, Germany Norway Sweden, and the United Kingdom; n = 267), which examined the association between mean birth weights and running mean (RM) temperatures. Thermal indices correspond to indices in Table 1, with running means of 0, 5 10, 20, 30, and 35 years. A model that only included location (i.e., the country) had an AIC value of 2786 and R2 = 0.76. Location was significant in all models (p < 0.001). R2*/AIC* provides values for models that include location.
The selection of countries in equatorial Africa had mean daily amplitudes in the range of 11.8 to 13.4 °C (Supplemental Table S4). Seasonal amplitudes and mean annual temperatures were in the range of 3.4 to 6.9 °C and 23.0 to 27.1 °C, respectively. The association between current thermal indices (running mean = 0) was significant for all thermal indices, whether the location was added to the model or not. Current thermal indices were thus a better expression of the location than the country, but the level of explanation was relatively low (R2 = 0.17). As the running mean increased, all indices also remained significant after adding location. The highest level of explanation and the lowest AIC value were observed for a running mean of 20 years, which offered a level of explanation of 25%. The outcome was the same as observed in the cross-sectional analysis (Table 6). It includes a negative association for daily amplitudes, seasonal amplitudes, and annual mean temperature, while there is a positive association for the interaction between annual mean temperature and seasonal amplitudes. When the interaction is removed from the model, the seasonal temperatures become positive (Table 5 and Table 6). Therefore, it can be inferred that the positive effect of seasonal amplitudes is enhanced by increasing the annual temperatures, but not proportionally, which results in a negative effect of seasonal amplitudes in the full model. For European countries, the impact of the interaction between annual mean temperatures and seasonal amplitudes is minimal, which permits the independent effect of temperature amplitudes to remain positive. Hence, the same associations were noted for the three data selections.

Table 6.
Outcomes of analyses that examined the association between mean birth weights and temperatures in equatorial African countries (Gambia, Nigeria, Ethiopia, and Kenya; n = 93), which examined the association between mean birth weights and running mean (RM) temperatures. Thermal indices correspond to indices in Table 1, with running means of 0, 5 10, 20, 30, and 35 years. A model that only included location (i.e., within a country) had an AIC value of 1171 and R2 = 0.11. Location/country was not significant in any model (p > 0.25). R2*/AIC* provides values for models that include location.
4. Discussion
Our global BW dataset included mean BWs from 2330 g to 3778 g, which compares well with Meredith’s compilation from 1970 [86] (2400 g to 3600 g). The more extensive range in our compilation is likely the product of a larger sample size. The global variation in BW aligns well with the patterns in various thermal indices. Higher BWs generally align with annual mean temperature, while lower BWs align with daily temperature variation or maximum temperatures (Figure 2A,B and Figure S1). These visual interpretations are supported by the statistical assessment of the global BW record, which shows that annual mean temperatures have a higher impact on the 50th and 75th percentiles than on the 25th percentile. The impact of daily amplitude appears to be lower (Table 3), but when the coefficient of variation is removed, the impact is approx. −30 g/°C for both the 25th and 75th percentiles. So, from a global perspective, mean annual temperatures and daily amplitudes have consistent effects, while the effects of seasonal amplitude appear more variable/uncertain.
In considering the alternative models, we can infer that models informing temperature extremes (Table 3 and Table 4, Models 5 and 6) have a higher level of explanation than models with lower temperature resolution (seasonal and annual means). Therefore, it seems that the consideration of daily temperature extremes is important—possibly critical—in accurately modeling the global variation in BW. However, it must be stressed that the given effects are unadjusted for proximate factors. When parental height, BMI, and calorie intake are introduced to the statistical models, we find no significant effects of mean annual temperature or seasonal amplitude [94]. The impact of daily amplitudes will remain, but its effect is reduced to half the size noted in these analyses. With this, we could argue that current human populations have appropriately adapted to differences in climates and that the variation in BW is the “natural” consequence of this.
We unexpectedly found that the variability in BW within even latitudes varied systematically across the world, and that the variability had a high correlation with mean BW (Figure 2C). As BWs increase, they become increasingly uniform, and the differences between the 25th and 75th percentiles disappear (Figure 2F); i.e., all communities have the same mean BW. The association (Figure 2C) also proposes that BW can be as high at 5° N as it can be at high latitudes. Admittedly, we made no special effort to ensure samples were taken from latitudes between the equator and 10° N; hence, these latitudes’ 50th and 75th percentiles may be underestimated. In searching specifically for reports that showed high mean birth weights in this region, we identified a few publications that indicate that populations in this region can have BWs that compare to those at high latitudes (Colombia, 3400 g [95]; Cameroon, 3600 g [96]). It would thus be reasonable to suggest that mean temperatures in the range of 23 to 27 °C do not necessarily compromise fetal growth or the development of maternal phenotypes capable of delivering neonates with high BW. However, this only occurs in humid regions with low daily amplitudes, e.g., in southern (coastal) but not northern Nigeria [97].
The coefficient of variation and the seasonal amplitude are highly correlated, suggesting that their contributions overlap (Table 3, Model 4). Consistently, we find that either the coefficient of variation or the seasonal amplitude has an effect (Table 3), which we interpret such that seasonal amplitudes do have an effect on heavier neonates (75th percentile), while other (or additional) “seasonal effects” are of importance for lower birth weights (Table 3, Models 1 and 2). The mixed outcome is consistent with other studies showing that seasonal variation in BW is poorly associated with seasonal variation in temperatures [64]. It should also be noted that sizable seasonal variation in BW (>200 g) can be observed in countries like Nepal [98] and Burkina Faso [99] under limited seasonal temperature variation, while variations of less than 50 g are seen at higher latitudes in highly seasonal climates (e.g., Israel [72] and Ireland [100]). A study of seasonal BW variation in the USA [101] identified significant seasonal variation in BW for neonates of African ancestry but not for Europeans (white), which suggests that BW seasonality is contingent on other factors. Given that we find little seasonal variation in BW and food intake when calorie availability is high (USA [102,103,104]) and higher variability when food availability is low (e.g., Nepal and Burkina Faso [104]), we suspect that seasonal variation in BW—i.e., the occurrence of lower mean BWs—has closer ties to seasonal variation in calorie availability, maternal BMI, and socioeconomic status than to seasonal variation in temperatures [105]. Seasonal occurrence of infectious diseases and the differential mortality rate between male and female fetuses [106] could also make marked seasonal contributions as males weigh approx. 100 g more than females at birth. Therefore, we expect a lower ability to predict BW variation from temperatures in low-income countries due to low food security (calorie availability), lower BMI, and higher perinatal mortality rates.
4.1. Temporal Integration of Thermal Cues and the Effect on Pregnancies and Maternal Phenotypes
Analyses performed on the datasets from Europe and equatorial Africa align with the comments given on the results from the global dataset. Our ability to explain the temporal variation in mean BW in equatorial Africa is thus far lower than that with respect to the European countries. However, the low accuracy is not simply a result of biological factors and sampling errors; it is also linked to large spatial heterogeneity within the countries [96]. Occurrences of socioeconomic disruption [42], shifts in perinatal mortality [45,46,47], and periods of severe food shortage (Ethiopia [41]) also reduce our ability to link temporal variation in BWs to thermal indices.
We found no association between thermal indices and shorter running means; thus, we provide no evidence that current weather conditions affect pregnancies [16,61]. However, it is questionable as to whether our data on annual mean BWs could reveal such information because half the pregnancies (born from January to May) would be influenced by previous years’ weather. Moreover, many data entries were assigned to the year of publication, which likely disrupted any association with shorter running means. Consistently, running means of 5 and 10 years also yielded unconvincing associations (Table 5 and Table 6), which meant that we only acknowledged effects that would be associated with the maternal phenotype. These would be channeled through changes in maternal anthropometry or physiological modulations associated with “environmental cues” [64,69,79].
The mean age of the mother is 30 years in all countries included in the two datasets [107], and there would be some logic in assuming that the period of integration of thermal cues would match the age of the mothers. This means that they continuously integrate thermal cues. The observations for Europe align with these notions, while the period of integration appears to be shorter for the dataset from equatorial Africa (20 y). It is impossible to account for this difference, especially when we also consider that the running means of 20 to 35 years are fairly similar in the European countries. We can, however, note that the period of integration for thermal cues spans several decades. This extended period of integration should, in theory, be sufficient to modulate the maternal effects that guide fetal growth/development [79,81,82,83].
4.2. The Accuracy of the Thermic Environment Models
We achieved high levels of explanation in our model, which supports the notion that BWs are predictable from thermal environment indices. However, this was the product of heavy-handed data aggregation, and the association with the original observations is far poorer (R2 = 0.35 vs. R2 = 0.63) (Figure 2A,B). If we examined data from individual pregnancies, we would find a poorer association, possibly R2 = 0.10, because the socioeconomic factors deliver marked contributions [30,31]. We should also be mindful that the level of explanation scales to the variation in the BWs, and that the thermal indices often simply reflect the “location”. This is, however, not the case for the equatorial Africa dataset, where the level of explanation is 25% (Table 6). Location does, however, influence the level of explanation in the European dataset, and when we run analog models for individual countries, we find levels of explanation of approx. 50%, i.e., two-thirds the level of explanation found for the group (Table 5). Our ability to explain the temporal variation in BW by decadal running mean indices is thus in the range of 25 to 50%, where the highest level of explanation is found in developed countries, where infectious diseases and other socioeconomic contributors [30,31] have less influence on annual mean BWs.
4.3. Further Model Development and the Impact of Other Putative Contributors
It is tempting to improve the thermic models with additional factors that would increase the level of explanation. In addition to proximate factors (e.g., human height [94]), several avenues could be pursued. In mentioning four examples, we note the following: (1) Increasing the sample size would lead to higher levels of explanation because it limits the number of outliers that emerge from lower sample sizes (Figure 2B,E). (2) Altitudes could be added to the statistical model as altitudes might modulate the impact of temperatures. An increase in altitude has been reported to lead to 75–150 g reductions per 1000 m increase [29], suggesting that this would lead to substantial improvement. Regrettably, the addition of altitude to Models 1 to 6 does not lead to improvement, and altitudes are not statistically significant (p > 0.63); it does, however, lead to improvements in Models 7 to 9, perhaps because altitude accurately informs daily amplitudes [76]. (3) We could also consider adjusting for relative humidity, permitting a tighter association with heat stress at higher mean temperatures [14]. This would, however, be quite challenging to incorporate, as relative humidity, like temperatures, varies over the day. (4) We could extend the analyses of temporal variation and include past decades such that we consider, in full, the thermal contributions across generations [79,81,108]. This will, however, require a larger dataset than we compiled for this study because the added requirement for thermal indices would limit the analyses to more recent years, when we also need to include the thermal indices for past generations. However, a visual inspection of the temporal data (Figure 1A) would suggest that an attempt to improve the model is unlikely to be successful simply because a large part of the variation is associated with spatial heterogeneity and variation caused by factors that are difficult to monitor and/or measure, such as the virulence of infectious agents and the impact, recovery, and lagged effects of sudden socioeconomic change. However, continuous, century-long data series with full coverage of entire nations should provide more apparent associations than those observed in our analysis.
It is inappropriate to comment on the possible impact on future pregnancies and BW based on the given associations because they mostly reflect adaptation, which has already been adopted among human populations. It should also be noted that thermal indices are mutually dependent; e.g., increments in mean annual temperatures are associated with systematic decrements in daily amplitudes [109]. Hence, reductions in BW due to increases in the mean temperature are associated with an increment resulting from reduced daily amplitudes.
5. Conclusions
We conclude that (1) thermal indices that report daily maximum temperatures, along with a measure of temperature variation, such as that given by the combined effect of annual mean temperatures and seasonal and daily amplitudes, provide accurate information on the differences and variation in human BWs. (2) Our assessment suggests that the integration period spans decades, and thermal cues are likely integrated continuously from birth to adulthood. (3) Monitoring BW can provide information on the biological impact of weather and/or climate changes with fair accuracy, but it requires data aggregation and/or large amounts of records. BWs that originate from nations with a low and/or varying food supply and elevated perinatal mortality have poorer associations than the BW records obtained from nations with low perinatal mortality and high food availability (>3000 calories per day per inhabitant); thus, they may not provide reliable/unambiguous indices of climate impacts.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/atmos16050569/s1: Table S1: Overview of the number of records for even latitude, the associated birth weight by percentiles, the mean birth weight, and the associated standard deviation (sd) for the southern hemisphere.; Table S2: Overview of the number of records for even latitude, the associated birth weight by percentiles, the mean birth weight, and the associated standard deviation (sd) for the northern hemisphere.; Table S3: Overview of thermal indices and birth weights for European countries. Table S4. Overview of thermal indices and birth weights for equatorial African countries.; Figure S1: Temperatures for 770 observations, as observed and aggregated by even latitudes. (A) The lowest daily temperatures in the coolest month of the year (T1, °C) vs. latitude (Ael). The data in A are aggregated to even-integer latitudes. (B) The highest daily temperatures in the year’s warmest month (T4, °C) vs. latitude (Bel). The data in B are aggregated to even-integer latitudes. (°C) Temperature amplitudes given as the lowest temperature in the warmest month (T3) minus the highest temperature in the coolest month (T2). (Cel) The data in C aggregated to even-integer latitudes. (D) The mean daily temperature amplitude for the warmest and coolest months (°C) vs. latitude. (Del) The data in D aggregated to even-integer latitudes. Error bars: ½ sd.
Author Contributions
P.M.J.: conceptualization, data curation, formal analysis, methodology, visualization, writing—original draft; M.S.: visualization, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
We acknowledge the free access to information on local temperatures from the World Meteorological Organization (WMO), World Weather Online (WWO), and Time and Date (TAD).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviation
The following abbreviation is used in this manuscript:
| BW | birth weight |
References
- IPCC. Climate Change 2022: Impacts, Adaptation, and Vulnerability; Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; p. 3056. [Google Scholar] [CrossRef]
- Neumann, J.E.; Price, J.; Chinowsky, P.; Wright, L.; Ludwig, L.; Streeter, R.; Jones, R.; Smith, J.B.; Perkins, W.; Jantarasami, L.; et al. Climate change risks to US infrastructure: Impacts on roads, bridges, coastal development, and urban drainage. Clim. Change 2015, 131, 97–109. [Google Scholar] [CrossRef]
- Yuan, X.; Li, S.; Chen, J.; Yu, H.; Yang, T.; Wang, C.; Huang, S.; Chen, H.; Ao, X. Impacts of global climate change on agricultural production: A comprehensive review. Agronomy 2024, 14, 1360. [Google Scholar] [CrossRef]
- Rupasinghe, R.; Chomel, B.B.; Martínez-López, B. Climate change and zoonoses: A review of the current status, knowledge gaps, and future trends. Acta Trop. 2022, 226, 106225. [Google Scholar] [CrossRef]
- Onoh, U.C.; Ogunade, J.; Owoeye, E.; Awakessien, S.; Asomah, J.K. Impact of climate change on biodiversity and ecosystems services. IIARD Int. J. Geogr. Environ. Manag. 2024, 10, 77–93. [Google Scholar]
- Gaitán-Espitia, J.D.; Hobday, A.J. Evolutionary principles and genetic considerations for guiding conservation interventions under climate change. Glob. Change Biol. 2021, 27, 475–488. [Google Scholar] [CrossRef]
- Fuller, A.; Mitchell, D.; Maloney, S.K.; Hetem, R.S.; Fonsêca, V.F.; Meyer, L.C.; van de Ven, T.M.F.N.; Snelling, E.P. How dryland mammals will respond to climate change: The effects of body size, heat load and a lack of food and water. J. Exp. Biol. 2021, 224 (Suppl. S1), jeb238113. [Google Scholar] [CrossRef] [PubMed]
- Haines, A.; Kovats, R.S.; Campbell-Lendrum, D.; Corvalán, C. Climate change and human health: Impacts, vulnerability and public health. Public Health 2006, 120, 585–596. [Google Scholar] [CrossRef]
- Litt, J.S.; Gerry Taylor, H.; Margevicius, S.; Schluchter, M.; Andreias, L.; Hack, M. Academic achievement of adolescents born with extremely low birth weight. Acta Paediatr. 2012, 101, 1240–1245. [Google Scholar] [CrossRef]
- Nobili, V.; Alisi, A.; Panera, N.; Agostoni, C. Low birth weight and catch-up-growth associated with metabolic syndrome: A ten year systematic review. Pediatr. Endocrinol. Rev. 2008, 6, 241–247. [Google Scholar] [PubMed]
- Del Giudice, M. Early stress and human behavioral development: Emerging evolutionary perspectives. J. Dev. Orig. Health Dis. 2014, 5, 270–280. [Google Scholar] [CrossRef]
- Wells, J.C.; Cole, T.J.; Cortina-Borja, M.; Sear, R.; Leon, D.A.; Marphatia, A.A.; Murray, J.; Wehrmeister, F.C.; Oliveira, P.D.; Goncalves, H.; et al. Low maternal capital predicts life history trade-offs in daughters: Why adverse outcomes cluster in individuals. Front. Public Health 2019, 7, 206. [Google Scholar] [CrossRef] [PubMed]
- Roberts, D.F. Race, genetics and growth. J. Biosoc. Sci. Suppl. 1969, 1, 43–67. [Google Scholar] [CrossRef]
- Wells, J.C.; Cole, T.J. Birth weight and environmental heat load: A between-population analysis. Am. J. Phys. Anthropol. 2002, 119, 276–282. [Google Scholar] [CrossRef]
- Jensen, P.M.; Sørensen, M. Differences in human birth weight and corollary attributes as a result of temperature regime. Ann. Hum. Biol. 2013, 40, 385–395. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.J. Effects of heat stress on mammalian reproduction. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 3341–3350. [Google Scholar] [CrossRef] [PubMed]
- Collier, R.J.; Baumgard, L.H.; Zimbelman, R.B.; Xiao, Y. Heat stress: Physiology of acclimation and adaptation. Anim. Front. 2019, 9, 12–19. [Google Scholar] [CrossRef]
- Choudhari, R.H. Multidimensional impact of climate change on human reproduction and fertility: A medical perspective on changing dynamics. In Research Anthology on Environmental and Societal Impacts of Climate Change; IGI Global: Hershey, PA, USA, 2022. [Google Scholar] [CrossRef]
- Johnson, R.E.; Kark, R.M. Environment and food intake in man. Science 1947, 105, 378–379. [Google Scholar] [CrossRef]
- Chaiyabutr, N.; Buranakarl, C.; Loypetjra, P. Renal regulation of urea excretion during urea infusion in acute heat exposed buffaloes. Asian-Australas. J. Anim. Sci. 1992, 5, 81–90. [Google Scholar] [CrossRef]
- McClelland, I.S.; Persaud, C.; Jackson, A.A. Urea kinetics in healthy women during normal pregnancy. Br. J. Nutr. 1997, 77, 165–181. [Google Scholar] [CrossRef]
- Roberts, D.F. Body weight, race and climate. Am. J. Phys. Anthropol. 1953, 11, 533–558. [Google Scholar] [CrossRef]
- Pomeroy, E.; Stock, J.T.; Wells, J.C. Population history and ecology, in addition to climate, influence human stature and body proportions. Sci. Rep. 2021, 11, 274. [Google Scholar] [CrossRef] [PubMed]
- GHO Global Health Observatory. Mean BMI (kg/m2) (Age-Standardized Estimate). 2020. Available online: https://apps.who.int/gho/data/node.main.A904?lang=en (accessed on 12 August 2020).
- Polgreen, P.M.; Polgreen, E.L. Infectious diseases, weather, and climate. Clin. Infect. Dis. 2018, 66, 815–817. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.; Fuerst, H.T. Low birth weight and maternal virus diseases: A prospective study of rubella, measles, mumps, chickenpox, and hepatitis. JAMA 1966, 97, 680–684. [Google Scholar] [CrossRef] [PubMed]
- Spencer, S.; Samateh, T.; Wabnitz, K.; Mayhew, S.; Allen, H.; Bonell, A. The challenges of working in the heat whilst pregnant: Insights from Gambian women farmers in the face of climate change. Front. Public Health 2022, 10, 152. [Google Scholar] [CrossRef]
- Mortola, J.P.; Frappell, P.B.; Aguero, L.; Armstrong, K. Birth weight and altitude: A study in Peruvian communities. J. Pediatr. 2000, 136, 324–329. [Google Scholar] [CrossRef]
- Yang, L.; Helbich-Poschacher, V.; Cao, C.; Klebermass-Schrehof, K.; Waldhoer, T. Maternal altitude and risk of low birthweight: A systematic review and meta-analyses. Placenta 2020, 101, 124–131. [Google Scholar] [CrossRef]
- Anekwe, C.V.; Jarrell, A.R.; Townsend, M.J.; Gaudier, G.I.; Hiserodt, J.M.; Stanford, F.C. Socioeconomics of obesity. Curr. Obes. Rep. 2020, 9, 272–279. [Google Scholar] [CrossRef]
- Kogan, M.D. Social causes of low birth weight. J. R. Soc. Med. 1995, 88, 611–615. [Google Scholar] [CrossRef]
- Wells, J.C.; Stock, J.T. Re-examining heritability: Genetics, life history and plasticity. Trends Endocrinol. Metab. 2011, 22, 421–428. [Google Scholar] [CrossRef]
- Kramer, M.S. Determinants of low birth weight: Methodological assessment and meta-analysis. Bull. World Health Organ. 1987, 65, 663–737. [Google Scholar] [PubMed]
- Jensen, P.M.; De Fine Licht, H.H. Predicting global variation in infectious disease severity: A bottom-up approach. Evol. Med. Public Health 2016, 1, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, S.; Sone, T.; Doi, T.; Kahyo, H. Seasonality of mean birth weight and mean gestational period in Japan. Hum. Biol. 1993, 65, 481–501. [Google Scholar] [PubMed]
- Lechtig, A.; Yarbrough, C.; Delgado, H.; Habicht, J.P.; Martorell, R.; Klein, R.E. Influence of maternal nutrition on birth weight. Am. J. Clin. Nutr. 1975, 28, 1223–1233. [Google Scholar] [CrossRef]
- Christian, P. Micronutrients, birth weight, and survival. Annu. Rev. Nutr. 2010, 30, 83–104. [Google Scholar] [CrossRef] [PubMed]
- De Rooij, S.R.; Bleker, L.S.; Painter, R.C.; Ravelli, A.C.; Roseboom, T.J. Lessons learned from 25 years of research into long term consequences of prenatal exposure to the Dutch famine 1944–1945: The Dutch famine birth cohort. Int. J. Environ. Res. Public Health 2022, 32, 1432–1446. [Google Scholar] [CrossRef]
- Han, C.; Hong, Y.C. Fetal and childhood malnutrition during the Korean War and metabolic syndrome in adulthood. Nutrition 2019, 62, 186–193. [Google Scholar] [CrossRef]
- Tolkunova, K.; Usoltsev, D.; Moguchaia, E.; Boyarinova, M.; Kolesova, E.; Erina, A.; Voortman, T.; Vasilyeva, E.; Kostareva, A.; Shlyakhto, E.; et al. Transgenerational and intergenerational effects of early childhood famine exposure in the cohort of offspring of Leningrad Siege survivors. Sci. Rep. 2023, 13, 11188. [Google Scholar] [CrossRef]
- Arage, G.; Belachew, T.; Hassen, H.; Abera, M.; Abdulhay, F.; Abdulahi, M.; Abate, K.H. Effects of prenatal exposure to the 1983–1985 Ethiopian great famine on the metabolic syndrome in adults: A historical cohort study. Br. J. Nutr. 2020, 124, 1052–1060. [Google Scholar] [CrossRef] [PubMed]
- Liczbińska, G.; Králík, M. Body size at birth in babies born during World War II: The evidence from Poland. Am. J. Mol. Biol. 2020, 32, e23421. [Google Scholar] [CrossRef]
- Kramer, M.S.; Victora, C.G. Low birth weight and perinatal mortality. In Nutrition and Health in Developing Countries; Semba, R.D., Bloem, M.W., Eds.; Humana Press: Totowa, NJ, USA, 2001; pp. 57–69. [Google Scholar]
- Wilcox, A.J.; Russell, I.T. Birthweight and perinatal mortality: III. Towards a new method of analysis. Int. J. Epidemiol. 1986, 15, 188–196. [Google Scholar] [CrossRef]
- Wilcox, A.J. On the importance—And the unimportance—Of birthweight. Int. J. Epidemiol. 2001, 30, 1233–1241. [Google Scholar] [CrossRef]
- Goldin, C.; Margo, R.A. The poor at birth: Birth weights and infant mortality at Philadelphia’s Almshouse Hospital, 1848–1873. Explor. Econ. Hist. 1989, 26, 360–379. [Google Scholar] [CrossRef]
- Graafmans, W.C.; Richardus, J.H.; Borsboom, G.J.; Bakketeig, L.; Langhoff-Roos, J.; Bergsjø, P.; Macfarlane, A.; Verloove-Vanhorick, S.P.; Mackenbach, J.P. EuroNatal Working Group. Birth weight and perinatal mortality: A comparison of “optimal” birth weight in seven Western European countries. Epidemiology 2002, 13, 569–574. [Google Scholar] [CrossRef]
- Ezechukwu, C.C.; Ugochukwu, E.F.; Egbuonu, I.; Chukwuka, J.O. Risk factors for neonatal mortality in a regional tertiary hospital in Nigeria. Niger. J. Clin. Pract. 2004, 7, 50–52. [Google Scholar]
- Liang, F.W.; Chou, H.C.; Chiou, S.T.; Chen, L.H.; Wu, M.H.; Lue, H.C.; Chiang, T.L.; Lu, T.H. Trends in birth weight-specific and-adjusted infant mortality rates in Taiwan between 2004 and 2011. Pediatr. Neonatol. 2018, 59, 267–273. [Google Scholar] [CrossRef] [PubMed]
- Boo, N.Y.; Nasri, N.M.; Cheong, S.K.; Sivamohan, N.A. 2-year study of neonatal mortality in a large Malaysian hospital. Singap. Med. J. 1991, 32, 142–147. [Google Scholar]
- Singh, M.; Tripathy, K.; Arya, L.S. Birth weight gestational age correlates of neonatal mortality. Indian J. Pediatr. 1982, 49, 511–517. [Google Scholar] [CrossRef]
- Jonsson, T. Metabolic theory predicts animal self-thinning. J. Anim. Ecol. 2017, 86, 645–653. [Google Scholar] [CrossRef]
- Prentice, A.M.; Rayco-Solon, P.; Moore, S.E. Insights from the developing world: Thrifty genotypes and thrifty phenotypes. Proc. Nutr. Soc. 2005, 64, 153–161. [Google Scholar] [CrossRef]
- Cox, E.; Takov, V. Embryology, ovarian follicle development. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2018. [Google Scholar] [PubMed]
- Meredith, H.V. Birth order and body size II. Neonatal and childhood materials. Am. J. Phys. Anthropol. 1950, 8, 195–224. [Google Scholar] [CrossRef]
- WHO. World Health Organization. Maternal Health and Safe Motherhood Programme. In Low Birth Weight: A Tabulation of Available Information; World Health Organization: Geneva, Switzerland, 1992. [Google Scholar]
- UN. United Nations: UN Data, Live Births by Birth Weight and Sex of Child. 2024. Available online: http://data.un.org/Data.aspx?d=POP&f=tableCode%3A60 (accessed on 21 June 2024).
- Ogston, F. On the Average Length and Weight of Mature New-Born Scotch Children. Edinb. Med. J. 1881, 26, 603. [Google Scholar] [PubMed]
- Wells, J.C. What was human birth weight in the past? Simulations based on data on stature from the palaeolithic to the present. J. Life Sci. 2009, 1, 115–120. [Google Scholar] [CrossRef]
- Yüzen, D.; Graf, I.; Diemert, A.; Arck, P.C. Climate change and pregnancy complications: From hormones to the immune response. Front. Endocrinol. 2023, 14, 1149284. [Google Scholar] [CrossRef] [PubMed]
- Carolan-Olah, M.; Frankowska, D. High environmental temperature and preterm birth: A review of the evidence. Midwifery 2014, 30, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Guo, T.; Wang, Y.; Zhang, H.; Zhang, Y.; Zhao, J.; Wang, Y.; Xie, X.; Wang, L.; Zhang, Q.; Liu, D.; et al. The association between ambient temperature and the risk of preterm birth in China. Sci. Total Environ. 2018, 613, 439–446. [Google Scholar] [CrossRef]
- Chodick, G.; Flash, S.; Deoitch, Y.; Shalev, V. Seasonality in birth weight: Review of global patterns and potential causes. Hum. Biol. 2009, 81, 463–477. [Google Scholar] [CrossRef]
- Foster, F.; Collard, M. A reassessment of Bergmann’s rule in modern humans. PLoS ONE 2013, 8, e72269. [Google Scholar] [CrossRef]
- Bogin, B.; Hermanussen, M.; Scheffler, C. Bergmann’s rule is a “just-so” story of human body size. J. Physiol. Anthropol. 2022, 41, 15. [Google Scholar] [CrossRef]
- Allen, J.A. The influence of physical conditions in the genesis of species. Radic. Rev. 1877, 1, 108–140. [Google Scholar]
- Serrat, M.A.; King, D.; Lovejoy, C.O. Temperature regulates limb length in homeotherms by directly modulating cartilage growth. Proc. Natl. Acad. Sci. USA 2008, 105, 19348–19353. [Google Scholar] [CrossRef]
- Betti, L.; Lycett, S.J.; von Cramon-Taubadel, N.; Pearson, O.M. Are human hands and feet affected by climate? A test of A llen’s rule. Am. J. Phys. Anthropol. 2015, 158, 132–140. [Google Scholar] [CrossRef]
- Bindon, J.R.; Baker, P.T. Bergmann’s rule and the thrifty genotype. Am. J. Phys. Anthropol. 1997, 104, 201–210. [Google Scholar] [CrossRef]
- Stelmach-Mardas, M.; Kleiser, C.; Uzhova, I.; Peñalvo, J.L.; La Torre, G.; Palys, W.; Lojko, D.; Nimptsch, K.; Suwalska, A.; Linseisen, J.; et al. Seasonality of food groups and total energy intake: A systematic review and meta-analysis. Eur. J. Clin. Nutr. 2016, 70, 700–708. [Google Scholar] [CrossRef] [PubMed]
- Varpe, Ø. Life history adaptations to seasonality. Integr. Comp. Biol. 2017, 57, 943–960. [Google Scholar] [CrossRef] [PubMed]
- Chodick, G.; Shalev, V.; Goren, I.; Inskip, P.D. Seasonality in birth weight in Israel: New evidence suggests several global patterns and different etiologies. Ann. Epidemiol. 2007, 17, 440–446. [Google Scholar] [CrossRef] [PubMed]
- Pereira, G.; Cook, A.; Haggar, F.; Bower, C.; Nassar, N. Seasonal variation in fetal growth: Accounting for sociodemographic, biological, and environmental exposures. Am. J. Obstet. Gynecol. 2012, 206, 74.e1–74.e7. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Peng, Y.; Zhou, H. Diurnal temperature range variation and its causes in a semiarid region from 1957 to 2006. Int. J. Climatol. 2014, 34, 343–354. [Google Scholar] [CrossRef]
- Jang, Y.S.; Shen, S.F.; Juang, J.Y.; Huang, C.Y.; Lo, M.H. Discontinuity of diurnal temperature range along elevated regions. Geophys. Res. Lett. 2022, 49, e2021GL097551. [Google Scholar] [CrossRef]
- Buklijas, T.; Al-Gailani, S. A fetus in the world: Physiology, epidemiology, and the making of fetal origins of adult disease. Hist. Philos. Life Sci. 2023, 45, 44. [Google Scholar] [CrossRef]
- Rocha, J.L.; Godinho, R.; Brito, J.C.; Nielsen, R. Life in deserts: The genetic basis of mammalian desert adaptation. Trends Ecol. Evol. 2021, 36, 637–650. [Google Scholar] [CrossRef]
- Kingma, B.; Frijns, A.; van Marken Lichtenbelt, W. The thermoneutral zone: Implications for metabolic studies. Front. Biosci. (Elite Ed.) 2012, 4, 1975–1985. [Google Scholar] [CrossRef]
- Kuzawa, C.W.; Bragg, J.M. Plasticity in human life history strategy: Implications for contemporary human variation and the evolution of genus Homo. Curr. Anthropol. 2012, 53, S369–S382. [Google Scholar] [CrossRef]
- Romero-Mujalli, D.; Fuchs, L.I.; Haase, M.; Hildebrandt, J.P.; Weissing, F.J.; Revilla, T.A. Emergence of phenotypic plasticity through epigenetic mechanisms. Evol. Lett. 2024, 8, 561–574. [Google Scholar] [CrossRef]
- Kuzawa, C.W.; Fried, R.L. Intergenerational memories of past nutritional deprivation: The phenotypic inertia model. In The Arc of Life: Evolution and Health Across the Life Course; Jasienska, G., Sherry, D., Holmes, D., Eds.; Springer: New York, NY, USA, 2017; pp. 7–20. [Google Scholar] [CrossRef]
- Gluckman, P.D.; Hanson, M.A.; Spencer, H.G. Predictive adaptive responses and human evolution. Trends Ecol. Evol. 2005, 20, 527–533. [Google Scholar] [CrossRef]
- Bateson, P.; Gluckman, P.; Hanson, M. The biology of developmental plasticity and the Predictive Adaptive Response hypothesis. Physiol. J. 2014, 592, 2357–2368. [Google Scholar] [CrossRef]
- Keys, A.; Henschel, A.; Mickelsen, O.; Taylor, H.L. The Biology of Human Starvation; University of Minnesota Press: Minneapolis, MN, USA, 1950; Volume 1 & 2, xxxii+1–764, pp. viii+765–1385. ISBN 9780816672332. [Google Scholar]
- Dulloo, A.G. Physiology of weight regain: Lessons from the classic Minnesota Starvation Experiment on human body composition regulation. Obes. Rev. 2021, 22, e13189. [Google Scholar] [CrossRef]
- Meredith, H.V. Body weight at birth of viable human infants: A worldwide comparative treatise. Hum. Biol. 1970, 142, 217–264. [Google Scholar] [PubMed]
- WMO. World Meteorological Organization, World Weather Information Service. 2021. Available online: http://worldweather.wmo.int/ (accessed on 12 August 2020).
- WWO. World Weather Online. Temperature Averages. 2021. Available online: https://www.worldweatheronline.com/ (accessed on 12 August 2020).
- TAD. Time and Date; Climate and Weather Records. 2021. Available online: https://www.timeanddate.com/weather/@7729880/climate (accessed on 12 August 2020).
- Barber, N. On the relationship between fertility and geographic latitude: A cross-national study. Cross-Cult. Res. 2002, 36, 3–15. [Google Scholar] [CrossRef]
- Pickett, S.T. Space-for-time substitution as an alternative to long-term studies. In Long-Term Studies in Ecology: Approaches and Alternatives; Springer: New York, NY, USA, 1989; pp. 110–135. [Google Scholar]
- Damgaard, C. A critique of the space-for-time substitution practice in community ecology. Trends Ecol. Evol. 2019, 34, 416–421. [Google Scholar] [CrossRef] [PubMed]
- WBCK. World Bank Climate Knowlegde Portal. 2024. Available online: https://climateknowledgeportal.worldbank.org/ (accessed on 12 August 2020).
- Jensen, P.M.; Sørensen, M. In search of environmental factors associated with global differences in birth weight and BMI. Am. J. Hum. Biol. 2025, 37, e70038. [Google Scholar] [CrossRef] [PubMed]
- Boerma, J.T.; Weinstein, K.I.; Rutstein, S.O.; Sommerfelt, A.E. Data on birth weight in developing countries: Can surveys help? Bull. World Health Organ. 1996, 74, 209–216. [Google Scholar] [PubMed]
- Tambi, M.D.; Effects of Maternal Immunization on Birth Weight in Rural Cameroon. African Economic Research Consortium, Nairobi (Research Paper: 413). 2021. Available online: https://publication.aercafricalibrary.org/handle/123456789/1284 (accessed on 12 August 2020).
- Airede, A.I. Birth weights of Nigerian newborn infants—A review. West Afr. J. Med. 1995, 14, 116–120. [Google Scholar] [PubMed]
- Hughes, M.M.; Katz, J.; Mullany, L.C.; Khatry, S.K.; LeClerq, S.C.; Darmstadt, G.L.; Tielsch, J.M. Seasonality of birth outcomes in rural Sarlahi District, Nepal: A population-based prospective cohort. BMC Pregnancy Childbirth 2014, 14, 310. [Google Scholar] [CrossRef]
- Wendl-Richter, H.U. Birthweight distribution in rural north-west Burkina Faso. Trop. Med. Int. Health 1997, 2, 404–408. [Google Scholar] [CrossRef]
- Murray, L.J.; O’Reilly, D.P.; Betts, N.; Patterson, C.C.; Smith, G.D.; Evans, A.E. Season and outdoor ambient temperature: Effects on birth weight. Obstet. Gynecol. 2000, 96, 689–695. [Google Scholar] [CrossRef]
- de Jonge, L.V.H.; Waller, G.; Stettler, N. Ethnicity modifies seasonal variations in birth weight and weight gain of infants. J. Nutr. 2003, 133, 1415–1418. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Olendzki, B.C.; Li, W.; Hafner, A.R.; Chiriboga, D.; Hebert, J.R.; Campbell, M.; Sarnie, M.; Ockene, I.S. Seasonal variation in food intake, physical activity, and body weight in a predominantly overweight population. Eur. J. Clin. Nutr. 2006, 60, 519–528. [Google Scholar] [CrossRef]
- Bernstein, S.; Zambell, K.; Amar, M.J.; Arango, C.; Kelley, R.C.; Miszewski, S.G.; Tryon, S.; Courville, A.B. Dietary intake patterns are consistent across seasons in a cohort of healthy adults in a metropolitan population. J. Acad. Nutr. Diet. 2016, 116, 38–45. [Google Scholar] [CrossRef]
- OWD. Our World in Data Daily Supply of Calories Per Person, 1274 to 2021, Measured in Kilocalories Per Person Per Day. 2024. Available online: https://ourworldindata.org/grapher/daily-per-capita-caloric-supply (accessed on 13 June 2024).
- Bantje, H. Seasonal variations in birthweight distribution in Ikwiriri village, Tanzania. J. Trop. Pediatr. 1983, 29, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Azeez, M.A.; Akinboro, A.; Bakare, A.A. Human sex ratio at birth in South West Nigeria. Indian J. Hum. Genet. 2007, 13, 59. [Google Scholar] [CrossRef][Green Version]
- OWD. Our World in Data. Average Age of Mothers at Childbirth, Estimated Average Age of Women Who Have Given Birth in Each Year. This Includes All Births that Year, not just Women’s First Childbirth. 2025. Available online: https://ourworldindata.org/grapher/period-average-age-of-mothers?time=latest (accessed on 3 March 2025).
- Jensen, P.M.; Sørensen, M.; Weiner, J. Human total fertility rate affected by ambient temperatures in both the present and previous generations. Int. J. Biometeorol. 2021, 65, 1837–1848. [Google Scholar] [CrossRef] [PubMed]
- Davy, R.; Esau, I.; Chernokulsky, A.; Outten, S.; Zilitinkevich, S. Diurnal asymmetry to the observed global warming. Int. J. Climatol. 2017, 37, 79–93. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).