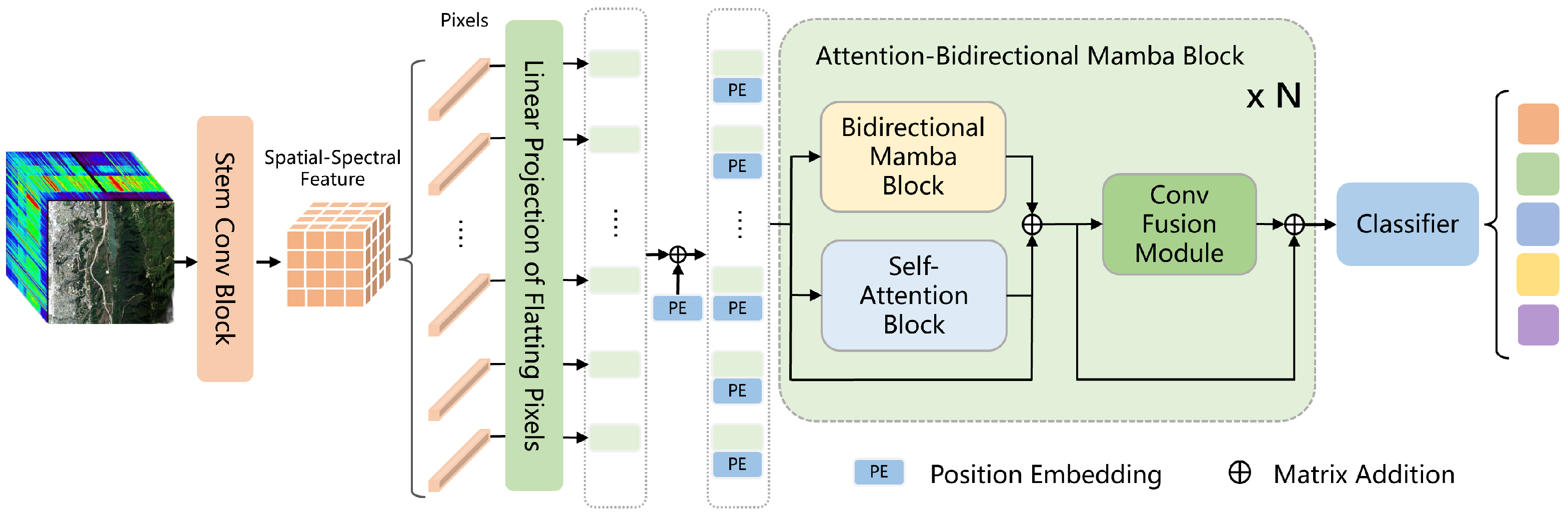
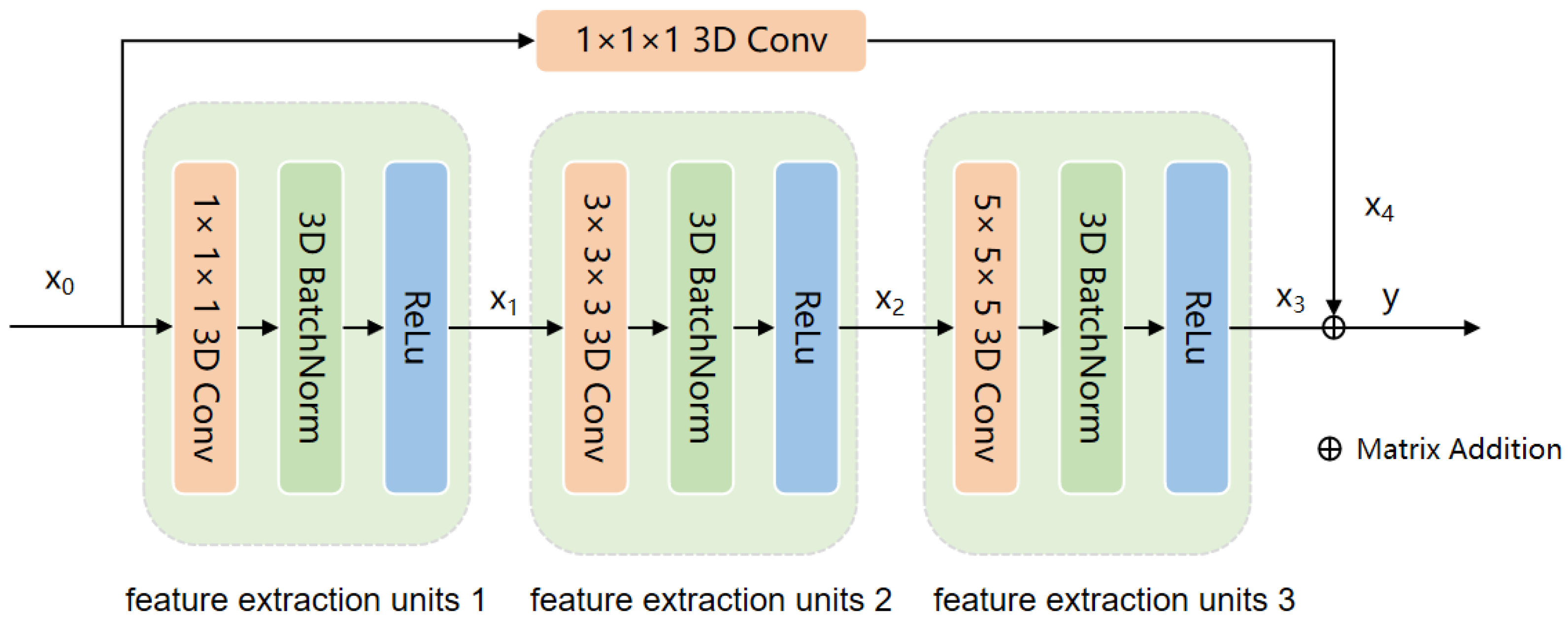
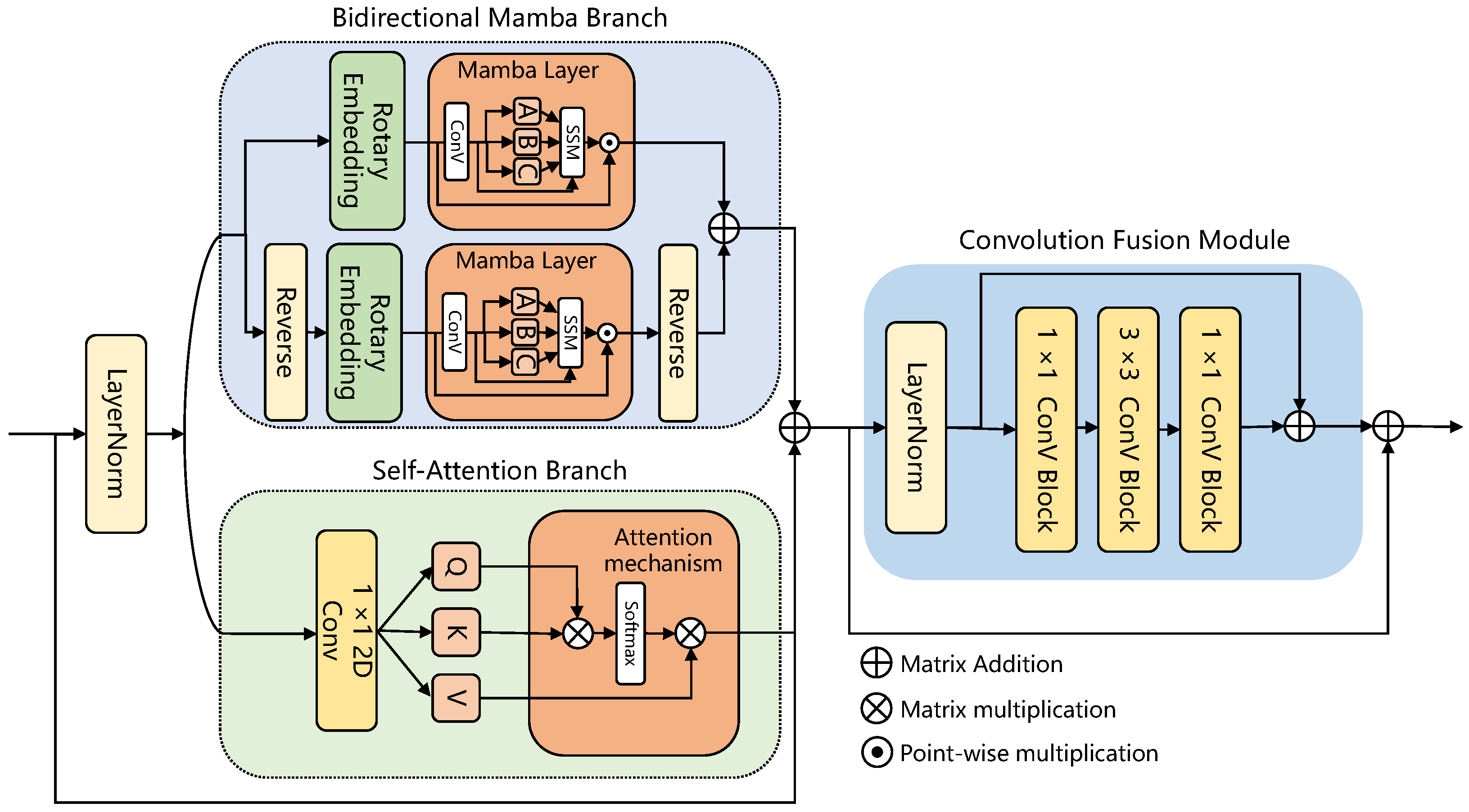
In this section, to demonstrate the superiority of our proposed AMamNet, we present a fair comparison of results with previous state-of-the-art (SOTA) methods. By employing the same experimental setup and evaluation metrics, we ensure that the performance gains achieved by AMamNet are attributed solely to its architectural advancements. Specifically, we choose SVM as the traditional machine learning-based method, and ABLSTM [
18], HybridSN [
35], SpectralFormer [
38], HiT [
39], SSFTT [
47], Hyper-E
T [
40], MorphFormer [
36], SMESC [
41], DBCTNet [
28], and HSIMamba [
29] as the deep-learning-based methods.
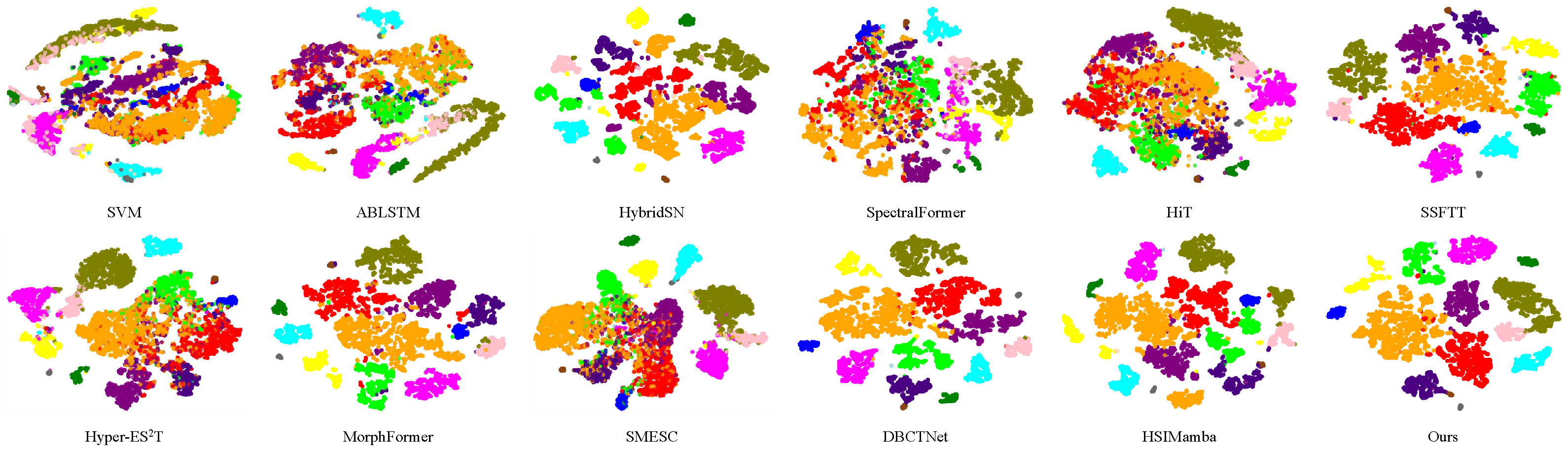
The distributions of features extracted using various methods are visualized with t-distributed stochastic neighbor embedding (t-SNE) [
48], as shown in
Figure 4. t-SNE, a widely used technique for dimensionality reduction, helps us understand how the model discriminates between classes in a lower-dimensional space. The visualization reveals that our model demonstrates a more cohesive separation, with greater distances between samples from different classes. In summary, the t-SNE visualization suggests that our model offers a high level of interpretability and practical effectiveness.
Additionally, quantitative classification results, encompassing OA, AA, Kappa, and per-class accuracies, are detailed in
Table 4,
Table 5 and
Table 6 for the Indian Pines, Pavia University, and WHU-Hi-LongKou datasets.
Figure 5,
Figure 6 and
Figure 7 illustrate the qualitative results for the IP, PU, and LK datasets, respectively. Background patches are included in the visualizations for illustrative purposes, but they are excluded from both training and quantitative evaluation. For datasets like IP and PU, some background pixels are not labeled and are excluded from the reported results; for the fully annotated LK dataset, all pixels are used in training and evaluation. Background pixels do not contribute to the loss computation, ensuring that the optimization is driven solely by labeled class samples.
4.3.1. Results Based on the Indian Pines Dataset
In this section, we compare the performance of SVM, ABLSTM, HybridSN, Spectral-Former, HiT, SSFTT, Hyper-E
T, MorphFormer, SMESC, DBCTNet, HSIMamba, and our proposed AMamNet on the IP dataset, as shown in
Table 4.
The comparison of classification results emphasizes the superior performance of deep learning methods over traditional machine learning approaches, such as SVM. The SVM model achieved an OA of only 73.68%, significantly lagging behind deep learning models. This stark difference highlights the unique advantages of deep learning methods in effectively handling complex HSI. Among the deep learning methods evaluated, several methods, including SMESC, DBCTNet, and MorphFormer, exhibited commendable performance, with OAs of 95.62%, 95.46%, and 93.60%, respectively. However, the proposed method, AMamNet, outperformed all competitors, achieving an impressive OA of 97.62%, an AA of 98.83%, and a Kappa coefficient of 0.9727. Notably, AMamNet not only surpasses the second-best performer, DBCTNet, by 2.00% in OA but also demonstrates superior robustness, as indicated by its higher Kappa coefficient.
In details, AMamNet achieved remarkable accuracy across 15 out of 16 categories, with perfect classification in multiple instances, demonstrating its effectiveness in distinguishing even the most challenging land cover types. This excellent performance is attributed to the model’s integration of the advantages of Mamba, self-attention mechanisms, and convolutional structures, enabling it to mitigate redundant spatial and spectral features and inter-class spectral overlap.
Building on its demonstrated superiority in classification performance, AMamNet further distinguishes itself, with significant advantages in model efficiency. Specifically, AMamNet requires only 0.5 M parameters, representing a reduction of 8.7 M compared to HSIMamba, another model based on the Mamba architecture. Furthermore, our training time is 32.65 s, which is significantly faster compared to Transformer-based methods. For instance, SpectralFormer takes 62 s, and MorphFormer requires 67.05 s, while DBCTNet takes 56.89 s. Additionally, our testing time is 1.24 s, which is 2.44 s faster than SpectralFormer. This shows that our method achieves high computational efficiency, outperforming most Transformer-based architectures in both training and inference time.
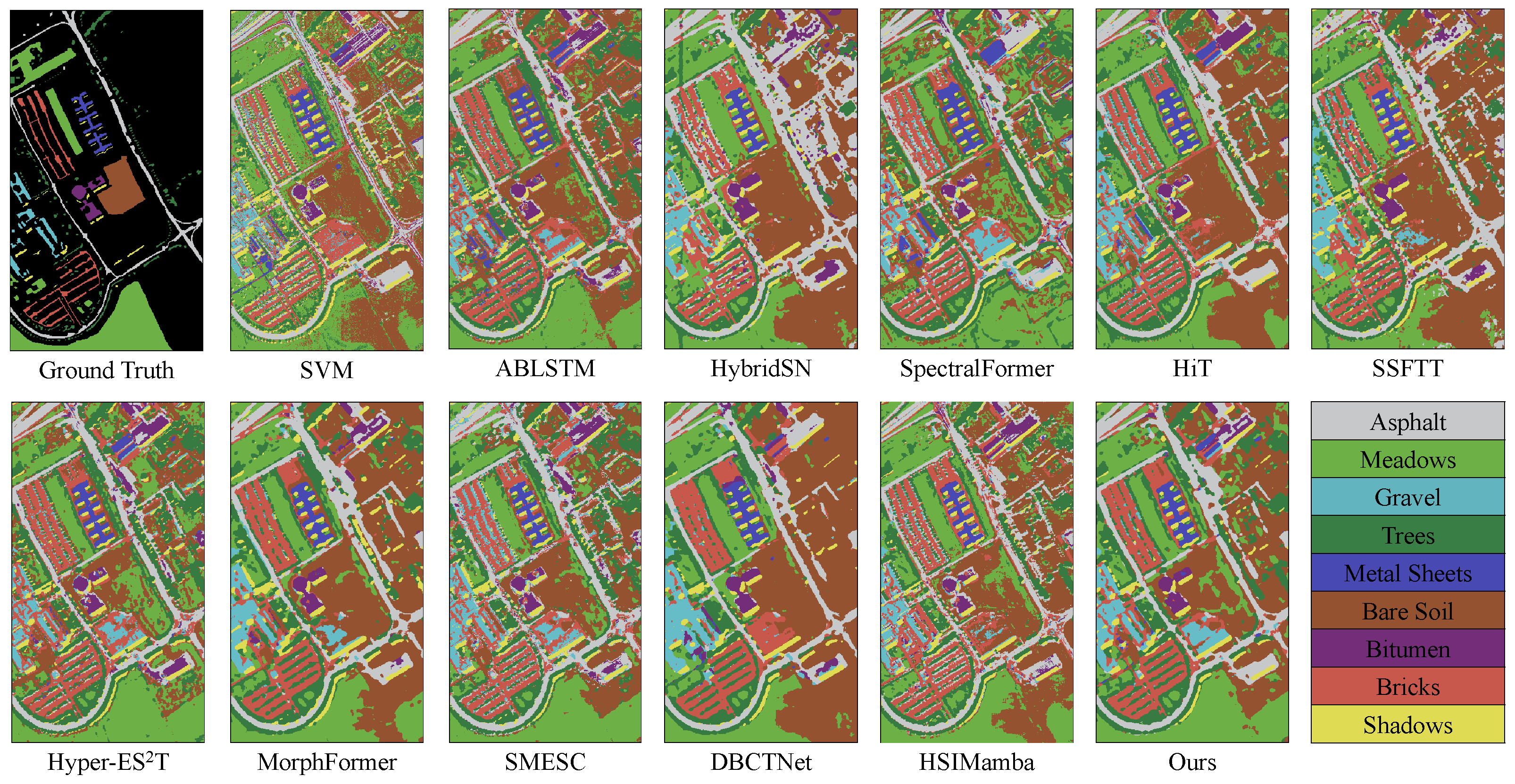
The classification results of various algorithms are illustrated in
Figure 5, clearly presenting the spatial distribution of different categories. The classification results of various algorithms are illustrated in
Figure 5, clearly presenting the spatial distribution of different categories. AMamNet demonstrates superior performance in challenging categories such as Soybean Mintill and Woods, with significantly reduced prediction noise compared to other models, achieving classification accuracies of 96.94% and 98.23%, respectively. This advantage is largely attributed to the 3D convolution-based Stem Conv Block module, which aggregates highly correlated spectral bands and smooths both local and global spatial features.
4.3.2. Results on Pavia University Dataset
The comparison of classification results based on the the PU dataset further confirms the superior performance of deep learning methods over traditional machine learning approaches, specifically SVM. As presented in
Table 5, SVM achieved an OA of only 77.61%, significantly trailing behind the deep learning models.
Figure 6 indicates that SVM tends to confuse Meadows and Bare Soil, primarily due to the similarity in reflectance values for these two categories in certain spectral bands. This similarity results in reduced classification accuracy when distinguishing between them, further highlighting the limitations of traditional machine learning methods in handling complex land cover types. In contrast, deep learning models can effectively identify these subtle differences through more advanced feature extraction mechanisms.
In the explicit comparison between deep learning methods, SMESC, DBCTNet, and MorphFormer achieved commendable OAs of 91.80%, 87.35%, and 88.89%, respectively. However, our proposed method, AMamNet, demonstrated superiority, attaining an impressive OA of 95.69%, an AA of 95.01%, and a Kappa coefficient of 0.9417, seamlessly outperforming the SSM-based method HSIMamba by a great margin. This improvement can be attributed to AMamNet’s incorporation of transformer-based dynamic tokenization, which enables the dynamic modeling of both local and global dependencies within spectral–spatial features. By leveraging this advanced mechanism, AMamNet demonstrates an enhanced capacity to capture subtle feature variations, facilitating the more accurate differentiation of complex and overlapping land cover types. Notably, AMamNet outperformed the second-best method, SMESC, by 3.89% in OA, demonstrating its superior robustness and effectiveness in HSI classification. Regarding the model’s parameters, training time and testing time, AMamNet achieves results comparable to SMESC, while demonstrating an approximately 4% improvement in the OA metric. Our training time of 141.69 s is considerably lower than HYPER-E2ST, which takes 524.25 s, and DBCTNet, the fastest Transformer-based method, by 23.22 s. In terms of testing time, our model performs well with a value of 10.01 s, which is lower than the average testing time of the compared methods, demonstrating strong efficiency in inference as well.
AMamNet, shown in
Figure 6, exhibits significant separation of features among various land cover types. Compared to other competitive models, such as SMESC and DBCTNet, AMamNet exhibits more precise class boundaries and superior overall classification performance, particularly in complex categories such as Meadows and Bitumen, with recognition accuracies of 98.21% and 97.86%, respectively. This advantage stems from the incorporation of ABMB, which captures fine-grained spectral variations via a bidirectional spectral scanning mechanism. This structure effectively preserves subtle spectral differences between overlapping categories, enabling the model to maintain excellent classification performance, even in the presence of blurred class boundaries and significant spectral confusion.
4.3.3. Results on the WHU-Hi-LongKou Dataset
Finally,
Table 6 displays the classification results of AMamNet in comparison to ten other algorithms on the WH-LK dataset. In this dataset, AMamNet outperforms all competitors across the three evaluation metrics, achieving an OA of 95.24%, which is 1.72% higher than that of the second-best method, DBCTNet. Specifically, in tackling challenging categories, some models, such as HybridSN, attain only 36.79% accuracy in category 4, while AMamNet excels, with an accuracy of 87.35%, the highest among all models. Furthermore, our method significantly outperforms HSIMamba, achieving an OA of 95.24%—a 4.25% improvement. This suggests that AMamNet, utilizing the ABMB and Stem Conv Block, excels at handling the complexities inherent in HSI data.
In terms of model complexity, AMamNet demonstrates a notable advantage. As shown in
Table 6, the parameter size of AMamNet is 0.8M, which is smaller than that of SMESC (1.0M) and other competing methods such as Hyper-ES
2T (23.1M) and HiT (64.8M). Despite its compact architecture, AMamNet achieves superior performance, highlighting the efficiency of its design. Additionally, AMamNet achieves competitive training time and testing time. In the LK dataset, due to the higher spectral dimensions, our training time of 135.8 s is slightly longer than DBCTNet’s 80.65 s, but still faster than SpectralFormer’s 111.53 s. When it comes to testing time, our method again excels, with a testing time of 24.42 s, which is much faster than HiT, which takes 65.70 s, further emphasizing our model’s superior testing speed.
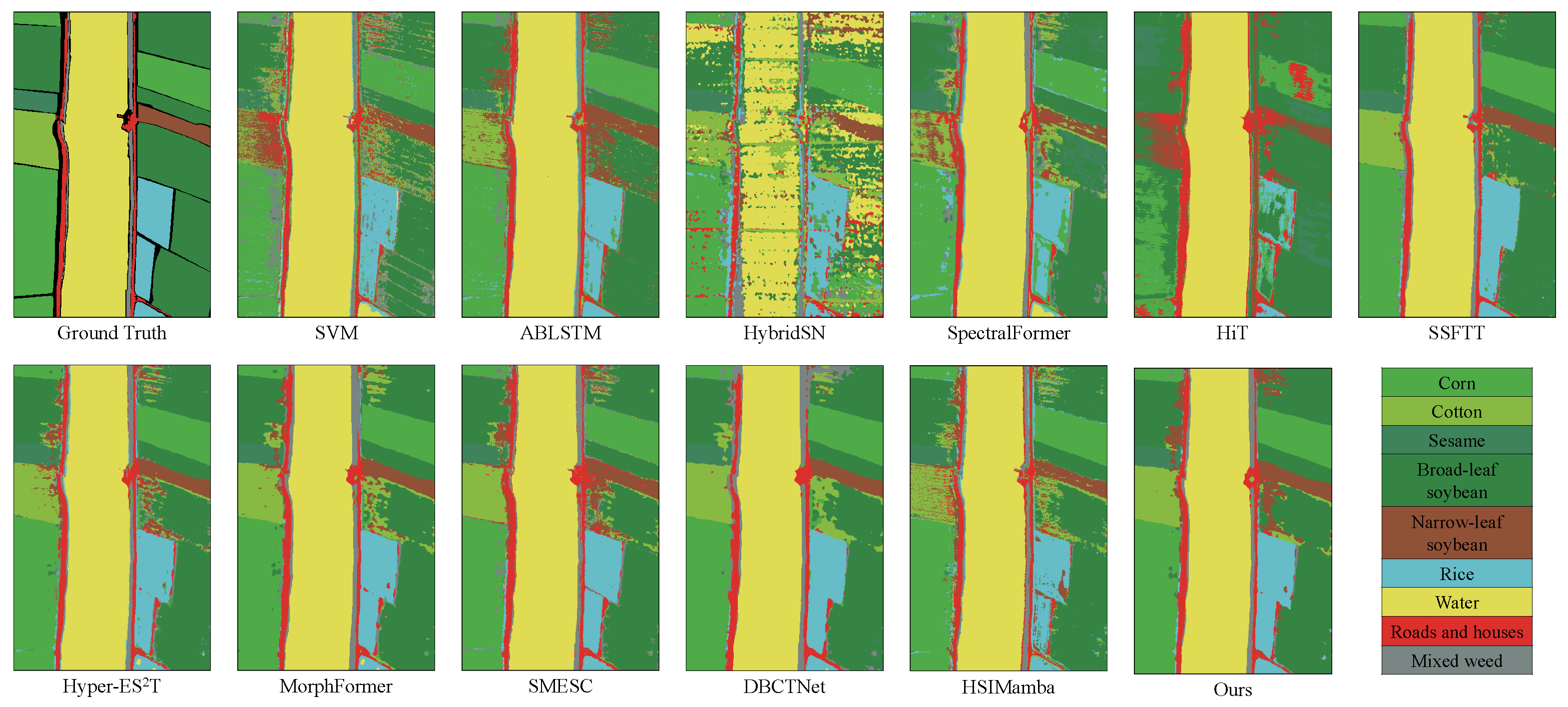
AMamNet, illustrated in
Figure 7, exhibits well-defined regions and clear boundaries, demonstrating its effectiveness in classification. For example, in categories that are generally challenging to identify, such as Broad-leaf soybean and Mixed weed, AMam-Net improved by 3.02% and 7.09%, respectively, compared to DBCTNet. From a visual perspective, AMamNet demonstrates clearer region boundaries with fewer classification noise. This significant improvement is primarily due to the integrated ABMB module. The module consists of two branches that work synergistically, leveraging their complementary strengths to model complex spectral relationships. The Self-Attention Branch introduces a context-aware attention mechanism, effectively capturing global spectral dependencies, enhancing key spectral features while suppressing irrelevant information. The Bidirectional Mamba Branch, based on the SSM, dynamically models the spectral sequence, deeply exploring and integrating trends within continuous spectral variations. The synergistic effect of these two branches enables the model to capture both local spectral relationships and long-range dependencies, effectively alleviating spectral indistinguishability and significantly improving classification accuracy for samples with high spectral similarity.