Evaluation of Large Eddy Effects on Land Surface Modeling Based on the FLUXNET Dataset
Abstract
1. Introduction
2. Theory, Model, and Data
2.1. Common Land Model (CoLM) and Classical Flux-Gradient Relations Under Unstable Conditions
2.2. Modified Flux-Gradient Relations Considering the Large Eddy Effects
2.3. FLUXNET2015 Dataset and Planetary Boundary Layer Height Data
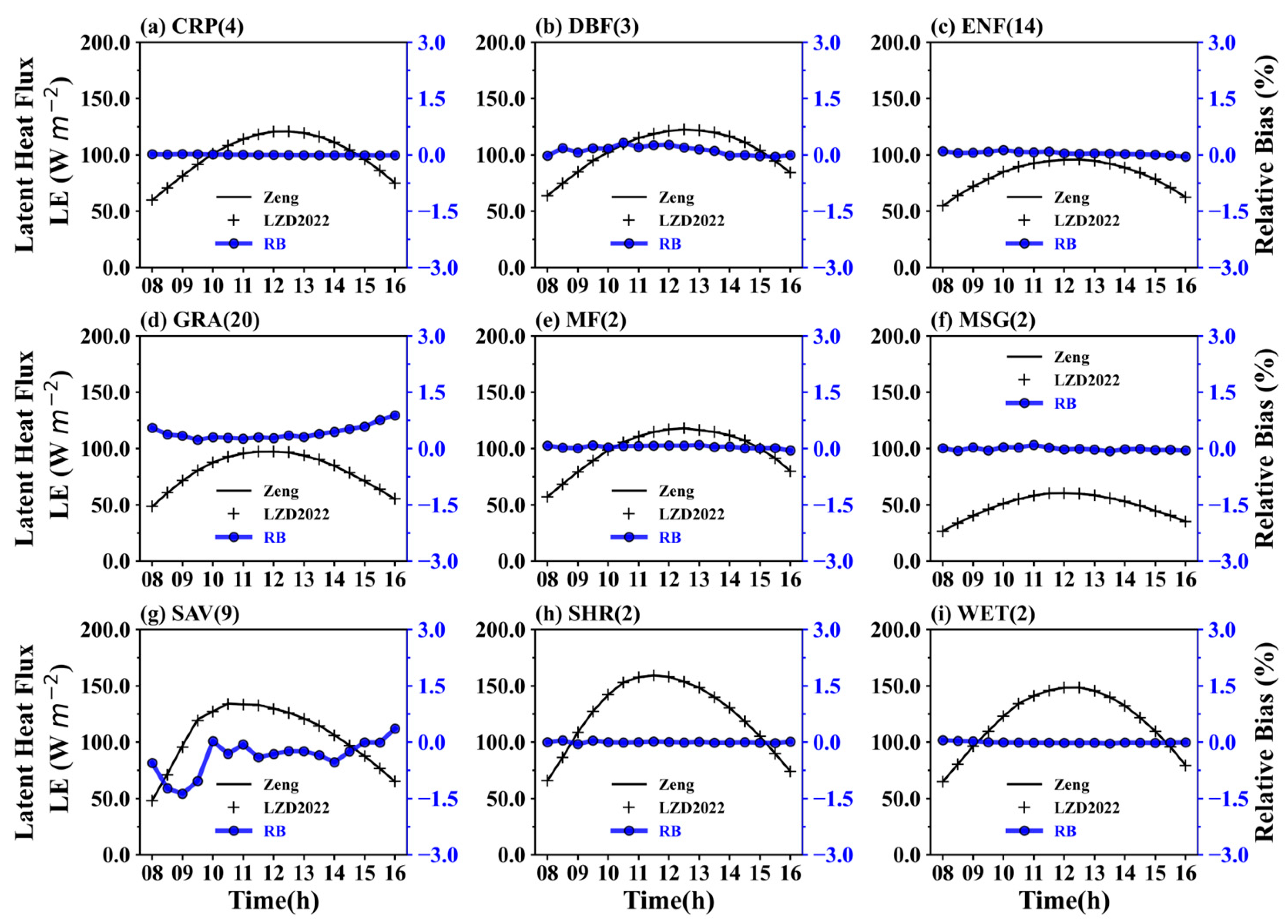
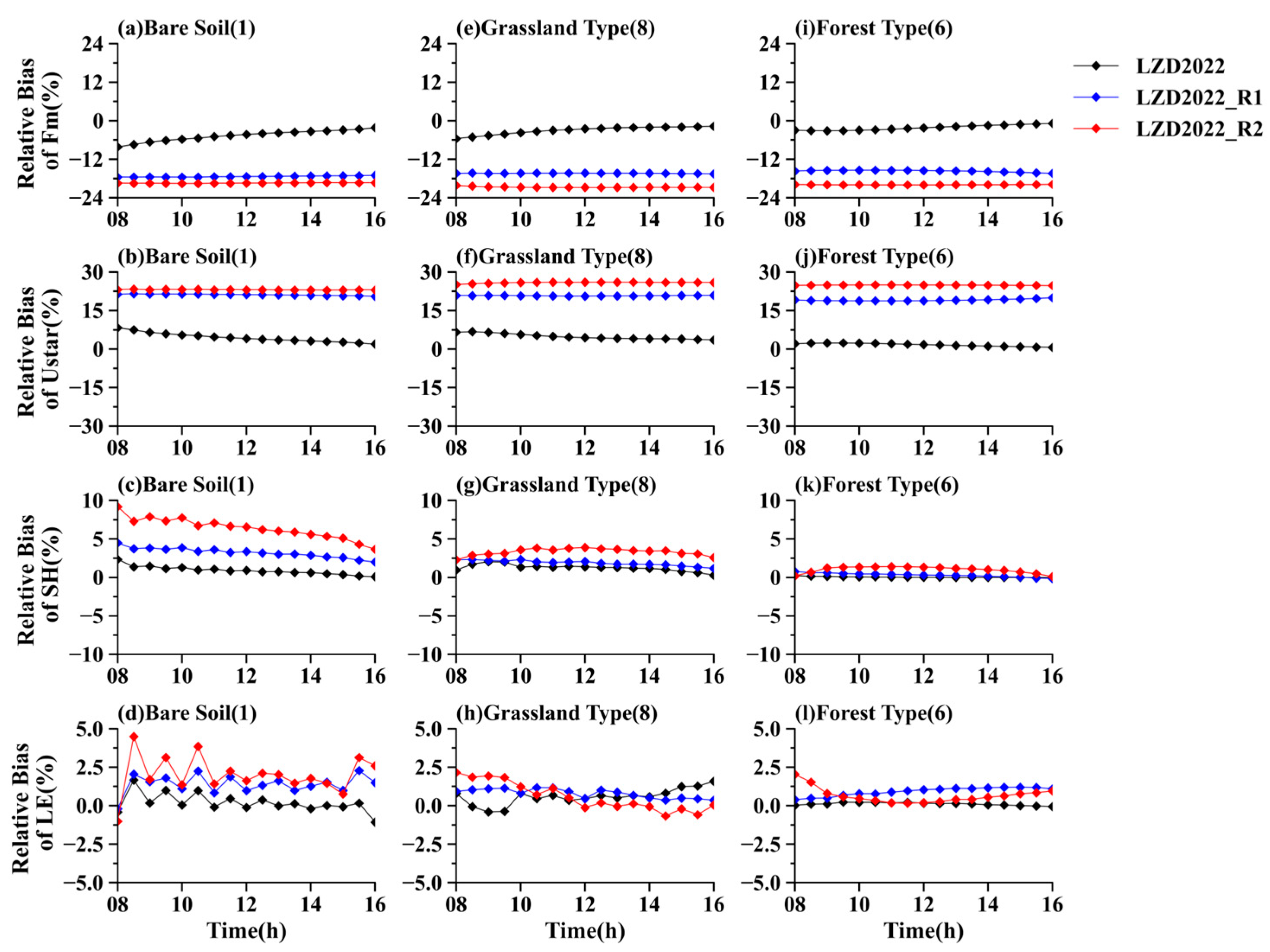
3. Results
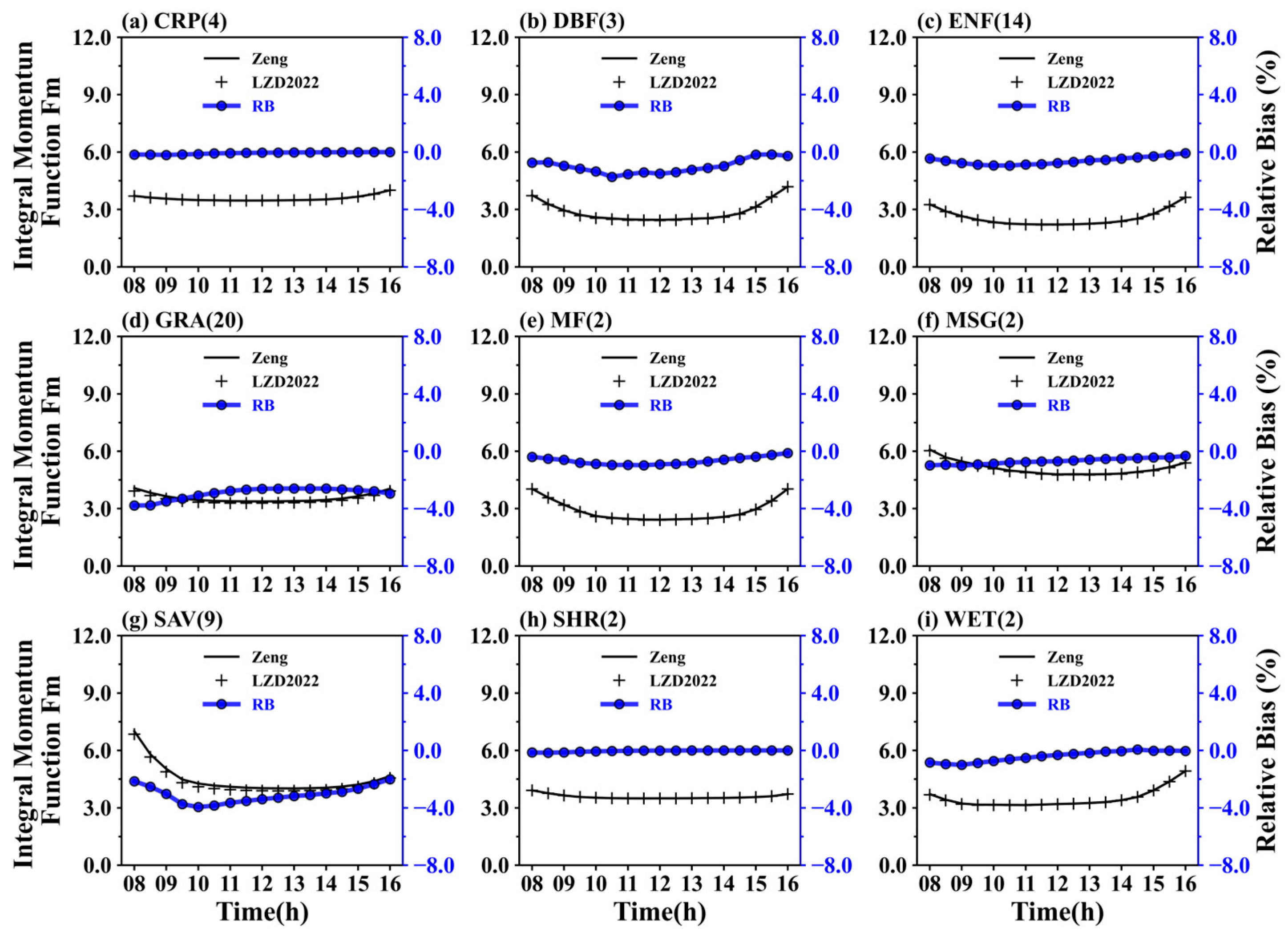
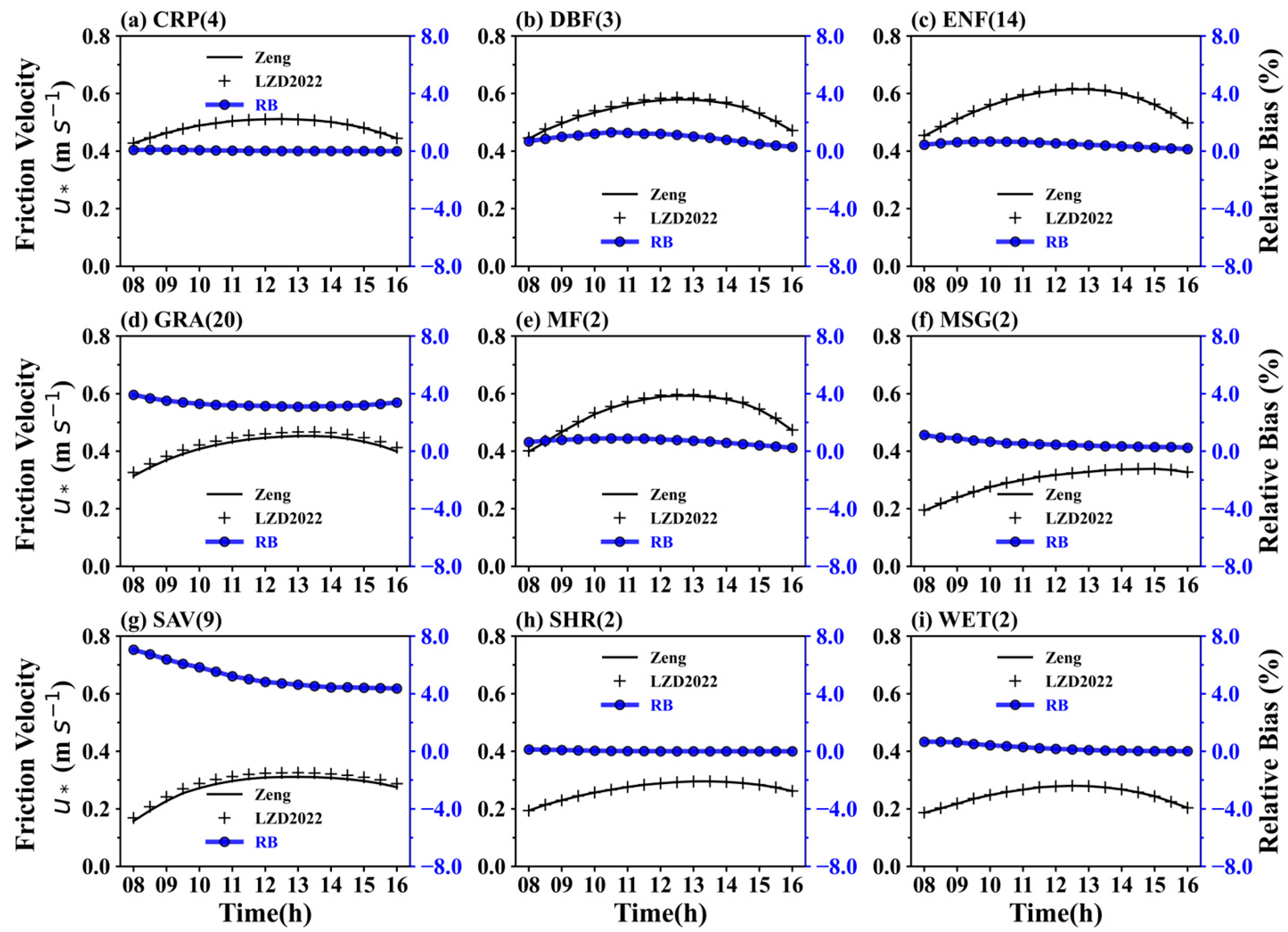
3.1. Comparison of Modified and Classical Flux-Gradient Relations
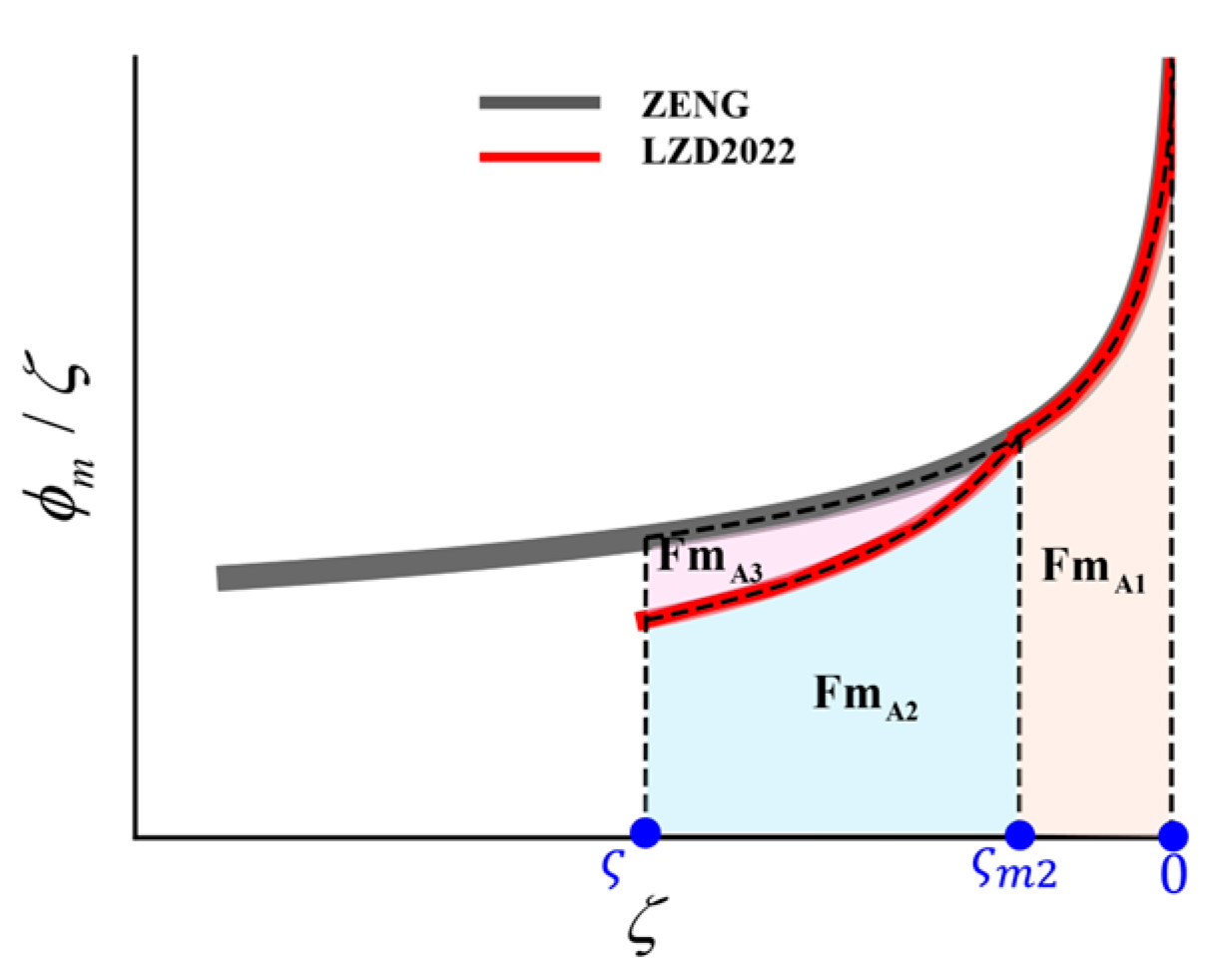
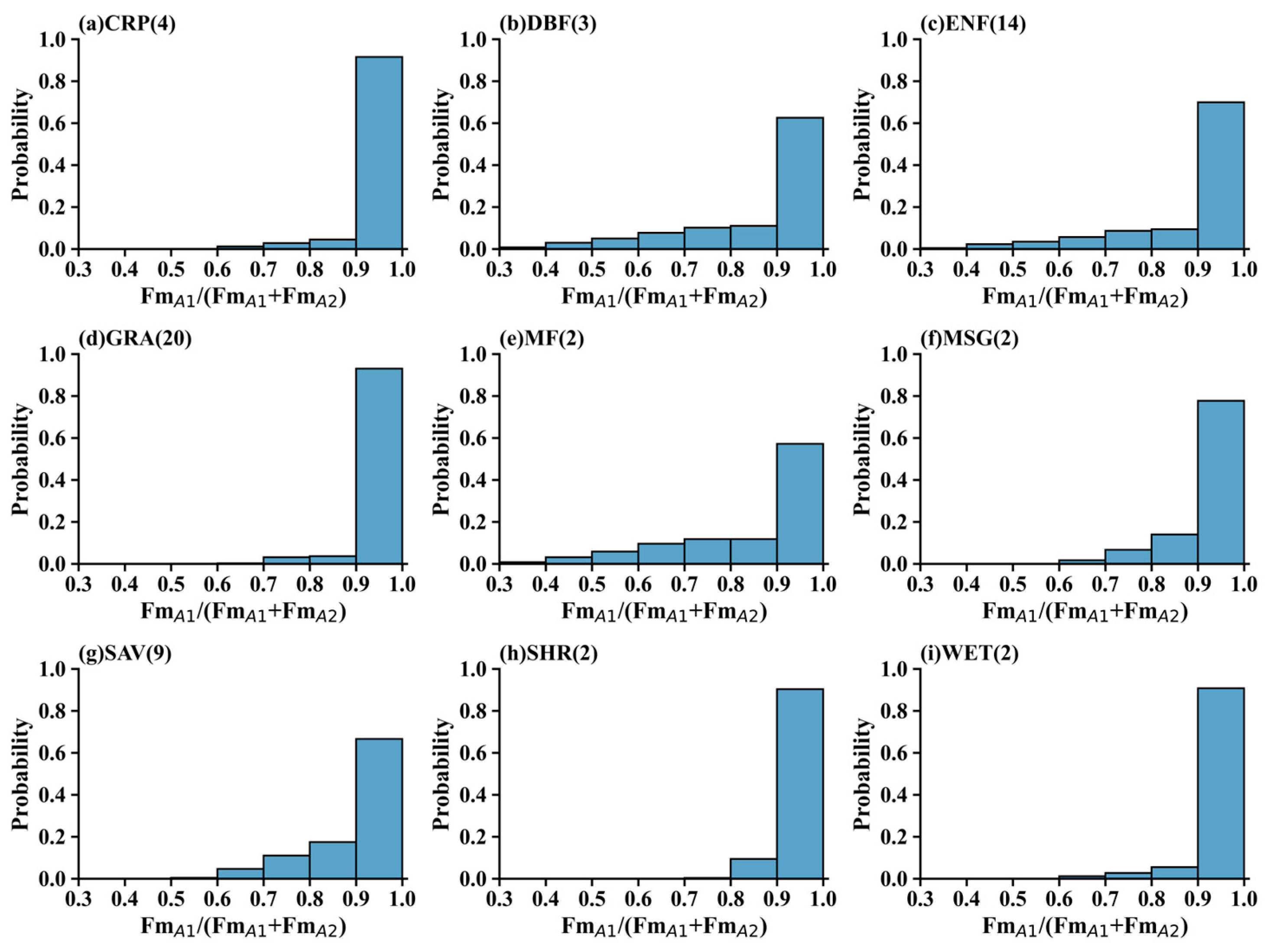
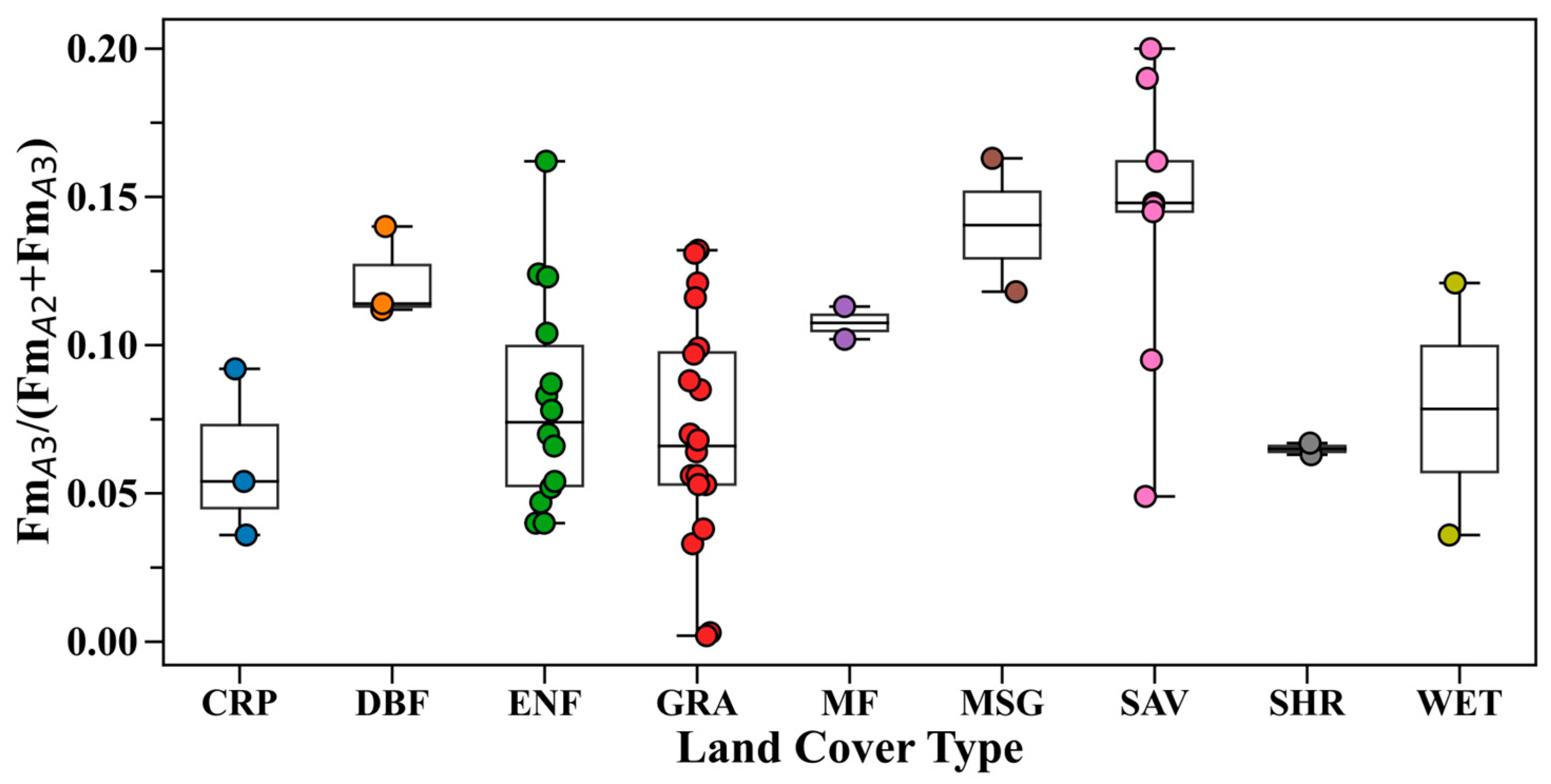
3.2. Factors Contributing to Minor Differences
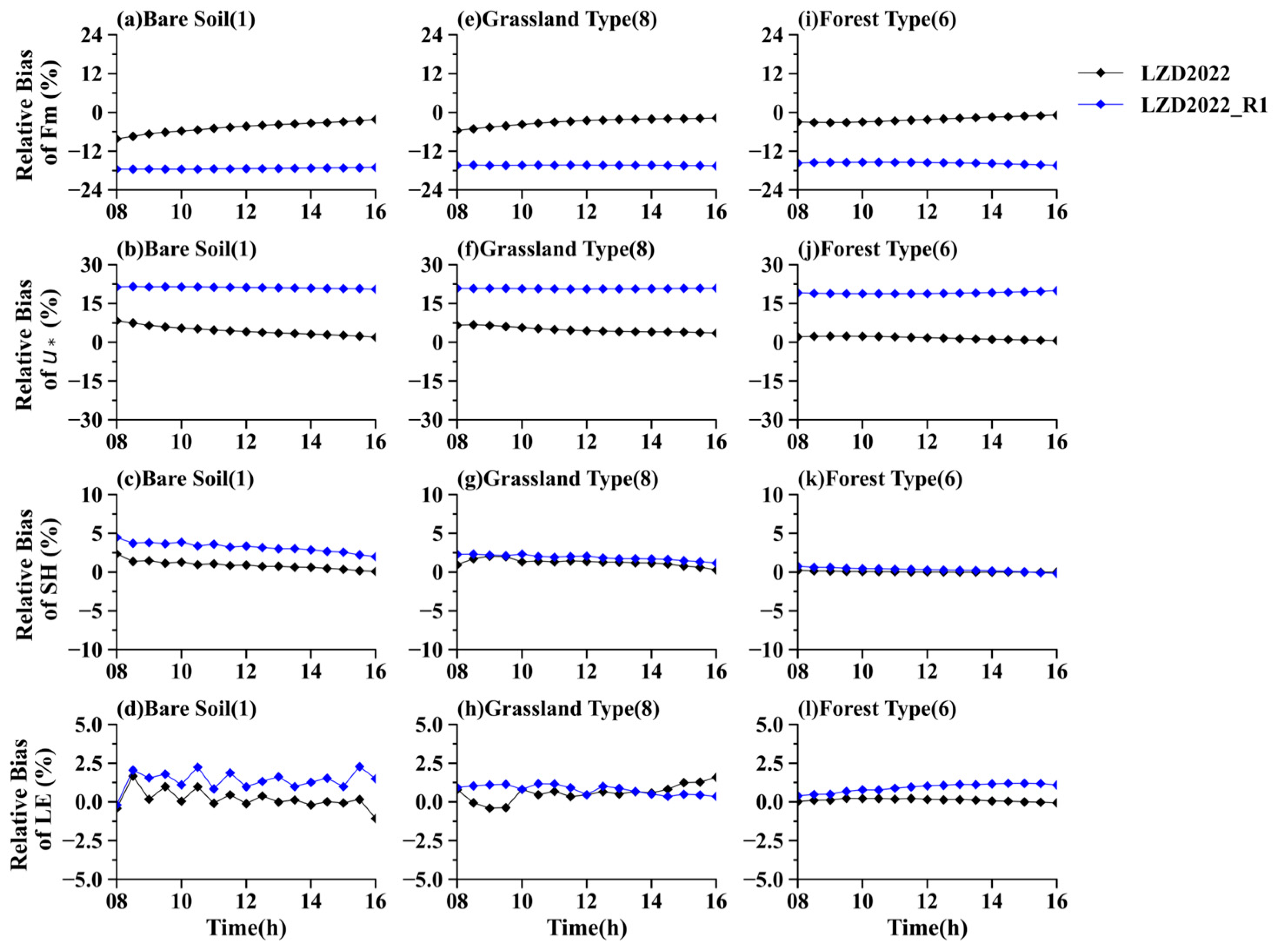
3.3. Overlapping Contributions and Indirect Influences
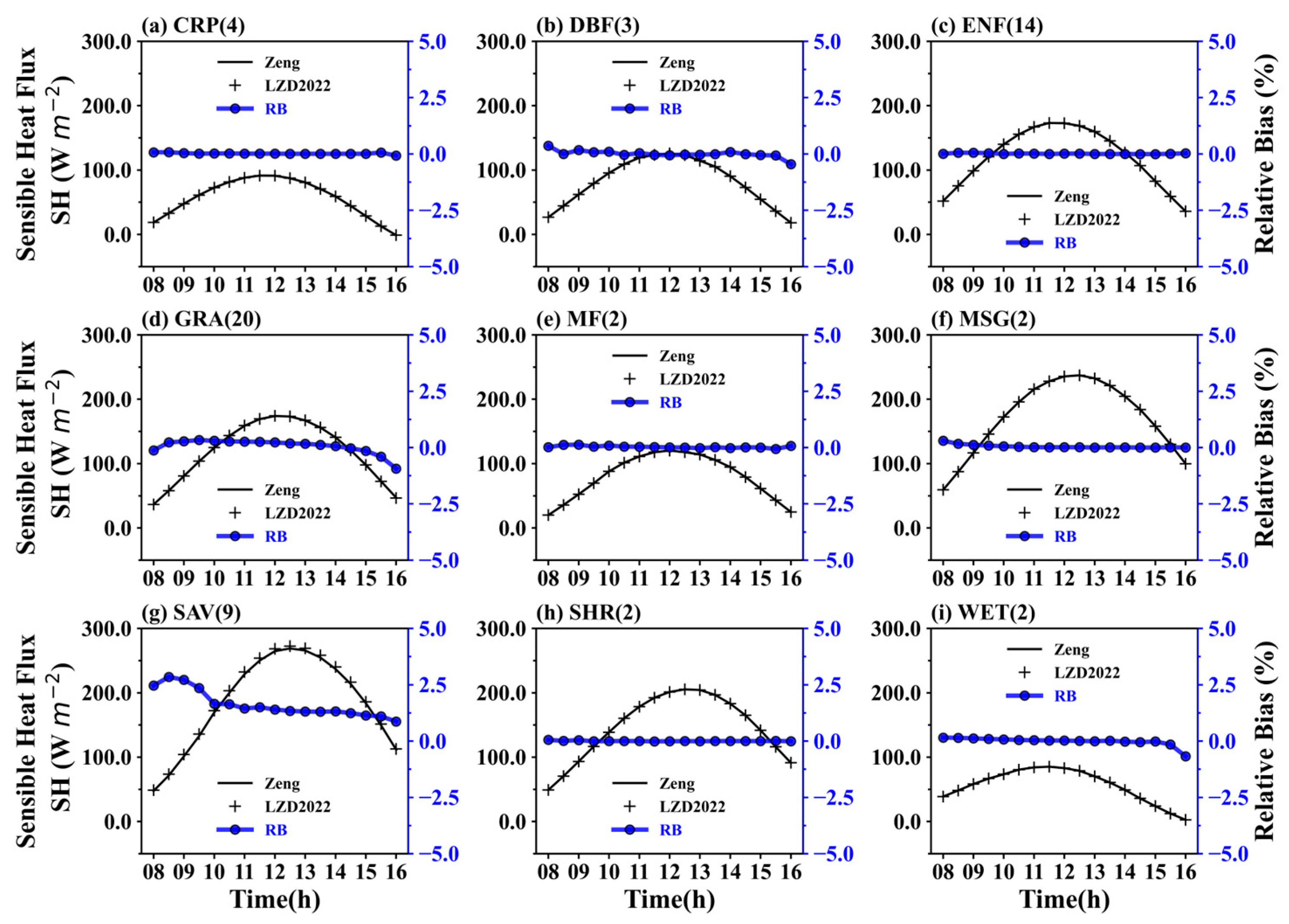
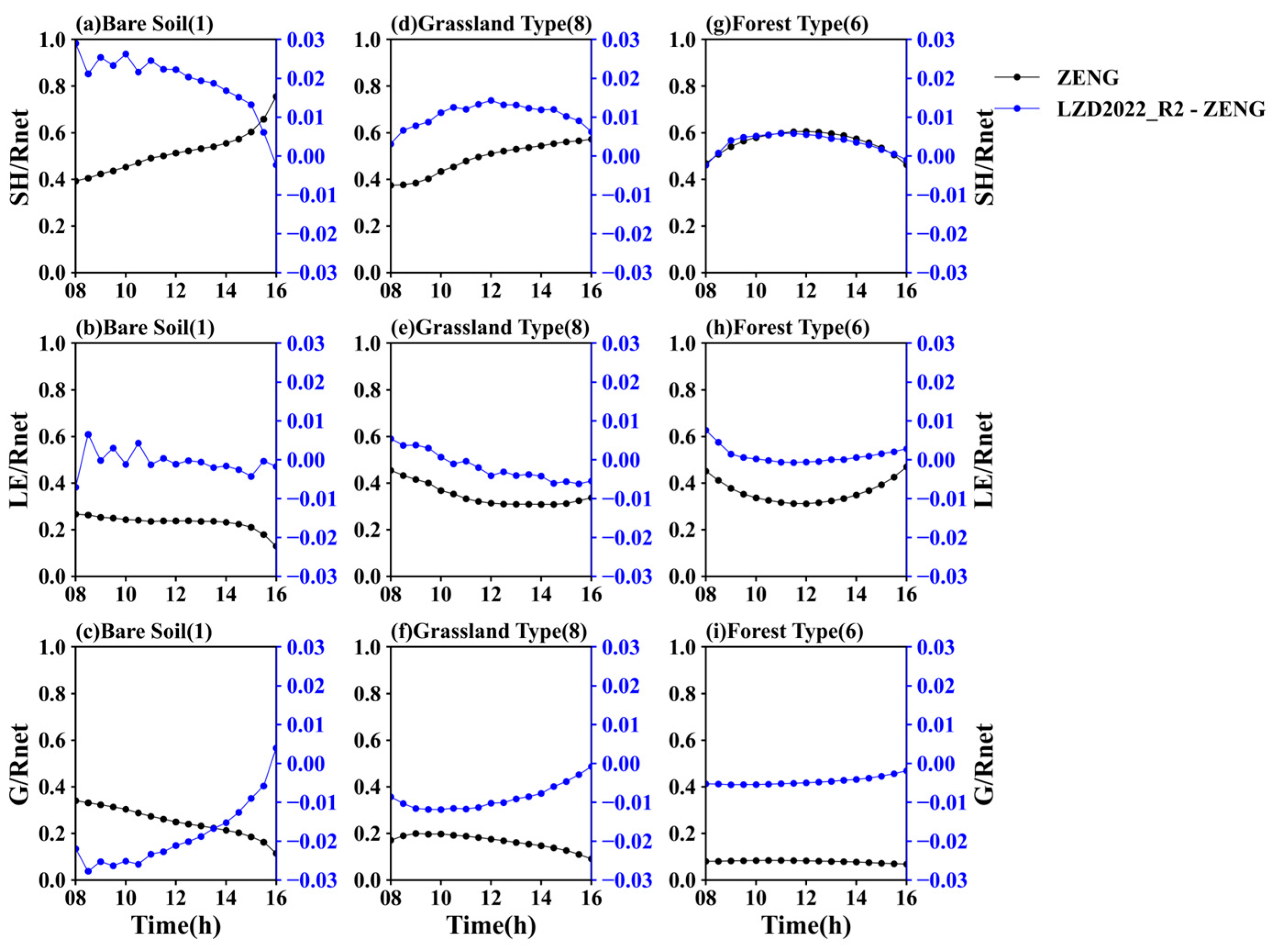
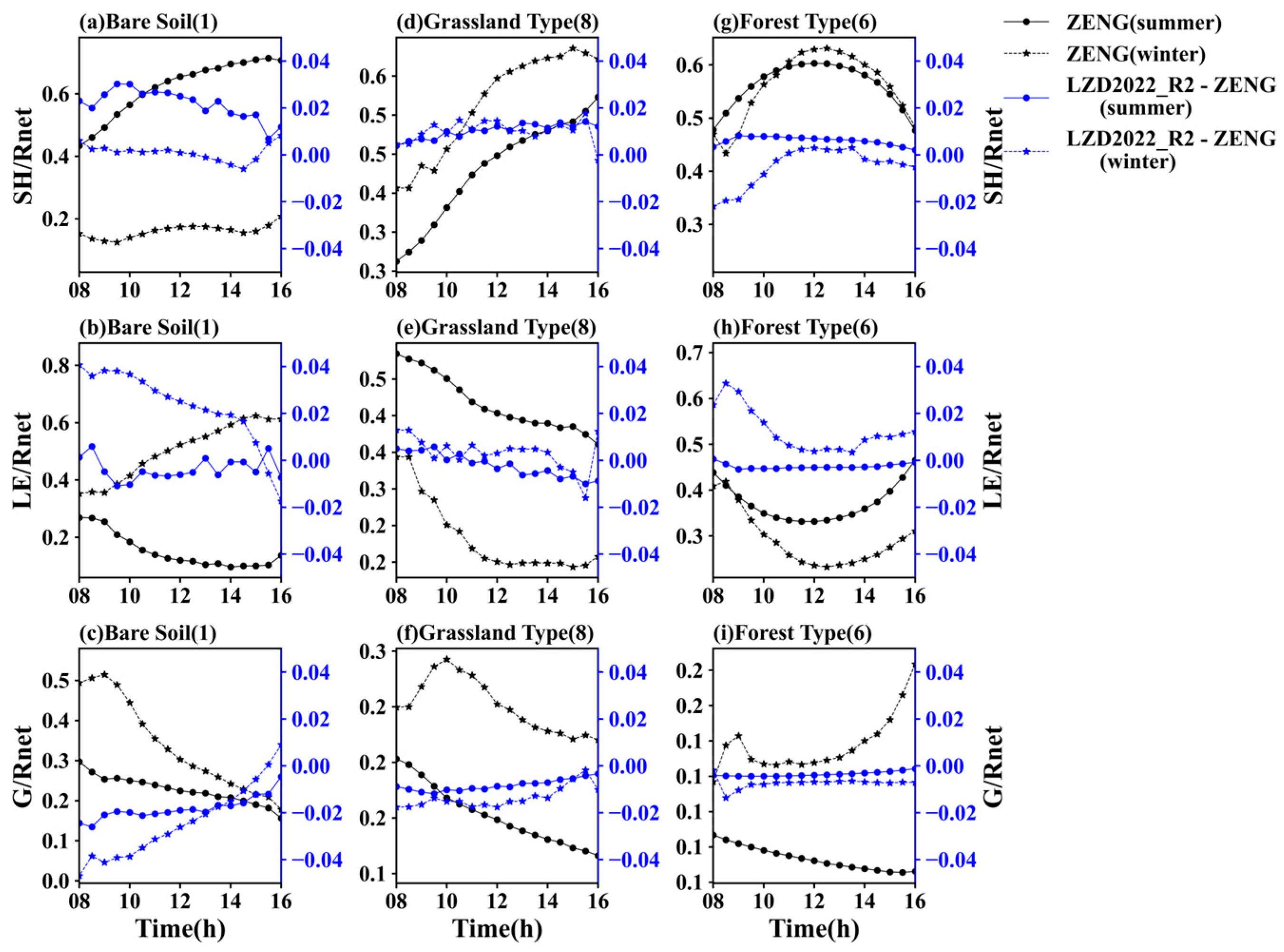
3.4. Surface Energy Balance
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ZENG | Classical flux-gradient relations scheme under unstable conditions. |
| LZD2022 | Modified flux-gradient relations scheme under unstable conditions. |
| LZD2022_R1 | Derived from the LZD2022 scheme after eliminating the overlapping effects of the ZENG scheme. |
| LZD2022_R2 | Derived from the LZD2022_R1 scheme by blocking the indirect influence on heat flux. |
| Integral momentum function in ZENG scheme. | |
| Integral momentum function in LZD2022 scheme. | |
| The overlapping component with ZENG in LZD2022 scheme. | |
| The term accounting large eddy effects in LZD2022 scheme. | |
| Difference between ZENG and LZD2022 scheme. |
Appendix A
Appendix A.1
Appendix A.2
References
- Dai, Y.; Williams, I.N.; Qiu, S. Simulating the effects of surface energy partitioning on convective organization: Case study and observations in the US Southern Great Plains. J. Geophys. Res. Atmos. 2021, 126, e2020JD033821. [Google Scholar] [CrossRef]
- Dai, Y.; Williams, I.N. Land surface effects on shear balance of squall lines. J. Geophys. Res. Atmos. 2022, 127, e2021JD035436. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Atmospheric Surface Layer. Contrib. Geophys. Inst. Slovak Acad. Sci. 1954, 51, e187. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A.J. A Review of Flux-Profile Relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Hogstrom, U. Non-dimensional Wind and Temperature Profiles in the Atmospheric Surface Layer: A Re-Evaluation. Bound.-Layer Meteorol. 1988, 42, 55–78. [Google Scholar] [CrossRef]
- Hogstrom, U. Review of Some Basic Characteristics of the Atmospheric Surface Layer. Bound.-Layer Meteorol. 1996, 78, 215–246. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Tennekes, H.; Lenschow, D.H.; Wyngaard, J.C. The Characteristics of Turbulent Velocity Components in the Surface Layer under Convective Conditions. Bound.-Layer Meteorol. 1977, 11, 355–361. [Google Scholar] [CrossRef]
- Khanna, S.; Brasseur, J.G. Analysis of Monin–Obukhov similarity from large-eddy simulation. J. Fluid Mech. 1997, 345, 251–286. [Google Scholar] [CrossRef]
- Katul, G.G.; Konings, A.G.; Porporato, A. Mean Velocity Profile in a Sheared and Thermally Stratified Atmospheric Boundary Layer. Phys. Rev. Lett. 2011, 107, 268502. [Google Scholar] [CrossRef]
- Banerjee, T.; Li, D.; Juang, J.-Y.; Katul, G. A Spectral Budget Model for the Longitudinal Turbulent Velocity in the Stable Atmospheric Surface Layer. J. Atmos. Sci. 2016, 73, 145–166. [Google Scholar] [CrossRef]
- Li, Q.; Gentine, P.; Mellado, J.P.; McColl, K.A. Implications of Nonlocal Transport and Conditionally Averaged Statistics on Monin–Obukhov Similarity Theory and Townsend’s Attached Eddy Hypothesis. J. Atmos. Sci. 2018, 75, 3403–3431. [Google Scholar] [CrossRef]
- Salesky, S.T.; Chamecki, M. Random Errors in Turbulence Measurements in the Atmospheric Surface Layer: Implications for Monin–Obukhov Similarity Theory. J. Atmos. Sci. 2012, 69, 3700–3714. [Google Scholar] [CrossRef]
- Deardorff, J.W. Numerical Investigation of Neutral and Unstable Planetary Boundary Layers. J. Atmos. Sci. 1972, 29, 91–115. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral Characteristics of Surface-Layer Turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Holtslag, A.A.M.; Debruin, H.A.R. Fluxes and Gradients in the Convective Surface Layer and the Possible Role of Boundary-Layer Depth and Entrainment Flux. Bound.-Layer Meteorol. 2005, 116, 237–252. [Google Scholar] [CrossRef]
- McNaughton, K.G. On the Kinetic Energy Budget of the Unstable Atmospheric Surface Layer. Bound.-Layer Meteorol. 2006, 118, 83–107. [Google Scholar] [CrossRef]
- Gioia, G.; Guttenberg, N.; Goldenfeld, N.; Chakraborty, P. Spectral Theory of the Turbulent Mean-Velocity Profile. Phys. Rev. Lett. 2010, 105, 184501. [Google Scholar] [CrossRef]
- Katul, G.G.; Li, D.; Chamecki, M.; Bou-Zeid, E. Mean Scalar Concentration Profile in a Sheared and Thermally Stratified Atmospheric Surface Layer. Phys. Rev. E 2013, 87, 023004. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, H.; Russell, E.S.; Huang, J.; Foken, T.; Oncley, S.P. Large Eddies Modulating Flux Convergence and Divergence in a Disturbed Unstable Atmospheric Surface Layer. J. Geophys. Res. Atmos. 2016, 121, 1475–1492. [Google Scholar] [CrossRef]
- McColl, K.A.; Katul, G.G.; Gentine, P.; Entekhabi, D. Mean-Velocity Profile of Smooth Channel Flow Explained by a Cospectral Budget Model with Wall-Blockage. Phys. Fluids 2016, 28, 035107. [Google Scholar] [CrossRef]
- Mellado, J.P.; Van Heerwaarden, C.C.; Garcia, J.R. Near-Surface Effects of Free Atmosphere Stratification in Free Convection. Bound.-Layer Meteorol. 2016, 159, 69–95. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Q.; Li, D.; Gentine, P. Logarithmic Profile of Temperature in Sheared and Unstably Stratified Atmospheric Boundary Layers. Phys. Rev. Fluids 2021, 6, 034606. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, X.; Dai, Y.; Yuan, H.; Wei, N.; Wei, Z.; Lu, X.; Zhang, S. A Surface Flux Estimation Scheme Accounting for Large-Eddy Effects for Land Surface Modeling. Geophys. Res. Lett. 2022, 49, e2022GL101754. [Google Scholar] [CrossRef]
- Bonan, G. A Land Surface Model (LSM Version 1.0) for Ecological, Hydrological, and Atmospheric Studies: Technical Description and User’s Guide; UCAR/NCAR: Boulder, CO, USA, 1996; 150p, NCAR/TN-417+STR. [Google Scholar]
- Dickinson, R.; Henderson-Sellers, A.; Kennedy, P. Biosphere-Atmosphere Transfer Scheme (BATS) Version 1e as Coupled to the NCAR Community Climate Model; UCAR/NCAR: Boulder, CO, USA, 1993; 72p, NCAR/TN-387+STR. [Google Scholar]
- Dai, Y.; Zeng, Q. A Land Surface Model (IAP94) for Climate Studies Part I: Formulation and Validation in off-Line Experiments. Adv. Atmos. Sci. 1997, 14, 433–460. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS Leaf Area Index Products for Land Surface and Climate Modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Duan, Q.; Liu, B.; Yuan, H. A Global Soil Data Set for Earth System Modeling. J. Adv. Model. Earth Syst. 2014, 6, 249–263. [Google Scholar] [CrossRef]
- Dai, Y.; Dickinson, R.E.; Wang, Y.-P. A Two-Big-Leaf Model for Canopy Temperature, Photosynthesis, and Stomatal Conductance. J. Clim. 2004, 17, 2281–2299. [Google Scholar] [CrossRef]
- Zeng, X.; Zhao, M.; Dickinson, R.E. Intercomparison of Bulk Aerodynamic Algorithms for the Computation of Sea Surface Fluxes Using TOGA COARE and TAO Data. J. Clim. 1998, 11, 2628–2644. [Google Scholar] [CrossRef]
- Kader, B.A.; Yaglom, A.M. Mean Fields and Fluctuation Moments in Unstably Stratified Turbulent Boundary Layers. J. Fluid Mech. 1990, 212, 637–662. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service (C3S); European Centre for Medium: Reading, UK, 2017. [Google Scholar]

| Site Name | Longitude | Latitude | Year | Land Cover Type (USGS) | Height (m) |
|---|---|---|---|---|---|
| AU-Cpr | 140.58 | −34.00 | 2011–2017 | Savanna | 20 |
| AU-DaP | 131.32 | −14.06 | 2009–2012 | Grassland | 15 |
| AU-DaS | 131.38 | −14.15 | 2010–2017 | Savanna | 23 |
| AU-Dry | 132.37 | −15.25 | 2011–2015 | Savanna | 15 |
| AU-How | 131.15 | −12.49 | 2003–2017 | Savanna | 23 |
| AU-Lit | 130.79 | −13.1 | 2016–2017 | Savanna | 31 |
| AU-Stp | 133.35 | −17.15 | 2010–2017 | Grassland | 4.8 |
| BE-Bra | 4.52 | 51.30 | 2004–2014 | Mixed Forest | 41.0 |
| BE-Lon | 4.74 | 50.55 | 2005–2014 | Irrigated Cropland and Pasture | 2.7 |
| BE-Vie | 5.99 | 50.30 | 1997–2014 | Mixed Forest | 40 |
| CA-Qfo | −74.34 | 49.69 | 2004–2010 | Evergreen Needleleaf Forest | 24 |
| CA-SF3 | −106.00 | 54.09 | 2003–2005 | Mixed Shrubland/Grassland | 18.29 |
| CH-Cha | 8.41 | 47.21 | 2006–2014 | Grassland | 2 |
| CH-Dav | 9.85 | 46.81 | 1997–2014 | Evergreen Needleleaf Forest | 35 |
| CN-Cng | 123.50 | 44.59 | 2008–2009 | Grassland | 6 |
| CN-Du2 | 116.28 | 42.04 | 2007–2008 | Grassland | 4 |
| CN-HaM | 101.18 | 37.37 | 2002–2003 | Grassland | 2.2 |
| CZ-wet | 14.77 | 49.02 | 2007–2014 | Herbaceous Wetland | 2.7 |
| DE-Bay | 11.86 | 50.14 | 1997–1999 | Evergreen Needleleaf Forest | 32 |
| DE-Geb | 10.91 | 51.10 | 2001–2014 | Irrigated Cropland and Pasture | 6 |
| DE-Gri | 13.51 | 50.94 | 2004–2014 | Grassland | 3 |
| DE-Hai | 10.45 | 51.07 | 2000–2012 | Deciduous Broadleaf Forest | 42 |
| DE-Kli | 13.52 | 50.89 | 2005–2014 | Irrigated Cropland and Pasture | 3.5 |
| DE-Obe | 13.72 | 50.78 | 2008–2014 | Evergreen Needleleaf Forest | 30 |
| DE-SfN | 11.32 | 47.80 | 2013–2014 | Herbaceous Wetland | 6 |
| DE-Tha | 13.56 | 50.96 | 1998–2014 | Evergreen Needleleaf Forest | 42 |
| DE-Wet | 11.45 | 50.45 | 2002–2006 | Evergreen Needleleaf Forest | 30 |
| DK-Lva | 12.08 | 55.68 | 2005–2006 | Grassland | 2.5 |
| DK-Sor | 11.64 | 55.48 | 1997–2014 | Deciduous Broadleaf Forest | 57 |
| ES-LMa | −5.77 | 39.94 | 2004–2006 | Savanna | 15.5 |
| FI-Hyy | 24.295 | 61.84 | 1996–2014 | Evergreen Needleleaf Forest | 23 |
| FI-Sod | 26.63783 | 67.36 | 2008–2014 | Evergreen Needleleaf Forest | 23 |
| HU-Bug | 19.60 | 46.69 | 2003–2006 | Grassland | 4 |
| IE-Dri | −8.75 | 51.98 | 2003–2005 | Grassland | 10 |
| IT-Amp | 13.60 | 41.90 | 2003–2006 | Grassland | 4 |
| IT-Isp | 8.63 | 45.81 | 2013–2014 | Deciduous Broadleaf Forest | 38 |
| IT-Noe | 8.15 | 40.60 | 2004–2014 | Shrubland | 2 |
| IT-SR2 | 10.29 | 43.73 | 2013–2014 | Evergreen Needleleaf Forest | 22.5 |
| NL-Ca1 | 4.92 | 51.97 | 2003–2006 | Grassland | 20 |
| NL-Loo | 5.74 | 52.16 | 1997–2013 | Evergreen Needleleaf Forest | 24.4 |
| RU-Fyo | 32.92 | 56.46 | 2003–2014 | Evergreen Needleleaf Forest | 29 |
| SD-Dem | 30.47 | 13.28 | 2005–2009 | Savanna | 9 |
| US-AR1 | −99.42 | 36.42 | 2010–2012 | Grassland | 2.84 |
| US-Aud | −110.50 | 31.59 | 2003–2005 | Grassland | 4 |
| US-Bkg | −96.83 | 44.34 | 2005–2006 | Grassland | 4 |
| US-Bo1 | −88.29 | 40.00 | 1997–2006 | Irrigated Cropland and Pasture | 10 |
| US-FPe | −105.10 | 48.30 | 2000–2006 | Grassland | 3.5 |
| US-Goo | −89.87 | 34.25 | 2004–2006 | Grassland | 4 |
| US-Ho1 | −68.74 | 45.20 | 1996–2004 | Evergreen Needleleaf Forest | 30 |
| US-KS2 | −80.6715 | 28.60858 | 2003–2006 | Shrubland | 3.5 |
| US-Me2 | −121.557 | 44.4523 | 2002–2014 | Evergreeen Needleleaf Forest | 32 |
| US-Me4 | −121.62 | 44.49 | 1996–2000 | Evergreeen Needleleaf Forest | 47 |
| US-SRG | −110.82 | 31.78 | 2009–2014 | Grassland | 3.25 |
| US-SRM | −110.86 | 31.82 | 2004–2014 | Savanna | 7.8 |
| US-Ton | −120.96 | 38.43 | 2001–2014 | Savanna | 23.5 |
| US-Var | −120.95 | 38.41 | 2001–2014 | Grassland | 2.2 |
| US-Whs | −110.05 | 31.74 | 2008–2014 | Mixed Shrubland/Grassland | 6.5 |
| US-Wkg | −109.94 | 31.73 | 2005–2014 | Grassland | 6.4 |
| Land Cover Type (USGS) | |
|---|---|
| CRP | 0.98 |
| DBF | 0.88 |
| ENF | 0.91 |
| GRA | 0.98 |
| MF | 0.87 |
| MSG | 0.95 |
| SAV | 0.92 |
| SHR | 0.98 |
| WET | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Li, L.; Shi, Q.; Liu, S. Evaluation of Large Eddy Effects on Land Surface Modeling Based on the FLUXNET Dataset. Atmosphere 2025, 16, 328. https://doi.org/10.3390/atmos16030328
Huang H, Li L, Shi Q, Liu S. Evaluation of Large Eddy Effects on Land Surface Modeling Based on the FLUXNET Dataset. Atmosphere. 2025; 16(3):328. https://doi.org/10.3390/atmos16030328
Chicago/Turabian StyleHuang, Huishan, Lingke Li, Qingche Shi, and Shaofeng Liu. 2025. "Evaluation of Large Eddy Effects on Land Surface Modeling Based on the FLUXNET Dataset" Atmosphere 16, no. 3: 328. https://doi.org/10.3390/atmos16030328
APA StyleHuang, H., Li, L., Shi, Q., & Liu, S. (2025). Evaluation of Large Eddy Effects on Land Surface Modeling Based on the FLUXNET Dataset. Atmosphere, 16(3), 328. https://doi.org/10.3390/atmos16030328





